税收是政府收入的重要来源之一。传统税收来源于实际经济活动之中, 铸币税则不同, 它来源于中央银行的货币创造过程。Obstfeld and Rogoff(1996)认为铸币税是一种价差:一国货币作为信用货币, 其本身除了制作材料等费用, 并没有其他的实际价值, 而一国政府却能通过货币的发行换取具有实际价值的商品, 实物资产与货币制作的费用的差价便是铸币税。Obstfeld and Rogoff(1996)研究的实际上是货币铸币税, Neumann(1992)的观点是高能货币剔除价格水平的影响就是货币铸币税(Frieman, 1971; Calvo, 1978, 1988; Grilli, 1989)。Klein and Neuman(1990)给出了铸币税的另一种定义——机会成本铸币税, 这是从持有货币的机会成本的角度来度量铸币税(Neuman, 1996; Honohan, 1996; Buiter, 2007)。所谓私人部门因持有货币而发生的机会成本是由于私人部门放弃持有可以带来利息的金融资产转而持有不能生息的货币而带来的利息方面的损失(Gros, 1989)。总的来说, 财政税收和铸币税都是税收, 只不过前者为显性税收(the explicit taxes), 后者是隐性税收(the implicit taxes)。两种税收的税率实质上是相通的, 都是对居民财富征收程度不同的税收。居民的货币财富会在无形中被通货膨胀抵消掉, 政府作为债务人获得间接获益。理论上, 铸币税也是政府税收的组成部分, 其征税比例就是通货膨胀率, 从某种意义上来说, 通货膨胀率反映了铸币税的税率。

中央银行垄断货币的发行权, 是唯一的货币发行机构。许多时候, 可以通过增加货币发行来向公众征收铸币税(Bruno and Fischer, 1990; Blanchard and Fisher, 1989)。中央银行除了可以获得铸币税以外, 作为一个独立的金融机构, 还可以获得利润。中央银行通过资产负债的管理, 有独立的收益和成本, 制定和实施国家货币政策, 会影响中央银行的净损益, 同时中央银行货币政策工具的操作, 也会对其净利润产生一定的影响。

Klein and Neumann (1990)和Neumann (1996)还定义了总铸币税, 即包括货币铸币税、央行收益以及所支付的利息。同时他们也考虑了总铸币税的分配及使用, 总铸币税的使用包含以下几个方面(Neumann, 1996):一是生产硬币和纸币的成本、国内和国外债务的净偿付、支付国外债务汇率变动的账面损失、支付政府净债务和扣除政府债务利息的拨定利润(财政铸币税); 二是转移给第三方的利润和(或)用作资本积累的资金。他们定义的财政铸币税是从央行获得政府债务的利息, 以及扣除政府债务利息而上交的央行利润。实际上, 中央银行获得的铸币税和利润又会上缴财政(王利民、左大培, 1999), 转移到财政部门。财政铸币税是从另一角度对铸币税进行研究(Neumann, 1992; Herrendorf and Valentinyi, 1999)。Hochreiter and Rovelli(2002)根据Drazen(1985), Klein and Neumann(1990)关于货币创造所带来总收入的探讨, 对铸币税做出了新的诠释。新的定义体现了总体测度的概念, 包括所有与货币创造相关的收益, 如货币扩张过程和购买资产过程中获取的收入等(Uzagalieva, 2005), 这种解释与财政铸币税(fiscal seigniorage)的定义非常相似。但是, 财政铸币税认为货币扩张兼具两种功能, 一是融资, 二是税收, 政府在这一过程中获得的净收益应该属于财政铸币税。

虽然关于铸币税定义较多, 但铸币税收入是政府融资的一个重要来源, 这一观点被很多学者认可(Bruni, Penati and Porta, 1989; Gros, 1993)。本质上, 铸币税就是央行独占货币发行权的垄断收益。不同的铸币税概念, 体现了从多个经济视角认识铸币税, 从财政、资产与负债等方面来研究铸币税, 可以清晰地发现其由来、分配和使用等一系列路径。实际上, 央行利润、财政铸币税和中央银行铸币税都有紧密联系, 财政铸币税不仅包含央行铸币税, 还包含央行和财政部之间债务债权、净利息所得等。

通常政府税收和税率之间存在倒"U"型的特征, 呈拉弗曲线形状, 即存在一个最优税率, 这个税率使得政府的边际税收为0, 总税收达到最大化。相应地, 从货币视角出发, 通货膨胀率和铸币税的关系是一样的, 即可用拉弗曲线表示铸币税随着通货膨胀率的变化而变动(Cagan, 1956; Easterly et al., 1995)。在货币市场均衡的前提下, 货币铸币税的变动特征受多重因素影响, 货币需求函数是关键要素。根据Cagan(1956)的研究结果来看, 使得中央银行铸币税最大化的条件是通胀水平与货币需求的利率水平的半弹性相等。现实经济中, 央行不一定要采取使自己获得最多铸币税的货币政策, 政府的主要融资工具目标中也不会有铸币税这一选项, 因为铸币税伴随央行货币发行而出现, 本质上是垄断货币发行的收益。不过, 如果出现政府财政资金紧张, 央行需要对政府大量财政赤字进行融通等特殊情况的时候, 央行也可能会按照政府的意愿追求铸币税的最大化。

国内关于铸币税的研究比较多, 这些研究从不同的侧面分析了我国铸币税的相关问题。陈玉宇(1997)对货币当局的铸币税进行简易测算, 依据其收支规模估算了利润情况。张明艳、江航翔(2003)在研究中得出结论:央行利用资产得到的收入扣减由于负债产生的利息支出和央行的各项必须开支与费用后, 剩下的就是央行利润。张健华、张怀清(2009)分析了我国央行铸币税的使用去向, 主要利用机会成本铸币税以及货币铸币税两种度量方式对1986年至2008年期间我国人民银行的铸币税规模进行了测度。近来, 一些学者在前人研究成果上, 又进一步探讨了中央银行铸币税收入的相关问题。王雅炯(2012)基于自身对央行收入成本的估计, 来预计央行盈亏, 进而挖掘货币政策实施后的央行收益。陆前进、朱丽娜(2014)在无限期假定的基础上探索了影响机会成本铸币税的关键因素之一——准备金付息制度, 并得出了机会成本铸币税小于货币铸币税的结论, 但没有对央行利润与财政铸币税进行探讨。陈宇峰、贵斌威(2015)给出了4种与Obstfeld and Rogogg(1996)对铸币税定义不一样的铸币税类型, 主要从金融抑制的方面将其分为传统铸币税、隐性铸币税、利差型铸币税以及金融抑制铸币税, 但是没有研究央行利润的形成机制。

综上所述, 本文的新意在于, 根据中国实际问题, 拓宽了央行铸币税的定义及测量口径, 运用中央银行资产负债表探究央行利润的形成机制, 并定义了转移的机会成本铸币税。在此基础之上, 本文定义了政府的财政铸币税。进一步本文在MIU(money-in-utility)典型代理人效用最大化(Obstfeld and Rogoff, 1995, 1996)的基础上, 研究央行利润、财政铸币税与通货膨胀率的非线性关系(包括"U型"特征和"倒U型"特征), 并在理论模型基础之上进行了实证研究。

考察中央银行利润, 首先从中央银行的资产负债表开始, 如表 1所示。从中央银行资产方来看, 首先是中央银行的对外债权, 即对外净资产, 是央行的主要资产, 在我国主要是央行购买外汇形成的外汇占款。对政府的债权主要包括央行购买或持有的政府债券。对存款商业银行的债权主要是中央银行以再贷款和再贴现等形式形成的对商业银行的债权。中央银行的负债方主要包括流通中的现金, 即央行发行的货币现金。银行储备是商业银行上缴的法定准备金和超额准备金。政府储蓄是政府在中央银行的存款, 中央政府的存款通常放在中央银行的账户上。央票作为央行的债务, 是主要的货币政策工具之一, 央行通过发行央票控制货币市场的流动性。

表 1

表 1 中国人民银行简化的资产负债表 资产 负债 对外净资产(NFA) 流通中现金(C) 对中央政府的债权(GB) 政府部门在央行的储蓄(DG) 对商业银行的债权(LB) 中央银行发行的票据(FP) 商业银行准备金存款(R)

表 1 中国人民银行简化的资产负债表

由资产负债表两边的平衡性可知, 此时, 机会成本铸币税^①为: ${i_t} = \frac{{{C_{t - 1}} + {R_{t - 1}}}}{{{P_t}}} = {i_t}\frac{{NF{A_{t - 1}}}}{{{P_t}}} + {i_t}\frac{{G{B_{t - 1}}}}{{{P_t}}} + {i_t}\frac{{L{B_{t - 1}}}}{{{P_t}}} - {i_t}\frac{{D{G_{t - 1}}}}{{{P_t}}} - {i_t}\frac{{F{P_{t - 1}}}}{{{P_t}}}$。假定央行资产和负债没有利息收入和支出, 则左右两侧的机会成本铸币税相等。上述等式的经济含义:等式左侧就是机会成本铸币税的含义, 代表央行机会成本铸币税的收入, 等式右侧表明央行转移出去的机会成本铸币税。因此, 央行的机会成本铸币税净收入为零。为了便于理解, 我们把前者称为机会成本铸币税, 后者称为转移的机会成本铸币税。此外, 对于等式右侧而言, 大于零的项代表其他方获取的转移支付的铸币税, 而小于零的项则表示央行获得的转移支付的机会成本铸币税。需要注意的是, 上式两侧减掉利息支付后的机会成本铸币税^②分别为: ${{S^0} = i\frac{C}{P} + \left( {i - {i^r}} \right)\frac{{RR}}{P} + \left( {i - {i^r}} \right)\frac{{ER}}{P},\left( {i - \left( {{i^f} + e} \right)} \right)\frac{{NFA}}{P} + \left( {i - {i^g}} \right)}$${\frac{{GB}}{P} + \left( {i - {i^o}} \right)\frac{{LB}}{P} - \left( {i - {i^d}} \right)\frac{{DG}}{P} - \left( {i - {i^{FP}}} \right)\frac{{FP}}{P}}$这样, 两个式子就不平衡了。扣除利息后机会成本铸币税与扣除利息后转移的机会成本铸币税是不同的。基于这一说法, 学界出现多种关于铸币税的含义和解释(陈宇峰、贵斌威, 2015)。假如中央银行转移的机会成本铸币税某一项大于零, 则意味着机会成本铸币税转移给了这一方; 如果这一数值小于零, 那么货币当局获得铸币税, 也就是说转移支付的机会成本铸币税恰好给了自己。

^①机会成本铸币税(Klein and Neuman, 1990; Neumann, 1992; Honohan, 1996): $S = i\frac{B}{P} = i\frac{{C + R}}{P}$, i是私人部门持有生息资产的收益率, 通常取市场化的基准利率, B是基础货币, P是一般价格水平。机会成本铸币税是市场利率与实际基础货币余额的乘积。如果考虑到我国对准备金付息, 则机会成本铸币税要扣除掉支付利息的那一部分, 公式可表示为: ${S^0} = i\frac{C}{P} + \left({i - {i^r}} \right)\frac{{RR}}{P} + \left({i - {i^e}} \right)\frac{{ER}}{P} = i\frac{B}{P} - {i^r}\frac{{RR}}{P} - {i^e}\frac{{ER}}{P}$, 其中, i是私人部门持有生息资产的收益率, RR是法定准备金, ER是超额准备金, i^r是法定准备金的利率, i^e是超额准备金的利率。

② 当然也包括对资产方支付利息。

中央银行的利润是其通过经营资产业务以及负债业务从而在创造货币时上缴政府机构的利息收入。其实现途径主要有四种:第一种是由于央行购入外汇导致资产项目中的外汇占款项增加, 同时央行将等量基础货币注入金融体系使得资产负债表中负债项的基础货币增加。央行能获得投资外汇储备的收入, 同时央行对商业银行上缴的准备金支付一定的利息, 商业银行不能再通过贷款获得更多利息收入, 这相当于向央行纳税。第二种是由于央行通过公开市场操作购入包括国债等在内的一些列金融资产而获得的利息以及其他潜在资产增值获得的收入。第三种是央行在与商业银行进行票据贴现业务时取得的利息收入。第四种是央行为了对基础货币的扩张进行冲销, 在发行央票的过程中付息导致其成本的增加, 即收入的减少。

央行资产负债表表明, 资产项目收入减去负债项目成本就等于自身所获得的收益。因此中央银行的利润(π^CB)可以由以下公式进行表示:

① (${i^f} + \dot e$)NFA表示持有外汇储备所获得的收益(用本币表示)。

i^f是国外基准利率, ${\rm{\dot e}}$代表汇率的变动率($\dot e$ > 0表示本币币值下降; $\dot e$ < 0表示本币币值上升), i^g是国债收益率, i^O是金融机构向货币当局支付的利率, i^d表示政府在央行存款的利率, i^FP指的是央行发债的利率。

对公式(1), 等式两边同时除以价格水平, 并进一步分解可以得到:

在实际问题中, 准备金分为法定准备金和超额准备金, 如果将两者进行区分的话, 则公式为:

其中, 第一项$\left({{i^f} + \dot e - i} \right)\frac{{NFA}}{P}$是代表央行本币资产收益率低于外汇资产收益率获得的收入; 第二项$\left({{i^g} - i} \right)\frac{{GB}}{P}$是央行持有的政府债券收益率高于市场利率的收入; 第三项$\left({{i^o} - i} \right)\frac{{LB}}{P}$是央行充当信贷者取得的大于市场利率的收益; 第四项$\left({i - {i^d}} \right)\frac{{DG}}{P}$是央行因支付低于市场利率的政府储蓄利率而获取的收益; 第五项$\left({i - {i^{FP}}} \right)\frac{{FP}}{P}$央行因支付低于市场利率的央票利率而获取的收益; 第六项$i\frac{B}{P} - {i^r}\frac{{RR}}{P} - {i^e}\frac{{ER}}{P}$是中央银行的机会成本铸币税。当然上述假定每一项都是正值, 代表中央银行获得的收益, 相反如果每一项都是负值, 则表示央行的损失。根据(3) 式:

其中$\left[ {\left({i - {i^f} - \dot e} \right)\frac{{NFA}}{P} + \left({i - {i^g}} \right)\frac{{GB}}{P} + \left({i - {i^o}} \right)\frac{{LB}}{P} - \left({i - {i^d}} \right)\frac{{DG}}{P} - \left({i - {i^{FP}}} \right)\frac{{FP}}{P}} \right]$是转移的机会成本铸币税, 从(4) 式中我们可以得到这样一个结论, 机会成本铸币税与其转移出去的部分之差就是央行的利润。如果机会成本铸币税与其转移的部分相等, 则利润值为零; 如果两者并不相等, 则央行的利润取决于两部分的相对大小。因此, 利润就是其机会成本铸币税中的未被转移的那一部分。假如完全转移出央行的机会成本铸币税, 那么央行没有利润; 假如部分转移央行的机会成本, 那么央行利润就是转移后余下的部分; 如果过度转移央行的机会成本, 那么亏损的局面将不可避免, 其净资产值将小于零。

综上, 我国央行利润就可以测算出来。市场利率i用一年期的定期存款利率来表示, i^f选取的是美国国库券1年期利率, ${\dot e}$是人民币对美元的汇率变动率, i^g指的是特别国债利率, i^O选用央行对金融机构发放一年期贷款的利率, i^d代表的是商业银行的活期存款利率, i^FP指的是央行发行票据需要支付的利率(以一年期为例并选取年末数值)。

观察表 2, 可以发现1985年至2007年, 中央银行利润总量整体趋势是上升的, 特别是2005年至2007年, 中央银行利润大幅上升。2008年至2014年, 中央银行利润呈现大幅下降的态势, 自2009年开始甚至为负值。这是由于:美联储为应对国际金融危机从而频繁地下调联邦基金利率后导致债券利率随之同方向变动, 由于对美国债券的投资使得我国外汇储备的收益率也相应下降。美国债券的利率已经低于央行票据的利率, 央行的冲销干预是亏损的, 中央银行利润因此大幅下降。另一方面, 中央银行利润占GDP和财政收入的比重变化趋势相似, 以央行利润占GDP的比重为例, 1989年, 1993年, 其占GDP的比重都出现了一个较大值, 这是基础货币、利率、政府存款和政府发行债券等因素共同影响的结果, 也反映了当时的宏观经济状况, 央行利润受国内外宏观经济变量影响明显。

表 2

表 2 1985年至2014年中央银行利润     单位:亿元, % (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) 1985 0.81 9.05 16.19 15.91 0.00 125.97 8.52 117.46 1.30 5.86 1986 -1.43 11.49 18.21 12.70 0.00 138.10 18.44 119.67 1.23 5.98 1987 -2.90 14.86 34.82 11.63 0.00 144.67 40.94 103.72 0.98 5.38 1988 -4.08 20.05 8.91 11.48 0.00 197.65 21.56 176.09 1.59 10.16 1989 -8.14 31.79 23.68 23.16 0.00 257.35 40.45 216.90 2.03 13.02 1990 -4.27 22.96 22.21 14.94 0.00 218.17 34.51 183.66 1.61 10.32 1991 -16.68 22.79 12.46 16.36 0.00 213.17 35.57 177.61 1.39 9.64 1992 -29.71 24.89 13.41 7.30 0.00 249.93 60.71 189.22 1.27 9.89 1993 -58.97 53.80 16.63 17.82 0.00 449.46 111.58 337.88 1.98 16.16 1994 -106.80 46.07 14.53 25.19 0.00 465.22 142.20 323.02 1.73 16.03 1995 -121.01 36.93 -6.84 25.15 0.00 459.24 125.95 333.29 1.65 16.18 1996 -71.43 17.18 -139.43 20.51 0.00 257.40 -71.33 328.72 1.51 14.55 1997 -24.07 8.27 -157.21 17.46 0.00 164.89 -142.34 307.23 1.30 11.97 1998 42.76 -0.62 -52.78 12.09 0.00 211.60 -108.25 319.85 1.26 10.82 1999 102.58 -7.96 -71.28 6.82 0.00 136.84 -188.64 325.48 1.19 9.39 2000 160.64 -7.94 -62.49 11.80 0.00 147.87 -242.92 390.75 1.30 9.66 2001 68.01 -14.06 -51.97 10.79 0.00 163.04 -144.84 307.87 0.93 6.26 2002 -24.55 -16.70 -38.00 11.75 0.00 160.73 -41.90 202.63 0.55 3.55 2003 -86.11 -16.71 -39.94 18.64 -8.51 192.95 19.33 173.62 0.43 2.68 2004 -115.73 -14.17 -43.65 25.64 -31.58 198.19 63.85 134.34 0.29 1.77 2005 156.53 -13.56 -35.78 32.53 19.44 238.87 -257.84 496.71 0.95 5.56 2006 511.03 -11.06 -24.51 51.20 -22.87 332.96 -574.92 907.88 1.50 8.41 2007 68.46 25.10 5.63 155.32 7.47 803.89 -200.51 1004.40 1.41 7.38 2008 -328.73 -53.17 -22.82 80.36 0.06 406.24 172.31 233.93 0.29 1.52 2009 -931.89 -51.81 -19.53 101.31 52.00 438.18 707.24 -269.06 -0.31 -1.56 2010 -1326.94 -30.54 -25.51 141.87 23.62 734.00 1105.41 -371.40 -0.37 -1.83 2011 -1698.76 -2.14 -8.32 158.24 0.54 1223.86 1529.52 -305.66 -0.27 -1.27 2012 -1543.75 -19.40 -32.12 124.43 -15.39 1206.99 1383.19 -176.20 -0.15 -0.66 2013 -1695.55 -18.90 -24.64 173.44 -8.21 1098.71 1486.78 -388.07 -0.30 -1.36 2014 -1561.74 -26.81 -59.40 162.23 -10.40 1005.91 1323.70 -317.79 -0.23 -1.05 注:数据来源为CEIC数据库, 国泰君安数据库, 中国资讯行—中国统计数据库, 国研网统计数据库, 中国人民银行网站和美联储网站。其中(1):$\left( {{i^f} + \dot e - i} \right)\frac{{NF{A^{CB}}}}{P}$; (2):$\left( {i - {i^g}} \right)\frac{{C{G^{CB}}}}{P}$; (3):$\left( {i - {i^o}} \right)\frac{{L{B^{CB}}}}{P}$; (4):$\left( {i - {i^d}} \right)\frac{{D{G^{CB}}}}{P}$; (5):$\left( {i - {i^{FP}}} \right)\frac{{FP}}{P}$; (6):$i\frac{B}{P} - {i^r}\frac{{RR}}{P} - {i^e}\frac{{ER}}{P}$; (7):转移的机会成本铸币税; (8):中央银行的利润; (9):中央银行利润占GDP之比(%); (10):中央银行利润占财政收入之比(%)。

表 2 1985年至2014年中央银行利润     单位:亿元, %

从表 2的数据结果来看, 1998年至2014年, 第一项和第六、八项的相关性分别为-0.8712, 0.8758, 并且第一项绝对值的均值也最大, 因此第一项是影响机会成本铸币税和中央银行利润的关键因素之一。同时央行的利润也会随着机会成本铸币税变化而同向变化。

根据一些学者的定义, 铸币税的现代最宽泛的说法是包括政府在货币发行流通过程中所获得的所有利润(王利民、左大培, 1999), 体现了央行和财政的结合, 这是从综合的角度来考察铸币税。这些主要因素有财政赤字的货币化, 即央行通过直接购买政府国债从而向财政融通资金; 央行直接发行货币的收益以及央行利润上缴财政的部分。

本文根据政府的预算约束平衡, 重新定义财政铸币税。现考虑政府的收入和支出, 可以得到以下等式: G_t+i_t^bB_t-1^P=T_t+(B_t^P-B_t-1^P)。此式中G_t为t期的政府购买支出, i_t^bB_t-1^P为对t-1期政府债券利息支出, T_t=τ_tP_tY_t(τ_t为t期税率)为政府t期的税收收入, (B_t^P-B_t-1^P)为t期新发行的债券数量, B_t-1^P为t-1期末t期期初的私人部门债券存量。

如果融入中央银行^①, 则可以得到以下等式:

① 本文中的政府包括财政部和中央银行, 财政铸币税也包括中央银行。

其中, DG_t-1为t-1期末的政府在央行存款。DG_t-DG_t-1为t期内政府存款的变动额, i_t^dDG_t-1为央行对政府存款的利息支付额。i_t^cGB_t-1为对t-1期央行持有政府债券进行的利息支出额, (GB_t-GB_t-1)为t期新发行的债券中央行持有的数量。π_t^CB为央行上缴政府部门的利润。

进一步, 从而得到下列等式:

其中, 括号内定义为财政铸币税(fiscal seigniorage)$\left\{ {\frac{{G{B_t} - G{B_{t - 1}} - i_t^cG{B_{t - 1}}}}{{{P_t}}} - \frac{{D{C_t} - D{C_{t - 1}} - i_t^dD{G_{t - 1}}}}{{{P_t}}} + \frac{{\pi _t^{CB}}}{{{P_t}}}} \right\}$, 具体包括央行对政府债权的变动, 政府存款的变动, 央行上缴的利润, 扣除对央行支付的利息, 再加上央行对政府存款所支付的利息等。

根据(4) 式, (6) 式可以写成:

大括号中仍然是财政铸币税, 这是对财政铸币税的另一种定义, 也是财政铸币税, 它反映了机会成本铸币税和财政铸币税的关系。该式意味着财政铸币税包含3部分:一是机会成本铸币税转移给政府这里的政府不包括中央银行。的那部分铸币税$\left({{i^f} + \dot e - i} \right)\frac{{NFA}}{P} + \left({{i^o} - i} \right)\frac{{LB}}{P} + \left({i - {i^{FP}}} \right)\frac{{FP}}{P} + \left({i\frac{B}{P} - {i^r}\frac{{RR}}{P} - {i^e}\frac{{ER}}{P}} \right)$, 二是政府债券发行的变动及市场利息支付$\left({\frac{{G{B_t} - G{B_{t - 1}}}}{{{P_t}}} - {i_t}\frac{{G{B_{t - 1}}}}{{{P_t}}}} \right)$, 三是政府存款的变动及获得市场利息$\left({ - \frac{{D{G_t} - D{G_{t - 1}}}}{{{P_t}}} + i\frac{{D{G_{t - 1}}}}{{{P_t}}}} \right)$。这两种定义是从不同的角度来看财政铸币税, 是对财政铸币税的不同理解, 两者是相等的。

由上可知, 转移的机会成本铸币税转移给政府部分的为$\left({i - {i^g}} \right)\frac{{GB}}{P} - \left({i - {i^d}} \right)\frac{{DG}}{P} - \left({i - {i^{FP}}} \right)\frac{{FP}}{P}$, 转移给非政府的部分为:$\left({i - {i^f} - \dot e} \right)\frac{{NFA}}{P} + \left({i - {i^o}} \right)\frac{{LB}}{P}$。央行的利润就来源于机会成本铸币税和转移的机会成本铸币税之差。而财政铸币税包括中央银行的利润、扣除中央银行转移给非政府的那部分机会成本铸币税, 以及政府债券发行、政府存款的变动和政府债券、政府存款获得的市场净利息。

接下来, 本文测算1985年至2014年我国的财政铸币税, 其中, i_t^gGB_t-1^CB为对t-1期央行持有政府债券进行的利息支出额, 在计算这个利息支出额时, GB_t-1选择的是央行对中央政府的债权, i_t^g选取的是特别国债利率, i_t^d选取的是活期存款利率^①, 其他变量选取同前。

① 特别国债利率的选取同前。

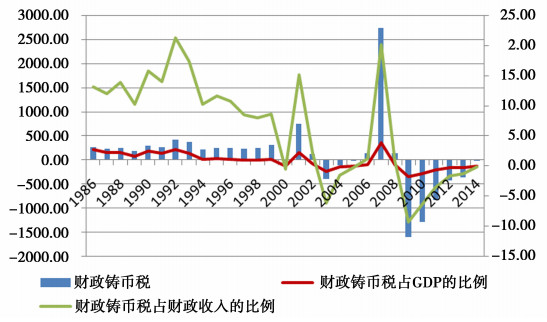
结合前文对中央银行利润的测算结果和图 1可以发现, 1985年至2014年财政铸币税在很大程度上是受到央行利润变动的影响, 央行利润也是财政铸币税的一部分, 是影响财政铸币税的重要因素。央行买卖政府债券或持有债券的变动, 政府存款的变动等也部分地解释了财政铸币税的数值变化。从1985年至1999年, 财政铸币税的绝对数额表现出较为稳定的特征, 2000年、2003年、2004年、2005年, 2009至2014年, 财政铸币税出现负的数值, 2007年财政铸币税达到一个最大值。从财政铸币税占GDP的比重来看, 基本上都在3%以内, 从1985年至2014年, 大致呈现出一个下降的趋势, 从财政铸币税占财政收入的比重来看, 波动幅度较为剧烈, 从1985年至2014年, 整体呈现出一个下降的趋势, 期间存在较大的上下波动, 其在2007年达到一个最大值, 主要原因还是由于中央银行发行的债券及上缴的利润等较大有关。财政铸币税的波动相对于其占GDP和财政收入的规模变动来看要大一些, 但财政铸币税比例并不低, 财政铸币税是在货币扩张、货币政策工具操作、财政赤字的变动等过程中形成的, 可以看出财政铸币税是对宏观经济的反映结果, 因此其造成的影响是不容忽视的。

图 1

图 1 1985年至2014年财政铸币税 注:数据来源为CEIC数据库, 国泰安数据库, 中国资讯行—中国统计数据库, 国研网统计数据库, 中国人民银行网站。

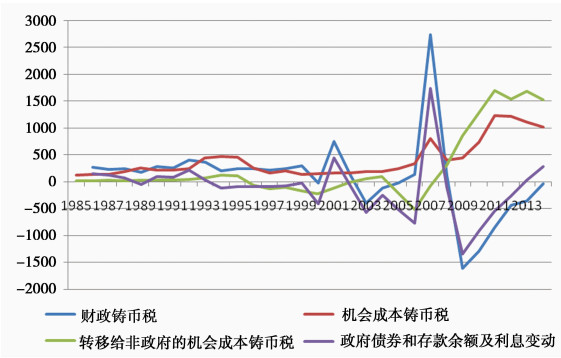
根据财政铸币税的分解可以看出, 在2000年以前, 财政铸币税、机会成本铸币税、转移给非政府的机会成本铸币税和政府债券、存款余额和利息的变动相对比较平缓, 2000年以后, 波动相对较大(见图 2)。这主要由于以下几个原因:一是外汇占款大幅度上升和央行票据大量发行, 转移给非政府的机会成本铸币税上升; 二是政府债券发行量增加, 政府发行的长期特别国债主要由央行持有, 导致政府债券和利息变动较大; 三是政府存款上升, 随着中国经济的增长和政府收入的上升, 政府在央行的存款也会增加, 因此政府存款和利息变化也较大。同时2008年金融危机的爆发, 货币政策调控的转变, 也加剧了这几者的变化, 财政铸币税的变动也相应增加。

图 2

图 2 1985年至2014年财政铸币税的分解 注:数据来源为CEIC数据库, 国泰安数据库, 中国资讯行—中国统计数据库, 国研网统计数据库, 中国人民银行网站。

综上所述, 我们可以看出央行铸币税、利润和财政铸币税特征不一。一是垄断货币发行权是铸币税征收的关键。央行被法律赋予的特殊垄断权利确保其能够取得铸币税收益; 铸币税能够影响央行利润, 除此之外, 央行利润的影响因素还包括资产负债运营管理与实施货币政策工具运用; 政府有财政赤字货币化和获得央行利润的权利, 因此就形成了特定主体的铸币税。二是任何一种铸币税都是由多个影响因子合力形成的结果。其中, 财政铸币税主要受央行对政府债权、央行利润、对央行支付的利息等因素的影响; 利率水平、实际货币余额共同作用于机会成本铸币税。此外, 机会成本铸币税及其转移的部分是央行利润的影响因素。三是多种铸币税不是孤立存在的, 它们是相互作用与相互制约的关系。比如, 财政铸币税与机会成本铸币税中都包含了央行利润, 央行利润的影响因素中又有机会成本铸币税, 因此通过相互影响, 机会成本铸币税也是财政铸币税中的重要组成部分。

与传统税收的显性性质不同, 隐形的货币铸币税是伴随着特定经济主体的社会活动而出现的潜在收入。因此, 铸币税也可以被视为相关经济现象与政策变化的风向标^①。

① 如央行铸币税的升高往往伴随通货膨胀的上升, 财政铸币税的上升往往是由于财政赤字的货币化导致的。

根据卡甘的研究(Cagan, 1956), 货币需求函数是影响最优铸币税的关键因素, 如果考虑到典型代理人的效用最大化, 则铸币税的变化与效用最大化的货币需求函数相联系。假定经济社会中存在代表性个体, 其他个体的约束条件、效用函数等与代表性个体相似, 那么就可以建立有微观基础的典型代理人跨期均衡模型, 可以得到消费者跨期效用最大化的货币需求函数(Blanchard and Fischer, 1989; Obstfeld and Rogoff, 1996; Walsh, 1998; Lucas, 2000)。假定典型代理人瞬间效用函数为u(c, m), 其中人均实际消费$c = \frac{C}{{PN}}$, 人均实际货币余额$m = \frac{M}{{PN}}$, C是总消费, M是名义货币余额, P是一般价格水平, N是总人口。我们假定u_c, u_m > 0, 且函数u(c, m)是严格凹的, 瞬间贴现率为ρ, 典型代理人一生的效用函数为: $V = \int_0^\infty {u\left({c, m} \right){e^{ - \rho t}}dt} $。

典型代理人面临的人均预算约束为:c+$\dot k + \dot m$=w+rk-n(k+m)-πm+x, 其中k是人均资本投入, 人均投资$\dot k = \frac{{dk}}{{dt}}$, 人均实际货币余额的变动:$\dot m = \frac{{dm}}{{dt}}$, w是实际工资水平, r是实际利率水平, 人均收入水平为w+rk, x表示典型代理人获得政府的实际人均转移支付, 通货膨胀率: $\pi = \frac{{\dot P}}{P}$, n是人口增长率。令人均总资产a=k+m, 则预算约束能够写成:${\dot a}$=[w+x+(r-n)a]-[c+(r+π)m], 其中(r+π)是名义利率, 是持有货币的机会成本。

为了求最优解, 我们构建哈密尔顿函数:H_t=u(c, m)e^-ρt+λe^-ρt{[w+x+(r-n)a]-[c+(r+π)m]}, 因此可以得到最优化的一阶条件: ${\frac{{\partial {H_t}}}{{\partial {c_t}}} = {u_c}\left( {c,m} \right){e^{ - \rho t}} - \lambda {e^{ - \rho t}} = 0,\frac{{\partial {H_t}}}{{\partial {m_t}}} = {u_m}\left( {c,m} \right)}$${{e^{ - \rho t}} - \lambda \left( {r + \pi } \right){e^{ - \rho t}} = 0,\frac{{\partial {H_t}}}{{\partial a}} = - \frac{{d\lambda {e^{ - \rho t}}}}{{dt}}}$。

进一步能够得到最优解:

假定"ponzi骗局"不存在, 横截性条件成立: $\mathop {\lim }\limits_{t \to \infty } \lambda {e^{ - \rho t}}a = 0$。将式(7) 与(8) 联立能够可以得到:

假设典型代理人定期效用函数存在等弹性特征:

将代理人的定期效用函数代入(10) 式可得出本模型的货币需求函数:

由货币需求函数, 名义利率与消费决定了实际货币需求。实际货币需求与持有货币的机会成本(i_t)反向变化, 利率下降, 货币需求上升; 与消费正向变动, 消费增加, 货币需求增加。以上是典型代理人效用最优化和宏观经济预算等式约束条件下的货币需求函数, 在货币供给等于货币需求的条件下, m_t^s=m_t^d=m_t, 实际货币余额: ${m_t} = \frac{{{M_t}}}{{{P_t}}} = \left({\frac{{1 - \gamma }}{\gamma }} \right){\left({\frac{1}{{{i_t}}}} \right)^\theta }{c_t}$。铸币税取决于实际货币余额, 如机会成本铸币税:${S^0} = {i_t}\frac{{{M_t}}}{{{P_t}}}$。

在理论分析中, 铸币税大小的衡量通常采用其占国内产出比这一指标来度量。例如扣除央行付息的机会成本铸币税: ${s^o} = i\frac{C}{{PY}} + \left({i - {i^r}} \right)\frac{{RR}}{{PY}} + \left({i - {i^e}} \right)\frac{{ER}}{{PY}}$, 因此扣除央行付息的机会成本铸币税能够写成货币需求函数乘积的形式:${{s^o} = i\frac{C}{{PY}} + \left( {i - {i^r}} \right)\frac{{RR}}{{PY}} + \left( {i - {i^e}} \right)\frac{{ER}}{{PY}} = }$${\left( {\frac{{iC + \left( {i - {i^r}} \right)RR + \left( {i - {i^e}} \right)ER}}{M}} \right)\frac{M}{{PY}}}$, 其中$\frac{M}{{PY}} = \left({\frac{{1 - \gamma }}{\gamma }} \right){\left({\frac{1}{{{i_t}}}} \right)^\theta }\frac{{{c_t}}}{{{Y_t}}}$, Y_t是人均实际GDP, 令$\frac{M}{{PY}} = \left({\frac{{1 - \gamma }}{\gamma }} \right){\left({\frac{1}{{{i_t}}}} \right)^\theta }\frac{{{c_t}}}{{{Y_t}}} = h\left(\pi \right)$, 并令$\left({\frac{{iC + \left({i - {i^r}} \right)RR + \left({i - {i^e}} \right)ER}}{M}} \right) = g\left(\pi \right)$, 定义g(π)为铸币税因子, 因此:s^O=g(π)h(π), 机会成本铸币税是铸币税因子和货币需求函数的乘积^①。机会成本铸币税两边取对数能够得到:lns^O=lng(π)+lnh(π), 我们对机会成本铸币税在均衡状态π=π^*的附近进行泰勒的二阶展开得到:

① 实际上, 货币铸币税、央行利润和转移的机会成本铸币税都可以转换成两者乘积的形式, 可以进行类似的分析。

令${\varepsilon _g} = \frac{{\pi g'\left(\pi \right)}}{{g\left(\pi \right)}}, {\varepsilon _h} = \frac{{\pi h'\left(\pi \right)}}{{h\left(\pi \right)}}$, 可知二次项系数:$\frac{1}{2}\left[ {\frac{{g'\left(\pi \right)}}{{g\left(\pi \right)}} + \frac{{h'\left(\pi \right)}}{{h\left(\pi \right)}}} \right]' = \frac{1}{2}\left[ {\frac{{{\varepsilon _g} + {\varepsilon _h}}}{\pi }} \right]' = \frac{1}{2}\left[ {\frac{{d\left({{\varepsilon _g} + {\varepsilon _h}} \right)}}{{d\pi }} - \frac{{\left({{\varepsilon _g} + {\varepsilon _h}} \right)}}{\pi }} \right]$。

因此:(1) 当$\left[ {\frac{{d\left({{\varepsilon _g} + {\varepsilon _h}} \right)}}{{d\pi }} - \frac{{\left({{\varepsilon _g} + {\varepsilon _h}} \right)}}{\pi }} \right]{|_{\pi = {\pi ^*}}} < 0$, 机会成本铸币税呈"倒U型"曲线;

(2) 当$\left[ {\frac{{d\left({{\varepsilon _g} + {\varepsilon _h}} \right)}}{{d\pi }} - \frac{{\left({{\varepsilon _g} + {\varepsilon _h}} \right)}}{\pi }} \right]{|_{\pi = {\pi ^*}}} > 0$, 机会成本铸币税呈"U型"曲线;

(3) 当$\left[ {\frac{{d\left({{\varepsilon _g} + {\varepsilon _h}} \right)}}{{d\pi }} - \frac{{\left({{\varepsilon _g} + {\varepsilon _h}} \right)}}{\pi }} \right]{|_{\pi = {\pi ^*}}} = 0$, 机会成本铸币税既不是"U型"曲线, 也不是"倒U型"曲线。

其中名义利率i_t等于实际利率r_t加上通货膨胀率π_t, i_t=r_t+π_t。如果考虑到[lnh(π)]″|_π=π^*=$\theta {\left({\frac{1}{{r + {\pi ^*}}}} \right)^2}$, 则意味着[lng(π)]″|_π=π^* < -$\theta {\left({\frac{1}{{r + {\pi ^*}}}} \right)^2}$, 机会成本铸币税呈"倒U型"曲线; 如果[lng(π)]″|_π=π^* > -$\theta {\left({\frac{1}{{r + {\pi ^*}}}} \right)^2}$, 机会成本铸币税呈"U型"曲线; 如果[lng(π)]″|_π=π^*=-$\theta {\left({\frac{1}{{r + {\pi ^*}}}} \right)^2}$, 机会成本铸币税既不是"U型"曲线, 也不是"倒U型"曲线。

当典型代理人实现效用最大化时, 实际货币余额h(π)与通货膨胀率反向变化, 这表示, 本国居民会随着通胀率的上升减持货币; 若g(π)与通货膨胀率正向变化, 即通货膨胀率变大时, g(π)变大。因此假如铸币税呈现U型曲线的形状, 通货膨胀率变大时, 货币余额h(π)下降, 实际货币余额h(π)下降的幅度大于g(π)上升的幅度, 因此铸币税持续下降; 当π > π^*时, 公众对于货币持有的负面态度改善, 因而会出现相反的情况, 实际货币余额h(π)下降的幅度小于g(π)上升的幅度, 铸币税持续上升。因此, 货币需求与通胀率是负相关的, 与通胀率正相关的变量是g(π)。假设通胀率不断上升, 铸币税的变化会呈现不同的趋势。在最大值左边, g(π)上升慢于实际货币余额h(π)下降, 铸币税相应下降; 在最大值的右边, g(π)上升快于实际货币余额h(π)下降, 铸币税相应上升。也就是说, 符合[lng(π)]″|_π=π^* > -$\theta {\left({\frac{1}{{r + {\pi ^*}}}} \right)^2}$, 铸币税呈"U型"曲线。

根据二次函数的特点, 机会成本铸币税的极大值点为(π^*, s^*):

假定机会成本铸币税是"倒U型"的曲线, 结合一阶和二阶导数的相关知识, 铸币税函数在其极大值的右侧是递减的凹函数, 相反, 在极大值的左侧是递增的凸函数。随着通货膨胀率上升, 经过最大值点后, 一阶导数转向下降, 二阶导数大于0, 最大值的右边是凹函数, 左边是凸函数。此外, 铸币税极大值点满足一阶导数为零, 二阶导数小于零。

因此, 我们利用跨期均衡模型可以得出以下结论:铸币税曲线满足U型或倒U型特征, 央行铸币税在典型代理人行为最优化的条件下存在最优化值。央行铸币税的变动趋势由实际货币余额h(π)和g(π)决定。其中, 实际货币余额h(π)随通胀率递减, 而g(π)与通胀率的变动关系或正或负。

本文实证研究是季度数据, 由于早期季度数据不可得, 我们选用的是1998年到2014年共计17年的数据。消费者物价指数采用环比数据(2005=100), 基础货币、物价水平以及国内生产总值等数据来自CEIC数据库、中国人民银行网站等, 并对相关变量进行季节调整。

类似于扣除利息的机会成本铸币税s^O=g(π)h(π), 其他的铸币税和央行利润等都能够表述这种形式, 如机会成本铸币税与GDP之比:${s^M} = \frac{{\Delta {M_t}}}{{{M_t}}}\frac{{{M_t}}}{{{P_t}{Y_t}}}$。扣除利息的货币铸币税:${s^M} = \left({\frac{{\Delta B}}{M} - \frac{{{i^r}}}{r}\frac{{\Delta RR}}{M} - \frac{{{i^e}}}{i}\frac{{\Delta ER}}{M}} \right)\frac{{{M_t}}}{{{P_t}{Y_t}}}$。机会成本铸币税占GDP的比例:${s^0} = {i_t}\frac{{{M_t}}}{{{P_t}{Y_t}}}$。央行利润与GDP之比:${{s^\pi } = [\left( {{i^f} + \dot e - i} \right)\frac{{NFA}}{M} + \left( {{i^g} - i} \right)\frac{{CG}}{M} + \left( {{i^o} - i} \right)\frac{{LB}}{M}}$${ + \left( {i - {i^d}} \right)\frac{{DG}}{M} + \left( {i - {i^{FP}}} \right)\frac{{FP}}{M} + \left( {i\frac{B}{M} - {i^r}\frac{{RR}}{M} - {i^e}\frac{{ER}}{M}} \right)]\frac{{{M_t}}}{{{P_t}}}}$。财政铸币税与GDP的之比:${s^F} = \left\{ {\frac{{G{B_t} - G{B_{t - 1}} - i_t^cG{B_{t - 1}}}}{{{M_t}}} - \frac{{D{G_t} - D{G_{t - 1}} - i_t^dD{G_{t - 1}}}}{{{M_t}}} + \frac{{\pi _t^{CB}}}{{{M_t}}}} \right\}\frac{{{M_t}}}{{{P_t}}}$。转移的机会成本铸币税占GDP的比例: ${{s^T} = [\left( {i - \left( {{i^f} + \dot e} \right)} \right)\frac{{NFA}}{M} + \left( {i - {i^g}} \right)\frac{{CG}}{M} + }$${\left( {i - {i^o}} \right)\frac{{LB}}{M} - \left( {i - {i^d}} \right)\frac{{DG}}{M} - \left( {i - {i^{FP}}} \right)\frac{{FP}}{M}]\frac{{{M_t}}}{{{P_t}{Y_t}}}}$。通货膨胀率:${\pi _t} = \ln \left({\frac{{{P_t}}}{{{P_{t - 1}}}}} \right)$。根据前面的理论分析和方程(13) 可知, 货币铸币税、机会成本铸币税等能够写成通货膨胀率和通货膨胀率二次项线性方程, 因此我们建立如下实证模型:

a₀是常数项, a₁, a₂, a₃分别是时间趋势、通货膨胀率、通货膨胀率平方的系数。其中a₃反映了铸币税关于通货膨胀的二阶导数(Ehrhart et al, 2009), 如果a₃ > 0, 表示铸币税曲线是"u"型的, 如果a₃ < 0, 表示铸币税曲线是"倒U"型的。

本部分选取自回归分布滞后的协整方法(ARDL cointegration approach), 并建立如下回归方程式:

首先, 检测变量间的协整关系, 采用F检验方法。Pesaran et al(2001)获得了F检验两个渐进的关键值, 一个是上限值, 一个是下限值。如果所有序列都是Ⅰ(0), 用下限值来检验长期稳定的关系, 其他情况都用上限值来检验协整关系。

为了检验变量平稳性, 我们选用ADF和PP两种方法对所有相关序列进行检验。结果如表 3:

表 3

表 3 序列的平稳性检验结果 原变量 一阶差分变量 变量 ADF检验形式 ADF统计量 PP检验值 变量 ADF检验形式 ADF统计量 PP检验值 stM (c, 0, 0) -6.6892*** -6.9926*** ΔstM (0, 0, 1) -10.9086*** -19.1554*** sMit(1) (c, 0, 1) -4.2653*** -6.3903*** ΔsMit(1) (0, 0, 0) -14.4941*** -18.7196*** stO (c, t, 1) -4.8067*** -3.6667*** ΔstO (c, 0, 0) -6.5227*** -6.74151*** sOit(2) (c, t, 1) -3.0314 -2.9169 ΔsOit(2) (c, 0, 0) -8.5855*** -8.5575*** stπ (c, t, 2) -3.1579 -2.0472 Δstπ (c, 0, 0) -4.2773*** -4.3035*** stF (c, 0, 0) -7.2530*** -7.2558*** ΔstF (0, 0, 1) -10.0885*** -31.6525*** stT (c, t, 2) -3.4264* -2.0037 ΔstT (0, 0, 1) -2.4366** -3.8714*** πt (c, 0, 0) -3.7553*** -3.7993*** Δπt (0, 0, 0) -11.2815*** -11.2815*** πt2 (c, 0, 1) -3.2195** -6.03116*** Δπt2 (0, 0, 0) -15.4322*** -15.6945*** 注:(c, t, m)分别表示常数项、趋势项和滞后阶数, 据AIC信息准则判定最优滞后阶数, (1) 代表扣除利息的货币铸币税, (2) 代表扣除利息的机会成本铸币税。***(**, *)分别表示在1%(5%, 10%)的水平下显著。

表 3 序列的平稳性检验结果

从检验结果来看, 在5%的显著水平下, 除了扣除利息的机会成本铸币税、转移的机会成本铸币税和央行利润, 所有序列ADF检验是平稳序列, PP检验也是平稳序列。平稳性检验的结果显示扣除利息的机会成本铸币税和央行利润是不平稳的, 但一阶差分都是平稳的。在10%的显著水平下, 转移的机会成本铸币税的ADF检验平稳, PP检验不平稳, 两者一阶差分都平稳。

首先检验货币铸币税和通货膨胀率、通货膨胀率的平方项等之间的协整关系。利用F统计量对s_t^M, π_t, π_t²的系数进行联合显著性检验。结果显示:F统计量=2.8117(p=0.050), 可以判定, 在10%的显著性水平下, s_t^M, π_t, π_t²之间存在长期协整关系。

然后, 估计ARDL的协整模型。经过比较, 本文选取标准误较小的ARDL(0, 0, 1) 模型, 参数估计如表 4。

表 4

表 4 ARDL(0, 0, 1) 模型 变量 系数 T值 P值 变量 系数 T值 P值 πt 1.2198 1.1884 πt2(-1) 58.6477 1.6522 πt2 58.6032 1.1478 t 0.3233E-3 1.2239 inpt 0.018972* 1.8788 R2 .31277 调整的R2值 .26618 F(4, 59) 6.7131 DW-统计量 2.2180 注:***、**、*分别表示在1%、5%、10%水平下拒绝原假设。

表 4 ARDL(0, 0, 1) 模型

最后, 进行诊断检验和稳定性检验。本文自相关检验采用拉格朗日乘数, 函数设定采用reset检验, 稳定性采用CUSUM和CUSUM平方进行检验, 此外还检验残差的正态性和异方差。表 5的结果显示该模型不存在自相关及异方差稳定, 且函数设定正确。

表 5

表 5 ARDL(0, 0, 1) 模型的误差诊断模型的诊断检验 检验类型 统计量值 伴随概率 F统计量值 伴随概率 自相关检验 CHSQ(4)=3.8346 F(4, 55)= 0.87635 RESET检验 CHSQ(1)= 0.038863 F(1, 58)=0.035241 残差的正态性检验 CHSQ(2)= 7.4160 方差 CHSQ(1)= 0.090008 F(1, 62)=0.087318 注:***、**、*分别表示在1%、5%、10%的水平下拒绝原假设。

表 5 ARDL(0, 0, 1) 模型的误差诊断模型的诊断检验

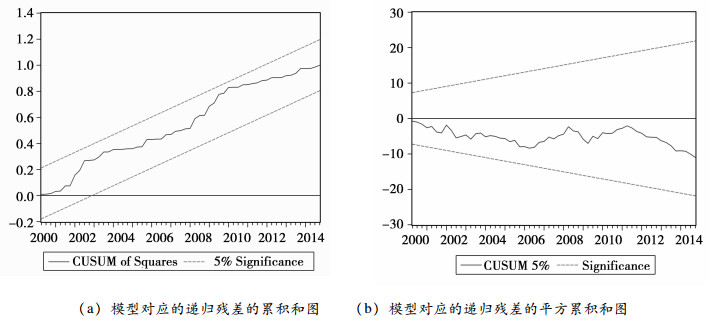
图 3结果显示, 在5%的显著水平下该模型是稳定的。

图 3

图 3 ARDL(0, 0, 1) 模型的的CUSUM和CUSUMSQ图

通过前文对模型联合检验的显著性判断滞后水平变量间存在长期稳定的协整关系, 其系数见表 6。

表 6

表 6 ARDL(0, 0, 1) 模型的长期系数 变量 长期系数 T值 P值 变量 长期系数 T值 P值 πt 1.2198 1.1884 t 0.3233E-3 1.2239 πt2 117.2509* 1.9160 inpt 0.018972* 1.8788 注:1、模型因变量是SM。2、***、**、*分别表示在1%、5%、10%的水平下拒绝原假设。

表 6 ARDL(0, 0, 1) 模型的长期系数

由上表可知, 通货膨胀率二次项的系数显著为正, 因此货币铸币税和通货膨胀率的关系呈"U"型曲线关系, 我们得到如下的货币铸币税函数:

s_t=1.2198π_t+117.2509π_t²+0.3233E-3t+0.018972inpt

首先, 我们可以考察扣除利息的货币铸币税、机会成本铸币税、央行利润、财政铸币税、转移的机会成本铸币税等的ARDL协整检验。边限协整检验的结果如表 7。

表 7

表 7 其他铸币税边限协整检验 类别 F检验 P值 扣除央行付息的货币铸币税 F(stM|πt , πt2)=9.2997 0.000 机会成本铸币税 F(sto|πt, πt2)=3.7021 0.018 扣除央行付息的机会成本铸币税 F(sto|πt, πt2)=6.3513 0.001 央行利润 F(stπ|πt, πt2)=6.4863 0.001 财政铸币税 F(stF|πt, πt2)=3.9671 0.013 转移的机会成本铸币税 F(stT|πt, πt2)=4.0026 0.014

表 7 其他铸币税边限协整检验

由F检验的结果我们可以判定, 在5%的显著水平下, 扣除利息的货币铸币税、机会成本铸币税、央行利润、财政铸币税、转移的机会成本铸币税等和π_t, π_t²之间存在长期协整关系。

其次, 同样我们继续估计ARDL-cointegration模型。按照AIC标准, 机会成本铸币税、央行利润、财政铸币税、转移的机会成本铸币税等的ARDL模型的具体参数估计如表 8。

表 8

表 8 ARDL模型① 扣除利息的货币铸币税ARDL(0, 0, 4) 机会成本铸币税ARDL(4, 0, 3) 扣除利息的机会成本铸币税ARDL(3, 0, 3) 央行利润ARDL(3, 4, 1) 财政铸币税ARDL(0, 3, 2) 转移的机会成本铸币税ARDL(3, 4, 1) 变量 系数 系数 系数 系数 系数 (-1) .66378***(6.0637) .61625***(5.6206) .99513***(8.5429) 1.0477***(8.7571) (-2) .34163**(2.6789) .39901***(3.4828) .26771(1.4396) .27857(1.4562) (-3) .019459(.15837) -.12995(-1.3479) -.35774***(-2.9767) -.42209***(-3.6291) (-4) -.13109(-1.5509) πt .014437(.024976) .12823***(4.0781) .12147***(3.9059) -.020327(-.48961) -1.6661***(-3.2767) .11893***(3.0526) πt(-1) -.10995**(-2.6751) -.89630(-1.5792) .040524(1.0076) πt(-2) .061098**(2.3386) 2.2737***(4.1858) -.064494**(-2.6980) πt(-3) -.034550(-1.4942) -.81751**(-2.2655) .5546E-3(.025867) πt(-4) -.041437*(-1.7719) .073726***(3.4202) πt2 25.5275(.97655) -2.3097*(-1.6957) -2.4203*(-1.852) 3.3184*(1.8868) 81.8373***(3.3651) -4.5179**(-2.6798) πt2(-1) 36.2516*(1.8519) 2.6791***(2.7031) 2.5849***(2.7698) 8.1170***(4.5743) 65.7312***(2.7132) -5.0827***(-2.9297) πt2(-2) 29.7676(1.3993) .23710(.22947) .43915(.44519) -79.1587***(-3.3564) πt2(-3) 51.1051**(2.6863) -2.7836***(-2.7417) -2.3381**(-2.4368) πt2(-4) -54.48**(-2.6041) t .2238E-3(1.5710) .1657E-5(.15930) -.2273E-5(-.20819) .4991E-4**(2.0411) -.4707E-4**(-2.2868) inpt .0083241(1.6427) .5406E-3(1.3409) .2907E-3(1.0813) -.0012346*(-2.0098) -.0070692**(-2.6623) .0013749**(2.2506) d2005 -.8874E-3(-1.6249) .7630E-3(1.4803) R2=0.45122 R2=0.93938 R2=0.91868 R2=0.98511 R2=0.38212 R2=0.98479 a-R2=.38138 a-R2=.92795 a-R2=.90512 a-R2=.98105 a-R2=.30488 a-R2=.98064 F(7, 55)=6.4604 F(10, 53)=82.1370 F(9, 54)=67.7801 F(12, 44)=242.6298 F(7, 56)=4.9475 F(12, 44)=237.3559 DW=2.0240 DW=1.5581 DW=1.7450 DW=1.9367 DW=1.5980 DW=1.9548 注:()-t检验值, -p值, ***、**、*分别表示在1%、5%、10%的水平下拒绝原假设。

表 8 ARDL模型①

① 受篇幅限制, 模型的诊断检验和稳定性检验不再一一列出, 如需要, 可向作者索取。

表 8显示, 根据有些铸币税变动的特点, 本文还考虑了时间趋势(Mankiw, 1987; Poterba and Rotemberg, 1990)。在央行利润和转移的机会成本铸币税中我们加入了2005年虚拟变量, 因为2005年第3季度我国进行了人民币汇率形成机制的改革, 以2005年第三季度作为转折点, 人民币汇率弹性增加, 并且我国的外汇储备也不断上升, 这对我国外汇占款及其收益的影响较大。

最后, 根据上述回归结果, 我们对各变量间长期协整关系给出长期系数。结果如表 9。

表 9

表 9 ARDL模型的长期系数 扣除利息的货币铸币税 机会成本铸币税 扣除利息的机会成本铸币税 央行利润 财政铸币税 转移的机会成本铸币税 变量 长期系数 长期系数 长期系数 长期系数 长期系数 长期系数 πt .014437(.024976) 1.2072(1.3916) 1.0592(1.1252) -1.5296*(-1.9088) -1.1062*(-1.9933) 1.7667**(2.1795) πt2 88.1694***(2.7766) -20.4935(-.74023) -15.1216(-.58556) 120.5011**(2.0366) 68.4099**(2.0184) -100.2206**(-2.1260) t .2238E-3(1.5710) .1560E-4(.17107) -.1982E-4(-.18464) .5259E-3***(3.7167) -.4913E-3***(-3.7573) inpt .0083241(1.6427) .0050888*(1.9783) .0025345(1.1567) -.013010***(-3.6284) -.0070692**(-2.6623) .014352***(4.3628) d2005 -.0093508*(-1.9611) .0079648*(1.8344) 注:***、**、*分别表示在1%、5%、10%的显著性水平下拒绝零假设。

表 9 ARDL模型的长期系数

由表 9可知, 扣除利息的货币铸币税和央行利润的通货膨胀率的二次项的系数显著为正, 即扣除利息的货币铸币税和央行利润对通货膨胀率的二阶导数大于0, 则扣除利息的货币铸币税和通货膨胀率呈"U"型曲线关系, 也就是说, 无论货币铸币税, 还是扣除利息的货币铸币税都有"U"型曲线关系, 央行利润和财政铸币税也呈"U"型曲线关系。机会成本铸币税与其扣除利息之后的二次项都为负且不显著, 因此机会成本铸币税和扣除利息的机会成本铸币税既没有"U"型特征, 也没有"倒U"型特征。转移的机会成本铸币税的通货膨胀率的二次项显著为负, 转移的机会成本铸币税对通货膨胀率的二阶导数小于0, 因此转移的机会成本铸币税与通货膨胀率呈现"倒U"型曲线关系。

央行利润就是机会成本铸币税减掉自身转移出去的部分, 两者之差就是中央银行的利润, 因此机会成本铸币税和转移的机会成本铸币税是影响中央银行利润的重要因素, 国际金融危机以后, 转移的机会成本铸币税影响中央银行利润的较大。转移的机会成本铸币税实际上是对铸币税另一种定义, 体现了中央银行机会成本铸币税是怎样被转移分配的。

进一步本文定义财政铸币税包括央行对政府债权的变动, 政府存款的变动, 央行上缴的利润, 扣除对央行支付的利息, 再加上央行对政府存款所支付的利息等, 它反映了央行获得的铸币税, 以及财政与央行资产和负债项目交易中所获得的收入和支付的成本变动情况。

本文研究显示机会成本铸币税、央行利润、财政铸币税等都可以分解为铸币税因子和货币需求的乘积的形式, 在一定条件下, 铸币税呈倒U型特征或U型特征。实证结果显示我国中央银行货币铸币税、央行利润和财政铸币税的变动存在U性特征; 但机会成本铸币税既没有U型特征, 也没有"倒U型特征"。转移的机会成本铸币税存在倒U型特征。实际上, 货币铸币税是无限期机会成本铸币税的近似值(陆前进、朱丽娜, 2014), 体现了铸币税的长期变化, 机会成本铸币税体现了铸币税的短期变动, 而典型代理人效用的最优化反映了经济主体长期追求的目标, 经济主体的最优化也会渗透在货币铸币税的长期变化上。短期内货币市场的均衡是主要的, 机会成本铸币税的变动主要体现货币市场的短期变化, 并不能够反映经济主体的福利变化, 可能也是货币铸币税和机会成本铸币税变动不一致的主要原因。

从理论上来看, 货币铸币税和机会成本铸币税直接和货币供给相联系, 在货币市场均衡的条件下, 货币需求也决定了货币铸币税和机会成本铸币税的变化, 而转移的机会成本铸币税体现了铸币税的转移支付, 和央行的外汇、债券买卖和再贷款相联系, 因此转移的机会成本铸币税呈现"倒U"型特征, 这可能也是转移的机会成本铸币税的不同之处。

从中央银行铸币税和中央银行的利润研究能够看出, 中央银行利润是铸币税的一部分, 是中央银行垄断货币发行而获得的是一种特许权价值。实际上, 转移的货币铸币税是央行铸币税的运用, 从另一个角度来看, 没有转移出去的铸币税, 也构成了央行利润的一部分, 即如果转移的机会成本铸币税为负, 则表示央行获得这部分铸币税, 央行的利润是增加的。因此央行利润和央行的机会成本铸币税相联系, 它反映了央行初次获得的铸币税一部分转化为央行的利润, 一部分又被央行转移出去。而财政铸币税就包含央行转给财政的那一部分铸币税, 以及财政与央行债权债务之间的关系, 这也构成了财政铸币税的一部分, 这可能也部分解释了央行利润和财政铸币税变动有共同的特点。

最后本文探讨的主要是央行铸币税和央行利润的来源, 是央行拥有货币发行特权而获得的, 下一步需要研究央行铸币税的最优分配和央行利润的合理运用。