随着国际金融活动的相互渗透和影响, 全球股市逐步形成了整体联动的发展态势(张兵等, 2010)。2008年全球金融危机致使全球股市暴跌, 中国股市更是暴跌65.39%①, 表明国际股市联动呈现出典型的"事件"驱动特征, 后金融危机时期国际股市一体化联动呈现出一种整体网络结构(梁琦等, 2015), 具有明显的非线性传导特征(李岸等, 2016)。上述新特征的出现, 使得国际股市一体化联动中的传导机制变得愈加复杂, 导致各国无法清晰认识风险事件的传导途径、影响程度及其控制方式, 进而加剧了事件冲击下的股市暴跌。为此, 刻画国际股市一体化联动网络结构, 探究中国股市在上述网络结构中的地位及其对传导关系的控制方式, 定量分析事件冲击下中国股市与国际股市之间的交互影响, 对揭示中国股市国际一体化联动中的传导机制, 防范和应对国际金融风险冲击具有重要的理论意义和现实价值。
① 采用中国上证综指07年和08年最后交易日点位计算所得。
当前国际股市联动已成为学术界研究的热点, 并逐渐形成了基于国际经济贸易和资本流动的"经济基础假说"和基于投资者心里预期和决策行为的"市场传染假说"(张兵等, 2010; 梁琦等, 2015)。在"经济基础假说"分析框架下, 现有研究更多关注股市联动的影响因素。Mensi et al.(2014)从宏观经济视角展开研究, 认为原油价格、黄金价格、美国经济政策的不确定性等因素是影响股市联动的重要原因。其他国外学者也集中探讨了汇率市场、债券市场、国际贸易、股市交易量、经济周期同步性以及地理因素等对股市联动的影响(Chinn and Forbes, 2003; Flavin et al., 2003; Dellas and Hess, 2005; Walti, 2011)。同时, 国内学者李稻葵、梅松(2009)在对美国及新兴市场宏观经济和资本流动的研究中发现, 跨境资本流动已成为传递风险引起股价波动的主要原因。此后, 龚金国、史代敏(2015)研究认为贸易强度是中美股市联动的主要原因, 贸易强度的增加促使两国股市的联动增加, 并且贸易渠道中的收入效应和价格效应也是促使股市联动的传导机制。此外, 国内学者研究发现全球化程度、汇率制度、金融管制、美国量化政策、外商直接投资等也是中国股市国际一体化联动的重要影响因素(游家兴, 2010; 李岸等, 2016)。
在"市场传染假说"分析框架下, 已有研究主要从股市联动关系和联动规律两个方面展开。这其中对股市联动关系的研究最为广泛和深入。自Jeon, B. N. and Furstenberg, G. M.(1990)较早关注到全球股票指数之间存在联动(co-movement)趋势以来, 针对中国股票市场与其他国家或地区股票市场之间联动关系的研究日益丰富。俞世典等(2001)、陈守东等(2003)在VAR框架下对中国上证指数与美国、日本及香港地区股票指数之间的联动性进行了分析, 结果均表明中国股市与国际市场之间不存在联动关系。高莹(2008)利用2005-2006年沪深300指数, 再次应用上述方法考察了国内外股指的关联性, 结果表明沪深300指数与世界主要股指之间存在短期相关关系, 且与除日经指数外的其他主要国家股指之间均存在长期协整关系。2008年金融危机的爆发, 使得中国股市与国际股市之间的联动逐渐增强, 中国股票市场的国际一体化进程成为众多学者关注的重点, 研究方法也得到进一步丰富, 提出了以信息论为基础的研究思路(费兆奇, 2011; 李红权等, 2011; Gilenko, E. and Fedorova, E., 2014; 梁琦等, 2015)。同时, 为进一步弥补传统的VAR分析框架中仅仅考察股市之间线性联动关系的不足, 周璞、李自然(2012)利用非线性格兰杰因果检验方法验证了中国和世界主要股市之间存在非线性联动关系, 揭示出后金融危机时期国际股市一体化联动已呈现出非线性特征。
对股市联动规律的研究则是建立在对股票市场联动关系分析基础上的拓展研究。Mantegna(1999)首次引入了复杂系统科学理论和方法, 对股票市场联动规律进行了研究, 随后Tumminello et al.(2006)、Tabak et al.(2010)、Cheong et al.(2012)对美国、日本、韩国等国家股票市场建立复杂网络, 并利用平均路径长度、节点介数和度数、幂律性质等拓扑指标揭示出股票市场联动的演变规律。同时, 国内学者则对国内股市联动网络的拓扑性质和聚类结构的演变规律进行了研究(庄新田等, 2007; 黄玮强等, 2008)。近年来, 刘惟枞、张巍(2014) 分析了2008年金融危机前后全球51只股票的网络演化规律, 揭示出各国股票市场的地位和作用不尽相同, 因其经济发展程度的不均衡特性而存在差异。李岸等(2016)则进一步丰富了上述研究, 从股市收益率和波动率两个方面, 研究了中国股市与其他40个国家股市之间联动的演化规律, 揭示出股市收益率和波动率联动模式已呈现出复杂网络结构特征。此外, 梁琦等(2015)则综合考察了17个国家和地区股票市场之间的网络联动规律, 揭示出中国股市全球一体化联动具有典型的"事件"驱动特征, 香港地区股市在风险联动中发挥了"唯一性"作用, 同时中国股市的国际影响力则呈现出非对称性特征, 而中国股市的信息联动和风险传染主要局限于亚洲地区, 表现出明显的区域性特征。
综上所述, 在"经济基础假说"分析框架下, 已有研究聚焦于国家宏观经济因素之间的国际流动对国际股市一体化联动的影响, 是基于"要素流动"视角下对国际股市之间传导机制的研究。同时, 在"市场传染假说"分析框架下, 现有研究认为投资者对股市变化的心里预期和决策行为像病毒传染一般在市场中扩散, 使得国际股票市场联动呈现出某种动态变化规律, 是基于"演变规律"视角下对国际股市之间传导机制的研究。事实上, 在股市联动模式已呈现出复杂网络结构的情境下, 国际股票市场之间的传导, 不仅受到贸易、资本、制度等国家宏观经济因素的影响, 而且也必然受到其所嵌入的股市联动"网络结构"的影响。依据格兰诺维特的"嵌入性"理论(Granovetter, M., 1985; 1992), 某国股票市场在联动网络结构中的国际"地位和角色", 将影响该国股票市场中投资者的心里预期和决策行为, 进而影响国际股市之间的传导机制, 而现有研究忽视了上述网络结构因素对国际股市联动产生的影响, 囿于现有研究更多关注经济因素和演变规律对国际股市之间传导机制的影响, 本文试图从"网络结构"视角探析国际股市之间的传导机制。为此, 本文采用网络分析方法, 通过刻画国际股市一体化联动网络结构, 揭示各国股市在上述联动网络结构中的地位, 以及解释因其地位不同产生的对传导关系控制方式的差异, 进而实现对国际股市一体化联动网络中事件的传导途径、影响程度及其控制方式的量化分析, 为科学阐释网络结构对国际股市之间传导机制的影响提供一种新思路。
鉴于此, 本文利用金砖国家和七国集团共十二个国家的股票收盘数据, 应用非线性格兰杰因果检验方法对国际股市收益率和波动率的非线性联动关系进行识别, 在此基础上使用社会网络分析方法刻画国际股票市场的联动网络及其结构特征, 利用广义脉冲函数揭示中国股市与国际股市之间的交互影响。与现有研究相比, 本文的主要创新在于利用网络分析方法揭示出中国股市在国际股票市场上的地位和角色, 及其对国际股市联动中传导关系的控制方式, 以及定量分析"事件"冲击下中国股市与国际股市之间动态交互影响的程度和趋势, 阐释出联动网络结构对国际股市之间传导机制的影响。
二、方法与数据 (一) 非线性格兰杰因果检验方法正如Granger and Newbold(1986) 所指出的, 真实世界几乎都是非线性关系的集合, 非线性模型是对真实世界的真实模拟。为此, Baek and Brock (1992)、Hiemstra and Jones(1994)、Diks and Panchenko(2006)提出了一种基于非参数统计量的非线性格兰杰因果检验方法, 从线性格兰杰因果模型中去掉序列间的线性"预测力", 基于残差信息揭示序列间非线性格兰杰因果关系。
1. BDS检验方法在非线性格兰杰因果检验之前, 通常采用BDS方法(Broock et al., 1996), 对残差序列进行非线性检验, BDS检验给定一个m维的时间序列Zt, 其观测值为(zt, zt+1, …, zt+m-1)。跨期空间概率的估计量关联积分(correlation integral)的定义是:
| ${C_{\rm{m}}}\left( {T,d} \right) = \sum _{{\rm{t}} = 1}^{{T_{\rm{m}}} - 1}\sum _{{\rm{s = t}} + 1}^{{T_{\rm{m}}} - 1}I(Z_t^m,Z_s^m,d) \times \frac{2}{{{T_m}({T_m} - 1)}}$ | (1) |
式(1) 中, I(Ztm, Zsm, d)是指标函数(Indicator Function), 当I函数满足条件//Ztm, Zsm// < d时, I(Ztm, Zsm, d)=1;否则, I(Ztm, Zsm, d)=0。//Ztm, Zsm//为两个序列Ztm、Zsm间的欧式空间距离, d是带宽, T是总样本数, 序列Zt可以分为Tm个m维的子样本, 且Ztm=(zt, zt+1, …, zt+m-1), Zsm=(zt, zt+1, …, zt+m)。
那么, 可对BDS检验的统计量做出定义:
| ${W_m}\left( {T,d} \right) = \frac{{\sqrt {T\left[ {{C_m}\left( {T,d} \right) - {C_1}{{\left( {T,d} \right)}^m}} \right]} }}{{{\sigma _m}\left( d \right)}}$ | (2) |
式(2) 中, σm(d)是给定m维样本的标准差。如果Wm(T, d)拒绝原假设, 则表明序列中存在非线性关系。
2. 非线性格兰杰因果关系检验Diks and Panchenko(2006)改进了Baek and Brock (1992)、Hiemstra and Jones(1994) 的检验方法。考虑Xt、Yt是两个时间序列变量, 定义Xt的m维先导向量(leading vector)为Xtm, Xt的Lx期滞后向量(lag vector)和Yt的Ly期滞后向量分别为Xt-LxLx和Yt-LyLy, 见公式(3):
| $\begin{array}{l} X_t^m = ({x_t},{x_{t + 1}}, \cdots \cdots ,{x_{t + m - 1}}),{\rm{ }}m = 1,2, \cdots \cdots ;t = 1,2 \cdots \cdots \\ X_{t - Lx}^{Lx} = ({x_{t - Lx}},{x_{t - Lx + 1}}, \cdots \cdots ,{x_{t - 1}}),{\rm{ }}Lx = 1,2, \cdots \cdots ;t = Lx + 1,Lx + 2 \cdots \cdots \\ {\rm{ }}Y_{t - Ly}^{Ly} = ({y_{t - Ly}},{y_{t - Ly + 1}}, \cdots \cdots ,{\rm{ }}{y_{t - 1}}),Ly = 1,2, \cdots \cdots ;t = Ly + 1,Ly + 2 \cdots \cdots \end{array}$ | (3) |
| $\begin{array}{l} {\rm{Pr}}\left( {\left\| {X_t^m - X_s^m} \right\| < d|\left\| {X_{t - Lx}^{Lx} - X_{s - Lx}^{Lx}} \right\| < d,\left\| {X_{t - Ly}^{Ly} - X_{s - Ly}^{Ly}} \right\| < d} \right)\\ {\rm{ = Pr}}\left( {\left\| {X_t^m - X_s^m} \right\| < d\left\| {X_{t - Lx}^{Lx} - X_{s - Lx}^{Lx}} \right\| < d} \right) \end{array}$ | (4) |
如果给定m、Lx、Ly > 1以及任意小的常数d > 0, 若Y满足公式(4) 的条件概率, 则Y不是X的严格非线性格兰杰原因。其中, Pr(·)表示概率, ‖·‖表示最大范数。s、t = max(Lx, Ly)+1, ..., T-m+1。如果给定(4) 式右边序列Xt的条件概率, 且无论有无序列Yt, 均不会对其产生影响, 则表明Y不是影响X的非线性格兰杰原因。(4) 式中的条件概率可表示为:
| $\frac{{CI\left( {m + Lx,Ly,d} \right)}}{{CI\left( {Lx,Ly,d} \right)}} = \frac{{CI\left( {m + Lx,d} \right)}}{{CI{\rm{ }}\left( {Lx,d} \right)}}$ | (5) |
其中:
| $ \begin{array}{l} CI = \left( {m + Lx,Ly,d} \right) = Pr\left( {\left\| {X_{t - Lx}^{m + Lx} - X_{s - Lx}^{m + Lx}} \right\| < d,\left\| {Y_{t - Ly}^{Ly} - Y_{s - Ly}^{Ly}} \right\| < d} \right)\\ CI = \left( {Lx,Ly,d} \right) = Pr\left( {\left\| {X_{t - Lx}^{Lx} - X_{s - Lx}^{Lx}} \right\| < d,\left\| {Y_{t - Ly}^{Ly} - Y_{s - Ly}^{Ly}} \right\| < d} \right)\\ CI = \left( {m + Lx,d} \right) = Pr{\rm{ }}\left( {\left\| {X_{t - Lx}^{m + Lx} - X_{s - Lx}^{m + Lx}} \right\| < d} \right)\\ CI = \left( {Lx,d} \right) = Pr\left( {\left\| {X_{t - Lx}^{Lx} - X_{s - Lx}^{Lx}} \right\| < d} \right) \end{array} $ |
假定Xt、Yt满足混合条件, 基于原假设"Yt不是Xt的严格非线性格兰杰原因", Diks and Panchenko(2006)构造了渐进正态分布的T检验量:
| $T = \left[ {\frac{{CI\left( {m + Lx,Ly,d,n} \right)}}{{CI\left( {Lx,Ly,d,n} \right)}} - \frac{{CI\left( {m + Lx,d,n} \right)}}{{CI\left( {Lx,d,n} \right)}}} \right] \sim N\left( {0,\frac{1}{{\sqrt n }}{\sigma ^2}\left( {m,Lx,Ly,d} \right)} \right)$ | (6) |
其中, n=T+1-m-max(Lx, Ly), σ2(·)是修正的检验统计量的渐进方差。根据(6) 式中的检验结果, 如果原假设被拒绝, 则两个序列间的因果关系一定是非线性的。
(二) 广义脉冲响应函数脉冲响应函数(Impulse Response Function, IRF)不同于格兰杰因果检验, 它关注随机扰动的影响是如何传递到各个变量, 这能够将模型所包含的经济意义较为完整而细致的表达出来, 可以提供脉冲条件下系统响应的正负方向、调整时期和过程趋势等信息。传统的IRF的正交化通常采用由Sims(1980) 提出的Cholesky分解方法来完成, 然而上述方法的结果严格依赖于模型中变量的先后检验次序。由Koop et al.(1996) 提出, Pesaran and Shin(1998) 进行拓展的广义脉冲响应函数(Generalized Impulse Response Function, GIRF)可以有效克服传统IRF的缺陷, 更加适合非线性脉冲响应函数分析。
(三) 社会网络分析方法社会网络分析方法以"关系"(relation)作为分析数据, 采用图论工具、代数模型技术探究关系模式中结构对成员整体和个体的影响, 是一种面向"关系数据"的分析方法, 其应用领域已广泛应用于社会学、经济学和管理学等领域(李敬等, 2014; 刘华军等, 2015), 逐渐成为一种新的研究范式(Freeman, 2011; Scott, 2013;刘军, 2014)。在社会网络分析中, 通常对整体网络结构和个体网络结构进行分析, 整体网络结构中常采用网络密度、网络关联度、网络效率、网络等级度等指标进行分析; 个体网络结构中常采用度数中心度、中介中心度、接近中心度等指标进行分析。本文将遵循上述研究范式揭示国际股票市场之间收益率和波动率的非线性联动网络结构特征。
(四) 样本选择与数据处理本文研究基于金砖国家和七国集团共十二个国家的每日收盘价数据, 即上证指数、巴西BOVESPA指数、印度孟买30指数、俄罗斯MICEX指数、南非股票指数、德国DAX指数、法国巴黎CAC40指数、美国道琼斯工业指数、日经225指数、伦敦金融时报100指数、加拿大股票指数和意大利股票指数。本文旨在探究分析后金融危机时期, 上述十二个国家股票市场收益率和波动率之间的联动效应及其联动网络结构特征。为此, 样本选择为时间跨度从2009年3月23日之后的12个国家股市日收盘价格。由于从2015年5月份至今, 中国股市的走势背离了世界主要股市, 进入到一个长时间的调整期, 通过检验整个研究数据的平稳性, 我们把处于调整期内的时间数据予以剔除, 不作为本次研究的样本数据。因此, 将样本数据的时间截止到2015年4月30日。全部数据来自雅虎财经网站(http://finance.yahoo.com)。由于各国的节假日有所不同, 本文删除了日期不重合的股票数据, 最终得到1632个数据。
现有研究认为, 股市联动一般从收益率与波动率两个方面揭示股票市场之间的价格联动和风险联动, 其中收益率联动常用于衡量金融市场的一体化水平, 而波动率联动则用于衡量金融风险传染(李岸, 2016)。对收盘价格序列采取自然对数差分, 得到连续复利收益率序列(杨科等, 2010)。波动率序列通常运用GARCH(1, 1) 模型估计股票指数收益率的日波动计算得出。标准的GARCH(1, 1) 模型为:
| ${R_t} = \mu + {\varepsilon _t},{\varepsilon _{\rm{t}}} \sim NID(0,\sigma _{\rm{t}}^2)$ | (7) |
| $\sigma _{\rm{t}}^2 = VAR({\varepsilon _t}|{\psi _t}_{ - 1}) = \omega + \alpha \varepsilon _{{\rm{t}} - 1}^2 + \beta \sigma _{{\rm{t}} - 1}^2$ | (8) |
模型由均值方程(7) 和条件方差方程(8) 构成, μ是常数项, εt是t时段收益率的误差项, 而σ2是εt的条件方差。
三、国际股市收益率和波动率的非线性联动关系 (一) 单位根检验非线性格兰杰因果检验只适用于平稳时间序列(杨子晖等, 2013; 杨子晖、赵永亮, 2014)。因此在格兰杰因果检验之前需要对变量的平稳性进行检验。选择Dickey-Fuller(1981) 提出的ADF单位根检验, 对收益率序列和波动率序列进行平稳性检验, 结果显示, 在1%的显著性水平下, 收益率序列是平稳序列, 在5%的显著性水平下, 波动率序列是平稳序列①。
① 限于篇幅, ADF单位根检验结果没有给出, 有需要的读者可向作者索要。
(二) BDS检验收益率序列和波动率序列均为平稳序列, 因此我们可以对两组数据进行非线性格兰杰因果检验。在这之前, 必须进行BDS检验以考察股票价格在国际传递中是否存在着非线性的动态变化趋势。检验结果如表 1和表 2所示。在1%显著性水平下, 基于回归残差的BDS检验均拒绝线性关系的原假设, 这意味着国际股市之间存在非线性关系。为此, 本文将采用非线性格兰杰因果检验方法考察十二个国家股市收益率和波动率的非线性传导关系。
| 表 1 收益率BDS检验 |
| 表 2 波动率BDS检验 |
本文采用由Diks and Panchenko(2006)改进的非线性格兰杰因果检验方法, 对12个国家股市收益率和波动率的非线性关系进行分析, 表 3、4分别报告了滞后2阶(Lx=Ly)的检验结果①。
① 本文测算了滞后4阶的非线性Granger关系, 限于篇幅未报告滞后3-4阶的测算结果, 如有需要可向作者索要。
| 表 3 收益率的非线性格兰杰因果检验 |
| 表 4 波动率的非线性格兰杰因果检验 |
根据表 3, 在10%显著性水平下, 结合1-4阶检验结果进行综合对比分析可知:(1) 滞后1-4阶, 中国的收益率对巴西、印度、俄罗斯、南非、法国、美国、英国、加拿大的收益均具有联动关系; 除此之外, 中国的收益率还对德国(滞后1、2、3阶显著)、意大利(滞后1、3阶显著)的收益率具有一定的联动关系。(2) 滞后1-4阶, 俄罗斯、南非、德国、法国、英国的收益率对中国的收益率均具有联动关系; 除此之外, 美国的收益率对中国(滞后2阶显著)的收益率具有一定的联动关系, 加拿大的收益率对中国(滞后2、3、4阶显著)的收益率具有一定的联动关系, 其他国家股市收益率之间非线性关系详见表 3。
根据表 4, 在10%显著性水平下, 结合1-4阶检验结果进行综合对比分析可知:(1) 滞后1-4阶, 中国波动率对印度、俄罗斯、日本、加拿大的波动率均具有联动关系; 除此之外, 中国波动率还对法国(滞后1、3阶显著)、英国(滞后1阶显著)、意大利(滞后1阶显著)的波动率具有一定的联动关系。(2) 滞后1-4阶, 德国、法国、美国、英国和加拿大的波动率对中国的波动率均具有显著的联动关系; 除此之外, 意大利的波动率对中国(滞后2阶显著)的波动率具有一定的联动关系, 其他国家股市波动率之间非线性关系详见表 4。
四、国际股市稳健性联动网络分析当前关于非线性格兰杰因果检验的最优滞后阶数并没有统一的选择标准(Ancis, 2010)。我们认为, 如果所有滞后阶数下检验结果均显著地拒绝"不存在非线性格兰杰因果关系"的原假设, 则变量间就存在"稳健"联动关系, 基于这种稳健的联动关系所形成的联动网络, 我们可以将其定义为"稳健性联动网络"(Robust Network, 简称R-Network)。
(一) 国际股市收益率稳健性联动网络分析根据非线性格兰杰因果检验结果, 按照稳健性联动关系的界定方法, 确定出12个国家股市收益率的稳健性联动关系。图 1对收益率稳健性联动网络(以下简称"收益网络")进行了可视化。
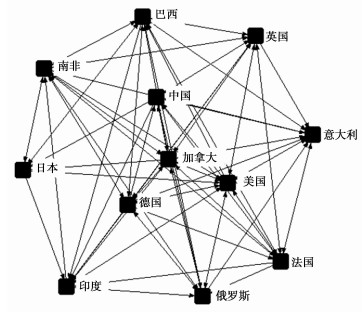
|
图 1 国际股市收益率稳健性联动网络 |
在收益网络中, 国际股市收益率之间联动关系数为56, 最大可能联动关系数为132, 网络密度为0.42, 这表明国际股市收益的联动程度较高。网络关联度为1.00, 说明整体网络联动性强, 均不存在孤立的国家。网络等级度为0.31, 表明收益网络的等级结构并不森严, 节点间对称可达程度较高, 各国股市收益之间存在互惠性。网络效率为0.49, 说明联动关系存在多重叠加现象, 国际股市收益网络较为稳定。
2. 国际股市收益网络的中心性为了揭示各个国家在国际股市收益网络中的地位和作用, 我们选择度数中心度、接近中心度、中介中心度三个中心性指标进行分析, 结果如表 5所示。
| 表 5 收益率稳健性联动网络的中心性 |
(1) 度数中心度。在收益网络中, 度数中心度排名最靠前的国家分别是加拿大、美国、德国, 它们的度数中心度分别是100.00、90.91和90.91, 这说明以上国家与其他国家的股票收益率间存在较多的联动关系, 在网络中处于中心地位。而中国和英国的度数中心度紧随其后, 度数中心度均为63.64。(2) 接近中心度。收益率网络中加拿大的接近中心度最高, 达到了100.00, 美国和德国并列第二, 这说明上述国家股市更加接近收益率网络的中心, 受到收益网络的影响较大, 表现出融入国际收益网络一体化的程度更高, 而日本、意大利的接近中心度排名靠后, 表明以上国家与国际股市收益网络中心国家股市的"距离"较远, 其国际收益网络一体化程度较低。(3) 中介中心度。加拿大的中介中心度最高, 美国和德国也紧随其后, 12个国家的中介中心度总量为47.3, 而加拿大的中介中心度占比为54.39%, 排名前3位的国家中介中心度之和占比超过86.32%, 说明这些国家股市在收益网络中易于调节其他国家股市收益, 发挥着"中介"作用。意大利、印度、日本的中介中心度最小, 表明上述国家股市收益易受其他国家影响。
综合以上分析, 国际股市收益的中心主要是传统成熟市场, 包括北美市场的加拿大和美国, 以及欧洲市场的德国、法国和英国。上述国家是带动国际股市上涨的源泉, 是国际股市收益率联动网络的中心, 进一步观察上述国家的中心度可以发现, 虽然上述国家是国际股市收益率联动网络的中心, 但加拿大中介中心度最高, 表明加拿大股市更多的在收益网络中心国家股市间扮演了"中继"的角色, 成为收益中心国家扩大溢出效应的"桥梁", 而英国、美国、德国等国家则是国际股市的绝对收益中心。而中国等金砖国家作为新兴股票市场, 其在国际股市收益率联动网络中的作用和地位已明显超过日本、意大利等国家的股市, 然而金砖国家股市普遍的收益传递较少, 更多扮演了股市上扬的追随者。中国在国际股市联动网络中的度数中心度仍较低, 但已经与英国相当, 而中国股市在联动网络中的出度远高于其他金砖国家, 表明中国股市已从金砖国家中脱颖而出, 正逐渐从追随者的角色, 迈向国际股市收益中心, 成为新兴的国际股市上涨的发动机。
(二) 国际股市波动率稳健性联动网络分析根据非线性格兰杰因果检验结果, 按照稳健性联动关系的界定方法, 确定出十二个国家股市波动率的稳健性联动关系。图 2描绘出国际股市波动率稳健性联动网络(以下简称"波动网络")。
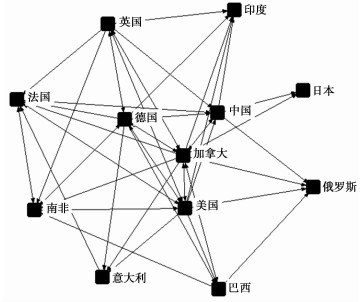
|
图 2 国际股市波动率稳健性联动网络 |
在波动网络中, 十二个国家股市波动率之间的联动关系数为52, 最大可能联动关系数为132, 网络密度为0.39, 这表明国际股市波动率的联动程度较高。网络关联度为1.00, 说明整体网络联动性强, 国际股市波动率之间联动关系十分稳健。网络等级度为0.31, 表明波动网络的节点间对称可达程度较高, 各国股市波动率之间存在相互传染性。网络效率为0.47, 说明联动关系存在多重叠加现象, 国际股市波动网络较为稳定。
2. 国际股市波动网络的中心性从表 6中心性结果可以得出, (1) 度数中心度。股票市场作为典型的"高风险高收益"类投资市场, 处于国际股市收益联动网络中心的加拿大、美国、德国、英国也成为了国际股市波动网络的中心, 其度数中心度分别为100、91.67、84.62和73.33, 这意味着上述国家不但是带动股市上扬的发动机, 也是导致股市波动风险的主要来源。(2) 接近中心度。国际股市波动网络中各国股市的接近中心度明显小于其在收益网络中的接近中心度, 加拿大、美国和德国接近中心度较大, 但也未超过60, 表明各国股市都竭力远离国际股市波动网络中心。(3) 中介中心度。加拿大的中介中心度仍为最高的20.42, 依旧在波动网络中心国家之间扮演着波动风险的"中继"角色, 而美国、德国和英国则是国际股市波动网络的绝对中心。
| 表 6 波动率稳健性联动网络的中心性 |
伴随着中国股市在国际股市收益率联动网络中地位的增长, 中国在波动网络中的度数中心度为78.57, 中国股市呈现出波动中心的趋势。但中国在国际股市波动网络中具有很高的中介中心度(8.09), 仅次于加拿大和美国, 比位列第四位的德国股市的中介中心度高出50%, 这表明中国股市在国际股市波动网络中扮演了重要的"中转"角色, 成为除加拿大和美国之外, 造成国际股市之间波动风险交叉影响的重要"桥梁"。比较中国在国际股市收益网络中的地位, 中国股市并未表现出"高风险高收益"的市场特点, 这一方面可能源于当前世界经济前景处于尚未明朗时期, 股市作为中国经济的晴雨表, 中国股市的波动风险更容易引起国际股市的波动。另一方面, 中国股市与发达国家股市比较, 股市投资者投机行为较强, 在监管机制尚未完善期间, 股市的波动促使投资者的投机行为表现出"羊群效应", 进而引起国际股市波动的"连锁反应"(李涛、郭杰, 2009)。综合分析国际股市收益网络和波动网络, 各国股市波动网络中的度数中心度普遍高于收益网络中的度数中心度, 而各国股市波动网络中的接近中心度普遍低于收益网络中的接近中心度, 这表明后金融危机时期, 在股市波动风险影响下各国股市之间的风险联动更加紧密, 同时各国股市普遍增强了风险管控机制, 尽可能远离股市波动风险的中心, 促进经济复苏和发展。
五、中国股市与国际股市之间的动态交互影响非线性格兰杰因果检验确定了国家股票收益和波动的相互联动关系, 在此基础上社会网络分析揭示出中国股市在国际股票市场上的地位和角色对国际股市联动中传导关系的控制方式, 但未能反映出事件冲击下国家股市之间动态交互影响的强弱程度、正负方向、调整时滞和稳定过程等信息, 为此, 本文采用广义脉冲响应函数刻画以上特征。
(一) 中国股市与国际股市收益的脉冲响应图 3中国股市对其他国家股市收益脉冲的响应, 大致呈现出了由正向响应转为负向响应, 并于5-6天后逐渐消失的变化趋势。中国股市紧随其他国家股市脉冲的衰减一起递减, 表明后金融危机时期中国股市紧跟国际股市收益变化, 同时在响应的后期呈现出负向增长趋势, 这与成熟国家股市对收益脉冲的响应趋势存在显著差别①, 这也表明中国股市在国际化进程中, 在受到国际利好脉冲的后期, 极易发生非理性投机行为(李涛、郭杰, 2009)。同时, 中国股市对美国股市收益脉冲则出现了先负向, 再正向, 而后负向的"一波三折"的响应趋势。这表明后金融危机时期, 在国际股市收益网络中, 虽然中国股市与收益网络中心的北美股市之间的联动十分紧密, 但中国股市更倾向于"追捧"美国股市, 且后期极易出现"恐慌"套现。
① 限于篇幅, 未列出其他国家脉冲响应趋势, 如需要可随时向作者索要。
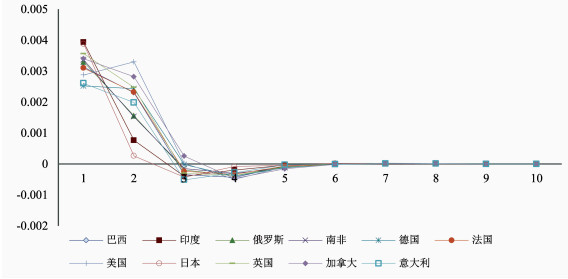
|
图 3 中国对国际股市收益率脉冲的响应 |
图 4国际股市对中国股市收益脉冲的响应, 大致呈现出由正向响应转为负向响应, 并最终于5-7天后逐渐消失的变化趋势。这与中国股市对其他国家股市收益脉冲的响应趋势类似, 反映出中国股市与国际股市之间存在交互影响关系, 这种关系对于持续提升中国股市在国际股市收益网络中的地位十分重要。相较于成熟国家股市对收益脉冲的响应, 因为中国股市存在"非理性"因素, 导致国际股市在中国股市利好脉冲的后期, 也表现出负向响应。进一步观察发现, 印度、日本等国家股市对中国利好脉冲影响的后期, 较早的呈现出负向响应, 表明中国股市对地缘临近国家股市具有更加快速的影响。
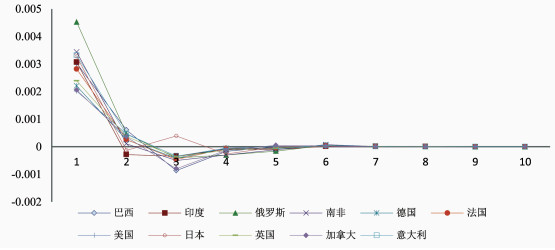
|
图 4 国际股市对中国收益率脉冲的响应 |
表 7左侧响应数值中, 中国对印度股市和日本股市的响应强度较大, 而对意大利股市的响应强度最小, 同时, 中国对加拿大、美国和英国股市的累积响应值较大。在表 7右侧响应数值中, 俄罗斯对中国股市的响应强度最大, 而巴西和加拿大对中国股市的响应强度最小, 俄罗斯、意大利、日本对中国股市的累积响应值较大。这表明, 从收益脉冲响应强度分析, 在国际股市收益网络中, 中国股市与临近国家股市之间, 如印度、日本、俄罗斯股市, 存在较大的收益脉冲响应强度, 而与地域较远的国家股市之间, 如意大利、巴西、加拿大股市, 具有较小的收益脉冲响应强度。换言之, 中国股市具有典型的"地缘特征"。同时, 从脉冲累积响应规模分析, 中国股市一方面对加拿大、美国和英国股市的脉冲产生了较大的累积响应, 另一方面俄罗斯、意大利、日本股市对中国股市的脉冲产生了较大的累积响应。这表明, 中国股市更倾向于将收益网络中心国家股市的利好, 持续传递给地缘临近国家股市, 中国股市在收益网络中具有典型的"地缘特征"。
| 表 7 中国股市与国际股市收益率的脉冲响应 |
图 5中国股市对国际股市波动脉冲的响应趋势, 大致呈现出整体快速递减的正向响应趋势。虽然中国股市对国际股市波动脉冲的响应中最小脉冲为负值, 但其数值较小, 中国股市对国际股市波动脉冲的负向响应趋势较弱。这表明, 中国股市作为国际股市波动网络中的"中介"角色, 使得国际股市的波动能够以更加迅速和直接的方式与中国股市联动。而从响应趋势中可看出, 中国股市并未识别出不同国家的波动脉冲, 以有针对性的分类监控国际股市波动对中国股市的脉冲影响。而中国股市对国际股市波动脉冲的负向影响较小, 则进一步突显出后金融危机时期, 如何最大限度的发挥中国股市在国际股市波动网络中的"中介"角色, 阻断国际股市的波动, 是今后中国重塑全球金融治理角色的重要内容。
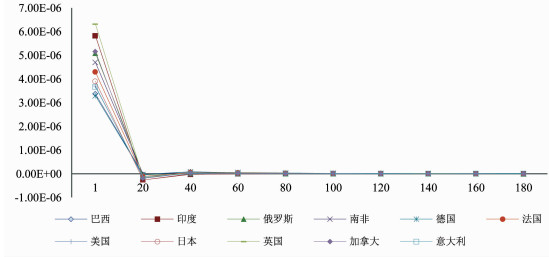
|
图 5 中国对国际股市波动率脉冲的响应 |
图 6国际股市对中国股市波动脉冲的响应趋势, 也呈现出递减的正向响应趋势。虽然其负向响应也较小, 但不同国家股市波动调整时间差异较大, 特别是股市发达国家, 如:美国、德国、英国、法国等国家, 对中国股市波动脉冲的调整时期超过200天。这一方面表明后金融危机时期, 随着中国股市国际一体化程度的提升, 中国股市在国际股市波动网络中对经济发达国家股市的影响更加深远。另一方面这也反映出, 上述国家股市去波动脉冲的能力不足, 这或许与上述国家较少采取直接行政干预股市的行为有关(韩萌萌, 2012)。相比较中国对国际股市波动脉冲的调整期数而言, 中国股市消除国际股市波动脉冲的时间较短, 这突显出后金融危机时期, 中国致力于股市的一系列改革取得了一定的成效。
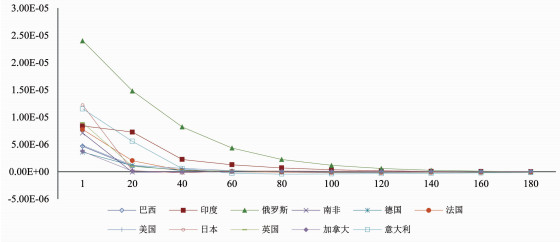
|
图 6 国际股市对中国波动率脉冲的响应 |
表 8左侧响应数值中, 中国股市对英国和印度等国家波动脉冲响应强度较大, 中国股市对英国和印度股市累积响应也较大, 表 8右侧响应数值中, 俄罗斯、日本、意大利对中国股市的波动脉冲响应强度较大, 而俄罗斯、意大利、日本对中国股市波动脉冲累积响应也较大。这表明, 在国际股市波动网络中, 初始波动冲击强度较大的国家股市, 往往是持续产生较大波动规模的国家。换言之, 当国际股市波动发生时, 应识别各国股市初始波动冲击强度, 有利于化解国际股市长期波动风险。在此基础上, 综合中国股市与国际股市之间的脉冲响应分析结果, 不难发现, 国际股市收益网络中各国脉冲响应的强度普遍大于波动网络的响应强度。这表明后金融危机时代, 国际股市联动网络中各国致力于提高本国股市在收益方面的联动强度, 而竭力规避波动联动的努力取得了显著成效, 这也从侧面反映出推动重塑新型全球治理格局的可行性和必要性。
| 表 8 中国股市与国际股市波动率的脉冲响应 |
本文利用金砖国家和七国集团共十二个国家股市收盘数据, 利用非线性格兰杰因果检验方法和社会网络分析方法, 对国际股市收益率和波动率的联动关系及其联动网络结构特征进行分析, 揭示出中国股市在国际股市联动网络中的地位和角色对国际股市联动中传导关系的控制方式, 并应用广义脉冲函数定量分析了事件冲击下国际股市之间的动态交互影响。主要研究结论如下:(1) 十二个国家构成的国际股市间收益率、波动率分别具有非线性联动关系, 同时上述非线性联动关系呈现出复杂的股市收益网络结构和波动网络结构。(2) 中国在国际股市收益率联动网络中的作用和地位与英国相当, 已明显超过日本、意大利等成熟国家股市, 表明中国股市已从金砖国家中脱颖而出, 正逐渐迈向国际股市收益中心, 成为带动国际股市上涨的发动机。(3) 中国在国际股市波动率联动网络中具有很高的中介中心度(8.09), 仅次于加拿大和美国, 比位列第四位的德国股市的中介中心度高出50%, 这表明中国股市在波动率联动网络中扮演了重要的"中转"角色, 是造成国际股市之间波动风险交叉影响的重要"桥梁"。(4) 中国股市的收益脉冲响应趋势, 大致呈现出了由正向响应转为负向响应, 并于5-7天时间内逐渐收敛为零的趋势。这与成熟国家股市收益脉冲响应趋势存在显著差别, 这表明中国股市推进国际化进程中, 在国际利好冲击的后期, 极易发生非理性投机行为引起的"恐慌"套现。(5) 中国股市的波动脉冲响应趋势, 大致呈现出整体快速递减的正向响应趋势。但中国股市消除国际股市波动脉冲的时间较短, 突显出后金融危机时期中国致力于股市监管的改革举措取得了显著成效。(6) 从收益率脉冲响应强度和累积规模分析, 在国际股市收益率联动网络中, 中国股市对国际股市的影响具有典型的"地缘特征", 倾向于将收益网络中心国家股市的利好"传递"给地缘临近国家股市。(7) 从波动脉冲响应强度和累积脉冲响应规模分析, 在国际股市波动率联动网络中, 初始波动脉冲强度较大的国家股市, 往往是持续大量产生波动脉冲的国家。以上结论清晰的揭示出中国股市国际一体化进程中承担的角色和地位, 对于应对未来金融风险, 稳定全球经济增长, 重塑新型全球治理框架具有重要的借鉴价值和指导意义。
| [] | 陈守东、韩广哲、荆伟, 2003, 《主要股票市场指数与我国股票市场指数间的协整分析》, 《数量经济技术经济研究》, 第 5 期, 第 124–129 页。 |
| [] | 范奎、赵秀娟、汪寿阳, 2010, 《全球主要股市间信息溢出的变异性研究》, 《管理科学学报》, 第 9 期, 第 87–97 页。 |
| [] | 费兆奇, 2011, 《股票市场的国际一体化进程》, 《世界经济》, 第 8 期, 第 127–145 页。 |
| [] | 高莹、靳莹莹, 2008, 《沪深300指数与世界主要股票指数的关联性分析》, 《管理评论》, 第 2 期, 第 3–8 页。 |
| [] | 龚金国、史代敏, 2015, 《金融自由化、贸易强度与股市联动—来自中美市场的证据》, 《国际金融研究》, 第 6 期, 第 85–96 页。 |
| [] | 黄玮强、庄新田、姚爽, 2008, 《中国股票关联网络拓扑性质与聚类结构分析》, 《管理科学》, 第 3 期, 第 94–103 页。 |
| [] | 李岸、粟亚亚、乔海曙, 2016, 《中国股票市场国际联动性研究—基于网络分析方法》, 《数量经济技术经济研究》, 第 8 期, 第 113–127 页。 |
| [] | 李稻葵、梅松, 2009, 《美元M2紧缩诱发世界金融危机:金融危机的内外因论及其检验》, 《世界经济》, 第 4 期, 第 15–26 页。 |
| [] | 李广众、杨子晖、杨铠维, 2014, 《汇率波动性与股市收益率联动性—来自国际样本的经验证据》, 《金融研究》, 第 7 期, 第 16–31 页。 |
| [] | 李红权、洪永淼、汪寿阳, 2011, 《我国A股市场与美股、港股的互动关系研究:基于信息溢出视角》, 《经济研究》, 第 8 期, 第 15–25 页。 |
| [] | 李敬、陈澍、万广华、付陈梅, 2014, 《中国区域经济增长的空间关联及其解释—基于网络分析方法》, 《经济研究》, 第 11 期, 第 4–16 页。 DOI:10.3969/j.issn.1002-5863.2014.11.001 |
| [] | 梁琪、李政、郝项超, 2015, 《中国股票市场国际化研究:基于信息溢出的视角》, 《经济研究》, 第 4 期, 第 150–164 页。 |
| [] | 李涛、郭杰, 2009, 《风险态度与股票投资》, 《经济研究》, 第 2 期, 第 56–67 页。 |
| [] | 李晓广、张岩贵, 《"我国股票市场与国际市场的联动性研究—对次贷危机时期样本的分析》, 《国际金融研究》, 第 11 期, 第 75–80 页。 |
| [] | 游家兴、陈珍珍、郑挺国, 2010, 《经济一体化与证券市场联动性—基于相关经验数据的分析》, 《厦门大学学报(哲学社会科学版)》, 第 2 期, 第 21–28 页。 |
| [] | 俞世典、陈守东、黄立华, 2001, 《主要股票指数的联动分析》, 《统计研究》, 第 8 期, 第 42–46 页。 |
| [] | 杨子晖、赵永亮、柳建华, 2013, 《CPI与PPI传导机制的非线性研究:正向传导还是反向倒逼》, 《经济研究》, 第 3 期, 第 83–95 页。 |
| [] | 杨子晖、赵永亮, 2014, 《非线性Granger因果检验方法的检验功效及有限样本性质的模拟分析》, 《统计研究》, 第 5 期, 第 107–112 页。 |
| [] | 张兵、范致镇、李心丹, 2010, 《中美股票市场的联动性分析》, 《经济研究》, 第 11 期, 第 141–151 页。 |
| [] | 周璞、李自然, 2012, 《基于非线性Granger因果检验的中国大陆和世界其他主要股票市场之间的信息溢出》, 《系统工程理论与实践》, 第 3 期, 第 466–475 页。 DOI:10.12011/1000-6788(2012)3-466 |
| [] | Ancis , Julie R. and Marshall D.S., 2010, "Using a Multicultural Framework to Assess Supervisees' Perceptions of Culturally Competent Supervision". Journal of Counseling & Development, 88(3), 277–284. |
| [] | Bekiros , 2015, "Business cycle (de)synchronization in the aftermath of the global financial crisis: implications for the Euro area". Studies in Nonlinear Dynamics & Econometrics, 19(5), 609–624. |
| [] | Borgatti , Stephen P., 2009, "Network Analysis in the Social Sciences". Science, 323(5916), 892–895. DOI:10.1126/science.1165821 |
| [] | Broock W. A, Scheinkman J. A. and Dechert W. D., 1996, "A test for independence based on the correlation dimension". Econometric Reviews, 15(3), 197–235. DOI:10.1080/07474939608800353 |
| [] | Cheong , Siew Ann, 2012, "The Japanese Economy in Crises: A Time Series Segmentation Study". Ssrn Electronic Journal, 6(5), 1–81. |
| [] | Dellas , Harris and Hess M., 2002, "Financial development and stock returns: A cross-country analysis". Journal of International Money & Finance, 24(6), 891–912. |
| [] | Denker , Manfred and Keller G., 1983, "On U-statistics and v". mise' statistics for weakly dependent processes. Zeitschrift Für Wahrscheinlichkeitstheorie Und Verwandte Gebiete, 64(4), 505–522. DOI:10.1007/BF00534953 |
| [] | Diks , Cees and Panchenko V., 2006, "A new statistic and practical guidelines for nonparametric Granger causality testing". Journal of Economic Dynamics & Control, 30(9-10), 1647–1669. |
| [] | Flavin , Thomas J, Hurley M. J. and Rousseau F., 2002, "Explaining Stock Market Correlation: A Gravity Model Approach". The Manchester School, 70(S1), 87–106. DOI:10.1111/manc.2002.70.issue-S1 |
| [] | Forbes , Kristin J. and Chinn M.D., 2003, "A Decomposition of Global Linkages in Financial Markets over Time". Review of Economics & Statistics, 86(3), 705–722. |
| [] | Gilenko , Evgenii and Fedorova E., 2014, "Internal and external spillover effects for the BRIC countries: Multivariate GARCH-in-mean approach". Research in International Business & Finance, 31, 32–45. |
| [] | Jeon B. N., Furstenberg G. M. V., 1990, "Growing International Co-Movement in Stock Price Indexes". Quarterly Review of Economics & Business, 30(3), 15–30. |
| [] | Mantegna R N, 1999, "Hierarchical structure in financial markets". The European Physical Journal B, 11(1), 193–197. DOI:10.1007/s100510050929 |
| [] | Mensi , Walid , 2014, "Do global factors impact BRICS stock markets? A quantile regression approach". Emerging Markets Review, 19(2), 1–17. |
| [] | Tabak , Benjamin M., Serra T.R. and Cajueiro D.O., 2010, "Topological properties of stock market networks: The case of Brazil". Physica A Statistical Mechanics & Its Applications, 389(16), 3240–3249. |
| [] | Wälti , Sébastien , 2011, "Stock market synchronization and monetary integration". Journal of International Money & Finance, 30(1), 96–110. |



