工业革命以来,人类社会生产高速发展,人们的物质生活得到了极大提高。与此相伴的是,自然资源的加速耗竭和生态环境的极大破坏将人类自身置于“资源-环境”双重压迫的窘境。尤其近年来,这一形势愈发严峻, 并引发了世界各国对能源安全、环境问题和全球气候变化的高度关注。这也使得当前以应对气候变化为主要内涵的国际环境谈判不再只是单纯的环境事务,而是涉及到未来各国争取发展空间和选择发展道路的问题,关乎各国重大的政治和经济利益。为抢占未来全球经济发展的制高点,各国政府纷纷寻求绿色发展之路。如美国提出绿色新政,出台了《美国清洁能源和安全法案》;日本已制定“绿色发展战略”总体规划;欧盟发布“2020发展战略”,将绿色增长作为提高欧盟国家竞争力的核心战略。在可预见的未来,绿色经济将引导出一个全球的经济新格局。同时,近年来,全球一方面面临日趋严重的资源环境危机,另一方面还面临经济增长不断下行的压力。因此,资源节约、环境友好和经济增长共同成为全球绿色发展内涵和评判的重要方面。在此背景下,构建“自然资源-生态环境-经济增长”三维的绿色发展效率评价模型,基于全球视角呈现绿色发展格局,揭示其中的内在逻辑进而探讨绿色发展的可行路径具有重要的现实意义。
现有文献关于绿色发展的研究主要集中于绿色发展的衡量和绿色发展的影响因素两个方面。在绿色发展的衡量方面,已有测度方法主要分为两类,一类是借助专家赋权法构建绿色发展指数,如欧洲环境署(EEA)使用绿色经济指标考察欧洲各国绿色发展水平(2012);李晓西等(2011)建立三级指标体系并综合各级指标信息构建了绿色发展指数;苏利阳等(2013)围绕绿色生产构建了基于综合指数法的“工业绿色发展绩效指数”。专家赋权法容易受到主观因素的干扰,存在一定的局限性。另一类是效率法,利用数据包络分析(DEA)方法等测度绿色发展效率,强调刻画以更少的资源投入实现更高的经济产出,同时减少环境污染。如YorüB K and Zaim O(2005)利用Malmquist-Luenberger指数测算比较了OECD国家的绿色生产率;Watanabe M and Tanaka K(2007)运用方向距离函数测算了中国各省的工业绿色发展效率;王兵等(2014)运用环境范围调整测度模型(RAM)研究了中国112个环保重点城市的绿色发展效率的差异;钱争鸣、刘晓晨(2013)基于SBM模型测算了中国各省绿色发展效率。在绿色发展的影响因素方面,已有研究主要考察的是产业结构(Samuels et al., 1984;曾晓文、刘金山,2016)、能源结构(胡根华、秦嗣毅,2012)、经济发展水平(钱争鸣、刘晓晨,2013)、产业集聚(岳书敬等,2015)、外商直接投资(赵广川等,2015)、资源开发利用(于成学、葛仁东,2015)、金融发展(黄建欢等,2014)等经济因素以及一些常规的自然环境因素如地形地貌、气温等(杨红亮等,2009)。
综上所述不难发现,相关学者大多局限于局部地域间绿色发展效率的测算,而当前以变暖为特征的气候变化是一个全球性问题。此外,已有研究较少考虑可能与绿色发展紧密相关的生态承载力、海拔等因素。鉴于此,本文基于全球视角,借助重心转移模型考察全球经济、资本、能源和碳排放的流动格局。并基于三维非参数方法对世界各国和地区的绿色发展进行更加宏观的评估,同时将低海拔地区人口数以及生态承载力等地理和环境因素纳入到绿色发展的影响因素指标体系中,对全球绿色发展的演变历程、收敛趋势及影响因素展开更加全面的探讨。
二、 研究方法 (一) 重心转移模型新世纪以来,世界经济风起云涌,东西方力量平衡正在逐渐倾斜,为了宏观把握全球经济、资本、能源以及碳排放等绿色发展关键要素的流动格局,本文引入重心转移模型对其进行分析。该模型概念来源于物理学求质心或者重心的方法,假设某个大区域上各小区域的某种属性值(如人口数、能源消费量)以带质量的点存在,求出这些点的重心,则可以得到整个区域该属性值的重心(Kumler and Goodchild, 1992)。美国学者Hilgard(1872)最早将该模型用于研究美国的人口问题。如今,重心转移模型被广泛用于各个领域的地理分布研究中,如人口(段学军等,2008),环境污染(彭远新、林振山,2010;Wang et al., 2009),土地利用(Chen and Zhou, 2011),商品消费(Fu et al., 2011)),生态系统服务(He et al., 2011),以及食品供给(Wang et al., 2012)。一些研究学者还将重心转移模型用于能源消费时空差异性的研究中(汪应宏等,2006;Zhang et al., 2012)。
根据重心转移模型,第t年的全球经济、资本、能源以及碳排放重心位置(Xt,Yt)可以由下式求出:
| ${X^t} = \frac{{\sum\limits_{i = 1}^n {M_i^t \times {x_i}} }}{{\sum\limits_{i = 1}^n {M_i^t} }}$ | (1) |
| ${Y^t} = \frac{{\sum\limits_{i = 1}^n {M_i^t \times {y_i}} }}{{\sum\limits_{i = 1}^n {M_i^t} }}$ | (2) |
Mit表示i区域第t年某属性值(即经济、资本、能源以及碳排放),(xi, yi)表示i区域的坐标。考虑到数据的可得性,本部分统计了全球总计165个国家和地区的数据,各国坐标取其首都的经纬度,其中经度采用360度计数法,即记东经0°为0°,西经1°为359°。
(二) 效率评价模型本文沿袭林伯强、刘泓汛(2015)的思路,构建“自然资源-生态环境-经济增长”三维的绿色发展效率评价模型。假设有K个被评价地区,x, x-, y, b分别为自然资源投入、非自然资源投入、合意产出和非合意产出,分别有N, I, M, J种。则绿色发展效率的评价模型可以表示为:
| $\left\{ {\begin{array}{*{20}{l}} {D({x^{k\prime }},{x^{{ - ^{k\prime }}}}{y^{k\prime }},{b^{k\prime }};g|CRS) = {\rho ^{k\prime }}}\\ { = {\rm{max}}{{\rm{w}}_y}(\sum\limits_{m = 1}^M {\varpi _m^y} \alpha _m^{k\prime }) + {w_b}(\sum\limits_{j = 1}^J {\varpi _j^b} \beta _j^{k\prime }) + {w_x}(\sum\limits_{{\rm{n}} = 1}^N {\varpi _n^x} \gamma _n^{k\prime })}\\ {s.t.\sum\limits_{k = 1}^K {{z_k}{y_{mk}}} \ge {y_{mk\prime }} + \alpha _m^{k\prime }g_m^y,{\rm{ }}form = 1,...,M;}\\ {\sum\limits_{k = 1}^K {{z_k}{b_{jk}}} = {b_{jk\prime }} - b_j^{k\prime }g_j^b,{\rm{ }}forj = 1,...,J;}\\ {\sum\limits_{k = 1}^K {{z_k}{x_{nk}}} \le {x_{nk\prime }} - \gamma _n^{k\prime }g_n^x,{\rm{ }}forn = 1,...,N;}\\ {\sum\limits_{k = 1}^K {{z_k}{x_{\overline {ik} }}} \le {x_{\overline {ik\prime } }},{\rm{ }}fori = 1,...,I;}\\ {{w_y} + {w_b} + {w_x} = 1;\sum\limits_{m = 1}^M {\varpi _m^y} {\rm{ = }}1;\sum\limits_{j = 1}^J {\varpi _j^b} = 1;}\\ {\sum\limits_{{\rm{n}} = 1}^N {\varpi _n^x} = 1;{z_k} \ge 1,{\rm{ }}fork = 1,...,K} \end{array}} \right.$ | (3) |
其中,CRS表示规模报酬不变假定,g=(gx, gy, gb)为自然资源投入、合意产出和非合意产出的方向向量,w=(wx, wy, wb)为相应的指标权重,(α, β, γ)分别为自然资源投入、合意产出和非合意产出对应的无效率水平,zk为链接投入和产出向量以构成凸集的强度变量。方向向量设定为g=(x, y, b),同时选取各指标权重分别为
| ${\rm{GDE}} = \frac{1}{2}\left[ {\frac{{1 - {\alpha ^*}}}{{1 + {\beta ^*}}} + \frac{{1 - {\gamma ^*}}}{{1 + {\beta ^*}}}} \right]$ | (4) |
| ${\rm{RCE}} = \frac{{1 - {\alpha ^*}}}{{1 + {\beta ^*}}}$ | (5) |
| ${\rm{CERE}} = \frac{{1 - {\gamma ^*}}}{{1 + {\beta ^*}}}$ | (6) |
参考Li and Song(2016),Li and Lin(2016)对模型的处理,选取投入指标为劳动力、资本存量、能源消费总量,GDP为合意产出指标,CO2排放量为非合意产出指标。采用国际面板数据,样本的时间区间为2000-2014年,区域跨度为全球各国。为便于比较且考虑到数据的可得性,本文借鉴Klimont Z et al.(2013)的做法,将统计到的全球165个国家和地区划分为41个地区,具体划分见表 1。
| 表 1 国家和地区划分 |
(1) 资本存量。对于资本存量的估算,本文借鉴Hall and Jones(1999)的思路,采用“永续存盘法”来估计各地区年度资本存量。具体公式如下:
| ${K_{i,t}} = \frac{{{I_{i,t}}}}{{{p_{i,t}}}} + (1 - {\delta _{i,t}}){K_{i,t - 1}}$ | (7) |
其中,Ki, t为地区i第t年的资本存量;Ii, t为地区i第t年的投资;pi, t为投资品价格指数;δi, t为地区i第t年的固定资本形成总额的经济折旧率。本文以2000年为基期,并认为地区i第t年的不变价固定资本形成总额即为地区i第t年的投资Ii, t,pi, t为固定资产投资额平减指数。其中,基期资本存量的测算公式为:
| ${K_{i,0}} = \frac{{{I_{i,0}}}}{{{\delta _0} + {g_{i,r}}}}$ | (8) |
其中Ki, 0为地区i的基期资本存量;δ0为基期折旧率,Hall and Jones(1999)指定其为0.06,本文借鉴叶宗裕(2010)的方法,采用各国2000年折旧率的算术平均值(0.0404);gi, r为地区i的GDP年均增长率。其中,固定资本投资额数据来源于世界银行数据库(2000-2014),2000-2011年各国固定资产折旧率数据来源于佩恩表P.W.T 9.0。
(2) 劳动力和国内生产总值(GDP)数据来源于世界银行数据库,并以2000年为不变价;能源消费总量和二氧化碳排放量数据来源于《BP世界能源统计2015》,并折算成石油标准量;劳动力数据来源于世界银行的原始数据。
三、 实证结果分析本部分主要从三方面对全球绿色发展格局及其逻辑展开讨论。首先,通过对新世纪以来全球经济、资本、能源以及碳排放等绿色发展关键要素重心的测算与分析,从整体上把握全球绿色发展格局及变迁。然后通过测算绿色发展效率对各地区绿色发展水平进行量化,通过效率值的对比分析更加直观地呈现全球绿色发展格局。最后通过收敛性分析推测全球绿色发展格局的演化趋势。
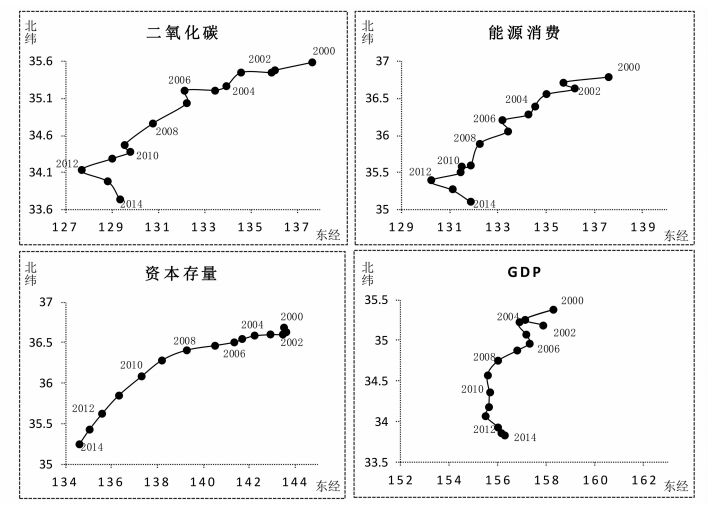
(一) 关键要素流动格局为清晰呈现全球经济、资本、能源以及碳排放的流动格局,本文首先使用重心转移模型对其进行整体把握。如图 1,整体来看,全球经济、资本、能源消费以及碳排放重心均位于东北半球,分布在127°E~159°E,33.5°N~37°N之间,具体位置为日本韩国一带,其中资本、能源消费与碳排放重心在日韩之间的日本海海域抉择移动,而经济重心则位于日本以东的太平洋。
|
图 1 2000-2014年资本、经济、能源消费以及碳排放重心的转移路径 |
各重心历年所处纬度高度一致,稳定在33°N至37°N之间,这主要是因为南北半球经济发展的差异所导致。但在2000年至2014年表现出向南迁移的趋势,这与南半球以及北半球低纬度国家的经济发展以及碳排放的相对增长有关。而从经度上看,2000-2011年全球经济、资本、能源消费以及碳排放重心整体上向亚洲内陆移动,表明随着中国、印度、东南亚等亚洲发展中国家/地区的崛起,东半球经济发展、能源消费以及碳排放等相对西半球有所增长;2012-2014年间,资本重心仍然继续向亚洲移动,而其它重心开始偏离原有轨道,表明随着经济发展阶段的转变,亚非地区新兴国家资本投入对提振本地区经济的边际效用有所下降。同时,新世纪以来,经济重心在东西方向上移动的幅度要明显小于资本、能源以及碳排放移动幅度,表明亚非地区新兴国家的崛起在带来经济增长的同时,更多的是导致本国能耗以及污染的增加。相对于欧美国家,亚非新兴国家尚处于粗放型发展阶段。
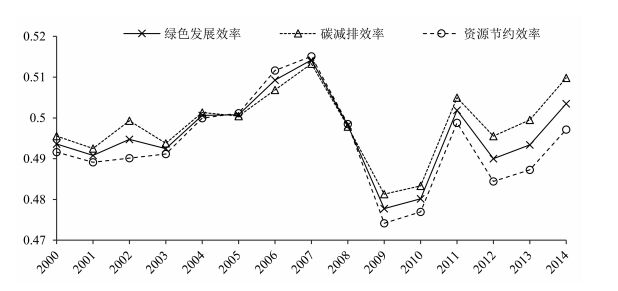
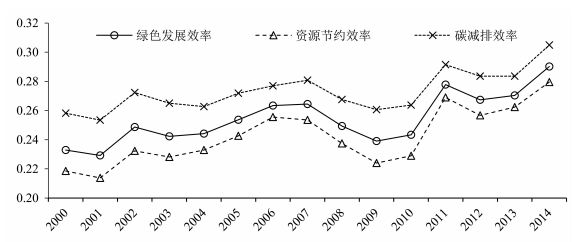
(二) 绿色发展现状分析整体层面如图 2所示,样本区间内,全球绿色发展效率、资源节约效率和碳减排效率均稳定在0.47-0.52之间,其中绝大部分年份,全球碳减排效率值要大于资源节约效率值,这表明全球范围来说实现绿色发展的主要路径是碳减排而不是资源节约。各指标增长趋势相似,2001-2007年稳步增长,2007-2009年急剧下跌,2010-2014年震荡回升。笔者分析认为,以2007、2008年为开端的金融危机极有可能对全球绿色发展产生了一定冲击,本文将在绿色发展的影响因素分析部分对此予以更进一步探讨。
|
图 2 2000-2014年全球绿色发展效率、资源节约效率与碳减排效率 |
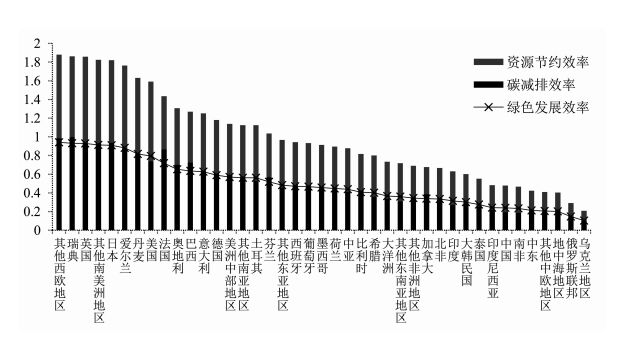
如图 3所示,各地区2000-2014年绿色发展效率、碳减排效率以及资源节约效率差异明显。绿色发展效率最高的前五个地区依次是其他西欧国家、英国、阿根廷、智利、日本,最低的五个国家或地区依次是中东、其他中欧国家、地中海地区、俄罗斯以及乌克兰地区。图 3中折线为碳减排效率以及资源节约效率的均值线(即绿色发展效率),通过均值线所处的位置,可以判断出资源节约效率与碳减排效率对绿色发展的贡献率。均值线明显位于碳减排效率值下方的国家有瑞典、法国、奥地利、巴西、芬兰、加拿大以及俄罗斯,反映出这些国家更加重视降低本国碳排放来实现其绿色发展。而均值线明显处于碳减排效率值上方的有美国、土耳其、希腊、印度、中国、南非以及其他东南亚地区,相比而言这些国家实现绿色发展的路径更加偏向于资源节约。
|
图 3 2000-2014年各地区绿色发展效率、资源节约效率与碳减排效率 |
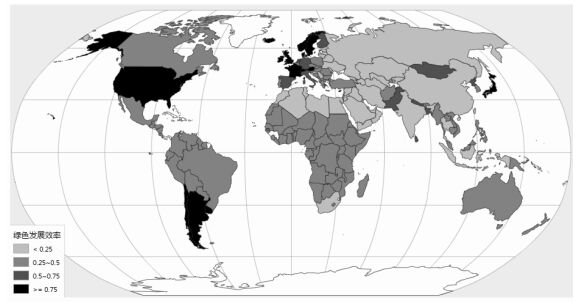
为更加清晰呈现当前全球绿色发展格局,本文绘制2014年全球绿色发展效率分布图,如图 4所示。整体来看,全球绿色发展水平非常不均衡,其中西半球绿色发展效率高于东半球,而且亚洲地区绿色发展效率要显著低于其他地区。具体国家层面,美国、日本、南美洲南部以及西欧绝大部分国家绿色发展效率大于0.75,已经抢占了绿色发展的制高点,而全球大部分地区绿色发展效率低于0.5,中国、俄罗斯、印度、中东以及中亚新兴国家绿色发展效率甚至低于0.25,绿色发展水平暂时落后①。
|
图 4 2014年全球绿色发展格局 |
① 结合公式(3) 和环境库兹涅茨曲线可根据未来发展趋势进一步将绿色发展水平落后的国家分为三类:第一类是处于工业化初期,人均GDP尚未跨过库兹涅茨曲线拐点的国家,随着人均GDP的增长,其绿色发展效率水平将可能进一步下降,如印度;第二类是人均GDP已经跨过库兹涅茨曲线拐点的国家,随着经济的继续增长,其绿色发展水平将会逐步提升,如中国;第三类是绿色发展水平较低,且经济停滞不前,绿色发展水平可能将持续维持低位,如中亚。
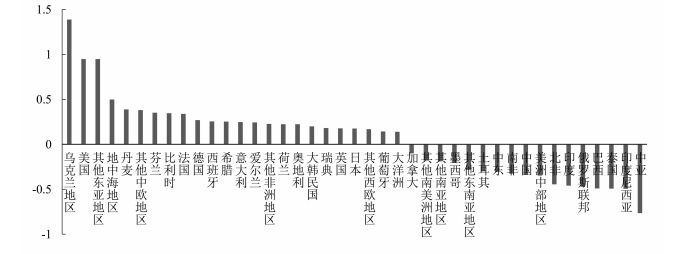
(三) 绿色发展变化趋势 1. 变化情况初步分析全球各国绿色发展效率变动情况如图 5所示。样本区间内,美国、日本、韩国以及欧洲等绝大多数发达地区绿色发展效率总体上升,表明发达国家在全球绿色发展道路上走在了前列。其它发展中国家如印度、巴西、泰国、印尼等绿色发展效率总体下降,表明当前大多数发展中国家逐步偏离绿色发展的轨道。这一现象与环境库兹涅茨曲线(EKC)基本吻合,本文将在影响因素分析部分作更进一步分析。同时,结合图 3可知,美国、丹麦、芬兰等绿色发展效率基数大的国家其增幅反而大于印度、俄罗斯等效率基数小的国家,因此全球绿色发展水平的差距可能将会进一步扩大,本文将在敛散性分析部分进行进一步探讨。
|
图 5 2000-2014年各地区绿色发展效率变化率 |
综合上述分析知,不同国家和地区绿色发展水平的差距有扩大趋势。为进一步探究各国绿色发展效率在时间维度上的离散趋势,本文利用σ进行收敛性检验(曾先峰,2008),具体表达式为:
| ${\sigma _t} = \sqrt {{N^{ - 1}}\sum _{m = 1}^N{{\left\{ {{R_m}\left( t \right) - \left[ {{N^{ - 1}}\sum _{k = 1}^N{R_k}\left( t \right)} \right]} \right\}}^2}} $ | (9) |
Rm(t)表示第m个地区在t时期的效率值;N表示全球41个地区。当σt+1<σt时,表示全球不同国家的效率呈现收敛状态,反之则呈现发散状态。
由图 6可知,整体来看,绿色发展效率、资源节约效率以及碳减排效率没有表现出足够明显的收敛或发散趋势。具体来说不同阶段收敛性有所不同,2000-2001年、2002-2003、2007-2009年以及2011-2012年这四个时期三种效率值均收敛,表明这些年份全球各国绿色发展效率、资源节约效率以及碳减排效率的差距相对于上一年有所缩小,而其他时期则表现为发散,呈现出收敛与发散反复交替的局面。
|
图 6 绿色发展效率、资源节约效率与碳减排效率σ收敛状态 |
鉴于α收敛趋势并不明显,本文对绿色发展效率、资源节约效率以及碳减排效率再进行绝对β收敛检验。借鉴Barro and Sala-i-Martin (1992)的方法并构造适合测度各效率收敛性的绝对β收敛模型如下:
| $\sqrt[t]{{\frac{{\theta _{it}^r}}{{\theta _{i0}^r}}}} = \beta {\rm{ln}}\theta _{i0}^r + \alpha _i^r + \varepsilon _{it}^r$ | (10) |
其中,θitr为i地区第t年的效率值,其中r=1, 2, 3分别表示绿色发展效率、资源节约效率、碳减排效率;θi0r为i地区初始年的效率值;αir为个体影响;εitr为随机误差项。若βr为负表示绝对β收敛,若βr为正则表示不存在β收敛。
本文采取41个国家和地区的面板数据估计,用Husman检验判断,应该采用面板数据固定效应模型,估计结果见表 2。
| 表 2 绿色发展效率、资源节约效率与碳减排效率绝对收敛结果表 |
由表 2可以看出,三种效率的系数β均显著为正,表明全球绿色发展效率、资源节约效率以及碳减排效率在2000-2014年呈现出发散趋势。因此三种效率值既不存在明显的σ收敛也不存在β收敛,即绿色发展水平更高的地区其增长幅度要大于绿色发展水平低的地区,世界各国绿色发展水平差距将会逐步扩大,若不寻求改变,全球绿色发展将越来越不均衡。
四、 绿色发展影响因素分析 (一) 变量说明参考相关研究并考虑数据可得性及本文研究的目的,本文选取绿色发展效率的影响因素如下:
结构因素,包括能源结构和产业结构,分别用非化石能源在能源消费中占比(Nen)和第二产业增加值在国内生产总值中的占比(Inr2) 来表示。马丽梅、张晓(2014) 运用空间计量方法对雾霾污染及其影响因素进行研究,发现污染水平与能源结构以及产业结构变动息息相关。因而从环境的视角看,绿色发展与能源和产业结构存在紧密联系。此外,胡根华、秦嗣毅(2012)在对金砖五国的能源效率研究中发现能源结构以及产业结构对能源效率影响明显,从能源效率方面佐证了绿色发展与能源和产业结构存在相关关系。
自然环境因素,包括生态环境承载力以及低海拔地区人口数,分别用森林面积占比(Forest)以及海拔低于5米常住人口占比(Lap)来表示。自然因素如气温、光照时间以及地形地貌对能源效率有一定程度的影响(杨红亮等,2009)。生态环境承载力决定一国环境污染的底线,而低海拔地区对过量碳排放造成的温室效应以及海平面上升更具危机感,一定程度上会影响其绿色发展的积极性。
其他控制变量,包括经济发展水平与能源价格,分别用人均GDP的自然对数(lnPGDP)以及市场综合油价(Oilp)来表示。环境库兹涅茨曲线(EKC)假说指出,环境质量会随着经济发展水平的提高而恶化,但当经济发展到一定水平后,环境质量会逐渐改善,即绿色发展与经济发展水平存在U型关系(Grossman and Krueger, 1991)。能源价格与经济增长负相关,且其影响具有滞后性(吴振信等,2011),另一方面,刘玲、丁浩(2010)发现,油价对碳减排潜力的影响因行业的不同而不同,对于整个能源系统而言其影响具有不确定性。因此能源价格是否会会影响绿色发展效率还有待本文进行验算。此外,为了探究2008年全球金融危机对各国绿色发展效率的影响(黄建欢等,2014),本文引入金融危机为虚拟变量。
(二) 模型构建与数据说明由于绿色发展效率、资源节约效率以及碳减排效率是介于0和1之间的双截尾数据,传统OLS、GLS和GMM得到的估计结果存在偏差。在此,本文采用Tobit模型以期得到更为精确的参数估计值。参考黄金波、周先波(2013)以及龚秀全(2016)对模型的处理,构建如下计量模型:
| $\left\{ {\begin{array}{*{20}{l}} {Lny_{i,t}^* = {\beta _0} + \sum\limits_{j = 1}^6 {{\beta _j}Lnx_{i,t}^j} + {\beta _7}Lnpric{e_{i,(t - 2)}} + \lambda Lncrisis + {\varepsilon _{i,t}}}\\ {{y_{i,t}} = y_{i,t}^*\;ify_{i,t}^* \in \left[ {{a_i},1} \right]}\\ {{y_{i,t}} = 0\;ify_{i,t}^* \in \left( { - \infty ,{a_i}} \right)}\\ {{y_{i,t}} = 1\;ify_{i,t}^* \in \left( {1, + \infty } \right)} \end{array}} \right.$ | (11) |
其中y是实际测算得到的效率值,i=1, 2, 3,分别表示绿色发展效率,资源节约效率,碳减排效率,y*是对应的隐藏变量,ai为样本区间内对应效率的最小值,其中a1=0.0633,a2=0.0660,a3=0.0606。εi, t为随机误差项,服从均值为0的正态分布。βj为各解释变量的回归系数,xj(j=1, 2, 3, 4, 5, 6) 代表前6个影响因素,pricei, (t-2)表示能源价格,考虑到能源价格变动对能源结构以及绿色发展效率的影响有滞后性,参考吴振信等(2011)的研究,本文选取滞后期为两期,crisis为虚拟变量金融危机。其中经济发展水平选取以2000年不变价计算的人均GDP并取其对数(lnPGDP),同时考虑其平方项来考察人均GDP对绿色发展的影响是否存在环境库兹涅茨曲线(EKC)。能源结构选取各国非化石能源消费占比(Nen)来衡量,数据来源于《BP世界能源统计2015》;产业结构以第二产业占比(Inr2) 来衡量;生态环境承载力选择各国森林面积占比(Forest)来衡量;低海拔地区居住人口选取海拔低于五米地区人口数(Lap)来衡量;市场油价水平选取各国柴油和汽油的市场综合油价(Oilp)来衡量,按照国际原油冶炼水平,一吨原油冶炼产生0.29吨汽油,0.49吨柴油的比例对市场油价进行加权平均。以上原始数据来源于世界银行数据库。虚拟变量金融危机(crisis)选取2007年及以前年度为0,2008年及以后为1。
(三) 计量结果分析表 3汇报了绿色发展效率的影响因素的检验结果。总体而言,主要解释变量与绿色发展效率、资源节约效率以及碳减排效率具有较显著的关系,且回归系数的符号符合预期。
| 表 3 Tobit回归结果表 |
(1) 结构因素中,绿色发展效率、资源节约效率以及碳减排效率与能源结构呈显著正相关关系,表明提高非化石能源在一次能源消费中的比重将有效促进绿色发展;与产业结构(Inr2) 相关系数为负但不显著,因此没有充分的证据说明全球工业具有“高能耗、高污染、高排放”的典型特征,笔者分析认为这可能与当前世界各国极不均衡的工业发展程度有关,如德国的工业4.0就是绿色低碳的典型,与此形成鲜明对比,中国的工业常常被贴上“污染”的标签。
(2) 地理环境因素中,森林面积占比与绿色发展效率、资源节约效率以及碳减排效率显著负相关,意味着生态环境承载力弱的国家,更加注重节能减排;海拔低于五米地区的居住人口数占比与绿色发展效率、碳减排效率存在显著的负相关,与资源节约效率则不存在显著关系,表明低海拔地区人口数占比高的国家或地区对绿色发展更加敏感,且其实现绿色发展的路径主要是通过降低碳排放而不是节约资源。究其原因可能是因为过量碳排放引起的温室效应以及海平面上升等对低海拔地区造成的威胁更加直接,其推行低碳发展的意愿也更加强烈。此发现能够较好的解释在相似的经济发展水平以及产业结构等条件下,沿海国家绿色发展效率与碳减排效率要高于内陆国家,如日本高于德国,英国显著高于法国等。
(3) 绿色发展效率、资源节约效率以及碳减排效率与经济发展水平(lnPGDP)呈“U”型关系,这与环境库兹涅茨曲线基本一致。其中,拐点依次为2430美元、2756美元以及2535美元(以2000年为不变价格)。2014年全球人均GDP(6456美元)高于这一水平,中国人均GDP(3481美元)也在近几年跨过这一拐点,全球41个地区仅有印度、非洲等8个地区尚处于“下坡”阶段,因此整体来说全球经济发展将有效提高绿色发展水平;三种效率与金融危机虚拟变量显著负相关,与滞后两年的市场油价显著正相关,表明金融危机对全球绿色发展产生了强烈冲击。而油价高涨会促进能源资源节约以及新能源与节能技术的开发,从而促进绿色发展。
五、 结论与启示本文测算了2000-2014年全球资本、经济、能源和碳排放几何重心的变化,以及绿色发展效率、资源节约效率与碳减排效率,并探讨了绿色发展格局的变化趋势及其内在逻辑。主要结论有:(1)2000-2014年全球二氧化碳、能源消费、GDP、资本存量的重心分布在127°E~159°E,33.5°N~37°N之间。其中,各指标重心在2000-2011年间整体向亚洲移动,2012-2014年经济、能源消费和碳排放重心开始偏离原有轨道。(2)2000-2014年全球绿色发展效率变化轨迹呈倒“S”状,欧美日韩等发达国家绿色发展效率逐年上升,而新兴国家则整体呈现出下降趋势,全球绿色发展效率呈发散趋势。(3) 绿色发展与能源结构、能源价格、低海拔地区居住人口占比正相关,与森林面积显著负相关,与经济发展水平呈“U”型关系,且当前的全球经济发展水平已经越过“U”型曲线拐点,金融危机对全球绿色发展影响显著。
以上结论蕴含的启示包含:(1) 经济、能源以及碳排放重心从原有轨道的偏离显示出亚非地区新兴国家近几年发展的疲软,而且资本投入带来的边际效用有所递减。新兴国家须摆脱投资驱动的增长模式,向更加节能环保的绿色发展方式转变。(2) 欧美发达国家与新兴国家绿色发展水平两极分化,欧美发达国家在绿色发展方面已经占得先机,相比而言新兴国家绿色发展水平滞后。然而,当前大部分新兴国家人均GDP已经跨过库兹涅茨曲线的拐点,未来有望成为全球绿色发展的引擎。(3) 气候变暖是一个全球性的问题,受到海平面上升威胁更小的国家同样也应该对绿色发展引起重视,积极主动承担节能减排的国际责任。同时生态承载力强的国家不宜过度依赖本国强大的生态环境而进行粗放式的发展,一旦本国生态失衡,将需要花费数倍的成本来弥补这一过失。
| [] | 段学军、王书国、陈雯, 2008, 《长江三角洲地区人口分布演化与偏移增长》, 《地理科学》, 第 2 期, 第 139–144 页。 |
| [] | 龚秀全, 2016, 《居住安排与社会支持对老年人医疗服务利用的影响研究——以上海为例》, 《南方经济》, 第 1 期, 第 11–27 页。 |
| [] | 胡根华、秦嗣毅, 2012, 《"金砖国家"全要素能源效率的比较研究——基于DEA-Tobit模型》, 《资源科学》, 第 3 期, 第 533–540 页。 |
| [] | 黄金波、周先波, 2013, 《中国粮食生产的非线性随机前沿面和技术效率研究》, 《南方经济》, 第 8 期, 第 18–30 页。 |
| [] | 黄建欢、吕海龙、王良健, 2014, 《金融发展影响区域绿色发展的机理——基于生态效率和空间计量的研究》, 《地理研究》, 第 3 期, 第 532–545 页。 DOI:10.11821/dlyj201403012 |
| [] | 李晓西、潘建成, 2011, 《中国绿色发展指数的编制——《2010中国绿色发展指数年度报告——省际比较》内容简述》, 《经济研究参考》, 第 2 期, 第 36–64 页。 |
| [] | 刘玲、丁浩, 2010, 《石油价格变动对碳减排潜力的影响分析——以电力和交通运输行业为例》, 《价格理论与实践》, 第 6 期, 第 50–51 页。 |
| [] | 林伯强、刘泓汛, 2015, 《对外贸易是否有利于提高能源环境效率——以中国工业行业为例》, 《经济研究》, 第 9 期, 第 127–141 页。 |
| [] | 马丽梅、张晓, 2014, 《中国雾霾污染的空间效应及经济、能源结构影响》, 《中国工业经济》, 第 4 期, 第 19–31 页。 |
| [] | 彭远新、林振山, 2010, 《能源消费产生的SO2和工业烟尘排放量时空演变分析》, 《自然资源学报》, 第 1 期, 第 52–59 页。 DOI:10.11849/zrzyxb.2010.01.006 |
| [] | 钱争鸣、刘晓晨, 2013, 《中国绿色经济效率的区域差异与影响因素分析》, 《中国人口·资源与环境》, 第 7 期, 第 104–109 页。 |
| [] | 苏利阳、郑红霞、王毅, 2013, 《中国省际工业绿色发展评估》, 《中国人口·资源与环境》, 第 8 期, 第 116–122 页。 |
| [] | 吴振信、薛冰、王书平, 2011, 《基于VAR模型的油价波动对我国经济影响分析》, 《中国管理科学》, 第 1 期, 第 21–28 页。 |
| [] | 王兵、唐文狮、吴延瑞, 2014, 《城镇化提高中国绿色发展效率了吗?》, 《经济评论》, 第 4 期, 第 38–49+107 页。 |
| [] | 汪应宏、郭达志、张海荣, 2006, 《我国煤炭资源势的空间分布及其应用》, 《自然资源学报》, 第 2 期, 第 225–230 页。 |
| [] | 杨红亮、史丹、肖洁, 2009, 《自然环境因素对能源效率的影响——中国各地区的理论节能潜力和实际节能潜力分析》, 《中国工业经济》, 第 4 期, 第 73–84 页。 |
| [] | 叶宗裕, 2010, 《中国省际资本存量估算》, 《统计研究》, 第 12 期, 第 65–71 页。 DOI:10.3969/j.issn.1002-4565.2010.12.011 |
| [] | 岳书敬、邹玉琳、胡姚雨, 2015, 《产业集聚对中国城市绿色发展效率的影响》, 《城市问题》, 第 10 期, 第 49–54 页。 |
| [] | 于成学、葛仁东, 2015, 《资源开发利用对地区绿色发展的影响研究——以辽宁省为例》, 《中国人口·资源与环境》, 第 6 期, 第 121–126 页。 |
| [] | 曾先锋、李国平, 2008, 《我国各地的农业生产率与收敛:1980-2005》, 《数量经济技术经济研究》, 第 5 期, 第 82–93 页。 |
| [] | 曾晓文、刘金山, 2016, 《广东产业生态化的发展战略与路径》, 《广东财经大学学报》, 第 5 期, 第 104–112 页。 |
| [] | 赵广川、郭俊峰、陈颖, 2015, 《我国FDI流入的经济效率分析——基于地级市动态面板数据模型》, 《南方经济》, 第 9 期, 第 41–51 页。 |
| [] | Barro , Robert T. and Xavier Sala-i-Martin , 1992, "Regional Growth and Migration:A Japan-United States Comparison". Journal of the Japanese and International Economies, 6(4), 312–346. DOI:10.1016/0889-1583(92)90002-L |
| [] | Grossman, Gene M. and Alan B. Krueger, 1991, "Environmental Impacts of a North American Free Trade Agreement", NBER Working Paper, No.3914. |
| [] | Fu , Juan , 2011, "The Movement Route of Consumption Gravity Center of Xinjiang from 1965 to 2009 Based on GIS". Procedia Earth and Planetary Science, 2, 321–326. DOI:10.1016/j.proeps.2011.09.050 |
| [] | He , Yingbin , 2011, "Exploring Spatial Change and Gravity Center Movement for Ecosystem Services Value Using a Spatially Explicit Ecosystem Services Value Index and Gravity Model". Environmental Monitoring and Assessment, 175(1-4), 563–571. DOI:10.1007/s10661-010-1551-z |
| [] | Hall , Robert E., Charles I. and Jones , 1999, "Why Do Some Countries Produce So Much More Output Per Worker than Others?". The Quarterly Journal of Economics, 114(1), 83–116. DOI:10.1162/003355399555954 |
| [] | Hilgard J.E, 1872, "The Advance of Population in the United States". Scribner's Monthly, 4(2), 214–218. |
| [] | Kumler, Mark P. and Michael F.Goodchild, 1992, "The Population Center of Canada-just North of Toronto", Geographical Snapshots of North America, Guilford, New York, 275-279. |
| [] | Klimont Z., Steven J., Smith and Janusz Cofala , 2013, "The Last Decade of Global Anthropogenic Sulfur Dioxide:2000-2011 Emissions". Environmental Research Letters, 8(1), 014003. DOI:10.1088/1748-9326/8/1/014003 |
| [] | Li , Ke and Malin Song , 2016, "Green Development Performance in China:A Metafrontier Non-Radial Approach". Sustainability, 8(3), 219. DOI:10.3390/su8030219 |
| [] | Li Jianglong, Boqiang Lin, 2016, "Green Economy Performance and Green Productivity Growth in China's Cities:Measures and Policy Implication". Sustainability, 8(9), 947. DOI:10.3390/su8090947 |
| [] | Martin, Jock et al., 2012, "Environmental Indicator Report 2012:Ecosystem Resilience and Resource Efficiency in A Green Economy in Europe", European Environment Agency. |
| [] | Samuels G., 1984, "Potential Production of Energy Cane for Fuel in the Caribbean". Energy Prog (United States), 4(4). |
| [] | Yörük , Barıs K. and Osman Zaim , 2005, "Productivity Growth in OECD Countries:A Comparison with Malmquist Indices". Journal of Comparative Economics, 33(2), 401–420. DOI:10.1016/j.jce.2005.03.011 |
| [] | Watanabe , Michio and Katsuya Tanaka , 2007, "Efficiency Analysis of Chinese Industry:A Directional Distance Function Approach". Energy Policy, 35(12), 6323–6331. DOI:10.1016/j.enpol.2007.07.013 |
| [] | Wang Q.Q., 2009, "Movement of the Gravity of Carbon Emissions Per capita and Analysis of Causes". Journal of Natural Resources, 24(5), 833–841. |
| [] | Wang Q., 2012, "Spatial-temporal Variations of Food Provision in China". Procedia Environmental Sciences, 13, 1933–1945. DOI:10.1016/j.proenv.2012.01.187 |
| [] | Xiaolin, Chen and Zhou Fei, 2011, "Gravity Center Change in the Coastal Area of the Pearl River Estuary Based on GIS and RS", International Conference on Information and Management Engineering, Springer Berlin Heidelberg:281-286. |
| [] | Zhang , Yan , 2012, "Analysis of the Distribution and Evolution of Energy Supply and Demand Centers of Gravity in China". Energy Policy, 49, 695–706. DOI:10.1016/j.enpol.2012.07.012 |