中国债券市场经过近20年的改革与发展,市场化程度不断得到深化。2015年债券市场全年发行各类债券规模达22.3万亿元,较去年同期增长87.5%,增速上升55.2个百分点参见央行发布的《2015年金融市场运行情况》报告。。同时利率管制机制在利率价格形成中的作用逐步消退,国债利率已被研究者认为基准利率,其价格形成受宏观经济环境及货币政策调整的影响。供给与需求的波动、货币政策冲击、国内外经济金融事件等因素都会使国债利率期限结构发生变化或平移。研究认为,中国宏观基本面显著影响国债收益率曲线及期限结构特征 (尚玉皇等,2015),收益率曲线与宏观变量之间存在双向互动关系 (吴吉林等,2010)。
利率期限结构金融模型是基于无套利条件下不可观测因子 (潜因子) 的VAR结构,虽然拟合效果好,能够刻画利率动态演化轨迹,但模型无法提供驱动利率变动的因子的宏观经济含义,也无法反映宏观冲击和货币政策冲击对收益的影响 (Duffie et al., 1996;Dai et al., 2000)。为了研究宏观经济与利率期限结构的关系,Ang and Piazzesi (2003)在不可观测因子向量中增加宏观因子构建了宏观-金融模型的开山之作,但模型中宏观因子外生给定,不受宏观结构约束,这类模型也称为内基宏观金融模型。实证研究中为了减少估计难度和复杂性,对模型参数施加的约束条件往往没有经济学理论支持,随意性较强。
为了进一步明确模型的经济含义,学者们构建了结构型宏观金融模型,也称为外基模型。因子向量可以全部为宏观经济变量,也可包含不可观测变量,因子动态采用基于新凯恩斯理论的动态一般均衡框架,从效用最大化的消费理论推导利率因子或随机折现因子 (定价核) 的运动形式,因而具有很强的微观理论基础,实证中用结构VAR进行估计和检验。模型一方面可以反映央行适时调整短期利率的行为,解释收益曲线的短期部分,另一方面,在金融无套利假设下,短期利率和长期利率是一致的,长期利率是经风险调整的未来短期利率预期,因而模型中投资者对宏观经济变量的预期值能够很好地解释收益曲线的中长期部分。内生的结构化因子解释了宏观经济对利率预期、风险溢价波动及期限结构变化等的影响,同时利用宏观经济信息进一步提高了收益率曲线的预测能力,因而广泛获得国内外学者青睐。Hördahl et al.(2006)最早用结构型宏观金融模型研究德国债券市场,得出预测效果要优于一般仿射类模型。Rudebusch et al. (2008)估计了美国国债市场,发现潜因子有重要的宏观和货币政策含义。Bekaert et al.(2010)构建的结构型宏观金融模型对美国历史收益率数据有很强的拟合能力,收益率曲线和三个潜在因子与宏观经济变量 (通货膨胀率和实际产出) 都高度相关。
近年来一些学者基于动态随机一般均衡模型 (DSGE) 导出期限结构,将前瞻型新凯恩斯模型与最大化效用导出的随机折现因子结合起来,使随机折现因子与总需求方程一致,通过高阶逼近得到时变风险溢价 (Rudebusch et al., 2008;Hördahl et al., 2007;Jules et al., 2012)。鉴于DSGE模型的开放性和灵活性,可以嵌入更多的经济结构和偏好,将无套利条件下的宏观金融利率期限结构模型与动态随机一般均衡模型有机结合,可以更深层次地挖掘利率期限结构的微观形成机理、货币政策规则的微观作用机制及风险溢价的微观生成来源。由于DSGE模型最终体现为差分方程组,一般不能给出解析解,需要数值逼近,因而模型求解有很大难度,这方面研究成果相对较少。结构型宏观金融模型是目前研究宏观经济、货币政策与利率期限结构、风险溢价关系的主流框架。
宏观经济和国债利率期限结构存在相互影响已是不争的事实,但我国宏观经济因素对利率期限结构影响并不稳定 (丁志国等,2014)。当宏观变量、货币政策或者投资者的宏观经济预期发生结构性变化时,国债利率期限结构可能会随之而变。研究表明,我国宏观经济和金融总量近20年来表现出明显的区间转换和非线性特征,为分段趋势平稳 (王琨等,2012;梁琪、滕建州,2006)。通货膨胀率序列和人民币名义汇率在此期间也具有明显的结构转变特征 (刘金全等,2006;项后军等,2011)。货币政策在从紧、适度从紧、适度宽松、稳健之间数次相机抉择。在此背景下,我国国债利率期限结构是否受影响发生显著的结构性间断,这对于经济计量建模来说是非常重要的问题。如果对短期、中长期的不同期限的利率方程分别进行结构突变检验,发现它们均在同一个时间点显著拒绝稳定性假设,则说明我国利率期限结构在此时出现了结构性变化。
我国由于利率市场化时间较晚, 目前对利率期限结构的研究仍然有限,多数学者使用金融模型研究国债市场,少数学者在金融模型中加入宏观信息,但均把样本期作为一个整体研究,并未考虑利率期限结构在样本期内是否发生了结构变化。如孙皓、石柱鲜 (2011),袁靖、薛伟 (2012)通过构建结构型宏观金融模型,研究货币政策与国债利率期限结构及风险溢价的关系。曾耿明、牛霖琳 (2013),周生宝等 (2015)基于内基宏观金融模型将利率期限结构分解为实际利率与通胀预期,分析实际利率与通胀预期的动态特征。刘澜飚等 (2014)基于动态随机一般均衡模型研究我国宏观经济对国债利率期限结构的影响。以上研究均未考虑模型稳定性,而忽视模型结构的稳定性将直接影响宏观经济决策的准确性,并进而影响宏观经济系统平稳运行和政策效果。
进一步考虑如果国债利率期限结构发生了显著突变,那么促发间断的主导因素是什么?股票、汇率、银行等金融子市场的改革对债券市场带来哪些变化,这些变化与债券间断有什么关联,相关研究结论关系到如何制定和实施政策制度以稳定债券价格、减少金融市场波动,所以研究具有理论价值和现实意义。目前国内外类似相关研究是从区制转移角度分析经济周期性变化与利率期限结构变化的关系。如Kang (2010),Zhu (2011),Kaya (2013)分别用区制转移模型考察了美国、日本和土耳其的货币政策对国债利率期限结构变化的影响。我国也有学者试图使用与经济周期或利率政策相关的区制转移序列捕捉利率变化动态,如潘敏等 (2012)对外生的货币政策代理变量和Nelson-Siegel模型估计出的水平和斜率因子建立了马尔科夫区制转移向量自回归模型,研究不同货币政策周期对国债利率期限结构的影响。虽然利率区制转移模型也刻画了结构性变化,反映了影响因素与利率的非线性关系,但本文除了关注检验结构突变点外,还分析各个因素对结构突变的影响程度以及结构变化的主导动因,因而本文研究主旨与区制转移模型文献不同。
综上所述,虽然我国已有学者针对银行间同业拆解市场利率在不同区制下运动特征进行了研究 (孙皓等,2012;刘金全、郑挺国,2006;王志强、熊海芳,2012),但对国债市场利率结构性变化或非线性特征鲜有相关研究,建立的利率期限结构模型均未进行结构稳定性检验,也较少考虑宏观经济结构变化对资产价格变化的影响。针对以上问题,本文首先基于未知间断点的结构突变方法实证检验中国国债利率期限结构在2002年到2015间是否发生了结构突变;其次对间断前后两组子样本分别构建结构型宏观金融模型,因子动态方程由新凯恩斯一般均衡理论推导,内生化宏观变量和货币政策规则,从经济金融联合视角刻画国债利率形成机制;最后定量计算两组宏观金融模型参数的变化对结构突变的影响程度,解释结构突变的宏观动因。模型采用极大似然法估计,为了避免陷入局部最优和初值选择带来的繁重工作量,我们采用自适应遗传算法进行最优化计算。研究发现2005年金融市场发生的利率市场化、股权分置改革、权证上市交易、浮动制汇率改革、商业银行上市等重大事件对债券市场造成联动效应,显著影响了债券定价的风险价格水平和收益率结构特征。这将为管理利率风险,稳定债券市场提供实证经验和理论依据。
二、 利率期限结构的结构突变检验 (一) 长期利率回归方程Campbell and Shiller (1991)为了检验预期假设理论,提出了长期利率回归方程,用长期利率的变化对长短期利差做回归。本文通过检验此方程斜率回归系数在不同样本期是否显著不同,来推断利率期限结构是否发生了结构突变,检验方程为:
| $ {i_{m - 1, t + 1}} - {i_{m, t}} = {\alpha _m} + {\beta _m}({i_{m, t}} - {i_{1, t}})/\left({m - 1} \right) + {\varepsilon _{m, t}} $ | (1) |
折现债券的长期收益率可以分解为未来短期收益率的均值和风险溢价项,在理性预期下由于短期利率预期不可预测,所以εm, t设为白噪音。若斜率回归系数βm显著偏离1,则拒绝预期假设理论,说明风险溢价存在且时变。同时βm也是结构变化的指示器,若前后两组样本的回归系数βm存在显著差异,则证明利率期限结构不稳定,发生了结构突变。
(二) 结构突变检验结构间断有多种检验方法,Chow检验需要先验设定断点时间;Quandt-Andrews扩展了Chow方法对未知断点进行检验,Andrews (1993)给出此方法中3个统计量的真实分布;CUSUM和CUSUM平方检验是对均值和方差稳定性检验;Bai和Perron (2003)提出的BP方法可以检验多重未知结构变点。本文首先选取2002年1月至2015年12月中国银行间国债市场10个交易品种的收益率数据估计方程 (1),10种国债的剩余期限分别为3、6、12、24、36、48、60、84、120、180个月①,接着用Quandt-Andrews方法检验斜率系数βm,得到最大似然比统计量 (Maximum LR F-statistic) 的时间点,然后用chow检验方法对每种利率在Maximum LR F-statistic时间点做间断性检验。
① 数据为中国银行间零息国债的名义即期利率月平均值,采自Wind数据库。
表 1列出了Quandt-Andrews和chow结构突变检验结果,Quandt-Andrews检验出有7种利率 (12、24、36、48、60、84、120个月) 的最大似然比统计量时间点均为2005年11月,其余3种利率 (3、6、180个月) 分别为2004年9月、2007年11月和2004年12月。Chow检验结果为3、6个月利率在10%显著水平下也不能拒绝在其最大似然比统计量时点无间断原假设,12、24、36、48、60、84个月利率均能在5%水平下拒绝2005年11月时无间断原假设,120个月利率在10%的显著水平下拒绝。而180个月利率在其最大似然比统计量时间点以10%的显著水平拒绝原假设,但在2005年11月时未能拒绝原假设 (p值为0.3130)。所以10个单方程线性回归检验结果为:在2005年11月时,在5%显著水平下3、6、120、180个月利率不能拒绝无结构间断的原假设,而其余6种利率均拒绝原假设。
| 表 1 结构性间断检验和长期利率方程斜率回归系数 |
为了进一步考察2005年11月前后两段时期回归斜率系数βm的差异,把样本分成子样本A (2002.01-2005.11) 和子样本B (2005.12-2015.12),分别估计10种利率在整样本和两个子样本的斜率回归系数。表 1下半部分显示了10种利率的斜率回归系数βm在3个样本中一致为负,且随着期限的增长稳步降低。但同时也直观地显示出两组样本的差异,子样本A中的斜率系数明显小于子样本B对应值,说明A区间的斜率系数偏离1更远。A区间的系数标准误至少为B区间对应值的2倍,说明A区间利率波动更大。方括号中的p值说明,在5%显著水平下,整样本中10种利率都拒绝理性预期假设,A样本中期限低于36个月的利率不能拒绝预期假设,其余中长期拒绝,而B样本中的120、180个月长期利率不能拒绝预期假设,其余短中期显著拒绝。表 1反映出的两组子样本斜率回归系数的差异,一定程度上辅证了利率期限结构在2005年11月出现结构突变。
如表 1所示上述单方程回归标准误偏大,这在一定程度上影响了估计和推断结果的准确性。由于不同期限利率运动特征都能被状态因子所捕捉,所以不同期限回归方程的误差项具有相关性,可以用似不相关回归技术 (SUR) 估计。利用误差项相关信息估计后的标准误要比单方程估计时小,因而推断结果会更可信。本文接下来对在5%显著性下不能拒绝原假设的4种利率分两组进行似不相关回归,再一次检验斜率系数变化的显著性具体检验方法为:添加虚拟变量与虚拟变量系数,把两项乘积加到回归方程斜率系数中,设A样本虚拟变量值为0,B样本虚拟变量值为1,联合检验三个虚拟变量系数同时为0的概率。。3、6、180个月的SUR回归方程为:
| $ \left[ {\begin{array}{*{20}{c}} {{i_{2, t + 1}} - {i_{3, t}}}\\ {{i_{5, t + 1}} - {i_{6, t}}}\\ {{i_{179, t + 1}} - {i_{180, t}}} \end{array}} \right] = \left[ \begin{array}{l} {\alpha _3}\\ {\alpha _6}\\ {\alpha _{180}} \end{array} \right] + \left[ {\begin{array}{*{20}{c}} {{\beta _3}}&0&0\\ 0&{{\beta _6}}&0\\ 0&0&{{\beta _{180}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {({i_{3, t}} - {i_{1, }}_t)/2}\\ {({i_{6, t}} - {i_{1, }}_t)/5}\\ {({i_{180, t}} - {i_{1, }}_t)/179} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\varepsilon _{3, t}}}\\ {{\varepsilon _{6, t}}}\\ {{\varepsilon _{180, t}}} \end{array}} \right] $ | (2) |
表 2显示了此组SUR回归结果,两组子样本的斜率回归系数值差异仍然很大,但标准误比表 1小,说明此次估计结果更有效、推断结果更可信。联合检验三个方程斜率系数无变化的P值为0.0491,说明在5%显著水平下3、6、180个月利率联合拒绝了无间断原假设。第二组3、120、180个月SUR回归后联合检验P值为0.0468,同样显著拒绝原假设。单方程和SUR回归检验结果推断得出,中国国债利率期限结构在5%水平上显著拒绝2005年11月无结构间断原假设。
| 表 2 SUR回归斜率系数和联合检验p值 |
2005年是中国金融改革年,5月证监会启动“股权分置改革”,7月阔别9年的权证重返股市,汇率改革为浮动制,9月商业银行被授予除定期和活期存款外的6种存款利息的定价权,这是利率市场化进程中迈出的重要一步,10月建行上市,四家国有商业银行开始走向国际资本市场。这些改革事件的叠加集聚使整个社会的资源配置效率得到提升,投资市场环境更加成熟,价格发现和风险规避功能进一步完善。
随之债券市场产生联动效应,一方面,利率和汇率的市场化、商业银行开放上市等促进了资本融通,加快了债券市场流动性,同时使债券价格更多地受市场供求关系影响,政策波动因素影响减弱;另一方面,股改、权证上市交易等增强了企业信息披露,使投资理念更加理性,风险对冲和抵御能力增强,两方面影响可能会引起债券市场风险水平发生变化。本文第四节实证部分对间断前后两组子样本建立无套利宏观金融模型,发现2005年后,与货币政策相关的斜率因子风险价格减小,投资者对货币政策波动的风险补偿要求降低,验证了我们的推断。实证还得出斜率因子风险价格减小是突变的关键动因。因而2005年多起金融改革事件的积聚发酵显著影响了债券市场的风险价格,致使利率期限结构于11月发生结构性变化。
三、 结构型宏观金融模型本文参考Rudebusch et al.(2008)的研究利用泰勒规则把新凯恩斯动态一般均衡模型和仿射无套利期限结构模型结合起来,驱动利率变动的因子具有了宏观经济含义,反映了宏观经济环境、货币政策对利率期限结构的影响。本节首先定义金融仿射无套利利率期限结构模型,接着定义新凯恩斯宏观均衡模型,之后通过对期限结构中短期利率的变化把宏观结构嵌入金融模型中,构建出利率期限结构的宏观金融模型。
(一) 仿射无套利期限结构模型根据资产定价第一基本定理,如果一个金融市场中存在风险中性测度,就不存在套利机会。Duffie and Kan (1996)和Dai and Singleton (2000)等一些研究者认为,收益曲线的主要变动都可以在无套利框架下得到刻画,所以从风险中性定价出发可以推导出无套利利率模型。基本思想为首先在风险中性世界定义状态因子随机扩散过程,债券价格是状态因子和期限的函数,之后根据伊藤引理得到债券价格的随机过程,此时资产的平均收益率等于无风险利率,进而得到风险中性世界里债券价格的偏微分方程。借助特定的拉东-尼克迪姆导数过程,通过哥萨诺夫定理把风险中性世界里的布朗运动转换到真实世界里,就得到了真实测度下的状态因子及债券价格的偏微分方程,此时债券平均收益率等于无风险利率加上风险价格与波动率的乘积。为了使债券价格为状态因子的仿射函数形式,定义状态因子的漂移项、波动率和短期利率 (无风险利率) 均为状态因子的仿射函数。离散时间模型为:
定义n个因子的状态向量Ft为高斯VAR (1) 过程:
| $ {F_t} = \mu + \rho {F_{t - 1}} + \Sigma {\varepsilon _t} $ | (3) |
设ρ为下三角矩阵,Σ为对角矩阵,εt服从独立正态分布N (0, In)。
定义短期利率it (无风险利率) 为常量和状态因子的线性函数:
| $ {i_t} = {\delta _0} + \delta {^\prime _1}{F_t} $ | (4) |
定义风险价格Λt为常量和状态因子的线性函数:
| $ {\Lambda _t} = {\lambda _0} + {\lambda _1}{F_t} $ | (5) |
定义J期零息债券的对数价格ln (bJ, t) 是状态因子的仿射函数:
| $ {\rm{ln}}({b_{J, t}}) = {A_J} + B{^\prime _J}{F_t} $ | (6) |
通过对债券价格的偏微分方程进行迭代求解可得到:
| $ \begin{array}{l} {A_1} = - {\delta _0};{B_1} = - {\delta _1}\\ {A_{j + 1}} = {A_j} + B{^\prime _j}(u - \Sigma {\lambda _0}) + \frac{1}{2}B{^\prime _j}\Sigma \Sigma ^\prime {B_j} + {A_1}\\ {B_{j + 1}} = B{^\prime _j}(\rho - \Sigma {\lambda _1}) + {B_1}, j = 1, 2, ..., J \end{array} $ | (7) |
则J期零息债券的连续复利名义收益率iJ, t为:
| $ {i_{J, t}} = - {\rm{ln}}({b_{J, t}})/J = - \frac{{{A_J}}}{J} - \frac{{B{^\prime _J}}}{J}{F_t} $ | (8) |
新凯恩斯宏观均衡模型由总供给、总需求和货币政策方程组成,是宏观分析的主流框架。
总供给AS方程 (菲利普斯曲线):
| $ {\pi _t} = {\alpha _\pi } + {\mu _\pi }{E_t}{\pi _{t + 1}} + (1 - {\mu _\pi }){\pi _{t - 1}} + {\alpha _y}{y_t} + {\varepsilon _{\pi, t}} $ | (9) |
πt为通胀率,yt为产出缺口或工业设备利用率。方程 (9) 表示通胀率由通胀预期、通胀滞后值、产出缺口及外生的供给冲击决定。(1-μπ) 刻画了通胀的内生持久性,αy反映通胀和产出之间的调整成本。
总需求IS方程:本文从消费者效用最大化框架推出跨期欧拉方程,采用与Fuhrer (2000)相似的外部习性形式,产出由产出预期、产出滞后值、真实利率及需求冲击决定。
| $ {y_t} = {\alpha _y} + {\mu _y}{E_t}{y_{t + 1}} + (1 - {\mu _y}){y_{t - 1}} - {\beta _r}({i_t} - {E_t}{\pi _{t + 1}}) + {\varepsilon _{y, t}} $ | (10) |
货币政策规则:学者们通常用泰勒规则或其扩展式研究央行货币政策行为,基准泰勒规则为:
| $ {i_t} = {r^*} + {\pi ^*}_t + {g_y}{y_t} + {g_\pi }({\pi _t} - {\pi ^*}_t) + {\varepsilon _{s, t}} $ | (11) |
r*为均衡真实利率,在短期内变动不大,一般设为常数。πt*为央行设定的通胀目标,εs, t为外生的货币政策冲击。r*+πt*代表了利率的长期水平,所以短期利率等于长期水平加上货币当局对通胀与通胀目标偏离和产出与均衡自然产出偏离时的利率调整。
(三) 宏观金融模型本文用泰勒规则把宏观和金融两种视角下的短期利率统一起来,进而为期限结构的潜在因子提供宏观经济含义,将新凯恩斯动态一般均衡框架纳入利率期限结构模型中。
定义状态向量Ft=(Ltm, Stm)'满足方程 (3),短期利率it设为常量和标准化单位因子的和:
| $ {i_t} = {\delta _0} + \delta {^\prime _1}{F_t} = {\delta _0} + L_{_t}^{^m} + S_{_t}^{^m} $ | (12) |
(11) 式和 (12) 式分别从宏观和金融两种视角下定义短期利率。Ang、Piazzesi (2003)和Dewachter、Lyrio (2006)实证说明了这两种定义形式有很强的关联。考虑到 (11)、(12) 式两种视角下短期利率的对应关系,本文模型只选择了“水平”和“斜率”两个因子,经过主成分分析这两个因子已经能捕捉样本收益率曲线95.3%的变化。
(12) 式中的Ltm通常表示收益率曲线分解出的水平因子,可以捕获名义利率的长期水平值,所以Ltm是 (11) 式中r*+πt*的一个很好近似;Stm通常代表收益率曲线分解出的斜率因子,可以反映 (11) 式中货币当局对政策目标偏离时所做的调整反应。此外Bekaert et al. (2010)研究也发现“水平因子”的变化主要由通胀目标冲击解释,“斜率与曲率因子”的变化主要由货币政策冲击解释。
所以本文设Ltm为πt*的近似值,即为代理人感知的央行货币政策通胀目标,代理人经过对信息加工学习后,其感知的通胀与央行设定的通胀目标存在差异。姚余栋、谭海鸣 (2011)把中国国债无套利期限结构模型分解出的水平因子和储户、朗润通胀预期指数及通胀数据进行对比研究,得出水平因子能够代表我国金融市场投资者对通胀的预期。这一结论也为本文水平因子经济含义的设定提供了实证支持。Dewachter and Lyrio (2006),Hordahl et al.(2006)的宏观金融模型也做相同设定。考虑到当通胀变化时代理人会逐步修正Ltm,所以Ltm设定为其滞后值和通胀率的加权平均:
| $ L_{_t}^{^m} = {\rho _L}L_{_{t - 1}}^{^m} + (1 - {\rho _L}){\pi _t} + {\varepsilon _{L, t}} $ | (13) |
设定了Ltm为πt*的近似值,则可以用Stm因子刻画 (11) 式中央行对通胀偏离和产出偏离后的动态反应。鉴于货币政策制定的复杂性,央行需要权衡多方面因素,可能会对通胀和产出以外的其它相关事件做出反应,因而斜率因子Stm设定为:
| $ S_{_t}^{^m} = {\rho _s}S_{_{t - 1}}^{^m} + (1 - {\rho _s})({g_y}{y_t} + {g_\pi }({\pi _t} - L_{_t}^{^m})) + {u_{s, t}} $ | (14) |
| $ {u_{s, t}} = {\rho _u}{u_{s, t - 1}} + {\varepsilon _{s, t}} $ | (15) |
ρs表示货币政策自身惯性 (利率平滑性),us, t表示除通胀和产出以外其它序列相关冲击,εs, t为货币政策冲击。ρs和ρu反映出货币政策连续性的两种不同来源,如果ρs等于0,则说明央行对通胀和产出以外其它相关事件冲击存在持续性反应;如果ρu等于0,则说明央行对其它事件不反应,政策的连续性源于利率惯性。单独估计泰勒规则方程时由于需要区分当期和滞后期回归元的影响,很难识别Stm的两种不同动态方式,但宏观金融模型中包含的利率期限结构的大量信息,有助于准确设置货币政策规则。
(13)-(15) 定义了潜因子的宏观经济含义,接着定义其中的宏观变量。由于工资合约、调整成本等因素使得价格存在刚性,所以宏观模型中变量通常为季度或年度频率。本文为了与利率数据月度频率一致,宏观变量也采用月度频率数据,这样就需要为总供给AS方程 (9)、总需求IS方程 (10) 增加更多期的滞后项,并把短期预期改为中长期预期。把 (9)、(10) 式中的通胀预期项用Ltm代替,并增加通胀和产出的滞后项得到 (16)、(17) 式:
| $ {\pi _t} = {\mu _\pi }L_{_t}^{^m} + (1 - {\mu _\pi })({\alpha _{\pi 1}}{\pi _{t - 1}} + {\alpha _{\pi 2}}{\pi _{t - 2}}) + {\alpha _y}{y_{t - 1}} + {\varepsilon _{\pi, t}} $ | (16) |
| $ {y_t} = {\mu _y}{E_t}{y_{t + 1}} + (1 - {\mu _y})({\beta _{y1}}{y_{t - 1}} + {\beta _{y2}}{y_{t - 2}}) - {\beta _r}({i_{t - 1}} - L_{_{t - 1}}^{^m}) + {\varepsilon _{y, t}} $ | (17) |
本文构建的结构型宏观金融模型的状态因子包括潜因子、产出缺口和通胀率,状态转移方程动态由方程组 (13)-(17) 刻画,其中επ, t, εy, t, εL, t和εS, t相互独立且服从正态分布,短期利率为 (12) 式。为了降低估计难度,我们把风险价格设为常量、Ltm和Stm的仿射函数。虽然如此设置风险价格不会受πt, yt的直接影响,但由于επ,t和εy,t会影响Ltm, Stm,所以风险价格仍然会受到πt和yt的间接影响。债券名义收益率由 (6)-(8) 式求解。
四、 实证分析 (一) 样本数据本文选取2002年1月至2015年12月中国银行间零息国债6种即期收益率月平均值估计宏观金融模型。对于无风险利率,国外多数学者使用3月期国债或3月期TIPS债券利率。鉴于我国并未发行类似TIPS等通胀保值债券,发行的最短期国债为3个月,但考虑到我国通胀水平高于西方国家,为使短期利率不含通胀风险溢价,本文选取剩余期限1个月的即期利率作为无风险利率,其余5种为半年、1年、3年、5年、10年期即期利率,数据采自wind数据库。参照kaya (2013)方法,对我国季度GDP数据用三次样条法得到月度数据,经季节调整后用HP滤波计算出潜在产出,产出缺口为GDP月度数据相对潜在产出的缺口百分比。同比通胀率为我国居民消费价格指数当月值与去年同期值的对数差。宏观数据来自中经网。
(二) 模型估计设定状态因子向量:Xt=[πt πt-1 yt yt-1 Lt St uS, t Etyt+1]′,设ηt=yt-Et-1yt,则由方程组 (13)-(17) 定义的因子动态为①:
① 限于篇幅原因,本文没有具体显示 (18) 式中Γ0, Γ1, ψ, Π矩阵,可参考Rudebusch et al.(2008)。
| $ {\Gamma _0}{X_t} = {\Gamma _1}{X_{t - 1}} + \Psi {\varepsilon _t} + \Pi {\eta _t} $ | (18) |
采用Sims (2001)提出的线性理性预期模型求解方法,将 (18) 式由结构VAR化为简约式VAR模型:
| $ {X_t} = \Gamma {X_{t - 1}} + \Omega {\varepsilon _t} $ | (19) |
由于Et-1yt可由状态向量Xt中的其它因子表示,去掉Et-1yt得状态向量Ft=[πt πt-1 yt yt-1 Lt St uS, t]′,动态方程为:
| $ {F_t} = \rho {F_{t - 1}} + \Sigma {\varepsilon _t} $ | (20) |
其中ρ为 (19) 式中Γ的左上7×7矩阵,Σ是Ω的左上7×4矩阵。
为了估计潜因子Ltm, Stm, u,本文参照Ang and Piazzesi (2003)的方法,设1、12、60个月收益率数据为观测无误差,6, 36, 120个月收益率数据观测有误差,这样潜因子就可用无误差收益率表示出来。设观测向量Zt=[πt yt r6 r36 r120]满足方程Zt=ΓzFt-1+Ωzξt,则Zt的对数似然函数为:
| $ \begin{array}{l} LF = \sum\limits_{t = 2}^T {{\rm{ln}}} {f_{{z_t}|zt - 1}}, \ldots {z_1}({z_t}|{z_{t - 1}}, \ldots {z_1};\theta)\\ = \sum\limits_{t = 2}^T {(- \frac{1}{2}{\rm{ln}}\left({2\pi } \right)} - \frac{1}{2}{\rm{ln}}({\rm{det}}({\Omega ^z}{\Omega ^z}^\prime)) - \frac{1}{2}{({Z_t} - {\Gamma ^z}{F_{t - 1}})^\prime }\\ {({\Omega ^z}{\Omega ^z}^\prime)^{ - 1}}({Z_t} - {\Gamma ^z}{F_{t - 1}})) \end{array} $ |
本文采用极大似然法估计,该法通常采用无约束多维极值最优化算法对似然函数求极值,估计过程经常会遇到以下两个问题:无约束多维极值算法是局部最优算法,所以估计结果很可能不是全局最优;拟合过程需要大量尝试参数初值,一种生成参数初值的方法是设参数在一定区间内服从某种分布,由Sobol伪随机数列生成初始点序列;另一种方法是把每个参数区间划分为多个子区间,所有参数的子区间进行不同组合生成参数初值向量。无论用哪种方法设置初值,当参数较多时,计算量都很大。本文模型似然函数形式复杂,曲面极值点不唯一,且模型参数多达23个,为了避免陷入局部最优和初值选择带来的繁重工作量,我们采用最优化计算中的自适应遗传算法对似然函数求极值。自适应性使得当种群趋于局部最优或分布分散时,交叉概率和变异概率随适应度自动改变,同时也能实现个体的“优胜劣汰”,所以自适应遗传算法较易收敛到全局最优,且不需要设置模型参数初值。考虑到本文似然函数的复杂度和参数个数,我们设置500个初始种群,最大进化代数为1000,杂交概率k1、k2设为0.5和0.9,变异概率k3、k4设为0.02和0.05,离散精度取0.01。本文用MATLAB编程构建模型和估计参数。
(三) 估计结果依据结构突变的检验结果,我们把样本划分为子样本A (2002.01-2005.11) 和子样本B (2005.12-2015.12)。分别对两组样本构建结构型宏观金融模型,参数估计值如表 3所示,标准误用Fisher信息矩阵计算。
| 表 3 两组子样本的宏观金融模型参数估计值 |
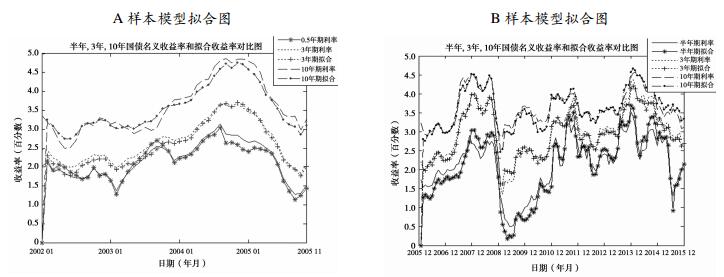
图 1给出了两组样本的6、36、120个月名义收益率和拟合收益率曲线图,左图为样本A,右图为样本B,在估计过程中这3种利率被设为有观测误差,其余3种设为无观测误差。拟合结果显示两组样本拟合收益率的平均绝对误差小于0.05,均方误差小于0.01,表明本文模型能够较好地刻画我国宏观经济和国债利率期限结构运动形态。
|
图 1 两组样本的名义收益率曲线和拟合收益率曲线 |
表 3显示两组样本估计结果有共同之处。对于因子动态,水平因子ρL在两组样本中均接近1,说明我国债券市场主观感知的通胀预期有很强的惯性;ρS的值都达到0.9以上,即我国利率有很强的平滑倾向;两组ρu值虽然显著,但相对较小,说明我国央行对产出和通胀以外其它相关信息反应很小,货币政策持续性主要源于利率惯性;(1-ρs) 与gπ, gy相乘后得到货币政策反应系数,两组样本中估计值均在5%水平上显著,A组对通胀偏离和产出缺口的反应系数为0.2346和0.2539,B组对应值为0.222和0.1974;各个因子的波动率均显著。关于通胀动态,两组μπ都不显著,表明代理人的预期通胀目标对我国当前通胀率几乎不具有影响;απ1在两组样本中均显著且估计值分别为1.1247和1.1401,说明通胀率滞后一期值对我国当期通胀率具有显著的主要影响;两组αy均显著且为正,说明通货膨胀率与产出缺口之间呈正相关关系,产出缺口的增大 (减小) 将引起通货膨胀率的上升 (下降)。对于产出动态,两组μy均显著,值为0.5510和0.5242,产出一期滞后值系数为0.4113和0.4277,表明产出缺口的预期值和滞后项对当前产出缺口均有影响,且影响程度相当;两组βr为正但较小,说明真实利率与产出缺口之间呈负相关关系,真实利率增大 (减小) 会引起产出缺口减小 (增大)。最后两组样本的风险价格系数都显著不为0,同样表明我国国债利率期限结构不满足理性预期假说,投资者对交易中存在的风险要求有相应的风险补偿,这与第二节用长期利率回归方程检验的结果一致。
两组样本参数估计值也存在差异。关于因子动态,A中的ρS小于B中的,反映了间断前利率持续性低于间断后;A时期货币政策对通胀和产出缺口的反应系数均大于B,且A中产出缺口反应系数略大于通胀反应系数,而B中情况相反,差异表明间断前央行对产出的变化更敏感,货币政策更偏向提高产能,而间断后央行希望更好地保持物价平稳;B组ρu大于A组,说明间断后央行对通胀和产出以外其它相关事件的反应增强。关于因子波动率的差异,A组的水平因子波动率略大于B组近3个基点,反映出间断后主观通胀预期的波动性略有下降;A中斜率因子波动率σS高出B组近8个基点,间断前货币政策波动性更强;A组的通胀率和产出缺口波动率均略小于B组。关于风险价格两组样本也有明显差异,A中λ0、λ1比B中对应值大,特别是A中的λSS比B中对应值大0.0121,反映出我国期限溢价及其波动性随着时间变小了,早期投资者对利率风险更敏感。
以上实证结果可进一步解释我国货币政策发展进程。事实上,为了应对亚洲金融危机和国内通货紧缩,央行从1998年开始采取“努力发挥作用的适度宽松”货币政策,实施了多次大幅政策调整,使得货币政策惯性相对较低、波动率较大,主观通胀预期波动率也较大;且此阶段以提高国内生产总值为主要目标,货币当局对产出的反应大于对通胀的反应,对产出和通胀以外其它事件的反应也很小。经过数年一系列多方面的协同改革发展,我国货币政策操作规范逐渐由“相机抉择”向“规则型”转变,货币政策目标由货币供应量、社会融资总规模等数量型目标逐渐向长短期利率等价格型目标转换,因而B样本期水平因子波动率减小,斜率因子持续性增强、波动率减小,反映出2005年后我国主观通胀预期波动率减小,货币政策更加持续、平稳;且此时国内社会投资明显加快,经济活力充沛,实施7年的积极财政政策和稳健货币政策转为稳健财政政策和从紧货币政策,通胀水平和波动水平相较前期有所增大,央行增强了对通胀的反应,并且由于国内外经济形势更加复杂多变,此阶段央行也加强了对通胀和产出以外其它事件的反应。
(四) 结构突变的动因分析长期利率回归方程 (1) 中斜率回归系数βm的显著变化表明我国国债利率出现结构突变,那么βm的变化主要由哪些因素引起,各个因素的影响程度以及谁是关键动因正是本节研究内容。根据回归方程最小二乘估计原理,结合债券定价公式 (6)-(8),我们推导出βm与利率期限结构模型参数的关系为:
| $ \begin{align} & {{\beta }_{m}}\equiv \frac{\text{cov}[({{i}_{m-1,t+1}}-{{i}_{m,t}}),({{i}_{m,t}}-{{i}_{1,t}})/\left( m-1 \right)]}{\text{var}[({{i}_{m,t}}-{{i}_{1,t}})/\left( m-1 \right)]} \\ & =\frac{\text{cov}[({{B}^{\prime }}_{m-1}{{F}_{t+1}}-{{B}^{\prime }}_{m}{{F}_{t}}),({{B}^{\prime }}_{m}{{F}_{t}}-{{B}^{\prime }}_{1}{{F}_{t}})]}{\text{var}[{{B}^{\prime }}_{m}{{F}_{t}}-{{B}^{\prime }}_{1}{{F}_{t}}]}\left( m-1 \right) \\ & =\frac{({{B}^{\prime }}_{m-1}\rho -{{B}^{\prime }}_{m})\Omega {{({{B}^{\prime }}_{m}-{{B}^{\prime }}_{1})}^{\prime }}}{({{B}^{\prime }}_{m}-{{B}^{\prime }}_{1})\Omega {{({{B}^{\prime }}_{m}-{{B}^{\prime }}_{1})}^{\prime }}}\left( m-1 \right) \\ \end{align} $ | (21) |
(21) 式中βm由债券定价模型参数导出,其中Bm′是 (6) 式中债券对数价格仿射函数的系数,是债券价格的因子负载,由ρ, Σ, λ1矩阵决定;Ω为因子的方差协方差矩阵,由ρ, Σ矩阵决定,所以βm的变化与ρ, Σ, λ1三个矩阵相关。
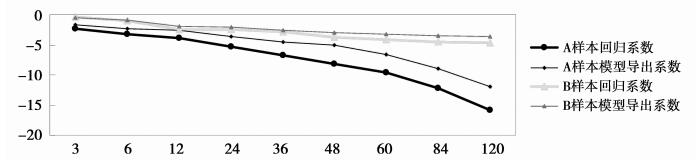
图 2描绘出两组样本中βm的模型统计值和回归估计值。粗线为公式 (21) 计算出的模型统计值,细实线为方程 (1) 中斜率系数回归估计值。结果显示样本A的2条斜率系数曲线均比样本B低,这是因为如表 1所示,A样本的各个期限利率斜率系数βm都小于B中对应值。A、B两组样本中,βm的模型统计值均随着期限的增加快速下降,且与相应的回归估计值都非常接近,所以 (21) 式计算的模型统计值可以充分反映 (1) 式回归估计值的变化动态。
|
图 2 两组样本βm的模型统计值与回归估计值对比图 |
公式 (21) 揭示了斜率系数βm的决定因素为ρ, Σ, λ1中的参数。定量计算每个参数对βm变化的影响程度,可以解释导致两组样本利率动态显著差异的关键因素。具体计算过程如下:把样本A中与βm有关的参数依次改为样本B中相应值,通过计算βm的变化大小来比较每个参数的影响程度。选择期限为120个月的国债利率作为分析对象,由于βm是m的单调递减函数,所以结论也适用于其它期限国债①。
①图 2显示出随着期限的增长,公式 (21) 计算出的βm模型统计值单调递减。
βm是模型参数的非线性函数,为了考察某个参数的影响效果,需要控制其它参数。本文主要考察与β120相关的13个关键参数,当计算某个参数的变化对斜率系数β120的影响时,其它12个参数将有212种组合,如果分别计算β120的变化值和参数贡献度后求均值计算量太大。所以本文将13个参数分为3组:因子自回归系数参数、因子波动率参数、风险价格参数,对8种取值分别计算后取均值,表 4显示模型参数改变对β120的平均影响和平均贡献度。
| 表 4 模型参数的改变对β120的平均影响和平均贡献度 |
当我们把样本A中3组参数同时替换为样本B中对应值后,β120上升了8.321,这再一次验证了两组样本中β120发生了显著性变化。表 4显示13个参数影响程度不一,其中产生较大影响的是ρS, λSL, λSS, σS。斜率因子系数ρS从样本A中值变化为样本B时引起β120较大幅度地下降了2.064,平均贡献度为-25.1;而水平因子的波动率σL和斜率因子的波动率σS的变动对β120的影响方向相反,分别下降0.739和上升1.951,平均贡献度为-8.9和23.4;通胀波动率σπ和产出波动率σy的影响作用微弱;风险价格系数的改变导致β120大幅上升,尤其是与斜率因子有关的风险价格系数λSL, λSS的变化对β120发挥了决定性作用,为β120的上升提供了27.5和75.1的平均贡献度;为了检验A样本较小的通胀反应系数对结构间断是否也有影响,本文把gπ减小一半计算其影响度,但只是使β120降低-0.028,影响非常有限。对比表 4贡献度可以看到,参数λSS对β120的上升起到了关键决定性作用,是我国国债利率期限结构发生结构突变的关键动因。
表 4定量计算结果表明由于样本A中斜率因子的风险价格系数比样本B中对应值大,所以当给定因子波动率水平时,会生成更加波动的时变风险溢价,同时样本A中更大的斜率因子波动率一定程度上又增强了这种效果,这两个因素叠加起来使得A样本期对预期假说的偏离更大。但A中斜率因子自回归系数ρS比B小,对预期假设的偏离产生了反向拉动作用,部分程度地抵消了以上两因素的影响,这三种因素的综合影响使得A样本的利率斜率系数βm显著不同于B,样本发生了结构性间断。这表明与货币政策相关的风险补偿变化和货币政策稳定性变化是我国利率期限结构发生变化的主要影响因素,其中与货币政策相联系的斜率因子风险价格的减小是我国国债利率期限结构发生结构突变的关键动因。
事实上,我国银行间债券市场于1999年9月才开始实施招标发行,所以A样本期间债券市场定价机制还不够完善,市场交易品种有限,二级市场交易贫乏,利率风险抵御和风险对冲能力较弱,风险价格高。且此期间央行推行多项改革,货币政策波动大 (更大的σS)。在这样的背景下,央行货币政策波动对国债市场的影响很大,投资者对货币政策波动要求更多的风险补偿 (较大的λSS),所以2006年前我国国债市场偏离预期假说的程度较大。2005年以后,金融市场利率风险防范措施和货币政策波动率都发生了较大的转变。随着利率市场化程度加深,债券价格越来越受市场供求关系的影响,货币政策等政策性因素的影响逐步减弱。股改、汇改、权证上市交易等重大改革事件极大地促进了我国资本市场的价格发现功能的实现,丰富了投资者利率风险管理意识和风险控制工具,市场风险价格开始降低。且B样本期间货币政策波动降低 (更小的σS),市场预期比前期稳定。因而2005年后投资者减少了对货币政策波动的风险补偿要求 (较小的λSS),导致国债利率市场偏离预期假说的程度锐减,利率期限结构发生显著性结构变化。
五、 结论本文实证检验得出我国国债利率期限结构在近15年并不稳定,发生了结构性变化。为了刻画宏观经济对国债收益率的影响,分析导致结构突变的原因,本文构建了因子为新凯恩斯一般均衡结构的宏观金融模型,潜在因子具有了丰富的宏观经济含义。其中“水平”因子解释为投资人预期的通胀目标,“斜率”因子解释为央行货币政策行为。此外在泰勒规则中增加了除通胀和产出以外的其它序列相关事件,借助利率期限结构刻画和识别出导致货币政策持续的两种不同来源:利率自身惯性和央行应对其它相关事件连续冲击的反应。单独估计泰勒规则由于信息缺乏无法准确识别。实证研究结果发现:
第一、通过对10种不同期限的利率回归方程做Quandt-Andrews和Chow检验,以及对拒绝突变假设的两组利率进一步做似不相关回归后联合检验回归斜率系数,得出在5%显著水平下我国国债利率期限结构于2005年11月发生结构变化,间断前后两组子样本的斜率系数发生了显著性变化;回归方程检验结果也说明,预期假说理论在我国国债市场并不成立。间断前利率的斜率回归系数小,并且斜率因子风险价格显著大于间断后,这两个结果一致表明间断前利率期限结构对预期假设的偏离程度显著大于间断后。
第二、两组子样本的宏观金融模型估计结果表明,我国债券市场主观通胀预期有很强的惯性;利率自身具有很强的平滑倾向,央行对除产出和通胀以外其它相关冲击反应较小,货币政策持续性主要源于利率自身惯性;我国通胀率几乎不受主观通胀预期的影响,通胀滞后值是其主要影响因素。两组子样本也呈现出显著差异。间断前斜率因子的自回归系数小,反映出间断后利率持续性增强,水平因子和斜率因子的波动率大,反映出前期通胀预期和货币政策波动大;间断后斜率因子的波动率及风险价格随着时间下降了,斜率因子的动态演变反映出2005年后央行希望更好地控制物价,并且加大了对通胀和产出以外其它相关事件冲击的反应。
第三、通过定量计算两组子样本宏观金融模型参数值的变化对结构间断的影响,得出λSS和σs的变化是导致结构性突变的主要因素,其中斜率因子风险价格λSS的减小是关键动因。斜率因子在模型中与央行货币政策相关,间断前由于投资者对风险抵御能力较低,货币政策波动大,对货币政策的波动更敏感,表现出对货币政策波动风险要求更多的补偿 (较大的λSS),利率偏离预期假设程度大。随着利率市场化进程的推进以及股改、汇改、权证重返股市、银行全面开放等革新使投资者的投资理念随之更加丰富和理性,开始将价值投资与风险控制结合起来,积极利用推出的金融工具对冲利率风险。因而2005后,投资者利率风险管理能力增强,且此时货币政策波动率也减小,从而降低了与货币政策波动相关的风险溢价 (较小的λSS)。减小的风险溢价使国债利率市场偏离预期假说的程度锐减,利率期限结构发生显著性结构变化。
因而从实证分析结果可以得出稳定利率期限结构的关键是降低债券市场的风险水平,尤其是货币政策波动生成的风险溢价。相关建议为:(1) 货币当局应保持货币政策稳定性,以降低因政策波动而引起的投资者对未来预期不确定性所要求的风险补偿; (2) 继续深化利率市场化改革,使国债收益率曲线更好地反映市场资金供求关系,减小政策性波动对价格的冲击与影响; (3) 从2005年一系列金融改革事件对债券市场风险价格的影响可以得出,有效管理利率风险对稳定期限结构非常重要。因而本文建议建立一个以管理利率风险为核心的,以利率期货、期权为主的、更健全和多元的利率衍生品市场,为市场参与者提供更多对冲利率风险的工具,这对稳定我国债券市场价格,促进金融市场繁荣稳定发展具有重要意义。
| [] | 丁志国、徐德财、李雯宁, 2015, 《宏观经济因素影响利率期限结构的稳定性判别》, 《数量经济技术经济研究》, 第 9 期, 第 55–75 页。 |
| [] | 梁琪、滕建州, 2006, 《中国宏观经济和金融总量结构变化及因果关系研究》, 《经济研究》, 第 1 期, 第 11–22 页。 |
| [] | 刘金全、金春雨、郑挺国, 2006, 《我国通货膨胀率动态波动路径的结构性转变特征与统计检验》, 《中国管理科学》, 第 2 期, 第 1–8 页。 |
| [] | 刘金全、郑挺国, 2006, 《利率期限结构的马尔科夫区制转移模型与实证分析》, 《经济研究》, 第 11 期, 第 81–89 页。 DOI:10.3969/j.issn.1002-9605.2006.11.031 |
| [] | 刘澜飚、沈鑫、王博, 2014, 《中国宏观经济对国债利率期限结构的影响研究》, 《金融研究》, 第 11 期, 第 49–64 页。 DOI:10.3969/j.issn.1006-169X.2014.11.012 |
| [] | 潘敏、夏庆、张华华, 2012, 《货币政策周期与国债利率期限结构》, 《财贸研究》, 第 1 期, 第 1–10 页。 |
| [] | 尚玉皇、郑挺国、夏凯, 2015, 《宏观因子与利率期限结构:基于混频Nelson-Siegel模型》, 《金融研究》, 第 6 期, 第 14–30 页。 |
| [] | 孙皓、石柱鲜、俞来雷, 2012, 《中国利率期限结构的非线性动态研究》, 《管理科学》, 第 2 期, 第 57–75 页。 |
| [] | 孙皓、石柱鲜, 2011, 《中国的货币政策与利率期限结构:基于宏观—金融模型的研究途径》, 《经济科学》, 第 4 期, 第 49–60 页。 |
| [] | 吴吉林、金一清、张二华, 2010, 《潜在变量、宏观变量与动态利率期限结构—基于DRA模型的实证分析》, 《经济评论》, 第 1 期, 第 34–45 页。 |
| [] | 王琨、滕建州、石凯, 2012, 《中国宏观经济和金融总量的非线性研究》, 《财经科学》, 第 6 期, 第 34–45 页。 |
| [] | 王志强、熊海芳, 2012, 《结构变点、时变期限溢价与预期假说—来自国内银行同业拆借利率的证据》, 《数量经济技术经济研究》, 第 5 期, 第 104–120 页。 |
| [] | 项后军、孟祥飞、潘锡泉, 2011, 《开放框架下的中国货币需求函数稳定性问题研究—基于结构突变的视角》, 《经济评论》, 第 5 期, 第 47–56 页。 |
| [] | 姚余栋、谭海鸣, 2011, 《中国金融市场通胀预期—基于利率期限结构的度量》, 《金融研究》, 第 6 期, 第 61–71 页。 |
| [] | 袁靖、薛伟, 2012, 《中国利率期限结构与货币政策联合建模的实证研究》, 《统计研究》, 第 2 期, 第 42–49 页。 |
| [] | 曾耿明、牛霖琳, 2013, 《中国实际利率与通胀预期的期限结构—基于无套利宏观金融模型的研究》, 《金融研究》, 第 2 期, 第 24–40 页。 |
| [] | 周生宝、王雪标、郭俊芳, 2015, 《我国国债市场的通胀预期研究—基于宏观金融仿射无套利期限结构模型》, 《数理统计与管理》, 第 4 期, 第 67–80 页。 |
| [] | Ang A., Piazzesi M., 2003, "A No-Arbitrage Vector Autoregression of Term Structure Dynamics with Macroeconomic and Latent Variables". Journal of Monetary Economics, 50(4), 745–787. DOI:10.1016/S0304-3932(03)00032-1 |
| [] | Bekaert G., Cho S. and Moreno A., 2010, "New Keynesian Macroeconomics and the Term Structure". Journal of Money, Credit and Banking, 42(1), 33–62. DOI:10.1111/jmcb.2010.42.issue-1 |
| [] | Clarida R., Gali J. and Gertler M., 2000, "Monetary Policy Rules and Macroeconomic Stability: Evidence and some Theory". Quarterly Journal of Economics, 115(1), 147–180. DOI:10.1162/qjec.2000.115.issue-1 |
| [] | Dai Q., Singleton K. and Yang W., 2007, "Regime shifts in a Dynamic Term Structure Model of US Treasury Bond Yields". Review of Financial Studies, 20(5), 1669–1706. DOI:10.1093/rfs/hhm021 |
| [] | Dai Q., Singleton K., 2000, "Specification Analysis of Affine Term Structure Models". Journal of finance, 55(5), 1943–1978. DOI:10.1111/0022-1082.00278 |
| [] | Dewachter H., Lyrio M., 2006, "Macro Factors and the Term Structure of Interest Rates". Journal of Money, Credit, and Banking, 38(1), 119–140. DOI:10.1353/mcb.2006.0014 |
| [] | Duffie D., Kan R., 1996, "A Yield-factor Model of Interest Rates". Mathematical Finance, 6(4), 379–406. DOI:10.1111/mafi.1996.6.issue-4 |
| [] | Gürkaynak R., Sack B. and Swanson E., 2005, "The Sensitivity of Long-term Interest Rates to Economic News: Evidence and Implications for Macroeconomic Models". American Economic Review, 95(1), 425–436. DOI:10.1257/0002828053828446 |
| [] | Hördahl p., Tristani o. and Vestin D., 2006, "A Joint Econometric Model of Macroeconomic and Term Structure Dynamics". Journal of Econometrics, 131(2), 405–444. |
| [] | Hördahl P., Tristani O., 2012, "Inflation Risk Premia in the Term Structure of Interest Rates". Journal of the European Economic Association, 10(3), 634–657. DOI:10.1111/j.1542-4774.2012.01067.x |
| [] | Jules H., Jesús F., Ralph S. and Juan R., 2012, "The Term Structure of Interest Rates in a DSGE Model with Recursive Preferences". Journal of Monetary Economics, 59(7), 634–648. DOI:10.1016/j.jmoneco.2012.09.002 |
| [] | Kang K.H., 2010, "Essays on Macro-Finance Asset Pricing Models and Estimation", published by Washington University press. |
| [] | Kaya H., 2013, "The Yield Curve and the Macro-economy Evidence from Turkey". Economic Modeling, 32(5), 100–127. |
| [] | Rudebusch G., Wu T., 2008, "A Macro-finance Model of the Term Structure Monetary Policy and the Economy". The Economic Journal, 118(530), 906–926. DOI:10.1111/ecoj.2008.118.issue-530 |
| [] | Rudebusch G., Swanson E., 2008, "Examining the Bond Premium Puzzle with a DSGE Model". Journal of Monetary Economics, 55(8), 111–126. |
| [] | Sims C.A., 2002, "Solving Linear Rational Expectations Models". Computational economics, 20(2), 1–20. |
| [] | Zhu X.N., 2011, "Revisiting the Expectations Hypothesis:The Japanese Term Structure and Regime shifts". Journal of Economics and Business, 63(3), 237–249. DOI:10.1016/j.jeconbus.2011.01.001 |



