消费不足和投资过度等特征暴露了我国经济持续平稳发展的顽疾。它们的存在意味着经济发展成果分配存在扭曲,经济跛足前行的危险性在不断增加。诚然,它们的形成并非一蹴而就,自上个世纪90年代以来,大体经历了三个阶段 (如图 1所示①):第一阶段,1996-2000年,消费产出比相对稳定维持在46.5%的均值,而投资产出比不断下降,并维持在35.6%的均值;期间,我国于1996年3月将基础设施建设和发展重工业作为战略计划,并于1997年9月开始私有化改革 (Chang et al., 2015),各级政府也相继推出鼓励投资的政策。第二阶段,2001-2007年,消费产出比在逐渐下降,而投资产出比却在不断上升:2000-2004上升速度较快,2004-2007年波动上升;期间,我国于2001年加入了WTO,2005年汇率政策也经历了变更。第三阶段,2008-2014年,消费产出比在低位调整后开始上升,而投资产出比跳升并维持在46.7%左右;期间,我国受到了2008年金融危机的冲击,进而引发政府“四万亿”政策救市。在各个阶段中,中国经历了多个政策性或者突发性事件,而消费和投资趋势性和波动性各具特色而又相互关联,究竟哪些政策或者因素才是导致消费不足和投资过度等特征的关键?
① 原始数据中,季度数据来源于Chang et al. (2015) 2016年3月份整理的数据,样本区间是1996年一季度-2014年四季度。投资指的是资本形成。
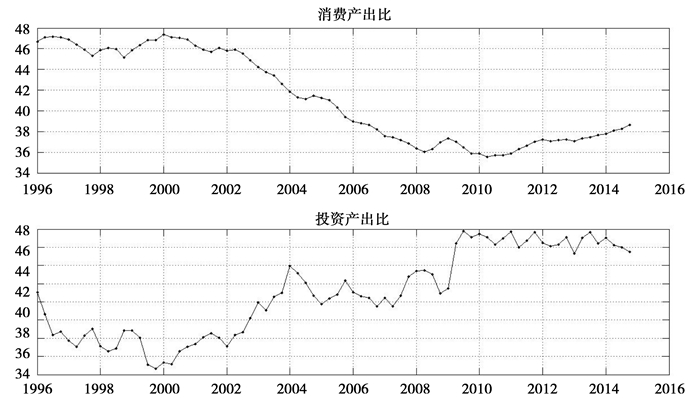
|
图 1 消费产出比和投资产出比 |
为此,国内学者针对这一问题进行了大量研究。林毅夫和苏剑 (2007)以要素价格为视角,对中国通过鼓励投资驱动经济的做法提出了质疑;中国经济增长前沿课题组 (2012, 2013, 2014) 则对中国政府主导的工业化投资进行了辩证的分析;王文甫等 (2014)进一步以产能过剩为切入点,对政府干预投资的行为进行正反两面的分析。Song et al. (2011)尝试用偏向国有企业的信贷政策,来解释中国持续较高增速的投资;Chang et al. (2015)转向偏向重工业的信贷政策视角,认为中国政府实施偏向性低利率借贷政策或者信贷配给造成中国投资较高增速;Chen and Naughton (2016)强调政府推动不同产业发展政策造成投资过度。其他相关的文献还有很多 (罗党论等,2012;吕冰洋、毛捷,2014;曹春方等,2014;贺振华,2006;黄俊、李增泉,2014;唐雪松等,2010;王彦超,2009;Hsieh and Song, 2015等等),其共同点是将投资过度归因于偏向投资的政策因素。与上述文献相比,本文则以投资偏向性金融政策作为分析消费不足和投资过度的切入点。文中投资偏向性金融政策主要是指偏向性产业政策及特有的金融信贷配给政策,其特点是通过改变投资品的成本进而影响投资和生产行为,并进一步通过信贷和收入影响消费。
为探究导致消费不足和投资过度的关键因素,既需要分析消费和投资的趋势影响因素,也需要分析消费和投资的波动影响因素。目前,动态随机一般均衡模型 (简称DSGE) 已成为宏观经济学的主流范式,具有其他宏观模型难以比拟的定量分析优势。基于这样的考虑,本文也将采用DSGE模型分析消费和投资趋势性和波动性的影响因素,并且此DSGE模型能够内生化趋势变动。就分析中国经济而言,构建内生化趋势的DSGE模型才能对中国经济的典型事实有更充分解释,理解经济变量间的增速差异,达到更深层次认识消费不足和投资过度等特征的关键成因。
然而前述文献中,无论是单方面分析消费不足或者投资过度,还是联合分析消费不足和投资过度,除了王文甫等 (2014)采用DSGE模型分析政策性因素对企业投资行为和及其产能利用情况的影响外,其余文献均非DSGE模型框架,难以对消费和投资趋势性和波动性解释因素进行全面分析。国内虽有采用DSGE方法研究经济波动,但缺乏对内生化趋势的处理。例如,许伟和陈斌开 (2009)构建了金融市场不完美,就中国的银行信贷摩擦对经济波动的影响进行分析;李成等 (2010)讨论了价格因素与中国货币规则的互动;李成等 (2011)详细分析了中国的通胀目标;林仁文和杨熠 (2014)就中国市场化改革和货币政策的变化进行了深入的讨论;马理、娄田田 (2015)讨论了零利率下限约束时的中国财政和货币政策;张伟进和方振瑞 (2013)就2008年金融危机成因和后果,通过贝叶斯方法估计模型参数的基础上,进行了详细的探讨;张伟进等 (2014)就户籍制度改革对中国城乡二元经济的影响进行分析;何青等 (2015)从信贷摩擦和房地产偏好两个角度,辩证分析了中国房地产建设对经济的影响。相比之下,趋势性特征的内生化设定在美国经济波动分析中占扮演重要角色,在NK-DSGE和RBC-DSGE两类框架下均有文献涉及。Ireland and Schuh (2008)和Ireland (2013)分别从封闭经济体和开放经济体两个角度,在RBC-DSGE模型中,阐述并解释美国投资增速高于消费增速的现象;而Smets and Wouters (2007)在NK-DSGE模型中,将美国趋势性特征内生为确定性增速,分析美国经济波动主因、通胀与产出等问题,并使模型具有不输于VAR的预测性特质;Liu et al. (2013)在NK-DSGE模型中,内生具有随机特性的趋势特征,突出投资增速相对较高,以分析美国土地价格和投资的联动,对宏观经济波动的扩大和传到作用。
本文所构建内生化趋势的DSGE模型,借鉴了上述国外文献的内生化趋势设定方法,具有以下几个方面特征:(1) 在DSGE模型中构建投资偏向性金融政策,联合考察中国的消费不足与投资过度等特征;(2) 内生化中国经济的趋势性特征,且突出资本投资速率相对较高的现象;(3) 鉴于鼓励投资的政策必然影响收入分配,文中产出收入分配份额采用模型贝叶斯估计而非校准,增加了模型的准确性。本文模型分析结果表明:单纯依靠刺激消费,或者通过刺激短期投资的方法,均难以改变消费产出比下降而投资产出比上升等趋势现象。改变投资偏向性金融政策,完善市场化的投资机制,将是实现中国经济平稳可持续发展的关键所在;且生产技术的进步也能够达到改善消费不足和投资过度的目的。换句话讲,从鼓励投资转向建立完善的市场机制及鼓励创新,可以做到从本质上改善消费不足和投资过度等趋势性特征。
与现有研究相比,本文主要创新体现为三个方面:(1) 鲜有文献尝试将中国消费不足和投资过度等特征,共同放置在构建了投资偏向性金融政策的DSGE框架中进行分析。尽管消费和投资是产出构成元素,但消费和投资趋势性和波动性解释因素并不尽相同,通过内生化趋势特征,本文将有机会区分两者的趋势性和波动性解释因素。同时,鉴于政府实施投资偏向性金融政策只是必要条件,这项政策的有效性与否,也只有内生化到模型中才能够得到验证。(2) 鲜有文献在DSGE模型中内生化趋势性差异特征,以匹配中国消费产出比下降和投资产出比上升等现象,并采用样本数据估计模型进行分析。目前,除了不需要数据进行参数估计,仅进行校准参数的文献,多数利用数据估计模型参数的文献,通过BP和HP等方法已经将趋势性特征丢弃。如果议题中可以忽略趋势性特征,并不造成什么影响;但是,类似于本文的议题中,趋势性差异特征显著且不可避免,忽视了趋势性的设定必定会造成系统性偏差。(3) 鲜有文献在DSGE模型中,用贝叶斯方法估计产出收入分配份额。就本文的议题来讲,能够估计出这个参数将是大有裨益。
本文余文安排如下:第二节理论模型,包含趋势性内生化设定,及基本模型的设立和求解;第三节是参数估计;第四节是消费和投资阶段性变化成因分析;第五节是结论及相关启示。
二、 理论模型鉴于国内DSGE文献对内生化趋势性特征的运用较少,而趋势内生设定又具有多种类型和方法,有必要针对这一设定进行简单的介绍,并结合本文议题对模型内生化趋势进行初步阐述。由于中国投资和资本增长百分比均值是产出、消费等变量增长百分比的两倍以上,模型将以此为出发点内生化趋势性特征。接下来,首先,用简化DSGE来叙述内生化趋势性特征设定,并进一步介绍本文的将要采用的设定情况;然后,详细展开基本模型的设定和求解。
(一) 增长趋势设定DSGE模型中内生化趋势性特征,可通过设定固定外生变量或者非平稳外生冲击两种形式来实现。首先,就经济趋势性特征而言,整体经济及各个经济变量有较为相近的趋势,则经济在等速趋势上运行;反之,整体经济及各个经济变量的趋势有显著差异,则经济体有非等速趋势性特征。正因如此,内生化趋势性特征时:固定外生变量多用于在模型中,实现有稳定统一的趋势性特征;而非平稳外生冲击的选择和组合,用来实现随机的等速或非等速趋势性特征。鉴于中国消费不足和投资过度属于非等速趋势性特征,分析中国的经济波动,应采用非平稳外生冲击的组合。
中国非等速趋势性特征表现为整体经济具有较高增速,但消费、投资及产出等观测变量增速不同。考虑到,虽然外生变量不必与观测变量相对应,但非平稳外生冲击需要与相应的观测变量相对应;兼顾中国非等速趋势性特征,那么,外生变量或者外生冲击的设定多表现为 (1)-(4) 式中,参数的设定情况,即Ai,i=0, 1, 2, 3, 4。
| $ U=U\left( {{C}_{t}},\left( {{L}_{t}}/{{A}_{0}} \right),\left( {{M}_{t}}/{{A}_{1}} \right) \right) $ | (1) |
| $ {{Y}_{t}}={{A}_{2}}*F({{K}_{t-1}},{{A}_{3}}*{{L}_{t}})~ $ | (2) |
| $ {{C}_{t}}+\left( {{I}_{t}}/{{A}_{4}} \right)={{Y}_{t}} $ | (3) |
| $ {{C}_{t}}+{{B}_{t-1}}={{Y}_{t}}-\left( {{I}_{t}}/{{A}_{4}} \right)+\left( {{B}_{t}}/{{R}_{t}}~ \right) $ | (4) |
其中,(1) 是消费者效用函数,Ct是消费,Lt是劳动时间,Mt是货币持有量;(2) 是生产函数,Yt是产出,Kt-1是投入的资本,Lt是雇佣的劳动时间;(3) 是商品市场出清,It是投资;(4) 是预算约束,Bt是买卖的债券量①。
① (1)-(4) 式,意在介绍如何通过冲击项设定内生化趋势,为了节省篇幅省略掉不涉及冲击项的方程。
1. 等速趋势设定经济体中生产技术或者人力资本持续的提高,描述整体经济在相同增速趋势上运行。在DSGE的模型设定中,等速增长趋势主要体现在生产函数 (2) 式中,A2和A3的设定,但是这两个参数设定形式的不同,可以用两种趋势特征:固定或者随机的均衡趋势。第一,固定的均衡趋势设定;Smets and Wouters (2007)设定A2=εta是稳定的全要素生产技术冲击,而A3=γ,其中γ是人力资本的确定性增速;这样的设定保证模型无论是否在平稳状态,都有相同的确定增速γ;该文将美国看作在确定性增速γ,即等速趋势特征下,来讨论其经济波动问题。第二,随机的等速趋势性特征设定;A2和A3的组合中,选择一个为非平稳外生冲击,另外一个为1;这样的设定下:模型平稳状态时,其经济变量均有相同的随机均衡增速;稳态时,则是相等的固定均衡增速;不过这样的设定,多用于与其他非平稳外生冲击组合,来描述经济中存在非等速趋势性特征。
2. 非等速趋势设定非等速趋势性特征设定,可以通过设定一个或者多个相互兼容和匹配的非平稳冲击来实现。以下面三篇文章为例,来分析非等速趋势性特征的设定:
第一,Ireland and Schuh (2008)在描述美国消费和投资增速不同的RBC-DSGE模型中,采用分别生产消费品和投资品的两个生产函数,即模型中有两个 (2) 式,其中 (2) 式中的A2=1,而A3是一个非平稳的外生冲击;用两个不同的人力资本外生冲击,来描述同一经济体内消费和投资的增速不同。
第二,在美国和欧盟的两国模型中,Ireland (2013)为了解释美国消费增速低于投资增速,而欧盟消费增速快于投资增速的事实,采用的是 (2) 式、(3) 和 (4) 式联合的形式,此时的 (4) 式是消费者预算约束;而 (2) 式中A2=1,而A3是非平稳人力资本冲击,这样的设置,保证两个经济体均有来自于人力资本的共同增速;(3) 和 (4) 式中It/A4项,非平稳外生冲击A4的设定,其直觉源于Greenwood et al. (1997)生产技术进步使得投资品相对于消费品价格下降,从而购买单位投资品的支出减少,或者相同的投资支出购买更多的投资品;而Justiniano et al. (2011)和Liu et al. (2013)等均指出,当投资品相对价格不是观测变量时,投资技术冲击可以看作是金融摩擦,并且可能会对宏观经济波动产生很大的影响。那么,非平稳外生冲击A3和A4的设定,确保模型平稳均衡状态时,观测变量的趋势性参数是人力资本永久性冲击和投资技术永久性冲击的函数,且投资和资本相对于其他经济变量有更高的增速;另外,Ireland (2013)在RBC-DSGE框架下,效用函数 (1) 式中没有货币,增设A0为平稳外生冲击和非平稳外生冲击两种形式的模型,进行对比分析;尽管这样的设定会使得趋势性函数构成发生变化,但并不改变投资增速高于其他观测变量的设定。
第三,Liu et al. (2013)为了确认土地价格和投资正相关,是土地价格变化驱动经济波动的原因,将土地和资本作为抵押信贷资产,在NK-DSGE模型中,同样采用 (2) 式、(3) 和 (4) 式联合的形式,此时的 (4) 式是企业家预算约束;但不同的是 (2) 式中A2是一个非平稳的生产技术冲击,而A3=1,相当于假定经济变量的趋势性参数是全要素生产率永久性冲击和投资技术永久性冲击的函数。同样,模型平稳均衡状态时,模型经济体有趋势特征,且投资和资本增速高于其他经济变量。
3. 本文趋势设定图 1展示的产出构成比例、Song et al. (2011)和Chang et al. (2015)均指出中国持续较高的投资增速,道出了中国的趋势性特征。Chang et al. (2015)进一步指出偏向重工业的金融信贷政策,是解释中国五个趋势性特征的关键;引言提到的众多文献,均指出中国投资过度的症因在于鼓励投资的政策因素以及鼓励若干产业发展的策略。这些文献均发现了中国的非均衡趋势特征,但他们没有内生化趋势特征,且将重点集中在信贷政策、产业政策及其他投资鼓励政策因素,又或者强调企业投资行为,往往忽略了资金提供者的行为。事实上,家户部门的消费行为也是金融市场的重要因素。鉴于此,本文模型准备在NK-DSGE框架下,内生化偏向投资的政策因素和趋势性差异特征,并完善供求双方的行为,更为深入的分析消费不足和投资过度的成因和后果。
投资偏向性金融政策及趋势性特征的内生化等,将是本文的特点和进行讨论的基础。首先,模型中拥有两类代表性个人。引入劳动力和信贷的供给者——家户部门,及劳动力和信贷的需求者,也是资本的拥有者——企业家,通过信贷市场,将两个代表性个人联系在一起,资金将在这两个代表性个人之间进行调配,以完善金融摩擦对投资的影响。其次,投资偏向性金融政策的模型,用企业家资本超额收益与永久性金融冲击的联合来完成。Liu et al. (2013)采用卢卡斯树的方式证明:当企业家有低于家户部门的主观折现因子时,企业家资本有超额收益,愿意借贷到最大化的信贷约束。此时,若企业家享有永久性金融冲击,将会持续有利于投资,即投资偏向性金融政策。最后,是非平稳外生冲击的设定。采用 (3)、(4) 式中A4设定为非平稳外生冲击的形式;(1) 式中的A0和A1将设定为1,另外设定消费偏好冲击来完善消费者行为的模型,同时也是完善金融市场摩擦设定;(2) 式中A2是平稳的生产技术冲击,A3=1。至此,本文模型不但构建了完整的信贷市场供需两方的行为,也将中国投资偏向性金融政策和非等速趋势特征内生到模型中来。当然,本文也会将政府行为纳入到模型中,接下来将是详细的描述。
(二) 基本模型中国经济存在产出比例变动,尤其消费不足和投资过度等趋势性特征,潜在成因是投资偏向性金融政策、该政策下的资源调配和调配过程中相关的外生冲击。本文将以此为基础进行建模:理论模型中假定资金提供者和资本拥有者是不同的代表性个人。假定经济中有三类经济主体:家户部门、企业家两类代表性个人及政府部门。家户部门通过消费、休闲、持有货币以及跨期储蓄来实现其终生效用最大化目标;企业家选择消费、生产和跨期投资来实现其终生效用及利润最大化目标;而政府部门实施财政和货币政策。
1. 家户部门鉴于模型有内生化趋势性特征的需要,选择在Smets and Wouters (2007)中效用函数的基础上,结合Walsh (2010) CES形式的MIU效用函数,得到家户部门的效用函数是:
| $ \text{E}\sum\limits_{t=0}^{\infty }{{{({{\beta }_{h}})}^{t}}}{{\omega }_{at}}\left( \text{exp}-\frac{{{\psi }_{h}}}{1+{{\sigma }_{hn}}}{{({{N}_{ht}})}^{1+{{\sigma }_{hn}}}} \right)\\ {{\left[ {{\alpha }_{h}}{{({{C}_{ht}}-{{H}_{ht}})}^{\frac{{{\sigma }_{hc}}-1}{{{\sigma }_{hc}}}}}+(1-{{\alpha }_{h}}){{\left( \frac{{{M}_{ht}}}{{{P}_{t}}} \right)}^{\frac{{{\sigma }_{hc}}-1}{{{\sigma }_{hc}}}}} \right]}^{\frac{{{\sigma }_{hc}}}{{{\sigma }_{hc}}-1}}} $ | (5) |
其中,Nht是劳动时间;Cht是家户部门消费,消费习惯Hht=γhCh, t-1与上期的消费成比例,比例系数是γh;Mht/Pt是实际货币持有量,即名义货币量Mht与价格水平Pt的比值。βh∈(0, 1) 是家户部门主观折现因子,βe是企业家主观折现因子,βh > βe表示家户部门比企业家更有耐心,愿意储蓄;ωat是家户部门消费偏好冲击①;ψh是劳动时间的效用贡献程度;σhn是劳动供给弹性倒数;αh是效用函数中消费对效用的贡献比例。
① 外生冲击形式在第四小节有展示,下同。
参考Iacoviello (2005)及Liu et al. (2013)的设定,去掉家户部门土地和房屋的交易,保留债券和货币的跨期选择。在t期,家户部门的预算约束是:
| $ {{C}_{ht}}+\frac{{{S}_{t}}}{{{R}_{t}}{{P}_{t}}}+\frac{{{M}_{ht}}}{{{P}_{t}}}+{{T}_{ht}}\le \frac{{{W}_{t}}}{{{P}_{t}}}{{N}_{ht}}+\frac{{{S}_{t-1}}}{{{P}_{t}}}+\frac{{{M}_{h,t-1}}}{{{P}_{t}}} $ | (6) |
其中,St是家户部门可购买债券数量、Rt是单位债券的本利和、Tht是家户部门缴纳的从量税、Wt是名义工资水平。
家户部门在预算约束 (2) 下,选择Cht, Nht, St, Mht最大化效用 (1),得到最优决策一阶条件,依次是,边际消费效用和边际收入效用μht的等式、劳动供给曲线、债券需求曲线、货币需求曲线:
| $ \begin{align} & {{\alpha }_{h}}{{\omega }_{at}}({{C}_{ht}}-{{\gamma }_{h}}{{C}_{h,t-1}}){{~}^{-\frac{1}{{{\sigma }_{hc}}}}}~\text{exp}\left( -\frac{{{\psi }_{h}}}{1+{{\sigma }_{hn}}}{{({{N}_{ht}})}^{1+{{\sigma }_{hn}}}} \right)* \\ & {{\left[ {{\alpha }_{h}}{{({{C}_{ht}}-{{\gamma }_{h}}{{C}_{h,t-1}})}^{\frac{{{\sigma }_{hc}}-1}{{{\sigma }_{hc}}}}}+(1-{{\alpha }_{h}}){{\left( \frac{{{M}_{ht}}}{{{P}_{t}}} \right)}^{\frac{{{\sigma }_{hc}}-1}{{{\sigma }_{hc}}}}} \right]}^{\frac{{{\sigma }_{hc}}-1}{{{\sigma }_{hc}}}}}={{\mu }_{ht}} \\ \end{align} $ | (7) |
| $ {{\psi }_{h}}{{({{N}_{ht}})}^{{{\sigma }_{hn}}}}\left[ {{\alpha }_{h}}{{({{C}_{ht}}-{{\gamma }_{h}}{{C}_{h,t-1}})}^{\frac{{{\sigma }_{hc}}-1}{{{\sigma }_{hc}}}}}+(1-{{\alpha }_{h}}){{\left( \frac{{{M}_{ht}}}{{{P}_{t}}} \right)}^{\frac{{{\sigma }_{hc}}-1}{{{\sigma }_{hc}}}}} \right]=\\ \frac{{{W}_{t}}}{{{P}_{t}}}{{\alpha }_{h}}{{({{C}_{ht}}-{{\gamma }_{h}}{{C}_{h,t-1}})}^{-\frac{1}{{{\sigma }_{hc}}}}} $ | (8) |
| $ \frac{1}{{{R}_{t}}}={{\beta }_{h}}{{E}_{t}}\frac{{{\mu }_{h,t+1}}}{{{\mu }_{ht}}}\frac{{{P}_{t}}}{{{P}_{t+1}}} $ | (9) |
| $ (1-{{\alpha }_{h}}){{\left( \frac{{{M}_{ht}}}{{{P}_{t}}} \right)}^{-\frac{1}{{{\sigma }_{hc}}}}}=\left[ 1-\frac{1}{{{R}_{t}}} \right]{{\alpha }_{h}}{{({{C}_{ht}}-{{\gamma }_{h}}{{C}_{h,t-1}})}^{-\frac{1}{{{\sigma }_{hc}}}}} $ | (10) |
在生产部门中产出:最终品、同质中间品和异质中间品。其中,同质中间品在完全竞争市场上卖给异质中间品厂商j;假定异质中间品厂商j∈[0, 1]具有连续性,将同质中间品生产成异质中间品,并有一定的垄断定价能力以确定概率最优化价格,在垄断竞争市场上销售给最终品生产企业;最终品厂商将异质中间品加工成最终品,作为消费品和投资品在完全竞争市场销售。
(1) 最终品生产企业
在垄断竞争市场上,最终品生产企业从异质中间品厂商购得Yjt;用以生产最终品Yt,并在完全竞争市场上,作为消费品或投资品销售。最终品的生产函数:
| $ {{Y}_{t}}={{\left( \int_{0}^{1}{Y_{jt}^{\frac{1}{1+\lambda }}}dj \right)}^{1+\lambda }} $ | (11) |
其中,λ > 0是最终品产品价格在边际成本上的加成,最终品生产企业将最终品价格Pt和异质中间品价格Pjt看作外生给定,最大化利润,得到异质中间品的需求函数
| $ {{Y}_{jt}}={{\left( \frac{{{P}_{jt}}}{{{P}_{t}}} \right)}^{-\frac{1+\lambda }{\lambda }}}{{Y}_{t}} $ | (12) |
完全竞争市场利润为零,结合 (11) 式,可以得到最终品价格和异质中间品价格的关系:
| $ {{P}_{t}}={{\left( \int_{0}^{1}{{{({{P}_{jt}})}^{-\frac{1}{\lambda }}}}dj \right)}^{-\lambda }} $ | (13) |
(2) 同质中间品生产企业
依照Iacoviello (2005)、Liu et al. (2013)及林仁文等 (2014)的设定,加入企业家代表性个人。本文的企业家是仅有消费的CES效用函数,企业家采用Cobb-Douglas生产函数,雇佣资本和劳动力来生产,并通过抵押资本融资。首先,企业家的效用函数:
| $ \text{E}\sum\limits_{t=0}^{\infty }{\beta _{e}^{t}}\left\{ \frac{{{\sigma }_{ec}}}{{{\sigma }_{ec}}-1}{{({{C}_{et}}-{{H}_{et}})}^{\frac{{{\sigma }_{ec}}-1}{{{\sigma }_{ec}}}}} \right\} $ | (14) |
其中,Cet是企业家消费,消费习惯Het=γeCe, t-1与上期消费成比例,γe是比例系数,σec > 0。
同质中间品生产函数:
| $ Y_{t}^{w}={{\omega }_{bt}}K_{t-1}^{\alpha }N_{et}^{1-\alpha } $ | (15) |
其中,Ytw是同质中间品产出,Kt-1和Net分别是投入的资本和雇佣的劳动;α是资本收入份额;ωbt是生产技术冲击。
综合Greenwood et al. (1997)、Liu et al. (2013)及Karabarbounis and Neiman (2014)投资技术冲击的特点,以及中国趋势性特征,兼顾Iacoviello (2005)及Liu et al. (2013)对企业家预算约束的设定,采用非平稳的投资技术冲击,能够在模型中实现两个不同的增长率,以突出中国投资增速较高的事实,以完成趋势性特征的内生化。企业家预算约束条件是:
| $ {{C}_{et}}+\frac{{{B}_{t-1}}}{{{P}_{t}}}+{{T}_{et}}=\frac{P_{t}^{w}}{{{P}_{t}}}Y_{t}^{w}-\frac{{{I}_{t}}}{{{Q}_{t}}}-\frac{{{W}_{t}}}{{{P}_{t}}}{{N}_{et}}+\frac{{{B}_{t}}}{{{R}_{t}}{{P}_{t}}}+{{F}_{t}} $ | (16) |
其中,Bt-1是需偿还债券总量、Bt/Rt是本期发行债券的现值、Ptw是同质中间品价格、Tet是企业家的纳税、It是投资、Ft是企业家获得的异质中间品的垄断利润。Qt=Qtpωit是投资技术的变化,称ωit投资技术暂时性冲击①;投资技术冲击的永久性部分Qtp=Qt-1pωct,称ωct是投资技术永久性冲击。其中,Γt=Qtα/(1-α)是投资和资本之外变量的去趋势 (Detrending) 函数,ΓtQt是资本、投资的去趋势函数。定义gγt=Γt/Γt-1,gqt=Qt/Qt-1=ωct(ωit/ωi, t-1),其稳态值分别是:gγ,gq;则gqtgγt-1是每期投资和资本的增长率,gγt-1是每期其他经济变量的增长率。
① 投资技术冲击 (investment-specific technological shocks) 不同于资本增广型技术冲击 (capital-augmenting technological shocks) 的供给面技术变化,没有投资品相对价格作为观测变量时,投资技术是在金融市场上,从投资增长速率变化的角度来影响投资的难易程度。
第0期企业家拥有K-1 > 0的资本,第t期的资本累计方程式:
| $ {{K}_{t}}=\left( 1-\delta \right){{K}_{t-1}}+\left[ 1-S\left( \frac{{{I}_{t}}}{{{I}_{t-1}}} \right) \right]{{I}_{t}} $ | (17) |
其中,δ是折旧率,S(·) 是投资调整成本函数,满足:S(gqgγ)=S′(gqgγ)=0和S″(gqgγ) > 0;而ω=S″(gqgγ) 是投资调整成本的变动程度。
企业家面临的借贷约束:
| $ {{B}_{t}}\le {{\omega }_{dt}}{{\text{E}}_{t}}{{Q}_{k,t+1}}{{K}_{t}} $ | (18) |
其中,Qk, t+1是名义商品衡量的资本影子价格;企业家的借贷约束占企业家账面资产的比重为ωdt。作为资产的流动性表现,称ωdt为金融信贷冲击。
企业家以生产技术 (15)、预算约束 (16)、资本投资 (17)、信贷约束 (18) 为约束,选择Cet、Net、It、Kt、Bt来最大化终身效用 (14),得到一节条件,依次是,消费与收入的边际效用μet的等式、劳动需求曲线、投资欧拉方程、资本欧拉方程、债券供给曲线:
| $ {{({{C}_{et}}-{{\gamma }_{e}}{{C}_{e,t-1}})}^{-1/{{\sigma }_{ec}}}}={{\mu }_{et}} $ | (19) |
| $ \left( 1-\alpha \right)\frac{P_{t}^{w}}{{{P}_{t}}}\frac{Y_{t}^{w}}{{{N}_{et}}}=\frac{{{W}_{t}}}{{{P}_{t}}} $ | (20) |
| $ \frac{1}{{{Q}_{t}}}=\frac{{{Q}_{kt}}}{{{P}_{t}}}\left[ 1-S\left( \frac{{{I}_{t}}}{{{I}_{t-1}}} \right)-S\prime \left( \frac{{{I}_{t}}}{{{I}_{t-1}}} \right)\frac{{{I}_{t}}}{{{I}_{t-1}}} \right]+\\ {{\beta }_{e}}{{E}_{t}}\frac{{{\mu }_{e,t+1}}}{{{\mu }_{et}}}\frac{{{Q}_{k,t+1}}}{{{P}_{t+1}}}S\prime \left( \frac{{{I}_{t+1}}}{{{I}_{t}}} \right)\left( \frac{{{I}_{t+1}}}{{{I}_{t}}} \right){{~}^{2}} $ | (21) |
| $ \frac{{{Q}_{kt}}}{{{P}_{t}}}=\frac{{{\mu }_{bt}}}{{{\mu }_{et}}}{{\omega }_{dt}}\frac{1}{{{P}_{t}}}{{\text{E}}_{t}}{{Q}_{k,t+1}}+{{\beta }_{e}}{{\text{E}}_{t}}\frac{{{\mu }_{e,t+1}}}{{{\mu }_{et}}}\left[ \alpha \frac{P_{t+1}^{w}}{{{P}_{t+1}}}\frac{Y_{t+1}^{w}}{{{K}_{t}}}+\frac{{{Q}_{k,t+1}}}{{{P}_{t+1}}}\left( 1-\delta \right) \right] $ | (22) |
| $ \frac{1}{{{R}_{t}}}=\frac{{{\mu }_{bt}}}{{{\mu }_{et}}}+{{\beta }_{e}}{{\text{E}}_{t}}\frac{{{\mu }_{e,t+1}}}{{{\mu }_{et}}}\frac{{{P}_{t}}}{{{P}_{t+1}}} $ | (23) |
其中,μbt是信贷约束乘子。
(3) 异质中间品生产企业
异质中间品Yjt由完全竞争市场上的同质中间品Ytw,组装生产而来,并在垄断竞争市场卖给最终品生产企业。异质中间品厂商具有垄断定价能力,采用Calvo定价机制:每期有ξ的概率不能够最优化调整价格,厂商可以根据上期通货膨胀进行指数化调整当期价格。即
| $ {{P}_{j,t+1}}={{\left( \frac{{{P}_{t}}}{{{P}_{t-1}}} \right)}^{\chi }}{{P}_{jt}}~ $ | (24) |
其中,χ是指数化程度。第t期,异质中间品厂商可以最优化调整价格时,会选择价格Pjt使得不能够最优化调整价格i≥0期内的利润最大化,即:
| $ \underset{{{P}_{jt}}}{\mathop{\text{max}}}\,{{\text{E}}_{t}}\sum\limits_{i=0}^{\infty }{{{\beta }_{e}}\xi {{)}^{i}}}\frac{{{\mu }_{e,t+i}}}{{{\mu }_{et}}}\left[ {{\left( \frac{{{P}_{t+i-1}}}{{{P}_{t-1}}} \right)}^{\chi }}\frac{{{P}_{jt}}}{{{P}_{t+i}}}-\frac{P_{t+i}^{w}}{{{P}_{t+i}}} \right]{{Y}_{j,t+i}} $ | (25) |
由最终品生产企业对异质中间品的需求函数,可以得到t+i期,异质中间品的需求函数:
| $ {{Y}_{j,t+i}}={{\left( {{\left( \frac{{{P}_{t+i-1}}}{{{P}_{t-1}}} \right)}^{\chi }}\frac{{{P}_{jt}}}{{{P}_{t+i}}} \right)}^{-1+\lambda \lambda }}{{Y}_{t+i}} $ | (26) |
异质中间品生产企业最大化利润的一节条件,可以得到最优价格Pt*调整方程:
| $ {{\text{E}}_{t}}\sum\limits_{i=0}^{\infty }{{{({{\beta }_{e}}\xi )}^{i}}}\frac{{{\mu }_{e,t+i}}}{{{\mu }_{et}}}\left[ {{\left( \frac{{{P}_{t+i-1}}}{{{P}_{t-1}}} \right)}^{\chi }}\frac{P_{t}^{*}}{{{P}_{t+i}}}-\left( 1+\lambda \right)\frac{P_{t+i}^{w}}{{{P}_{t+i}}} \right]Y_{j,t+i}^{*}=0 $ | (27) |
其中,
| $ P_{t}^{-\frac{1}{\lambda }}=\xi {{\left[ {{\left( \frac{{{P}_{t-1}}}{{{P}_{t-2}}} \right)}^{\chi }}{{P}_{t-1}} \right]}^{-1\lambda }}+\left( 1-\xi \right){{(P_{t}^{*})}^{-\frac{1}{\lambda }}} $ | (28) |
总物价水平调整方程与异质中间品最优价格调整方程相结合,线性化以后是有理性预期的菲利普斯曲线。异质中间品厂商的垄断定价行为,可以获得垄断利润Ft=(1-Ptw/Pt)Yt,并将这部分利润分配给企业拥有者——企业家。
3. 政府部门当一个经济体,以调整货币增速为政策手段时,货币数量法则将是货币政策模拟的首选;且货币流通速率足可反映一个经济体货币政策 (陈彦斌等,2015)。因而,本文货币政策采用Sargent and Surico (2011)的货币数量法则:
| $ \frac{{{V}_{t}}}{V}={{\left( \frac{{{V}_{t-1}}}{V} \right)}^{{{{\tilde{n}}}_{m}}}}{{\left[ {{\left( \frac{{{\Pi }_{t}}}{\Pi } \right)}^{-{{\varphi }_{p}}}}{{\left( \frac{{{Y}_{t}}}{{{Y}_{t-1}}} \right)}^{-{{\varphi }_{y}}}} \right]}^{1-~{{{\tilde{n}}}_{m}}}}{{\omega }_{et}} $ | (29) |
其中,Vt≡Mt/Mt-1是货币增长速度,ωet是货币政策冲击,V、Π分别是稳态时的货币增长率、通货膨胀率;
政府财政支出预算约束限制:
| $ {{G}_{t}}={{T}_{t}}+\frac{{{M}_{t}}-{{M}_{t-1}}}{{{P}_{t}}} $ | (30) |
政府支出Gt由税收Tt和铸币税 (Mt-Mt-1)/Pt来支付。假定财政支出与产出水平的关系式:Gt/Yt=1-1/ωft,其中,ωft是财政政策冲击。
4. 外生冲击外生冲击是与每个观测变量相对应的,衡量外生因素的数量化形式。外生冲击ωsh, t服从如下随机过程:
| $ \text{ln}{{\omega }_{sh,t}}=\left( 1-{{\rho }_{sh}} \right)\text{ln}{{{\bar{\omega }}}_{sh}}+{{\rho }_{sh}}\text{ln}{{\omega }_{sh,t-1}}+{{\sigma }_{sh}}{{\varepsilon }_{sh,t}} $ | (31) |
其中,sh∈{a, b, c, d, e, f, i},ωsh > 0是ωsh, t稳态时的值,ρsh∈(0, 1) 是冲击持续程度,σsh是标准差,εsh, t是标准正态分布数列。
5. 市场出清家户部门、生产部门和政府部门的经济活动,在每一期都会保证供给与需求相等;即市场出清。与Smets and Wouters (2003, 2007)、Iacoviello (2005)及Liu et al. (2013)等一般均衡模型相同,不受冲击影响时,模型有唯一均衡。即竞争性均衡时,模型中商品、劳动力及债券等市场出清:在t期的价格体系下,最终品市场出清,即Ct+It/Qt+Gt=Yt,其中,Cht+Cet=Ct是总消费;劳动力市场出清Nht=Net=Nt;债券市场出清St=Bt;货币市场出清Mht=Mt;两类代表性个人交税总额等于政府的税收Tht+Tet=Tt,并假定企业家缴纳的税Tet=τTt。即竞争性均衡时,存在一系列价格,确保商品、劳动力及债券等市场供求相等;本文市场出清的表现就是价格体系{Wt, Qkt, Rt, Pt, Ptw, Pt*}t=0∞下,商品分配{Cht, Cet, It, Mht, Nht, Net, St, Bt, Kt, Gt, Vt, Tt, Ft}t=0∞保证家户部门和企业家的最优化问题得以解决,及所有市场得以出清。
6. 平稳状态模型中非稳定外生冲击的设定,使得1到5部分中的一节条件、预算约束、市场出清及政策法则等,每条方程式中的经济变量,除了利率、资本相对价格、通胀、劳动时间、中间品通胀等变量,其余变量均需去趋势处理,并将名义变量变为实质变量,确保最优决策行为方程体系在平稳状态路径 (stationary processes),进而才能够进行对数线性化 (log-linearized) 处理。标准化去趋势处理如下,
| $ {{{\rm{\tilde X}}}_{st}} = {X_{st}}/{\Gamma _t},{{{\rm{\tilde X}}}_{kit}} = {X_{kit}}/{Q_t}{\Gamma _t},{\Pi _t} = {P_t}/{P_{t - 1}},\\ \Pi _t^{ws} = P_t^{ws}/{P_t},{\rm{ }}{{\tilde \mu }_{ebt}} = {\mu _{ebt}}\Gamma _t^{1/{\sigma _{ec}}},{q_{kt}} \equiv {Q_{kt}}{Q_t}/{P_t} $ | (32) |
其中,Xst={Wt/Pt, Ct, Cht, Cet, Mt/Pt, Yt, Bt/P, Ft, Vt, Mht/Pt, Gt, Tt},Xkit={Kt, It},Ptws={Ptw, Pt*},
样本资料的选取和处理,是模型结构参数校准和贝叶斯估计的前提和基础。而贝叶斯估计则是在前文介绍的线性化方程体系基础上,通过理性预期的求解得到状态空间模型的方程体系①,此方程体系结合参数先验特征和样本资料,通过计算观测变量数据的似然函数值,来确定参数的后验分布特征。因而,这一部分将阐述三个内容:首先,介绍样本数据的来源和处理情况;其次,结合样本及文献资料,介绍部分结构参数的校准情况;第三,介绍其余结构参数的贝叶斯估计情况。
① 最优决策行为方程体系的线性化形式,如Smets and Wouters (2007)文中所展示,是进行模型估计前需要完成的工作,限于篇幅不再展示。
(一) 样本数据本文采用六组中国经济变量的季度数据,作为样本数据:消费 (Ctdata)、产出 (Ytdata)、M1(M1tdata)、GDP平减指数 (Ptdata)、资本形成总额 (Itdata)、政府财政支出 (Gtdata)。样本区间是1996年一季度至2014年四季度,其中,M1来自于统计局;其余数据来自Chang et al. (2015)2016年3月份整理的数据。
由于Chang et al.(2015)将整理的中国宏观经济变量已经进行了季节性调整,且GDPdeflator是以2005年为基期,所以,来自统计局的M1也先进行了季节性调整;接下来,用GDPdeflator将名义的消费、产出、资本形成变成实际变量Ctreal、Ytreal、Itreal;然后计算得出投资产出比 (Rtiy=Itreal/Ytreal)、政府支出产出比 (Rtgy=Gtreal/Ytreal)、投资消费比 (Rtic=Itreal/Ctreal);最后,选取Itreal、M1tdata、Ptdata、Rtiy、Rtgy、Rtic均采用对数差分的处理作为观测变量数据①,即完成观测变量数据的选择和处理。
① 对数差分的处理使得观测变量,有显著不等于零的期望均值,投资的期望均值是2.4,通胀的期望均值是0.78,货币增速的期望均值是3.5,投资产出比的期望均值是0.15,投资消费比的期望均值是0.4。贝叶斯估计时需要校准这些观测变量的期望值。
(二) 参数校准单单一个理论模型,如要精确地估计出中国宏观模型的每一个结构参数值,将是一项艰巨的任务,本文的结构参数中有五个参数属于此列。幸而,未被采用作为观测变量的数据,以及其他相关文献可以给出解答,即这五个参数可以采用校准的方法来确定。家户部门主观折现因子βh=0.99,资本折旧率δ=0.025,这与国内多数DSGE文献相一致;企业家主观折现因子借鉴Liu et al. (2013)中的数值βe=0.956;由样本期间内M1与GDP年度比值均值,得M/Y=0.55;同样,样本期间财政支出与GDP季度比值均值,可确定G/Y=0.145。
(三) 贝叶斯估计参数先验特征的设定,依据样本观测数据并参照现有文献进行调整。而参数后验分布采用贝叶斯方法估计。模型中有31个估计变量。表 1中2-4列给出了需要估计参数的先验分布特性;5-8列给出了参数后验分布的众数、均值、5%分位数和95%分位数。
| 表 1 结构参数先验与后验分布 |
1.先验分布。表 1中2-4列给出了需要估计参数的先验分布;原则上参考已有文献并结合数据特征,选择参数先验分布,保证参数的先验分布均值和方差 (自由度) 取值在合理的范围。具体来讲,通过Smets and Wouters (2003, 2007)、Liu et al. (2013)来设定参数先验分布;参考李成等 (2010, 2011),张伟进等 (2013, 2014) 来调整先验分布均值和方差 (自由度) 取值大小。诚然,本文确定了参数的先验分布之后,通过贝叶斯的方法估计模型参数,还需要根据观测变量数据特征及中国经济事实,来调整某个参数分布的均值和方差 (自由度),以达到解释中国经济的目的。
2.后验分布。表 1中5-8列给出了参数后验分布的众数、均值、5%分位数和95%分位数。参数后验分布采用的是Random-Walk Metropolis算法,进行30万次模拟抽样,舍掉前面10万次。模型的收敛性通过验证,说明模型设计具有合理性,可以用来解释样本期间的中国经济。参数后验分布大体位于合理区间,不再一一讨论,有几个参数是本文分析议题的关键。
第一,产出分配α估计的均值是0.51,90%的置信区间是[0.49, 0.54],基本可以描述中国产出资本收入份额相对其他经济体较高的事实,即中国劳动收入份额较少的事实。
第二,趋势性特征内生化的参数rate,1+rate/100是投资技术永久性冲击稳态时的值,rate估计的均值是2.53,90%的置信区间是[2.09, 3.03],相当于产出的季度增长均值是2.66,90%的置信区间是[2.19, 3.19],换算成年度增长率约为10.6%,尽管略高于样本期间的年度GDP指数值9.6%,但两个数值均位于90%的置信区间;同时,rate估计的数值,经模型稳态方程式的计算,相当于投资年度增长率均值约为20.66%,略低于样本期间投资完成额年度增长率均值23.26%,而这两个值也均位于90%的置信区间数据来源于统计局,一,GDP采用季度数据,用上年同期的当季值增长率计算年度均值,样本期间是1995年1季度-2014年4季度;二,投资数据采用月度数据,投资完成额累计增长率计算年度均值,样本期间是1998年2月-2014年12月。。说明模型的内生化趋势性差异特征的设定,及内生化参数rate估计均较为合理,可以用来描述消费不足和投资过度等差异趋势性特征。
第三,货币数量法则中,参数φp估计的均值是1.20,相对于张伟进、方振瑞 (2013) 设定的先验参数 (1.7) 和估计值 (1.88) 均低,90%置信区间是[0.74, 1.70];参数φy相对于Smets and Wouters (2003, 2007)、张伟进、方振瑞 (2013)设定的先验参数 (0.12) 及估计值 (0.16) 均高,估计的均值是0.49,90%置信区间是[0.33, 0.66],说明在考虑了内生化趋势性差异特征以后,中国产出增速的变动,在货币政策法则中的重要性相对较高。
四、 消费和投资阶段性变化的成因分析模型及其贝叶斯估计得到中国经济事实认可之后,在模型和估计参数的基础上,参照Smets and Wouters (2003, 2007)、Liu et al. (2013)、张伟进等 (2013, 2014),所采用的分析方法。用脉冲响应、方差分解和历史拆解等系列方法,分析外生冲击对观测变量波动性和趋势性的影响,重点分析外生冲击对投资消费比波动性和趋势性的解释,进一步找出中国消费和投资经历阶段变化的解释主因;同时,判断这些外在因素对中国趋势性特征和经济波动解释的相对重要性。
(一) 脉冲响应脉冲响应分析其他外生冲击不变的情况下,某时点,某个外生冲击一单位标准差的改变,在一定时段内,对某一观测变量偏离趋势百分比的影响;简单的讲,脉冲响应是冲击发生后的一段时间内,观测变量的动态调整路径。可以直观也更纯粹的了解某一个外生冲击改变时,对特定观测变量偏离趋势的解释情况。
外生冲击的脉冲响应图形,由后验分布中20万组参数的50%计算得到10万组脉冲响应数据;在此基础上,计算得到脉冲响应的均值 (黑色实线) 和90%置信区间 (暗色部分)。图 2是外生冲击对投资消费比的脉冲响应图像,鉴于信贷行为中,资金是通过其在金融市场上的调配,建立了投资和消费的关联,本文将从金融市场摩擦和非金融市场因素两方面来分析脉冲响应:消费偏好冲击、投资技术冲击、金融信贷冲击在金融市场上直接影响着消费者和企业家的行为;而生产技术冲击、货币政策和财政政策冲击属于非金融市场因素。
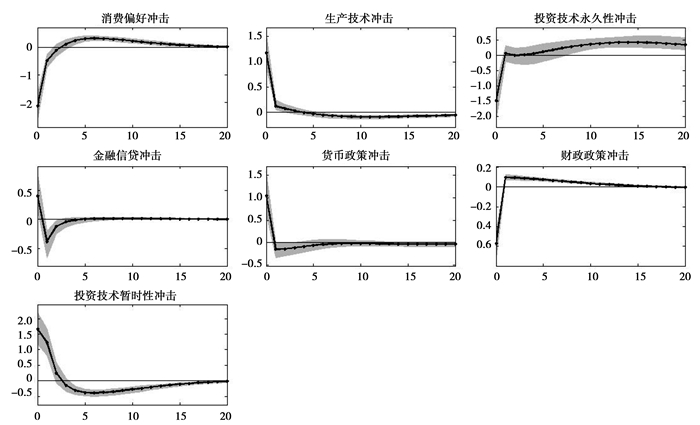
|
图 2 投资消费比的脉冲响应 |
在金融市场上,(1) 消费偏好冲击的发生致使投资消费比快速下降,第3期开始正向偏离趋势,经过一个上升过程后逐渐回归趋势;(2) 金融信贷冲击发生伊始,投资消费比上升,但很快降到趋势水平之下,之后回归趋势;(3) 投资技术暂时性冲击发生之后,也会促使投资消费比上升,相比金融信贷冲击上升幅度更高,持续期限更长,同样经过3期之后,投资消费比开始负向偏离趋势,经过一个缓慢下降过程后才回归趋势;(4) 投资技术永久性冲击发生之后,首先使得投资消费比下降,因为投资技术永久性冲击相当于降低了投资品的实际价格,即相同的投资量,只需要支付更少,就可以完成;2期之后,由于投资变得更为有利,加之企业家通过拥有资本,能够获得相比信贷成本更高的收益,从而使得投资消费比长期正向偏离趋势。事实上,投资技术永久性冲击同样可以促使投资、投资产出比长期正向偏离趋势,而其他金融市场摩擦只是使得投资消费比暂时偏离趋势水平。
从非金融市场角度看,(1) 生产技术冲击伊始促使投资快速增加,从而使得投资消费比上升显著,之后缓慢下降,第5期之后,投资消费比将长期低于趋势水平。事实上,生产技术冲击对投资产出比的脉冲响应,也有相似于投资消费比的动态调整路径;但是生产技术冲击会小比率促进投资正向偏离趋势。既然生产技术冲击可缓解消费产出比的下降,意味着生产技术冲击促使消费增速相对投资增速上升;(2) 货币政策冲击会促使投资消费比快速升到趋势水平之上,但很快会降低到趋势水平线之下,然后缓慢的回归趋势;(3) 财政政策冲击对消费和投资的挤出效应差异,可以清晰的从投资消费比的脉冲响应图像看出来,冲击发生之后,投资消费比会很快下降,之后迅速升到趋势水平之上,然后缓慢的回归趋势,说明财政政策对投资波动的影响相对消费而言较高。总之,非金融市场因素中,生产技术冲击可以持续的降低投资消费比,而财政和货币政策冲击只是使得投资消费比暂时偏离趋势状态,最终会回归趋势。
综上,脉冲响应的分析告诉我们,投资技术永久性冲击是造成投资、投资产出比和投资消费比长期持续上升的主因;而生产技术冲击长期则可抑制投资消费比和投资产出比上升,并促使投资小比率上升,即促使消费增速追赶投资增速;其他冲击仅仅是引起投资、投资产出比和投资消费比的波动。换句话讲:投资技术永久性冲击是促成中国形成消费不足和投资过度等趋势性差异特征的主因,而生产技术冲击有机会缓解这两个特征,增加消费并调节投资。而其他的外生冲击因素,仅仅是使得消费和投资出现波动,并不会改善根本问题。
(二) 方差分解方差分解意在考察外生冲击发生后,各个外生冲击分别对观测变量预测误差方差的解释程度。而脉冲响应考察的是外生冲击致使观测变量偏离趋势的期望值;脉冲响应从一阶矩的角度考察外生冲击对观测变量的影响,而方差分解则是从二阶矩的角度分析外生冲击对观测变量波动的解释情况。即方差分解是外生冲击对观测变量预测误差方差的贡献百分比。表3列出t=4,10,40季度的情况:
方差分解表明:(1) 投资消费比的方差主要解释因素是消费偏好冲击、投资技术永久性冲击和投资技术暂时性冲击,在t=4时,分别解释30%、14.7%、33.3%,随着期限至延长t=40时,投资技术永久性冲击的解释力度增加至24.6%,而消费偏好冲击和投资技术暂时性冲击分别降至26.1%和31.3%。(2) 投资产出比的方差主要解释因素相对集中,t=4时,71%被投资技术暂时性冲击所解释,接下来是消费偏好冲击可以解释10.6%的波动;随着期限的延长,t=40时,投资技术暂时性稍有降低,可以解释63.1%的投资产出比波动,而消费偏好冲击可解释10%的波动,此时投资技术永久性冲击增加到14.5%。(3) 投资的方差解释因素相对分散,t=4时,较为突出的是投资技术暂时性冲击,可以解释35.1%的投资波动;而消费偏好冲击、生产技术冲击和投资技术永久性冲击可分别解释:16.6%、19.3%、14.3%;随着期限延长,t=40时,投资技术永久性冲击上升至26.8%,而投资技术暂时性冲击下降至21.5%,消费偏好冲击和生产技术冲击稍稍下降,可分别解释13.8%、15.8%。
将方差分解与脉冲响应相结合可知,(1) 消费偏好冲击和投资技术暂时性冲击是解释投资、投资产出比和投资消费比波动的主因;(2) 尽管投资技术永久性冲击可以使得投资消费比、投资和投资产出比正向偏离趋势水平,但是对它们的波动解释力度并不占主导地位,说明投资技术永久性冲击,对三者的脉冲效应,是趋势性的确定性的影响,而波动性解释相对较小;(3) 生产技术冲击对投资、投资产出比和投资消费比同样有趋势性解释力,但对三者的波动解释并不占支配地位,说明生产技术的改进对三者主要体现在趋势性方面,而非波动性角度。至此,基本上可以判定,样本观测期间,投资技术永久性冲击和生产技术冲击,是解释中国趋势性的主因,而消费偏好冲击和投资技术暂时性冲击,是解释中国波动性的主因。
| 表 2 方差分解结果 |
首先,外生冲击平滑值的变动反应的是样本观测期间,外生冲击偏离趋势水平的变动情况,文中联合参数估计和模型设计的特色,及脉冲响应的特点,可以用来分析消费和投资阶段性特征的变化。其次,历史拆解用于分析外生冲击对观测变量刺激的波动性和方向性 (增加还减少) 的解释,也是样本期间内有限持续性的解释;不同于用于分析外生冲击对观测变量方向性及持续性影响的脉冲响应;也不同于用于分析外生冲击激励观测变量波动性和持续性情况的方差分解,是脉冲响应和方差分解很好的补充。历史拆解适用于分析样本期间内外生冲击如何解释投资消费比等观测变量的波动;历史拆解和方差分解联合分析,可以与历史事件和政策因素相结合,来分析观测变量与外生冲击的动态互动,更具有说服力,且便于找出经济改变的时点和成因。在历史拆解分析之前,先来分析外生冲击平滑值。
1. 平滑值外生冲击平滑值是根据数据和贝叶斯估计的参数计算,得到外生冲击在样本间内的变化走势。外生冲击平滑值是独立于观测变量之外的变动情况,是历史拆解分析的背景。图 3中,展示的是全样本时段的外生冲击平滑值,零值水平线代表着某一平滑值的趋势保持不变,高于该线是平滑值有上升趋势的百分比;反之,是下降趋势百分比。需要讲明的是,外生冲击中,投资技术永久性冲击是非平稳外生冲击,其他外生冲击是平稳外生冲击。模型平稳均衡时,投资技术永久性部分有增长率rate/100,其趋势水平值是1+rate/100,其他外生冲击均保持水平不变。图 3的平滑值有三点启示:
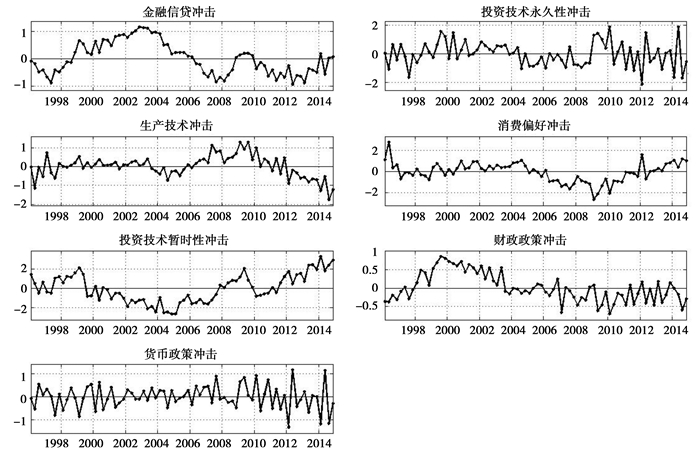
|
图 3 外生冲击平滑值 |
第一,用金融信贷冲击平滑值与大的经济事件相匹配:1997年的东南亚金融危机使得资本抵押信贷能力下降,此时金融信贷冲击平滑值远低于趋势水平;2000年以来中国经济发展迅速,资本抵押信贷能力得到显著的扩张,这一时段该平滑值一直维持在趋势水平线之上;直到2006年金融危机前夕,金融信贷冲击平滑值已经开始大幅负向偏离趋势水平;受金融危机影响,2008年前后,金融信贷冲击平滑值负向偏离趋势降到低点,中国资本的抵押信贷能力大幅降低;而后,“四万亿”的拯救措施使得资本的信贷能力增加,金融信贷冲击平滑值短暂的高于趋势水平;而2011年以来,中国经济增速显著放缓,资本也放缓了抵押信贷的步伐,金融信贷冲击平滑值也显著低于趋势水平。因而,金融信贷冲击平滑值再次证明了本文模型具有一定的可行性。
第二,投资技术永久性冲击平滑值是去掉趋势值1+rate/100后的变动情况,是解释消费和投资阶段性变动的关键。由脉冲响应和方差分解可知,稳定的投资技术永久性冲击消费不足与投资过度等趋势性差异特征的主因。因而,此冲击平滑值的变动,可以解释消费和投资变动的阶段变化:
(1) 消费产出比和投资产出比的快速变动期。图 1显示2000-2010年期间,消费产出比从最高点下降到最低点,而投资产出比从最低点快速上升到一定比值,出现了波动性上升,在2009年跳升至较高比率。期间,中国产出增长率也相当可观,而投资增速犹高于产出增速,消费增速则在产出增速之下,即使如此,它们同样保持了较快的增速。图 3显示这一时段,投资技术永久性冲击平滑值均在趋势附近做小比率的调整。图 2中,投资技术永久性冲击对投资消费比的脉冲响应,冲击伊始并不能够促进投资消费比上升,反倒是下降,两期之后才逐渐表现为正向偏离趋势水平,说明稳定的投资技术永久性冲击是这两种比率快速变动的关键。
究竟是什么因素在2000-2010年主导了这两种趋势性特征?样本观测期间,经历了1996年3月推出发展重工业的信贷政策,1997年东南亚金融危,以及同年9月进行的私有化改革,2001年加入WTO,2005年人民币汇率制度变革,以及2008年金融危机。其中,发展重工业的政策、私有化、加入WTO及汇率制度改革,有机会影响趋势性特征。如果没有2008年金融危机,很难将这几个要素的重要性进行划分,以投资产出比为例:2000-2004年投资技术永久性冲击平滑值处于正向小比率高于趋势状态,同期的投资产出比快速上升;从2004年直到2008年底投资技术永久性冲击平滑值,大多处于小比率负向偏离趋势的水平,同期的投资产出比处于波动上升期;金融危机之后,政府主导的“四万亿”财政支出,使得投资产出比突然跳升,投资技术永久性冲击平滑值也从负向偏离均衡,跳升至正向偏离。金融危机的“实验”表明,其他因素变动不大的情况下,作为鼓励投资的政策因素,投资技术永久性冲击平滑值稳定与否,是解释投资产出比阶段性变化的主因。至于2004-2008年期间,投资产出比在40%-45%之间的波动,说明即使没有金融危机,政府主导的通过投资实现的增长也遭遇了瓶颈,其政策的效力在逐渐消失,而金融危机只是转移了注意力。至于消费产出比的变动可用同样的分析思路,而消费产出比的变动之所以相对平滑,应归因于消费的影响因素,消费偏好冲击和生产技术冲击的平滑值可就两个趋势的差异给出解释。总之,促进投资的政策性条件的有效性和持续性,是解释这两个趋势性差异特征的主因。
(2) 消费产出比高比率平稳和投资产出比低比率下降期。图 1显示,1996-2000年期间,消费产出比比值较高且相对稳定,而投资产出比比值较低却在下降。1996年实施鼓励投资的政策,从投资技术永久性冲击平滑值的变动情况来看,政策稳定性尚待改进,结合该冲击对投资消费比的脉冲响应可知,投资技术永久性冲击开始时,会降低投资消费比而非增加;尤其经历了1997年的东南亚金融危机,中国经济也难免受损,1997年9月开始的私有化改革,也有资源再分配的效果,也可能会影响到投资的进展。图 3中,投资技术永久性冲击平滑值在改革初期相对稳定,东南亚金融危机之后波动性比较大,先是显著低于趋势水平,而后逐渐升到趋势水平以上,充分说明此时鼓励投资的政策尚未稳定。从而解释了图 1两种比率的变动情况。
(3) 消费产出比从低比值上升恢复,而投资产出比比值高且相对稳定。图 1显示,发生金融危机后,2008年11月推出扩大内需的政策,消费产出比于2009年有短期的上升,2010年开始逐渐稳步上升,而投资产出比由于“四万亿”的作用,2009年底跳升至高位以后,基本在相同的比值上波动。由2000-2008年期间两种产出比变动分析,可知金融危机之前政府主导的工业化投资已经遭遇了瓶颈期,金融危机只是转移了注意力,危机的拯救措施反倒使得投资产出比有机会跳升到高比值,这也说明鼓励投资政策可能正在失效;2011年中国经济增速放缓,扩大内需诉求强烈,消费产出比稳步上升,而投资产出比相对稳定。图 3中,投资技术永久性冲击平滑值在2008年之后持续大幅度波动,说明这一时段鼓励投资的政策条件开始变得不稳定,也就解释了图 1中两种比值的变化情况。
综上,投资技术永久性冲击平滑值的变动,基本上与中国促进投资政策有效性相匹配,与其促进投资的可行性高度相关。是解释消费产出比和投资产出比各阶段变化及趋势性差异的主因。而且,稳定有效的投资技术永久性冲击是投资、投资产出比和投资消费比逐渐上升,而消费产出比不断下降的主因;反之,投资技术永久性冲击频繁的调整反倒不利于投资产出比上升,却有可能提高消费产出比。
第三,其他外生冲击平滑值:(1) 生产技术冲击平滑值在2006年之前较为平稳,2007年到2011年正向偏离趋势,同时期内,统计局数据显示科研和开发机构研究与试验发展人员投入,及科研经费支出都有显著提高,从而改善了全要素生产率;而2012年之后又逐渐低于趋势水平,本文无法解释。但由脉冲响应可知,生产技术冲击5期之后会迫使投资消费比下降,与图 1中消费产出比上升,而投资产出比平稳波动相吻合。(2) 消费偏好冲击平滑值在2006年-2011年出现了负向偏离趋势水平的现象,同期内消费产出比降至低点。2011开始恢复上升,而投资产出比稳定在高比率波动。(3) 投资技术暂时性冲击平滑值,在投资产出比和投资消费比变动较为缓慢的时段1996年-1999年、2009年期间以及2011年-2014年间,投资技术暂时性冲击平滑值均高于趋势水平,而投资产出比和投资消费比上升速率较高的时段,2000年-2004年间,投资技术暂时性冲击平滑值均低于趋势水平。可知,在投资速率较高时段,任何形式的投资技术暂时性冲击都有可能会影响到投资的效率。只是2004-2008年间,鼓励投资的政策遭遇瓶颈,投资技术暂时性冲击平滑值低于趋势值。(4) 政策性外生冲击中,财政政策冲击平滑值在2003年之前多是高于趋势水平,2004年以后则大多低于趋势水平;货币政策冲击平滑值相对平稳的时期,2001年-2009年期间,正是投资消费比和投资产出比,乃至于产出均是上升速率较高的时段,说明稳定性政策可能是维持中国经济趋势的因素。
总之,(1) 金融信贷冲击平滑值显示,本文模型可以捕捉到较大的金融事件;(2) 投资技术永久性冲击平滑值变动反应的是促进投资政策条件的变动,与此冲击对投资消费比的脉冲响应相结合,可以较完善的解释消费产出比和投资产出比的阶段性变化。得知,较为稳定的投资技术永久性冲击是促使投资、投资消费比、投资产出比上升的主因; (3) 生产技术冲击平滑值变动反映的是科研创新的变动,与其对投资消费比的脉冲响应相结合,可知生产技术冲击的确可以提高消费并稳定投资,并可解释2004-2008年消费产出比和投资产出比变动差异。
2. 历史拆解样本观测期间,受外生冲击的影响,观测变量会偏离其稳态趋势一定比例,模型中所有外生冲击致使该观测变量偏离趋势百分比的加总,即该观测变量在某一时期偏离趋势的百分比变动,这一分析过程即为历史拆解。这里主要分析外生冲击对投资产出比、投资消费比波动的解释情况。图 4中,实线是观测变量偏离趋势百分比,条状图是各个冲击项对观测变量偏离趋势百分比的贡献。外生冲击对投资产出比、投资消费比的历史拆解可以划分为两种类型:
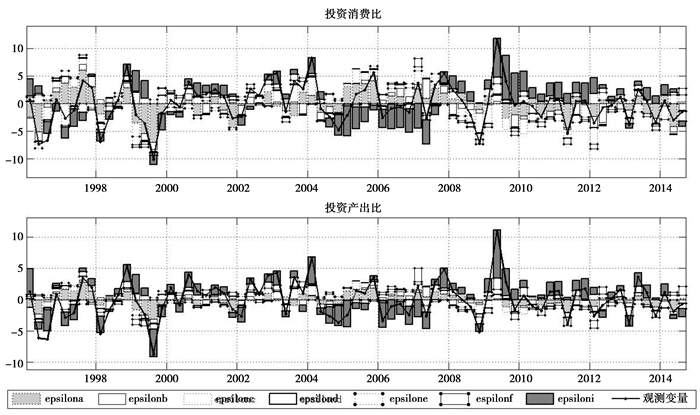
|
图 4 历史拆解 注:条形图的参数分别是:消费偏好冲击epsilona;生产技术冲击epsilonb;投资技术永久性冲击epsilonc;金融信贷冲击epsilond;货币政策冲击epsilone;财政政策冲击epsilonf;投资技术暂时性冲击epsiloni。 |
首先,对投资消费比和投资消费产出比偏离趋势波动解释显著的因素是:消费偏好冲击和投资技术暂时性冲击。图 4中,有颜色填充的条状图,即消费偏好冲击和投资技术暂时性冲击,解释了大部分投资产出比和投资消费比的偏离趋势的变动。尽管二者对投资消费比偏离其趋势百分比变动贡献较多,但他们对投资消费比偏离其趋势的贡献,并非单一的促进上升,或者促使下降,而是交替出现的,多数情况下是出现在观测变量趋势水平线两侧,对投资消费比和投资产出比的波动有平复作用。较特殊的时段:(1) 东南亚金融危机时,采取人民币汇率不贬值的策略,短期投资和消费偏好冲击均出现不利变化,致使1999年中国的投资和消费受到限制,二者对投资产出比和投资消费比均是负向偏离趋势有贡献。(2) 中国汇率制度改革时,2005年有接近于5%的负向偏离,有可能是汇率改革影响了投资的速度,因为这一时点,投资技术暂时性冲击对投资消费比,尤其投资产出比的负向偏离,有超额贡献。(3)2008年金融危机时,受危机的影响,2009年初投资消费比和投资产出比下降显著,中国推出“四万亿”拯救措施,于2009年内,两个观测变量均出现正向偏离,这部分偏离大多被投资技术暂时性冲击解释。总之,消费偏好冲击和投资技术暂时性冲击时解释消费和投资波动性的主因。
其次,对投资消费比和投资产出比历史拆解解释力不强的外生冲击。(1) 根据脉冲响应的特点,投资技术永久性冲击和生产技术冲击是解释投资产出比和投资消费比的趋势性因素,历史拆解中二者对投资产出比、投资消费比偏离趋势的贡献有限,不过由于生产技术冲击大多反映的是全要素生产率的外生变动情况,因而生产技术冲击平滑值对投资消费比的贡献,多是同方向的变动;相比之下,作为解释趋势性特征的主因,投资技术永久性冲击除了在1998年东南亚金融危机和2008年金融危机时期,促使投资消费比负向偏离趋势水平,而2000年-2007年之间大多是少量促进投资消费比正向偏离其趋势。(2) 政策性冲击平滑值对投资产出比、投资消费比偏离趋势的贡献同样较少。不同于投资技术永久冲击和生产技术冲击,尽管脉冲响应显示政策性冲击会对投资产出比、投资消费比等产生影响,而方差分解显示任何时段政策性冲击对观测变量的解释都很少;且历史拆解显示,这两种政策因素对投资产出比、投资消费比的趋势偏离贡献也很少。这说明暂时性政策冲击,在消费不足和投资过度等特征形成过程中,对消费和投资增速差异的波动性解释力相对较小。
总之,外生冲击对投资产出比、投资消费比的历史拆解分析显示,消费偏好冲击和投资技术暂时性冲击,是解释投资消费比偏离趋势的主因;而消费不足和投资过度等趋势性特征解释主因,生产技术冲击和投资技术永久性冲击,对投资产出比、投资消费比偏离趋势的解释较少;而暂时性政策冲击对投资产出比、投资消费比的偏离趋势的解释力也很小,也就是对消费和投资增速差异暂时偏离趋势解释很少。
五、 结论及启示自1996年以来,中国宏观经济波动展现出消费不足和投资过度两大显著特征。为了详细分析这两个特征的成因,即消费和投资增速差异的趋势性和波动性解释因素,本文通过在动态随机一般均衡模型中,设定投资偏向性金融政策和内生化趋势性特征,构建了可以刻画消费和投资增速差异的理论模型,并进一步分析消费和投资经历的阶段性变化及两个特征的成因和后果。采用中国1996年1季度至2014年4季度的六组季度数据作为观测变量,结合贝叶斯方法估计模型参数,并利用脉冲响应、方差分解、平滑值分析和历史拆解方法识别内生化趋势特征及外生冲击对中国经济运行的影响。分析结果表明:
首先,用脉冲响应来辨明观测变量的趋势性和波动性解释因素。分析表明:生产技术冲击5期之后,会促使投资消费比、投资产出比等负向偏离趋势水平,投资技术永久性冲击2期之后,会促使投资消费比、投资、投资产出比等正向偏离趋势水平,这两类冲击对投资消费比来讲,是趋势性解释因素;其他外生冲击对投资消费比的脉冲响应,无论动态调整路径如何变化,最终会回到趋势水平,均是波动性解释因素。
其次,用方差分解辨明观测变量波动性解释因素的相对重要性。分析表明:投资消费比的波动解释因素中,消费偏好冲击、投资技术永久性冲击和投资技术暂时性冲击最为突出,短期可以分别解释30%、14.7%和33.3%的波动;而长期可以分别解释26.1%、24.6%、31.3%的投资消费比波动。当然,这三者也是投资、投资产出比波动的解释主因,只不过投资技术暂时性冲击解释百分比会变的更高。
最后,用平滑值来深入分析消费产出比和投资产出比等所经历的阶段性变化,用历史拆解分析投资消费比和投资产出比的波动性变化。平滑值分析表明:鼓励投资政策的持续稳定性,及市场可行性是划分消费产出比和投资产出比阶段性变化的关键。与脉冲响应相结合可知:较为稳定的投资技术永久性冲击,是促使消费产出比和投资产出比按各自趋势快速变动的主因,而投资技术永久性冲击稳定性较差的时期,这两种比值相对稳定。样本期间内,投资消费比和投资产出比历史拆解表明:消费偏好冲击和投资技术暂时性冲击是解释投资消费比和投资产出比波动的主因。
基于上述研究结论,可以得到以下三点启示:一是,由于偏向性金融政策的存在,带来了投资技术永久性冲击,最终形成了过度投资。由此引发了严重的产能过剩问题,并造成了资源错配,因而化解这一问题需要从其根源出发,建立市场化的投资环境,提高资源配置效率。同时,由图 1可知,2010年以来,由于政府一系列政策改革,使得消费产出比有上升的势头,而投资产出比维持在了高位水平没有进一步升高的迹象。二是,短期的消费刺激计划虽然可以影响短期经济波动,但无法逆转长期以来形成的消费不足问题。因而使得家户部门很难从经济的快速成长当中,获得相同增速的福利水平提升。在本文的分析框架下,要根本上改变这一趋势,需要通过市场化改革淡化偏向性金融政策对投资的影响。此外,技术水平的提高也可以有效提升消费占总产出的比重。三是,本文分析结果表明,即便是没有发生2008年金融危机,偏向性金融政策所带来的投资增长效果也将缺乏动力。从而使经济增速放缓,进入所谓的“新常态”。倒逼企业进行结构性改革,通过技术进步而非扩大规模获得竞争优势。同时,也从客观上要求进一步完善市场机制,形成以市场为导向的投资环境。
| [] | 曹春方、马连福、沈小秀, 2014, "财政压力、晋升压力、官员任期与地方国企过度投资", 《经济学 (季刊)》, 第 04 期, 第 1415–1436 页。 |
| [] | 陈彦斌、郭豫媚、陈伟泽, 2015, "2008年金融危机后中国货币数量论失效研究", 《经济研究》, 第 04 期, 第 21–35 页。 |
| [] | 何青、钱宗鑫、郭俊杰, 2015, "房地产驱动了中国经济周期吗?", 《经济研究》, 第 12 期, 第 41–53 页。 |
| [] | 贺振华, 2006, "寻租、过度投资与地方保护", 《南开经济研究》, 第 02 期, 第 64–73 页。 |
| [] | 黄俊、李增泉, 2014, "政府干预、企业雇员与过度投资", 《金融研究》, 第 08 期, 第 118–130 页。 |
| [] | 李成、马文涛、王彬, 2011, "学习效应、通胀目标变动与通胀预期形成", 《经济研究》, 第 10 期, 第 39–53 页。 |
| [] | 李成、王彬、马文涛, 2010, "资产价格、汇率波动与最优利率规则", 《经济研究》, 第 03 期, 第 91–103 页。 |
| [] | 林仁文、杨熠, 2014, "中国市场化改革与货币政策有效性演变——基于DSGE的模型分析", 《管理世界》, 第 06 期, 第 39–52 页。 |
| [] | 林毅夫、苏剑, 2007, "论我国经济增长方式的转换", 《管理世界》, 第 11 期, 第 5–13 页。 |
| [] | 罗党论、应千伟、常亮, 2012, "银行授信、产权与企业过度投资:中国上市公司的经验证据", 《世界经济》, 第 03 期, 第 48–67 页。 |
| [] | 吕冰洋、毛捷, 2014, "高投资、低消费的财政基础", 《经济研究》, 第 05 期, 第 4–18 页。 |
| [] | 马理、娄田田, 2015, "基于零利率下限约束的宏观政策传导研究", 《经济研究》, 第 11 期, 第 94–105 页。 |
| [] | 唐雪松、周晓苏、马如静, 2010, "政府干预、GDP增长与地方国企过度投资", 《金融研究》, 第 08 期, 第 99–112 页。 |
| [] | 王文甫、明娟、岳超云, 2014, "企业规模、地方政府干预与产能过剩", 《管理世界》, 第 10 期, 第 17–36 页。 |
| [] | 王彦超, 2009, "融资约束、现金持有与过度投资", 《金融研究》, 第 07 期, 第 121–133 页。 |
| [] | 许伟、陈斌开, 2009, "银行信贷与中国经济波动:1993-2005", 《经济学 (季刊)》, 第 03 期, 第 969–994 页。 |
| [] | 张伟进、方振瑞, 2013, "金融冲击与中国经济波动", 《南开经济研究》, 第 05 期, 第 3–20 页。 |
| [] | 张伟进、胡春田、方振瑞, 2014, "农民工迁移、户籍制度改革与城乡居民生活差距", 《南开经济研究》, 第 02 期, 第 30–53 页。 |
| [] | 中国经济增长前沿课题组, 2012, "中国经济长期增长路径、效率与潜在增长水平", 《经济研究》, 第 11 期, 第 4–17 页。 |
| [] | 中国经济增长前沿课题组, 2013, "中国经济转型的结构性特征、风险与效率提升路径探讨", 《经济研究》, 第 10 期, 第 5–17 页。 |
| [] | 中国经济增长前沿课题组, 2014, "中国经济增长的低效率冲击与减速治理", 《经济研究》, 第 12 期, 第 4–17 页。 |
| [] | Chang, C., K. Chen, D. Waggoner and T. Zha, 2015, "Trends and Cycles in China's Macroeconomy", The NBER Macroeconomics Annual 2015, University of Chicago Press. |
| [] | Chen, L. and Naughton, B. , 2016, "An Institutionalized Policy Making Mechanism: China's Return to Techno-Industrial Policy". Research Policy, 45(10), 2138–2152. DOI:10.1016/j.respol.2016.09.014 |
| [] | Greenwood, J. , Hercowitz, Z. and Krusell, P. , 1997, "Long Run Implications of Investment Specific Technological Change". American Economic Review, 87(3), 342–362. |
| [] | Hsieh, C. and Z. M. Song, 2015, "Grasp the Large, Let Go of the Small: The Transformation of the State Sector in China", Brookings Papers on Economic Activity, 295-346. |
| [] | Iacoviello, M. 2015, "House Prices, Borrowing Constraints, and Monetary Policy in the Business Cycle". American Economic Review, 95(3), 739–764. |
| [] | Ireland, P. N. 2013, "Productivity and US macroeconomic performance: Interpreting the past and predicting the future with a two-sector real business cycle". Journal of the European Economic Association, 11(1), 1–24. DOI:10.1111/j.1542-4774.2012.01108.x |
| [] | Ireland, P. N. and Schuh, S. , 2008, "Productivity and US macroeconomic performance: Interpreting the past and predicting the future with a two sector real business cycle model". Review of Economic Dynamics, 11(3), 473–492. DOI:10.1016/j.red.2007.10.001 |
| [] | Justiniano, A. , Primiceri, G. E. and Tambalotti, A. , 2011, "Investment shocks and the relative price of investment". Review of Economic Dynamics, 14(1), 102–121. DOI:10.1016/j.red.2010.08.004 |
| [] | Karabarbounis, L. and Neiman, B. , 2014, "The Global Decline of the Labor Share". Quarterly Journal of Economics, 129(1), 61–103. DOI:10.1093/qje/qjt032 |
| [] | Liu, Z. , Wang, P. and Zha, T. , 2013, "Land Price Dynamics and Macroeconomic Fluctuations". Econometrica, 81(3), 1147–1184. DOI:10.3982/ECTA8994 |
| [] | Sargent, T. J. and Surico, P. , 2011, "Two Illustrations of the Quantity Theory of Money: Breakdowns and Revivals". American Economic Review, 101(1), 109–128. DOI:10.1257/aer.101.1.109 |
| [] | Smets, F. and Wouters, R. , 2003, "An Estimated Dynamic Stochastic General Equilibrium Model of The Euro Area". Journal of the European Economic Association, 1(5), 1123–1175. DOI:10.1162/154247603770383415 |
| [] | Smets, F. and Wouters, R. , 2007, "Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach". American Economic Review, 97(3), 586–606. DOI:10.1257/aer.97.3.586 |
| [] | Song, Z. , Storesletten, K. and Zilibotti, F. , 2011, "Growing Like China". American Economic Review, 101(1), 196–233. DOI:10.1257/aer.101.1.196 |
| [] | Walsh, C. E., 2010, "monetary theory and policy", Third edition. |




