自Lucas (1988)以来,关于人力资本和经济增长的讨论已经非常多,人力资本投资能够显著促进经济增长的观点已经是一个共识,这里不再赘述。如果仅仅关注增长,那么只需要提高社会资源对人力资本的配置即可,问题在于近些年人们逐渐开始关注人力资本投资对收入差距的影响 (Shea, 2000)。当社会平均收入水平达到一定程度以后,“不患寡而患不均”成为一个日益重要的问题,而“寒门难出贵子”是由此引致的一个被广为关注的现象。这主要源于人们生活中的一些观察性结果,家庭背景较好的子女更容易就读优质中学、大学,在就业方面资源也更加广泛,这会使得社会不同阶层间的财富流动更加缓慢,固化了社会阶层。反对者认为,贫苦家庭的子女更可能上进,这主要源于他们勤奋努力的边际收益高于富裕家庭子女,因而这批学生的教育回报更高,底层家庭的子女收入会因为教育而得到改善。
应当说,如果一般家庭子女的教育回报更高的假设成立,那么反对者的意见是有合理的。问题在于,事实是否真是如此?目前的研究集中于家庭收入差距是否影响教育水平选择,或者不同收入水平的个人教育回报率的差异。但这些研究还不够,政府即使通过政策手段,使不同家庭背景的个人获得同等教育机会,也未必能够缩小收入差距。如果一般家庭的子女受大学教育的回报低于富裕家庭的子女受同样大学教育的回报,那么不同社会阶层的收入差距仍将扩大。
这并非没有根据。就目前的社会现象来看,对初等教育而言,富裕家庭能够支付昂贵的学区房,使子女入读更好的小学、中学,甚至幼儿园。除此以外,在课外辅导班、省市级课余比赛上的支出,也都需要以家庭的财力为支撑。对于高等教育,富裕家庭的子女优势主要体现在专业选择、社会实践、实习经历上,这些隐性资源对未来收入有至关重要的作用。以金融业为例,尽管劳动者平均收入更高,但收入不确定性也很大,一般家庭子女往往风险规避意愿更强,所以选择高学费专业的概率更小。从宏观层面加总来看,这意味着一般家庭子女的期望收入很可能因为专业选择而低于富裕家庭子女。不过,社会现象并不总是与经济分析的表现一致,对“寒门难出贵子”的真实性及背后原因进行严谨的经济学讨论是有必要的。
“新常态”自2014年被用来描述中国新阶段的经济发展状况,除去关于新常态的经济及政治模式不论,单从经济发展角度来讲,新常态指的是中国未来的均衡经济增速将显著低于2012年以前的经济增速的状况,从国务院报告来看,决策层对新时期经济增速的预期是7%,低于前三十年的8.8%。对新常态经济增速较低的解释是中国的人口红利在消失,资本回报率在降低,其中,人力资本既是人口红利转变的重要方向,也是资本结构转型的一个渠道,在“新常态”的经济发展中将起到重要作用。这里之所以特别讨论“新常态”的影响,是因为人力资本投资与收入差距的关系会随着经济增长的变化而变化。当经济增速较高时,一方面,教育回报的不确定性变小,教育选择受家庭收入的影响可能更小;另一方面,在同等教育水平下,能够支付各种教育费用的家庭会越来越多。这些都有助于缩小收入差距。但当经济增速较低时,教育回报不确定性变大,家庭收入增长也更为缓慢,这意味着,在“新常态”下,人力资本投资与收入差距之间的问题很可能更为严重。
本文的贡献首先在于,我们从理论上证明了当家庭财富影响教育回报率时,社会整体收入差距确实会增大,并在实证检验中证明了这个结论。此外,我们还发现,尽管增大普通家庭的教育回报率有利于提高社会平均收入水平,但客观上社会整体的收入差距也会增大,在某些条件下,收入差距增大的速度甚至高于富裕家庭教育回报率提高的情况。基于这两个结论,我们对目前现有或将有的高等教育政策,如“高奖学金高学费”、“金融、法律专业硕士高收费”等进行了评价,认为这些政策将在长期使得社会收入差距进一步扩大。最后,我们第一次从一个极长的时间跨度 (1991-2009) 来探讨不同家庭教育回报率差异的趋势变化,并据此对教育产业化与收入差距的关系进行了讨论。
全文结构安排如下:第二部分是文献综述与理论模型的提出;第三部分提出计量模型;第四部分是数据和实证结果;第五部分讨论家庭财富与收入差距的长期趋势,以及对收入差距的一个反事实检验;第六部分是“新常态”下的研究展望,第七部分是结论和政策建议。
二、 文献综述与理论假说 (一) 文献综述关于教育对社会收入差距影响的研究有很多。作为一种人力资本投资,不同的教育水平对收入的影响最先被人们关注,个体接受的教育程度不同会带来社会收入分化,这已经是一个共识 (Mincer, 1974; Becker, 1975; Perotti, 1996; Sylwester, 2002)。后续的劳动经济学开始关注个人能力在教育与收入关系中起到的作用,由于到能力越强的人越有可能接受高水平教育,所以教育引致的收入不平等程度经常被高估。除此以外,教育这个概念本身也被扩展,更广义的人力资本或者人类发展指数对收入差距的影响也被纳入讨论 (Theyson and Heller, 2015)。
早期的研究关注个人的教育选择和教育回报,而没有考虑家庭在教育选择与收益中的影响。Jencks (1977)全面讨论了之前关于教育、家庭和收入差距的研究,认为家庭在子女是否能够接受教育、接受教育的质量以及教育回报率方面都有明显的影响。Atkinson et al. (2011)更是在一个较长的历史时期内,讨论了高收入阶层是如何通过教育传递财富的。
如果把教育视为一种投资,那么这个投资决策在大多数时候是由父母为子女选择的。这时候,尽管有智力遗传、代际财富转移的因素被纳入进来,但简单而言,家庭面对的也是成本收益之间的权衡。大多数研究关注收益侧,传统的观点认为,低收入家庭的教育投资由于信贷约束的存在而受到抑制, 因此他们的教育投入低于最优水平, 其子女的教育收益率应该远远高于高收入家庭子女的教育收益率 (Becker and Tomes, 1986; Jerrim and Macmillan, 2014)。但袁诚、张磊 (2009)使用2002年CHIP数据所做的截面分析,提出了相反的观点,他们认为这样的判断没有考虑教育、能力以及收入在代际间的传递, 因此与现实中贫困学生的高等教育结果并不完全一致。父母的收入水平不仅影响子女的受教育水平, 而且也影响他们的受教育结果。特别是在发展中国家, 贫困学生的就业和毕业收入情况仍然受到自身家庭的社会和经济背景的显著影响, 较高的教育收益率对于他们而言是一个过于乐观的判断。
李任玉等 (2014)研究了教育在代际传承之外的影响路径,他们使用CHNS数据,将观测样本的家庭分为高、低收入两个样本,通过构建反事实样本,发现高、低收入家庭的子女之间的收入差距主要来源于教育不平等,而两组子女的教育回报也有差异。值得一提的是,这个研究使用了多年的CHNS数据,不过可能因为样本数量所限,最后仍然采用了一般的OLS方法,没有分析时间趋势上的变化。Qin et al. (2014)也使用CHNS数据研究了1989-2009年中国家庭代际人力资本转移与收入差距的关系,发现父辈的收入不平等通过健康、教育途径直接引致了子辈的收入不平等,而且这种转移效应越来越大。周兴、张鹏 (2015)则发现职业的代际传承也阻碍了代际间的收入流动,而这种传承效应在高收入家庭弹性影响更强。陈永伟、陈双双 (2015)将将收入差距进行分解,分为公平和非公平的差距,教育回报不同带来的差距被视作公平的,地区、行业等因素导致的收入差距被视作不公平的,他们发现大学教育回报率上升是公平收入差距上升的主因,地区因素和高利润行业 (房地产等) 因素是不公平收入差距上升的主因。
近20年来,对教育成本侧的研究逐渐兴起。这是由于很多对收益侧的研究很难回答一个问题,即既然教育的期望回报率很高,而且信贷约束在变宽松,为何很多贫困家庭仍然不选择让子女接受更多教育,这并不符合理性人最大化个人收益的假设。Maoz and Moav (1999)构建了一个理论模型,试图说明教育成本保持较低增速能够降低社会收入不平等水平。Nakamura and Yu (2011)对这个模型进行了拓展,指出这个理论框架对教育成本的增速设定极为敏感,不同的增速假设会带来截然相反的结果,但他们仍然认为教育成本增速的影响至关重要。Yang and Qiu (2016)研究了中国的教育成本、收入差距问题,发现不同家庭在孩子义务教育阶段的成本投入直接影响子女的收入水平。张川川 (2015)则研究了教育的机会成本,发现出口增长带来的需求冲击增加了非农就业,这增大了教育的机会陈本,导致适龄人口的高中和大学入学率显著下降,但农村和城市的家庭教育选择有明显差别,农村青年进入高中和大学学习的概率都随着就业增长出现了显著下降,城镇青年进入大学学习的概率有显著下降,但进入高中的概率有显著上升。
不论是成本侧还是收益侧的文献,在这一类研究框架下,教育常常被视为同质的,但越来越多的研究者开始关注不同质的教育对收入不平等的影响。Pritchett (1996)进行了一项大规模的跨国比较,发现人力资本投资对经济增长的作用差别极大,其中一项很重要的原因在于同等年限下的教育质量差异很大。即便对于同质的两个人,由于家庭不同,对教育质量的选择也不同 (即使受教育年限相同)。这里除了家庭对成本因素的考虑以外,还有教育回报存在不确定性的问题,而低收入家庭对不确定性的规避意愿更强 (才国伟、刘剑雄,2014),所以低收入家庭更倾向于让子女接受普通质量的教育,反映在具体行为上,就是选择略为普通的中学,不参加提高全面技能的大学生培训,不填报金融硕士等高学费的研究生专业等,这些行为选择本身就意味着未来的预期回报下降,而从社会整体来看,这就代表高收入家庭群体与低收入家庭的差距会进一步拉大。杨娟等 (2015)构建了一个四期的世代交叠模型,从理论层面说明,贫困家庭由于受预算约束限制,对孩子的早期教育投入较少,所以义务教育阶段的人力资本积累较低,而这拉低了贫困家庭的高等教育参与率,使得社会收入差距扩大。他们用校准方法模拟了各种教育经费的投入模式,发现增大义务教育阶段的经费投入有助于降低收入差距。
值得一提的是,从宏观层面来看,社会收入差距本身是否与教育选择存在反向因果关系是应当考虑的,不过很多研究并未注意这个问题。在Lundberg and Squire (2003)对收入差距和经济增长的研究、以及Barro (2000)对于增长、投资和收入差距的讨论中,教育都没有被作为内生变量来处理。而陆铭等 (2005)的研究考虑了内生性问题,他们建立了一个教育方程,并考察教育如何受到收入差距的影响,不过他们发现收入差距对教育的影响极弱。本文所构建的理论模型里,教育选择仅仅跟个体家庭收入相关,社会整体的收入差距本身不会影响家庭决策的既有标准。不过从实证研究的角度,仍然存在收入差距影响教育选择的可能性,因此对实证结果进行稳健性检验仍然是有必要的。
在教育水平之外,教育质量和就业行业选择的影响正在越来越大。仅就教育年限来看,低收入家庭在初等教育上的回报率是否高于高收入家庭这个问题本身就存在争议 (Bishop et al., 2005; Knight and Song, 2003; 罗楚亮,2006;张车伟,2006;高梦滔、姚洋,2006)。因此,教育能够缩小社会整体的收入差距这个推断本身并非是一个共识。而这些研究的统计方法也存在问题,这些研究基本使用了分位数回归,数学上,基于个体条件分布的分位数回归结果,是否能够被用来解释社会整体的收入差距是不确定的,邢春冰 (2008)构建了一系列数值样本,证明即使高分位数收入的教育回报率低于低分位数,既可能带来社会整体收入差距缩小的结果,也可能得到增大的结果。
尽管如此,“寒门难出贵子”仍然是日益引人关注的一个话题 (王婧,2013),诚然农村人口比例下降是一个原因,但这个原因不足以解释“寒门”越来越难提高个人以及家庭收入的状况。出于人力资本投资会带来高回报,而高回报的投资则可以要求高成本的直观理论,政策层推出了很多增大教育成本的提议,学界也提供了相应的理论支持 (蒋和胜等,2013),其中“教育产业化”、“高价金融、法律专业硕士”、“高学费高奖学金”(张维迎,2006) 等政策是代表,而“学区房”、课外竞赛则是伴生产物。
用同样的逻辑,我们可以预计如果部分学者建议的名校“高学费高奖学金”制度出台,那么低收入家庭将更倾向于不填报这类名校,尽管名校的期望回报率会更高。那么可以预见,由人力资本投资差异带来的社会总体的收入差距会更大。尽管理论上可以将高学费转化为对低收入家庭子女的助学金,但在收入上报相对不透明的环境下,这种做法的可行性很低。
此外,对金融、法律这类专业的高收费,还会引发不同家庭的自选择问题,使得中低收入家庭倾向于不选择此类专业,降低这类家庭的子女未来进入金融、法律行业的可能性。由于这些行业的平均收入水平高于其他行业,所以这种自选择也会加大贫富差距。
“新常态”在这里之所以重要,是因为自2009年以来家庭教育费用支出快速增大,这一方面反映了经济结构转型时候消费的扩大,另一方面则隐含着不同家庭教育开支差异扩大的状况,后者对收入差距的影响尤为重要。
人力资本积累一方面靠培训,而更重要的方面是教育。良好的教育模式,不仅应当使经济持续稳定高速增长,也应当使得社会收入差距稳定在一个合理的水平。本文通过构建一个理论模型,同时依靠实证结果的支持,试图说明降低优质教育的学费门槛,能够促进社会转向一个良好的人力资本培养环境,而“教育产业化”的模式,以及目前正在实质性发生的高等教育高奖学金高学费的方式 (金融硕士、法律硕士等),不仅会拉低经济增速,而且会扩大社会收入差距,其中原因在于,一方面中国的低收入人群仍然很多,高学费门槛会增加突破“贫困陷阱”的难度;另一方面教育回报存在不确定性,收入较低家庭的高成本教育的回报不确定性更加敏感,从而倾向于接收低成本教育,拉开与高收入家庭的差距。
(二) 理论假说在本文的理论模型里,人力资本是唯一的投资,物质资本没有被考虑在内,所以经济的长期增长几乎完全由人力资本投资带动 (除去家庭财富的自然增长)。
我们设定一个无限期延续的代际交迭模型,代表性个人存活两期 (青年期和老年期)。为了研究方便,我们假设每个家庭每代有且仅有一个子女 (后续我们将讨论扩展层面的多子女模型)。这样,对任意第t(t > 0) 期,每个代表性家庭各有一个处于老年期的个人和青年期的子女。每个家庭初始期 (第0期) 的财富被随机分配,假设第i个人的初始财富为Yi0Yi0,其中i=1, 2, …, N, 而N为社会总人数。如果没有教育投资,那么家庭财富值以一个外生的速度a增长。
在随后各期,家庭的财富增长依靠个人的教育投资回报。代表性个人仅能在青年期接受教育,教育回报自动进入家庭财富。根据家庭原先积累财富的差异,个人接受的教育选择也有所差别:富裕家庭的教育类型H,普通家庭的教育类型L,或者不接受教育 (零教育)。H和L并非一定是有差异的教育环境,两个个体的教育环境可以相同 (如同一所学校),这里用不同标记是为了说明二者所处的家庭环境有差异。富裕家庭接受教育H的成本为CH,而教育回报是不确定的,可能以πH的概率实现收益1+rH,或者以1-πH的概率实现收益1+rL。普通家庭接受教育L的成本为CL,而教育回报也是不确定的,可能以πL的概率实现收益1+rH,或者以1-πL的概率实现收益1+rL。我们假设CH > CL, πH > πL, rH > rL,直观意义就是,富裕家庭接受教育的成本更高,同时教育的期望收益也更高。CH > CL在很大程度上是家庭的主动选择,富裕家庭可以负担更多的培训班、家庭教师等,而这些额外的教育投入也能够提高子女的期望教育回报率。最后,如果不接受教育,那么个人的教育投入及回报都为零。H、L的教育成本都按照外生固定增速g增长。
在这个模型里,家庭财富通过两种渠道增长,第一是上一代留存下来的财富的自然增长,第二则是下一代通过教育投资来提高收入。
在第1期,若个人i来自富裕家庭,则接受教育H,其期望收益如下所示
| $ EY_{iH}^{1}=[{{\text{ }\!\!\pi\!\!\text{ }}_{H}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{H}} \right)\left( 1+{{r}_{L}} \right)]\left( Y_{i}^{0}-{{C}_{H}} \right) $ | (1) |
若是普通家庭,则接受教育L,期望收益为
| $ EY_{iL}^{1}=[{{\text{ }\!\!\pi\!\!\text{ }}_{L}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{L}} \right)\left( 1+{{r}_{L}} \right)]\left( Y_{i}^{0}-{{C}_{L}} \right) $ | (2) |
若不接受教育,收益为
| $ Y_{i}^{1}=\left( 1+a \right)Y_{i}^{0} $ | (3) |
由于 (CH, CL, πH, πL, rH, rL) 均确定且外生给定,所以Y0iYi0是唯一影响受教育选择的参数。
首先考虑受教育门槛值 (threshold),也就是“贫困陷阱”的临界点,接受教育的充要条件为
| $ Y_{i}^{0}\ge \frac{\left[ {{\text{ }\!\!\pi\!\!\text{ }}_{H}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{H}} \right)\left( 1+{{r}_{L}} \right) \right]{{C}_{H}}}{{{\text{ }\!\!\pi\!\!\text{ }}_{H}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{H}} \right)\left( 1+{{r}_{L}} \right)-1-a} $ | (4) |
或
| $ \text{Y}_{\text{i}}^{\text{0}}\ge \frac{{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}}\left( 1+{{\text{r}}_{\text{H}}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right){{\text{C}}_{\text{L}}}}{{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}}\left( 1+{{\text{r}}_{\text{H}}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right)-1-\text{a}} $ | (5) |
所以受教育门槛收入水平为
| $ \text{Y}_{\text{th}}^{\text{0}}\text{=min(}\frac{\text{ }\!\![\!\!\text{ }{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}}\text{1}+{{\text{r}}_{\text{H}}}+\text{1}-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}}\text{1}+{{\text{r}}_{\text{L}}}\text{ }\!\!]\!\!\text{ }{{\text{C}}_{\text{H}}}}{{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}}\left( \text{1}+{{\text{r}}_{\text{H}}} \right)+\left( \text{1}-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}} \right)\left( \text{1}+{{\text{r}}_{\text{L}}} \right)-\text{1}-\text{a}}\text{,}\frac{\text{ }\!\![\!\!\text{ }{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}}\text{1}+{{\text{r}}_{\text{H}}}+\text{1}-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}}\text{1}+{{\text{r}}_{\text{L}}}]{{\text{C}}_{\text{L}}}}{{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}}\left( 1+{{\text{r}}_{\text{H}}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right)-1-\text{a}}) $ | (6) |
为方便起见,记
| $ A={{\pi }_{H}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\pi }_{H}} \right)\left( 1+{{r}_{L}} \right),\text{B}={{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}}\left( 1+{{\text{r}}_{H}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right) $ |
则有
| $ \text{Y}_{\text{th}}^{\text{0}}=\text{min}\left\{ \frac{\text{A}{{\text{C}}_{\text{H}}}}{\text{A}-1-\text{a}},\frac{\text{B}{{\text{C}}_{L}}}{\text{B}-1-\text{a}} \right\} $ | (7) |
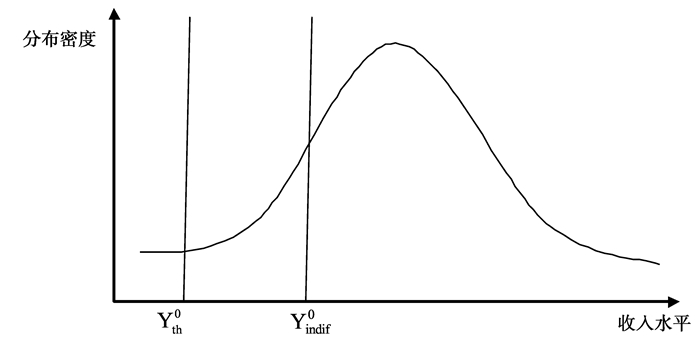
家庭财富高于Yth的人接受类型为H或者L的教育,而低于Yth的人将选择不接受教育。
然后我们考虑两种教育类型H与L间的无差异条件,即
| $ \text{EY}_{\text{iH}}^{1}=\text{EY}_{\text{iL}}^{1} $ | (8) |
变形后,可得到
| $ Y_{indif}^{0}=\frac{A{{C}_{H}}-B{{C}_{L}}}{A-B} $ | (9) |
家庭财富高于
此外,为了简化讨论,我们预先假定
|
图 1 教育门槛与无差异点 |
第2期,原先个人的收入将作为财富留存在家庭中,其回报率为1+a。家庭的新一代个体重新开始选择是否接受教育,与第1期类似,若个人i所处家庭进入富裕阶层,则接受教育H,其期望收益如下所示
| $ E{{Y}_{iH}}^{2}=A\cdot [Y_{i}^{1}\left( 1+a \right)-\left( 1+g \right){{C}_{H}}] $ | (10) |
若进入普通家庭,则接受教育L,期望收益为
| $ E{{Y}_{iL}}^{2}=B\cdot [Y_{i}^{1}\left( 1+a \right)-\left( 1+g \right){{C}_{L}}] $ | (11) |
若不接受教育,则收益为
| $ Y_{i}^{2}=\left( 1+a \right)Y_{i}^{1} $ | (12) |
与第1期方法相同,可以得到受教育门槛收入水平为
| $ Y_{th}^{1}=\text{min }\left\{ \frac{\left( 1+g \right){{C}_{H}}}{{{\pi }_{H}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\pi }_{H}} \right)\left( 1+{{r}_{L}} \right)},\frac{\left( 1+g \right){{C}_{L}}}{{{\pi }_{L}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\pi }_{L}} \right)\left( 1+{{r}_{L}} \right)} \right\} $ | (13) |
两种教育类型H与L间的无差异条件为
| $ Y_{indif}^{1}=\frac{\left( 1+g \right)(A{{C}_{H}}-B{{C}_{L}})}{\left( 1+a \right)\left( A-B \right)} $ | (14) |
第3期,第4期,……,与前面过程类似,不再赘述。
1. “贫困陷阱”问题对各期家庭而言,财富值低于Yth的家庭的最优决策是不接受教育,也就是说,这批家庭在世代财富积累中只能获得财富自然增长的收益率1+a,而无法从教育中获益。由此,尽管所有家庭的财富都会获得增长,但处于门槛线以下的家庭与受教育家庭的财富差距可能会越来越大。
容易推出,财富门槛值在各期的增长率为1+g,而对于不接受教育的家庭,其财富增长率为1+a,“贫困陷阱”是否出现,或者是否会消褪,将取决于g和a的大小关系。直观地,若g > a,那么门槛值的增速将超过财富自然增速,贫困陷阱不仅会持续存在,而且会覆盖越来越多的人口。其经济学意义是,对家庭而言,教育负担的增速若超过社会的自然财富增长速度,那么即使教育本身能够带来高回报,最终处于“贫困陷阱”区域内的人口也会越来越多。
2. 贫富差距问题即便“贫困陷阱”问题解决,家庭的绝对收入水平能够稳定上升,问题也只解决了一半,因为“不患寡而患不均”,所以贫富差距问题也非常重要,而且正在显得越来越重要。
在这个模型里,贫富差距的来源除了是否接受教育之外,还在于接受教育的回报率。尽管教育回报的不确定性导致很难解出降低贫富差距的充要条件,但直观来看,降低受教育的无差异收入水平Yindif在社会收入序列中的位置一定是减轻贫富差距的一个必要条件。
考虑一个足够大的样本,当期家庭的收入水平从小到大依次为{Y1, Y2, Y3, …, YN},由于样本足够大,所以我们可以用期望收益替代真实收益来近似样本整体的收入排序状况,因此,下一期家庭的收入水平可以记做如下形式:
| $ \left\{ \left( 1+\text{a} \right){{\text{Y}}_{1}},\cdots ,\text{B}\left( {{\text{Y}}_{\text{th}}}-{{\text{C}}_{\text{L}}} \right),\cdots ,\text{A}\left( {{\text{Y}}_{\text{indif}}}-{{\text{C}}_{\text{H}}} \right),\cdots ,\text{A}\left( {{\text{Y}}_{\text{N}}}-{{\text{C}}_{\text{H}}} \right) \right\} $ |
理论上,计算出该期社会群体的收入分布函数F·,我们就可以得到无差异收入水平Yindif所处的分位数位置F-1(Yindif)。由于计算概率分布函数并非本文的研究重点,所以我们选择计算特定情况下的分布函数,所谓特定情况,指的是我们由回归分析以及前人研究得到的结果,来直接设定模型相关参数的值 (参数设定细节见附录),然后使用数值模拟方法就可以得到世代交迭的社会收入分布状况。
为便于直观研究,我们着重研究了富裕家庭教育回报增大或者普通家庭教育回报增大的情况下,整个社会的收入增速和差距状况。由于教育回报存在不确定性,所以我们没有选择直接提高富裕家庭的教育回报率,而是采用了间接的方法,提高富裕家庭 (或者普通家庭) 获得高教育回报率的概率。三种情形如下所示:情形一:基准情形;情形二:富裕家庭获得高回报的几率提高0.2;情形三:一般家庭获得高回报的几率提高0.2。
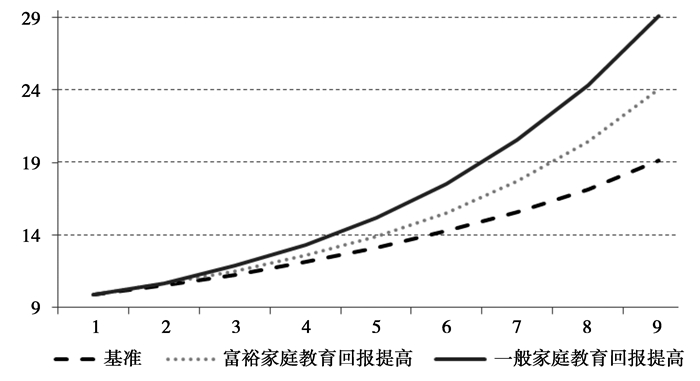
下图是数值模拟方法得到的三种情形下收入增速图。在基准情形下,社会收入水平以对数线性速度稳定增长,之所以增长,是因为在模型设定下,教育的期望回报率高于教育成本的提高速度,人力资本投资带来了收入的增长。在富裕家庭教育回报提高的情况下,社会平均的期望教育回报率也提高,所以收入增速高于基准情形。而在普通家庭教育回报提高的情况下,收入增速提高在三种情形里最快,这是因为普通家庭教育回报本身就低于富裕家庭,所以提高的边际效果高于富裕家庭。
|
图 2 收入增速模拟 |
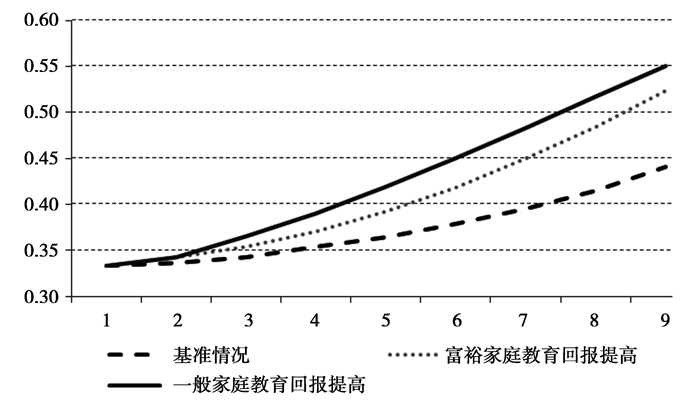
下图是三种情形下社会基尼系数的变化图。从图中可见,增大富裕家庭的回报 (增加富裕家庭教育获得高回报的概率),会导致社会整体的收入差距扩大。这是因为富裕家庭与普通家庭的组间收入差距增大,进而导致基尼系数增大。
出乎意料的是,提高一般家庭的教育回报 (增加一般家庭教育获得高回报的概率) 也会拉大收入差距。从常理来讲,提高一般家庭教育回报率,会缩小两组家庭的组间收入差距,应当有助于降低基尼系数。但从模拟结果来看,组内收入差距扩大带来的影响不容忽视。即便两组家庭的平均收入差在降低,但由于一般家庭组内的收入差距扩大,社会总体的基尼系数也可能增加,甚至超过第二种情形下组间收入差距增大的影响。①
① 如图 3所示,在某些参数设定下,提高一般教育回报率会增大社会总体基尼系数。作者同时验证了这不是极端状况,在很多正常条件的参数设定下,这个结果仍然成立。
|
图 3 基尼系数模拟 |
一个家庭仅有一个子女的假设过于严格。尽管有计划生育政策,但子女超过一个的家庭不是少数,本文有必要讨论多子女情况下的家庭教育选择与收入差距的关系。在放松假设的情况下,检验原有结论是否会有变化。
考虑内生的生育决策,一个家庭生育m个孩子。与只生育一个的情形不同,这里的教育决策不再是两个 (受教育或者不受教育),而是多个,即选择m1个孩子接受教育,m2个孩子不接受教育,其中m1和m2非负,且m1+m2=m。
假设家庭财富在子女中均分。在第1期,对富裕家庭i,子女接受教育的类型为H,其期望收益如下所示
| $ EY_{iH}^{1}=[{{\pi }_{H}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\pi }_{H}} \right)\left( 1+{{r}_{L}} \right)](\frac{{{m}_{1}}}{m}Y_{i}^{0}-{{m}_{1}}{{C}_{H}})+\left( 1+a \right)\frac{{{m}_{2}}}{m}Y_{i}^{0} $ | (15) |
若是普通家庭,则接受教育的类型为L,期望收益为
| $ EY_{iL}^{1}=[{{\pi }_{L}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\pi }_{H}} \right)\left( 1+{{r}_{L}} \right)](\frac{{{m}_{1}}}{m}Y_{i}^{0}-{{m}_{1}}{{C}_{L}})+\left( 1+a \right)\frac{{{m}_{2}}}{m}Y_{i}^{0} $ | (16) |
与单个子女情形下只需要讨论收入的门槛水平Yth0不同,这里还需要家庭对生育子女数m以及受教育子女数m1做出选择。本文采用逆推法求解,首先给定家庭子女总数m,家庭选择最优化m1。以富裕家庭为例,考虑以下最优化问题
| $ \begin{align} & \underset{{{\text{m}}_{1}}}{\mathop{\text{max}}}\,\left[ {{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}}\left( 1+{{\text{r}}_{\text{H}}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right) \right](\frac{{{\text{m}}_{1}}}{\text{m}}\text{Y}_{\text{i}}^{0}-{{\text{m}}_{1}}{{\text{C}}_{\text{H}}})+\left( 1+\text{a} \right)\frac{{{\text{m}}_{2}}}{\text{m}}\text{Y}_{\text{i}}^{0} \\ & \text{is}.\text{t}.\text{ }{{\text{m}}_{1}}+{{\text{m}}_{2}}=\text{m},{{\text{m}}_{1}}\ge 0,{{\text{m}}_{2}}\ge 0 \\ \end{align} $ |
改写 (15),得到
| $ \begin{align} & \text{EY}_{\text{iH}}^{1}~=\left[ {{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}}\left( 1+{{\text{r}}_{\text{H}}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right) \right](\frac{{{\text{m}}_{1}}}{\text{m}}\text{Y}_{\text{i}}^{0}-{{\text{m}}_{1}}{{\text{C}}_{\text{H}}})+\left( 1+\text{a} \right)\frac{{{\text{m}}_{2}}}{\text{m}}\text{Y}_{\text{i}}^{0} \\ & \ \ \ \ \ \ \ =\frac{{{\text{m}}_{1}}}{\text{m}}\left[ {{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}}\left( 1+{{\text{r}}_{\text{H}}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right)(\text{Y}_{\text{i}}^{0}-\text{m}{{\text{C}}_{\text{H}}})+\left( 1+\text{a} \right) \right]+\left( 1+\text{a} \right)\text{Y}_{\text{i}}^{0} \\ \end{align} $ | (17) |
由此可知,EYiH1是一个关于m1的单调函数,因此,极值只可能在角点处存在。当πH(1+rH)+(1-πH)(1+rL(Yi0-mCH) > (1+a) 时,接受教育的期望回报率较高,所以所有子女都接受教育;当πH(1+rH)+(1-πH)(1+rL(Yi0-mCH) < (1+a) 时,接受教育的回报率较低,所以所有子女都不接受教育。由于不存在内点解,所以当子女总数给定时,家庭子女的教育选择只能是全部接受教育,或者全部不接受教育。
现在考虑生育子女数m的选择。由于家庭的最优决策只会是子女全部接受教育或者全部不接受教育,所以这里只需要讨论这两种情况。以富裕家庭为例,在第1期,对富裕家庭i,若子女全部接受教育H,其期望收益如下所示
| $ EY_{iH}^{1}=[{{\pi }_{H}}\left( 1+{{r}_{H}} \right)+\left( 1-{{\pi }_{H}} \right)\left( 1+{{r}_{L}} \right)]\left( Y_{i}^{0}-m{{C}_{H}} \right) $ | (18) |
若子女全部不接受教育,收益为
| $ Y_{i}^{1}=\left( 1+a \right)Y_{i}^{0} $ | (19) |
普通家庭的情况可以类比得到。将 (18)、(19) 与单子女情况下的收益 (1)、(3) 对比可以发现,多子女情形下,家庭的教育决策并不会发生实质改变。因此,简单情形下的推论仍然适用于多子女情形。不过值得注意的是,教育回报本身存在不确定性,在教育期望回报相等的条件下,多子女家庭的收入不确定性会随着子女数增加而降低。
另外,受教育的门槛收入水平会因为家庭子女增多而提高,也就是家庭子女越多,他们受教育的概率越小。这在直观上是可以理解的,因为子女多直接增大了受教育的总成本。对于有m个子女的家庭而言,受教育的门槛收入水平为:
| $ \text{Y}_{\text{th}}^{0}=\text{min}\left\{ \frac{[{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}}\left( 1+{{\text{r}}_{\text{H}}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right)]\text{m}{{\text{C}}_{\text{H}}}}{{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}}\left( 1+{{\text{r}}_{\text{H}}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{H}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right)-1-\text{a}},\frac{[{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}}1+{{\text{r}}_{\text{H}}}+1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}}1+{{\text{r}}_{\text{L}}}]\text{m}{{\text{C}}_{\text{L}}}}{{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}}\left( 1+{{\text{r}}_{\text{H}}} \right)+\left( 1-{{\text{ }\!\!\pi\!\!\text{ }}_{\text{L}}} \right)\left( 1+{{\text{r}}_{\text{L}}} \right)-1-\text{a}} \right\} $ | (20) |
这是一个关于子女数的单调减函数。由此我们可以得出一个推论,个人的受教育程度与其兄弟姐妹数量负相关。值得注意的是,家庭子女数越多,教育的总支出越大,这意味着子女数较多的家庭选择让子女受教育的可能性下降。
三、 计量模型 (一) 估计教育回报率我们从估计教育回报的最基本回归方程开始:
| $ \text{ln}(wag{{e}_{it}})={{\beta }_{0}}+{{\beta }_{1}}\cdot Ed{{u}_{it}}+{{\lambda }_{indu}}+{{\lambda }_{prov}}+{{\lambda }_{year}}+{{\varepsilon }_{it}} $ | (21) |
ln (wageit) 是城镇劳动者真实工资的自然对数形式,Eduit代表劳动者的受教育年限。λinduλprov和λyear分别是行业、省份和年度虚拟变量。β1则是估计出来的教育回报。如果β1大于0,即说明教育回报率为正。
我们在方程 (1) 的基础上依次加入代表个人、家庭特征的一系列控制变量,回归方程如下所示:
| $ \text{ln}(wag{{e}_{it}})={{\beta }_{0}}+{{\beta }_{1}}\cdot Ed{{u}_{it}}+\varphi \cdot I{{C}_{it}}+\gamma \cdot H{{C}_{it}}+{{\lambda }_{indu}}+{{\lambda }_{prov}}+{{\lambda }_{year}}+{{\varepsilon }_{it}} $ | (22) |
其中,ICit代表个人特征向量,包括了性别、在国有企业工作的虚拟变量、年龄、工作经验以及工作经验的平方项;HCit代表劳动者所在家庭的特征向量,包括家庭总收入、规模大小、60岁以上老人数目以及6岁以下小孩数目。
(二) 家庭收入与教育回报率为了衡量家庭收入对教育回报率的影响,我们构造了家庭收入与受教育年限的交叉项,建立如下回归方程:
| $ \text{ln}(wag{{e}_{it}})={{\beta }_{0}}+{{\beta }_{1}}\cdot Ed{{u}_{it}}+\varphi \cdot I{{C}_{it}}+\gamma \cdot H{{C}_{it}}+{{\lambda }_{indu}}+{{\lambda }_{prov}}+{{\lambda }_{year}}+{{\varepsilon }_{it}} $ | (23) |
ln (FI)it为对数化的家庭收入,β1刻画了当家庭收入不同时,个人的教育回报率之间的区别,如果β1大于0,则表明了富裕家庭的教育回报率更高,从而进一步拉大高收入家庭与低收入家庭之间的收入差距。
(三) 工具变量为了更好地解决方程 (17) 存在的内生性问题,我们选取了兄弟姐妹的数量作为个人受教育水平的工具变量 (Wooldridge, 2006)。子女数增加会增大家庭的基本生活成本,所以家庭的孩子数量应当与个人的受教育水平负相关,这也是劳动经济学领域常用的对教育水平的工具变量之一。回归方程中的交叉项Eduit*ln (FI)it同样也使用了对应的工具变量。
四、 数据及实证结果 (一) 数据描述本文采用的数据是1992-2009年国家统计局城镇住户调查数据。城镇住户调查数据覆盖北京、辽宁、浙江、安徽、湖北、广东、四川、陕西、甘肃九个省和直辖市①。该数据采用分层多阶段抽样方法,以确保样本的随机性和代表性。城镇住户调查提供了详细的个人以及家庭信息。本文使用的个人数据主要有受教育程度、性别、年龄、工作经验、就业单位类型以及工资收入,家庭数据则包括家庭总收入、规模大小、60岁以上老人数目以及6岁以下儿童的数目。我们将个人数据样本限定在有劳动收入的非农就业人群,排除了个体经营者、离退休再就业人员、离退休人员、在校学生等人群。本文侧重分析家庭收入状况对于个人教育回报的影响,进一步,我们只保留了男性年龄处于16至60岁、女性年龄处于16至55岁之间,且与户主的关系为子女的劳动人口。
① 数据来源:清华大学中国经济社会数据中心。
首先,本文按照城镇住户调查数据提供的文化程度定义了受教育年限,接受最高一级教育水平为小学、初中、高中、专科、大学本科和研究生的受教育年限分别为6、9、12、15、16和19年。在此基础上,本文也同时分别构造了各教育水平的虚拟变量。家庭总收入是指调查户中生活在一起的所有家庭成员的收入总和。
在定义本文的工具变量时,我们将城镇住户调查数据中与户主关系同为子女的人口数量定义为兄弟姐妹数,由于该数据并未区分媳婿,我们便进一步按照婚姻状况排除媳婿的影响,即如果该子女为已婚,我们便将兄弟姐妹数减去1。
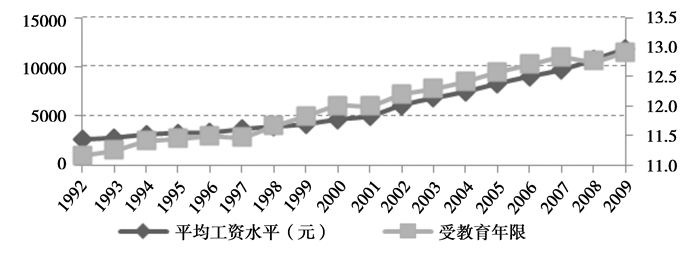
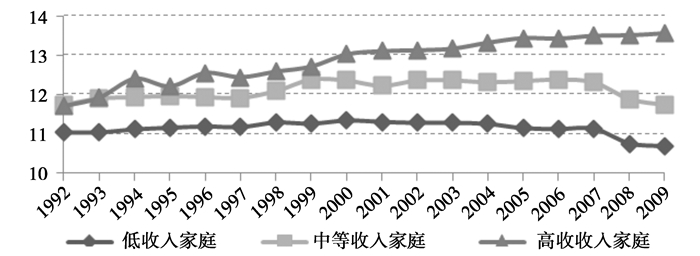
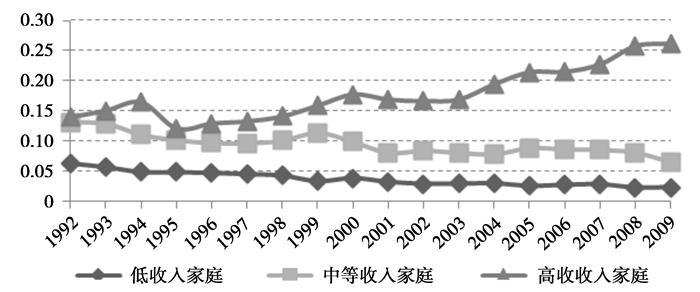
图 5刻画了从1992年至2009年间个人的平均工资水平与受教育年限的年度趋势,从图中我们可以看出整个社会的受教育水平逐年上升,且与工资水平的上涨保持较为一致的速度从数据上这也印证了“寒门”的减少。但是,如果按照家庭收入将整个样本分为低收入家庭、中等收入家庭和高收入家庭,进而比较这三类家庭的平均受教育年限,图 6表明了高收入家庭的平均受教育年限呈现出逐年上升的趋势,然而中低等收入家庭的平均受教育年限却几乎维持不变,在2008年经济危机之后甚至出现下降趋势。再进一步观察接受高等教育的比例与家庭收入之间的关系,可以很直观地从图 7中看出,高收入家庭有能力为子女提供高等教育的机会,而中低收入家庭的子女接受高等教育的概率却随年份缓慢下降。
|
图 4 工资水平与受教育年限趋势 |
|
图 5 家庭收入与受教育年限 |
|
图 6 家庭收入与接受高等教育比例 |
|
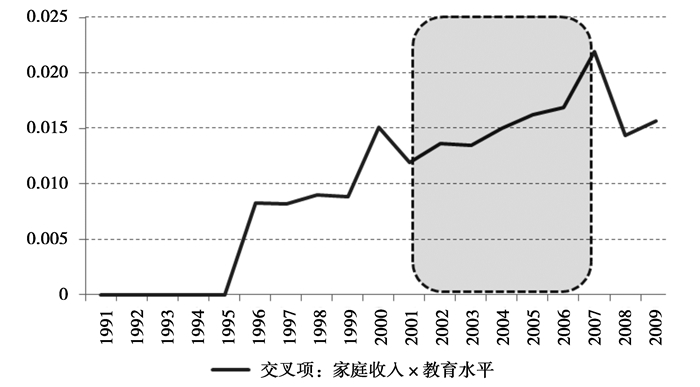
图 7 家庭财富对教育回报的影响趋势 |
我们首先利用最小二乘法,对 (1) 式进行回归。如表 1的第1列中所示,如果只控制年份固定效应和省固定效应,教育回报率的系数为0.075,并且在1%的显著水平上显著,表明多接受一年的教育,工资水平上升7.5%。表 2第2列至第6列的回归结果显示,当我们逐步控制了代表职工个人特征的相关变量时,受教育年限的系数并没有受到太大的影响,基本维持在0.075左右。在表 1第6列的基础上,表 2第1列加入了家庭收入的变量,可以看到教育年限的系数有很大程度的下降 (从0.075下降至0.034),表明在未控制家庭收入之前,教育回报率被明显高估。表 2中第2列至第4列又逐步控制了其他的家庭特征变量,发现受教育年限的系数维持在0.022。
| 表 1 教育回报的回归结果 |
| 表 2 教育回报的回归结果 (控制家庭特征) |
家庭收入对教育回报率的影响的回归结果如表 3所示,受教育年限与对数家庭收入的交叉项系数为0.009,且在1%的水平上显著,但是在加入交叉项之后,受教育年限的系数却变为了负数。表 3第1列的结果表明,富裕家庭的个人教育回报率更高,而对于低收入家庭来说,教育回报率甚至有可能为负。在表 3第2列和第3列中,我们分别将受教育年限替换为最高学历为大学及以上和最高学历为专科的虚拟变量。大学及以上虚拟变量与对数家庭收入的交叉项为0.026,不仅在数值上较第1列的结果有了很大的提高,同时还在10%水平上显著,表明在有足够家庭财富的基础上,高质量的教育回报率更高,而出身“寒门”的子女只能选择较为普通的教育机会,获得较低的回报,这也进一步证明了本文的推断。第3列中的回归结果显示,最高学历为专科的虚拟变量与对数家庭收入的交叉项为-0.061,且在1%的水平上显著。来自低收入家庭的子女在学校选择上有时只能选择接受时间较短、收效较快的专科学校,此时他们的教育回报率才有可能为正。而对于来自富裕家庭的子女,选择专科学校的回报率则更低,但是由于他们对于学校选择更加灵活,所以他们会转而选择接受高质量的教育,获取更高的回报。
| 表 3 家庭收入对教育回报的影响 (最小二乘法) |
进一步,我们将家庭收入进行排序,并分为十等分,将处于90分位数的家庭定义为富裕家庭,而家庭收入位于第50分位数的家庭定义为一般家庭,展开了分组回归检验,结果如表 4所示。回归结果再一次验证了处于富裕家庭的子女的教育回报率更高,而对于一般家庭来说,教育回报率有可能不显著。使用大学及以上虚拟变量以及专科虚拟变量,也得出与之前类似的结论。作者还尝试了多种对家庭财富的分类方法,结果类似。
| 表 4 家庭收入对教育回报的影响 (最小二乘法) |
对于教育与个人收入之间存在的内生性问题,本文选择使用工具变量法处理。如前文计量模型部分所述,这里使用家庭的兄弟姐妹数量作为工具变量。表 5报告了工具变量法第一阶段的回归结果,兄弟姐妹数量对个人受教育水平的影响显著为负,且在1%的水平上显著,这与之前的预测相一致。另外,城镇住户调查数据从2002年才开始提供个人婚姻状况的变量,因此在使用工具变量法进行分析时,我们将样本控制在2002年至2009年期间。
| 表 5 兄弟姐妹个数对受教育水平的影响 (使用2002-2009样本) |
表 6汇总了分别使用最小二乘法和工具变量的实证结果,表 6第1列报告了了使用2002年至2009年样本的最小二乘法回归结果,第2列则是使用工具变量法的回归结果。从结果可以看出,两种方法得到的估计系数略有差异,但数值差别不大,系数的正负更没有发生变化。
| 表 6 家庭收入对教育回报的影响 (使用2002-2009样本) |
图 7给出了分年度数据对方程 (3) 的回归结果 (篇幅所限,详细回归结果表格已省略),图中的各个点代表使用当年数据回归得到的家庭收入与教育水平交叉项的回归系数。1991-1995年间不同阶层家庭子女的教育回报率几乎无差异。1995年以后,差异开始增大,尽管经历了短时间的缩短,但一直到2007年,总体趋势是向上的。
2002年开始,富裕家庭的教育回报率明显相对上升,这个趋势延续到2007年。这段时间也是中国“教育产业化”发展最快的时期,“教育产业化”的得失不是本文研究的内容,但产业化本身确实使得不同社会阶层受教育类型的差异扩大,反映在教育回报率上,就是富裕家庭教育回报率更高。而在2007年以后,这个差异开始缩小,由于数据所限,我们无法得知2010-2014年间不同社会财富阶层的教育回报率差异,但根据之前19年的数据以及由回归结果进行的推理,我们有理由认为那些会促使不同阶层所接受教育的差异增大的改革应当实质上强化了不同阶层的教育回报率差异。
如果富裕家庭的教育回报率降低至与普通家庭子女相等,我们可以预计两组家庭的组间收入差距会下降,进而可以得出结论,社会整体的收入差距会降低。基于这个考虑,我们构建了如下的反事实检验
| $ \begin{align} &\text{ln}(wag{{e}_{it}})=counterfactual[\text{ln}(wag{{e}_{it}})]+\text{ln}(wag{{e}_{it}})-counterfactual[\text{ln}(wag{{e}_{it}})] \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ={{\beta }_{0}}+{{\beta }_{1}}\cdot Ed{{u}_{it}}*commonincome+{{\beta }_{2}}\cdot Ed{{u}_{it}}+{{\beta }_{3}}\cdot \text{ln }{{\left( FI \right)}_{it}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\varphi \cdot I{{C}_{it}}+\gamma \cdot H{{C}_{it}}+{{\lambda }_{indu}}+{{\lambda }_{prov}}+{{\lambda }_{year}}+{{\varepsilon }_{it}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +{{\beta }_{1}}\cdot Ed{{u}_{it}}*\text{ln}{{\left( FI \right)}_{it}}-{{\beta }_{1}}\cdot Ed{{u}_{it}}*commonincome \\ \end{align} $ |
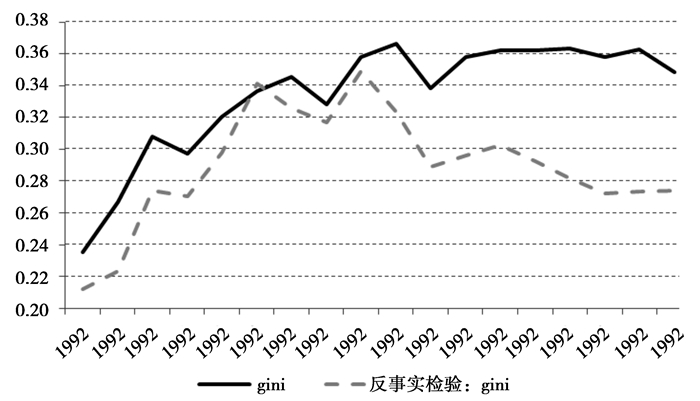
结果如图 8所示,总体而言,城镇住户的基尼系数呈扩大趋势,从1992年的0.23上升到2009年的0.35,这个数值低于统计局公布的0.47(2009年数据),是因为本文所选取的样本全部是城镇住户调查数据,而统计局的数据则是城镇、农村住户综合调查所得。尽管总体基尼系数很高,但如果把城乡分开来看,基尼系数并不高。
|
图 8 对基尼系数的反事实检验 |
在2000年之前,反事实检验得到的基尼系数与原样本差别不大。但2001年以后,差距开始扩大,差距最大的是2008年,城镇居民收入差距的24.5%来自不同家庭的教育回报率差异。平均来看,由家庭财富带来的教育回报差异贡献了19.1%的城镇居民收入差距 (2001-2009年)。如果消除家庭收入带来的教育回报率差异,2009年的城镇基尼系数会从0.35下降到0.27。
六、 “新常态”下的研究展望随着教育产业化政策的终止,我们能够观察到城镇局面收入基尼系数的缩小,如果其他条件不变,贫富差距减轻将会是一个自然而然的变化结果。问题在于,“新常态”下宏观经济发生了诸多结构性变化,在新的结构下,贫富差距是否会进一步缩小值得讨论。
由于数据的缺乏,本文无法探讨“新常态”下教育回报与贫富差距之间关系的变化情况,但我们仍然可以根据“新常态”的一些公认特征,来模拟贫富差距变化的趋势。“新常态”在这里包括两层含义,即社会整体经济增速的下滑和不同家庭教育回报率差异的扩大。前者在模型中表现为收入外生增速a的下降,由于教育支出增速不变,所以这会带来受教育门槛的相对提高;后者在模型中表现为富裕家庭教育回报率的进一步提高,为了与后文实证结果相互参照,这里把回报率差异扩大的程度设定为9.0%。
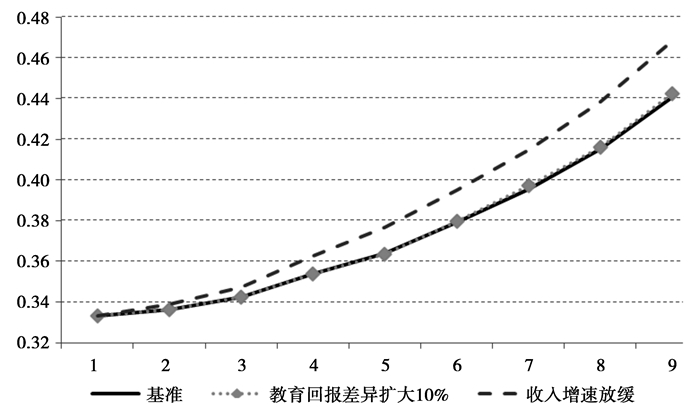
图 9是模拟“新常态的”的结果。从图中可以看出,经济潜在增速下降是基尼系数扩大的主要原因。8年期的数值结果表明,潜在外生收入增速下降使得基尼系数从第8年的0.441扩大到0.468,增幅为6.1%。相比之下,富裕家庭教育回报提高的影响微乎其微。值得一提的是,富裕、普通家庭教育回报差异在这里作用微小,不代表在真实经济中也是如此,后文的实证结果表明,在真实经济中,不同家庭的教育回报差异对收入基尼系数的贡献也是非常显著。
|
图 9 基尼系数模拟——“新常态” 注:教育回报差异扩大10%与基准情形的差异很小。 |
从模拟结果可以看到,经济潜在增速的下滑对贫富差距缩小有不利影响,这意味着政策需要有比以往更大幅度的倾斜,才能够维持原先经济条件下的收入差距缩小的趋势。
七、 结论及政策建议本文首先构建了代际交迭模型,将人力资本的投资作为内生选择变量,推导出不同收入家庭的最优教育选择。数值模拟的结论表明在假设富裕家庭子女的教育回报率更高的情况下,尽管社会平均收入水平提高,但是整个社会的贫富差距扩大。反映在社会现实中,就是尽管绝对收入低的群体占比越来越低,但收入的相对差距在扩大。所谓“寒门难出贵子”,并非绝对意义下的情况,教育确实起到了带动收入增长的作用。然而相对来讲,收入较低的家庭其子女通过教育改善收入的难度更大,这会造成收入差距的拉大。
使用1992年至2009年中国城镇住户调查的数据,作者进行了实证分析,结果不仅支持了理论模型的假设,也支持理论模型的结论,富裕家庭的子女能够获取更高的回报,进一步拉开与出身“寒门”的群体之间的收入差距。具体到“新常态”,由于数据只有2009年可以归入这种经济状态,所以作者进行了数值模拟,结果表明,在社会整体潜在收入增速下降的背景下,不同家庭教育回报差异所带来的影响会变得更大。总而言之,教育投资确实提高了中国1992年以来的收入平均水平,从这点而言,增长问题得以解决。但收入差距的严重性在逐渐扩大,由于富裕家庭的教育回报更大,并且在17年的观察中,不同家庭的教育回报差异还在扩大,我们应该把更多资源放在解决不同家庭的教育回报上。由于回报率的差异,仅仅提供均等的受教育机会是不够的,对贫穷家庭的教育补贴应当更加倾斜。
除此以外,提高学费同时提高奖学金的政策,以及对某些未来高收入专业征收高学费的措施,从个人的教育回报而言是合理的,高的教育回报确实定价可以更高。然而,教育本身并不是商品,对微观个体而言合理的措施,从宏观层面来看往往是不合理的。从社会总体来看,这些教育改革措施实质上扩大了不同阶层、不同个体的教育回报率差异,客观上使得社会整体的收入分布更加离散,增大了基尼系数。
仅仅关心教育的机会均等已经不足以降低收入差距,在机会均等之外,政策应当更注意结果公平。对于大学教育的专业,高收入专业高学费有合理之处,但贫困学生的学费应当在一定程度上被减免,未来可能的高收入不能成为现阶段高成本的理由。而助学金方面,目前的助学金发放标准过于严苛,致使很多相对低收入家庭的子女无法申请到补助,而国家的核定补助又无法完全发放,这是一种资源的浪费。对于中学和小学的教育,学费本身已经不再是家庭的沉重负担,但不同中小学之间的硬件差距极大,而不同地区的师资水平及教师待遇也相差悬殊,这种受教育环境的不公平也应当被改善。提高学校硬件投资的统筹级别,设定最低学校投资标准,减轻同一地区城乡教师的待遇差异,都有利于解决中小学教育环境不公平问题。
| [] | 才国伟、刘剑雄, 2014, "收入风险, 融资约束与人力资本积累——公共教育投资的作用", 《经济研究》, 第 7 期, 第 67–80 页。 |
| [] | 陈永伟、陈双双, 2015, "中国城镇居民收入差距的公平与不公平分解及度量", 《经济学动态》, 第 3 期, 第 44–51 页。 |
| [] | 蒋和胜、何兴容、杨柳静, 2007, "非义务教育产业化发展的理论基础与现实依据", 《财经科学》, 第 2 期, 第 51–57 页。 |
| [] | 李任玉、杜在超、何勤英, 2014, "富爸爸, 穷爸爸和子代收入差距", 《经济学 (季刊)》, 第 1 期, 第 231–258 页。 |
| [] | 陆铭、陈钊、万产华, 2005, "因患寡, 而患不均——中国的收入差距, 投资, 教育和增长的相互影响", 《经济研究》, 第 12 期, 第 4–14 页。 |
| [] | 罗楚亮, 2007, "城镇居民教育收益率及其分布特征", 《经济研究》, 第 6 期, 第 119–130 页。 |
| [] | 王婧, 2013, "社会性话题的媒体报道实证研究", 《新闻世界》, 第 9 期。 |
| [] | 邢春冰, 2008, "分位回归, 教育回报率与收入差距", 《统计研究》, 第 5 期, 第 43–49 页。 |
| [] | 杨娟、赖德胜、邱牧远, 2015, "如何通过教育缓解收入不平等?", 《经济研究》, 第 9 期, 第 86–99 页。 |
| [] | 袁诚、张磊, 2009, "对低收入家庭子女大学收益的观察", 《经济研究》, 第 5 期, 第 42–51 页。 |
| [] | 张车伟, 2006, "人力资本回报率变化与收入差距:'马太效应'及其政策含义", 《经济研究》, 第 12 期, 第 120–135 页。 |
| [] | 张川川, 2015, "'中等教育陷阱'?——出口扩张、就业增长与个体教育决策", 《经济研究》, 第 12 期, 第 115–127 页。 |
| [] | 张维迎, 2006, "高学费对穷人有好处", 《经济研究信息》, 第 5 期, 第 31–32 页。 |
| [] | 周兴、张鹏, 2015, "代际间的职业流动与收入流动——来自中国城乡家庭的经验研究", 《经济学 (季刊)》, 第 1 期, 第 351–372 页。 |
| [] | Atkinson, Anthony, B. , Thomas, Piketty and Emmanuel, Saez , 2011, "Top Incomes in the Long Run of History". Journal of Economic Literature, 49(1), 3–71. DOI:10.1257/jel.49.1.3 |
| [] | Barro, R. J. 2000, "Inequality and growth in a panel of countries". Journal of Economic Growth, 5(1), 5–32. DOI:10.1023/A:1009850119329 |
| [] | Becker, G. S., 1975, "Human capital: a theoretical and empirical analysis, with special reference to education", second edition. Nber Books, 18. |
| [] | Becker, G. S. and Tomes, N. , 1986, "Human capital and the rise and fall of families". Journal of Labor Economics, 4(3), S1–39. DOI:10.1086/298118 |
| [] | Bishop, J. A. , Luo, F. and Wang, F. , 2005, "Economic transition, gender bias, and the distribution of earnings in china". Economics of Transition, 13(2), 239–259. DOI:10.1111/ecot.2005.13.issue-2 |
| [] | Jencks, C. 1977, "Inequality: a reassessment of the effect of family and schooling in America". Journal of Marriage & Family, 28(1), 121–123. |
| [] | Jerrim, J. and Macmillan, L. , 2014, "Income inequality, intergenerational mobility, and the great gatsby curve: is education the key?". Social Forces, 94. |
| [] | Knight, J. B. and Song, L. , 2003, "Increasing urban wage inequality in china: extent, elements and evaluation". Economics of Transition, 11(4), 597–619. DOI:10.1111/ecot.2003.11.issue-4 |
| [] | Lucas, R. E. 1988, "On the mechanics of economic development". Journal of Monetary Economics, 22(88), 3–42. |
| [] | Maoz, Y.D. and Moav, O. , 1999, "Intergenerational mobility and the process of development". Economic Journal, 109(458), 677–697. |
| [] | Mattias, L. and Lyn, S. , 2003, "the simultaneous evolution of growth and inequality". Economic Journal, 113(487), 326–344. |
| [] | Mincer, J. 1974, "Unemployment effects of minimum wages". Journal of Political Economy, 84(4), 87–104. |
| [] | Nakamura, T. and Yu, M. , 2011, "Education cost, intergenerational mobility, and income inequality". Economics Letters, 112(3), 266–269. DOI:10.1016/j.econlet.2011.05.011 |
| [] | Perotti, R. 1996, "Growth, income distribution, and democracy: what the data say". Journal of Economic Growth, 1(2), 149–87. DOI:10.1007/BF00138861 |
| [] | Pritchett, L. 1997, "Where has all the education gone?.world bank working paper#1581". World Bank Economic Review, volume, 15(3), 367–391. |
| [] | Qin, X., Wang, T., and Zhuang, C. C., 2014. "Intergenerational transfer of human capital and its impact on income mobility: evidence from china", China Economic Review. in Press (DOI: 10.1016/j.chieco.2014.10.005). |
| [] | Shea, J. 2000, "Does parents' money matter?". Journal of Public Economics, 77(99), 155–184. |
| [] | Sylwester, K. 2002, "Can education expenditures reduce income inequality?". Economics of Education Review, 21(1), 43–52. DOI:10.1016/S0272-7757(00)00038-8 |
| [] | Theyson, K. C. and Heller, L. R. , 2015, "Development and income inequality: a new specification of the kuznets hypothesis". Journal of Developing Areas, 49(3), 103–118. DOI:10.1353/jda.2015.0153 |
| [] | Wooldridge, J. M., 2006. Introductory econometrics: a modern approach. Thomson/South-Western. 4 Edition. |
| [] | Yang, J. and Qiu, M. , 2016, "The Impact of Education on Income Inequality and Intergenerational Mobility". China Economic Review, 37, 110–125. DOI:10.1016/j.chieco.2015.12.009 |



