效率是经济学研究的核心问题之一,是公司管理追求的目标,反映出公司的资源利用效果以及整体经营状况,体现了公司竞争力和可持续发展能力。作为资本市场的重要组成部分,证券公司运营效率的高低对于整个资本市场的健康高效运行以及资源的高效配置无疑具有举足轻重的影响。研究我国证券公司的效率及其影响因素、进而探索提升效率的路径对于促进形成具有国际竞争力、品牌影响力和系统重要性的证券公司无疑具有重要的现实意义。
国内外学者对证券公司的效率进行了大量研究,取得了丰硕的成果。如Fukuyama and Weber (1999)、Wang et al.(2003)、Zhang et al.(2006)以及Serifsoy and Wei(2007)分别研究了日本、中国台湾、美国以及欧洲证券业的效率。樊宏(2002)、朱南、刘一(2008)、王晓芳、程可胜(2009)、李兰冰等(2011)、杨光兵等(2013)以及翟永会(2014)对我国证券公司的效率进行了研究。
在学者们的研究中,影响证券公司效率的因素,大体上可以划分为证券公司的特征因素和外部的环境因素两大类。在证券公司的特征因素方面,一些因素是作为焦点因素来研究,而另一些因素则是作为控制因素。其中研究的焦点因素包括:
(1) 股权结构,具体包括股权性质(国有与否)、股权集中度和股权制衡度。其中股权集中度的具体测度指标有第一大股东的持股比例、前三大股东的持股比例以及前五大股东的持股比例。股权集中度与证券公司效率的关系是研究的热点,而得到的结论不尽一致。如Yeh et al.(2010)的研究结果表明,对加入金融控股集团的证券公司,其运营效率与大股东持股比例正相关;而对于没有加入金融控股集团的证券公司而言,运营效率与大股东持股比例没有显著的关系。冯根福、丁国荣(2011)的研究表明:证券公司第一大股东持股比例与经营效率呈显著正相关关系。沙浩(2011)的研究表明,前三大股东持股比例与证券公司的经营效率正相关。王聪、宋慧英(2012)的研究表明,第一大股东持股比例与证券公司成本效率之间是一种U型关系。杨志明等(2015)的研究表明,第一大股东持股比例与证券公司效率之间是倒N型的三次曲线关系,该结果验证了谢军(2007)所述的“区间特征”;其研究结果还表明大股东绝对控股(持股比例大于50%)的证券公司效率最高,往下依次分别为参股情形(持股比例小于30%)和相对控股(持股比例在30~50%)情形。
(2) 董事会特征、监事会特征以及管理层报酬等。冯根福、丁国荣(2011)的研究表明,中国证券公司的董事会规模、独立董事比例与公司经营效率呈显著负相关关系;董事长与总经理的两职分离有利于提高公司经营效率;监事会规模、监事会独立性与公司经营效率负相关, 但均不显著; 中国证券公司管理层规模、管理层报酬与公司经营效率呈显著正相关关系。沙浩(2011)的研究结论是董事会规模与效率负相关,且董事持股比例越高,券商拥有的市场风险越大;独立董事比例与效率和风险承担之间的关系不显著,表明独立董事尚未充分发挥职能。
(3) 员工知识结构,用本科以上员工占员工总数的比例来测度。边晓磊、陈学彬(2009)的研究表明,员工知识结构对证券公司技术效率有显著的正向作用。
在影响效率的证券公司特征因素中,作为控制因素的有:
(1) 公司规模,用总资产测度。如李兰冰等(2011)、冯根福、丁国荣(2011)、王聪、宋慧英(2011、2012)以及杨志明等(2015)都考虑了公司规模因素对证券公司效率的影响,大多得到了公司规模对证券公司效率具有显著正向作用的结论。
(2) 财务杠杆,用资产负债率测度。如李兰冰等(2011)、王聪、宋慧英(2011、2012)以及杨志明等(2015)都考虑了财务杠杆因素对证券公司效率的影响,并且研究结论非常一致:财务杠杆对证券公司效率具有显著的正向作用。
(3) 成立年限。李兰冰等(2011)在研究海峡两岸证券业经营效率时将成立年限作为控制因素,但并未发现其对效率有显著影响。
(4) 上市与否。蒋绵绵等(2014)在研究中考虑了上市与否对证券公司效率的影响。
而影响证券公司效率的外部环境因素主要包括:
(1) 市场结构,具体包括用Panzar-Rosse模型(PR模型)测度的市场竞争度和赫芬达尔-赫希曼指数(Herfindahl-Hirschman Index)。如王聪、宋慧英(2011、2012)运用PR模型测度市场竞争度,测度我国证券业的市场结构,研究表明,市场竞争度与证券公司效率之间呈倒U型关系,且现阶段处于下降区间。杨志明等(2015)用全部证券公司营业收入市场占比的平方和来计算赫芬达尔-赫希曼指数,测度中观层面的市场集中度。他们的研究结果表明,市场集中度与证券公司效率之间呈现“U”型关系。
(2) 宏观经济环境变量,包括上证指数的年度均值、实际经济增长率、经济自由度、地区生产总值等。如李兰冰等(2011)在研究海峡两岸证券业经营效率时将当地股票市场指数、经济自由度、地区生产总值、国际金融危机等指标纳入环境变量。王聪、宋慧英(2011、2012)以及杨志明等(2015)在研究中都将上证指数的年度均值作为宏观经济环境控制变量。
在研究证券公司效率与上述因素之间的关系时,学者们的研究步骤大多为“两步法”,即先用一些模型测度效率,后采用一些回归方法研究影响因素与效率之间的具体关系。如边晓磊、陈学彬(2009)先用数据包络分析(DEA)方法测度证券公司效率,再进行Tobit回归分析。沙浩(2011)和冯根福、丁国荣(2011)也是先用DEA方法测度证券公司效率,再用回归方法进行分析。李兰冰等(2011)将Metafrontier思想与DEA模型相结合构建共同边界模型测度证券公司效率,之后进行Tobit回归分析。王聪、宋慧英(2011、2012)首先用随机前沿分析(SFA)方法测度证券公司效率,然后用固定效应模型研究市场结构、股权结构与证券公司成本效率之间的关系。杨志明等(2015)首先采用基于松弛的方向距离函数测算证券公司的生产效率,然后选择面板数据回归模型(固定效应模型)进行分析。
在研究其他金融业的效率(或全要素生产率)及其影响因素方面,学者们大多采用“两步法”。如何康(2015)首先采用EBM模型和GML指数来测算城市商业银行的静态效率和动态全要素生产率,然后采用面板Tobit模型研究了利率市场化是否有利于改善城市商业银行效率。但也有学者选用基于产出导向距离函数的随机前沿分析方法进行研究,该方法为“一步法”,即测度效率和分析效率的影响因素同步进行。如张健华、王鹏(2009、2011)采用基于产出导向距离函数的随机前沿分析方法对中国不同类型银行的技术效率及其影响因素进行了研究,还对中外银行业进行了比较研究。于研、孙磊(2010)应用随机前沿分析(SFA)方法,构建超越对数产出距离函数,对我国12家代表性商业银行的技术效率和全要素生产效率指数进行了分析。目前,基于产出导向距离函数的随机前沿分析方法已经在各领域的研究中得到了应用,如何晓萍(2011)、续竞秦、杨永恒(2012)、刘婕、魏玮(2014)、王文、牛泽东(2014)、李春米、毕超(2015)等学者在研究中均采用这种方法。
本文采用基于产出导向距离函数的随机前沿分析方法研究2007-2015年95家中国证券公司的技术效率及其影响因素。与以往关于中国证券业效率的研究相比,本文的创新在于:(1)所采用的研究方法--基于产出导向距离函数的随机前沿分析方法有独特优势。与一般的随机前沿分析方法只能处理单产出相比,该方法能处理多产出问题;与通常的研究效率及其影响因素的“两步法”相比,该方法为“一步法”,即测度证券公司技术效率和分析技术效率的影响因素同步进行;与非参数的DEA方法相比,该方法考虑了随机因素的影响。检索结果表明,迄今为止,尚无采用产出导向距离函数的随机前沿模型分析我国证券业效率的文献。(2)在数据可获得的前提下,比较全面地考察了影响证券公司技术效率的因素并进而分析效率提升的路径。
二、 基于产出导向距离函数的随机前沿分析方法随机前沿分析具有分离技术无效率项与随机误差项的特点,其中Battese and Coelli (1995)的模型更有“一步法”分析效率影响因素的优势,成为评价效率的常用方法,其适应性得到了广泛验证。本文将其和产出导向距离函数相结合,对作为一个多投入/多产出系统的中国证券业进行技术效率分析。
距离函数有投入导向和产出导向之分。根据Lovell et al.(1994),产出导向的距离函数定义为:Do(x, y)=min{θ:y/θ∈P(x)}。对y而言,Do(x, y)满足非减的、正齐次性以及凸性;而对x是非增的。如果产出y落在生产可能性集合P(x)内,Do(x, y)的取值小于或等于1;如果产出y落在生产可能性集合的边界上,Do(x, y)取值为1。
在距离函数的具体设定方面,与C-D生产函数相比,超越对数生产函数具有形式上较为灵活、受到的限制少等优势,因而在已有文献中被广泛使用。本研究采用Orea (2002)提出的超越对数产出距离函数来测度证券业多投入/多产出系统的技术效率。一个n项投入、m项产出的超越对数产出距离函数可表示为:
| $ \begin{align} & \ln {{D}_{o}}\left({{x}_{it}}, {{y}_{it}}, t \right)={{\alpha }_{0}}+\sum\limits_{k=1}^{n}{{{\alpha }_{k}}\ln {{x}_{kit}}}+ \\ & \sum\limits_{j=1}^{n}{{{\beta }_{j}}\ln {{y}_{jit}}}+\frac{1}{2}\sum\limits_{k=1}^{n}{\sum\limits_{h=1}^{n}{{{\alpha }_{kh}}\ln {{x}_{kit}}\ln {{x}_{hit}}}} \\ & +\frac{1}{2}\sum\limits_{j=1}^{m}{\sum\limits_{l=1}^{m}{{{\beta }_{jl}}\ln {{y}_{jit}}\ln {{y}_{lit}}}}+\sum\limits_{k=1}^{n}{\sum\limits_{j=1}^{m}{{{\gamma }_{kj}}\ln {{x}_{kit}}\ln {{y}_{jit}}}} \\ & +{{\varphi }_{0}}t+\frac{1}{2}{{\varphi }_{00}}{{t}^{2}}+\sum\limits_{k=1}^{n}{{{\xi }_{kt}}t\ln {{x}_{kit}}}+\sum\limits_{j=1}^{m}{{{\tau }_{jt}}t\ln {{y}_{jit}}} \\ \end{align} $ | (1) |
其中,i为公司,t为时间,yit为产出,xit是要素投入。α、β、γ、φ、ξ以及τ为需要估计的参数。Do(xit, yit, t)为基于时期t技术的产出距离函数,下标“o”表示基于产出导向。产出距离函数Do(xit, yit, t)关于产出yit满足线性齐次性,即:
| $ {{D}_{o}}\left({{x}_{it}}, {{\omega }_{it}}, t \right)=\omega {{D}_{o}}\left({{x}_{it}}, {{\omega }_{it}}, t \right) $ | (2) |
因此,如果选择任意一种产出,譬如选择第m种产出ymit,并设定ω=1/ymit,则有
| $ {{D}_{o}}\left({{x}_{it}}, {{y}_{it}}/{{y}_{mit}}, t \right)={{D}_{o}}\left({{x}_{it}}, {{y}_{it}}, t \right)/{{y}_{mit}} $ | (3) |
式(3)两边取对数,变换可得:
| $ \ln {{y}_{mit}}=-\ln {{D}_{o}}\left({{x}_{it}}, {{y}_{it}}/{{y}_{mit}}, t \right)+\ln {{D}_{o}}\left({{x}_{it}}, {{y}_{it}}, t \right) $ | (4) |
采用TL表示式(1)的超越对数产出距离函数,(4)式变换为:
| $ \ln {{y}_{mit}}=-TL\left({{x}_{it}}, y_{it}^{*}, t;\theta \right)+\ln {{D}_{o}}\left({{x}_{it}}, {{y}_{it}}, t \right) $ | (5) |
其中,yit*=yit/ymit为经ymit标准化后的产出向量,θ=[α, β, γ, φ, ξ, τ]为一系列需要估计的参数。设uit=-lnDo(xit, yit, t),并且在式(5)中加入随机误差项,得到如下随机前沿模型:
| $ \begin{align} & ln{{y}_{mit}}=-TL\left({{x}_{it}}, y_{it}^{*}, t;\theta \right)+{{v}_{it}}-{{u}_{it}}=-{{\alpha }_{0}}-\sum\limits_{k=1}^{n}{{{\alpha }_{k}}ln{{x}_{kit}}}- \\ & \sum\limits_{j=1}^{m-1}{{{\beta }_{j}}lny_{jit}^{*}}-\frac{1}{2}\sum\limits_{k=1}^{n}{\sum\limits_{h=1}^{n}{{{\alpha }_{kh}}ln{{x}_{kit}}ln{{x}_{hit}}}} \\ & -\frac{1}{2}\sum\limits_{j=1}^{m-1}{\sum\limits_{l=1}^{m-1}{{{\beta }_{jl}}lny_{jit}^{*}lny_{lit}^{*}}}-\sum\limits_{k=1}^{n}{\sum\limits_{j=1}^{m-1}{{{\gamma }_{kj}}ln{{x}_{kit}}lny_{jit}^{*}}} \\ & +{{\varphi }_{0}}t-\frac{1}{2}{{\varphi }_{00}}{{t}^{2}}-\sum\limits_{k=1}^{n}{{{\xi }_{kt}}tln{{x}_{kit}}}-\sum\limits_{j=1}^{m-1}{{{\tau }_{jt}}tlny_{jit}^{*}}+{{v}_{it}}-{{u}_{it}} \\ \end{align} $ | (6) |
vit为一般意义上的随机误差项,包括测量误差以及其他各种不可控因素的影响,服从相互独立的正态分布N(0, σv2),并且与uit相互独立;uit是非负的技术无效率项,Battese and Coelli (1995)假定其服从相互独立的截断正态分布N+(μit, σu2),其中μit=zitδ,zit代表影响技术效率的因素,δ是需要估计的未知参数。(6)式是一个标准的随机前沿分析模型,其包含的所有未知参数可以通过极大似然估计一个阶段求出。其优势在于能处理多投入/多产出系统,并且在估算技术效率的同时能进行效率影响因素分析。至于(1)式中其他的参数,可以根据如下线性齐次性约束条件求解:
| $ \begin{align} & \sum\limits_{j=1}^{m}{{{\beta }_{j}}}=1, \sum\limits_{l=1}^{m}{{{\beta }_{jl}}}=0\left(j=1, 2, \cdots, m \right), \sum\limits_{j=1}^{m}{{{\gamma }_{kj}}}=0\left(k=1, 2, \cdots, n \right), \\ & \sum\limits_{j=1}^{m}{{{\tau }_{jt}}}=0, {{\beta }_{jl}}={{\beta }_{lj}}, {{\alpha }_{kh}}={{\alpha }_{hk}}. \\ \end{align} $ | (7) |
前述技术无效率项uit服从的截断正态分布N+(μit, σu2)是同方差假定。Wang (2003)、连玉君、苏治(2009)使用异质性随机前沿模型进行相关研究,该模型假定uit服从截断正态分布N+(μit, σit2),是异方差假定,并假定μit=c0+zitδ、σit2=exp (c1+zitγ),即uit和σit是相同变量的函数,当然允许它们的系数不同。从理论上来说这种模型设定更好,但就本文的研究数据以及所采用的影响效率的变量而言,这个模型尤其是异方差的设定过于复杂。采用Wang (2003)以及连玉君、苏治(2009)的估计异质性随机前沿模型的Stata程序都得不到有效的结果,要么运行出不了结果,要么对几个模型估计出了各个回归系数,但计算得到的证券公司效率值异常,无法使用。即使违反前述假定,在方差方程中仅仅使用少数几个甚至一个变量,也得不到有效结果。因此只能放弃选用异质性随机前沿模型。本文选用Frontier4.1软件进行模型估计,就本研究的数据而言,该软件的运行非常稳健。
三、 样本及变量的确定 (一) 样本的确定2015年参与中国证监会分类评价的119家证券公司中,有24家公司按规定与其母公司合并评价。由于中国国际金融有限公司(中金公司)没有披露职工薪酬,不纳入样本。申银万国证券与宏源证券在2014年合并为申万宏源证券,考虑到两家公司的规模,在2014年之前,将申银万国证券与宏源证券都纳入样本。上海证券在2014年成为国泰君安证券的控股子公司,在2014年之前将其纳入样本。上海华信证券是2014年受让原财富证券的控股子公司财富里昂证券100%股权而来,因只有两年,不纳入样本。总之,从2007年到2015年以总共95家公司为备选样本。一些证券公司由于成立时间晚、在某些年份部分变量数据缺失以及产出变量数据为负值不符合模型对数据首先要进行对数化处理的要求等原因,在相应年份也未被纳入到样本中。最终,本研究的样本容量为776。
(二) 投入/产出变量的选择进行效率评价首先要确定投入/产出变量,对于金融机构投入产出变量的确定,主要有生产法、中介法和资产法。这三种方法并无绝对的优劣之分,目前越来越多的学者的做法是以中介法为主,综合采用三种方法,同时根据实际研究的需要进行投入产出变量的选取。本文综合考虑这三种方法,并结合证券行业的特点来确定投入/产出变量。证券公司是使用劳动和资本作为生产要素投入获取证券服务收入、投资收益及其他收入的金融企业。
1. 投入变量的选择综合考虑,选择资本和劳动力两个方面作为投入。(1)关于资本投入,学者们选择的具体变量有:注册资本或实收资本(樊宏,2002;边晓磊、陈学彬,2009)、净资本(杨志明等,2015)以及净资产(杨光兵等,2013)等。(2)关于劳动力投入,有学者选择员工人数(朱南等,2008),但大多数学者选择职工薪酬(王晓芳等,2009;王聪等,2012;杨志明等,2015)。借鉴以往学者采用的投入变量和数据的可获得性,选用净资产(所有者权益x1)和本年度实际支付的职工薪酬(x2)作为投入变量。由于一些证券公司在某些年份缺失实际支付的职工薪酬,本文用合并现金流量表中的“支付给职工以及为职工支付的现金”做近似代替,但两者的统计口径略有差异。
2. 产出变量的选择关于产出,学者们选择的具体变量有:净利润(杨光兵等,2013;杨志明等,2015)、营业收入(程可胜,2009)、手续费(朱南等,2008)、佣金净收入和投资收益(陈芳平等,2011)等。
由于经纪业务、投资银行业务、资产管理业务以及投资业务为证券公司的主要收入来源,因此本文选择证券公司手续费及佣金净收入(y1),包括经纪业务、投资银行业务以及资产管理业务手续费净收入)和投资收益(y2)作为产出变量。这两个变量一个反映了证券公司对外提供证券服务获得的收益,一个反映了证券公司对自有资金的营运收益。
由于模型要求首先对投入/产出数据进行对数化处理,而部分证券公司在某些年份投资收益为负值,不符合要求。张健华、王鹏(2009)的处理方法是:在某一变量出现负值的年份,将该变量的原始数值统一加上一个正值,从而将该变量在这一年度的所有数值都变为正值。如果按照这个方法对本研究的投资收益进行处理,将可能高估那些投资收益较少的证券公司的技术效率。在本文选择的样本中,2007-2015年投资收益为负值的证券公司家数分别是:0、27、7、3、26、5、2、0和0,仅有2008年和2011年家数较多。本研究把投资收益为负值的70个样本剔除,这些样本不处于生产前沿面上,剔除这些样本不会对其他样本技术效率的估算产生实质影响。由于这70个样本中的证券公司在其余年份仍然保留,其独特的信息(比如股权结构等)仍然存在于研究样本中,所以也不会对技术效率的因素影响分析产生实质性影响。还有部分证券公司在一些年份的投资收益为0元,本研究将其处理为1元,这种处理对研究结果的影响可忽略不计。
3. 投入/产出变量的数据说明为了与职工薪酬、手续费及佣金净收入以及投资收益等流量指标在时间上保持一致,净资产采用年初值和年末值的平均值,所有投入/产出变量的单位均为元。变量净资产、职工薪酬、手续费及佣金净收入以及投资收益的统计口径为合并口径,数据来源于证券公司的合并财务报表及附注。证券公司的年度报告、审计报告来源于中国证券业行业协会网站、证券公司官方网站、沪深两大证券交易所网站、中国债券信息网和上海清算所网站等。
另外,张健华、王鹏(2009)在研究1999-2008年间银行业前沿效率时,对投入/产出数据按照GDP折算指数折算到2000年价格水平。本文进行类似的处理,根据按当年价格计算的2007-2015年国内生产总值(名义GDP)、按2005年不变价计算的2007-2010年国内生产总值(实际GDP)以及按2010年不变价计算的2010-2015年国内生产总值(实际GDP)计算折算系数,将投入/产出价值量统一折算为2010年的价格水平。国内生产总值数据来源于国家统计局网站。
(三) 效率影响变量的确定 1. 证券公司自身特征变量本文借鉴学者们的研究从证券公司自身特征和环境因素两方面来选择影响效率的变量。
(1) 上市与否。检验上市类证券公司整体效率水平是否显著优于非上市类证券公司。
(2) 成立年限。检验证券公司是否会随着经营年限的增长而形成独特的核心竞争力,进而相比成立时间短的证券公司有明显的效率优势。具体数值根据证券公司年报信息确定。
(3) 企业规模。企业规模是影响效率的重要因素之一。资产规模可以反映规模经济效应。王聪、宋慧英(2012)在研究股权结构、市场结构与成本效率的关系时将证券公司的总资产作为控制变量,用来衡量证券公司的规模水平。杨志明等(2015)也选择总资产作为控制指标。考虑到证券公司的效率和总资产可能存在相互影响,本文选择年初的总资产来衡量证券公司的规模水平,数据来自合并资产负债表,和前文中对投入/产出价值量一样折算为2010年价格水平,实证时再取其对数值。
(4) 成本管理能力。成本管理能力无疑会影响企业的效率,成本管理能力越强,企业的效率应该越高。计算公式为:成本管理能力=(营业收入-投资收益-公允价值变动收益)/营业支出,根据合并利润表中的数据计算。考虑到证券公司的效率与成本管理能力可能存在相互影响,本文选择上一年度的营收数据来计算成本管理能力。
(5) 股权结构。本文从股权集中度和股权制衡度两方面来描述我国证券公司股权结构特征。同时为了考察股权集中度与证券公司的效率之间是否存在复杂的曲线关系,在研究中还加入股权集中度的平方以及三次方。分别采用第一大股东的持股比例、前三大股东的持股比例以及前五大股东的持股比例具体衡量股权集中度。数据来源于证券公司年报,部分证券公司的股权结构参考中国证监会公告。由表 1可知,2007-2015年第一大股东持股比例平均大约为48%,前三大股东持股比例平均大约为73%,前五大股东持股比例平均大约为82%。正如王聪、宋慧英(2012)所进行的国际比较,我国证券公司的股权集中度普遍偏高。
| 表 1 2007-2015年大股东平均持股比例 |
(6) 财务杠杆变量。选用资产负债率来衡量证券公司的财务杠杆水平。同样,资产负债率和效率可能存在相互影响,本文选用年初的资产负债率,合并口径。
2. 控制(环境)因素。(1) 时间因素。把时间因素作为一个控制变量,借此考察我国证券公司的效率是否随时间的推移而上升。
(2) 市场集中度(竞争度)。本文用赫芬达尔-赫希曼指数(HHI)来度量市场集中度。计算公式为
(3) 国内生产总值(GDP)的实际增长率。采用GDP实际增长率来衡量宏观经济环境对证券公司效率的影响。
四、 模型估计结果及分析 (一) 估计结果和模型适用性分析实证中选择证券公司的投资收益(y2)作为(5)式中的比较基准,对手续费及佣金净收入(y1)进行标准化,记为y1*。借助Frontier4.1c软件对(6)式进行估计,表 2给出了超越对数距离函数和无效率方程的估计结果。
| 表 2 超越对数距离函数和无效率方程估计结果 |
关于模型的适用性:(1)从γ=σu2/(σu2+σv2)看,模型的γ显著不为0,表明存在显著的无效率成分。(2)进行似然比检验,原假设H0:应采用普通线性模型,备择假设H1:采用随机前沿模型。检验的统计量都服从自由度为12的混合卡方分布,显著性水平为0.01时,临界值为25.549,由表 2的似然比值LR,很容易得到拒绝原假设H0的结论。综合上述两点,采用随机前沿分析模型是合适的。(3)通过似然比检验样本期内中国证券业是否存在技术进步,检验的假设如下:H0:不存在技术进步(即超越对数距离函数中包含t的项系数全部为0),H1:存在技术进步。经计算,检验的似然比LR为529,检验的统计量都服从自由度为5的混合卡方分布,显著性水平为0.01时,临界值为14.325,因此得到的结论是拒绝H0,也就是说,样本期内中国证券业存在显著的技术进步。
(二) 证券公司技术效率分析表 3报告了2007-2015年间我国证券公司技术效率描述统计指标,全部均值仅为0.6772,2015年年度均值达到最高0.8353,我国证券公司的效率尚有较大的提升空间。从方差来看,2015年的最小,表明这一年证券公司的效率差异最小,总体而言2015年是我国证券公司效率表现最好的一年。
| 表 3 中国证券公司2007-2015年技术效率描述统计分析表 |
图 1给出了2007-2015年证券公司年度均值的趋势图。从趋势上看,2008年有明显下降,这主要是由于金融危机的影响,然后上升,之后又略微下降,而近几年则有缓慢上升的趋势,这与证券公司的现实表现比较相符。我国证券公司的平均技术效率2008年最低,2011年次低,恰与这两年股票市场行情低迷相对应,2008年上证指数下跌了65.39%,2011年上证指数下跌了21.68%,这两年也是研究期间上证指数跌幅最大的两年。在这两年中,市场的持续下跌造成证券公司的投资收益锐减,近30家证券公司甚至出现投资亏损。尽管由于模型的限制,研究时将投资收益为负的证券公司剔除,但毫无疑问保留下来的证券公司在这两年的投资收益相比其他年份也是偏低的,从而导致这两年证券公司的技术效率普遍偏低。相比2008年,2009-2010年证券公司的技术效率算是回归正常,当然作为重要的金融中介之一,肯定也受益于由中央政府牵头从2009年开始的四万亿经济刺激计划。2010年融资融券业务正式启动,从2011年至2015年,随着融资融券等创新业务的大力推进和发展,证券公司的营收能力、创新能力和风险管理能力均有所提升,证券公司正逐步摆脱对传统经纪业务的依赖。相应地,这几年证券公司的技术效率是稳步上升的。
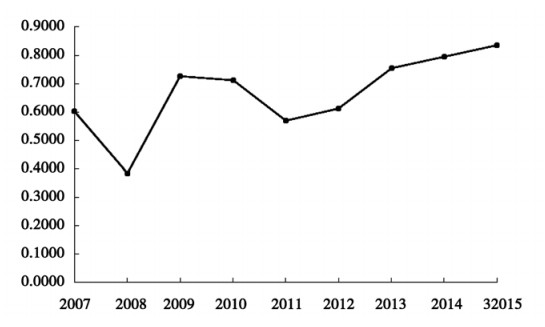
|
图 1 2007~2015年中国证券业效率均值 |
图 2给出了我国证券业技术效率核密度曲线,很明显效率分布是左偏分布,有效率非常低的证券公司,从表 3可以看到,效率最低的证券公司仅为0.0913。我国证券公司的效率普遍不高,有相当一部分证券公司效率值在0.8以下,其中效率值在0.5~0.7之间的证券公司占了很大的比例。
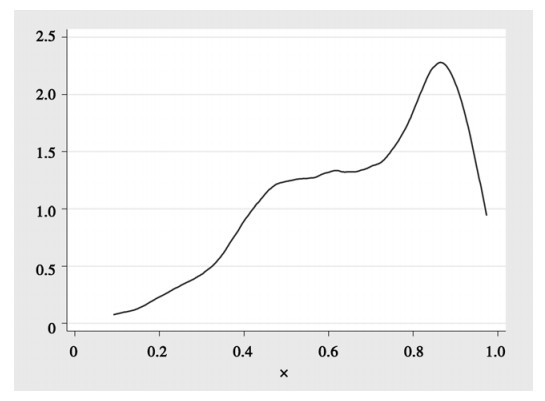
|
图 2 中国证券业技术效率核密度图 |
下面对影响证券公司技术效率的因素进行分析,无效率方程估计结果见表 2。
1. 证券公司自身特征变量(1) 上市证券公司和非上市证券公司的效率没有显著差别。非上市证券公司在效率方面的表现并不比上市证券公司差,应该大力支持符合法定上市条件的证券公司上市,促进证券行业进一步发展壮大。
(2) 成立年限对证券公司的技术效率没有显著影响。这说明证券公司并没有随着经营年限的增长而形成公司的核心竞争力进而促进效率提升,另外也可能与证券行业内部同质化竞争严重,普遍存在“靠天吃饭”现象有关。应该积极推动证券公司实施差异化、专业化、特色化发展战略,促进证券公司形成核心竞争力。
(3) 总资产与无效率显著负相关,这也就意味着其与效率显著正相关。这表明证券公司的效率具有规模效应。应该鼓励证券公司上市,积极推动证券公司市场化并购重组,促进证券公司做大做强。
(4) 成本管理能力与无效率显著负相关,当然就与效率显著正相关。这是符合预期的,证券公司的成本管理能力越强,当然经营就会越有效率,所以证券公司应该加强内部管理,提升公司的成本管理能力。
(5) 前三大股东持股比例与无效率之间是一种U型关系,因而其与效率之间是一种倒U型关系,其顶点位置为0.5705。这意味着当前三大股东持股比例小于57.05%时,证券公司的效率随前三大股东持股比例的提高而上升;前三大股东持股比例在57.05%附近时,效率达到最佳;而当前三大股东持股比例超过57.05%时,证券公司的效率会随着前三大股东持股比例的增加而下降。
本文还把模型中前三大股东持股比例的平方剔除进行估计,结果是无效率回归方程中其他变量的符号以及显著性没有变化,而前三大股东持股比例与无效率显著正相关(0.01显著性水平),因而与证券公司的效率显著负相关。这与两者之间是一种U型关系看似不一致,实则不然。根据上面倒U型关系的计算,当前三大股东持股比例超过55.40%时,前三大股东持股比例与证券公司的效率是负相关的。而从2007年到2015年,每年我国证券公司前三大股东持股比例平均都大约是73%(见表 1),远高于57.05%,所以才会呈现出前三大股东持股比例与证券公司的效率是负相关的情形。由此可见,我国证券公司前三大股东持股比例过高对效率产生了不利影响,所以应该适度降低前三大股东持股比例。本文还采用前五大股东的持股比例进行类似研究,结果表明,前五大股东持股比例与效率之间也是倒U型关系。
本文还在模型中进一步加入前三大股东持股比例的三次方,以此来检验前三大股东持股比例与无效率之间是否还存在更复杂的非线性关系。估计结果表明,在加入前三大股东持股比例的三次方之后,前三大股东持股比例、其平方以及三次方均不显著(显著性水平0.10),而无效率回归方程中其他变量回归系数的符号以及显著性没有发生任何变化。前三大股东持股比例与无效率之间不存在复杂的三次曲线关系。
本文也检验了第一大股东持股比例与无效率之间的关系。保持其他变量不变,将前述模型中的前三大股东持股比例及其平方剔除:(1)加入第一大股东持股比例,记为模型1;(2)加入第一大股东持股比例及其平方,记为模型2;(3)加入第一大股东持股比例、其平方以及三次方,记为模型3。这三个模型的估计结果见表 4。在模型1中,第一大股东持股比例与无效率显著正相关,这也就意味着其与效率是显著负相关的,第一大股东持股比例越高,证券公司的效率越低。在模型2中,第一大股东持股比例及其平方并不显著。而在模型3中,第一大股东持股比例、平方以及三次方均不显著。第一大股东持股比例与效率之间并不存在显著的二次曲线和三次曲线关系,这与王聪、宋慧英(2012)、杨志明、郑明高、鄢哲明(2015)等学者的研究结论并不相同,这种不同可能与学者们的研究视角、选择的样本范围、时间跨度以及效率估算方法不同有关。
| 表 4 三个模型无效率回归结果比较 |
(6) 资产负债率与无效率之间显著负相关,也就是说资产负债率与效率之间显著正相关,财务杠杆高有益于证券公司效率的提升。2014年新修订的《证券公司风险控制指标管理办法》放宽了风险控制限制、净资产比率要求以及自营投资净资本的要求,放大了券商业务空间。据专业人士测算券商杠杆率有望大幅提升至6倍左右。无疑,这一举措将拓展行业发展空间,提升证券公司的效率。但对于这种在诸多行业去杠杆之际,证券行业出现的“加杠杆”做法,无论是证券公司还是监管部门都应该保持清醒的认识,毕竟高杠杆意味着高风险。
2. 控制因素的影响(1) 时间因素t与无效率显著负相关。这意味着,2007~2015年间证券公司的效率总体上是趋于上升的,这一点也可以从图 1看出来,尤其是从2011-2015年间证券公司的效率是稳步上升的。在经历了2008年金融危机的严峻考验之后,近些年来证券行业在人员素质、业务创新能力、业务范围以及资本实力等方面都有了很大的提升,这些无疑会有助于效率的提升。
(2) 赫芬达尔指数与无效率显著正相关,因而与效率显著负相关。赫芬达尔指数数值越大,意味着证券行业集中度越高,市场竞争程度越低,证券公司的效率越低。这一结果与传统产业组织理论哈佛学派的理论相一致,竞争可以提高企业效率。本文也检验了赫芬达尔指数与效率之间是否存在二次曲线关系。但在加入赫芬达尔指数的平方之后,赫芬达尔指数项不显著,其平方项在0.05显著性水平显著,无效率方程中其他回归系数的符号和显著性没有发生任何变化。而王聪、宋慧英(2012)的研究表明,市场竞争度与证券公司成本效率之间呈现倒U型。杨志明、郑明高、鄢哲明(2015)的研究结论是市场集中度(HHI指数)与证券公司效率之间呈现“U”型关系。本文的研究结果与他们的不尽一致。
(3) GDP实际增长率与无效率显著负相关,进而与效率显著正相关。这符合预期,经济的高速增长无疑会带给证券行业更多的红利。
五、 结论和建议本文使用2007-2015年中国95家证券公司的数据和基于产出导向距离函数的随机前沿分析方法对中国证券业的技术效率及其影响因素进行了系统研究。
主要结论为:(1)证券公司前三大股东的持股比例与技术效率之间呈倒U型关系。(2)2007-2015年间证券公司的技术效率总体上是上升趋势。(3)市场竞争度与证券公司的技术效率显著正相关。(4)国内生产总值实际增长率与证券公司的技术效率显著正相关。(5)证券公司的总资产、成本管理能力以及资产负债率与技术效率显著正相关。(6)证券公司上市与否以及成立年限对证券公司的技术效率没有显著影响。
以上结论具有以下几点启示:(1)应该大力支持符合法定上市条件的证券公司公开发行上市,积极推动证券公司市场化并购重组,促进证券公司扩充资本,扩大规模,以实现效率的规模效应。(2)推动证券公司实施差异化、专业化、特色化发展战略,促进证券公司培育和提升核心竞争力,提升效率。(3)科学调控杠杆率,在有效控制风险的前提下合理放大行业业务规模空间、提高公司自有资金使用效率。(4)股权结构合理化是促进效率提升的重要举措,前三大股东的持股比例不应过低,也不要过高,以实现效率最佳。目前,我国证券公司前三大股东持股比例过高,应该适度降低前三大股东持股比例。
相信在不久的将来将会涌现出一批与我国经济实力和资本市场规模相匹配、具有中国特色和品牌影响力的一流证券公司。
| [] | 边晓磊、 陈学彬 , 2009, "基于DEA方法的我国证券公司经营效率分析", 《新金融》 , 第 4 期 , 第 50–55 页。 |
| [] | 陈芳平、 习斌 , 2011, "我国证券公司效率的实证分析", 《兰州大学学报(社会科学版)》 , 第 4 期 , 第 104–108 页。 |
| [] | 程可胜 , 2009, "中国证券公司效率的实证分析", 《华东经济管理》 , 第 8 期 , 第 82–87 页。 |
| [] | 樊宏 , 2002, "基于DEA模型的我国证券公司评价方法及应用", 《数量经济技术经济研究》 , 第 4 期 , 第 118–121 页。 |
| [] | 冯根福、 丁国荣 , 2011, "中国证券公司内部治理影响公司经营效率的实证分析", 《财经理论与实践》 , 第 169 期 , 第 30–36 页。 |
| [] | 何康 , 2015, "利率市场化有利于改善城市商业银行效率吗-来自中国24家城市商业银行的经验证据", 《南方经济》 , 第 8 期 , 第 50–62 页。 |
| [] | 何晓萍 , 2011, "中国工业的节能潜力及影响因素", 《金融研究》 , 第 10 期 , 第 34–46 页。 |
| [] | 蒋绵绵、 杜朝运、 王滨江 , 2014, "证券公司经营效率影响因素分析-基于超效率DEA模型与Tobit模型", 《财会通讯》 , 第 11 期 , 第 21–24 页。 |
| [] | 李春米、 毕超 , 2015, "中国西部地区环境全要素生产率增长研究", 《兰州大学学报(社会科学版)》 , 第 4 期 , 第 48–59 页。 |
| [] | 李兰冰、 胡均立、 黄国彰 , 2011, "海峡两岸证券业经营效率比较研究:基于Metafrontier方法", 《当代经济科学》 , 第 1 期 , 第 40–47 页。 |
| [] | 连玉君、 苏治 , 2009, "融资约束、不确定性与上市公司投资效率", 《管理评论》 , 第 1 期 , 第 19–26 页。 |
| [] | 刘婕、 魏玮 , 2014, "城镇化率、要素禀赋对全要素碳减排效率的影响", 《中国人口·资源与环境》 , 第 8 期 , 第 42–48 页。 |
| [] | 沙浩 , 2011, "证券公司治理机制对其市场风险与效率的影响", 《金融与经济》 , 第 4 期 , 第 59–61 页。 |
| [] | 王聪、 宋慧英 , 2011, "市场结构、股权结构与证券公司成本效率", 《投资研究》 , 第 11 期 , 第 93–107 页。 |
| [] | 王聪、 宋慧英 , 2012, "中国证券公司股权结构、市场结构与成本效率的实证研究", 《金融研究》 , 第 5 期 , 第 80–92 页。 |
| [] | 王文、 牛泽东 , 2014, "中国装备制造业技术创新的静态与动态效率-基于二位码行业数据的分析", 《经济管理》 , 第 5 期 , 第 24–36 页。 |
| [] | 王晓芳、 程可胜 , 2009, "中国证券业效率的动态分析", 《产业经济研究》 , 第 2 期 , 第 49–54、78 页。 |
| [] | 谢军 , 2007, "第一大股东持股和公司价值:激励效应和防御效应", 《南开管理评论》 , 第 1 期 , 第 21–25 页。 |
| [] | 续竞秦、 杨永恒 , 2012, "我国省际能源效率及其影响因素分析-基于2001~2010年面板数据的SFA方法", 《山西财经大学学报》 , 第 8 期 , 第 71–78 页。 |
| [] | 杨光兵、 张爱武、 刘亚 , 2013, "证券公司效率评价:一种经过风险调整的方法", 《财经理论与实践》 , 第 9 期 , 第 51–54 页。 |
| [] | 杨志明、 郑明高、 鄢哲明 , 2015, "金融控股与中国证券公司效率", 《浙江社会科学》 , 第 6 期 , 第 15–23、130、155 页。 |
| [] | 于研、 孙磊 , 2010, "我国商业银行收益结构转型对经营效率的影响", 《财经研究》 , 第 2 期 , 第 99–109 页。 |
| [] | 翟永会 , 2014, "市场结构、获利能力与证券公司效率", 《财经理论与实践》 , 第 190 期 , 第 43–47 页。 |
| [] | 张健华、 王鹏 , 2009, "中国银行业前沿效率及其影响因素研究-基于随机前沿的距离函数模型", 《金融研究》 , 第 12 期 , 第 1–18 页。 |
| [] | 张健华、 王鹏 , 2011, "银行效率及其影响因素研究-基于中、外银行业的跨国比较", 《金融研究》 , 第 5 期 , 第 13–28 页。 |
| [] | 朱南、 刘一 , 2008, "中国证券公司生产效率的数据包络分析", 《金融研究》 , 第 11 期 , 第 120–137 页。 |
| [] | Battese, G.E. and Coelli, T.J. , 1995, "A Model for Technical Inefficiency Effects in a Stochastic Frontier Production Function for Panel Data". Empirical Economics , 20 (2) , 325–332. DOI:10.1007/BF01205442 |
| [] | Coelli, T. and Perelman, S. , 1999, "A Comparison of Parametric and Nonparametric Distance Functions:With Application to European Raiways". European Journal of Operational Research , 117 (2) , 326–339. DOI:10.1016/S0377-2217(98)00271-9 |
| [] | Coelli, T and Perelman, S. , 2000, "Technical Efficiency of European Railways:A Distance Function Approach". Applied Economics , 32 (15) , 1967–1976. DOI:10.1080/00036840050155896 |
| [] | Fukuyama, H. and W. L. Weber and Weber, W. L. , 1999, "The Efficiency and Productivity of Japanese Securities Firms, 1988-1993". Japan and the World Economy , 11 (1) , 115–133. DOI:10.1016/S0922-1425(97)00033-9 |
| [] | Grosskopf, S. , Margaritis, D. and Valdmanis, V. , 1995, "Estimating Output Substitutability of Hospital Services:A Distance Function Approach". European Journal of Operational Research , 80 (3) , 575–587. DOI:10.1016/0377-2217(94)00138-3 |
| [] | Lovell, C. A. K., S. Richardson, P. Travers, and L. L. Wood, 1994, "Resources andFunctionings:A New View of Inequality in Australia", in W. Eichhorn, ed., "Models and Measurement of Welfare and Inequality", Springer Verlag, Berlin:787-807. |
| [] | Orea, L. 2002, "Parametric Decomposition of a Generalized Malmquist Productivity Index". Journal of Productivity Analysis , 18 (1) , 5–22. DOI:10.1023/A:1015793325292 |
| [] | Serifsoy, B. and Weiß, M. , 2007, "Settling for efficiency-A framework for the European Securities Transaction Industry". Journal of Banking & Finance , 31 (10) , 3034–3057. |
| [] | Wang, Hung-Jen 2003, "A Stochastic Frontier Analysis of Financing Constraints on Investment:The Case ofFinancial Liberalization in Taiwan". Journal of Business & Economic Statistics , 21 (3) , 406–419. |
| [] | Wang, K.-L. , Tseng, Y.-T. and Weng, C.-C. , 2003, "A Study of Production Efficiencies of Integrated Securities Firms in Taiwan". Applied Financial Economics , 13 (3) , 159–167. DOI:10.1080/09603100110111105 |
| [] | Yeh, C-P , Wang, K-M and Chai, K-C , 2010, "Measuring the Efficiency of Securities Companies by Corporate Governance in a Financial Holding and Non-financial Holding System". Expert Systems with Applications , 37 (6) , 4671–4679. DOI:10.1016/j.eswa.2009.12.041 |
| [] | Zhang, WD , Zhang, S. and Luo, X. , 2006, "Technological Progress, Inefficiency and Productivity Growth in the US Securities Industry, 1980-2000". Journal of Business Research , 59 (5) , 589–594. DOI:10.1016/j.jbusres.2005.10.011 |



