股指期货作为一种重要的金融衍生品,自1982年在美国诞生以来,就发展非常迅速,目前己成为世界上交易量最大、流动性最好的期货品种之一。我国在2010年4月16日正式推出了沪深300股指期货,之后又陆续推出了上证50和中证500股指期货品种。股指期货的推出对我国资本市场来说是一件大事,给投资者带来了许多美好期待,增加了可以套期保值和规避市场波动的工具,但在股指期货推出后3个月内大盘的快速下跌近30%,其所起到的稳定市场功能和作用似乎并不显著。这可能和我国的股指期货推出时间较短,品种结构和市场监管不完善有关。股指期货作为一种国际通行的金融工具,其在资本市场的地位和功能是非常重要的。价格发现功能是衡量其发展程度的一大重要标志,也是学术界、实业界以及监管层十分关心的问题。
本文从股市上升、下跌、震荡的三个状态下来分别探讨股指期货与现货市场的价格引导关系。这是目前众多文献中,学者们尚未进行的领域,但却是观察问题一个不可忽视的角度。因为股市的快速上升和下跌通常是股指期货发挥其避险和套期保值功能的良好机会,同时也潜藏着利用它进行投机的机会。所以本文从实证的角度,按照时变的思路,根据股指期货可能在不同市场环境下的作用和表现,将市场区别为上升、下跌和震荡三种情况下来分析价格发现功能的差别,以更细致地解释在不同环境下价格引导和发现能力的差异。
二、 文献回顾股指期货的一个重要功能是价格发现。按照Schreiber and Schwartz (1986)的解释,价格发现就是将市场相关信息迅速而有效融入到资产价格中的行为过程,是对均衡价格的探寻过程。在已有的文献中,一般认为期货市场具有成本低、流动性好、可加杠杆、指令执行快速等优点,会吸引知情交易者率先参与。因此,期货市场就能对市场信息做出更快的反应,期货价格的变化也通常会领先于现货价格的变化。Fleming等(1996)认为,知情交易者倾向于选择在低交易成本的期货市场来进行交易,所以期货价格也会首先做出反映。Kim (1999)应用VAR模型检验了S & P500、MMI and NYSE composite三种指数的期货市场与现货市场,研究表明期货市场是以S & P500领先,而现货市场是以MMI指数为主导,两个结果都证明低交易成本赋予市场价格发现的优势。Booth等(1999)利用协整和VECM模型分析了德国DAX指数现货、期货和期权的价格发现过程,结果表明DAX期货的价格发现能力明显优于期权,该结果符合低交易成本具价格发现优势的假说。其后,也有一些研究者对市场信息的种类做出更加细致的区别。肖辉和吴冲锋(2004)认为当信息是反映少数公司的信息时,知情交易者倾向于在股市做交易,而对于系统信息,则更倾向于在期货市场做交易。所以在面对同样的信息冲击时候,微观市场结构的不同就是导致该市场能否价格领先的基本原因,哪一个市场具有使交易者快速获利的响应机制和低成本优势,就会成为交易者的首选,也就随之带来了价格的优先表现。当然,信息也会有二次的叠加与确认,因为其他市场也会收到同样有关经济和信息的数据,也有相应的资产可作为操作对象,只是响应的机制和行动方式可能会慢一点。
在对价格发现机制的定性描述研究以外,国内外更多的是对这种的机制的定量化描述与检验。在这个过程当中,随着现代计量工具的改进与发展,大致经历了三个阶段:
第一阶段是简单线性回归方法。这种方法通常把现货、期货市场的价格作为因变量和自变量,利用简单线性回归求其系数,然后对系数进行约束性检验。Bigman等(1983)提出了首个对期货市场有效性进行检验的模型St=a+bFt+et,其中St为现货价格,Ft为期货价格。他认为如果期货市场具有价格发现功能,那么回归系数就应该具有a>0,b=1的约束。但之后Elam和Dixon (1988)的研究却认为由于金融时间序列是非平稳的,因此a>0,b=1的假定就可能存在伪回归,所依赖F统计量就可能存在偏误。因此,学者们逐渐放弃了这一类研究。
第二阶段是以协整关系和VECM为基础的研究。这类研究是迄今为止有关期货和现货关系以及价格发现功能所见到的数量最多的研究。VECM不仅克服了不稳定时间序列建模的难题,而且建模后,可以测定变量之间的短期关系,也可以测定变量偏离长期均衡后的调整关系。另外,VECM也是格兰杰因果关系、脉冲响应关系、方差分解、长短期模型(PT)和信息份额(IS)分析的基础。Gonzalo and Granger (1995)以VECM模型为基础,采用长短期模型,把价格的变化解释为永久冲击P和短暂冲击T,通过对永久冲击构成系数的分解来研究每个市场对共因子的贡献。Hasbrouck (2003)采用信息份额IS模型,对美国股指期货的价格发现功能进行了研究,发现规模较小的期货市场在价格发现过程中的贡献更大,而像S & P500指数和纳斯达克100这样规模较大的指数却贡献更小。在IS和PT这两类较为典型的研究方法提出之后,也有研究者做了对比试验,发现这两者的结果在残差不相关时候较为一致,而残差较为严重相关时候,则会很不一致。Brooks et al.(2001)利用VAR模型和VECM模型同时研究了FTSE-100指数现货和期货之间的关系,结果表明期货指数的变化可能导致现货市场的变化。在国内,严敏等(2009)利用VECM、公共因子模型和带有误差修正的双变量EGARCH模型,发现指数现货市场在价格发现中起到主导作用,且两个市场之间不存在显著的非对称双向波动溢出效应。何诚颖(2011)从股指期货和现货对新信息的反应速度、新信息融入比率两个角度,采用了沪深300指数期货和现货的1分钟数据和向量误差修正模型和脉冲响应函数研究了沪深300股指期货的价格发现能力,发现沪深300指数期货市场的价格发现能力都要强于指数现货市场。方匡南、蔡振忠(2012)研究表明我国指数期货和现货价格存在相互引导关系,而现阶段现货市场能更快反应全部市场的冲击,且现货市场在价格发现功能中的作用相对较大。
第三阶段是时变阶段。这是目前开展比较少的,但却是更为细致和接近现实的阶段。这种研究的假定是期货和现货市场之间不是一种固定关系,而是一种时变关系,即随着时间而变化的关系,这种关系在某些时候甚至可以为零(即没有关系)。Chiang (2003)提出了带有机制转换的协整关系模型,并对CAC40, S & P500 and Nikkei的股指期货进行了实证研究,发现附加转换机制的协整模型相对传统模型有更好的拟合效果。Li (2009)采用具有马尔科夫转换机制VECM模型进行研究,结果发现在不同波动机制下股指期货具有引领现货的价格发现功能是有差异的。顾京、叶德磊(2013)利用递归协整的方法,发现在我国股指期货运行之初,股指期货和现货市场之间并不具有稳定的协整关系,而随着市场的不断发展和完善,二者之间开始出现稳定的协整关系。
在对以上文献的梳理和研究过程中,发现已有的研究对股指期货的价格发现能力存在不一致结论,有的认为我国股指期货市场已具备了价格发现能力,而有的则认为不然。这些差异产生的原因一方面可能是使用的数据阶段和频率有差别,二则也可能是使用的计量手段不同。另外,许多研究将期货和现货市场二者的关系固定化,不利于体现在不同环境下二者间的时变(Time Varying)关系。本文将按照时变的思路,根据股指期货可能在不同市场环境下的作用和表现,将市场区别为上升、下跌和震荡三种情况下来分析价格发现功能的差别,以更细致地解释在不同环境下价格引导和发现能力的差异。
三、 研究方法对股指期货和现货的互动关系分析首先是建立在协整分析基础上的,即这两者之间在长期是否具有稳定的协同变化关系,所以就有必要检验两个价格序列的平稳性以及协整关系。序列的平稳性检验可以采用ADF (Augmented Dickey-Fuller)检验,协整检验采用Johansen and Juselius提出的JJ检验。如果检验结果符合同阶单整和具有协整关系,就可以进行VECM分析。
(一) 向量误差修正模型(VECM)分析两个I (1)过程的期货和现货价格时间序列可以写成如下的向量误差修正模型(VECM)形式:
| $ \Delta LNI{{F}_{t}}={{\lambda }_{f}}{{e}_{t-1}}+\sum\limits_{i=1}^{p}{{{a}_{fi}}\Delta lnH{{S}_{t-i}}}+\sum\limits_{i=1}^{p}{{{b}_{fi}}\Delta lnI{{F}_{t-i}}}+{{\varepsilon }_{f, t}} $ | (1) |
| $ \Delta LNH{{S}_{t}}={{\lambda }_{s}}{{e}_{t-1}}+\sum\limits_{i=1}^{p}{{{a}_{si}}\Delta lnH{{S}_{t-i}}}+\sum\limits_{i=1}^{p}{{{b}_{si}}\Delta lnI{{F}_{t-i}}}+{{\varepsilon }_{f, t}} $ | (2) |
其中:Δ为一阶差分符号,LNIF、LNHS分别为股指期货和现货市场价格的对数,et-1为误差修正项,λf和λs分别为股指期货和现货误差修正项的调整系数,afi、bfi、asi、bsi为短期调整系数,p为方程阶数,εf, t和εs, t为残差项。VECM模型可以从长期和短期两个角度来描述期货和现货价格之间的动态变化关系,其中的协整关系就是二者的长期均衡关系。
从价格序列向长期均衡调整的角度看,ECM项的系数λf和λs的数值可能有以下三种情形:(1)λf < 0,λs>0,这种情形意味着所建模型是适合的,在期货和现货价格偏离均衡状态时候,下一期会有一个回调的机制,同时,系数值越大,则回调的速度越快。(2)λf>0,λs < 0,这种情形意味着在期货和现货价格偏离均衡状态时候,下一期不仅不会回调,而且是发散状态,否定了长期存在协整的关系。(3)在λf=0时候,λs可能有三种情形:λs>0或λs=0,λs < 0。当λs>0的情形是合适的,意味着期货市场虽然不会受均衡关系约束,但现货市场却受到长期均衡关系约束,会自动向期货市场靠拢。而λs=0或λs < 0的情形是对协整关系的一种否定,也即长期关系对短期是没有约束的。
从短期关系来看,若式(1)中ΔlnHSt-i的某些系数afi显著不为零,则说明这些时期的现货价格能影响期货价格,并且,如果时期跨度越长,则说明越能更早预测期货价格。同样,若式(2)中ΔlnIFt-i的某些系数bsi显著不为零,则说明这些时期的期货价格能影响现货价格,并且,如果时期跨度越长,则说明越能更早预测现货价格,即期货价格领先现货价格几个时期。
(二) 公共因子模型通过VECM虽然可以得到两个市场的相互引导的方向和领先关系,但依然不能确定不同市场在价格决定中的比例,所以Hasbrouck (1995)和Gonzalo-Granger (1995)分别提出信息份额(Information Share,简写为IS)模型和长短期模型(Permanent Transitory,简写为PT)来研究价格发现过程中的数量关系。这两个模型的共同之处都是建立在VECM之上的,只是采用了不同的分解技术,PT分解的是共因子,而IS分解的是共因子的方差。当两方程的残差完全不相关时,这两者的结果差别不大,但当残差严重相关时,则会有较大差别(Baillie,2002)。
1. 长短期(P-T)模型Stock-Watson (1988)的研究认为期货和现货价格的协整序列Yt可以表示为Yt=Ft+Gt,其中Ft代表共同因子,Gt代表暂时成分。Gonzalo-Granger (1995)证明了共同因子Ft可以分解为两个价格的线性组合Ft=bYt,b=(b1,b2)’为公共因子系数向量,由于b与误差修正系数向量α=(α1,α2)’正交,对b标准化后得两个市场价格发现的贡献度为:
| $ \begin{matrix} {{\text{ }\!\!\beta\!\!\text{ }}_{1}}=\frac{\left| {{\alpha }_{2}} \right|}{\left| {{\alpha }_{1}} \right|+\left| {{\alpha }_{2}} \right|} & {{\text{ }\!\!\beta\!\!\text{ }}_{2}}=\frac{\left| {{\alpha }_{1}} \right|}{\left| {{\alpha }_{1}} \right|+\left| {{\alpha }_{2}} \right|} \\ \end{matrix} $ | (3) |
Hasbrouck (1995)将共同因子Ft的方差进行分解,通过计算对方差的贡献大小来测度每个市场的价格发现功能。当两个市场的新息完全没有相关性的时候,第i个市场所占的信息份额为:
| $ {{s}_{i}}=\frac{\gamma _{i}^{2}\sigma _{i}^{2}}{\sum\limits_{i=1}^{n}{\gamma _{i}^{2}\sigma _{i}^{2}}} $ | (4) |
当两个市场的存在同期新息相关时,可以利用侨力斯基(Cholesky)方法进行分解,但侨力斯基方法受变量次序改变的影响,因此,调整两个变量的次序就可以得到每个市场IS的上限和下限:
| $ \begin{matrix} IS_{F}^{U}=\frac{{{\left({{\lambda }_{s}}{{\sigma }_{f}}-{{\lambda }_{f}}\rho {{\sigma }_{s}} \right)}^{2}}}{\lambda _{s}^{2}\sigma _{f}^{2}-2{{\lambda }_{f}}{{\lambda }_{s}}\rho {{\sigma }_{f}}{{\sigma }_{s}}+\lambda _{f}^{2}\sigma _{s}^{2}}&IS_{F}^{L}=\frac{\lambda _{s}^{2}\sigma _{f}^{2}{{\left(1-\rho \right)}^{2}}}{\lambda _{f}^{2}\sigma _{s}^{2}-2{{\lambda }_{f}}{{\lambda }_{s}}\rho {{\sigma }_{f}}{{\sigma }_{s}}+\lambda _{s}^{2}\sigma _{f}^{2}} \\ \end{matrix} $ | (5) |
本文取ISFU和ISFL的均值作为期货市场在价格发现中所占份额的有效估计,同理,现货市场也按照这种方法进行估计。
四、 数据选取本文的数据样本对象是沪深300指数,该指数横跨沪深两市的权重股,很好地代表了我国股市发展的情况。而沪深300期指是我国上市最早的股指期货,数据周期最长,能较好第反映我国股指期货市场的发展情况。另外,数据频率的选择对于能否得出正确结论是有很大影响的。在已有文献中,有些研究选择日数据来进行(严敏、巴曙松等,2009),这样的频率对于反映迅捷的股市和期货市场来说,可能稍显长了一点。因为套利交易者会很快弥补市场的缺口,不会留那么长时间,所以更多研究者选择时期很短的数据。本文选择1分钟数据,这样可以很细致地观察到两个市场的互动关系。在样本数据的阶段划分上,从2010年4月16日期指上市以来,本文选择三段较有代表性的数据来研究:
第一阶段股市急速上升时期(2015年3月9日-2015年4月28日)。在这一时期,沪深300股指在短短37个交易日内,从3440点上升到4741点,升幅达37.8%,日均升幅1%。
第二阶段股市急速下跌时期(2015年6月9日-2015年7月9日)。在这一时期,沪深300股指在短短23个交易日内,从5349点下跌到3897点,跌幅达27%,日均跌幅-1.17%。
第三阶段股市平稳震荡时期(2014年5月12日-2014年7月21日)。在这一时期,沪深300股指在50个交易日内,从2155点到2166点,变化幅度0.5%。
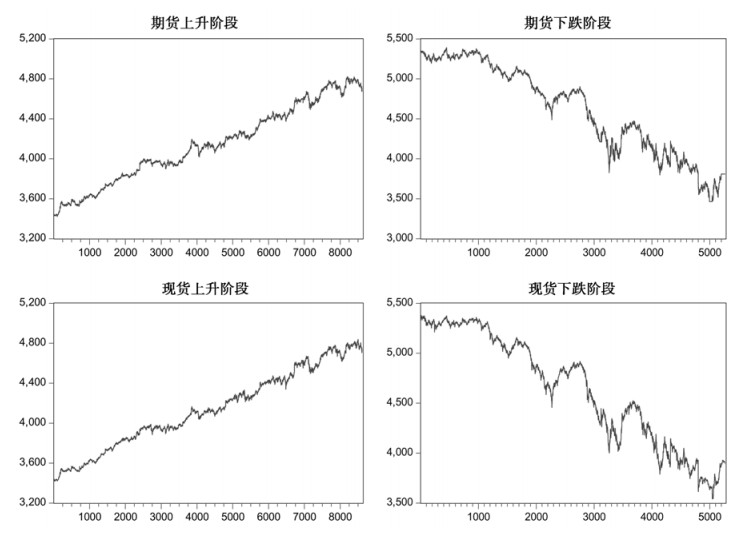
本文选择沪深300IF所构成的连续指数作为期货指数。由于期货和现货的交易时间不同,只保留期货和现货市场每日相同时段的数据,即上午9:31-11:30,下午13:01-15:00,这样每天有240个1分钟数据,数据来源于wind数据库。为了减少异方差和基期的影响,本文对期货和现货序列取自然对数,分别记为LNIF和LNHS。沪深300上升和下跌阶段的走势如图 1,三个阶段序列统计特征如表 1所示。
|
图 1 股指期货与现货序列上升和下跌阶段的走势图 |
| 表 1 三个不同阶段下股指期货与现货序列的描述性统计量 |
从图 1和表 1可以看出,本文所选时段内股指期货和现货的走势很明显,具备显著的上升和下跌趋势。从2015年3月9日至2015年4月28日的短短36个交易日内,股指期货和现货的升幅为37%,从2015年6月9日至2015年7月9日的短短22个交易日内,股指期货和现货的跌幅为27%。三个阶段数据的偏度、峰度和J-B统计量基本拒绝正态分布,具有一般金融序列所有“尖峰厚尾”特征。
五、 实证分析 (一) 单位根和协整检验股指期货和现货的互动关系分析首先是建立在协整分析基础上的,即这两者之间在长期是否具有稳定的协同变化关系,所以就有必要检验两个价格序列的平稳性以及协整关系。本文利用ADF (Augmented Dickey-Fuller)来检验数据平稳性,从表 2可以看出股指期货和现货的原始序列在1%的显著性水平下是不平稳的,但一阶差分后的序列是平稳的,是I (1)过程,具备做协整分析的基础。
| 表 2 沪深300期货和现货的ADF检验结果 |
对二者间的协整关系检验,由于E-G检验的缺点,本文采用Johansen and Juselius (1990)提出的迹统计量(Trace Statistic),检验形式采用序列有趋势项而协整方程只包括常数项的形式,阶数的确定依据VAR模型的阶数减1准则选择。从表 3的检验结果可以看出,第一行所假定的没有协整关系,在1%的显著性水平下被拒绝;而第二行所假定的至少存在一个协整关系被接受。所以股指期货和现货在长期有一个稳定的协同变化趋势。
| 表 3 沪深300期货和现货的Johansen协整关系检验结果 |
在沪深300期货和现货序列存在协整关系的前提下,本文按照上升、下跌和震荡三个阶段分别研究价格互动关系。
第一阶段上升时期(2015年3月9日至4月28日)。2015年春夏之交的大牛市是距今最近的一个牛市,本文选择这个阶段五条均线全部向上的时段,共计36个交易日。根据AIC和SC最小准则,VECM模型的阶数最终确定为8阶,AR根全部在单位圆内,表示模型是稳定的。具体结果见表 4中的上升阶段,从长期均衡关系对短期变动的约束看,期货收益率的调整系数λf不显著,而现货的调整系数λs在1%水平下显著不为0且λs>0,这样的实证结果说明期货市场的收益率不受长期关系的约束,而现货市场受到长期均衡关系约束,会主动向期货市场靠拢。从短期关系看,现货市场收益率(ΔLNHSt)所对应的方程中受到期货市场的前1期、2期、3期、4期、5期、6期的影响都是显著不为零的(置信度99%)。因此,可以看出期货市场在6分钟前就可以引导现货市场价格。而在期货收益率方程中,现货市场只在1分钟前有0.092的影响力,在其余时间段并不显著。所以,在股市上升阶段,期货市场的价格引导功能都要胜过现货市场。
| 表 4 三个阶段VECM模型的估计结果 |
第二阶段下跌时期(2015年6月9日至7月9日),共计22个交易日,跌幅28%。根据AIC和SC最小准则,VECM模型的阶数最终确定为5阶,AR根全部在单位圆内,表示模型是稳定的。具体结果见表 4中的下跌阶段,从长期关系对短期的约束看,期货收益率和现货收益率的调整系数都很显著(5%水平),且为一负一正(期货为负,现货为正),但期货调整系数的绝对值大于现货。这样的实证结果说明期货和现货市场都受到长期均衡关系约束,都会向彼此靠拢,但期货市场的调节速度要快一点。从短期变化看,现货市场收益率所对应的方程中受到期货市场的前1期、2期、3期、4期、5期的影响都是显著不为零(置信度99%)。因此,可以看出期货市场在5分钟前就可以引导现货市场价格。而在期货收益率方程中,现货市场只在4分钟前有影响力,在其余时间段并不显著。所以,在股市下跌阶段,现货市场对期货的价格引导功能有所增加,但起主导作用的还是期货市场。
第三阶段震荡时期(2014年5月12日至7月21日),共计50个交易日。根据AIC和SC最小准则,VECM模型的阶数最终确定为9阶,AR根全部在单位圆内,表示模型是稳定的。具体结果见表 4中的震荡阶段,从长期关系对短期的约束看,现货收益率的调整系数λs在5%水平下不显著,但在10%水平下显著,期货收益率的调整系数在1%水平下显著,且小于0,同时期货调整系数的绝对值大于现货调整系数。这样的实证结果说明现货市场虽然也受长期均衡关系的约束,但期货市场受到长期均衡关系约束力更大,会主动向现货市场靠拢。所以,在股市震荡阶段,从长期对短期关系的约束看,现货市场的价格引导功能都要胜过期货市场。
(三) 公共因子模型在VECM分析的基础上,本文应用PT模型和IS模型来量化不同市场在价格决定中的比例。具体结果见表 5,在股市快速上升的阶段,不论是PT模型还是IS模型的检验结果都显示,期货市场对价格发现所占的比例都较大,分别为73.8%和68.6%,明显胜过现货市场所占比例26.2%和31.4%。另外,期货和现货市场的相关系数达到0.667,有较大的相关性,IS模型的可信度较好。这个结果与之前的VECM模型也相呼应,基本认可期货市场在股市快速上升阶段的价格发现能力要远远大于现货市场。
| 表 5 IS和PT模型检验结果 |
在股市急速下跌的阶段,IS模型的检验结果表明期货和现货市场价格发现所占比例分别为49.5%和50.5%,基本无差异;而PT模型表明二者分别为40.8%和49.2%。虽然PT模型和IS模型的检验结果有所差别,但由于期货和现货市场的相关系数达到0.65,二者有较大的相关性,所以IS模型的结论更可靠,也就是两个市场对价格决定的力度基本持平。
在股市盘整阶段,不论是PT模型还是IS模型的检验结果都显示,现货市场对价格发现所占的比例都较大,分别为78.1%和71.2%,明显胜过期货市场所占比例21.9%和28.8%。另外,期货和现货市场的相关系数为0.443,相关性并不大,两模型的结果无显著差异。这个结果与之前的VECM模型也相呼应,基本认可现货市场在此阶段的价格发现能力要大于期货市场。
(四) 稳健性检验为了进一步验证股指期货市场在不同行情下的价格发现功能,增加上述结论的可靠性和稳定性,本文增加两个时段(共6个时期)来做验证,具体时期选择如表 6。
| 表 6 股指期货与现货序列的两个时间段表 |
从IS和PT模型的检验结果来看,第二、三阶段中,上升和下跌时期中期货市场的价格发现所占比例较大,大致在71.5%~76.1%,远大于现货市场的价格发现比例。其中,在股市大跌时期,期货市场的价格发现能力更大一点。这可能与金融市场更易于受到市场负面信息影响,下尾相关性增大有关。相对来说,在市场震荡阶段,现货市场的价格发现功能要大很多,在两个阶段平均为72.5%左右,这与第一阶段结论是相一致的。
| 表 7 阶段二和阶段三的IS和PT模型检验结果 |
股指期货在我国目前尚属新生事物,对其如何监管以及其对我国资本市场发展所起到的作用都是需要探索的问题。本文采用VEC模型、PT模型和IS模型,从股市上升、下跌、震荡的三个不同状态来分别探讨了股指期货与现货市场的价格引导和发现关系。通过对不同状态下股指期货价格发现能力的实证分析,发现在大牛市时期,股指期货的所起到的作用会很明显。在股市急速上升的时期,股指期货由于对宏观经济的信息吸收较好和反映较快,加上自身市场特有的微观结构,所以领先现货市场6个时期,并且在价格发现中所占比例为70%左右。在股市急速下跌(熊市)的时期,股指期货领先现货市场5个时期,在价格发现中所占比例与现货市场基本持平,这可能与我国的期货市场目前规模较小和品种单调有关,也可能与本文所用样本数据有关。在股市平盘震荡时期,股指期货的价格发现能力要弱于现货市场,只占25%左右比例。这可能与市场缺乏热点,投资者也缺少动力来应用股指期货来进行套利或避险的行为有关。因为股指期货通常在大起大落的市场中才能体现其“用武之地”,而平淡的市场则无法凸现其价值。
本文的建议是在股市快速上升和下跌阶段,投资者要更加重视股指期货的作用,可以充分利用股指期货进行避险或套期保值。同时,我国要在结合境外经验与自身实际情况的基础上,加快发展股指期货市场,在已有的品种基础上,进一步增加市场供给,以拓展金融期货产品的深度和广度,增加市场交易的活跃程度。在股指期货的品种与合约设计方面,要大胆引进国外的先进设计理念,创新品种设计,改善目前较为单一的产品体系。在市场交易方面,进一步协调期货与现货市场的交易制度,取消对股指期货交易的一些限制措施,完善市场交易制度。总之,只有不断改革创新,加快发展股指期货市场,减少对它的不必要限制措施,才会发挥出股指期货对资本市场的促进功能,使之成为更加规范和成熟的股指期货市场。
| [] | 方匡南、 蔡振忠 , 2012, "我国股指期货价格发现功能研究", 《统计研究》 , 第 5 期 , 第 73–78 页。 |
| [] | 顾京、 叶德磊 , 2013, "股指期货价格发现功能动态研究", 《上海经济研究》 , 第 11 期 , 第 22–31 页。 |
| [] | 何诚颖 , 2011, "基于高频数据的沪深300指数期货价格发现能力研究", 《数量经济技术经济研究》 , 第 5 期 , 第 139–151 页。 |
| [] | 肖辉、 吴冲锋 , 2004, "股指与股指期货日内互动关系研究", 《系统工程理论与实践》 , 第 5 期 , 第 15–21 页。 |
| [] | 严敏、 巴曙松、 吴博 , 2009, "我国股指期货市场的价格发现与波动溢出效应", 《系统工程》 , 第 10 期 , 第 32–38 页。 |
| [] | Booth, G.G. , So, R.W. and Tse, Y. , 1999, "Price discovery in the German equity index derivatives markets". Journal of Futures Markets , 19 (6) , 619–643. DOI:10.1002/(ISSN)1096-9934 |
| [] | Bigman, D. and Goldfarb, D. , 1983, "Futures market efficiency and the time content of the information sets". Journal of Futures Markets , 3 (3) , 321–334. DOI:10.1002/(ISSN)1096-9934 |
| [] | Brooks, C. and Rew, A.G. , 2001, "Ritson S. A trading strategy based on the lead-lag relationship between the spot index and futures contract for the FTSE 100". International Journal of Forecasting , 17 (1) , 31–44. DOI:10.1016/S0169-2070(00)00062-5 |
| [] | Chiang, M.H. 2003, "Price discovery and changes in regimes for stock index futures". Global Finance Journal , 14 (3) , 287–301. DOI:10.1016/j.gfj.2003.05.001 |
| [] | Elam, E. and Dixon, B.L. , 1988, "Examining the validity of a test of futures market efficiency". Journal of Futures Markets , 8 (3) , 365–372. DOI:10.1002/(ISSN)1096-9934 |
| [] | Fleming, J. , Ostdiek, B. and Whaley, R.E. , 1996, "Trading costs and the relative rates of price discovery in stock, futures, and option markets". Journal of Futures Markets , 16 (4) , 353–387. DOI:10.1002/(ISSN)1096-9934 |
| [] | Gonzalo, J. and Granger, C.W.J. , 1992, "Estimation of Common Long-Memory Components in Cointegrated System". Journal of Business & Economic Statistics , 13 (1) , 27–35. |
| [] | Hasbrouck, J. 1995, "One Security, Many Markets:Determining the Contributions to Price Discovery". Journal of Finance , 50 (4) , 1175–99. DOI:10.1111/j.1540-6261.1995.tb04054.x |
| [] | Kim, M. , Szakmary, A. C. and Schwarz, T. V. , 1999, "Trading costs and price discovery across stock index futures and cash markets". Journal of Futures Markets , 19 (4) , 475–498. DOI:10.1002/(ISSN)1096-9934 |
| [] | Schreiber, P. S. and Schwartz, R. A. , 1986, "Price discovery in securities markets". Journal of Portfolio Management , 12 (4) , 43–48. DOI:10.3905/jpm.1986.409071 |



