长期以来,国内学术界对消费和资产价格的研究集中于股价涨跌对消费的财富效应和传导机制方面上,鲜有涉及消费对股票价格的影响研究。中国股市经历二十多年的高速发展,2015年底总市值已达58.4万亿,上市公司高达2862家,位居全球第二。中小投资者作为市场微观主体,提供了消费作为股票收益率预测变量的良好基础:一方面,中小投资者投机泛滥、羊群效应叠加,行为高度一致,市场价格和收益率可根据居民的经济行为总量变化进行预测。另一方面,中小投资者具有典型的风险厌恶特征,会迅速根据预期资产收益率变化调整消费和家庭资产配置,消费变量对居民预期变化反应灵敏。直觉似乎告诉我们,居民消费扩张或收缩多少会对股票市场产生影响。
消费对股票定价研究一直是国际学术界研究的热点,大量学者从消费资本资产定价模型(CCAPM) 对该问题展开了深入研究。CCAPM围绕着预期收益折现值展开,将预期收益表示为消费者风险厌恶系数和跨期消费边际替代率的函数形式(Breeden,1979)。然而CCAPM模型在解释股权溢价(equity premium) 和无利率风险之谜(risk-free rate puzzle) 遭遇困境。Mehra and Prescott(1985)研究表明,代表型经济人具有高得令人难以置信的风险厌恶系数,不愿参与任何证券投资,甚至会为了避免任何损失而购买巨额保险,与此前投资者风险厌恶系数较低的先验分析相悖。Bansal and Yaron(2004)后续提出用代表性个体的消费增长率来反映宏观长期风险,成功地解释了美国股权溢价之谜和股市长期可预测性现象。
国内对消费资本资产定价研究较少,主要有:陈国进等(2014)验证Bansal and Yaron长期风险模型对中国股市适用性,研究发现中国股票价格可以预测未来消费增长率和时变波动。胡召平(2010)引入“效用成本风险异质性”的概念,将CCAPM模型中的效用成本区分为“消费效用成本”和“风险效用成本”,解释了中国股权溢价之谜和无风险利率之谜。游家兴(2005)则指出研究方法存在选择偏差,股权溢价之谜和无风险利率之谜本身不具备很强的稳定性和可靠性。同时,鉴于中国处于转轨时期,经济呈现政府政策主导,居民储蓄率过高等特征,无风险利率之谜在我国的具体含义有别于美国。
纵观国内现有文献,直接采用CCAPM考察沪深股市收益率的研究都难以得到满意结论,需要修改模型设定或改变研究对象,即以资产价格作为出发点研究消费变动情况。究其根因,CCAPM模型的前提假设对于中国股市过于严苛,中国居民消费和金融行为难以满足“理性经济人以消费期望效用最大化为原则来对所持有的资产组合和各期消费进行决策”的前提条件(汪昌云、汪勇祥,2007)。中国金融市场相比美国发展滞后,居民受到的消费信贷约束较大,加之传统保守的储蓄意识和社会保障体制不完善等因素,呈现消费不振和储蓄率过高的特点,CCAPM模型不一定适用于中国股票市场定价。
基于此,本文提出采用Lettau and Ludvigson(2001)消费财富比的分析思路来探讨中国居民消费和财富对沪深股指收益率的可预测性。Lettau and Ludvigson(2001)研究中发现宏观经济中消费、资产(asset holding) 和劳动力收入之间存在长期共同变化趋势,居民根据预期资产回报率变化而改变消费行为,最终反映成消费对价值中枢(长期趋势) 的短期偏离。这一短期偏离量为消费财富比所测度,对美国股市收益率短期波动具有显著预测效力。对研究问题的探讨有利于提供市场参与者的投资决策与风险管理理论依据,对我国政府推动供给侧资本市场改革、逐步提高直接融比重和构建多层次资本市场具有重要参考价值。
本文具有以下几个主要贡献:首先,提供一个全新研究视角,以消费财富比作为代理指标,探讨中国城镇居民的消费扩张或收缩是如何影响和预测股票市场收益率。其次,充分考虑到中国宏观经济与金融的具体情况,根据我国股市的定价规律和发展阶段,选取2010年1月至2016年6月作为样本区间,实现预测的科学性和合理性。再次,本文运用周期图谱分析消费财富比序列,创新采用递归HP滤波方法处理数据,提高HP滤波数据处理的灵活性和准确性,实现消费财富比对沪深股票市场收益率的预测,该方法也适用于类似金融时间序列数据处理。余下部分安排如下:第二部分介绍消费财富比的理论基础;第三部分构建消费财富比序列;第四部分汇报预测模型估计参数和预测有效性;第五部分总结全文。
二、 消费财富比的理论基础考虑典型代理人经济体(representative agent economy),总财富Wt定义为第t时期理性代理人所掌握的全部经济资源①,Ct代表同一时期的消费,Rw,t+1为第t+1期的资本回报率,总财富从第t期累积到第t+1期的表达式为:
| ${{W}_{t+1}}=1+{{R}_{w,t+1}}{{W}_{t}}-{{C}_{t}}$ | (1) |
①本文的资产和财富是同一概念,并无区别。
令rw,t+1=log(1+Rw,t+1),其他变量以对应小写字母表示自然对数处理。借鉴Campbell and Mankiw(1989)推导,当ct-wt平稳时,对式(1) 进行一阶泰勒展开:
| $\Delta {{w}_{t+1}}\approx k+{{r}_{w,t+1}}+1-1/{{\rho }_{w}}{{c}_{t}}-{{w}_{t}}$ | (2) |
ρw代表稳态下新增投资占总财富比例,典型代理人的财富增长率Δwt+1取决于未来的投资回报率rw,t+1以及当期所做投资增量决策1-1/ρwct-wt,k为常数项②。加入
| ${{c}_{t}}-{{w}_{t}}={{E}_{t}}\sum\limits_{i=1}^{\infty }{{{\rho }_{w}}^{i}\left( {{r}_{w,t+i}}-\Delta {{c}_{t+i}} \right)}$ | (3) |
②为简化分析过程,本文接下来推导省略不重要常数项。
Et表示第t时期信息下的条件期望,式(3) 为典型代理人事前(ex-post) 消费跨期预算约束,由投资回报率水平rw,t+i(流入项)、消费增长率Δct+i(漏出项) 和新增投资占比ρwi共同决定。将总财富进一步细分为人力资产(ht)和非人力资产(at),对应的资本回报率也分为人力资产回报率(rh,t) 和非人力资产回报率(ra,t) 两部分,并以劳动力收入(yt) 作为人力资产衡量标准。式(3) 进一步可推导为式(4),ω为非人力财富占总财富比例:
| ${{c}_{t}}-\omega {{a}_{t}}-\left( 1-\omega \right){{y}_{t}}={{E}_{t}}\sum\limits_{i=1}^{\infty }{{{\rho }_{w}}^{i}}\text{ };\text{ }\left\{ \left[ \omega {{r}_{a,t+i}}+\left( 1-\omega \right){{r}_{h,t+i}} \right]\text{ }-\Delta {{c}_{t+i}} \right\}\text{ }+\left( 1-\omega \right){{z}_{t}}\text{ }$ | (4) |
zt是均值为零的平稳随机误差项,式(4) 是典型代理人的消费跨期预算约束式。变量均为对数形式,等式左边表示了典型代理人当期消费占总财富的比例,称之为消费财富比,简写为cay(Lettau and Ludvigson,2001)。假设式(4) 右边各项均为平稳序列,左边各项经济变量ct、at和yt通常呈现随时间增长的非平稳特性,根据计量理论可知,三者之间存在长期均衡的协整关系。消费财富比以协整变量的线性组合方式衡量了在外部冲击下代理人消费对长期均衡的短期偏离程度。
式(4) 可视为包含最优消费的广义市场投资组合收益预期的函数表达形式,预期改变将最终体现在代理人的消费行为中。当代理人预期资产回报率上升和资产价值增加,财富效应会刺激当期消费支出。相比之下,资产和劳动力收入变动较为滞后,预期回报率改变使消费暂时偏离长期均衡,表现为消费财富比同向变化。同作为市场资金价格的衡量方式,预期资产收益率涨跌应与股票收益率高度正向相关。消费财富比刻画了代理人预期收益率、消费和实现收益率间相继出现的扩张与收缩交替更迭、循环往复的运动规律,并将这个过程中不可直接被观测的预期收益率转换成可测度的短期偏离量,是后续实证的关键。模型具有一般性,不需要依赖于特定偏好设定,放宽了消费和资产收益等变量随机性的前提假设。
三、 消费财富比的协整估计 (一) 变量与数据说明本节选取2005年1月到2016年6月期间中国城镇居民数据构建消费财富比序列,数据均来源于wind数据库。首先,研究对象选择城镇居民是因为中国城乡发展二元化,金融市场在城市充分发展,城镇居民可通过抵押住房、信用贷款和金融投资等方式实现提前或推迟消费。而农村居民由于户籍制度、消费观念、抵押品不足以及农村金融发展水平等约束,难以通过借贷实现平滑消费,无法构建出相应的消费财富比。
其次,采用城镇居民人均非耐用消费品和服务性支出作为消费的代理变量。非耐用消费品和服务更能反映与财富和收入预期对应的消费流形式(Lettau and Ludvigson,2001)。依据国家统计局分类标准,相应选取城镇居民人均食品、衣着、教育文化娱乐服务以及其他商品和服务的人均消费性支出。同时,以城镇居民人均可支配收入作为劳动力收入的代理变量。
由于消费和收入代理变量只公布了年度和季度的统计数据,本节以月度社会消费品零售总额占当季值比重为权重将季度数据月度化,其合理性和有效性分析如下:第一,消费财富比测度了代理人由收益率预期变化而产生的消费短期趋势偏离量,本身是高频经济变量。将消费和收入季度数据月度化能使消费财富比更好地发挥先导预测的功能,充分运用消费和收入数据中所包含的高频信息,增强消费财富比模型的预测准确性与及时性。第二,为尽可能地提高数据频率转化时信息含量,采用月度社会消费品零售总额占比作为权重指导数据调整。社会消费品零售总额是企业通过交易售给个人、社会集团非生产、非经营用的实物商品金额,以及提供餐饮服务所取得的收入金额①,月度社会消费品零售总额占比可直接调整消费序列。同时,大量实证研究表明消费和收入之间存在长期稳定均衡关系(韩立岩,1998;苏良军等,2006;刘轶,马赢,2015),以月度社会消费品零售总额占比拆分城镇居民可支配收入,极大程度上提取收入季度数据中的有用信息,还原序列高频变化情况,避免由其他估算方法导致的信息误差和耗损等问题。
①定义来源于中国国家统计局网站http://www.stats.gov.cn/tjsj/zxfb/201607/t20160715_1377679.html。
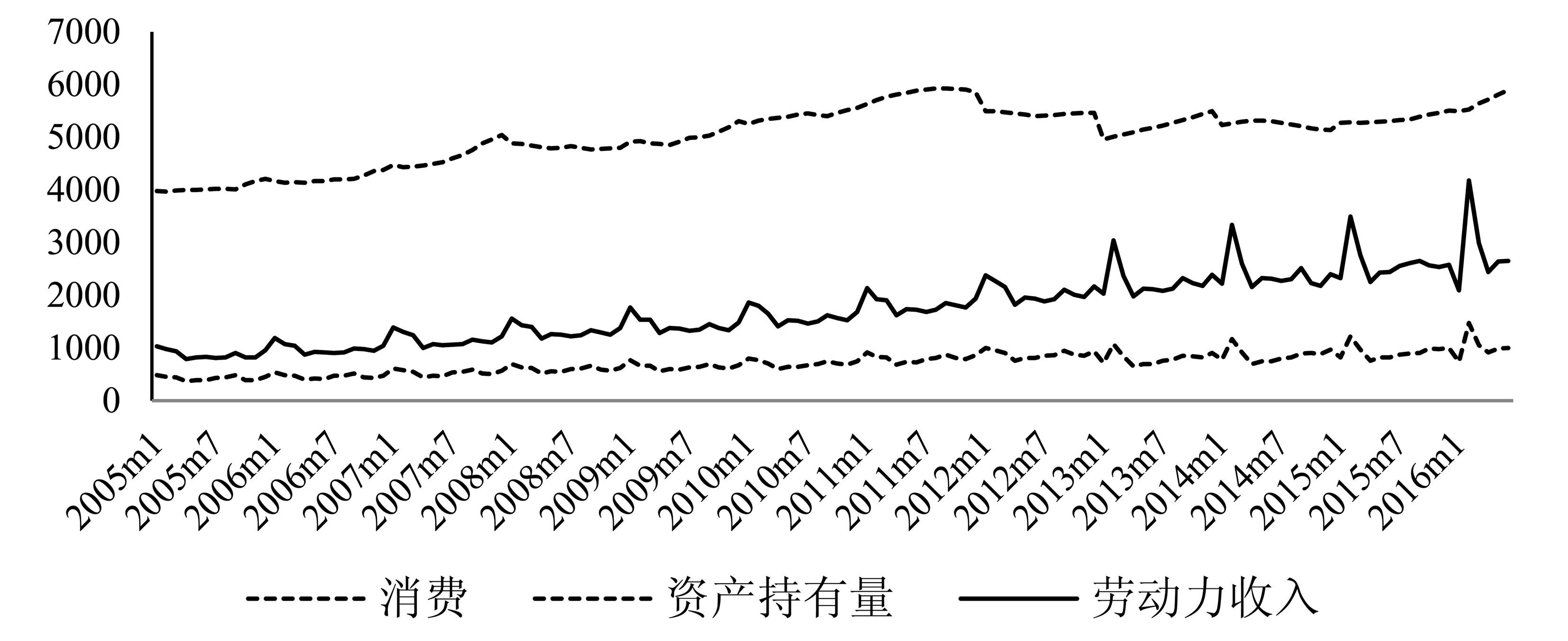
最后,受到城镇居民资产数据可得性限制,本文借鉴Caporale and Sousa(2016)构建思路,以房屋价格指数和股票市场指数之和作为居民资产的代理变量。在此基础上,以中国社科院公布的房地产与股票占居民总资产比重进一步优化资产序列(见表 1)①。具体而言,中国城镇居民资产序列是由当月房地产每平方米平均销售价格和上证综指收盘价的加权平均和构建而成,其中房地产平均销售单价和股票指和数对应权重详情参见表 1。图 1给出了2005年1月至2016年6月期间消费、资产收入序列的走势情况。
①关于居民部门资产负债表详情参见附录1。
| 表 1 2005年至2014年中国居民资产及其构成 |
|
图 1 2005年1月至2016年6月的消费、财富与收入(单位:元) |
根据上述方法构建的消费、资产及收入序列均呈现随时间推移共同缓慢上升趋势,虽然每个变量均存在各自短期波动特征。收入因为年终奖等因素,短期波动特征尤为显著,消费也通常在春节长假前后出现明显的偏离。房地产“金九银十”现象导致资产往往在九月和十月达到该年的峰值。表 2显示,样本期间内城镇居民人均非耐用品消费、人均可支配收入、资产均值分别为706.61元/月、1699.92元/月和5045.23元/月。
| 表 2 变量的描述性统计(样本数:138) |
对变量进行ADF和Phillips-Perron单位根检验,结果均表明消费、财富和收入的对数值具有一阶单整性I(1)。接着采用Johansen检验方法对消费、财富和收入变量进行协整检验,根据各项信息准则确定滞后阶数为1或3。进而对一阶和三阶滞后项进行检验,根据Johansen检验、似然比检验(LR) 和Wald检验结果可知,消费、收入与资产三个变量都进入同一个协整关系(详情参见附录 2至5)。以上实证结论表明,尽管消费、收入与资产短期内具有各自变动规律,但在长期内三者间存在着协同变化的趋势。
(三) 向量误差修正模型根据Granger表示性定理,如果非平稳变量之间存在协整关系,则变量之间存在短期误差修正机制。当消费、资产和收入组成的经济系统受到外界干扰时(如财政和货币政策等),系统偏离均衡状态,误差修正机制将努力使系统重回均衡。从表 3上看,消费和收入表现出较强地内在均衡修正机制,而资产却缺乏短期调节功能。短期误差修正机制以消费作为主导,以-0.688的速度调整回归均衡。进一步说明了由于医疗、住房、养老等支出不确定性,当经济体发生意外冲击时,中国城镇居民主要靠调整消费以适应新的环境,城镇居民谨慎消费心理显著和总量消费呈现波动较大特征。特别是当第t-1期资产受到正向冲击时对消费的抑制效应显著,城镇居民会迅速调整非耐用品消费以回归均衡状态。
| 表 3 向量误差修正模型 |
①ECM(t-1)所代表的协整方程的误差项为:
借鉴Lettau和Ludvigson(2001)动态最小二乘法(Dynamic Ordinary Least Squares,DOLS) 进行协整估计。DOLS优点在于,在“超级一致性(superconsistent)”性质下,即使残差εt与解释变量相关,系数估计量仍然是一致的。DOLS还加入领先或滞后差分项消除变量间内生性问题①,协整回归方程如下(括号中为Newey-West修正t统计量,θ为常数):
①本文领先/滞后差分项阶数为6,确定标准是根据Johansen的完全信息极大似然比估计方法(full information maximum-likelihood),6阶之前的领先/滞后项加入对模型没有任何的改善。
| ${{c}_{t}}=\underset{\left( 10.51 \right)}{\mathop{0.638{{a}_{t}}}}\,+\underset{\left( 23.24 \right)}{\mathop{0.492{{y}_{t}}}}\,+\theta $ | (5) |
ct,at和yt分别是第t期中国城镇居民的非耐用品消费、资产和收入,校正后的R2为95.82%。收入和资产的边际消费弹性系数在1%置信水平显著为正。居民资产的边际消费弹性为0.638,通过表 2可得样本期间人均非耐用品消费—资产比值为0.133,城镇居民资产的边际非耐用品消费倾向约为0.085,可支配收入的边际非耐用品消费倾向约为0.21②,大于资产的边际消费倾向,与张卫涛、陈杰(2009)的结论相似,资产和收入变动对消费具有显著的财富效应。系数之和稍大于1是因为统计误差以及由插值法造成的偏误。
②城镇居民资产的边际消费倾向=0.638×0.133=0.085,城镇居民可支配收入的边际消费倾向=706.61/1699.92×0.492=0.416×0.133×0.492=0.205
根据理论模型,得到相应的短期偏离项——消费财富比序列(cayt)。
| $ca{{y}_{t}}=~{{c}_{t}}-0.638{{a}_{t}}-0.492{{y}_{t}}$ | (6) |
消费财富比变量的描述性统计均值为-2.56,标准差为0.09,偏度为1.03,峰度为5.70,最大值和最小值分别为-2.21和-2.73。
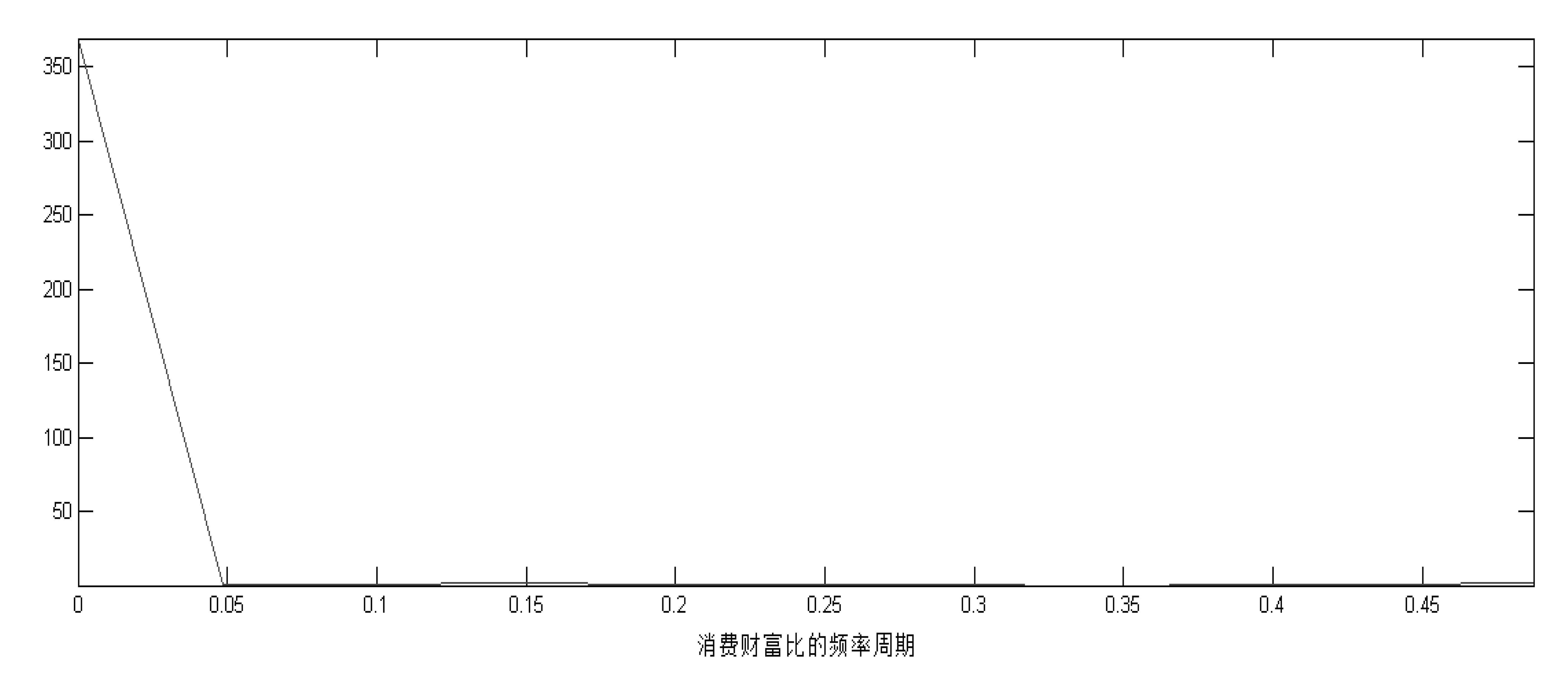
(五) 递归HP滤波去势消费财富比预测模型的基本原理是:在股价均值回归的基础上,消费、收入与资产三者间存在的长期共同趋势提供了股指收益率的价值中枢;消费短期偏离量(消费财富比) 衡量了由外部冲击引起的预期收益率变化,可预测股指收益率对价值中枢的短期偏离程度。消费财富比本质属于高频经济变量,但经周期图谱分析,上述消费财富比序列中仍保留大量的低频趋势信息(见附录 7),原序列无法拥有高频特性,难以实现对股指收益率预测作用。进而采用HP滤波处理消费财富比,通过傅里叶变换去除原序列的低频趋势成分:
| ${{y}_{t}}=g{{}_{t}}+{{c}_{t}}\text{ }其中,t=1,2,3\ldots T$ | (7) |
趋势序列{gt}t=1T和周期序列{ct}t=1T是下列损失函数最小化问题的解:
| ${{g}_{t}}=\underset{\left\{ {{g}_{t}} \right\}_{t=1}^{T}}{\mathop{\min }}\,\left\{ \sum\limits_{t=1}^{T}{{{\{{{y}_{t}}-{{g}_{t}}\}}^{2}}}+\lambda \sum\limits_{t=1}^{T}{{{[\left( {{g}_{t}}-{{g}_{t-1}} \right)-\left( {{g}_{t-1}}-{{g}_{t-2}} \right)}^{2}}} \right\}$ | (8) |
式(8) 右侧大括号多项式的第一项是高频周期成分,是对低频趋势{gt}t=1T的偏离程度。第二项是趋势项“平滑”程度,λ用于调节二者权重。当λ取0时,序列{gt}t=1T和原序列重合。当λ趋于无穷大时,趋势序列{gt}t=1T非常光滑,以直线形式呈现。本文λ取值为129600。
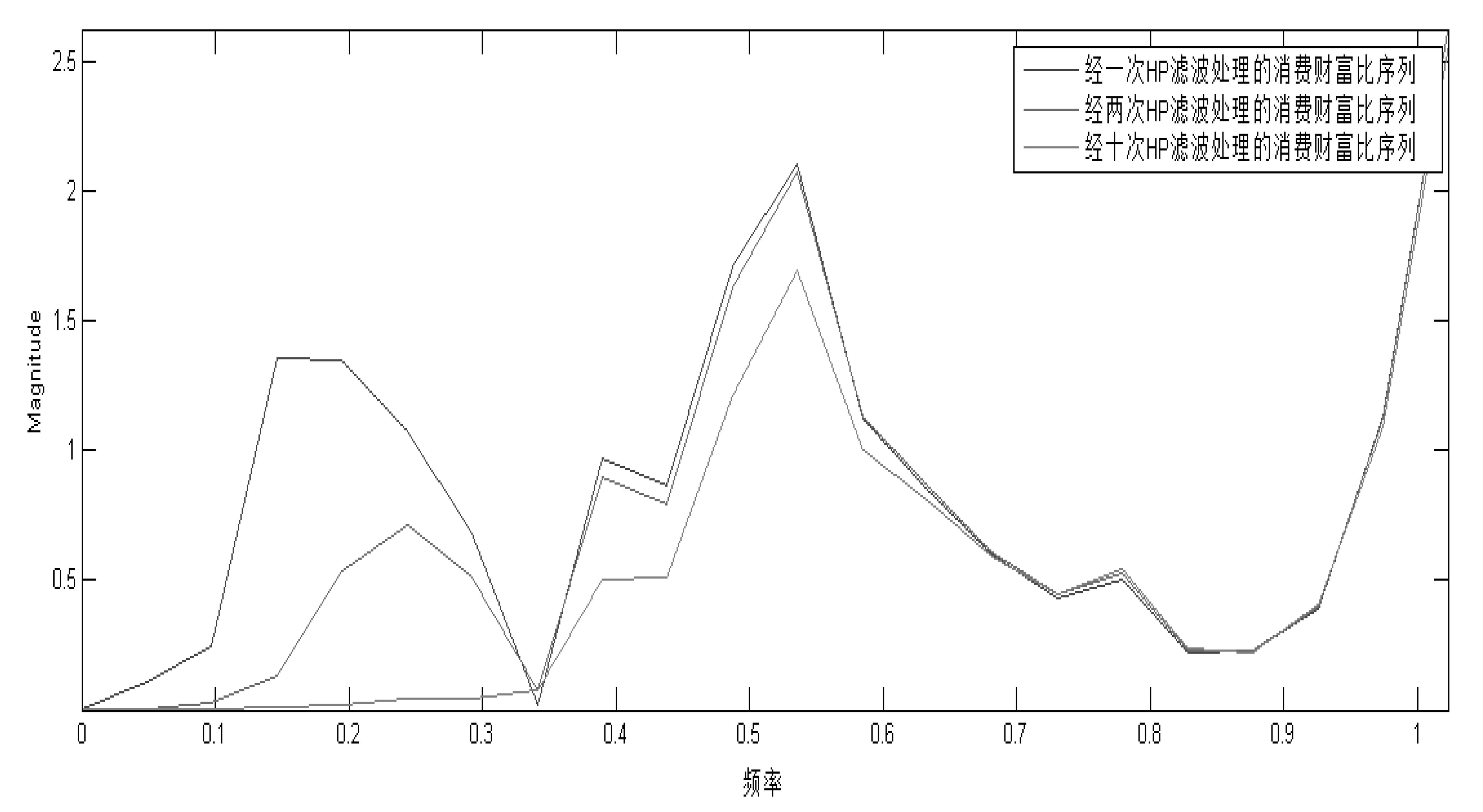
通过周期图谱(见附录8) 发现,采用上述单次HP滤波分解的消费财富比周期部分{ct}t=1T中仍然存在大量低频信息,在频率为0.15处有明显的谱峰,第一主频率的时间周期约为7个月①,属于低频范畴。作为时间序列去趋(Detrend) 的基准方法之一,HP滤波的高通属性(High-Pass Filter) 难以完全分离序列中的低频信息,仅凭单次提取的消费财富比周期部分仍包含大量低频信息“噪音”,依旧难以实现消费财富比的高频属性。
①第一主频率的时间周期计算方式为:T=1/f
为了获得目标高频范围内的消费财富比序列,本文借鉴Ma(2016)的递归HP滤波优化方法,进一步分解周期部分{ct1}t=1T,得到序列中低频趋势序列{gt2}t=1T和更高频周期序列{ct2}t=1T。对{ct2}t=1T序列进行周期图谱检验,如达到目标频率则不再进行HP滤波分解;若尚未达到目标频率则继续采用HP滤波对{ct2}t=1T序列进行分解,得到{gt3}t=1T和{ct3}t=1T。依次重复,直至{ctm+1}t=1T经周期图谱检测达到目标频率为止。
| ${{y}_{t}}={{g}_{t}}^{1}+{{c}_{t}}^{1}$ | (9) |
| ${{c}_{t}}^{1}={{g}_{t}}^{2}+{{c}_{t}}^{2}$ | (10) |
| ${{c}_{t}}^{2}={{g}_{t}}^{3}+{{c}_{t}}^{3}$ | (11) |
$\vdots $
| ${{c}_{t}}^{m}={{g}_{t}}^{m+1}+{{c}_{t}}^{m+1}$ | (12) |
周期序列{ct1}t=1T经过m次递归HP滤波分解得到{gtm+1}t=1T和高频周期序列{ctm+1}t=1T,将周期项逐次从式(12) 代回至式(9),最终可得式(13):
| ${{y}_{t}}=\sum\limits_{i=1}^{m+1}{{{g}_{t}}^{m+1}+{{c}_{t}}^{m+1}}$ | (13) |
定义递归HP滤波处理后的趋势项为
| ${{y}_{t}}={{y}_{t}}^{*}+{{c}_{t}}^{m+1}$ | (14) |
通过周期图谱最终确定消费财富比序列的次数为10次②。去势后的消费财富比均值为0.00,方差为0.07,偏度为-0.22,峰度为2.80,最大值为0.16和最小值为-0.24。
②详情参见附录8,ctm+1第一主频率的时间周期小于2个月,可得m=10次
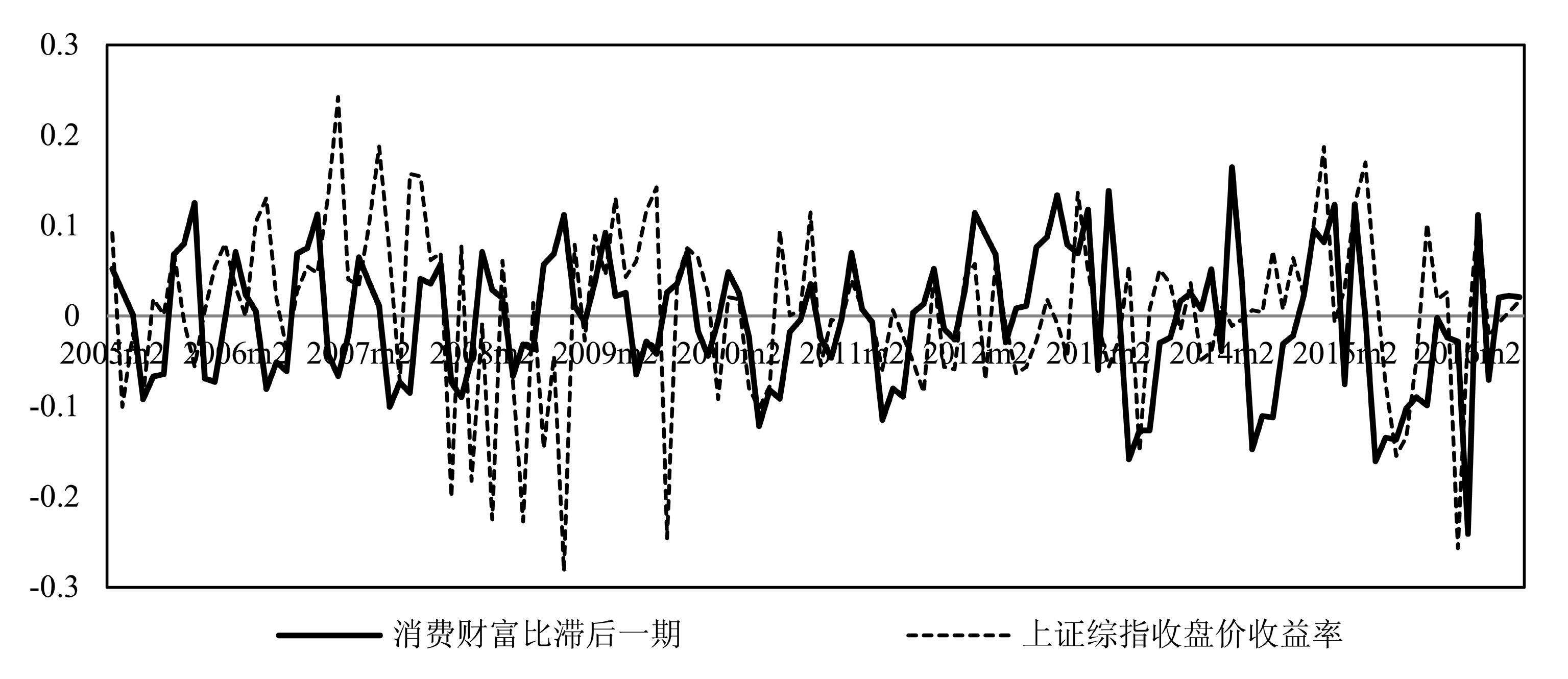
四、 消费财富比对市场收益率预测 (一) 消费财富比预测基础消费财富比体现了城镇居民根据时变预期回报率变化而不断调整的消费行为,反映出股票价值中枢和短期波动之间关系。图 2和图 3显示,消费财富比滞后一期与上证综指或深证成指收益率呈现均值回归的运动规律,2010年后几乎是同步波动,有些时间段内甚至重合,存在较强的正相关。消费财富比通过度量城镇居民非耐用品消费对共同趋势的短期偏离量,反映出城镇居民对未来资产价格预期变化情况。预期改变将会影响城镇居民在股票市场未来的交易行为,进而对股指收益率产生影响①。
①沪深股指收益率计算方式:r=lnPt+1/Pt,其中Pt是第t期的上证综指或深证成指当月收盘价。
|
图 2 消费财富比滞后一期与上证综指收益率关系 |
如图 2所示,去势后消费财富比围绕着均值(0值) 上下变动。当经济景气时,城镇居民会开始对所拥有财富抱有乐观预期,预期资产收益率增加或工资水平提高刺激当期消费扩张。此时财富价值和劳动工资还维持在原有水平,消费财富比对共同趋势短期正向偏离程度随之增大。反之,宏观经济下行,房地产进入拐点或股市疲软,城镇居民预期资产收益率下降会导致当期消费缩减,消费财富比会向下偏离。因此,消费财富比将不可直接测度的城镇居民预期资产收益转化为可测度指标,加之中国城镇居民的消费文化和消费习惯,消费财富比变化更敏感,领先于收益率变动,预示着下期上证指数或深证成指收益率同向变动。
不得不提的是图中2006年至2009年间股指收益率与消费财富比的背离走势,中国股市在此期间存在的“投机市”和“政策市”是深层原因。2006年中国经济高位增长、股权分置等利好消息促使资金大量流入股市,上证综指从2006年6月998点一路飙升至2007年10月6124点,此时投资者更多的是跟风炒作和从众追涨等非理性投机特征。之后,大小非解禁、国际经济局势衰败、出口受挫、内需不足和利率上调等负面消息冲击下股价迅速下挫,中小投资者竞相抛售和“杀跌止损”,上证指数暴跌至2008年底1838点,累计跌幅高达73%。后续政府出台一系列积极财政和货币政策,推出四万亿计划等释放出大量流动性,股价又反弹至2009年3471点。这一时期反映基本面的消费财富比失去对股指波动的解释预测能力。
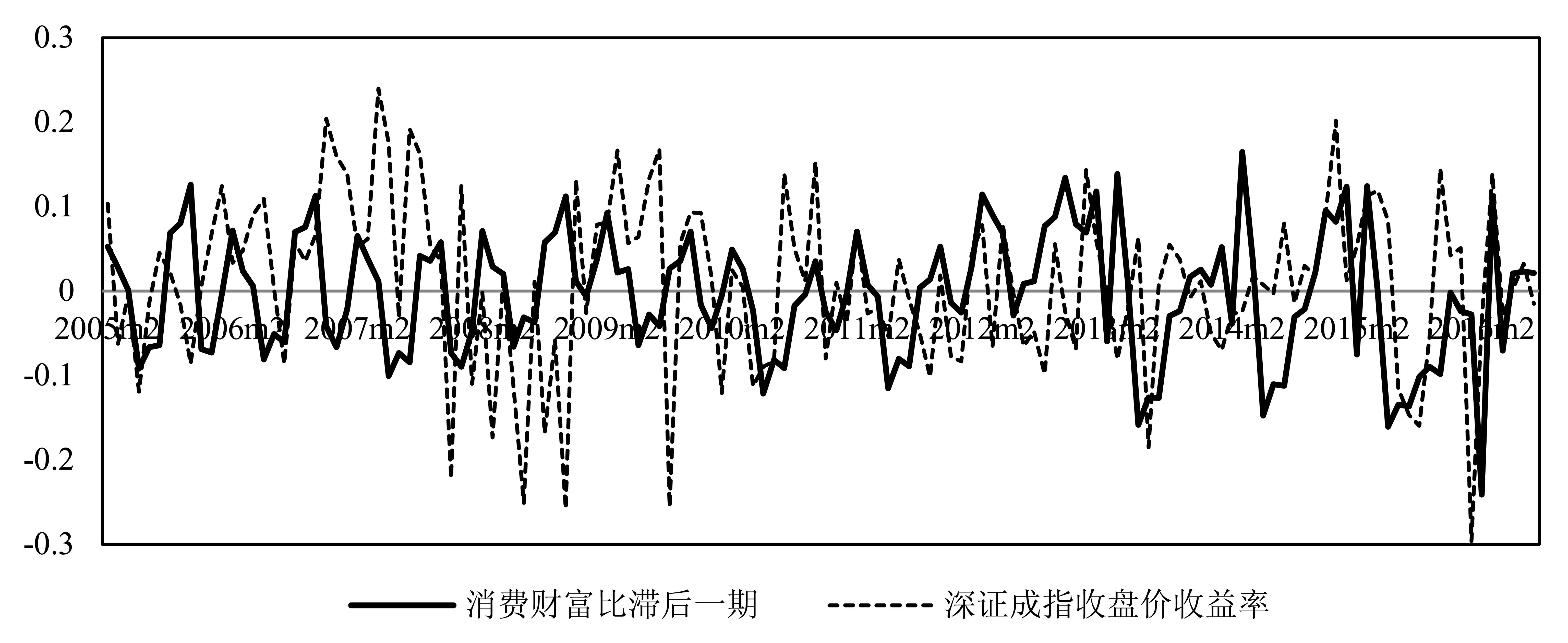
(二) 预测样本时期的确定本文选取2010年1月至2016年6月的消费财富比与沪深两市股指收益率进行经验研究①,原因如下:首先,由图 2和图 3可知,自2010年以来消费财富比领先于股指收益率变动,两者呈现高度同步走势,两者存在较强的正向相关。其次,从股票市场发展阶段来看,2010年以后股市开始充分扩容。2001年至2009年新股上市数为546家,总计1700家公司,而2010年1月至2016年6月之间,中国股市经历IPO重启,上市公司迅速扩大到2929家,整体上市公司与宏观经济愈发密切关联。最后,政策面从银行主导融资模式转向加强多层次资本市场功能方向发展,股市与经济各部门关联性增强。综上所述,最终确定以2010年1月到2016年6月期间沪深股指收益率作为考察样本,共计79个样本量。
①因为消费财富比序列是2010年1月2016年6月,采用滞后一期及两期消费财富比进行预测,从而对应的沪深股指收益率样本区间为2010年2月至2016年8月。
|
图 3 消费财富比滞后一期与深证综指收益率关系 |
采用最小二乘回归(OLS) 方法对消费财富比预测模型进行估计,计量模型具体如下:
| ${{r}_{i,t+1}}=\alpha +\beta ca{{y}_{t}}+{{\varepsilon }_{t+1}}$ | (15) |
ri,t+1是第t+1时期市场指数收益率,cayt是第t期的消费财富比,εt+1为预测模型的随机误差项(error term)。考虑到统计数据公布存在滞后性,分别选取滞后一期和滞后两期的消费财富比逐次回归,分别记为lcay和lcay2。同时,sh和sz代表上证指数收益率和深证成指收益率,lsh和lsz为对应变量的滞后一期。表 4报告了主要变量的相关性分析结果,表中右上部分是spearman相关系数,左下部分是pearson相关系数。解释变量和被解释变量之间相关系数不超过0.3,不存在共线性问题。
| 表 4 变量之间的相关系数矩阵 |
采用Newey-West稳健性标准误来控制在小样本下分布可能面临序列相关和异方差问题,据此进行统计推断。表 5给出了对应的实证结果,可得到以下两个重要结论:第一,消费财富比对沪深股指收益率的预测拟合效果较好。消费财富比模型校正后的R2均大于5%,其中滞后一期模型的可解释预期上证指数回报率方差占实际回报率方差的7.83%,深证成指为7.30%,仅稍微低于Lettau和Ludvigson(2001)原模型的9%。
| 表 5 消费财富比对沪深股指收益率的预测模型 |
中美两国消费财富比拟合优度差异源于中美两国经济和金融异质性。首先,两国消费特征不同。美国是典型的高消费低储蓄国家,居民通过调整资产来维持消费水平稳定,消费和资产的联动性更强。其次,股票市场结构不同。中国股市是一个倒金字塔形,截止至2015年12月,主板市场1593家公司挂牌,中小企业板是800个公司挂牌,创业板是536个。美国是正金字塔型股票市场,股市结构更为合理,与宏观经济联系更密切。最后,投资者结构不同。美国市场主体是各类指数基金及对冲基金等成熟机构投资者。相比之下,中国股市的投资主体是中小投资者。中小投资者喜好短线操作、投机倾向严重、换手率极高、平均持股时间短暂。中小投资者非理性交易使得随机误差增大,降低消费财富比模型的拟合优度。
另一方面,消费财富比模型优于姜富伟等(2011)的多变量预测模型,他们采用传统资产定价文献中十二种常用变量对中国股市进行预测,发现股息率、通胀率、换手率、M1以及M2增长变动率具有显著预测能力,对应的R2在1.04%到3%之间。预测性回归模型R2通常较小,消费财富比对沪深股指收益率的拟合能力较强。
第二,消费财富比滞后一期和两期的系数均在10%置信水平下显著异于零,对沪深股指收益率具有显著的解释和预测效力。滞后一期消费财富比每变动1%,上证指数收益率变动0.273%,深证成指收益率变动0.264%;滞后两期消费财富比每变动1%,上证综指和深证成指收益率相应变动0.263%和0.272%。
表 5结果还表明消费财富比的预测模型显著优于股指收益率自回归模型。上证综指滞后一阶收益率对当期收益率的预测系数仅在10%的置信水平下显著,校正后R2为2.02%,远低于消费财富比的7.83%。深证成指滞后一阶收益率预测系数则不显著,模型解释力较低。
(四) 预测模型有效性检验本文采用嵌套模型的平均误差平方(Mean Squared Error,MSE) 来衡量消费财富比预测模型的有效性①。先选定一个基准模型,计算出其平均误差平方,记为MSEr。然后在基准模型基础上,加入消费财富比得到比较模型的MSEu。若比较模型与基准模型的平均误差平方比值(MSEu/MSEr) 小于1,说明加入消费财富比后的预测模型精度高于基准模型。
①平均误差平方(Mean Squared Error,MSE) 定义如下:
表 6和7给出两对嵌套模型的检验结果,第一对是以股市收益率滞后一阶自回归模型为基准模型,第二对是以常数项(标记为α) 为基准模型。同时还增加了MSE-F检验实现多维度检验,MSE-F检验的原假设是基准预测模型和比较测模型具有相同的平均误差平方,并分别采用非对称分布(表 6和7中记为Asy. CV) 和自体抽样重复(bootstrap,记为BS CV)95%的置信水平临界值作为检验标准。MSE比值和MSE-F检验结果均显示,消费财富比预测模型效果优于基准模型,具有较好的解释预测能力。
| 表 6 消费财富比对上证指数收益率的预测精度检验 |
| 表 7 消费财富比对深证成指收益率的预测精度检验 |
进一步采用消费财富比对市场长期收益率进行预测。长期收益率由单期收益率加总得到,其预测模型是单期收益率预测模型的补充,反映了单期消费财富比对未来多期市场收益率的预测持续程度(persistency)。为简化模型分析,忽略常数项①,计量模型如下:
①表 4估计结果也显示,常数项在1%水平下不显著。
| ${{r}_{i,t+2}}=\beta ca{{y}_{t+1}}+{{\varepsilon }_{t+2}}$ | (16) |
| $ca{{y}_{t+1}}=\varphi ca{{y}_{t}}+{{\delta }_{t+1}}$ | (17) |
以两期市场收益率为例,结合式(16)—(17) 可得
| $\begin{align} & {{r}_{i,t+2}}+{{r}_{i,t+1}}=\beta ca{{y}_{t}}+{{\varepsilon }_{t+1}}+\beta \varphi ca{{y}_{t}}+ \\ & {{\delta }_{t+1}}+{{\varepsilon }_{t+2}}=\beta 1+\varphi ca{{y}_{t}}+\gamma \\ \end{align}$ | (18) |
γ=βδt+1+εt+1+εt+2是两期市场收益率模型的误差项。表 8和9给出长期收益率实证结果,sh1至sh12分别为对应1至12个月的上证指数收益率之和,表 9中命名规则类似。
| 表 8 消费财富比对上证指数收益率的长期预测 |
| 表 9 消费财富比对深证成指收益率的长期预测 |
表 8结果显示,在10%的置信水平下,消费财富比能解释和预测4个月内的上证指数长期收益率,但超过4个月就失去解释预测能力。校正后R2呈现了先增后降的趋势,侧面证明了单期消费财富比预测模型的有效性。由表 3可知中国城镇居民消费的波动较大,消费财富比对股票市场价格产生的主要是暂时性冲击。对式(17) 回归发现,φ=0.37,不难得到φ4=0.02,在4期之后失去冲击影响力。这一结论不同于Lettau and Ludvigson(2001)的研究,美国是消费型国家,当消费偏离长期趋势时,会给整个经济体带来持续的影响。下表 9给出深证成指的长期收益率预测估计情况,结果与表 8类似。
五、 小结本文从宏观经济消费变量出发,借鉴Lettau和Ludvigson的研究思路,考察消费财富比对沪深市场收益率的预测解释能力及有效性。研究发现:(1) 中国城镇居民人均非耐用品消费、资产和人均可支配收入之间存在着一个协整关系。2005年1月至2016年6月的协整回归结果显示,城镇居民资产和可支配收入的边际非耐用品消费倾向分为为0.089和0.21。(2) 消费财富比模型可视为包含最优消费的广义市场投资组合收益预期的函数表达形式,预期改变将引起典型代理人消费决策的调整。消费财富比刻画了预期回报率、消费和资产收益率之间相继出现的扩张与收缩交替更迭、循环往复的运动规律,并以协整变量线性离差的方式间接测度了代理人的预期资产收益率。(3) 消费财富比本质上是高频经济变量,本文创新采用递归HP滤波方法去除序列中包含的低频趋势信息,实现消费财富比对沪深股指收益率的预测和解释。经过10次递归HP滤波去势后的消费财富比滞后一期与上证综指或深证成指收益率均呈现出均值回归的运动规律,并在2010年以后几乎同步波动,存在较强的正相关。(4)2006年至2009年间上证综指与消费财富比序列走势背离,中国股市此期间存在的“投机市”和“政策市”是其深层次原因,以代理人最优消费跨期决策为理论基础的消费财富比难以解释和预测这一时期的股指收益率波动。(5)2010年1月至2016年6月期间,消费财富比对股指收益率具有显著预测能力。消费财富比滞后一期每偏离1%,预测着上证指数和深证成指收益率将相应变动0.273%和0.264%。这说明中国城镇居民消费、资产和收入之间存在的长期趋势提供了股票价值中枢,消费财富比通过测度由预期收益率变动引起的消费短期偏离量,显著预测股指收益率对价值中枢的短期偏离程度。(6) 根据平均误差平方结果,消费财富比预测模型较优。同时,消费财富比仅对4个月以内的上证指数收益率之和有显著的解释和预测能力,单期消费财富比对长期市场收益率预测的持续性不强。
本文意义在于实现美国学术界公认的具有股市预测能力的消费财富比对中国股指收益率的预测性检验,为资产定价研究提供中国经验。消费财富比是从理性代理人的预算约束模型出发,无法解释沪深两市“政策市”和“投机市”等非理性因素造成的收益率极端情况。后续研究可以在消费财富比的基础上,加入反映政府政策和投资者情绪的变量,进一步探索宏观经济基本面、政府政策和投资者行为三者对股指收益率的解释和预测能力。本文的创新是采用递归方法优化HP滤波,克服HP滤波单次分解的伪周期提取问题,提高HP滤波数据处理灵活性和准确性。本文局限性是样本量较小,同时沪深股市在股票结构、发行制度和交易者群体方面与美国有根本性差异,所得结论难以与美国百年股市的大样本相媲美。结论的可靠性除了寄望于计量方法的改进,更多地需依靠股市深化发展和数据的更新。
附录
| 附录 1 2005年至2014年中国居民资产构成 (单位:亿元) |
| 附录 2 变量的单位根检验 |
| 附录 3 Johansen 检验滞后期检验结果 |
| 附录 4 Johansen 变量一阶协整关系检验结果 |
| 附录 5 Johansen 变量三阶协整关系检验结果 |
| 附录 6 进入协整关系的序列检验 |
|
附录 7 消费财富比原始序列的周期谱图 |
|
附录 8 消费财富比原始序列的周期谱图 |
| [] | 陈国进、 黄伟斌、 PuriTribhuvan , 2014, "宏观长期风险与资产价格:国际比较与中国经验", 《世界经济》 , 第 6 期 , 第 51–72 页。 |
| [] | 韩立岩 , 1998, "中国收入——消费关系的协整分析与模糊分析", 《管理世界》 , 第 5 期 , 第 50–58 页。 |
| [] | 胡召平 , 2010, "基于效用成本风险异质性的消费资本资产定价模型", 《经济理论与经济管理》 , 第 5 期 , 第 51–58 页。 |
| [] | 姜富伟、 凃俊、 RapachDavid E.、 StraussJack K和周国富 , 2011, "中国股票市场可预测性的实证研究", 《金融研究》 , 第 9 期 , 第 107–121 页。 |
| [] | 刘轶、 马赢 , 2015, "股价波动、可支配收入与城镇居民消费", 《消费经济》 , 第 2 期 , 第 7–11 页。 |
| [] | 汪昌云、 汪勇祥 , 2007, "资产定价理论一个探索股权溢价之谜的视角", 《管理世界》 , 第 7 期 , 第 136–151 页。 |
| [] | 游家兴 , 2005, "理性定价、选择偏差与消费资本资产定价谜团——来自中国证券市场的经验证据", 《经济科学》 , 第 6 期 , 第 161–173 页。 |
| [] | 宋玉臣、 寇俊生 , 2005, "沪深股市均值回归的实证检验", 《金融研究》 , 第 12 期 , 第 55–61 页。 |
| [] | 苏良军、 何一峰、 金赛男 , 2006, "中国城乡居民消费与收入关系的面板数据协整研究", 《世界经济》 , 第 5 期 , 第 65–72 页。 |
| [] | 张卫涛、 陈杰 , 2009, "居民资产如何影响消费?——基于1998-2007中国城镇的实证研究", 《南方经济》 , 第 10 期 , 第 18–28 页。 |
| [] | Bansal, , Ravi, and and, AmirYaron. , 2004, "Risks for the Long Run:A Potential Resolution of Asset Pricing Puzzles". The Journal of Finance , 59 (4) , 1481–1509. DOI:10.1111/j.1540-6261.2004.00670.x |
| [] | Breeden, and Douglas, T. , 1979, "An Intertemporal Asset Pricing Model with Stochastic Consumption and Investment Opportunities". Journal of financial Economics , 7 (3) , 265–296. DOI:10.1016/0304-405X(79)90016-3 |
| [] | Caporale, , Guglielmo, Maria and and Ricardo, M.Sousa. , 2016, "Consumption,Wealth,Stock and Housing Returns:Evidence from Emerging Markets". Research in International Business and Finance , 36 , 562–578. DOI:10.1016/j.ribaf.2015.01.001 |
| [14] | Campbell,John Y.,and N.Gregory Mankiw.,1989, "Consumption,Income and Interest Rates:Reinterpreting the Time Series Evidence",NBER Working Paper,No.246. |
| [] | Lettau, , Martin, and and Sydney, Ludvigson. , 2001, "Consumption,Aggregate Wealth,and Expected Stock Returns". Journal of Finance , 56 (3) , 815–849. DOI:10.1111/0022-1082.00347 |
| [16] | Ma,Jinpeng,and Max Tang.,2016, "A FIR Filter to Date Post-WWⅡ Recessions",Available at SSRN 2717905. |
| [] | Mehra, , Rajnish, and and Edward, C.Prescott , 1985, "the Equity Premium:A Puzzle". Journal of monetary Economics , 15 (2) , 145–161. DOI:10.1016/0304-3932(85)90061-3 |




