“银行晴天送伞,雨天收伞。”日剧《半泽直树》中的这句台词曾引发社会热议,许多企业家恐怕对此也是深有同感。我国长期存在的企业融资难问题(尤其是对于中小企业而言)一直是政府、工商界和学术界十分关注的议题,商业银行也不可避免地被大众舆论打上了“嫌贫爱富”的标签。但是,从《半泽直树》中来看,这些现象在日本也是广泛存在的。那么,这是否意味着商业银行的“送伞”和“收伞”并不是中国的特有现象,而是商业银行这一金融机构普遍拥有的一个特征,甚至这一问题的存在本身就具备一定的合理性呢?
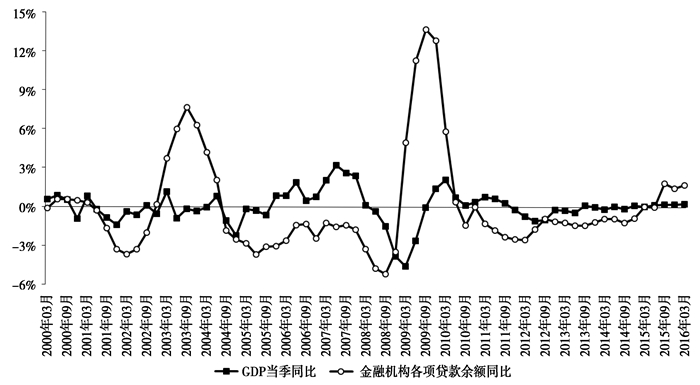
商业银行“晴天送伞,雨天收伞”这一微观行为在宏观总量上的表现就是银行信贷的顺周期性。我们使用HP滤波法提取了我国GDP和金融机构各项贷款余额同比增长率的周期波动部分。如图 1所示,银行信贷呈现出比较明显的顺周期性特征。当然,我们还注意到2003年和2009年异常的巨量信贷投放。银行信贷的顺周期性同样在众多国家广泛存在,比如Apostoaie et al.(2014)在十个欧洲国家以及Kollintzas et al.(2011)在九个OECD国家均发现了这一共性。
|
图 1 GDP和银行信贷周期波动 |
关于信贷周期的研究和争论源远流长,至少可以上溯至亚当·斯密(1776),具体可参见巴曙松、刘海博(2009)。他们将现代信贷周期理论归结为以下三个角度:“一是基于信息经济学理论,从信贷市场的不完全性和信息不对称角度阐述了经济波动的信贷观点;二是从银行信贷行为的角度,认为银行的行为具有内在的顺周期性,从而加剧了经济的波动;三是从银行业风险管理和监管的角度考察。”
宏观经济学较常采用的是上述的第一种解释,即信贷市场存在信息不对称问题。Bernanke and Gertler(1989)构建了一个OLG(代际交叠)模型,其中需要对固定规模的投资项目进行融资的企业面临Townsend(1979)以及Gale and Hellwig(1985)提出的所谓“有成本状态证实”(costly state verification)问题。Bernanke et al.(1999)进一步将上述设定纳入到一个动态一般均衡模型之内,并将其命名为“金融加速器”(financial accelerator)机制,即信贷市场的内生发展能够将遭遇的冲击放大并传导至宏观经济。
而在2008年的全球金融危机之后,宏观经济学家们意识到金融体系对宏观经济周期波动存在着重要影响,开始将视线聚焦到如何将金融体系整合进原有的主流宏观经济模型当中。其中的一个典型是Christiano et al.(2010、2014),他们将Bernanke et al.(1999)中的“金融加速器”机制整合进标准的DSGE(动态随机一般均衡)模型当中,并将其视作“金融摩擦”(financial frictions)。他们发现,金融中介感知的“风险冲击”是此次金融危机的触发器,而金融摩擦的存在使得金融中介将原本分散的个别风险变为了系统性风险。
国内对这方面的研究也在不断跟进。杜清源、龚六堂(2005)在RBC(真实经济周期)模型中引入了“金融加速器”机制来分析信贷市场中存在的信息不对称问题对宏观经济造成的影响,并采用数值模拟的方法与传统RBC理论进行了比较。仝冰(2010)也参照Christiano et al.(2010、2014)的早期工作论文版本对我国的宏观经济状况进行了分析。王立勇等(2012)研究了粘性价格、粘性信息和混合粘性条件下“金融加速器”效应及其作用机制,并发现我国经济中存在显著的“金融加速器”效应。王国静、田国强(2014)则对企业贷款施加了一个强制的融资约束,并将与之相关的随机波动定义为“金融冲击”,研究其对我国经济波动的影响。
本文的研究基于上述文献的创见,但又有不同的创新之处。首先,与王国静、田国强(2014)等文献不同,本文所构建的DSGE模型具备更加合理的微观基础,银行信贷是基于商业银行的理性决策之上的,而不是强制性的外部设定,因此能够将商业银行的微观行为和宏观上的信贷周期纳入到一个一致的框架之内。其次,尽管本文的模型与包含“金融加速器”机制的文献相一致,但是分析的侧重点不同。文献重在理论模型的创新和研究金融摩擦对经济波动影响的重要性,而本文则重在分析信贷市场在微观和宏观表现上的一致性和合理性,并据此就我国当前存在的企业融资难问题提供了一些具有理论依据的政策建议。
本文余下的结构安排如下:第二部分构建一个带有金融摩擦的新凯恩斯主义的中等规模的DSGE模型,第三部分介绍数据的选取和模型中结构参数的估计,并对估计结果做了稳健性检验,第四部分分析金融摩擦和银行信贷周期问题,第五部分提出缓解企业融资难问题的对策,第六部分总结全文。
二、 理论模型本文参照Del Negro et al.(2013),在Christiano et al.(2005)以及Smets and Wouters(2003、2007)的经典新凯恩斯主义模型中按照Christiano et al.(2010、2014)的方式引入了Bernanke et al.(1999)的“金融加速器”机制,因此本文构建的模型是带有金融摩擦的新凯恩斯主义的中等规模的DSGE模型。
模型中的经济主体主要有家庭、劳动加总者、最终产品生产者、中间产品生产者、资本品生产者、企业家、银行、中央银行和政府等九大类。各经济主体均通过在各自的约束条件下最大化其目标函数来做出理性决策。同时,整个经济会受到多种外生随机冲击,包括劳动供给冲击、价格加成冲击、全要素生产率冲击、投资边际效率冲击、风险冲击、政府支出冲击和货币政策冲击等七种。最后,各个市场同时出清,亦即“一般均衡”。总之,模型遵循了“动态随机一般均衡模型”的标准设定。
(一) 家庭和劳动加总者连续的家庭j∈[0,1]拥有如下相同的效用函数:
| ${E_t}\left\{ {\sum\limits_{s = 0}^\infty {{\beta ^s}} \left[ {\ln \left({{C_{t + s}}\left(j \right) - h{C_{t + s - 1}}\left(j \right)} \right) - \frac{{{\varphi _{t + s}}}}{{1 + {v_L}}}{L_{t + s}}{{\left(j \right)}^{1 + vL}}} \right]} \right\}$ | (1) |
其中Ct(j)是消费,Lt(j)是劳动供给,h是家庭的消费习惯系数,φt则是劳动供给冲击,服从如下的外生冲击过程:
| $\ln {\varphi _t} = \left({1 - {\rho _\varphi }} \right)\ln \varphi + {\rho _\varphi }\ln {\varphi _{t - 1}} + \varepsilon _t^\varphi,\varepsilon _t^\varphi \sim N\left({0,\sigma _\varphi ^2} \right)$ |
家庭受到如下的预算约束:
| $\begin{array}{l} {P_{t + s}}{C_{t + s}}\left(j \right) + {B_{t + s}}\left(j \right) + {D_{t + s}}\left(j \right) \le {R_{t + s - 1}}{B_{t + s - 1}}\left(j \right) + R_{t + s - 1}^d{D_{t + s - 1}}\left(j \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + {W_{t + s}}\left(j \right){L_{t + s}}\left(j \right) + \prod\nolimits_{t + s} { + T{r_{t + s}}} - {T_{t + s}} \end{array}$ | (2) |
其中Pt是消费品的价格,Bt(j)和Dt(j)分别是家庭选择持有的政府债券和银行存款的数量,Rt和Rtd则分别是政府债券和银行存款的名义总利率。Wt(j)是名义工资,Πt是家庭从拥有的企业中获得的人均利润,Trt是家庭从企业家中获得的人均转移支付,Tt是总额税。
存在竞争性的劳动加总者,它们将家庭的异质性的劳动供给Lt(j)通过如下的生产技术打包成同质的Lt后卖给中间产品生产者:
| ${L_t} = {\left[ {\int_0^1 {{L_t}{{\left(j \right)}^{\frac{1}{{1 + {\lambda _w}}}}}dj} } \right]^{1 + {\lambda _w}}}$ | (3) |
由劳动加总者的利润最大化的一阶条件可得家庭劳动供给的需求函数为:
| ${L_t}\left(j \right) = {\left({\frac{{{W_t}\left(j \right)}}{{{W_t}}}} \right)^{ - \frac{{1 + {\lambda _w}}}{{{\lambda _w}}}}}{L_t}$ | (4) |
其中Wt(j)和Wt分别是支付给Lt(j)和Lt的名义工资。
结合公式(4)和劳动加总者的零利润条件可得如下的工资加总等式:
| ${W_t} = {\left[ {\int_0^1 {{W_t}{{\left(j \right)}^{ - \frac{1}{{{\lambda _w}}}}}dj} } \right]^{ - {\lambda _w}}}$ | (5) |
每个家庭提供异质性的劳动供给,而且由于劳动力市场的设定,家庭拥有市场力量,所以他们能够决定各自的名义工资水平。假设存在Calvo(1983)中的名义工资刚性,即:在每一期,只有1-ζw比例的家庭可以自由地设定自己的工资,剩下的ζw比例的家庭则只能简单地根据稳态的工资增长率(稳态的通货膨胀率π*乘以稳态的经济增长率γ)来调整其工资。因此,在t期,当家庭能够自由地调整其工资时,它会选择最优工资水平
| $\mathop {\max }\limits_{{{\bar W}_t}\left(j \right)} {E_t}\left\{ {\sum\limits_{s = 0}^\infty {\zeta _w^s{\beta ^s}} \left[ { \cdots - \frac{{{\varphi _{t + s}}}}{{1 + {v_L}}}{L_{t + s}}{{\left(j \right)}^{1 + {v_L}}}} \right]} \right\}$ | (6) |
同时服从预算约束公式(2)、劳动供给的需求函数公式(4)以及如下的粘性工资的简单调整规则:
| ${W_{t + s}}\left(j \right) = {\tilde W_t}\left(j \right){\left({{\pi _ * }\gamma } \right)^s}$ | (7) |
存在竞争性的最终产品生产者,它们将异质性的中间产品Yt(i)通过如下的生产技术打包成同质的最终产品Yt:
| ${Y_t} = {\left[ {\int_0^1 {{Y_t}{{\left(i \right)}^{\frac{1}{{1 + {\lambda _{p,t}}}}}}di} } \right]^{1 + {\lambda _{p,t}}}}$ | (8) |
其中λp,t为价格加成冲击,服从如下的外生冲击过程:
| $\ln {\lambda _{p,t}} = \left({1 - {\rho _p}} \right)\ln {\lambda _p} + {\rho _p}\ln {\lambda _{p,t - 1}} + \varepsilon _t^p,\varepsilon _t^p \sim N\left({0,\sigma _p^2} \right)$ |
由最终产品生产者的利润最大化的一阶条件可得中间产品的需求函数为:
| ${Y_t}\left(i \right) = {\left({\frac{{{P_t}\left(i \right)}}{{{P_t}}}} \right)^{ - \frac{{1 + {\lambda _{p,t}}}}{{{\lambda _{p,t}}}}}}{Y_t}$ | (9) |
其中Pt(i)和Pt分别是中间产品和最终产品的价格。
结合公式(9)和最终产品生产者的零利润条件,同样可得最终产品的价格加总等式为:
| ${P_t} = {\left[ {\int_0^1 {{P_t}{{\left(i \right)}^{ - \frac{1}{{{\lambda _{p,t}}}}}}di} } \right]^{ - {\lambda _{p,t}}}}$ | (10) |
连续的中间产品生产者i∈[0,1]通过如下的生产技术将投入的资本和劳动加工成异质性的中间产品并卖给最终产品生产者:
| ${Y_t}\left(i \right) = {Z_t}{K_t}{\left(i \right)^\alpha }{\left[ {{\gamma ^t}{L_t}\left(i \right)} \right]^{1 - \alpha }}$ | (11) |
其中Kt(i)和Lt(i)分别是资本和劳动投入,γ是稳态的经济增长率,Zt是全要素生产率冲击,服从如下的外生冲击过程:
| $\ln {Z_t} = \left({1 - {\rho _Z}} \right)\ln Z + {\rho _Z}\ln {Z_{t - 1}} + \varepsilon _t^Z,\varepsilon _t^Z\~N\left({0,\sigma _Z^2} \right)$ |
中间产品生产者从竞争性的市场上购买同质的资本和劳动,并且面临相同的资本租金率Rtk和名义工资Wt,因此中间产品生产者的利润函数是:
| ${P_t}\left(i \right){Y_t}\left(i \right) - R_t^k{K_t}\left(i \right) - {W_t}{L_t}\left(i \right)$ | (12) |
同样地,根据Calvo(1983),假设每一期只有1-ζp比例的中间产品生产者能够自由地设定中间产品的价格,而剩下的ζp比例的中间产品生产者只能简单地根据稳态的通货膨胀率π*来调整其产品价格。所以,当能够自由地调整其产品价格时,中间产品生产者会选择最优价格水平
| $\mathop {\max }\limits_{{{\tilde P}_t}\left(i \right)} {E_t}\left\{ {\sum\limits_{s = 0}^\infty {\zeta _p^s{\beta ^s}\Xi _{t + s}^p} \left[ {{{\tilde P}_t}\left(i \right){\pi ^s}_ * - M{C_{t + s}}} \right]{Y_{t + s}}\left(i \right)} \right\}$ | (13) |
| $s.t.\;\;\;{Y_{t + s}}\left(i \right) = {\left({\frac{{{{\tilde P}_t}\left(i \right){\pi ^s}_ * }}{{{P_{t + s}}}}} \right)^{ - \frac{{1 + {\lambda _{p,t + s}}}}{{{\lambda _{p,t + s}}}}}}{Y_{t + s}}$ |
其中MCt是中间产品生产者的名义边际成本,βsΞt+sp是折现因子(Ξtp是家庭预算约束公式(2)的拉格朗日乘子)。
(四) 资本品生产者竞争性的资本品生产者在每一期期初向企业家购买x单位的资本品,并向最终产品生产者购买It单位的最终产品,最后将两者通过如下的生产技术转变为新的资本品后重新卖给企业家:
| $x' = x + {\mu _t}\left[ {1 - S\left({\frac{{{I_t}}}{{{I_{t - 1}}}}} \right)} \right]{I_t}$ | (14) |
其中x′是新的资本品,资本品生产者在该期期末将其重新卖给企业家,x则是在期初向企业家购买的资本品。It是投资支出,即资本品生产者所购买的最终产品,S(·)是投资调整成本,而且S′(·)>0,S″(·)>0。μt是投资边际效率冲击,服从如下的外生冲击过程:
| $\ln {\mu _t} = \left({1 - {\rho _\mu }} \right)\ln \mu + {\rho _\mu }\ln {\mu _{t - 1}} + \varepsilon _t^\mu,\varepsilon _t^\mu \sim N\left({0,\sigma _\mu ^2} \right)$ |
资本品生产者选择投资It来最大化其未来利润的期望折现总和:
| $\mathop {\max }\limits_{{I_t}} {E_t}\left\{ {\sum\limits_{s = 0}^\infty {{\beta ^s}\Xi _{t + s}^p} \left\{ {Q_{t + s}^k{\mu _{t + s}}\left[ {1 - S\left({\frac{{{I_{t + s}}}}{{{I_{t + s - 1}}}}} \right)} \right]{I_{t + s}} - {P_{t + s}}{I_{t + s}}} \right\}} \right\}$ | (15) |
其中βsΞt+sp是和上文一样的折现因子,Qtk则是资本品的名义价格。
(五) 企业家和银行连续的企业家e在t-1期期末用自有的净资产Nt-1(e)和银行贷款Bt-1d(e)从资本品生产者那里购买Kt-1(e)单位的安装资本(installed capital),即:
| $Q_{t - 1}^k{\bar K_{t - 1}}\left(e \right) = {N_{t - 1}}\left(e \right) + B_{t - 1}^d\left(e \right)$ | (16) |
在下一期,企业家选择一个资本利用率水平ut(e)将有效资本(effective capital)Kt(e)以资本租金率Rtk租给中间产品生产者,即:
| ${K_t}\left(e \right) = {u_t}\left(e \right){\bar K_{t - 1}}\left(e \right)$ | (17) |
在t期期末,企业家将折旧后的资本卖给资本品生产者,结合资本品生产者的生产函数公式(14)可得安装资本Kt(e)的积累过程为:
| ${\bar K_t}\left(e \right) = \left({1 - \delta } \right){\bar K_{t - 1}}\left(e \right) + {\mu _t}\left[ {1 - S\left({\frac{{{I_t}}}{{{I_{t - 1}}}}} \right)} \right]{I_t}$ | (18) |
其中δ是资本的折旧率。
在每一期,企业家会遭受到一个异质性的冲击ωt(e),该冲击会增加或者减少其拥有的资本,因此捕捉了实际经济运行中企业经营所面临的风险。根据Bernanke et al.(1999),ωt(e)服从对数正态分布:
| $\ln {\omega _t}\left(e \right) \sim N\left({{m_{\omega,t - 1}},\sigma _{\omega,t - 1}^2} \right)$ |
其中mω,t-1满足E[ωt(e)]=1,标准差σω,t是风险冲击,服从如下的外生冲击过程:
| $\ln {\sigma _{\omega,t}} = \left({1 - {\rho _{{\sigma _\omega }}}} \right)\ln {\sigma _{{\omega ^ * }}} + {\rho _{{\sigma _\omega }}}\ln {\sigma _{\omega,}}_{t - 1} + \varepsilon _t^{{\sigma _\omega }},\varepsilon _t^{{\sigma _\omega }}\~N\left({0,\sigma _{{\sigma _\omega }}^2} \right)$ |
假设企业家在t-1期便得知ωt(e)在t期的累积分布函数为Ft-1(ωt(e))。在得知该冲击之后,企业家将选择一个最优的资本利用率水平ut(e)。当然,在调整资本利用率时,企业家还需要对每单位资本承担一个相对于最终产品的调整成本a(ut(e))。
因此,企业家的资本净收益可记为:
| ${\omega _t}\left(e \right)\tilde R_t^k\left(e \right)Q_{t - 1}^k{\bar K_{t - 1}}\left(e \right)$ | (19) |
其中:
| $\tilde R_t^k\left(e \right) = \frac{{R_t^k{u_t}\left(e \right) + \left({1 - \delta } \right)Q_t^k - {P_t}a\left({{u_t}\left(e \right)} \right)}}{{Q_{t - 1}^k}}$ | (20) |
是企业家的资本的名义总回报率。
由于最优的资本利用率水平ut(e)可由一阶条件Rtk/Pt=a′(ut(e))得到,所以所有企业家的资本利用率水平ut(e)和资本的名义总回报率
企业家向银行贷款时签订了一份债务合约,约定了贷款金额以及相应的利率。但是由于企业家受到ωt(e)的冲击,持有的资本在不断波动,企业经营面临风险,因此可能会发生违约。假设存在企业家违约的临界值ωt(e),当ωt(e)<ωt(e)时,企业家就会对债务进行违约,那么违约临界值可由下式定义:
| ${\bar \omega _t}\left(e \right)\tilde R_t^kQ_{t - 1}^k{\bar K_{t - 1}}\left(e \right) = R_t^c\left(e \right)B_{t - 1}^d\left(e \right)$ | (21) |
其中Rtc(e)和Bt-1d(e)分别是贷款利率和贷款金额。
银行向家庭吸收存款,储蓄利率为Rtd,并贷款给企业家。由于存在信息不对称,银行对贷款进行监管是有成本的,即债务合约是“有成本状态证实”的(costly state verification):银行在回收违约的企业家的残值时需要支付μe比例的费用。因此,银行的零利润条件是:
| $\begin{array}{l} \left[ {1 - {F_{t - 1}}\left({{{\bar \omega }_t}\left(e \right)} \right)} \right]R_t^c\left(e \right)B_{t - 1}^d\left(e \right) + \left({1 - {\mu ^e}} \right)\int_0^{{{\bar \omega }_t}\left(e \right)} {{\omega _t}\left(e \right)} d{F_{t - 1}}\left({{\omega _t}\left(e \right)} \right)\tilde R_t^kQ_{t - 1}^k{{\bar K}_{t - 1}}\left(e \right)\\ = R_{t - 1}^dB_{t - 1}^d\left(e \right) \end{array}$ | (22) |
企业家在遵循融资约束公式(22)的条件下选择资本和银行贷款的数量来最大化预期利润:
| $\int_{{{\bar \omega }_t}\left(e \right)}^\infty {\left[ {{\omega _t}\left(e \right)\tilde R_t^kQ_{t - 1}^k{{\bar K}_{t - 1}}\left(e \right) - R_t^c\left(e \right)B_{t - 1}^d\left(e \right)} \right]} d{F_{t - 1}}\left({{\omega _t}\left(e \right)} \right)$ | (23) |
因此,企业家的净利润是:
| ${V_t} = \int_{{{\bar \omega }_t}\left(e \right)}^\infty {{\omega _t}\left(e \right)\tilde R_t^kQ_{t - 1}^k{{\bar K}_{t - 1}}\left(e \right)d{F_{t - 1}}\left({{\omega _t}\left(e \right)} \right) - \left[ {1 - {F_{t - 1}}\left({{{\bar \omega }_t}\left(e \right)} \right)} \right]R_t^c\left(e \right)B_{t - 1}^d\left(e \right)} $ | (24) |
假设每一期都有1-γe比例的企业家退出市场,而剩下的γe比例的企业家则继续经营。退出市场的企业家需要消耗Θ比例的净资产,并且将剩余的净资产转移支付给家庭。同时,在每一期,新进入市场的企业家将从家庭收到Wte单位的净值转移。由于Wte非常小,所以该退出和进入机制确保了企业家无法积累足够的净资产来进行自我融资,从而必须向银行进行贷款。企业的净资产为:
| ${N_t}{\rm{ = }}{\gamma ^e}{V_t} + W_t^e$ | (25) |
企业家向家庭的净转移支付为:
| $T{r_t}{\rm{ = }}\left({1 - \Theta } \right)\left({1 - {\gamma ^e}} \right){V_t} - W_t^e$ | (26) |
中央银行遵循如下的简单名义利率规则:
| $\frac{{{R_t}}}{{{R_ * }}} = {\left({\frac{{{R_{t - 1}}}}{{{R_ * }}}} \right)^{\rho R}}{\left[ {{{\left({\prod\limits_{j = 0}^3 {\frac{{{\pi _{t - j}}}}{{{\pi _ * }}}} } \right)}^{\psi \pi }}{{\left({\frac{{{Y_t}}}{{{Y_{t - 4}}}}{\gamma ^{ - 4}}} \right)}^{\psi Y}}} \right]^{1 - \rho R}}{e^{\varepsilon _t^R}}$ | (27) |
其中R*、π*和γ分别是稳态的名义利率、通货膨胀率和经济增长率。
| $\varepsilon _t^R \sim N\left({0,\sigma _R^2} \right) \circ $ |
政府服从如下的预算约束:
| ${P_t}{G_t} + {R_{t - 1}}{B_{t - 1}} = {T_t} + {B_t}$ | (28) |
政府支出Gt遵循如下的简单规则:
| ${G_t} = \left({1 - 1/{g_t}} \right){Y_t}$ | (29) |
其中gt是政府支出冲击,服从如下的外生冲击过程:
| $\ln {g_t} = \left({1 - {\rho _g}} \right)\ln g + {\rho _g}\ln {g_{t - 1}} + \varepsilon _t^g,\varepsilon _t^g \sim N\left({,\sigma _g^2} \right)$ |
结合家庭和政府的预算约束以及劳动加总者、最终产品生产者和资本品生产者的零利润条件可得总的资源约束条件如下:
| ${C_t} + {I_t} + a\left({{u_t}} \right){\bar K_{t - 1}} = \frac{1}{{{g_t}}}{Y_t}$ | (30) |
上述模型中最优化问题的一阶条件描绘了宏观经济变量之间的动态关系,再结合该市场出清条件,它们共同刻画了模型经济的均衡行为。
三、 数据选取和参数估计第二部分已经介绍了模型的设定,现在需要选择实际的经济数据对模型中的结构参数进行估计。按照主流的DSGE模型的求解和参数估计方法,本文对一部分参数进行校准,对其余参数则进行贝叶斯估计,并且选用不同时间段的数据以检验研究结果的稳健性。
(一) 数据选取本文选取了总产出、通货膨胀率、银行存贷利差和存款利率的季度数据作为模型中的观测变量,并据此挑选相应的经济统计数据。总产出选择GDP当季同比增长率,通货膨胀率由CPI当月同比增长率经简单加权平均得到,银行的贷款利率和存款利率则分别选择金融机构人民币贷款一般贷款加权平均利率和法定的一年定期存款利率,银行存贷利差由上述两个利率相减可得。数据的时间段为2010年第一季度至2015年第四季度,之所以选择这个区间,一是因为主要考察我国经济进入“新常态”以来所呈现出的新特征,二是避免2008年的经济危机和2009年的特殊的巨量信贷投放对模型的参数估计产生误导。数据均来源于Wind数据库。
(二) 参数校准对模型中的部分参数进行校准,如表(1)所示。
| 表 1 参数校准 |
对其余的参数进行贝叶斯估计,具体的参数设置及估计结果如表 2和表 3所示。
| 表 2 结构参数的先验分布和后验估计结果 |
| 表 3 外生冲击过程的先验分布和后验估计结果 |
为了检验研究结果的稳健性,本文选取了几个不同时间段的数据对模型的结构参数进行贝叶斯估计以及后续的脉冲响应函数分析。除了上文提及的2010年第一季度至2015年第四季度,本文还选取了2000年第一季度至2009年第四季度,以及完整的2000年第一季度至2015年第四季度。结果发现:不同时间段数据下的模型的结构参数的估计值相对稳定,而且脉冲响应函数的结果也相一致,差别仅在于经济变量响应程度的大小,而这与各个时间段中经济周期波动的大小有关。出于论文的简洁性,稳健性检验的具体结果就不在此赘述了。
四、 金融摩擦和信贷周期宏观层面上的银行信贷呈现出的顺周期性特征和微观层面上的商业银行“晴天送伞,雨天收伞”的行为特征在逻辑上是一致的。由于DSGE模型将宏观模型建立在坚实的微观基础之上,因此上文所构建的理论模型为解释信贷周期和商业银行行为提供了很好的理论视角。
由于信贷市场存在信息不对称问题,因此就产生了Bernanke et al.(1999)所提出的“外部融资溢价”(external finance premium)渠道。外部融资溢价是指企业向外部(主要是银行)借款和内部融资之间存在利息差。由于银行在企业经营状况方面处于信息的劣势方,因此需要向企业收取风险溢价。而外部融资溢价又和两方面因素有关,一是贷款企业的杠杆率,二是银行观测到的风险冲击,参见下面的公式(31)。该公式是根据模型中企业家和银行的最优化问题的一阶条件经过对数线性化和整合得到的,其中带“^”的小写字母表示去趋势后的对应的经济变量的对数偏离(log-deviation)。
| ${{E}_{t}}\left[ \hat{\tilde{R}}_{t+1}^{k}-{{{\hat{R}}}_{t}} \right]={{\zeta }_{SP,b}}\left( \hat{q}_{t}^{k}+{{{\hat{\bar{k}}}}_{t}}-{{{\hat{n}}}_{t}} \right)+{{\zeta }_{SP,{{\sigma }_{\omega }}}}{{\hat{\sigma }}_{\omega ,t}}$ | (31) |
公式左侧是外部融资溢价,或者是商业银行的存贷利差;公式右侧第一项小括号内是企业的杠杆率,第二项则是银行观测到的风险冲击。其中ζSP,b和ζSP,σω分别是外部融资溢价对杠杆率和风险冲击的弹性,两者均大于0。
从中我们可以看出,当企业的杠杆率越高,银行对贷款收取更高的利率;当银行发现风险冲击增大,比如遭遇金融危机,银行同样会提高贷款利率。贷款利率的提高也就意味着银行信贷的收缩。企业的杠杆率和企业净资产成反比,当宏观经济繁荣时,企业资产状况良好,风险冲击也较小,因此贷款利率较低,从而贷款规模较大,当宏观经济萧条时则相反。所以信贷周期呈现出明显的顺周期性的特征。
近年来我国经济进入“新常态”,经济增速放缓,尽管市场上资金十分充裕,但是许多企业却面临融资困难的问题,原因就在于此。商业银行虽然拥有大量可贷资金,但是想要贷款的诸多企业经营困难,杠杆率非常高,财务状况非常差,而且银行对经济前景比较悲观,不确定性风险较高,即公式(31)右侧的两项都很高,所以要求较高的贷款利率。银行要求更高的风险溢价,许多经营状况较差的企业根本无法负担,甚至即便有些企业愿意支付高额利息,银行也不愿意贷款给他们,这就是我们当前观察到的一些企业存在融资难问题的原因所在。
总而言之,商业银行“晴天送伞,雨天收伞”是其在金融市场存在信息不对称问题下的理性决策,并且正是因为这一“金融摩擦”的存在导致了信贷周期呈现出顺周期性的特征。
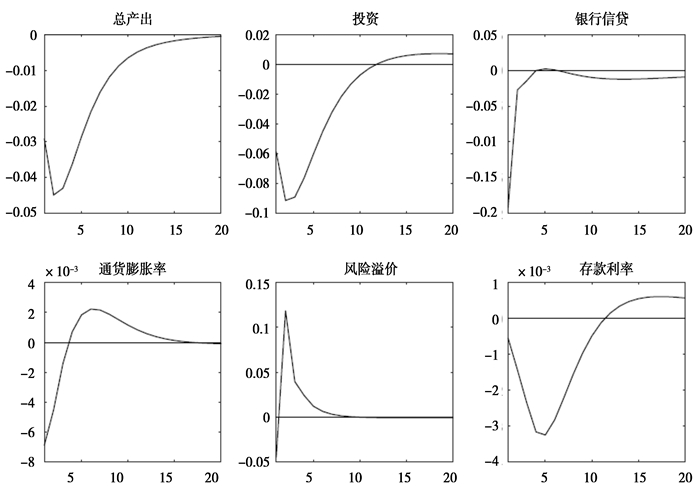
此外,我们从公式(31)中看到风险冲击在其中扮演了重要的角色。风险冲击会影响外部融资溢价,从而导致信贷的紧缩或扩张。现在假设宏观经济受到一单位标准差的风险冲击,其他主要经济变量对该冲击的脉冲响应函数如图 2所示。从图中可以看到,当受到一单位风险冲击时,银行所要求的风险溢价上升了,由此导致银行信贷收紧,从而致使投资和总产出下降。
|
图 2 主要经济变量面临风险冲击的脉冲响应函数 |
尽管银行信贷的顺周期性难以避免,经济增速下行趋势下企业融资难问题的存在也是事出有因,但是我们依然可以采取相应的措施降低信贷周期的波动,缓解企业融资难问题。
最广为人知的措施就是政府的逆周期性操作,例如中央银行可以制定和实施降息降准等货币政策。如前文的图 2所示,在一个具备自动稳定器作用的货币规则下,当经济遭受风险冲击时,利率将会下降,以此应对其对经济造成的不良影响。无风险利率的下降能够部分对冲风险溢价的上升,从而在一定程度上缓解银行信贷的收紧。
另一个比较直观的措施是将风险冲击控制在一定范围之内。风险是无法完全消除的,但是至少可以将其控制在一定区间之内。比如在爆发金融危机这样的极端时刻,巨大的风险冲击无疑会对经济造成灾难性的影响。这时,中央银行要迅速反应并坚定地充当“最后贷款人”的角色,阻断风险冲击的继续蔓延。此外,在经济状况良好的时候,监管者应该加强对银行等金融机构的监管,避免系统性风险的爆发。同样如图 2所示,如果遭遇的一单位的风险冲击降低了,那么主要经济变量的波动自然也会降低,银行信贷的紧缩程度也会缓解。
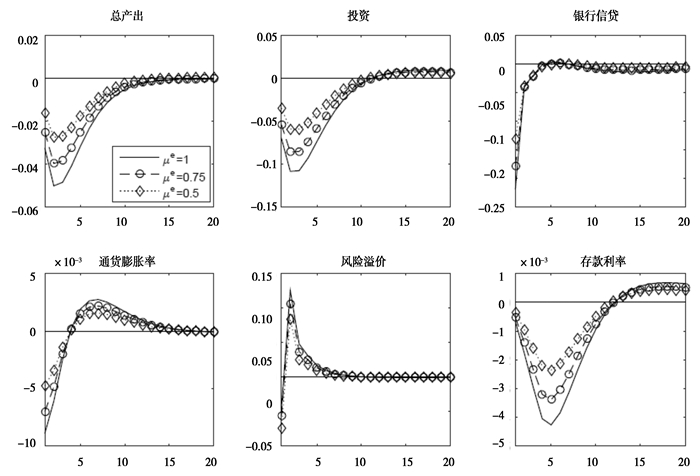
最后,按照模型的解释,商业银行之所以在经济下行时紧缩贷款,是因为存在信息不对称问题所导致的代理成本。如果能够降低代理成本,那么至少可以在一定程度上缓解银行信贷的收紧。代理成本的大小由参数μe控制,图 3画出了当μe不变以及变为原来的0.75和0.5大小时的情况。如图 3所示,当μe减少时,面临相同的风险冲击之下,主要经济变量的波动变小了,其中银行信贷的下降幅度也缩减了。
|
图 3 不同μe大小下,主要经济变量面临风险冲击的脉冲响应函数 |
根据上述模型模拟的结果,缓解企业(尤其是中小企业)融资难问题的具体措施有以下这些:第一,综合运用多种货币政策工具,保持银行体系流动性合理适度,引导货币信贷适度增长,加强宏观信贷政策指导力度,引导金融机构优化信贷结构,加大对中小企业的信贷投放;第二,加强对银行等金融机构的监管,认真执行《巴塞尔协议Ⅲ》的相关决议,提升金融机构抗击风险的能力,坚决防止局部性风险转化为系统性风险;第三,积极推动征信体系和中小企业信用体系建设,完善企业信用信息服务体系,优化企业金融生态环境。
六、 结论本文在一个具有坚实的微观基础的新凯恩斯主义DSGE模型的框架下,分析了微观层面上商业银行“晴天送伞,雨天收伞”的行为特征和宏观层面上银行信贷的顺周期性特征的原因。通过在模型中加入“金融加速器”机制,本文探讨了金融摩擦如何导致信贷周期以及风险冲击对经济周期波动的影响。研究发现:微观层面上,商业银行的信贷紧缩和扩张行为是其在金融市场存在信息不对称问题下的理性决策;宏观层面上,银行信贷的顺周期性是由于存在金融摩擦所导致的;在如今经济增速下行阶段,风险冲击增强了银行的惜贷慎贷情绪,加剧了企业融资难问题。
尽管商业银行“晴天送伞,雨天收伞”的行为以及银行信贷的顺周期性无法完全消除,但是我们依然可以采取相应的措施降低其波动和不利影响。本文根据模型模拟为如何缓解企业融资难问题提出了一些实际的可操作的政策建议:第一,综合运用多种货币政策工具,加强信贷政策指导,确保企业贷款合理增长;第二,加强对银行等金融机构的监管,坚决防止局部性风险转化为系统性风险;第三,完善企业信用信息服务体系。
| [] |
巴曙松、 刘海博 ,
2009, "信贷周期理论研究综述", 《湖北经济学院学报》 , 第 3 期 , 第 45–54 页。
( 0) 0)
|
| [] |
杜清源、 龚六堂 ,
2005, "带'金融加速器'的RBC模型", 《金融研究》 , 第 4 期 , 第 16–30 页。
( 0) 0)
|
| [] |
仝冰,2010,"货币、利率与资产价格",北京大学博士论文。
( 0) 0)
|
| [] |
王国静、 田国强 ,
2014, "金融冲击和中国经济波动", 《经济研究》 , 第 3 期 , 第 20–34 页。
( 0) 0)
|
| [] |
王立勇、 张良贵、 刘文革 ,
2012, "不同粘性条件下金融加速器效应的经验研究", 《经济研究》 , 第 10 期 , 第 69–81 页。
( 0) 0)
|
| [] |
Apostoaie, C.-M.
, Percic, S.
, Cocris, V.
and Chirlesan, D.
, 2014, "Research on the Credit Cycle and Business Cycle with a Focus on Ten States from Central Eastern, and Southeastern Europe". , Emerging Markets Finance and Trade , 50 , 63–77.
( 0) 0)
|
| [] |
Bernanke, B.
and Gertler, M.
, 1989, "Agency Costs Net Worth, and Business Fluctuations". , American Economic Review , 79 (1) , 14–31.
( 0) 0)
|
| [] |
Bernanke, B., M. Gertler and S. Gilchrist, 1999, "The Financial Accelerator in a Quantitative Business Cycle Framework", in Handbook of Macroeconomics (Vol. 1C):1341-1393. Eds. by Taylor, J. B. and M. Woodford. Published by North-Holland.
( 0) 0)
|
| [] |
Calvo, G. A.
1983, "Staggered Prices in a Utility-Maximizing Framework". , Journal of Monetary Economics , 12 (3) , 383–398.
( 0) 0)
|
| [] |
Christiano, L. J.
, Eichenbaum, M.
and Evans, C. L.
, 2005, "Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy". , Journal of Political Economy , 113 (1) , 1–45.
( 0) 0)
|
| [] |
Christiano, L. J., R. Motto and M. Rostagno, 2010, "Financial Factors in Economic Fluctuations", European Central Bank Working Paper, No.1192.
( 0) 0)
|
| [] |
Christiano, L. J.
, Motto, R.
and Rostagno, M.
, 2014, "Risk Shocks". , American Economic Review , 104 (1) , 27–65.
( 0) 0)
|
| [] |
Del Negro, M.
, Eusepi, S.
, Giannoni, M.
, Sbordone, A.
, Tambalotti, A.
, Cocci, M.
, Hasegawa, R.
and Linder, M. H.
, 2013, "The FRBNY DSGE Model". , Federal Reserve Bank of New York Staff Reports No.647 .
( 0) 0)
|
| [] |
Gale, D.
and Hellwig, M.
, 1985, "Incentive-Compatible Debt Contracts:The One-Period Problem". , Review of Economic Studies , 52 (4) , 647–663.
( 0) 0)
|
| [] |
Kollintzas, T.
, Konstantakopoulou, I.
and Tsionas, E.
, 2011, "Stylized Facts of Money and Credit over the Business Cycles". , Applied Financial Economics , 21 (22-24) , 1735–1755.
( 0) 0)
|
| [] |
Smets, F.
and Wouters, R.
, 2003, "An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area". , Journal of the European Economic Association , 1 (5) , 1123–1175.
( 0) 0)
|
| [] |
Smets, F.
and Wouters, R.
, 2007, "Shocks and Frictions in US Business Cycles:A Bayesian DSGE Approach". , American Economic Review , 97 (3) , 586–606.
( 0) 0)
|
| [] |
Townsend, R. M.
1979, "Optimal Contracts and Competitive Markets with Costly State Verification". , Journal of Economic Theory , 21 (2) , 265–293.
( 0) 0)
|



