已有的理论研究与经验研究均表明一个显在的事实:作为财政政策的重要构成部分,政府支出在实现宏观经济稳定、促进经济增长与社会就业过程中具有重要的作用 (Céspedes and Galí,2012;陈利锋,2015a;迟诚和马万里,2015)。2007年至2009年金融危机期间,世界各国政府纷纷采用财政政策来抵御逆向外生冲击对于本国经济的不利冲击,使得研究者重新关注并重视政府支出 (以及财政政策) 的效应,进而使得政府支出重新成为理论研究与政策分析的热点话题。
那么,政府支出对于宏观经济具有怎样的影响呢?不同的研究流派对于这一问题具有不同的解答。Burnside et al.(2004)、McGrattan and Ohanian (2010)、Pappa (2009)以及Traum and Yang (2011)等则采用新古典的分析范式即设定完全竞争的市场环境对政府支出的宏观经济效应进行了分析。研究结果无一例外的指出,政府支出对于消费和投资具有挤出效应。基于这些研究的结论,在熨平宏观经济波动时政府应该对支出政策的使用保持审慎的态度。在此基础上,Céspedes and Galí(2012)以及Galí(2013)等已有的研究表明,在经济周期波动分析中新古典的设定可能与现实存在严重的不符,而以非完全竞争为特征的新凯恩斯主义动态随机一般均衡 (即NK-DSGE) 模型则与现实更为贴近。
然而,作为近十年来主流宏观经济学与政策分析的标准范式的NK-DSGE模型却较少对政府支出进行深入的分析 (Mattini and Rossi, 2009)。具体表现为:(1) 政府支出被看作为一个外生冲击,进而无法有效的刻画政府支出与实际经济变量之间的联系 (王文甫,2015;陈利锋,2015a);(2) 政府支出被看做一个整体进而忽略了政府支出的不同构成成分,因而也忽略了政府支出不同构成成分宏观经济效应的差异 (Mattini and Rossi, 2012)。
针对已有的NK-DSGE模型第一个方面的不足,Christiano et al.(2011)、Eggertsson (2011)、Roulleau-Pasdeloup (2013)、Benjamin et al.(2013)等均将政府支出作为内生变量引入NK-DSGE模型框架并考察政府支出的宏观经济效应。这一做法既克服了第一个方面的不足,研究的结果也发现这一做法可以更好的拟合现实数据。然而这些研究仍主要分析的是政府支出的整体经济效应,因而仍忽略了政府支出不同构成部分宏观经济效应的差异。
针对已有的NK-DSGE模型第二个方面的不足,部分研究在建模过程中考虑了政府支出的不同构成成分。①胡永刚和郭新强 (2012)、饶晓辉和刘方 (2014)以及Bouakez et al.(2014a)等分别考察了政府生产性支出冲击对于一国经济波动和居民消费的影响。研究结果表明,政府生产性支出是推动经济波动的重要力量,而生产性支出对于居民消费具有促进作用,即“挤入效应”。显然,这一结论与基于完全竞争的新古典分析范式所得到的结论是相反的:后者认为政府支出对于居民消费具有“挤出效应”。Bouakez et al.(2013)与Albertini et al.(2014)等则分别考察了政府生产性支出与政府消费性支出的影响,研究结果均发现生产性政府支出冲击与消费性政府支出冲击对于美国主要宏观经济变量均具有不同的冲击效应。因此,在NK-DSGE模型中引入政府支出不同构成成分之后,已有的研究均发现生产性支出与消费性支出具有不同的宏观经济效应。这一发现意味着,在考察政府支出的宏观经济效应时,基于忽略政府支出不同构成成分的NK-DSGE模型所得到的结论可能存在一定的偏误。
① 需要说明的是,部分研究采用其他的划分方式对政府支出进行分类。易行健 (2013)基于政府支出对于消费影响的差异性将政府支出划分为民生性支出与非民生性支出。刘吕吉和张凤 (2015)则基于福利的角度将政府支出划分为福利性支出与非福利性支出。
尽管已有的研究已经考察了政府支出不同构成成分对于宏观经济的影响,但是这些研究仍忽略了现实经济中不同部门之间的差异,部门之间的差异可能使得相同的政府支出冲击对于不同部门具有不同的影响。换言之,政府支出 (无论是消费性政府支出还是生产性政府支出) 的宏观经济效应具有部门依赖性。然而已有的现就并未对这一问题进行深入的分析。需要说明的是,已有的研究已经开始关注财政政策的部门效应。Monacelli和Perotti (2008)基于开放经济NK-DSGE模型考察了财政政策冲击的部门效应;Bénétrix和Lane (2010)则分析了财政政策冲击对于不同部门产出的影响;Bouakez et al.(2014b)使用结构向量自回归模型对减税和政府支出的整体效应和部门效应进行了分析。①因此,对政府支出进行分类并依据现实经济中不同部门之间的差异构建NK-DSGE模型,进而分析政府支出不同构成成分对于不同部门的影响,是对已有研究的一个重要的补充。然而,仍然存在的一个问题是,政府支出的不同构成成分对于我国现实经济中不同的部门以及宏观经济波动具有怎样的影响呢?
① 这些研究的结果无一例外的发现,财政政策对于不同部门具有不同的冲击效应。
为了更好的回答这一问题,基于我国的相关数据,本文首先建立了一个包含产出、制造业部门产出、服务部门产出等6变量向量自回归 (VAR) 模型,并基于这一模型发现两个关于政府支出不同构成成分的宏观经济效应的经验性证据:(1) 相对政府消费性支出而言,政府生产性支出对于整体经济 (以产出变量为代表) 具有更大的冲击效应;(2) 政府支出冲击的宏观经济效应具有部门依存性 (Sector-Dependence) 特征,具体表现为:无论是生产性政府支出冲击还是消费性政府支出冲击,其对于制造业部门产出和服务部门产出均具有不同的冲击效应。VAR模型所得到的经验性证据为我们提供了政府支出不同构成成分影响宏观经济以及不同部门的经验上的直觉,从而也构成了本文NK-DSGE模型建立的现实依据。
基于已有NK-DSGE模型存在的不足以及VAR模型所得到的经验证据,本文建立了一个包含政府支出不同构成成分的多部门NK-DSGE模型,并基于这一模型分析政府支出的不同构成成分对于我国实际经济波动的影响。与Wesselbaum (2014)类似,我们在NK-DSGE模型中引入制造业部门与服务部门。当在NK-DSGE模型中引入多个不同的部门时,劳动力可以跨部门流动。为了对劳动力跨部门流动进行有效的刻画,与Blanchard and Galí(2010)类似,在本文的模型中,我们设定不同部门具有不同的雇佣成本,而雇佣成本的差异是引起劳动力跨部门流动的外在引力。更重要的,在相同的外生冲击下,雇佣成本的差异引起不同部门生产企业雇佣决策的改变,进而使得不同部门的产出、就业、实际工资等变量均呈现出不同的动态反应。基于我国的现实数据,我们对这一模型进行了贝叶斯估计,进而生产性政府支出与消费性政府支出冲击的贝叶斯脉冲响应函数证实了我们基于VAR模型所得到的经验证据。贝叶斯冲击分解的结果则表明,相对于政府消费性支出而言,政府生产性支出冲击对于我国宏观经济波动具有更大的影响。在此基础上,本文采用福利分析法考察了生产性政府支出冲击与消费性政府支出冲击引起的社会福利损失,研究结果发现生产性政府支出冲击引起了相对较大的社会福利损失。
国际金融危机之后,欧美发达国家的经济呈现“缓慢复苏”的特征 (Galí et al.,2012),表现为产出增长速度相对更为缓慢,并且失业相对金融危机之前更具持续性 (Ravenna and Walsh, 2014;Galí,2016)。由于金融危机期间财政政策在各国经济摆脱金融危机过程中具有显著性重要作用,因而部分研究者倾向于使用政府支出政策以及与之相关的财政政策对经济进行干预以促进劳动力市场乃至整体经济的复苏 (Karras,2012;Wesselbaum,2014;Karras,2015)。对于我国而言,政府支出政策是我国政府宏观调控的重要政策工具,“西部大开发”以及“经济刺激计划”等展现了大国政府支出政策强大的现实影响力。然而,金融危机之后,我国经济增长形势并不乐观,整体经济下行的趋势日益明显,社会就业问题也更为严重。在这一背景下,分析政府支出政策不同构成成分的宏观经济效应及其对于不同部门的影响,对于我国政府支出政策的制定与调整均具有重要的现实意义。
二、 政府支出宏观经济效应的经验特征 (一) 样本说明本部分建立一个包含制造业部门产出、服务部门产出、政府生产性支出、政府消费性支出、产出以及通胀的6变量VAR模型。其中,制造业部门产出采用国家统计部门公布的由农副产品加工业等31个部门销售收入的加总数据表示;总产出采用支出法核算的GDP表示;服务部门产出采用第三产业产值数据表示;采用饶晓辉和刘方 (2014)的办法,政府生产性支出以财政基本建设支出、教育支出和科研支出之和表示,而政府消费性支出则采用财政支出与生产性支出之差表示;通胀则采用经过环比处理之后的CPI数据表示。所有数据均来源于中经网数据库,样本时期为2002Q1至2013Q4。
鉴于季度GDP平减指数难以获得,我们采用季度CPI数据对除通胀之外的其他变量进行处理使之转变为实际值 (Actual Value)。在此基础上,采用X12方法将季节性趋势从各变量观测数据中予以剔除。最后,使用CF滤波法分离出各个变量的周期性成分。
(二) 模型分析在对VAR (6) 模型系统估计之前,需要确定最优滞后长度。一般而言,关于VAR模型最优滞后长度的选取依据的是赤茨信息准则 (AIC)、施瓦茨信息准则 (SC)、似然比 (LR)、最终预测偏误 (FPE) 和汉南-昆准则 (HQ) 等。本文VAR (6) 模型的滞后长度检验结果显示最优滞后长度为2;进一步,VAR (6) 模型的特征根全部位于单位圆内,表明本文VAR (6) 模型系统是平稳的。在此基础上,我们对VAR (6) 模型进行了估计,进而得到政府生产性支出冲击与消费性支出冲击的脉冲响应函数。
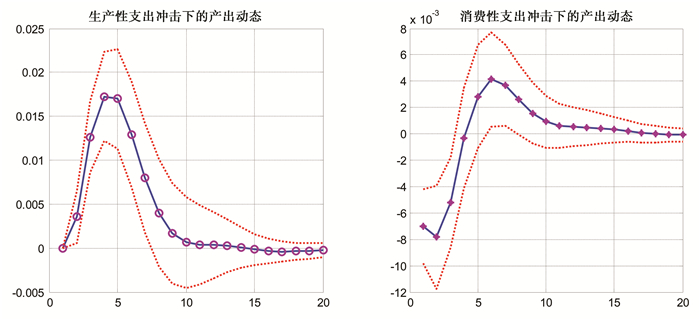
图 1给出了生产性政府支出冲击与消费性政府支出冲击下总产出的动态反应函数。显然,在两类政府支出冲击下,总产出表现出显著的“驼峰状”动态变化路径,这与已有的研究如Hall (2011)等是一致的。两类政府支出冲击最终均推动了产出的增加,不过在两类政府支出冲击下,总产出的动态变化轨迹却存在显著差异,具体表现为:(1) 生产性政府支出冲击下,产出迅速上升并在4个时期之后达到冲击效应的最大值 (约0.018个单位),之后则逐渐收敛至稳态;而在消费性政府支出冲击下,产出首先呈现出短暂的下降趋势,然后在逐渐上升并在冲击发生之后的第6个时期到达冲击效应的峰值 (约为4×10-3个单位),然后再逐渐向稳态收敛;(2) 比较生产性政府支出冲击与消费性政府支出冲击下产出的动态反应可以发现,生产性政府支出冲击对于产出具有更大的冲击效应。这一发现与Tapp (2011)、饶晓辉和刘方 (2014)、Wesselbaum (2014)等研究所得到的结论是一致的。
|
图 1 生产性政府支出冲击与消费性政府支出冲击下的产出动态 |
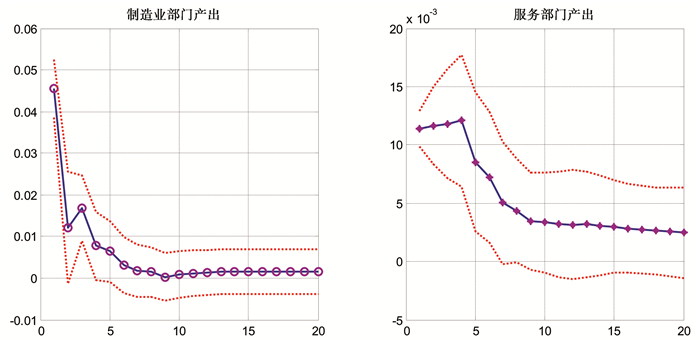
在此基础上,我们进一步考察不同政府支出冲击对于制造业部门与服务部门产出的冲击效应。图 2给出了生产性政府支出冲击下两类不同部门产出的动态反应路径。显然,在相同的外生冲击下,两类部门产出做出不同的动态反应,具体表现为:在生产性政府支出冲击下,制造业部门产出迅速上升,之后逐渐下降并向稳态收敛;而服务部门产出则在冲击发生之后缓慢上升并在第4个时期达到冲击效应的峰值,之后则逐渐下降并向稳态收敛。这一结果意味着在相同的外生冲击下,不同部门的同一变量的动态反应具有显著差异。
|
图 2 生产性政府支出冲击下的两部门产出动态 |
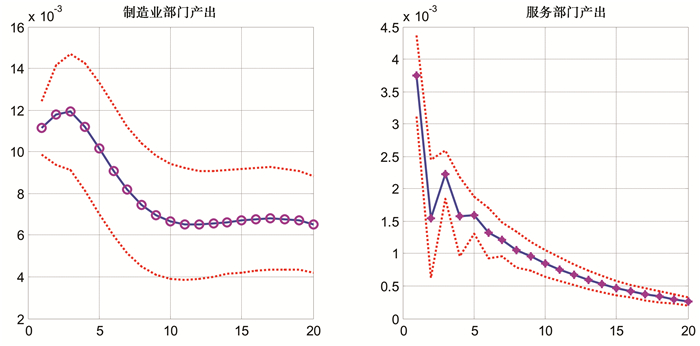
图 3给出了消费性政府支出冲击下制造业部门与服务部门产出的动态反应。与生产性政府支出冲击类似,消费性政府支出冲击对于制造业部门产出与服务部门产出的冲击效应业存在显著的差异。因此,综合图 2与图 3可以发现,政府支出冲击对于制造业部门与服务部门具有不同的冲击效应,即政府支出的冲击效应存在部门依存性特征。
|
图 3 消费性政府支出冲击下的两部门产出动态 |
基于以上经验研究的结果,政府支出冲击的宏观经济效应具有如下经验特征:
(1) 相对政府消费性支出而言,政府生产性支出对于整体经济具有更大的冲击效应;
(2) 政府支出冲击的效应具有部门依存性特征。
三、 理论模型本部分所建立的NK-DSGE模型中包含了家庭、制造业部门与服务部门生产企业、、中间产品生产企业、最终产品生产企业以及政府等主体。与Iacoviello et al.(2011)、Wesselbaum (2014)、Hara et al.(2014)以及陈利锋 (2016)等类似,中间产品生产企业中包含了两个部门:制造业部门与服务部门。然而与陈利锋 (2016)等不同的是,本文的模型中引入了物质资本。物质资本的引入从两个方面改变了模型经济:首先,家庭可以进行物质资本投资,进而改变了家庭的优化行为;第二,改变了企业的生产行为,进而也改变了外生冲击下模型各变量的动态反应。制造业部门与服务部门生产企业雇佣劳动力并租赁物质资本进行生产,其产品作为投入品为中间产品生产企业所购买。为了分析的便利,我们设定制造业部门与服务部门均为中间产品生产企业所有,因而中间产品生产企业可以无成本的获得生产投入。①
① 需要注意的是,这并不意味着中间产品生产企业的生产成本为零。其生产成本来源于制造业部门与服务部门雇佣家庭的劳动力以及租赁物质资本所支付的工资和租金。
(一) 劳动力市场任意时期t,定义Ntm和Nts为家庭成员在两类部门的就业,显然经济中的总就业Nt为两部门就业之和,即:Nt=Ntm+Nts。为便于分析,经济中的劳动力供给设定为单位1。①定义Ut为失业,因此:Ut=1-Nt。
① 这一设定意味着在本文的模型中,就业与就业率、失业与失业率的含义相同。基于便利性考虑,建模过程中,我们统一使用就业、失业。
定义δ为离职率,那么时期t两类部门的就业Ntx(x=m, s) 均为上一期未离职的就业者与本期新雇佣的劳动力 (Htx) 之和,即:
| $ N_t^x = \left( {1 - \delta } \right)N_{t - 1}^x + H_t^x $ | (1) |
经济中新雇佣的劳动力为两类部门新雇佣的劳动力数量之和,因此:Ht=Htm+Hts。定义Jt为经济中待业的劳动力,显然,Jt中包含了上一时期原本处于失业状态的劳动力和上一时期末新离职的劳动力。因此,Jt满足:
| $ {J_t} = {U_{t - 1}} + \delta {N_{t - 1}} = 1 - \left( {1 - \delta } \right){N_{t - 1}} $ | (2) |
定义Xtm和Xts分别为制造业部门与服务部门失业者找到工作的概率,依据Blanchard和Galí(2010),两类部门失业者找到工作的概率定义为本部门新雇佣的劳动力与待业劳动力之比,即:Xtx=Htx/Jt(x=m, s)。因此,总的找到工作的概率Xt为:Xt=Xtm+Xts。企业雇佣劳动力需要花费雇佣成本,如招聘成本、培训成本以及除工资之外的福利等。与Blanchard和Galí(2010)相同,本文设定两类部门企业的雇佣成本满足:
| $ F_t^x = A_t^x{(X_t^x)^{{\gamma _x}}} $ | (3) |
其中:Ftx为两类部门企业的雇佣成本;参数γx为雇佣成本对于找到工作的概率的弹性系数;Atx为两类部门的技术冲击,定义εtax=lnAtx,那么εtax服从平稳的AR (1) 过程。
(二) 家庭家庭的目标为最大化效用函数:
| $ {E_t}\sum\nolimits_{_{t = 0}}^\infty {{\beta ^t}{\rm{exp}}(\varepsilon _t^d)} [{\rm{ln}}{C_t} - {\rm{exp}}(\varepsilon _t^l)N_t^{1 + \eta }{\left( {1 + \eta } \right)^{ - 1}}] $ |
其中:β为贴现因子;Ct为消费;η为劳动供给弹性系数的倒数;εtd和εtl分别为偏好冲击与劳动力供给冲击,且二者均服从平稳的AR (1) 过程。家庭成员可以在制造业部门就业,也可以在服务部门就业,其对应的名义工资率分别为Wtm和Wts。为了实现一生消费的平滑化,家庭还使用储蓄进行物质资本投资。具体的,物质资本积累方程为:
| $ K_{t + 1}^x = (1 - {\delta _k})K_t^x + {\rm{exp}}(\varepsilon _t^k)K_t^kS(I_t^k/K_t^k)\left( {x = m,s} \right) $ | (4) |
上式中:δk为物质资本折旧率;Ktx和Itx分别为两类部门的物质资本和投资;S(·) 为投资调整成本并且:S(δk)=δk,S′(δk)=1,S′ > 0,S″≤0。Altig et al.(2011)认为产生物质资本调整成本的原因在于投资的不可逆性。与Galí et al.(2007)不同的是,上式中包含了投资冲击εtk。已有的研究如Justiniano et al.(2011)认为这一冲击度量了由最终产品转化为物质资本投资的效率或者生产投资物品的特定技术冲击;Justiniano et al.(2010)以及Furlanetto and Seneca (2014)均发现投资冲击是推动经济周期波动的重要力量。与已有的研究类似,我们设定投资冲击εtk服从平稳的AR (1) 过程。定义Kt为经济中总的物质资本,因此:Kt=Ktm+Kts,即总的物质资本为两部门物质资本之和。对应的,经济中的总投资为两类部门投资之和,即:It=Itm+Its。
任意时期家庭的收入包括:在两类部门获得的工资收入、上期购买的债券带来的收益、失业救济、租金收入以及其他收入;家庭的支出则包括消费支出、投资支出 (It)、购买债券支出以及缴纳的税收 (Tt)。因此,家庭的预算可行集为:
| $ {C_t} + \frac{{{B_{t + 1}}}}{{{P_t}}} + {I_t} + {T_t} \le W_t^mN_t^m + W_t^sN_t^s + {R_t}\frac{{{B_t}}}{{{P_t}}} + R_t^k{K_t} + {W^u}{U_t} + {O_t} $ | (5) |
其中:Pt为价格水平;Bt为家庭持有的政府债券,Rt为名义利率;Wtm和Wts分别为家庭成员就业于制造业部门与服务部门获得的实际工资;Wu为失业救济金,Ut为失业;Ot为其他收入。具体的,家庭效用最大化问题对应的优化条件为:
| $ {\lambda _t} = {\rm{exp}}(\varepsilon _t^d)/{C_t} $ | (6) |
| $ \beta {E_t}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}{R_{t + 1}}\frac{{{P_t}}}{{{P_{t + 1}}}} = 1 $ | (7) |
| $ \begin{array}{l} Q_t^x = \beta {\rm{exp}}(\varepsilon _t^k){E_t}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}\{ R_{t + 1}^k + {Q_{t + 1}}[{\rm{exp}}( - \varepsilon _{t + 1}^k)(1 - {\delta _k}) + \\ S(I_{t + 1}^xK_{t + 1}^x) - (I_{t + 1}^xK_{t + 1}^x)S'(I_{t + 1}^xK_{t + 1}^x)]\} \end{array} $ | (8) |
其中:λt为预算可行集 (5) 的动态拉格朗日乘子。式 (6) 为家庭效用最大化时的最优消费;式 (7) 为效用最大化时的最优债券持有;式 (8) 为效用最大化时的最优物质资本投资,Qtx=[S′(Itx/Ktx)]-1为Tobin (托宾) 的“Q”。
(三) 中间产品生产企业的行为制造业部门与服务部门的生产企业采用如下技术进行生产:
| $ Y_{it}^x = A_t^x{(K_{it - 1}^x)^{{\alpha _x}}}{(N_{it}^x)^{1 - {\alpha _x}}}{(G_t^k)^{{\alpha _G}}} $ | (9) |
上式中,Yitx为两类部门的产出;Gtk为由政府的生产性支出所形成的生产性资本;αx为物质资本的产出弹性;v为生产性资本的产出弹性。式 (9) 表明,物质资本的引入改变了厂商的生产行为。中间产品生产企业使用两类部门生产企业的产品,并采用如下技术进行中间产品的生产:
| $ {Y_{it}} = {A_t}{(Y_{it}^m)^v}{(Y_{it}^s)^{1 - v}} $ | (10) |
上式中:Yit为中间产品的产出;参数v为制造业产品的产出弹性;At为整体生产率冲击,且εta=lnAt服从平稳的AR (1) 过程。定义Ft(Witx, Nit-1x) 为中间产品生产企业的利润函数,那么其目标为最大化如下以递归形式表述的方程:
| $ \begin{array}{l} {F_t}(W_{it}^x,N_{it - 1}^x){\rm{ }} = {P_{it}}{P_t}{Y_{it}} - W_{it}^mN_{it}^mW_{it}^sN_{it}^s - R_t^kK_{it - 1}^x\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - F_t^mH_{it}^m - F_t^sH_{it}^s + \beta {E_t}{\Lambda _{t,t + 1}}{F_{t + 1}}(W_{it + 1}^x,N_{it}^x) \end{array} $ |
其对应的一阶条件为:
| $ R_t^k = \frac{{{P_{it}}}}{{{P_t}}}\frac{{\partial \;{Y_{it}}}}{{\partial \;K_{it - 1}^m}} = \frac{{{P_{it}}}}{{{P_t}}}\frac{{\partial \;{Y_{it}}}}{{\partial \;K_{it - 1}^x}} \Leftrightarrow R_t^k = {\alpha _m}v\frac{{{Y_{it}}}}{{K_{it - 1}^m}} = {\alpha _s}\left( {1 - v} \right)\frac{{{Y_{it}}}}{{K_{it - 1}^s}} $ | (11) |
| $ v(1 - {\alpha _m})\frac{{{P_{it}}}}{{{P_t}}}\frac{{{Y_{it}}}}{{N_{it}^m}} - W_{it}^m - F_t^m + \beta \left( {1 - \delta } \right){E_t}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}F_{t + 1}^m = 0 $ | (12) |
| $ \left( {1 - v} \right)(1 - {\alpha _s})\frac{{{P_{it}}}}{{{P_t}}}\frac{{{Y_{it}}}}{{N_{it}^s}} - W_{it}^s - F_t^s + \beta \left( {1 - \delta } \right){E_t}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}F_{t + 1}^s = 0 $ | (13) |
定义Vtm和Vts分别为工人就业于制造业部门与服务部门获得的就业价值,Vtu为失业者获得的收益。工人既可以在部门内部流动,也可以在部门之间流动。决定工人流动的因素为就业的收益。如果在制造业部门就业,那么工人可以获得如下收益:(1) 制造业部门提供的工资收入Wtm;(2) 未来不离职 (概率为1-δ) 与离职之后重新在本部门其他企业就业而获得的就业价值 (概率为δXt+1m);(3) 未来离职之后就业于服务部门而获得的就业价值 (概率为δXt+1s);(4) 离职之后失业所获得的失业价值 (概率为δ(1-Xt+1))。工人就业的成本为在工作时间中牺牲的闲暇,已有的研究采用消费与闲暇的边际替代率表示,因而就业的成本为:MRSt=exp (εtd)CtNtη。具体的,工人在制造业部门就业获得的就业价值Vtm为:
| $ \begin{array}{l} V_t^m = W_t^m - MR{S_t} + \beta {E_t}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}[(1 - \delta + \delta X_{t + 1}^m)V_{t + 1}^m + \\ \delta X_{t + 1}^sV_{t + 1}^s + \delta (1 - {X_{t + 1}})V_{t + 1}^u] \end{array} $ | (14) |
工人在服务业部门就业获得的就业价值包括:(1) 服务部门企业提供的工资收入Wts;(2) 未来不离职 (概率为1-δ) 与离职之后在本部门其他企业就业获得的就业价值 (概率为δXt+1s);(3) 未来离职之后在制造业部门就业获得的就业价值 (概率为δXt+1m);(4) 离职后失业获得的失业价值 (概率为δ(1-Xt+1))。因此,工人在服务部门就业获得的就业价值Vts为:
| $ \begin{array}{l} V_t^s = W_t^s - MR{S_t} + \beta {E_t}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}[(1 - \delta + \delta X_{t + 1}^s)V_{t + 1}^s + \\ \delta X_{t + 1}^mV_{t + 1}^m + \delta (1 - {X_{t + 1}})V_{t + 1}^u] \end{array} $ | (15) |
失业者获得的失业价值包括:(1) 失业救济金Wu;(2) 失业者未来在制造业部门得到工作岗位而获得的就业价值,其对应的概率为Xt+1m;(3) 失业者未来在服务部门得到工作岗位获得的就业价值,其对应的概率为Xt+1s;(4) 失业者未来仍处于失业状态而获得的失业价值,其对应的概率为1-Xt+1。具体的,工人失业获得的失业价值为:
| $ V_t^u = {W^u} + \beta {E_t}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}[X_{t + 1}^mV_{t + 1}^m + X_{t + 1}^sV_{t + 1}^s + \\ (1 - {X_{t + 1}})V_{t + 1}^u] $ | (16) |
定义Stm=Vtm-Vtu和Sts=Vts-Vtu分别为工人在制造业部门与服务部门获得的就业剩余,ϑ为反映工人议价能力的模型参数,依据Blanchard and Galí(2010),均衡时,家庭成员在各个部门承担的雇佣成本与家庭成员在各个部门就业所获得的就业剩余相等,即ϑFtx=Stx。因此,工资决定方程为:
| $ \begin{array}{l} \partial F_t^m = W_t^m - MR{S_t} - {W^u} + \beta \vartheta \left( {1 - \delta } \right)\\ {E_t}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}[(1 - X_{t + 1}^m)F_{t + 1}^m - X_{t + 1}^sF_{t + 1}^s] \end{array} $ | (17) |
| $ \begin{array}{l} \partial F_t^s = W_t^m - MR{S_t} - {W^u} + \beta \vartheta \left( {1 - \delta } \right)\\ {E_t}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}[(1 - X_{t + 1}^s)F_{t + 1}^s - X_{t + 1}^mF_{t + 1}^m] \end{array} $ | (18) |
最终产品生产企业投入中间产品,并使用Dixit-Stiglitz技术进行最终产品的生产。定义θp为名义价格刚性,价格设定方式为:
| $ {E_t}[\sum\nolimits_{_{t = 0}}^\infty {{\beta ^k}} \frac{{{\lambda _{t + k}}}}{{{\lambda _t}}}{Y_{t + k}}(P_t^*{P_{t + k}} - \frac{\varepsilon }{{\varepsilon - 1}}M{C_{t + k}})] = 0 $ | (19) |
与谢平与罗雄 (2002)类似,我们设定模型经济中的货币政策机制为:
| $ \frac{{{R_t}}}{R} = {(\frac{{{Y_t}}}{Y})^{{r_y}}}{(\frac{{{\Pi _t}}}{\Pi })^{{r_p}}}{\rm{exp}}(\varepsilon _t^r) $ | (20) |
其中:Πt=Pt/Pt-1为通胀;R、Y和Π分别为名义利率、产出和通胀的稳态值;ry和rp分别反映了货币政策当局对于产出和通胀变化的敏感程度;εtr为货币政策冲击并且服从平稳的AR (1) 过程。需要说明的是,国内部分已有的研究在标准的泰勒规则中引入利率平滑机制。事实上,利率平滑机制的引入将改变货币政策冲击下各变量的持续性特征,而本文主要考察的是政府支出不同构成成分对于我国经济波动的影响,因而货币政策规则的设定对于模型的结论并不存在显著性影响。
政府的财政政策原则为:Tt+(Bt+1/Pt)Rt-1=(Bt/Pt)+Gtc+GtI,Tt为税收收入和债券收入。与Galí et al.(2007)类似,税收收入为债券和政府支出的函数,且满足:
| $ {T_t} = {\varphi _g}{G_t} + {\varphi _b}\frac{{{B_t}}}{{{P_t}}} $ | (21) |
上式右边为政府支出,其包含了偿还上期债券、政府消费性支出Gtc和政府生产性投资GtI。与Wesselbaum (2014)类似,政府消费性支出满足如下规则:
| $ \frac{{G_t^c}}{{{G^c}}} = {(\frac{{{Y_t}}}{Y})^{ - {\gamma _c}}}{(\frac{{{B_t}/{P_t}}}{{B/P}})^{ - {\lambda _c}}}{\rm{exp}}(\varepsilon _t^c) $ | (22) |
其中:Gc为政府消费性支出的稳态值;B/P为政府债券的稳态值;γc和λc为政府消费性支出对于产出和政府债券的反应系数;εtc为政府消费支出的外生成分,且服从平稳的AR (1) 过程。政府生产性支出形成的生产性资本Gtk为上期未折旧的资本与政府本期的生产性支出之和,即:
| $ G_t^k = (1 - {\delta _k})G_{t - 1}^k + G_t^I $ | (23) |
与消费性支出类似,生产性支出满足如下规则:
| $ G_t^I{G^I} = {(\frac{{{Y_t}}}{Y})^{ - {\gamma _k}}}{(\frac{{{B_t}/{P_t}}}{{B/P}})^{ - {\lambda _k}}}{\rm{exp}}(\varepsilon _t^I) $ | (24) |
其中:GI为政府生产性支出的稳态值;γk和λk分别为生产性支出对于产出和政府债券的反应系数;εtI为政府生产性支出冲击且服从平稳的AR (1) 过程。最后,定义政府支出Gt=Gtc+GtI为政府消费性支出与生产性支出之和。因此,模型经济的均衡条件为:
| $ {Y_t} = {C_t} + F_t^mH_t^m + F_t^sH_t^s + {I_t} + {G_t} $ | (25) |
至此,包含异质性部门与政府支出不同构成成分的多部门NK-DSGE模型介绍完毕。
四、 模型的参数化本部分对包含异质性部门与政府支出不同构成成分的多部门NK-DSGE模型中的参数进行校准和贝叶斯估计。
(一) 部分参数的校准家庭的贴现因子β,与已有的研究类似,我们采用2002年第1季度至2014年第4季度的物价数据进行估算,估算的结果表明这一参数的取值约为0.98。稳态时的就业率N,采用2002年至2013年的就业人口与适龄劳动人口比值的平均值表示,估算的结果表明这一参数的取值约为0.8。制造业部门的就业与总就业的比值n1=Nm/N,依据2002年至2013年制造业就业数量与总就业数量比值的平均值表示,估算的结果表明其取值约为17%;政府生产性支出与消费性支出与产出的比值sGI=GI/Y和sGC=Gc/Y的取值,依据本文经验研究中的样本进行估算,估算的结果表明这两个参数的取值分别为23.16%和17.8%;物质资本折旧率δk,依据He et al.(2007)将其取值为0.04。失业救济Wu,我们采用Ravenna and Walsh (2011)的取值,将其设定为0.54。家庭的议价能力参数ϑ,采用Gertler and Trigari (2009)的设定,将其取值为0.5。具体的参数校准的结果见表 1。
| 表 1 参数的校准 |
包含异质性部门与政府支出不同构成成分的多部门NK-DSGE模型中的其他参数,本文对其进行贝叶斯估计。本文分别选取如下7组观测值序列:产出、消费、制造业部门产出、名义利率、通胀、政府生产性支出以及政府消费性支出。产出采用剔除净出口之后的GDP数据;消费采用社会消费总额数据;制造业部门产出采用国家统计部门公布的由农副产品加工业等31个部门销售收入的加总数据;名义利率采用已有经验研究中使用的同业拆借利率数据;通胀采用经环比方法处理之后的CPI数据;政府生产性支出与政府消费性支出采用相应的政府支出数据。除通胀和名义利率数据外,其余数据在经CPI调整为实际值之后取自然对数。所有数据均来源于中经网数据库,样本时期为2002Q1至2013Q 4。由于季度数据可能具有季节性趋势,因而我们首先使用X12方法对观测值序列进行季节调整,并使用CF滤波技术从各观测值序列中得到各变量的周期成分。
(三) 参数的贝叶斯估计表 2给出了各参数贝叶斯估计的后验估计值、90%置信域以及对应的标准误。①劳动供给弹性的倒数η的贝叶斯估计值为6.2077,这一估计值与已有的研究如Zhang (2009)等关于这一参数的取值较为接近,后者将这一参数取值设定为6.16;离职率δ的贝叶斯估计值为0.1081,与Blanchard and Galí(2010)对于美国和欧洲劳动力市场离职率的估算结果相比,我国劳动力的流动性低于美国但高于欧洲;制造业部门资本的产出弹性系数αm以及对应的服务部门资本的产出弹性系数αs的估计值分别为0.6556和0.4328,这一估计值反映出我国制造业部门的资本密集程度高于服务部门;政府生产性支出形成的生产性资本的产出弹性系数αG的贝叶斯估计值为0.1105,这一估计值与饶晓辉和刘方 (2014)较为接近,后者对于这一参数的估计结果为0.1063;制造业部门提供的投入品的产出弹性系数v的贝叶斯估计值为0.6617,这一估计值表明中间产品生产过程中制造业部门占据相对较大的份额。
| 表 2 参数贝叶斯估计的结果 |
① 我们依据已有的相关研究对待估计参数的先验均值与分布进行了设定,基于篇幅考虑,本文省略了这一部分内容,感兴趣的读者可以向作者本人索取。
制造业部门与服务部门的雇佣成本对于找到工作的概率的反应系数γm和γs的估计值分别为0.6364和0.4303,这一估计值表明制造业部门雇佣成本对于劳动力市场状况具有更强的敏感性。相对于服务部门而言,制造业部门对工人技能、技术以及教育培训经历等方面的要求相对较高以及技术工人的稀缺,因而具有相对更高的雇佣成本。名义价格刚性系数θp的估计值为0.5999,这一估计值与国内的相关研究所得到的取值较为接近。不同中间产品的替代弹性系数ε的估计值为5.9698,国内的相关研究如王君斌和王文甫 (2010)等将其取值为6,显然这一取值在本文贝叶斯估计的90%置信域内。
名义利率对于产出的反应系数ry及其对于通胀的反应系数rp的估计值分别为0.1418和1.6004。显然,这两个参数的取值均大于先验均值。这意味着,相对于标准的泰勒规则而言,我国货币政策当局对于产出的变化或经济增长更加敏感。政府消费性支出对于产出与政府债券的反应系数γc和λc的估计值分别为0.1443和0.3107,二者均大于先验均值;政府生产性支出对于产出与政府债券的反应系数γk和λk的估计值分别为0.1906和0.6462,二者与先验均值均存在一定的差异。
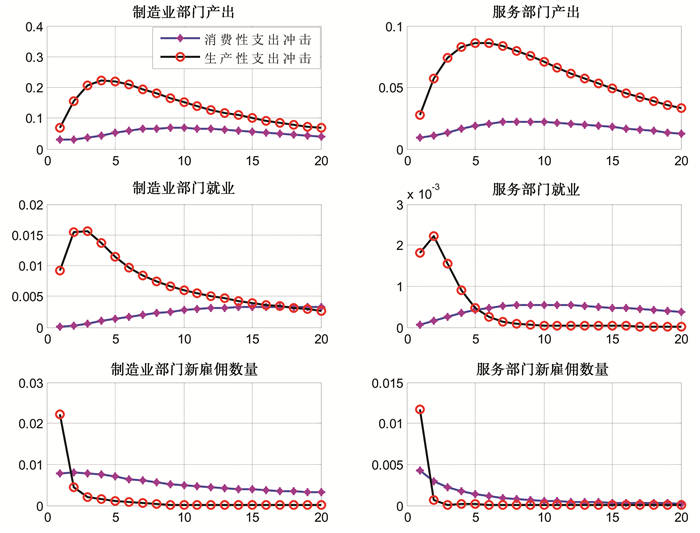
五、 模型动态分析 (一) 政府支出不同构成成分对于不同部门的冲击效应出于本文的研究目的考虑,这里我们仅给出政府生产性支出冲击与政府消费性支出冲击的贝叶斯脉冲响应函数。我们首先考察不同的政府支出冲击对于制造业部门与服务部门的部门冲击效应,具体的,图 4给出了政府生产性支出冲击与消费性支出冲击下两类部门产出、就业以及新雇佣的劳动力数量等变量的动态变化路径。
|
图 4 政府生产性支出冲击与消费性支出冲击对于不同部门的冲击效应 |
显然,扩张性政府生产性支出冲击与消费性支出冲击增加了社会总需求,总需求的增加推动了制造业部门与服务部门生产规模的扩张,进而使得两部门增加劳动力的雇佣。因而,图 4显示出政府生产性支出与消费性支出冲击下两类部门新雇佣劳动力数量均表现出上升的趋势。依据定义可知,新雇佣的数量的增加推动了两类部门就业的增加;生产规模的扩张和就业的增加进一步推动了两类部门产出的增加。因而在两类政府支出冲击下,两类部门的产出均在冲击发生之后呈现出上升的趋势,之后则随着冲击的衰减而逐渐向稳态收敛。因此,政府支出不同构成成分的部门效应较好的反映了本文基于VAR模型所得到的经验性事实。
政府生产性支出冲击与消费性支出冲击下,尽管制造业部门与服务部门的主要宏观经济变量均表现出相同的动态变化趋势,但是相对于政府消费性支出冲击,政府生产性支出冲击对于两类部门各个变量均具有较大的冲击效应。以两类部门产出为例,在积极的政府生产性支出冲击发生的4个时期之后,制造业部门产出达到最大值 (即0.23个单位);而在积极的政府消费性支出冲击发生之后的第7个时期,制造业部门产出才达到最大值 (即0.08个单位)。类似的,在积极的生产性支出冲击下,服务部门的产出在冲击发生之后的第5个时期达到冲击效应的峰值即0.8个单位;而在积极的消费性支出冲击下,服务部门的产出在冲击发生之后的第8个时期才达到冲击效应的峰值即0.02个单位。
另外,图 4还表明,在相同的外生冲击下,制造业部门与服务部门产出、就业、新雇佣的劳动力数量等宏观经济变量的动态反应轨迹也呈现显著的差异,换言之,政府支出冲击的效应具有部门依存性特征,这一发现与陈利锋 (2016)是一致的。以两类部门产出为例,图 4中,在积极的生产性支出冲击下,两类部门产出对于冲击的反应程度存在显著差异。具体表现为,制造业部门产出对于生产性支出冲击反应的峰值为0.23个单位,而服务部门产出反应的峰值为0.8个单位。当然,这一结论与本文基于VAR模型所得到的经验性事实是一致的。由于两类部门的产出、就业、新雇佣的劳动力数量等变量对于同一外生冲击具有不同的动态反应,因而基于建模的角度,考虑不同部门差异的NK-DSGE模型可能更为合理。
(二) 政府支出不同构成成分对于整体经济的冲击效应我们进一步分析政府生产性支出冲击与消费性支出冲击对于整体经济的影响。与政府支出冲击的部门效应类似,图 5显示出,扩张性政府生产性支出冲击与消费性支出冲击均推动总需求的增加,总需求的增加使得两类部门生产企业扩大生产规模。生产规模的扩张增加了两类部门生产企业对于劳动力的需求,进而推动了整体经济中新雇佣的劳动力的数量以及就业的增加,对应的,也引起了失业与待业劳动力数量的下降。依据找到工作的概率的定义可知,新雇佣数量的增加和待业劳动力数量的下降将引起整体找到工作的概率的上升。就业的增加与生产规模的扩张最终扩大了经济中的总供给能力,进而推动了总产出的增加。显然,政府支出不同构成成分的贝叶斯脉冲响应函数较好的拟合了本文第二部分基于VAR模型所得到的经验性事实。换言之,本文所建立的包含政府支出不同构成成分以及部门异质性的多部门NK-DSGE模型较好的拟合了我国的现实数据。

|
图 5 政府生产性支出冲击与消费性支出冲击对于整体经济的冲击效应 |
图 5还表明,政府生产性支出冲击与消费性支出冲击下,总产出的动态反应表现出完整的“驼峰状”特征,这与已有的研究所得到的结论是一致的。另外,就冲击的效应而言,相对于政府消费性支出,政府生产性支出冲击对于产出、就业、新雇佣的劳动力数量、找到工作的概率、失业以及待业的劳动力数量等均具有相对更大的冲击效应。这一发现与政府支出冲击的部门效应是相同的。当然,这一发现也与已有的研究如饶晓辉和刘方 (2014)等是一致的,后者在一个忽略部门异质性的NK-DSGE模型中得到了类似的结论。
(三) 经济周期特征与已有的关于经济周期的相关研究类似,我们通过对模型经济的周期性特征进行分析,并且将其与实际经济的周期性特征进行匹配,进而可以发现模型经济对于现实经济的拟合程度。与Galí et al.(2012)类似,我们以模型变量的AR (1) 系数 (即ρx) 和标准差 (即σx) 分别作为其持续性 (Duration) 特征与的波动性特征的度量指标;以模型变量与实际数据的相关系数ρxy反映模型经济中的变量与实际经济变量在数据上的匹配程度;而以模型变量的波动性与实际变量的波动性之比 (即σx/y) 作为反映模型经济中的变量在波动性上与实际经济变量的匹配程度。具体的结果在表 3中。
| 表 3 周期性特征 |
表 3第1列给出了制造业部门产出、服务部门产出、产出、就业、消费、政府消费性支出、政府生产性支出以及投资等变量模型拟合的数据呈现出的持续性特征。在所有的变量中,投资表现出最强的持续性特征,这可能源于我国长期依靠投资拉动经济增长的做法。两类部门产出以及总产出均表现出一定的持续性,模型经济拟合的数据表明,制造业部门与服务部门产出的持续性分别为0.65和0.71,而总产出的持续性为0.64。与已有的研究如吕光明 (2009)等相比,本文模型拟合的产出持续性相对较小。原因在于本文选取的样本空间为2002年第1季度至2013年第4季度,在这一期间,金融危机对我国经济的冲击以及金融危机之后我国经济步入“新常态”,经济增长的速度相对放缓,这些因素均在一定程度上对我国产出的持续性产生了影响。
表 3的第2列给出了各个变量模型拟合数据的波动性特征。显然,模型拟合数据中,投资数据表现出最大的波动性,总产出则次之。这一发现与已有的研究如吕朝凤等 (2013)是一致的,后者在一个包含政府支出的实际经济周期模型中也发现了同样的事实。另外,制造业部门产出的波动大于服务部门产出的波动,原因在于我国制造业具有较大的对外依存度,金融危机期间以及欧洲债务危机引起国外需求的萎缩,进而通过贸易渠道导致我国制造业部门产出的波动,因而制造业部门产出比服务部门产出呈现出更大的波动性特征。
表 3第3列给出了各个变量模型拟合数据与现实数据之间的相关系分别为0.80、0.89、0.87、0.85、0.91、0.88、0.81和0.88。这表明,模型经济实现了对现实数据相对较好的拟合。表 3第4列还给出了不同变量模型拟合数据与实际数据的波动性之比,从中可以看出:(1) 与现实数据相比,两类部门产出、总产出、就业、消费、政府消费性支出的模型拟合数据均表现出更大的波动性;(2) 相对于现实数据而言,政府生产性支出与投资等变量的模型拟合数据表现出较小的波动性;(3) 整体而言,各个变量的模型拟合数据所表现出的波动性与现实数据的波动性均较为接近。
(四) 贝叶斯冲击分解为了得到不同外生冲击在我国经济波动过程中的作用,我们采用贝叶斯冲击分解方法对两类部门产出、总产出、就业、消费以及投资等变量进行贝叶斯冲击分解,进而得到不同外生冲击在推动这些变量波动过程中的推动力量的大小。
表 4第1列给出了制造业部门产出波动的贝叶斯冲击分解的结果。显然,货币政策冲击可以解释17.4%的制造业部门产出波动,进而构成了推动制造业部门产出波动最为重要的力量;生产性政府支出可以解释16.26%的制造业部门产出波动,其构成了推动制造业部门产出波动第二重要的因素;与之对应的,消费性政府支出冲击仅可以解释制造业部门产出波动的7.66%。制造业部门技术冲击与投资冲击分别可以解释制造业部门产出波动的15.47%和14.17%。
| 表 4 贝叶斯冲击分解 |
表 4第2列指出,与制造业部门类似,在所有外生冲击中,货币政策对于服务部门产出波动具有最强的推动作用,其可以解释服务部门产出波动的19.07%;投资冲击、生产性政府支出冲击以及服务部门技术冲击分别可以解释服务部门产出波动的13.82%、13.24%和12.29%,而消费性政府支出冲击可以解释服务部门产出波动的6.87%。与制造业部门产出波动情况不同,劳动力供给冲击可以解释4.88%的服务部门产出波动,而这一冲击对于制造业部门产出波动的推动力量相对较小,其仅仅可以解释制造业部门产出波动的1.30%。
表 4第3列给出了总产出波动贝叶斯冲击分解的结果。从中可以看出:(1) 货币政策冲击是推动我国总产出波动最为重要的力量,这一结果与饶晓辉和刘方 (2014)是一致的,后者同样发现货币政策冲击在推动我国产出波动过程中具有最重要的作用;(2) 投资冲击以及技术冲击分别可以解释总产出波动的13.82%和13.11%。这一结果与已有的研究如Justiano et al.(2010)不同,后者发现投资冲击是推动美国经济波动最为重要的因素,并且其对于产出波动的效应远大于技术冲击;(3) 政府生产性支出冲击与消费性政府支出冲击分别可以解释总产出波动的15.93%和11.36%,即相对于政府消费性支出而言,政府生产性支出对于产出波动具有更大的推动作用。
表 4第4至6列分别给出了就业、消费与投资的贝叶斯冲击分解的结果。同样可以发现:(1) 货币政策在推动这些变量波动过程中具有最为重要的作用;(2) 相对于消费性政府支出而言,生产性政府支出在推动这些变量波动过程中具有更为重要的作用;(3) 投资冲击在推动这些变量波动过程中均具有重要的作用,但其并不是最为重要的因素。
基于贝叶斯冲击分解的结果可以发现:(1) 在本文的考察期内,货币政策冲击是推动我国经济波动最为重要的力量;(2) 尽管国外已有的研究发现投资冲击是推动宏观经济波动最为重要的力量,但是本文贝叶斯冲击分解的结果却发现,投资冲击并不是推动我国经济波动最为重要的因素;(3) 相对于消费性政府支出冲击而言,生产性政府支出冲击对于我国宏观经济波动具有更大的推动作用。
(五) 福利分析与大多数已有的国内外相关研究如Ranenna and Walsh (2012)、Galí(2013)以及陈利锋 (2015b)等类似,本文采用Benigno and Woodford (2012)改进的Linear-Quadratic (即LQ) 方法,可以得到如下社会福利损失函数:①
① Galí(2015)给出了社会福利损失函数详细的证明,感兴趣的读者可以参考这一著作。
| $ W = - \frac{1}{2}{E_0}\sum\nolimits_{t = 0}^\infty {{\beta ^t}} [(\frac{\varepsilon }{{{\lambda _p}}}){({{\hat \pi }_t})^2} + (1 + \frac{{v + \eta }}{{1 - v}})({{\hat y}_t})2] $ | (26) |
其中:
|
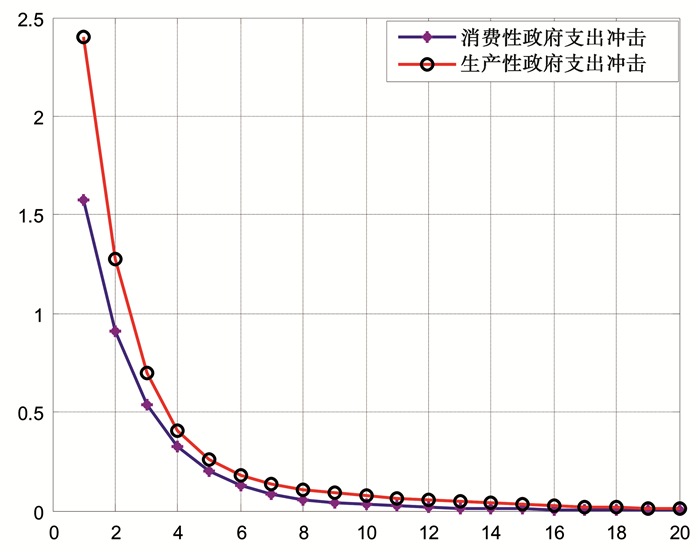
图 6 政府支出冲击与社会福利 |
图 6给出了生产性政府支出冲击与消费性政府支出冲击发生之后社会福利损失随时间变化的轨迹。显然,生产性政府支出冲击所引起的社会福利损失大于消费性政府支出冲击。不过,图 6还表明,随着时间的推移,生产性政府支出冲击与消费性政府支出冲击所引起的社会福利损失之间的差距逐渐缩小并收敛。
基于图 6可以发现,整体而言,政府生产性支出冲击所引起的社会福利损失大于消费性政府支出冲击。那么为什么不同类型政府支出所引起的社会福利损失存在差异呢?原因在于不同类型政府支出对于宏观经济具有不同的冲击效应。基于式 (26) 可知,如果外生冲击引起产出和通胀更大的波动,那么政策制定者稳定产出和通胀所付出的努力 (也即稳定经济的代价) 也越大,相应的社会福利损失也越大。本文贝叶斯冲击分解的结果表明,政府生产性支出对于产出和通胀的波动具有相对更大的作用,因而其导致了更大的社会福利损失。
(六) 政策含义由于积极的生产性政府支出冲击以及消费性政府支出冲击对于两类部门产出和就业、总产出等变量均具有显著的冲击效应,因而当经济下行时政府可以通过扩张性政府支出政策以缓解乃至扭转经济下行的趋势,进而达到稳定产出的目的。类似的,当劳动力市场遭遇逆向外生冲击进而引起就业下降和失业增加时,财政政策当局也可以采用扩张性政府支出的方法实现劳动力市场的稳定。基于本文贝叶斯脉冲响应函数分析的结论,相对于增加消费性政府支出而言,增加生产性政府支出可能具有更大的政策冲击效应。因此,在经济下行时期,如果使用扩张性政府生产支出政策,其对于劳动力市场乃至宏观经济均具有较强的政策效果。
不过,基于贝叶斯冲击分解的结果可以发现,相对于消费性政府支出,生产性政府支出冲击在各宏观经济变量的波动过程中具有更为重要的作用。这一结论意味着生产性政府支出的增加可能会引起产出等变量更大的波动。由于社会福利损失则来源于宏观经济变量的波动,因此,相对于增加消费性政府支出而言,生产性政府支出的增加则意味着相对较大的社会福利损失。已有的相关研究表明,我国政府偏好生产性政府支出。显然,依据本文的研究可知,相对于消费性政府支出冲击,生产性政府支出的增加无论是对于部门经济变量还是整体经济变量均具有更大的积极效应,然而也可能意味着宏观经济波动以及更大的社会福利损失。因而,依据宏观经济形势,积极调整政府支出的结构,在积极利用政府支出不同构成成分的积极效应的同时,也要注意其社会福利效应。
六、 结论基于一个包含不同部门与政府支出不同构成成分的NK-DSGE模型,我们对政府支出不同构成成分对于不同部门以及整体宏观经济的冲击效应进行了考察。贝叶斯脉冲响应函数的结论发现:(1) 政府支出的不同构成成分对于同一宏观经济变量具有不同的冲击效应,并且一般而言,生产性政府支出相对于消费性政府支出而言具有更大的冲击效应;(2) 制造业部门与服务部门的变量对于相同的外生冲击具有不同的动态反应,这意味着考虑不同部门之间差异的NK-DSGE模型可能更为合理。在此基础上,我们采用矩匹配的方法对模型拟合数据与现实数据进行匹配以考察模型对于现实数据的拟合程度。研究的结果表明,本文的模型相对较好的拟合了现实数据。贝叶斯冲击分解的结果指出:(1) 在本文考察的所有外生冲击中,货币政策冲击对于我国宏观经济波动具有最为重要的推动作用;(2) 对比消费性政府支出冲击而言,生产性政府支出冲击对于我国宏观经济各个变量的波动均具有更大的推动作用。
本文尝试将政府支出不同构成成分引入包含不同部门的多部门经济NK-DSGE模型中,并考察政府支出不同构成成分对于我国经济 (包括整体宏观经济与不同部门经济) 波动的影响。作为一种尝试,本文仍存在一些可以扩展的方向。第一,更多部门的引入。本文基于便利性考虑,仅将现实经济划分为制造业部门与服务部门,这一设定显然无法有效的刻画现实经济不同部门之间的差异。因此,一个可能拓展的方向是在本文的模型中引入更多的部门,并分析政府支出不同构成成分对于我国整体经济波动与不同部门经济波动的影响。①第二,本文分析了政府支出不同构成成分对于我国经济波动的影响,但并未分析最优政府支出的构成。在政策实践中,政府支出政策的目标包含了熨平宏观经济波动。因此,本文另一个可行的拓展是分析旨在熨平宏观经济波动的最优政府支出政策。
① 通过引入更多的部门可以更为完整的反应不同部门之间的差异以及联系,进而可以更为精确的分析政府支出的部门效应。关于更多部门的引入可以参考Foerster et al.(2011)所使用的结构动态因子模型以及陈利锋 (2014)使用的包含结构因子的NK-DSGE模型。
| [] | Albertini, J., Poirier, A., Roulleau-Pasdeloup, J., 2014, "The Composition of Government Spending and the Multiplier at the Zero Lower Bound, " Humboldt-Universität zu Berlin SFB Discussion Paper, No. 2014-017. |
| [] | Bénétrix, A. and Lane, P. , 2010, "Fiscal Shocks and the Sectoral Composition of Output". Open Economies Review, 21(3), 335–350. DOI:10.1007/s11079-009-9161-5 |
| [] | Benigno, P. and Woodford, M. , 2012, "Linear-Quadratic Approximation of Optimal Policy Problem". Journal of Economic Theory, 147(1), 1–42. DOI:10.1016/j.jet.2011.10.012 |
| [] | Benjamin, B. , Alexandra, P. and Johannes, P. , 2013, "Fiscal News and Macroeconomic Volatility". Journal of Economic Dynamics and Control, 37(12), 2582–2601. DOI:10.1016/j.jedc.2013.06.011 |
| [] | Blanchard, O. and Galí, J. , 2010, "Labor Markets and Monetary Policy: A New Keynesian Model with Unemployment". American Economic Journal: Macroeconomics, 2(2), 1–30. |
| [] | Bouakez, H. , Chihi, F. and Normandin, M. , 2014, "Measuring the Effects of Fiscal Policy". Journal of Economic Dynamics and Control, 47(c), 123–151. |
| [] | Bouakez, H., Guillard, M., Roulleau-Pasdeloup, J., 2014, "Public Investment, Time to Build, and the Zero Lower Bound, " CIRPEE Working Paper, No. 14-02. |
| [] | Bouakez, H., Larocque, D., Normandin, M., 2013, "Seperating the Wheat from the Chaff: A Disaggregate Analysis of the Effects of Public Spending in the U.S., " CIRPEE Working Paper, Mimeo. |
| [] | Burnside, C. , Eichenbaum, M. and Fisher, J. , 2004, "Fiscal Shocks and Their Consequences". Journal of Economic Theory, 115(1), 89–117. DOI:10.1016/S0022-0531(03)00252-7 |
| [] | Céspedes, L. F., Galí, J., 2012, "Fiscal Policy and Macroeconomic Performance: An Overview, " In Céspedes, L. F., Galí, J., editor, Fiscal Policy and Macroeconomic Performance: Central Bank of Chile Press, pp. 293-332. |
| [] | Christiano, L. , Eichenbaum, M. and Rebelo, S. , 2011, "When is the Government Spending Multiplies Large?". Journal of Political Economy, 119(1), 78–121. DOI:10.1086/659312 |
| [] | Eggertsson, G. B. 2011, "What Fiscal Policy is Effective at Zero Interest Rate?". NBER Macroeconomics Annual 2010, 25, 59–112. |
| [] | Foerster, A. T. , Sarte, P. D. and Watson, M. W. , 2011, "Sectoral versus". Aggregate Shocks: A Structural Factor Analysis of Industrial Production. Journal of Political Economy, 119(1), 1–38. |
| [] | Furlanetto, F. and Seneca, M. , 2014, "Investment Shocks and Consumption". European Economic Review, 66(c), 111–126. |
| [] | Galí, J., 2011, "Monetary Policy and Unemployment, "In Friedman, B., Woodford, M., editor, Handbook of Monetary Economics, 3(A), pp. 487-546. |
| [] | Galí, J. 2013, "Notes for a New Guide to Keynes (I): Wages, Aggregate Demand, and Employment". Journal of European Economic Association, 11(5), 973–1003. DOI:10.1111/jeea.12032 |
| [] | Galí, J., 2015, "Monetary Policy, Inflation and Business Cycle: An Introduction to the New Keynesian Framework, " Princeton: Princeton University Press, 2nd Edition. |
| [] | Galí, J., 2016, "Insider-Outsider Labor Market, Hysteresis and Monetary Policy, "Universitat Pompeu Fabra, Department of Economics Working Papers, No. 1506. |
| [] | Galí, J. , López-Salido, J. D. and Valles, J. , 2007, "Understanding the Effects of Government Spending on Consumption". Journal of the European Economics Association, 5(1), 227–270. DOI:10.1162/JEEA.2007.5.1.227 |
| [] | Galí, J. , Smets, F. and Wouters, R. , 2012, "Slow Recovery: A Structural Interpretation". Journal of Money, Credit and Banking, 44(S2), 9–30. |
| [] | Gertler, M. and Trigari, A. , 2009, "Unemployment Fluctuations with Staggered Nash Wage Bargaining". Journal of Political Economy, 117(1), 38–86. DOI:10.1086/597302 |
| [] | Hara, N., Katayama, M., Kato, R., 2014, "Rising Skill Premium?: The Roles of Capital-Skill Complementarity and Sectoral Shifts in a Two-Sector Economy, " Bank of Japan Working Paper Series, No. 14-E-9. |
| [] | He, D. , Zhang, W. and Shek, J. , 2007, "How Efficient has been China's Investment? Empirical Evidence from National and Provincial Data". Pacific Economic Review, 12(5), 596–617. |
| [] | Iacoviello, M. , Schiantarelli, F. and Schuh, S. , 2011, "Input and Output Inventories in General Equilibrium". International Economic Review, 52(4), 1179–1214. DOI:10.1111/iere.2011.52.issue-4 |
| [] | Justiniano, A. , Primiceri, G. and Tambalotti, A. , 2010, "Investment Shocks and Business Cycles". Journal of Monetary Economics, 57(2), 132–145. DOI:10.1016/j.jmoneco.2009.12.008 |
| [] | Justiniano, A. , Primiceri, G. and Tambalotti, A. , 2011, "Investment Shocks and the Relative Price of Investment". Review of Economic Dynamics, 14(1), 101–121. |
| [] | Karras, G. 2012, "Trade Openness and the Effectiveness of Fiscal Policy: Some Empirical Evidence". International Review of Economics, 59(3), 303–313. DOI:10.1007/s12232-011-0126-9 |
| [] | Karras, G. 2015, "Fiscal Activism in European Regions: Evidence on Fiscal Rules before and after the Euro". Regional Science Inquiry, 0(1), 21–34. |
| [] | Mattini, F. and Rossi, L. , 2009, "Optimal Monetary Policy in Economies with Dual Labor Markets". Journal of Economics Dynamics and Control, 33(7), 1469–1489. DOI:10.1016/j.jedc.2009.01.008 |
| [] | Mattini, F. and Rossi, L. , 2012, "Monetary Policy and Automatic Stabilizers: The Role of Progressive Taxation". Journal of Money, Credit and Banking, 44(5), 825–862. DOI:10.1111/j.1538-4616.2012.00512.x |
| [] | McGrattan, E. and Ohanian, L. , 2010, "Does Neoclassical Theory Account for the Effects of Big Fiscal Shocks? Evidence from World War Ⅱ". International Economic Review, 51(2), 509–532. DOI:10.1111/(ISSN)1468-2354 |
| [] | Monacelli, T. and Perotti, R. , 2008, "Openness and the Sectoral Effects of Fiscal Policy". Journal of the European Economic Association, 6(2-3), 395–403. DOI:10.1162/JEEA.2008.6.2-3.395 |
| [] | Obstbaum, M., 2011, "The Role of Labour Markets in Fiscal Policy Transmission, "Bank of Finland Discussing Papers, No.16/2011. |
| [] | Pappa, E. 2009, "The Effects of Fiscal Shocks on Employment and Real Wage". International Economic Review, 50(1), 217–244. DOI:10.1111/iere.2009.50.issue-1 |
| [] | Ravenna, F. and Walsh, E. C. , 2011, "Welfare-Based Optimal Monetary Policy with Unemployment and Sticky Prices: A Linear-Quadratic Framework". American Economic Journal: Macroeconomics, 3(2), 130–162. DOI:10.1257/mac.3.2.130 |
| [] | Ravenna, F. and Walsh, E. C. , 2012, "Monetary Policy and Labor Market Frictions: A Tax Interpretation". Journal of Money, Credit and Banking, 59(2), 180–195. |
| [] | Ravenna, F., Walsh, E. C., 2014, "Slow Recoveries, Worker Heterogeneity, and the Zero Lower Bound, "UCSC Department of Economics Working Papers, No. 2014-10. |
| [] | Roulleau-Pasdeloup, J., 2013, "The Productive Government Spending Multiplier, in and out of the Zero Lower Bound, "CREST Working Paper, No. 2013-02. |
| [] | Tapp, S. 2011, "The Dynamics of Sectoral Labor Adjustment". Canadian Journal of Economics, 44(4), 1264–1296. DOI:10.1111/caje.2011.44.issue-4 |
| [] | Traum, N. and Yang, S. , 2011, "Monetary and Fiscal Policy Interactions in the Post-War U.S.". European Economic Review, 55(1), 140–164. DOI:10.1016/j.euroecorev.2010.11.009 |
| [] | Wesselbaum, D., 2014, "Sectoral Labor Market Effects of Fiscal Spending, "MPRA Working Paper, No. 58761. |
| [] | Zhang, W. 2009, "China's Monetary Policy: Quantity Versus Price Rules". Journal of Macroeconomics, 31(3), 473–484. DOI:10.1016/j.jmacro.2008.09.003 |
| [] | 陈利锋, 2014, 《部门冲击与整体冲击的宏观经济效应分析——以8大部门供给冲击对整体通货膨胀的影响为例》, 《西部论坛》, 第 6 期, 第 43–51 页。 |
| [] | 陈利锋, 2015, 《累进性工薪所得税、失业回滞与中国劳动力市场波动——基于新凯恩斯主义动态随机一般均衡的视角》, 《南京师大学报 (社会科学版)》, 第 2 期, 第 37–47 页。 |
| [] | 陈利锋, 2015, 《异质性雇佣成本、失业波动与货币政策——Evans规则在我国具有适用性吗?》, 《国际金融研究》, 第 5 期, 第 26–36 页。 |
| [] | 陈利锋, 2016, 《我国政府支出的部门效应与整体效应》, 《制度经济学研究》, 第 2 期, 第 22–39 页。 |
| [] | 迟诚、马万里, 2015, 《财政分权对城乡收入差距的影响机理与传导机制》, 《经济与管理研究》, 第 9 期, 第 19–27 页。 |
| [] | 胡永刚、郭新强, 2012, 《内生增长、政府生产性支出与中国居民消费》, 《经济研究》, 第 9 期, 第 57–71 页。 |
| [] | 刘吕吉、张凤, 2015, 《基于福利性财政支出的城乡收入差距研究》, 《首都经济贸易大学学报》, 第 6 期, 第 12–21 页。 |
| [] | 吕朝凤、黄梅波、陈燕鸿, 2013, 《政府支出、流动性冲击与中国实际经济周期》, 《金融研究》, 第 3 期, 第 30–43 页。 |
| [] | 吕光明, 2009, 《供求冲击与中国经济波动:基于SVAR模型的甄别分析》, 《统计研究》, 第 7 期, 第 20–27 页。 |
| [] | 饶晓辉、刘方, 2014, 《政府生产性支出与中国的实际经济波动》, 《经济研究》, 第 11 期, 第 17–30 页。 |
| [] | 王君斌、王文甫, 2010, 《非完全竞争市场、技术冲击与中国劳动力就业》, 《管理世界》, 第 1 期, 第 23–36 页。 |
| [] | 王文甫, 2015, 《中国政府支出宏观效应及其传导机制研究》. 北京: 经济科学出版社, 第 21-37 页. |
| [] | 谢平、罗雄, 2002, 《泰勒规则及其在中国货币政策中的检验》, 《经济研究》, 第 3 期, 第 3–12 页。 |
| [] | 易行健, 2013, 《民生性财政支出对我国居民消费的影响》, 《上海财经大学学报》, 第 2 期, 第 55–62 页。 |



