1998年以来,我国房地产业迅猛发展,对国民经济增长起到了重要的拉动作用(张清勇和年猛,2012;王鹤等,2014)。但与此同时,各地商品住宅价格不断攀升,呈现一定空间联动性(洪涛等,2007;陈浪南和王鹤,2012),并且这种联动关系随着一系列房价调控措施的实施而不断增强。伴随市场化改革的稳步推进,人口迁移、资本流动、企业迁址、跨区投资等更加频繁,在市场“无形之手”的作用下,各地房价联动关系变得广泛而普遍。根据黄飞雪等(2009)的研究,16个大中城市(包括4个直辖市和12个副省级城市) 之间房价格兰杰意义上的单向溢出关系达到125个,单个城市对其它城市房价的溢出关系数均值为7.81。张衔和林仁达(2015)的研究则发现,在35个大中城市中,有14个城市对其它城市房价格兰杰意义上的单向溢出关系数超过25个。这些结论表明多个城市之间房价的联动关系已经突破了单纯地理学意义上“近邻”效应,而呈现出多线程的复杂结构,即网络形态。在此背景下,各地房价调控进程及其政策效果将不仅取决于自身传导因素,还取决于其它地区与之的空间联动关系。鉴于此,本文主要回答以下三个问题:各地房价联动的网络结构特征如何?各地房价在这种联动网络中的地位和作用如何?这种联动网络结构受到哪些因素的影响?基于上述问题的回答,对提高房价调控政策的精准性、构建跨区域房价协同调控机制具有重要的理论意义和应用价值。
关于房价联动关系的形成机理,大部分学者依据“波纹效应”理论进行解释,他们认为房价的空间传导具有一定规律性,某些地区房价率先变动后会带动周围地区房价发生变化,家庭迁移、财富转移、空间套利等空间联系因素,以及住房交易成本和搜寻成本、区域房价影响因素的领先滞后关系、空间异系数性等市场异质性因素是房价“波纹效应”产生的主要原因(Meen,1999;Wood,2003;Cook,2003;Oikarinen,2006;徐迎军和李东,2008;王松涛等,2008;张衔和林仁达,2015)。也有学者认为房价“波纹效应”与地理区域的范围界定有关,房价只在连续地理区域之间传导的模式比较明显(Drake,1995; Pollakowski and Ray, 1997;王松涛等,2008)。关于房价联动关系及其影响因素,已有文献运用相关性检验、协整分析、格兰杰因果检验、脉冲响应、误差修正模型、广义空间动态面板数据模型等计量方法证实了地区间房价联动关系的存在(MacDonald and Taylor, 1993;Giussani and Hadjumatheou, 1991;Holmes,2007;Luo et al., 2007;洪涛等,2007;王松涛等,2008;苑德宇和宋小宁,2008;陈浪南和王鹤,2012;王鹤,2012);少数文献运用共同因子模型对区域房价联动的影响因素进行了实证检验,结论表明区域房价联动主要受经济环境和调控政策的影响(王鹤等,2014)。总体上看,已有研究对我国房价联动关系给予了一定解释和实证检验,为进一步明确房价波动的关联关系及其网络结构奠定了基础,但仍存在一定局限,具体表现为:第一,已有研究主要考虑了地理上的“近邻”效应或“区域”效应,难以从整体上把握房价联动的全局特征。第二,已有研究主要基于“属性数据”展开,忽视了反映结构特征的“关系数据”的重要作用,难以刻画城市房价联动的整体网络结构特征。第三“波纹效应”对房价联动关系给出了合理解释,但已有实证研究主要使用传统计量方法分析地区房价的影响因素,难以揭示地区房价联动“关系”的影响因素。
鉴于已有研究局限,本文基于2011年1月至2015年2月中国69个大中城市①50个月的商品住宅销售月度价格指数,借助社会网络分析方法(Social Network Analysis, SNA) 揭示城市房价联动的网络结构特征及其影响因素。文章结构如下:首先,构建城市房价VAR模型并进行Granger因果关系检验,以确定城市房价的空间联动关系。其次,借助社会网络分析方法对城市房价联动的网络结构特征进行考察。通过测度网络密度、网络关联度、网络等级度、网络效率等指标刻画城市房价联动的整体网络结构特征;通过点度中心度、中介中心度和接近中心度等中心性分析考察各城市在房价联动网络中的地位和作用;通过块模型分析揭示城市房价联动网络的空间聚类方式。再次,使用QAP相关分析及回归分析方法实证检验城市房价联动网络结构的影响因素。最后,针对上述分析从全局视角得出相应结论及政策启示。
① 大中城市是房价调控的主要载体,70个大中城市中,大理是唯一的县级市,其它69城市都是地级市,因此,本文基于除大理之外的其它69个大中城市数据展开研究。
二、 方法与数据社会网络分析是基于“关系数据”的一种跨学科研究方法。该方法以“关系”作为基本分析单位,采用图论、代数模型等技术探究关系模式及其对结构中成员或整体的影响,在管理学、经济学、社会学等领域已得到广泛应用,逐渐成为一种新的研究范式(徐振宇,2013)。
(一) 城市房价联动关系确定及网络构建方法“关系”的确定是网络分析的关键(Scott,2013)。本文聚焦于房价动态关联关系,作为内生变量的城市房价也要引入模型,那么OLS估计的经典假设将不再满足,参数估计和推断变得困难,而向量自回归模型(VAR) 能有效克服这一问题(高铁梅,2009);另外,格兰杰因果关系检验能够较好地衡量地区变量间在时间先后上的动态引导关系。基于以上考虑,本文选择VAR 格兰杰因果关系检验方法确定城市房价联动关系。城市房价是网络中的点,城市房价联动关系是网络中的线,通过VAR格兰杰因果关系检验能够确定两两城市间的“因”和“果”,从而得到一条有向连线,这些点和线共同组成城市房价的空间联动网络。
(二) 城市房价联动的网络结构特征分析方法1. 整体网络结构特征刻画。整体网络结构特征一般由网络密度(Density)、网络关联度(Connectedness)、网络等级度(Hierarchy)、网络效率(Efficiency) 来刻画。
网络密度是指网络中的实际连线数与最大可能连线数之比,反映城市房价联动网络的疏密程度,取值介于0~1之间。网络密度越大,意味着城市房价之间的关联就越紧密。假设网络中有N个节点,L代表节点间实际关联数量,那么网络密度D可以表示为:
| $D = L/\left[ {N \times \left( {N - 1} \right)} \right]$ | (1) |
网络关联度反映城市房价联动网络自身的稳健性和脆弱性,取值介于0~1之间。如果网络中很多线都与某一个城市相连,那么网络对该城市的依赖性就很高,如果排除该城市,网络就可能崩溃,此时网络关联度较低;如果多数节点之间均存在直接或间接连接路径,那么网络关联度就较高。假设网络中不可达点的对数为V,那么网络关联度C可表示为:
| $C = 1 - \left\{ {V/\left[ {N \times \left( {N - 1} \right)/2} \right]} \right\}$ | (2) |
网络等级度表示网络中城市间非对称可达程度,反映网络中各城市的等级结构,取值在0~1之间。网络等级度越高,等级结构就越森严,越多的城市处于从属和边缘地位。假设网络中对称可达点对数为K,max(K) 代表网络中最大可能的对称可达点对数,那么等级度H可表示为:
| $H = 1 - [K/{\rm{max}}\left( K \right)]$ | (3) |
网络效率反映城市房价联动网络中各城市间的连接效率,取值介于0~1之间。网络效率越低,意味着城市间存在越多的冗余连线,房价关联越紧密,网络就越稳定。假设网络中冗余连线个数为M,max(M) 代表网络中最大可能的冗余连线个数,那么网络效率E可表示为:
| $E = 1 - \left[ {M/{\rm{max}}\left( M \right)} \right]$ | (4) |
2. 各节点的网络结构特征刻画。各节点的网络结构特征一般由点度中心度(Degree Centrality)、接近中心度(Closeness Centrality) 和中介中心度(Betweenness Centrality) 来刻画。
点度中心度是根据连接数来衡量各城市在房价联动网络中所处中心程度。点度中心度越高,意味着该城市与其它城市间联系越多,也就表明该城市处于网络更加中心的地位。根据城市间联系方向,点度中心度分成点出度和点入度,点出度是指该城市指向其它城市的连线数,反映该城市对其它城市的辐射程度;点入度是指其它城市指向该城市的连线数,反映其它城市对该城市的影响程度。对于N个节点的有向网络,X节点的点出度为C1,点入度为C2,那么点度中心度可以表示为:
| ${C_{AD}} = ({C_1} + {C_2})/\left( {2N - 2} \right)$ | (5) |
接近中心度用来刻画某个城市在网络中“不受其它城市控制”的程度,可以用某个城市与其它城市的捷径“距离”(捷径中包含的线数) 之和的倒数值来表示。接近中心度越高,意味着该城市与其它城市的“距离”越短,通达性越好,联系越紧密,对其它城市的影响控制程度越强,该城市也就越居于网络中心的位置。假设dij代表节点i与j之间的捷径距离(即捷径中包含的线数),那么接近中心度可表示为:
| $C_{AP}^{ - 1} = \sum\limits_{j = 1}^N {{d_{ij}}} $ | (6) |
中介中心度反映某个城市对其它城市间房价联动关系的控制程度。中介中心度越高,意味着该城市越能控制其它城市间房价联动程度,该城市也就更加处于网络中心的位置。中介中心度可分成绝对中介中心度和相对中介中心度。假设网络中共N个节点,其中节点j和k之间存在gjk条捷径,j和k之间存在的经过第三个节点i的捷径数为gjk(i),节点i对j、k两点交往的控制能力用bjk(i) 表示,bjk(i)=gjk(i)/gjk, 那么中介中心度可表示为:
| ${C_{RB}} = 2\sum\limits_j^N {\sum\limits_k^N {{b_{jk}}\left( i \right)/({N^2} - 3N + 2),} } 其中,j \ne k \ne i,且j < k$ | (7) |
3. 块模型(Block Modeling) 分析法。块模型分析法基于“块”在网络中的角色展开,能够从板块个数、板块成员构成、板块关联关系等新的维度揭示和刻画城市房价联动网络的内部结构状态,是社会网络中空间聚类分析的常用方法。按照角色位置,本文将69个大中城市划分为四类板块:(1) 净溢出板块,该板块成员向其它板块成员的溢出关系明显多于接收关系,且该板块内部成员间溢出关系较少。(2) 经纪人板块,该板块成员既对其它板块溢出关系,也接收其它板块成员发出的关系,该板块成员与其它板块成员间联系较多。(3) 双向溢出板块,该板块成员向板块内部成员、其它板块成员均发出较多关系。(4) 净受益板块,该板块成员向其它板块成员的溢出关系明显小于接收关系,且该板块内部成员间溢出关系较多。
(三) QAP分析法本文研究变量均选取关系数据,解释变量之间可能具有高度相关性,从而引起多重共线性。如果使用传统计量方法,将导致参数估计量不准确、变量显著性检验失去意义,严重时参数经济意义将与现实不一致。而QAP(Quadratic Assignment Procedure) 是一种非参数估计方法,不需假定解释变量之间相互独立,能够有效避免多重共线性问题(李敬等,2014)。鉴于此,本文将选用QAP分析法就城市房价联动网络的影响因素进行相关分析和回归分析。QAP相关分析以矩阵数据置换为基础,通过比较方阵各元素的相似性给出矩阵相关系数并进行非参数相关性检验。首先,计算已知矩阵的实际相关系数;其次,对其中一个矩阵的行与相应的列进行随机置换,并将置换后的矩阵与另一矩阵计算相关系数,重复这种过程足够过次,可得相关系数分布,然后进一步计算大于或等于实际相关系数的比例;最后,根据相关系数分布判断实际相关系数落入拒绝域还是接受域,进而实现对相关系数的显著性检验。QAP回归分析通过研究一个矩阵对多个矩阵的回归关系,得出可决系数并进行显著性经验。首先,将被解释变量矩阵对应长向量与解释变量矩阵对应长向量进行常规的多元回归,可得实际参数估计值和可决系数;其次,将被解释变量矩阵的各行和对应的各列同时进行随机置换,并与解释变量矩阵重新回归,重复这种过程足够多次,保存所有的系数值和可决系数,可得相应的分布,在此基础上,能够实现对参数估计值和可决系数的显著性检验(刘军,2014)。
(四) 数据来源本文以中国69个大中城市作为网络节点,基于2011年1月至2015年2月的月度数据深入考察城市房价联动的网络结构特征及其影响因素。城市房价以新建商品住宅销售价格同比指数为代表,为剔除物价的影响,我们将房价以2010年为基期做了平减处理,数据来自《中国统计年鉴》①;各城市人口、人均GDP、工资收入、金融存贷款、产业结构、人均用地面积等数据根据《中国城市统计年鉴》整理计算得到;城市地理距离根据ArcGis计算得到。
① 环比月度数据,分子、分母可能涉及不同季节因素的影响,需要进行季节调整;而同比月度数据,分子、分母是相同的季节因素,所以本文未将同比月度数据进行季节调整。
三、 城市房价联动的网络结构特征 (一) 城市房价联动网络的构建本文使用69个大中城市新建商品住宅销售价格月度数据、基于VAR格兰杰因果关系检验法确定城市间房价关联关系,进而构建联动网络。VAR格兰杰因果关系检验对于滞后期数的选择较为敏感,因此本文依据LR、PRE、AIC、SC、HQ五种方法进行最优滞后期数的选择。通过VAR格兰杰因果关系检验,本文最终确定了城市间3023个有向关联关系,利用UCINET可视化工具Netdraw可绘制城市房价联动的网络结构图(如图 1),由图 1可以直观的发现中国城市房价联动呈现出显著的网络结构形态。
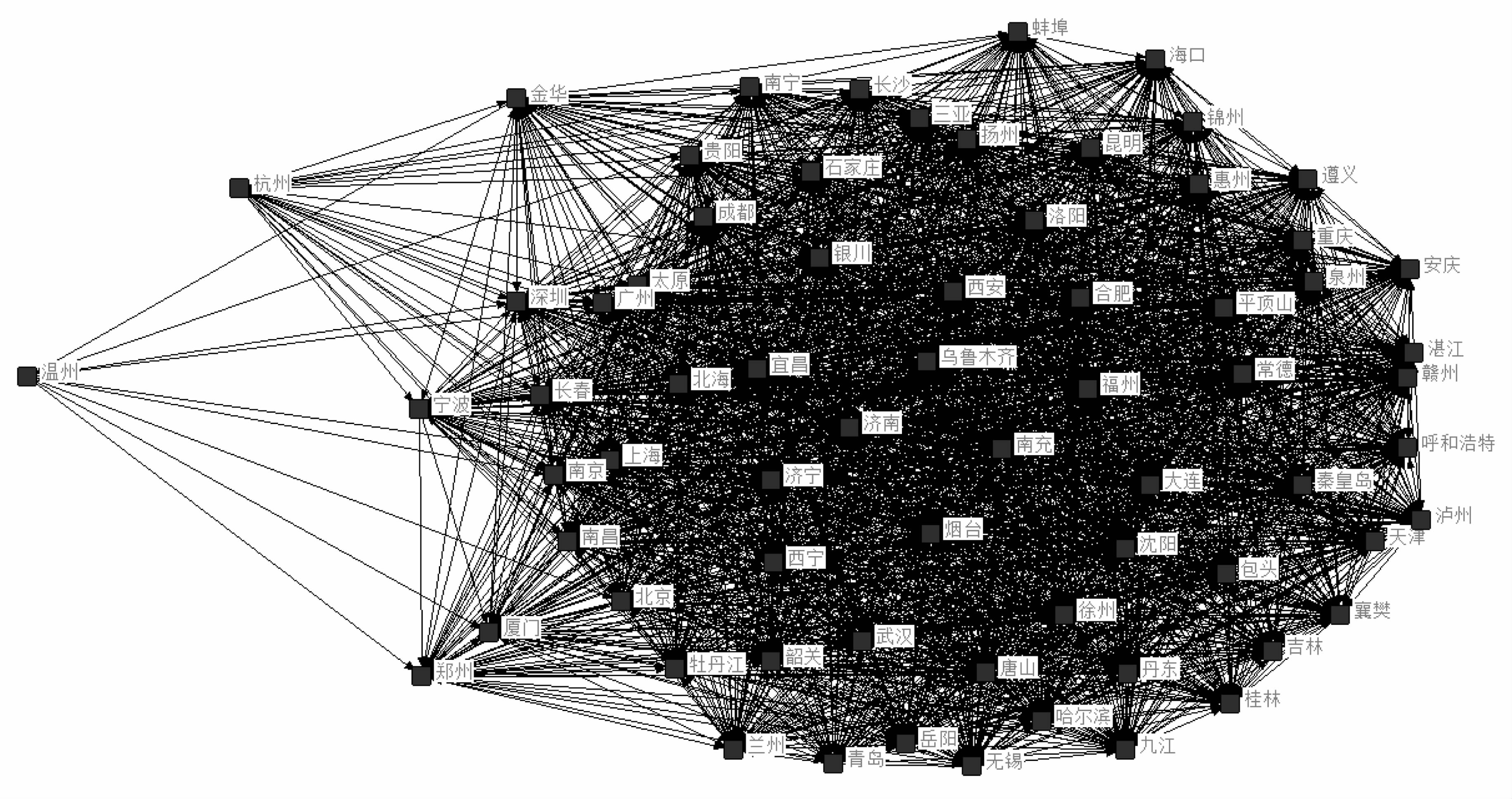
|
图 1 中国城市房价的联动网络 |
1. 整体网络结构特征分析
69个大中城市间房价联动关系数为3023,最大可能关联关系数为4692,网络密度为0.64,表明“全国城市房价一张网”的联动效应显著。网络关联度为1,表明城市房价整体联动性强,城市房价普遍存在溢出效应,网络通达性好,稳健性强,网络不会因为哪一个城市的缺失而出现崩溃的现象。网络等级度为0,表明房价联动网络中城市间等级结构并不森严,网络节点间对称可达程度较高,处于从属和边缘地位的城市较少,即使房地产市场发展水平差异较大的城市间也可能存在较强的关联效应和溢出效应。网络效率为0.10,说明房价联动网络中城市间存在较多的冗余连线,关联较为紧密,网络较为稳定。
2. 中心性分析
为了考察并揭示各城市在房价联动网络中的地位和作用,本部分选择点度中心度、接近中心度、中介中心度三个指标进行网络中心性分析,结果如表 1所示。
| 表 1 网络中心性分析 |
(1) 点度中心度。表 1测算结果显示,69个大中城市的点度中心度均值为91.41。其中,排名靠前的城市依次是上海、广州、济南、济宁、南昌、北海、银川,说明这些城市房价与其它城市间存在较多联动关系,在网络中处于中心的地位;排名靠后的城市依次是金华、郑州、杭州、温州,说明这些城市房价可能较多地取决于本地因素,而与其它城市关联性较弱。另外,点出度均值为43.81,排名靠前的城市依次是广州、北京、上海、南京、济南、武汉、深圳,说明这些城市房价具有较强溢出效应,在网络中起“引领”作用。点入度排名靠前的城市依次是长春、唐山、济宁、韶关、银川、哈尔滨和泉州,说明这些城市房价受到其它城市的较强影响,在网络中处于“跟随”地位。从点度中心度、点出度和点入度综合排名看,与其它城市联动性较强、且处于房价“引领”地位的城市主要位于东部地区。
(2) 接近中心度。表 1测算结果显示,69个大中城市的接近中心度均值为92.13。其中,上海、广州、济南、济宁、南昌、北海、银川的接近中心度均达到98.55,排名并列第一,说明这些城市与其它城市的捷径“距离”较短、通达性好、联系紧密,在信息资源、权力、声望及影响力方面较强,居于房价联动网络的中心位置。究其原因,这些城市大多位于东部地区,房地产市场相对完善,对于区域内生因素及政策调控因素的反应速度较快,在网络中扮演房价调整的中心行动者角色。排名靠后的城市依次是金华、郑州、杭州、温州,说明这些城市与网络中心点的“距离”较远,在房价联动网络中受控制于其它城市,扮演边缘行动者的角色。
(3) 中介中心度。表 1测算结果显示,69个大中城市的中介中心度均值为0.14。其中,排名靠前的城市依次是上海、广州、南京、长沙、深圳、北京,说明这些城市更加处于其它城市间关联捷径上,因此控制着其它城市房价联动关系。上海中介中心度最高,达到0.52,远高于其它城市,说明上海处于房价联动网络的核心位置。69个大中城市的中介中心度总量为9.88,而排名前6位的城市中介中心度之和占了总量的29%以上,这些城市主要位于房地产市场较为完善的东部地区,在房价联动网络中发挥着 “中介”作用。而排名靠后的城市分别是泸州、湛江、蚌埠、安庆、杭州、温州,它们中介中心度之和只占总量的2%以下,这些城市处于网络中较为“偏远”的位置,与其它城市的房价联动关系受制于排名靠前城市。
3. 块模型分析
本文按照最大分割深度2,收敛标准0.2,基于CONCOR(Convergent Correlations) 方法把69个大中城市分为四个板块。其中,第一板块包括9个城市,分别是北京、南京、温州、深圳、郑州、宁波、上海、广州、杭州。第二板块包括17个城市,分别是长沙、青岛、乌鲁木齐、厦门、武汉、兰州、重庆、沈阳、天津、南充、襄阳、成都、合肥、太原、济南、西安、宜昌。第三板块包括25个城市,分别是北海、锦州、徐州、常德、福州、南昌、烟台、赣州、呼和浩特、丹东、南宁、遵义、秦皇岛、洛阳、泉州、包头、石家庄、无锡、惠州、平顶山、昆明、吉林、湛江、大连、泸州。第四板块包括18个城市,分别是九江、唐山、济宁、扬州、桂林、哈尔滨、牡丹江、金华、海口、安庆、贵阳、岳阳、长春、三亚、韶关、西宁、银川、蚌埠。四个板块在东、中、西地区的分布情况如表 2所示。
| 表 2 板块分布情况 |
表 3测算了大中城市房价联动板块的溢出效应。板块内部关系数为949个,板块间关系数为2074个,板块间关联关系和溢出关系较为明显。(1) 第一板块,溢出关系总数为423个,接收关系总数为109个,板块内部关系数为35个;期望内部关系比例为12%,实际内部关系比例为8%,在四板块中均为最低,根据前文定义,该板块属于净溢出板块。该板块成员主要分布在东部和中部地区,在网络中扮演着房价“引导”角色。(2) 第二板块,溢出关系总数为922个,其中板块内部关系数为204个;接收关系总数为595个,其中接收其它板块关系数391个;期望内部关系比例为24%,实际内部关系比例为22%,因此该板块属于经纪人板块。该板块成员主要分布在东部和中部地区,在网络中扮演着“桥梁”角色。(3) 第三板块,溢出关系总数为1135个,其中向板块内其它成员溢出关系数为506个,向板块外溢出关系数为629个,另外接收关系总数为1286个;期望内部关系比例为35%,实际内部关系比例为45%,因此该板块属于双向溢出板块。该板块成员主要分布在东部和西部地区,在网络中扮演着内部、外部双向“引导”角色。(4) 第四板块,溢出关系总数为543个,接收关系总数为1033个,板块内部关系数为204个;期望内部关系比例为25%,实际内部关系比例为38%,因此该板块属于净受益板块。该板块成员多数在分布西部地区,在网络中处于较为被动的地位,扮演着“跟随”角色。以上结果表明我国东部地区房地产市场发展较为成熟,当人口、土地、住房投资、产业结构、购房政策等影响因素发生变化时,房价调整较为敏感,这种调整引导了本板块成员及其它板块成员的房价波动;西部地区房地产市场发展相对落后,分布在净受益板块的城市较多,该地区城市房价较大程度上受到其它地区城市的影响;中部地区房地产市场发展情况居中,在四大板块的分布较为平均,受益与溢出关联关系较为均衡,在房价联动网络中主要起桥梁作用。
| 表 3 城市房价联动板块的溢出效应 |
为进一步考察溢出关系在各板块的分布情况,接下来引入密度矩阵和像矩阵进行分析。用板块间城市房价实际溢出关系数除以可能的最大溢出关系数,可得各板块的网络密度矩阵。整体网络密度代表房价联动网络疏密的整体平均水平,如果板块网络密度大于整体网络密度,则表明房价溢出关系在该版块更加集中。整体网络密度为0.64,将大于0.64的板块网络密度赋值“1”、将小于0.64的板块网络密度赋值“0”,可得像矩阵。网络密度矩阵和像矩阵如表 4所示,图 2直观描述了四大板块之间的关联关系。其中第一板块溢出效应主要表现为对第二板块、第三板块、第四板块的溢出关系,而第一板块内部成员间的溢出效应并不明显。第二板块溢出效应主要表现为对第二板块内部、第三板块、第四板块的溢出关系。第三板块溢出效应主要表现为对第三板块内部、第四板块的溢出关系。第四板块溢出效应主要表现为第四板块内部成员间的溢出关系。像矩阵对角线上的元素只有第一板块对应为零,说明二、三、四板块内部成员间均具有较强的溢出关系,“俱乐部效应”显著。另外,还可以看出四大板块间的溢出关系具有明显的“梯度效应”。当宏观经济政策或微观经济变量发生调整时,在网络中扮演“引导”角色的北京、深圳、上海、广州等第一板块城市房价首先出现波动,然后向第二、三、四板块城市传导;第二板块城市房价波动后,继续向第三、四板块城市传导;第三板块城市房价波动后,又传向第四板块城市。换言之,作为城市房价联动发动机的第一板块不仅直接影响第二、三、四板块,还通过第二板块间接影响第三、四板块,通过第三板块间接影响第四板块,因此第二、三板块是维系城市房价联动关系的重要枢纽。
| 表 4 城市房价联动板块的密度矩阵与像矩阵 |
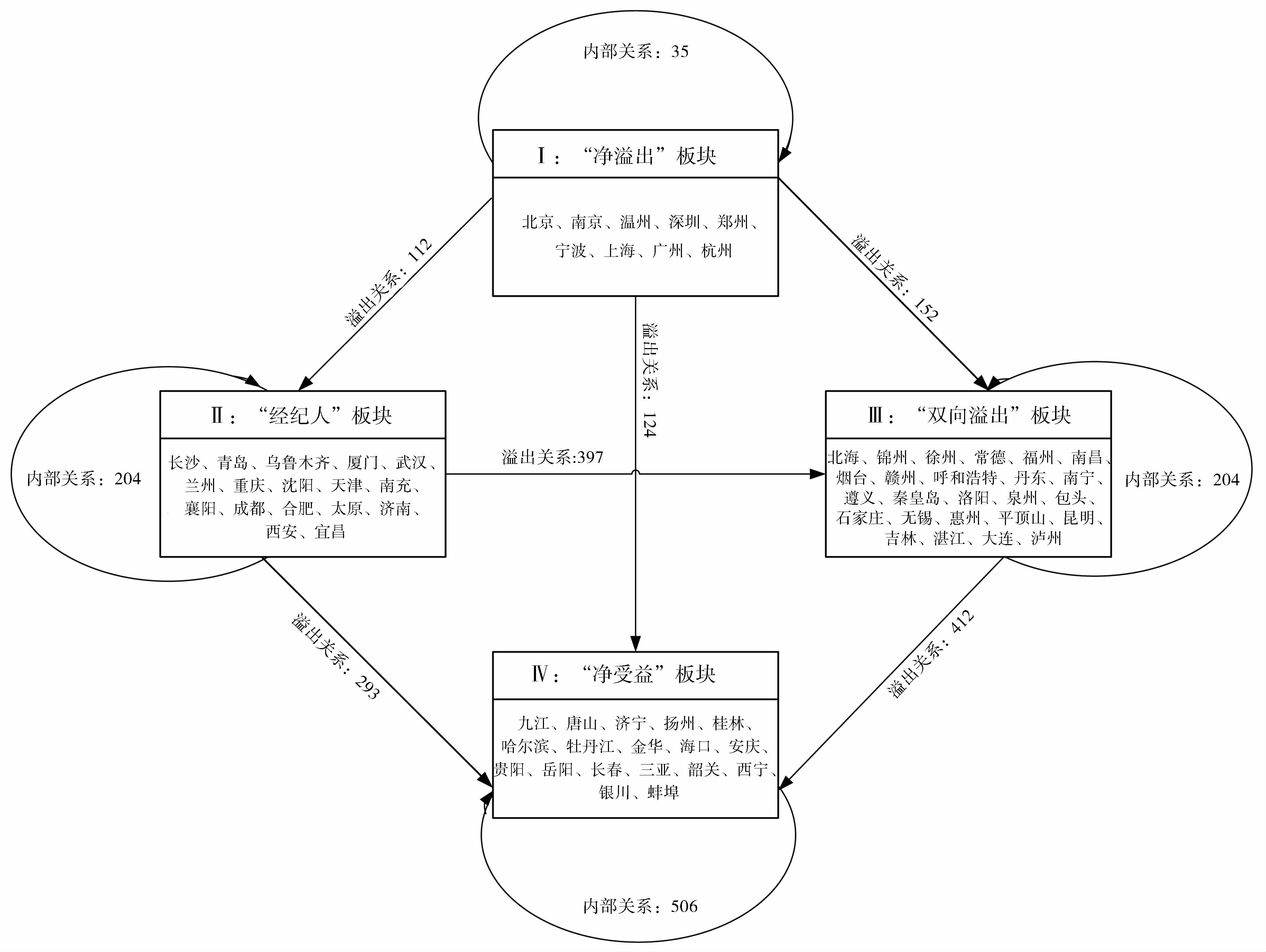
|
图 2 房价联动四大板块间的关联关系 |
房价波动的影响因素有很多,主要涉及供给、需求和政策三个方面。其中供给因素包括开发成本、土地价格、企业数量、投资状况、人均资源占用量等方面(梁云芳和高铁梅,2006;白霜,2008);需求因素包括居民购买力、人口密度、人口迁移、住房租金等方面(Berry and Dalton, 2004;杜红艳和马永开,2009);政策因素包括房贷政策、利率调整、汇率变化、税收政策等方面(Meen,2002;Gerlach and Peng, 2005;况大伟,2009;周京奎,2005)。另外,根据潘文卿(2014)、刘华军等(2015)的研究,区域差异是空间关联的重要影响因素,因此我们认为各地房价波动影响因素的区域差异对房价联动关系具有重要影响。借鉴上述研究,本文将城市房价联动关系的影响因素设定如下:(1) 人口数量的区域差异。购房需求量是影响房价的重要因素,而人口数量与购房需求量密切相关,因此,随着经济一体化发展,人口数量差异可能会引发城市间人口流动,从而增强住房需求及价格变化的联动关系。(2) 经济发展水平的区域差异。城市间经济发展水平的差异可能会促进要素流动以及投资贸易往来,从而提高建房成本、房价波动的关联性。(3) 收入水平的区域差异。城市间收入水平的差异可能会引起攀比效应、促进劳动力人员流动,从而增强住房需求及价格联动性。(4) 金融发展水平的区域差异。城市间金融发展水平的差异可能会引发房地产需求方空间套利行为,同时促进地区间资本流动,从而增强住房需求、投资及价格联动关系。(5) 产业结构的区域差异。相似的产业结构意味着城市可能处于相同的发展阶段,从而促进住房需求、供给乃至房价呈现具有较强的关联性。(6) 其它方面的区域差异。还有一些因素可能对城市间房价联动关系具有影响作用,比如购房政策的区域差异、地理距离的区域差异、人均居住用地面积的区域差异等。
基于上述因素,构建以下线性模型:Y=F(Xi),i=1, 2,…, 8。模型中,Y为69个大中城市房价联动矩阵,是根据VAR格兰杰因果关系检验确定的二值关系矩阵;X1为城市间人口数量(取期初与期末之均值) 差异;X2为城市间人均GDP差异;X3为城市间在岗职工平均工资差异;X4为金融相关率(城市间存贷款之和占GDP比重) 差异;X5为城市间第三产业占GDP比重差异;X6为城市是否在同一省份,同省取“1”,不同省取“0”;X7为城市中心球面距离,可根据ArcGis计算得到;X8为城市间人均居住用地面积差异。除Y、X6、X7外,其它指标数据根据2011-2013平均值计算绝对差异矩阵得到。
(二) QAP相关分析本文采用QAP相关分析法检验城市房价联动矩阵与其影响因素之间的相关性,随机置换次数选择5000次,结果如表 5所示。表 5中实际相关系数基于两个矩阵实际值计算得到;相关系数均值依据随机置换计算得到;最大值、最小值是指随机置换后计算的相关系数中出现的最大值、最小值;P≥0反映随机置换后计算的相关系数不小于实际相关系数的概率;P≤0反映随机置换后计算的相关系数不大于实际相关系数的概率(刘军,2014)。
| 表 5 QAP相关分析结果 |
相关分析结果表明:(1)X6、X7与Y的相关系数分别为-0.008、-0.021,但显著性概率分别为0.300、0.241,这表明城市房价联动关系与城市是否在同一省份、城市间距离远近的相关性并不强。可能的原因是,一方面随着网络、通讯技术的普及,房产信息在不同城市间的传递能够瞬间完成,城市间“信息化距离”逐渐缩短,即使地理距离较大的城市间也可能存在较强的关联性(张衔和林仁达,2015);另一方面,统一的房价调控政策对于城市房价联动关系跨越省份、跨越空间距离的限制也具有一定推动作用。X8与Y相关系数为-0.028,显著性概率为0.349,这表明城市房价联动关系与城市间人均居住面积差异的相关性并不强。可能的原因是,随着住房需求的不断攀升,房地产开发商为谋求更高的投资利润,将更多住宅项目由多层开发转向高层开发,从而弱化了人均居住用地面积与房价波动关联性。(2)X1、X2、 X3、X4与Y的相关系数分别为0.282、0.221、0.281、0.106,对应的显著性概率均小于0.10,这表明城市间的人口数量差异、经济发展水平差异、工资收入水平差异、金融发展水平差异与城市房价联动矩阵呈现显著正相关;换言之,以上因素的区域差异越大,城市间要素流动、财富转移、投资及贸易往来等经济活动越频繁,房价联动性越强。X5与Y的相关系数为-0.093,显著性概率小于0.10,这表明产业结构差异与城市房价联动矩阵呈现显著负相关;换言之,城市间相似的产业结构可能会带动相似的购房需求及投资需求,从而增强房价联动性。
(三) QAP回归分析接下来,选择与房价联动矩阵相关系数较为显著的变量作为解释变量,进一步检验各影响因素对城市房价联动矩阵的影响关系。为避免解释变量间的多重共线性,本文采用QAP回归分析法进行考察。随机置换次数选择5000次,结果如表 6所示。回归结果中,调整后的可决系数为0.115,且在1%显著性水平下显著,这说明城市间的人口数量差异、经济发展水平差异、收入水平差异、金融发展水平差异、产业结构差异只能解释中国城市房价联动关系的11.5%。
| 表 6 QAP回归分析结果 |
表 6回归分析结果表明:(1)X1标准化回归系数为0.177,并且通过了10%的显著性水平检验,这表明在其它影响因素不变的情况下,城市间人口数量差异越大,房价联动性就越强。一方面,人口数量较大的城市,住房需求一般更加旺盛,房价相对较高,迫于住房成本的压力,人们可能从高房价城市向低房价城市迁移,从而引起低房价城市住房需求增加,进而带动城市房价上升;而反过来,迁出城市人口数量减少,住房需求相对下降,房价上涨压力得以缓解甚至可能出现下跌,其结果是人口数量差异较大的不同城市间房价出现了较强的联动性。另一方面,人口数量较大的城市,劳动力一般更加富裕,随着劳动力市场不断完善,部分劳动力为了追求更高收入,可能会转向某些劳动力稀缺城市工作,人口流动往往伴随家庭迁移、财富转移,这一过程必然也会引起迁入、迁出城市住房需求联动变化,从而增强城市间房价联动性(王松涛等,2008)。(2)X2标准化回归系数为0.139,并且通过了显著性检验,这表明城市间经济发展水平差异越大,房价联动性就越强。经济发展水平较高的城市一般具备良好的基础设施和完善的交通运输条件,劳动、资本、技术等生产要素也相对丰富,但随之而来的是过度拥挤而造成企业运营成本上升。根据克鲁格曼的外围理论(2002),某些企业可能会迁址到运营成本较低的其它城市,而为了吸引这些企业的到来,其它城市也积极改善基础实施及交通运输条件,一旦企业迁址到这些城市,必然带动人口及财富的相应转移,从而引起迁入、迁出城市住房消费需求变化,进而导致城市间房价联动变化。从另一方面来看,当运营成本较低的城市改善了自身基础条件之后,它们与其它城市之间的要素流动、贸易往来、房地产跨区投资等可能会相应增加,这些经济联系将提升建房成本乃至住房价格的关联性。(3)X3标准化回归系数0.116,并且通过了显著性检验,这表明城市间工资收入水平差异越大,房价联动性越强。一方面,较高的工资收入对劳动力通常具有较强的吸引力,城市间工资收入差异越大,劳动力跨地区流动倾向就越强。一旦劳动力群体选择从低收入城市迁入高收入城市,家庭财富也会随之转移,从而可能带动高收入城市住房需求增长、住房价格上涨,低收入城市住房需求下降、住房价格下跌,在此情况下,城市间房价波动可能呈现较强的关联性。另一方面,根据结构性通货膨胀理论,工资收入水平差异容易引起攀比效应。城市间工资收入差异越大,攀比效应可能越强,即工资收入调整的联动性就越强,从而导致城市间购房需求、房价波动的关联性可能就越强。(4)X4标准化回归系数0.101,并且通过了显著性检验,这表明城市间金融发展水平差异越大,房价联动性越强。一方面,金融发展水平不同,城市间住房信贷约束条件可能存在较大差异,金融发展水平较高城市的房地产市场或行为个体可能会对外来冲击做出较快反应,从而使得该城市房价波动表现出领先效应,而其它城市房价波动则表现为滞后效应,Meen(1999)基于空间异系数性采用数值模拟对此做了解释。另一方面,信息流动不充分、交易成本高等因素使得城市房地产市场不是绝对有效的(王松涛等,2008),金融发展水平差异为住房需求方进行空间套利提供了客观条件,当跨城市间空间套利发生时,城市间房价联动关系随之增强。另外,金融发展水平的差异还对资本流动具有一定推动作用,可能会引起城市间房地产开发投资资本的相对变动,进而影响城市间房价联动关系。(5)X5标准化回归系数为-0.086,并且通过了显著性检验,表明城市间产业结构差异越小,房价联动关系越强。可能的原因是,相似的产业结构意味着城市可能处于相同的经济发展阶段,从而具有相似的住房购买需求及投资需求,进而导致城市房价呈现相似波动态势,表现出较强的联动性。
五、 结论与启示本文基于2011年1月-2015年2月中国69个大中城市商品住宅销售价格指数,利用社会网络分析(SNA) 方法对城市房价联动的空间网络结构特征及其影响因素进行了经验考察。研究结论如下:(1) 从整体网络结构特征看,城市间房价联动程度较高,普遍存在较强的关联效应和溢出效应;网络中存在较多的冗余连线,网络通达性好,网络稳定性高;城市间等级结构并不森严,网站节点对称可达程度较高,处于从属和边缘地位的城市较少。(2) 中心性分析结果显示上海、广州、北京、深圳等城市中心度较高,在网络中处于中心位置,具有房价“引领”作用;金华、郑州、杭州、温州等城市中心度较低,在网络中处于“跟随”地位,扮演边缘行动者的角色。(3) 块模型分析结果显示,北京等9个城市属于净溢出板块,在网络中扮演“引导”角色;长沙等17个城市属于经纪人板块,在网络中扮演“桥梁”角色;北海等25个城市属于双向溢出板块,在网络中扮演内、外部双向“引导”角色;九江等18个城市属于净受益板块,在网络中扮演“跟随”角色。东部城市分布在双向溢出板块的最多;西部城市分布在净受益板块的最多;而中部城市在四大板块的分布较为平均。另外,板块间还存在显著的“俱乐部效应”、“梯度效应”。(4)QAP相关分析结果表明,在10%显著性水平下,城市间人口数量差异、经济发展水平差异、收入水平差异、金融发展水平差异与城市房价联动矩阵呈现显著正相关;产业结构差异与城市房价联动矩阵呈现显著负相关;城市是否在同一省份、城市间距离远近、人均居住用地面积与城市房价联动矩阵相关性并不显著;QAP回归分析结果表明,在10%显著性水平下,城市间人口数量差异、经济发展水平差异、收入水平差异、金融发展水平差异和产业结构差异对城市房价联动性具有显著影响。
基于以上研究结论,可得出如下启示:(1) 城市房价联动关系及其多线程网络结构特征可以为调整房价调控政策提供新的视角。由前文分析可知,69个大中城市房价之间普遍存在空间联动关系,这种关系不是单个城市对单个城市简单线程关系,而是多个城市之间多线程的复杂网络结构关系。对于点出度、接近中心度、中介中心度较高的城市,国家在制定房价调控政策时应予以区别对待。一方面,要充分考虑这些城市房价波动的自身传导因素;另一方面,还要更加重视这些城市对其它城市的空间溢出效应。如果这些城市房价能够得到定向调控和精准调控,那么通过它们在房价联动网络中的引领作用或中介作用则可能更好地调控其它城市房价。总之,城市房价联动关系为房价空间协同调控创造了条件,同时也为房价调控整体政策的实施增加了难度,要求政府不仅要高度关注各地区自身“属性数据”的表现,还要充分重视城市间房价的空间联动性,房价调控政策应从“点”转向“面”、从“数量”转向“结构”、从“局部”转向“整体”。(2) 城市房价联动网络的板块结构特征可以为制定差别化的区域房价调控政策提供新的借鉴。为稳定房价,近年来中央及地方政府先后出台了一系列房地产调控政策,但调控效果并不理想(尹虹潘,2012),本文以为应充分重视城市房价联动网络中板块的空间聚类特征,以及板块间的关联效应和溢出效应,进而针对不同板块特点制定区域性房价调控政策。对于净溢出板块城市,应利用其在房价联动网络中扮演的发动机角色,以及其房价波动对其它板块城市的引导作用,实施从严调控策略,从源头上稳定城市房价。对于净受益板块城市,因其在网络中较多地受制于其它板块,处于较为被动的地位,扮演着“跟随”角色,所以基于这一板块的房价调控政策可适当从松。对于经纪人板块城市,因其在联动网络中扮演“桥梁”角色,直接影响整个房价联动网络的关联程度,所以基于这一板块的房价调控政策应充分考虑其在网络中的传递作用。对于双向溢出板块城市,因其向内部成员及其它板块成员均发出较多的关系,所以基于这一板块的房价调控政策应充分考虑其内部、外部双向“引导”作用。(3)QAP分析结果可以为影响城市房价联动关系从而提升房价调控效果提供新的思路。QAP分析结果从另一视角印证了城市房价联动关系的复杂性,房价联动不仅受到房地产市场自身因素的影响,还受到人口流动、就业状况等一系列其它因素的影响。因此,在调控城市房价的过程中,一方面应不断完善房地产市场体系建设,继续发挥其“看不见的手”作用,利用供求、价格、竞争等市场工具进一步影响城市间房价联动关系;另一方面应发挥政府“看见的手”作用,通过调节城市间人口规模、经济发展水平、收入水平、金融发展水平及产业结构等方面的差异程度,进一步影响城市间房价联动关系,从而为提升房价调控效果创造有利条件。
| [] | Berry M., Dalton T, 2004, "Housing Prices and Policy Dilemmas:A Peculiarly Australian Problem". Urban Policy and Researeh, 22(1), 69–91. DOI:10.1080/0811114042000185509 |
| [] | Cook S., Thomas C, 2003, "An Alternative Approach to Examining the Ripple Effect in UK House Prices". Applied Economics Letters, 10(13), 849–851. DOI:10.1080/1350485032000143119 |
| [] | Drake L, 1995, "Testing for Convergence between UK Regional House Prices". Regional Studies, 29(4), 357–366. DOI:10.1080/00343409512331349023 |
| [] | Gerlach S., Peng W.S., 2005, "Bank Lending and Property Prices in Hong Kong". Journal of Banking & Finance, 29(2), 461–481. |
| [] | Giussani B., Hadjimatheou G, 1991, "Modelling Regional House Prices in the UK". Papers in Regional Science, 70(2), 201–219. DOI:10.1007/BF01434329 |
| [] | Holmes M.J, 2007, "How Convergent Are Regional House Prices in the United Kingdom? Some New Evidence from Panel Data Unit Root Testing". Journal of Economic and Social Research, 9(1), 1–17. |
| [] | LUO Z.Q., Chunlu LIU C. and Picken D, 2007, "Housing Price Diffusion Pattern of Australia's State Capital Cities". International Journal of Strategic Property Management, 11(4), 227–242. |
| [] | Macdonald R., Taylor M., 1993, "Regional Housing Prices in Britain:Long-Run Relationships and Short-run Dynamics". Scottish Journal of Political Economy, 40(1), 43–55. DOI:10.1111/sjpe.1993.40.issue-1 |
| [] | Meen G., 1999, "Regional House Prices and the Ripple Effect:A New Interpretation". Housing Studies, 14(6), 733–753. DOI:10.1080/02673039982524 |
| [] | Meen G., 2002, "The Time-Series Behavior of House Prices:A Transatlantic Divide?”,". Journal of Housing Economies, 11(1), 1–23. DOI:10.1006/jhec.2001.0307 |
| [] | Oikarinen E., 2006, "The Diffusion of Housing Price Movements from Center to Surrounding Areas". Journal of Housing Research, 15(1), 3–28. |
| [] | Pollakowski H.O., Ray T.S., 1997, "Housing Price Diffusion Patterns at Different Aggregation Levels:An Examination of Housing Market Efficiency". Journal of Housing Research, 8(1), 107–124. |
| [] | ScottJ.,2013,“Social Network Analysis”,Published by Sage. |
| [] | Wood R., 2003, "The Information Content of Regional House Prices:Can They Be Used To Improve National House Price Forecasts?". Bank of England Quarterly Bulletin,Autumn, 304–314. |
| [] | 保罗·克鲁格曼,2002,《地理和贸易》,北京大学出版社2002年6月第一版。 |
| [] | 陈浪南、王鹤, 2012, 《我国房地产价格区域互动的实证研究》, 《《统计研究》》, 第 7 期, 第 37–43 页。 |
| [] | 白霜, 2008, 《房地产价格的决定因素分析》, 《《财经问题研究》》, 第 8 期, 第 107–110 页。 |
| [] | 杜红艳、马永开, 2009, 《我国房价与租金Granger因果关系的实证研究》, 《《管理评论》》, 第 1 期, 第 94–99 页。 |
| [] | 苑德宇、宋小宁, 2008, 《中国区域房价泡沫测度及空间传染性研究——基于 2001~2005 年 35 个大中城市面板数据的实证分析》, 《《上海财经大学学报》》, 第 3 期, 第 78–85 页。 |
| [] | 高铁梅,2009,《计量经济分析方法与建模——Eviews应用与实例(第二版)》,清华大学出版社2009年5月第二版。 |
| [] | 洪涛、西宝、高波, 2007, 《房地产价格区域间联动与泡沫的空间扩散》, 《《统计研究》》, 第 8 期, 第 64–67 页。 |
| [] | 黄飞雪、周筠、李志洁、侯铁珊, 2009, 《基于协整和向量误差修正模型的中国主要城市房价的联动效应研究》, 《《中大管理研究》》, 第 2 期, 第 122–143 页。 |
| [] | 况大伟, 2009, 《住房特性、物业税与房价》, 《《经济研究》》, 第 4 期, 第 151–160 页。 |
| [] | 梁云芳、高铁梅, 2006, 《我国商品住宅销售价格波动成因的实证分析》, 《《管理世界》》, 第 8 期, 第 76–82 页。 |
| [] | 李敬、陈澍、万广华、付陈梅, 2014, 《中国区域经济增长的空间关联及其解释—基于网络分析方法》, 《《经济研究》》, 第 11 期, 第 4–16 页。 |
| [] | 刘华军、刘传明、孙亚男, 2015, 《中国能源消费的空间关联网络结构特征及其效应研究》, 《《中国工业经济》》, 第 5 期, 第 83–95 页。 |
| [] | 刘军,2014,《整体网分析——UCINET软件实用指南(第二版)》,格致出版社2014年8月第二版。 |
| [] | 潘文卿, 2014, 《中国的区域关联与经济增长的空间溢出效应》, 《《经济研究》》, 第 1 期, 第 54–65 页。 |
| [] | 王鹤, 2012, 《基于空间计量的房地产价格影响因素分析》, 《《经济评论》》, 第 1 期, 第 48–56 页。 |
| [] | 王鹤、潘爱民、陈湘州, 2014, 《经济环境、调控政策与区域房价——基于面板数据同期强相关视角》, 《《南方经济》》, 第 6 期, 第 56–74 页。 |
| [] | 王松涛、杨赞、刘洪玉, 2008, 《我国区域市场城市房价互动关系的实证研究》, 《《财经问题研究》》, 第 6 期, 第 122–129 页。 |
| [] | 徐迎军、李东, 2008, 《关于我国住宅价格波纹效应的研究》, 《《统计与决策》》, 第 21 期, 第 15–17 页。 |
| [] | 徐振宇, 2013, 《社会网络分析在经济学领域的应用进展》, 《《经济学动态》》, 第 10 期, 第 61–72 页。 |
| [] | 尹虹潘, 2012, 《不同房地产调控政策在城市层面的运行机制——基于城市房价空间分析曲线的理论分析》, 《《经济学家》》, 第 12 期, 第 67–73 页。 |
| [] | 张清勇、年猛, 2012, 《中国房地产业关联度高、带动力强吗?—兼论房地产业的定位》, 《《财贸经济》》, 第 10 期, 第 123–129 页。 |
| [] | 张衔、林仁达, 2015, 《我国城市房价短期波纹效应的实证》, 《《财经科学》》, 第 9 期, 第 132–140 页。 |
| [] | 周京奎, 2005, 《货币政策、银行资款与住宅价格》, 《《财贸经济》》, 第 5 期, 第 22–27 页。 |




