随着资本市场的快速发展和全球经济、金融一体化程度的不断提高,通货膨胀的影响因素日益多元化和复杂化。其中,有关股票、债券、房地产等资产价格与通货膨胀之间关系的研究更是受到了学者和政策制定者的广泛关注。尤其在2008年金融危机爆发后,这一问题再次引起了高度的重视。一方面,危机前近三十年高增长、低通胀的“大缓和”(Great Moderation) 使得西方经济学家和政府确信盯住通货膨胀的货币政策极为成功,而金融危机的爆发使传统的通货膨胀和货币政策理论与实践受到质疑和挑战;另一方面,深受金融危机影响的国家其资产价格均出现剧烈波动,但通货膨胀却得到了很好的控制。因此,资产价格波动是否必然影响通货膨胀、其影响方向为何、消费品价格的稳定是否意味着宏观经济的稳定、货币政策是否需要盯住资产价格等成为当前饱受争论和亟待解决的重要问题,而解决上述问题的基础和关键在于要对资产价格和通货膨胀的影响关系形成科学的认知,在经济新常态背景下,对资产价格波动所隐含的通货膨胀信息更需要合理分析和预判。
事实上,关于资产价格对通货膨胀的影响,国内外学者均已进行了大量的研究,但并未得出一致的结论。Irving Fisher (1911)首先肯定了通货膨胀受资产价格的影响,指出货币当局应当不仅关注生产、消费和服务价格的稳定,还应充分关注资产价格的稳定。以此为基础,国外学者展开了深入研究,或构建更为广义的价格指数 (Alchian and Klein, 1973),或分析消费、投资和预期等传导途径 (Smet,1997;Mishkin,2001;Lettau and Ludvigso, 2004),均得出资产价格波动隐含未来通货膨胀的信息,应当提高解读水平或者将其“内置”于价格指数中。此外,以股票价格 (Ray and Chatterjee, 2000)、房地产价格 (Goodhart and Hofmann, 2000;Aoki et al., 2004) 和综合指数 (Goodhart and Hofmann, 2001) 等衡量资产价格的一系列实证研究也为上述观点提供了经验证据。鉴于此,有学者认为货币政策有必要盯住资产价格以控制通货膨胀和维持经济和金融稳定,预防“泡沫”破裂造成的系统性风险 (Cecchetti et al., 2000;Roubini,2006;Allen and Rogoff, 2011;Bernanke,2012)。
但是,也有研究者得出截然相反的观点。一方面,有别于消费品价格,资产价格具有波动频率高、幅度大、合理价值难以度量以及推动力多元化等特点。因此,其和通货膨胀之间的关系十分脆弱,以纳入资产价格的广义价格指数来衡量价格总水平更容易导致调控目标的非最优化 (Filardo,2000;Trichet,2003)。另一方面,合理价值度量的困难导致无法对“资产价格泡沫”进行识别,而“盲目的”、大幅的政策调整则会加剧“泡沫”的破灭进而使得经济陷入痛苦的衰退期,因此货币政策不应该对资产价格作出反应 (Bernanke,2002;Bean,2004;Iacoviello,2005;Goodhart and Persaud, 2008)。此外,从货币需求理论和货币数量论的角度出发,Fama (1981)指出股票收益率和通货膨胀呈负相关关系。可见,资产价格对通货膨胀的影响表现出较大的不确定性。
对此,我国学者也进行了一定的研究。主要观点均认为资产价格影响通货膨胀,货币当局应积极关注并解读其波动信息,但房地产价格和股票价格的影响存在较大差异,需要区别对待。如陈继勇等 (2013)指出,股票、房地产价格波动均隐含了一定程度的未来产出和通货膨胀信息,中国货币政策在必要时应干预资产价格,在条件完备时甚至可以盯住房地产价格。戴国强和张建华 (2009)以及纪敏等 (2012)基于中国数据的实证研究得出,资产价格波动影响通货膨胀,但房地产价格的影响更为明显,而股票价格的作用较弱或者无影响。也有学者将资产价格“内置”于价格指数,对我国通货膨胀的度量指标进行了修正,使修正后的价格指数预测效果更优,同时还可以使既定的货币政策更为有效 (汪恒,2007;罗忠洲和屈小粲,2013)。
综合现有研究来看,理论分析虽得出资产价格变动可以通过消费、投资等渠道影响通货膨胀,但由于不同国家经济运行状况和金融市场化程度的不同,实证研究得出的结论并不一致。而由于数据、变量以及模型选取的不同,我国学者得出的结论也存在一定程度差异。其中,基于中国数据的实证研究多数采用向量自回归模型 (VAR),但固定系数的模型难以体现经济结构的变化,无法捕捉系数的变化规律,由此得出的结果也难免存在偏误。与此同时,经济新常态背景下,随着经济结构的不断调整和经济环境的日益复杂化,变量之间的影响关系必然会表现出时变性,尤其是互联网金融不断创新, 改变了金融市场经济主体行为,使货币需求和资产结构处于复杂多变状态 (邹新月等,2014)。因此,使用时变系数模型判断资产价格与通货膨胀的关系,将使估计结果更加精确,更能反映经济运行的客观规律。
近年来,国外学者对传统向量自回归模型进行了一系列扩展,其中引入时变系数的扩展模型成为最重要的进展,受到了广泛的关注,并在相关领域取得了显著的成果 (Baumeister et al., 2008;Nakajima and Watanabe, 2011)。其后,Nakajima and West (2013)提出了包含潜在门限的时变参数向量自回归 (LT-TVP-VAR) 模型。一方面,该模型不仅包含了传统向量自回归模型的特点,而且其时变特性可以更好地捕捉系数及变量影响关系的变化;另一方面,该模型中潜在门限的设定可以对系数的异常变动进行处理,进而能有效克服变量之间影响关系的“不稳定性”,使估计结果更加合理、稳健。
鉴于此,本文构建LT-TVP-VAR模型,将通货膨胀率、房地产价格和股票价格纳入统一分析框架进行实证研究,以期回答资产价格对通货膨胀是否具有指示作用这一问题,并为科学分析和解读资产价格波动信息提供有益的经验参考。
二、 资产价格影响通货膨胀渠道的理论分析从理论方面看,目前多数学者均认为资产价格 (股票和房地产) 变动可以通过居民财富效应、预期、信贷和货币激活效应等渠道影响居民消费和投资需求进而总需求的变动,形成需求拉动的通货膨胀。
(一) 居民财富效应在弗里德曼持久收入假说和莫迪利亚尼生命周期理论的经典消费理论框架下,居民消费需求由现期收入、预期收入和持有资产价值 (财富) 共同决定。资产价格波动使居民持有财富发生变动,导致居民消费需求的变动,最终引致市场消费品价格发生变化。值得注意的是,居民财富效应在金融市场和资本市场较为完善的发达经济体较为显著,而在部分发展中国家则表现不甚明显或呈现非对称性 (齐红倩和黄宝敏,2013)。此外,发展中国家在一定经济周期内,由于持有房地产资产价值的稳定性高于股票资产价值,其风险性也相对低于股票财富的风险波动,因而房地产财富效应大于股票财富效应,这一点与我国部分学者的实证结果相符。
(二) 预期经济参与者对未来的预期不仅影响消费行为,同时还将影响投资行为,进而通过消费和投资两个渠道交叉影响着总需求和通货膨胀。从消费方面来看,当资产价格处于上升期时,消费者预期未来资产价格还会不断上升,即预期资产收益率将提高,导致永久收入上升,因此在边际消费倾向不变时,消费支出将会相应增加;同理,当资产价格缩水时,消费者在悲观预期作用下将会相应减少消费支出。从投资方面看,在股票市场或房地产市场发展的繁荣期,投资者预期未来一段时期其价格将会继续上升并扩大投资;反之,在股票或房地产市场发展萧条时期,投资者趋于谨慎,将逐步减小投资规模。
(三) 信贷信贷是金融市场影响实体经济的重要途径,而资产价格的波动也会造成信贷的扩张和收缩,从而影响企业投资行为。当资产价格上涨时,企业的净财富增加,借款信用和还款能力相应提高,因此企业会选择投资的扩张。当资产价格下跌时,企业净财富减少,借款信用和还款能力都将降低,即便企业对资金和投资扩张的需求仍较大,但综合考虑流动性约束和信用风险后,借款人对于企业的贷款行为将趋于谨慎。因此,企业投资将减少,甚至整个经济会出现信贷紧缩的情况,造成投资全面下滑,经济陷入衰退。
(四) 货币激活效应随着资产市场的发展,货币供给的流向不再仅限于交易和储蓄,部分货币会脱离传统的实体经济循环体系流向资产市场,并专门用于资产交易,进而引起资产价格的变动。这部分脱离实体经济货币循环体系而滞留在金融系统中用于资产交易的货币,就是Binswanger (1998)提出的金融窖藏 (Financial Hoarding)。由此可知,货币总量分布于实体经济循环体系和金融窖藏两个部分,而这两个部分中的货币并非固定不变,而是处于不断的流动中,在二者收益率相等处达到动态平衡。当金融窖藏的货币不断增多,资产价格膨胀,或居民的货币需求结构发生变化时,金融窖藏的货币便会流向实体经济循环系统,造成通货膨胀的上升,这便是“货币激活效应”,即资产价格膨胀在货币循环系统中所造成的通货膨胀效应 (刘鹏,2014)。
由上述分析可知,资产价格波动可以通过多种渠道影响通货膨胀,但在现实经济运行中,由于金融市场发展的不完善以及传导途径不畅等因素影响,资产市场对通货膨胀的影响可能并不显著或者表现出很强的时变性和复杂性,因此,需要进一步通过实证分析揭示其影响的内在规律及关联性。
三、 实证分析 (一) 模型、数据和参数估计 1. LT-TVP-VAR模型为便于描述,我们首先引入传统的SVAR模型,其次引入时变参数将其扩展为TVP-VAR模型,最后引入待估参数的潜在门限设定,完成对LT-TVP-VAR的描述。一个典型的SVAR模型可以表示为:
| $ A{y_t} = {B_1}{y_{t - 1}} + \cdots + {B_s}{y_{t - s}} + {\mu _t}, t = s + 1, \cdots, n, $ | (1) |
其中,A为 (k×k) 阶的联立参数矩阵,B1……BS为 (k×k) 阶的系数矩阵,yt是 (k×1) 维观察向量,μt为 (k×1) 维的结构性冲击,且μt~N(0, ΣΣ),其中,
| $ \Sigma {\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{{\rm{\sigma }}_{\rm{1}}}}&{\rm{0}}&{\rm{\Lambda }}&{\rm{0}}\\ {\rm{0}}&{\rm{O}}&{\rm{O}}&{\rm{M}}\\ {\rm{M}}&{\rm{0}}&{\rm{0}}&{\rm{o}}\\ {\rm{o}}&{\rm{\Lambda }}&{\rm{0}}&{{{\rm{\sigma }}_{\rm{k}}}} \end{array}} \right]\;\;\;\;{\rm{A = }}\left[ {\begin{array}{*{20}{c}} {\rm{1}}&{\rm{0}}&{\rm{\Lambda }}&{\rm{0}}\\ {{{\rm{\alpha }}_{{\rm{21}}}}}&{\rm{O}}&{\rm{O}}&{\rm{M}}\\ {\rm{M}}&{\rm{0}}&{\rm{0}}&{\rm{o}}\\ {{{\rm{\alpha }}_{{\rm{k1}}}}}&{\rm{\Lambda }}&{{{\rm{\alpha }}_{{\rm{k, k - 1}}}}}&{\rm{1}} \end{array}} \right] $ |
设βi=A-1Bi,Xt=Is⊗(yt-1, …, yt-s)(⊗表示克罗内克乘积)。引入时变参数后,方程 (1) 可以进一步简写为:
| $ {y_t} = {X_t}{\beta _t} + A_t^{ - 1}{\Sigma _t}{\varepsilon _t}, t = s + 1, \cdots, n, $ | (2) |
参照Nakajima and West (2013)的思路,本文假定模型参数遵循如下的演进过程:
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{\beta _t} = {\mu _\beta } + {\Phi _\beta }\left({{\beta _{t - 1}} - {\mu _\beta }} \right) + {v_t}, t = s + 1, \cdots n, }\\ {{\alpha _t} = {\mu _\alpha } + {\Phi _\alpha }\left({{\alpha _{t - 1}} - {\mu _\alpha }} \right) + {\zeta _t}, t = s + 1, \cdots n, }\\ {{h_t} = {\mu _h} + {\Phi _h}\left({{h_{t - 1}} - {\mu _h}} \right) + {\xi _t}, t = s + 1, \cdots n, } \end{array}\\ V = Var\left({\left[ {\begin{array}{*{20}{c}} {{\varepsilon _t}}\\ {{V_t}}\\ {{\zeta _t}}\\ {{\xi _t}} \end{array}} \right]} \right) = \left({\begin{array}{*{20}{c}} {{I_n}}&0&0&0\\ 0&{{\Omega _\beta }}&0&0\\ 0&0&{{\Omega _\alpha }}&0\\ 0&0&0&{{\Omega _h}} \end{array}} \right) \end{array} $ | (3) |
其中,βt和αt分别为模型系数和联立参数构成的向量,ht=log (σ2t)。vt、ζt和ξt分别为相应的随机波动。(1)-(3) 式即构成了典型的TVP-VAR模型形式。在此基础上,本文引入如下的潜在门限设定:
| $ \begin{array}{l} {b_t} = {\beta _t}{s_{bt}}\\ {s_{bt}} = I\left({|{\beta _t}| \ge {d_b}} \right) \end{array} $ | (4) |
| $ \begin{array}{l} {a_t} = {\alpha _t}{s_{at}}\\ {s_{at}} = I(|{\alpha _t}| \ge {d_a}) \end{array} $ | (5) |
其中,I(.) 为指示变量 (取值为0和1),db和da分别表示系数和联立参数的待估潜在门限值。(1)-(5) 式即为一个一般化的LT-TVP-VAR模型。对于此类时变参数模型的估计,需要充分利用样本外的信息,而贝叶斯分析方法是最为常用的手段。因此,本文在贝叶斯框架下利用马尔科夫蒙特卡洛模拟方法 (MCMC) 对参数进行估计,并进一步计算时变脉冲响应函数进行深入分析。关于该模型以及参数估计过程更为详细的描述和论证参见Primiceri (2005)和Nakajima and West (2013)。
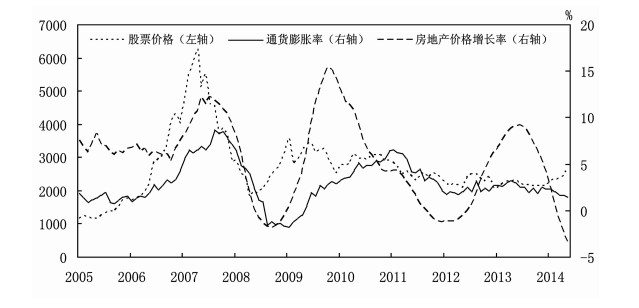
2. 数据选取和描述本文选取我国2005年7月到2014年11月的月度时间序列数据,建立包含有股票价格、房地产价格以及通货膨胀率的LT-TVP-VAR模型,实证分析两类资产价格对通货膨胀率的影响及差异。其中,股票价格以上证综合指数月末收盘值表示,为使序列更加平滑,对其进行对数处理;通货膨胀率以当月居民消费价格指数 (CPI) 同比增长率表示;房地产价格以国家统计局发布的70个大中城市新建住宅价格指数同比增长率表示。由于2011年1月起,统计局对住宅销售价格统计方案进行调整,不再公布70个大中城市总体价格指数,该数据自2011年1月后为70个大中城市新建住宅价格指数同比数据的算术平均值。原始数据均来自于国家统计局官方网站及Wind数据库 (图 1),在季节调整和初步处理后,经检验可得,参与计算的所有序列均至少在5%的显著性水平下平稳①。
|
图 1 原始数据序列 |
① 本文使用ADF单位根方法检验了数据的平稳性,具体结果不再赘述。
由图 1可以看出,在样本期内,我国股票、房地产价格以及通货膨胀率均经历了大幅的波动,2008年以后股票价格和通货膨胀的变动趋于平缓且趋势较为一致,但房地产价格仍出现较大幅度波动。具体来看,上世纪90年代我国建立股票市场后,经历10年的发展,2005年中国股市已逐渐走向成熟。从2005年6月至2007年10月,为改善上市公司治理结构,证监会于2005年9月出台《上市公司股权分置改革管理办法》,中国股市随之出现了目前为止最强的一轮上涨,上证指数从998点持续上升至6124点。2007年10月之后,受国际金融危机等多重因素的影响,上证指数从最高点不断回落。2014年下半年,受央行降息、降准、沪港通以及其他利好的带动,上证指数从2000点附近不断上升至3000点以上,现阶段,虽然经历了较大幅度的下跌和剧烈波动,但仍处于近几年以来的高位。
2005年至今,房地产价格表现出较强的周期性变动规律,分别出现三个“波峰”(2007、2010和2013年) 和两个“波谷”(2009和2012年)。2005年至2008年上半年,房地产市场呈现过热态势,价格不断攀升,同比增长率高至10%。此后,由于国际金融危机影响蔓延至我国,国内外需求增长大幅放缓,投资、消费增速均出现下降,导致房地产价格的下行,2009年价格连续6个月下降。为应对经济危机,稳定经济增长,政府出台大规模刺激计划,导致了房地产行业的快速回升,房地产市场于2010年出现了新一轮的过热,价格涨幅再次高达10%以上。鉴于房地产市场过热造成的一系列经济和社会问题,中央和地方政府出台了包括限购在内的一系列调控措施,使得楼市出现短暂降温,2012年房地产价格再次出现下降。但是,调控政策的作用并未能持续,2013年房价出现了新一轮的上涨,但幅度相对较为温和。2014年以后,我国经济增速继续下降、结构深入调整、改革继续推进,经济发展进入“新常态”,房地产供求格局也发生了变化,土地购置、投资和房价增长均不断放缓,除个别城市外,整体的房地产市场再次出现低迷,现阶段虽略有回暖,但复苏基础并不稳固。
在通货膨胀方面,2005年以来,我国通货膨胀率总体经历了两轮“上升-回落”的走势。2005年至2008年上半年,由于货币供给 (M2) 的快速增长,导致了投资过热现象 (固定资产投资增速达20%以上),进而通货膨胀率不断攀升,并于2008年4月达到8.5%的峰值。此后,受国际金融危机的影响,国内外需求迅速萎缩,投资、消费增长急剧下降,通货膨胀率亦不断回落,2009年CPI连续9个月负增长。为应对危机,我国实施适度宽松的货币政策和积极的财政政策,2009-2010年,M2和固定资产投资增长持续加快,M2月度同比增速和投资季度累计同比增速最高均达到30%左右,通货膨胀随之由负转正,并于2011年7月进一步上升至6.5%的峰值。近两年,前期刺激政策的增长效应已然消失,但间接加剧了部分行业尤其是上游能源类行业的产能过剩,与此同时,危机后世界经济弱势复苏,出口需求大幅下滑。在国内外需求增长乏力的背景下,从2011年开始,产出和通货膨胀整体均呈现下行趋势,2014年CPI同比增长仅为2%,创近5年新低,2015年上半年CPI月度增长均低于1.5%,通缩风险加大。
从上述分析看出,股票价格、房地产价格以及通货膨胀率均表现出一定的周期性变化规律,同时三者的变动共同受到宏观经济运行及其他冲击的影响。而这其中股票价格、房地产价格的波动信息是否对通货膨胀具有指示作用、作用机理如何、在经济运行的不同阶段其隐含信息对通货膨胀的真实影响是否存在差异等问题,需要依赖充分的实证研究加以明确。需要说明的是,本文选取的房地产价格指数自2005年开始统计,因此无法进一步扩充样本容量。但是,现有的样本容量已超过100,对于模型构建而言样本容量是充分的。并且更具积极意义的是,本文选定的样本期覆盖了股票市场发展的极度繁荣期 (2007年)、房地产市场发展的繁荣期 (2007和2010年) 和低迷期 (2012和2014年) 以及经济危机时期 (2008-2009年) 等典型时期,对于展开全面的分析具有充分的样本数据基础。
3. 模型参数估计结果和适用性的进一步说明本文在贝叶斯框架下运用MCMC方法进行模型估计。根据VAR模型中滞后阶数的判定准则,选用二阶滞后构建模型,并选择M=10000的模拟样本长度,其中,包含有1000个样本的预模拟期 (Burn-in Period)。表 1给出了模型中部分参数后验分布的均值、标准差、95%置信区间,Geweke收敛诊断值和无效影响因子 (inefficiency factors) ①。表 2为潜在门限值的可接受率,用于衡量其显著性。
| 表 1 模型部分参数估计结果 |
| 表 2 潜在门限值可接受率 (%) |
① 模型中的协方差矩阵 (Ωβ)、(Ωα) 和 (Ωh) 分别为18阶、3阶和3阶对角矩阵,由于篇幅有限,表 1参数估计结果只列出了各矩阵对角线元素的部分后验估计结果 (第一个元素)。
Geweke收敛诊断值和无效影响因子均是判断MCMC模拟和估计效果的重要依据,前者用于测定得到的马尔科夫链的收敛性,后者则用于测定模拟所产生不相关样本的个数。可以看出 (表 1),在5%的显著性水平下 (临界值为1.96),所有参数均没有拒绝收敛于后验分布的原假设,表明10000次的模拟次数即可以产生有效的样本,对于参数估计而言是足够的;同时,所有参数估计结果的无效影响因子均较小,其中最大的为220.35(μh),即至少可以产生10000/220.35≈45个不相关样本,可以用以进行有效的后验推断。综合两个统计量的诊断结果来看,本文模型取得了良好的估计效果。
模型估计效果良好仅仅表明模型在统计意义上成立,进一步,我们对LT-TVP-VAR模型的在文章实证模型中的适用性和必要性进行说明。
首先,从模型选择来看,本文重点研究对象是资产价格通货膨胀效应的时变特征,从时间序列模型出发,可用于设定参数时变的常用模型有状态空间模型和时变参数向量自回归模型 (TVP-VAR)。然而,状态空间模型对时变参数随机过程的假定较为主观,估计所得的结果也难免存在偏差,而TVP-VAR的系列模型在贝叶斯框架下的非参数估计方法可以有效避免人为设定随机过程所带来的这一偏差。就现有关于资产价格问题的实证研究而言,本文得出的结论也与之存在一定差异,我们认为这一差异可能是由于模型选择差异而导致的。比如,纪敏等 (2012)建立可变参数状态空间模型研究了股票和房地产价格对通货膨胀影响,与本文研究内容十分接近,但是,在其模型设定下得出了“房地产价格对通货膨胀影响显著,而股票价格影响不明显”的结论。从现实经验来看,股票是居民财富配置的重要组成部分,其财富效应一定程度会对通货膨胀产生影响,本文基于LT-TVP-VAR模型的实证结果则证实了这一结论。
其次,在TVP-VAR和LT-TVP-VAR模型的选择方面,本文选择包含潜在门限的时参数向量自回归模型 (LT-TVP-VAR) 的原因在于:TVP-VAR模型适用于变动较为平缓、序列较为平滑的时间序列数据,如利率、通货膨胀、货币供给和产出等,也有较多学者使用这一模型进行了实证研究,如陈守东等 (2014)分析了我国货币供给对通货膨胀和产出的动态影响。但是,对于波动较为剧烈,本身极具不平滑性的时间序列,在使用TVP-VAR模型时,其协方差矩阵容易出现无限放大的问题,进而导致估计结果的非有效,而LT-TVP-VAR模型中潜在门限的设定可以平滑掉剧烈波动部分数据,使得协方差矩阵趋于收敛,在有效避免这一问题的同时,还能分析参数的时变特性。从本文选取的数据来看,股票价格和房地产价格均具有剧烈波动的特性,其中股票价格表现尤为明显,比如2007-2008年和2014-2015年股票市场的剧烈震荡。鉴于此,本文选择LT-TVP-VAR模型进行实证具有适用价值。
最后,本文在统计意义上进行了一定的比较。由表 2可以看出,模型估计的所有潜在门限值可接受率均高于20%,最高可达64.3%,表明资产价格和通货膨胀的相互影响存在较为显著的门限效应,在估计过程中有效过滤了部分剧烈波动的数据,从而构建LT-TVP-VAR模型具有一定合理性。同时,本文利用同样的数据和设定估计了TVP-VAR模型,对协方差矩阵中部分对角线元素的统计量进行对比①,可以看出 (表 3),无论Geweke诊断值还是无效影响因子,TVP-VAR模型参数值均大于LT-TVP-VAR模型,统计上亦表明在本文的数据基础上,构建LT-TVP-VAR模型更具合理性。
| 表 3 LT-TVPVAR模型和TVP-VAR模型中部分参数的统计量对比 |
① 由于潜在门限的设定最主要是影响协方差矩阵的收敛性,因此在对比中,我们仅仅比较三个对角线元素的统计量。
(二) 资产价格影响通货膨胀的时变特征分析本节我们利用时变系数和时变脉冲响应函数分析房地产价格和股票价格对通货膨胀的作用规律,并重点关注不同阶段作用效果的差异性,以此揭示资产波动可能隐含的通货膨胀信息。
由上节的模型设定可知,系数落入门限范围的概率越高,变量间的影响关系越弱 (系数更小)。图 2显示,四个影响系数均表现出一定的门限选择效应,二阶滞后系数选择效应更为显著。具体来看,房地产价格和股票价格对通货膨胀的一阶滞后影响系数落入门限范围的概率均较低 (低于0.2),相应的系数值也较高,表明二者对通货膨胀存在着持续稳定的影响。相对而言,房地产和股票价格二阶滞后影响系数落入门限范围的概率表现出很强的时变性,部分时点的概率极高 (达到0.8左右),即其二阶滞后影响具有一定程度的不稳定性。但是,综合来看,房地产和股票价格对通货膨胀的影响系数均为正,表明在不考虑其他因素的前提下,资产价格攀升可以直接推动通货膨胀上升。

|
图 2 时变影响系数及其落入门限范围的概率 |
时变影响系数虽然可以表示变量之间的直接影响,但是在VAR模型中,变量之间不仅存在直接影响,而且还存在系统性的间接影响。因此,本文进一步计算时变脉冲响应函数,考察资产价格对通货膨胀的时变影响。
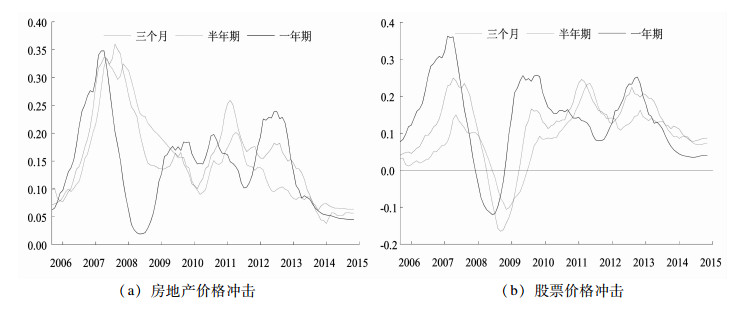
由图 3(a)可以看出,在整个样本期内,房地产价格的正向冲击均可以造成通货膨胀的上升,即房地产资产价格波动具有明显的通货膨胀效应。同时还可以看到,在不同时期,房地产价格对通货膨胀的影响存在明显差异。2005-2007年,房地产市场整体处于过热时期,房价持续上升,对通货膨胀的推升作用也不断增强并达到峰值。2008年,受金融危机的影响,总需求急剧下滑,直接导致房地产市场的低迷,其影响作用亦明显减弱。此后,房地产价格对通货膨胀的影响再次经历了一轮“增强-减弱”的走势,即从2010年开始逐渐增强出现峰值,之后影响不断减弱 (其间,一年期响应出现一次上升)。从上述分析可以得出,无论经济处于繁荣还是萧条时期,房地产价格上升均可以导致通货膨胀的上升,反之亦然。与此同时,房地产价格对通货膨胀的影响强度受房地产业自身周期的影响较大,即表现出较强的顺周期性:其影响强度的持续上升期和峰值点均出现在房地产业过热时期 (2005-2007年,2010年前后),而影响强度的下降期和谷值也基本出现在房地产业发展的低迷期 (2008和2012年前后,2014年)。
|
图 3 通货膨胀对资产价格冲击的时变脉冲响应 |
从股票价格对通货膨胀的影响来看 (图 3(b)),在整个样本期内,不同期限的响应基本保持了一致的形态,并且除2008至2009年上半年外,股票价格的正向冲击均造成了通货膨胀的上升。进一步来看,在不同经济周期阶段,股票价格冲击对通货膨胀的影响差异明显。2005-2007年,随着货币供给和固定资产投资的快速增长,股票价格急剧攀升,上证指数一路升至6124的最高点,相应造成了较大的通货膨胀压力。从实证结果也可以看出,期间股票价格对通货膨胀的推升作用不断增强。2008年美国首先爆发次贷危机并迅速蔓延至全球,经济衰退伴随着股市“泡沫破裂”,导致对通货膨胀的影响趋弱甚至出现通货紧缩。值得注意的是,金融危机期间,股票价格的正向冲击并未能造成通货膨胀的上升。可见,在经济衰退期间,经济和金融风险不断释放,诸多影响通货膨胀的因素交织,使得资产价格的波动难以传导至实体经济。此后,随着刺激政策的推出,经济快速复苏,股市逐渐回暖,其对通货膨胀的影响亦不断增强,并于2009年下半年再次达到峰值 (期间,上证指数达到3478的阶段性高点)。以上分析表明,除经济危机时期外,在其他各个时期股票价格上升均可以导致通货膨胀的上升。并且和房地产价格类似,其作用强度也表现为明显的顺周期性:脉冲响应先后出现的4个峰值均处于股票价格的阶段性上升期,而1个明显的谷值则位于经济危机时期,亦即股票市场发展的极度低迷期 (期间,上证指数创出1664的低点)。
我们进一步分析资产价格冲击对通货膨胀影响的传导渠道,可以发现居民财富效应、预期、信贷以及货币激活渠道均较为畅通。无论通过何种渠道,资产价格首先是影响消费和投资行为,然后传导至通货膨胀。
从消费来看,2005-2007年股票和房地产市场均处于繁荣期,极大推动了通货膨胀水平的上升,期间在财富效应、预期以及货币激活的影响下,居民消费增速持续上升。2005-2007年,社会消费品零售总额增速从12%左右持续上升至20%左右。而2010年股票市场相对低迷,房地产市场处于繁荣期,出现了典型的周期错配,但房地产市场对消费的影响大于股票市场,2010年消费增长也基本维持在18%-20%。在股票和房地产市场发展低迷期 (2008、2012以及2014年上半年),消费增长明显低于繁荣期,尤其从2012年至今,消费增速持续下滑,2014年仅增长12%。当然,需要说明的是消费水平增长和总体宏观经济走势高度相关,难以单独区分资产价格对其的影响程度,但仅从统计数据来看,资产价格的上升切实促进了居民消费的增长。同时,资产价格对消费的影响渠道直观体现在居民财富效应方面,2005-2007年,受资产性收入大幅增长的带动,城镇居民人均可支配收入同比增速维持在10%左右,2007年3月高达16.6%,而预期及货币激活效应无法量化考察,但二者可以强化资产价格的财富效应进而促进消费提升。
从投资来看,在资产市场发展的繁荣期,受预期、信贷以及货币激活的影响,固定资产投资快速增长,2005-2007年,在无大规模财政扩张的情况下,固定资产投资总额累计同比增速高达25%-30%,2010年投资增速亦保持在25%左右。其中,从信贷渠道来看,2010年贷款期末环比增速维持在20%的高位,而预期和货币激活对投资的影响虽难以量化考察,但无疑三者在一定程度上促进了信贷进而投资的增长①。在资产市场发展的低迷期,信贷和投资增长也相应放缓,尤其2013年之后,固定资产投资增长持续下滑,2014年仅增长15.7%。②
① 2009年之前贷款期末环比增速指标并未统计,但从2005-2007年M2的快速增长和贷款规模的总量水平也可以看出信贷的快速扩张。
② 上述数据均来自于国家统计局网站和中经网统计数据库,2009年政府出台了4万亿大规模刺激政策,因此期间投资的快速增长不能算作常态。
综合上述分析可知,房地产和股票资产价格均可以对通货膨胀产生显著影响。并且,其影响均表现出一定的时变特征:即无论房地产价格还是股票价格,其价格波动对通货膨胀的影响强度具有明显的顺周期特性,这一点在房地产和股票市场发展的“极度繁荣”和“极度低迷”期表现的尤为明显。进一步分析可知,“预期”这一渠道虽然无法度量,但在资产价格对消费和投资进而通货膨胀的影响方面,一定程度扮演着“加速器”的作用,即可以强化其他渠道的作用效果。当房地产或股票市场开始出现繁荣迹象时,投资者预期市场进入了新一轮的上升周期,会更多地购买资产进行投资进而推升了通货膨胀,而通货膨胀的攀升将进一步加剧市场的过热,如此循环往复,资产价格对通货膨胀的推升力度便不断增强。反之,当资产市场或宏观经济整体低迷时,即使价格出现上升,投资者也会认为只是暂时性现象,因此并不会大规模购买资产,进而对通货膨胀的推升作用有限。
四、 结论和政策建议资产价格变动可以通过财富效应、预期、信贷以及货币激活等渠道影响消费、投资行为,导致总需求的变动,进而影响通货膨胀,但其影响强度和时变特性需要进一步研究,对其波动信息的解读水平也有待提高。本文建立包含潜在门限的时变参数向量自回归模型 (LT-TVP-VAR),实证研究了房地产和股票价格对通货膨胀影响的时变特征。结合实证结果和我国当前实际,得出如下结论和政策建议:
(一) 我国资产价格具有一定的通货膨胀指示作用,应对其波动及隐含的通胀信息予以高度关注。经历了20年的发展,我国股票市场已达到较大规模,房地产市场对于国民经济的影响也变得举足轻重,二者对消费、投资行为进而物价水平的影响已十分明显。从实证结果来看,不论股票价格还是房地产价格的变化均可以导致通货膨胀同方向的变化,即资产市场的变动可以有效传导至消费品市场,消费品价格稳定不再意味着价格总水平的稳定。因此,仅就控制通胀这一调控目标而言,在货币政策制定时,中央银行应适当加强前瞻性,将资产价格因素充分考虑在内,避免出现经济政策的发力不足和过度调控。
(二) 在资产市场“繁荣期”和“低迷期”,其通胀效应存在明显差异,应区别、审慎对待。实证结果显示,房地产价格和股票价格对通货膨胀的影响均存在较强的时变特性,在资产市场发展的“繁荣期”和“低迷期”表现尤为明显。在市场 (房地产或股票) 发展的“繁荣期”,二者对通货膨胀的影响强度呈不断增强的趋势;相反,在萧条期,其影响强度逐渐趋弱甚至无效,即表现为顺周期性。鉴于此,在资产市场发展的不同时期,应制定差别化政策,使得调控更具针对性。一方面,在资产市场发展的“繁荣期”,面临较大的通胀压力时,中央银行不仅需要适当紧缩货币,而且还需针对性地制定相关政策以抑制资产价格的过度上升,防止“泡沫”的发生,维持物价稳定。另一方面,在资产市场发展的“低迷期”,资产价格对通货膨胀的影响极其有限。如果经济面临低通胀或通缩压力,在实施积极财政政策的同时,中央银行应更加注重定向宽松,使得金融更多支持实体经济。此时,宽松的财政和货币政策将有效刺激实体经济需求,使通货膨胀回升至正常合理区间,同时实体经济的回升亦会刺激资产市场复苏。
需要注意的是,上述结论仅仅代表房地产和股票市场景气状况趋同时的情境,当两个市场运行出现周期错配时,通货膨胀变动可能表现出更大的不确定性和复杂性,宏观调控难度也相应加大。此时,仅仅依靠货币政策难以有效调控,需根据两个市场的运行情况分别制定针对性的制度及行政政策,既要避免资产市场的“泡沫”化,还要防止其低迷,以此维持物价水平和通货膨胀预期的稳定。
(三) 货币政策制定应积极关注资产价格,但尚不具备直接将其纳入调控框架的条件,需继续提高金融市场化程度。鉴于资产价格具有较强的通胀效应,货币政策是否应该盯住资产价格以提高调控的前瞻性和有效性呢。诚然,资产价格波动不仅影响到未来的通货膨胀,而且关系到金融稳定。因此,货币政策制定应该重点关注资产价格。但是,资产价格的合理区间难以确定,或者说难以对“泡沫”进行识别,同时资产价格的波动相对大于消费品价格,导致将其纳入货币政策调控框架存在较大难度,这一点也是几乎所有国家中央银行所面临的问题。并且,相对于发达国家而言,我国金融市场发展尚不成熟,市场化程度还有待进一步提高,货币政策制定仍不具备直接将资产价格纳入调控框架的条件。当然,对于资产价格的调控不能单一依靠货币政策,针对资本市场和房地产市场的相关制度的制定和行政政策的使用也是有效的调控方式。
2015年,“三期叠加”的影响仍然持续,受部分行业产能过剩和总体需求不足的影响,CPI延续低增长态势,PPI更是连续三年多下降,通缩压力加大。从资产市场运行来看,房地产投资增长继续下行,在相关政策刺激下,房地产价格初显企稳迹象,但市场复苏基础并不稳固;而股票价格虽然经历了一定的下滑和剧烈波动,但总体仍处于近年来的高点。房地产和股票市场运行出现典型的周期错配,对通货膨胀影响的不确定性增大。对此,在“松紧适度”的基础上,中央银行宜继续通过“降准”、“降息”等手段施以更为宽松的货币政策,释放更多的流动性,以稳定经济增长,预防通缩风险。与此同时,仍需继续坚持2014年以来的“定向调控”策略,引导资金更多流向实体经济,防止股票和房地产市场的“泡沫化”。
| [] | Allen, F and Rogoff, K, 2011, "Asset Prices, Financial Stability and Monetary Policy, "Swedish Riksbank Workshop on Housing Markets, Monetary Policy and Financial Stability. |
| [] | Alchian, A A. and Klein, B , 1973, "On a Correct Measure of Inflation". Journal of Money, Credit and Banking, 5(1), 173–191. DOI:10.2307/1991070 |
| [] | Aoki, K , Proudman, J and Vlieghe, G , 2004, "House Prices, Consumption, and Monetary Policy:a Financial Accelerator Approach". Journal of financial intermediation, 13(4), 414–435. DOI:10.1016/j.jfi.2004.06.003 |
| [] | Binswanger, M 1998, "The Finance Process on a Macroeconomic Level From a Flow Perspective:A New Interpretation of Hording". International Review of Financial Analysis, 6(2), 107–131. |
| [] | Bernanke, B, 2012, "Monetary Policy Since the Onset of the Crisis, "Federal Reserve Bank of Kansas City Economic Symposium, Jackson Hole, Wyoming. |
| [] | Bernanke, B, 2002, "Asset-price 'Bubbles' and Monetary Policy, "Speech before the New York Chapter of the National Association for Business Economics. |
| [] | Bean, C R 2004, "Asset Prices, Financial Instability, and Monetary Policy,". American Economic Review, 94(2), 14–18. DOI:10.1257/0002828041301795 |
| [] | Baumeiste, C, Durinck, E and Peersman, G, 2008, "Liquidity, Inflation and Asset Prices in a Time-varying Framework for the Euro Area, "National Bank of BelgiumWorking Paper, No.142. |
| [] | Cecchetti, et al., 2000, "Asset Prices and Central Bank Policy, " Working Paper, Geneva Report on the World Economy CEPR and ICMB, NO.1222. |
| [] | Fisher, I, 1911, The Purchasing Power of Money, New York Press. |
| [] | Filardo, A 2000, "Monetary Policy and Asset Prices". Economic Review-Federal Reserve Bank of Kansas City, 85(3), 11–38. |
| [] | Fama, E 1981, "Stock Return, Real Activity, Inflation and Money". American Economic Review, 71(4), 545–565. |
| [] | Goodhart, C and Hofmann, B, 2001, "Asset Prices, Financial Conditions, and the Transmission of Monetary Policy, "Conference on Asset Prices, Exchange Rates, and Monetary Policy, Stanford University, pp.2-3. |
| [] | Goodhart, C and Hofmann, B , 2000, "Do Asset Prices Help to Predict Consumer Price Inflation?". The Manchester School, 68(s1), 122–140. DOI:10.1111/manc.2000.68.issue-s1 |
| [] | Goodhart, C and Persaud, A , 2008, "How to avoid the next crash,". Financial Times, 30, 14. |
| [] | Iacoviello, M 2005, "House Prices, Borrowing Constraints, and Monetary Policy in the Business Cycle,". American Economic Review, 95(3), 739–764. DOI:10.1257/0002828054201477 |
| [] | Lettau, M and Ludvigson, S C , 2004, "Understanding Trend and Cycle in Asset Values: Reevaluating the Wealth Effect on Consumption". American Economic Review, 94(1), 276–299. DOI:10.1257/000282804322970805 |
| [] | Mishkin, F S, 2001, "The Transmission Mechanism and the Role of Asset Prices in Monetary Policy, "National Bureau of Economic Research, NO.w8617. |
| [] | Nakajima, J and West, M , 2013, "Bayesian Analysis of Latent Threshold Dynamic Models". Journal of Business and Economic Statistics, 31(2), 151–164. DOI:10.1080/07350015.2012.747847 |
| [] | Nakajima, J and Watanabe, J , 2011, "Bayesian Analysis of Time-varying Parameter Vector Autoregressive Model for the Japanese Economy and Monetary Policy". Japanese Int.Economies, 25(3), 225–245. DOI:10.1016/j.jjie.2011.07.004 |
| [] | Primiceri, G E 2005, "Time Varying Structural Vector Autoregression and Monetary Policy". Review of Economics Studies, 72(3), 821–852. DOI:10.1111/roes.2005.72.issue-3 |
| [] | Ray, P and Chatterjee, S, 2001, "The Role of Asset Prices in Indian Inflation in Recent Years: Some Conjectures, " BIS Working Papers, NO.8. |
| [] | Roubini, N 2006, "Why Central Banks Should Burst Bubbles". International Finance, 9(1), 87–107. DOI:10.1111/infi.2006.9.issue-1 |
| [] | Smets, F, 1997, Financial Asset Prices and Monetary Policy: Theory and Evidence. Published by Bank for International Settlements, Monetary and Economic Department. |
| [] | Trichet, J C, 2003, "Asset Price Bubbles and Their Implications for Monetary Policy and Financial Stability, "The Implications for Monetary, Regulatory and International Policies, pp.15-22.Published by Federal Reserve Bank of Chicago. |
| [] | 陈继勇、袁威、肖卫国, 2013, 《流动性, 资产价格波动的隐含信息和货币政策选择--基于中国股票市场与房地产市场的实证分析》, 《经济研究》, 第 11 期, 第 43–55 页。 |
| [] | 陈守东、易晓溦、刘洋, 2014, 《货币供给、通货膨胀与产出波动的动态效应研究:1992-2013》, 《南方经济》, 第 2 期, 第 24–41 页。 |
| [] | 戴国强、张建华, 2009, 《我国资产价格与通货膨胀的关系研究--基于ARDL的技术分析》, 《国际金融研究》, 第 11 期, 第 19–28 页。 |
| [] | 纪敏、周源、彭恒文, 2012, 《资产价格影响通货膨胀了吗? --基于中国月度数据的实证分析》, 《国际金融研究》, 第 11 期, 第 23–29 页。 |
| [] | 罗忠洲、屈小粲, 2013, 《我国通货膨胀指数的修正与预测研究》, 《金融研究》, 第 9 期, 第 30–43 页。 |
| [] | 刘鹏, 2014, 《通货膨胀、资产价格波动与货币激活效应》, 《财经科学》, 第 6 期, 第 12–21 页。 |
| [] | 齐红倩、黄宝敏, 2013, 《房地产财富效应与中国城镇居民消费不对称性》, 《南京社会科学》, 第 6 期, 第 8–13 页。 |
| [] | 汪恒, 2007, 《资产价格对核心通货膨胀指数的修正》, 《数量经济技术经济研究》, 第 2 期, 第 92–98 页。 |
| [] | 邹新月、罗亚南、高杨, 2014, 《互联网金融对我国货币政策影响分析》, 《湖南科技大学学报 (社会科学版)》, 第 2 期, 第 84–89 页。 |



