美国货币政策利率工具的高效性,受到广泛的认可,然而其近年来以通胀为单一目标的货币政策体系也暴露出潜在的风险与执行效果上的欠缺,特别是在反思2008年美国金融危机前后的货币政策实施过程中,受到部分学者的质疑。在货币政策的执行过程中,如何有效地跟踪货币政策的执行效果,客观评价政策工具实施代价,对于正在推进利率市场化与发展货币政策工具的中国来说,更加重要。早在1995年,著名经济学家Solow, Taylor与Friedman在反思美国货币政策的过程中 (Solow et al., 1998),Solow讨论“美联储应该如何谨慎行事”时,强调了由Fuhrer (1995)提出的通货膨胀惯性 (简称通胀惯性, 也称作通胀持久性) 的概念与模型的重要性,通胀惯性为跟踪货币政策的执行效果与评价政策工具的实施代价,提供了一种理论框架与计量模型。2010年,在Friedman与Woodford组织的对2008年美国金融危机与货币政策的反思过程中,Fuhrer (2011)进一步定义和解释了通胀惯性的经济含义。
通胀惯性,最初的定义来自于对反通胀过程的研究。Fuhrer (1995)将其定义为通胀过程在受到货币政策冲击后,偏离均衡状态所持续的时间。由此,通胀惯性通常被认为是导致货币政策滞后效应的原因,此处的货币政策是指以货币供给量作为中介目标的货币政策体系。通胀惯性作为通胀率动态的结构性特征,从通胀过程受到单位冲击的角度考虑,主要以通胀率自回归过程的AR系数之和来衡量。考虑到近年来以利率为中介目标的货币政策体系的发展,Fuhrer (2011)在菲利普斯曲线与利率规则的基础上,推导出通胀惯性在以利率为中介目标的货币政策体系下,作为独立指标的经济含义。Fuhrer (2011)从通胀率前后期关系的角度考虑通胀惯性,依然是主要以通胀率自回归过程的AR系数之和来衡量。除了对货币政策效果的影响,作为以通胀率自回归过程的AR系数之和来度量的通胀惯性,也能代表更广泛意义上的整体价格的平稳性,其变动会直接导致通胀率自回归过程的结构性变化。由于通胀惯性无法直接观测且缺乏实时有效度量的计量方法,对该指标的认识并不充分,通常被简单的认为是一个接近1且长期稳定的数值。因此,其刻画通胀过程稳定性,乃至于广泛意义上的中长期整体价格稳定性的含义,容易被忽视。
早期以货币供给量为目标的货币政策,其现实操作中的滞后性缺点十分明显。但是其具备良好的自动反周期特性,货币紧缩政策导致实际GDP下降后,利率也会下降,从而缓解了实际GDP的下降。相比之下,以利率为中介目标的货币政策在现实执行中的滞后期大为缩短,但是对其实施的代价,目前还缺乏深入的认识与有效的度量方法。在理论分析上,流动性偏好理论认为两种政策工具没有本质区别。货币政策既可以用货币供给量来描述,也可以用利率来描述。增加货币供给量的操作将导致利率的降低,调低利率的操作也会导致实际货币供给量的增加,反之亦然。从近期粘性信息经济学理论的角度分析,两种类型的货币政策工具具有显著的区别,粘性信息经济学认为公众对利率信息更加敏感。不同经济学理论对菲利普斯曲线模型进行了不同方式的扩展,以解释社会实践过程中的通胀惯性和与其紧密相关的货币政策滞后性现象。例如Gali和Gertler (1999)提出结合理性预期与适应性预期的混合式菲利普斯曲线模型,来解释通胀惯性。Mankiw和Reis (2002)从信息更新过程的角度理解通胀惯性,建立了粘性信息菲利普斯曲线模型。
理论上的分析判断需要通过计量模型对数据的实证分析来检验,更多的计量经济学者尝试采用计量模型对通胀惯性进行度量和分析。Pivetta和Reis (2007)列举了三种度量通胀惯性的方法,包括 (1) 通胀率动态AR过程的滞后项系数之和; (2) 通胀率动态AR过程的最大特征根 (简称LAR) 的方式; (3) 计算单位冲击对通胀影响维持在0.5个单位根以上时间的半衰期法。其中第一种方法,得到最广泛的认可,被包括Taylor (2000)、Levin和Piger (2004)、Mishkin (2007)在内的文献所广泛采用。但是不管采用哪种方法,通胀惯性的度量都是以对通胀率动态的分析为基础的。有充分多的文献证实通胀率时间序列可能包含局部单位根过程,数据存在局部不平稳性,结构也存在不稳定性和结构断点。这不仅增加了研究通胀率动态本身的困难,更使得依赖其AR结构度量的通胀惯性指标,成为一个不可直接观测的潜变量。
为了通过研究通胀率过程以度量通胀惯性,各种能够兼容不平稳性和分析结构断点的方法与非线性模型被广泛的采用。Cogley和Sargent (2001)采用多元时变参数模型的贝叶斯方法判断美国的通胀惯性在20世纪70年代早期出现过上涨,在保持了10年左右的高通胀惯性后,转为下降。Levin和Piger (2004)分析了包含美、日等十二个工业国家的通胀惯性,认为多国的通胀惯性自20世纪80年代后,明显下降。Mishkin (2007)的结论支持Levin和Piger (2004)的判断。Nobay et al.(2010)采用平滑转移自回归模型 (简称STAR) 分析了2004年之前美国的通胀率,指出该数据全局平稳且局部存在单位根,并认为美国通胀惯性在1983年之后降低了。这些结论与包括Stock (2001)、Pivetta和Reis (2007)在内的研究结果相悖。Stock (2001)通过传统方法用最大特征根的估计值来说明在20世纪末的40年里,美国的通胀惯性一直居于高位,且几乎没有改变过。
在对我国通胀惯性水平与通胀动态的研究过程中,张屹山和张代强 (2008)认为我国通胀率是一个具有局部单位根的门限自回归过程,在减速通胀过程中是平稳的自回归过程,在加速通胀过程是具有单位根的自回归过程,且在两种状态下都存在高通胀惯性;张成思采用断点检验与“Grid Bootstrap”方法,对我国1980年-2007年的通胀过程进行分析,认为我国的通胀惯性即使在低通胀环境下,依然相当高。张凌翔和张晓峒 (2001)采用非线性单位根检验方法检验了我国通胀率过程的整体平稳性。也有学者从Friedman (1977)提出的通胀不确定性的角度分析通胀率过程的波动性,如何奇志和范从来 (2011)采用了Markov区制转移模型,认为通胀水平与波动性有着正相关关系。
学者们希望通过对通胀惯性的有效度量解释货币政策滞后效应的变化,而Keen (2007)基于Mankiw和Reis (2002)的粘性信息经济学模型的研究发现,货币政策的滞后效应与货币工具的选择具有关。当以货币供应为政策工具并存在真实刚性时,通胀对政策冲击的响应具有滞后性。若以名义利率为政策工具,通胀会在货币政策冲击之后立即达到峰值,不存在滞后效应。与过去相比,目前的货币政策多已转变为以利率为中介目标的政策工具来实施,这也促使Fuhrer (2011)重新定义和解释通胀惯性的经济含义。Fuhrer (2011)把简化菲利普斯曲线纳入通胀惯性模型,在以利率为中介目标的货币政策体系下,推导出通胀惯性作为独立指标的经济含义,并以此通胀惯性的经济理论模型为基础,分析认为频繁的使用货币政策工具以实现通胀率目标,将付出通胀惯性的代价。
本文从Fuhrer (2011)的基于菲利普斯曲线与利率规则的通胀惯性经济理论的模型出发,引入Fox et al.(2011)的Sticky HDP-HMM分层Dirichlet过程,将通胀率过程扩展为非线性的无限状态Markov区制转移的计量经济模型,以实现对通胀惯性的有效度量,检验利率工具对通胀惯性的影响与货币政策的代价。重点检验了金融危机前美国的货币政策工具对通胀惯性的影响,分析美国货币政策的执行效果与付出的代价。进而分析我国的通胀惯性与货币政策的执行效果,检验我国的通胀惯性近期受货币政策的影响情况。最后将中美放在共计十个国家的通胀惯性的对比中进行分析,全面总结通胀惯性的共性规律,进一步确认本文的实证结论。
二、 基于菲利普斯曲线与利率规则的通胀惯性模型 (一) 宏观调控过程中的菲利普斯曲线与通胀过程无论是从近期经济理论发展的角度,还是从货币政策的实践过程中分析,将通胀惯性仅作为通胀过程的动态特征来研究,是远远不够的。只有从通胀惯性的形成机理与经济活动内在关联的角度进行分析,才能全面的解释通胀惯性。
首先,从反通胀的货币政策执行过程中分析通胀惯性的含义。按照短期菲利普斯曲线的经济理论,在实施反通胀的紧缩货币政策后,经济沿着短期菲利普斯曲线向下移动,即更高的失业率与更低的通胀率位置。等完成短期向长期的转变后,通胀预期下降,短期菲利普斯曲线向左移动,失业率重回自然失业率水平。从政策执行的效果上看,通胀过程在受到货币政策冲击后,如果没有经过足够长的时间便达到了目标通胀率,那显然是通胀惯性受到了冲击,否则在高通胀惯性的情况下,通胀率只会缓慢达到控到政策目标。Fuhrer (1995)认为在反通胀过程中,较高通胀惯性推升反通胀成本,使“牺牲率”提高,即需要为降低一个百分点的通胀率付出更高的产出代价。例如,美国在1979年实施反通胀的货币政策后,于1983年实现通胀目标,而失业率在1987年才恢复到1979年的水平。在这次反通胀过程之前,持理性预期理论的经济学者认为,如果能传递更多的信息给公众,让公众相信通胀会下降,可以直接影响和降低通胀预期。从这种观点出发,降低通胀的代价应该比以“牺牲率”估算的小很多,甚至根本没有代价。其后的社会实践证明,美国在1979年开始实施的反通胀过程中,付出的代价虽然很大,但确实比“牺牲率”所计算的要低。而且当时向公众传递信息的渠道,也被证明确实还没有发挥出完全的作用。可见,影响通胀预期是达成最终政策目标的关键,而影响通胀预期的传导机制有两种:一种是存在滞后期的传导机制,即透过实际的经济过程调节总需求,改变社会中物品与劳务的供应量,在经济环境对政策敏感性不变的情况下,经过一个滞后期,在完成从短期向长期的转变后,改变通胀预期。另一种是不存在滞后期的传导机制,或者被称为“无代价”的方法,即没有经过实际的经济过程,也不需要等待短期向长期的转变,通过信息的传递或者其他手段,增强经济环境对政策敏感性,直接去影响通胀预期。显然每种货币政策都同时包含这两种传导机制。而Reis (2006)基于粘性信息理论认为,信息粘性对利率的敏感性要大得多,即利率工具所包含的第二种传导机制的成分更多。
相反,当采取扩张性货币政策时,经济沿着短期菲利普斯曲线向上移动,通胀率升高,失业率降低,在完成短期向长期的转变之前,货币政策体现出其非中性的作用。直到通胀预期上升,短期菲利普斯曲线向右移动,失业率回升到之前的水平,通胀率还保持在上升后的水平,货币政策恢复中性特征。可见在采取扩张性货币政策时,如果经济环境对政策敏感性较强,通胀预期改变得更快。在研究宏观经济的过程中,不能忽略货币政策本身的影响因素。
(二) 通胀惯性独立的经济含义与计量经济模型考虑到货币政策本身在经济过程中不可忽视的影响力,Fuhrer (2011)认为目前的政策制定者,有必要首先搞清楚目前本国的通胀惯性是否是源于经济结构自身特点的,具有独立于通胀率过程的经济含义,可以被认为是经济形势的稳定特征的经济指标,还是其货币政策行为作用于经济结构的结果。从通胀惯性具有的独立经济含义出发,对其结构性根源进行分析,可概括为三个方面:(1) 继承自可驱动通胀过程的行为,例如产出缺口与边际成本; (2) 独立于其驱动过程的,通胀过程自身的内在特征; (3) 央行在明确通胀目标并付诸实施的行为。Benati (2008)指出央行在达成本国通胀目标的过程中,可以感受到惯性的下降。
理论上的分析,需要建立计量经济模型来检验。Fuhrer (2011)把简化的菲利普斯曲线与货币政策纳入通胀惯性模型,简单而全面的刻画了通胀、产出、利率的关联,以及宏观经济环境中的敏感性与通胀惯性的关系。Fuhrer (2011)为通胀惯性定义的计量模型由 (1)-(5) 式组成。其中 (1) 式事实上是菲利普斯曲线的简化形式,表示当期通胀率πt对滞后一期通胀率πt-1的改变与产出缺口xt成正比,系数是a,代表通胀变化对产出缺口的敏感性。(2) 式表达了产出缺口xt与代表货币政策的短期政策利率ft的负相关关系,系数是b,代表产出缺口对货币政策的敏感性。而 (3) 式表示短期政策利率ft作为通胀的正相关函数 (隐含通胀目标是0),系数是c, 代表货币政策对通胀的积极响应程度。
| $ {\pi _t} = {\pi _{t - 1}} + a{x_t} $ | (1) |
| $ {x_t} = - b{f_t} $ | (2) |
| $ {f_t} = c{\pi _t} $ | (3) |
而通胀率与其滞后项关系,被简化为 (4) 式所表述的AR (1) 过程,其AR系数之和g,用于度量通胀惯性。将 (2)-(4) 式先后带入 (1) 式可得 (5) 式,(5) 式左侧代表通胀惯性的g由 (1)-(3) 式中的a、b、c三个系数标出。
| $ {\pi _t} = g{\pi _{t - 1}} $ | (4) |
| $ g \equiv \frac{1}{{1 + abc}} $ | (5) |
从Fuhrer (2011)的通胀惯性模型可以看出,其对通胀惯性的理解,与Fuhrer (1995)之前对通胀惯性的定义相比已经有所推进,新定义从更多变化的角度考虑通胀惯性,并可以得出两点重要的判断:首先,当利率对通胀的响应更加频繁,导致c增大时,通胀惯性g将随之降低。其次,当通胀预期对货币政策的通胀目标更加敏感时,(4) 式所代表的通胀率AR结构的稳定性将被打破,其AR系数之和可能产生倾向于通胀目标的方向变化,使通胀过程加速达到通胀目标。本文的实证分析将对Fuhrer (2011)的通胀惯性理论的新模型加以检验,分析频繁的利率政策工具对通胀惯性的影响。
三、 通胀惯性的无限状态Markov区制转移模型 (一) 基于分层Dirichlet过程的无限状态Markov区制转移模型Fuhrer (2011)的通胀惯性理论模型中的描述的通胀率过程,实际上是一个结构不稳定的动态过程,为了全面的反映其结构变化,有效度量通胀惯性。本文从 (4) 式所描述的通胀动态过程出发,扩展为无限状态Markov区制转移模型 (简称IMS)。对其可能存在不平稳性与结构不稳定性的AR过程进行无限状态的区制拟合。有别于有限状态数量的区制模型,这种IMS模型可以通过其MCMC过程中,由后验分布产生的不限状态数量的不同区制的AR结构对数据的充分拟合,得到AR系数之和的后验中值无偏估计。虽然具体形式不同,但各种基于区制假设的模型,在分析的过程中都存在检验区制数量的问题。除了通过某种方法检验再确定区制数的方法以外,在无限状态的先验假设下,进行区制分析的方法体系,被越来越多的学者所采用。必须给定区制数量作为约束条件的根源,是模型的迭代过程中依赖于Dirichlet分布 (两区制时退化为Beta分布) 作为区制演化过程的先验分布或前提假设。Dirichlet分布只能在给定维度的有限状态下迭代更新,而基于动态变化的Dirichlet分布形成的Dirichlet过程 (Dirichlet Process),是可以在迭代中,自主更新区制数量的无限状态随机过程Ferguson (1973)。这种可以从数据中挖掘出更多信息的方法,在不断解决多个领域的复杂数据问题的过程中,业已成为一个完善的非参数方法体系,且应用广泛。Fox et al.(2011)将分层Dirichlet过程与隐性Markov模型相结合,提出了带有粘性的无限状态隐性Markov模型 (Sticky Infinite Hidden Markov model, 简称Sticky HDP-HMM,这是一种最新的分层Dirichlet过程),并采用这种模型,实现了对混杂语音记录的有效识别。在计量经济学领域,Jensen和Maheu (2011)将其引入随机波动率模型 (简称SV-DPM),捕捉更多未知信息,提升了分布预测效果。Jensen和Maheu (2013)亦将其引入多元GARCH模型 (简称MGARCH-DPM),提高了投资组合的波动预测效果。Jochmann (2015)基于Fox et al.(2011)的Sticky IHMM模型实现针对美国通胀率动态的区制结构断点的检验方法。Song (2012)基于Fox et al.(2011)的Sticky HDP-HMM模型,将区制转移与结构断点检验方法融合起来,分析美国实际汇率问题。本文设计并实现的IMS模型,其实质是以Fox et al.(2011)的Sticky HDP-HMM分层Dirichlet过程为先验条件,将Kim和Nelson (1999)的贝叶斯Markov区制转移模型扩展到无限状态,结合K-Means算法构建出的无限状态Markov区制转移模型。为通胀惯性构建的IMS模型,可实现对通胀惯性的有效度量与区制分析,为检验通胀惯性的变化与Fuhrer (2011)模型的有效性提供了工具。
通胀惯性是以通胀率过程的AR系数之和度量的,其IMS计量模型以 (6) 式所示的通胀率过程为基础,其中πt代表t时期的通胀率,数据的总长度是T。β0, St代表截距项,其下角标中的0代表它是截距项,其下角标中的st代表t时期πt所处的区制状态序号,在无限状态的假设条件下,该值在理论上可以为任意正整数。st在后续各式中保持与此相同的含义。m代表模型所考察的最大滞后阶数。每个滞后项πt-i的系数β0, St的下角标代表它是滞后i期的系数,且处于序号为st的区制状态。包括截距项β0, St,滞后项系数β0, St与如 (11) 式所示的服从正态分布的随机误差项εt的方差σ2st都被设计为区制转移项,用以充分适应通胀率过程的动态特征,使其滞后项系数与波动特征得以被充分度量。通胀惯性由 (7) 式中的gt表示,即t时刻的滞后项系数之和。由于区制转移过程的存在,所以gt是时变的,而且在无限状态假设下,gt可以重复已有的区制,也可以转换到未知的全新区制,这使得IMS模型既可以度量到通胀率过程的极端情况,也可以充分刻画其短期结构的变化。(6) 式中的参数在每个区制状态下的值以双层分布过程抽取,类似Kim和Nelson (1999)所设计的贝叶斯方法,这些分布的设定也是根据共轭分布族来确定的。其中的截距项和滞后项系数,如式 (8) 所示,服从多元正态分布,该分布的均值向量μ与多元协方差矩阵Σ的值由 (9) 式与 (10) 式所示的第二层分布来抽取。第二层分布依旧是根据共轭分布族确定,如μ的先验分布是正态分布,其均值b0与方差Β0的数值是作为超参数设定的。Σ的先验分布是逆Wishart分布,m0是该分布的自由度参数,Z0是其尺度矩阵参数,这两个参数也是作为超参数设定的。σ2st如 (12) 式所示服从逆Gamma分布,c0是其形状参数,d0为尺度参数。在 (8) 至 (12) 所描述的双层共轭分布结构中的状态参数潜变量st,它的后验边缘分布是由分层Dirichlet过程动态模拟形成的。
| $ {\pi _t} = {\beta _{0, {s_t}}} + \sum\limits_{i = 1}^m {{\beta _{i, {s_t}}}{\pi _{t - i}} + {\varepsilon _t}}, \;\;\;\;\;\;t = 1, \cdots, T. $ | (6) |
| $ {g_t} = \sum\limits_{i = 1}^m {{\beta _{i, {s_t}}}}, \;\;\;\;\;\;\;t = 1, \cdots, T. $ | (7) |
| $ {\beta _{., {s_t}}}\sim{\rm{N}}\left({\mu, \sum } \right), \;\;\;\;\;\;\;t = 1, \cdots, T. $ | (8) |
| $ \mu \sim{\rm{N}}\left({{{\rm{b}}_0}, {{\rm{B}}_0}} \right), $ | (9) |
| $ \sum \sim{\rm{Inv - Wishart}}\left({{Z_0}, {{\rm{m}}_0}} \right) $ | (10) |
| $ {\varepsilon _t}\sim{\rm{N}}\left({0, \sigma _{{s_t}}^2} \right), \;\;\;\;\;\;\;t = 1, \cdots, T. $ | (11) |
| $ \sigma _{{s_t}}^2\sim{\rm{Inv - Gamma}}\left({{{\rm{c}}_0}, {{\rm{d}}_0}} \right), \;\;\;\;\;\;\;t = 1, \cdots, T. $ | (12) |
所谓分层结构的Dirichlet过程是由 (13) 与 (14) 式所示的,一个两层结构的随机抽取过程。其中第一层的γ是由 (13) 式所代表的stick-breaking过程即“断棍过程”所产生的分布特征参数向量,也是第二层Dirichlet过程的超参数之一。DP代表一个标准的Dirichlet过程,α, η, κ是超参数,在 (14) 式所表达的DP过程中,第一个设定参数值α+κ对应可能新出现的状态,第二个参数是由δj值与α, η, κ组成的如 (14) 式所示的计算结果得到的向量,对应于已出现过的既有状态。其中δj的下角标j与ωj的相同时,δj的值为1,否则为0。κ代表粘性系数,从 (14) 式中不难发现,κ的值越大,DP过程向自转移收敛的速度更快,不同的粘性系数κ适用于处理不同学科领域中自转移倾向的数据,Fox et al.(2011)给出了这些超参数设定的法则。第二层的DP过程不仅捕获出可能存在状态数量,同时为序号为j的状态抽取代表该状态向包括其自身的所有状态转移的概率测度向量ωj,进而用于在 (13) 所示的从t-1时点的状态st-1抽取下一时点的状态即st的多项式分布的参数向量。Fox et al.(2011)设计的Sticky HDP-HMM分层Dirichlet过程即由 (13) 至 (15) 式表示的,可抽取代表不同时期所处区制状态的潜变量向量S=(s1, …, sT) 的边缘后验分布。
| $ \gamma \sim {\rm{stick}} - {\rm{breakin}}g\left(\eta \right) $ | (13) |
| $ {\omega _j}|\alpha, \gamma, \kappa ~{\rm{DP}}\left({\alpha, \kappa, \frac{{\alpha \gamma + \kappa {\delta _j}}}{{\alpha + \kappa }}} \right), \;\;\;\;j = 1, \cdots, \infty, $ | (14) |
| $ {s_t}~multinomial\left({{\omega _{{s_{t - 1}}}}} \right), \;\;\;\;\;t = 1, \cdots, T. $ | (15) |
与Kim和Nelson (1999)基于贝叶斯方法的Markov区制转移模型相比,本文将无限状态的假设条件下,基于以上分层Dirichlet过程设计的此模型称之为无限状态的Markov区制转移模型,其状态的数量随着Gibbs过程的循环迭代过程,通过Dirichlet过程不断与数据本身的特征相匹配而更新。
(二) 混合分层结构的Gibbs算法实现通过本文对所构建的无限状态Markov区制转移模型的描述,可以看出该模型的设定充分考虑到了通胀率过程可能存在单位根过程的不平稳性,过程中的结构不稳定性,随机扰动项波动方差的不确定性。该模型借助对通胀率过程的拟合,度量通胀率的滞后项系数之和,即通胀惯性的计量指标,并通过区制分析的方式识别通胀惯性的区制状态,为研究与监控通胀惯性,扫清了技术障碍。
本文通过将 (13) 至 (15) 式所表示的分层结构Dirichlet过程与 (8) 至 (12) 式所表示的分层结构的共轭分布族过程,耦合于两种分层结构共同包含的区制状态潜变量向量S,以Chib (1996)的向前滤波与向后抽样算法 (Forward-Filtering,Backward-Sampling) 对耦合过程进行模拟抽样,以此为核心实现IMS模型的混合分层结构的Gibbs算法,进而完成模型中所有无限状态区制转移变量的后验无偏估计。具体步骤描述于本文的附录A,并由C++编程实现,以用于本文的实证研究,其中矩阵运算部分采用了著名的lapack与blas开放标准运算库,以确保计算过程的准确性和提高程序运行的整体性能。
四、 通胀惯性与货币政策的实证分析 (一) 美国通胀率动态分析美国的通胀惯性一直是众多学者关注与争论的焦点,直到近期才达成相对接近的结论。在Stock (2001)对持美国通胀惯性有所下降观点的Cogley和Sargent (2001)进行评论时,作出四点与之相反的判断,Stock (2001)认为:第一,美国在20世纪末的40年时间里,通胀惯性大致是不变的,并且始终较高; 第二,通胀与通胀惯性不存在正相关的关系; 第三,通胀的自回归过程的结构是稳定的,至少是很难做出拒绝其稳定性的假设; 第四,从真实经济活动和通胀的关系上来说,简化形式的菲利普斯曲线是稳定的。
进入21世纪之后,更多的社会实践经验与实证分析显示美国的通胀惯性已经悄然改变。自美国1979年为治理了其20世纪70年代的大通胀过程,付出较高成本后,还曾在1989年前后通过十多次连续提高联邦基金基准利率的方式,以两年的微弱经济衰退的代价平抑了通胀率。在2001年为应对网络泡沫破灭与恐怖袭击后可能的衰退,下调利率十多次。2008年应对金融危机后可能的衰退,把联邦基金基准利率调到了接近0利率的0.25%。从社会实践上可以看出,美国在20世纪80年代之后的货币政策操作,其政策效应显现的滞后期明显变短了。包括Taylor (2000)、Levin和Piger (2004)、Mishkin (2007)的研究也都认为美国的通胀惯性在20世纪80年代之后明显降低了。Fuhrer (2011)在对比和总结了通胀惯性相关文献的研究成果后,认为可以得出美国的通胀惯性已经发生变动的结论,并以基于菲利普斯曲线与利率规则的通胀惯性模型做出解释,从理论的角度分析是频繁的利率操作,使美国经济付出了通胀惯性的代价,本文的实证研究首先检验Fuhrer (2011)的理论观点。
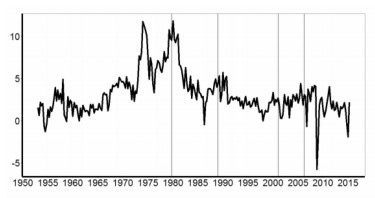
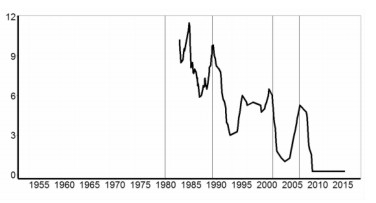
本文采用被广泛认为能充分代表美国通胀过程的,如图 1a所示的1953年至2015年第2季度的美国个人消费支出平减指数 (简称PCE) 的季度数据来分析美国通胀惯性,数据来源于美国联邦储备局网站,并根据贝叶斯信息准则选择滞后3阶进行分析。并检验美国通胀惯性与图 1b所示的美国联邦基金利率之间的一致性关联关系。
|
图 1a 美国PCE通胀率 |
|
图 1b 美国联邦基金利率 |
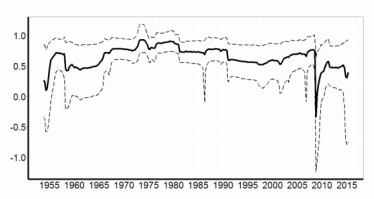
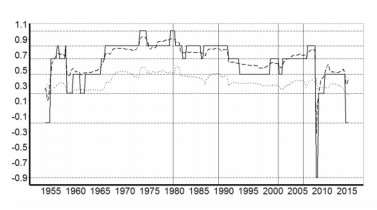
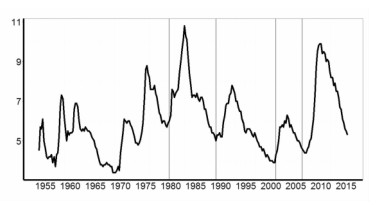
图 2a显示了本文采用IMS模型对美国PCE通胀惯性的后验中值估计,图 2a的AR系数和与图 2b的最大特征根相比,形态相似,但是后者要更加平坦一些。两种方法虽然都反映了相同AR过程的结构变化,但是毕竟计量的方式不同。本文主要以大多数文献采用的AR系数和的方式对通胀惯性进行度量,并参考最大特征根的结果,检验通胀率存在单位根过程的可能性。图 2a与图 2b中的实线代表后验中位数估计,上下虚线分别代表 10%与90%分位数估计。其中1972年至1986年左右的度量结果与Stock (2001)的结果相近,即美国“大通胀”期间,AR系数和与最大特征根局部接近或超过1的概率较高。1953年至2012年的度量结果与Jochmann (2015)得出的估计值接近。从AR系数和与最大特征根都可以判断出1986年之后,通胀惯性的短期变化趋势明显。特别是将图 2a的通胀惯性估计值与图 1a所示的美国PCE通胀率数据的短期变化相比,发现自从1989年前后美国采用利率工具调控通胀之后,在越接近2008年的时间里,通胀惯性与通胀率的短期变化趋势越显得一致。而在此之前,即便通胀率的波动更加剧烈,通胀惯性亦基本保持稳定。进一步通过图 2c的区制分析,发现在1989年的调控之后,伴随着调控效果的逐步显现,通胀惯性明显下降了两个区制。图 2c中的实线代表最大概率的区制状态,虚线是以AR系数和估计的通胀惯性指标,下方点线代表处于此区制状态的概率,多条水平的虚线代表不同区制状态的通胀惯性指标水平,四条竖线突出标注出相关事件的关键时点。对照图 2b的美国联邦基金利率的操作过程可以发现,在1989年之后频繁的利率工具的作用下,通胀率在2006年之前,一直被控制在目标区域范围内,波动也明显降低了。在此过程中,通胀惯性没有使货币政策执行效果像1979年那样产生很长的滞后期,而且还明显的与通胀率一起在响应利率工具的调控作用。此时的通胀惯性在利率上升时下降,在利率下降时转为上升。直到2008年金融危机期间,通胀惯性短期触底之后,由于美国联邦基金利率已无再降空间而保持在接近0利率的水平后,通胀惯性开始逐渐恢复,至今仍明显低于金融危机前的水平。与通胀过程越发及时的响应利率操作的现象不同,图 2d所示的美国失业率数据滞后于利率操作的时长,似乎一直保持在3年左右滞后期水平。可见,频繁的利率操作加快了通胀率的调控效率,付出了通胀惯性的代价,却对实际经济的影响有限。
|
图 2a AR系数和的后验分位数 |

|
图 2b 最大特征根的后验分位数 |
|
图 2c 美国PCE通胀惯性的区制分 |
|
图 2d 美国失业率 |
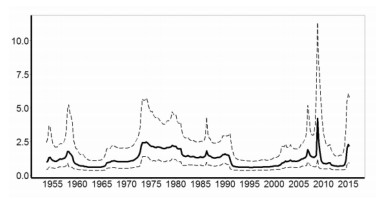
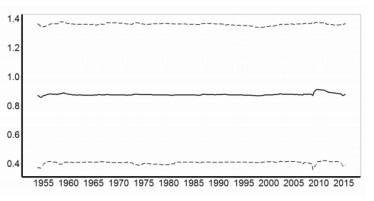
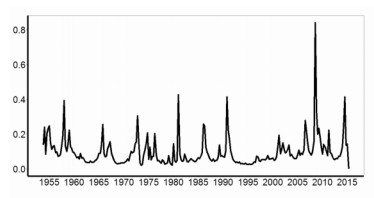
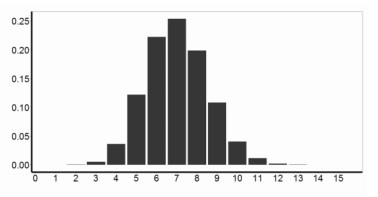
进一步对图 3a显示的扰动项方差估计结果进行分析,可以看出,通胀率过程的不同阶段受到的冲击扰动因素不同,其扰动项方差存在明显的不确定性,并且在“大通胀”与“金融危机”期间波动较大。从图 3b可以看出整个通胀率过程的截距项相对平稳,其动态过程主要受AR结构变化的驱动。从图 3c可以看出通胀率过程存在多个概率超过30%的结构断点。从图 3d显示的区制数量分布来看,通胀过程最大可能性的区制数量是7。
|
图 3a 扰动项方差的后验分位数 |
|
图 3b 截距项的后验分位数 |
|
图 3c 区制断点概率图 |
|
图 3d 区制数量的后验分布 |
为确认是利率调控对通胀惯性的影响,特别是在2008年美国爆发金融危机之前的这段时期,利率调控与通胀惯性变化之间的相关性,本文借鉴Dionísio et al.(2006)采用互信息手段检验非线性时间序列相关性的方法,检验美国利率数据与美国通胀惯性之间的一致性关联指数。所谓两个变量之间的互信息即I(X, Y) 由 (16) 式所示,为其联合熵H(X, Y) 与条件熵H(Y|X) 之差,也可表示为两个变量的熵与其联合熵H(X, Y) 之差。进一步可由 (17) 式中的联合密度函数pX, Y(x, y) 与边缘密度函数的计算公式得出。将互信息即I(X, Y) 作形如 (18) 式的变化,即得到两个变量的一致性关联指数,即式 (18) 中表示的λ(X, Y)。该指数介于0和1之间,数值越高相关度越高,接近于1代表接近于完全的一致性关系。
| $ I(X, Y) = H(X, Y) - H(Y|X) = H(X) + H(Y) - H(X, Y) $ | (16) |
| $ I(X, Y) = \int {\int {{p_{x, y}}\left({x, y} \right)\ln \frac{{{p_{x, y}}\left({x, y} \right)}}{{{p_x}\left(x \right){p_y}\left(y \right)}}} } dxdy $ | (17) |
| $ I(X, Y) = \left\{ {1 - {e^{ - 2I\left({X, Y} \right)}}} \right\} $ | (18) |
本文所采用的互信息检验工具为R软件平台中的entropy软件包。通过互信息检验发现,美国2001年至2007年之间的利率与通胀惯性的一致性相关指数达到了0.94的极高水平,而在2001年之前,该指数维持在0.76至0.89之间。本文也采用美国CPI通胀率数据对美国的通胀惯性进行了分析和检验,结果与基于PCE通胀率的分析结论一致。这说明通胀惯性在频繁的利率调控影响下,在特定期间内几乎受控于货币政策工具的调整而改变,短期内已经部分脱离了经济结构自身的特点,更倾向于反映货币政策行为作用的结果。
综上所述,美国的通胀惯性在采取单一的利率工具,单一的通胀目标后,其通胀惯性不断受到利率政策的影响而下降,验证了Fuhrer (2011)的分析,即当利率对通胀的响应更加频繁时,将付出通胀惯性的代价。在美国央行不断加快达到其通胀目标的同时,也加快了对通胀预期的直接影响,联系着实际通胀率与通胀预期目标的通胀惯性指标,不仅不能对货币政策产生足够的滞后效应,而且还表现出顺应通胀率达到通胀目标的变化趋势。由此可见,美国单一工具与单一通胀目标制的货币政策,对短期调控效率的提升,是以损失经济环境中广泛意义上的中长期整体价格稳定性作为代价的,为经济埋下了隐患。
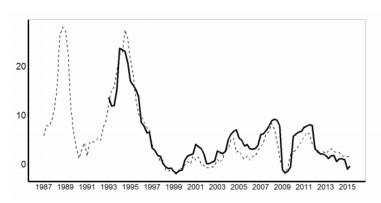
(二) 从通胀惯性看我国宏观调控政策的执行效果前述的实证分析表明,在利率市场化体系成熟的美国,频繁的利率操作在提高通胀调控效率的同时,付出了通胀惯性的代价,却对实际经济的影响有限。对于坚持实行多目标制的我国,在逐步推进利率市场化的进程之中,是否也存在或者将会出现类似美国的现象?这需要通过实证的检验来分析。本文重点选取了被广泛认为能全面反映我国通胀总体状况的GDP平减指数 (GDP_D) 与居民消费价格指数 (CPI) 的季度数据,对我国的通胀惯性进行实证研究。数据来源于国家统计局网站。GDP_D选取1993年1季度至2015年2季度时间段的季度数据,通过贝叶斯信息准则选取滞后2阶模型进行分析。CPI选取1987年1季度至2015年2季度时间段,通过贝叶斯信息准则选取滞后6阶的模型进行分析。如图 4a所示,其中实线代表的是GDP_D,虚线代表CPI。
|
图 4a 中国GDP_D与CPI通胀率 |
结合图 4b所示的1年期人民币贷款基准利率与图 5a、图 5b的我国通胀惯性估计值与区制分析的结果,可以发现在1996年实现“软着陆”之前,我国投资建设的扩张阶段,通胀惯性出现过类似美国在20世纪70年代的“大通胀”时期的峰状特征。我国的GDP_D与CPI通胀过程的最大概率区制数均为5,在“软着陆”之前通胀惯性甚至存在达到或超过1的区制状态,对应的是高通胀的通胀率单位根过程。“软着陆”之后我国的GDP_D通胀惯性一直比较稳定。GDP_D通胀惯性在2003年之后转换进入高位运行,暗示之后的潜在通胀风险,但一直在过程中保持稳定。直至2007年与2008年间出台连续密集的紧缩政策后,GDP_D通胀惯性在2008年中向下探底,其后又受到金融危机期间扩张性政策的影响,于2009年末回到了高惯性区制。货币政策在2010年再次紧缩,2011年末适度放松后,GDP_D通胀惯性降到稍低的区制水平。从图 5a中可以看出,我国的GDP_D通胀惯性在稳定了十多年之后,于近期开始对货币政策做出相对频繁的响应,由于相对谨慎的使用利率工具,使我国的通胀惯性在被货币政策短暂影响后,及时恢复到依然较高的稳定水平。

|
图 4b 中国人民币贷款基准利率 |

|
图 5a 中国GDP_D通胀惯性 |

|
图 5b 中国CPI通胀惯性 |
如果从图 5b所示的CPI通胀惯性的来看,即便是近期相对密集的货币政策,也没有撼动我国CPI通胀惯性的稳定水平。这说明,我国的货币政策主要对生产与投资过程中的通胀惯性产生了影响。为了确认这一判断,本文进一步对我国的商品零售价格指数 (RPI),工业生产者出厂价格指数 (PPI) 与工业生产者购进价格指数 (RPIRM) 的通胀惯性进行检验, 通过贝叶斯信息准则选取RPI滞后5阶、PPI滞后1阶、RPIRM滞后1阶进行分析。
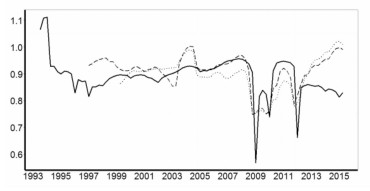
图 6b中的虚线代表RPI通胀惯性,虽然没有以CPI估计的结构一样平稳,但是与图 6a中虚线代表的PPI与点线代表的RPIRM的通胀惯性度量结果相比,可以确认我国的货币政策主要对生产与投资过程中的通胀惯性产生了影响。由此可见,虽然与美国相比,我国的通胀惯性依然稳固,但是随着我国利率市场化体系的发展,传导效率的提高,Fuhrer (2011)提示的利率工具对通胀惯性的冲击效应初步显现。警示我国在货币政策的实施过程中应慎用价格型政策工具。从图 4b可以看到,自2014年以来,我国央行已较为谨慎的使用利率工具。2015年,随着经济下行压力持续加大,我国央行两次交错使用了降息和降准的货币政策工具,两次同时执行了降息降准的货币政策,用以降低社会融资成本和释放流动性。从图 6a中可以看出, GDP_D与生产和成本环节的PPI与PPIRM指数的通胀惯性近期呈现分化趋势。PPI与PPIRM指数的通胀惯性增强,说明其近期的通缩状态将趋于常态化。而被投资相关的价格水平占据更大权重的GDP_D,其通胀惯性的持续低迷,体现了投资增速放缓对经济的不利影响。随着降息降准等货币政策工具的持续作用,GDP_D的下降态势将有所缓和。
|
图 6a 中国GDP_D、PPI与PPIRM通胀惯性 |

|
图 6b 中国CPI与RPI通胀惯性 |
为了进行对比分析,确认通胀惯性的一些共性规律,本文进一步选取了加拿大、英国、法国、德国、意大利、日本、韩国与泰国等国家的CPI通胀率数据①,借助IMS模型进行对比分析,图 7给出了包含中美在内的十个国家的CPI通胀惯性指标后验中值估计。

|
图 7 各国通胀惯性的后验中值估计 |
① 本文选取的季度同比数据包括:中国CPI (1987Q1-2015Q2)、美国CPI (1953Q1-2015Q2)、加拿大CPI (1945Q1-2015Q2)、英国CPI (1989Q1-2015Q2)、法国CPI (1999Q1-2015Q2)、德国CPI (1992Q1-2015Q2),意大利CPI (1997Q1-2015Q2)、日本CPI (1971Q1-2015Q2)、韩国CPI (1976Q1-2015Q2) 与泰国CPI (1977Q1-2015Q2)。数据来自中国国家统计局网站,美国联邦储备银行网站与Wind数据库。
通过对十个国家通胀惯性的对比分析,可以看到不同国家的通胀惯性都存在较为稳定的区制状态。在加速通胀时期,各国通胀惯性的形态基本一致,即出现“大通胀”时期特征的峰状形态。例如二战后加速投资建设时期的加拿大,20世纪70年代的美国、日本、韩国、泰国,20世纪90年代的我国。在这种加速通胀时期,通胀过程的AR系数和或最大特征根 (LAR) 的估计值往往存在达到或超过1的情况,即存在单位根过程。在这种AR结构驱动的通胀的过程中,通胀惯性在稳定状态偏上的位置震荡,驱动加速通胀过程。在相对稳定的时期,通胀惯性也会出现相对平坦的峰状特征过程,如果不加以重视,放任其发展,存在逐渐演变出为高通胀过程的风险,进而被迫进行更大代价的反通胀操作。
各国在经历与应对经济危机的过程中,例如1992年的欧洲货币危机期间的英国与德国;1997年亚洲金融危机期间韩国与泰国;2007-2009年金融危机期间的美国;受危机冲击与本国政策的影响,通胀惯性都出现了短暂的急促变化,通胀过程在相对短期内出现结构断点的概率短促拉升,波动的幅度也随之短暂拉升。总之,无论是由内部结构驱动的持续通胀过程,还是受到政策与环境冲击的短期结构变化,通胀惯性从长期看都会在经济环境稳固后回到稳定状态。其中韩国的通胀惯性在亚洲金融危机之后,稳定在了下降后的水平。而泰国在走出危机后,通胀惯性依然相对缺乏稳定性。
为了对比各国通胀惯性的曲线形态,图 7的纵坐标被设置为根据数据的差异而不同,如果还原图 7的纵坐标为统一尺度,将很容易的看出,在十国之中大部分国家的通胀惯性的实际变化范围是非常有限的。例如加拿大的通胀惯性,几乎可以被看作是一条水平直线。可见虽然很多国家都实施了单一目标制与基准利率工具,但是由于各国的经济情况不同,货币政策工具的效率与执行方式也不同,其货币政策的影响与实施效果也不尽相同。
本文对各国通胀惯性在其状态的平稳期,进行简单的均值统计,如表 1所示。相比之下,我国属于通胀惯性较高的国家,但这并不意味着我国的货币政策的滞后期一定很长,因为通胀惯性在货币政策的过程中并非一定是固定不变的。同时这也从一个侧面表明,我国的宏观经济的运行具有一定的稳定性。
| 表 1 各国的通胀惯性比较 |
本文的研究证实货币政策工具在加速实现政策效果的同时,也导致了通胀惯性的不稳定,甚至打破了通胀惯性所代表的经济形势的整体稳定性,暴露出单一目标货币政策框架的缺陷。正如包括Mishkin (2010)在内的针对2007年至2009年金融危机的反思文献所达成的共识:单纯的或者过分的强调通胀目标的达成,可能付出更大的成本。通胀预期在通货膨胀决定与货币政策向宏观经济传导的过程中,起到非常关键的作用。货币政策与金融体系的影响力,可能超过了原本的认识水平,仅通过中介目标实现的货币政策,不能达成所有的目标,必须强调稳定通胀预期与宏观审慎监管的重要性。
本文的实证分析表明:第一,通胀率过程存在结构不稳定性,包含结构变点,并在高通胀区域内,存在单位根过程。第二,通胀率的动态过程除了受不确定性波动因素的影响之外,主要受AR过程的结构性变化所驱动,即以其AR系数之和度量的通胀惯性并非稳定不变,其脱离稳定状态的变化可直接驱动通胀率过程。第三,虽然通胀惯性存在相对稳定的区制状态,但是在高通胀过程中,通胀惯性会向上震荡,并形成峰状特征,这种特征在不同国家的实证分析中普遍存在,有助于分析通胀风险。第四,美国近期通胀惯性产生了区制变动,与其基准利率政策高度相关,证实了Fuhrer (2011)通胀惯性模型的有效性,警示利率工具频繁使用的代价。利率工具在加速实现政策效果的同时,也导致了通胀惯性的不稳定,甚至在金融危机期间短暂失效,打破了通胀惯性所代表的广泛意义上中长期整体价格的稳定性,暴露出单一目标货币政策框架的缺陷。第五,我国的通胀惯性也明显对近期的利率政策做出了值得关注的响应,显示我国已经初步形成了较为敏感和有效的市场化利率体系与传导机制,提升了我国货币政策效率的同时,也凸显了组合政策工具与完善宏观审慎政策框架的重要性。第六,合理的政策滞后期效应,使我国的通胀惯性在被货币政策短暂影响后,可以有足够的时间有效恢复。第七,2014年至2015年,我国央行多次降准降息等系列货币政策工具的采用,辅以综合利用其他多种提供流动性的工具,可在维持通胀惯性基本稳定的状态下,实现抵御通缩的作用。
我国目前处于经济转型升级的过程中,且受到国内外多重因素的影响,为保持经济的平稳增长,要求货币政策同时兼顾维护低通胀、促增长,保就业、维护国际收支平衡与维护价格总水平基本稳定等多重目标。在这种环境下,科学的货币政策与合理的政策滞后期,综合利用多种提供流动性的工具,有利于保持通胀惯性的长期稳定。这表明坚持实行多目标、多手段与宏观审慎政策相结合的调控模式,对我国经济中长期发展与维护经济环境稳定的重要性。
| [] | Beal, M.J. , Ghahramani, Z. and Rasmussen, C.E. , 2002, "The infinite hidden Markov model,". Advances in Neural Information Processing Systems, 14, 577–584. |
| [] | Chib, S. 1996, "Calculating posterior distributions and modal estimates in Markov mixture models,". Journal of Econometrics, 75, 79–97. DOI:10.1016/0304-4076(95)01770-4 |
| [] | Cogley, T. and Sargent, T.J. , 2001, "Evolving post-world war Ⅱ U.S.inflation dynamics,". NBER Macroeconomics Annual, 16, 331–373. |
| [] | Cecchetti, S.G. and Debelle, G. , 2006, "Has the inflation process changed?,". Economic Policy, 21, 311–352. |
| [] | Dionísio, A. , Menezes, R. and Mendes, D. , 2006, "Entropy-Based Independence Test,". Nonlinear Dynamics, 44, 351–357. DOI:10.1007/s11071-006-2019-0 |
| [] | Ferguson, T S. 1973, "A Bayesian analysis of some nonparametric problems,". The Annals of Statistics, 1, 209–230. DOI:10.1214/aos/1176342360 |
| [] | Friedman, M. 1977, "Inflation and Unemployment,". Journal of Political Economy, 85, 451–472. DOI:10.1086/260579 |
| [] | Frühwirth-Schnatter, S. 2008, "Comment on article by Rydén,". Bayesian Analysis, 3, 689–698. DOI:10.1214/08-BA326A |
| [] | Fuhrer, J.C. 1995, "The Persistence of Inflation and the Cost of Disinflation,". New England Economic Review, 1, 3–16. |
| [] | Fuhrer, J.C., 2011, "Inflation Persistence", in Handbook of Monetary Economics (Vol.3A).Eds.by Benjamin, M.Friedman and Michael, Woodford., pp.423-486.Published by North-Holland. |
| [] | Fox, E. , Sudderth, E. , Jordan, M. and Willsky, A. , 2011, "A sticky HDP-HMM with application to speaker diarization,". Annals of Applied Statistics, 5, 1020–1056. DOI:10.1214/10-AOAS395 |
| [] | Gali, J., and Gertler, M., 1999, "Inflation Dynamics: A Structural Econometric Analysis", Journal of Monetary Economics, No.44, pp.195-222. |
| [] | Jensen, M.J. and Maheu, J.M. , 2013, "Bayesian semiparametric multivariate GARCH modeling,". Journal of Econometrics, 1, 3–17. |
| [] | Jensen, M.J.and Maheu, J.M., 2010, "Bayesian semiparametric stochastic volatility Modeling, " Journal of Econometrics.157, pp.306-316. |
| [] | Jochmann, M. 2015, "Modeling U.S.Inflation Dynamics: A Bayesian Nonparametric Approach,". Econometric Reviews, 34, 537–558. DOI:10.1080/07474938.2013.806199 |
| [] | Keen, B.D. 2007, "Sticky Price and Sticky Information Price-Setting Models: What is the Difference?,". Economic Inquiry, 45, 770–786. DOI:10.1111/ecin.2007.45.issue-4 |
| [] | Kivinen, J.J., Sudderth, E.B.and Jordan, M.I., 2007, "Learning multiscale representations of natural scenes using Dirichlet processes, " Proceedings of the 11th IEEE International Conference on Computer Vision.pp.14-21 |
| [] | Kim, C.J.and C.R.Nelson., 1999, State-space models with regime switching, Published by Cambridge, Mass: MIT Press. |
| [] | Levin, A.T.and J.M.Piger., 2004, "Is Inflation Persistence Intrinsic in Industrial Economics?, " European Central Bank Working Paper, No.334. |
| [] | Mankiw, N.G. and Reis, R. , 2002, "Sticky Information Versus Sticky Prices: A Proposal to Replace the New Keynesian Phillips Curve,". The Quarterly Journal of Economics, 117, 1295–1328. DOI:10.1162/003355302320935034 |
| [] | Mishkin, F. 2007, "Inflation Dynamics". International Finance, 10, 317–334. DOI:10.1111/j.1468-2362.2007.00205.x |
| [] | Mishkin, F., 2010, "Central Banking After the Crisis" in Central Bank of Chile, Monetary Policy and Financial Stability, " Sixteenth 16th Annual Conference of the Central Bank of Chile. |
| [] | Pivetta, F. and Reis, R. , 2007, "The persistence of ination in the United States,". Journal of Economic Dynamics and Control, 31, 1326–1358. DOI:10.1016/j.jedc.2006.05.001 |
| [] | Reis, R. 2006, "Inattentive Consumers,". Journal of Monetary Economics, 53, 1761–1800. DOI:10.1016/j.jmoneco.2006.03.001 |
| [] | Robert, M.Solow., John, B.Taylor., Benjamin, M.Friedman., 1998, Inflation, Unemployment, and Monetary Policy, Published by MIT Press. |
| [] | Stock, J.H. 2001, "Evolving post-world war Ⅱ U.S.inflation dynamics,". Comment.NBER Macroeconomics Annual, 16, 379–387. |
| [] | Taylor, J. 2000, "Low inflation, pass-through, and the pricing power of firms,". European Economic Review, 44, 1389–1408. DOI:10.1016/S0014-2921(00)00037-4 |
| [] | Yong Song, 2012, "Modelling Regime Switching and Structural Breaks with an Infinite Hidden Markov Model, " The Rimini Centre for Economic Analysis Working Paper Series 28_12. |
| [] | 何奇志、范从来, 2011, 《中国通货膨胀的动态特征研究》, 《经济研究》, 第 7 期, 第 91–101 页。 |
| [] | 张成思, 2008, 《中国通胀惯性特征与货币政策启示》, 《经济研究》, 第 2 期, 第 33–43 页。 |
| [] | 张凌翔、张晓峒, 2011, 《通货膨胀率周期波动与非线性动态调整》, 《经济研究》, 第 5 期, 第 17–30 页。 |
| [] | 张屹山、张代强, 2008, 《我国通货膨胀率波动路径的非线性状态转换-基于通货膨胀持久性视角的实证检验》, 《管理世界》, 第 12 期, 第 43–50 页。 |



