当前我国的利率和汇率市场化改革都在加速进行。利率市场化改革方面,国内债券市场利率、同业拆借利率、贴现利率都已经实现了市场定价,外币存贷款和人民币贷款利率也已基本实现了利率市场化,仅剩下存款利率上限还受到一定的管制。2015年5月11日,中国人民银行在下调存贷款基准利率的同时,将存款利率浮动区间上限调整为基准利率的1.5倍,利率市场化改革提速。汇率市场化改革方面,当前实行的是以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度。2012年4月16人民币对美元汇率的日波幅从±0.5%扩大到±1%,2014年3月17日该波幅进一步扩大至±2%。
可以看出,利率和汇率市场化正在齐头并进。一个重要的问题是利率和汇率市场化的先后完成次序问题。他国经验表明(参见中国人民银行调查统计司课题组《协调推进利率汇率改革和资本账户开放》,2012),两者之间并没有确定的先后完成次序,应该根据本国具体情况确定改革次序。经济理论表明两者不是孤立存在的,它们互相影响,不能割裂来分析。为了分析两者改革的次序问题,对相关文献的观点以及研究方法进行梳理。
从结论观点来看,利率市场和汇率市场化改革的先后次序学界存在争论:支持利率市场化应该先于汇率市场化(张宗新,2006;罗鹏和张莹,2010) 的理由:其一:利率市场化是在国内进行,相对来讲风险可控性比汇率可控程度要高,且利率工具可以有效调节经济,金融体系受到的冲击较小;其二:汇率市场化优先于利率市场化步伐会加大经济结构调整的压力和代价。汇率市场化将使国内经济承受着来自国际的更大压力和冲击,要求一国的金融体系具备较强的抵御风险的能力。反对利率市场化应该先于汇率体制改革(陈光磊,2012) 的理由:其一:高息差是由人民币有效汇率高估导致的,如果没有汇率高估加剧中国经济的持续低迷、造成坏账积累,可能并不需要建立这样一种利差保护机制;其二:双向提幅增频的浮动汇率政策将促进利率市场化。浮动汇率提幅增频,政府保持外汇的易变性,实行双向浮动,有利于提高企业对汇率和利率的敏感度提高,有利于利率市场化。支持两者应同时进行(樊祎斌,2001) 的理由:其一:汇率市场化和利率市场化两者之间没有先后顺序,也不互为前提条件,都属于市场建设、放松对交易过程和行为的政治约束;其二:利率市场化、汇率形成机制改革、人民币国际化与资本账户开放是循序渐进、协调配合、相互促进的关系,不失时机,果断启动,成熟一项,推进一项。
从使用方法来看,汇率和利率的关系研究在利率平价说、蒙代尔弗莱明模型以及汇率决定的资产市场说等经典理论的深化过程中不断发展。进入20世纪90年代,随着协整理论、面板数据技术的快速发展和广泛应用,许多经济学家针对经典模型,就具有代表性的国家或地区的汇率和利率关系进行实证检验。Simone and Razzak(1999)使用了协整单位根证明了名义汇率和长期利差是单位根过程,验证了汇率和利差之间存在协整关系。Macdonald and Nagayasu(2000)利用面板数据以及协整检验的方法研究了汇率和利率间的互动关系。Basurto and Ghosh(2000)使用汇率决定的标准货币模型, 实证发现紧缩的货币政策通常伴随着本币升值。Wu and Chen(2001)基于汇率和利率的数据特征建立了考虑时变系数和马尔可夫转换异方差模型。So(2001) 建立了多变量EGARCH模型, 研究美元汇率和利率的短期动态关系。刘万锋(2009)基于定性响应模型, 研究发现相对浮动汇率制,固定汇率制度可以降低通胀发生的概率。张萌、蒋冠(2014)通过构建包含金融因素的DSGE 模型分析货币、通货膨胀率与其他宏观经济变量之间互动与联动机制,认为坚持规则性货币政策原则,控制货币存量及其增长率,能使房地产相对价格与实际利率趋于合理。
从以上文献可以看出,现有关于两者市场化完成次序的研究多从定性角度分析,已有的定量分析多关注利率与汇率的联动关系,少见直接针对该问题的定量研究。其中一个重要的原因在于很难构建一个统一的分析框架既能反映利率与汇率之间的关系,又能刻画利率市场化和汇率市场化进程。近年来,小型开放经济宏观经济学--动态随机一般均衡(DSGE) 模型逐渐成为国际宏观经济学的新方法(陈云, 2010),不少学者运用其研究汇率相关问题,如卞志村和孙俊(2011),袁申国等(2011),梅冬州和龚六堂(2011),Guillermo J. Escudé(2014) 等。本论文参考Gali and Monacelli(2005)、Justiniano and Preston (2010)构建小型开放动态随机一般均衡模型,仿照金中夏(2013)用长期均衡利率的上升来度量利率市场化进程,借鉴袁申国、陈平和刘兰凤(2011)货币政策函数来反映汇率制度选择,设置情形模拟,从波动性、脉冲响应和社会福利函数三个方面综合分析利率和汇率市场化改革的宏观经济效应,探讨利率、汇率市场化改革次序。考虑到利率与汇率市场化改革容易引起经济环境、政策体制、预期等变化,使用普通的线性模型容易引起卢卡斯批判,而使用向量自回归模型又无法体现经济微观机制,基于微观经济机制的DSGE框架能够避免卢卡斯批判,本文选择小国开放经济DSGE模型。之所以选择小国开放经济体来描述我国宏观经济主要有以下两点原因:首先,从贸易的角度看,我国支出法GDP分项统计显示,近5年来我国进出口总额占GDP比重平均为46%,说明我国经济和世界经济互有很强的依赖性,表示我国经济具有很强的开放性特征;其次,从金融的角度分析,由于我国货币还不是储备货币,金融市场规模与发达国家相比仍然较小,我国还不具备可以影响世界利率水平的定价权,国际资本流动还未给我国经济波动带来很大影响。需要指出的是,“小型”是指在世界资产市场和外国商品市场中的份额小,而不是指起产出在世界市场中的份额。
本文后续内容安排如下: 第二部分构建小型开放经济的动态随机一般均衡理论模型; 第三部分为模型参数的校准与估计; 第四部分为模拟分析,从主要经济变量受到冲击后的波动、脉冲响应和社会福利损失三个角度综合分析利率和汇率市场化改革的宏观经济效应;第五部分为主要结论。
二、 模型基本框架模型主体包括居民、企业和中央银行。居民在面对预算约束的条件下,对消费、劳动力供给和期末资产进行选择,进而达到预期效用函数最优化。企业生产的产品分为两类:最终产品和中间产品。假定最终产品市场处于完全竞争状态,而中间产品市场处于垄断竞争状态,并进一步假定企业对中间产品的价格采取Calvo(1983)定价的形式,企业通过对产品数量和价格的选择达到利润最大化的目的。货币政策由中央银行负责制定并执行,货币政策目标包括物价、经济增长及汇率在合理均衡水平上的稳定。
假设世界由本国和外国构成,本国生产的产品用H表示,外国生产的产品用F表示,本国和外国生产的产品都包括H和F,假设H和F之间的替代弹性为η。
(一) 居民行为决策假设国内居民和国外居民拥有相似的效用函数和预算约束,经济中存在无穷同质且无限生命的代表性家庭,代表性家庭的决策问题是选择消费、劳动供给和实际货币持有额的持有量来最大化其终生效用。
国内居民在其预算约束下最大化其效用函数:
| ${\rm{max}}:{E_0}\sum\limits_{t = 0}^\infty {{\beta ^t}} [\frac{{{C_t}^{1 - \sigma }}}{{1 - \sigma }} + \frac{{{{({M_t}/{P_t})}^{1 - v}}}}{{1 - v}} - \frac{{{N_t}^{1 + \varphi }}}{{1 + \varphi }}]$ | (1) |
其中,β为贴现因子,ct、Mt/Pt、lt分别表示居民消费国内产品和消费国外产品的复合消费、实际货币余额、居民劳动时间。σ、v、φ 均大于0,分别表示消费的跨期替代弹性的倒数、货币需求对利率的弹性的倒数、劳动供给对真实工资的弹性的倒数。消费品篮子为关于国内和国外产品的不变替代弹性(CES) 指数形式:
| ${C_t} = {[{\alpha ^{\frac{1}{\eta }}}{({C_{H,t}})^{\frac{{\eta - 1}}{\eta }}} + {\left( {1 - \alpha } \right)^{\frac{1}{\eta }}}{({C_{F,t}})^{\frac{{\eta - 1}}{\eta }}}]^{\frac{{\eta - 1}}{\eta }}}$ | (2) |
这里1-α表示进口的外国产品在本国篮子中的权重,CH, t表示国内居民消费国内产品的数量,CF, t表示国内居民消费进口商品的数量。参数η>0表示国内产品与国外产品的替代弹性.
居民消费支出满足:
| ${P_t}{C_t} = {P_{H,t}}{C_{H,t}} + {P_{F,t}}{C_{F,t}}$ | (3) |
其中,Pt, PH, t, PF, t分别表示消费品总价格,居民消费的国内产品总价格,居民消费的国外产品用人民币表示的总价格。
在(2) 式约束下最小化(3) 式,对CH, t,CF, t分别求一阶导数,得到:
| ${C_{H,t}} = \alpha {\left( {\frac{{{P_{H,t}}}}{{{P_t}}}} \right)^{ - \frac{1}{\eta }}}{C_t},{C_{F,t}}\left( j \right) = \left( {1 - \alpha } \right){\left( {\frac{{{P_{H,t}}}}{{{P_t}}}} \right)^{ - \eta }}{C_t}$ | (4) |
| ${P_{H,t}} = {P_t}{\left( {\frac{{{C_{H,t}}}}{{\alpha {C_t}}}} \right)^{ - \frac{1}{\eta }}},{P_{F,t}} = {P_t}{\left( {\frac{{{C_{H,t}}}}{{\alpha {C_t}}}} \right)^{ - \frac{1}{\eta }}}$ | (5) |
将(5) 式代入(2) 可得下式:
| ${P_t} = {[\alpha {({P_{H,t}})^{1 - \eta }} + \left( {1 - \alpha } \right){({P_{F,t}})^{1 - \eta }}]^{\frac{1}{{1 - \eta }}}}$ | (6) |
定义贸易条件为本国产品和外国产品的相对价格,即
| $\frac{{{P_t}}}{{{P_{H,t}}}} = {[\alpha + \left( {1 - \alpha } \right)s_t^{1 - \eta }]^{1/(1 - \eta )}} \equiv g\left( t \right)$ | (7) |
本国居民可以在消费、本国货币、债券持有以及商品直接选择,即本国居民的预算约束可以由下面的形式表示:
| ${P_t}{C_t} + {B_t} + {M_t} = {R_t}{B_{t - 1}} + {W_t}{N_t} + {M_{t - 1}} + {T_t}$ | (8) |
这里Bt是居民在t期持有的债券量;Wt是居民的名义工资;Tt是一次性转移支付;Rt表示名义利率。居民效用最大化条件下求得一阶方程为:
| ${C_t}^\sigma {N_t}^\varphi = \frac{{{W_t}}}{{{P_t}}}$ | (9) |
| ${\left( {\frac{{{W_t}}}{{{P_t}}}} \right)^{ - v}}{C_t}^\sigma = \frac{{{R_t} - 1}}{{{R_t}}}$ | (10) |
| $\beta {R_t}{E_t}\{ {\left( {\frac{{{C_{t + 1}}}}{{{C_t}}}} \right)^{ - \sigma }}\frac{{{P_t}}}{{{P_{t + 1}}}}\} = 1$ | (11) |
| $\beta {E_t}\{ {\left( {\frac{{C_{t + 1}^*}}{{{C_t}^*}}} \right)^{ - \sigma }}\frac{{{P_t}^*}}{{{P_{t + 1}}^*}}\} = \frac{{{Q_t}}}{{{Q_{t + 1}}{R_t}}}$ | (12) |
其中Qt表示名义汇率。(11)(12) 式子联立,得到最优风险分担条件:
| $\frac{{{Q_{t + 1}}{P_{t + 1}}^*C_{t + 1}^{ - \sigma }}}{{{P_{t + 1}}{{(C_{t + 1}^*)}^{ - \sigma }}}} = \frac{{{Q_t}{P_t}^*{C_t}^{ - \sigma }}}{{{P_t}{{({C_t}^*)}^{ - \sigma }}}}$ | (13) |
上面式子含义是:1单位货币(无论是本币还是外币) 用于购买外国商品篮子和用于购买本国商品篮子所带来的边际效用之比,是不随时间变动的常数。假设本国和外国是对称的,那么这一比值为1。可以得到:
| $\frac{{{C_t}}}{{{C_t}^*}} = {q_t}^{\frac{1}{\sigma }}$ | (14) |
厂商问题是在给定的技术和产品需求的约束下,选择最优的定价和产量。垄断竞争厂商的定价方式采取Calvo(1983)定价,本国代表性厂商的生产函数为:
| ${Y_t} = {Z_t}{N_t}^\gamma $ | (15) |
其中Nt为企业雇佣的劳动,Zt为外生技术水平,假设其服从一阶自回归过程:
| ${\rm{ln}}({Z_t}) = {\rho _z}{\rm{ln}}({Z_{t - 1}}) + \varepsilon _t^z\varepsilon _t^z \sim N(0,\sigma _z^2),0<{\rho _z}<1$ | (16) |
对任意产品j的需求为:
| ${Y_{H,t}}\left( j \right) = {[\frac{{{P_{H,t}}\left( j \right)}}{{{P_t}}}]^{ - \varepsilon }}{C_t}$ | (17) |
对于处在垄断市场的中间商品,模型假定企业价格设定追寻Calvo(1983)定价方式,即并不是所有厂商都在同一时间段对自己的价格水平进行调整,假定有ρ部分厂商在每一期不能调整产品的价格。厂商问题是在技术约束(15) 和需求约束(17) 下,选择最优的定价PH, t#,产量Yt+k|t和要素需求Lt+k|t以最大化如下利润流现值的期望:
| ${E_t}\{ \sum\limits_{k = 0}^\infty {{\rho ^k}{Q_{t,t + k}}} [P_{H,t}^\# {Y_{t + {k_{|t}}}} - {W_{t + {k_{|t}}}}{L_{t + {k_{|t}}}}]\} $ | (18) |
其中Qt, t+k为随机贴现因子,
| $m{c_t} = \frac{1}{\gamma }{\omega _t}{g_t}{Y_t}^{\frac{{1 - \gamma }}{\gamma }}Z_t^{ - \frac{1}{\gamma }}$ | (19) |
最终,可以得到厂商的最优定价PH, t#为:
| $P_{H,t}^\# = \frac{{{E_t}\{ {{\left( {\beta \rho } \right)}^k}C_{t + k}^{1 - \sigma }[{P_{H,t + k}}/{P_{t + k}})P_{H,t + k}^\varepsilon m{c_{t + k}}\} }}{{{E_t}\{ {{\left( {\beta \rho } \right)}^k}C_{t + k}^{1 - \sigma }({P_{H,t + k}}/{P_{t + k}})P_{H,t + k}^{\varepsilon - 1}\} }}$ | (20) |
定义
| $\Pi _{H,t}^{1 - \eta } = \rho + \left( {1 - \rho } \right){(\Pi _{H,t}^\# )^{1 - \eta }}$ | (21) |
以CPI度量的通胀率Πt和本国产品度量的通胀率ΠH, t之间的关系为:
| $\frac{{{\Pi _t}}}{{{\Pi _{H,t}}}} = \frac{{{g_t}}}{{{g_{t - 1}}}}$ | (22) |
国外企业行为类似。
(三) 央行货币政策国内有不少文献均将汇率引入到货币政策规则中,进行拓展研究。如王晓天(2007)、卞志村(2008)、袁申国等(2011)。本文参考以上文献,以利率作为货币政策的操作变量:
| ${R_t}/R = {({R_{t - 1}}/R)^{{\rho _R}}}{({E_t}{\pi _{t + 1}}/\pi )^{{\varphi _\pi }}}{({y_t}/y)^{{\varphi _y}}}{({E_t}{Q_{t + 1}}/{Q_t})^{{\varphi _q}}}{\rm{exp}}(\varepsilon _t^R)$ | (23) |
其中R、π、y为各自稳定状态值,εtR为货币政策冲击项。该式子表明中央银行采用反馈规则通过调整名义利率Rt对预期通膨Etπt+1、产出yt偏离其稳定做出反应,还对汇率的预期变化EtQt+1做出调整。 上式引入汇率项,系数φq反映了本国货币政策对名义汇率变动的敏感度。若系数φq=0,表示货币当局不干预汇率的波动,即本国实行完全浮动的汇率制度;若系数φq≠0,表示货币当局面对名义汇率波动会做出反映,相应的汇率制度为一种管理浮动的汇率制度,φq越大表明我国货币政策对汇率波动的管制越强。国外的货币政策用标准的泰勒规则表示。
(四) 产品市场均衡国内
| ${Y_t} = \frac{{{P_{H,t}}}}{{{P_t}}}{]^{ - \eta }}[\alpha {C_t} + {\alpha ^*}{C_t}^*]$ | (24) |
国外
| ${Y_t}^* = {[\frac{{P_{F,t}^*}}{{P_t^*}}]^{ - \eta }}[\left( {1 - \alpha } \right){C_t} + (1 - {\alpha ^*}){C_t}^*]$ | (25) |
模型中反映稳态特性的参数用校准法,刻画模型动态特征的参数需要用统计方法估计。货币政策方程包含预期变量,因此普通的最小二乘法估计其参数不是有效的,常用广义矩估计方法。估计时根据方程包含的变量需要用到的数据:产出、通胀率、利率、汇率。数据样本选取1996Q1-2014Q3,数据来源国家统计局网站和中国人民银行网站、CEIC数据库、Wind数据库。国外货币政策方程用标准泰勒规则,国外技术冲击一阶自回归系数取值和国内相同。
为了消除通胀的影响,需要将名义GDP转化为实际GDP,实际GDP=名义GDP/定基通胀率,定基通胀率选取基期为1995年第4季度;产出缺口由被广泛应用又比较容易处理的HP滤波方法得到;通胀率采用CPI反映;张屹山和张代强(2007)认为相比而言,管制利率对我国居民以及企业的经济活动影响较大,而且当前中央银行主要价格型调控工具为一年期存贷款利率,故选择一年期存款名义利率为本文的名义利率数据,实际利率采用名义利率减去通胀率;实际汇率计算时采用q=S·CPI*/CPI,其中,q, S分别是实际汇率和名义汇率,CPI*表示定基的美国消费者物价指数,CPI表示定基的中国消费者物价指数,美国通胀率数据来自于美国劳工部统计年鉴,两国通胀率数据均需要进行定基处理,基期为1995年12月。名义汇率数据来自于中国人民银行货币政策司网站。取月末的数据为本月名义汇率数据,季度数据通过月度平均得到。
(二) 参数的校准大部分参数的赋值借鉴相关研究文献中的参数值。不失一般性设定外生技术水平冲击稳态值为1。文章表格中π=Pt/Pt-1,稳态时各期价格相同,故设定稳态通胀为1;R和R*时分别用样本期内的平均值代替;由(11) 式得稳态时β=1/R,国外参数β*同样如此。σ, ψ, v, η, γ的取值分别来自于张卫平(2012),ρ=0.75取值参考Parrado(2004)和何国华、张龙翔(2013); ρπ*, ρy*为标准泰勒规则的系数,其取值来自Taylor(1993);ρz和σz的取值来自于金中夏等(2013);α, α*的取值参考刘斌(2008)和张卫平(2012);σRZ, ρz*, σz*取值参考刘斌(2008)。
| 表 1 模型部分参数校准值 |
广义矩估计是一个常用的方法,主要是因为GMM的限制条件较少。广义矩估计是基于在模型实际参数满足一定矩条件下形成的一种参数估计方法。在随机抽样中,样本统计量将依概率收敛于某个常数。这个常数又是分布中未知参数的一个函数。在分布未知下,依然可以利用样本矩构造方程(包含总体的未知参数),求得总体的未知参数。只要模型设定正确,则总能找到该模型实际参数满足的若干矩条件,从而对未知参数进行估计。有关该方法在DSGE模型中的具体应用可参加刘斌(2008),此处不详细介绍。估计时工具变量选择滞后期的通货膨胀、实际利率、汇率和产出缺口。由估计结果t统计量的DW值可以看出,估计结果是显著的。估计结果与刘斌(2008)基本相同。结果见表 2。
| 表 2 模型动态参数估计结果 |
下面设置几种情形进行模拟,从经济变量受到冲击后的波动性、脉冲响应和社会福利损失三个方面综合分析利率和汇率市场改革的政策效应。
由货币政策方程式(22) 可知,若系数φq=0,表示本国实行自由浮动的汇率制度;若系数φq≠0,表示本国实行有管理浮动的汇率制度,并且φq越大表明我国货币政策对汇率波动的管制越强。随着汇率市场化的逐步推进,系数φq=0.2将逐步减小,情形设定时假定其减小至0.1,汇率完全市场化后减小至0。根据金中夏、洪浩和李宏瑾(2013)的研究成果,逐步实施利率市场化将使市场均衡利率上升。本文为了度量逐步实施汇率市场化改革,设置如下情形:管理浮动汇率制情形1:φq=0.2,管理浮动汇率制情形2 :φq=0.1,自由浮动汇率制:φq=0。
(一) 波动性分析下面表 3给出各种情形下主要宏观经济变量在各种均衡利率下受到模型中所有冲击后的波动(标准差)。
| 表 3 不同长期利率水平下的各变量受到冲击后的波动(标准差) (单位:10-2) |
由表 2估计结果可知,当前我国实施的管理浮动汇率为情形1。表 3横向比较表示管理浮动汇率情形既定,实施利率市场化带来的宏观经济变量波动情况:随着均衡利率的上升,产出、通胀、利率和汇率的波动都呈现一定程度的放大。表 3纵向比较表示均衡利率不变,实施汇率市场化时,货币政策对于汇率的反应系数变小,产出和汇率的波动增大,但是通胀和利率的波动减小。
中国2015年经济增长和通胀控制目标分别降为7%左右和3%左右,2015年一季度GDP增长率为7%,通胀率同比上涨1.2%。在此宏观经济环境下,推进利率和汇率市场化改革时机合适。温和的物价水平下,商业银行的名义利率水平与实际利率相差较小,利率市场化的推进不会引起存贷款利率的大幅波动,因而有利于金融市场的稳定。但是波动性分析结论提醒我们,实施利率市场化要警惕市场利率升高过快导致的产出波动进一步加大。因为如果过快取消存款利率上限,将推高无风险利率,提升银行资本金成本,从而进一步推升贷款利率水平,企业融资成本将大幅上升,引起较大的经济波动。
自2014年11月21日以来,中国人民银行三次扩大存款利率上限浮动区间,并且每次都伴随着下调存款基准利率。以上的模拟结论表明,央行这一举措一方面为平稳推进利率市场化改革,另一方面能避免防止利率过快上升带来的经济波动。同样可以看出,当前宏观经济情况下,汇率改革也应遵循逐步推进的原则防止造成产出的过度波动。
(二) 脉冲响应分析 1. 模拟分析均衡利率不变下逐步实施汇率市场化的宏观经济效应四个冲击中,国内技术冲击和利率冲击对国内的经济影响较大。下面给出当前均衡利率(R=1.035) 下,技术冲击和利率冲击的经济影响。
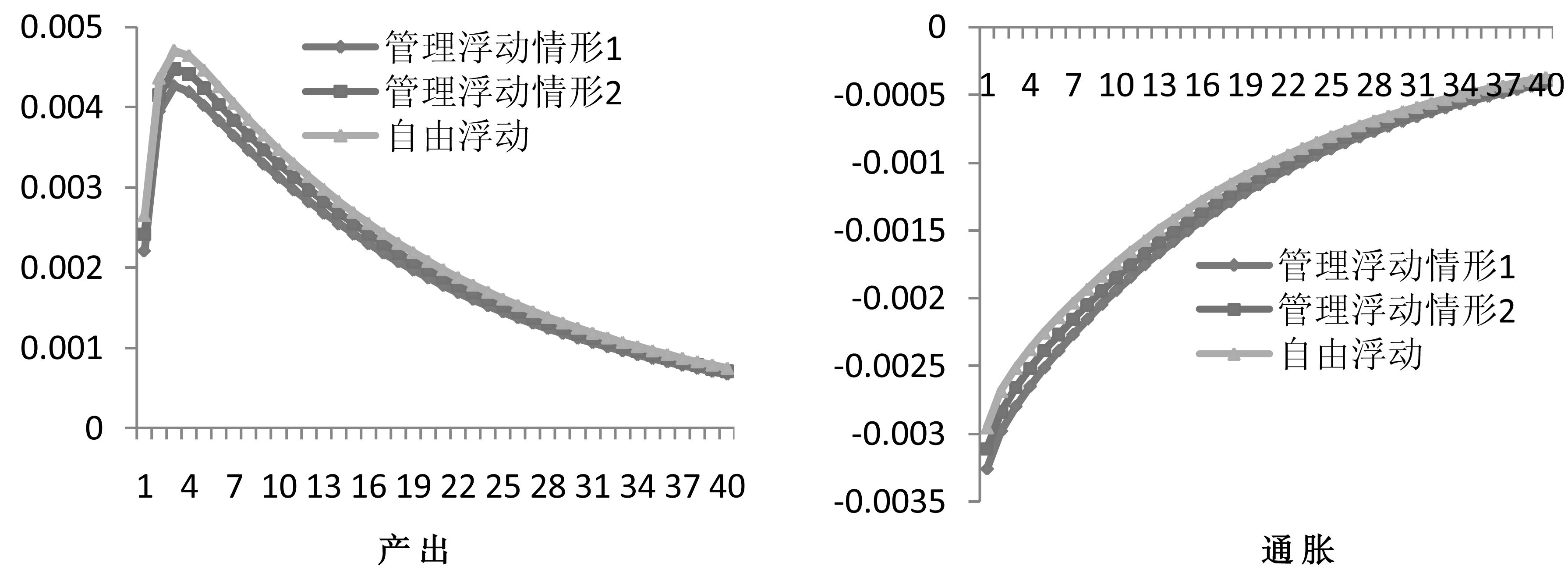
|
图 1 国内技术冲击的脉冲响应 |
图 1看出,技术进步使产出增加而通胀降低,主要原因是国内技术进步使企业边际生产成本降低,从而降低通胀率,物价的下降刺激总需求增加,使总产出水平在短期内增加。通过比较看出:随着汇率市场化的改革深入,技术冲击导致的产出波动将逐步增大,而通胀波动将逐步减小。
图 2看出,利率提高一个百分点能有效的抑制了通货膨胀,降低投资从而引起产出下降。货币政策调整的冲击效应包括影响程度和作用时间两个部分,一个合意的情形是利率在该请形下能最短时间内发挥最大的政策效应。通过比较图 2看出,不同的汇率制度情形下,利率调控效应的不同主要表现在初始影响程度。随着汇率市场化改革的深入,货币政策调控产出和通胀的能力逐步提高。
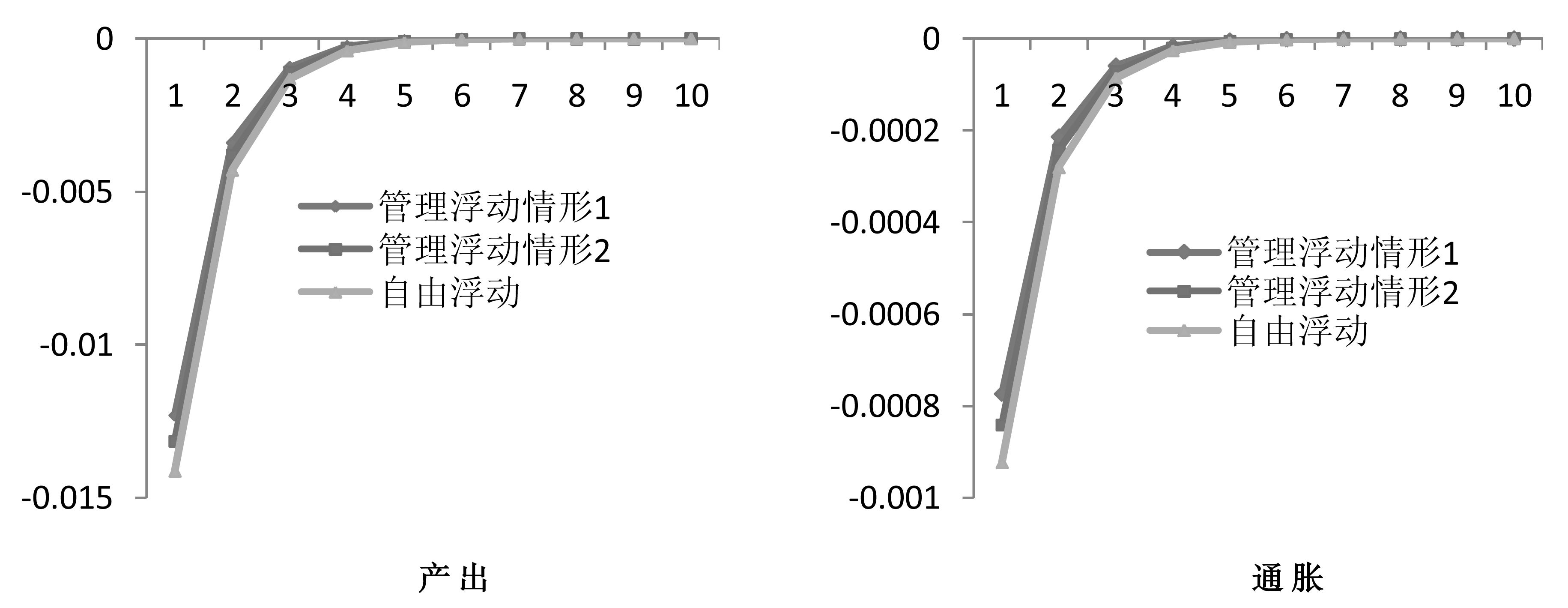
|
图 2 国内利率冲击的脉冲响应 |
当前我国人民币汇率虽然是“浮动”的,但从是历年数据观察,我国的浮动区间过于窄小,而且大多数是单边升值浮动,没有真正意义上的双边浮动。随着我国对外贸易额度的不断增长,贸易顺差的绝对值也在不断增大,由此通过资本账户和经常账户进入国内变成我国的外汇储备也越来越多,央行为吞吐这些巨额的外汇,不得不被动地超发货币,释放流动性,导致近年央行在货币市场通过各种货币工具不断回收对冲的成本也越来越大,货币政策目标和汇率政策目标存在冲突矛盾,保持货币政策的独立性也受到影响。以上脉冲响应分析结果显示,随着汇率市场化改革的深入,利率调控通胀和产出的效应增强。基于我国经济现实情况,应当逐步推进汇率市场化改革,适当加大汇率的双边浮动幅度,提升货币政策独立性以及利率的调控能力。
2. 模拟分析当前汇率弹性下,均衡利率上升的宏观经济效应下面模拟当前汇率弹性下(即货币政策对汇率的反应系数不变,φq=0.2),利率市场化改革逐步推进的宏观经济效应。
比较图 3和图 4:当前汇率制度不变下,随着利率市场化改革的深入,均衡利率上升使技术进步造成的产出和通胀波动增大;利率作为货币政策工具调控产出的能力没有显著变化,但是调控通胀的能力明显提高。
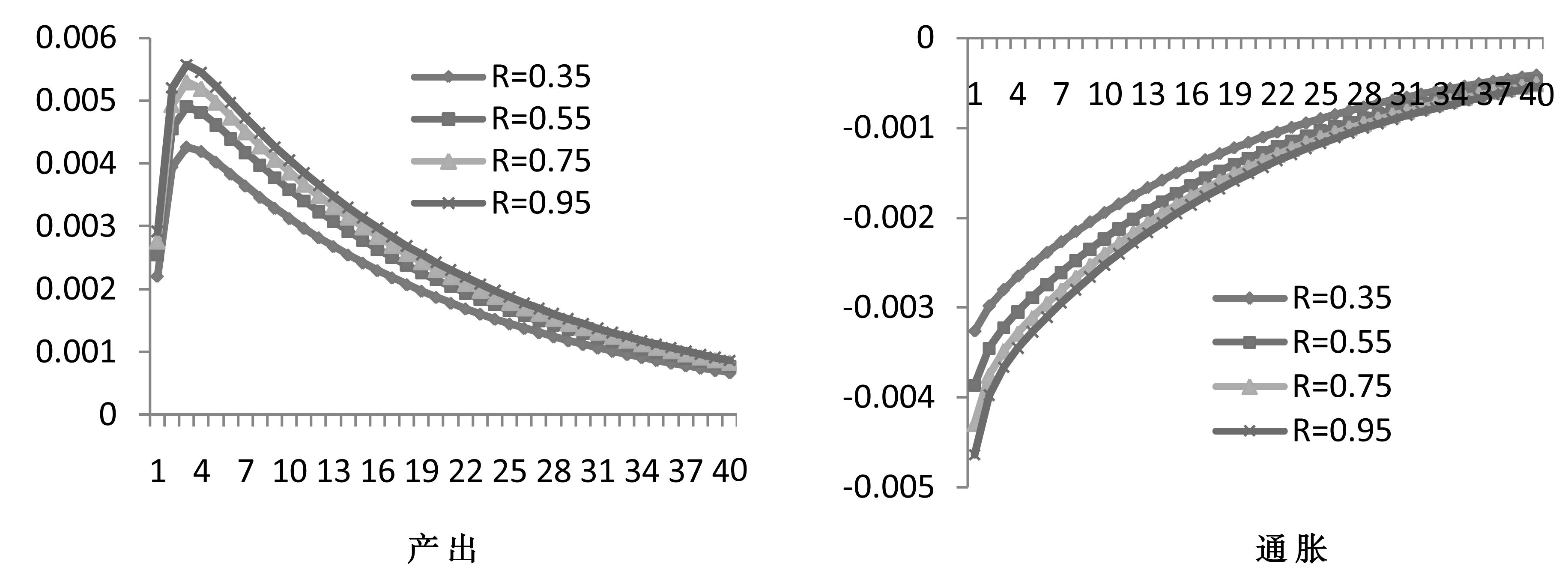
|
图 3 国内技术冲击的脉冲响应 |
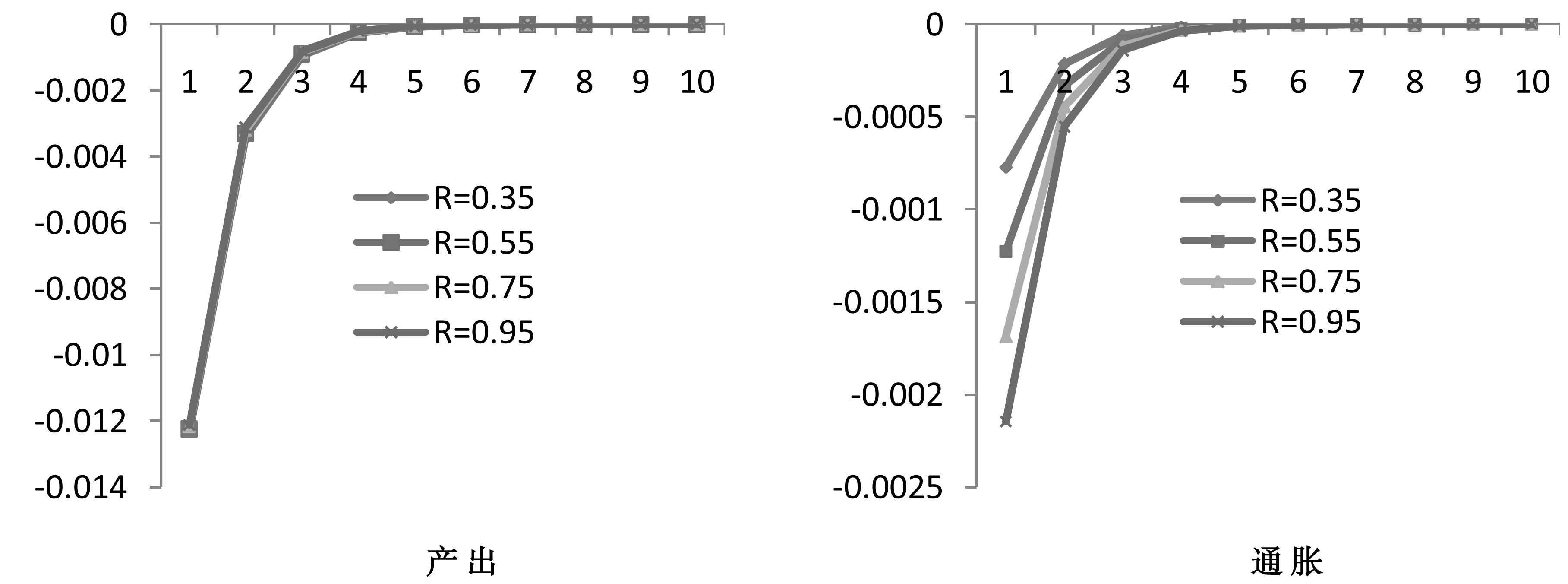
|
图 4 国内利率冲击的脉冲响应 |
当前,我国货币政策实际执行中主要承担保证经济增长和稳定物价这两大目标。货币政策目前处于数量型调控模式和价格型调控模式并用,市场化和行政性手段兼施的阶段。2008年金融危机爆发,央行主要通过数量型放松来挽救经济,虽然拉动经济强劲反弹,但却带来了自2009年底至2011年中持续通胀、实际利率持续陷入负区间、房地产价格飙升、银行体系不良贷款隐忧浮现等种种问题。因此,数量型调控模式下央行是否有能力合理确定并有效控制货币供应量受到了广泛质疑和诸多诟病,呼吁加速利率市场化改革的声音也更加强烈,希望利率市场化改革提升价格型货币政策的调控效果。本文此处的脉冲响应分析显示出利率改革能够增强利率调控的有效性,我国经济现实也要求价格型货币政策工具利率作为货币政策调控工具的调控能力要提高。
(三) 社会福利损失函数分析不同于封闭条件,开放条件下的社会福利损失函数中需要考虑汇率的波动。参考Woodford(1997)思路,福利标准是基于下面的跨时损失函数:
| $L = {E_t}\sum\limits_{i = 1}^n {{\vartheta ^i}} [\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } _{t + i}^2 + {\lambda _y}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over y} _{t + i}^2 + {\lambda _q}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} _{t + i}^2]$ | (26) |
其中
由前面的脉冲响应分析知道,技术冲击的影响最大。此处综合分析技术冲击对主要经济变量产出、通胀和汇率的影响,用社会福利损失表示,计算结果如下表:
表 4的横向比较发现,当均衡利率处于3.5%-5.5%之间,汇率市场化改革造成的福利损失增大,当利率高于6.5%,福利损失减小;这个结果说明汇率市场化改革造成的福利损失与利率市场化改革所处的阶段有关。表 4纵向比较发现,在各种汇率浮动制不变情况下,均衡利率的升高,技术冲击引起的社会福利损失逐渐增大。综合比较发现,若均衡利率上升过快,利率市场化改革引起的社会福利损失大于汇率市场化改革引起的社会福利。这个分析结果的经济启示意义在于:一方面,利率市场化改革引起的社会福利损失变化大,汇率市场化引起的福利损失变化小,因此先行推行汇率市场化改革有利于稳定经济波动;另一方面,汇率市场化改革受到利率市场化改革阶段的制约,当利率市场化改革进行到一定阶段后,再推进汇率市场化改革,有利于减少汇率市场化改革引起的福利损失,减缓经济波动。因此,为避免经济波动过大,引起社会福利损失增加,要逐步协调推进利率和汇率市场化改革。
| 表 4 技术冲击下不同长期利率水平下的损失函数值(单位:10-4) |
一直以来,我国政府担心过快的金融改革改革会导致宏观经济的动荡,因此利率和汇率市场化改革均是逐步协调推进。如2005年7月启动人民币汇率制度改革,人民币对美元汇率浮动幅度为03%,2007年5月扩大至0.5%,2012年4月扩大至1%,2014年3月扩大至2%。2014年以来,中国人民银行推动存款利率市场化改革又迈出新的重大步伐,2014年11月21日,在调整人民币贷款和存款基准利率水平的同时,推出利率市场化的重要举措,将人民币存款利率浮动区间上限由基准利率的1.1倍扩大至1.2倍。截止2015年5月11日,存款利率浮动区间上限又经历了1.2倍扩大至1.3倍、1.3倍至1.5倍,并且每次扩大浮动区间的同时都下调存款基准利率防止利率的过快上升。本文的实证分析也充分的印证了这一点。
五、 研究结论本文通过构建小型开放经济的新凯恩斯动态随机一般均衡模型,在同一个框架下设置情形模拟,从波动性、脉冲响应和社会福利函数三个方面综合分析利率和汇率市场化改革的宏观经济效应,实证研究得到如下结论:
第一, 当前情况下,实施利率市场化改革引起各宏观经济变量波动的增加,而实施汇率市场化改革引起产出和汇率波动增大,但通胀和利率的波动减小。利率的过快上涨会导致经济波动明显增大,需要逐步推进利率和汇率市场化改革。第二,脉冲响应分析显示出利率和汇率市场化改革能够增强利率调控的有效性,提升我国价格型货币政策工具利率作为货币政策调控工具的调控能力。第三,汇率市场化改革造成的福利损失与利率市场化所处的阶段有关。若均衡利率升高过快,利率市场化改革引起的社会福利损失将大于汇率市场化改革引起的社会福利,因此要协调推进利率和汇率市场化改革,扩大利率浮动区间的同时扩大汇率浮动区间,逐步降低利率和汇率政策目标的矛盾冲突。
近期,在人民币贬值压力下,中国资金面临外流压力。国际方面,美国经济复苏和美联储加息预期持续推升美元走强,带动国际资本回流美国,从而进一步加大中国资金外流和货币跃值双重压力。随着中国金融市场开放、资本项目开放和人民币国际化步伐的加快,国际资本双向流动频繁,汇率波动幅度继续加大,国际资本流动冲击国内金融稳定风险加大。建议当前协调推进利率和汇率市场化改革的同时,应完善调控工具并实施进行必要的资本管制,加强跨境资金流动双向监测预警,防范跨境资本双向流动冲击,应警惕跨境资金流动和人民币贬值可能引发中国金融市场波动的风险。
| [] | Barry E,Ricardo H.,1999, “Exchange Rates And Financial Fragility”, Working Paper,No.7418. |
| [] | Gertler,G.and Natalucci.,2003, “External Constraints on Monetary Policy and the Financial Accelerator”, Draft. |
| [] | Guillermo J. Escudé, 2014, "The Possible Trinity: Optimal Interest Rate, Exchange Rate, and Taxes on Capital Flows in a DSGE Model for a Small Open Economy". The open-Acess, Open-Assessment E-Journal, 8, 1–59. |
| [] | Jordi Gali, Tommaso Monacelli, 2005, "Monetary Policy and Exchange Rate Volatility in a Small Open Economy". Review of Economic Studies, 72, 707–734. DOI:10.1111/roes.2005.72.issue-3 |
| [] | Justiniano A, B. Preston, 2010, "Monetary Policy and Uncertainty in an Empirical Small Open Economy Model". Journal of Applied Econometrics, 25(1), 93–128. DOI:10.1002/jae.1153 |
| [] | Panayiotis F, Diamandis A and Drakos , 2011, "Financial liberalization, exchange rates and stock prices: Exogenous shocks in four Latin America countries". Journal of Policy Modeling(3), 381–394. |
| [] | Parrado E.,2004,“Inflation Target and Exchange Rate Rules in a Open Economy”, IMF Working Paper, 21. |
| [] | Sebastian Edwards.,2006,“The Relationship Between Exchange Rates and Inflation Targeting Revisited”, NEBR Working Paper ,No. 12163. |
| [] | Woodford ,M.,1999,“Optimal Monetary Policy Inertia”, NEBR Working Paper ,No.7261,July. |
| [] | 卞志村, 2008, 《开放经济下的最优货币政策, MCI及在中国的检验》, 《数量经济技术经济研究》, 第 4 期, 第 17–28 页。 |
| [] | 陈光磊,2012,《汇率和利率市场化孰先孰后》,证券分析报告第4-16页。 |
| [] | 陈云, 2010, 《国际宏观经济学的新方法: NOEM-DSGE模型》, 《经济学家》, 第 2 期, 第 38–45 页。 |
| [] | 樊祎斌, 2001, 《中国利率市场化改革与汇率制度的选择》, 《金融教学与研究》, 第 9 期, 第 11–13 页。 |
| [] | 何国华、张龙翔, 2013, 《贸易开放度对中国最优货币政策规则选择的影响》, 《经济与管理研究》, 第 7 期, 第 77–85 页。 |
| [] | 金中夏、洪浩、李宏瑾, 2013, 《利率市场化对货币政策有效性和经济结构调整的影响》, 《经济研究》, 第 4 期, 第 69–82 页。 |
| [] | 黄志刚, 2010, 《资本流动、货币政策与通货膨胀动态》, 《经济学季刊》, 第 4 期, 第 1332–1360 页。 |
| [] | 陆前进, 2011, 《人民币汇率增加弹性和参考一篮子货币汇率形成机制研究》, 《数量经济技术经济研究》, 第 11 期, 第 83–111 页。 |
| [] | 刘斌,2010,《动态随机一般均衡模型及其应用》,中国金融出版社第一版。 |
| [] | 刘斌, 2008, 《我国DSGE模型的开发及在货币政策分析中的作用》, 《金融研究》, 第 10 期, 第 3–21 页。 |
| [] | 刘敏、李颖, 2008, 《三元悖论”与人民币汇率制度改革浅析》, 《国际金融研究》, 第 6 期, 第 69–75 页。 |
| [] | 刘万峰, 2009, 《新兴市场经济国家通货膨胀发生概率与汇率制度选择——基于定性响应模型的实证研究》, 《南方经济》, 第 4 期, 第 44–54 页。 |
| [] | 梅冬州、龚六堂, 2011, 《新兴市场经济国家的汇率制度选择》, 《经济研究》, 第 11 期, 第 73–88 页。 |
| [] | 马文涛, 2011, 《货币政策的数量型工具和价格型工具的调控绩效比较: 来自动态随机一般均衡模型的证据》, 《数量经济技术经济研究》, 第 10 期, 第 93–103 页。 |
| [] | 王晓天、张淑娟, 2007, 《开放条件下货币政策目标规则的比较—个简单的理论框架与中国货币政策名义锚的选择》, 《金融研究》, 第 4 期, 第 14–29 页。 |
| [] | 熊芳、黄宪, 2008, 《中国资本账户开放次序的实证分析》, 《国际金融研究》, 第 3 期, 第 32–39 页。 |
| [] | 徐高,2008,《基于动态随即一般均衡模型的中国经济波动数量分析》,博士学位论文第85-123页。 |
| [] | 张萌、蒋冠, 2014, 《纳入金融因素的DSGE模型与宏观经济稳定研究》, 《经济经纬》, 第 1 期, 第 155–160 页。 |
| [] | 袁申国、陈平、刘兰凤, 2011, 《汇率制度、金融加速器和经济波动》, 《经济研究》, 第 1 期, 第 57–70 页。 |
| [] | 张卫平,2012,《货币政策理论:基于动态一般均衡方法》,北京大学出版社第一版第23-29页。 |
| [] | 张屹山、张代强, 2007, 《前瞻性货币政策反应函数在我国货币政策中的检验》, 《经济研究》, 第 3 期, 第 20–32 页。 |
| [] | 张宗新, 2006, 《金融开放条件下利率改革和汇率改革的协同效应分析》, 《国际金融研究》, 第 9 期, 第 9–14 页。 |



