利率市场化的本质是充分发挥市场在资金配置中的基础性作用,形成由供需双方自主决定的资金定价机制,有效实现资金最优化配置的过程。利率市场化是中国经济发展的客观要求与必然举措,通过利率市场化建立有效的金融市场进而不断完善现代金融体系是金融改革的基本路径。2013年7月20日,中国人民银行宣布全面放开贷款利率管制,取消贷款利率下限,让金融机构自主决定贷款利率,表明贷款利率市场化已初步实现。尽管存款利率市场化仍未取得实质性进展,但2014年3月央行行长周小川表示,存款利率放开已在计划之内,很可能会在最近两年实现。可见,存贷款利率的完全市场化已经是一个无法阻挡的趋势。
利率市场化可通过储蓄效应、渠道效应和收入效应来深化金融市场功能和优化金融资源配置,以提高商业银行效率;但利率市场化也会造成银行的净利差缩窄,净利息收入减少,利率波动幅度加大。商业银行间价格竞争加剧,引发商业银行更高的系统性风险,有可能降低商业银行效率。可见,利率市场化对商业银行效率的影响存在一定的不确定性。城市商业银行作为股份制中小银行,在资产规模、业务齐全、新产品开发及风险规避方面与国有商业银行、全国性股份制银行相比仍有较大差距。当利率市场化所引致的同业竞争加剧时,城市商业银行很有可能因为竞争而降低投融资效率及压缩利润空间。因此,若以城市商业银行为研究对象,深入探究利率市场化对银行效率的影响具有重要的现实指导意义的。本文试图要探究的问题是:中国城市商业银行的综合效率如何?利率市场化是否有助于改善城市商业银行效率?本文的研究结论可为城市商业银行如何采取措施应对利率市场化带来的负面效应提供客观的理论依据。
|
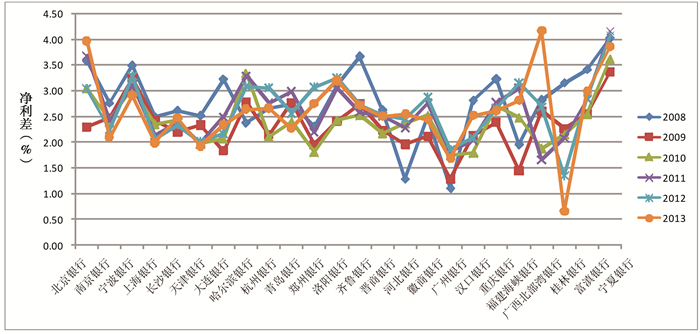
图 1 2008-2013年中国24家城市商业银行净利差变动图 |
国内外相关研究文献集中于探讨商业银行效率的测算及影响因素分析,银行效率测算方法多集中于采用非参DEA方法和参数SFA方法。相比而言,参数SFA方法要求对所有研究样本数据的无效率分布做出事先假设并要确定函数形态,若函数形式设定不合理或主观性较强将对测算结果造成巨大偏差。非参方法则不限定具体函数形式,仅根据投入产出数据即可测算银行效率,因而得到广泛应用。Park and Weber (2006)、Elena (2007)和Pasiouras (2008)均采用DEA-Malmquist指数测算商业银行的静态效率与动态全要素生产率,并实证分析影响因素。陈刚 (2002)运用DEA模型的Malmquist指数对我国商业银行1994-1999年的效率进行测算,研究发现我国商业银行一直在创新但成效却不显著。郑录军和曹廷求 (2005)采用DEA方法对我国商业银行效率进行估计并探究其影响因素,研究结果显示国有商业银行、股份制商业银行和城市商业银行在效率方面并不存在明显差异,集中型股权结构和公司治理机制是影响我国商业银行效率的重要因素。袁晓玲和张宝山 (2009)、张健华和王鹏 (2010)均采用基于DEA技术的Malmquist生产率指数对商业银行效率进行测算,研究发现中国上市商业银行的全要素生产率总体略有下降,但纯技术生产率和规模生产率却略有提高。
鉴于前述研究文献没有考虑不良贷款等非期望产出,迟国泰等 (2006)、王兵和朱宁 (2011)、姜永宏和蒋伟洁 (2014)在研究中将不良贷款引入作为一种坏产出,研究发现不考虑不良贷款约束时商业银行的全要素生产率存在高估。所不同的是迟国泰等 (2006)研究的是静态效率,而王兵和朱宁 (2011)采用的是考虑非期望产出的径向ML指数进行测算,姜永宏和蒋伟洁 (2014)采用的是基于SBM的Luenberger生产率指标法。此外,现有研究中仅有谭元戎等 (2013)专门以城市商业银行为研究对象,对技术效率及影响因素进行实证分析,其他相关文献集中于对商业银行进行效率测算。而且现有研究文献并未就利率市场化与商业银行效率改善之间的关系进行研究,相关研究主要探讨审慎性监管和商业银行效率改善 (魏琪等,2014)、信贷调控与商业银行效率 (章晟和杜灵青,2013) 及利率市场化与企业创新效率的关系研究 (李程,2014)。综合可知,一方面现有关于银行效率测算的研究文献很少涉及城市商业银行的测算,而且现有测算方法要么是径向的要么是SBM的,技术参考集也非全局的,这些模型均存在一定的缺陷。此外,很多研究文献并没有考虑不良贷款等非期望产出,测算结果存在一定的偏差。另一方面,现有文献没有就利率市场化与城市商业银行效率间的关系进行研究,未对利率市场化进行有效区分,也缺乏相应的理论和实证研究成果。因此,本文首先采用基于考虑非期望产出的并综合径向和非径向特点的EBM模型和GML指数来测算城市商业银行的静态效率和动态全要素生产率,然后在将利率市场化区分为存款利率市场化和贷款利率市场化的基础上,采用Tobit模型实证检验利率市场化对城市商业银行效率的影响,以期为理清两者之间的作用机制提供相应的理论依据。
二、 城市商业银行效率测算及评价 (一) 研究方法1.生产技术。鉴于传统的Malmquist-Luenberger生产率指数使用两个当期ML指数几何平均的形式,导致在测度跨期方向性距离函数时可能面临一个潜在的线性规划无解问题,并且以几何平均形式不具有循环性或传递性,因此本文采用Oh (2010)提出的基于全局技术的GML指数来衡量银行全要素生产率。根据Fare (2007)定义的环境技术函数,本文构造一个包含投入、期望产出与非期望产出的生产可能性集。假设生产系统中有m个决策单元,使用n种投入要素,生产u种期望产出和v种非期望产出。定义矩阵X=(xij)∈Rn×m+表示投入要素对应的向量,Yg=(yijg)∈Ru×m+表示期望产出对应的向量,Yb=(yijb)∈Rv×m+为非期望产出对应的向量。假设生产可能性集满足闭集和凸集、联合弱可处置性、零结合性及期望产出与投入的强可处置性,运用数据包络分析法 (DEA),传统环境技术可模型化为:
| $ P\left( x \right) = \{ (x,{y^g},{y^b})|x \geqslant X\lambda ,{y^g} \leqslant {Y^g}\lambda ,{y^b} = {Y^b}\lambda ,\sum mi = 1{\text{ }}\lambda = 1,\lambda \geqslant 0\} $ |
其中λ表示横截面观察值的权重,若
2.基于EBM模型的静态银行效率测度。传统以径向测算为基础的规模报酬不变模型,即CCR模型假定在保持产出不变的前提下测度投入导向的效率值,但其假定的所有投入要素均以相同比例缩减的条件过于严格,与现实经济背离。而以非径向测算为基础的SBM模型 (Tone, 2001),通过考虑非径向的松弛变量来规避投入要素同比例缩减的假设条件,但却以损失效率前沿投影值的原始比例信息为代价,并且在求解线性规划过程中SBM模型存在较大的不足。针对径向和非径向模型的不足,Tone and Tsutsui (2010)构建一个综合径向和非径向特点的EBM模型。考虑具有n种投入要素和s种产出的m个决策单元,EBM模型表示为:
| $ {\gamma ^*} = \mathop {\min }\limits_{\theta ,\lambda ,s} \theta - {\varepsilon _x}\sum\limits_{i = 1}^n {\frac{{{{\bar w}_i}{{\bar s}_i}}}{{{x_{i0}}}}} ,s.t.\;\theta {x_0} - X\lambda - \bar s = 0\lambda Y \geqslant {y_0},\lambda \geqslant 0,\bar s{\text{ }} \geqslant 0 $ |
其中γ*为EBM模型测度的最优效率值,θ为CCR模型计算的径向效率值,s为非径向的投入要素松弛向量,λ为权重向量,wi表示第i变量的权重并满足
3.GML指数-银行全要素生产率模型。本文在全局技术集的基础上引入方向性距离函数,即设定一个方向向量g=(-gx, gy, -gb),对于选定的方向性向量g,方向性距离函数可以最大的限度增加“好”产出及减少非期望产出和投入。纳入方向性向量后可得到方向性距离函数的表达式:
| $ \begin{gathered} \overrightarrow D _0^G({x^t},{y^t},{b^t};{y^t}, - {b^t}) = max\beta \hfill \\ s.t.\;\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {z_k^ty_{kj}^t} } \geqslant \left( {1 + \beta } \right){y_j}^t,j = 1,2,...u \hfill \\ \sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {z_k^ty_{ks}^t} } = \left( {1\beta } \right){b_s}^t,s = 1,2,...v \hfill \\ \sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {z_k^ty_{ki}^t} } \leqslant \left( {1\beta } \right){x_i}^t,i = 1,2,...n \hfill \\ \end{gathered} $ |
其中,zkt为第t期的权重值,k=1, 2, ...K。通过测算基于全局技术集的方向性距离函数,本文将GML全要素生产率指数定义为:
| $ GML_t^{t + 1} = \frac{{1 + \overrightarrow D _0^G({x^t},{y^t},{b^t};{y^t},{b^t})}}{{1 + \overrightarrow D _0^G({x^{t + 1}},{y^{t + 1}},{b^{t + 1}};{y^{t + 1}},{b^{t + 1}})}} = EFFCH_t^{t + 1} \times TECH_t^{t + 1} $ |
如果GML>1,意味着银行全要素生产率呈现增长,如果GML≤1,说明银行全要素生产率呈现下降或不变。
(二) 指标与数据本文以中国24家城市商业银行为研究对象,投入产出数据的时间跨度为2008-2013年,相关数据主要来源于各城市商业银行年报。银行效率测算中投入和产出的合理确定是最为关键的,现有对银行经营活动进行测度的方法主要有生产法、中介法和资产法。鉴于中介法的指标数据可得性强并且其采用的存贷款总额指标可最直接体现商业银行的资金融通功能,因此本文采用中介法来对各城市商业银行的静态效率与动态全要素生产率进行测算。银行投入方面,本文主要采用利息支出、营业支出和存款总额来衡量;银行产出方面,本文选用利息收入、非利息收入及贷款总额来衡量期望产出,而采用不良贷款率衡量非期望产出。其中,利息支出=总计息负债利息支出=客户存款利息支出+同业及其他金融机构和拆入款项利息支出+发放债券及其他利息支出;营业支出=营业收入-营业利润;利息收入=总生息资产利息收入=贷款和垫款利息+债券投资利息+存放中央银行款项利息+存放或拆放同业及其他金融机构存款利息+金融资产;非利息收入=手续费及佣金收入+投资收益+公允价值变动损益+汇兑损益+其他业务收入。本文采用MAXDEA PRO 6.4软件进行考虑非期望产出的EBM模型和GML模型效率测算。
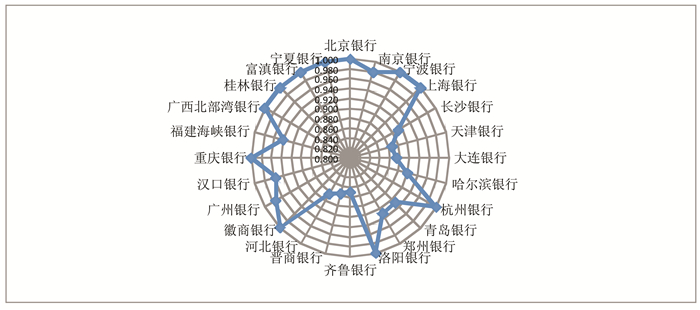
(三) 城市商业银行效率分析1.综合效率分析。2008-2013年中国24家城市商业银行中,考虑不良贷款率的银行效率值为1的城市商业银行有北京银行、宁波银行、上海银行、杭州银行、洛阳银行、徽商银行、重庆银行、广西北部湾银行、桂林银行、富滇银行和宁夏银行,这些银行处于效率前沿,其他银行则仍存在无效率成分。处于效率前沿的银行可分为两类:第一类是资产规模较大、实力雄厚并能较好化解各种风险的城市商业银行,主要有4家上市银行北京银行、宁波银行、徽商银行和重庆银行,还有即将上市的东部沿海城市商业银行,包括上海银行、杭州银行,这类银行在面对利率市场化时可能会有更多的选择性;第二类是资产规模一般的中西部城市商业银行,尽管其在实力和创新方面仍存在不足,但其不良贷款水平控制较好,因而仍处于效率前沿。其他未达到效率前沿的城市商业银行,可能更多是因为资产规模、创新水平、赢利能力及对不良贷款的控制力度不够等造成的。
2.全要素生产率分析。其一,2008-2013年中国24家城市商业银行的平均GML指数值为1.016,表明城市商业银行全要素生产率呈现增长趋势,其中技术效率指数为1.006,说明期间技术效率有所改善但却幅度不大,而技术进步指数为1.010,则显示技术进步对全要素生产率的贡献大于技术效率改善的贡献程度,可见城市商业银行仍需通过改善自身的技术效率来提高全要素生产率。其二,2008-2013年间,只有长沙银行、青岛银行、晋商银行、广州银行、富滇银行和宁夏银行的全要素生产率并未实现增长,其他城市商业银行的全要素生产率均有不同程度的增长。技术效率改善方面,除天津银行、哈尔滨银行、郑州银行、晋商银行、河北银行、广州银行、汉口银行和福建海峡银行外,其他银行的技术效率均未改善甚至出现技术效率恶化现象。技术进步方面,除长沙银行、晋商银行、广州银行、福建海峡银行、富滇银行和宁夏银行外,其他银行均实现技术进步。综合可知,一般而言上市城市商业银行的全要素生产率要高于非上市银行,东部沿海城市商业银行的全要素生产率要高于中西部城市商业银行,而未实现技术效率改善和技术进步的城市商业银行主要集中于中西部地区。此外,技术进步一直是城市商业银行全要素生产率提高的关键因素。
|
图 2 2008-2013年中国24家城市商业银行综合效率 |
尽管很少有文献探究利率市场化对城市商业银行综合效率和全要素生产率的影响,但并不缺乏对其影响因素进行分析的文献,代表性的影响因素主要有银行的资产规模、资本充足率、自有资本比率、营业费用比率及非利息收入比率等。根据本文要探究的研究主题,并结合其他影响银行效率的主要因素,本文设定下述实证分析模型:
| $ \begin{gathered} {E_{it}} = {\gamma _0} + {\gamma _1}Iga{p_{it}} + {\gamma _2}Iga{p_{it}} \times Lerne{r_{it}} + \hfill \\ {\gamma _3}Year{13_{it}} + {\gamma _4}Yea{r_{it}} \times Lerne{r_{it}} + {\gamma _5}Lnsiz{e_{it}} \hfill \\ + {\gamma _6}Eq{t_{it}} + {\gamma _7}Ca{r_{it}} + {\gamma _8}Co{d_{it}} + {\gamma _9}I{d_{it}} + {\mu _i} + {\varepsilon _{it}} \hfill \\ \end{gathered} $ |
其中,i代表银行,t代表年份,μi为不可观测的个体效应,εit为随机扰动项。Eit为被解释变量,即本文测算的静态综合效率与动态全要素生产率,Igapit为存款利率市场化变量,Year13it为贷款利率市场化变量,同时考虑到利率市场化会通过加剧城市商业银行价格竞争从而对银行效率产生影响,本文还分别加入价格竞争变量Lernerit与存贷利率市场化变量的交叉项。本文还加入银行个体特征变量来控制相关因素对银行效率的影响,主要有银行规模Lnsizeit、自有资本比率Eqtit、资本充足率Carit、营业费用比率Codit和非利息收入占比Idit等。
| 表 1 2008-2013年中国24家城市商业银行全要素生产率 |
本文与银行相关数据均来源于中国24家城市商业银行2008-2013年年报,2008年之前各城市商业银行年报缺失严重故并未考虑。除被解释变量采用本文测算的静态综合效率与动态全要素生产率外,其他变量选取如下:
1.存贷利率市场化变量。尽管存款利率市场化仍未完全实现,但存款利率市场化进程却表现为存贷利差的逐步缩小,本文采用净利差来表示存款利率市场化进程。净利差的计算公式为:IGAPi=LRi-DRi,其中LRi为实际贷款利率,由银行的利息收入除以总生息资产得到,DRi为实际存款利率,由利息支出除以存款与短期借款之和得到。因为2013年7月20日央行宣布全面放开贷款利率管制,取消贷款利率下限,表明贷款利率市场化已初步实现,本文采用虚拟变量来表示贷款利率市场化,2013年之前取0,2013年之后取1。
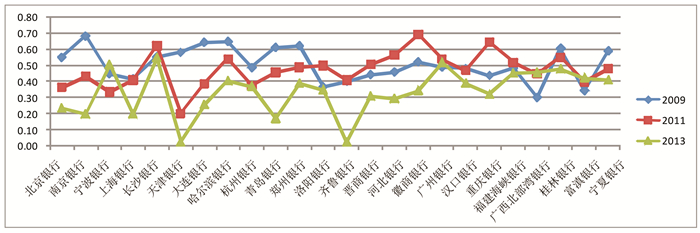
2.银行价格竞争变量。本文采用研究中广泛使用的勒那指数作为银行竞争的代理变量,其能度量银行产出的边际价格超过边际成本的百分比。勒那指数的计算公式为:LERNER=(P-MC)/P,其中P为银行产品的价格,本文采用银行贷款利息收入与总贷款之比来衡量;MC为银行贷款的边际成本,包括借入资金价格=利息支出/总借入资金及非利息运营支出=营业费用/总资产两部分。勒那指数是介于0和1之间的数值,该值越大表明银行越垄断,即银行间竞争越弱。
3.其他控制变量。资产规模采用城市商业银行资产额来表示并取对数,自有资本比率采用所有者权益与资产总额的比值来衡量,营业费用比率采用营业费用与营业收入的比值来衡量,非利息收入比率采用非利息收入占营业收入的比重来衡量,资本充足率数据来源于各年年报。
| 表 2 变量描述性统计 |
|
图 3 中国24家城市商业银行的勒那指数 |
考虑到本文测算得到的城市商业银行综合效率值介于0和1之间,全要素生产率均大于0,若采用传统线性回归方法进行拟合得到的效率值可能为负,这是与现实相矛盾的。因此,本文采用面板Tobit模型来实证检验利率市场化对城市商业银行效率的影响,同时鉴于存款利率市场化和贷款利率市场化对银行效率的影响存在异质性,本文分别设置模型来进行检验。
面板Tobit模型估计结果显示,一方面Igap与EB显著正相关,即城市商业银行综合效率与存贷净利差正相关,表明存款利率市场化引致存贷净利差逐步收窄时不利于提高银行综合效率。而且Igap×Lerner显著为负,鉴于Igap和Lerner均为负向指标,那么该交叉项系数为负表明存款利率市场化引致的城市商业银行价格竞争会降低综合效率。贷款利率市场化变量的系数显著为负,其与价格竞争变量的系数显著为正,这同样表明贷款利率市场化不利于城市商业银行综合效率的提高。原因在于:其一,利率市场化逐渐引致银行净利差缩小,银行之间价格竞争加剧。而城市商业银行作为股份制中小银行,在资产规模、业务齐全、新产品开发及风险规避方面与国有商业银行、全国性股份制银行相比仍有较大差距。当利率市场化所引致的同业竞争加剧时,城市商业银行很有可能因为竞争力缺乏而降低投融资水平,从而压缩利润空间、降低净资产收益率,这无疑会使得银行综合效率的下降。其二,利率市场化的推进加大城市商业银行的不良贷款水平。利率市场化改革对不同效率企业的影响截然不同,高效率企业具有较强的偿债能力,可在城市商业银行竞争中获得较为优惠的低贷款利率,而低效率企业为获得借贷资金必定以高市场利率进行融资,客观上增加城市商业银行的债务成本和违约风险,从而加大城市商业银行的不良贷款水平。此外,城市商业银行作为中小规模银行,倾向于制定更高的存款利率来追求资金规模,从而引致更高的流动性风险问题并加大破产风险,不良贷款率的上升必然降低城市商业银行的综合效率。另一方面Igap与EG显著正相关,Year13与EG显著负相关,这仍然表明利率市场化的逐步推进,短时间内不利于城市商业银行全要素生产率的提高。正如上述所分析的机理,利率市场化的推进将会加剧银行价格竞争,加大收入波动性及降低净资产收益率,加大破产概率及提高不良贷款率,均不利于城市商业银行技术效率的改善和技术创新,这必然会降低城市商业银行的全要素生产率。
| 表 3 面板Tobit模型的估计结果 |
控制变量方面,银行规模的扩大整体而言仍有利于综合效率和全要素生产率的提高,原因在于城市商业银行可通过扩大规模来降低成本,创造新的规模效益空间,实现技术效率的提高。但这并不意味着城市商业银行要一味扩大资产规模,其实城市商业银行应该充分发挥其服务社区和中小企业的优势,通过创新赢利模式发展社区银行的方式来创造新的规模收益空间,而不应该盲目增加营业网点扩大规模。银行自有资本比率和资本充足率无疑会对城市商业银行的效率产生正向影响,这是因为风险控制能力是衡量商业银行经营管理效率高低的重要标准,而银行自有资本比率和资本充足率与风险控制能力高度相关,这两个比率越高则银行安全性越好,不良资产比率越低,资产质量越好。城市商业银行一直寻求通过增资扩股和上市融资来实现提高自有资产比率和资本充足率的目标,这必然也会有利于本身技术效率的提高。营业费用比率的提高不利于城市商业银行综合效率和全要素生产率的提高,原因在于营业费用过高必定压缩城市商业银行的利润,不利于银行收入的稳定性,并加大其破产风险。意外的是,非利息收入占营业收入比重的提高对城市商业银行效率的制约作用并不显著。可能的原因是,非利息收入占营业收入的比重可反映城市商业银行的创新能力水平,但城市商业银行仍未改变依靠净利差来赚取利润的盈利模式,非利息收入水平不高并且缺乏中间业务创新的激励,因此可能对城市商业银行效率有着负面影响效应。不过鉴于非利息收入在城市商业银行营业收入中所占比重较小,因而未形成较为显著的制约作用。
四、 结论与启示本文基于2008-2013年中国24家城市商业银行的相关数据,采用考虑非期望产出并综合径向和非径向特点的EBM模型和GML指数来测算城市商业银行的静态效率和动态全要素生产率,在将利率市场化区分为存款利率市场化和贷款利率市场化的基础上,运用Tobit模型实证检验利率市场化对城市商业银行效率的影响。研究结果表明,城市商业银行全要素生产率呈现增长趋势,技术效率有所改善但却幅度不大,技术进步一直是城市商业银行全要素生产率提高的关键因素;利率市场化及其引致的价格竞争效应会通过降低净资产收益率和加大不良贷款风险的方式不利于银行综合效率和全要素生产率的提高,而银行自有资本比率和资本充足率的上升却有利于化解不良贷款风险而有利于提高银行效率。
利率市场化已经是无法阻挡的趋势,因而如何采取科学合理的措施来应对利率市场化带来的负面影响效应具有重要的理论和现实指导意义。本文的研究结论表明,短时间内利率市场化的推进引发的价格竞争效应不利于城市商业银行综合效率和全要素生产率的提高。城市商业银行作为中小股份制银行,将面临利率市场化、金融脱媒、互联网金融及金融自由化等带来的挑战,经营环境更趋复杂。那么,城市商业银行如何进行自我定位,采取科学合理的政策措施来成功化解利率市场化带来的危机和挑战则显得日益紧迫。本文认为可以从投融资及风险规避两个方面来应对:其一,虽然城市商业银行与国有商业银行及股份制银行的网络和规模优势无法比拟,但却可以充分利用其规模较小、机制灵活及服务地方的特点创造生存空间和管理效率。城市商业银行要不断提升经营管理能力,需要多层次、全方位及更好地服务中小企业,满足中小企业对于融资的需求,积极扩展中小企业融资和信贷业务,同时大力开展中间业务及资产证券化业务创新,通过推进信贷资产证券化,将一部分风险较大的资产在资本市场出售,迅速回收资金,获得中间价差,提高资产的周转速度和收益率,这样既可以成功应对利率市场化可能对城市商业银行利润和资产收益率造成的负面影响,还可以通过业务创新提高技术效率。其二,城市商业银行还需提升自主利率风险意识,建立适当的利率风险预测与评价系统,密切跟踪市场利率走势,结合资金来源和运用情况,合理调整生息资产及付息负债重定价期限结构,减少利率变动对盈利能力的潜在负面影响,降低破产风险概率。此外,城市商业银行还需通过资产重组、引进境外战略投资者和民营资本等方式推动自身发展,不断在竞争中创造规模收益,切实提高自身的技术效率和全要素生产率。
| [] | Elena, B. 2007, "Does IT Invest Improve Bank Performance?". Journal of Banking and Finance(7), 2205–2230. |
| [] | Fare, R. , Grosskopf, S. and Carl, A. P. , 2007, "Environmental Production Functions and Environmental Directional Distance Functions". Energy(7), 1055–1066. |
| [] | Oh, D.H. 2010, "A Global Malmquist-Luenberger Productivity Index". Journal of Productivity Analysis(3), 183–197. |
| [] | Park, K.H. and Weber, W.L. , 2006, "A Note on Efficiency and Productivity Growth in the Korean Banking Industy 1992-2002". Journal of Banking and Finance(12), 2371–2386. |
| [] | Pasiouras, F. 2008, "Estimating the Technical and Scale Efficiency of Greek Commercial Banks". Research in International Business and Finance(3), 301–318. |
| [] | Tone, K. 2001, "A Slack-based Measure of Efficiency in Data Envelopment Analysis". European Journal of Operational Research(3), 498–509. |
| [] | Tone, K. and Tsutsui, M. , 2010, "An Epsilon-based Measure of Efficiency in DEA-A Third Pole of Technical Efficiency". European Journal of Operational Research(3), 1554–1563. |
| [] | 陈刚, 2002, 《评价我国商业银行生产有效性动态变化的Malmquist指数》, 《管理科学》, 第 5 期, 第 31–35 页。 |
| [] | 郑录军、曹廷求, 2005, 《我国商业银行效率及其影响因素的实证分析》, 《金融研究》, 第 1 期, 第 91–101 页。 |
| [] | 袁晓玲、张宝山, 2009, 《中国商业银行全要素生产率的影响因素研究-基于DEA模型的Malmquist指数分析》, 《数量经济技术经济研究》, 第 4 期, 第 93–104 页。 |
| [] | 张健华、王鹏, 2010, 《中国银行业广义Malmquist生产率指数研究》, 《经济研究》, 第 8 期, 第 128–140 页。 |
| [] | 迟国泰, 2006, 《基于DEA方法的中国商业银行综合效率的研究》, 《中国管理科学》, 第 5 期, 第 52–61 页。 |
| [] | 王兵、朱宁, 2011, 《不良贷款约束下的中国银行业全要素生产率增长研究》, 《经济研究》, 第 5 期, 第 32–45 页。 |
| [] | 姜永宏、蒋伟洁, 2014, 《不良贷款约束下中国上市商业银行全要素生产率研究-基于Luenberger指数的分析》, 《南方经济》, 第 4 期, 第 62–79 页。 |
| [] | 谭元戎, 2013, 《中国城市商业银行的技术效率及其影响因素的实证分析》, 《经济问题探索》, 第 6 期, 第 47–53 页。 |
| [] | 魏琪, 2014, 《审慎性监管有助于改善银行效率吗-基于门限模型的实证研究》, 《经济科学》, 第 3 期, 第 85–96 页。 |
| [] | 章晟、杜灵青, 2013, 《信贷调控对商业银行效率影响的实证研究》, 《中南财经政法大学学报》, 第 3 期, 第 100–106 页。 |
| [] | 李程, 2014, 《利率市场化与企业创新效率-基于随机前沿函数的大中型工业企业实证研究》, 《金融经济学研究》, 第 1 期, 第 90–99 页。 |



