1978年以来, 我国经历了长达三十多年的经济高速增长, GDP年均增长率高达10%, 人均GNI从1978年的165美元增加到2011年的2635美元①(World Development Indicators, 2013) , 并于1997年和2010年先后迈入中低和中高收入国家行列。但长期以来, 中国高增长过程中一直伴随着高投入和高消耗、经济结构失衡等诸多弊病, 同时, 中国能否跨越中等收入陷阱并成功过渡到高等收入水平, 更成为各方关注的焦点。然而, 思考进而解决这一系列问题都绕不开对中国增长模式的反思, 尤其是克鲁格曼“亚洲无奇迹”的论断后, 学界对我国经济增长来源、增长模式及其可持续性进行了激烈讨论。
① 均以2000年不变价计算。
学者们一般使用全要素生产率(Total factor productivity, TFP)的方法来对经济增长进行分解, 计算各种要素对经济增长的贡献, 判断经济增长的来源。在经济核算理论中, 全要素生产率是剔除要素投入贡献后所剩余的部分, 最早由索洛(Solow, 1957)提出。索洛首先引入一个Hicks中性和规模报酬不变的新古典生产函数Yt=AtKtαLtβ, 在该函数基础上, 将经济增长扣除劳动和资本投入两个生产要素之后的部分, 即At对经济增长的贡献, 称为技术进步。由于计算出的技术进步是一个残差项, 因此也称为索洛残差。为理解中国经济增速的来源, 过去已有若干学者使用全要素生产率方法对中国经济增速进行了分解, 得到了物质资本、劳动力和全要素生产率的贡献。例如, 李京文等(1996) 对我国1978-1995年的经济增长进行了分解, 发现物质资本、劳动力和TFP依次分别贡献了46.9%、13.3%和39.9%的增长; 沈坤荣(1997) 发现物质资本、劳动力和TFP增长对1979-1994年间的经济增长的贡献依次分别占到38.7%、17.5%和43.8%; 叶裕民(2002) 对1979-1998年间经济增长分解得到的结果也非常类似; 孙琳琳和任若恩(2005) 测算了1981-2002年各要素对经济增长的贡献, 发现物质资本、劳动力和TFP的贡献分别占49%、16%和35%; 李宾和曾志雄(2009) 拉长了样本区间, 研究覆盖1979-2007间的29年, 他们的测算结果显示在改革后的近三十年间, 物质资本对经济增长的贡献最大, 高达71.2%, 劳动力和TFP分别只贡献了9.0%和19.8%。虽然对不同要素贡献的估算差异很大, 但上述研究的测算结果, 基本都认为, 物质资本积累和全要素生产率的增长对中国经济增长是尤为重要的, 而劳动力对经济增长的贡献则最小, 不足20%。
但是, 仅仅以此来判断各要素对经济增长的贡献是有局限性的。原因在于, 上述文献在考察劳动力的贡献时, 只计入了劳动力的数量, 而并未考虑劳动力质量的影响。我国近三十年来劳动力质量大幅提升。以教育指标衡量, 从1982年至2010年, 我国受过高中以上教育的人口比例已经从7.03%上升至22.96%, 增加了2.3倍, 而其中受过大专以上教育的人口比例上升更快, 从0.58%上升至8.93%, 增加了14.4倍, 文盲和半文盲的比例则从22.85%下降至4.08%①。很多学者在使用TFP方法研究中国经济增长源泉时, 也加入了人力资本的考量。例如, Wang and Yao(2003) 对中国1952-1999年的经济增长进行了分解, 发现从1978-1999年, 物质资本、劳动力数量、劳均人力资本和TFP对GDP增长的贡献分别为47.7%、15.9%、11.0%和25.4%。Zhu(2012) 将1978-2007年的人均GDP增长分解为劳动参与率、资本产出比、人均人力资本和TFP的贡献, 得到这四者的贡献分别为7.05%、0.51%、14.55%和77.89%。
① 根据国家统计局公布的人口普查公报计算。
然而, 上述研究也仅采用了受教育年限这一指标来间接表示个体的人力资本存量。在改革开放以后, 我国劳动力除受教育年限大幅上升外, 教育的质量也在不断提高, 同时, 人们的健康水平也伴随生活水平的改善有很大的提高。尤其值得注意的是, 每年有大量劳动力从农村转移到城镇, 其知识、技能和生产率都得到了相当大的提升。因此, 应该考虑使用一个更加完善的刻画劳动力质量增长的人力资本指标来考察劳动力对经济增长的贡献。本文采用梁润(2012) 基于劳动力当期收入衡量的人力资本指数来对劳动力数量和质量的贡献进行测算。
准确测算各要素对经济增长的贡献, 尤其是劳动力数量和质量的贡献, 在当前的背景下尤为重要。2012年我国15-59岁的劳动年龄人口比上年末减少345万人①, 是相当长时期内的第一次绝对下降。同时, 全社会人口也会进入快速老龄化时期。2010年65岁以上人口占总人口的比例为8.87%②。根据人口学家的预测, 这个比例将在2020年超过12%, 并迅速增至2030年的16.4%和2050年的24.1%(曾毅, 2005)。人口老龄化, 以及由此所带来的劳动力短缺将在何种程度上影响中国经济未来的走势, 这也是学术界和政策制定部门都非常关心的问题。而本文的工作有助于更深入的了解中国经济的长期可持续性, 以及未来经济增长的来源。
① 见国家统计局网站发布的《2012年国民经济和社会发展统计公报》。
② 见国家统计局网站发布的《2010年第六次全国人口普查主要数据公报》。
下文的结构如下:第二部分介绍测算方法和要素投入测量方法; 第三部分是本文的测算结果; 第四部分对测算结果进行分析和比较; 第五部分是结论和政策含义。
二、 TFP测算方法及要素投入测量要估计历年来的TFP以及其对经济增长的贡献, 关键是使用何种测算方法以及如何准确测量各要素投入水平。下文介绍TFP测算方法和本文所用的人力资本总量与物质资本存量数据。
(一) TFP测算方法常见的测算TFP的方法有两种, 一种是增长会计法, 基本思路是基于新古典增长理论, 将经济增长中要素投入贡献剔除掉, 从而得到全要素生产率增长的估算值。另一种是经济计量学方法, 一般是借助各种经济计量模型, 将总产出或增加值作为因变量, 将不同的投入变量作为自变量, 通过参数估计的方法来得到TFP。增长会计法是OECD(2001) 生产率手册推荐的方法, 其理论模型简洁, 易于操作, 所得结果更为稳定, 经济含义也较强, 是目前应用最广的TFP测算方法。经济计量学方法虽然可以放松增长会计法中的完全竞争和规模报酬不变的假设, 但却需要对参数作出其他的先验假定, 而且受样本量的影响, 还容易出现估计参数不稳定甚至与常识相悖的结论。基于以上原因, 本文使用增长会计法来进行测算。
与孙琳琳和任若恩(2005) 以及李宾和曾志雄(2009) 一样, 我们假定总量生产函数可以表示为超越对数生产函数的形式, 具体为:
| $\begin{align} & \text{log}\left( Y \right)={{\alpha }_{0}}+{{\alpha }_{H}}\cdot \text{log}\left( H \right)+{{\alpha }_{K}}\cdot \text{log}g\left( K \right)+{{\alpha }_{tt}}+{{\beta }_{KK}}/2\cdot \text{log}{{\left[ K \right]}^{2}} \\ & +{{\beta }_{HH}}/2\cdot \text{log}{{\left[ H \right]}^{2}}+{{\beta }_{tt}}/2\cdot {{t}^{2}}+{{\beta }_{KH}}\cdot \text{log}\left( K \right)\cdot \text{log}\left( H \right) \\ & +{{\beta }_{Kt}}\cdot \text{log}\left( K \right)\cdot t+{{\beta }_{Ht}}\cdot \text{log}\left( H \right)\cdot t \\ \end{align}$ | (1) |
其中的Y、K和H分别表示总产出、物质资本存量和人力资本总量。
文献中已证明, 在规模报酬不变的假设下, 希克斯中性的TFP增长率可以表示为:
| $\text{ln}\left( \frac{{{A}_{t}}}{{{A}_{t-1}}} \right)=\text{ln}\left( \frac{{{Y}_{t}}}{{{Y}_{t-1}}} \right)-{{{\bar{s}}}_{k}}\left( t \right)\cdot \text{ln}\left( \frac{{{K}_{t}}}{{{K}_{t-1}}} \right)-(1-{{{\bar{s}}}_{k}}\left( t \right))\cdot \text{ln}\left( \frac{{{H}_{t}}}{{{H}_{t-1}}} \right)$ | (2) |
其中
① 见Barro and Sala-i-Martin(2004) 第435页。
由于人力资本总量H可以表示为劳动力数量L和劳均人力资本存量h之积, (2) 式还可以写为:
| $\begin{align} & \text{ln}\left( \frac{{{Y}_{t}}}{{{Y}_{t-1}}} \right)=\text{ln}{{A}_{t}}{{A}_{t-1}}+{{{\bar{s}}}_{k}}\left( t \right)\cdot \text{ln}\left( \frac{{{K}_{t}}}{{{K}_{t-1}}} \right)+(1-{{{\bar{s}}}_{k}}\left( t \right))\cdot \text{ln}\left( \frac{{{H}_{t}}}{{{H}_{t-1}}} \right) \\ & =\text{ln}\left( \frac{{{A}_{t}}}{{{A}_{t-1}}} \right)+{{{\bar{s}}}_{k}}\left( t \right)\cdot \text{ln}\left( \frac{{{K}_{t}}}{{{K}_{t-1}}} \right)+(1-{{{\bar{s}}}_{k}}\left( t \right))\cdot \text{ln}\left( \frac{{{L}_{t}}}{{{L}_{t-1}}} \right)+ \\ & (1-{{{\bar{s}}}_{k}}\left( t \right))\cdot \text{ln}\left( \frac{{{h}_{t}}}{{{h}_{t-1}}} \right) \\ \end{align}$ | (3) |
因此, 我们可以把经济增长分解为TFP增长、物质资本存量增长和人力资本总量增长的贡献三部分, 而人力资本总量的贡献还可进一步分解为劳动力人数(数量)增长和劳均人力资本(质量)增长的贡献。
估算各要素的产出弹性有两种方法, 计量回归和收入份额法。前者需假定产出弹性为常数, 后者可测算出随时间变动的产出弹性但需假设市场完全竞争及规模报酬不变。一般认为后者即收入份额法相对较优, 尤其是对快速发展的经济体而言。OECD(2001) 生产率手册中推荐使用此种方法, 孙琳琳和任若恩(2005) 也使用这种方法来确定投入要素的产出弹性。本文也使用收入份额法, 用历年收入法GDP中资本所得份额作为当年的资本产出弹性。具体的, 将第t年各地区收入法生产总值构成项目中的劳动者报酬、固定资产折旧和营业盈余按地区加总, 得到第t年全国的劳动者报酬、固定资产折旧和营业盈余, 则第t年的全社会的资本所得份额为:
| ${{s}_{k}}\left( t \right)=\frac{固定资产折旧\left( t \right)+营业盈余\left( t \right)}{劳动者报酬\left( t \right)+固定资产折旧\left( t \right)+营业盈余\left( t \right)}$ | (4) |
历年收入法GDP构成的数据来源分别为:1983-1992年数据来自Hsueh and Li(1999) , 1993-2004年数据来自《中国国内生产总值核算历史资料(1952-2004) 》, 2005-2011年来自历年《中国统计年鉴》。所得资本份额最大值为53.3%, 最小值为39.1%, 平均值为43.6%。
(二) 人力资本总量在本文的研究中, 人力资本总量的测算是准确估计全要素生产率及各要素对经济增长贡献的关键。在传统文献中, 个体的人力资本存量表示该个体所拥有的知识、技能和能力, 全社会劳动力的人力资本总量为个体的人力资本存量之和。由于人力资本依附于个体并且不可直接测量, 估算其存量比较困难。从全要素生产率测算的原理可以看出, 我们需要找到一个既能反映当期社会全体劳动力的生产能力又在时间序列上具有可比性的人力资本总量指标。
传统文献中对人力资本总量的线性测算方法主要有成本法, 教育指标法、未来收益贴现法和基于劳动收入的方法等四类。我国学者也基于这四种方法对中国的人力资本总量进行了估计。
成本法类比于物质资本的形成, 将形成个体人力资本的投入累计相加, 用该累计投入来表示人力资本存量。基于成本法的人力资本测算主要有张帆(2000) 、钱雪亚等(2008) 、焦斌龙和焦志明(2010) 等。但目前大家对于应该将哪些投入作为形成人力资本的投入看法不一, 并且投入的成本与当期劳动者的生产率并非一一对应, 因而由此计算的人力资本总量不适宜用于全要素生产率测算。
教育指标法仅关注教育这一形成人力资本的手段。出于数据易得性的考虑, 很多研究使用这一类指标表征人力资本存量。例如蔡昉和王德文(1999) 、徐现祥和舒元(2005) 、郑京海等(2008) 等研究采用劳动力平均受教育年限, 许和连等(2006) 使用中等及以上在校学生人数, 郭庆旺等(2007) 用中小学师生比等指标代理个体的人力资本存量。但鉴于教育指标未考虑教育的质量、工作经验、城乡转移等因素对个体劳动生产率的影响, 因此并不能准确地衡量人力资本存量的变动。
未来收益法(Jorgenson and Fraumeni, 1989和1992) 假定个体能像物质资本一样在市场上交易, 其价格即为该个体预期未来终生劳动收入的贴现值, 可以用于表示该个体的人力资本存量。国内使用这类方法的测算结果主要有王德劲和向蓉美(2006) 以及李海峥等(2010) 。由于一个个体的终生劳动收入贴现值还取决于他在未来各时期的劳动生产率大小, 以及未来的物质资本存量, 而不仅仅是当期的劳动生产率, 因此也不宜用于全要素生产率的测算。
基于劳动收入的人力资本测算方法(LIHK方法)由Mulligan和Sala-i-Martin提出(Mulligan and Sala-i-Martin, 1997)。该方法认为, 在要素市场完全竞争的情况下, 由于同一经济体中的个体面临相同的物质资本存量和技术水平, 工资差别就反映了当期劳动者生产能力的差异。假定没有受过教育也没有工作经验的劳动者(简单工人)的生产能力是固定的, 不随时间和地域的改变而变化, 就可以将简单工人作为衡量人力资本的基本单位。全社会劳动收入总和除以简单工人的工资即可表征此时全社会的人力资本总量。Mulligan和Sala-i-Martin使用美国人口普查的数据, 通过回归Mincer工资方程来估计简单工人的工资, 从而估计了各普查年份美国的人力资本总量。这一方法直接从劳动者的收入出发, 包含了教育质量、工作经验、物质资本等因素对个体生产能力的影响, 是表征人力资本总量最直接的指标。从经济意义上看, 该指标反映了当期全社会劳动力的生产能力, 同时又在时间上具有可比性, 符合全要素生产率的测算要求。朱平芳和徐大丰(2007) 基于这种方法对中国城市人力资本进行了测算。梁润(2012) 则结合中国的实际情况, 对原方法进行了适当改进, 测算了全国的人力资本总量。作者对全国人口按年龄、性别、受教育程度和城乡进行分组, 估计了历年各组的劳动力人数, 并结合CHNS调查数据, 估算了每年各组的人力资源存量, 并加总获得了1982-2011年全国的人力资本总量。本文所用的历年劳动力人口数量、劳均人力资本存量以及人力资本总量数据来自梁润(2012) , 详细数据见表 1。
除了线性加总以外, 也有学者考虑人力资本加总的非线性。例如陈晓光(2005) 考虑了人力资本向下兼容性, 并进行了跨国收入核算。人力资本向下兼容的含义是, 高水平人力资本的劳动力可以从事低水平的工作, 但反过来却不可以。作者得出的结论是, 在考虑人力资本向下兼容后, 人力资本对经济增长的贡献大幅提高。在考虑这种非线性加总情况下, 一般而言, 工资之比依然等于人力资本之比, 但由于加总的非线性, 在劳动力人力资本水平不断提高的过程中, 人力资本总量的增长率会高于按线性加总的增长率。如果采用非线性加总, 人力资本的贡献率可能比本文测算更高。然而人力资本非线性加总涉及到较为复杂的参数选择和估计, 估算结果也受到分组数量的影响, 为简单起见, 本文仍然使用LIHK方法计量的人力资本总量。
需要进行说明的是, 由于人力资本本身的复杂性和测算的困难, 以及中国劳动力市场存在各种扭曲, 所有试图对中国的人力资本总量进行测算的研究都会遇到使用何种指标更为准确的问题。Mulligan和Sala-i-Martin提出的方法也仅仅是对于人力资本总量的一个较为合理的近似。然而, 相比于其他测算方法, 使用相对工资收入来测算的人力资本总量对于研究人力资本对经济增长的贡献而言可能是更为合理的。原因有以下两方面:一方面, 虽然由于劳动力市场的各种扭曲, 劳动力工资水平可能与劳动者本身的能力并不相符。然而若从经济增长的角度看, 劳动力工资可能更好的表示了该劳动力的边际贡献。另一方面, 从TFP方法对经济增长的贡献进行分解的公式可以看出, 人力资本总量的增长率比其绝对水平更加重要。如果中国劳动力市场的各种扭曲随时间的变化相对缓慢, 那么测算出的人力资本总量的增长率与真实增长率的误差是相对较小的。
(三) 物质资本存量许多实证研究都涉及到对资本存量K的估计, 例如计算投资回报率、分析投资需求、估计经济的潜在产出、经济增长分解等。由于我国目前还没有可用的官方资本存量或资本服务量的数据, 因此, 需要在一定的假设下对物质资本存量进行估算。
本文使用最常用的永续盘存法估计我国的物质资本存量。具体方法和参数设置主要参考了张军等(2004) , 并根据《中国国内生产总值核算历史资料(1952- 2004) 》和历年统计年鉴更新了近年的数据。但本文选取的折旧率与该文有所不同, 张军等(2004) 中假定各省全部建筑和设备的平均寿命期分别是45年和20年, 其他类型的投资假定为25年, 从而三者的折旧率分别是6.9%, 14.9%和12.1%, 再根据1952-2000年各年三类资本品的比重, 加权得到各省固定资本形成总额的经济折旧率9.6%。在其他文献中, 由于使用数据和方法的不同, 对资产折旧的处理也存在差异, 折旧率的选取从3.6%(Hu and Khan, 1997)到10%(龚六堂和谢丹阳, 2004)甚至更高不等。本文沿用Perkins(1988) 、王小鲁和樊纲(2000) 与Wang and Yao(2003) 的处理方法, 选取整体折旧率为5%。主要原因为, 本文是对整个社会的物质资本存量进行估计, 不仅包含建筑和设备这类折旧较快的物质资本, 还包括公路、桥梁和其他公共设施等折旧相对较慢的物质资本, 因而应选取一个较为适中的折旧率。另外, 用5%的折旧率所计算的折旧额, 与从地区生产总值收入法构成项目加总而得的折旧额基本相符。计算得到的历年物质资本存量数据见表 1。
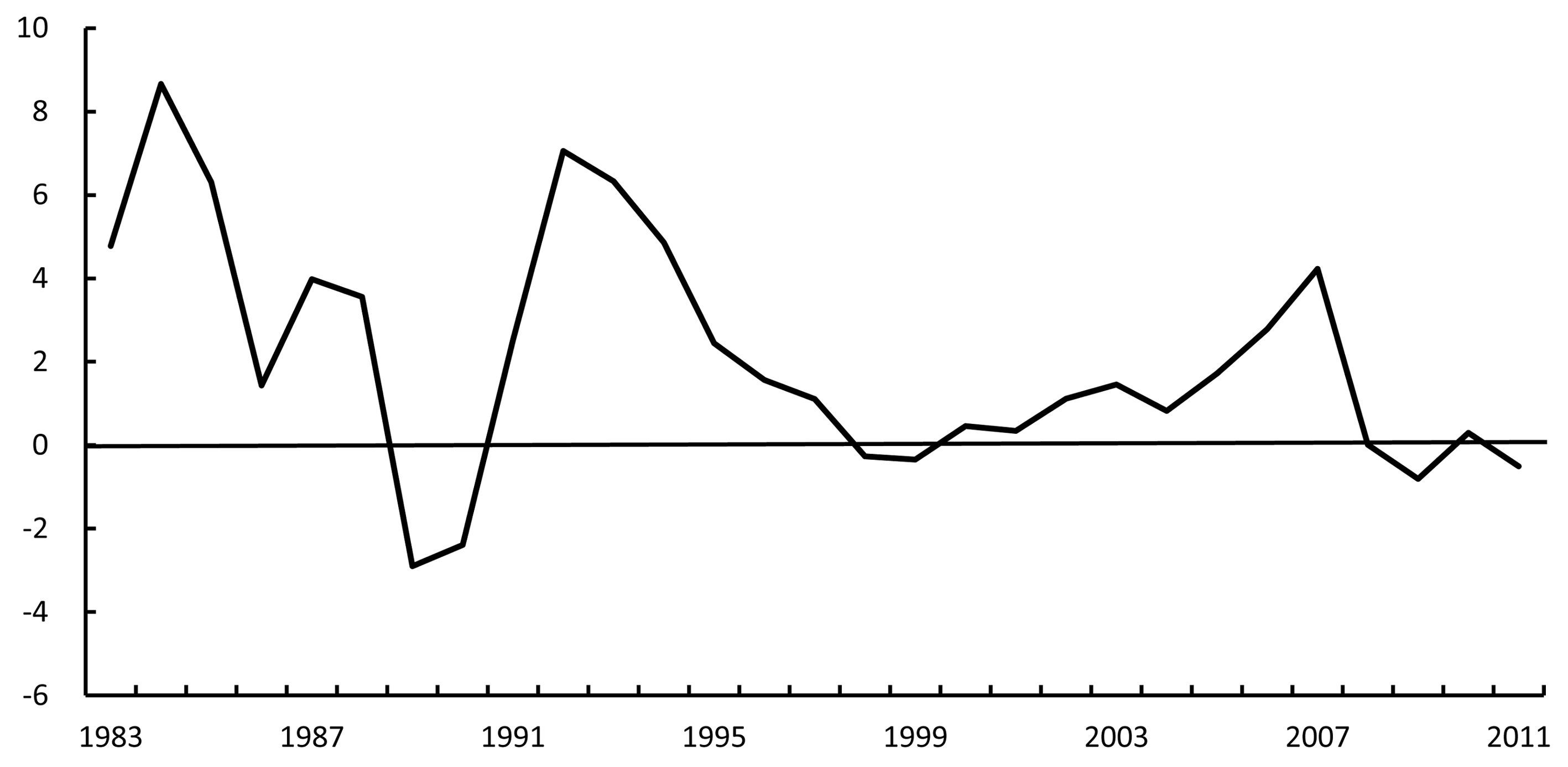
三、 估计结果和比较使用上述物质资本存量和人力资本总量数据及资本所得份额, 根据式(2) 可得到历年的全要素生产率(TFP)增长率, 见表 1。从中可看出, TFP增长率在改革开放初期比较高, 波动也最为剧烈, 最高点在1984年, 达到8.7%, 最低时为1989年的-2.9%。近年来, TFP的波动逐渐降低, 增速也趋缓。图 1更清楚的显示了TFP增长率的变化趋势。从中可看出, TFP增长率与我国经济制度改革和技术进步密切相关。1982-1985年是包产到户深入发展的时期, 产权制度的明晰使得劳动者的积极性更高, TFP增长率在这一阶段也快速上升。随着1988年的物价闯关失败以及当时企业和居民的错误预期, 再加上1989年政府猛烈的宏观调控①, 以及当时国内和国际上的一些政治因素, 企业的生产受到很大负面影响, TFP的增长率也跌到了谷底, 甚至为负。1992年邓小平南巡, 被认为是中国改革过程中历史性的转折, 其后的一系列改革政策和刺激措施使得生产快速恢复, TFP增长率迅速攀升。1998年受亚洲金融危机的影响, TFP增长率又再次下滑。进入新世纪以来, 随着我国加入WTO、参与国际分工、释放生产潜力, TFP增长率的波动减小, 趋势上呈稳步上升态势并在2007年达到了另一高点, 但2008年以来的全球金融危机对TFP造成了显著的负面影响。此后, 在内需刺激政策下, TFP增长率在2010年有所回升, 但2011年又继续降为负值。
① 参见宋国青(1995) 对此次错误预期的讨论, 以及杨冶(1995) 对这次经济紧缩的研究。
| 表 1 中国的人力资本、物质资本和TFP |
|
图 1 TFP增长率估计 |
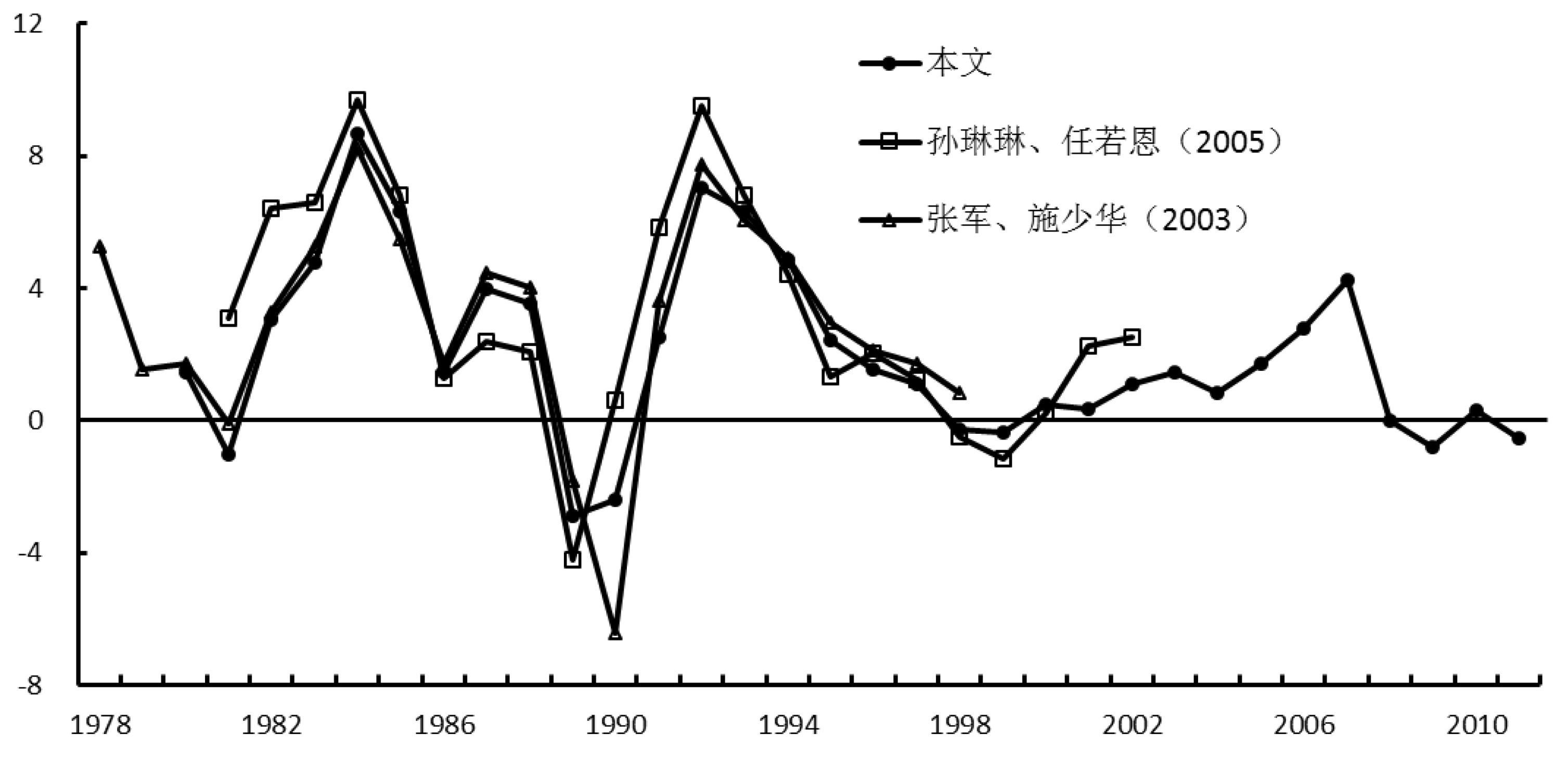
为了考察考虑了人力资本贡献后全要素生产率的测算效果, 图 2比较了表 1中的TFP增长率与其他一些学者测算的结果。从中可以看出, TFP增长率的波动大体上都是一致的, 说明在考虑人力资本后TFP增长率的波动方向依然没有改变, 但本文测算的TFP增长率水平与其他测算结果存在差异。在大部分时期, 本文的估计结果低于孙琳琳和任若恩(2005) 以及张军和施少华(2003) 的估计(以及其他一些类似方法估计出的TFP增长率), 原因在于, 这些研究只简单的考虑了劳动力的人数, 而没有考虑(或没有考虑完全)人力资本对产出的影响, 因此劳动力质量上升的因素部分被计入TFP中, 导致TFP增长率被高估。
|
图 2 与其他TFP增长率测算结果的比较 |
为了对过去的经济增长模式有更加深刻的认识, 我们可以按(3) 式定量分析物质资本存量、人力资本总量和TFP增长对过去经济增长的贡献, 并可进一步将人力资本总量的贡献分解为劳动力人数(数量)的贡献和劳均人力资本存量(质量)的贡献。
1983-2011年, 我国GDP的年均增长率高达10.3%, 这其中, 物质资本存量增长贡献了5.0个百分点, 占48.7%, 表示我国过去三十年的经济增长几乎一半得益于物质资本的积累, 这与其他研究如孙琳琳和任若恩(2005) 以及郭庆旺和贾俊雪(2005) 的结果也比较一致。人力资本总量的贡献为3.2个百分点, 占31.0%, 低于物质资本存量的贡献。在人力资本总量对GDP贡献的3.2个百分点中, 劳动力人数上升的贡献仅为0.9个百分点, 占27.1%, 而劳均人力资本存量上升的贡献为2.3个百分点, 占72.9%, 说明过去三十年人力资本总量的贡献主要是通过劳动力质量的提高来体现的。TFP的增长的贡献为2.1个百分点, 占20.3%。
我们进一步将1983-2011的30年分为三个阶段, 并分别估计了每个阶段各要素对经济增长的贡献, 如表 2所示。从中可以看出, 1983-1990年、1991-2000年和2001-2011年这三个阶段的的GDP年平均增长率分别为9.9%、10.5%和10.4%。由于社会总投资的增长非常快, 投资占GDP的比重也在快速上升, 物质资本对经济增长的贡献越来越大, 从上世纪80年代的3.8个百分点上升至本世纪初的6.3个百分点, 贡献率也从38.0%上升至60.5%。人力资本总量的贡献比较稳定, 但从分解来看, 劳动力数量和质量对GDP增长的相对贡献发生了很大变化。1983-1990年, 劳动力数量上升与质量增长的贡献几乎相等, 都约为1.6个百分点。但随后, 数量的贡献逐渐下降而质量的贡献不断上升。在2001-2011年期间, 劳动力数量的贡献已下降到仅0.4个百分点而质量的贡献则上升至2.7个百分点, 分别占人力资本总量贡献的12%和88%。由此可见, 近年来人力资本总量对经济增长的贡献绝大部分来自劳动力质量的上升, 数量变动的贡献已经很小。从上世纪80年代至今, TFP增长的贡献相对变化较大, 上世纪80年代为2.9个百分点, 近十年内则下降至1.2个百分点。从贡献率来看, TFP的贡献率从上世纪80年代的29.6%下降至近十年的11.5%, 说明TFP的增长对经济增长的促进作用越来越小。
| 表 2 分时段各要素对经济增长的贡献 |
在使用综合人力资本总量指标测算后, 人力资本总量对经济增长的贡献与仅考虑劳动力数量或简单考虑劳动力教育水平的测算结果差别很大。仅考虑劳动力数量的研究测算出劳动力对经济增长的贡献均低于20%, 而TFP增长对经济增长的贡献则相对较大。由于这些研究未考察劳动力质量的变化, 因此会将劳动力质量上升的部分即劳均人力资本的贡献计入TFP中, 导致测算的TFP偏高, 并得出劳动力对经济增长贡献不大的结论。考察劳动力教育水平后, 劳动力对经济增长的贡献增加, 例如Wang and Yao(2003) 估计的1978-1999年劳动力数量和质量的贡献之和为25.9%。本文测算发现, 过去三十年中国的经济增长约有31%是由人力资本总量的增长所贡献的, 其中劳动力质量上升的贡献率为22.6%, 占人力资本总量贡献的73%。
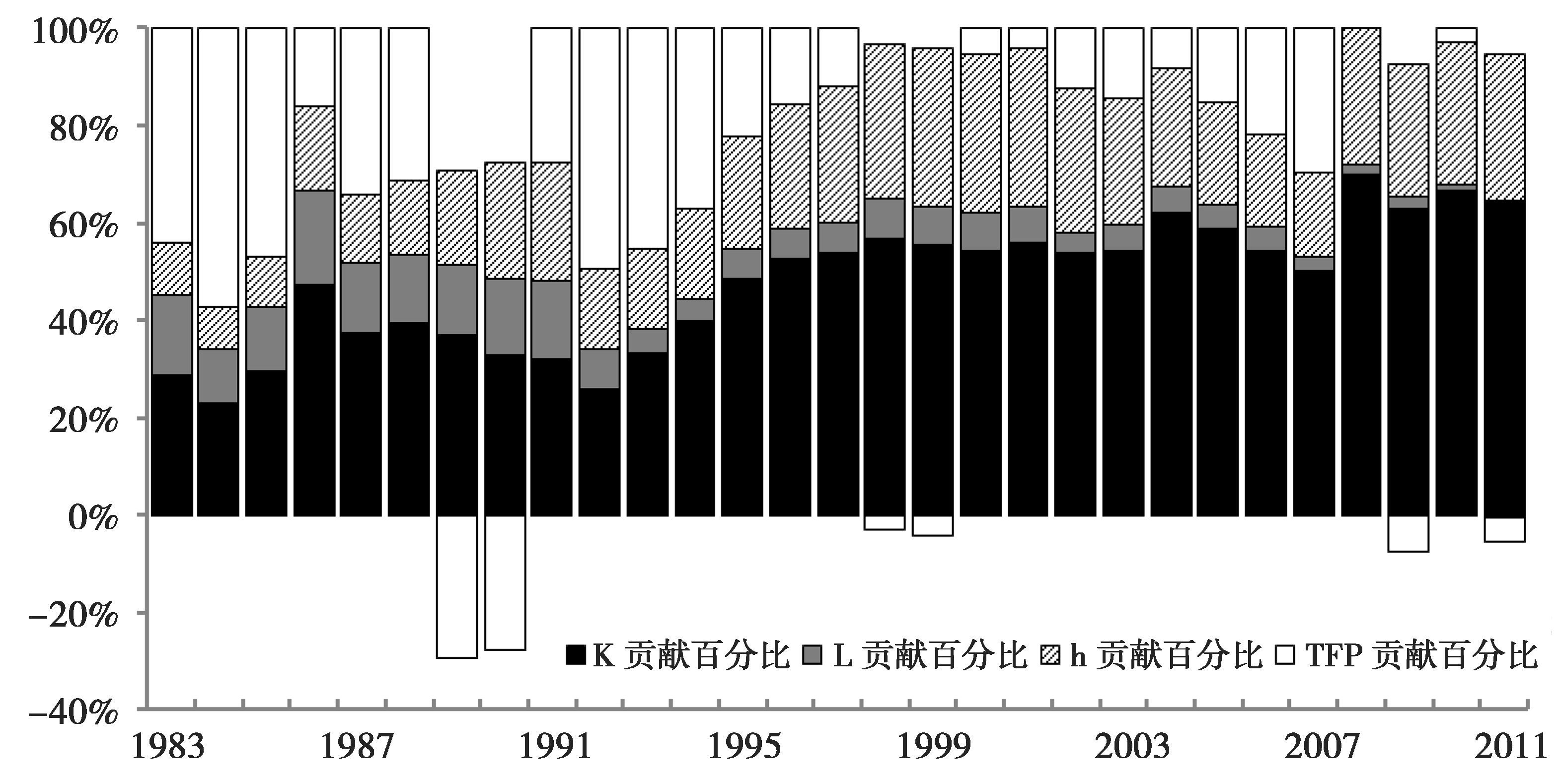
表 3和图 3对历年各要素对经济增长的贡献进行了分解。从中可看出, 物质资本存量和劳均人力资本存量对经济增长的贡献在逐渐增加, 而劳动力人数的贡献在逐渐减小。这三者的波动相对较小, TFP的波动最大, 贡献率最高为57.1%, 最低为-71.4%, 而且在改革开放初期的波动尤为剧烈。这与改革初期我国的宏观经济治理经验不足、经济政策不稳定有关。近年来, 我国在熨平经济周期方面有了更多的经验和更好的方式, 因此经济波动和TFP贡献的波动都大为减小。
| 表 3 历年各要素对经济增长的贡献 |
|
图 3 各要素对经济增长的贡献率 注:K表示物质资本存量, L表示劳动力数量, h表示劳均人力资本存量。 |
在对中国全要素生产率进行测算的文献中, 大多直接使用劳动力人数来衡量劳动力的贡献, 或使用受教育年限来近似代替劳动力的质量。然而, 在中国这样一个高速发展并正经历结构转型的经济体中, 劳动力人数或受教育年限远不能刻画劳动力质量的变化。本文使用最新的人力资本测算结果, 对中国1983-2011年的全要素生产率重新进行了测算。
总体来看, 中国的经济增长仍然属于投入推动型增长, 尤其是物质资本投入的推动。本文的测算结果表明, 过去三十年我国的经济增长中, 有48.7%得益于物质资本存量的积累, 有31.0%得益于人力资本总量的增长, TFP增长的贡献仅为20.3%。在人力资本总量的贡献中, 有27%来自劳动力数量的上升, 73%来自于劳动力质量的增长。与仅考虑劳动力数量的测算结果相比, 考虑质量后劳动力对经济增长的贡献大幅上升。
过去三十年, 我国物质资本经历了快速积累的过程, 其对经济增长的贡献也在逐步增加——从八十年代的3.8个百分点上升至本世纪初的6.3个百分点, 贡献率从38%上升至60.5%。但随着物质资本存量基数的变大, 加上近年来产能过剩问题的恶化, 未来物质资本存量的增速可能大幅放缓, 过去依靠物质资本投入推动的增长可能无法延续。
改革开放初期, 通过引进技术、设备等方式, 我国实现了技术的快速发展, 而随着我国技术水平向世界前沿趋近, 技术进步也在逐渐放缓。从分时期经济增长的分解来看, TFP增长对经济增长的贡献从上世纪八十年代的2.9个百分点下降至本世纪初的1.2个百分点。由此可见, 中国经济转型的迫切性进一步提高。
人力资本是一个国家的宝贵资源。在我国1983-2011年的经济增长中, 人力资本总量贡献了3.2个百分点, 占31.0%。我国即将进入老龄化社会, 劳动力绝对数量已经开始下降。但幸运的是, 我国劳动力质量在不断快速上升, 并已经成为全社会人力资本总量增长的主要来源。随着我国升学率的不断提高以及整体教育质量的逐年上升, 未来若干年里将会有更多的高质量劳动力进入社会。城镇化的深入也能使更多人通过在职培训、干中学等因素提升技能, 促进现有劳动力的人力资本不断增长。在未来若干年中, 我国劳动力质量的增长可能成为支撑经济增长的重要动力。要维持经济的长期、可持续增长, 需要将我国经济增长从物质资本推动型转换为人力资本推动型, 这需要全社会加大对人力资本的投资, 以及发展高人力资本附加值产业。
| [] | Barro R. J., X. Sala-i-Martin X, 2004, "Economic Growth (2nd Edition)", Cambridge, Massachusetts: MIT Press. |
| [] | Hsueh, T. and Li, Q, 1999, China's National Income: 1952-1995, Westview Press. |
| [] | Hu Z., Khan M. S., 1997, "Why is China Growing So Fast?". IMF Staff Papers, 103–131. |
| [] | IMF, 2013, “World economic outlook”, April 2013. |
| [] | Jorgenson, D.W. and Fraumeni, B.M., 1989, “The Accumulation of Human and Non-Human Capital, 1948-1984”, in The Measurement of Saving, Investment and Wealth. Eds. by R. Lipsey and H. Tice, Published by University of Chicago Press. |
| [] | Jorgenson D.W., Fraumeni B.M., 1992, "Investment in Education and U.S. Economic Growth". Scandinavian Journal of Economics, S51–S70. |
| [] | Mulligan C.B., Sala-i-Martin X., 1997, "A Labor Income-based Measure of the Value of Human Capital: An Application to the States of the United States". Japan and the World Economy, 9(2), 159–191. DOI:10.1016/S0922-1425(96)00236-8 |
| [] | OECD, 2001, Productivity Manual: A Guide to the Measurement of Industry - level and Aggregate Productivity Growth, OECD, Paris. |
| [] | Perkins , D. H., 1998, "Reforming China's Economic System". Journal of Economic Literature, 26(2), 601–645. |
| [] | Solow R.M., 1957, "Technical Change And the Aggregate Production Function". The review of Economics and Statistics, 39(3), 312–320. DOI:10.2307/1926047 |
| [] | The World Bank, 2013, “World Development Indicators”, May 2013. |
| [] | Wang, Y. and Yao Y., 2003, “Sources of China's Economic Growth, 1952-1999: Incorporating Human Capital Accumulation”, China Economic Review, 14(1), pp.32-52. |
| [] | Zhu X., 2012, "Understanding China's growth: Past, present, and future". The Journal of Economic Perspectives, 26(4), 103–124. DOI:10.1257/jep.26.4.103 |
| [] | 蔡昉、王德文, 1999, 《中国经济增长可持续性与劳动贡献》, 《经济研究》, 第 10 期, 第 62–68 页。 |
| [] | 陈晓光, 2005, 《人力资本向下兼容性及其对跨国收入水平核算的意义》, 《经济研究》, 第 4 期, 第 46–56 页。 |
| [] | 龚六堂、谢丹阳, 2004, 《我国省份之间的要素流动和边际生产率的差异分析》, 《经济研究》, 第 1 期, 第 45–53 页。 |
| [] | 郭庆旺、贾俊雪, 2005, 《中国全要素生产率的估算:1979—2004》, 《经济研究》, 第 6 期, 第 51–60 页。 |
| [] | 国家统计局, 2007, 《中国国内生产总值核算历史资料1952-2004》, 中国统计出版社。 |
| [] | 焦斌龙、焦志明, 2010, 《中国人力资本存量估算: 1978-2007》, 《经济学家》, 第 9 期, 第 27–33 页。 |
| [] | 李宾、曾志雄, 2009, 《中国全要素生产率变动的再测算: 1978-2007 年》, 《数量经济技术经济研究》, 第 3 期, 第 3–15 页。 |
| [] | 李海峥、梁赟玲、BarbaraFraumeni、刘智强、王小军, 2010, 《中国人力资本测度与指数构建》, 《经济研究》, 第 8 期, 第 42–54 页。 |
| [] | 李京文、龚飞鸿、明安书, 1996, 《生产率与中国经济增长》, 《数量经济技术经济研究》, 第 12 期, 第 27–40 页。 |
| [] | 梁润, 2012, 《中国的人力资本与经济增长:1978-2030》, 博士论文。 |
| [] | 钱雪亚、王秋实、刘辉, 2008, 《中国人力资本水平再估算: 1995-2005》, 《统计研究》, 第 12 期, 第 3–10 页。 |
| [] | 沈坤荣, 1997, 《中国综合要素生产率的计量分析与评价》, 《数量经济技术经济研究》, 第 11 期, 第 53–62 页。 |
| [] | 舒尔茨, 1990, 《论人力资本投资》, 中译本, 北京经济学院出版社。 |
| [] | 宋国青, 1995, 《利率、通货膨胀预期与储蓄倾向——从两次高通胀期间的储蓄倾向看预期的作用》, 《经济研究》, 第 7 期, 第 3–10 页。 |
| [] | 孙琳琳、任若恩, 2005, 《中国资本投入和全要素生产率的估算》, 《世界经济》, 第 12 期, 第 3–13 页。 |
| [] | 王德劲、向蓉美, 2006, 《我国人力资本存量估算》, 《统计与决策》, 第 10 期, 第 100–102 页。 |
| [] | 王小鲁和樊纲, 2000, 《中国经济增长的可持续性——跨世纪的回顾与展望》, 经济科学出版社。 |
| [] | 徐现祥、舒元, 2005, 《物质资本、人力资本与中国地区双峰趋同》, 《世界经济》, 第 1 期, 第 47–57 页。 |
| [] | 许和连、亓朋、祝树金, 2006, 《贸易开放度、人力资本与全要素生产率》, 《世界经济》, 第 12 期, 第 3–11 页。 |
| [] | 许宪春, 2002, 《中国国内生产总值核算》, 《经济学(季刊)》, 第 4 期, 第 23–36 页。 |
| [] | 叶裕民, 2002, 《全国及各省区市全要素生产率的计算和分析》, 《经济学家》, 第 3 期, 第 115–121 页。 |
| [] | 杨冶, 1995, 《中国80年代三次经济紧缩评述》, 《中国工业经济》, 第 6 期, 第 28–31 页。 |
| [] | 曾毅, 2005, 《中国人口老化、退休金缺口与农村养老保障》, 《经济学(季刊)》, 第 3 期, 第 1043–1066 页。 |
| [] | 张帆, 2000, 《中国的物质资本和人力资本估算》, 《经济研究》, 第 8 期, 第 65–71 页。 |
| [] | 张军、施少华, 2003, 《中国经济全要素生产率变动:1952-1998》, 《世界经济文汇》, 第 2 期, 第 17–24 页。 |
| [] | 张军、吴桂英、张吉鹏, 2004, 《中国省际物质资本存量估算:1952-2000》, 《经济研究》, 第 10 期, 第 35–44 页。 |
| [] | 郑京海、胡鞍钢、ArneBigsten, 2008, 《中国的经济增长能否持续?一个生产率视角》, 《经济学(季刊)》, 第 3 期, 第 777–808 页。 |
| [] | 朱平芳、徐大丰, 2007, 《中国城市人力资本的估算》, 《经济研究》, 第 9 期, 第 84–95 页。 |




