经国务院批准,中国人民银行决定从2013年7月20日起全面放开金融机构贷款利率管制,将我国利率市场化改革推进到新的阶段。随着利率市场化改革不断推进,各类利率相互关联度不断提高,相互影响更为迅速,利率在经济当中所起的杠杆作用日渐凸显,对宏观经济的调节作用日益显现 (戴国强和梁福涛,2006)。形成鲜明对照的是,货币供应量稳定宏观经济波动的效力逐渐降低,没有形成逆周期性的供给机制,反而表现出明显的内生性供给 (于泽,2008;黄武俊和陈漓高,2010)。这促使了大量学者呼吁我国应该构建以利率为货币政策中间目标的货币政策体系。
泰勒规则为利率政策制定提供一个很好的参考标准,该理论认为应该根据通货膨胀缺口和产出缺口来调节利率 (Taylor,1993)。Taylor (1993)对比了不同货币政策规则下美国、法国、德国、意大利、日本、英国和加拿大7个国家的经济表现,发现利率规则,即泰勒规则,最有利于实现物价稳定和产出稳定。鉴于这一货币政策规则的良好表现,许多国家的货币当局在制定货币政策时直接或间接地借鉴了泰勒规则。
基于泰勒规则良好的实践基础与其简易操作方式,在当前经济背景下,检验泰勒规则在我国的适用性显得很有必要,然而,这一规则的适用性检验需对我国的货币政策环境进行特殊考虑:
第一,我国利率并没有完全实现市场化。泰勒规则是在利率实现完全市场化的环境下提出,其适用性理应满足此条件。我国利率市场化是一个逐步改革过程。我国在1996年放开了同业拆借利率,开始实施利率市场化改革,并在2003年公布的《2002年中国货币政策执行报告》中明确了利率市场化改革的思路:先外币,后本币;先贷款,后存款;先长期、大额,后短期、小额。然而,我国利率市场化至今依然没有完成。进而,我们在付诸于计量检验时,有必要将传统泰勒规则设定为时变参数的泰勒规则,以考虑利率市场化的改革历程。
第二,我国货币政策多目标性。周小川多次强调,我国货币政策坚持盯准四个目标——低通货膨胀、经济增长、保持较高就业和国际收支平衡。此外,有些经济变量对货币政策的影响可能只是存在阶段性影响,如影响国际收支平衡的汇率在我国很长时期内是固定的,并且国际收支并未表现严重失衡,因此货币政策制定在此期间可能并不会考虑国际收支与汇率因素。郭福春和潘锡泉 (2012)的研究也显示,汇改后汇率波动幅度的加大对货币政策的冲击效应明显,而汇改前及整体层面上的效应并未显现,体现了我国货币政策的“区间效应”特性。因此,泰勒规则中货币政策目标的维数也可能是时变的。
基于此,本文将传统泰勒规则拓展为货币政策目标与参数都是时变的泰勒规则,以期更好检验泰勒规则在我国的适用性。本文余下内容结构安排如下:第二部分是文献综述;第三部分具有货币政策目标与参数时变的泰勒规则模型的设定与估计;第四部分为实证结果分析,考察我国利率影响因素的维度时变性和强度时变性,综合判断泰勒规则在我国的适用性;最后为本文的结论与政策含义。
二、 文献综述已有文献对泰勒规则的完善与拓展主要有两个方向:一是增加传统泰勒规则中的货币政策目标,二是使用不同的计量分析方法。
在泰勒规则的政策目标维度方面,学者们的拓展主要体现为:第一,平滑调整机制的引入。当利率目标值与当期利率差距较大时,利率一步式地调向目标值将对资本市场形成巨大冲击,同时对货币当局的信誉度也会造成负面影响,因此大量研究偏向于引入利率滞后项以刻画利率调整的平滑特征 (Sack and Wieland, 1999;Clarida et al., 2000;谢平和罗雄,2002)。第二,袁靖 (2007)则在传统泰勒规则中进一步考虑了资产价格的因素,认为资产价格波动也应纳入我国货币政策操作规则之内。第三,随着世界经济互动关系日益增强,Clarida et al.(2001)、王胜和邹恒甫 (2006)等考虑了开放经济的因素,在传统泰勒规则中考虑了国外因素,并发现国外经济发展也对国内的货币政策制定产生影响。第四,Svensson (2000)、Mohanty and Klau (2004)、陈晓莉 (2008)、郭福春和潘锡泉 (2012)等进一步在泰勒规则中引入汇率因素,以考虑汇率对宏观经济这一传导渠道和刻画货币当局针对汇率变动的货币政策调整。第五,中国人民银行营业管理部课题组 (2009)认为,鉴于货币供应量在我国货币政策操作中的中介目标职能,对我国泰勒规则的估计应对这一重要指标有所反映,因此,传统泰勒规则需要加入货币供应量变量;最后,部分学者批判了传统泰勒规则引入当期经济变量的做法,认为货币当局在制定货币政策时更多基于对未来宏观经济的预测,政策调整具有前瞻性,进而以前瞻性的经济变量替代传统泰勒规则中相应的当期经济变量 (Clarida et al., 1998;张屹山和张代强,2007)。
在计量分析方法方面,部分文献考虑了经济体制的转变、领导团体的变更等现实背景因素,从某些侧面体现泰勒规则模型的时变性,以探讨货币政策行为中的非线性特征。最简单的做法是分阶段回归,Clarida et al.(2000)、Orphanides (2004)、王建国 (2006)将样本划分为不同时期,采用分段估计的简单方法,考虑了货币政策规则在不同时段之间的转变。Martin and Milas (2004)、Petersen (2007)、赵进文和闵捷 (2005)等则采用Logistic平滑转换模型分析了货币政策制定的非线性特征。Cogley and Sargent (2005)、Primiceri (2005)、Koop et al.(2009)等进一步将货币政策的非线性特征推进到时变性情境下,以依靠“数据说话”的形式探讨货币政策操作的时变性,发现美国货币政策对宏观经济的反应存在明显的时变特征。刘金全和张小宇 (2012)应用时变参数泰勒规则模型检验了我国利率调整机制,发现我国利率对产出缺口和通货膨胀缺口调整存在明显的时变性。
此外,很多发展中国家的货币政策制定并不是采用单一通货膨胀目标制,而是具有目标维数多样性和时变性的特征。在我国,周小川也多次在公共场合强调我国货币政策具有多目标性。因此,在传统泰勒规则中引入不同因素以检验泰勒规则在我国的适用性显得很有必要。另一方面,经济体内自发变革因素和政府主动改革动力都将改变经济运行机制和经济变量之间互动关系,而具有时变特征的计量方法能更好地刻画这一客观现实,挖掘经济变量之间的作用关系。因此,我们认为,在研究泰勒规则或其变种在中国的适用性时,有必要将这两个方面进行结合,以度量货币政策制定影响因素的时变性和货币政策对各因素反应的时变性。
Koop and Korobilis (2012)(以下简称KK) 通过动态模型平均 (DMA) 和动态模型选择 (DMS) 预测了美国的通货膨胀率,考察了通货膨胀成因的时变性,并且时变性不仅表现在影响因素个数,还体现在影响强度上。结果显示,相比于传统方法,这一模型维数与系数时变性兼具的方法在预测通货膨胀率方面表现更为出色。因此,本文借鉴DMS方法,检验泰勒规则在我国的适用性。由于研究对象的不同,本文对KK进行了相应拓展:第一,KK的DMS并没有关注系数的显著性,因而偏向于选择包含因素众多的“大”模型,而本文考虑了系数的显著性问题,重点分析了泰勒规则模型维度与系数的时变性;第二,KK重点在于预测通货膨胀率,即样本外预测,而本文主要考察泰勒规则在我国货币政策操作中的适用性,主要关注模型在样本内的拟合效果,即样本内预测。
综上所述,本文将考虑我国货币政策目标的多样性与变化性,兼顾我国经济处于转型期的现状,拓展KK的DMS方法,研究目前我国货币政策制定是否具备泰勒规则的性质。
三、 模型设定与估计 (一) 传统泰勒规则泰勒规则可以表述为以下一般形式:
| $ {i_t} = {r^ * } + {\pi _t} + \alpha \left( {{\pi _t} - {\pi ^ * }} \right) + {\beta _{{{\tilde y}_t}}} $ | (1) |
其中it为联邦基金利率,r*为均衡实际利率,πt为前4季度平均通货膨胀率,π*为目标通货膨胀率,
α和β可视为对经济的实现值与目标值偏离的容忍度。α和β越大表明,货币当局将对通货膨胀偏离目标值或产出偏离潜在产出的现象越不能容忍,并以大幅的利率调整做出反应。特别是α的大小,当α>0时,it调整幅度大于通货膨胀率,实际利率下降,进而降低通货膨胀,避免“经济增长→实际利率下降→经济进一步膨胀”的恶性循环。α>0是稳定经济的重要条件,也是泰勒规则是否适合作为一国货币政策规则的条件。在研究美国联邦基金利率的调整时,Taylor (1993)将r*和π*都具体设定为2,并将α和β设定为0.5,发现模型较好地拟合了联邦基金利率的走势。
(二) “双重时变”的前瞻性泰勒规则公众决策时不仅会考虑历史与现状,还将预测未来,以更好地平滑消费或投资,因而预期在公众决策过程中至关重要。中央银行也会将这一行为纳入货币政策制定中,使得货币政策制定具有前瞻性。基于此,大多数研究者倾向于应用前瞻性泰勒规则而不是基于当期或历史信息的泰勒规则 (Clarida et al., 1998;卞志村,2006)。
另一方面,除了传统泰勒规则当中的通货膨胀与产出①,国内学者从不同视角对传统泰勒规则进行了扩展 (王胜和邹恒甫,2006;袁靖,2007),引入了众多经济因素。于是,在Clarida et al.(1998)的前瞻性泰勒规则基础上,可进一步扩展为②:
①正如2007年4月12日,周小川在湖南调研发表演讲时说:“世界上很多央行是单一目标制的,就是治理通货膨胀。中国央行还是多目标的,要促进经济发展、促进就业扩大、促进国际收支平衡,但最主要的目标还是保持低通货膨胀。”
②参考张屹山和张代强 (2007)和以股票市场代理的资产价格已经包括未来的信息,因此ω中的货币供应量和资产价格没有采用前瞻性,而对于其他因素同样没有考虑前瞻性,在稳健性检验时进一步考虑前瞻性。
| $ i_t^ * = {i^ * } + \alpha \left( {E\left[ {{\pi _{t + n}}\left| {{\Psi _t}} \right.} \right] - {\pi ^ * }} \right) + \beta E\left[ {{y_{\widetilde {t + p}}}\left| {{\Psi _t}} \right.} \right] + \sum\limits_{j = 1}^q {{\lambda _j}{\omega _{t,j}}} $ | (2) |
其中it*为t期时目标利率,i*为长期均衡名义利率,E[πt+n|Ψt]为基于在t期的信息Ψt对通胀的向前k期预测,
进一步考虑利率调整存在的平滑行为,并假定利率的动态变化满足:
| $ {i_t} = \left( {1 - \rho } \right)i_t^ * + \rho {i_{t - 1}} + {\xi _t} $ | (3) |
其中ρ∈[0, 1]为平滑系数,(3) 式表示当前利率的确定是目标利率与上期利率的加权平均,以避免利率向目标利率一次调整带来的金融市场与宏观经济过度波动。将 (2) 式加入 (3) 式可以得到:
| $ {i_t} = c + \left( {1 - \rho } \right)\alpha {\pi _{t + n}} + \left( {1 - \rho } \right)\beta {y_{\widetilde {t + p}}} + \sum\limits_{j = 1}^q {{\tau _j}{\omega _{t,j}}} + \rho {i_{t - 1}} + {v_t} $ | (4) |
其中υt=-(1-ρ){α(πt+n-E[πt+nΨt])+
进一步将上述模型的参数设定为如下时变形式:
| $ {i_t} = {c_t} + \left( {1 - {\rho _t}} \right){\alpha _t}{\pi _{t + n}} + \left( {1 - {\rho _t}} \right){\beta _t}{y_{\widetilde {t + p}}} + \sum\limits_{j = 1}^{{q_t}} {{\tau _{tj}}{\omega _{t,j}}} + {\rho _t}{i_{t - 1}} + {v_t} $ | (5) |
此时,(5) 式的时变性不仅体现在参数上,还体现在ω内包含其他因素的个数上,即qt具有时变性,这就是本文“双重时变性”的核心定义。这一设定将便于我们分析每一期利率调控考虑的因素和对各因素的反应强弱。
(三) “双重时变”前瞻性泰勒规则的估计为了表示方便,我们将 (5) 式简化为:
| $ {i_t} = {X_t}{\theta _t} + {v_t} $ | (6) |
将参数的运动过程设定如下形式:
| $ {\theta _t} = {\theta _{t - 1}} + {\zeta _t} $ | (7) |
所有参数的时变过程被设定为随机游走形式,这也是文献中降低待估参数空间维度的常用做法。其中,υt~N(0, Ht),ζt~N(0, Qt)。由于 (6) 式中Xt内所含的变量个数是时变的,我们将t期的可能模型设定为:
| $ \begin{array}{l} {i_t} = X_t^{\left( k \right)}\theta _t^{\left( k \right)} + v_t^{\left( k \right)}\\ \theta _t^{\left( k \right)} = \theta _{t - 1}^{\left( k \right)} + \zeta _t^{\left( k \right)} \end{array} $ | (8) |
其中υt(k)~N(0, Ht(k)),ζt(k)~N(0, Qt(k))。我们事先无法判断t期的具体模型,只知在t期存在K=25个可能模型①因此,对 (8) 式的估计不仅涉及时变参数的估计,还需确定每一期的具体模型。
①由于我们在每一期都加入了截距项、通货膨胀与产出缺口,t期可能加入额外变量为ω和it-1,其最大维度为5,即包括了货币供应量、资产价格、汇率、国际因素以及it-1,因而在t期存在K=25个可能模型。在每一期都加入通货膨胀与产出缺口是为了保持泰勒规则的完整性和分析两者系数的时变性,同时我们研究也显示,两者的系数在任何一期都是显著的。而截距项的引入可以吸收变量之间的低频协动性 (comovement),进而克服潜在的估计扭曲问题 (Gambetti, 2006;Fernald, 2007;Galí and Gambetti, 2009)。
1. 参数的估计参考KK与Raftery et al.(2010),本文采用卡尔曼滤波方法对参数进行估计,首先先验设定参数的分布和初始值,进而采用递归方法来实现参数的估计,具体过程是:假定①
①参考研究中普遍的做法,本文将初始值设定为OLS估计值。
| $ \theta _{t - 1}^{\left( k \right)}\left| {{i^{t - 1}}} \right. \sim N\left( {\widehat {\theta _{t - 1}^{\left( k \right)}},\sum _{t - 1}^{\left( k \right)}} \right) $ | (9) |
| $ \theta _t^{\left( k \right)}\left| {{i^{t - 1}}} \right. \sim N\left( {\widehat {\theta _{t - 1}^{\left( k \right)}},\sum _{t\left| {t - 1} \right.}^{\left( k \right)}} \right) $ | (10) |
(9) 式表示给定i从第1期到t-1期的信息,θt-1(k)的分布。KK等都将Σt|t-1(k)设定为:
| $ \sum _{t\left| {t - 1} \right.}^{\left( k \right)} = \frac{1}{\lambda }\sum _{t - 1}^{\left( k \right)} $ | (11) |
其中λ∈(0, 1]。大多数研究者偏向于采用 (11) 式的递归形式不仅源自其设定的简便,也因为其在实践应用中的良好表现。在具体设定中,本文将λ设为0.99,这也是研究中常用的设定。进一步,我们应用卡尔曼滤波方法得到所有的参数②。
②具体估计过程备索。
2. 时变的货币政策目标模型中货币政策目标维数的时变性,即意味着模型维度本身存在的时变性。模型维度的跨期变化需要设定相邻两期模型之间的转换过程。自从Hamilton (1989)将马尔科夫转换过程引入到时间序列模型之后,其在宏观经济研究中得到广泛应用;然而,面对维数庞大的模型,马尔科夫转换过程所采用的贝叶斯方法在计算上并不可行 (KK)。因此,Raftery et al.(2010)做了如下简化:
| $ {\pi _{t\left| {t - 1} \right.,k}} = \frac{{\pi _{t - 1,k}^\alpha }}{{\sum\limits_{l = 1}^K {\pi _{t - 1,l}^\alpha } }} $ | (12) |
α被设定为接近1的数值,其满足α∈(0, 1],本文取α=0.99。(12) 式的设定大大缩减了计算过程,并在应用中表现很稳健。而对于πt, k,我们设定如下③:
③KK的研究是用于预测通货膨胀,因此其在 (13) 式中的pk(it) 为pk(yt|yt-1),其思路是基于1到t-1期的信息,t期时在模型k下取得yt的概率。本文也主要采用了此思路。
| $ {\pi _{t,k}} = \frac{{{\pi _{t\left| {t - 1} \right.,k}}{p_k}\left( {{i_t}} \right)}}{{\sum\limits_{l = 1}^K {{\pi _{t\left| {t - 1} \right.,l}}{p_l}\left( {{i_t}} \right)} }} $ | (13) |
其中pk(it) 表示在t期基于模型k下取得it的概率。(8) 式可知,
| $ {i_t} \sim N\left( {\begin{array}{*{20}{c}} {X_t^{\left( k \right)}}&{\widehat {\theta _t^{\left( k \right)}}}&{,\widehat {H_t^{\left( k \right)}}} \end{array}} \right) $ | (14) |
由 (14) 式便可得到pk(it),并计算πt, k,即货币当局在t期应用了模型k的概率。(13) 式表明,当在t期模型k的拟合效果较好,那么πt, k也将较高。接下来,我们将基于此判断每期的最优模型,进而确定每一期影响利率的因素。一个自然的思路是,选择πt, k最高的那个模型,这也是DMS方法的选择方式。
然而,更多变量的引入倾向于提高模型的拟合优度,或提高KK当中的预测效果,因此仅仅基于πt, k的DMS方法偏向于选择包含变量众多的“大”模型。在样本量有限和双重时变性设定的情形下,过多参数的估计将降低估计的准确性。现有的模型选择准则一般是通过考察增加额外变量对残差平方和的改善与设定增加额外变量的惩罚来综合选择最优的模型,如AIC和BIC准则。然而,这些准则并不能引入到时变的情境,这是因为在每一期内选择模型时只有一期残差而并不存在残差平方和。
为此,本文遵循计量经济学中“一般到简单”的准则,注重于系数统计上的显著性,将不显著的系数从模型中删除,即剔除除了截距项、通货膨胀和产出缺口的系数显著性之外包含系数不显著的模型。此外,为了避免出现多个变量的系数单独不显著而联合显著,和存在遗漏变量的问题,本文参考Doan (2004)以[0.16, 0.84]较窄的分位点构造置信区间和判断显著性水平①。概而言之,本文对KK的DMS方法进行做出了如下改进:
①选择较窄置信区间的另一个原因是,当包含了多余的变量时,估计结果依然是无偏的,而遗漏变量时则将使得估计结果有偏。
首先,判断每个模型当中系数是否显著异于0。虽然根据
②我们通过10000次的Boostrap来得到系数模拟分布。
其次,除了截距项、通货膨胀和产出缺口的系数显著性之外,我们将包含变量系数不显著的模型进行剔除;
最后,从剩余模型中选择πt, k最高的模型,以作为每一时期的最优模型。
这一方法既考虑系数的显著性以克服KK方法选择“大”模型的倾向,又兼顾了模型的拟合优度。
四、 实证结果分析 (一) 变量与数据本文数据样本区间为1996年第1季度到2014年第2季度,数据来自于中经网统计数据库,指标数据的选择与处理过程如下。
1.利率 (i)。银行间同业拆借利率和债券回购利率是我国市场化程度最高的利率,基本体现了市场中资金的紧缺程度和资金的价格。此外,相比于债券回购利率,同业拆借是各机构凭借信用在银行间市场拆借资金,其利率水平较回购利率更能体现资金的真实价格 (刘金全和张小宇,2012)。因此,本文选取7天的同业拆借利率作为利率的代理变量。由于7天同业拆借利率是以月度数据的形式公布,本文根据月度交易量进行加权平均得到季度数据。
2.产出缺口 (y)。为计算产出缺口,首先需要将公布的名义GDP转换为实际GDP。为此,我们把1996年第1季度定基为1,然后根据公布的环比CPI数据,计算各季度的累积CPI,实际GDP=名义GDP/累积CPI①。其次,应用X-12季节调整方法,剔除实际GDP的季节成分,得到除季度因素的实际GDP。再次,利用HP滤波方法,推算出潜在GDP。最后,产出缺口y=(除季度因素的实际GDP-潜在GDP)/潜在GDP×100。
①我国的环比CPI是以月度形式公布,因而需要计算季度环比CPI。我们首先将环比CPI进行累积,然后累积之后CPI进行季度平均,并除以1996年第一季度CPI值,即将1996年第一季度定基为1,最终得到累积季度CPI值。
3.通货膨胀率 (π)。本文以同比CPI作为通货膨胀的代理变量,并将月度CPI平均得到季度CPI。
4.汇率 (ER)。国际收支平衡是我国货币政策的目标之一,而汇率与国际收支情况密切相关,汇率变动也成为了货币当局核心关切指标。本文选取人民币/美元名义汇率作为的汇率代理变量,并将月度汇率数据平均得到季度汇率数据②。
②在研究中,采用何种汇率,尤其是名义汇率还是实际汇率,则没有达成一致。借鉴赵文胜和张屹山 (2012)的观点,在汇率的弹性和波动性方面,实际有效汇率更真实地反映了人民币汇率的走势,但是在分析经济变量与人民币汇率的关系时,名义汇率更为合适,因此本文选取名义汇率作为汇率的代理变量。
5.货币供应量 (M1R)。为与CPI同比数据对应,我们对货币供应量M1进行年度对数差分处理,以获取M1同比增长率数据,再进行平均得到季度数据。此外,与张屹山和张代强 (2007)、中国人民银行营业管理部课题组 (2009)等的研究一致,本文将M1同比增长率滞后一期的数据引入模型③。
③我们将货币供应量M1样本期扩充为1994年10月到2014年6月,使得滞后一期的样本量与其他变量一致。为了保持样本量大小,利率、国际因素和汇率因素也做了类似处理,其中1995年第4季度利率数据的选取参考了国内大多数研究,选择上海融资中心同业拆借利率。
6.股票市场 (SM)。2007年4月12日,周小川也表示:“央行的货币政策调控会关注资产价格。通货膨胀跟资产价格一起上涨的时候,那央行的政策是要收缩流动性,使得物价和资产都能往下走;两者走势不是一致方向的时候,货币政策就要取舍,那就主要是针对通货膨胀。”虽然货币政策的主要目的是通货膨胀,但是当资产价格波动较大以至于影响宏观经济的平稳发展时,货币政策可能会对其做出相应反应。为刻画这一可能,本文以股票价格作为资产价格的代理变量,借鉴袁靖 (2007)的做法,选用上证综合指数,对其取对数并采用HP滤波法推算潜在价格水平,在此基础上以上证综合指数对数值与其HP滤波值的差值作为股票价格泡沫。
7.国际因素 (IN)。本文以美国GDP代理国际经济的发展,以分析国外经济的发展对我国货币政策制定的影响。王胜和邹恒甫 (2006)在度量国外经济的发展时采用了Δyt*=100log (Yt+1*/Yt*) 形式,然而,为了与CPI数据类型统一,本文将美国GDP数据进行年度对数差分,即Δyt*=100log (Yt+4*/Yt*)。
(二) 时变泰勒规则模型估计结果在进行模型估计之前,我们对所有数据进行平稳化处理。根据ADF单位根检验,只有汇率数据是在10%的显著性水平上是不显著的,因而对其差分处理。
1. 时变的货币政策目标由于每期具体模型的确定,即货币政策目标多少,依赖于 (5) 式中n和p,因此首先需要选择前瞻期n和p。为了便于分析,我们假定n=p,即货币当局对通货膨胀和产出缺口的前瞻期数一样。当然,此时允许n < 0,其表示后顾性泰勒规则;n=0表示同期性泰勒规则;n>0表示前瞻性泰勒规则。在不同n选择下,模型估计的均方误差 (RMSE) 见表 1①。
| 表 1 取不同值时模型估计的均方误差 |
①我们将国际因素和汇率都设定为前瞻性数据,结果是稳健的。
由表 1来看,前瞻一期泰勒规则估计结果的均方误差最小,明显占优于其他估计结果。刘斌 (2006)研究也发现,在总需求和总供给中,前瞻性行为的权重都超过了0.6,预期对我国的产出及通胀率的决定均起到重要的作用。
鉴于n=1时均方误差最小,本文结果都是n=1下得到。当n=1时,各期货币政策目标估计结果见表 2。表 2表明,我国利率变动存在明显调整上的平滑性、因素上的时变性、与央行目标一致性的特点:
| 表 2 时变的货币政策目标 |
首先,在任何时段内,模型都包含了利率的滞后项,我国利率表现显著的平滑化调整。这与国内大多数研究一致 (谢平和罗雄,2002;张屹山和张代强,2007;刘金全和张小宇,2012;等等)。
其次,在不同阶段,利率目标存在时变性:在1996年第1、2季度,2002年第4季度到2004年第1季度,和2008年第1季度到2014年第1季度三个阶段,汇率变动与国际收支显著影响了利率;1996年第3季度到2002年第3季度以及2004年第2季度到2007年第4季度,利率并不受汇率的影响。
再次,我国货币政策的目标是,低通货膨胀、经济增长、保持较高就业和国际收支平衡。由于就业与经济增长目标具有一定的一致性,货币政策目标主要为通货膨胀、经济增长和国际收支平衡,而表 2估计结果体现了,利率调整也主要关注了这几个目标。
最后,我国利率并没有直接对股票市场、美国经济、货币供应量做出明显反应。在股票市场方面,正如周小川所强调,通货膨胀与资产价格一起上涨时,货币政策更多关注的是通货膨胀。袁靖 (2007)的研究也指出,我国在制定货币政策操作时较不重视应对资本市场价格较大波动。在国外经济方面,与王胜和邹恒甫 (2006)结论不同是,我们研究发现,我国利率调整并没有针对以美国经济为代理的国外经济,这可能源自于王胜和邹恒甫 (2006)并没有考虑利率的平滑效应。当不考虑利率的平滑因素时,我们同样得到美国经济对我国利率具有显著影响。在货币供应量方面,本研究与张屹山和张代强 (2007)、Fendel and Frenkel (2006)、Surico (2007)等研究一致。
2. 时变参数泰勒规则的估计结果(1) 利率对通货膨胀缺口的反应。图 1为利率对通货膨胀缺口的反应系数,其存在明显时变性。在具体数值方面,反应系数都在 (0.92, 1.02) 区间内,并且其在绝大多数时期是小于1,表明利率对通货膨胀的反应不足,利率调整没有起到稳定通货膨胀的作用,这与国内现有研究结论一致。然而,与国内现有研究结论不同的是,我们的研究发现,当经济出现通货紧缩并且具有长期持续之势时,货币当局在对抗通货紧缩表现出较强力度,比如1998年到2002年期间。这也表明,货币当局在对抗通货膨胀与通货紧缩的力度上表现出明显的不对称。
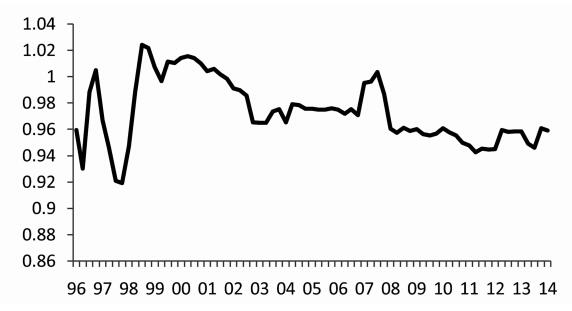
|
图 1 利率对通货膨胀缺口反应系数 |
从反应系数的时变性趋势来看,我们的结论总体上与刘金全和张小宇 (2012)的结论一致。1998年以前,利率对通货膨胀反应存在明显不足,这更进一步降低了实际利率并恶化了通货膨胀,酿成了当时的高通货膨胀。1998年至2002年期间,反应系数处于历史高位,这一时期也是我国经历通货紧缩时期。这表明,在此时期,央行积极对抗通货紧缩,大幅降低利率以缓解物价下降带来的实际利率上升,但是由于反应仍然不足,最高的反应系数也只是1.02,与Taylor (1993)在对美国研究中设定的1.5还具有较大差距,这也促使了我国经济较长时间处于通货紧缩。在2002年之后,利率对通货膨胀缺口的反应强度总体上逐渐减弱,这说明货币当局调控通货膨胀面临的压力逐步增加 (刘金全和张小宇,2012)。其中,在2007年时反应系数存在明显的凸起,这可能原因是:在2007年时,我们物价存在明显上扬的趋势。为了治理高启的通货膨胀,央行实施了紧缩型货币政策。然而在2008年,全球正面临金融危机并逐步恶化、扩散,我国政府和央行基于社会各界的压力进行救市,缓解金融危机对我们经济的冲击,因而提高了对通货膨胀的容忍度。
(2) 利率对产出缺口的反应。图 2为利率对产出缺口的反应系数。相比通货膨胀缺口,利率对产出缺口的反应没有明显趋势,但是波动范围较大,尤其是1999年之前。利率对产出缺口的反应数值位于 (0.45, 0.76) 之间,与Taylor (1993)对美国的研究中设置的0.5相当。利率对产出缺口的正向作用表明,利率能够稳定产出波动。在产出高于潜在产出时,利率将升高,抑制产出增长,促使产出回归至潜在产出,而当产出低于潜在产出时,利率将下行以促进产出增长,使产出恢复至潜在水平。因此,在稳定产出波动方面,泰勒规则是一个合适我国经济运行的货币政策规则。
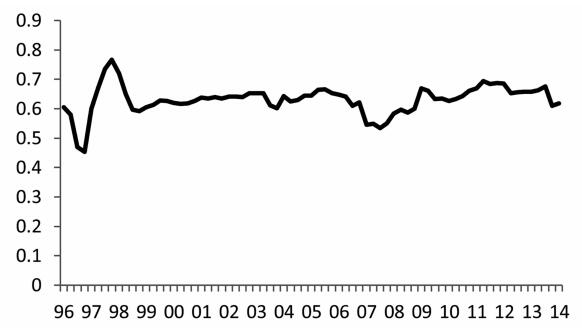
|
图 2 利率对产出缺口反应系数 |
此外,利率对产出缺口的反应存在两个波动较大时期:第一,在1997年左右,利率对产出缺口的反应存在明显凸起,我国经济在此之前保持高速增长,GDP增长速度都超过了10%,而较强的反应系数目的在于遏制经济快速增长,实现经济软着陆 (刘金全和张小宇,2012)。第二,2007年至2008年期间,利率对产出缺口的反应系数下挫。此时是我国经济又一快速发展时期,GDP增长速度达到14%,同时美国经济正经历金融危机,并大有蔓延之势。因此,反应系数下挫的合理解释是,国际经济形势使政府和央行承受着巨大的救市压力,实施宽松的政策,进而对当时已经出现的经济过热反应不足。
(3) 利率平滑系数。为了避免金融市场和宏观经济剧烈波动,货币当局偏向于将现有利率逐步调向目标值,而不是一步到位的方式,因而利率往往表现出很明显的渐进式变化和显著的自相关。图 3显示,我国利率变化也存在明显的平滑效应,平滑系数位于 (0.89, 0.92) 高位水平,波动的幅度非常小。从走势来看,平滑系数整体上呈现下降趋势,尤其是1997年以来。这表明,利率调整逐渐变得更为快速,政策灵活性日益增强,以迅速应对外部冲击,这在2008年左右的金融危机时期表现得更为明显。
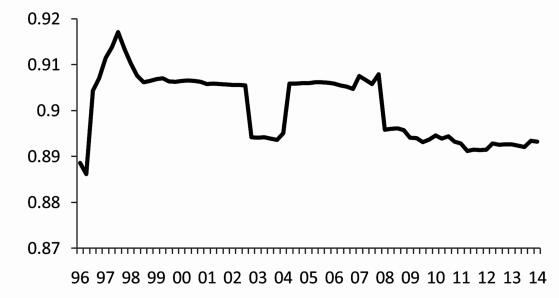
|
图 3 利率平滑系数 |
(4) 利率对汇率的反应。由图 4可知,我国利率对汇率的反应呈现出阶段性的特征:在1996年第1、2季度,2002年第4季度到2004年第1季度以及2008年第1季度到2014年第1季度三个阶段,利率会对汇率做出反应;而在其余时间,利率并不会对汇率做出反应。
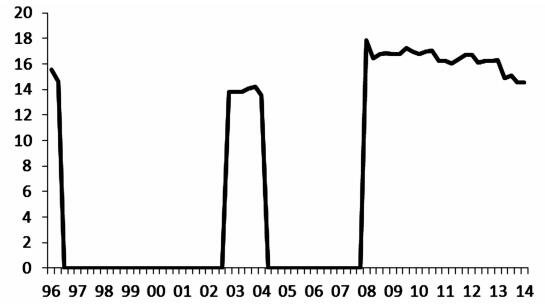
|
图 4 利率对汇率的反应系数 |
从历史背景看,我国1994年1月1日取消了双重汇率制度,人民币官方汇率与市场汇率并轨,实行以外汇市场供求为基础的、单一的、有管理的浮动汇率制。人民币/美元汇率也从1993年的低于6一跃到1994年的高于8,人民币大幅贬值,此后,人民币反向缓慢升值,这大幅促进了出口而抑制了进口。从1994年到1996年,经常项目和资本项目出现了大幅顺差,尤其是资本项目。而2001年11月成功加入WTO使得我国在2002之后经常项目和资本项目同样出现了大幅顺差,并且呈现逐步扩大的趋势。这些因素导致我国在1996年左右和2002到2004年出现了大幅的国际收支顺差,这不仅会通过影响进出口相对大小来影响GDP规模,而且在强制结售汇体制下,汇率变化带来的经常项目和资本项目顺逆差调整将改变央行外汇占款,并进一步改变基础货币投放规模和国内物价水平。这些因素促使了货币当局调整货币政策,而从利率对汇率反应的作用方向来看,人民币加速贬值和国际收支出现大幅顺差时,利率会上升。因此,利率的上升能够在一定程度上抑制国际收支不平衡给我国经济带来的剧烈波动,起到有效的调节作用。
从1996年到2002年,我国国际收支并未出现严重不平衡,因此,利率也并未对其做出反应。从2004年到2007年,虽然我国在此期间经常项目和资本项目都出现了大幅顺差,但是我国央行从2003年开始发行央票,并且发行央票的规模与顺差规模相当 (见图 5与图 6),有效地回收了基础货币,市场资金并未受到过度影响,因而利率并未对国际收支做出反应。在2008年以后,虽然我国在2012年左右国际收支有所改善,但是大部分时间国际收支依然表现出大幅顺差。与此同时,央票的发行量却出现了大幅缩减,这使得央行向市场注入了过多流动性。利率上升则减缓了因国际收支不平衡对物价和GDP带来的冲击。因此,利率在汇率冲击和国际收支变动时对经济体起到了有效调节作用。
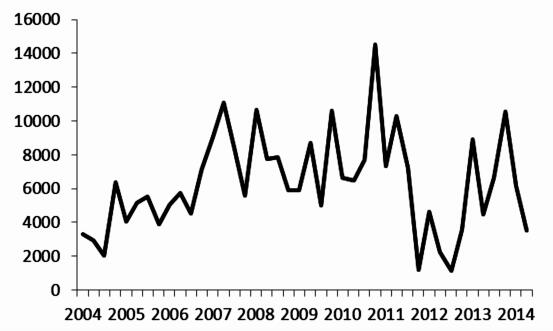
|
图 5 我国国际收支顺差额度 (单位:亿元)① 数据来源:数据来自于中国经济信息中心 (CEIC) 数据库。 |
①根据相应时期的人民币/美元汇率换算成以人民币表示的国际收支顺差额度。
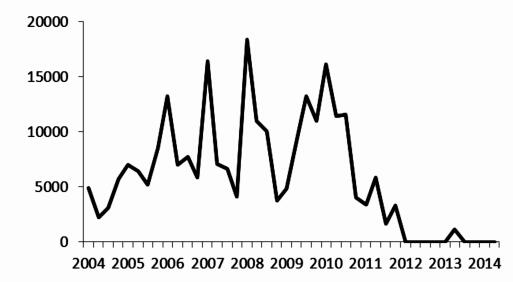
|
图 6 我国央票发行规模 (单位:亿元) 数据来源:根据中国人民银行网站的中央银行票据发行公告整理而成。 |
基于我国货币政策多目标性、经济处于转型期、货币政策制定的前瞻性等性质,本文扩展了传统泰勒规则,构建了兼顾货币政策目标与系数时变性的动态模型选择 (DMS) 方法,并藉此更好地考察泰勒规则在中国的适用性。本文构造的DMS方法主要借鉴了KK的DMS方法,并根据研究目的,做出了相应拓展:第一,考虑了系数的显著性,并在此基础上进行模型选择,避免了KK选择包含因素众多“大”模型的倾向;第二,改变了KK基于预测拟合效果的模型选择方法,设定为以样本内模型拟合效果为基础的模型选择方法。
我们研究发现,我国利率调整无论是在目标维度方面,还是各目标对利率的影响强度,都存在明显的时变性。在目标维度方面,我国利率调整因素存在明显的阶段性:1996年第3季度到2002年第3季度和2004年第2季度到2007年第4季度两个时期,利率会对产出缺口和通货膨胀做出反应,并具有平滑调整特征;在1996年第1、2季度,2002年第4季度到2004年第1季度以及2008年第1季度至2014年第1季度,利率还会对汇率波动与国际收支状况做出调整。此外,在整个样本期间,利率始终并没有对股票市场、美国经济、前期货币供应量做出反应。
在各因素对利率的作用强度方面,估计结果发现:首先,利率对通货膨胀存在显著反应,并且表现明显的时变性,然而由于系数估计值大部分时期小于1,利率对通货膨胀的反应不足,利率并没有起到降低通货膨胀波动的作用。故而,我国货币政策制定目前并未遵循严格意义上的泰勒规则。但是,当经济长期处于通货紧缩时,系数估计值则略大于1,这表现出对于通货紧缩的积极响应。因此,我国利率调整对通货膨胀与通货紧缩的反应存在明显的不对称性。其次,利率对产出缺口的反应并不存在明显的趋势,但是在经济面对外部冲击较大时,这一反应强度亦表现明显波动性。最后,利率平滑系数呈现下降趋势,利率调整的幅度逐渐上升,政策灵活性日益增强。
近年以来,我国以货币供应量为主的货币政策框架在稳定经济波动方面变得越来越力不从心。货币供应量表现明显的内生性供给与顺周期性 (于泽,2008)。社会各界对构建以利率为中间变量的货币政策框架的呼声日益强烈。然而,中国呈现出不完全的泰勒规则,最主要的原因可能就是利率并未实现完全市场化 (卞志村,2006;张屹山和张代强,2007;等等)。因此,我国应该尽快构建以市场供求为基准的利率形成机制,培育利于以利率为中间变量的金融环境。一方面应该发展同业拆借利率、债券回购利率等市场利率的市场化程度,放宽市场准入,使其能够真正反映资金的紧缺性,并排除各货币市场之间的壁垒,提高各种利率互动关系。另一方面,增加各期国债的发行数量,丰富、增加央行资产构成,提高央行调节利率的能力。
| [] | Clarida, R. , Gali, J. and Gertler, M. , 1998, "Monetary Policy Rules in Practice: Some International Evidence,". European Economic Review, 42(6), 1033–1067. DOI:10.1016/S0014-2921(98)00016-6 |
| [] | Clarida, R. , Gali, J. and Gertler, M. , 2000, "Monetary Policy Rules and Macroeconomics Stability : Evidence and Some Theroy,". Quarterly Journal of Economics, CXV(1), 147–180. |
| [] | Clarida, R., J. Gali, and M. Gertler, 2001, "Optimal Monetary Policy in Open versus Closed Economies: an Integrated Approach, "NBER Working Paper. No. 8604. |
| [] | Cogley, T. and Sargent, T. J. , 2005, "Drifts and Volatilities: Monetary Policies and Outcomes in the post WWII US". Review of Economic Dynamics, 8(2), 262–302. DOI:10.1016/j.red.2004.10.009 |
| [] | Doan, T. Rats Manual, version 6[M], 2004, Evanston. |
| [] | Fendel, R. and Frenkel, M. , 2006, "Five Years of Single European monetary Policy in Practice: Is the ECB Rule-based?". Contemporary Economic Policy, 24(1), 106–115. DOI:10.1093/cep/byj002 |
| [] | Fernald, J. G. 2007, "Trend Breaks, Long-run Restrictions, and Contractionary Technology Improvements". Journal of Monetary Economics, 54(8), 2467–2485. DOI:10.1016/j.jmoneco.2007.06.031 |
| [] | Galí, J. and Gambetti, L. , 2009, "On the Sources of the Great Moderation". American Economic Journal: Macroeconomics, 1(1), 26–57. DOI:10.1257/mac.1.1.26 |
| [] | Gambetti, L., 2006, "Technology Shocks and the Response of Hours Worked: Time-Varying Dynamics Matter, " unpublished manuscript. |
| [] | Hamilton, J. 1989, "A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle,". Econometrica, 57(2), 357–384. DOI:10.2307/1912559 |
| [] | Koop, G. , Leon-Gonzalez, R. and Strachan, R.W. , 2009, "On the Evolution of the Monetary Policy Transmission Mechanism,". Journal of Economic Dynamics and Control, 33(4), 997–1017. DOI:10.1016/j.jedc.2008.11.003 |
| [] | Koop, G. and Korobilisi, D. , 2012, "Forecasting Inflation Using Dynamic Model Averaging,". International Economic Review, 53(3), 867–886. DOI:10.1111/iere.2012.53.issue-3 |
| [] | Martin, C. and Milas, C. , 2004, "Modelling Monetary Policy: Inflation Targeting in Practice". Economica, 71(282), 209–221. DOI:10.1111/ecca.2004.71.issue-282 |
| [] | Mohanty M.S and M. Klau, 2004, " Monetary Policy Rules in Emerging Market Economies: Issues and Evidence, " BIS Working Papers, No 149. |
| [] | Orphanides, A. 2004, "Monetary Policy Rules, Macroeconomic Stability and Inflation: A View from the Trenches,". Journal of Money, Credit and Banking, 36(2), 151–175. DOI:10.1353/mcb.2004.0013 |
| [] | Petersen, K., 2007, "Does the Federal Reserve Follow a Non-linear Taylor rule? " Department of Economics Working Paper Series, No.2007-37. University of Connecticut. |
| [] | Primiceri, G. E. 2005, "Time Varying Structural Vector Autoregressions and Monetary Policy". The Review of economic studies, 72(3), 821–852. DOI:10.1111/roes.2005.72.issue-3 |
| [] | Raftery, A. , Karny, M. and Ettler, P. , 2010, "Online Prediction under Model Uncertainty via Dynamic Model Averaging: Application to a Cold Rolling Mill". Technometrics, 52(1), 52–66. DOI:10.1198/TECH.2009.08104 |
| [] | Riskmetrics, 1996, "Technical Document—Fourth Edition, "Available at: http://www.riskmetrics.com/system/files/private/td4e.pdf. |
| [] | Sack, B. and V. Wieland, 1999, "Interest-rate Smoothing and Optimal Monetary Policy: a Review of Recent Empirical Evidence, "Finance and Economics Discussion Series, 1999-39, Federal Reserve Board. |
| [] | Surico, P. 2007, "The Monetary Policy of the European Central Bank,". Scandinavian Journal of Economics, 109(1), 115–135. DOI:10.1111/sjoe.2007.109.issue-1 |
| [] | Svensson, L.E.O, 2000, " Open-economy Inflation Targeting, "NBER working paper, No.6545. |
| [] | Taylor, J. B. 1993, "Discretion versus Policy Rules in Practice,". Carnegie-Rochester Conference Series on Public Policy, 39, 195–214. DOI:10.1016/0167-2231(93)90009-L |
| [] | 卞志村, 2006, 《泰勒规则的实证问题及在中国的检验》, 《金融研究》, 第 8 期, 第 56–69 页。 |
| [] | 陈晓莉, 2008, 《汇率变动对货币政策操作变量的影响》, 《经济科学》, 第 5 期, 第 40–47 页。 |
| [] | 戴国强、梁福涛, 2006, 《中国金融市场基准利率选择的经验分析》, 《世界经济》, 第 2 期, 第 3–11 页。 |
| [] | 郭福春、潘锡泉, 2012, 《开放框架下扩展泰勒规则的再检验——基于汇改前后及整体层面的比较分析》, 《财贸经济》, 第 11 期, 第 63–69 页。 |
| [] | 黄武俊、陈漓高, 2010, 《外汇资产、基础货币供应与货币内生性》, 《财经研究》, 第 1 期, 第 66–76 页。 |
| [] | 刘斌, 2006, 《稳健的最优简单货币政策规则在我国的应用》, 《金融研究》, 第 4 期, 第 12–23 页。 |
| [] | 刘金全、张小宇, 2012, 《时变参数"泰勒规则"在我国货币政策操作中的实证研究》, 《管理世界》, 第 7 期, 第 20–28 页。 |
| [] | 王建国, 2006, 《泰勒规则与我国货币政策反应函数的实证研究》, 《数量经济技术经济研究》, 第 1 期, 第 43–49 页。 |
| [] | 王胜、邹恒甫, 2006, 《开放经济中的泰勒规则——对中国货币政策的检验》, 《统计研究》, 第 3 期, 第 42–46 页。 |
| [] | 谢平、罗雄, 2002, 《泰勒规则及其在中国货币政策中的检验》, 《经济研究》, 第 3 期, 第 3–12 页。 |
| [] | 于泽, 2008, 《我国M2顺周期性的原因分析》, 《管理世界》, 第 12 期, 第 24–31 页。 |
| [] | 袁靖, 2007, 《由泰勒规则货币政策对我国股票市场货币政策传导效力的实证研究》, 《统计研究》, 第 8 期, 第 60–63 页。 |
| [] | 张屹山、张代强, 2007, 《前瞻性货币政策反应函数在我国货币政策中的检验》, 《经济研究》, 第 3 期, 第 20–32 页。 |
| [] | 赵进文、闵捷, 2005, 《央行货币政策操作政策拐点与开关函数的测定》, 《经济研究》, 第 12 期, 第 90–101 页。 |
| [] | 赵文胜、张屹山, 2012, 《货币政策冲击与人民币汇率动态》, 《金融研究》, 第 8 期, 第 1–15 页。 |
| [] | 中国人民银行营业管理部课题组, 2009, 《非线性泰勒规则在我国货币政策操作中的实证研究》, 《金融研究》, 第 12 期, 第 30–44 页。 |



