2013年5月份公布的《2013年深化经济体制改革重点工作的意见》明确提出“扩大个人住房房产税改革试点范围”,而国家税务总局近期则下发通知,首次明确表态将研究扩大个人住房房产税改革试点范围。然而,对于开征房产税是否能对我国住房价格产生影响许多专家学者纷纷给出不同的观点。中国指数研究院上海公司研究总监陈延彬认为房价环比上涨较快的原因主要在于,首先是供应量较少,如北京,可售量只有6万套左右,供需非常不平衡,其次则在于部分城市成交火热,日光盘的频频出现,进一步加大了购房者房价上涨的预期。而中国社会科学院金融研究所研究员易宪容则认为房产税征收增加了房价上涨的预期。本文认为,在此次房产税试点期间,导致房价上涨较快的原因不止有陈延彬所述的两个原因,就像易宪容所说的那样,人们对征收房产税的预期也可能是此次房产税试点期间房价继续升温不减的一个不可忽视的因素。
目前,我国学术界已有关于预期与住房价格互动性的研究。然而,上述文献少有从理论的角度来探讨预期与住房价格的互动关系。如况伟大 (2012)使用1980-2009年23个OECD国家的住房市场数据,考察了住房房产税对房价的影响,研究发现,预期比房产税对房价影响更大。然而,试图从理论上探讨预期驱动住房价格波动的原因和机制的文献仍是空白。本文尝试建立加入金融摩擦的消息推动下的经济周期 (News-Driven Business Cycle with Financial Frictions) 模型,分析房产税试点消息和信贷政策对公众预期形成、公众行为改变的重要性,同时结合脉冲反应对比分析预期到的房产税和信贷政策和未预期到的房产税和信贷政策对住房价格的影响,以便于我们正确分析房产税和信贷政策对住房价格的影响。本文试图探究的是:关于房产税和信贷政策的“消息冲击”是否会对住房价格产生影响?如果会产生影响,它会对住房价格产生怎样的影响?本文的主要研究贡献在于:本文第一次将房产税预期和信贷预期实际运用于住房价格的影响分析上,并首次探讨了经济人在混合预期下的行为对住房价格的影响,并验证了预期效应的可加性,也即当经济人对未来同时产生多种预期时,由多种预期所产生的对内生变量 (在本文里就是住房价格) 的影响具有相互增强的性质。消息冲击下的脉冲反应显示,当政府过早宣布房产税或信贷政策并形成公众预期时,这种政策的实际效果可能会与实施政策的初始目标产生背离,从而会在一定程度上减弱政策的实施效果。这表明政策的执行效率和执行时机选择都是确保政策效果的重要因素。其次,本文把房地产贷款具体分为房地产开发商贷款和个人购房贷款两类,并分别详细探讨了这些不同政策的混合预期对于房地产价格的作用效果。
二、 相关研究文献其实在很早以前人们就认识到了预期可能是导致经济波动的重要因素。例如,早在1927年,英国著名经济学家阿瑟·庇古 (Arthur Pigou) 就指出:“商人们的预期变化——此外再没有别的东西,构成了产业波动的直接原因或者前导。”遗憾的是,早期的经济学家仅对预期变化如何影响经济波动进行了定性描述。后来,Beaudry和Portier (2004)的研究跨出了重要的一步。他们构建了一个包含预期冲击的三部门模型,并在此模型基础上讨论了预期冲击导致经济波动的机制和效应。Beaudry和Portier (2004)开创性的研究引起了学术界对预期理论更为深入的研究,如,Beaudry和Portier (2007),Jaimovich和Rebelo (2009),Denhaan和Kaltenbrunner (2007),Fujiwara (2007),Kobayashi、Nakajima和Inaba (2007),Christiano、Ilut、Motto和Rostagno (2008),Grohe和Uribe (2008),Khan和Tsoukalas (2009)等等。在理论方面,Feve、Matheron和Sahuc (2009)在一个一维的纯前瞻性的理性预期模型中考察了预期冲击对内生经济变量的波动性的影响。他们的研究表明,与不可预期的冲击相比,预期冲击反而增加了经济的波动性。但是Winkler和Wohlmann (2009)的研究则表明,即使在纯理论模型中,预期冲击对宏观经济波动的影响也是不确定的。因为预期冲击增加了某些经济变量的波动性,但同时也减少了某些经济变量的波动性。在经验方面,Winkler和Wohlmann (2009)在一个实际经济周期模型 (即,Smets和Wouters (2003)的模型) 中考察了各种预期冲击对宏观经济波动的影响。有意义的是,他们对可预期的政策冲击的分析表明:(a) 可预期的财政政策 (政府支出) 冲击降低了大部分关键宏观经济变量 (产出、就业和通货膨胀等) 的波动性。因此,可预期的财政政策具有反周期的宏观调控功能。(b) 可预期的货币政策冲击 (利率冲击) 对宏观经济波动的影响效果却与财政政策冲击截然相反。除了资本的实际价格,可预期的利率冲击 (即,人们事前预期到央行要加息) 增加了几乎所有宏观经济变量的波动性。因此,可预期的货币政策冲击往往并不能起到稳定经济的作用。
关于住房价格、房产税与信贷政策三者之间的关系,国内外学者也纷纷做了大量的研究。对于房产税和房价关系的研究,Seth Payton (2004)通过实证研究指出房产税实际税率与住宅价格呈显著负相关,是影响住宅价格的主导因素。Wood (2006)采用微观模拟的方法得出,征收房产税会在一定程度上对住房的相对价格产生影响。而Lai et al.(2010)则从福利经济学的视角探讨了开征房产税对房地产价格的作用效果。国内学者对此也做过大量研究,祝伟大 (2009)通过建立一个静态模型对开征房产税与房地产价格之间的关系做了比较静态分析。
骆永民和伍文中 (2012)采用DSGE模型研究了开征房产税以及房地产价格变动对整个宏观经济所造成的影响。在信贷政策对住房价格的影响上,大部分学者多采用计量方法建立模型阿里研究二者之间的影响关系。赵进文和高辉 (2009)根据实证研究结果得出,房地产价格是中央银行利率政策决策中一个重要的影响因素,而谭政勋和王聪 (2011)认为我国信贷规模扩张能够引起房价上涨,而且我国房价上涨和信贷扩张是双向的相互驱动而造成的。谭政勋和陈铭 (2012)还通过采用实证分析得出,我国商业银行的贷款量可能是造成我国房地产价格攀升的一个重要原因。上述研究所运用的计量手段大多是向量误差修正模型 (VEC) 以及结构向量自回归模型 (SVAR),如梁云芳、高铁梅和贺书平 (2006),王晓明 (2010),以及徐承明和王安兴 (2006)等。但是,简单的计量手段比较难以进行政策之间的组合效应研究,并且有些计量模型由于所采用的数据以及指标的不准确也会在一定程度上影响计量结果的稳健性。
与上述文献相比,本文的主要边际贡献在于:首先,上述学者在模型中并没有考虑对经济变量产生重要影响的预期因素对住房价格的影响。本文将消息预期理论与房产税试点与信贷政策相结合,通过建立一个带有金融摩擦效应的DSGE模型对房产税试点消息与预期信贷政策和房地产价格之间的关系进行分析。其次,庄子罐、崔小勇和龚六堂 (2012)对预期因素对宏观经济变量的影响只停留在单个预期冲击对宏观经济变量的影响,但是却忽略了混合预期的影响。鉴于此,本文探讨了经济人在混合预期下的行为对住房价格的影响,并验证了预期效应的可加性,也即当经济人对未来同时产生多种预期时,由多种预期所产生的对内生变量 (在本文里就是住房价格) 的影响具有相互增强的性质。
三、 理论模型介绍本文的模型共包括三个主体部分,他们分别是家庭部门,企业部门以及政府部分。为了实现理论模型和现实经济情况的契合,突出现实经济体中家庭与企业所存在的异质性,本文又进一步将家庭部门细分为两类,他们分别是耐心型家庭和非耐心型家庭。耐心型家庭在消费时并不通过跨期贷款来实现当期不能承担得起的消费,而非耐心型家庭由于耐心程度不够因而愿意通过跨期贷款来实现当期不能承担得起的消费。对于企业的异质性,本文将企业部门细分为房地产开发商和最终产品部门。本文模型中的房地产开发商可以看成Iacoviello (2005)和Iacoviello and Neri (2010)的DSGE模型的中间商,同样的假设可见诸于郑忠华和邸俊鹏 (2012)以及谭政勋和王聪 (2011)。为了讨论预期的企业信贷政策对住房价格的影响,本文将房地产资源也作为房地产开发商的生产要素之一,这样的话,房地产开发商不仅使用两类家庭所提供的劳动力以及经济体中的资本存量而且还利用房地产资源作为投入要素来生产中间产品,在实现中间产品的销售后,将销售利润一部分支付给耐心型家庭和非耐心型家庭,剩下的另一部分用于企业的当期消费和下一期投资需求。为了讨论预期的个人抵押贷款政策和预期的企业信贷政策对住房价格的不同影响,以及体现真实经济体中贷款来源的异质性,本文又将房地产贷款进一步细分为房地产开发商贷款和个人购房贷款两种,这样就可以讨论房地产开发商和非耐心型家庭对企业信贷政策和个人抵押贷款政策的不同预期所产生的对住房价格影响的差异。为了考察不同的预期稳态税率下房产税试点消息冲击对房价的影响,本文将政府部门的收入来源设定为两类家庭和房地产开发商的房产税之和,而政府支出则体现为购买性日常支出。由于篇幅所限,各个经济主体的具体设置可参见赵胜民和罗琦 (2013)。在赵胜民和罗琦 (2013)一文中,作者只是对传统的房产税冲击和信贷冲击进行模拟分析,并没有考虑到经济中的预期因素对与结果的影响,这主要体现在经济体中的冲击形式表示为:
| $ln{\omega _t} = \left( {1 - {\rho _\omega }} \right)ln\bar \omega + {\rho _\omega }ln{\omega _{t - 1}} + {\sigma _\omega }{\varepsilon _{\omega ,t}}$ | (1) |
| $ln\omega _t^{"} = \left( {1 - {\rho _{{\omega ^{"}}}}} \right)ln{{\bar \omega }^{"}} + {\rho _\omega }ln\omega _{t - 1}^{"} + {\sigma _{{\omega ^{"}}}}{\varepsilon _{\omega ,t}}$ | (2) |
| $ln\tau _t^h = \left( {1 - {\rho _\tau }} \right)ln{{\bar \tau }^h} + {\rho _\tau }ln\tau _{t - 1}^h + \sigma _\tau ^h\varepsilon _{\tau ,t}^j$ | (3) |
而在本文中,由于考虑到预期因素的存在,经济体中的冲击形式表示为:
| $ln{\omega _t} = \left( {1 - {\rho _\omega }} \right)ln\bar \omega + {\rho _\omega }ln{\omega _{t - 1}} + \sigma _\omega ^0\varepsilon _{\omega ,t}^0 + \sum\nolimits_{j = 1}^4 {\sigma _\omega ^j\varepsilon _{\omega ,t}^j} $ | (4) |
| $ln\omega _t^{"} = \left( {1 - {\rho _{{\omega ^{"}}}}} \right)ln{{\bar \omega }^{"}} + {\rho _\omega }ln\omega _{t - 1}^{"} + \sigma _{{\omega ^{"}}}^0\varepsilon _{{\omega ^{"}},t}^0 + \sum\nolimits_{j = 1}^4 {\sigma _{{\omega ^{"}}}^j\varepsilon _{{\omega ^{"}},t}^j} $ | (5) |
| $ln\tau _t^h = \left( {1 - {\rho _\tau }} \right)ln{{\bar \tau }^h} + {\rho _\tau }ln\tau _{t - 1}^h + \sigma _\tau ^{0\;h}\varepsilon _{\tau ,t}^{0\;h} + \sum\nolimits_{j = 1}^4 {\sigma _\tau ^{j\;h}\varepsilon _{\tau ,t}^{j\;h}} $ | (6) |
之所以在附加预期的状态下,经济体中的冲击形式表示为上述形式的原因是:假设经济信息冲击可以划分为不可预期冲击和可预期冲击。不可预期冲击与一般经济冲击的经济学含义相同,可预期冲击指的是那些在当期之前 (包括当期) 被经济人意识到经济信息,但这种经济信息的要等到当期之后 (也就是下一期) 才能发挥作用,第 (7) 和 (8) 式从数学上描述了这个过程。假设某外生冲击变量xt,满足:
| ${x_t} = \rho {x_{t - 1}} + \eta _t^x,\eta _t^x{\sim }i.i.d.N\left( {0,{\sigma ^2}} \right)$ | (7) |
| $\eta _t^x = \mu _t^0 + \mu _{t - 1}^1 + {\phi ^2}\mu _{t - 2}^2 + {\phi ^3}\mu _{t - 3}^3 + \cdots + {\phi ^n}\mu _{t - n}^n$ | (8) |
其中,μt0代表的冲击为不可预期的,μt0+φμt-11+φ2μt-22+φ3μt-33+ …+φnμt-nn代表的冲击为可预期的,φ指的是冲击的衰减速度,其取值范围一般为0≤φ≤1。加入在模型中嵌入冲击衰减速度可以在一定程度上降低冲击对整个经济系统的冲击强度,从而可以在一定程度上避免把经济的波动过多归咎于预期冲击,让理论模型的分析结果与现实经济更加匹配。下面给出模型求解的具体方程:
总需求方程:
| ${{\hat Y}_t} = \left( {c/Y} \right){{\hat c}_t} + \left( {\hat c/Y} \right){{\hat c}_t} + \left( {{c^{"}}/Y} \right)\hat c_t^{"} + \left( {I/Y} \right){{\hat I}_t} + \left( {G/Y} \right){{\hat G}_t}$ | (9) |
| $\hat c_t^{'} = \hat c_{t + 1}^{'} - \hat R_t^f + {{\hat \pi }_{t + 1}}$ | (10) |
| $\begin{gathered} {{\hat I}_t} = {{\hat K}_{t + 1}} + \gamma \left( {{{\hat I}_{t + 1}} - {{\hat K}_t}} \right) + \left\{ {\left[ {1 - \gamma \left( {1 - \delta } \right)} \right]/{\phi _k}} \right\} \hfill \\ \left( {{{\hat Y}_t} + {{\hat X}_{t + 1}} - {{\hat K}_t}} \right) + \left( {1/{\phi _k}} \right)\left( {{{\hat c}_t} - {{\hat c}_{t + 1}}} \right) \hfill \\ \end{gathered} $ | (11) |
房价动态变化方程:
| $\begin{array}{l} {{\hat q}_t} + {{\bar \tau }^h}\left( {{{\hat q}_t} + \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \tau } _t^h - {{\hat c}_t}} \right) = \left[ {\omega \beta + \gamma \left( {1 - \omega } \right)} \right]{{\hat q}_{t + 1}} + \\ \left[ {1 - \omega \beta - \gamma \left( {1 - \omega } \right)\\ + {{\bar \tau }^h}} \right]\left( {{{\hat Y}_{t + 1}} - {{\hat X}_{t + 1}} - {{\hat h}_t}} \right)\\ \;\;\;\; - \left( {\omega \beta /w} \right)\left( {\hat R_t^b - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } }_{t + 1}}} \right)\\ + \left[ {1 - \left( {\omega \beta /w} \right)} \right]\left( {{{\hat c}_t} - {w_2}{{\hat c}_{t + 1}}} \right) + \left[ {\left( {\beta /w} \right) - \gamma } \right]{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \omega } }_t} \end{array}$ | (12) |
| $\begin{array}{l} {{\hat q}_t} + {{\bar \tau }^h}\left( {{{\hat q}_t} + \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \tau } _t^h - \hat c_t^{"}} \right) = \left[ {{\beta ^{"}} + {\omega ^{"}}\left( {\beta - {\beta ^{"}}} \right)} \right]{{\hat q}_{t + 1}} + \left[ {1 - {\beta ^{"}} - {\omega ^{"}}\left( {\beta - {\beta ^{"}}} \right) + {{\bar \tau }^h}} \right]\\ \;\;\;\;\;\left( {{{\hat J}_t} - \hat h_t^{"}} \right) - \left( {{\omega ^{"}}\beta /{w_0}} \right)\left( {\hat R_t^l - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } }_{t + 1}}} \right) + \left[ {1 - \left( {{\omega ^{"}}\beta /{w_0}} \right)} \right]\left( {\hat c_t^{"} - {w_1}\hat c_{t + 1}^{"}} \right) + \\ \;\;\;\;\;\left[ {\left( {\beta /{w_0}} \right) - {\beta ^{"}}} \right]{\omega ^{"}}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \omega } _t^{"} \end{array}$ | (13) |
| $\begin{array}{l} {{\hat q}_t} + {{\bar \tau }^h}\left( {{{\hat q}_t} + \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \tau } _t^h - \hat c_t^{'}} \right) = \beta {{\hat q}_{t + 1}} + \left( {1 - \beta + {{\bar r}^h}} \right){{\hat j}_t} + \left\{ {\left[ {\left( {1 - \beta + {{\bar r}^h}} \right)h} \right]/{h^{'}}} \right\}\hat h_t^{"}\\ \;\;\;\; + \left\{ {\left[ {\left( {1 - \beta + {{\bar r}^h}} \right){h^{"}}} \right]/{h^{'}}} \right\}\hat h_t^{"} + \hat c_t^{'} - \beta \hat c_{t + 1}^{'} \end{array}$ | (14) |
借贷约束和金融摩擦约束方方程:
| ${{\hat b}_t} = {{\hat q}_{t + 1}} + {{\hat h}_t} - \left( {\hat R_t^b - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } }_{t + 1}}} \right) + {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \omega } }_t} + \left[ {{{\bar r}^h}/\left( {1 + {{\bar r}^h}} \right)} \right]\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over r} _t^h$ | (15) |
| $\hat b_t^{"} = {{\hat q}_{t + 1}} + \hat h_t^{"} - \left( {\hat R_t^l - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } }_{t + 1}}} \right) + \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \omega } _t^{"} + \left[ {{{\bar \tau }^h}/\left( {1 + {{\bar \tau }^h}} \right)} \right]\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \tau } _t^h$ | (16) |
| $\hat R_t^l - \hat R_t^f = \xi \left( {\hat b_t^{"} - {{\hat q}_t} - \hat h_t^{"}} \right) - \left[ {{{\bar \tau }^h}/\left( {1 + {{\bar \tau }^h}} \right)} \right]\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \tau } _t^h$ | (17) |
| $\hat R_t^b - \hat R_t^f = \xi \left( {\hat b_t^{'} - {{\hat q}_t} - \hat h_t^{'}} \right) - \left[ {{{\bar \tau }^h}/\left( {1 + {{\bar \tau }^h}} \right)} \right]\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \tau } _t^h$ | (18) |
总供给方程:
| $\begin{array}{l} {{\hat Y}_t} = \left\{ {\eta /\left[ {\eta - \left( {1 - \mu - \upsilon } \right)} \right]} \right\}\left( {{{\hat A}_t} + \upsilon {{\hat h}_{t - 1}} + \mu {{\hat K}_{t - 1}}} \right) - \left\{ {\eta /\left[ {\eta - \left( {1 - \mu - \upsilon } \right)} \right]} \right\}\\ \left[ {{{\hat X}_t} + \alpha \hat c_t^{"} + \left( {1 - \alpha } \right)\hat c_t^{"}} \right] \end{array}$ | (19) |
| ${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } }_t} = \beta {E_t}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } }_{t + 1}} - \kappa {{\hat X}_t}$ | (20) |
状态变量演进方程:
| ${{\hat K}_t} = \delta {{\hat I}_t} + \left( {1 - \delta } \right){{\hat K}_{t - 1}}$ | (21) |
| $\begin{array}{l} \left( {b/Y} \right){{\hat b}_t} = \left( {c/Y} \right){{\hat c}_t} + \left( {qh/Y} \right)\left( {{{\hat h}_t} - {{\hat h}_{t - 1}}} \right) + \left( {I/Y} \right){{\hat I}_t} + \left( {wb/\beta Y} \right)\\ \left( {\hat R_{t - 1}^b + {{\hat b}_{t - 1}} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } }_t}} \right) - \left( {1 - {s_1} - {s_2}} \right)\left( {{{\hat Y}_t} - {{\hat X}_t}} \right) + \left( {{{\bar r}^h}qh/Y} \right)\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over r} _t^h + {{\hat q}_t} + {{\hat h}_t}} \right) \end{array}$ | (22) |
| $\begin{array}{l} \left( {{b^{"}}/Y} \right)\hat b_t^{"} = \left( {{c^{"}}/Y} \right)\hat c_t^{"} + \left( {q{h^{"}}/Y} \right)\left( {\hat h_t^{"} - \hat h_{t - 1}^{"}} \right) + \left( {{w_0}{b^{"}}/\beta Y} \right)\left( {\hat R_{t - 1}^l + \hat b_{t - 1}^{"} - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } }_t}} \right)\\ - {s_2}\left( {{{\hat Y}_t} - {{\hat X}_t}} \right) + \left( {{{\bar r}^h}q{h^{"}}/Y} \right)\left( {\hat r_t^h + {{\hat q}_t} + \hat h_t^{"}} \right) \end{array}$ | (23) |
政府部门决策方程及外生冲击方程:
| $\hat R_t^f = \left( {1 - r_R^f} \right)\left( {{r_\pi }{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \pi } }_t} + {r_Y}{{\hat Y}_t} + {r_q}\Delta {{\hat q}_t}} \right) + r_R^f\hat R_{t - 1}^f$ | (24) |
| ${{\hat G}_t} = {{\hat q}_t} + \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \tau } _t^h$ | (25) |
| $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \tau } _t^h = {\rho _{{r^h}}}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over r} }_{r - 1}}^h + \sigma _\tau ^{0\;h}\varepsilon _{\tau ,t}^{0\;h} + \sum\nolimits_{j = 1}^4 {\sigma _{{\tau ^h}}^j} \varepsilon _{{r^h},t}^j$ | (26) |
| ${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \omega } }_t} = {\rho _\omega }{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \omega } }_{t - 1}} + \sigma _\omega ^0\omega _{\omega ,t}^0 + \sum\nolimits_{j = 1}^4 {\sigma _\omega ^j} \varepsilon _{\omega ,t}^j$ | (27) |
| $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \omega } _t^{"} = {\rho _\omega }\omega _{t - 1}^{"} + \sigma _{{\omega ^{"}}}^0\varepsilon _{{\omega ^{"}},t}^0 + \sum\nolimits_{j = 1}^4 {\sigma _{{\omega ^{"}}}^j} \varepsilon _{{\omega ^{"}},t}^j$ | (28) |
| ${{\hat A}_t} = {\rho _A}{{\hat A}_{t - 1}} + {\sigma _A}{\varepsilon _{A,t}}$ | (29) |
其中,在上述线性系统中某些代理变量所表示的实际值为:
| $\begin{array}{*{20}{l}} {w = {{\left( {\beta \omega } \right)}^{\left( {\xi /\xi + 1} \right)}},}&{{w_0} = {{\left( {\beta {\omega ^{"}}} \right)}^{\left( {\xi /\xi + 1} \right)}},}\\ {{w_1} = \left( {\gamma - \gamma \omega } \right)/\left[ {1 - \left( {\omega \beta /w} \right)} \right],}&{{w_2} = \left( {\beta - {\beta ^{"}}\omega } \right)/\left[ {1 - \left( {{\omega ^{"}}\beta /{w_0}} \right)} \right],}\\ {{s_1} = \left[ {\alpha \left( {1 - \upsilon - \mu } \right) + X - 1} \right]/X,}&{{s_2} = \left[ {\left( {1 - \alpha } \right)\left( {1 - \upsilon - \mu } \right)} \right]/X,\; \\ \kappa = \left[ {\left( {1 - \theta } \right)\left( {1 - \beta \theta } \right)} \right]/\theta } \end{array}$ |
参数校准根据现实经济中的真实数据进行估计而得,也有一部分参数为借鉴现有文献获取,本文在校准过程中所采用的数据为中经网数据,校准过程如下:
在对耐心型家庭的主观贴现因子的设置时,本文根据陈彦斌等 (2009)将耐心型家庭的主观贴现因子设置为0.985,根据Iacoviello (2005)对非耐心型家庭的主观贴现因子设置为0.95。对劳动供给的Frisch弹性η′和η″的设置本文参照仝冰 (2010)的设置,将劳动供给的Frisch弹性都设置为1。本文在房地产开发商的折现因子γ的设置上参照封北麟 (2009)的校准结果,将其设置为0.886,根据黄赜琳 (2005)将资本收入比μ设置为0.499。根据中经网统计数据库数据,本文将房地产占收入的比例υ设为0.012。根据肖争艳 (2011)将耐心型家庭的劳动产出弹性α设置为0.73。在校准资本折旧率δ时,本文参照黄赜琳 (2005)将其设置为0.025。
为了体现模型参数和现实经济情况的契合,在借贷型家户的抵押贷款比例的稳态值的设定上,本文认为近年来随着国家加大对房地产市场的调控力度,房贷首付比例不断升高,虽然全国各个地区有所差异,例如,东部沿海地区像浙江、广东等地提高至40%,即借贷部分占房款总额的60%,而中西部地区像河南、陕西等地也提高至30%,即贷款部分占房款总额的70%。为了体现普遍性,本文取这两个数值的平均值,即贷款比例为0.75。对于企业抵押贷款比例,在国内大约为50%~60%,我们取为0.5。对于风险溢价弹性系数ζ的设定,在Carlstrom和Fuerst (1997)、Fukunaga (2002)和Céspedes et al.(2005)的等模型中,风险溢价弹性系数一般在0~0.4中取值。为了考虑金融摩擦效应对经济体中各种预期冲击的影响,同时鉴于我国金融中介服务体系相比欧美发达国家发展尚不完善的情况,金融摩擦系数应该低于美国等发达国家,因而本文的ζ分别取0.02。对于外生冲击相关参数的设定如下实际上,只要外生冲击相关参数的设定在合理的范围内,参数的具体取值不影响模拟结果 (刘鹏和鄢莉莉,2012)。:技术冲击的持续性系数和标准差的设置,本文参照许伟和陈斌开 (2009)的估计结果,设技术冲击的持续性系数为0.78,标准差为0.02。通货膨胀冲击的持续性系数和标准差的设置;本文参照骆永民和伍文中 (2012)对房产税冲击的贝叶斯估计结果,设房产税冲击的持续性系数为0.7329,标准差为0.0372;本文参照Zheng Liu et al.(2013)对贷款价值比的贝叶斯估计结果,相对于美国等发达经济体我国信贷市场发展尚不完善,信贷冲击强度应该低于美国等发达经济体,并且波动性会大于美国等发达经济体,故设我国企业信贷冲击的持续性系数为0.7,标准差为0.2896,非耐心型家庭的住房按揭贷款额度冲击持续性系数为0.45,标准差为0.8691。
五、 数值模拟分析DSGE模型的数值模拟分析为考察纳入金融摩擦与否对房产税对住房价格的整体影响提供了一个合适的方法。本文在不改变其他模型参数的基础上,通过改变税率,考察房价受到不同税率时的房产税冲击、个人抵押贷款冲击、企业信贷冲击的脉冲响应。
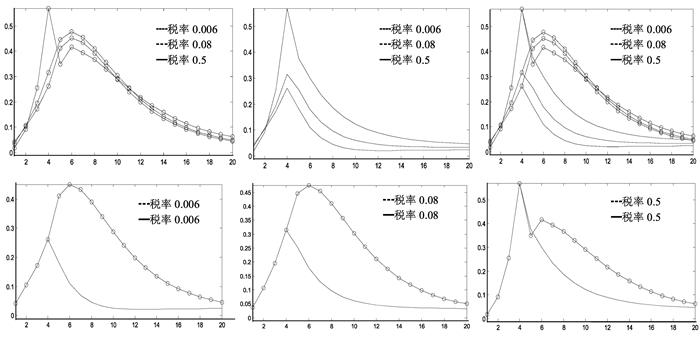
(一) 不同的预期稳态税率下房产税试点消息冲击对房价的影响图 1是预期稳态税率分别取0.006、0.08和0.5时,滞后4期的房产税试点消息冲击 (意思是政府将于4个季度,也即1年后实施房产税) 对房价的影响。第一行的第一个图是房产税试点消息实现下住房价格的反应,第一行的第二个图是房产税试点消息未实现下住房价格的反应,第三个图是前两个图的合并。在模型中引入大小为一单位标准差的滞后4期的房产税试点消息冲击之后,观察前两个图可以发现,无论是最后房产税试点消息实现与否,随着预期稳态税率 (即预期房产税实施的政策力度) 的增加,当前的住房价格也随之上涨。
|
图 1 不同的预期稳态税率下房产税试点消息冲击对房价的影响 注:上图中纵轴表示住房价格对稳态的偏离值,横轴表示季度。o线:消息实现,无o线:消息未实现。 |
在房产税试点消息实现的情况下 (在第一行的第一个图中),当预期稳态税率取0.006时,滞后4期的房产税试点消息冲击最多能导致当期房价上涨0.2,但当预期稳态税率取0.08时,滞后4期的房产税试点消息冲击最多能导致当期房价上涨0.56。也就是说,随着预期稳态税率 (即预期房产税实施的政策力度) 的增加,当前的住房价格上涨得就越快。
在房产税试点消息未实现的情况下 (在第一行的第二个图中),如果预期稳态税率的值设为0.006时,房产税试点消息冲击在滞后4期的情形下最多能导致当期房价上涨0.4左右。然而,如果预期稳态税率设为0.08时,房产税试点消息冲击在滞后4期的情形下最多能使得房价在当期上涨0.56。换句话说,随着预期房产税实施的政策力度的增加,住房价格在当前上涨的速度就会加快。这说明了当经济人预期到房产税政策可能会实施时,经济人购买住房的需求就会上升,原因是房产税政策的实施可能会导致住房价格的进一步上涨,这一点与近期深圳楼市供需两旺,最近部分深圳热销楼盘将原计划明年推出的房源提前放出以满足当前住房需求的增加的事实相吻合,业内人士表示此举或与房产税出台预期有关①。
①来源于《中国证券报》2013年6月13日第A07版。
从第二行的三个图可以清楚地看到,对于实现了的房产税试点消息冲击,住房价格会继续增加一段时期,在第5期开始将将沿着新的均衡路径继续增加,然后再缓慢地回到稳态。这说明了当经济人最终发现房产税政策由试点变成真正实施的政策时,经济人出于对征税而导致的房价上涨的恐慌,会继续增加对住房的需求,从而导致住房价格继续上涨一段时间,但是当房产税实施了一段时间后,人们便逐渐淡化了房产税对房价的影响,于是理性的经济人对住房的需求又会缓慢回到正常水平,于是住房价格就会缓慢下降。
而对于未实现的房产税试点消息冲击,住房价格会在第5期突然下降,然后从第5期开始将将沿着新的均衡路径快速回到稳态。这说明了当经济人最终发现房产税政策由试点变成没有实施的政策时,经济人购买住房的需求就会立即下降,原因是住房价格这时并不会再上涨了,因为房产税政策不再实施了。
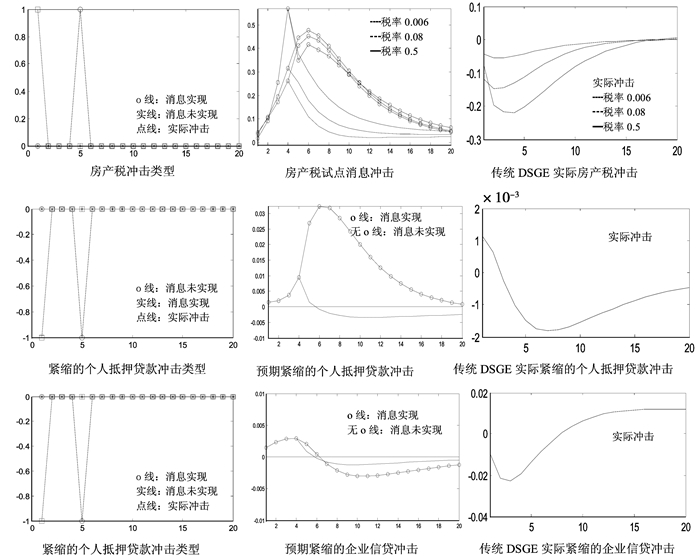
(二) 房产税试点消息冲击,预期紧缩的个人抵押贷款政策和预期紧缩的企业信贷政策与传统DSGE实际房产税冲击对房价的影响比较图 2考察的是房产税试点消息冲击,预期紧缩的个人抵押贷款政策和预期紧缩的企业信贷政策与传统DSGE实际冲击对房价的影响比较。从上图的第一行可以看出,正向的房产税试点消息冲击均是在房产税政策实施前导致了房价的上涨,这一点与中国社会科学院金融研究所研究员易宪容的观点相一致,即征收房产税增加了房价上涨的预期。而传统DSGE实际房产税冲击却产生的是抑制房价上涨的作用,这一点与陈多长和踪家峰 (2004)与况伟大 (2012)的研究结论相一致,即房产税对房价具有显著负向作用。
|
图 2 房产税试点消息冲击,预期紧缩的个人抵押贷款政策和预期紧缩的企业信贷政策与传统DSGE实际房产税冲击对房价的影响 注:上图中纵轴表示住房价格对稳态的偏离值,横轴表示季度,o线:消息实现,无o线:消息未实现。 |
从图 2的第二行可以看出,预期紧缩的个人抵押贷款政策在紧缩政策实施前导致了房价的上涨,然后在政策实施后住房价格才开始缓慢回落,而传统DSGE实际冲击却产生的是抑制房价上涨的作用,这一点和谭政勋和陈铭 (2012)的结论比较相符,他们利用面板模型分析房价失衡与房价变化对金融危机的影响,研究得出银行贷款是短期房价上涨最主要的推动力。预期紧缩的个人抵押贷款政策在紧缩政策实施前导致了房价的上涨的原因可以解释为:目前我国工薪阶层主要还是依赖于向银行获取住房按揭贷款来购买住房的,当经济人预期到政府可能会在未来一段时期后实施紧缩性的个人抵押贷款政策 (比如,提高个人按揭贷款的首付比例) 时,理性经济人为了降低以后购房的成本就会在当期 (即,紧缩性的个人抵押贷款政策实施前) 选择购房,这样就会导致紧缩性的个人抵押贷款政策实施前住房需求量增加,在住房供应量一定的情况下,预期到的紧缩的个人抵押贷款政策在紧缩政策就会导致住房价格的进一步上涨。
从图 2的第三行可以看出,预期紧缩的企业信贷政策在紧缩政策实施前导致了房价的上涨,然后在政策实施后住房价格迅速回落,而传统DSGE实际冲击却产生的是抑制房价上涨的作用。预期紧缩的企业信贷政策在紧缩政策实施前导致了房价的上涨的原因可以解释为:
在我国,房地产开发商的资金来源大部分仍以贷款为主,当房地产企业预期到政府可能会在未来一段时期后实施紧缩性的企业信贷政策 (比如,降低房地产企业贷款规模) 时,理性的房地产开发商为了降低以后的房地产开发成本就会在当期 (即,紧缩性的个人抵押贷款政策实施前) 选择增加住房建设量,在住房需求一定的情况下,开发商的这种行为就会在一定程度上降低住房价格的上涨程度,从而预期紧缩的企业信贷政策是上述三种政策中在政策实施前导致房价上涨幅度最小的政策。
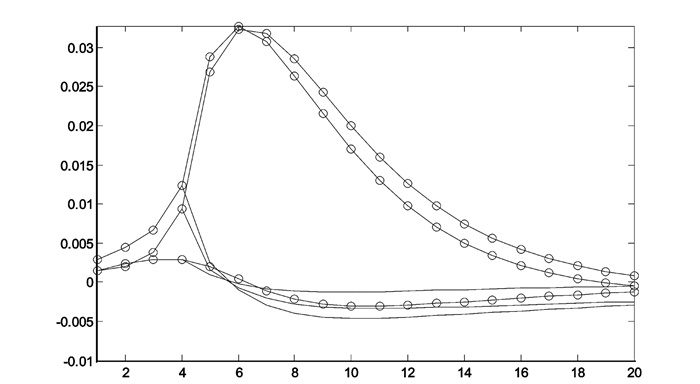
(三) 房产税试点消息、预期紧缩的个人抵押贷款政策以及预期紧缩的企业信贷政策三者的两两混合预期对住房价格的影响图 3-图 6考察的是税率取0.006时,房产税试点消息,预期紧缩的个人抵押贷款政策和预期紧缩的企业信贷政策三者之间两两组合与三者组合所产生的四组混合预期对对住房价格的影响。从上面的第一个图可以看出,预期紧缩的个人抵押贷款政策与预期紧缩的企业信贷政策的混合预期在紧缩政策实施前导致的房价上涨幅度均大于单纯预期紧缩的个人抵押贷款政策和单纯预期紧缩的企业信贷政策,由此可见预期效应具有可加性,也即当经济人对未来同时产生多种预期时,由多种预期所产生的对内生变量的影响具有相互增强的性质。同样,在接下来的三个图中,预期效应的可加性也同样得到体现,即混合预期在政策实施前对住房价格的影响总是最大的,换句话说混合预期在政策实施前所产生的推高住房价格的作用比起单纯存在一种预期的情形下都要大。另外,通过对比上面的四个图我们发现,房产税试点消息始终是三种预期中导致住房价格上涨的最主要因素,预期紧缩的个人抵押贷款政策位居其次,而预期紧缩的企业信贷政策对住房价格的推高作用是这三者之中最弱的,这意味着在抑制房价上涨的作用上,预期紧缩的企业信贷政策是最有效的,其次是预期紧缩的个人抵押贷款政策,房产税试点消息则是在抑制房价上涨方面最不利的预期因素。
|
图 3 预期紧缩的个人抵押贷款政策与预期紧缩的企业信贷政策的混合预期 (实o线) 注:o线表示消息实现情形下:实o线表示预期紧缩的个人抵押贷款政策与预期紧缩的企业信贷政策的混合预期,虚o线表示单纯预期紧缩的个人抵押贷款政策,点o线表示单纯预期紧缩的企业信贷政策。无o线表示消息未实现情形下:实线表示预期紧缩的个人抵押贷款政策与预期紧缩的企业信贷政策的混合预期,虚线表示单纯预期紧缩的个人抵押贷款政策,点线表示单纯预期紧缩的企业信贷政策。 |

|
图 4 房产税试点消息与预期紧缩的企业信贷政策的混合预期 (实o线) 注:o线表示消息实现情形下:实o线表示房产税试点消息与预期紧缩的企业信贷政策的混合预期,虚o线表示单纯预期紧缩的企业信贷政策,点o线表示单纯房产税试点消息。无o线表示消息未实现情形下:实线表示房产税试点消息与预期紧缩的企业信贷政策的混合预期,虚线表示单纯预期紧缩的企业信贷政策,点线表示单纯房产税试点消息。 |

|
图 5 房产税试点消息与预期紧缩的个人抵押贷款政策的混合预期 (实o线) 注:o线表示消息实现情形下:实o线表示房产税试点消息与预期紧缩的个人抵押贷款政策的混合预期,虚o线表示单纯预期紧缩的个人抵押贷款政策,点o线表示单纯房产税试点消息。无o线表示消息未实现情形下:实线表示房产税试点消息与预期紧缩的个人抵押贷款政策的混合预期,虚线表示单纯预期紧缩的个人抵押贷款政策,点线表示单纯房产税试点消息。 |

|
图 6 房产税试点消息,预期紧缩的个人抵押贷款政策和预期紧缩的企业信贷政策三者的混合预期 (实o线) 注:o线表示消息实现情形下:实o线表示预期紧缩的个人抵押贷款政策的混合预期和预期紧缩的企业信贷政策的混合预期,虚o线表示单纯预期紧缩的个人抵押贷款政策,点o线表示单纯房产税试点消息,点划o线表示单纯预期紧缩的企业信贷政策。无o线表示消息未实现情形下:实线表示预期紧缩的个人抵押贷款政策的混合预期和预期紧缩的企业信贷政策的混合预期,虚线表示单纯预期紧缩的个人抵押贷款政策,点线表示单纯房产税试点消息,点划线表示单纯预期紧缩的企业信贷政策。图 3-图 6中纵轴表示产出对稳态的偏离值,横轴表示季度。 |
对于实现了的混合预期,通过对比上面的四个图我们发现,预期紧缩的个人抵押贷款政策与预期紧缩的企业信贷政策的混合预期在实现之后所引起的住房价格下降幅度是四组混合预期在实现情形下效果最好的,这一点进一步补充了预期未实现的情形下我们得出的结论。预期未实现的情形下我们得出预期紧缩的企业信贷政策是最有效的,其次是预期紧缩的个人抵押贷款政策,房产税试点消息则是在抑制房价上涨方面最不利的预期因素,而在预期实现情形下我们得出的是企业信贷和个人抵押贷款政策的组合是抑制房地产价格上涨的最有效政策组合,房产税与企业信贷或个人抵押贷款政策的组合在抑制住房价格上涨的作用上明显低于企业信贷和个人抵押贷款政策的组合,这一结论与中国社会科学院金融研究所研究员易宪容的观点比较一致①。
①资料来源于http://business.sohu.com/20130521/n376605089.shtml。
六、 结论随着我国经济社会的发展,经济主体 (家庭、企业组织、政府) 面临的不确定性和决策风险在不断增加,预期冲击将成为导致中国宏观经济在短期内发生大幅波动的一个重要因素。值得注意的是,国内少数学者也认识到了预期冲击是驱动我国宏观经济波动的重要因素。本文引人加入金融摩擦的消息推动下的经济周期 (News-Driven Business Cycle with Financial Frictions) 模型来分析预期对住房价格的影响,研究发现预期冲击对住房价格具有重要作用。具体来说,本文发现房产税试点的消息冲击,预期紧缩的个人抵押贷款政策和预期紧缩的企业信贷政策均对房价具有重要作用,并且消息冲击影响下的住房价格与传统周期模型下实际政策冲击的影响下的住房价格之间具有明显的区别。同时,本文通过对房产税试点消息,预期紧缩的个人抵押贷款政策和预期紧缩的企业信贷政策三者之间两两组合与三者组合所产生的四组混合预期对住房价格的影响发现:预期效应具有可加性,也即当经济人对未来同时产生多种预期时,由多种预期所产生的对内生变量的影响具有相互增强的性质。最后,本文发现在导致房价上涨的预期冲击中,预期紧缩的企业信贷政策是最微弱的,其次是预期紧缩的个人抵押贷款政策,房产税试点消息预期则是导致房价上涨方面最不利的预期因素。
消息推动的经济周期 (NDBC) 研究刚刚起步,本文第一次将房产税预期和信贷预期实际运用于住房价格的影响分析上,并首次探讨了经济人在混合预期下的行为对住房价格的影响,并验证了预期效应的可加性,也即当经济人对未来同时产生多种预期时,由多种预期所产生的对内生变量 (在本文里就是住房价格) 的影响具有相互增强的性质。由本文所得的脉冲相应结果可以看出,一旦经济主体对政府过早宣布的经济政策形成预期,便将以自己的特殊行为来抵消政府的影响,从而这种预期效应可能会在一定程度上抵消政府实施政策的初衷,使政府的政策的作用减至最低。这充分说明了政府在制定政策时应充分考虑政策执行的时机与政策执行的效率之间的关系。
| [] | Beaudry, P. and Portier, F. , 2004, "An Exploration into Pigou's Theory of Cycles". Journal of Monetary Economics, 51(7), 1183–1216. |
| [] | Beaudry, P. and Portier, F. , 2007, "When can changes in expectations cause business cycle fluctuations in neo-classical settings?". Journal of Economic Theory, 135(1), 458–477. DOI:10.1016/j.jet.2006.06.009 |
| [] | Bernanke, Ben, Mark Gertler and Simon Gilchrist, 1999, "The Financial Accelerator in a Quantitative Business Cycle Framework", In John Taylor and Michael Woodford (eds.), Handbook of Macroeconomics, North-Holland, Amsterdam, pp.1341-1393. |
| [] | Cespedes, L. F. and Chang, R. , 2005, "Balance Sheets and Exchange Rate Policy". American Economic Review, 94(4), 1183–1193. |
| [] | Christiano, L., Motto, R. and M. Rostagno, 2007, "Monetary policy and the stock market boom bust cycle", Manuscript, Northwestern University. |
| [] | Christiano, L. , Eichenbaum, M. and Evans, C. , 2005, "Nominal Rigidities and the Dynamic Effects of a shock to Monetary Policy". Journal of Political Economy, 113(1), 1–45. DOI:10.1086/426038 |
| [] | Christiano, L. J., Motto, R. and Rostagno, M., 2010, "Financial Factors in Business Cycles", European Central Bank Working Paper Series, No 1192 / MAY. |
| [] | Daria Finocchiaro and Virginia Queijo von Heideken, 2010, "Do central banks react to house prices? ", Sveriges Riksbank Working Paper Series, No. 21. http://www.riksbank.se/Documents/Forskning/FinocchiaroRB_CV2016.pdf |
| [] | Feve, P. , Matheron, J. and Sahuc, , 2009, "On the dynamic implications of news shocks"". Economic Letters, 102(6), 96–98. |
| [] | Fujiwara, I., Hirose, Y. and Shintani, M., 2008, "Can news be a major source of aggregate fluctuations? a Bayesian DSGE approach", IMES discussion paper 2008-E-16, Bank of Japan. http://www3.grips.ac.jp/~econseminar/20110117jmcb_363.pdf |
| [] | Gertler, M., and Kiyotaki, N., 2010, "Financial Intermediation and Credit Policy in Business Cycle Analysis", N.Y.U. and Princeton, mimeo. |
| [] | Goodfriend, M. and McCallum, B.T. , 2007, "Banking and Interest Rates in Monetary Policy Analysis: A Quantitive Exploration". Journal of Monetary Economics, 55(6), 1480–1507. |
| [] | Iacoviello, and Matteo, , 2005, "House Prices, Borrowing Constraints and Monetary Policy in the Business Cycle". American Economic Review, 95(5), 739–764. |
| [] | Jaimovich, N. and Rebelo, S. , 2009, "Can news about the future drive the business cycle?". American Economic Review, 171(2), 112–133. |
| [] | Kobayashi, K. and Nutahara, K.: 2008, "Nominal rigidities, news-driven business cycles, and monetary policy", Discussion paper 08-E-018, REITI. |
| [] | Lai, F.C. , McDonald, J. F. and Merriman, D.F. , 2010, "Housing Appreciation (Depreciation) and Owner's Welfare". Journal of Housing Economics, 19(4), 66–73. |
| [] | Margarita Rubio, Jose A.Carrasco-Gallego, 2012, "Macroprudential Measures, Housing Markets, and Monetary Policy", Dynare Working Papers, No.023. https://www.nottingham.ac.uk/cfcm/documents/papers/13-05.pdf |
| [] | Matteo, Iacoviello and Stefano, Neri , 2010, "Housing Market Spillovers: Evidence from an Estimated DSGE Model". American Economic Journal: Macroeconomics, 93(7), 125–164. |
| [] | Rebelo, Sergio, 2005, "Real Business Cycle Models: Past, Present, and Future", NBER Working Paper, No.11401. |
| [] | Smets, F. and Wouters, R. , 2003, "An estimated dynamic stochastic general equilibrium model of the euro area". Journal of the European Economic Association, 52(1), 1123–1175. |
| [] | Suh, and Sangwon, , 2011, "Currency Hedging Failure in International Equity Investments and an Efficient Hedging Strategy: The Perspective of Korean Investors". Pacific-Basin Finance Journal, 19(8), 390–403. |
| [] | Seth Payton, 2004, "Property taxes and local policy affect housing values", Indiana University, Center for Urban Policy and Environment Report. |
| [] | Winkler and Wohlmann, 2009, "On the (de) stabilizing effects of news shocks", Kiel Working Paper No.1542. |
| [] | Wood, G.A. and Flatau, P. , 2006, "Microsimulation Modeling of Tenure Choice and Grants to Promote Home Ownership". Australian Economic Review, 39(4), 14–34. |
| [] | Liu, Zheng , Wang, Pengfei and Zha, Tao , 2013, "Land-price Dynamics and Macroeconomic Fluctuations". Econometrica, 213(3), 1147–1184. |
| [] | 陈多长、踪家峰, 2004, 《房地产税收与住宅资产价格:理论分析与政策评价》, 《财贸研究》, 第 1 期, 第 57–60 页。 |
| [] | 陈彦斌、霍震、陈军, 2009, 《灾难风险与中国城镇居民财产分布》, 《经济研究》, 第 11 期, 第 144–158 页。 |
| [] | 封北麟, 2009, 《资产价格波动与货币政策反应》. 经济科学出版社, 第 30-213 页. |
| [] | 黄绩琳, 2005, 《中国经济周期特征与财政政策效应——一个基于三部门RBC模型的实证分析》, 《经济研究》, 第 6 期, 第 27–39 页。 |
| [] | 刘斌, 2008, 《我国DSGE模型的开发及在货币政策分析中的应用》, 《金融研究》, 第 10 期, 第 1–21 页。 |
| [] | 刘鹏、鄢莉莉, 2012, 《银行体系、技术冲击与中国宏观经济波动》, 《国际金融研究》, 第 3 期, 第 69–76 页。 |
| [] | 梁云芳、高铁梅、贺书平, 2006, 《房地产市场与国民经济协调发展的实证分析》, 《中国社会科学》, 第 3 期, 第 21–40 页。 |
| [] | 骆永民、伍文中, 2012, 《房产税改革与房价变动的宏观经济效应——基于DSGE模型的数值模拟分析》, 《金融研究》, 第 5 期, 第 1–14 页。 |
| [] | 况伟大, 2009, 《住房特性、物业税与房价》, 《经济研究》, 第 4 期, 第 151–160 页。 |
| [] | 仝冰, 2010, 《货币、利率与资产价格—基于DSGE模型的分析和预测》, 《北京大学博士研究生学位论文》. |
| [] | 谭政勋、王聪, 2011, 《中国信贷扩张, 房价波动的金融稳定效应研究——动态随机一般均衡模型视角》, 《金融研究》, 第 8 期, 第 57–71 页。 |
| [] | 谭政勋、陈铭, 2012, 《房价波动与金融危机的国际经验证据:抵押效应还是偏离效应》, 《世界经济》, 第 3 期, 第 146–159 页。 |
| [] | 王晓明, 2010, 《银行信贷与资产价格的顺周期关系研究》, 《金融研究》, 第 3 期, 第 21–37 页。 |
| [] | 徐承明、王安兴, 2006, 《风险转移规制和房地产价格泡沫的控制》, 《世界经济》, 第 9 期, 第 15–29 页。 |
| [] | 许伟、陈斌开, 2009, 《银行信贷与中国经济波动: 1993—2005》, 《经济学季刊》, 第 3 期, 第 969–994 页。 |
| [] | 赵进文、高辉, 2009, 《资产价格波动对中国货币政策的影响——基于1994-2006年季度数据的实证分析》, 《中国社会科学》, 第 2 期, 第 98–114 页。 |
| [] | 赵胜民、罗琦, 2013, 《金融摩擦视角下的房产税、信贷政策与住房价格》, 《财经研究》, 第 12 期, 第 75–81 页。 |
| [] | 庄子罐、崔小勇、龚六堂, 2012, 《预期与经济波动——预期冲击是驱动中国经济波动的主要力量吗?》, 《经济研究》, 第 6 期, 第 46–59 页。 |



