随着全球气候变暖和2009年哥本哈根气候会议的召开,以低能耗、低污染为基础和以“低碳技术”为核心的“低碳经济”发展模式已成为全球经济转型发展的焦点。中国作为世界第二经济体和CO2排放第一大国,减排不力将会导致其碳排放量高出其它国家越来越多,那么中国在国际碳减排会议上的责任越来越重 (李宾,2014)。《2009年中国可持续发展战略报告》的低碳发展目标确定为:到2020年,单位GDP的CO2排放降低约50%,这个战略目标无疑为我国成功走向低碳经济发展道路起到了极大的推动作用。为进一步深化落实该低碳目标,2010年起我国先后启动了两批共6省和36市的国家低碳试点省市,其中包括了广东省、深圳市和广州市,并陆续开展7个碳排放交易试点等控制碳排放的重点措施。可见,广东省作为我国的经济强省,理应成为发展低碳经济的积极先行者和领导者。同时,为了加快低碳技术的进步及普及,缓解资源环境压力,协同减少二氧化碳等温室气体的排放,国家发改委于2014年制定《节能低碳技术推广管理暂行办法》。鉴于此,当一个地区或工业企业由于受到碳排放管制等政策约束而采用低碳技术来减少碳排放时,我们难免会质疑这些地区或工业企业是否会以降低经济增长和生产率为代价来换取碳排放的减少和环境质量的提高,即在促进经济发展与控制温室气体减排等环境保护方面能否否实现双赢?
传统观点认为,诸如碳排放管制等环境管制政策会额外耗费生产性资源,是以牺牲生产率提高和经济增长为代价的 (如Gray, 1987; Barbera and McConnell, 1990)。不过1991年“波特假说”的提出,重新审视了此观点,认为制定适宜且比较严格的环境管制政策能引致企业创新和技术进步 (Porter, 1991)。2014年世界银行报告也指出,通过实施低碳技术等政策,到2030年全球GDP可望每年额外增加高达2.6万亿美元或2.2%,防止约85亿公吨温室气体的排放①。节能减排的技术进步是提高广东地区工业的环境全要素生产率和实现双赢发展的核心动力 (王兵和杜敏哲,2013)。在节能减排约束下,地区工业要从根本上创新和改进污染处理技术及其生产技术,为此,广东省在强化科技支撑、研发推广低碳技术方面也做出了不少的努力,设立节能减排专项资金支持节能减排技术改造、应用和循环经济、资源综合利用、清洁生产项目。但是,政府相关的环境管制 (如碳排放管制等) 毕竟会增加企业购买治污设备和引进治污技术的减排成本。那么,利用这些低碳技术,一个地区或工业企业会产生多大的减排成本或者能否用较低的减排成本来实现双赢?
①引自http://www.tanpaifang.com/ditanjingji/2014/0709/35015.html。
为澄清以上几个问题,本文根据广东省21个地级市的要素资源投入、工业产出和碳排放污染数据,以低碳经济发展理念为出发点,设计出一个基于数据包络分析和方向性环境距离函数的低碳行为分析模型,并利用该模型衡量出环境中碳排放管制下地区工业的产值增长和碳排放减少潜力及其边际减排成本,并比较不同低碳技术下的工业生产率、效率和技术进步状况,这对于以低碳理念考察工业经济发展模式具有重要的理论与实践意义。
本文接下来的结构安排是:第二节综述有关环境管制与边际减排成本的国内外文献;第三节基于数据包络分析和方向性环境距离函数,拓展出一个低碳行为分析模型;第四节数据处理及其数据分析;第五节是实证结果的分析;第六节为结论。
二、 文献综述技术作为长期经济增长的驱动力,决定了经济活动的环境后果。如果一个工业企业使用低碳等清洁技术,这对于减缓资源环境压力发挥着重要的作用。但是,工业企业对环境污染物所采取的处理技术,不仅取决于自身的技术水平、对待污染物的态度、可用的资源投入,以及政府相关的环境管制政策等因素。“波特假说”认为,适宜且比较严格的环境管制政策能引致企业创新和技术进步,由此实施的节能减排技术可以为企业带来环境质量和生产率或经济增长同时提高的双赢发展机会,甚至会弥补环境管制所带来的减排成本 (Porter and Van der Linde, 1995)。此外,Greaker (2006)通过研究环境减排技术的外溢性,也发现在缺乏环境管制时,环境技术的供给不足会造成很高的环境R & D成本,但严格的环境管制会使得污染企业对环境技术的需求增加,刺激创新技术的供给,进而降低减排成本和获取减排红利。
虽然环境管制下的技术创新可为企业带来双赢,但环境管制并非“免费的午餐”,减排难免需要付出成本的。现有文献对污染物的边际减排成本或影子价格的研究,一方面,很多都通过距离函数法度量环境管制下环境污染物的边际减排成本或影子价格来分析环境管制带来的减排成本 (如Boyd et al., 2002;Choi et al., 2012;Wei et al., 2012;涂正革,2009;袁鹏和程施,2011;陈诗一,2011;刘明磊等,2011等)。涂正革 (2009)发现工业SO2的影子价格不仅取决于SO2变化的方向, 还与SO2排放的规模有很大的关系,排放规模处于较高水平时,影子价格较小,反之,影子价格较高。陈诗一 (2011)基于方向性距离函数构成的节能减排行为分析模型,度量了各行业因时而变的CO2排放的历史边际减排成本,并以此作为未来碳税征收税率大小的依据。Wei et al.(2012)运用SBM模型测算出我国1995-2007年29省份的碳排放减少潜力及其边际减排成本,东部碳排放效率最低和边际减排成本最高,而西部拥有最大的碳排放减少潜力和最低的边际减排成本。Choi et al.(2012)和Wang and Wei (2014)则利用非径向DEA方法对中国地区的碳排放边际减排成本测度分析,认为碳排放的边际减排成本与CO2排放效率成正相关关系。
另一方面,对污染排放与减排成本的研究,除了距离函数法外,还有学者利用关于能源经济的成本函数法分析。例如,Kuosmanen and Kortelainen (2007)和Kuosmanen et al.(2009)利用环境成本收益法 (ECBA) 研究了温室气体减排的环境政策对经济的影响,发现如果一个国家只关心以最低的经济成本进行温室气体减排,那么随着时间的推移,等量减少温室气体排放是首要的选择。Park and Lim (2009)通过对韩国发电厂的碳边际减排成本研究,发现韩国发电厂CO2平均影子价格为14.04欧元/吨。高鹏飞等 (2004)则应用能源、环境、经济耦合的中国MARKA-MACRO模型发现碳边际减排成本将随着减排率的提高而增大,而且越早开始实施碳减排的约束,在等同的减排量下,二氧化碳边际减排成本将越高。通过对污染物的边际减排成本测度后,也有学者继而分析污染排放量和技术变化等因素对边际减排成本曲线 (MACC) 的影响 (如Ellerman and Decaux, 1998;Baker et al., 2008;Loschel, 2004等)。一般情况下,边际减排成本随减排量上升而增加,通过对MACC求和或积分可得到总减排成本 (潘勋章等,2013)。Kuik et al.(2009)分析了由于温室气体减少政策和碳价格引致的技术进步对边际减排成本的影响,表明技术进步在2025年和2050年对碳排放的边际减排成本分别是呈现出增加和减少效应。
综观以上研究,一方面,虽然环境管制政策可以诱使企业技术创新和应用清洁的技术,但不同的环境政策会刺激企业技术革新的动力和方向 (Baker, 2008),而不同的技术变化方向使得经济活动对环境产生不同的影响 (Michida, 2006)。然而上述研究尚未厘清不同管制程度下企业可以采取的减排技术或者低碳技术的方向。如果环境管制不严或企业有足够优势进行谈判,那么企业或许不太会利用先进的技术进行减排,而是采取一般的技术把污染控制在既定的原有水平;相反,严格的管制会迫使企业利用先进的清洁技术或低碳技术,进而把污染排放减少至原有水平之下。另一方面,这些研究主要衡量和分析了环境管制下污染排放的边际减排成本曲线及其影响。虽然减排成本曲线是一个可以识别企业能否获得经济和环境的双赢的有效的环境治理方法 (Beaumont and Tinch, 2004),但它们忽略了环境管制下应该如何选择不同程度的低碳技术来以较低的边际减排成本实现环境保护和经济发展或者生产率增长的双赢前景。
针对以上的研究局限,本文试图从以下两个方面进行拓展研究:(1) 本文根据企业视环境政策的不同而捕获出三种不同减排程度的技术,即基准技术、弱低碳技术、强低碳技术。基准技术意味着企业利用传统的生产技术使得污染排放随着产出增加而增加,弱低碳技术意味着企业针对政府温和的环境管制政策而采取使得碳排放控制在既定的原有水平的低碳技术,强低碳技术则使得企业减少原有的碳排放量以适应政府严格的环境政策,从而设计出一个低碳行为分析模型。(2) 利用该模型,测度低碳技术下碳排放减少、产值增长、边际减排成本和生产率等指标,比较不同低碳技术下碳排放减少和产值增长变化及其碳排放边际减排成本的变化,以及减排技术是否有利生产率的提高,进而分析工业能否以较低的减排成本实现环境与经济的双赢。
三、 研究方法 (一) 环境技术模型在经济与社会的可持续发展中,资源与环境不仅是促进经济发展的内生变量,而且还是制约经济发展规模和经济增长速度的因素 (王兵等,2010)。为了将资源和环境因素纳入经济增长核算的分析框架中,本文利用Färe et al. (2007)提出的环境技术 (Environmental Technology),构造出一个既包括生产投入、期望产出 (如地区生产总值,GRP等),又包括伴随生产过程而产生的环境污染物 (如CO2等) 等非期望产出的联合生产可能性集合①:
| $S\left(t \right) = \left\{ {\left({{L^t}, {K^t}, {E^t}, {Y^t}, {C^t}} \right):\left({{L^t}, {K^t}, {E^t}} \right)能够产生\left({{Y^t}, {C^t}} \right)} \right\}$ | (1) |
①该生产可能性集合满足闭集和有界集、“好”产出和投入是自由可处置、零结合公理以及产出弱可处置性公理。
其中,L、K、E分别表示劳动、资本和能源要素投入,Y、C分别表示生产过程中的期望产出 (如GRP) 和非期望产出 (如CO2排放量)。
假设生产技术在规模报酬不变 (CRS) 条件下,运用数据包络分析 (DEA) 可以将t期的联合生产可能性集合转化为如下的环境技术模型:
| $\begin{gathered} S\left( t \right) = \hfill \\ \left\{ {\left( {{Y^t},{C^t}} \right):\sum\limits_{i = 1}^I {z_i^tY_i^t \geqslant Y,} \sum\limits_{i = 1}^I {z_i^tC_i^t = C,\sum\limits_{i = 1}^I {z_i^tL_i^t \leqslant L,\sum\limits_{i = 1}^I {z_i^tK_i^t \leqslant K,} \\ \sum\limits_{i = 1}^I {z_i^tE_i^t \leqslant E,} } } z_i^t \geqslant 0} \right\} \hfill \\ \end{gathered} $ | (2) |
其中,i表示每个观测值;zkt表示每一个横截面观察值的权重,zkt≥0表示规模报酬不变。t+1期的环境技术Tt+1只需将式 (2) 的t改为t+1。
(二) 低碳行为分析模型传统的生产函数并不能同时刻画期望产出和非期望产出随着生产过程中各种环境技术的变化而变化,因此,Chambers et al.(1996)依据Luenberger (1992)短缺函数的思想,构造了方向性距离函数。该函数衡量了观测值到生产边界上的距离,可以有效地评估一个经济体的经济和环境绩效。以当期环境技术作为参考技术,基于产出导向型 (output-oriented) 的方向性环境距离函数可定义为:
| $\vec D_o^t\left({{L^t}, {K^t}, {E^t}, {Y^t}, {C^t};g} \right) = \sup \left\{ {\beta :\left({{Y^t}, {C^t}} \right) + \beta g \in S\left(t \right)} \right\}$ | (3) |
其中,式 (3) 中方向向量g表示期望产出和非期望产出同比例增减的方向。
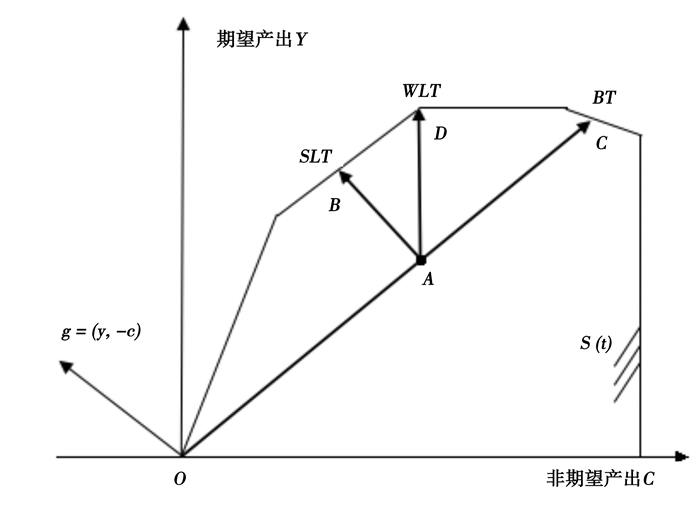
当企业尚未受到相关的碳排放管制或征收类似排污费用等措施制约时,这些企业自然不会增加额外的资金、人力等成本来减少CO2排放,那么碳排放量将会随着企业总产值的增加而上升,本文把此时这些企业采取的生产技术称之为基准技术 (Baseline Technology, BT),即忽视环境保护的传统生产技术。如图 1所示,期望产出与非期望产出在同一方向同比例扩增,即生产由A点移向C点。传统的经济学理论认为,污染排放作为一种非期望产出,具有弱可处置性的,即减少碳排放是需要成本的。那么此基准技术下的方向性距离函数表示为:
|
图 1 产出导向型的方向性环境距离函数 |
| $\begin{array}{*{20}{l}} {\vec D_{{\rm{BT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right) = Max\;\beta _{BT}^w}\\ {s.t.\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tY_i^t \ge Y_i^{t"}\left({1 + \beta _{BT}^w} \right)} } ;\;\;\;\;\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tC_i^t \ge C_i^{t"}\left({1 + \beta _{BT}^w} \right)} } ;}\\ {\;\;\;\;\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tL_i^t \le L_i^{t"};\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} } \sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tK_i^t \le K_i^{t"};} } }\\ {\;\;\;\;\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tE_i^t \le E_i^{t"};\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} z_k^t \ge 0, \;\;\;\;i = 1, \ldots, I, \;\;\;\;t = 1, \ldots, T} } \end{array}$ | (4) |
然而,如果政府为了实现该地区的低碳经济发展模式,对该地区的工业企业进行环境管制。那么,该地区工业企业对环境污染物是弱可处置的,对其进行处理是需要付出成本的,如消耗劳动、资本等投入要素,或者通过节约能源消耗来减少污染物排放。在这种政策环境下,所有的工业企业都希望能革新现有的生产技术,采用更加清洁的低碳技术来实现工业总产值的增加和碳排放的减少的双赢发展。它们创新和使用清洁的技术,将会可能导致企业的碳排放水平出现两种结果,即要么保持原有的碳排放水平,要么减少碳排放量至原有水平之下。对于前者,如图 1,生产者能同时增加期望产出和保持非期望产出不变,即生产由A点移向D点,其对应的碳排放减少技术称之为弱低碳技术 (Weak Low-Carbon Technology, WLT),对应的碳排放管制政策称之为温和的低碳政策,其意味着适宜的低碳政策会诱导企业采取弱低碳技术。在非期望产出具有弱可处置性时,对应的方向性距离函数表示为:
| $\begin{array}{*{20}{l}} {\vec D_{{\rm{WLT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right) = Max\;\beta _{WLT}^w}\\ {s.t.\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tY_i^t \ge Y_i^{t"}\left({1 + \beta _{WLT}^w} \right)} } ;\;\;\;\;\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tC_i^t = C_i^{t"}} } ;}\\ {\;\;\;\;\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tL_i^t \le L_i^{t"};\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} } \sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tK_i^t \le K_i^{t"};} } }\\ {\;\;\;\;\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tE_i^t \le E_i^{t"};\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} z_k^t \ge 0, \;\;\;\;i = 1, \ldots, I, \;\;\;\;t = 1, \ldots, T} } \end{array}$ | (5) |
对于后者,如果企业采取更加先进和清洁的技术,使得企业能同时增加总产值和减少碳排放。如图 1,生产由A点移向B点,生产者能同时增加期望产出和减少非期望产出,其对应的碳排放减少技术称之为强低碳技术 (Strong Low-Carbon Technology, SLT),对应的碳排放管制政策称之为严格的低碳政策,其意味着严格的低碳政策会诱导企业采取强低碳技术。在非期望产出具有弱可处置性时,对应的方向性距离函数表示为:
| $\begin{array}{*{20}{l}} {\vec D_{{\rm{SLT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right) = Max\;\beta _{SLT}^w}\\ {s.t.\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tY_i^t \ge Y_i^{t"}\left({1 + \beta _{SLT}^w} \right)} } ;\;\;\;\;\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tC_i^t = C_i^{t"}} } \left({1 - \beta _{SLT}^w} \right);}\\ {\;\;\;\;\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tL_i^t \le L_i^{t"};\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} } \sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tK_i^t \le K_i^{t"};} } }\\ {\;\;\;\;\;\sum\limits_{t = 1} {\sum\limits_{i = 1}^I {z_i^tE_i^t \le E_i^{t"};\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} z_k^t \ge 0, \;\;\;\;i = 1, \ldots, I, \;\;\;\;t = 1, \ldots, T} } \end{array}$ | (6) |
根据上述的低碳行为分析模型,本文可以测度出工业企业采用的生产技术由基准技术转为弱或强低碳技术后的潜在产值增长变化 (PTG):
| $PTG_{BT}^{WLT, t} = {Y^t} \times \left\{ {\vec D_{{\rm{WLT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right) - \vec D_{{\rm{BT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)} \right\}$ | (7) |
| $PTG_{BT}^{SLT, t} = {Y^t} \times \left\{ {\vec D_{{\rm{SLT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right) - \vec D_{{\rm{BT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)} \right\}$ | (8) |
同理,本文也可以测度出工业企业采用的生产技术由基准技术转为弱或强低碳技术后的潜在碳排放减少变化 (PCR):
| $PCR_{BT}^{WLT, t} = {C^t} \times \vec D_{{\rm{BT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)$ | (9) |
| $CR_{BT}^{SLT, t} = {C^t} \times \left\{ {\vec D_{{\rm{SLT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right) + \vec D_{{\rm{BT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)} \right\}$ | (10) |
目前对边际减排成本的测算主要有两种方法:成本函数法和距离函数法。参照Boyd et al.(2002)、陈诗一 (2011)利用距离函数对控制排放在既定水平和标准节能减排行为两种政策下边际减排成本 (Marginal abatement cost,MAC) 的计算方法,本文可度量出工业企业采用的生产技术由基准技术转为弱或强低碳技术后二氧化碳排放的边际减排成本,即在适宜或严格的低碳政策下每减排一个单位二氧化碳需要牺牲的工业总产值大小:
| $MAC_{BT}^{WLT, t} = \frac{{{Y^t} \times \left\{ {\vec D_{{\rm{BT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right) - \vec D_{{\rm{SLT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)} \right\}}}{{{C^t} \times \vec D_{{\rm{BT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)}}$ | (11) |
| $MAC_{BT}^{SLT, t} = \frac{{{Y^t} \times \left\{ {\vec D_{{\rm{BT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right) - \vec D_{{\rm{SLT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)} \right\}}}{{{C^t} \times \left\{ {\vec D_{{\rm{SLT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right) + \vec D_{{\rm{BT}}, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)} \right\}}}$ | (12) |
在上述给定的低碳行为分析模型下,依据Chung et al. (1997),基于t期和t+1期之间的基准技术下的Malmquist-Luenberger (ML) 生产率指数及其分解可定义为:
| $\begin{array}{l} M{L_{BT}} = {\left[ {\frac{{1 + \vec D_{BT, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)}}{{1 + \vec D_{BT, w}^t\left({L_i^{t + 1}, K_i^{t + 1}, E_i^{t + 1}, Y_i^{t + 1}, C_i^{t + 1};{g^{t + 1}}} \right)}} \times \frac{{1 + \vec D_{BT, w}^{t + 1}\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)}}{{1 + \vec D_{BT, w}^{t + 1}\left({L_i^{t + 1}, K_i^{t + 1}, E_i^{t + 1}, Y_i^{t + 1}, C_i^{t + 1};{g^{t + 1}}} \right)}}} \right]^{\frac{1}{2}}}\\ \;\;\;\;\;\;\;\;\;\; = \frac{{1 + \vec D_{BT, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)}}{{1 + \vec D_{BT, w}^{t + 1}\left({L_i^{t + 1}, K_i^{t + 1}, E_i^{t + 1}, Y_i^{t + 1}, C_i^{t + 1};{g^{t + 1}}} \right)}}\\ \;\;\;\;\;\;\;\;\;\; \times {\left[ {\frac{{1 + \vec D_{BT, w}^{t + 1}\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)}}{{1 + \vec D_{BT, w}^t\left({L_i^t, K_i^t, E_i^t, Y_i^t, C_i^t;{g^t}} \right)}} \times \frac{{1 + \vec D_{BT, w}^{t + 1}\left({L_i^{t + 1}, K_i^{t + 1}, E_i^{t + 1}, Y_i^{t + 1}, C_i^{t + 1};{g^{t + 1}}} \right)}}{{1 + \vec D_{BT, w}^t\left({L_i^{t + 1}, K_i^{t + 1}, E_i^{t + 1}, Y_i^{t + 1}, C_i^{t + 1};{g^{t + 1}}} \right)}}} \right]^{\frac{1}{2}}}\\ \;\;\;\;\;\;\;\;\;\; = EFFC{H_{BT}} \times TEC{H_{BT}} \end{array}$ | (13) |
对于弱或强低碳技术下的ML生产率指数及其分解的定义类似,其中,ML、EFFCH、TECH分别表示全要素生产率变化指数、技术效率变化指数和技术进步指数。对此,本文利用序列DEA测算这三个指标,并比较和分析下工业企业采取两种不同的低碳技术 (即适宜的或严格的低碳政策) 的经济与环境绩效。
四、 数据来源及处理 (一) 投入产出指标的选择与处理按照上述研究方法,我们选取2000-2010年广东省21个地级市的全部国有及规模以上非国有工业作为为研究对象,在《广东统计年鉴》和各地级市统计年鉴中选取了能源、资本和劳动力作为投入要素,工业总产值作为期望产出,CO2排放量作为非期望产出。
1.劳动投入。依据国外的研究,衡量劳动投入的最准确的指标应当是工业从业人员的有效劳动时间。但由于我国对劳动时间统计数据的缺乏,本文选择2000—2010年广东省21个地级市规模以上工业从业人员平均人数表示劳动投入量。
2.资本投入。本文选择各地级市工业的固定资产净值平均余额作为资本投入量 (李小平和朱钟棣,2005)。其基本思路是首先是按照国家统计局固定资产投资统计司的方法对对固定资产投资价格指数进行推算;接着以2005年为基期,利用固定资产投资价格指数折算出可比价的2000年固定资产净值平均余额Kt0;然后基于固定资产净值原值计算固定资产名义净投资额;最后,我们对各市2000-2010的固定资产净值平均余额进行如下计算,从而得出t年的实际资本存量Kt:
| ${K_t} = {K_{t0}} + \sum\limits_{{t_0} \pm 1}^t {\Delta {K_t}/{P_i}\left(t \right)} $ | (14) |
3.能源投入。能源 (尤其是化石能源) 不仅仅是工业企业生产过程中的中间投入要素,更是环境污染物 (如CO2排放) 的主要来源。本文选择广东各省21个地级市统计年鉴中提供的2000—2010年规模以上工业能源消费总量作为能源投入量。其中,东莞市的能源数据来自于《东莞市能源保障“十二五”规划》。为了统一计算口径,本文选择的能源消费量是经过能源折标准煤参考系数折算出的能源消费总量。
4.期望产出。由于本文在上述的投入指标中选取了具有中间投入品性质的能源消费量 (陈诗一,2009、王兵和杜敏哲,2013),所以本文选取工业总产值作为期望产出指标,同时利用各地区工业品出厂价格指数对其进行平减,构造出以2005年为可比价的2000-2010年实际工业总产值数据。
5.非期望产出。由于我国并没有官方统计的CO2排放量数据,而世界银行指出CO2主要源于原煤、洗精煤、焦炭、原油、煤油、汽油、燃料油、天然气等化石能源或一次性能源的消耗而排放在大气。根据《2006年IPCC国家温室气体清单指南》提供的各种能源i的平均低位发热量NCV、碳排放系数CEF和碳氧化因子COF,我们可利用此指南中的公式对CO2排放进行估算:
| $C{O_2} = \sum\limits_{i = 1}^{\rm{n}} {C{O_{2, i}}} = \sum\limits_{i = 1}^{\rm{n}} {{E_i} \times NC{V_i}} \times CE{F_i} \times CO{F_i} \times \left({44/12} \right)$ | (15) |
为了便于探索低碳行为分析模型对各市及各经济区域工业经济的影响,本文根据广东省四大经济区域划分的方法,划分为珠三角地区、东翼地区、西翼地区以及粤北山区①,表 1给出了相关数据的统计概述。
①珠三角地区:广州、深圳、佛山、珠海、东莞、中山、惠州、江门、肇庆;东翼地区:汕头、汕尾、潮州、揭阳;西翼地区:湛江、茂名、阳江;粤北山区:清远,韶关、河源、梅州、云浮。
| 表 1 广东21个地级市工业投入产出变量 (2000-2010) |
1.工业的快速增长与能源消费量缓慢增长和CO2排放增长缓慢。
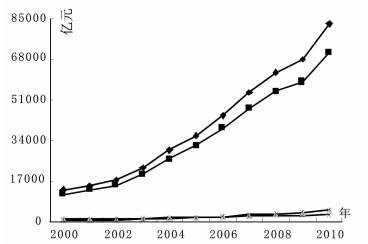
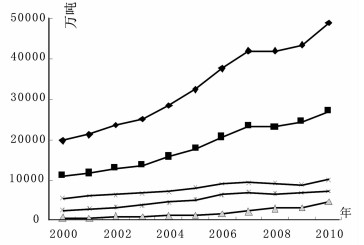
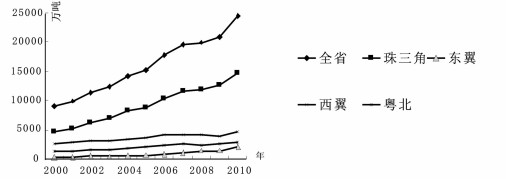
由图 2.a看出,以2005年作为不变价格,全省工业总产值从2000年的13124.84亿元增长到2010年的82878.06亿元,10年翻了三翻以上,年均增长19.08%。而在工业快速发展的同时,能源消费和CO2排放也缓慢增长。广东工业在2000-2010年间能源从9116.65万吨增长到24519.38万吨,年均增长8.89%;CO2排放从19715.75万吨增加至48747.94万吨,年均增长6.33%。从能源消费、CO2排放增长趋势图中发现,CO2排放与能源消费几乎一直保持着相似的增长趋势。2007-2009年能源消费和CO2排放增长最缓慢,这主要由于这几年新能源及新减排技术的不断开发与利用,使得两者增长减缓;但2009年后一改减缓的增长趋势,呈现出大幅度的反弹,工业能源消费和CO2排放伴随着工业总产值的高速增长而增长。从工业能源消费和CO2排放的地区分布来看,2000-2010年能源消费和CO2排放总量 (或者增长率) 最高的是珠三角地区,其它3个经济区域相对低很多。总体上,CO2排放的速度远远低于工业的快速增长速度。
|
图 2.a 工业总产值增长趋势 (2000-2010) |
|
图 2.b 工业CO2排放量 (2000-2010) |
|
图 2.c 工业能源消费量 (2000-2010) |
2.工业总产值增长的CO2排放弹性。
为了比较工业增长与CO2排放之间的静态关系,本文计算了2000年至2010年工业增长对CO2排放的弹性,即工业总产值每增长1%,CO2排放增加的比率。广东21市的地区工业CO2排放弹性平均值为0.89。其中,广州、深圳、东莞、中山、肇庆、清远、云浮在工业快速增长的同时,CO2排放弹性都比较低,保持在1以内。产出CO2排放弹性最严重的地区是河源 (1.15)、惠州 (1.17) 和揭阳 (1.19)。
从产出CO2排放弹性可以大概知道工业经济增长与CO2排放的静态关系,下文将基于低碳行为分析模型深入解析低碳技术、工业经济增长与CO2排放之间的动态关系。
| 表 2 各地区工业产出的CO2排放弹性 |
从理论上来说,适宜的或者基于经济激励导向的严格环境管制从较长时期来看可以激发创新、促进节能减排技术或新能源技术的研发、改进生产无效性和提高投入生产率,最终部分或全部抵消短期执行环境管制的成本 (陈诗一,2010)。换句话而言,如果工业企业的生产技术从原来的传统技术转变为清洁的低碳技术,这会导致技术进步和生产率提高,最终会使得这些企业拥有碳排放减少和工业总产值增加的潜力,而这些潜力所带来的效益会有利于抵消碳排放的减排成本。利用低碳行为分析模型,本文测度出2001-2010年广东省各地区工业总产值和碳排放在强弱不同的低碳技术下的潜在变化的平均结果 (如表 3)。
| 表 3 低碳技术下工业的潜在产值增长和潜在碳排放减少结果 (2001-2010) |
从表 3来看,不同低碳技术下的潜在产值增长和潜在碳排放减少的趋势分布都呈现出一定的规律性。随着企业受环境约束而采取低碳技术的提高或低碳政策的严格,潜在产值增长和潜在碳排放减少幅度是逐步上升的,其中潜在产值增长由全省的年均152亿元提高至316亿元,潜在碳排放减少的幅度最大,由弱低碳技术下全省的年均133万吨上升至强低碳技术下的787万吨。可见,工业生产技术的创新与进步会创造出更大的产值增长和碳排放减少的空间。具体到各个地区工业而言,深圳和惠州分别在2001-2005年、2006-2010年潜在产出增减变化为0,茂名在弱低碳技术下的潜在产值增长和潜在碳排放减少均为0,表明这三个地区工业在最佳的生产实践边界上,它们在这些时期都已充分利用企业的资源 (如劳动、资本、能源等) 和有效率地生产。大部分地区在强低碳技术下比弱低碳技术下能获得更高的潜在产值增长量,如珠三角的广州、珠海、佛山、东莞、惠州、江门、西翼的阳江、湛江、茂名、粤北的韶关、梅州、清远和云浮。而所有地区都在强低碳技术下比弱低碳技术下能获得更高的潜在碳排放减少量,且在强低碳技术下珠三角地区 (780万吨) 比西翼 (964万吨) 和粤北 (948万吨) 地区的潜在碳排放减少量更少,说明强低碳技术下珠三角地区碳排放的无效率水平较低,但在弱低碳技术下,珠三角地区碳排放的无效率水平是最高的。由此可见,所有的地区工业都应该尽可能地提高低碳技术水平,降低生产和碳排放的无效率,从而促进产值的增加和碳排放的减少;同时,在利用更强的低碳技术来减少碳排放等污染物或受到更严厉的低碳发展政策约束时,经济发展水平越高的地区 (如珠三角地区) 越会得到更高的潜在产值增长,王兵、杜敏哲 (2013)也发现经济较为发达的珠三角地区工业是节能减排的最大获利者,这与珠三角地区拥有更大的节能减排技术的比较优势以及更多的资金投入有关。
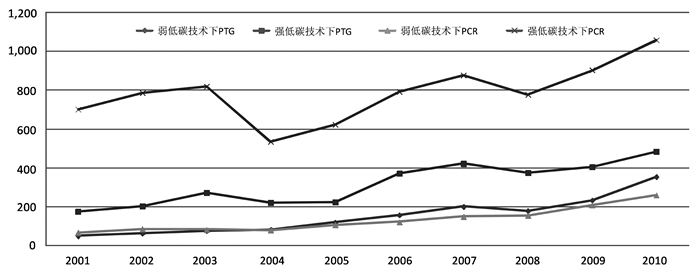
在不同的低碳技术下,表 3显示广东工业的潜在产值年均增长幅度分别从2001-2005年的79、220亿元增加到2006-2010年的226、412亿元,潜在碳排放年均减少分别从2001-2005年的85、693万吨到2006-2010年的180、881万吨。从每个时段的平均结果难以探析各个时期的具体变化状况及其原因,图 3报告了在强弱两种不同的低碳技术下广东工业在2001-2010年的潜在产出结果。从2001年至2010年,无论工业企业使用何种低碳技术或政府实施适宜还是严格的低碳政策,广东工业的潜在产值增长和潜在碳排放减少的幅度呈现出波动上升的趋势。其中,由弱低碳技术转为强低碳技术,工业的潜在碳排放减少幅度远远大于潜在产值增长的幅度。特别需要说明的是,潜在产出变化在2004年出现了较大幅度的下降,究其原因,主要是2004年广东重工业的企业数突然由2003年的9660家增加至14879家①,增长54%左右,重工业化程度加深,这一时期的能耗和碳排放污染量等迅速抬高,导致工业企业现有的技术水平难以改变和提升现有的生产水平和碳排放等污染减少的空间。这与陈诗一 (2012)发现本世纪初以来的经济高速增长以及能耗和污染排放的疯狂飙升导致2003-2005年中国低碳经济转型掉入了历史低谷的研究结论相似。在2008年,潜在产值增长和潜在碳排放减少的幅度都出现了小幅回落,这反映出国际金融危机对工业企业的冲击。
①数据来源于2005年《广东统计年鉴》。
|
图 3 低碳技术下广东工业的潜在产值增长和碳排放减少结果 (2001-2010) |
综合表 3与图 3,不管企业采用弱低碳技术还是强低碳技术,或者政府实施适宜的还是严格的低碳政策,工业企业都能实现在潜在产值增加的同时,减少碳排放量。也就是说,在低碳技术下,工业企业既能保持产值增长,又能减少环境污染,创造出一个提质增效型的双赢发展机会。并且,企业采取更强的低碳技术或政府制定更为严格的低碳政策会降低生产的无效率,这会更有利碳排放等环境污染物的减少和经济的增长,双赢前景更为可观。包群等 (2013)也发现,只有在环保执法力度严格,通过环保立法才能起到明显的环境改善效果。
(二) 碳排放的边际减排成本工业企业可以采取低碳技术能实现经济与环境的双赢,其带来的经济效益可以弥补甚至超过由环境管制所带来的经济成本 (Porter and Van der Linde, 1995),这也意味着不可以零成本地减少碳排放等污染物。表 4报告了低碳技术下2001-2010年广东各地区工业碳排放的边际减排成本的平均结果。
| 表 4 低碳技术下工业碳排放的边际减排成本结果 (2001-2010) |
碳排放的边际减排成本大小决定了企业创新和利用低碳技术的动力。如表 4,几乎所有地区 (汕尾、茂名除外) 在弱低碳技术下需要为碳排放付出的边际减排成本都要比强低碳技术下的边际减排成本要高,这揭示了当企业受到严格的低碳政策或环境管制约束且有能力采取更加先进的低碳技术进行生产时,企业理应尽量利用自已先进的低碳技术来尽可能地降低碳排放的边际减排成本。不过,各地区碳排放的边际减排成本存在较大差异,这与碳排放强度存在一定负相关性,二氧化碳排放强度越高的地区,减排成本一般也越低,说明继续进行减排的难度会更大 (刘明磊等,2011)。当工业企业的生产技术由弱低碳技术转为强低碳技术后,全省工业碳排放的边际减排成本平均从0.8035万元/吨降至0.3158万元/吨,其中粤北地区碳排放边际减排成本的下降幅度最大 (平均1.3796万元/吨降至0.2330万元/吨),其次是西翼地区 (平均0.5844万元/吨降至0.1698万元/吨)、东翼地区 (平均0.7711万元/吨降至0.3863万元/吨),降幅最小的是珠三角地区,这表明经济和技术相对落后的粤北、西翼、东翼地区具有很大的低碳技术
提升的空间,如果它们加大技术创新和引进的资金投入,提高该地区的生产和减排技术水平,缩小与珠三角地区的技术差异,这三个区域将会以较低的减排成本来获得较大的经济效益。当然,如果企业受到严格的环境管制且没有相应的减排技术时,其面临的减排成本是相当大。细心发现,在工业潜在碳排放减少相对较大的地区往往具有较低的碳排放边际减排成本,例如,在强低碳技术下,潜在碳排放减少最大的是西翼,最小的是东翼,而碳排放边际减排成本最大的是东翼,最小是西翼,对于弱低碳技术下也表现出类似的现象,这与Choi et al.(2012)和Wei et al.(2012)的研究发现相似。在弱低碳技术下,相对于“十五”期间 (2001-2005年),大部分地区在“十一五”期间 (2006-2010年) 的碳排放边际减排成本提高了,如广州、惠州、佛山、东莞、江门、肇庆、汕头、潮州、揭阳、河源、茂名等地区,而西翼的湛江、粤北的韶关、梅州、清远等地区的成本下降得较为明显。不过,在强低碳技术下,除深圳、阳江、河源和汕尾外,其他地区在“十一五”期间的的碳排放边际减排成本都要比“十五”期间的要高。
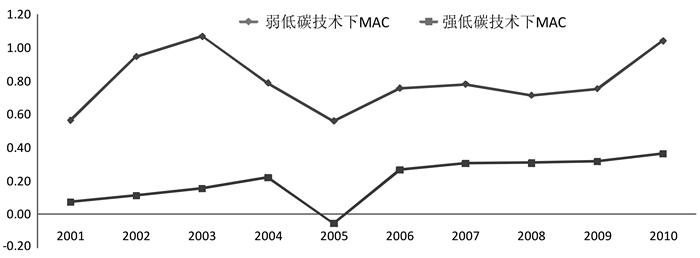
图 4描述了2001年至2010年广东省工业在两种不同的低碳技术水平下碳排放的边际减排成本波动上升的趋势,其基本上与潜在产值增长和潜在碳排放减少变化的趋势相近,且伴随着技术的进步,强低碳技术下的边际减排成本一直低于弱低碳技术下的边际减排成本。全省碳排放边际减排成本分别由2001年的0.5637、0.0724万元/吨增加至1.0438、0.3637万元/吨,其中2005年跌至最低,2005年后继续上升。Choi et al.(2012)发现我国碳排放的边际减排成本从2001年至2002年持续上升,2003、2004年则出现下降,而后其成本继续上升;Wei et al.(2012)也发现中国碳排放的边际减排成本由1995年开始上升至2002年的最高点,2002年后则出现下降,并认为这是我国2002年后城镇化和工业化积累而导致的结果 (Liao et al., 2007)。如前所述,广东在2004年重工业化进程迅速加速,所以我们的研究结果也与现有研究一致。随着碳排放边际减排成本的不断上升,广东省对二氧化碳等污染物排放的管制也会面临较大的压力。在刚开始采用尚未成熟的或先进的低碳技术来减缓碳排放时,工业企业难以避免会付出较大的代价,但随着低碳技术的成熟与深化,技术的创新与进步会给工业以较低的成本带来很大的碳排放等污染降低的空间,从而更好地应对政府实行严格的环境管制或低碳政策。同时,以上的结果也表明了工业企业可以使用较低边际减排成本的强低碳技术来实现环境保护和经济发展的双赢。
|
图 4 广东省碳排放的边际减排成本MAC:2001-2010 |
上文从总量上分析低碳技术下碳排放与工业经济发展的双赢发展状况,说明了温和的或严格的低碳政策诱导企业使用的弱或强的低碳技术会同时实现碳排放减少与工业经济增长。但是,采用清洁和先进的低碳技术措施可能会高估环境 (碳排放) 管制带来的经济成本,因为这样的减排可能会提高生产率。为了澄清低碳技术减排是否有利于生产率的提高的问题,表 5比较了2001-2010年广东省各地区工业分别在基准技术、弱低碳技术和强低碳技术下的生产率、效率和技术进步的平均结果。
| 表 5 低碳技术下各地区工业的生产率及其分解的平均结果 (2001-2010) |
根据表 5,整体而言,相比于基准技术 (即不控制污染排放的传统生产技术),两种低碳技术下的工业生产率、效率和技术进步指数在总体上都得到了较大的提高。且随着低碳技术的提高或需要面对的环境管制强度的增强,工业的生产率、效率和技术进步指数也随之提高,这也与Murty and Kumar (2003)、王兵等 (2008)的研究结论一致。在两种低碳技术下,全省工业的生产率比基准技术下的生产率分别年均增长2.77%和6.73%,效率分别年均增长0.11%和0.57%,技术进步率分别年均增长2.73%和6.22%。可见,技术进步对生产率的提高贡献最大,由低碳行为引起的吸收前沿生产技术的追赶效应并不明显,技术进步已成为工业生产率提高的重要驱动力。上述结果意味着,工业企业应通过创新和提高低碳技术水平,这样才能使得环境管制不仅不会降低生产率,反而能为工业经济的增长和环境的改善提供切实的保证。而对于相关的环境政策制定者来说,它们理应制定适宜且严格的低碳政策来促使工业经济获取提高环境质量和生产率增长的双赢结果。值得说明的是,在环境管制下,利用低碳技术进行碳减排,的确有利于生产率的提高;但环境管制并非“免费的午餐”,由管制引起的生产率增长收益也不一定能够完全抵消环境管制的经济成本 (李树、陈刚,2013)。
具体而言,采用更加先进和清洁的强低碳技术对经济发展较为落后的西翼和粤北地区的工业生产率、效率和技术进步的促进作用更大,尤其是湛江、茂名、梅州和清远等地区。在低碳技术的推动下,东翼、西翼和粤北地区的生产率、效率和技术进步率都表现出随着低碳技术的增强而递增的态势,而珠三角部分地区则并不明显。东翼地区的生产率由弱低碳技术下的年均增长3.04%提高至强低碳技术下的8.37%,西翼地区由年均增长6.21%提高至12.44%,粤北地区由年均增长5.56%提高至18.92%,这说明了东翼、西翼和粤北地区更加要利用清洁的强低碳技术来控制碳排放,提高工业的生产率。而珠三角地区在2001-2010年间生产率、效率和技术进步率在两种不同的技术下分别年均增长10.63%和8.12%、1.04%和0.58%、9.4%和7.59%,强弱低碳技术下三个指标之间相差并不大,但它们都高于基准技术下度量出的数值,这意味着珠三角地区为兼顾较低的减排成本,应该采取弱偏强的低碳技术来应对温和偏向严格的环境管制政策,以使其生产更有效率。
六、 结论为缓解资源环境压力,减少二氧化碳等温室气体的排放,以资源高效利用为前提,以低碳技术为核心的低碳经济转型已势在必行。对于政府,它们会针对污染企业出台一系列的限制环境污染物排放、碳税等管制政策;而对于企业,创新和应用诸如低碳的技术是企业持续发展与提升竞争力的关键。理论上,严格的环境管制能够诱导企业技术创新,提高生产率和环境质量。虽然由管制带来的双赢效益不一定能够完全弥补由环境管制引起的减排成本,但由于采用先进的低碳技术,企业以较低的减排成本实现双赢也未尝不可。因此,本文根据广东省21个地级市的要素资源投入、工业产出和碳排放污染数据,以低碳经济发展理念为出发点,设计出一个基于方向性环境距离函数的低碳行为分析模型,探析了在强弱不同的低碳技术下边际减排成本与工业经济的双赢发展问题。
基于产出增减潜力的角度表明,随着企业受环境约束而采取低碳技术的提高或低碳政策的严格,潜在产值增长和潜在碳排放减少幅度是逐步上升的。同时,在利用更强的低碳技术来减少碳排放等污染物或受到更严厉的低碳发展政策约束时,由于各地区的经济基础和资源禀赋的差异,经济发展水平越高的地区 (如珠三角地区) 越会得到更高的潜在产值增长。
基于碳排放的边际减排成本的结果表明,几乎所有地区 (汕尾、茂名除外) 在弱低碳技术下需要为碳排放付出的边际减排成本都要比强低碳技术下的边际减排成本要高,这揭示了当企业受到严格的低碳政策或环境管制约束且有能力采取更加先进的低碳技术进行生产时,企业理应尽量利用自已先进的低碳技术来尽可能地降低碳排放的边际减排成本。同时,在各种低碳技术下,工业生产率、效率和技术进步指数在总体上都得到了较大的提高,且随着低碳技术的提高或需要面对的环境管制强度的增强而提高。总而言之,工业企业从减少碳排放等污染、提高生产率和较低的减排成本这几方面考虑,工业企业应该利用强低碳技术实行碳排放的真正减少,而不是把碳排放维持在既定的原有排放水平,从而应用较低边际减排成本的强低碳技术来实现环境保护和经济发展的双赢。
因此,为加速工业的低碳经济发展进程,首先要强化科技支撑,研发推广低碳技术。重点开展科技促进工业节能减排,加大基础性研究、开放合作以及产学研结合的力度,进一步推进低碳领域的试点工作。其次,实行低碳政策要统筹和兼顾地区间经济基础、资源禀赋和技术等差异,采取切实有力的措施向经济欠发达或技术落后的地区转移技术或资本投入,共同促进节能减排。最后,强化低碳技术不仅要考虑新兴战略产业等产业之间的结构、以及地区间重工业和轻工业之间能源消耗结构,还要适应政府对相关行业的环境管制政策。
当然,需要说明的是,本文对低碳技术只划分出强弱两种,在一定程度上会影响地区间差异分析的准确性。另外,影响低碳经济发展中碳排放的因素不只是技术或环境管制强度,还受到各地区的资源禀赋、现有的能源结构、产业结构,以及碳减排目标的影响,这些为我们的后续研究提供了方向。
| [] | Baker, E. , Clarke, L. and Shittu, E. , 2008, "Technical Change and The Marginal Cost of Abatement". Energy Economics, 30, 2799–2816. DOI:10.1016/j.eneco.2008.01.004 |
| [] | Barbera, A. J. and McConnell, V.D. , 1990, "The Impact of Environmental Regulation on Industry Productivity: Direct and Indirect Effects". Journal of Environmental Economics and Management, 18, 50–65. DOI:10.1016/0095-0696(90)90051-Y |
| [] | Beaumont, N. J. and Tinch, R. , 2004, "Abatement Cost Curves: A Viable Management Tool for Enabling the Achievement of Win-Win Waste Reduction Strategies?". Journal of Environmental Management, 71(3), 207–215. DOI:10.1016/j.jenvman.2004.03.001 |
| [] | Boyd, G. A. , Tolley, G. and Pang, J. , 2002, "Plant Level Productivity, Efficiency and Environmental Performance of the Container Glass Industry". Environmental and Resource Economics, 23, 29–43. DOI:10.1023/A:1020236517937 |
| [] | Chambers, R. G. , Chung, Y. and Färe, R. , 1996, "Benefit and Distance Functions". Journal of Economic Theory, 70(2), 407–419. DOI:10.1006/jeth.1996.0096 |
| [] | Choi, Y. , Zhang, N. and Zhou, P. , 2012, "Efficiency and Abatement Costs of Energy-related CO2 Emissions in China: A Slacks-based Efficiency Measure". Applied Energy, 98, 198–208. DOI:10.1016/j.apenergy.2012.03.024 |
| [] | Chung, Y. H. , Färe, R. and Grosskopf, S. , 1997, "Productivity and Undesirable Outputs: A Directional Distance Function Approach". Journal of Environmental Management, 51, 229–240. DOI:10.1006/jema.1997.0146 |
| [] | Ellerman, D. A. and A. Decaux, 1998, "Analysis of Post-Kyoto CO2 Emission Trading Using Marginal Abatement Curves," Report 40, Massachusetts Institute of Technology, Joint Program on the Science and Policy of Global Change. |
| [] | Färe, R. , Grosskopf, S. and Pasurka, C.A. , 2007, "Environmental Production Functions and Environmental Directional Distance Functions". Energy, 32, 1055–1066. DOI:10.1016/j.energy.2006.09.005 |
| [] | Gray, W. B. 1987, "The Cost of Regulation: OSHA, EPA and the Productivity Slowdown". American Economic Review, 77(5), 998–1006. |
| [] | Greaker, M. 2006, "Spillovers in the Development of New Pollution Abatement Technology: A new look at the Porter-hypothesis". Journal of Environmental Economics and Management, 52, 411–420. DOI:10.1016/j.jeem.2006.01.001 |
| [] | Kuik, O. , Brander, L. and Tol, R. , 2009, "Marginal abatement costs of greenhouse gas emissions: A meta-analysis". Energy Policy, 37, 1395–1403. DOI:10.1016/j.enpol.2008.11.040 |
| [] | Kuosmanen, T. and Kortelainen, M. , 2007, "Valuing Environmental Factors in Cost-benefit Analysis using Data Envelopment Analysis". Ecological Economics, 62(1), 56–65. DOI:10.1016/j.ecolecon.2007.01.004 |
| [] | Kuosmanen, T. , Bijsterbosch, N. and Dellink, R. , 2009, "Environmental Cost Benefit Analysis of Alternative Timing Strategies in Greenhouse Gas Abatement: A Data Envelopment Analysis Approach". Ecological Economics, 68(6), 1633–1642. DOI:10.1016/j.ecolecon.2008.07.012 |
| [] | Liao, H. , Fan, Y. and Wei, Y.M , 2007, "What Induced China's Energy Intensity to Fluctuate: 1997-2006?". Energy Policy, 35, 4640–4649. DOI:10.1016/j.enpol.2007.03.028 |
| [] | Loschel, A. 2004, "Technological Change, Energy Consumption, and the Costs of Environmental Policy in Energy-Economy-Environment Modeling". International Journal of Energy Technology and Policy, 2(3), 250–261. DOI:10.1504/IJETP.2004.005157 |
| [] | Luenberger, D. G. 1992, "New Optimality Principles for Economic Efficiency and Equilibrium". Journal of Optimization Theory and Applications, 75(2), 221–264. DOI:10.1007/BF00941466 |
| [] | Michida, E., 2006, "Are There Win-Win Opportunities in Developing Countries", Environmental and Resource Economists, Kyoto, Japan, 3rd World Congress, 3-7 July. |
| [] | Murty, M. N. and Kumar, S. , 2003, "Win-Win Opportunities and Environmental Regulation: Testing of Porter Hypothesis for Indian Manufacturing Industries". Journal of Environmental Management, 67(2), 139–144. DOI:10.1016/S0301-4797(02)00203-7 |
| [] | Park, H and Lim, J. , 2009, "Valuation of Marginal CO2 Abatement Options for Electric Power Plants in Korea". Energy Policy, 37(5), 1834–1841. DOI:10.1016/j.enpol.2009.01.007 |
| [] | Porter, M. E., 1991, "America's Green Strategy, " Scientific American, 264. |
| [] | Porter, M. E. and Van der Linde, C. , 1995, "Toward a New Conception of the Environment Competitiveness Relationship". The Journal of Economic Perspectives, 9, 97–118. DOI:10.1257/jep.9.4.97 |
| [] | Wei, C. , Ni, J. and Du, L. , 2012, "Regional Allocation of Carbon Dioxide Abatement in China". China Economic Review, 23, 552–565. DOI:10.1016/j.chieco.2011.06.002 |
| [] | Wang, K. and Wei, Y.M. , 2014, "China's regional industrial energy efficiency and carbon emissions abatement costs". Applied Energy, 130, 617–131. DOI:10.1016/j.apenergy.2014.03.010 |
| [] | 包群、邵敏、杨大利, 2013, 《环境管制抑制了污染排放吗?》, 《经济研究》, 第 12 期, 第 42–54 页。 |
| [] | 陈诗一, 2009, 《能源消耗、二氧化碳排放与中国工业的可持续发展》, 《经济研究》, 第 4 期, 第 41–55 页。 |
| [] | 陈诗一, 2010, 《节能减排与中国工业的双赢发展: 2009-2049》, 《经济研究》, 第 3 期, 第 130–143 页。 |
| [] | 陈诗一, 2011, 《边际减排成本与中国环境税改革》, 《中国社会科学》, 第 3 期, 第 85–100 页。 |
| [] | 陈诗一, 2012, 《中国各地区低碳经济转型进程评估》, 《经济研究》, 第 8 期, 第 32–44 页。 |
| [] | 高鹏飞、陈文颖、何建坤, 2004, 《中国的二氧化碳边际减排成本》, 《清华大学学报 (自然科学版)》, 第 9 期, 第 1192–1195 页。 |
| [] | 李宾, 2014, 《我国碳减排的定量评估》, 《南方经济》, 第 8 期, 第 56–70 页。 |
| [] | 李小平、朱钟棣, 2005, 《中国工业行业资本形成、全要素生产率变动及其趋异化:基于分行业面板数据的研究》, 《世界经济》, 第 9 期, 第 51–62 页。 |
| [] | 刘明磊、朱磊、范英, 2011, 《我国省级碳排放绩效评价及边际减排成本估计:基于非参数距离函数方法》, 《中国软科学》, 第 3 期, 第 106–114 页。 |
| [] | 李树、陈刚, 2013, 《环境管制与生产率增长——以APPCL2000的修订为例》, 《经济研究》, 第 1 期, 第 17–31 页。 |
| [] | 潘勋章、滕飞、王革华, 2013, 《不同碳排放权分配方案下各国减排成本的比较》, 《中国人口·资源与环境》, 第 12 期, 第 16–21 页。 |
| [] | 涂正革, 2009, 《工业二氧化硫排放的影子价格:一个新的分析框架》, 《经济学季刊》, 第 1 期, 第 259–282 页。 |
| [] | 王兵、吴延瑞、颜鹏飞, 2008, 《环境管制与全要素生产率增长: APEC的实证研究》, 《经济研究》, 第 5 期, 第 19–32 页。 |
| [] | 王兵、吴延瑞、颜鹏飞, 2010, 《中国区域环境效率与环境全要素生产率增长》, 《经济研究》, 第 5 期, 第 95–109 页。 |
| [] | 王兵、杜敏哲, 2013, 《节能减排约束下广东地区工业经济的可持续发展: 2011-2020》, 《产经评论》, 第 4 期, 第 60–72 页。 |
| [] | 袁鹏、程施, 2011, 《我国工业污染物的影子价格估计》, 《统计研究》, 第 9 期, 第 66–73 页。 |



