2015年3月,人力资源与社会保障部提议尽快制定延迟退休方案,再次引发了社会各界对延迟退休政策的热议。目前,关于延迟退休政策的理论研究主要从三个方面开展:一是讨论延迟退休的必要性和可行性,主要从预期寿命、老龄化趋势、养老保险基金收支平衡、延迟退休的相关理论等角度进行。多数学者认为预期寿命理应成为延迟退休的决策基础,我国的退休年龄与人均预期寿命延长的趋势不相称,需要适度调整 (乐章和刘二鹏,2015)。人口老龄化提高了养老保险的制度赡养率,增加了医疗和护理需求,养老保险即将出现资金缺口 (殷俊和黄蓉,2013),面临隐性债务和个人账户空账的双重危机 (林宝,2001),延迟退休能提升养老保险的风险抵御能力。还有一些学者利用生命周期理论、收益激励模型来阐述延迟退休对个人储蓄的激励作用 (邵国栋等,2007;汪泽英和曾湘泉,2004)。二是讨论延迟退休的政策效应,主要是对养老保险制度和就业的影响。这类研究存在较大争议,一部分学者反对延迟退休政策推行,认为延迟退休无法弥补养老保险基金的缺口 (李雪,2008),政策推行会导致覆盖率降低,加重剩余劳动力问题 (李绍光,2008)。另外一部分学者则认为,相比提高替代率和缴费率水平,延迟退休是当下缓解养老保险支付压力的有效方法。延迟退休对就业产生压力的观点,建立在老年人和年轻人工作存在替代关系的假设前提下,但这种假设前提不一定存在 (李珍,2007),延迟退休对就业的影响未知。三是讨论延迟退休的实施方案,在选择时机和方案上存在分歧:一部分学者认为延迟退休应该尽早推行,最佳时机是劳动力年龄人口达到峰值时 (邓大松和刘昌平,2002),另一些学者则建议在养老压力急剧增大,劳动就业压力较小的情况下推行延迟退休政策 (林宝,2010)。大部分学者支持了弹性退休制度,提出最低工作年限法、逐步渐进法等具体改革方案 (朱棱,1999;林宝,2014)。
可以看出,相关研究主要从政府角度出发,以分析退休年龄和宏观经济之间的相互关系为重点,主要讨论了延迟退休政策的宏观经济效应。事实上,延迟退休政策的制定与实施是相关利益群体的博弈过程,未来退休政策的调整需要平衡个人决策和政府选择之间的利益,才能降低改革的阻力,保证政策的顺利推行。以此理念为基础,本文首先从个人决策角度出发,建立个人退休年龄决策模型,着重分析了初始就业年龄、人口预期寿命、利率对个人退休决策的影响,指出提高养老金的收益水平,可以增强个人延迟退休的意愿。在低利率、低初始就业年龄的前提下,强制延迟退休政策必然造成个人福利损失。然后,依据第六次人口普查数据建立Leslie人口预测模型,并将Leslie人口模型引入养老保险基金平衡测算过程,对养老保险的制度抚养比进行了修正,在此基础上,测算了渐进式延迟退休时间表对养老保险基金缺口变动的影响。模型结果表明,渐进式的延迟退休政策能够有效降低基金缺口率,尽早统一男女退休年龄政策能够收到良好的预定成效。但在人口结构严重老龄化时,基金依然面临10%左右的缺口,不能依赖延迟退休政策来解决基金缺口问题。面对个人决策和政策选择之间的冲突,政府应该采取多种其他配套措施,降低养老保险基金的支付缺口,并延缓老龄化的进程,以降低延迟退休政策制定和执行的阻力。
二、 个人退休年龄决策根据我国《社会保险法》的规定,个人缴费满15年,男女达到法定的退休年龄才能领取养老保险。假设个人追求自身利益最大化,想尽量领取较多的养老保险,但是个人退休选择不受法定退休年龄的限制,达到缴费15年的标准后可自由选择退休年龄。设定个人从t0开始工作,实际退休年龄为t(t≥t0+15),t年龄的当年养老保险支付水平为xt,年利率为r1,国家法定退休年龄为T,Td为死亡年龄,Vt表示养老保险制度下实际退休年龄t时的全部养老保险给付贴现值。
若个人缴费已经达到15年,在达到法定退休年龄之前选择提前退休,即t≤T时退休,则可以获得从法定退休年龄到死亡年龄的全部养老保险给付,将这部分养老保险给付贴现到法定退休年龄T,则
设定初始就业年龄在18-29岁之间,预期寿命在74-85岁之间,在年利率为2%、3%、4%、5%的情况下,分别估算个人的最优退休年龄。表 1显示了初始就业年龄、个人预期寿命、利率水平和退休年龄选择四者之间的关系,可以看出,在给定初始就业年龄的前提下,利率对个人退休年龄选择的影响明显,利率水平越高,个人延迟退休的意愿越强。人均预期寿命对退休年龄选择有一定的影响,随着预期寿命的延长,个人也倾向于延迟退休。另外,初始就业年龄也会影响个人的退休意愿,但是影响非常有限。目前,我国的人口预期寿命约为75岁,当初始就业年龄为18岁时,按照目前的养老保险收益水平,如果没有法定退休年龄,个人会选择在50岁左右提前退休。
| 表 1 个人最优退休年龄选择 |
根据估算数据结果,预期寿命、初始就业年龄、利率的提升,都能在不同程度上提高个人延迟退休的意愿,但是个人最优退休年龄对三个因素变动的敏感程度不同。其中,利率的提高,可以明显提升个人延迟退休的意愿。如表 1估算数据显示,5%的年利率可以大大提高个人延迟退休的意愿,在初始就业年龄为18岁的情况下,个人的意愿退休年龄在64.61岁。在低利率2%的情况下,即使预期寿命提高到85岁,出于自身利益的考虑,个人并不愿意将退休年龄延迟到56岁。然而,当利率提升到3%,根据最优退休年龄的测算结果,预期寿命提高到85岁,个人初始就业年龄提高到26岁时,个人会考虑在60岁以后退休。
相比个人退休年龄对利率的敏感性,人均预期寿命对个人退休年龄选择的影响有限,从表 1的估算数据结果可见一斑。以3%的年利率为例,个人初始就业年龄为18岁时,即使将人均预期寿命从74岁提高到85岁,个人最优年龄从50.19岁上升到57.21岁。然而,人均预期寿命的延长,受到科技水平、医疗卫生条件、遗传因素等诸多因素影响,其提高过程是一个缓慢而漫长的过程,且预期寿命达到一定水平,增速逐步放缓。从1990年到2010年,我国人口平均预期寿命从68.55岁提升到74.83岁,20年提高了6.28岁①。相比之下,1990年到2012年,欧洲发达国家的平均预期寿命从72岁提高到76岁,22年提高了4岁②。这样,实际上人口预期寿命成为非可控因素,不能通过迅速提高人口预期寿命,从而增强个人延迟退休的意愿。
①国家统计局.第六次全国人口普查数据.[EB/OL]. http://www.stats.gov.cn/tjsj/tjgb/rkpcgb/qgrkpcgb/201209/t20120921_30330.html
②WHO. Life Expectancy Data by WHO Region. [EB/OL]. http://apps.who.int/gho/data/view.main.690?lang=en
相比人均预期寿命的外生性特征,初始就业年龄则可以通过推行义务教育,提高受教育年限和受教育水平进行,继而影响到个人退休年龄的理性选择。但是值得注意的是,初始就业年龄虽然可以抑制个人提前退休行为,但对提高个人退休年龄的影响效果非常有限。表 2显示了个人初始就业年龄对最优退休年龄选择的影响,在3%利率、当前人均预期寿命的现实条件下,当个人在18岁高中毕业直接参加工作,预期寿命为74岁时,其最优退休年龄为50.19岁。同等条件下,个人在22岁完成大学教育进入劳动力市场,最优退休年龄为51.68岁,此时,个人初始就业年龄延长4年,最优退休年龄提升了大约1.5岁。当个人选择攻读研究生学位,25岁进入劳动力市场,最优退休年龄提高到52.82岁;攻读博士学位后,28岁进入劳动力市场,最优退休年龄为53.97岁。相比利率对退休年龄的影响,初始就业年龄对个人最优退休年龄选择的影响要小的多。
| 表 2 个人初始就业年龄与最优退休年龄的选择 (r1=3%) |
由此可见,在目前养老保险收益率和个人初始就业年龄较低的情况下,出于自身利益最大化的考虑,当个人可以自由选择退休年龄时,多数人会在50岁到55岁之间退休,当推迟法定退休年龄时,个人面临福利损失,因此多数人缺乏支持退休年龄政策改革的意愿。当前退休年龄政策约束下,由于女性退休年龄低于男性,法定退休年龄带给女性的福利损失小于男性。最优退休年龄选择模型也在一定程度上可以用来解释提前内退行为,当法定退休年龄明显高于个人最优退休年龄,劳动力供大于求的状态长期存在,提前内退行为不可避免。应该意识到,当进一步提高法定退休年龄时,受低利率和初始就业年龄的限制,个人福利会遭受进一步损失,届时个人通过自动失业、提前内退、降低缴费等行为来降低延迟退休政策对个人福利的负面影响,也是不可避免的。为了降低延迟退休政策的负面效应,可以考虑通过养老保险基金的保值增值、提高个人初始就业年龄来降低政策执行的阻力。
三、 延迟退休:养老保险基金平衡的现实选择随着人口老龄化的加剧,养老保险制度的财政支付压力增大,面临基金平衡的难题。养老保险基金采用社会统筹与个人账户相结合的部分积累制,个人账户并不具有再分配的性质,按照目前的计发办法,能够实现一生个人收入的自我平衡,而统筹基金账户的财务平衡由当期收入和支出共同决定,最终达到代际之间的收支平衡,面临着收支不平衡的风险。因此,养老保险基金平衡实际上是社会统筹账户的平衡问题。维持基金平衡的方法主要有降低养老金替代率、提高劳动者参与率、提高缴费水平和延迟退休,在养老金实际替代率水平低下和缴费水平较高无法调整的前提下,延迟退休由此成为政府提高养老金支付能力的现实选择。本文基于养老保险基金平衡公式,建立Leslie人口模型确定参保人口参数,以测算延迟退休对制度赡养率的影响,继而测算养老保险基金缺口的变动,估计延迟退休的政策效应。
(一) 养老保险基金平衡模型设L(c)、L(p) 分别为当期养老保险的缴费人数和受益人数;P(t) 为养老保险的缴费率,即养老保险缴费额与计费工资总额的比率;B(t) 为养老保险替代率①,即t年退休职工的平均养老金与当年在职职工平均工资之比;W(t) 为t年工资收入,等同于计费工资总额。则养老保险基金平衡公式为 (邓大松,2007):
①养老金替代率的含义不一,本文采取普遍使用的社会平均工资替代率。
| $ L(c) \times p(t) \times W(t) = L(p) \times B(t) \times W(t) $ | (1) |
设d(t) 为制度赡养率,则d(t)=L(p)/L(c),公式 (1) 可转化为关于缴费率P(t) 的公式:
| $ p(t) = d(t) \times B(t) $ | (2) |
设养老保险缺口率为n(t),即t年养老金缺口金额与当年在职职工工资总额的比例。如果t年的养老金缴费小于当年应支付退休职工的养老金,即养老金出现缺口,那么养老金财务平衡式将被打破。此时,下面等式成立:
| $ n(t) = B(t) \times d(t) - P(t) $ | (3) |
其中,制度赡养率d(t) 与劳动年龄人口结构紧密相关,可用d1(t) 退休年龄人口与工作年龄人口之比②去推算,但由于并非所有退休年龄人口都能领取退休金,并非所有工作年龄人口都工作并缴纳养老保险金,所以d(t) 并不等同于d1(t)。设定C(t)=d(t)/d1(t),即退休职工数占退休年龄人口的比例与在职职工占工作年龄人口总数的比例之比 (姜向群,2006),养老保险缺口率公式转化为:
②退休人口指男60岁及以上人口,女干部55岁及以上人口,女工人50岁及以上人口。工作年龄人口指男16-60岁人口,女干部16-55岁人口,女工人16-50岁人口。
| $ n(t) = B(t) \times d(t) \times C(t) - P(t) $ | (4) |
制度赡养率d(t) 随着老龄化的加重不断提高,如果维持缴费率P(t) 不变,则需要降低养老金的替代率B(t);而如果替代率B(t) 保持不变,则需要提高基金的缴费率P(t),才能换取养老基金的财务平衡。然而,我国的养老金的名义缴费率已经达到计费工资总额的28%,位列世界较高水平。缴费率过高,既不利于解决劳动力市场的供需矛盾,也会产生替代效应,企业和个人难有余力参加企业年金和进行个人养老储蓄,阻碍多支柱养老保险体系的建立。另一方面,替代率P(t) 受到经济发展水平和养老金支付刚性等因素制约,目前企业退休人员平均养老金替代率已经低于60%的制度设计目标,2013年降低为44.13%(李珍和王海东,2012)。如果考虑到我国目前缴费工资大大低于实际工资总收入的现状,退休人员养老金的实际替代率将更低。在多支柱养老金体系尚未建立的前提下,降低养老金替代率,意味着直接影响到退休人员的生活水平,通过降低养老金替代率来缓解老龄化带来的养老金支付危机也不可行。因此,无论提高养老金的缴费率还是降低替代率,对减轻老龄化负担,都困难重重。在缴费率和替代率都无法做出大幅调整的现实情况下,只能通过抑制制度赡养率,来维持养老基金的平衡,解决养老金支付的困境。
相比之下,制度赡养率是一个关于退休年龄、预期寿命和年龄别死亡概率的函数。预期寿命和死亡概率建立在生物遗传、生存环境、医疗条件的基础上,属于外生不可控因素,只有退休年龄是可以设定和改变的,并且延迟退休对于基金平衡的影响是双向的:一方面,不仅可以增加缴费人数和缴费年限,从而提高养老保险基金的收入,另一方面,可以通过减少养老金的支付年限和领取人数来减少养老保险基金的支出,从而降低制度赡养率,养老金的收支缺口压力可能得以缓解。
(二) 制度赡养率的测算以往研究大多用老年人口抚养比来估算制度赡养率,我国的老年抚养比是指60岁及以上老人占14-59岁人口的比例,这样用老年抚养比代替制度赡养率的测算,人为减少了退休年龄人口,增加了工作年龄人口,导致制度赡养率的测算值低于实际水平,而实际上目前养老保险的制度赡养率,是指领取养老金的老人占适龄就业人口的比例。在当下养老保险制度普遍覆盖的前提下,制度赡养率用退休年龄人口与工作年龄人口之比、劳动参与率测算更为准确。因此,本文利用2010年第六次人口普查的年龄别数据,建立Leslie人口预测模型,测算2010年到2060年之间的制度赡养率。
1. Leslie人口模型人口预测的方法一般为场景预测和数学模型预测,主要包括回归模型、BP神经网络模型、Leslie模型和队列模型。队列模型对数据质量要求高,依赖于场景方案人为设置,而回归模型和BP神经网络模型不能够反映年龄别人口的变动趋势。相比之下,Leslie模型建立在年龄结构的离散分析基础上,考虑到年龄别人群之间的生育率和死亡率,预测的结果较为精确,能够呈现年龄别人口的变动趋势,因此本文选用Leslie模型进行2010年到2060年之间的年龄别人口测算。
假定年龄别生育率、男女比率和死亡率保持一个相对稳定的水平,将人口分为0~99岁、99岁以上101个阶段,设定Xi=(xi0, xi1, ...xi99, xi99+)T,i=0, 1, ..., k,xij(j=0, 1, ...100) 为第i年j年龄段女性数量,那么初始值X0=(x00, x01, .., x099, x099+)T,则经过k年后,Xk=(xk0, xk1, ...xk99, xk99+)T。设定bik为第k年i年龄女性的生育率,dik为第k年i年龄女性的死亡率,sik为第k年i年龄女性的生存率,则sik=1-dik,wk为第k年出生人口中女性新生儿所占比例,则第k+1年0年龄组的女性人数为:
| $ L = \left( {\begin{array}{*{20}{c}} {w{b_0}}&{w{b_1}}& \cdots &{w{b_{99}}}&{w{b_{100}}}\\ {{s_0}}&0& \cdots & \cdots &0\\ 0&{{s_1}}&0& \cdots &0\\ \cdots & \cdots &0&0& \cdots \\ 0& \cdots &0&{{s_{99}}}&0 \end{array}} \right),则{x^{k + 1}} = L{x^k} $ |
通过递推公式,推出Leslie矩阵模型的公式:xk=Lkx(0),当L矩阵和初始女性人口分布向量x(0),可以求出第k年女性人口的数量,然后根据各年龄段男女性别比得出人口总量和年龄别人口数量 (任强,候大道,2011)。
2. 修正制度赡养率参数依据Leslie矩阵模型,设定2010年的年龄别人口为初始值,由《中国2010年人口普查资料》获取女性年龄别生育率、年龄别男女比例和女性年龄别死亡率,在MATLAB软件中编程,预测2010年-2060年的年龄别人口数量,从而计算出d1(t) 各个年份的数值。设定城镇化进度和劳动参与率在短期内保持不变,根据《2010年中国统计年鉴》数据,计算出C(t) 的值为0.9582,修正d1(t),得出养老保险的制度赡养率。如表 3所示,在老龄化的影响下,2010年的制度赡养率为0.373,2045年左右,制度赡养率接近1,2050年达到峰值,2060年前后开始回落。
| 表 3 2010年-2060年养老保险的制度赡养率 |
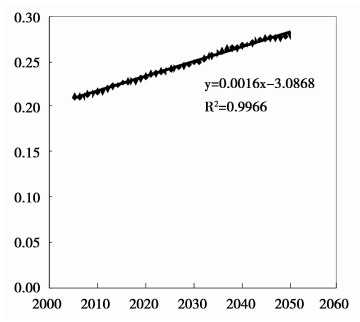
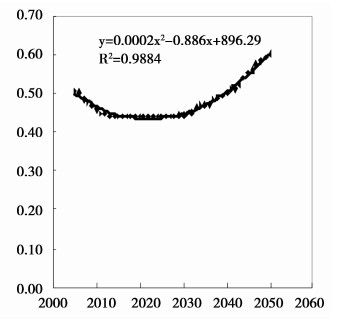
按照我国养老保险制度的设计,单位与职工负担的养老金缴费率各占工资的20%和8%,但由于收费制度的漏洞,实际缴费率低于28%。假定实际缴费率水平逐年线性上升,能够在2050年前后达到名义缴费率水平,然后保持不变。根据2005-2010年的实际缴费率测算数据 (李珍和王海东,2012),绘制散点图,然后对实际缴费率曲线进行拟合和测算,得出缴费率的拟合曲线为y=0.0016x-3.0868,R2=0.9966, p < 0.01。而替代率则参照我国现阶段养老保险制度的替代率目标设计,由2005-2013年的替代率进行曲线拟合 (林宝,2014),在2050年达到目标替代率0.60,然后保持不变,根据拟合曲线预测2010年以后的替代率水平。实际替代率的二次拟合曲线为y=0.0002x2-0.886x+896.29,其中R2=0.9884,p < 0.01。实际缴费率和实际替代率曲线拟合和数据估算过程在SPSS软件中完成。
|
图 1 缴费率拟合曲线 |
|
图 2 替代率拟合曲线 |
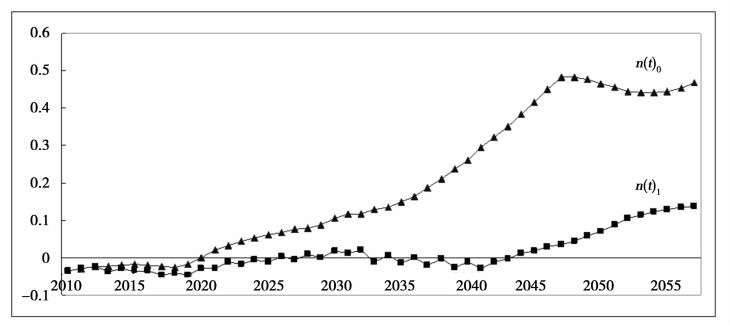
2014年养老金收入增幅开始低于支出的增幅,基金的支付压力逐渐显现。由于老龄化带来的收支平衡压力,人力资源与社会保障部决定制定和推进渐进式延迟退休政策。延迟退休政策坚持“小步徐趋,渐进到位”的方法逐年推进,最后达到法定退休年龄。为此,中国社科院推出了渐进式延迟退休时间表:从2016年起,企业单位女职工退休年龄每年延长半年,在2025年企业单位女职工的退休年龄达到55岁;从2026年起,企业女职工、事业单位女职工和女公务员的退休年龄每年延迟半年,在2035年达到60岁;从2036年起,城镇职工养老保险的全体参保者的退休年龄每年延长半年,到2045年达到65岁 (葛倩等,2015)。基于此,本文在制度赡养率、实际缴费率、实际替代率的参数估算前提下,依据养老保险基金平衡公式和延迟退休时间表,对养老保险2010年到2060年的基金缺口n(t) 进行了测算。测算结果如图 3所示,n(t)0为不推行延迟退休政策时,养老保险基金的缺口变动,n(t)1为渐进式延迟退休时间表下,养老保险基金的缺口变动。
|
图 3 延迟退休与养老保险基金缺口变动 |
从图中可以直观看出:目前,我国养老保险基金依然可以维持年度收支平衡,略有结余。在2020年前后,基金开始出现缺口,其主要原因为人口年龄结构趋于成熟型,劳动力年龄人口稳定并开始减少,老年人口逐渐增多。基金缺口在2025年以后加速增大,于2050年前后达到峰值,达到0.483左右,2050年-2060年之间略有回落,主要原因是老龄化程度加剧,导致人口总量缩减,从而改变了制度抚养比。按照现行的退休年龄政策,养老保险基金的未来缺口巨大,无法维持年度的收支平衡,在缴费率和替代率变动受限的情况下,只能通过延迟退休政策,来降低制度赡养率。相比之下,在2025年将企业女职工的退休年龄调整到55岁以后,基金基本可以实现收支平衡,2035年将女性参保者的退休年龄调整到60岁以后,基金略有结余,2045年全部参保者的退休年龄调整到65岁后,基金出现了10%左右的缺口,主要原因是人口年龄结构的根本改变以及人口总量的萎缩。这样,渐进式退休年龄方案可以大大减少养老保险基金的缺口率,政策对缺口变动的影响最大为2050年前后,政策前后基金的对比缺口率达到0.447。
因此,退休年龄和养老金的收支平衡之间有着极为密切的关系。在老龄化的现实背景下,通过提高退休年龄的确可以有效缓解养老保险基金支付压力,逐步减轻国家的财政负担,有利于实现基本养老保险制度的可持续性,但是并不是解决基金缺口的根本途径。在预测期2055年之后,基金保持着10%左右的缺口率,并且有一定程度的上升趋势,但是进一步提高退休年龄来降低缺口率是不可行的,只能通过其他措施,比如增加缴费基数、提高劳动参与率、经济稳定持续发展、建立多支柱的养老保险体系、调整生育政策等措施,来直接或间接降低养老保险基金的缺口。基金平衡模型建立在实际缴费率和实际替代率的实证数据基础上,进行曲线拟合和预测,实际上是假定实际缴费率和实际替代率水平经过一段时间能够达到目标替代率和名义缴费率,在养老保险制度发展过程中,如果不能如期达到目标替代率和名义缴费率,基金的缺口势必进一步拉大。以上分析可以得出:渐进性的延迟退休政策可以降低制度赡养率,将养老保险基金缺口维持在一个稳定的水平,缓解老龄化带来的养老金支付危机,减轻国家财政的负担。但是,缓解养老保险基金支付压力并不是只有提高退休年龄才能做到,只是结合我国现实状况,它是目前最适合的办法。
应该意识到,退休年龄进行改革的决定性因素是人口预期寿命,根据人口预期寿命科学厘定退休年龄是对现有人力资本的充分利用,而缓解养老金支付压力只是退休年龄改革的客观效应之一。建国后至今,在预期寿命不断延长的前提下,现行男女之间、职业之间的退休年龄差距始终不变,大部分的女性劳动力处于“未老先退”的状态,这既是对人力资本和人口红利的浪费,又引发了基金缺口率的上升。从模型分析结果来看,渐进式的退休年龄改革,在将男女退休年龄同步调整后,基金可实现当年收支平衡。在人口尚未高龄化,制度抚养比小于1时,尽早统一退休年龄能够收到良好的成效。因此,当前退休年龄改革的首要应该在于统一退休年龄。
但是,我们不应该本末倒置,把对退休年龄改革的根本目标设定为应对养老保险支付压力,依赖提高退休年龄来解决基金缺口问题。加之个人提前退休的决策倾向,这种政策目标取向必将遭受国民反对,政策改革难以推行。当采取强制的、逐步渐进的延迟退休政策,2035年之后当人口高龄化时代降临,制度抚养比大于1,即使进一步将男女退休年龄从60岁提高到65岁,养老保险基金依然无法实现收支平衡,应提早看到人口结构转变和退休年龄之间的密切关系,及时把握退休年龄改革的时机,并意识到延迟退休政策的局限性。
四、 结论与建议本文建立养老金个人决策模型和基金平衡模型,讨论了个人退休意愿和政府退休政策的现实选择。在个人缴费满15年的前提下,如果没有法定退休年龄的限制,目前养老金利率水平过低,个人倾向提前退休。尽管预期寿命、初始工作年龄、利率水平都和个人最优退休年龄的选择存在密切关系,但预期寿命和初始工作年龄的调整非常有限,如果能够将目前养老金的利率水平从2%提高到5%,个人延迟退休意愿将大大提高,在初始就业年龄为18岁的情况下,个人最优退休年龄将提高到65岁。然而,低利率、低初始就业年龄的现实条件下,强制延迟退休,会造成个人福利损失。
养老保险基金平衡受实际缴费率、制度替代率和实际替代率的相互制约和影响,但目前名义缴费率居高不下,实际养老金替代水平逐年下降,通过延迟退休降低制度替代率是政府当下的现实选择。在模型测算中发现,渐进式的延迟退休政策从2016年开始实施,在老龄化加速平稳,人口结构没有重大变化的情况下,同步男女退休年龄到60岁,基金基本上可以实现收支平衡。但在生育率保持不变,老龄化速度加速时,人口结构发生重大变化,从稳定结构向“倒三角”结构急剧转变,即使将男女退休年龄同步提高到65岁,养老保险基金也仍旧存在10%左右的缺口,并且缺口有着进一步稳定扩大的趋势。并且,延迟退休政策调整具有一定的局限性,过高的退休年龄设置,会对劳动力市场造成一定的压力,在养老金利率水平低下的情况下,个人实际上缺乏延迟退休的动力。因此,延迟退休政策应该在人口预期寿命的科学厘定基础上进行,当下,政府可以考虑首先统一退休年龄,以降低执行阻力,能够收到良好的预定成效。
养老保险基金缺口问题的解决,可以通过其他政策的配合使用进行,从而减轻延迟退休政策的负面效应,实现基金的动态均衡。可选择政策包括以下几个方面:第一,效仿企业年金制度,建立基本养老金个人账户的信托投资机制,实现养老保险个人账户基金的保值增值,从而分担养老保险统筹账户的筹资压力。另外,在安全性和流动性的原则下,目前养老保险基金的每年积累盈余和风险准备基金可以通过投资基础设施建设、国债、短期金融债券的方式,进行适度投资。这样,提高养老金的投资收益率,增加个人退休积累,提高个人延迟退休的意愿。第二,逐渐建立多支柱的养老保险体系,将基本养老保险、企业年金和个人储蓄结合起来,从而提高企业年金和个人储蓄对基本养老保险的替代效应,降低基本养老基金的名义替代率。第三,养老保险的征缴实行费改税,以填补保险缴费的制度漏洞,削减个人工资缴费中普遍存在的基本工资缴费和全额工资缴费的差异,以扩大缴费基数,保证实际缴费率水平和名义缴费率水平的一致。第四,适度放宽生育政策,提高生育率,延缓老龄化的趋势。根据本文人口模型的预测数据,在目前的生育率水平下,人口结构在2045年到2060年之间将发生根本变化,老龄化问题严重。我国目前的经济发展水平尚不具备应对严重老龄化的能力,应该及时适度调整生育率水平,延缓老龄化浪潮。
| [] | 邓大松、刘昌平, 2002, 《中国养老社会保险基金敏感性实证研究》, 《社会保障制度 (人大复印资料)》, 第 4 期, 第 22。 |
| [] | 邓大松, 2007, 《社会保险》, 中国与劳动社会保障出版社2007年6月第二版. |
| [] | 葛倩、刘佳和王道斌等, 2015, 《延迟退休方案后年推出, 你能轮上延迟退休吗?》, http://finance.ifeng.com/a/20150311/13545119_0.shtml. |
| [] | 姜向群, 2006, 《人口老龄化对退休金负担影响的量化研究》, 《人口研究》, 第 2 期, 第 51–55 页。 |
| [] | 林宝, 2001, 《中国退休年龄改革的时机和方案选择》, 《中国人口科学》, 第 1 期, 第 25–31 页。 |
| [] | 林宝, 2010, 《人口老龄化对企业职工基本养老保险制度的影响》, 《中国人口科学》, 第 1 期, 第 84–92 页。 |
| [] | 林宝, 2014, 《延迟退休年龄对养老金资金平衡的影响》, 《财经问题研究》, 第 12 期, 第 41–46 页。 |
| [] | 李雪, 2008, 《延长退休年龄解决养老金"空账"问题的可行性研究》, 《中共长春市委党校学报》, 第 1 期, 第 75–77 页。 |
| [] | 李绍光, 2008, 《建立可持续的养老保险制度》, 《中国社会保障》, 第 3 期, 第 20–21 页。 |
| [] | 李珍, 2007, 《社会保障理论》, 中国劳动与社会保障出版社2007年6月第二版. |
| [] | 李珍、王海东, 2012, 《基本养老保险目标替代率研究》, 《保险研究》, 第 2 期, 第 97–103 页。 |
| [] | 任强、侯大道, 2011, 《人口预测的随机方法:基于Leslie矩阵和ARMA模型》, 《人口研究》, 第 2 期, 第 28–42 页。 |
| [] | 邵国栋、朱小玉、刘伟, 2007, 《基于生命周期理论的延迟退休年龄合理性研究》, 《云南社会科学》, 第 5 期, 第 53–56 页。 |
| [] | 汪泽英、曾湘泉, 2004, 《中国社会养老保险收益激励与企业职工退休年龄分析》, 《中国人民大学学报》, 第 4 期, 第 74–78 页。 |
| [] | 殷俊、黄蓉, 2013, 《人口老龄化视角下的基础养老金长期精算平衡研究》, 《统计与决策》, 第 13 期, 第 164–167 页。 |
| [] | 乐章、刘二鹏, 2015, 《延迟退休年龄:研究进展与若干争议》, 《社会保障研究》, 第 2 期, 第 107–112 页。 |
| [] | 朱棱, 1999, 《论法定退休年龄的界定与调整》, 《辽宁大学学报》, 第 5 期, 第 25–27 页。 |




