“爱美之心,人皆有之”这句话清楚地表明,人对美的认识是有共同性的。“情人眼里出西施”这句话则明确地指出,人对美的认识是有差别的。一个科学工作者在科研工作中感受到的科学之美,与他们在生活中看到的美,是既有共同性,也有差异性的;而不同领域的科学工作者所感悟到的科学之美,也不尽相同。一般说来,在数学和一些理论性较强的学科里,人们比较容易体验到科学之美。而在一些工程科学或应用性较强的领域里,科学之美的展现似乎要少一些,人们关注和研究的也比较少。本文希望就工程科学的美,做一些探讨。
工程热物理学是工程科学中理论体系比较完整、研究方法比较完备、应用对象比较广泛的学科之一。它是在世界航空航天技术发展的时代诞生的,研究对象是有化学反应的高温、高压、高速流动的规律和应用,包括工程热力学、工程流体力学、传热传质学、燃烧学和多相流动几门分支学科。如今,它在航空航天推进、能源洁净高效利用和可再生能源开发中,发挥着巨大的作用,在信息科技、生物技术等领域也越来越显示出重要性。
上个世纪40年代末期、50年代初期,航空科技和航空产业在第二次世界大战后的全球经济复苏中率先高速发展。在航空推进中,燃气轮机很快在各种动力装置中脱颖而出,在航空推进中占据了统治地位,并且对飞行速度突破“声障”做出了决定性的贡献。西方各国纷纷加大投入,期望航空发动机技术有巨大的进展,大幅度提高飞行器的性能。
作为航空发动机的核心,叶轮机械(包括风扇、压气机、涡轮)的研究有重大意义。但同时,这种研究也是十分困难的。由于叶轮机械有许多片叶片,必须考虑这些叶片之间复杂的相互作用,这使得传统的孤立翼型的理论模型不能适用,因为按照这一模型,只能得到叶片平均半径处的参数,而无法考虑叶片的扭转。因此,必须创建新的理论模型,推导相应的数学方程,提出简化的物理假定,并给出相应的基本方程和求解方法。正是在这种迫切的重大需求下,吴仲华先生在50年代初期创立了叶轮机械三元流动理论[1],大大促进了航空发动机和燃气轮机科技和产业的发展。
一、 叶轮机械三维流动理论的诞生叶轮机械内部流动是研究在一定空间范围内的流动现象,揭示共同的、普遍的规律和主要特征,为工程设计提供理论依据和设计计算方法,并在工程实践中不断加以应用、改进和完善。可见,叶轮机械内部流动理论和工程热物理学科属于技术科学的范畴,这里既有大量的知识创新内容,也有更多的技术创新内容,是一个完整的学科体系。
在控制方程、边界条件和研究方法等方面,叶轮机械等内部流动与机翼等外部流动都有很大的不同。
叶轮机械流动控制方程[2]是
连续方程
动量方程
能量方程
这里ρ、p、
在边界条件方面,内部流动通常有一定的空间范围,与外部流动的无限空间有很大的不同。
在研究方法上,除了流体力学中常用的理论分析、数值计算和实验研究外,内部流动还大量使用经验方法和经验数据。
由此可见,叶轮机械内部流动,除了通常外部流动的特征外,还有其许多独自的特点和方法,需要根据研究对象的不同情况,在专门设计的实验装置上开展深入、系统的研究,进行多种可靠、细致的测量,以得出其特有的规律和特征,为设计提供理论依据和计算方法。
正是在这种环境中,刚刚在NIT获得科学博士(Science Doctor)的吴仲华先生投身到航空发动机的研究,他加入了美国航空咨询委员会(NACA,是NASA 的前身)的路易斯实验室(Lewis Lab.,现在更名为Glenn研究中心),并且选择了困难的叶轮机械流动作为自己的研究方向。
对于上述这组非线性程度很高的叶轮机械内部流动基本方程,解析求解是根本不可能的,即使在十分简化的情况下,可以得到非常有限的解析解,在工程设计中也没有什么实际意义。40年代末期、50年代初期,正值世界上第一台电子计算机问世不久,它在科学计算中的巨大作用还没有被人们充分认识。正是在这种背景下,年轻的吴仲华已经洞察到计算机的巨大潜力,毅然决然地抛弃了当时流体力学界推崇为高水平的解析求解方法,勇敢地迈上数值求解的道路。可以毫不夸张地说,吴仲华先生是国际上系统地从事大规模工程科学数值计算的开拓者之一。
面对非常复杂的叶轮机械流动方程组,要把非定常性、粘性和三维性这三个因素都准确地加以考虑,不仅在当时是不可能的,即使在60年后的今天,仍然是不可能的。而且,在许多情况下,也不需要同时准确计算这三者。因此,如何根据叶轮机械流动的主要特点来提出简化的模型,使数值求解成为可能,就是首先必须解决的问题。从流动的基本方程来看,非定常性和粘性都十分复杂,只有三维性比较简单一点,而这一点又与叶片之间的相互作用紧密相关,这正是当时学术界最为关心的。因此,以三维性为主要考虑因素,尽可能地兼顾非定常性和粘性,有可能是一种可行的办法。
实际上,在一般流动中通常假定为定常流动,基本方程中的∂/∂t均为零;而在叶轮机械实验测量中容易测得的流动损失不难转换为熵的变化量,而熵是叶轮机械流动研究者和设计者所熟悉的,这样就可以在基本方程中方便地用熵的梯度来代替粘性项。经过仔细的分析和进一步的严格推导,动量方程中形式复杂、难以求解的粘性项就代之以熵的梯度,能量方程也以相对滞止转子焓I来简洁地表达:
| $\begin{align} & \nabla \cdot \left( \rho \overrightarrow{W} \right)=0 \\ & \overrightarrow{W}\times \left( \nabla \times \overrightarrow{W} \right)\approx \nabla \rho -T\nabla s \\ & \frac{dI}{dt}\approx 0 \\ & \frac{ds}{dt}\ge 0 \\ \end{align}$ |
我们看到,能量方程可以表为相对滞止转子焓沿流线基本不变,成为极易求解的代数方程;而其他流动方程也被大大简化,形式非常简单,这为以后的数值求解打下了坚实的基础。当然,上述方程组在当时的计算机条件下仍然是无法进行计算的,需要进一步加以简化。
现在,我们来考虑叶片之间的三维相对定常流动。这种三维流场,可以想象充满着无数条流线,而这些流线又可以按照不同的规律组成各种类型的流面。因此,也可以认为三维流场是由各种不同的流面组成的,这样,我们就把流场、流面和流线三者联系在一起了:只要知道了每一条流线上流体的参数,就知道了整个三维流场。同样,只要知道了每一个流面上流动的参数,也就知道了全流场。因此,我们既可以按照三维的流动方程来求解得到流线上的流动参数,也可以从三维流动方程来建立流面上二维流动的方程,求解得到流面上的流动参数。这就是说,可以把求解叶片中的三维空间流动转化为求解一系列流面上二维流动。这种降维的求解方法,使叶片间复杂的三维流动的求解成为可能。
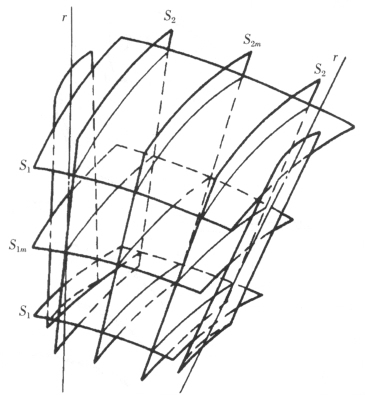
对流面上流动特点的分析发现,按照不同规律形成的流面千变万化,没有必要求解所有流面上的流动,而只要选择按某种原则构成的流面来求解就可以了。进一步,不难注意到,这些流面上的流动相互之间是紧密相关的,而这种关联关系必须通过与之交叉并按不同规律形成的另一类流面才能得到。至此,叶片之间的三维流动就可以转化为相互交叉的两类流面上的二维流动,这给数值求解带来了极大的简化和方便(图 1和图 2)。
|
图 1 叶片间的两类流面 |
|
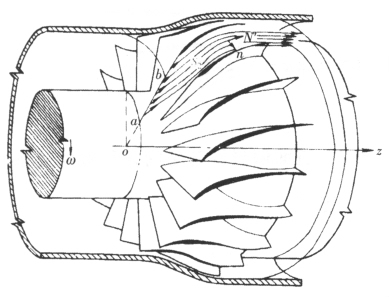
图 2 S2相对流面 |
为了建立两类不同流面之间的关系,根据流面流动的特点,需要导入与通常的空间偏导数不同的流面偏导数。
对任意非正交曲线坐标系下空间的任意流面S,可以表达为:
| $S\left( {{x}^{i}} \right)=0,i=1,2,3$ |
在这个流面上,流面偏导数与空间偏导数之间有着关系:
| $\frac{\bar{\partial }q}{\partial {{x}^{\alpha }}}=\frac{\partial q}{\partial {{x}^{\alpha }}}-\frac{{{N}_{\alpha }}\sqrt{{{g}^{33}}}}{{{N}_{3}}\sqrt{{{g}^{\alpha \alpha }}}}\frac{\partial q}{\partial {{x}^{3}}},\left( \alpha =1,2 \right)$ |
其中,
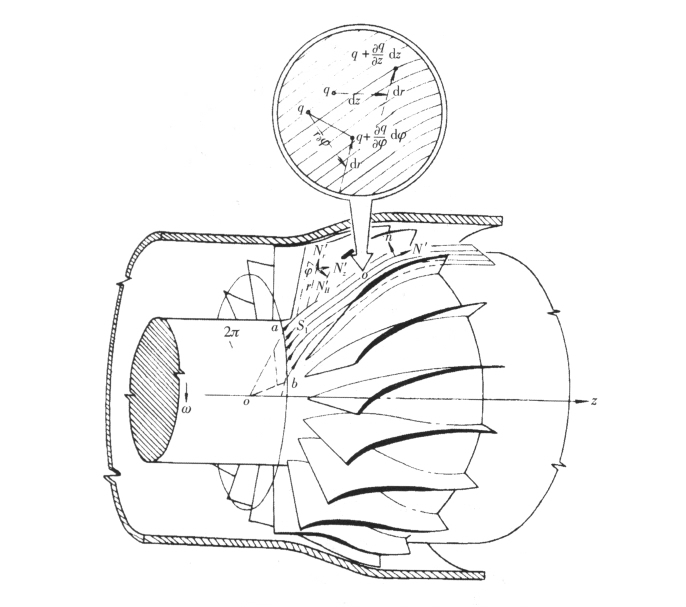
|
图 3 流面偏导数与空间偏导数的关系 |
连续方程
| $\frac{\partial \left( \sqrt{{{g}^{ii}}\rho {{w}^{i}}} \right)}{\partial {{x}^{i}}}=0\Rightarrow \frac{\bar{\partial }\left( b\sqrt{g}\rho {{w}^{\alpha }} \right)}{\partial {{x}^{\alpha }}}=0$ |
在这个方程中,除了用流面偏导数代替空间偏导数外,出现了参数b:
| $\frac{\bar{D}\left( \ln b \right)}{\bar{D}t}=\frac{{{n}^{\alpha }}}{{{n}_{3}}}\frac{\partial {{w}^{\alpha }}}{\partial {{x}^{i}}}$ |
从数学上和物理上都可以证明,b代表流片厚度。
X1 方向动量方程
| $\begin{align} & \vec{W}\times \left( \nabla \times \vec{V} \right)\approx \nabla I-T\nabla s \\ & \Rightarrow {{w}^{2}}\left( \frac{\bar{\partial }{{w}_{2}}}{\bar{\partial }{{x}^{1}}}-\frac{\bar{\partial }{{w}_{1}}}{\bar{\partial }{{x}^{2}}}+2{{\omega }^{3}}\sqrt{g} \right)+{{w}^{3}}\left( \frac{\bar{\partial }{{w}_{3}}}{\bar{\partial }{{x}^{1}}}-2{{\omega }^{2}}\sqrt{g} \right) \\ & +\frac{1}{2}{{w}_{\alpha }}{{w}_{\beta }}\frac{\partial {{g}^{\alpha \beta }}}{\partial {{x}^{3}}}\frac{\bar{\partial }{{x}_{3}}}{\bar{\partial }{{x}^{1}}}=\frac{\bar{\partial }I}{\bar{\partial }{{x}^{1}}}-T\frac{\bar{\partial }s}{\bar{\partial }{{x}^{1}}}-{{F}_{1}} \\ \end{align}$ |
可以看到,这个方程中出现了参数F1。类似地,X2 方向的动量方程也可以转化为用流面偏导数表达的方程,其中出现F2,从数学上和物理上都不难证明,F1和F2是矢量
| $\overrightarrow{F}=-\left( \frac{1}{n\varphi }\frac{1}{\rho }\frac{1}{r}\frac{\partial p}{\partial \varphi } \right)\overrightarrow{n}$ |
至此,已经建立了叶轮机械内三维流动基本方程与两类流面上二维流动基本方程之间的关系。可以看出,在流面的流动方程中出现了两个有明确物理意义的量:流片厚度b和流面之间的作用力
现在要决定如何选取两类流面了。从有利于工程计算考虑,可以选取如图 1所示的S1和S2两类流面:从叶片上游的一条圆弧出发,在流动中形成的是S1流面;而从上游的一条径向线出发,在流动中形成S2流面。在设计计算中,可以进一步作出简化的决定:把S1流面取作任意回转面,或者更方便地假定为圆锥面,甚至圆柱面;而把S2流面取作流道的中心线,甚至子午面。不难看出,S1和S2两类流面都有明确的物理含义,易于与工程设计中的几何概念相结合,给设计计算带来巨大的便利。
二、 工程科学之美分析这个理论不难发现,新引入的流面偏导数是一座桥梁,它把叶片空间内三维流动的物理量与流面上二维流动的物理量联系在一起,把三维的运动方程转换为流面上的二维流动方程。而在导出的流面上流动基本方程中出现了流片厚度和流面之间的作用力,它们是流动三维性的表征,也是流面上流动方程与通常的二维流动方程的不同之处,可以认为它们是流面理论模型的两大支柱。还应当注意到,在这一理论中,引入了一个沿流线的不变量———相对滞止转子焓I,它使方程更为简洁,计算更为简便。这一座桥梁、两个支柱和一个不变量,可以认为是两类流面理论的精华。
我们看到,一个在当时计算机条件下无法求解的叶轮机械内十分复杂的三维流动就这样被分解为S1和S2两族流面上的二维流动,使数值求解成为可能。这样一个理论将丰富的想象力、清晰度物理概念、严格的数学演绎和方便的工程应用完美地结合在一起,全方位地体现了工程科学之美。可以毫不夸张地说,它是全面展示工程科学之美的优秀范例。
因此,这个理论一经发表,就引起了国际学术界的高度重视。两类流面理论被称为“吴氏三维流动理论”或“吴氏理论”,两类流面上的流动基本方程被称为“吴氏方程”。正是基于两类流面的理论模型和方法,国际上对叶轮机械内部流动进行了深入、系统的研究,发现了许多新的流动规律和特征,大大提高了叶轮机械的性能。同时,各国在叶轮机械的流动设计中普遍应用这一理论和方法,成功地设计和研制出许多航空发动机。事实上,在一些著名的航空发动机,如Spey、RB211、JT3D、JT9D、F404等的设计中都用到两类流面理论。直到现在,在直接求解三维流动的计算方法已经比较成熟的情况下,这一理论和方法,由于物理概念明确和计算简便易行,仍然广泛地用在先进航空发动机和燃气轮机的设计计算中。
很明显,吴仲华先生奠基的叶轮机械三维流动理论是一个无比巨大的贡献,对推动叶轮机械的发展,对促进航空发动机和燃气轮机的发展,发挥了极其重大的作用。他逝世后不久,从1995年开始,在每两年一届的国际吸气式发动机学术会议(International Symposium on Air-Breathing Engines)上专门设立了“吴仲华讲座”,以缅怀这位杰出科学家和他做出的划时代贡献。
| [1] | Wu,Chung-Hua:“A General Theory of Three-Dimensional Flow in Subsonic and Supersonic Turbomachines of Axial,Radial,and Mixed-Flow Types,"ASME Paper Number 50-A-79,ASME Transactions,November 1952,or NACA TN 2604,1952. |
| [2] | Wu,Chung-Hua:“Three-Dimensional Turbomachine Flow Equations Expressed with Respect in Non-orthogonal Curvilinear Coordinates and Methods of Solution,"Proceedings of 3rd International Symposium on Air-Breathing Engines,1976:233-252. |
 2012, Vol. 2
2012, Vol. 2
