2. 香港城市大学媒体与传播系
互联网极大地提高了人们信息获取与知识分享的效率。一方面,互联网作为日益主流的媒介,与报纸、电视等传统媒体共同具备信息传播功能。另一方面,互联网用户不仅仅是信息接收者,还同时扮演信息发布者的角色。因其互动性和实时性特征,互联网改变了传统的“广播式(Broadcasting)”信息传播模式,极大地提高了信息传播的速度和广度。但与此同时,信息技术的发展也可能衍生出诸多社会问题。互联网在不同地区、不同人群间的发展速度不同,导致人们对于信息技术的获取出现了差异。例如,1994年,美国政府发布了《被互联网遗忘的角落:一项有关美国城乡信息穷人的调查报告》。该报告认为,不同人群之间的信息技术使用差异造成人们获取信息机会的不平等,影响了人们政治参与、意见表达等更深层次的不平等[1-2]。该报告使得“数字鸿沟”这一概念在学术研究、政策制定等层面引起了广泛重视。
尽管“数字鸿沟”这一议题获得了广泛关注,但如果将数字鸿沟放在一个“历时性”视角中,不同学派对于数字鸿沟的社会影响则呈不同观点。一派观点认为,数字鸿沟的不断扩大导致社会进行更深层次的阶层分化;而另外一派观点则认为,随着信息技术的进步和社会政治、经济等因素的干预,数字鸿沟本身在消弭,他们认为,长远来说数字鸿沟不会成为影响社会不平等的因素之一。因此,本文旨在通过不同国家和地区的互联网采纳实际数据,对数字鸿沟演化做一经验性的描述。
一、 数字鸿沟的概念化定义和操作化定义在讨论数字鸿沟演化问题之前,有必要首先厘清数字鸿沟的概念。本节从概念化定义和操作化定义两个层面阐述“数字鸿沟”概念。前者旨在说明数字鸿沟的理论内涵;后者旨在对数字鸿沟进行可量化的操作性定义。
1. 概念化定义(Conceptualization)一般意义而言,数字鸿沟指在既定社会中不同社会群体对于信息技术的使用差异(Disparity)[3-4]。狭义的数字鸿沟指群体间对某一种信息技术的采纳差异,例如互联网的使用[5-7]。本研究使用数字鸿沟的狭义定义,即指互联网的使用差异。出于对比的目的,我们同时引入了手机作为数字鸿沟研究的另一案例。
2. 操作化定义(Operationalization)数字鸿沟的操作化定义为数字鸿沟提供了可执行的定量测量方法。既往互联网采纳研究提出了多个衡量互联网使用差异的指标。例如,欧洲的SIBIS项目发展了一套指标体系,通过测量个体网络使用技能、ICT技术获取、以及网络使用频度来衡量个体的互联网使用。另外一些学者将数字鸿沟定义为社会各个群体间互联网采纳指标的均值差异[8]。本研究采纳后一种定义方式,并进一步引入和对比四种不同的测量方式。
(1) 基于方差的算法(Variance-based algorithm)
基于方差的算法是最基础也是最直接的测量方法。本研究引入两种基于方差的测量方法:互联网扩散率在各个群体间分布的标准差(以下简称“标准差算法”)和简化的“数码沟”指数(以下简称“Zhu算法”)[9]。Zhu算法将社会内各群体按照年龄、性别和教育程度分成多个子群体。数字鸿沟即各群体互联网扩散率差异的绝对值的和。表 1列出了本研究所用的所有数字鸿沟计算公式。
| 表 1 数字鸿沟指数计算方法 |
(2) 基于比率的算法(Proportion-based algorithm)
基于比率的算法旨在计算各个群体所占比率的差异,本研究引入“熵”和“基尼系数”两种算法。熵出自于Shannon和Weaver的传播理论。熵这个概念被广泛应用于计算“多样性”。简单来说,熵值越大,研究对象的分布越平均[10-12]。在Krippendorff看来,以方差为基准的测量方式,只对单峰分布的数据类型适用,而对数据的概率分布没有任何假设[13]。“熵”这个概念能够从更广义上来测量不平等或差异。因此,本研究引入了“熵”这个概念和算法来测量互联网使用率在各群体之间的分布不平等(以下简称“熵”算法)。熵值越小,互联网使用率的差异越小。
在经济学领域中,对数、帕累托、幂律公式等多种曲线也被广泛用于测量不平等。基于这些算法提出的不平等计算指标有基尼系数,Atkinson度量以及Theil’s MLD[8]。基尼系数是上述这些指标中在测量收入或财富不平等问题中被最为广泛使用的一个指标。基尼系数也已被用于测量不同的年龄、性别和教育水平群体的互联网使用的不平等[2, 14-15]。本研究将基尼系数作为测量数字鸿沟的一个测量方法(以下简称“基尼系数算法”)。
尽管学界已经提出多种测量互联网采纳不平等的指标,但各个指标对于互联网数字鸿沟现象的测量效果尚不一致。例如,Chen等学者认为,使用不同的标准,数字鸿沟的演化趋势也随之变化。他们的研究表明,数字鸿沟在不同的社会经济阶层群体之间扩大,而在不同性别群体之间缩小[16]。加拿大的一项研究发现,使用Gini系数作为数字鸿沟测量方式,数字鸿沟在不同收入的群体间从1996至1997年间扩大(.37到.4),继而从1998年至2000年开始缩小(.37到.27)[14]。因此,出于比较的目的,本文将引入上述四种不同的测量方式,并对其刻画数字鸿沟演化的灵敏度进行检验。
二、 数字鸿沟的演化互联网数字鸿沟的演化从本质上来说是群体/国家间互联网采纳扩散的差异变化。因此,为了计算数字鸿沟的演变,我们首先刻画不同群体/国家间互联网采纳率的变化。根据Rogers的创新扩散理论[17],互联网采纳的扩散应遵循S曲线。如果我们将一个社会根据经济政治指标分为不同的子群体,这些子群体的互联网采纳的扩散也应遵循S曲线。这些S曲线的起飞点、饱和点和拐点可能各不相同。
数字鸿沟产生的根本原因是教育、收入、种族等因素导致不同人群互联网采纳的概率和速度不同[18]。从这个意义上来说,互联网使用的扩散与数字鸿沟的产生演化和经济增长与收入差距不平等问题类似,其本质皆是增长与不平等的关系问题。因此,我们借助于经济学理论,来考察互联网的增长与数字鸿沟的演化。三种经济学理论对该问题提供了不同的理论解释和理论预测。
第一种理论是Kuznets假说[19]。该假说认为,随着经济的增长,贫富差距会首先增大。但随着公共政策、婚姻以及社会形态的改变(例如,从农业社会向现代社会的转变)等因素的干预,这种贫富差异会继而缩小[19-20]。该理论一经发表,已经在多个领域得到了广泛应用。在互联网采纳率增长与数字鸿沟演化的关系问题上,Kuznets假说可能成立。在一个社会中,社会经济地位较高的人会首先采纳互联网。随着政府对互联网的政策鼓励以及互联网接入的价格变低,社会经济地位较低的群体会随之采纳,并有可能追赶。换言之,在处于较高阶层的人群中,互联网扩散率在早期较快;随着上层人群互联网扩散率增长变慢到最终趋于饱和,处于较低阶层的人群互联网扩散速率增长开始变快——用Rogers的创新扩散理论解释,不同的社会群体间对于新技术的采纳存在时间差。如果该假设成立,数字鸿沟应该在早期变大,继而缩小。Chen等的研究发现,数字鸿沟在发展中国家扩大,而在发达国家已在缩小[16]。该研究间接印证了上述假说。
另一派理论认为,数字鸿沟的演化存在一个“天花板效应”。“滴漏”经济学理论(Trickle Down Economics)认为,不平等是刺激经济增长的“必要之恶(Necessary Evil)”——因为财富会从富人“下渗”到穷人[21-22]。该观点隐含的逻辑是,富人会将他们的财富返还到社会中,从而使得财富在未来得到重新分配。因此,资本积累的越多,能够返还的财富也越多[22]。“滴漏”经济学理论也能够用于描述互联网采纳率增长与数字鸿沟演化的发展路径。上层社会群体对互联网的采纳,会促使网络供应商的商业策略及商业模式转变,从而促使互联网技术价格的降低,最终使得政治经济地位较高的社会群体与政治经济地位较低的社会群体的互联网扩散率很快到达饱和。换言之,各个阶层之间的数字鸿沟会很快弥合。
第三类观点,被称为“马太效应”。该观点认为,社会群体之间存在着“剪刀差(scissors gap)”。由于相对弱势,处于较低层次的社会群体很难赶超处于较高层次的社会群体。如果该假说成立,处于较高层次的社会群体的互联网扩散率会比低层次群体的互联网扩散率快。而低层次群体的互联网扩散率会停在某个点上,使得数字鸿沟最终无法弥合。Chen等发现,在发展中国家,互联网普及率增长非常快。而截至2004年,不同社会间的数字鸿沟仍在扩大[16]。一项OECD报告显示,自1997年至2000年,在OECD国家与非OECD国家的数字鸿沟不断扩大[23]。
总而言之,数字鸿沟的演化目前依然是一个有争议性的议题。数字鸿沟的演化很大程度上取决于互联网扩散率的变化。上述三种不同的经济学理论,对数字鸿沟的演化给出了不同的驱动因素解释和预测。因此,本研究选取多个不同地区的数据,采用多种数字鸿沟的测量方式,来刻画数字鸿沟的演化。本研究通过比较全球各个国家以及不同国家内各个社会群体间的互联网使用数字鸿沟演化趋势,来寻找数字鸿沟的演化规律,并对比不同的数字鸿沟测量指标的测量精度。此外,出于比较的目的,本研究还引入了手机数字鸿沟,作为互联网使用的参照组。
三、 研究方法 1. 数据收集本研究使用了四个数据集。世界互联网和手机的扩散率来自于国际电信联(International Telecommunication Union,ITU)。该组织收集了自1997至2008年间世界多个国家的互联网扩散率以及1965至2008年手机的扩散率。国家层面,我们选择了香港和美国作为两个地区的代表。美国的数据来自于常驻人口调查(Current Population Survey,CPS)和皮尤“互联网与美国生活”项目调研数据(Pew Internet and American Life Project,PEW)。前者包含了1997年,1998年,2000年,2001年,2003年和2007年的调查数据;后者包括了2000年到2007年的调查数据。香港的数据来自于香港互联网项目。该项目由香港城市大学互联网挖掘实验室负责,收集了自2000到2008年基于电话随机抽样的香港居民互联网使用数据。
2. 测量本研究选取了标准差算法、Zhu算法、熵以及基尼系数算法四种指标(详见表 1)。在表 1中,Pc指在一既定社会/国家中互联网扩散率,P指全球互联网扩散率;c指代国家(从1到k),Qc是国家C的累积互联网采纳的扩散率占总体扩散率的比例;Pi是累积互联网扩散率。在一个既定社会里,a、s和e分别指代年龄(age)、性别(sex)和教育水平(education),Pase指某一特定年龄、性别和教育群体的互联网采纳率。P指代该社会的总体互联网扩散率,Wase指每一个组别根据人口普查中该群体总数比例进行加权的权重。
在本研究中,我们将一个社会的总人口根据年龄(青年、中年、老年)、性别(男性、女性)和教育水平(大学以上、大学以下)分为12组(3×2×2)。
四、 研究结果 1. 不同数字鸿沟的测量方式比较我们首先用模拟(simulation)的方法,对比四种不同的数字鸿沟测量方法的测量效果。我们构建了三种互联网扩散率的增长模式。
情景1:社会经济地位较高的社会群体的互联网扩散率快于社会经济地位较低的社会群体的互联网扩散率;
情景2:社会经济地位较高的社会群体的互联网扩散率慢于社会经济地位较低的社会群体的互联网扩散率;
情景3:在早期社会整体互联网扩散率较低时,社会经济地位较高的社会群体的互联网扩散率快于社会经济地位较低的社会群体的互联网扩散率;到晚期,社会经济地位较低的群体开始追赶社会经济地位较高群体的互联网扩散率。
在所有拟合数据中,时间点均设为10个,社会群体设为20个。按照上文对数字鸿沟的定义,情景1的数字鸿沟指数应不断扩大;情景2的数字鸿沟指数应不断缩小;而情景3的数字鸿沟指数应先扩大后缩小。
| 表 2 数字鸿沟演化的模拟结果 |
表 2展示了利用四种算法对上述三种情景的数字鸿沟指数计算结果。我们发现,在四种算法中,两种基于比率的算法(即熵和基尼系数算法)之间的相关系数为-0.990 (N=30,p < 0.001),两种基于方差的算法(即Zhu算法和标准差算法)之间的相关系数为0.997 (N=30,p < 0.001),即熵和基尼系数算法高度相关;Zhu算法和标准差算法高度相关。但我们没有发现基于比例的算法与基于方差的算法之间的稳定关系。
更重要的是,基于比率的两种算法计算结果显示,三种情景的数字鸿沟皆在缩小;而基于方差的算法则能够较敏感的显示出三种情景中数字鸿沟的变化,与理论假设一致。该结果说明,对于数字鸿沟的计算,基于方差的算法更适用。
2. 世界互联网和手机的数字鸿沟演化本文分别考量了全世界不同国家间和一个社会内部的数字鸿沟演化规律。前者侧重于比较不同国家或社会之间互联网的使用差异;后者则侧重于比较一个社会中各群体的互联网使用差异。
互联网和手机的扩散,无论在跨国层面还是某一国家/社会内都在稳步增长。特别是,世界互联网扩散率从1997年的2%增长到2008年22%;手机扩散率从1965年的0%增长到2008年的59%。香港互联网扩散率从2000年的40%增长到2008年的68.7%, 美国互联网扩散率从2000年22%增长到2007年76%。
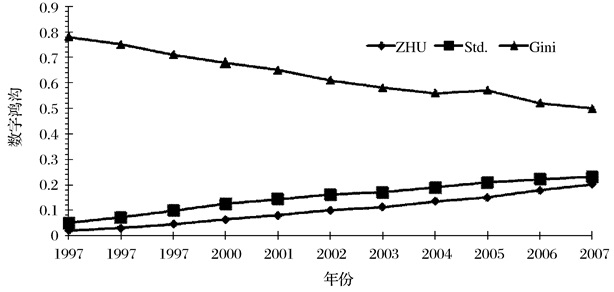
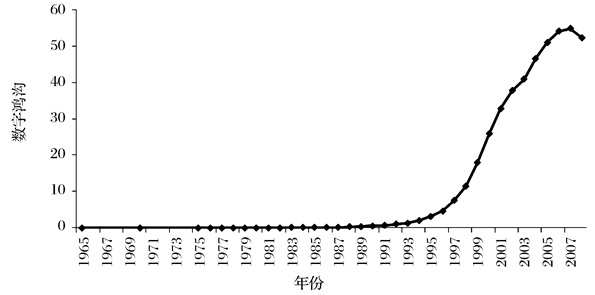
由于Gini系数算法和熵算法的高度相关性,我们采用三种数字鸿沟的计算指标来量化数字鸿沟,即标准差算法、Zhu算法以及基尼系数算法。如图 1所示,Zhu和标准差算法显示,全球不同国家的互联网数字鸿沟从1997年至2007年在不断扩大。与此同时,我们还计算了手机电话数字鸿沟的演化趋势。通过图 2可以看出,随着手机使用扩散率的提升,手机的数字鸿沟的演化呈“倒U”字型。具体而言,手机电话数字鸿沟在2007年扩散率为50%左右时达到顶峰。
|
图 1 全球互联网数字鸿沟演化趋势 |
|
图 2 全球手机数字鸿沟演化趋势 |
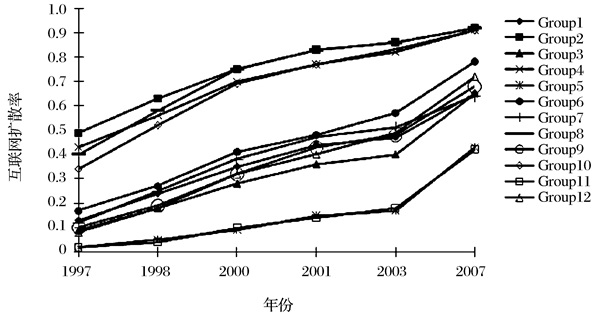
图 3a显示了美国自1997年到2007年的互联网扩散率的增长。如果按照年龄、教育、性别三个指标将人群分为12组,这12个群体显示出了明显的三种不同的趋势。互联网扩散率最高的第一集团(即组2、组4、组8和组10)是青年或中年人(低于35岁),具有较高教育水平。第一集团在1997年的互联网扩散率最高,到2007年,该群体的互联网采纳率已经接近100%。第二集团(即组3、组6、组7、组9和组12)是教育程度较低的中青年,以及教育程度较高的老年。第二集团的互联网扩散率在迅速追赶第一集团,在2007年,其互联网扩散率已经达到60%到70%。第三集团是教育程度较低的老年。尽管该集团的互联网扩散率出现了一定程度的增长,即1997年的10%到2007年的30%,但距离饱和点依然有很大距离。
|
图 3a 美国互联网扩散率演化趋势 |
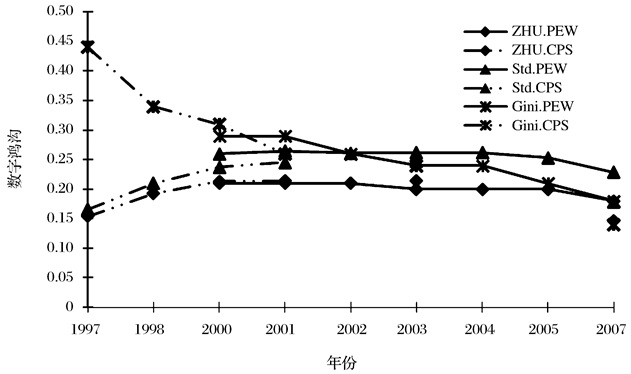
图 3b显示了来自两个独立数据库(CPS和PEW)的美国互联网数字鸿沟从1997年到2007年的演化趋势。Zhu算法(即ZHU.PEW和ZHU.CPS)和标准差算法(即Std.PEW和Std.CPS)显示,美国的互联网数字鸿沟演化也呈现出倒U字型,即在2003年互联网扩散率在59%时到达顶峰。与模拟的结果类似,基尼系数算法(即Gini.PEW和Gini.CPS)显示美国互联网数字鸿沟自产生之日起便在变小。这种结果显示了,基于方差的算法和基于比率的算法对数字鸿沟的演化刻画得更为细致。
|
图 3b 美国互联网数字鸿沟演化趋势 |
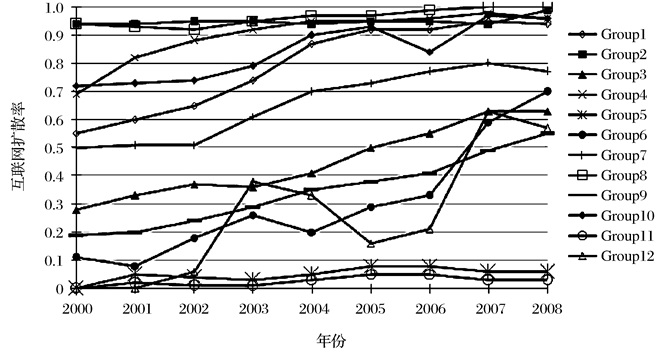
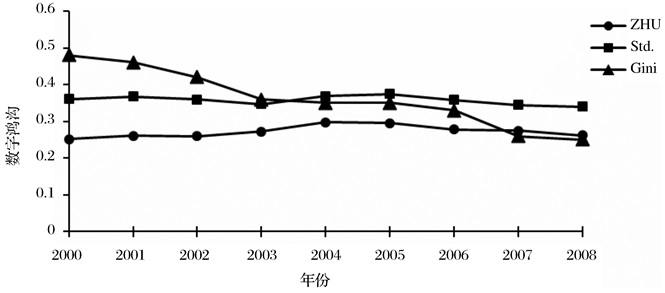
图 4a显示了香港自2000年到2008年的互联网扩散率的增长。与美国情况类似,图中出现了三大集团。第一集团(即组2、组4、组8和组10)为教育水平较高的组别。与美国不同,不同性别的人群在互联网扩散率上显示出了差异。即,在高学历人群中(组4和组10),互联网在男性中的扩散率要明显快于女性。第二集团(即组3、组6、组7、组9和组12)为教育程度较低的中年、教育程度较低的青年以及教育程度较高的老年。能够看出,男性和女性之间的差别依然存在。第三集团是组5和组11,即教育程度较低的老年人。香港的互联网数字鸿沟演化趋势与美国类似。如图 4b,Zhu算法(ZHU)和标准差算法(Std)显示,数字鸿沟的发展呈现出倒U字型,峰值在2003和2004年,其时扩散率为54%左右。
|
图 4a 香港地区互联网扩散率演化趋势 |
|
图 4b 香港地区互联网数字鸿沟演化趋势 |
数字鸿沟是一个已经在学界争论很久的问题,既往对数字鸿沟演化趋势研究所得结论不尽相同。这种不同可能由两种因素构成,其一,不同的研究使用的数字鸿沟测量方法不同;其二,各个地区国家的数字鸿沟演化趋势不同。
为了理清数字鸿沟的演化,我们首先利用模拟的方法,产生虚拟的数据,对基于比率的数字鸿沟算法(即基尼系数算法和熵算法)以及基于方差的算法(即Zhu算法和标准差算法)的敏感度进行检验。模拟结果显示,基于比率的算法对于数字鸿沟的刻画不敏感,即无论各群体采纳率的发展呈何种趋势,基于比率的算法皆不能敏感的显示群体间采纳差异的中心离散程度。相反,基于方差的算法则更为敏感。此外,我们还发现,基尼系数和熵的计算结果高度相关;而Zhu算法和标准差算法高度相关。
基于不同国家/地区的互联网和手机采纳数据,我们分别计算了全球以及地区间的数字鸿沟演化趋势。本研究发现,数字鸿沟的发展,在不同国家和地区,有着普遍规律可循。基于方差的算法显示,无论全球范围还是在某个地区,随着互联网采纳率的提升,数字鸿沟皆呈现出倒U字型的发展趋势;即数字鸿沟会先扩大随后缩小,且其峰值出现在总体扩散率达到50%左右时。此外,数字鸿沟的倒U演化趋势不仅仅在互联网这种媒体上适用,还适用于手机媒体。换言之,这种趋势可能适用于各种信息技术。未来的研究或许可以着重于使用不同类型的信息技术,计算多种信息技术的演化趋势。
综上所述,数字鸿沟的演化并非遵循“马太效应”路径或“瓶颈效应”。相反,随着互联网采纳扩散率的增长,不同阶层间的数字鸿沟在最初扩大,而最终会逐渐弥合。该发现对于媒体技术发展、媒介采纳等领域的政策制定具有一定启示意义。对于决策者而言,如何加快数字鸿沟的倒U字型发展趋势,从而使得数字鸿沟尽快弥合,或许是政策制定的关键。换言之,促进媒介技术的扩散,使其在社会-经济水平较低的阶层尽快普及,或许是促进数字鸿沟消弭的有效途径。而从长远视角来看,互联网技术的悲观论观点或许过于杞人忧天。互联网技术的发展,并未造成社会更深层次的不平等。相反,随着技术的发展,社会-经济地位较低的群体会在短短几年间逐步赶上社会——经济地位较高的群体,从而享受到新技术带来的便利。
2. City University of Hong Kong
| [1] | Dimaggio P., Hargittai E., Neuman R., Robinson J. Social implication of the Internet. Annual Review of Sociology, 2001, 27(1): 307-336. DOI: 10.1146/annurev.soc.27.1.307. |
| [2] | Martin S. P. Is the digital divide really closing? A critique of inequality measurement in a nation online. IT & Society, 2003, 1(4): 1-13. |
| [3] | Riccardini F., Fazio M.. Measuring the digital divide. IAOS Conference on Official Statistics and the New Economy, 2002. |
| [4] | Jin J., Cheong A. W. H. Measuring Digital Divide: The Exploration in Macao. Observatorio (OBS) Journal, 2008, 2(3): 259-2972. |
| [5] | Hargittai E. The digital divide and what to do about it. In D. C. Jones Ed., New Economy Handbook. San Diego, CA: Academic Press, 2005. |
| [6] | Vehovar V., Sicherl P., Husing T., Dolnicar V. Methodological challenges of digital divide measurements. The Information Society, 2006, 22(5): 279-290. DOI: 10.1080/01972240600904076. |
| [7] | Hoffman D. L., Novak T. P., Schlosser A. E. The evolution of the digital divide: How gaps in Internet access may impact electronic commerce. Journal of Computer-Mediated Communication, 2000, 5(3). |
| [8] | Jasso G., Kotz S. Two types of inequality: Inequality between persons and inequality between subgroups. Sociological Methods and Research, 2008, 37(1): 31-74. DOI: 10.1177/0049124108318971. |
| [9] | 祝建华.数码沟指数之操作定义和初步检验.载吴信训, 王军, 林爱君编.走向21世纪的新闻传播学研究.广东:汕头大学出版社, 2001: 203-211. |
| [10] | Chaffee S., Wilson D. Media rich, media poor: Two studies of diversity in agenda-holding. Journalism & Mass Communication Quarterly, 1977, 54(3): 466-476. |
| [11] | Mccombs M., Zhu J. Capacity, diversity, and volatility of the public agenda: Trends from 1954 to 1994. Public Opinion Quarterly, 1995, 59(4): 495-525. DOI: 10.1086/269491. |
| [12] | Shannon C. E., Weaver W. A mathematical theory of communication. Urbana: University of Illinois Press, 1949. |
| [13] | Krippendorff K. Information theory: structural models for qualitative data. London: Sage Publications, 1986. |
| [14] | Sciadas G. The digital divide in Canada. Ottawa : Statistic Canada. 2002. < http://publications.gc.ca/Collection/Statcan/56F0009X/56F0009XIE2002001.pdf > |
| [15] | U.S. Department of Commerce, Economics and Statistics Administration, National Telecommunications and Information Administration. A Nation Online: How Americans are expanding their use of the Internet. Washington, D.C. U.S.2002. |
| [16] | Chen W., Wellman B. The global digital divide: Within and between countries. IT & Society, 2004, 1(7): 39-45. |
| [17] | Rogers E. M.. Diffusion of Innovations. New York: Free Press, 2003. |
| [18] | Hsieh J. J. P.-A., Rai A., Keil M. Understanding digital inequality: comparing continued use behavioral models of the socio-economically advantaged and disadvantaged. Management information systems quarterly, 2008, 32(1): 97-126. |
| [19] | Kuznets S. Economic Growth and Income Inequality. The American Economic Review, 1995, XLV(1): 1-29. |
| [20] | Higgins M., Williamson H. G. Explaining inequality the world round: Cohort size, Kuznets Cures, and openness. NBER Working Paper 7224.1999. < http://www.nber.org/papers/w7224 > |
| [21] | Adelman I., Robinson S. Income distribution and development. In C. H. T. N. Srinivisan Ed., Handbook of Development Economics. New York: North Holland, 1989. |
| [22] | Aghion P., Bloton P. A theory of trickle-down growth and development. Review of Economic Studies, 1997, 64(2): 151-172. DOI: 10.2307/2971707. |
| [23] | OECD. Understanding the digital divide. Paris. 2001. < http://www.oecd.org/sti/1888451.pdf > |
 2013, Vol. 3
2013, Vol. 3
