自从Reynolds(1883年)的圆管实验以来, 转捩一直作为流体力学的核心问题之一而受到高度重视。由于转捩现象非常复杂, 所以转捩的研究进展缓慢, 到目前为止还没有转捩的完整理论。人们基于湍流产生的原因是层流边界层不稳定的认识, 把注意力主要集中在层流的失稳上。在不可压缩流动中, 稳定性理论为了解不稳定波的特点, 以及边界层失稳的细节, 发挥了十分重要的作用。尤其值得一提的是小扰动的线性稳定性理论结合实验的半经验“ E-N”方法, 对在低背景扰动环境下的平板以及轴对称边界层的转捩预测, 收到了较好的效果。
可压缩边界层的稳定性问题在相当长一段时间里, 没有引起人们的关注。人们试图用不可压流中已得到的结果来类推可压缩流动的稳定性。直到Mack[1]的许多重要工作后, 人们对可压缩流, 尤其是高超声速流的稳定性特点与不可压流的一些本质差别有了较多的了解。然而这些认识主要集中在平板的简单边界层上。随着航天技术的发展, 人们迫切需要了解象球锥这样典型外形的稳定性特点。因为, 它的转捩预测对再入体的落点精度分析和采用新型弹道的飞行器的热防护设计都十分重要。低湍流度高超声速风洞的建成为这项研究提供了重要手段。Stetson[2]等人的试验表明, 球锥边界层稳定性的复杂性远非平板可比。因为, 其稳定性要受到钝度比等其它因素的影响。现在已经清楚:(1)小钝度比使球锥边界层临界雷诺数比相应尖锥的临界雷诺数大得多; (2)小钝度比球锥边界层一旦失稳, 其扰动放大率迅速增加至远大于尖锥的扰动放大率; (3)钝度比对稳定性的影响存在一个域值, 当在此域值以内, 增大钝度比对边界层起稳定作用。当超过此域值, 则会在边界层外的熵层中产生无粘扰动, 并随熵吞进入边界层, 从而大大降低临界雷诺数。需要指出一点, 从Mack[3]对零迎角尖锥边界层稳定性的理论分析与Stetson的实验比较来看, 除最大放大率所对应的频率比较吻合外, 其它特征参数尚有明显差别。并且Stilla[4]、Lysenko[5]等人根据不同背景湍流度风洞的实验得出的转捩增长因子值也出入较大。因此, “E-N”方法用于高超声速边界层需要更加慎重和更加详细的实验数据, 或者说经验成分更大。但这并不等于说小扰动的线性理论在高超声速中失去意义。事实上, 它已经在了解高超声速边界层稳定性的特点上, 至少在定性上起了十分重要的作用。“E-N”法仍是目前比较可行的转捩预测方法。同时, 还应看到高超声速稳定性实验难度较大, 不可能做得很多、很细。因此, 理论分析有其不可替代的作用。
本文以数值方法求解的球锥组合体绕流流场为基本流。利用Malik的两点四阶紧致格式, 分析了在不同来流马赫数、雷诺数, 以及球锥以不同角速度绕体轴旋转等条件下球锥的稳定性特点, 并对转捩问题进行了讨论。
1 问题的数学描述计算几何外形是半锥角为10°的球锥。基本层流流场是基于数值方法求解完全气体条件下的“ N-S”方程, 得到零迎角球锥绕流的计算结果后, 利用在边界层坐标系下, 二维或轴对称可压缩定常流动的边界层方程, 并经Mangler, 以及Cebeci定义的可压缩形式的Falkner-skan变换, 在以静焓he = hw原则确定的边界层位置处, 与球锥绕流的数值计算结果耦合, 采用盒子格式推进求解球锥上的边界层方程, 从而得到较高精度的基本流场。
考虑到所讨论的对象为零迎角轴对称物体, 因此采用贴体的直角曲线坐标系。设(x, y, θ)分别为沿物面的流向、法向以及周向坐标, 相应拉梅系数表示为
| $ {H_1} = \frac{{{R_0} + y}}{{{R_0}}},\quad {H_2} = 1,\quad {H_3} = {r_0} + y\cos \lambda = r $ |
式中R0是球锥当地曲率半径, r0为当地锥半径, λ为球锥当地角。速度(u, v, w)为相应坐标上的分量。则该坐标系下的可压缩“ N-S”方程可表述为如下矢量形式
| $ \frac{{\partial \bar U}}{{\partial t}} + \frac{{\partial \bar E}}{{\partial x}} + \frac{{\partial \bar F}}{{\partial y}} + \frac{1}{r}\frac{{\partial \bar G}}{{\partial \theta }} = H $ | (1) |
式中U, E, F, G分别与笛卡尔坐标下守恒型“ N-S”方程中t, x, y, z对应的五元素矢量类似, H为流向及横向曲率影响产生的五元素矢量, 这里从略。
在研究中采用了准平行流假定, 这个假定意味着给定点处的平均物理量只是到物面距离, 即y的函数。在此前提下, 我们可以假定扰动量具有如下行进波的形式
| $ \mathit{\tilde \Phi }(x,y,\theta ,t) = \mathit{\hat \Phi }(y){{\rm{e}}^{i(\alpha x + m\theta - \omega t)}} $ |
其中Φ表示扰动变量如速度、温度、压力等。ω是扰动频率, α是流向波数, β是展(周)向波数。将瞬时流动参数(平均场+扰动)代入方程式(1)中, 再减去平均流物理量满足的方程, 并进行线性化后得到扰动所满足的线性稳定性方程。
| $ \begin{array}{c} - \frac{{p - \rho \tau }}{T}\left( {\omega - \alpha U - \frac{\beta }{{{r_0}}}W} \right) + \rho \left( {\alpha u + \frac{\beta }{{{r_0}}}w} \right) + {\rho _y}v + \rho {v_y} = 0\\ - \rho u(\omega - \alpha U - \frac{\beta }{{{r_0}}}W) + \alpha \left[ {p - \frac{2}{3}\mu \left( {2\alpha u - {v_y} - \frac{\beta }{{{r_0}}}w} \right)} \right] + \rho {U_y}v - \frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{T_y}\left( {{u_y} + av} \right) - \\ \mu \left( {{u_{yy}} - \alpha {v_y}} \right) - \left[ {\left( {\frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{U_{yy}} + \frac{{{{\rm{d}}^2}\mu }}{{{\rm{d}}{T^2}}}{T_y}{U_y}} \right)\tau + \frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{U_y}{\tau _y}} \right] - \frac{\beta }{{{r_0}}}\mu \left( {\frac{p}{{{r_0}}}u + \alpha w} \right) = 0\\ - \rho v\left( {\omega - \alpha U - \frac{\beta }{{{r_0}}}W} \right) - \alpha \mu \left( {{u_y} + \alpha v} \right) - \\ \frac{2}{3}\left[ {\frac{{{\rm{d}}\mu }}{{{\rm{d}}{T_y}}}\left( { - \alpha u + 2{v_y} - \frac{\beta }{{{r_0}}}w} \right) + \mu \left( { - \alpha {u_y} + 2{v_{yy}} - \frac{\rho }{{{r_0}}}{w_y}} \right)} \right] + \\ {p_y} - \frac{\beta }{{{r_0}}}\mu \left( {\frac{\beta }{{{r_0}}}v + {w_y}} \right) - \left( {\alpha \frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{U_y} + \frac{\beta }{{{r_0}}}\frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{W_y}} \right)\tau - \frac{\rho }{{{R_0}}}\left[ {\left( {\frac{p}{P} - \frac{\tau }{T}} \right){U^2} + 2Uu} \right] - \\ \frac{{\cos {\theta _f}}}{{{r_0}}}\rho \left[ {\left( {\frac{p}{P} - \frac{\tau }{T}} \right){W^2} + 2Ww} \right] = 0\\ - \rho w\left( {\omega - \alpha U - \frac{\beta }{{{r_0}}}W} \right) - \alpha \mu \left( {\frac{\beta }{{{r_0}}}u + \alpha w} \right) + \rho v{W_y} - \frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{T_y}\left( {\frac{\beta }{{{r_0}}}v + {w_y}} \right) - \\ \mu \left( {\frac{\beta }{{{r_0}}}{v_y} + {w_{yy}}} \right) - \left[ {\left( {\frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{W_{yy}} + } \right.} \right.\left. {\left. {\frac{{{{\rm{d}}^2}\mu }}{{{\rm{d}}{T^2}}}{T_y}{W_y}} \right)\tau + \frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{W_y}{\tau _y}} \right] + \\ \frac{\beta }{{{r_0}}}\left[ {p - \frac{2}{3}\mu \left( { - \alpha u - {v_y} + \frac{{2\beta }}{{{r_0}}}w} \right)} \right] = 0\\ - \frac{p}{{\gamma - 1}}\left( {\omega - \alpha U - \frac{\beta }{{{r_0}}}W} \right) + \frac{{\gamma P}}{{\gamma - 1}}\left( {\alpha u + \frac{\beta }{{{r_0}}}w} \right) - \alpha \left( {2\mu {U_y}v + 2k\tau } \right) + \\ \left[ {\gamma \frac{{{P_y}v + P{v_y}}}{{\gamma - 1}} - 2\mu {U_y}{u_y} - \frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{T_y}{U_y}u - \frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}{T_y}{W_y}w - 2\mu {W_y}{w_y} - \mu {W_{yy}}w - } \right.\\ \left. {\frac{{{\rm{d}}k}}{{{\rm{d}}T}}{T_y}{\tau _y} - k{\tau _{yy}}} \right] - \frac{\beta }{{{r_0}}}\left( {2\mu {W_y}v + k\frac{\beta }{{{r_0}}}\tau } \right) - \left[ {\frac{{{\rm{d}}\mu }}{{{\rm{d}}T}}\left( {U_y^2 + W_y^2} \right)\tau + \left( {\frac{{{\rm{d}}k}}{{{\rm{d}}T}}{T_{yy}} + \frac{{{{\rm{d}}^2}k}}{{{\rm{d}}{T^2}}}T_y^2} \right)\tau + } \right.\\ \left. {\frac{{{\rm{d}}k}}{{{\rm{d}}T}}{T_y}{\tau _y} + \left( {{\alpha ^2} + \frac{{{\beta ^2}}}{{r_0^2}}} \right)\frac{{{\rm{d}}k}}{{{\rm{d}}T}}\tau } \right] = 0 \end{array} $ | (2) |
式中为方便起见, 略去波动量的“ ^ ”, 并以α、β、ω代替iα、iβ、iω。(U、V、W、T、P)与(u、v、w、τ、p)分别代表流场基本流与扰动的流向、法向、周向速度、温度和压力, ρ代表基本流密度。比热比γ = 1.4, θf为半锥角, 动力粘性系数μ服从Sutherland公式, k为热传导系数。这实际上构成了关于Re, α, m和ω的特征值问题。在本文所涉及的二维平板或轴对称边界层条件下, m是实数。对时间模式而言α是实数, ω是复数, 反之, 则是空间模式。此时, 稳定性方程可表示成如下形式
| $ \left( {A{D^2} + BD + C} \right)\hat \phi = 0 $ | (3) |
其中
| $\left\{\begin{array}{ll}{y=0} & {u=v=w=\tau=0} \\ {y \rightarrow \infty} & {u=v=w=\tau \rightarrow 0}\end{array}\right.$ |
上述方程式(2)也可以表示为一阶微分方程系统。若令
| $ \frac{\mathrm{d} \bar{\psi}}{\mathrm{d} y}=\bar{A} \bar{\psi} $ | (4) |
式中A是8×8矩阵(可以用A、B、C导出)。
| $ {\bar \psi^k} - {\bar \psi^{k - 1}} = \frac{{{h_k}}}{2}\left( {\frac{{{\rm{d}}{{\bar \psi}^k}}}{{{\rm{d}}y}} + \frac{{{\rm{d}}{{\bar \psi}^{k - 1}}}}{{{\rm{d}}y}}} \right) - \frac{{h_k^2}}{{12}}\left( {\frac{{{{\rm{d}}^2}{{\bar \psi}^k}}}{{{\rm{d}}{y^2}}} - \frac{{{{\rm{d}}^2}{{\bar \psi}^{k - 1}}}}{{{\rm{d}}{y^2}}}} \right) + o\left( {h_k^5} \right) $ |
将方程式(4)离散
| $ \left( {I - \frac{{{h_k}}}{2}{{\bar A}^k}\frac{{h_k^2}}{{12}}{{\bar B}^k}} \right){\bar \psi^k} - \left( {I + \frac{{{h_k}}}{2}{{\bar A}^{k - 1}} + \frac{{{h_k}}}{{12}}{{\bar B}^{k - 1}}} \right){\bar \psi^{k - 1}} = 0 $ | (5) |
式中
| $ {\bar B^k} = \frac{{{\rm{d}}{{\bar A}^k}}}{{{\rm{d}}y}} + {\bar A^k} \cdot {\bar A^k} $ |
然后, 依据方程式(5)解特征值问题。
对可压缩流, 转捩预测仍然借用不可压缩流中的“ E-N”法, 若以代“* ”号的量表示为有量纲的量时, “ N-E”方法可表述为, 对于某一特定频率的扰动先找到其放大率从负转为正的点x*, 设该处扰动幅值为A0*, 当该扰动以
| $ N = \ln \left( {\frac{{{A^*}}}{{A_0^*}}} \right) = \int_{x_0^*}^{{x^*}} - T\left( {{x^*}} \right){\rm{d}}{x^*} $ |
对应于转捩点的大小应由相应实验确定。不同流动转捩所对应的N大小亦不同。
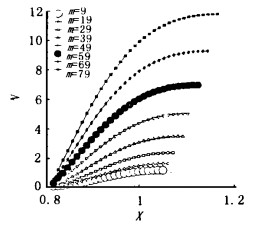
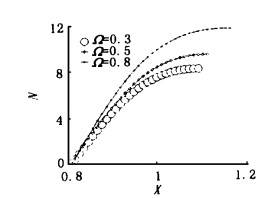
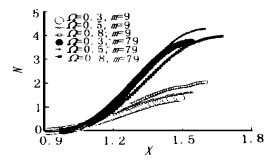
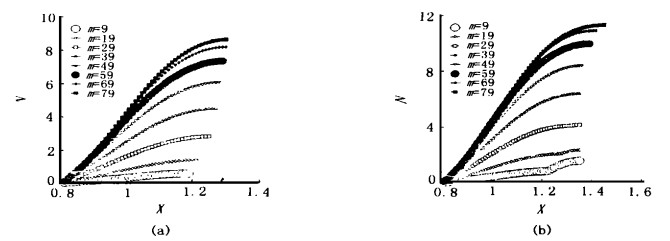
2 结果及分析由于考虑到钝锥端头前有一道弓形激波, 因而在波后的流速相对较低, 这样一来我们的计算域内整个或相当大的范围内找不到不稳定的第二模式。鉴于这种情况, 基于第一模式讨论球锥的稳定性特点和转捩预测。图 1分别表示在来流马赫数M∞ = 3, 雷诺数Re = 106条件下角速度Ω = 0.8(l/s)时, 不同周向波数的放大因子N随流向距离X的变化。由图可知放大因子N随周向波数的增加而增加。图 2反应了在同样来流条件下, 周向波数m = 79时, 在不同角速度情况下, 增长因子N随角速度的增加而增加。图 3中来流条件为M∞ = 7, Re = 106, (a)对应的角速度Ω = 0.3, (b)对应的角速度Ω = 0.8, 从该图我们发现来流马赫数较大时, 对应与最大N的周向波数并不是最大的。且随角速度的增加, 最大放大因子N所对应的周向波数会减小。图 4是在同一来流条件下, 周向波数m = 9, 79时放大因子在不同角速度下随流向坐标的变化曲线。由这张图我们看到, 当波数变大时, 最大因子逐渐由较大角速度移到较小角速度上。若把不同来流条件的四组图对照起来, 不难看出, 马赫数增大使流动趋于稳定。图 5与图 6对应的来流条件分别为M∞ = 5, Re = 106和M∞ = 5, Re = 107。这两组图都分别对应的是角速度Ω = 0.3, 0.8时放大因子随流向坐标的变化曲线。两组图对照起来, 我们不难看到来流雷诺数增大将使流动更不稳定, 而且周向速度越大, 反应越大。同时也使得最大放大因子向大周向波数方向移动。若都以N = 9作为判断转捩的准则, 我们将在表 1中看到在不同流动状态, 以及不同波角的扰动条件下的转捩位置。
|
图 1 在M∞ = 3, Re = 106时, 对在不同周向波数最大放大频率下的放大因子N随距离X的变化 Fig.1 N factor Variation with position X and azimuthal wave number for the most amplified frequence at M∞ = 3.0, Re = 106 |
|
图 2 在M∞ = 3, Re = 106时, 对在不同周向速度最大放大频率下的放大因子N随距离X的变化 Fig.2 N fact or Variation with position X for the azimuthal speed and the most amplified frequence at M∞ = 3, Re = 106 |

|
图 3 M∞ = 7, Re = 106对在不同周向波数最大放大频率下的放大因子N随距离X的变化 Fig.3 N fact or Variation with position X for the azimuthal wave number and the most amplified frequence at M∞ = 7.0, Re = 106 |
|
图 4 M∞ = 7, Re = 106在最大放大频率下的放大因子N随距离X的变化 Fig.4 N factor Variation with position X for the azimuthal speed and the most amplified frequence at M∞ = 7.0, Re = 106 |

|
图 5 M∞=5, Re=106时,对在不同周向波数最大放大频率下的放大因子N随距离X的变化 Fig.5 N fact or Variation with position X for the azimuthal wave number and the most amplified frequence at M∞ = 5.0, Re = 106 |
|
图 6 M∞=5, Re=107时,对在不同周向波数最大放大频率下的放大因子N随距离X的变化 Fig.6 N fact or Variation with position X for the azimuthal wave number and the most amplified frequence at M∞ = 5.0, Re = 107 |
| 表 1 不同条件下的转捩位置 Table 1 Transition position at dif f erent condition |
|
|
由表 1可知, 在来流马赫数不太大, 或来流雷诺数较高时, 并且有较大的周向速度时转捩点更靠前, 此时, 周向波数也较大。
定性地说, 在飞行器再入大气层时, 在初始阶段, 即马赫数还很高时, 发生转捩的可能性较小。随着飞行器的下降, 马赫数减小, 雷诺数增加, 将发生转捩。且转捩点会朝前移动, 这与实验得到的结论是一致的。当然, “ E-N”法是个半经验法, 究竟N应取多大, 必须与实验或飞行器遥测的数据结合起来, 才能确定。
袁湘江衷心感谢中国空气动力研究与发展中心的张涵信教授, 在本文完成过程中所给予的热情帮助和支持; 并特别感谢中国空气动力研究与发展中心的黎作武博士为本文提供了球锥绕流的数值计算结果。
| [1] |
Mack L M. Boundary Layer Linear Stability Theory. AGARD Report No.709, June 1984.
|
| [2] |
Stetson K F, Thompson E R, Donaldson J C, Siler L G, Laminar Boundary Layer Stability Experiments on a Coneat Mach 8, Part 2: Blunt Cone, AIAA paper, 84-0006, 1984.
|
| [3] |
Mack L M. Stability of Axisymmetric Boundary Layerson Sharp Cones at Hypersonic Mach Numbers, AIAA Paper, 87-1413, 1987.
|
| [4] |
Stilla J. Engineering Transition Prediction for a Hypersonic Axisymmetric Boundary Layer, AIAA Paper, 93-5114.
|
| [5] |
Lysenko V I. Stability Characteristics of a Supersonic Boundary Layer and Their Relation to the Position of the Laminar-Turbulent Transition Point, NASATM -88533.
|
 1999, Vol. 17
1999, Vol. 17
