为满足民用方面日益严格的适航噪声要求和军用方面声隐身能力提升需求,直升机的噪声问题需要持续深入研究[1-2]。旋翼气动噪声作为直升机的最主要噪声源之一,对其进行准确预估是十分必要的[3-4]。目前直升机旋翼噪声预测领域的大部分研究都集中在开发工具上,这些基于桨叶几何外形输入的计算模型在设计阶段就能够确定旋翼噪声特性[5-9]。
对于飞行中的直升机,其旋翼桨叶运动是非常复杂的。除了跟随机体的运动(加速、滚转、倾转、偏航)和自身的旋转运动(耦合变距、挥舞、摆振),桨叶几何外形还会经历显著的弹性形变,包括弯曲和扭转。弹性形变对于旋翼气动力存在很大影响。当桨叶在负载作用下扭转时,局部的迎角可能和刚性桨叶运动时所设置的迎角有很大不同。相应的,这一现象会改变桨叶表面的升力和阻力分布,同样也会影响桨叶尾迹。旋翼桨叶在结构上是细长的柔性体,尤其是目前的桨叶大多采用复合材料,在负载的作用下可以轻易使桨尖位置弯曲超出旋翼平面一倍弦长,相应的会影响桨尖涡位置和桨涡干扰的方向。任何气动力方面的改变都会通过载荷噪声部分来影响声学特性。因此,在设计阶段将刚性桨叶外形作为模型输入是不准确的。
研究者们意识到了这一点,开始考虑桨叶弹性形变。在之前大多数考虑桨叶形变研究中,使用包含柔性桨叶动力学和空气动力学的载荷计算,用来使声学代码能够分析大部分由于桨叶形变带来的噪声影响。但是,这些研究在噪声计算方面并没有考虑桨叶的弹性形变,导致噪声预测是不准确的[10-11]。载荷噪声并非只与载荷相关,而且还和声源位置和声源位置的时间导数有关,精确的载荷计算并不足以纠正这些声源位置和运动的错误。进一步讲,旋翼平面内的噪声主要是厚度噪声,厚度噪声强烈的依赖于桨叶表面的位置、速度和加速度。这些量都需要根据桨叶弹性形变进行重新计算。
鉴于此,本文基于Camrad Ⅱ软件和FW-H方程建立旋翼悬停气动噪声计算模型,旋翼桨叶几何外形和旋翼非定常载荷计算均考虑了桨叶弹性形变的影响。旋翼的操纵量、形变量和非定常载荷均由Camrad Ⅱ软件计算得到。采用三维网格对形变桨叶的外形进行精确描述,结合Camrad Ⅱ计算得到的旋翼非定常载荷,之后基于FW-H计算方法进行形变旋翼悬停气动噪声计算。在风洞中采用双目立体视觉方法对模型旋翼进行形变测量试验,将Camrad Ⅱ的仿真数据与试验数据进行对比分析,验证Camrad Ⅱ计算桨叶形变的能力。最后,针对全尺寸旋翼的悬停噪声进行计算,分析桨叶形变对气动力和噪声的影响。
1 计算方法 1.1 旋翼载荷及形变计算Camrad Ⅱ软件具有强大的旋翼飞行器综合分析能力,在直升机领域中应用广泛。本文采用Camrad Ⅱ软件计算旋翼桨叶的非定常气动载荷,经数据后处理程序计算得到桨叶固定坐标系下沿桨叶展向分布的升力系数,配平后的旋翼操纵量也可以相应得到。
为考虑桨叶弹性形变的影响,分别采用Camrad Ⅱ的刚性桨叶模型和弹性桨叶模型计算形变前后的桨叶操纵量、桨叶外形和旋翼非定常载荷。桨叶截面翼型的形变量在本文中被合理忽略,Camrad Ⅱ只对桨叶扭转和弯曲变形进行仿真。非定常载荷计算中选用Camrad Ⅱ自带的配平模块。
1.2 声学计算方法FW-H方程是计算旋翼气动噪声的经典方程。对于亚声速状态的旋翼噪声,Farassat 1A公式(以下通称F 1A公式)是FW-H方程解的时域积分表达式:
| $p'\left( {\boldsymbol{x} ,t} \right) = {p'_T}\left( {\boldsymbol{x} ,t} \right) + {p'_L}\left( {\boldsymbol{x} ,t} \right)$ | (1) |
式中:
| $\begin{split} 4{\text{π}} {{p'}_T}(\boldsymbol{x} ,t) =& \int\limits_{f = 0} {{{\left[ {\frac{{{\rho _0}({{\dot v}_n} + {v_n})}}{{r{{\left| {1 - {M_r}} \right|}^2}}}} \right]}_{{\rm{ret}}}}{\rm{d}}S} + \\& \int\limits_{f = 0} {{{\left[ {\frac{{{\rho _0}{v_n}(r{{\dot M}_r} + {a_0}({M_r} - {M^2}))}}{{{r^2}{{\left| {1 - {M_r}} \right|}^3}}}} \right]}_{{\rm{ret}}}}{\rm{d}}S} \end{split}$ | (2) |
| $\begin{split} 4{\text{π}} {{p'}_L}(\boldsymbol{x} ,t) =& \frac{1}{{{a_0}}}\int\limits_{f = 0} {{{\left[ {\frac{{{{\dot l}_r}}}{{r{{\left| {1 - {M_r}} \right|}^2}}}} \right]}_{{\rm{ret}}}}{\rm{d}}S} + \\& \int\limits_{f = 0} {{{\left[ {\frac{{{l_r} - {l_M}}}{{{r^2}{{\left| {1 - {M_r}} \right|}^2}}}} \right]}_{{\rm{ret}}}}{\rm{d}}S} {\rm{ + }} \\& \frac{1}{{{a_0}}}\int\limits_{f = 0} {{{\left[ {\frac{{{l_r}(r{{\dot M}_r} + {a_0}({M_r} - {M^2}))}}{{{r^2}{{\left| {1 - {M_r}} \right|}^3}}}} \right]}_{{\rm{ret}}}}{\rm{d}}S} \end{split}$ | (3) |
以上公式的详细推导和参数定义可参考文献[12]。公式(3)中的桨叶表面分布载荷一般由CFD方法提供。
综合分析软件通常不能计算公式(3)中桨叶表面压力分布的载荷,而是输出沿展向分布的桨叶截面升力。一种不需要桨叶表面压力分布的载荷噪声预测方法就是基于紧致源模型,将F 1A公式中的载荷噪声部分写成紧致源形式[13-14]:
| $\begin{split} 4{\text{π}} {{p'}_L}\left( {\boldsymbol{x} ,t} \right) =& \frac{1}{{{a_0}}}\int_0^R {{{\left[ {\frac{{{{{\dot {\boldsymbol{L}}}}_r}}}{{r{{\left| {1 - {M_r}} \right|}^2}}}} \right]}_{{\rm{ret}}}}{\rm{d}}l\left( y \right) + } \\& \int_0^R {{{\left[ {\frac{{{{\boldsymbol{L}}_r} - {{\boldsymbol{L}}_M}}}{{{r^2}{{\left| {1 - {M_r}} \right|}^2}}}} \right]}_{{\rm{ret}}}}{\rm{d}}l\left( y \right)} {\rm{ + }} \\& \frac{1}{{{a_0}}}{\int_0^R {\left[ {\frac{{{{\boldsymbol{L}}_r}\left( {r{{\dot M}_r} + {a_0}\left( {{M_r} - {M^2}} \right)} \right)}}{{{r^2}{{\left| {1 - {M_r}} \right|}^3}}}} \right]} _{{\rm{ret}}}}{\rm{d}}l\left( y \right) \end{split} $ | (4) |
以上公式的详细推导和参数定义可参考文献[15]。文献[15]充分对比了Camrad Ⅱ/FW-H模型和CFD/FW-H模型,发现两种方法的计算精度相当,尤其对于悬停状态。本文将使用Camrad Ⅱ/FW-H模型进行噪声计算。
1.3 桨叶表面网格划分悬停状态下旋翼在每个方位角受到相同的负载,导致旋翼在旋转过程中的弹性形变是一样的,因此仅需要根据某一方位角下的形变量对桨叶外形进行网格划分。
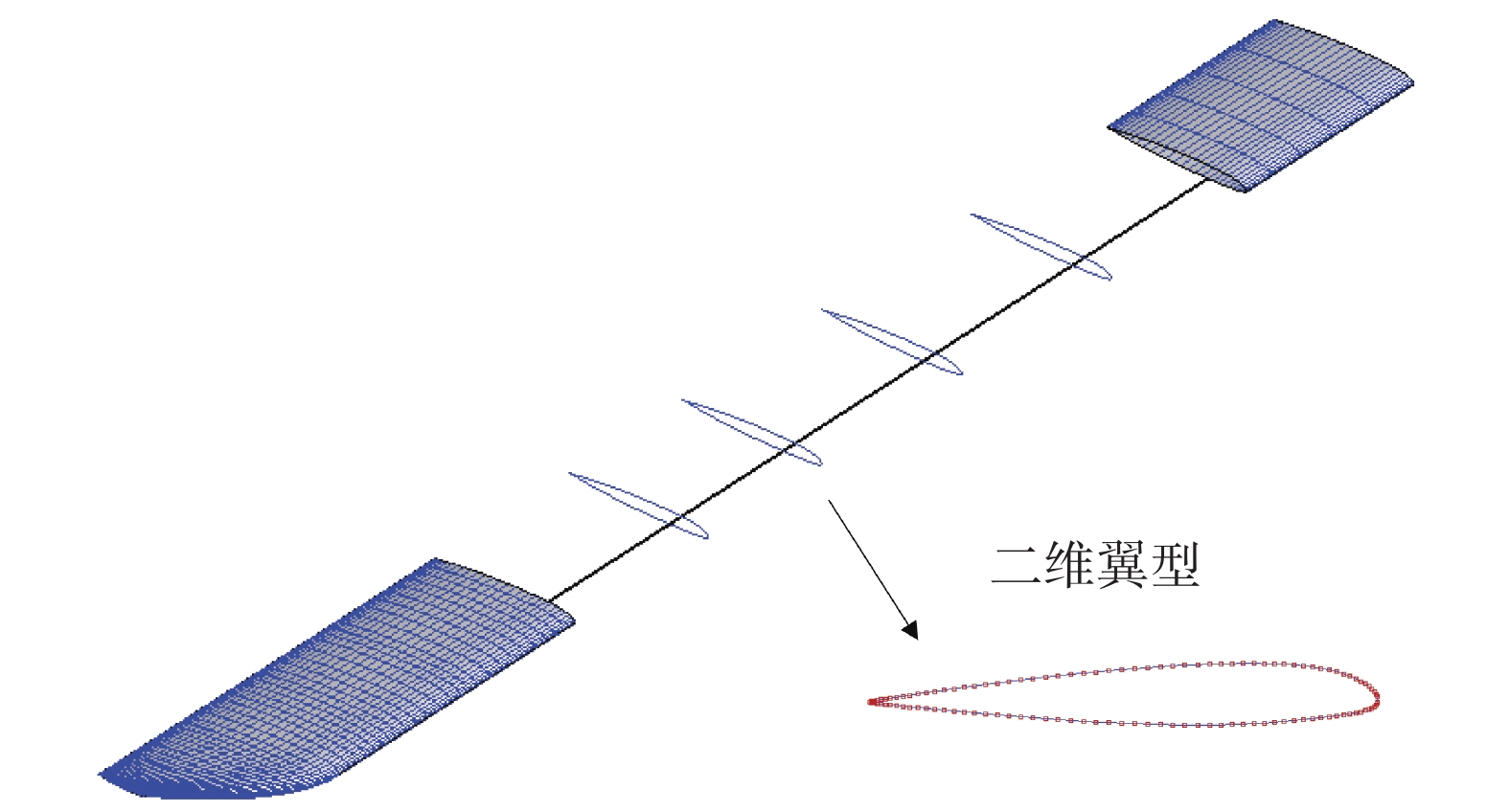
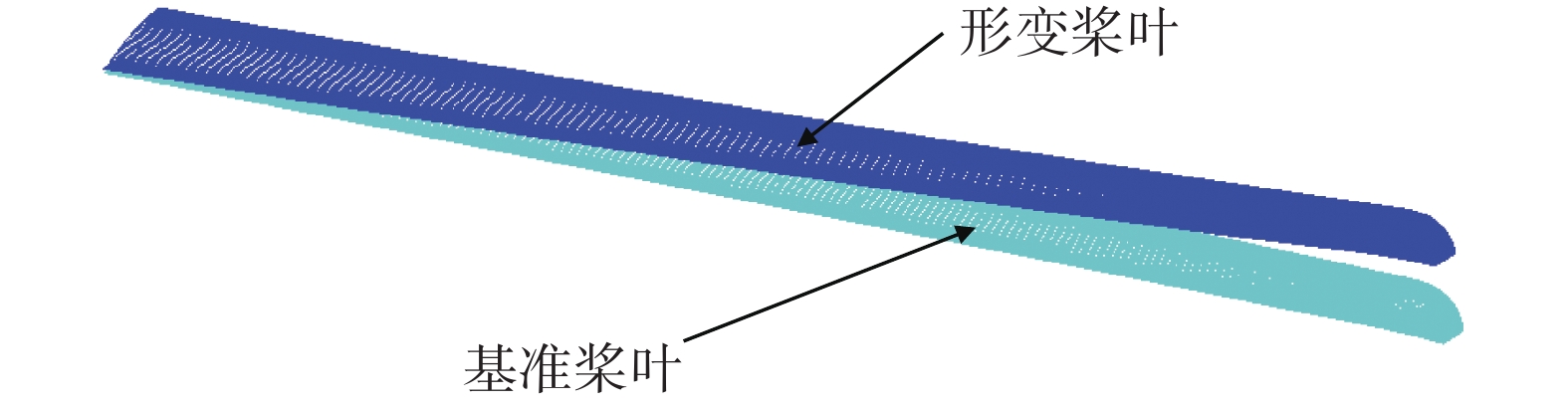
桨叶表面网格划分的简要步骤如下:首先将桨叶分解为二维翼型和一维展向站位点[15-16],之后将二维翼型按照展向站位点进行平铺,最后根据基准量和弹性形变量对各个站位的二维翼型进行坐标变换,得到桨叶表面的三维面网格,如图1所示。详细步骤可参考文献[16]。桨叶形变前后的示意图如图2所示。
|
图 1 单片桨叶网格划分 Fig.1 Grid for a single blade |
|
图 2 桨叶形变前后示意图 Fig.2 Original and deformed blades |
Camrad Ⅱ计算桨叶非定常载荷的能力已经在文献[17]中得到验证,但文献[17]中对Camrad Ⅱ计算桨叶形变能力的验证不充分。本文基于双目立体视觉方法对直升机旋翼桨叶形变进行测量[18-20],用于对比分析Camrad Ⅱ计算桨叶形变的能力。同时,还将对考虑桨叶弹性形变的旋翼悬停气动噪声计算模型进行验证。
2.1 桨叶形变测量设备与方法在中国空气动力学研究与发展中心4 m×5.5 m声学风洞开展了3 m级直径模型旋翼风洞试验,测量了模型旋翼的性能数据和形变数据。试验中采用无铰式桨榖,模型旋翼具有5片桨叶,直径为3 m,桨尖速度为221 m/s。桨叶弦长0.095 m,桨尖抛物线后掠,线性扭转。
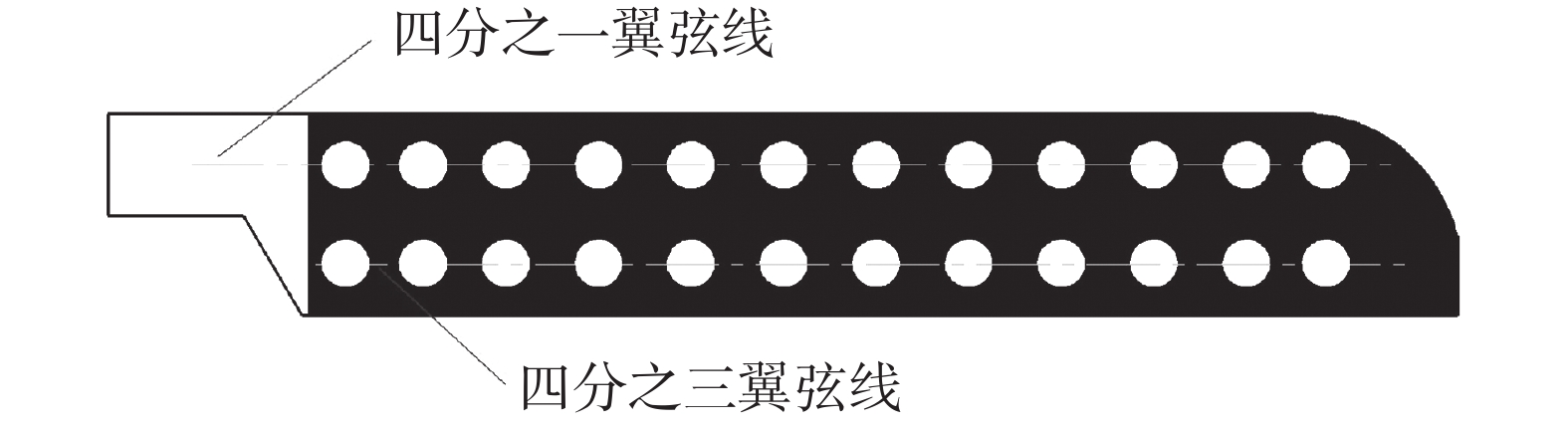
试验前,在旋翼桨叶表面1/4弦线和3/4弦线处粘贴具有唯一编码信息的标记点,如图3所示。
|
图 3 桨叶表面标记点布置示意图 Fig.3 Schematic diagram of sprayed markers on the blade |
试验中,采用高频激光器对稳定运转后的旋翼进行瞬态照明,照明同步触发两部高速相机进行桨叶图像采集。
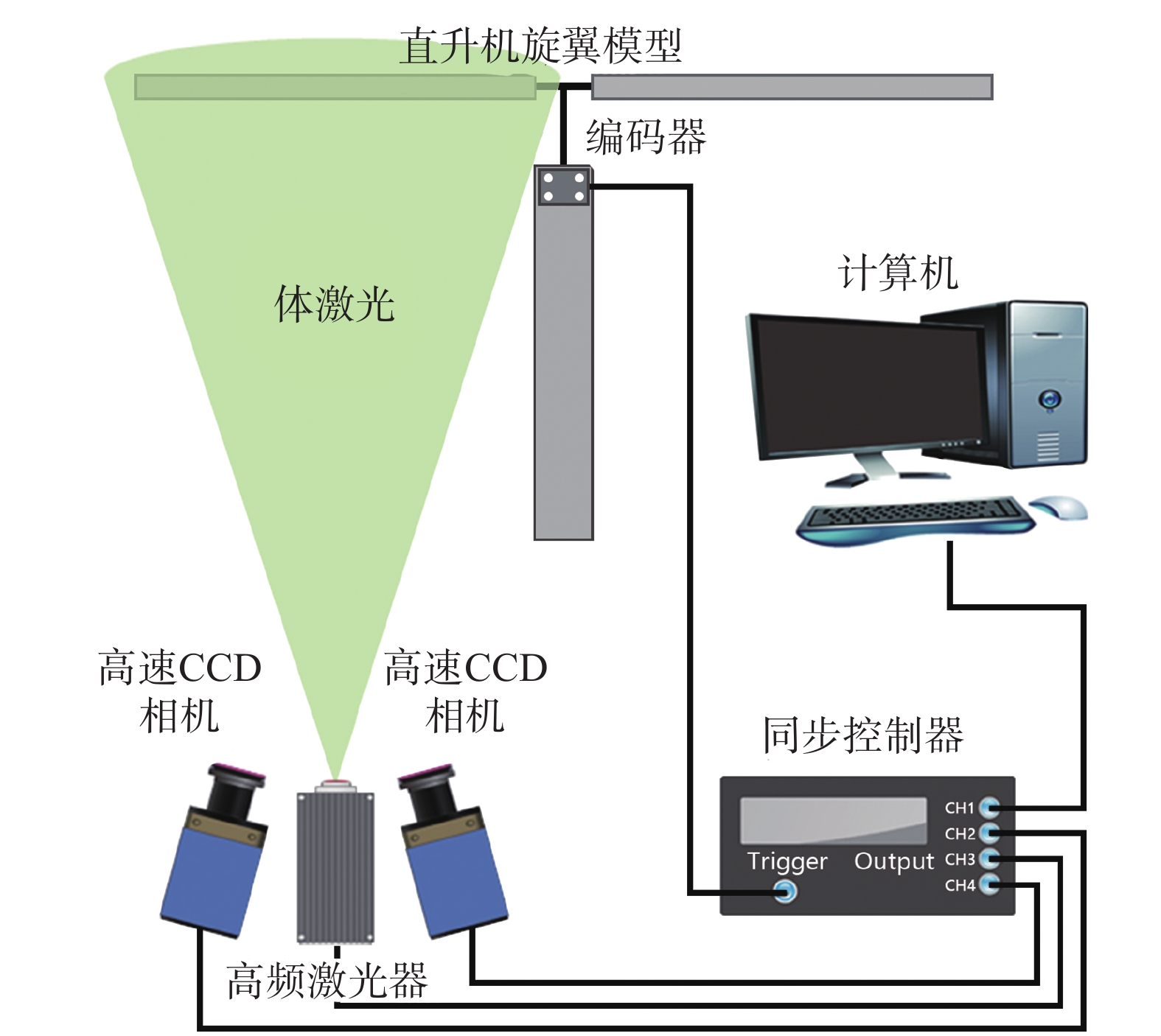
试验后,基于双目立体视觉原理对图像进行处理,计算得到所有标记点的三维坐标。最后,与基准状态进行对比,可以进一步得到旋翼桨叶的形变参数,在试验中忽略了翼型的几何外形变化。双目成像系统结构如图4所示,详细的测量原理可以参考文献[20],这里不再赘述。
|
图 4 双目成像系统结构[20] Fig.4 Binocular imaging system |
由于旋翼模型桨叶重力的作用,在静止状态下,桨尖挥舞位移相对桨盘平面为负值,因此试验中选取50 r/min、0°总距状态为基准状态,即认为这一状态下桨叶的挥舞位移和扭转形变量几乎为0。Camrad Ⅱ计算与试验的结果均扣除了50 r/min、0°总距状态下的桨叶基准形变量。
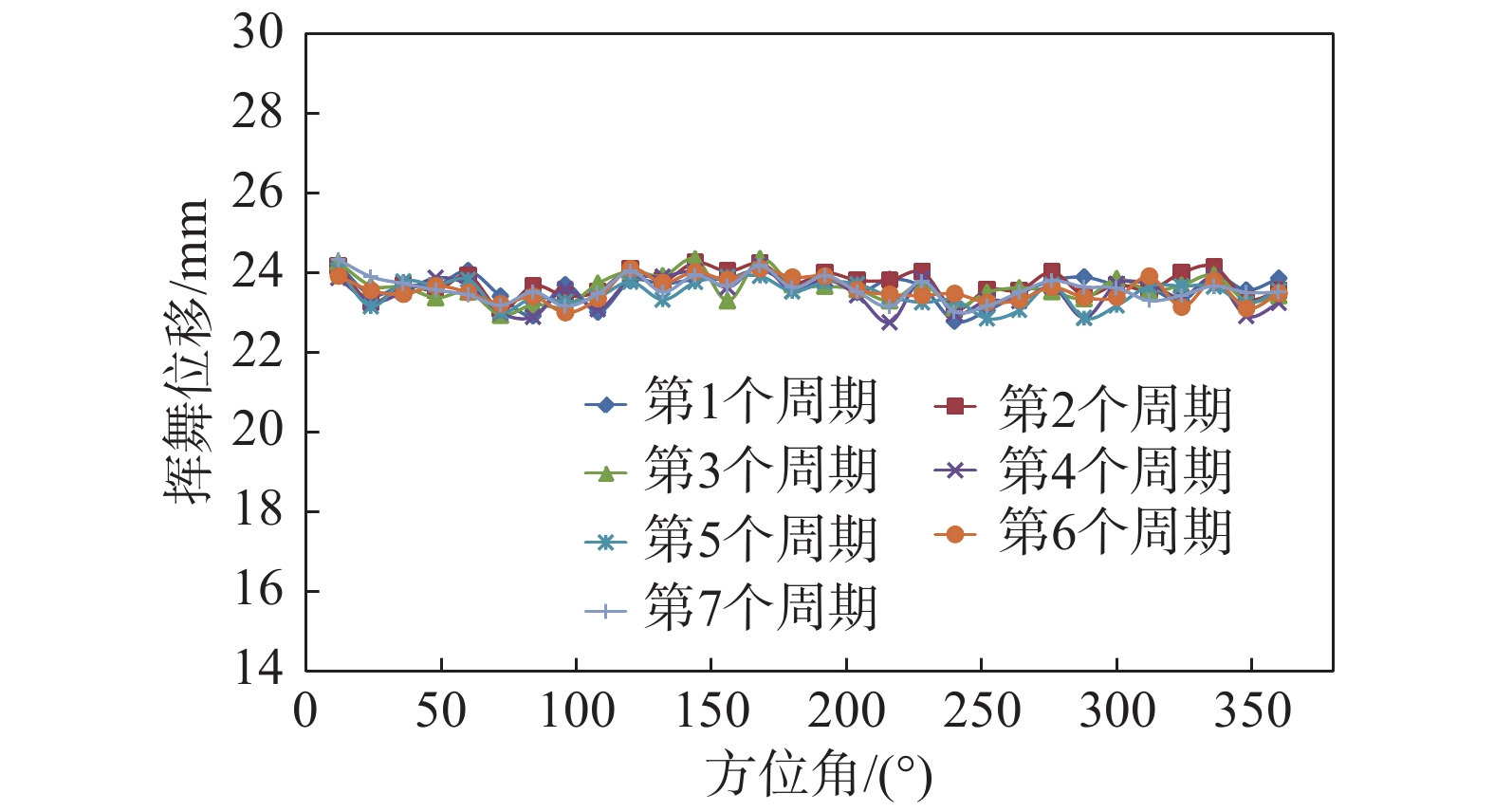
图5给出了旋翼桨叶形变测量重复性试验结果,对应的总距为8°、位置为0.7R。本文定义向上挥舞为正,与旋转方向相反的摆振为正。试验中每隔12°方位角对旋翼桨叶采集一次图像,进行桨叶形变分析。由于悬停状态几乎没有挥舞一阶量,因此在各方位角处测得的挥舞形变量相差不大。从图中可以看出,桨叶挥舞位移的七次重复性试验数据都重合得很好,证明了本次试验数据的有效性和可靠性。图6和图7中的试验结果均为一个周期各个方位角试验值算数平均后的结果。
|
图 5 悬停状态重复试验结果对比(总距8°、r = 0.7R) Fig.5 Repeatability test results of a blade in hover (Collective pitch = 8°, r = 0.7R) |
|
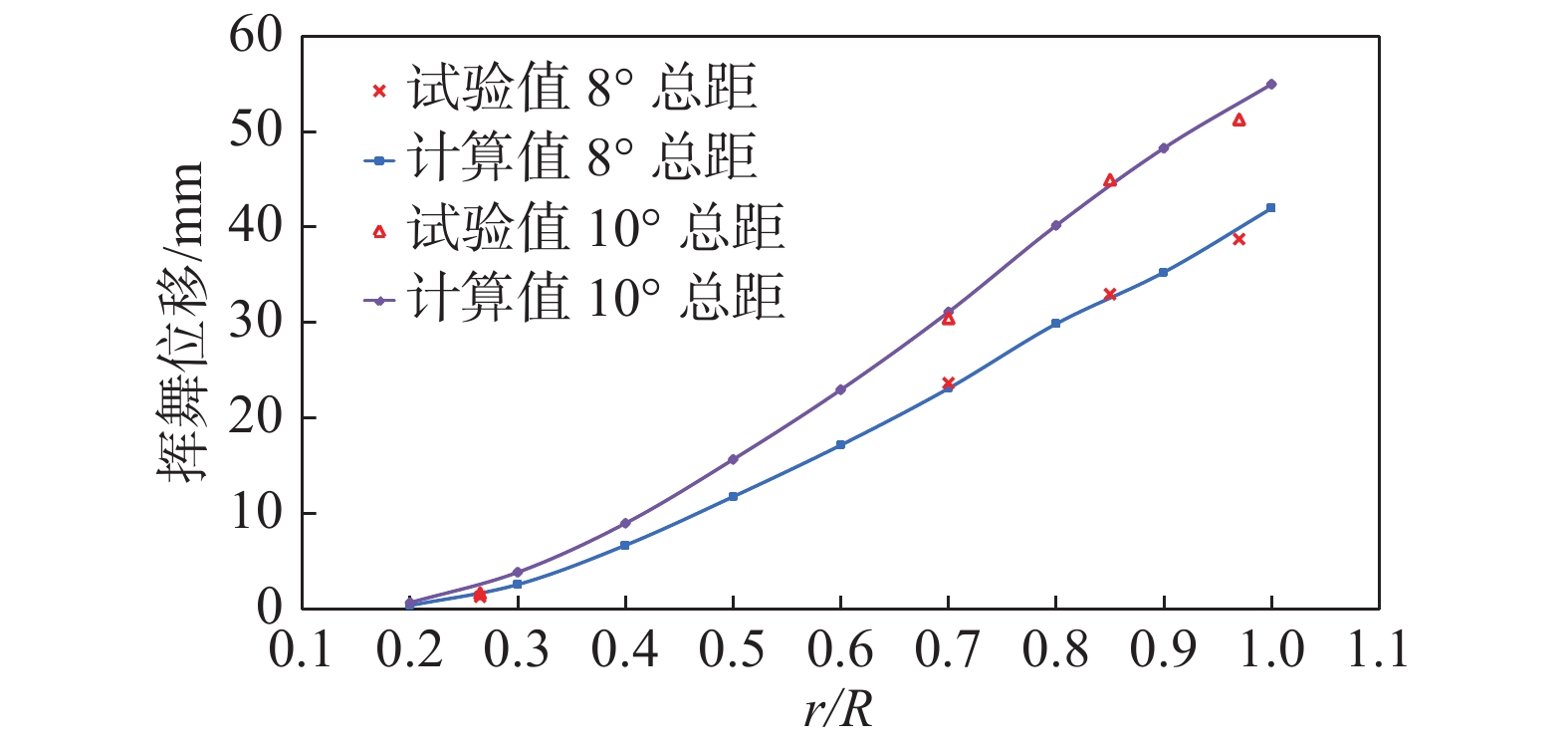
图 6 挥舞位移量对比 Fig.6 Comparison of the flap deformation |
|
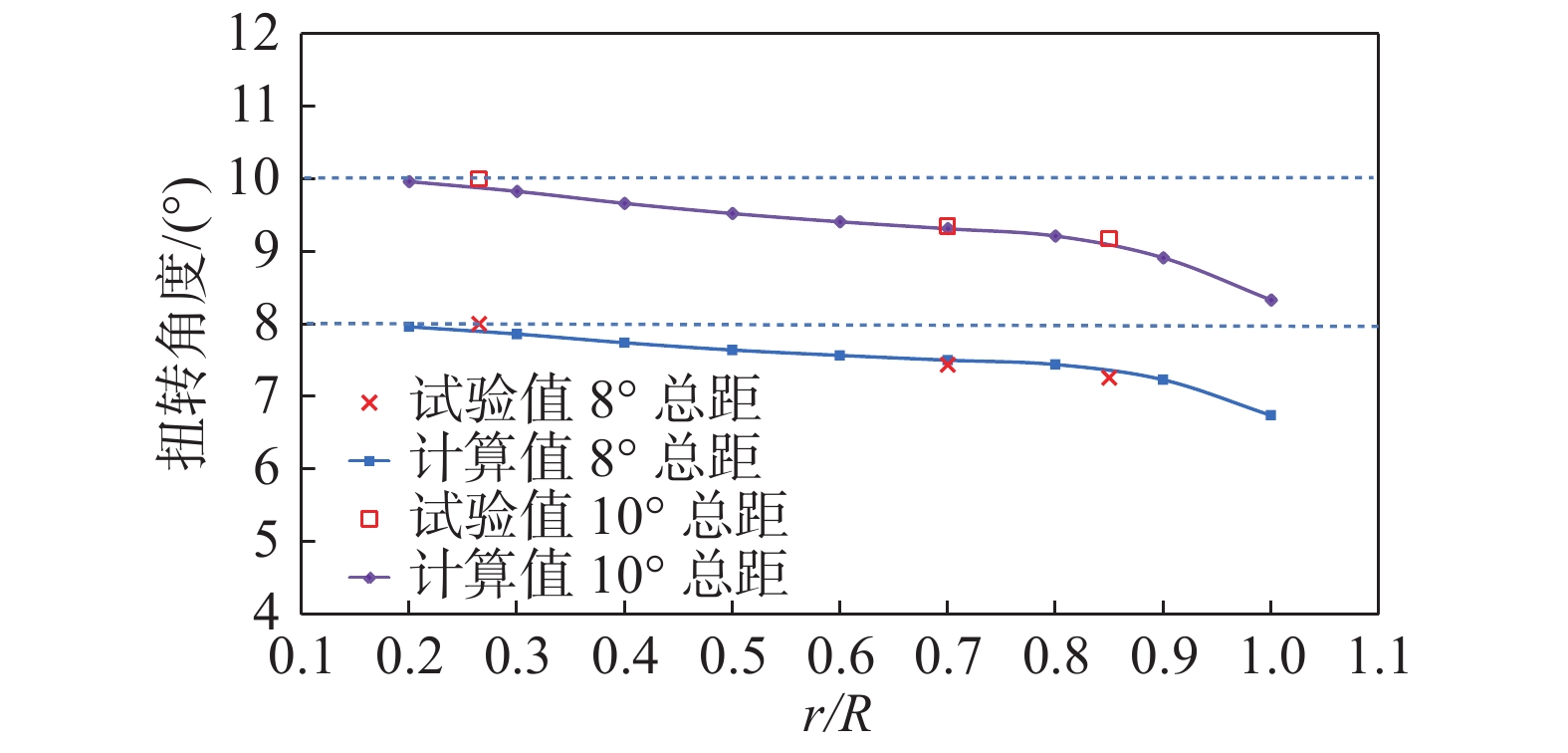
图 7 桨叶扭转角度对比 Fig.7 Comparison of the twist deformation |
图6为不同总距下桨叶挥舞位移试验与计算对比结果。由图中可以看出,随着总距增加,旋翼桨叶挥舞位移随之增大。Camrad Ⅱ计算得到的桨叶挥舞位移无论从趋势还是位移量方面均与试验结果吻合较好。针对10°总距的状态,桨尖沿挥舞方向的位移量达到0.5倍弦长。
图7为不同总距下桨叶扭转角度试验值与计算值对比结果,其中忽略了桨叶自身的扭转角。由于桨尖采用尖削结构,无法布置两个标记点,导致扭转角测试不准确,因此试验值并没有选在桨尖区域。从图中可以看出,Camrad Ⅱ计算得到的桨叶扭转角度与试验结果吻合较好。
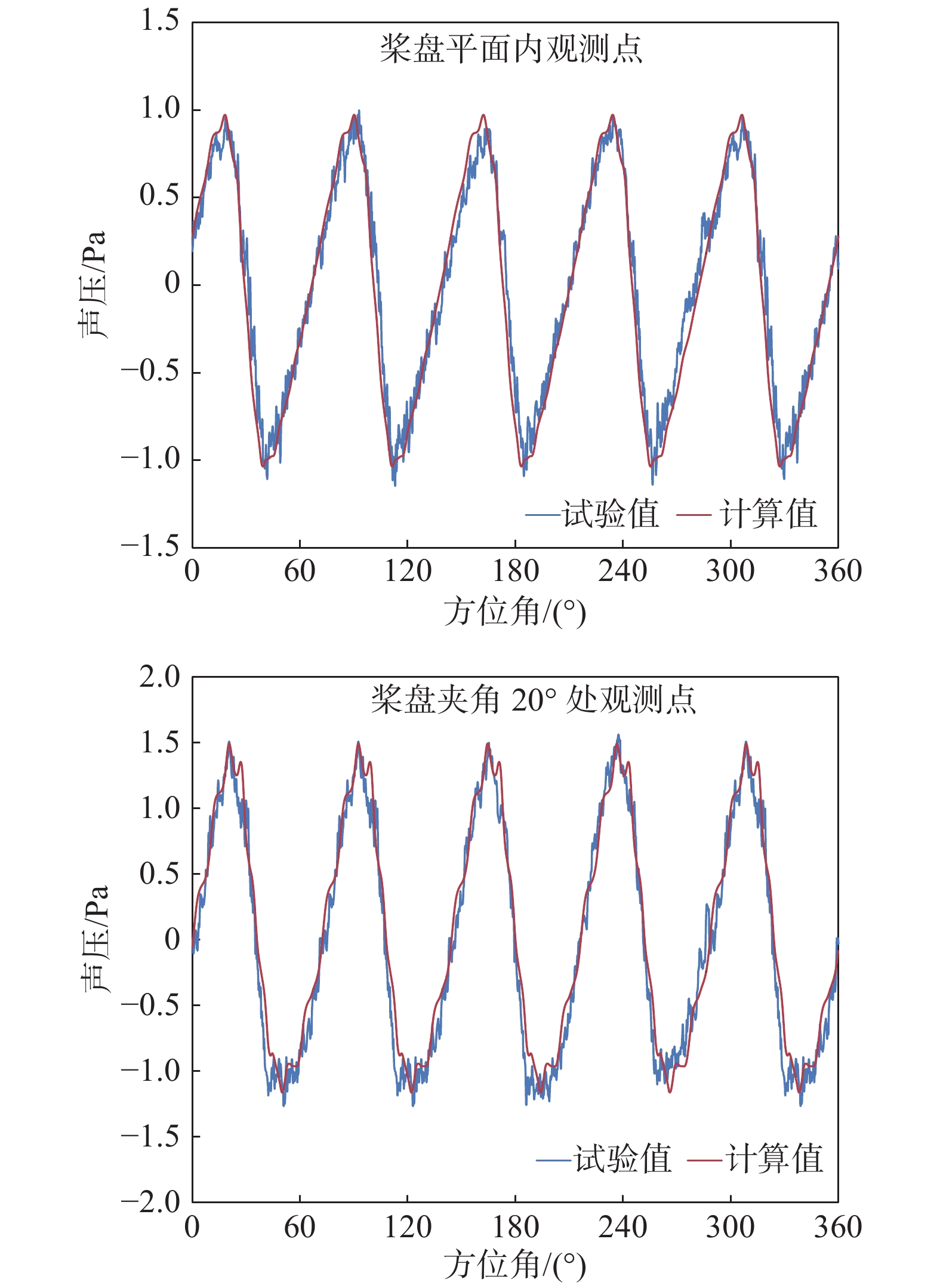
2.3 噪声计算方法验证在中国空气动力学研究与发展中心4 m×5.5 m声学风洞开展了2 m级直径模型旋翼风洞试验,测量了模型旋翼的性能数据和噪声数据。试验中的模型旋翼具有5片桨叶,直径为2 m。桨叶弦长0.062 m,桨尖抛物线后掠,线性扭转。试验中桨尖转速为208.3 m/s。图8中给出了桨盘平面内和桨盘夹角20°处声压历程的本文计算值与试验值对比。
|
图 8 模型旋翼声压时间历程对比 Fig.8 Time histories of sound pressure obtained by the experiment and numerical simulation |
从图中可以看出,本文建立的旋翼噪声计算模型计算得到的观测点处的声压历程与试验值吻合得很好,表明了本文建立的方法的有效性。
3 计算与分析本节针对全尺寸旋翼进行悬停状态噪声计算,分析了桨叶形变对噪声辐射特性的影响。此外,还对桨叶形变量和气动力特性进行了分析。
3.1 计算模型为开展桨叶形变对旋翼悬停状态气动噪声特性的影响分析研究,选用一副全尺寸旋翼作为研究对象。采用的旋翼半径为6.75 m,具有5片桨叶。桨叶采用的翼型为OA309,桨叶弦长0.42 m,桨尖抛物线后掠,−12°线性扭转。旋翼额定桨尖速度为216.4 m/s。
在对比噪声的计算结果时,必须保证是在旋翼负载相同的情况下,因此,必须要进行配平计算。选取该全尺寸旋翼典型使用状态下的拉力系数0.015作为配平目标量。
本文选取纵向平面内桨盘夹角0°~80°(桨盘下方)的9个观测点进行噪声计算,观测点与桨盘中心的距离为5R。观测点布置如图9所示。
|
图 9 观测点位置示意图 Fig.9 Diagram of the acoustic observing points |
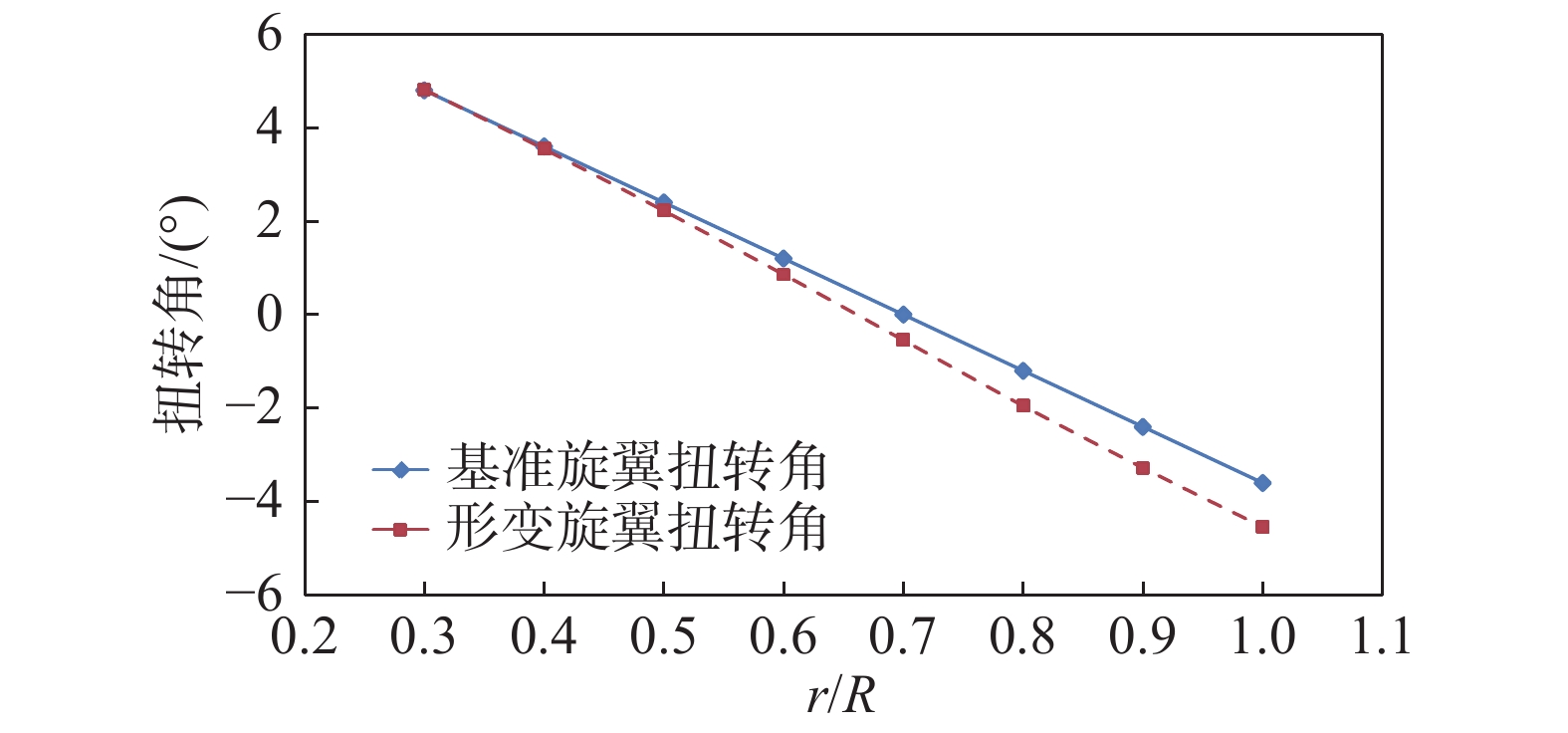
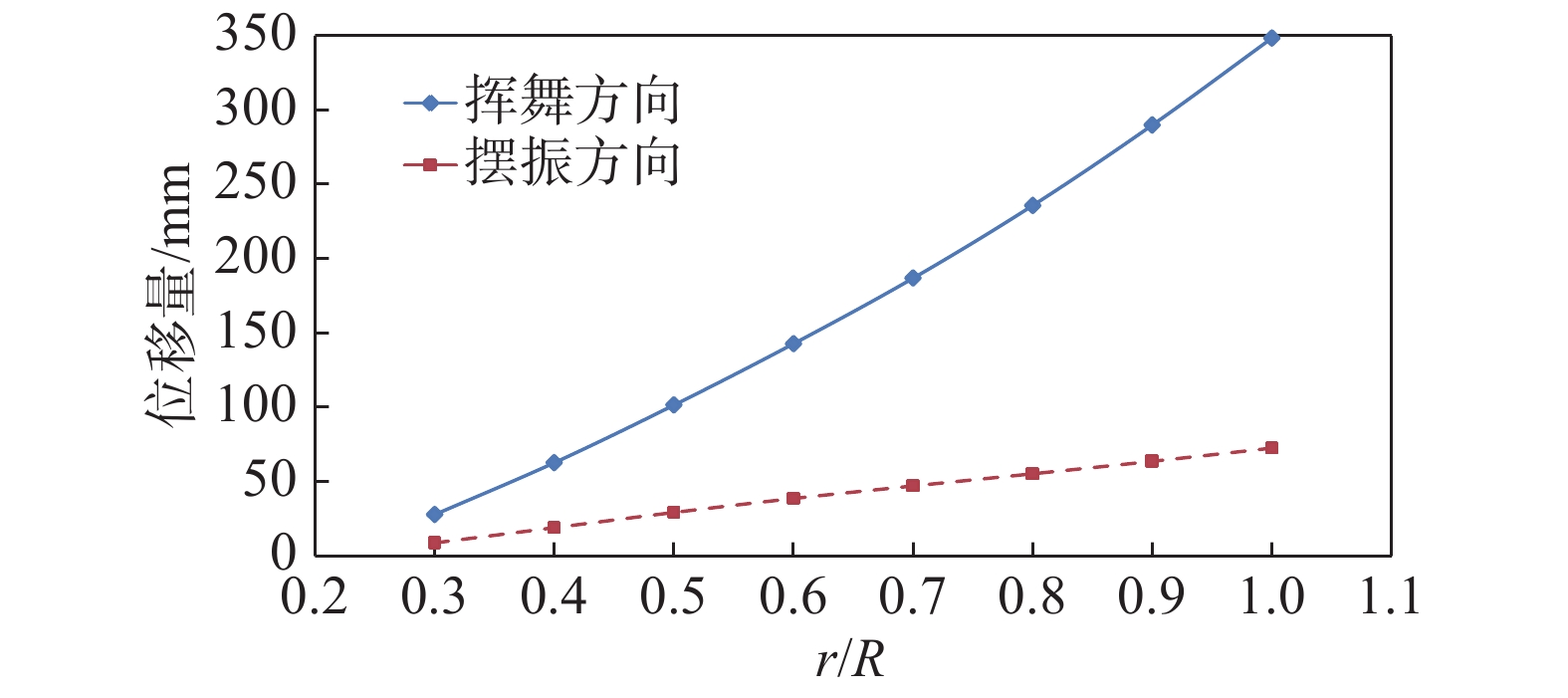
在旋翼非定常载荷计算模型中,每片桨叶采用11个非线性梁单元建模,每片桨叶包含15个桨叶载荷输出剖面。分别采用CAMRAD Ⅱ中的刚性桨叶模型和弹性桨叶模型对形变前后桨叶进行计算。图10为基准旋翼和形变旋翼的扭转角分布(不含操纵总距)。从图中可以看出,桨叶扭转形变量从桨叶根部到桨尖逐渐增大,扭转率从−12°/R近似变为−13°/R。图11为桨叶沿挥舞方向和摆振方向的形变量。从图中可以看出,两种形变量从桨根到桨尖均呈增大趋势,沿挥舞方向的形变量更大。桨尖沿挥舞方向的形变量达到了0.8倍弦长。
|
图 10 旋翼扭转角分布 Fig.10 Distribution of blade twist |
|
图 11 挥舞方向和摆振方向形变量分布 Fig.11 Distribution of blade deformation |
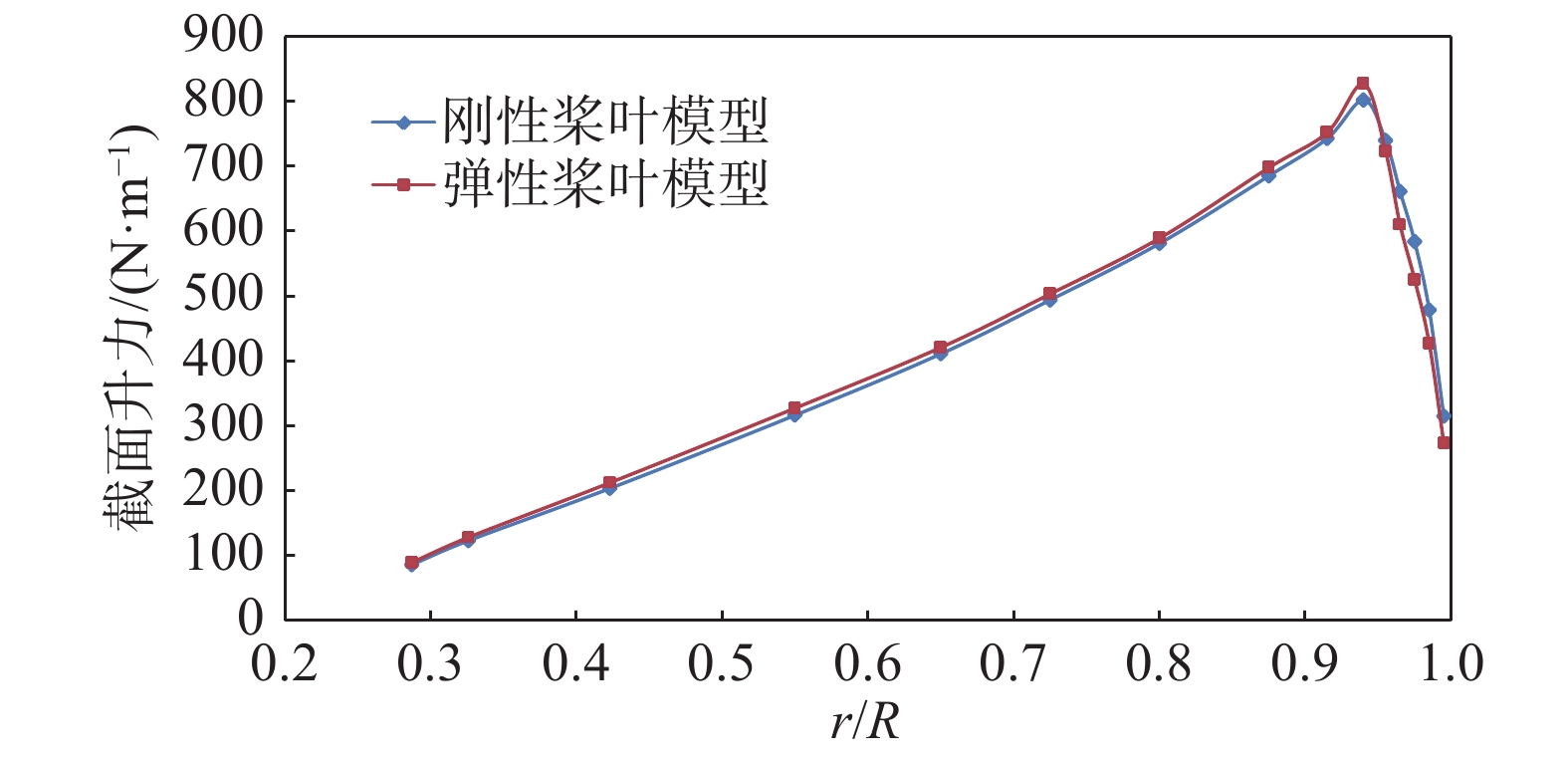
图12分别用刚性桨叶模型和弹性桨叶模型计算了悬停状态下桨叶升力展向分布,图中纵坐标为单位长度的截面升力。从图中可以看出,桨叶的形变并没有改变升力展向分布趋势。进一步对比后发现,考虑弹性形变的桨叶内侧产生略大的升力,桨叶外侧的升力略小。配平相同拉力系数Camrad Ⅱ采用刚性桨叶模型计算得到的总距操纵量为9.63°,弹性桨叶模型对应的操纵为10.41°,操纵量的不同是由于桨叶形变带来气动力变化导致的。从图10可以看出,考虑桨叶弹性形变后,桨叶外侧区域的迎角减小,导致桨尖部分升力减小。为了保持拉力系数不变,总距操纵量相应提高,最终产生了如图12所示的升力分布。
|
图 12 桨叶展向升力分布 Fig.12 Blade lift along the spanwise direction |
图13给出了不同方法计算得到的旋翼悬停状态气动总噪声辐射特性。方法1进行载荷计算时采用Camrad Ⅱ的刚性桨叶模型,桨叶网格采用基准外形,即未考虑弹性形变影响;方法2进行载荷计算时采用的Camrad Ⅱ的弹性桨叶模型,桨叶网格采用基准外形,即仅考虑桨叶弹性形变引起的载荷变化;方法3(本文方法)进行载荷计算时采用的Camrad Ⅱ的弹性桨叶模型,桨叶网格采用形变后外形,即兼顾桨叶形变引起的外形变化和载荷变化。从图13中可以看出,三种计算方法得到的噪声辐射方向特性是完全一致的,随着桨盘夹角的增大,总噪声呈现先增大后减小的趋势,在桨盘夹角20°处噪声级达到峰值。桨叶形变没有改变旋翼悬停气动噪声的方向特性。桨盘夹角0°~30°区域的噪声级较大,为旋翼气动噪声的主要传播方向。
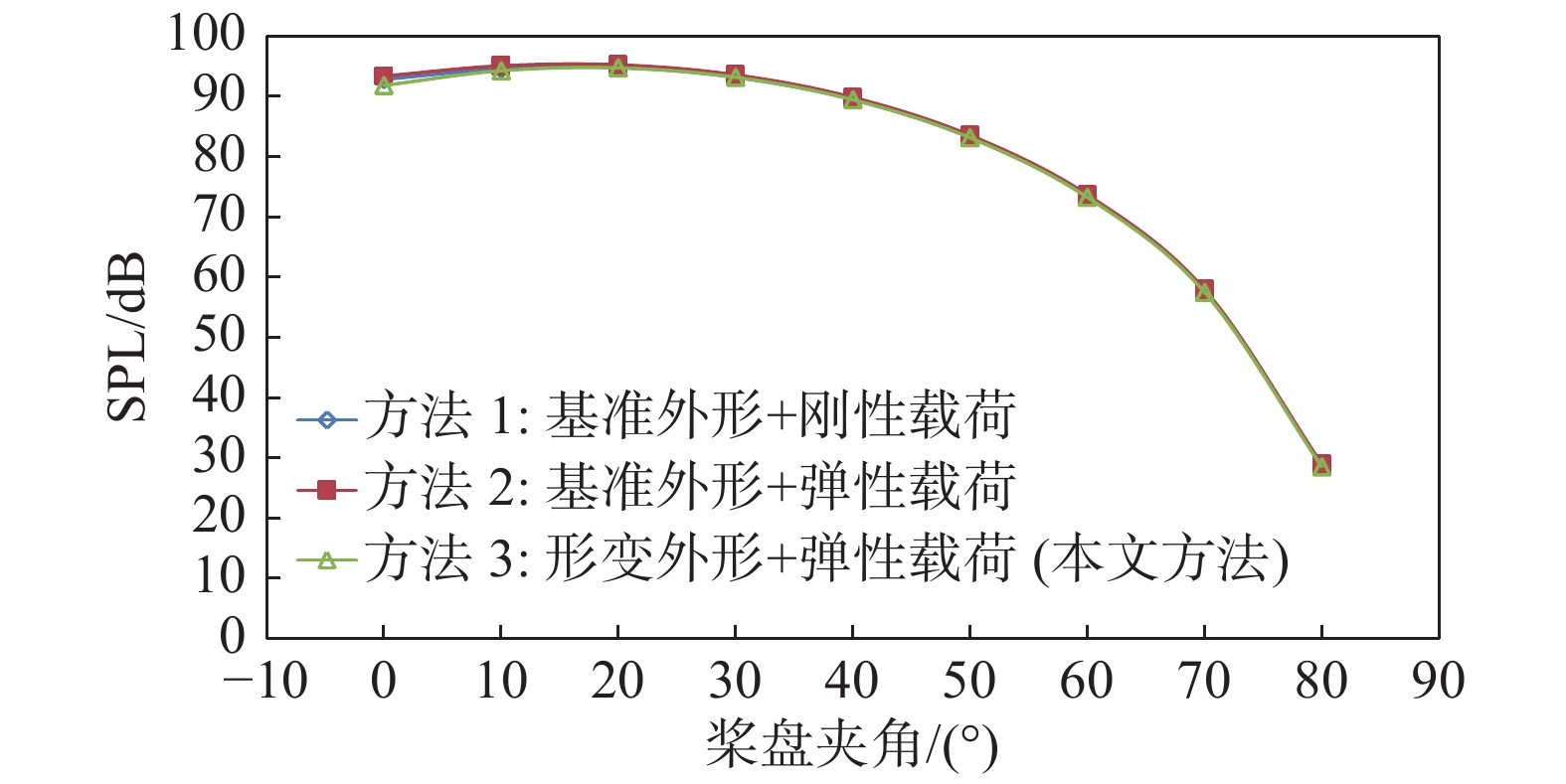
|
图 13 不同方法计算得到的总噪声辐射特性 Fig.13 Total in-hover noise obtained by different numerical methods |
图14显示的是三种方法计算得到的厚度噪声差值对比。从“方法2减去方法1”的曲线可以看出,两种方法的厚度噪声基本无差异。相比于前两种方法,方法3考虑桨叶外形形变之后,在桨盘平面以外区域的厚度噪声均有所降低,在噪声的主要传播方向上,噪声变化量在0.15 dB以内。在桨盘夹角70°观测点处,噪声差值达到了−0.3 dB,但该观测点位于非主要传播方向上,对总噪声影响很小。
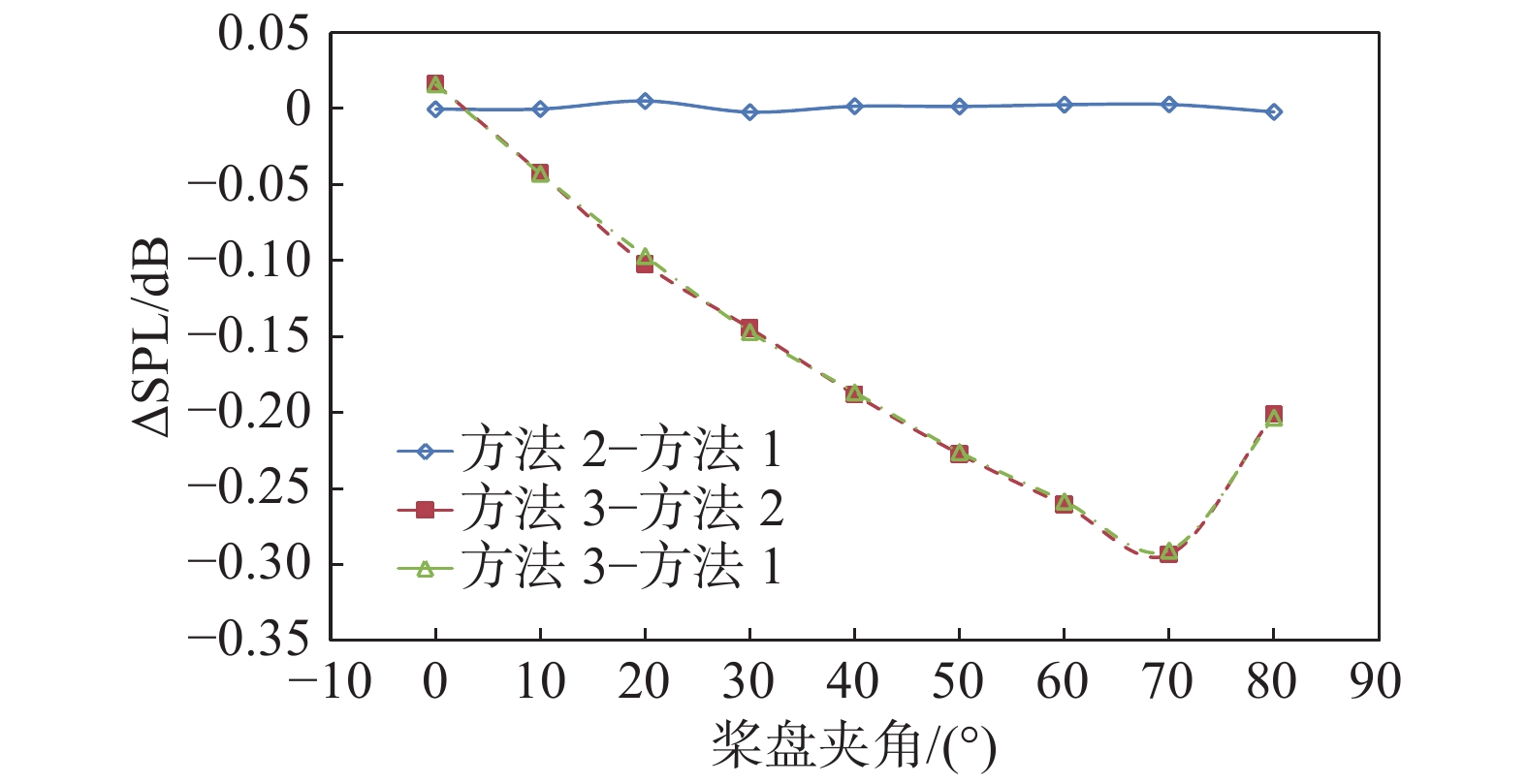
|
图 14 不同方法计算得到的厚度噪声差值 Fig.14 Difference of the thickness noise between different methods |
考虑形变后旋翼厚度噪声的变化较小,这是因为厚度噪声是由桨叶旋转运动排开空气而产生的。从公式(2)可以看出,影响厚度噪声的因素主要是桨叶旋转速度和运动速度。因此,扭转变化和总距变化对厚度噪声影响较小。
图15显示的是三种方法计算得到的载荷噪声差值对比。从图中可以看出,相比于方法1,后两种方法考虑弹性形变引起的载荷变化后,载荷噪声在所有观测点均有所增大,在桨盘平面内的载荷噪声增大约1.0 dB。方法2与方法3计算得到的载荷噪声存在一定差异,差值能够达到−0.3 dB,说明载荷噪声并非只与载荷相关,还受到桨叶外形变化的影响,精确载荷计算不足以包含桨叶形变带来的全部影响。
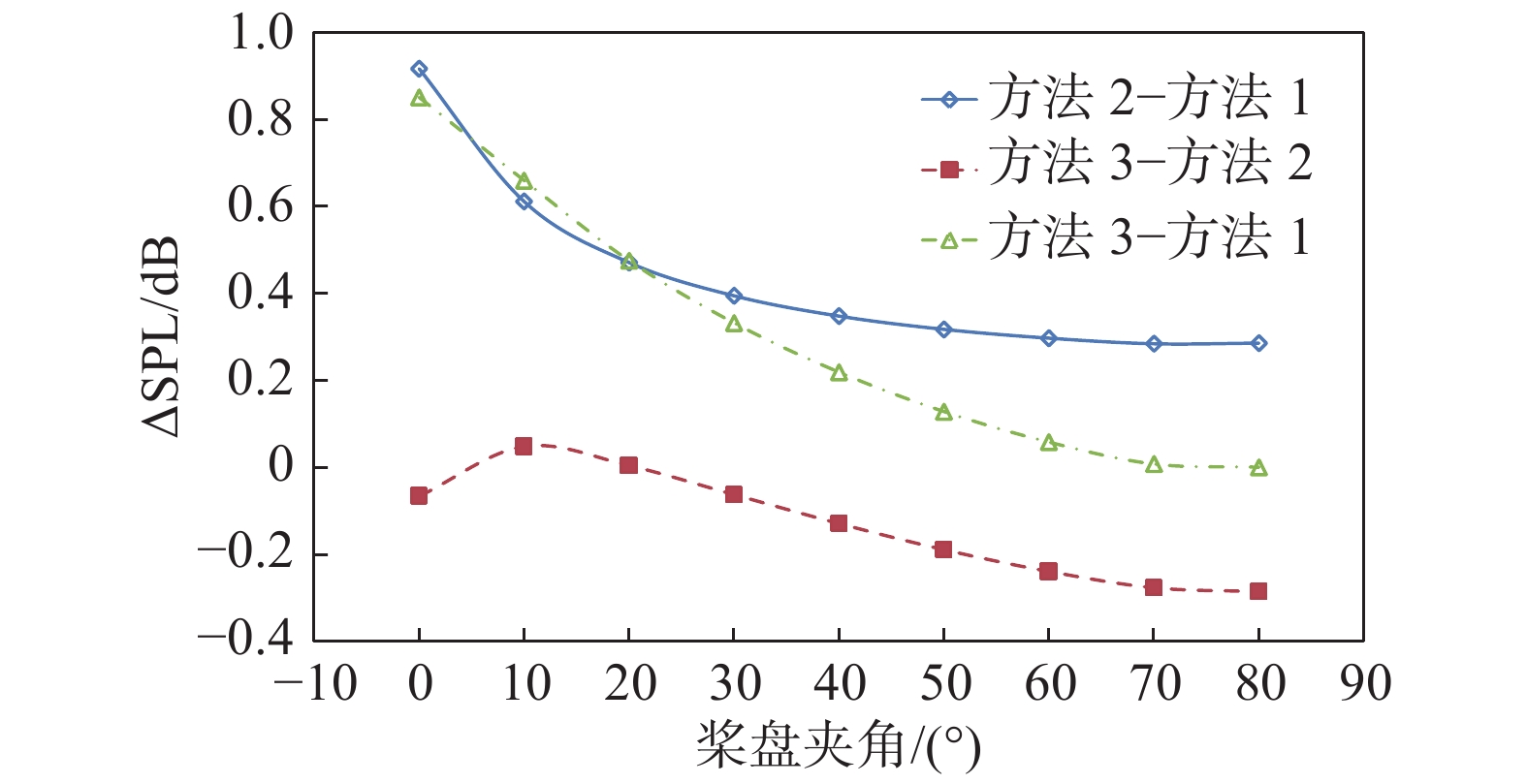
|
图 15 不同方法计算得到的载荷噪声差值 Fig.15 Difference of the loading noise between different methods |
图16显示的是三种方法计算得到的总噪声差值对比。从图中可以看出,相比于方法1,方法2的总噪声在所有观测点均有所增大,变化量在0.6 dB以内。相比于方法1,方法3的总噪声在所有观测点均有所减小,变化量最大处位于桨盘平面内,此处噪声差值为−1.0 dB。方法2和方法3的差异最为明显,噪声差值最大处位于桨盘平面内,此处噪声差值为−1.5 dB。
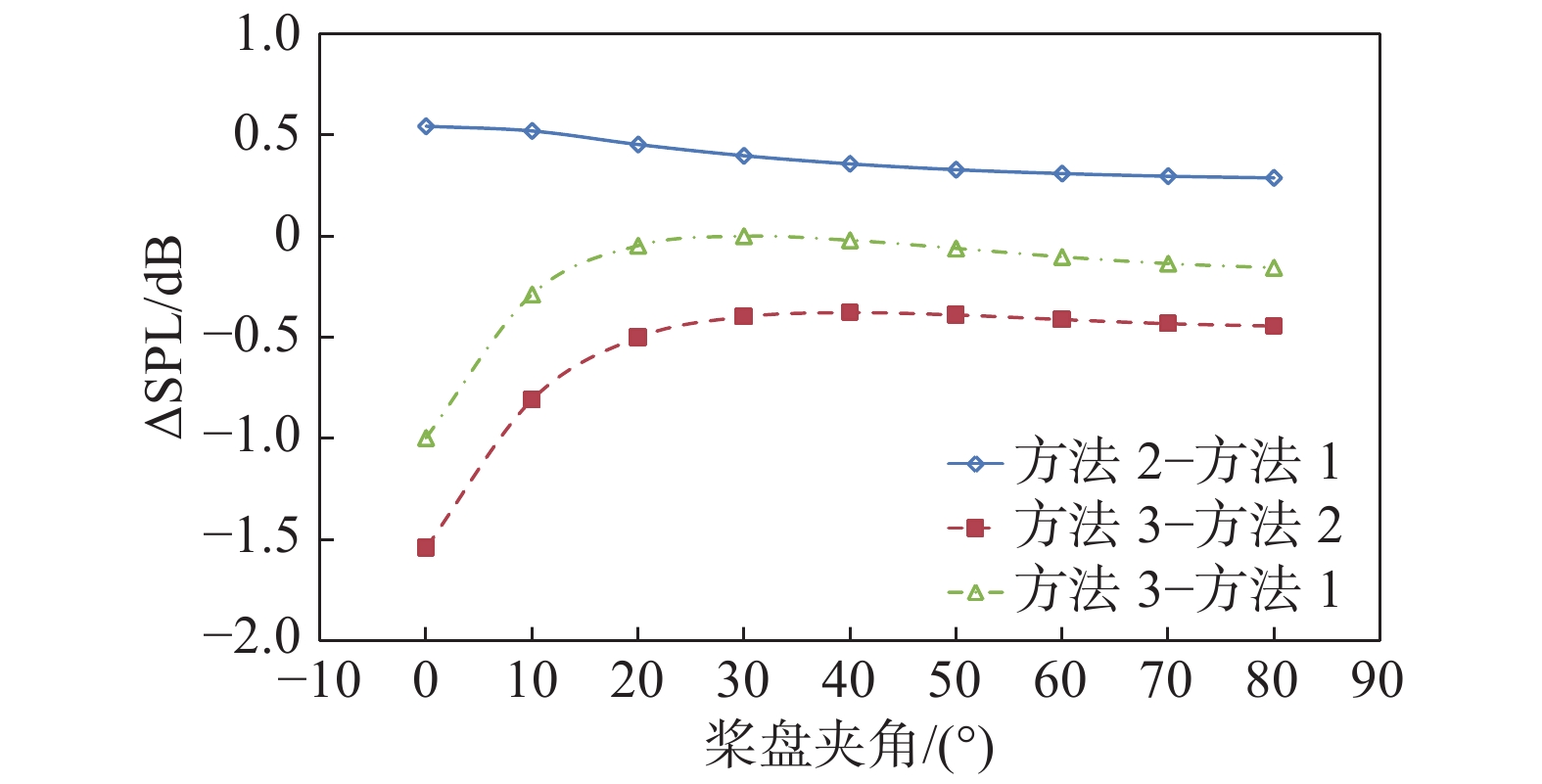
|
图 16 不同方法计算得到的总噪声差值 Fig.16 Difference of the total noise between different methods |
图17计算了悬停状态下桨盘平面内观测点处三种情况各类噪声的时间历程,图中显示的是单片桨叶旋转周期内的声压曲线。从图中可以看出,桨叶形变对厚度噪声和载荷噪声声压时间历程的幅值和相位均有一定影响,进而导致叠加后的总噪声幅值和相位均不一致。图18计算了悬停状态下最强观测点处(桨盘夹角20°)三种情况各类噪声的时间历程,也存在与图17相似的结果。
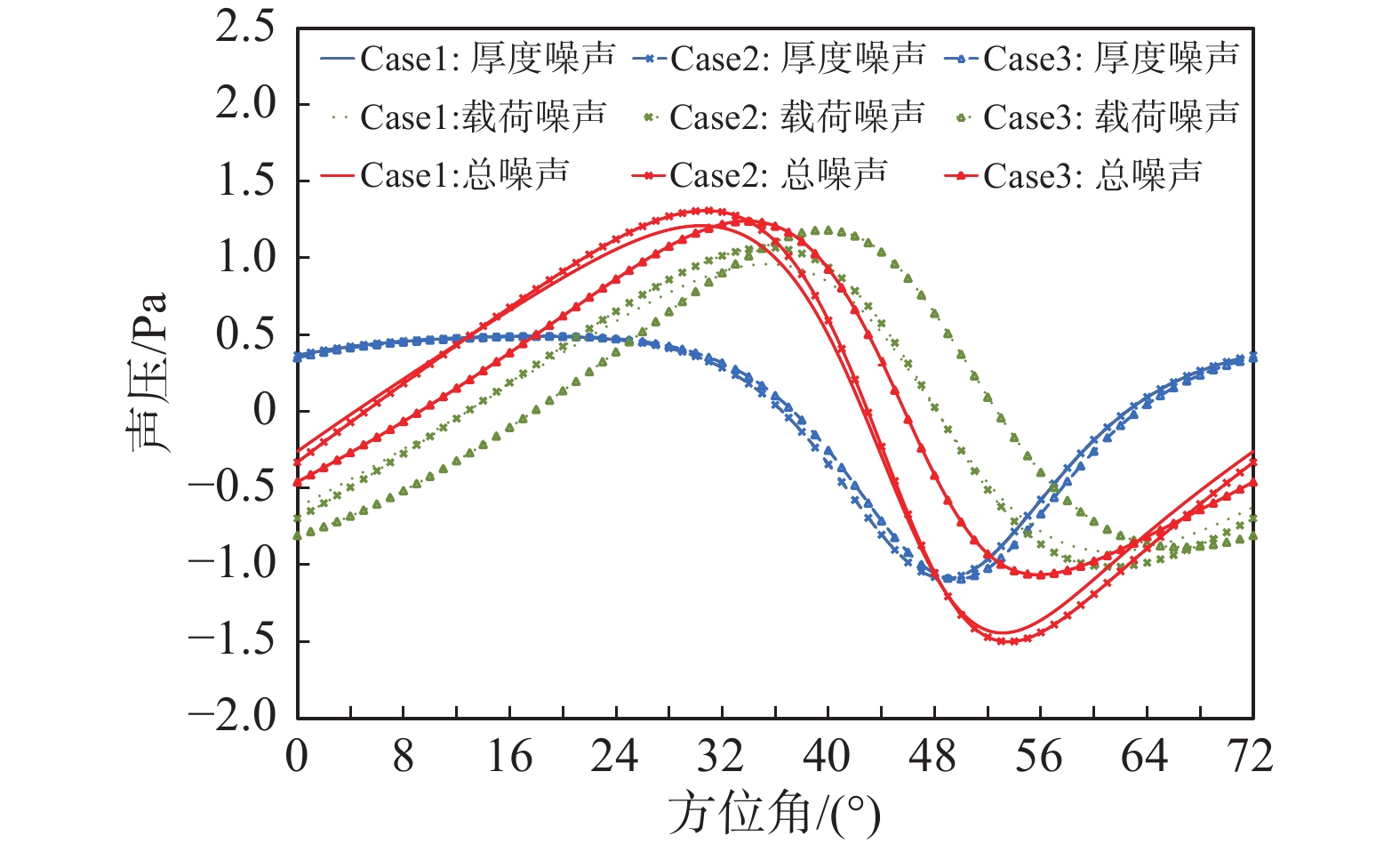
|
图 17 桨盘平面内观测点的声压时间历程对比 Fig.17 Time histories of the sound pressure at an observation point in the rotor plane |
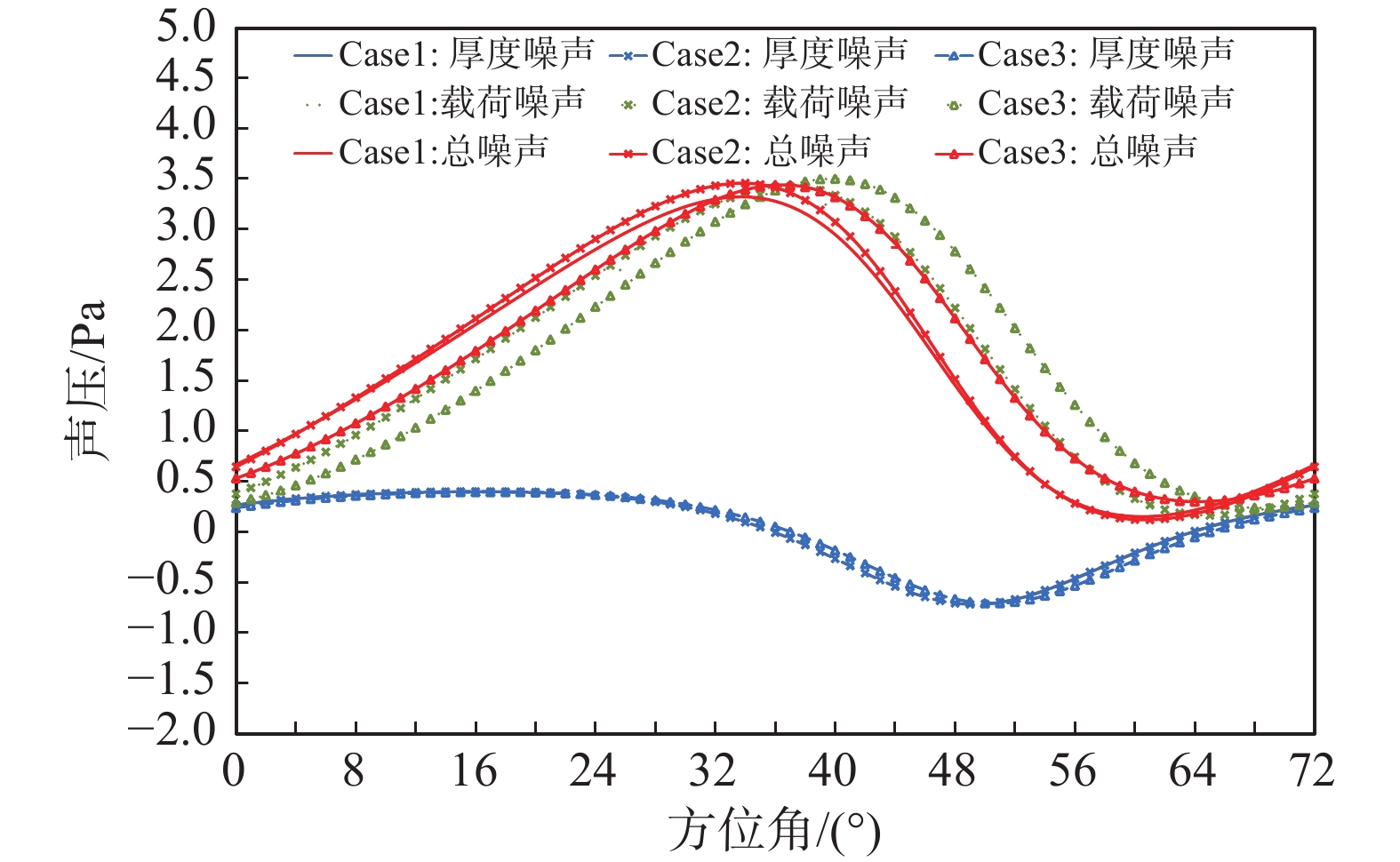
|
图 18 噪声最强观测点处的声压时间历程对比 Fig.18 Time histories of the sound pressure at the observation point with the strongest noise |
结合图14、图15和图16来看,在噪声最主要传播方向上(桨盘夹角20°),方法1与方法3的厚度噪声和载荷噪声的差值分别为−0.1 dB和0.47 dB,但叠加后的总噪声基本没有差别。针对桨盘平面内的观测点,方法2与方法3的厚度噪声和载荷噪声差值均非常小,但总噪声差值却达到了−1.5 dB。从图17和图18中可以看出,厚度噪声和载荷噪声叠加计算总噪声时要同时考虑幅值和相位,声波相位的干涉可能对总噪声幅值产生较大影响。这种声波相位干涉在本文分析中是普遍存在的。在对噪声进行预测时,噪声幅值与相位均要精确预测,尤其是想要利用相位相消原理进行噪声控制时,更应该考虑桨叶弹性形变引起的外形变化和载荷变化。
4 结 论通过本文研究,发现采用Camrad II的弹性桨叶模型能够正确预估悬停状态下桨叶的弹性形变量,具有较好的可靠性。计算结果表明:
1)在典型工作状态下,旋翼桨叶会发生明显的弹性形变,扭转率从−12°/R近乎变为−13°/R,挥舞方向形变量约0.8倍弦长,明显大于摆振方向形变量。
2)桨叶形变不会改变旋翼悬停气动噪声的方向特性,但会改变厚度噪声和载荷噪声声压时间历程中的幅值和相位,进而导致总噪声幅值改变。相较而言,桨叶形变对厚度噪声影响较小,对载荷噪声影响较大。
致谢:感谢中国空气动力研究与发展中心唐敏、左承林、尹星繁等人协助完成模型旋翼风洞试验。
| [1] |
BRENTNER K S. Prediction of helicopter rotor discrete frequency noise-a computer program incorporating realistic motions and advanced acoustic formulation: NASA-TM-87721[R]. Hampton, Virginia: National Aeronautics and Space Administration,, 1986.
|
| [2] |
RICHARD S. Modeling helicopter near-horizon harmonic noise due to transient maneuvers[D]. Maryland: University of Maryland College Park, 2012.
|
| [3] |
ALLEN C B. An unsteady multiblock multigrid scheme for lifting forward flight rotor simulation[J]. International Journal for Numerical Methods in Fluids, 2004, 45(9): 973-984. DOI:10.1002/fld.711 |
| [4] |
EDWARDS B, COX C. Revolutionary concepts for helicopter noise reduction: SILENT program: NASA/CR-2002-211650[R]. Hampton, Virginia: National Aeronautics and Space Administration, 2002.
|
| [5] |
FFOWCS-WILLIAMS J E, HAWKINGS D L. Sound generated by turbulence and surfaces in arbitrary motion[J]. Philosophical Transactions of the Royal Society, Series A, Mathematical and Physical Sciences, 1969, 264(1151): 321-342. DOI:10.1098/rsta.1969.0031 |
| [6] |
BRENTNER K. Modeling aerodynamically generated sound - Recent advances in rotor noise prediction[C]// 38th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 2000. doi: 10.2514/6.2000-345
|
| [7] |
PASSE B J, SRIDHARAN A, BAEDER J D. Computational investigation of coaxial rotor interactional aerodynamics in steady forward flight[C]// 33rd AIAA Applied Aerodynamics Conference, Dallas, TX. Reston, Virginia: AIAA, 2015. doi: 10.2514/6.2015-2883
|
| [8] |
SHARMA K, CORLE E, BRENTNER K, et al. Robust and automated coupling of RCAS and PSUWOPWOP[J]. AHS Aeromechanics Design for Transformative Vertical Flight, 2018. |
| [9] |
王博, 招启军, 樊枫, 等. 改进型CLOR桨尖旋翼悬停状态气动噪声特性试验与预估分析[J]. 空气动力学学报, 2013, 31(4): 454-461. WANG B, ZHAO Q J, FAN F, et al. Investigations on acoustic characteristics of rotor with improved CLOR blade-tip in hover based on experimental and prediction method[J]. Acta Aerodynamica Sinica, 2013, 31(4): 454-461. (in Chinese) |
| [10] |
AOYAMA T, YANG C, KONDO N, et al. Comparison of noise reduction effect between AFC and conventional IBC by moving overlapped grid method[C]// 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, Massachusetts. Reston, Virginia: AIAA, 2006. doi: 10.2514/6.2006-2609
|
| [11] |
AOYAMA T, YANG C, SAITO S. Numerical analysis of active flap for noise reduction using moving overlapped grid method[J]. Journal of the American Helicopter Society, 2007, 52(3): 189-200. DOI:10.4050/jahs.52.189 |
| [12] |
FARASSAT F. Linear acoustic formulas for calculation of rotating blade noise[J]. AIAA Journal, 1981, 19(9): 1122-1130. DOI:10.2514/3.60051 |
| [13] |
Misiorowski M, Gandhi F. Comparison of acoustic predictions using distributed and compact airloads[C]// 75th Annual Forum and Technology Display, May 13–16, Philadelphia, Pennsylvania, U.S.A, 2019.
|
| [14] |
BRENTNER K, JONES H. Noise prediction for maneuvering rotorcraft[C]// 6th Aeroacoustics Conference and Exhibit, Lahaina, HI. Reston, Virginia: AIAA, 2000. doi: 10.2514/6.2000-2031
|
| [15] |
李志彬, 孙伟, 袁明川. 旋翼气动噪声快速计算方法研究[J]. 直升机技术, 2021(1): 1-7. LI Z B, SUN W, YUAN M C. Research on the rapid calculation method of rotor aerodynamic noise[J]. Helicopter Technique, 2021(1): 1-7. DOI:10.3969/j.issn.1673-1220.2021.01.001 (in Chinese) |
| [16] |
樊枫. 直升机非定常干扰流场与声场的计算方法研究与应用[D]. 南京: 南京航空航天大学, 2013. FAN F. Research and application of computational methods for unsteady flow field and sound field of helicopter[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013 (in Chinese). |
| [17] |
刘婷, 刘平安, 樊枫. 升力偏置对共轴刚性旋翼桨叶载荷和形变的影响分析研究[J]. 航空科学技术, 2020, 31(4): 42-49. LIU T, LIU P A, FAN F. Influence of lift offset on coaxial rigid rotor blade loads and deformation[J]. Aeronautical Science & Technology, 2020, 31(4): 42-49. DOI:10.19452/j.issn1007-5453.2020.04.007 (in Chinese) |
| [18] |
熊邦书, 熊奎, 李新民, 等. 基于双目视觉的直升机旋翼桨叶挥舞角测量[J]. 测控技术, 2016, 35(1): 34-37. XIONG B S, XIONG K, LI X M, et al. Flapping angle measurement of helicopter rotor blade based on binocular vision[J]. Measurement & Control Technology, 2016, 35(1): 34-37. DOI:10.3969/j.issn.1000-8829.2016.01.009 (in Chinese) |
| [19] |
熊邦书, 罗院华, 黄建萍, 等. 基于立体视觉的直升机桨叶扭转角模拟测量方法[J]. 应用科学学报, 2018, 36(6): 950-957. XIONG B S, LUO Y H, HUANG J P, et al. Measurement method of torsion of helicopter rotor blades based on stereo vision[J]. Journal of Applied Sciences, 2018, 36(6): 950-957. DOI:10.3969/j.issn.0255-8297.2018.06.007 (in Chinese) |
| [20] |
左承林, 马军, 岳廷瑞, 等. 基于双目立体视觉的直升机旋翼桨叶位移变形测量方法[J]. 实验流体力学, 2020, 34(1): 87-95. ZUO C L, MA J, YUE T R, et al. Displacement and deformation measurements of helicopter rotor blades based on binocular stereo vision[J]. Journal of Experiments in Fluid Mechanics, 2020, 34(1): 87-95. (in Chinese) |
 2022, Vol. 40
2022, Vol. 40

