0 引　言

麦克风相阵列相阵列技术能给出声源位置、频率、强度和指向性等丰富的噪声信息，是气动噪声研究的重要手段。国外从20世纪90年代起利用相阵列测试技术针对飞机^[1-7]、高速列车^[8]等开展了大量气动噪声风洞试验、飞行试验研究。国内相阵列技术研究起步较晚，但发展很快。随着我国大飞机项目的立项，气动噪声问题已经成为我国航空领域研究的热点问题，各气动研究机构和院校相继建立起麦克风相阵列气动噪声测量技术，形成了气动噪声风洞试验能力，已应用于民机^[9-13]和高速列车^[14]气动噪声研究。

民机气动噪声风洞试验周期短，费用低，易实施，在民机型号的声学设计与研究中得到了广泛应用。但风洞试验由于存在雷诺数效应、模型失真以及来流流场差异等问题，难以给出如飞行试验结果般最真实、最具参考价值的噪声数据，甚至给出与飞行试验相左的结果。Stoker^[1]对比了波音777的6.3%缩比、26%缩比的两个缩比模型风洞试验与全尺寸飞行试验的气动噪声试验结果，显示缩比模型风洞试验结果均与飞行试验结果存在不同程度的差异。美国QTDⅡ项目中起落架降噪措施飞行演示验证试验显示，在风洞试验中得到验证、有显著降噪效果的起落架降噪措施，在飞行试验中毫无降噪效果，甚至在某些工况下还增加了低频噪声^[15]。因此气动噪声飞行试验仍然是民机气动噪声研究不可或缺的环节。

在飞行试验中使用地面阵列开展飞机气动噪声源识别的难点在于，由于飞机与阵列之间存在相对运动而出现的声传播多普勒效应，给阵列数据处理带来挑战，需要发展适用于飞行试验的相阵列技术，同步获取飞机的航迹，对噪声信号进行解多普勒效应处理，才能进行声源识别与定位。目前国内应用于飞行试验中运动声源识别的相阵列技术仍基础薄弱，相关研究开展较少。乔渭阳等于2001年在民机降落过程中利用相阵列技术开展了飞机进场着陆过程噪声研究^[16]，于2008年对某支线客机降落过程中的发动机噪声和襟翼噪声进行了研究^[17]，分别采用了光学传感器和激光测距传感器、GPS系统进行航迹监测，民用GPS定位精度为5 m量级。航迹监测是飞行试验的重要环节，精确的航迹信息是对声源实现精确定位的必要保证。另外，飞行试验中声波经过长距离大气传播而出现相关性丢失，距离较远的麦克风接收到的声波信号间的相关性降低，这给阵列设计提出了新的要求。

根据上述问题，针对气动噪声飞行试验中利用麦克风相阵列技术识别运动声源的难点，本文对时域波束形成算法、解多普勒效应技术、适用于飞行试验的阵列优化设计方法开展了研究。通过仿真声源分析了航迹误差对声源识别的影响。在此基础上，采用差分GPS系统进一步提高无人机航迹监测精度，基于某无人机噪声飞行试验开展了运动声源识别技术验证。

1 阵列数据处理算法 1.1 时域波束形成算法

阵列数据处理算法是麦克风相阵列气动噪声测试技术的核心。波束形成算法包括时域算法和频域算法。两类方法的基本假设在本质上是相同的，因而通常能给出相似的结果。但文献[1]指出，对于短时信号的处理，时域方法能给出比频域算法更好的结果。在运动物体的噪声试验中，噪声测试是在运动物体飞越阵列上方的过程中进行的，由于声源与麦克风阵列间存在相对运动，会发生多普勒频移。因此，将相阵列技术应用于运动声源时，只能截取较短的时域信号进行声源定位。目前，在应用于运动声源的相阵列技术中通常采用时域算法，在应用于静止声源的相阵列技术中通常使用频域算法。

本文采用了Dougherty^[18]提出的改进的时域波束形成算法。典型的时域波束形成算法公式为：

$ {b_{TD}}\left( {{{\boldsymbol{x}}_i}} \right) = \frac{1}{T}\int_0^T {{{\left[ {\sum\limits_{m = 1}^M {{p_m}\left( {t - {\tau _{im}}} \right)} } \right]}^2}{\rm{d}}t} = \left\langle {{{\left[ {\sum\limits_{i = 1}^M {{p_i}\left( {t - {\tau _{im}}} \right)} } \right]}^2}} \right\rangle $

(1)

其中： ${b_{TD}}\left( {{{\boldsymbol{x}}_i}} \right)$ 为声源面 ${{\boldsymbol{x}}_i}$ 位置的时域波束形成结果； $ {p_m}\left( t \right) $ 为第 $ m $ 个麦克风的时域信号， $ M $ 为阵列麦克风数目， $ {\tau _{im}} $ 为第 $ m $ 个麦克风对于声源面 ${{\boldsymbol{x}}_i}$ 位置的延时； $\left\langle {\;} \right\rangle$ 为时间平均。

频域波束形成算法中，互谱矩阵主对角元素为麦克风自噪声，将其置零能剔除麦克风自噪声，提高信噪比。而展开时域波束形成算法的公式（1）， $ \displaystyle\sum\limits_{m = 1}^M {p_m^2\left( {t - {\tau _{im}}} \right)} $ 项即为麦克风自噪声，对应频域算法中互谱矩阵主对角元素。改进的时域波束形成算法公式为：

$ {b_{TD,DD}}\left( {{{\boldsymbol{x}}_i}} \right) = \left\langle {{{\left[ {\sum\limits_{m = 1}^M {{p_m}\left( {t - {\tau _{im}}} \right)} } \right]}^2} - \sum\limits_{m = 1}^M {p_m^2\left( {t - {\tau _{im}}} \right)} } \right\rangle $

(2)

1.2 解多普勒效应

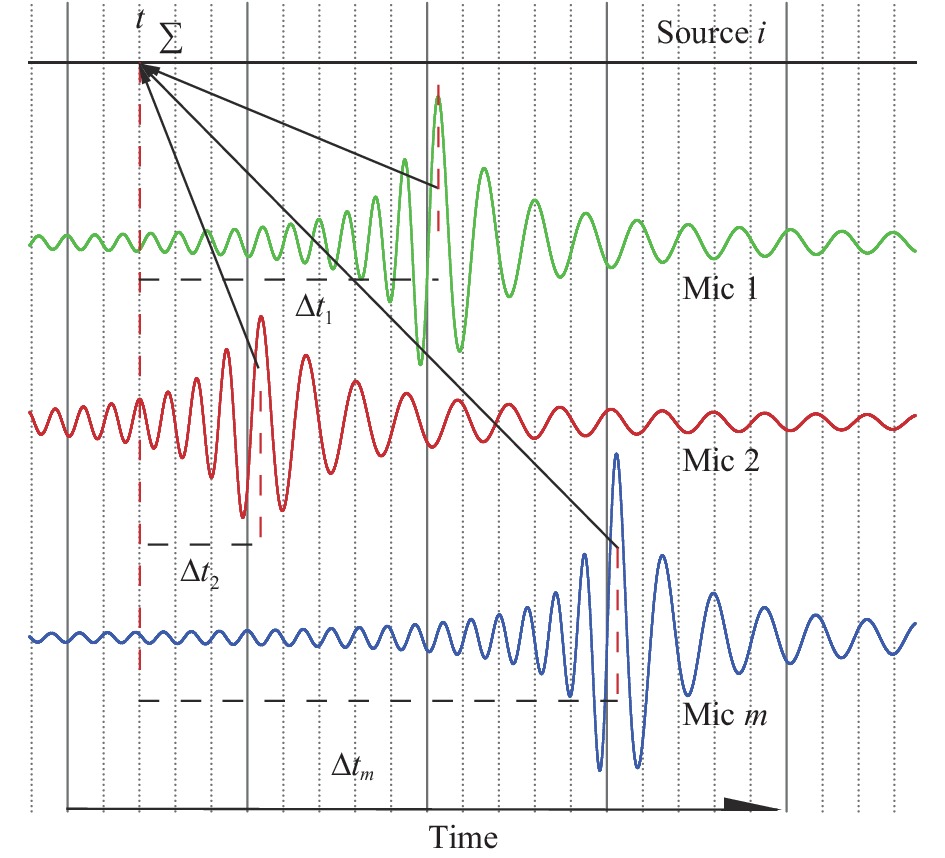
多普勒效应给阵列数据处理算法提出了新的要求，要求在做波束形成之前必须对阵列信号进行解多普勒效应的处理。本文采用了Zechel^[8]的解多普勒效应方法，即基于运动物体轨迹对麦克风信号进行重采样，如图1所示。计算延时需要用到与麦克风信号相同步的运动轨迹数据。

2 阵列优化设计 2.1 声传播相关性丢失

飞行试验中声场尺度较大，声波经过长距离大气传播而出现相关性丢失，距离较远的麦克风接收到的声波信号间的相关性降低。由于声传播相关性丢失问题的存在，使得大口径阵列被分割成若干个小阵列，阵列性能受到极大影响。因而设计应用于飞行试验的阵列时必须考虑声传播相关性丢失问题。

Sijtsma^[19]依据大型民机气动噪声飞行试验数据给出了一种声传播相关性丢失近似模型：在声传播相关性丢失的影响下，有效阵列半径与声源频率成反比，如式（3）所示：

$ {R_j} = {{4000} \mathord{\left/ {\vphantom {{4000} {{f_j}}}} \right. } {{f_j}}} $

(3)

基于有效阵列半径给出阵列中单元 $ n $ 在频率 $ {f_j} $ 下的权重系数如公式（4）：

$ {w_{n,j}} = \frac{1}{2}\left\{ {1 - {\text{Erf}}\left[ {8\left( {\frac{{{r_n}}}{{{R_j}}} - 1} \right)} \right]} \right\} $

(4)

其中： ${\text{Erf}}\left( {\;} \right)$ 为误差函数， $ {r_n} $ 为单元 $ n $ 距阵列中心的距离。该权重系数削弱了有效阵列半径以外阵列单元的权重。显然，飞行试验中的飞行高度、气象条件均会影响声传播相关性丢失的程度，实际应用中，可通过噪声测试数据进行评估，依据评估结果调整声传播相关性丢失模型。对于大型民机气动噪声飞行试验的阵列设计，可参考上述声传播相关性丢失模型。

2.2 阵列优化设计问题建模

将上述声传播相关性丢失模型，嵌入阵列性能评估过程中，以相关性丢失问题影响下的阵列旁瓣抑制水平和分辨率为目标函数，利用多目标优化算法，优化阵列单元坐标。对阵列多目标优化问题进行如下建模：

$ \left\{ {\begin{array}{*{20}{l}} {\min \left\{ {R\left( {{{\boldsymbol{x}}_i}} \right),{\rm{MSL}}\left( {{{\boldsymbol{x}}_i}} \right)} \right\}} \\ {{{\boldsymbol{x}}_i} \in \varOmega } \\ {\left| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right| \geqslant d} \end{array}} \right. $

(5)

其中： $R\left( {{{\boldsymbol{x}}_i}} \right)$ 和 ${\rm{MSL}}\left( {{{\boldsymbol{x}}_i}} \right)$ 分别是阵列分辨率和旁瓣抑制水平，阵列分辨率取主瓣峰值下降3 dB的主瓣宽度。阵列性能计算过程中均考虑了声传播相关性丢失； ${{\boldsymbol{x}}_i}(i = 1, \cdots, M)$ 为阵列单元坐标， $ M $ 为阵列单元数目； $\varOmega$ 为阵列口径所决定的区域； $\left| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right| \geqslant d$ 为约束条件，单元间最小间距不小于规定值 $ d $ 。

2.3 典型阵列设计结果

对比分析是否考虑声传播相关性丢失问题对阵列设计结果的影响。阵列设计条件如下：阵列样式为多臂对数螺旋阵列，阵列单元数目为63，口径为45 m×36 m，声源距离阵列平面50 m，声源频率范围为300～3000 Hz，使用了2.1节的相关性丢失模型，使用了多目标全局优化算法。

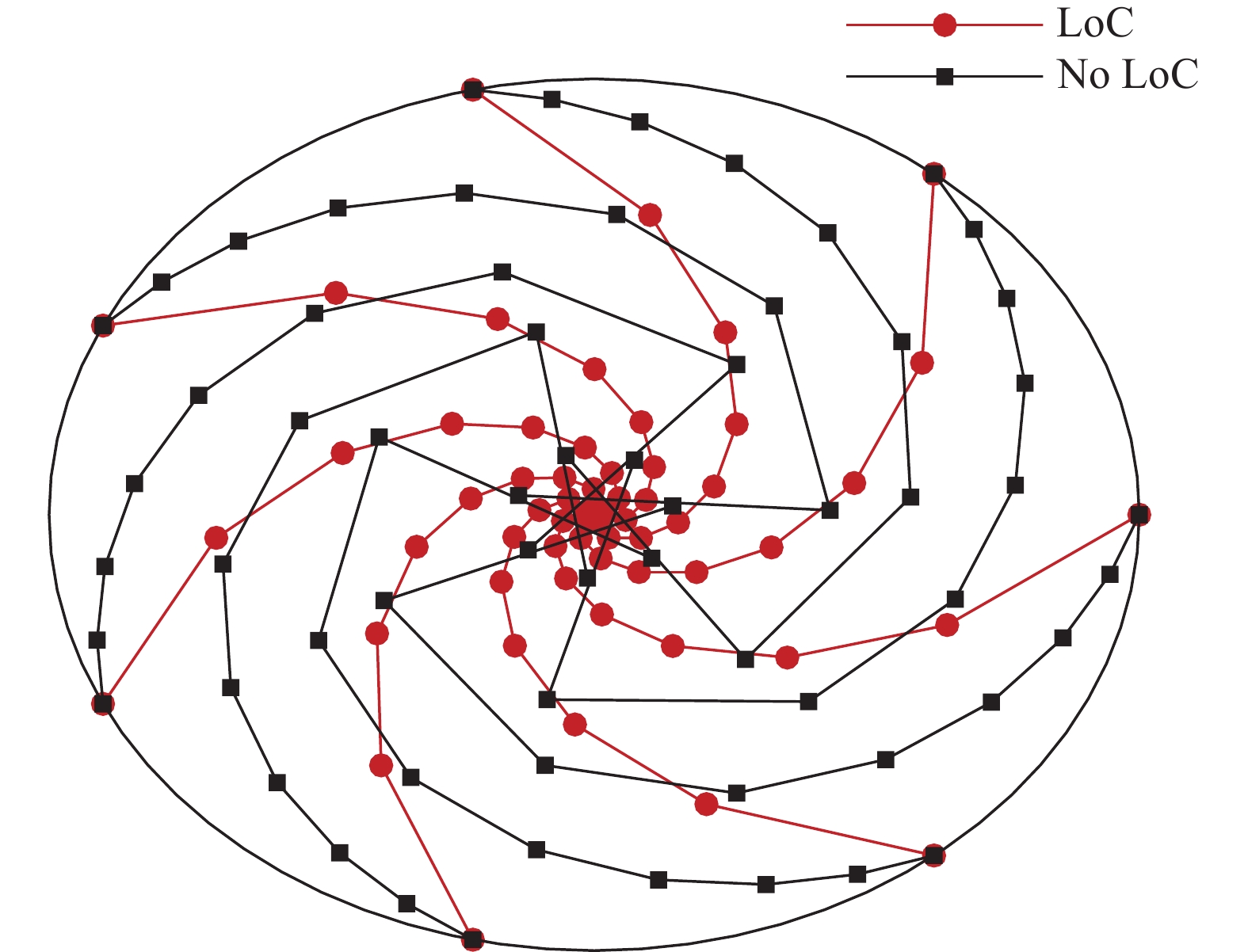
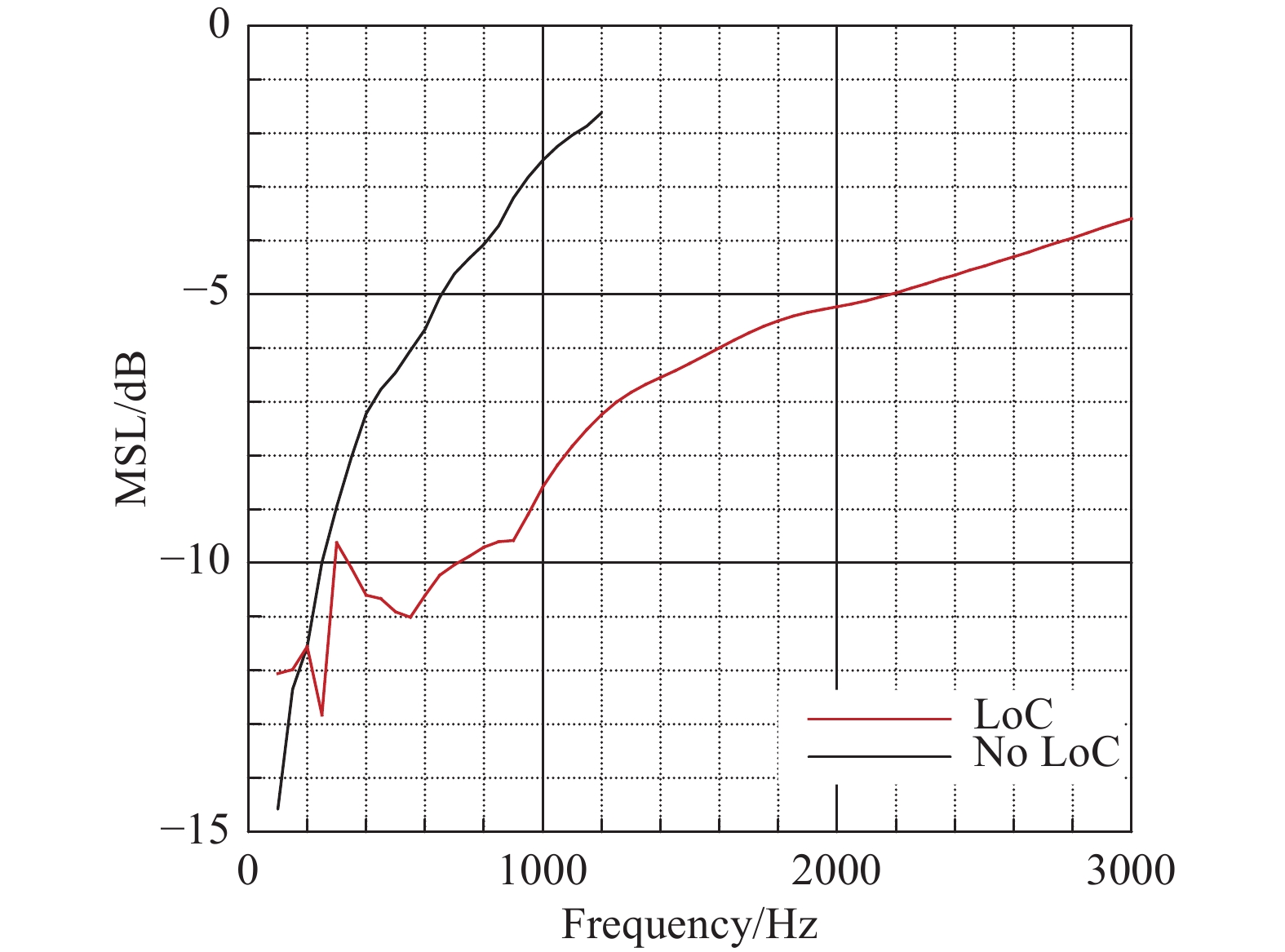
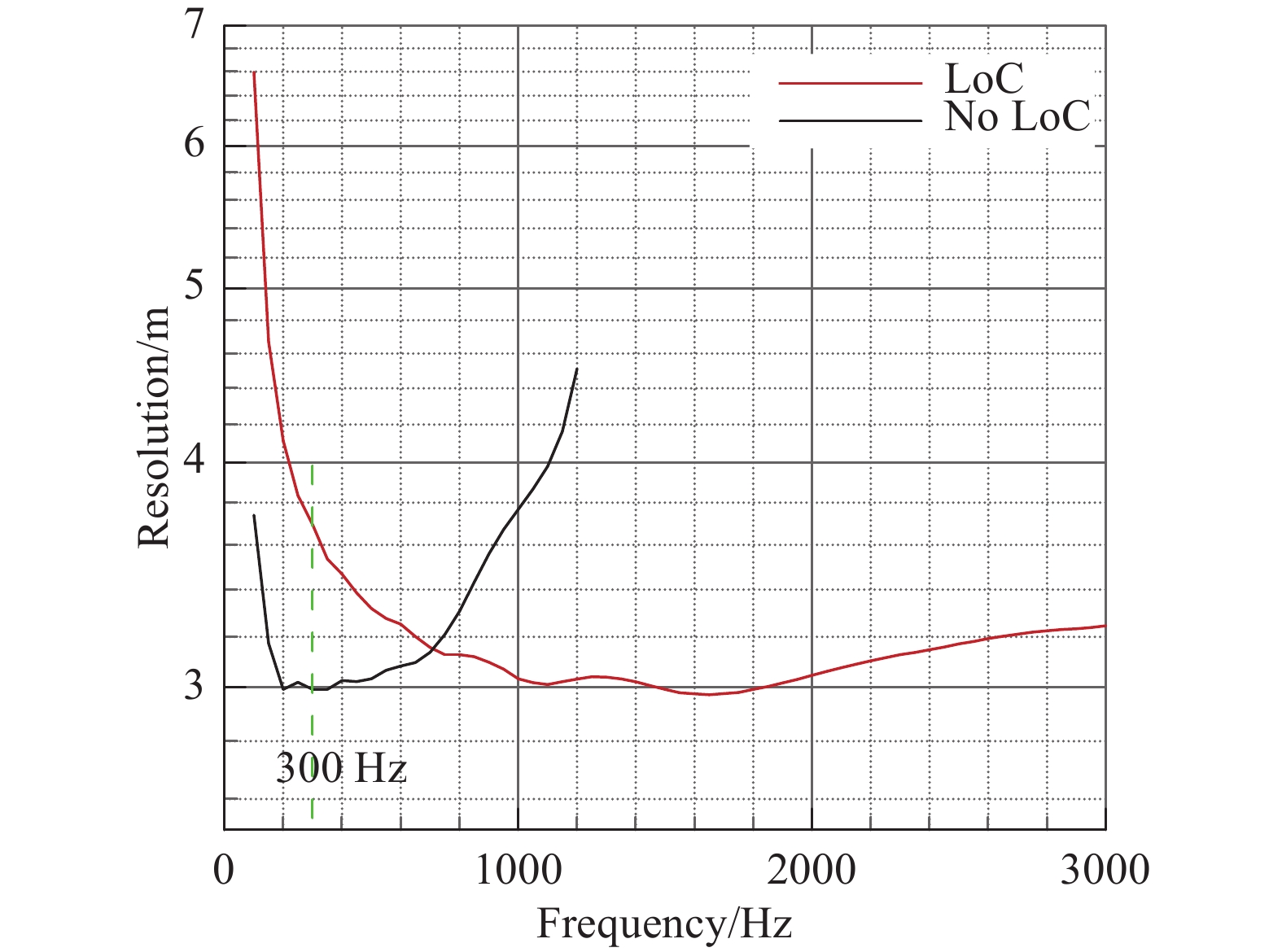
图2、图3和图4分别给出了两个最优阵列的阵列单元分布和在声传播相关性丢失影响下的阵列最大旁瓣水平和阵列分辨率，图中“LoC”表示考虑声传播相关性丢失的最优阵列设计，“No LoC”表示未考虑声传播相关性丢失的最优阵列设计。从图中可以看到，考虑声传播相关性丢失后，阵列单元向阵列中心靠拢，呈现出“外疏内密”分布，以保障在阵列外围单元由于相关性丢失而“失效”后，阵列中心区域仍有较多有效单元。从阵列性能曲线上看，在声传播相关性丢失问题影响下，“No LoC”阵列性能急剧下降，在1200 Hz彻底失效；而“LoC”阵列则直到3000 Hz仍保持了较好的阵列性能，可用频率范围大大增加。

3 运动声源识别仿真分析

对运动声源识别开展仿真，评估航迹数据误差、数据长度对声源识别的影响。仿真的工况为：阵列为35单元构成的对数螺旋阵列，口径3 m；点声源在阵列平面前10 m距离的直线上，以30 m/s的速度沿阵列X轴正向飞越阵列；声源信号为正弦波加随机噪声，频率为1000 Hz，噪声幅值为正弦波幅值的1%；声波信号的采样率为20480 Hz。

3.1 数据长度对阵列性能的影响

图5给出了使用不同长度的航迹和噪声数据给出运动声源识别仿真结果，数据长度分别为0.05、0.1、0.2 s，对应于航迹长度为1.5、3.0、6.0 m，航迹中点位于阵列正上方。从图中可以看到，基于更长的数据识别出的声源在航向的尺寸更小。表1给出了以上声源识别结果的性能参数，数据长度主要影响航向分辨率，对旁瓣抑制水平和横向分辨率影响很小。从以上分析可以看出，相阵列技术应用于运动声源时，通过增加噪声和航迹数据长度，一定程度上可提高声源识别的航向分辨率。

3.2 航迹误差的影响

将麦克风相阵列技术应用于运动声源探测时，其关键在于获取与噪声数据相同步的运动物体轨迹数据，轨迹误差对噪声源识别存在影响。轨迹误差可分为零点误差、漂移误差和随机误差。零点误差来源于阵列坐标系与运动物体坐标系的对标误差，是运动轨迹的整体偏移。漂移误差来源于测量系统的偏移，随时间积累。通过数值仿真手段分别模拟以上三种轨迹误差，分别分析其对噪声源识别的影响。

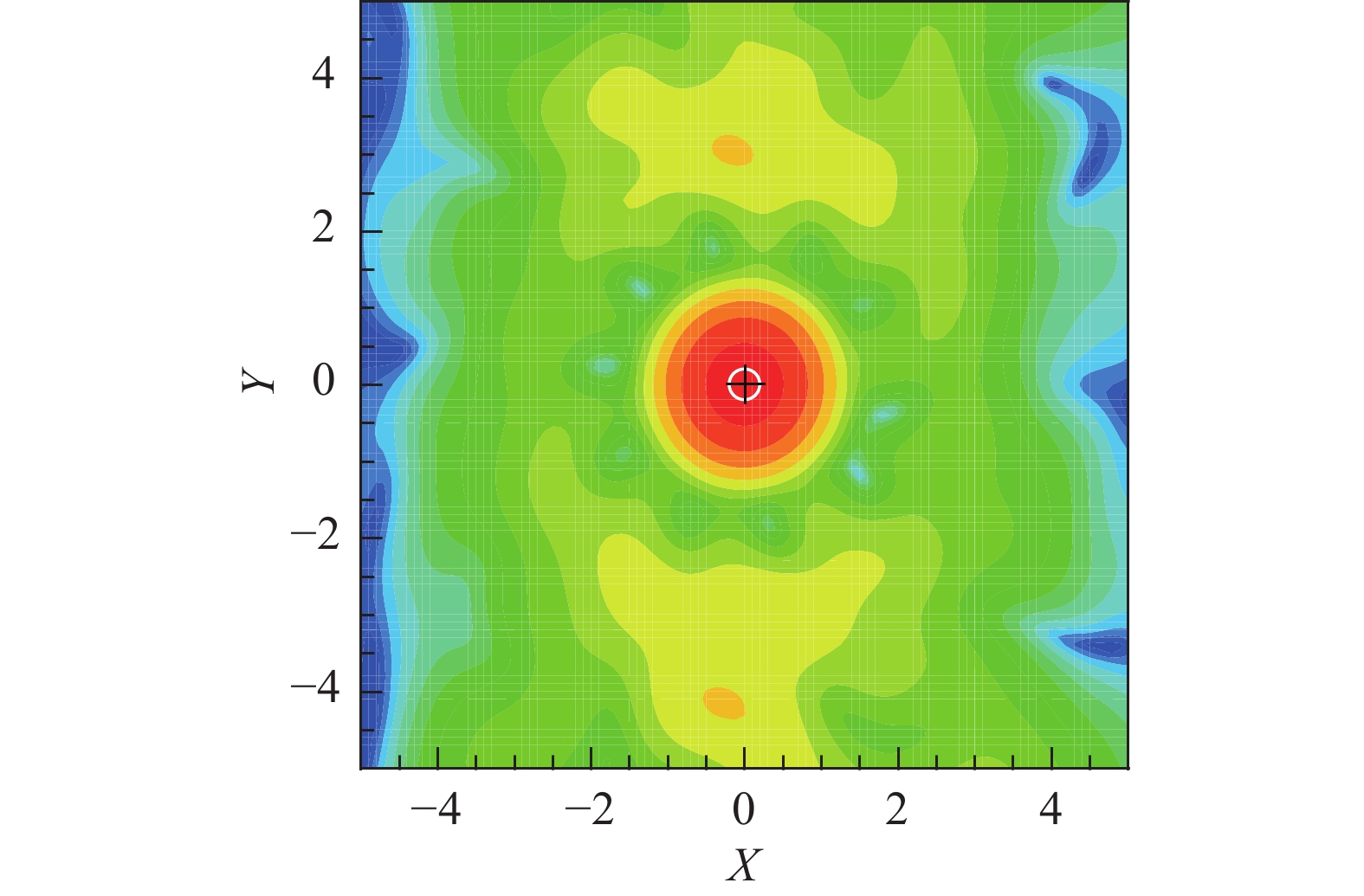
图6给出了上述运动声源识别仿真结果。所截取的阵列麦克风信号是点声源飞越阵列中心时发出的，时间长度为0.05 s，航迹长度为1.5 m。图中黑色十字标记的是声源的真实位置，白色圆圈为所识别的声源位置。从图中可以看到，清晰地识别出了声源，验证了上述时域波束形成算法和解多普勒效应方法的正确性。

在轨迹数据中人为加入1倍波长（0.34 m）的航向零点误差，即轨迹数据整体沿X轴正向偏移0.34 m，阵列麦克风信号不变。图7（a）给出了声源识别结果。从图中可以看到，声源被清晰地识别，但其位置存在偏移；轨迹的零点误差为沿X轴正向0.34 m，而识别出的声源位置反方向偏移约0.34 m。可见零点误差会导致识别出的声源位置反向等距偏移。在轨迹数据中人为加入5倍波长（1.7 m）的横向零点误差，从图7（b）中可以看到，航迹数据存在Y轴正向偏移时，在模型坐标系中声源位置出现反向偏移，偏移量为航迹数据偏移量。

图7（c）给出了漂移误差对声源识别的影响。在轨迹数据中人为加入航向漂移误差。在所截取的0.05 s航迹数据中，漂移误差从0线性增长到1倍波长，阵列麦克风信号不变。从图中可以看出，与图7（a）类似，清晰地识别出了声源，但其位置也存在方向偏移，约为0.17 m。可见漂移误差也会导致识别出的声源位置反向偏移；在漂移误差线性增长情况下，偏移距离为累积漂移误差的一半。

图7（d）给出了随机误差对声源识别的影响。在轨迹数据中人为加入最大幅值为0.1倍波长的随机误差。阵列麦克风信号不变。从图中可以看出，声源识别效果显著变差，主瓣变形，分辨率变差，在主声源出现很多旁瓣，主声源位置也出现偏移。可见随机误差对声源识别的影响较大。在实际应用中，应着力控制随机误差。

4 无人机噪声飞行试验 4.1 试验设置

在西北某机场对某型无人机噪声开展了飞行试验研究。该无人机螺旋桨为三叶推力桨，安装于机身尾部。根据机场周围地理条件，在机场外距机场跑道终点1 km处某平整、空旷的地面上布放麦克风阵列。在无人机起飞、平飞飞越阵列上空的过程中，采集阵列噪声信号。飞控系统同时记录无人机航迹（经纬高、时间）、发动机工作状态（转速、油门）、空速等数据。

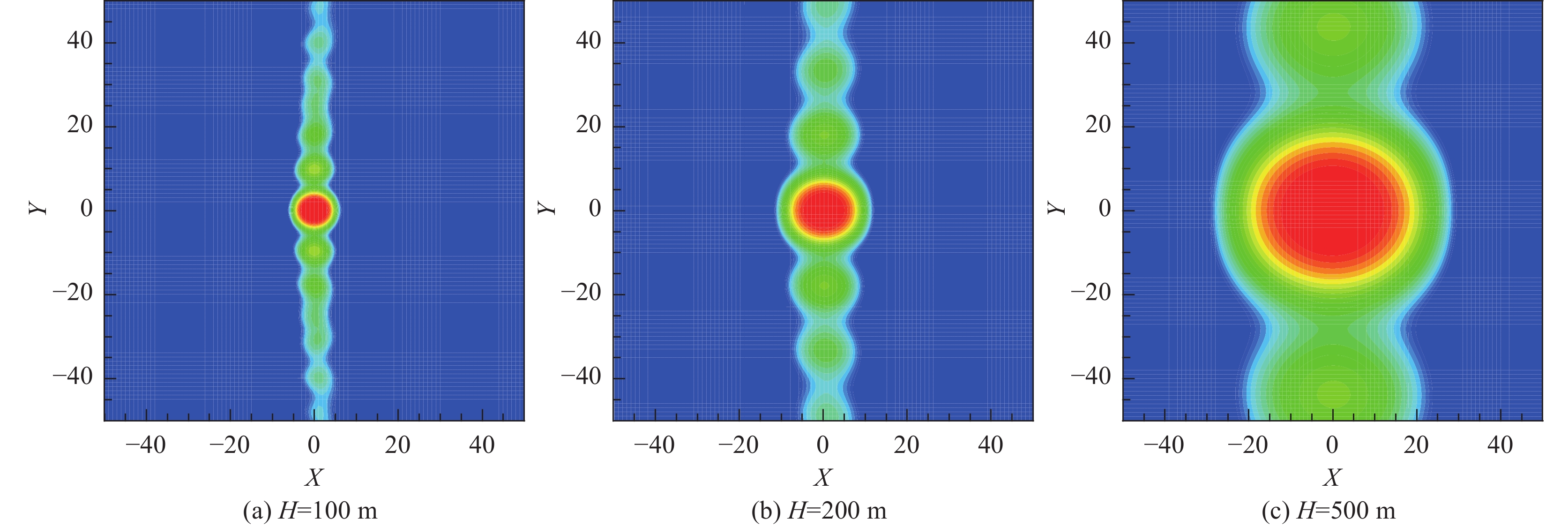
4.1.1 阵列设计

受场地限制，本次试验只能布置细长形的阵列。根据无人机的飞行状态以及螺旋桨工作状态，飞机平飞高度500 m，螺旋桨一阶叶片通过噪声频率分别为113 Hz和103 Hz，对阵列口径提出了很高的要求。根据3.2节数据长度对阵列性能的影响分析结果，增加数据长度在一定程度上可改善航向分辨率。故而采用了直线阵列样式，垂直于航向布置，在较小的阵列规模下最大限度保证横向分辨率。运用第2节中所述的考虑声传播相关性丢失的阵列优化设计方法得到了一个“外疏内密”分布的直线阵列，长度90 m，41个阵列单元。图8给出了该阵列对不同高度声源的基本响应，使用了以阵列正上方为中心的2 s长度的航迹数据。声源频率为100 Hz，飞行速度50 m/s。表2给出了该阵列的声源识别性能，表中也给出了一个典型平面阵列的对比结果，该阵列为2.3节中的“LoC”平面阵列放大2倍的阵列，63个阵列单元，横向口径90 m、航向口径72 m。从表中可以看到，直线阵列在航向分辨率和最大旁瓣水平方面略逊于平面阵列，而横向分辨率略优。

4.1.2 测试系统

测试系统由地面麦克风阵列、数据采集系统、GPS授时系统、机载差分GPS系统和便携式跑道标定设备组成。麦克风阵列由41个阵列麦克风构成，数据采集系统为东华DH8302动态数据采集系统，采用了西安同步电子SYN2304型串口时间服务器对数采系统的上位机进行GPS授时，记录的噪声数据包含了GPS时间。机载的差分GPS系统记录飞机航迹，通过GPS时间实现噪声数据与航迹数据的时间对标。使用便携式跑道标定设备测量阵列点GPS位置，实现阵列与航迹的空间对标。

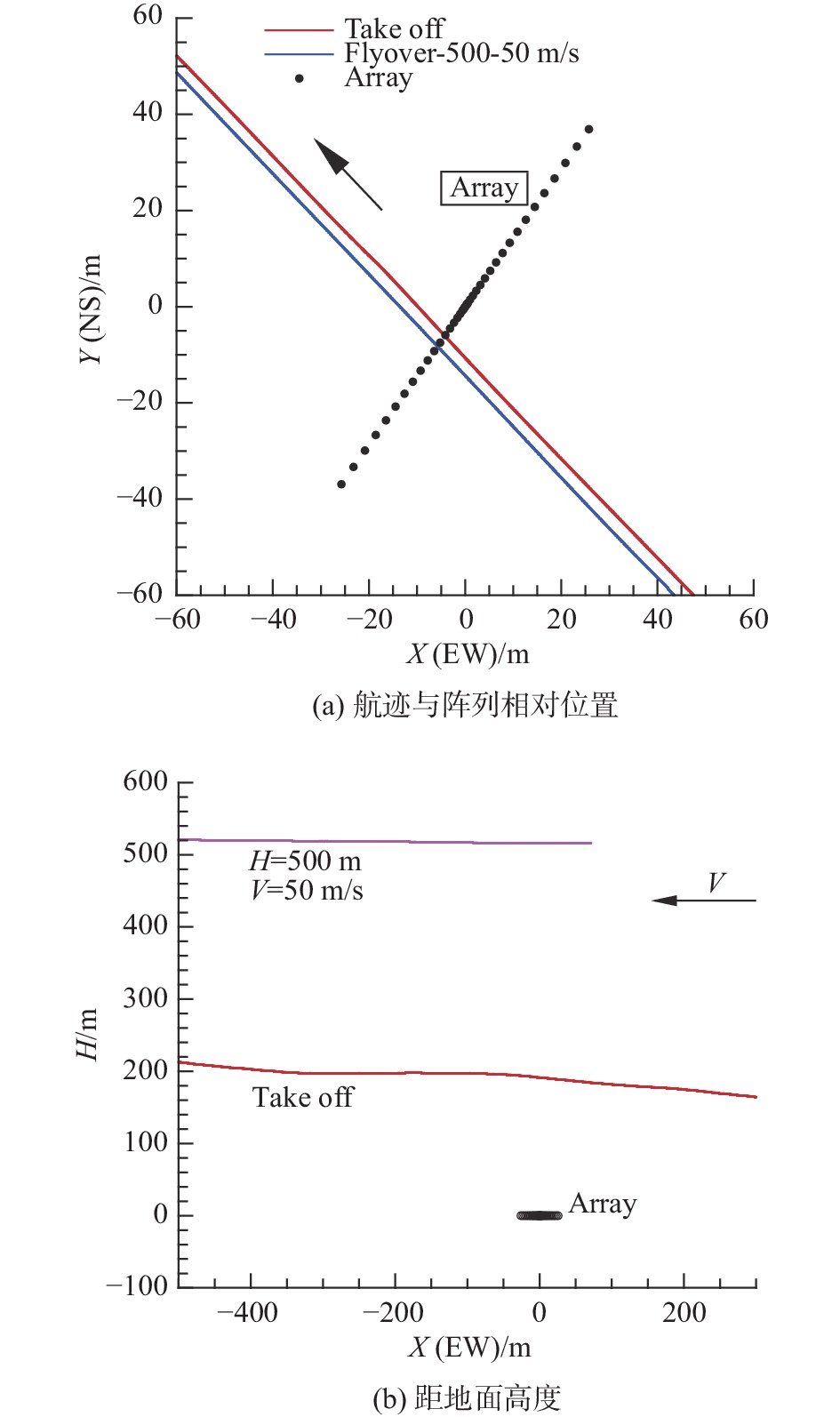
4.2 试验结果

图9给出了起飞和低空平飞状态无人机飞越阵列上空的航迹。X轴方向为自西向东，Y轴方向为自南向北。两次飞行航迹虽然略微偏离阵列中心，但均处于阵列探测范围内。

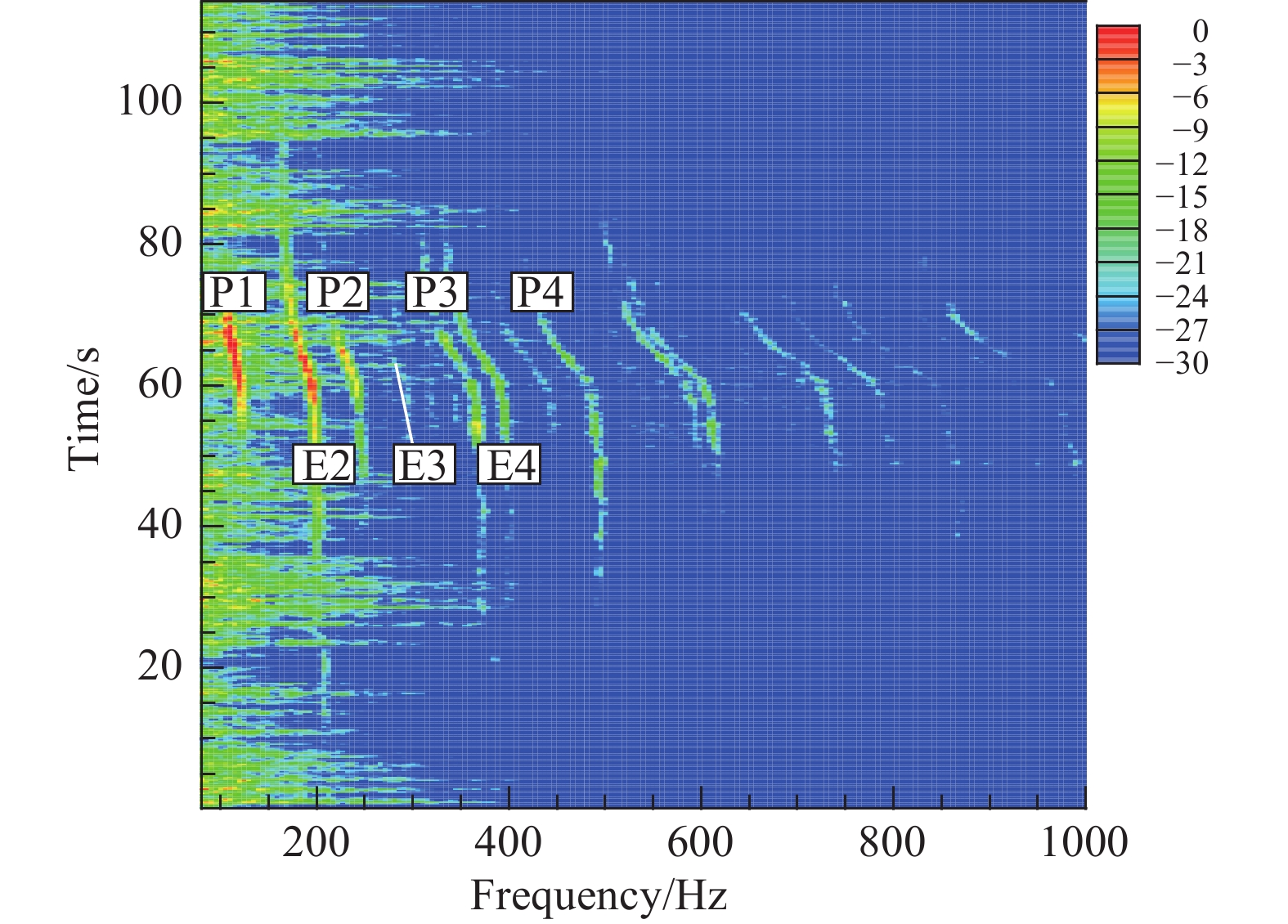
图10给出了起飞过程中无人机噪声的单麦克风频谱，图中“P1”、···、“P4”表示1～4阶螺旋桨噪声分量，“E2” 、···、“E4” 表示2～4阶螺旋桨驱动系统噪声分量。可以看到清晰的多普勒效应，表明麦克风信号正常，信噪比良好。无人机起飞过程中飞越阵列正上方时的高度为191.7 m，飞行速度为30 m/s。从图10中可以看到主要噪声分量呈现出了显著的多普勒效应。

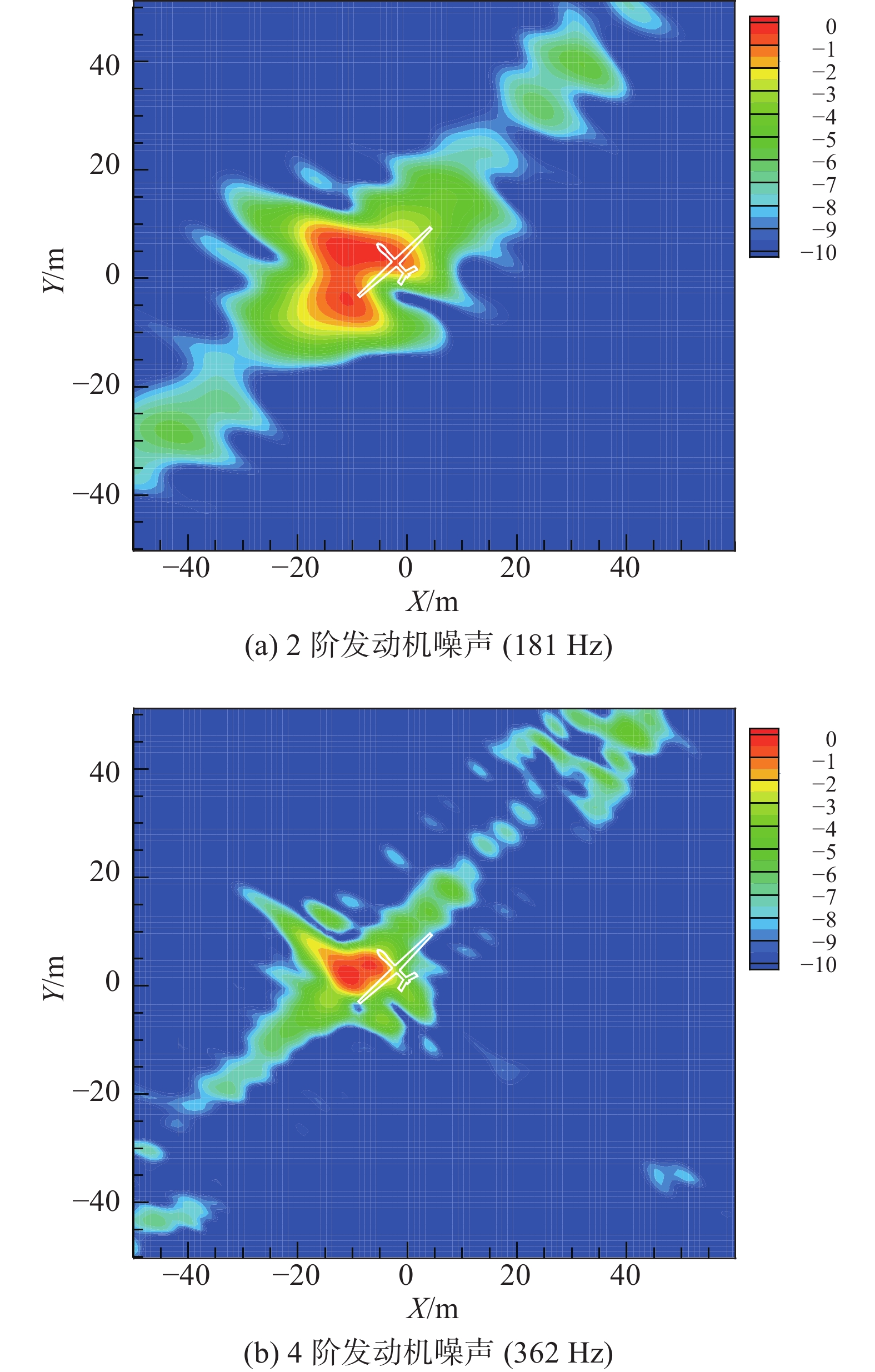
图11、图12给出了无人机起飞过程中螺旋桨噪声和发动机噪声的窄带波束形成结果，带宽0.6 Hz，数据长度为1.6 s，对应航迹长度为50 m。从图中可以看到，清晰地识别出了1～3阶螺旋桨噪声和2、4阶发动机噪声。随着声源频率提高，阵列分辨率提高。

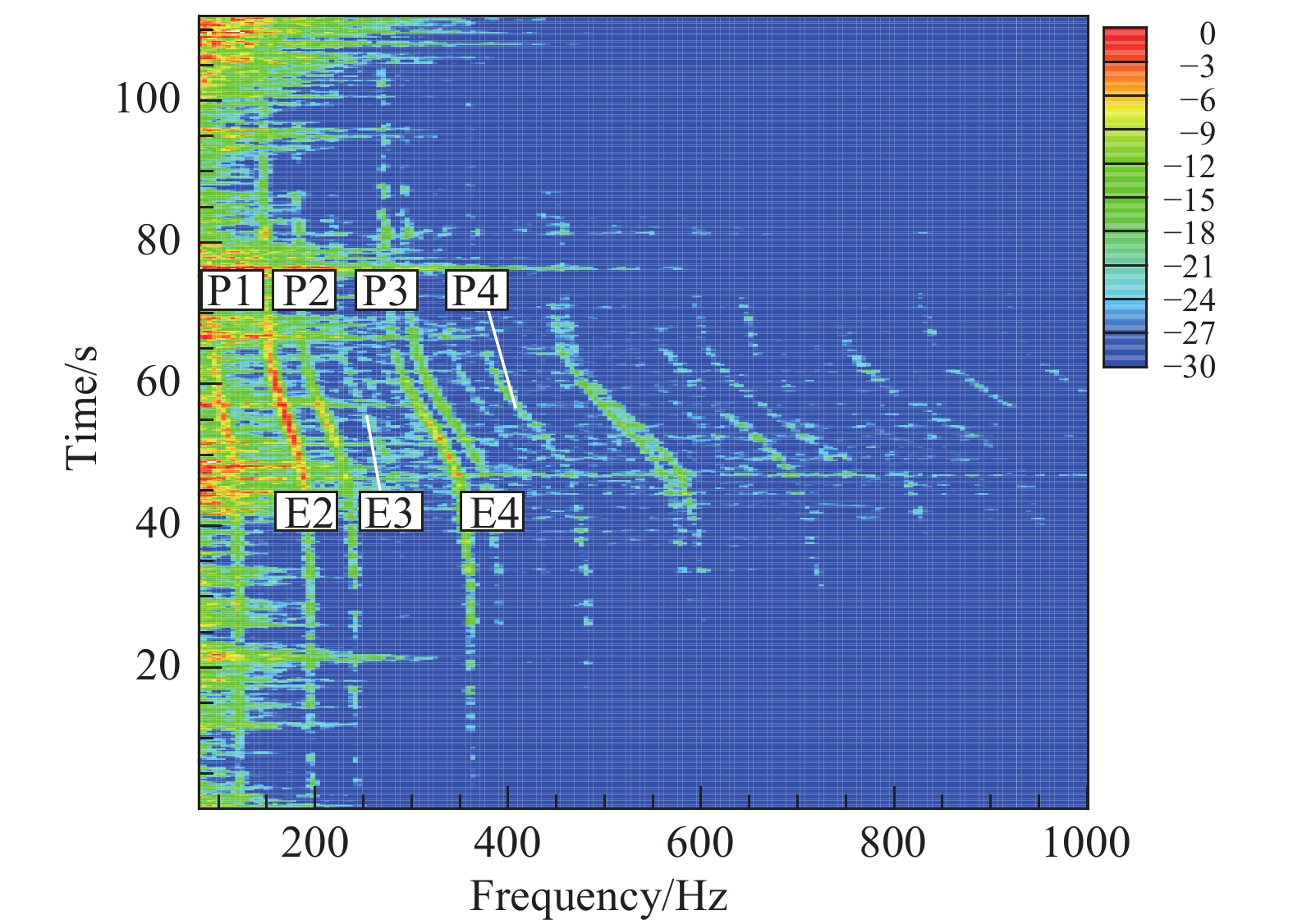
图13给出了无人机在高度500 m、飞行速度50 m/s的平飞过程中无人机噪声的单麦克风频谱，图中“P1”、···、“P4”表示1～4阶螺旋桨噪声分量，“E2” 、···、“E4” 表示2～4阶螺旋桨驱动系统噪声分量。可以看到较清晰的多普勒效应。图14和图15给出了无人机飞越阵列上空的过程中螺旋桨噪声和发动机噪声的窄带波束形成结果，带宽为0.6 Hz，数据长度为1.6 s，对应航迹长度为83 m。可以看到，清晰地识别出了1～3阶螺旋桨噪声和2～4阶发动机噪声。与起飞工况的声源识别结果相比，由于所用数据对应的航迹长度增大，航向分辨率得到改善，与横向分辨率相当。但飞行高度升高，阵列对声源分辨率降低，特别是横向分辨率，受阵列尺寸限制，难以有效改善。这也是影响定位精度的主要原因。此外，由于航迹偏离阵列中心，机身反射及声源指向性也对定位结果产生一定影响。

5 结　论

本文针对气动噪声飞行试验中运动声源识别的难点，对麦克风相阵列测量技术的时域波束形成算法、解多普勒效应技术开展了研究，建立了适用于运动声源识别的麦克风相阵列测量系统；提出了一种考虑声传播相关性丢失问题的阵列优化设计方法，基于该方法给出的阵列，在某型无人机噪声飞行试验中，实现了起飞和低空平飞状态螺旋桨和发动机噪声源的定位与识别。可得出以下结论：

1）考虑声传播相关性丢失问题的阵列优化设计方法给出的最优阵列，能够有效应对声传播相关性丢失问题，在较大频率范围内能够保持较好阵列性能。

2）轨迹数据的零点误差与漂移误差对声源识别的动态范围和分辨率的影响很小，随机误差对声源识别的动态范围和分辨率的影响很大，可为航迹监测系统搭建提供指导。

3）通过增加用于波束形成的噪声数据对应航迹的长度，一定程度上可提高阵列的航向分辨率，可用于指导较小规模的阵列方案设计。