2. 陕西省先进飞行器服役环境与控制重点实验室,西安 710049
2. Shaanxi Key Laboratory of Environment and Control for Flight Vehicle, Xi’an 710049, China
经过上亿年的进化,鸟类、昆虫、蝙蝠等生物均通过扑翼运动实现飞行。国内外学者受到扑翼生物的启发,研制了扑翼飞行器。扑翼飞行器主要在悬停、升力、能耗、控制等性能方面具有很大的优势。然而,目前扑翼飞行器的发展仍面临无法提供更高升力,飞行效率低,尺寸无法达到扑翼昆虫量级,无法做出更精确的飞行控制等问题[1]。因此,为了突破扑翼飞行器高升力、高效率、小尺寸等技术瓶颈,亟需开展更为细致的扑翼运动动力学研究,为设计更高效、高机动性的扑翼飞行器提供可靠的理论基础。扑翼飞行器在飞行过程中,相对来流方向与翼弦间的角度为迎角。迎角是影响扑翼飞行器飞行时升阻力系数的重要因素。当迎角超过一定范围,飞行器的飞行性能将会下降。因此,为了获得扑翼飞行器飞行时最佳的飞行姿态,开展不同迎角对扑翼运动的影响机理研究尤为重要。
目前关于迎角对扑翼运动的影响机理研究主要以实验为主:2007年,宁琦等[2]对扑翼飞行器进行了风洞试验,研究了迎角对其气动特性的影响;2014年,鲍锋等[3]基于色流实验与粒子图像测速(particle image velocimetry, PIV)技术,开展了迎角对单自由度扑翼运动升力的影响机理研究。此外,对扑翼运动其他运动参数的研究中,1989年,Ennos[4]等基于高速摄影技术,对扑翼昆虫飞行时的运动学规律进行了探索;1999年,Dickinson等[5]通过模型实验的方法确定了昆虫飞行时的雷诺数范围为40与400之间。然而,实验方法普遍存在代价大、成本高等问题,且实验能够提供的数据有限,难以精细地获得能够直观、全面反映其空气动力学机制的流场细节特征。因此,高效、准确地对扑翼运动进行数值模拟研究已成为近些年的热点。国内外学者主要通过求解N-S方程的方法对扑翼运动开展数值模拟研究。1998年,Liu等[6]通过求解三维非定常N-S方程的方法模拟并分析了昆虫飞行时的非定常流场结构;2000~2004年,Wang等利用二维计算[7-9]、三维实验[10]的方法研究了蜻蜓前飞时流场的变化与前后翼之间的影响,解释了蜻蜓飞行高升力机制;2002~2015年,孙茂等[11-14]通过求解N-S方程的方法,对扑翼昆虫运动时的稳定性高、能耗低等特点进行了研究,并对气动力机理进行了归纳;2008年,Young等[15]通过求解三维不可压N-S方程的方法模拟了昆虫扑翼运动,研究了振幅、频率等参数对扑翼运动性能的影响。
扑翼的运动方式复杂、外形复杂,可靠的模拟结果依赖于复杂边界条件易实施的数值方法与高分辨率网格。近年来,高效准确的格子Boltzmann方法(lattice Boltzmann method, LBM)[16]在计算流体力学(computational fluid dynamics, CFD)中得到普遍应用,由于其算法简单、边界条件易实施、质量动量严格守恒、适于并行等优点,被应用于各个领域,在扑翼运动的数值模拟中也得到快速发展。2014年,Keisuke等[17]采用浸没边界格子Boltzmann方法针对类蜻蜓扑翼模型前后翼相位滞后角开展了数值模拟研究,结果表明,扑翼运动的移动方向取决于相位滞后角。2020年,彭连松等[18]采用基于LBM的商业软件Xflow,对串列双翅扑翼和单对翅扑翼进行数值模拟,结果表明,双翅悬停效率高于单翅拍动的悬停效率。此外,对扑翼运动进行数值模拟时,对运动复杂边界的精确描述是十分重要的。动边界识别方法总体上分为拉格朗日法和欧拉法,基于拉格朗日法的动边界识别法,其重构网格计算时间长,计算效率低。而Level-Set方法[19]基于欧拉法,即使在规则分布的欧拉网格中也能精确捕捉到边界点的位置。同时,由于网格的规则性,更适合并行计算,使得重构网格的时间大大缩短,若在较高的网格分辨率下,可精准描述复杂物体边界运动。如2005年,李会雄等[20]基于Level-Set方法捕捉了气-液两相流运动相界面; 2006年,陈凡红等[21]基于Level-Set方法追踪了各种外形的物体在旋转流场中的变形还原效果,研究表明,Level-Set方法可以准确追踪运动界面,且容易实现,具有较大通用性。另一方面,在硬件上,近些年来,图形处理器(graphics processing unit,GPU)发展速度远超中央处理器(central processing unit, CPU),GPU开始逐渐应用于非显示的通用图形处理器(general purpose graphics processing unit, GPGPU),出现了较多基于CPU/GPU异构系统的CFD高性能计算在各类计算流体力学方法(如N-S、LBM等)上的应用研究,使得CFD计算效率更高。其中GPU的单指令多线程模式与LBM算法完美匹配,两者结合,较之CPU可达百倍以上的加速比[22]。
基于以上种种,本文针对扑翼运动问题,采用LB方法求解流场,Level-Set方法追踪复杂运动边界,并结合GPU并行加速技术,开发了扑翼运动三维高效数值模拟程序,对扑翼在不同迎角下,上下扑动时其气动性能开展数值研究。通过精细捕捉其流体力学特征量—涡系结构、压力场等,分析其升阻力产生的机制,获得其最佳运动迎角。同时,本文也为扑翼运动的研究提供了高效、可靠的数值方法。
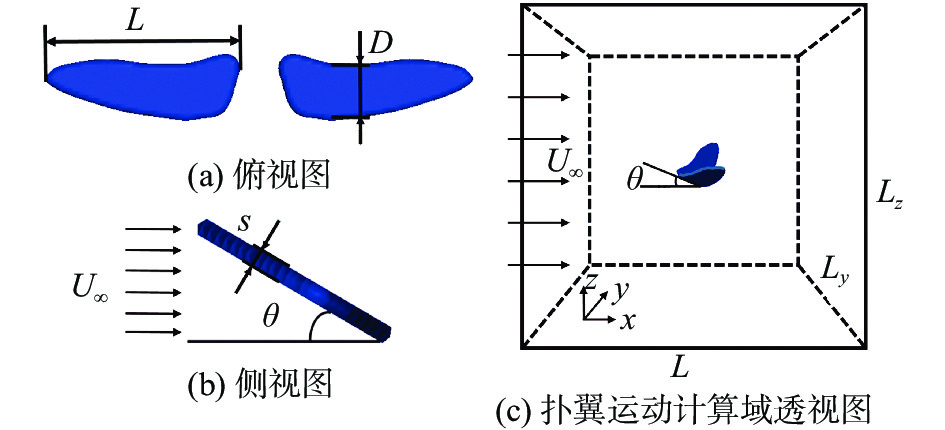
1 计算模型与数值方法 1.1 计算模型本文根据Liang[12]选用的扑翼模型进行建模,其几何模型如图1所示。
|
图 1 扑翼几何模型 Fig.1 Prototype of flapping-wing |
翼面的展长
| $ \alpha ={\alpha }_{{\rm{max}}}{{\rm{sin}}}\left(2{\text{π}} f+\varphi \right) $ | (1) |
其中,
雷诺数
| $ {C}_{L}=\frac{{F}_{z}}{0.5\rho {U}_{{\rm{ref}}}^{2}A},\;{C}_{D}=\frac{{F}_{x}}{0.5\rho {U}_{{\rm{ref}}}^{2}A} $ | (2) |
其中,
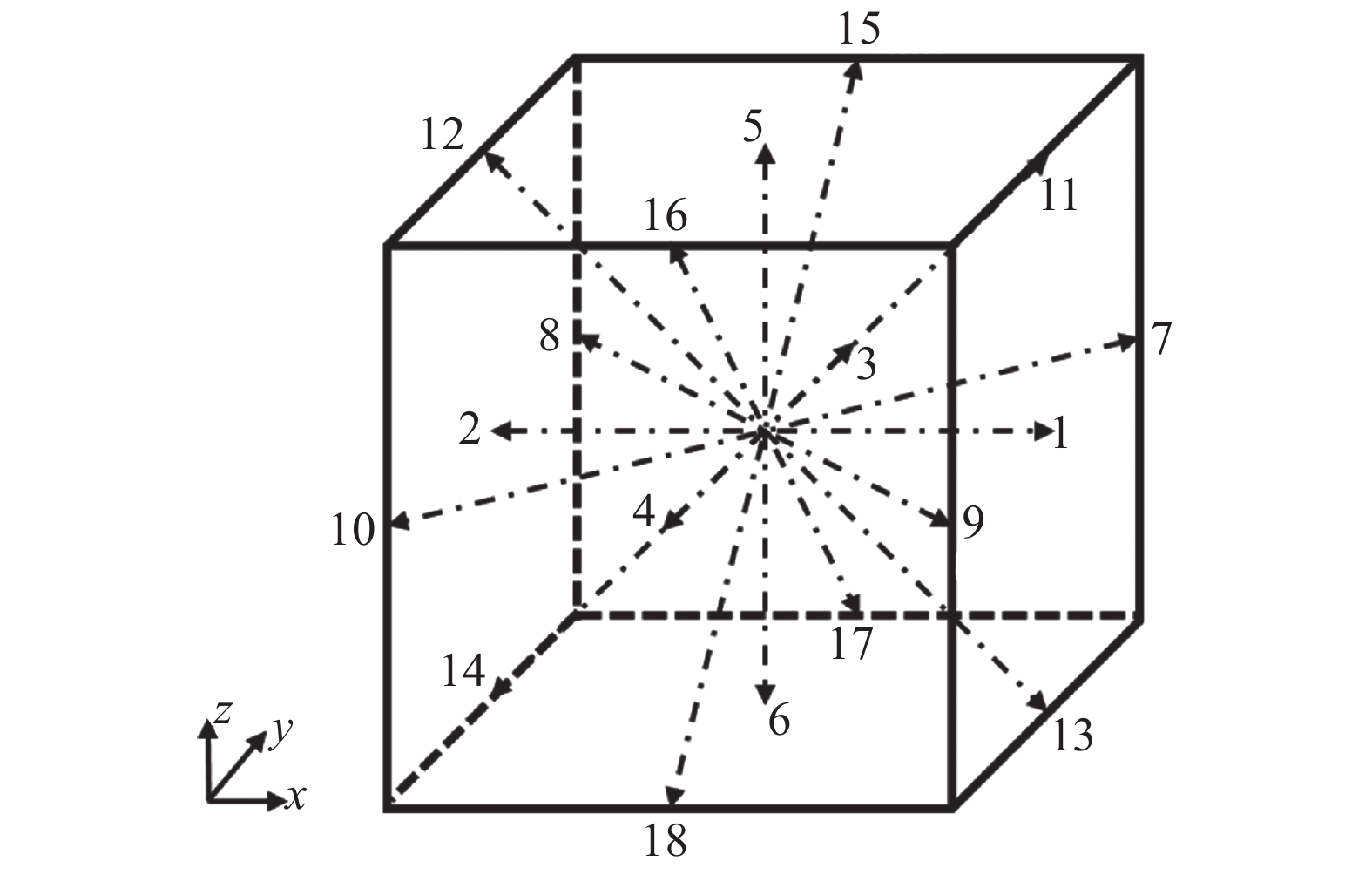
本文采用LBM-D3Q19模型[16](图2)求解流场,其离散方程如下:
| $ {f}_{i}\left({\boldsymbol{r}}+{{\boldsymbol{e}}}_{i}{\rm{\delta }}_{t},t+{\rm{\delta }}_{t}\right)-{f}_{i}\left({\boldsymbol{r}},t\right)=\frac{1}{\tau }\left[{f}_{i}^{{\rm{eq}}}\left({\boldsymbol{r}},t\right)-{f}_{i}\left({\boldsymbol{r}},t\right)\right] $ | (3) |
式中:
| $ {f}_{i}^{{\rm{eq}}}=\rho {w}_{i}\left[1+3\left({{\boldsymbol{e}}}_{i} \cdot {\boldsymbol{u}}\right)+\frac{9}{2}{\left({{\boldsymbol{e}}}_{i} \cdot {\boldsymbol{u}}\right)}^{2}-\frac{3}{2}{{\boldsymbol{u}}}^{2}\right] $ | (4) |
其中,每个方向上的分布函数的权系数
| ${w_i} = \left\{ {\begin{array}{*{20}{l}} {1/3,}&{i = 0}\\ {1/18,}&{i = 1,2, \cdots ,6}\\ {1/36,}&{i = 7,8, \cdots ,18} \end{array}} \right. $ | (5) |
离散速度模型
| $ {{\boldsymbol{e}}}_{i}=\left\{ {\begin{array}{*{20}{l}} {\left( {0,0,0} \right)},\quad i = 0\\ {\left( { \pm 1,0,0} \right),\left( {0, \pm 1,0} \right),\left( {0,0, \pm 1} \right)},\quad i = 1,2, \cdots ,6\\ {\left( { \pm 1, \pm 1,0} \right),\left( {0, \pm 1, \pm 1} \right),\left( { \pm 1,0, \pm 1} \right)},\quad i = 7,8, \cdots ,18 \end{array}} \right. $ | (6) |
宏观密度
| $ \rho ={\sum }_{i}{f}_{i} $ | (7) |
| $ {\boldsymbol{u}}={\sum }_{i}{{\boldsymbol{e}}}_{i}{f}_{i}/\rho $ | (8) |
对于流场,宏观边界条件为:进口
| $ {f}_{i}\left({{\boldsymbol{r}}}_{s},t\right)={f}_{i}^{{\rm{eq}}}\left({{\boldsymbol{r}}}_{s},t\right)+\left[{f}_{i}\left({{\boldsymbol{r}}}_{f},t\right)-{f}_{i}^{{\rm{eq}}}\left({{\boldsymbol{r}}}_{f},t\right)\right] $ | (9) |
其中,
|
图 2 D3Q19模型 Fig.2 D3Q19 model |
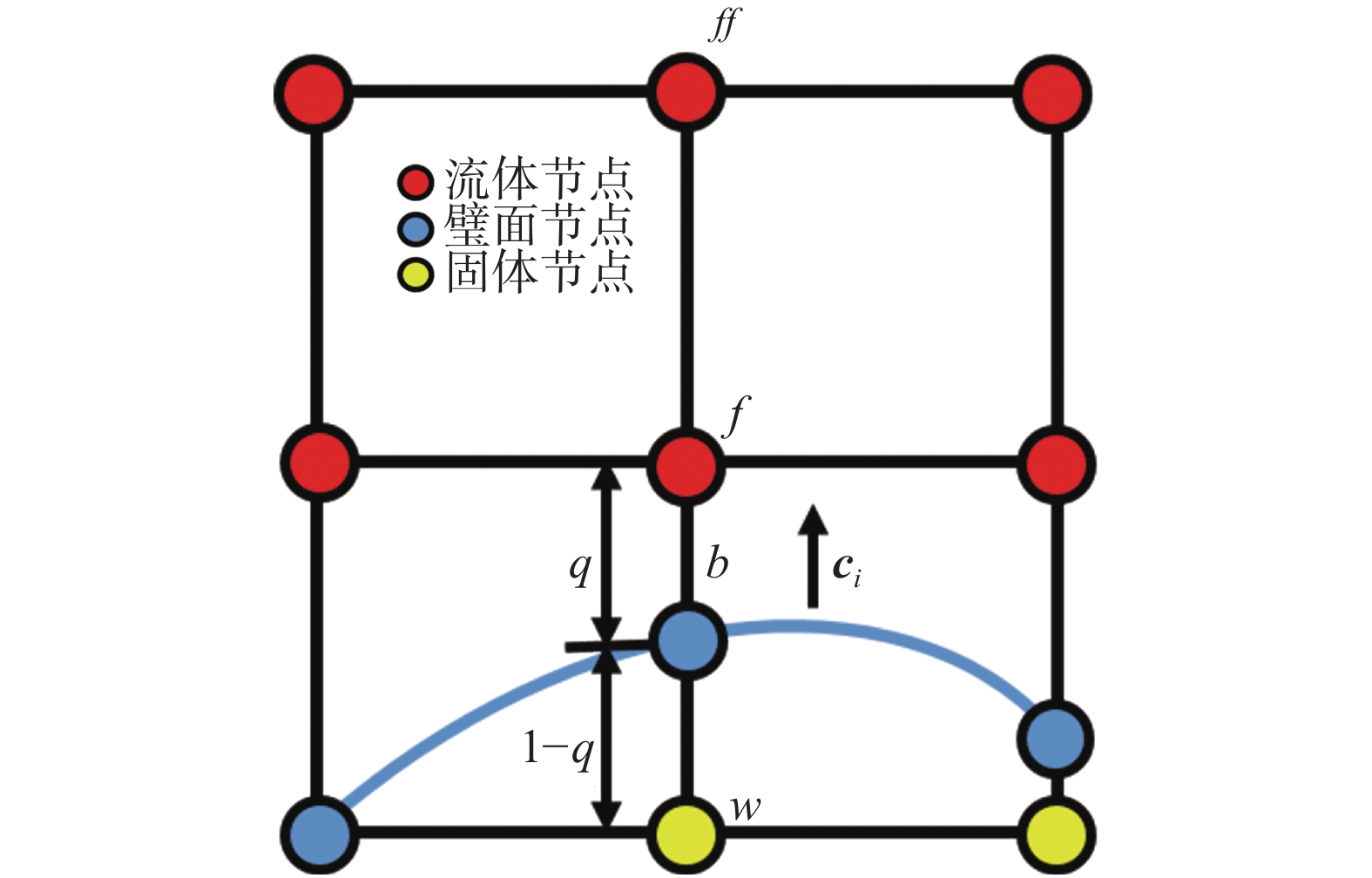
对于移动的固体壁面,本文采用非平衡态外推格式[23]确定固体边界。如图3所示,非平衡态外推格式将固体节点
非平衡态部分中,q表示与壁面相交一个网格间距中处于流体区域的比例:
| $ q=\frac{\left|{{\boldsymbol{r}}}_{f}-{{\boldsymbol{r}}}_{b}\right|}{\left|{{\boldsymbol{r}}}_{f}-{{\boldsymbol{r}}}_{w}\right|} $ | (10) |
其中,
| $ {{{{\bar {\boldsymbol{u}}}}_w}} = \left\{ {\begin{array}{*{20}{l}} {q{{\boldsymbol{u}}_{w1}} + \left( {1 - q} \right){{\boldsymbol{u}}_{w2}},}&{q < 0.75}\\ {{{\boldsymbol{u}}_{w1}},}&{q \geqslant 0.75} \end{array}} \right.$ | (11) |
其中,
| $f_i^{{\rm{neq}}}( {{{\boldsymbol{r}}_w},t} ) = \left\{ {\begin{array}{*{20}{l}} {qf_i^{{\rm{neq}}}( {{{\boldsymbol{r}}_f},t} ) + ( {1 - q} )f_i^{{\rm{neq}}}( {{{\boldsymbol{r}}_{ff}},t} ),}&{q < 0.75}\\ {f_i^{{\rm{neq}}}( {{{\boldsymbol{r}}_f},t} ),}&{q \geqslant 0.75} \end{array}} \right.$ | (12) |
综上,
| $ {f}_{i}\left({{\boldsymbol{r}}}_{w},t\right)={f}_{i}^{{\rm{eq}}}\left({{\boldsymbol{r}}}_{w},t\right)+\left(1-\frac{1}{\tau }\right){f}_{i}^{{\rm{neq}}}\left({{\boldsymbol{r}}}_{w},t\right) $ | (13) |
|
图 3 曲线边界非平衡态外推格式 Fig.3 Schematic of extrapolation method for curved boundary conditions in lattice Boltzmann method |
物体在流场中运动时,当前时刻是固体中的网格节点下一时刻可能会成为流体节点,此时需要重新填充新生流体节点[24]。如图4所示,蓝色虚线为
公式如下所示:
| $ \begin{split} {f}_{p}\left({{\boldsymbol{r}}}_{p},t+{\rm{\delta }}_{t}\right)=&{f}_{p}^{{\rm{eq}}}\left({{\boldsymbol{r}}}_{p},t\right)+{f}_{p}^{{\rm{neq}}}\left({{\boldsymbol{r}}}_{p},t\right)\\ \;\;\;\;\;\;\;\;\;\; =&{f}_{p}^{{\rm{eq}}}(\overline {\rho },{{\boldsymbol{u}}}_{b})+\left[{f}_{g}({{\boldsymbol{r}}}_{g},t)-{f}_{g}^{{\rm{eq}}}({{\boldsymbol{r}}}_{g},t)\right] \end{split}$ | (14) |
其中:在
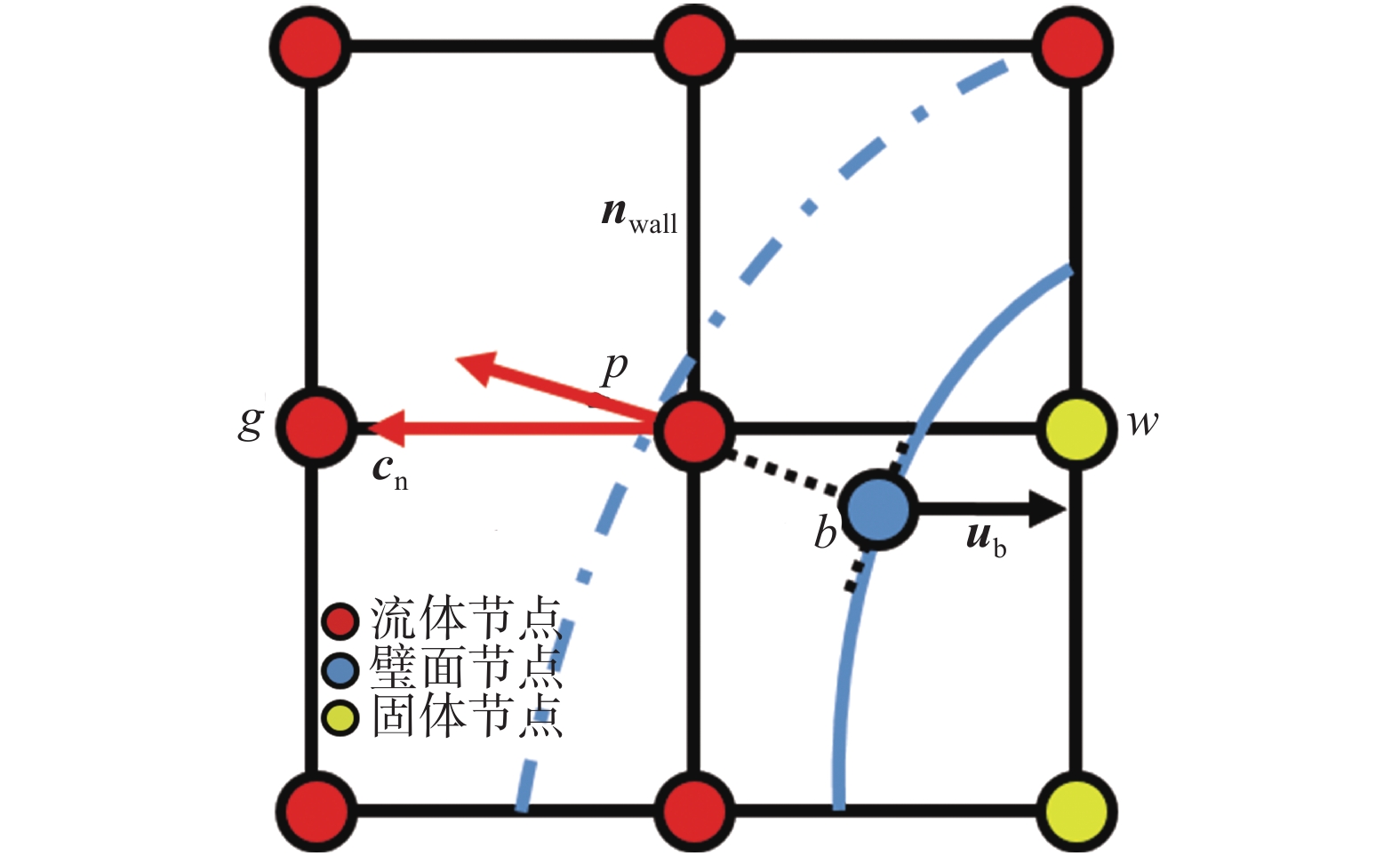
|
图 4 新生流体节点的重新填充 Fig.4 Schematic of initialization of new fluid nodes |
Level-Set算法是一种用隐函数描述边界运动的方法[19],利用等值面函数
| $ d\left({\boldsymbol{x}}\right)={{\rm{min}}}\left(\left|{\boldsymbol{x}}-{{\boldsymbol{x}}}_{I}\right|\right){}{{\boldsymbol{x}}}_{I}\in \varOmega $ | (15) |
其中,
符号距离函数表示的
| $ \phi \left({\boldsymbol{x}}\right)=\left\{ {\begin{array}{*{20}{l}}d\left({\boldsymbol{x}}\right)&,{\boldsymbol{x}}\in {\varOmega }^+\\ 0&, {\boldsymbol{x}}\in \varOmega \\ -d\left({\boldsymbol{x}}\right)&, {\boldsymbol{x}}\in {\varOmega }^-\end{array}} \right. $ | (16) |
其中,
针对流/固动边界的实时更新问题,采用Level-Set动边界识别方法对标准格子立方体网格的边界进行实时更新。如图5所示,图5(a)为物体运动前状态,每个节点存储
GPU并行模式是将数据分配于多条线程(thread),多条线程组成一个块(block),GPU中多个运算单元同时计算每个block中的threads,而每条thread中的数据则串行计算。
本文自主搭建了基于LBM-GPU与Level-Set动边界识别方法的数值计算平台,计算流程图如图6所示。在流场计算的每一个迭代中,经过分布函数的碰撞与迁移之后,对下一迭代步的边界位置采用Level-Set方法进行识别,并映射至LBM网格中,对网格节点属性,即固体内部、固体壁面及流体,进行更新,并对新生流体节点的分布函数进行填充,完成一次循环。
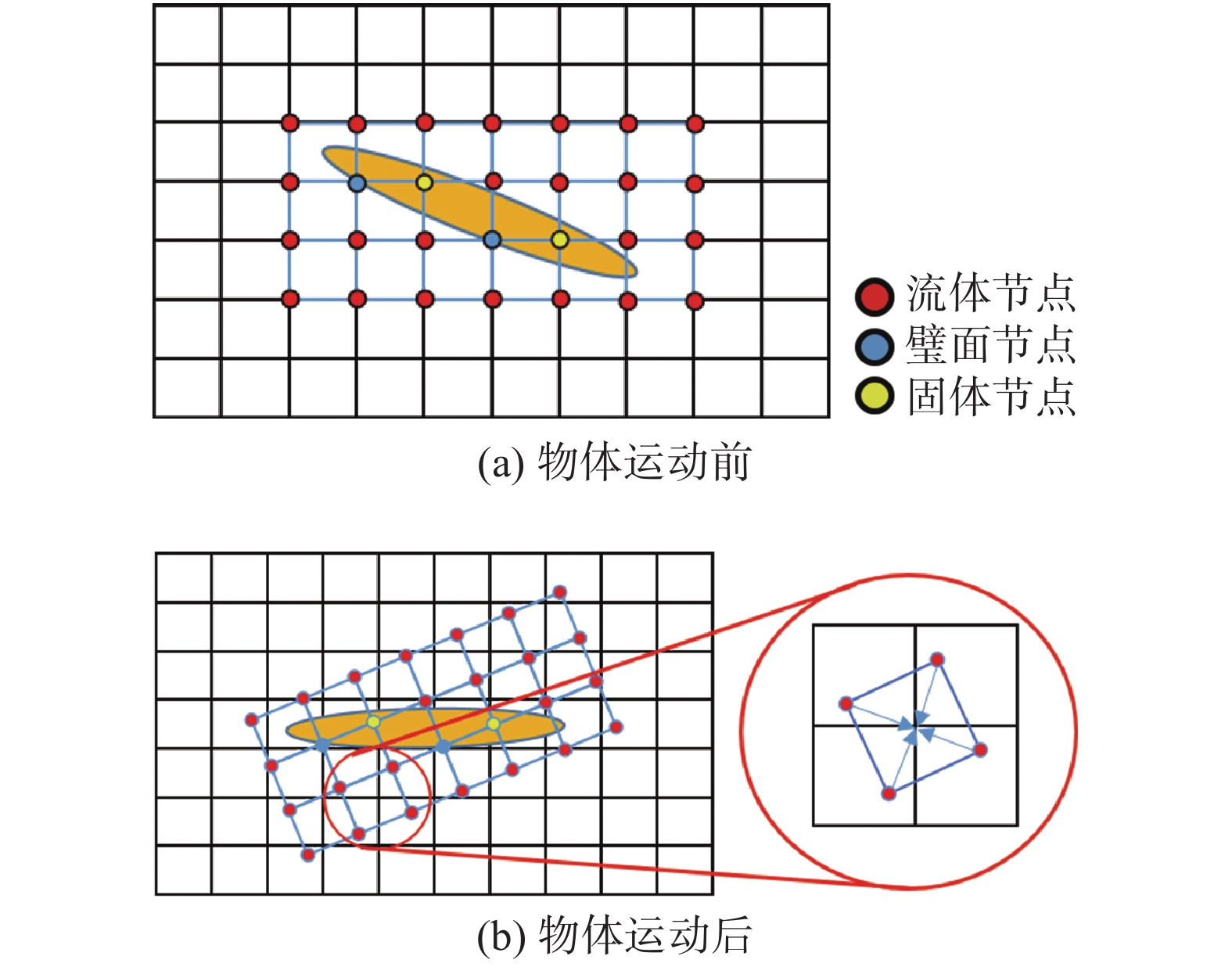
|
图 5 Level-Set动边界识别方法 Fig.5 Schematic of identification method of moving boundary of Level-Set |
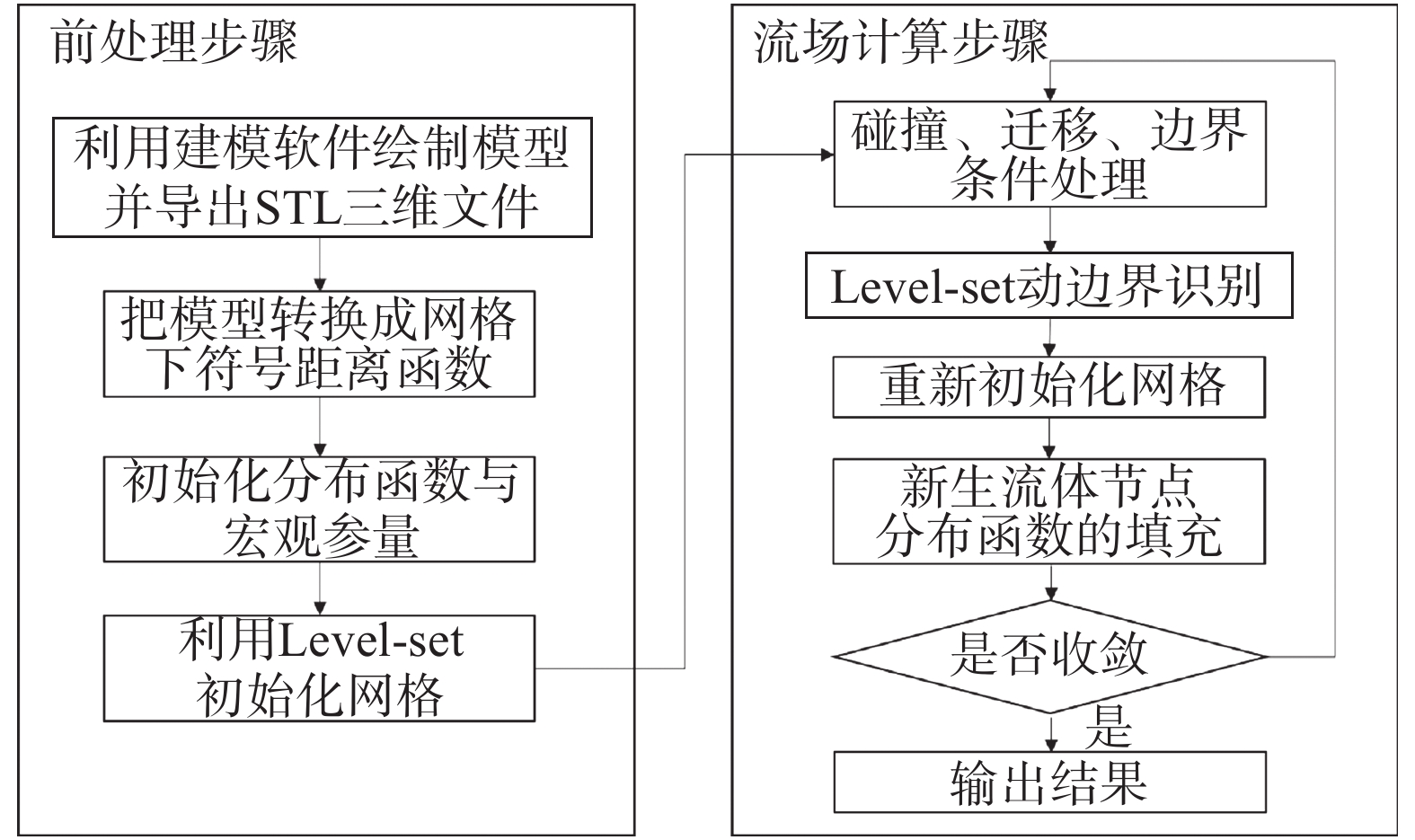
|
图 6 计算流程图 Fig.6 Flow chart of numerical method |
此外,本计算采用一颗NVIDIA Tesla K20M GPU加速,以2389万个网格计算工况为例,计算7200个LBM步长,总耗时4.20 h;相同情况下使用一颗Intel Core i7-3770 CPU计算共耗时298.2 h,加速比为71。
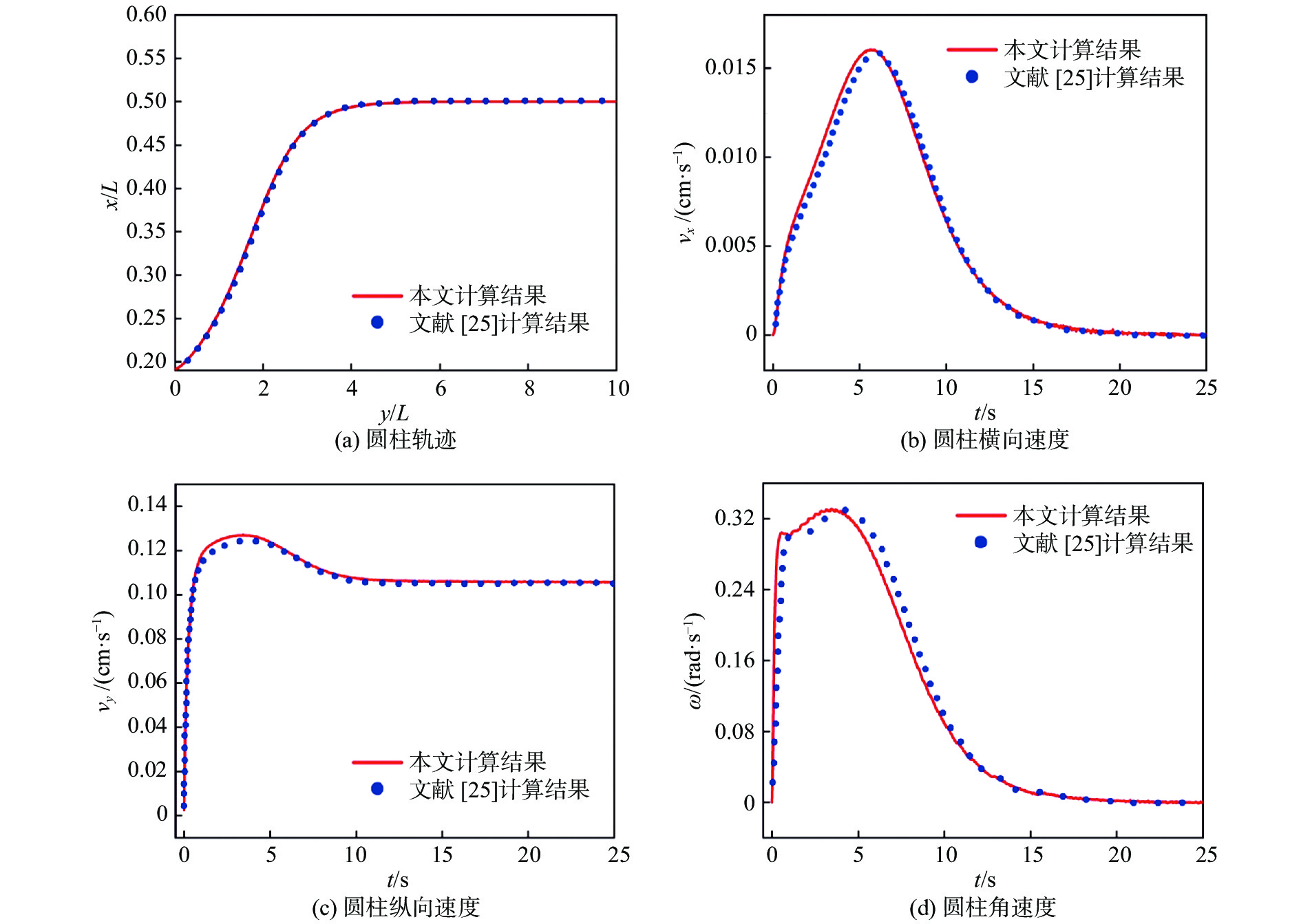
1.3 程序验证 1.3.1 正确性验证本文利用圆柱沉降问题进行程序验证,并与Li[25]的模拟结果进行对比。文献采用应力积分法求得物体受力,从而获得物体运动的轨迹,实现追踪动边界的效果。如图7所示,圆柱在一个充满流体的管道中自由下落,由于自身的重力以及流体的作用,圆柱会边旋转边平移地下沉。管道宽度
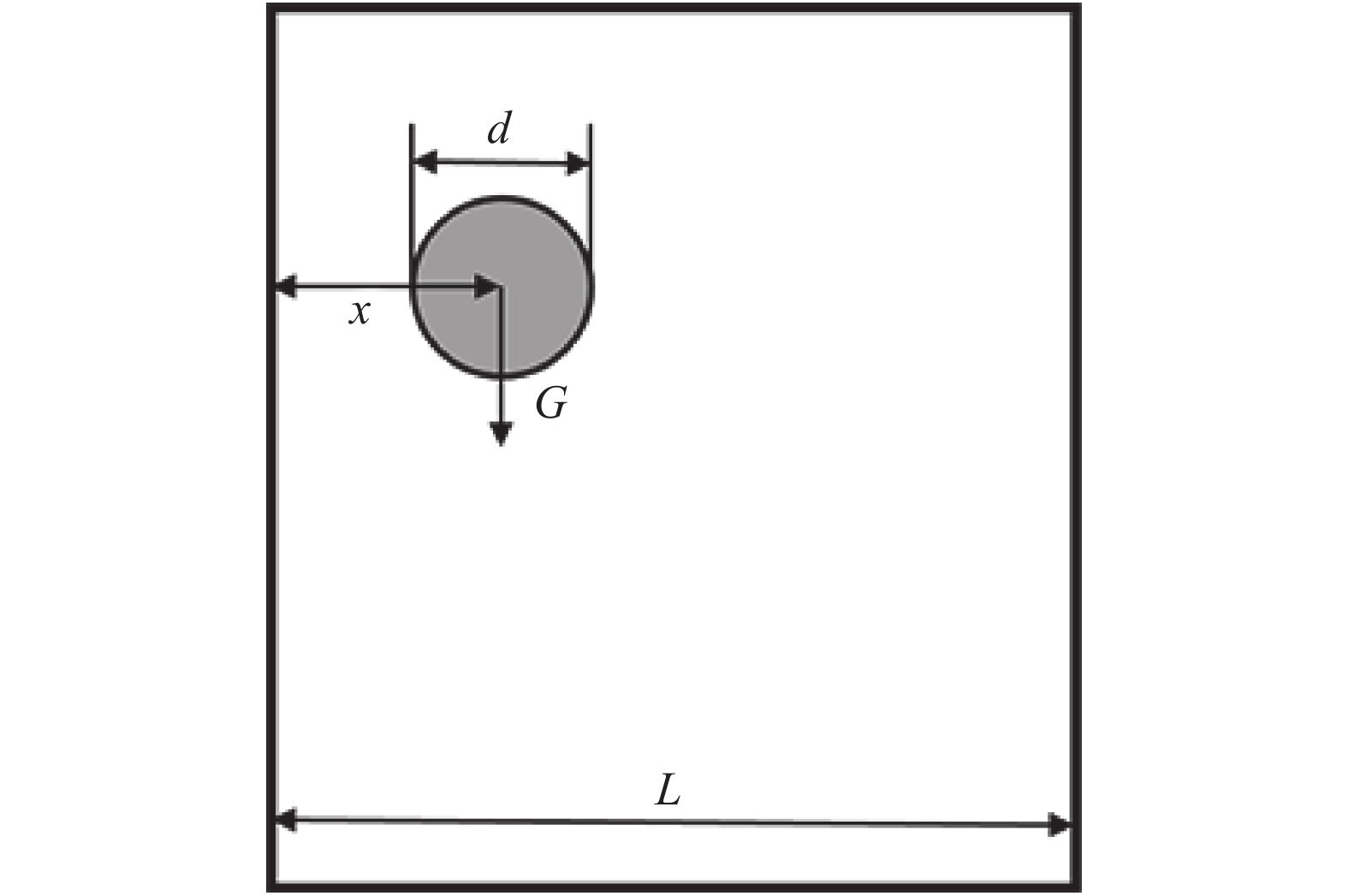
|
图 7 圆柱沉降示意图 Fig.7 Schematic of sedimentation of a circular cylinder |
图8为圆柱下沉过程中圆柱下落轨迹、水平方向速度、竖直方向速度和角速度随时间变化的曲线图。可以看出,本文结果与文献对比一致。此外,从图8(a)可以看出,圆柱运动最终达到了以恒定速度
本文使用不同三种网格分辨率模拟了图1所示的扑翼运动。计算参数
图9为三种网格分辨率下的翼尖处涡量云图。从图中可以看出,涡量云图基本一致。但随着网格分辨率的增加,在扑翼尾迹处的旋涡分离趋势更加明显,涡的细节也更清晰。

|
图 9 翼尖涡量云图 Fig.9 Vorticities contour at wing-tip |
图10为不同网格分辨率下的升力系数与阻力系数随时间变化曲线图,其中

|
图 10 网格无关结果图 Fig.10 Grid independence results |
本文计算6个扑动周期,一个扑动周期对应1200个LBM步长,共7200个LBM时间步长,对于A、B、C三种工况,计算时间分别为3.68 h、3.86 h、4.20 h。三种工况的计算均采用GPU加速,因计算时间较短,本文在之后的计算中均采取288×288×288的网格分辨率,以捕捉到更精细的流场细节。
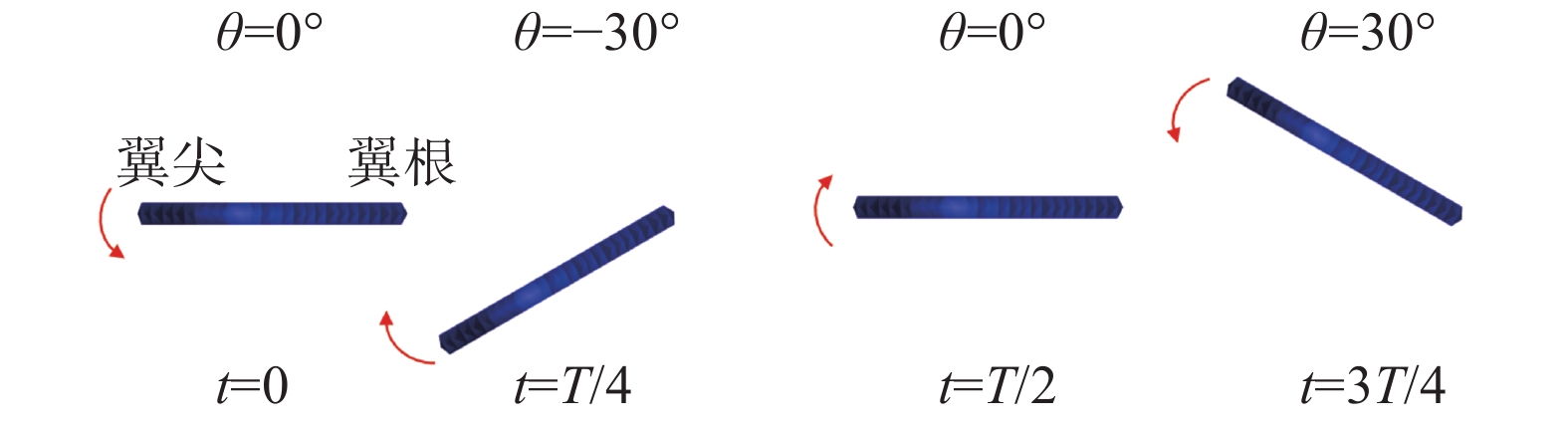
2 结果与讨论 2.1 迎角对升阻力系数的影响如图11所示,以
|
图 11 一个周期内扑翼运动示意图 Fig.11 Schematic of flapping-wing movement in a period |
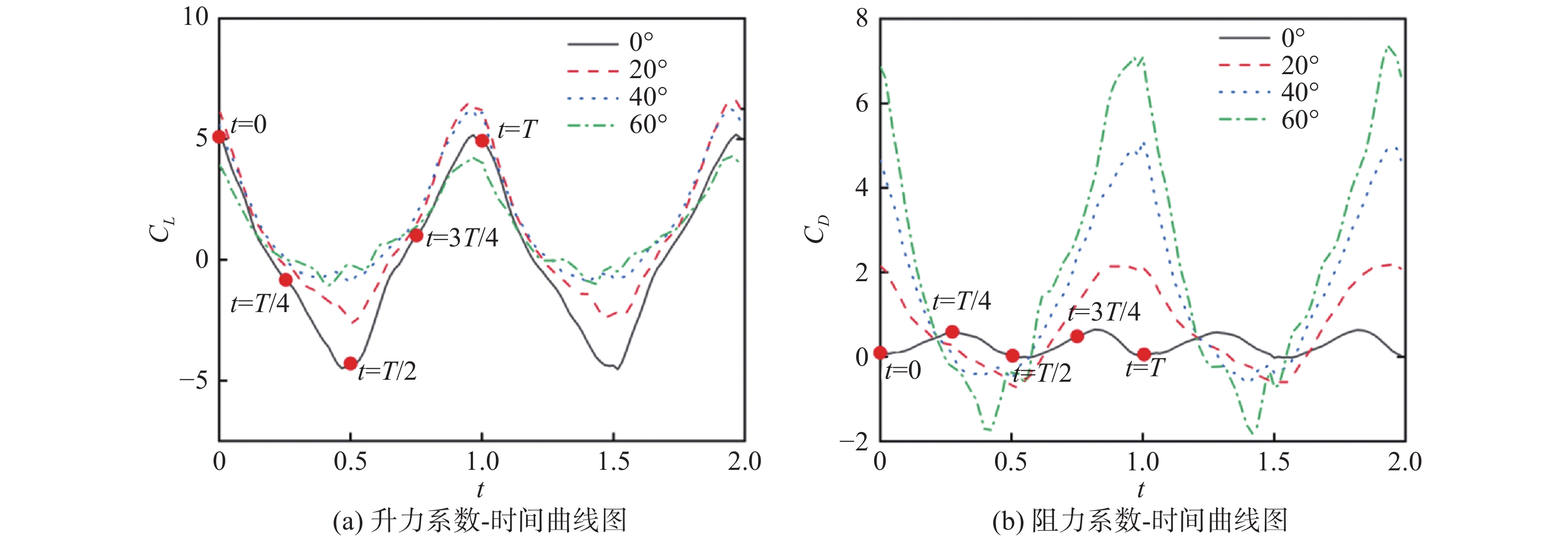
图12为不同迎角下升力系数
|
图 12 升阻力系数随时间变化曲线 Fig.12 Variation curve of lift and drag coefficient with time |
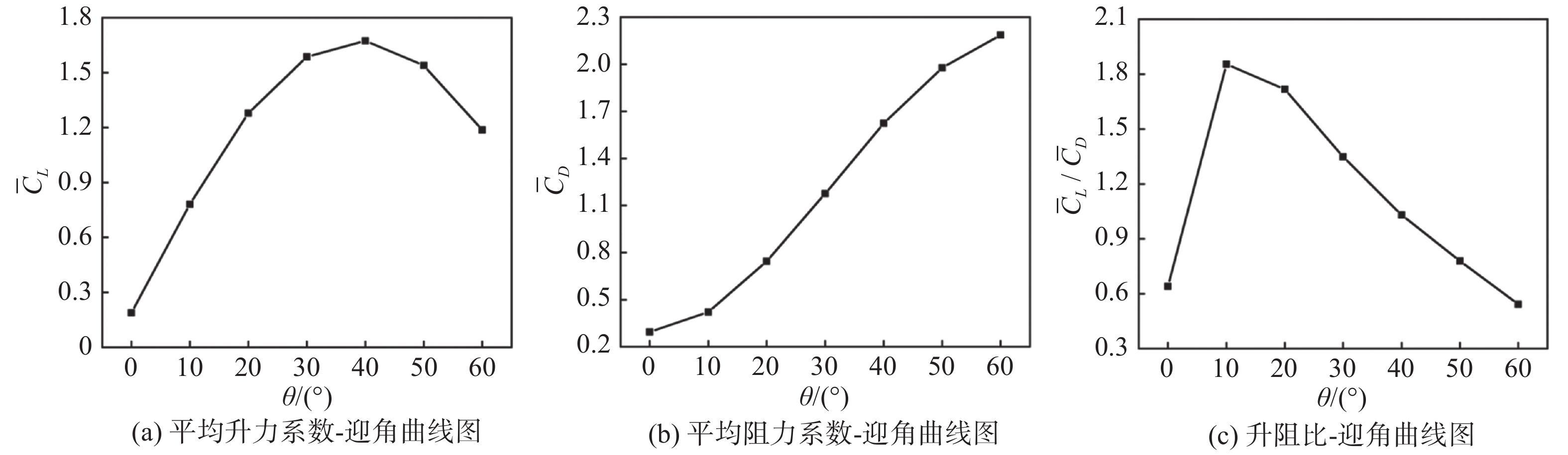
图13分别为平均升力系数
下文通过压力场和流场结构对扑翼运动的气动特性机理进行分析。
|
图 13 平均升阻力系数随迎角变化曲线 Fig.13 Variation curve of average lift and drag coefficient with angle of attack |
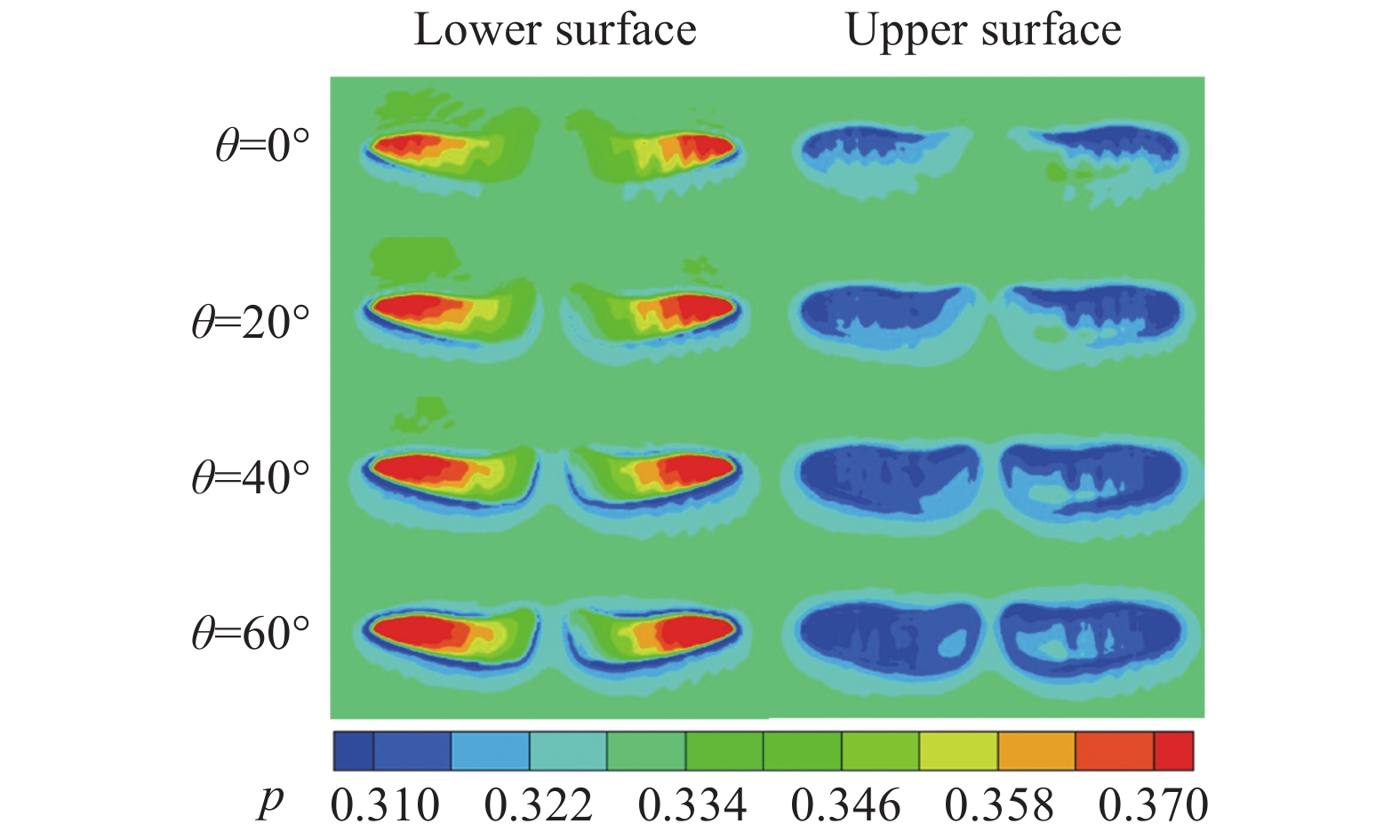
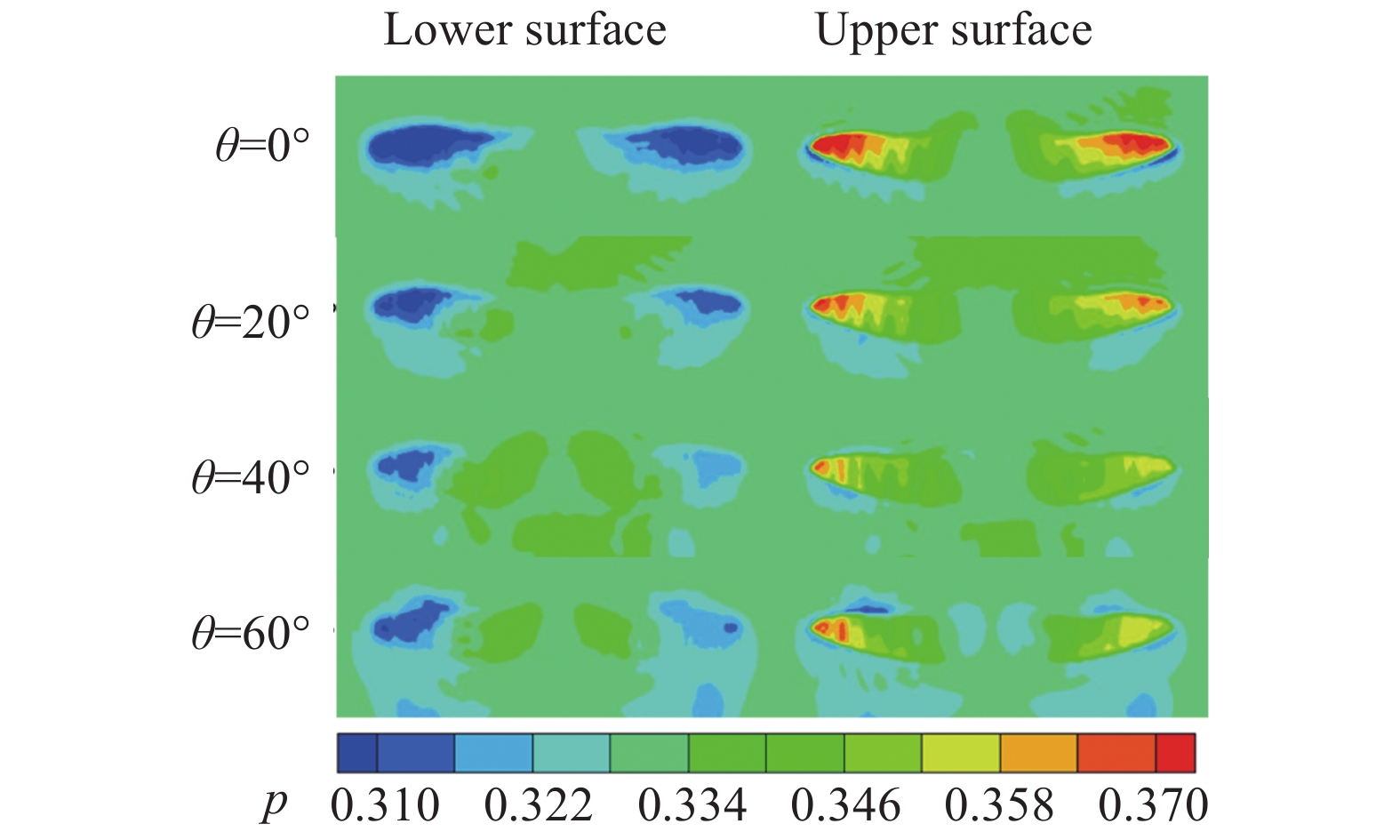
图14为不同迎角下,
|
图 14 |
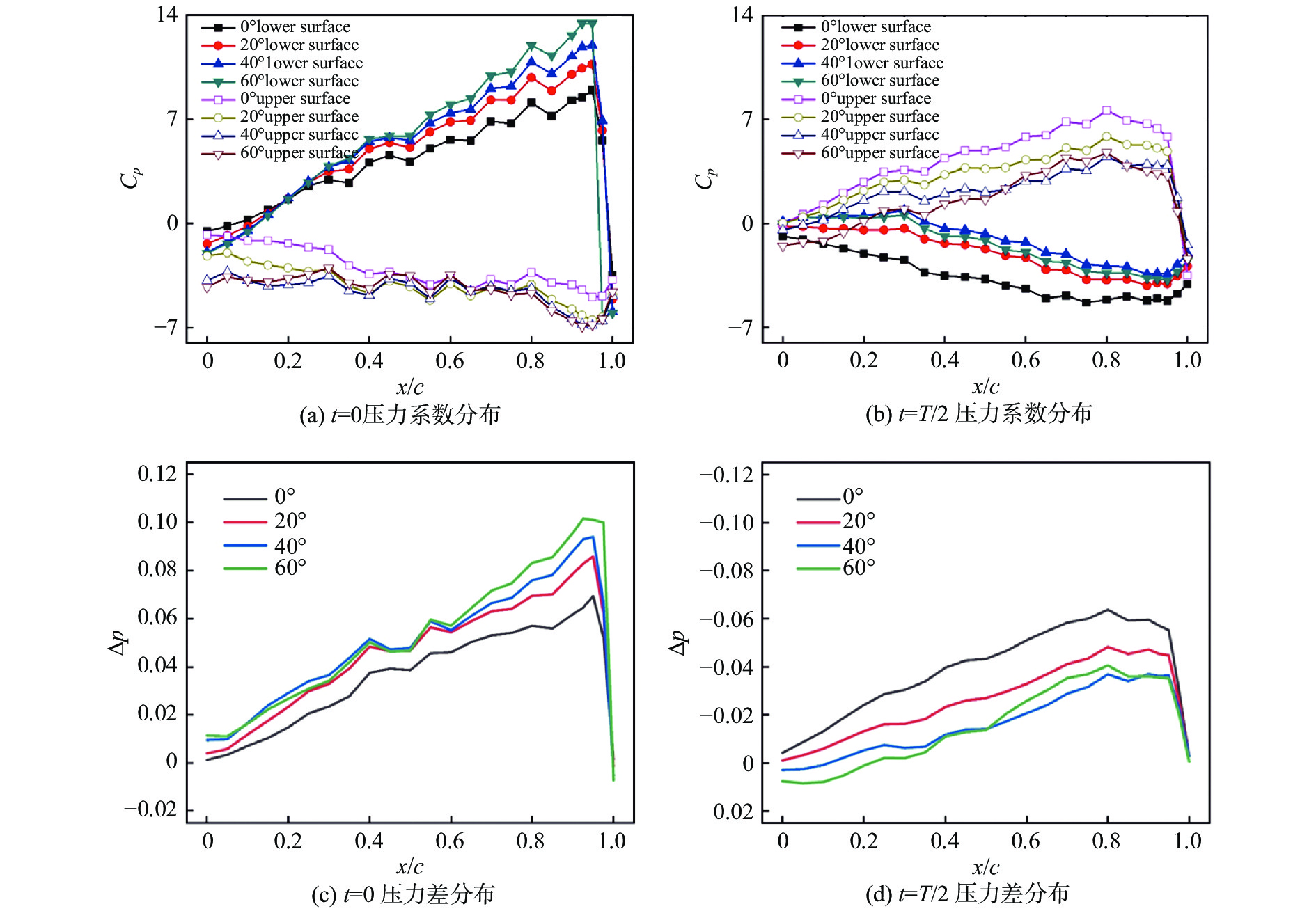
图15为不同迎角下,
|
图 15 |
图16为不同迎角下、
|
图 16 压力系数和压力差沿翼型弦长方向变化曲线图( |
同样地,分析图16(b、d),从翼根到翼尖方向,
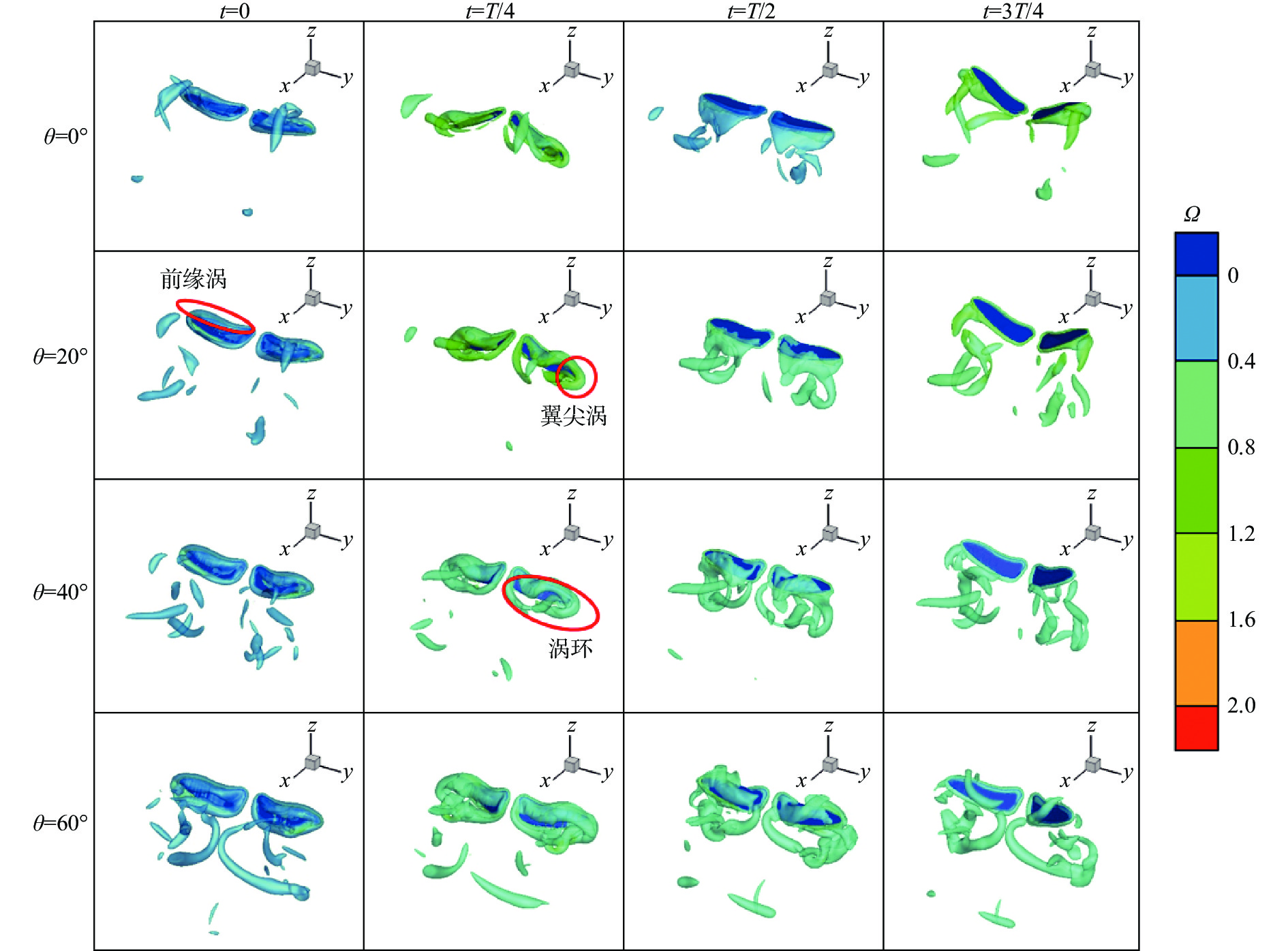
为了更直观地展现三维流场中由扑翼产生的涡系结构,图17给出了在一个周期内4个时刻的Q准则云图。Q准则定义为
图17为不同迎角下扑翼运动涡系结构随时间的演变,图中Ω 表示LBM格子单位下的涡量。从图中可以观察到前缘涡,扑翼拍动过程中,上翼面前缘开始产生前缘涡。前缘涡具有附着于扑翼表面不脱落的特性,附着于翼面的面积越大,提供的升力越大,而一旦当前缘涡从扑翼上脱落,升力系数将会大幅下降。可以看出,当
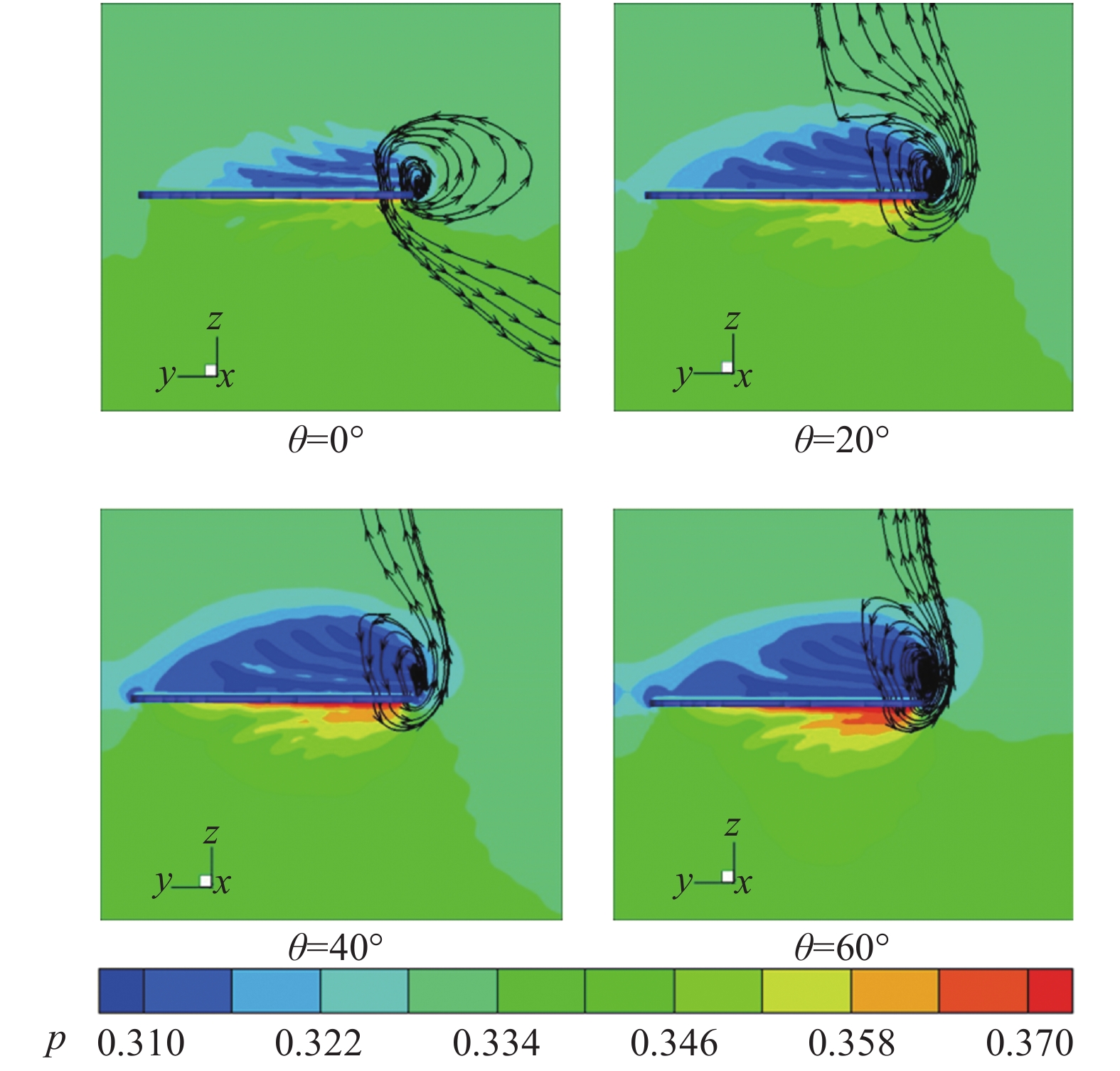
图18为不同迎角下,
|
图 17 不同迎角下扑翼运动涡系结构随时间的演变 Fig.17 Variation of vortices structure of flapping-wing for different angle of attack with time |
|
图 18 |
如图17所示,在
如图17所示,随着迎角的增大,前缘涡附着于翼面的面积明显增大,且与翼尖涡逐渐融合,并在扑翼尾迹处逐渐形成了封闭的涡环,不易耗散,且涡环与扑翼间的相互作用,使得涡环中的能量得以重复利用,使扑翼维持在一个高升力状态。
本文结合LBM与Level-set动边界识别方法,采用GPU加速,建立了三维含有运动边界流场的高效数值模拟方法并开发了相应程序。基于此,开展了不同迎角下扑翼运动气动特性机理分析。研究结果表明:
1) 随着迎角的增加,扑翼的平均升力系数先增大后减小,平均阻力系数逐渐增大。升阻比在10°时达到最大。此时,扑翼能够获得最佳气动性能。
2)
3) 随着迎角的增大,前缘涡附着于翼面的面积明显增大,扑翼后方脱落的涡旋也较难耗散,提高了扑翼的升力;同时,翼尖涡的强度与影响范围逐渐增大,导致涡致阻力增加,阻力系数增加。
LBM结合Level-Set方法可精确捕捉具有复杂外形的运动边界,同时,采用GPU加速能够获得极高的加速比。本文的数值方法可为扑翼运动提供高效、可靠的研究手段。
| [1] |
肖天航, 罗东明, 郑祥明, 等. 仿生飞行器非定常气动优化设计研究进展与挑战[J]. 空气动力学学报, 2018, 36(1): 80-87. XIAO T H, LUO D M, ZHENG X M, et al. Progress and challenges in unsteady aerodynamic optimization design of bionic flapping-wings[J]. Acta Aerodynamica Sinica, 2018, 36(1): 80-87. DOI:10.7638/kqdlxxb-2017.0171 (in Chinese) |
| [2] |
宁琦, 白存儒, 吴炯, 等. MAV0701微型扑翼飞机风洞试验研究[J]. 科学技术与工程, 2007, 7(16): 4239-4241. NING Q, BAI C R, WU J, et al. Investigation of flapping-wing MAV in wind tunnel[J]. Science Technology and Engineering, 2007, 7(16): 4239-4241. DOI:10.3969/j.issn.1671-1815.2007.16.065 (in Chinese) |
| [3] |
鲍锋, 杨琪, 何意. 单自由度扑翼模型脱落涡及其升力机制的实验研究[J]. 航空动力学报, 2014, 29(5): 1091-1098. BAO F, YANG Q, HE Y. Experimental investigation on shedding vortex and lift mechanism of flapping wing model with single degree of freedom[J]. Journal of Aerospace Power, 2014, 29(5): 1091-1098. (in Chinese) |
| [4] |
ENNOS A R. The kinematics and aerodynamics of the free flight of some Diptera[J]. Journal of Experimental Biology, 1989, 142(1): 49-85. DOI:10.1242/jeb.142.1.49 |
| [5] |
DICKINSON M H, LEHMANN F O, SANE S P. Wing rotation and the aerodynamic basis of insect flight[J]. Science, 1999, 284(5422): 1954-1960. DOI:10.1126/science.284.5422.1954 |
| [6] |
LIU H, KAWACHI K. A numerical study of insect flight[J]. Journal of Computational Physics, 1998, 146(1): 124-156. DOI:10.1006/jcph.1998.6019 |
| [7] |
WANG Z J. Vortex shedding and frequency selection in flapping flight[J]. Journal of Fluid Mechanics, 2000, 410: 323-341. DOI:10.1017/s0022112099008071 |
| [8] |
WANG Z J. Two dimensional mechanism for insect hovering[J]. Physical Review Letters, 2000, 85(10): 2216-2219. DOI:10.1103/PhysRevLett.85.2216 |
| [9] |
WANG Z J. The role of drag in insect hovering[J]. The Journal of Experimental Biology, 2004, 207(pt 23): 4147-4155. DOI:10.1242/jeb.01239 |
| [10] |
WANG Z J, BIRCH J M, DICKINSON M H. Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations vs robotic wing experiments[J]. The Journal of Experimental Biology, 2004, 207(pt 3): 449-460. DOI:10.1242/jeb.00739 |
| [11] |
孙茂. 昆虫飞行的空气动力学[J]. 力学进展, 2015, 45(1): 1-28. SUN M. Aerodynamics of insect flight[J]. Advances in Mechanics, 2015, 45(1): 1-28. DOI:10.6052/1000-0992-14-065 (in Chinese) |
| [12] |
LIANG B, SUN M. Dynamic flight stability of a hovering model dragonfly[J]. Journal of Theoretical Biology, 2014, 348: 100-112. DOI:10.1016/j.jtbi.2014.01.026 |
| [13] |
SUN M, LAN S L. A computational study of the aerodynamic forces and power requirements of dragonfly (Aeschna juncea) hovering[J]. The Journal of Experimental Biology, 2004, 207(pt 11): 1887-1901. DOI:10.1242/jeb.00969 |
| [14] |
SUN M, TANG J. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion[J]. The Journal of Experimental Biology, 2002, 205(pt 1): 55-70. |
| [15] |
YOUNG J, LAI J C S, GERMAIN C. Simulation and parameter variation of flapping-wing motion based on dragonfly hovering[J]. AIAA Journal, 2008, 46(4): 918-924. DOI:10.2514/1.31610 |
| [16] |
何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2009. HE Y L, WANG Y, LI Q. Lattice Boltzmann method: theory and applications[M]. Beijing: Science Press, 2009. (in Chinese) |
| [17] |
MINAMI K, SUZUKI K, INAMURO T. Free flight simulations of a dragonfly-like flapping wing-body model using the immersed boundary-lattice Boltzmann method[J]. Fluid Dynamics Research, 2015, 47(1): 015505. DOI:10.1088/0169-5983/47/1/015505 |
| [18] |
彭连松, 郑孟宗, 潘天宇, 等. 翼间干涉效应对蜻蜓悬停气动性能的影响[J/OL]. 2020-09-04. 航空学报. PENG L S, ZHENG M Z, PAN T Y, et al. Effect of tandem-wing interactions on aerodynamics of hovering dragonfly[J/OL]. 2020-09-04. Acta Aeronautica et Astronautica Sinica. (in Chinese) DOI: 10.7527/S1000-6893.20.24571 |
| [19] |
OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49. DOI:10.1016/0021-9991(88)90002-2 |
| [20] |
李会雄, 邓晟, 赵建福, 等. LEVEL SET输运方程的求解方法及其对气-液两相流运动界面数值模拟的影响[J]. 核动力工程, 2005, 26(3): 242-248, 267. LI H X, DENG S, ZHAO J F, et al. Numerical simulation of interface movement in gas-liquid two-phase flows with level set method[J]. Nuclear Power Engineering, 2005, 26(3): 242-248, 267. DOI:10.3969/j.issn.0258-0926.2005.03.008 (in Chinese) |
| [21] |
陈凡红, 王成, 郝莉, 等. 用Level Set方法追踪运动界面[J]. 力学与实践, 2006, 28(4): 23-27. CHEN F H, WANG C, HAO L, et al. Tracking moving interfaces by level set method[J]. Mechanics in Engineering, 2006, 28(4): 23-27. DOI:10.3969/j.issn.1000-0879.2006.04.005 (in Chinese) |
| [22] |
XIAN W, TAKAYUKI A. Multi-GPU performance of incompressible flow computation by lattice Boltzmann method on GPU cluster[J]. Parallel Computing, 2011, 37(9): 521-535. DOI:10.1016/j.parco.2011.02.007 |
| [23] |
GUO Z L, ZHENG C G, SHI B C. An extrapolation method for boundary conditions in lattice Boltzmann method[J]. Physics of Fluids, 2002, 14(6): 2007-2010. DOI:10.1063/1.1471914 |
| [24] |
CAIAZZO A. Analysis of lattice Boltzmann nodes initialisation in moving boundary problems[J]. Progress in Computational Fluid Dynamics, an International Journal, 2008, 8(1/2/3/4): 3. DOI:10.1504/pcfd.2008.018074 |
| [25] |
LI H, LU X, FANG H, et al. Force evaluations in lattice Boltzmann simulations with moving boundaries in two dimensions[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2004, 70(2 pt 2): 026701. DOI:10.1103/physreve.70.026701 |
 2022, Vol. 40
2022, Vol. 40