流体力学研究方法随研究工具的发展不断创新和变革,计算机的发展促使流体力学的研究方法从最开始的理论推导和实验模拟逐渐转向借助计算机对流体力学问题进行数值建模,这一转变直接导致计算流体力学(computational fluid dynamics, CFD)这一学科的出现。人工智能(artificial intelligence, AI)被称为第四次工业革命的催化剂,是21世纪被广泛提及的一个名词。AI依靠大数据和优秀的算法不断为传统领域赋能,突破传统领域的技术壁垒。流体力学作为经典学科,AI能否为其带来新的活力?2019年以来,流体力学智能化这个名词逐渐在会议和文章中被提及,越来越多的研究人员开始关注流体力学智能化这一领域。张伟伟[1]对流体力学智能化问题进行了系统性地归纳和总结,将其主要内容分为三部分:1)流体力学理论和方法的智能化,探索融合经典流体力学理论和人工智能算法的新理论,以解决经典方法存在的问题和不足;2)流动信息特征提取与融合的智能化,流体力学数据繁多复杂,人类大脑难以从这么庞大的数据信息中发掘一些有价值的信息,相反人工智能算法恰恰非常适合处理大数据问题,因此使用基于人工智能的算法可以挖掘和融合不同来源的流体数据信息;3)多学科、多场耦合模型的智能化,人工智能可以充当一种粘合剂将经典流体力学、计算机和自动控制学科紧密地联系起来,从而做到多学科之间的相互交融和协作。对此,国内外研究者们在近期开展了广泛的研究与探索,如应用人工智能技术研究湍流模型[2-7],以及在飞行器设计中的应用研究[8]。
流体力学智能化需要在经典流体力学研究方法和成果的基础上结合人工智能技术,流体力学大数据小样本的学科特点和背景是机器学习建模时需要考虑的客观问题。当前流体力学智能化的核心内容或许是提升人工智能赋能流体力学的可解释性,探索流体力学新的物理内涵和认知。因此,人工智能给流体力学的发展提供新的研究范式,流体力学为人工智能的发展提供足够复杂的研究对象,使传统学科和新型学科交叉融合相互促进。
物理问题尤其是流体力学问题其数据之间的隐含规律复杂多变,这导致传统机器学习模型在发掘数据之间的隐含规律时其表现往往差强人意。但是流体力学中的数据往往存在控制方程形式的约束,因此如何充分利用数据的约束方程作为机器学习模型的先验知识是改善机器学习解决物理问题的重点。融合物理先验知识的神经网络方法(physical-informed neural network, PINN)算法自Karniadakis[9]提出以来就受到广泛的关注和探索。作为一种融合物理方程信息的神经网络模型,它既拥有神经网络的强大学习能力,又能结合学科背景使其网络模型具备可解释性。本文结合课题组近期工作,以三维超声速可压缩槽流和不可压缩圆柱绕流为例,介绍PINN算法的原理及其在求解N-S方程、预测流动参数、确定方程待定系数的机理和可行性。
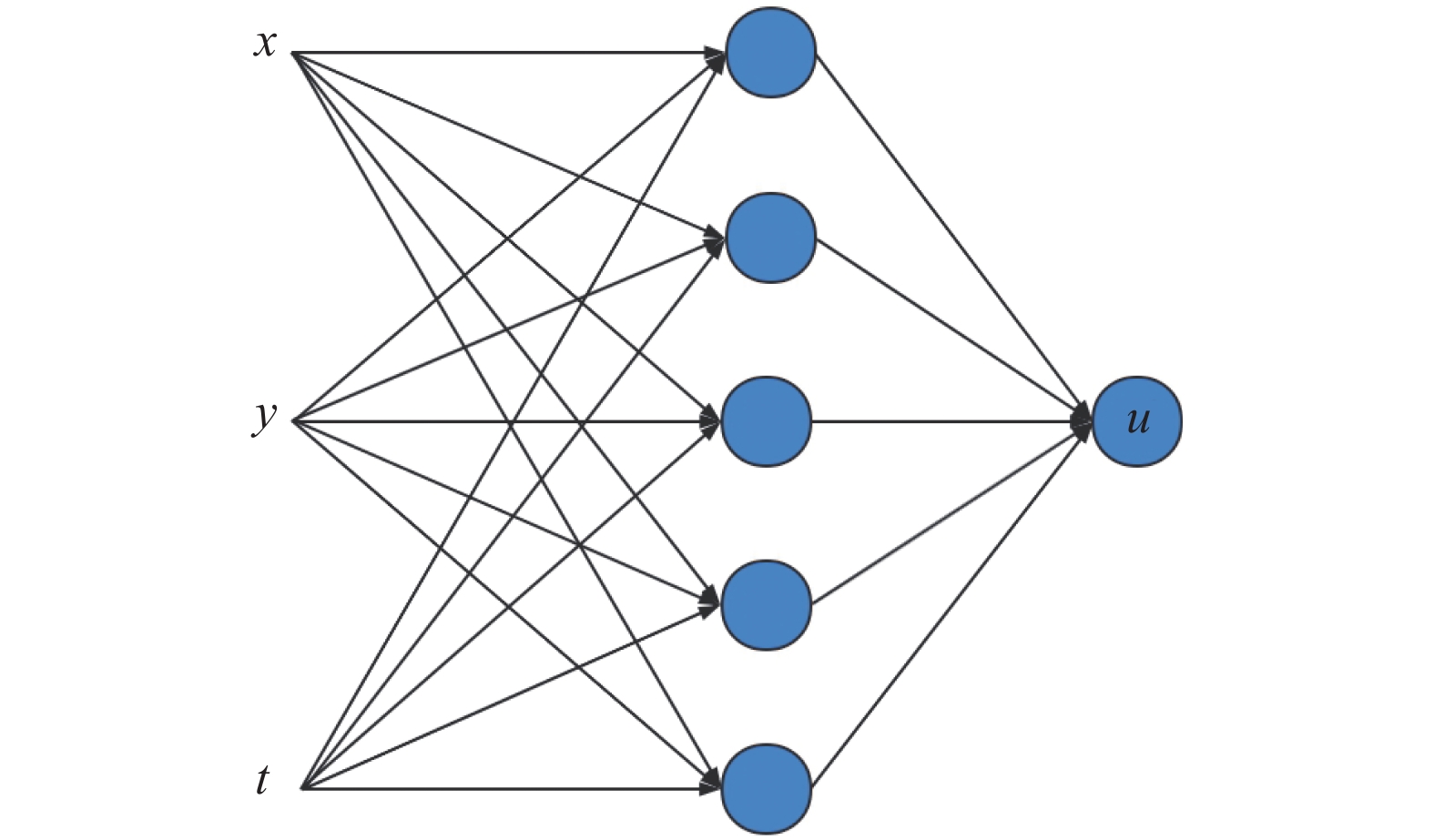
1 PINN原理神经网络属于参数模型(图1),使用多层神经网络构建输入特征
| $ u={g}_{NN}\left(x,y,t\right) $ | (1) |
并通过最小化输出的预测值和真实值之间的均方误差Loss指导自身的训练:
| $ \mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}=\frac{1}{n}\sum _{i=1}^{n}{({u}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}^{i}-{u}_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}^{i})}^{2} $ | (2) |
|
图 1 传统神经网络模型 Fig.1 Traditional neural network |
传统神经网络算法从数据中发掘隐含的相关关系,当数据量有限时,使用梯度下降计算网络参数
|
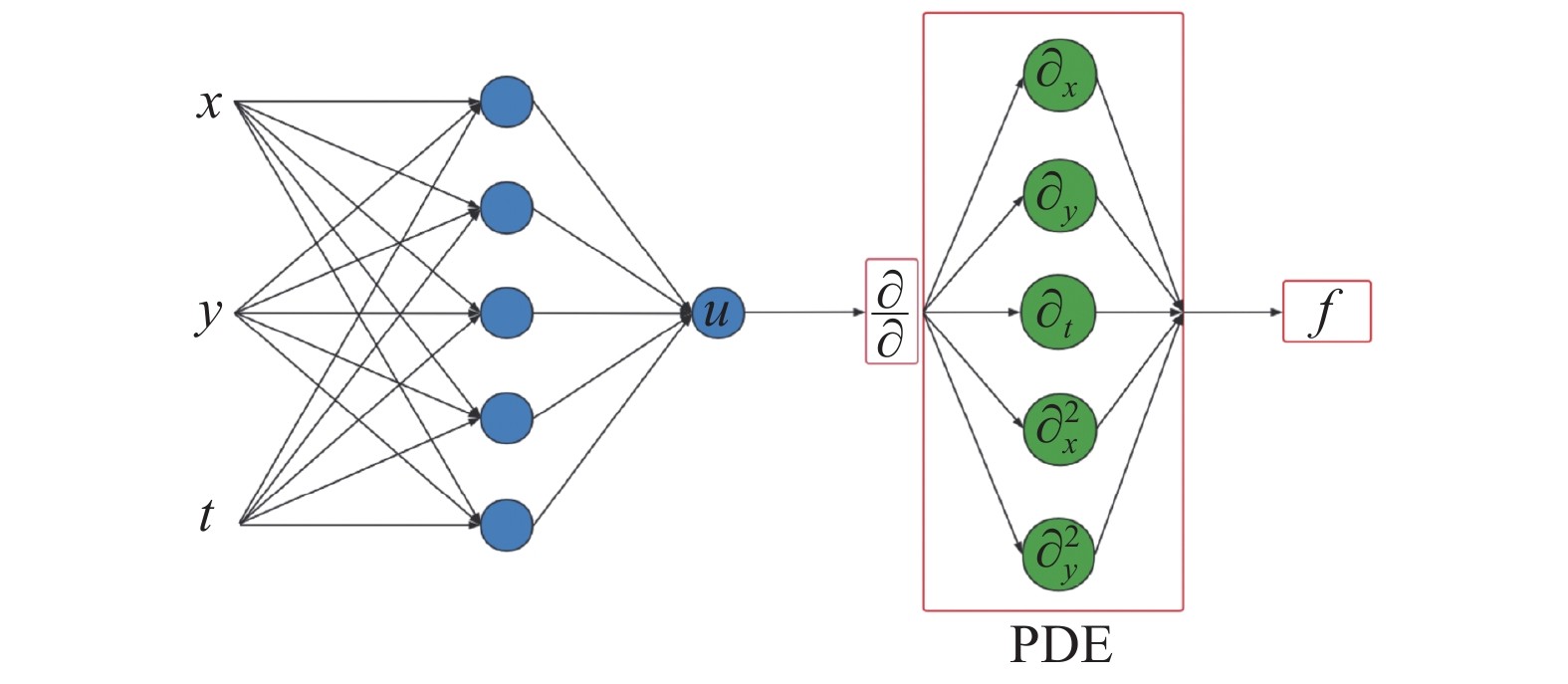
图 2 PINN网络结构 Fig.2 Physical-informed neural network |
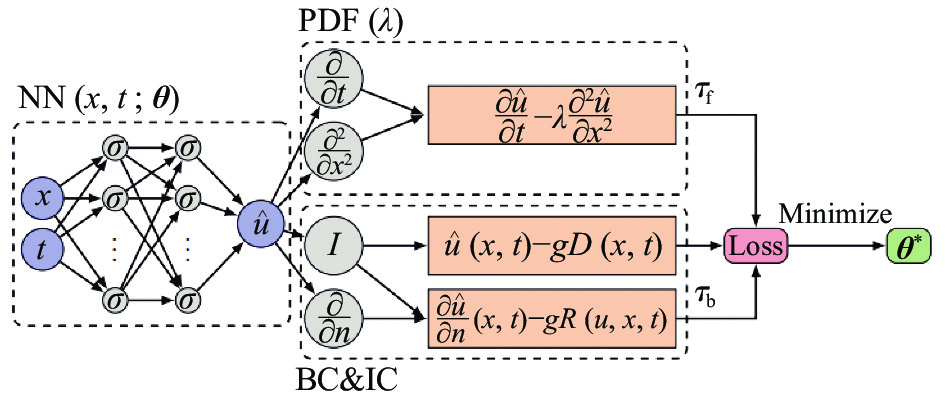
首先,PINN与传统神经网络相比,增加了将网络输出作为输入附加约束的偏微分方程的步骤。偏微分方程的形式复杂多样,考虑偏微分方程的一般形式:
| $ \frac{\partial u}{\partial t}+N\left(u,x,y,t\right)=0 $ | (3) |
PINN假设存在函数
| $ f\left(u,x,y,t\right)=\frac{\partial u}{\partial t}+N\left(u,x,y,t\right) $ | (4) |
当
其次,与传统NN方法损失函数式(2)相比,PINN网络的约束Loss如式(5)所示:
| $ \mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}=\frac{1}{n}\sum _{i=1}^{n}{({u}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}^{i}-{u}_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}^{i})}^{2}+\lambda {f({u}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}^{i},{x}_{i},{y}_{i},{t}_{i})}^{2} $ | (5) |
其中
故可见PINN通过最小化损失函数Loss实现两个目的:1)最小化PINN的预测值和样本真实值之间的误差使PINN预测值
再者,两者训练过程中,网络参数
| $ \mathrm{\omega }={\omega }_{0}-{\eta {\nabla }_{\omega }\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}(\omega )}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}-\lambda \eta {\nabla }_{\omega }\frac{1}{N}\sum _{i=1}^{n}{f({u}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}^{i},{x}_{i},{y}_{i},{t}_{i})}^{2} $ | (6) |
从式(6)可知PINN更新权重时增加了第二项
综上,通过对比图1和图2所示网络结构、损失函数Loss和网络参数
由于PINN融合神经网络和偏微分方程,发掘样本数据之间的潜在规律,因此PINN方法的应用前景十分广泛。结合笔者近期的研究工作,对其目前主要应用进行介绍。
2.1 PINN解偏微分方程神经网络方法求解偏微分方程的核心思想是:利用神经网络和符合偏微分性质的样本数据逼近数据所在区域偏微分方程的显式形式。偏微分方程可以用来描述系统状态随时间和空间的变化规律,因此物理问题的大多数控制方程是以偏微分方程形式存在。偏微分方程由于多变量耦合,常常难以获得精确的数学显式解,因此偏微分方程解的存在性和偏微分方程的求解一直是数学领域的热点[10-12]。
虽然一般情况下偏微分方程难以获得精确解,但是借助数值方法可以求解离散网格上变量状态,借此可以获得大量符合偏微分性质的网格点上的数据。接着利用这些数据进行机器学习训练,从而能够获得满足偏微分形式表征物理量隐含关系的机器学习模型。神经网络作为一种强大的数据分析算法,在发掘数据之间隐含的函数关系问题上发挥巨大的作用,理论证明多层非线性激活函数组成的神经网络能够逼近任意的函数关系[13]。近年来用深度神经网络等机器学习方法构造有效的物理模型一直是研究热点[14],在PINN之前,主要是用约束神经网络求解偏微分方程,采用数值微分的方式[9]。与之不同的是,PINN的特点是用误差的形式将物理控制方程融合入神经网络,某种程度上与迭代 Krylov线性解算器相似,其主要优点是采用自动微分的方式求解微分方程[15-16]。PINN求解偏微分方程模型结构如图3[17]。
将时空坐标输入神经网络,经过神经网络计算输出控制方程物理量。将输出的物理量与训练样本的标签物理量分别带入偏微分方程、边界条件(boundary condition,BC)约束以及初始条件(initial condition,IC)约束,并通过两者之间的差异构建损失函数,通过最小化损失函数调节神经网络中每个神经元之间的连接权重以达到训练收敛。
由于偏微分方程在其定义域与值域的关系数量是无限的,在整个域上进行训练约束是不现实的,所以只能取定义域与值域上离散的映射关系(训练数据)进行训练。训练样本的选取关系到模型的泛化性能,选取的样本分布尽可能地涵盖所研究的偏微分方程在其定义域与值域映射关系中所有关系特征,可以大大提升模型的泛化能力。
同理,边界条件的泛化性能也应考虑对不同边界条件函数的映射关系的特征分布进行训练样本选取,例如壁面上不同区域的时空坐标与物理量值的映射关系的特征选取。
2.2 PINN在流场重建中的应用流场重建指充分利用流场的已知信息或可观测信息挖掘流场未知信息或不可观测信息。实验是解决CFD和理论分析无法解决的流体力学问题的最后手段,但是实验通常只能获得有限的、可观测的数据样本,因此想要获取全流场的流动信息进行更细致地研究就需要涉及到流场重建,包括:1)基于流场快照的速度场构建;2)基于流场速度场的其他流动信息构建,比如压力场;3)基于稀疏流场和噪声流场的信息重建等。如何有效解决这些问题是获得高精度实验结果必须解决的难题。
针对特定流场重建已发展出各种算法,例如利用图像信号处理方法对原始流场图像进行图像增强和去噪后获得高质量图像;运用相关法和光流法从PIV(particle image velocity,PIV)流场快照中提取出速度场信息后,有限容积法、直接积分法和泊松公式能结合不可压缩流动的速度场重建压力场[18];本征正交分解(POD)方法对稀疏流场进行模态分解后重组模态基完成稀疏流场的重建等。这些方法都各有优势和局限,相关法和光流法其原理基于图像信号,缺乏流体力学先验信息约束,因此对实验图像质量要求苛刻。有限容积法、直接积分法和泊松法通过处理不可压缩N-S方程后,求解压力梯度获得流场的压力场,这要求高精度的速度场,并且存在误差积累的问题。此外,现有流场重建问题根据其背景不同,适用的算法也完全不同,算法之间难以相互联系和发展。而人工智能具备在大数据的基础上发掘数据之间的隐含规律这一特性,因此探索通过人工智能赋能流场重建,挖掘大量流场数据之间的隐含信息,从而可以构建流场变量和时空坐标之间的函数关系。直接使用传统机器学习模型回归数据样本的函数关系因缺乏物理信息的先验知识而不能获得较好的结果,而PINN方法通过对神经网络增加流场物理变量之间的N-S方程约束,使人工智能赋能流场重建变得可能。
本文使用张朋[19]计算的可压缩充分发展槽道湍流直接数值模拟(DNS) Case2的结果作为训练和测试数据。计算条件为来流马赫数
| 表 1 计算和训练区域设置 Table 1 The domain Setup for DNS & PINN |
|
|
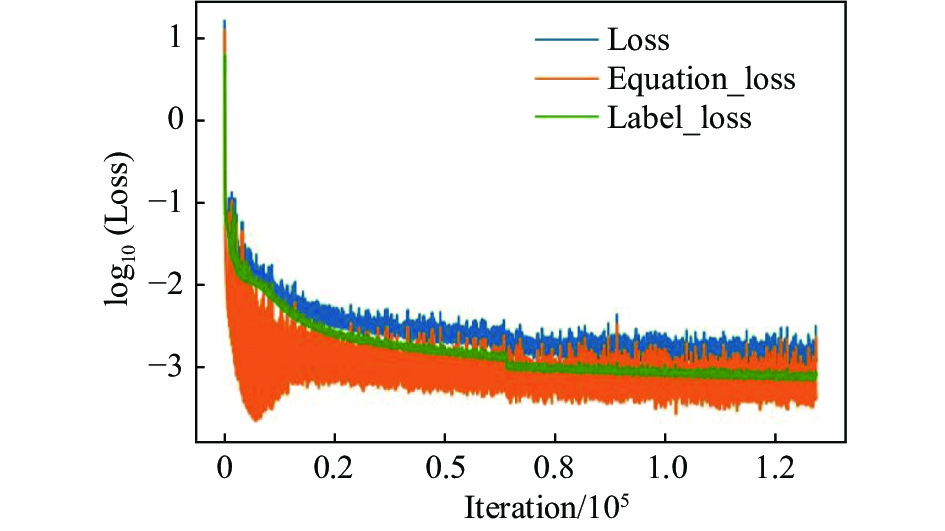
训练曲线如图4所示。从图中可知,方程约束项Equation_loss的波动要大于输入特征项Label_loss,两者的数值大小接近,这反映流场重建结果同时受数据样本和方程信息约束。
|
图 4 PINN重建Re= 6000槽道的Loss Fig.4 Reconstruction of loss of Re= 6000 channel based on PINN |
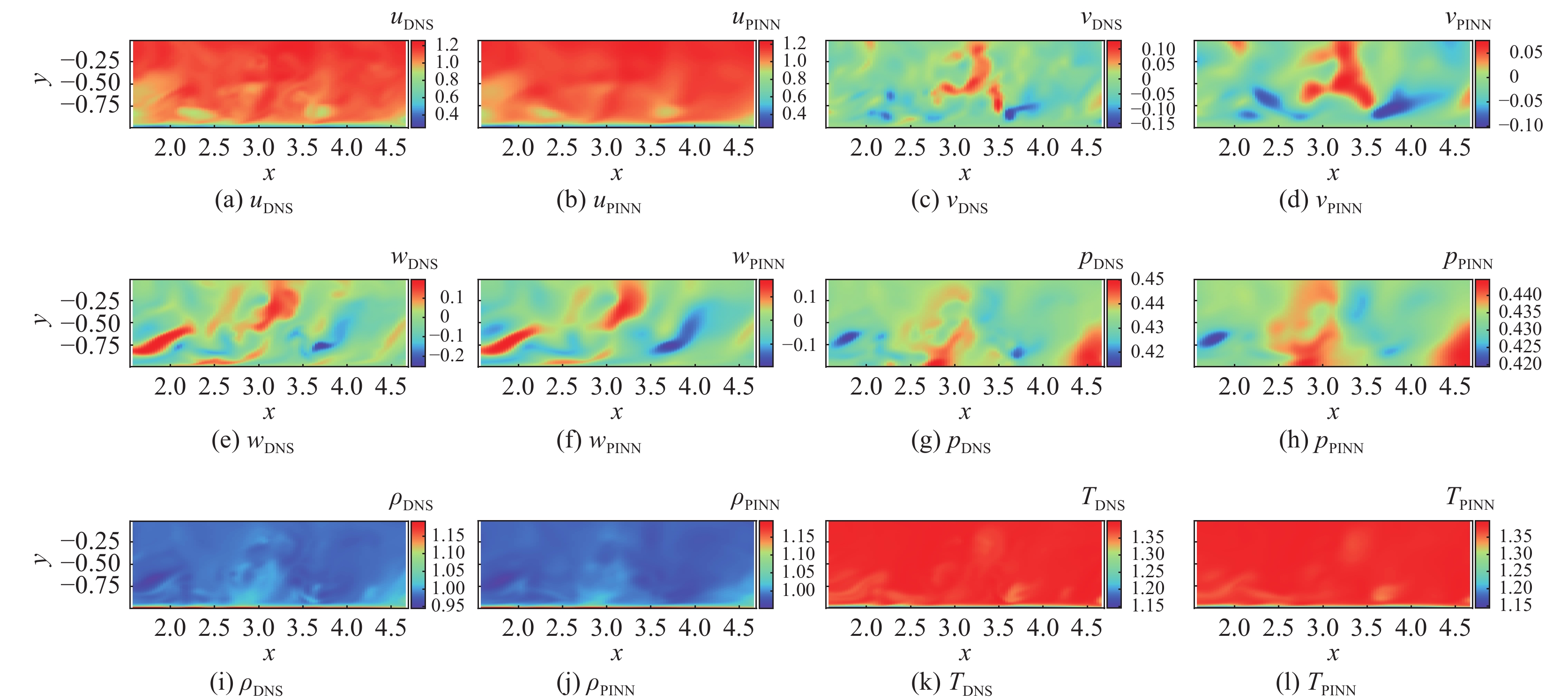
图5为从训练空间截取的t = 0时刻、z = 2.38流向x-y平面的DNS和PINN重建的瞬时物理量等值图对比,包括流向速度u、法向速度v、展向速度w、压力p、密度ρ、温度 T等。从图中可知,u、v、w、p、ρ、T在不同时刻的PINN重建结果与DNS结果十分接近。数据分析显示在其余时刻、以及不同平面包括展向y-z平面和法向x-y平面的物理量的等值线对比也显示了相近的结果。
|
图 5 流向平面DNS和PINN的瞬时物理量对比 (t= 0, x, y, z= 2.38) Fig.5 Comparison of instantaneous physical quantities between DNS and PINN in streamwise plane (t= 0, x, y, z= 2.38) |
图6(a)为从预测结果中随机选取的第40个时刻法向x-z平面((1−|y|)/H = 0.176,H为半槽高)上的流向脉动速度
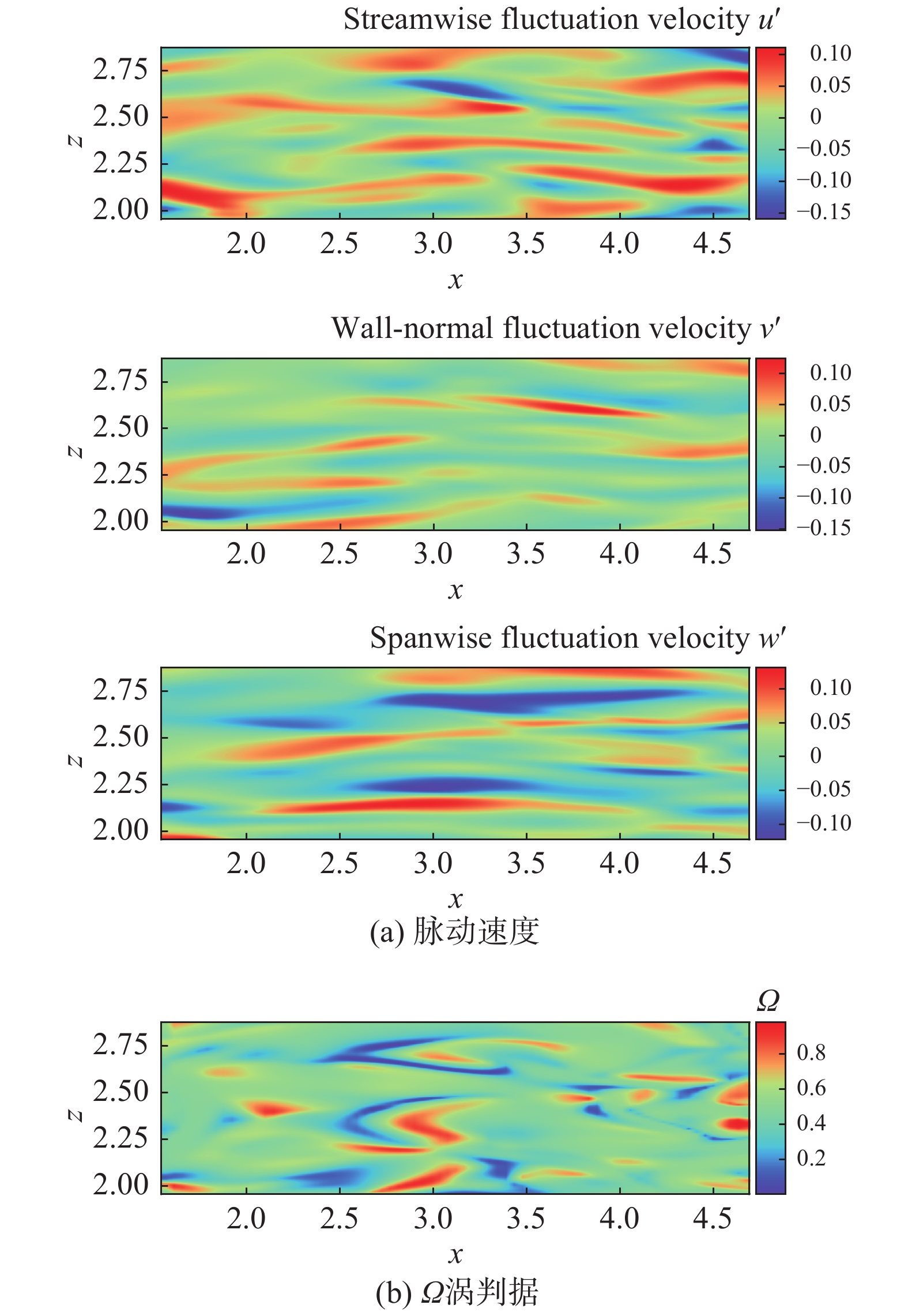
|
图 6 PINN重建流场瞬时量分布 Fig.6 Instantaneous flowfield by PINN |
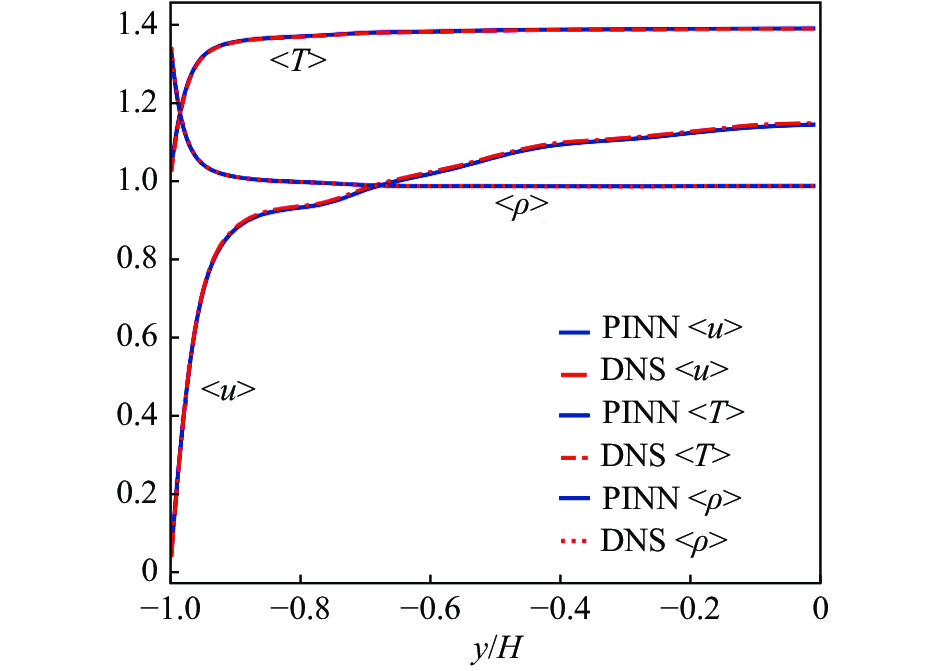
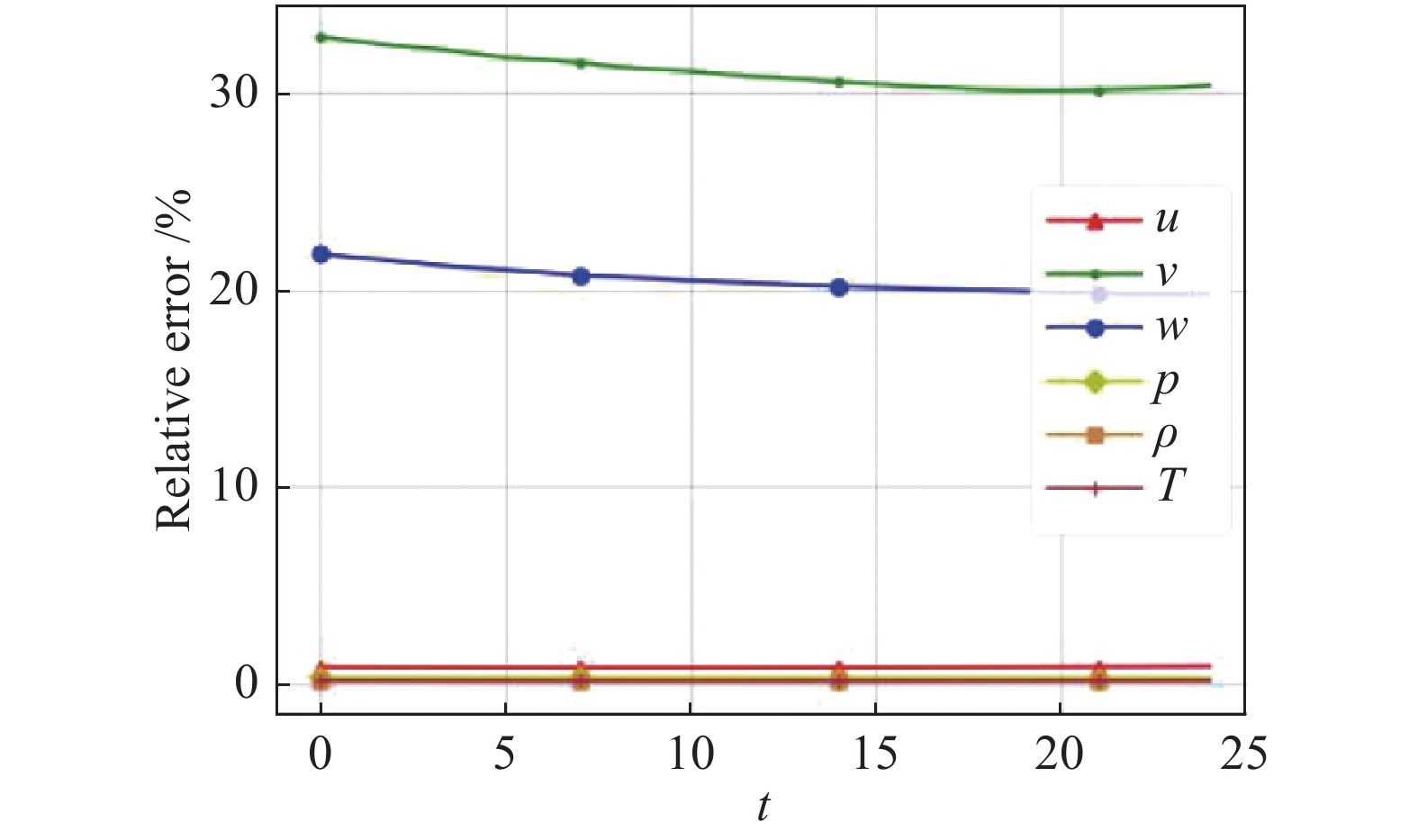
图7对比了PINN预测结果和所选区域的DNS结果的平均量,结果显示雷诺时均流向速度<u>、密度<ρ>、温度<T>沿发现法向分布均与DNS的统计平均值吻合良好,证明添加了物理先验知识约束后的神经网络具有良好的数据回归和流场重建能力。图8记录了瞬时物理量的PINN重建结果与对应时刻测试数据DNS数据的相对误差,横坐标t表示25个离散时刻,并显示
|
图 7 PINN方法和DNS的统计平均物理量的对比 Fig.7 Comparison of mean profiles between PINN and DNS |
|
图 8 PINN重建结果的相对误差 Fig.8 The relative error of the reconstruction result of the PINN |
上述内容验证了PINN重建流场的可行性,根据结果我们可以发现PINN的训练拟合的结果精度较高。
为了验证PINN的预测能力,采用同流场不同分布数据集进行训练并预测,从流场中抽取半槽道结果作为实验数据集:
| 表 2 训练测试样本算例 Table 2 Example of training and test samples |
|
|
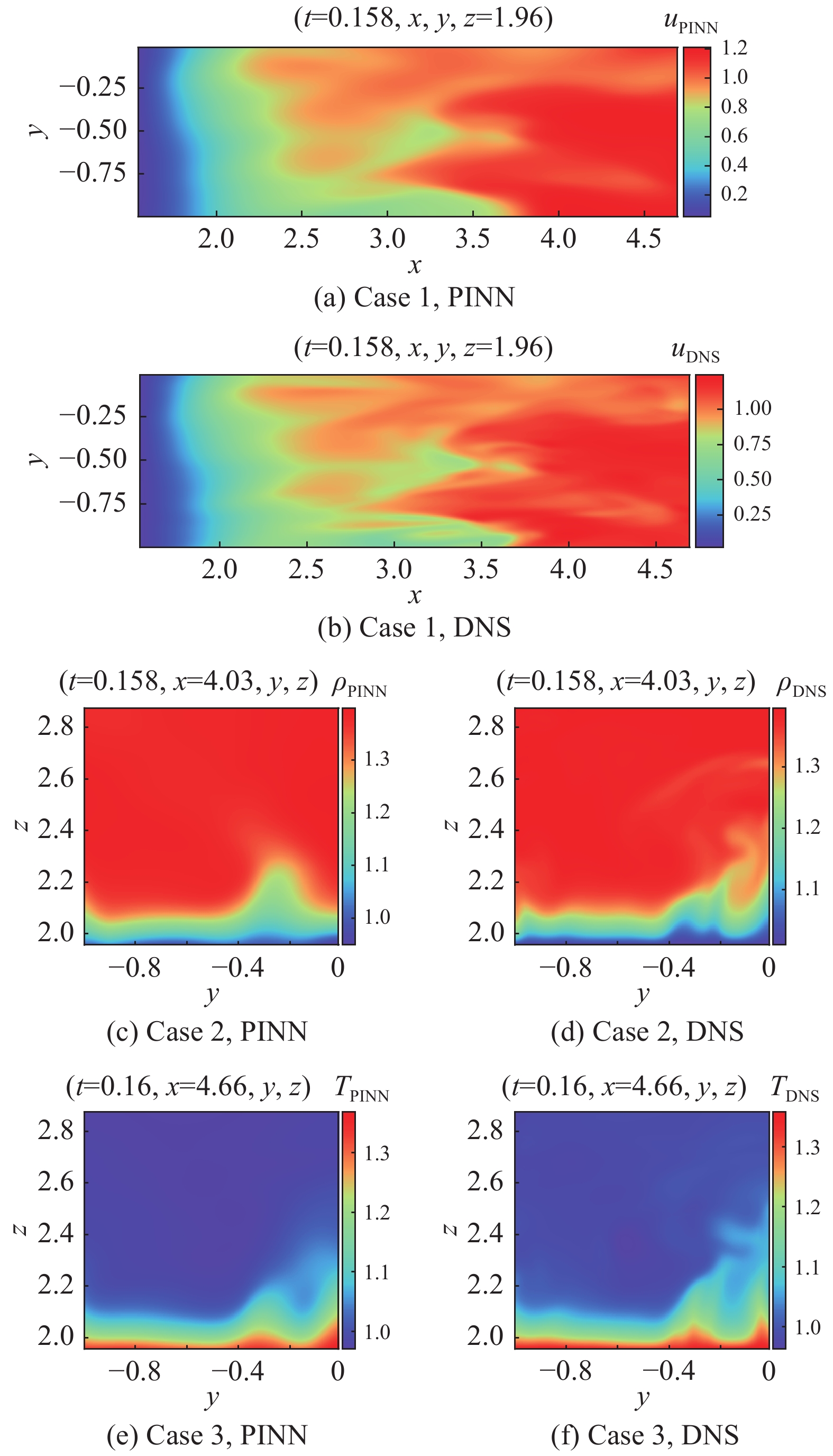
|
图 9 预测的瞬时流场 Fig.9 Training and prediction of instantaneous flow field |
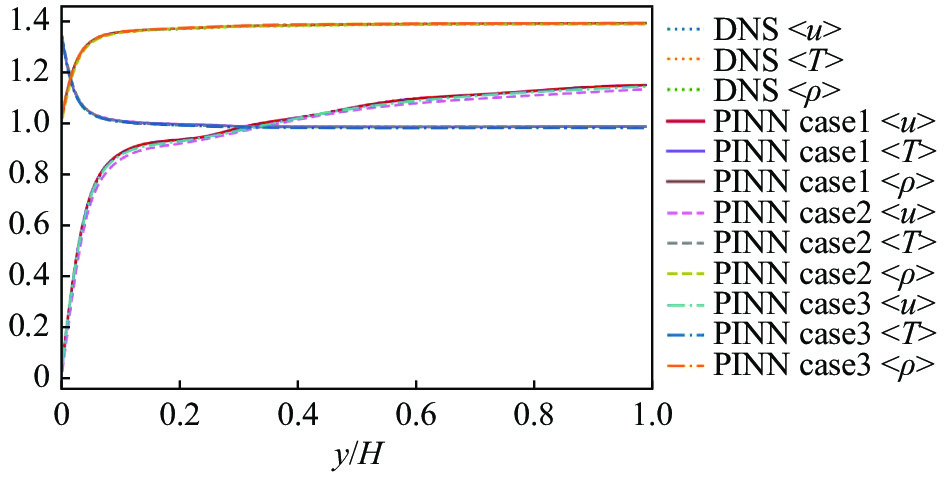
|
图 10 PINN方法和DNS的统计平均物理量的对比 Fig.10 Comparison of mean profiles between PINN and DNS |
| 表 3 流场训练结果 Table 3 Results of flow field training |
|
|
| 表 4 流场预测结果 Table 4 Results of flow field prediction |
|
|
由于预先融入了物理信息的约束,PINN相比普通的神经网络的拟合速度更快,效果也更好,效率更高。PINN对于同一特征流场的预测性能较好,但是由于其输入特征为时空坐标,以至于输入模型的信息量有限,导致其泛化性能较为一般。增加有效输入特征以及减少损失函数中关于特定流动的特征约束可以一定情况下提升PINN的泛化性能。对于高Re的非定常流动,流动的随机性大大提升,相比全连接网络,可以尝试采用时序、卷积等结构的神经网络模型,在一定情况下可以改善对于高Re非定常流动中的特征捕捉能力。
PINN在流场重建中具有实际应用价值。PINN可用于PIV流场重建,利用实验的流场数据,探索一种能够以较高精度重建流场变量连续状态变化的方法具有一定工程意义,以及PINN对于流场数据缺失复原的应用也具有较大的可行性。
2.3 PINN在参数重建中的应用模型的系数重建问题是一类较为重要的工程问题,其中渐近性原则常被用于解决此类问题。渐近性原则的思想是模型预测的方程输出结果应当和实验结果一致,本质是数据拟合。研究人员常使用渐近性原则来确定模型方程中的待定系数,其方法是在逼近模型系数时,率先确定对精度影响大的方程项的系数,再逐步确定其他系数,进而逐一确定系数。这一方式可以降低小项的影响,但难以同时获得最优的系数组合解。不同于传统做法,PINN具备结合样本数据反推方程属性的能力[21],可以同时确定方程中的待定系数组合,因此PINN方法可以在参数重建领域发挥巨大的作用。
如图11所示,建立PINN模型来说明PINN的参数重建。具体为针对二维不可压缩绕圆柱流动,设置N-S约束方程系数
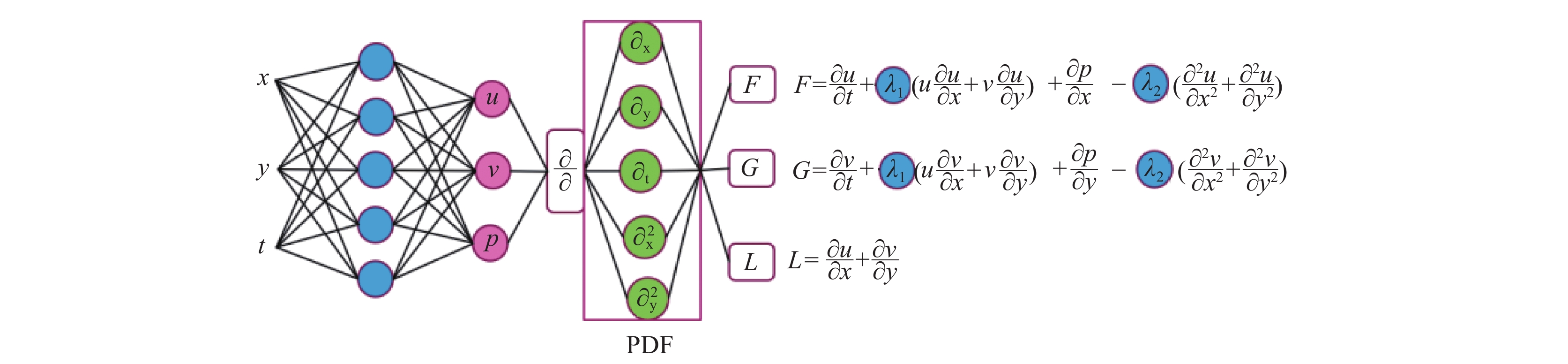
|
图 11 待定系数的PINN模型 Fig.11 PINN model with undetermined coefficients |
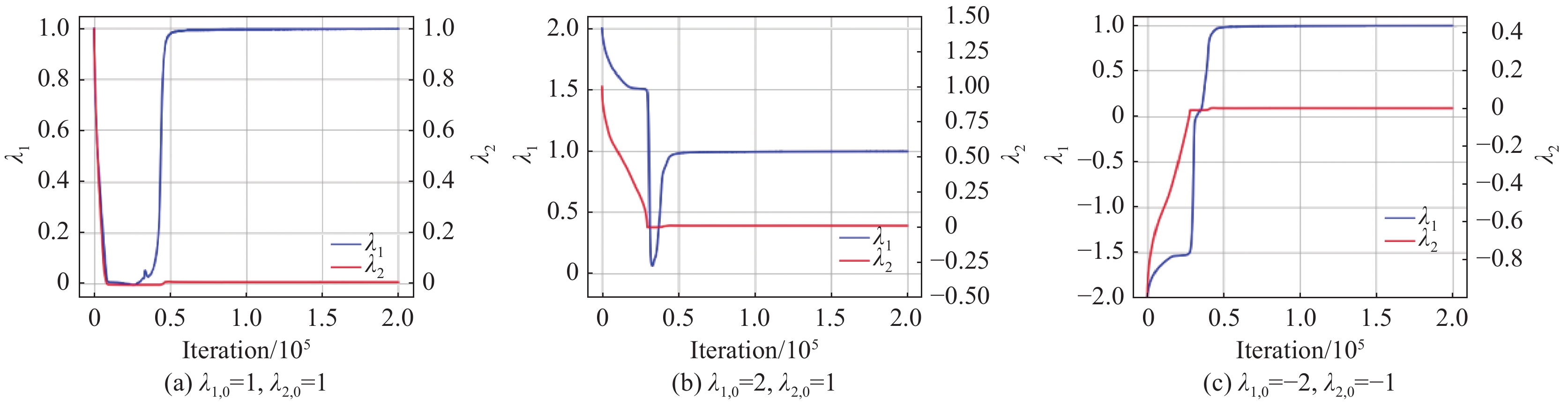
|
图 12 不同初始值 λ1、λ2随着训练次数的变化趋势 Fig.12 Different initial values λ1、λ2 with the change of training times |
表5为最终收敛值和对应的相对误差。从表5中可知,使用PINN重建流场时,PINN可以将N- S约束方程的系数当作自身的可训练参数,使其随着训练收敛至真实值。
| 表 5 不同初始值λ1、λ2的重构结果 Table 5 The reconstruction results of λ1、λ2 with different initial values |
|
|
此外,我们进一步尝试了通过2.2节中三维可压缩槽道流DNS数据对三维可压缩N-S方程中的体积力项
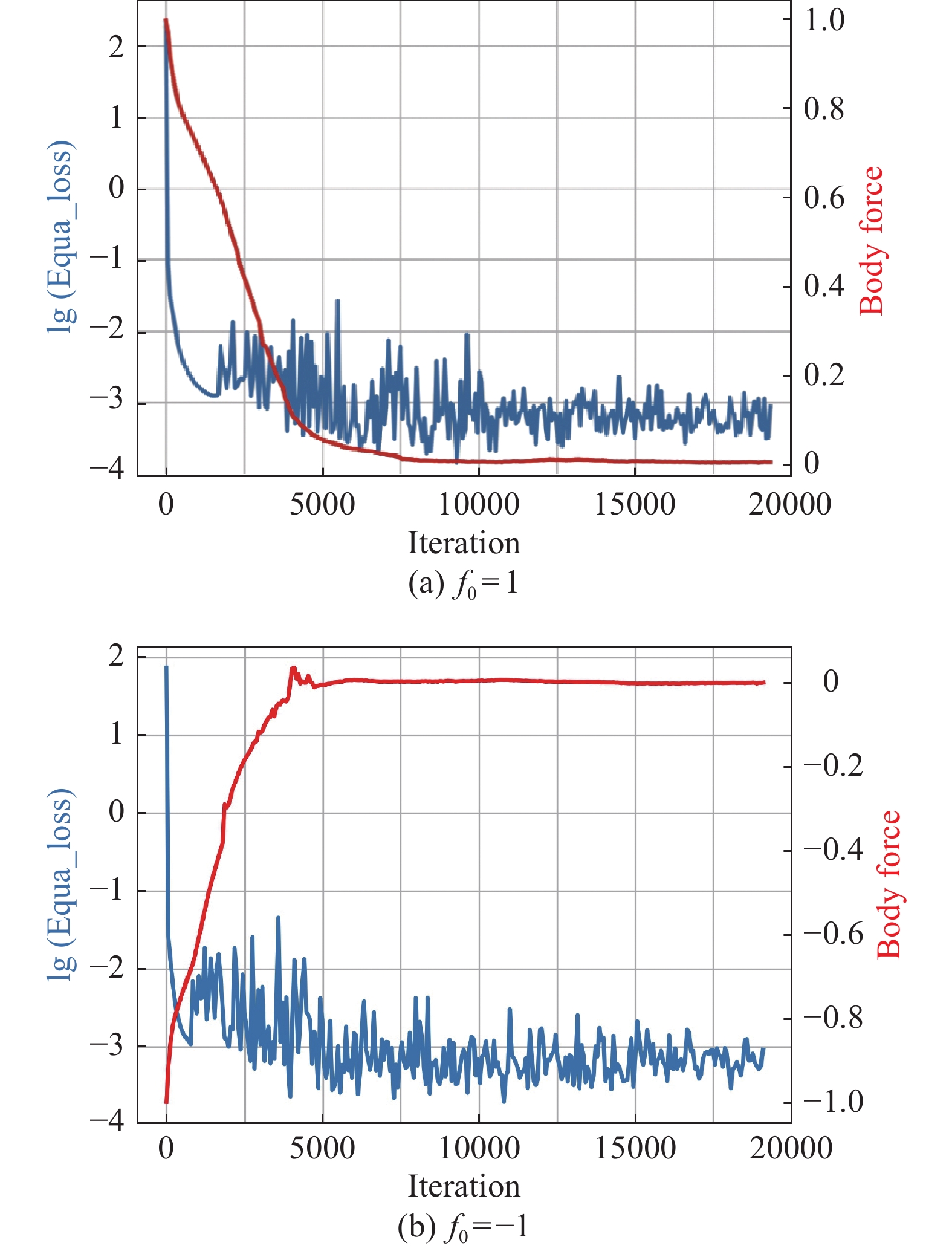
|
图 13 体积力与方程损失收敛曲线 Fig.13 Convergence curve of volume force and equation loss |
由图13可知不同初始值下,体积力
PINN作为融合人工智能和以数学方程表示的物理先验知识的一种新方法,其未来应用的方式还有更多可能,本文阐述了该方法并结合具体工作举例说明了其可适用场景:
1)PINN用于求解偏微分方程:应用神经网络来逼近高维复杂偏微分方程是人工智能目前重要研究方向之一,PINN将偏微分方程融入误差网络,结合自动微分方法提高了求解的效率和精度。
2)PINN用于流场信息重建:通过在损失函数中添加偏微分方程约束并利用自动微分技术,结合DNS训练数据集应用于可压缩槽道流动,可以重构瞬时湍流流场,并通过对预测参数的统计分析与DNS数据对照分析,验证了预测模型有效性及其用于更多流动场景的可能性。
3)PINN用于方程参数重建:结合不可压缩圆柱绕流与三维可压缩槽道流的控制方程和DNS数据训练集,通过训练可以获得方程中的待定系数与待定项,验证了该方法可以进一步应用于更广泛的模型构建场景。
但是在研究中也发现了PINN方法目前的泛化性欠佳,极大限制了其使用范围和能力,是急需克服的难点。
致谢:感谢浙江大学夏振华教授在本文研究工作开展中提出的各种有益讨论和建议。
| [1] |
张伟伟, 寇家庆, 刘溢浪. 智能赋能流体力学展望[J]. 航空学报, 2021, 42(4): 26-71. ZHANG W W, KOU J Q, LIU Y L. Prospect of artificial intelligence empowered fluid mechanics[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(4): 26-71. (in Chinese) |
| [2] |
KUTZ J N. Deep learning in fluid dynamics[J]. Journal of Fluid Mechanics, 2017, 814: 1-4. DOI:10.1017/jfm.2016.803 |
| [3] |
DURAISAMY K, IACCARINO G, XIAO H. Turbulence modeling in the age of data[J]. Annual Review of Fluid Mechanics, 2019, 51(1): 357-377. DOI:10.1146/annurev-fluid-010518-040547 |
| [4] |
XIAO H, WU J L, WANG J X, et al. Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier-Stokes simulations: a data-driven, physics-informed Bayesian approach[J]. Journal of Computational Physics, 2016, 324: 115-136. DOI:10.1016/j.jcp.2016.07.038 |
| [5] |
尹宇辉, 李浩然, 张宇飞, 等. 机器学习辅助湍流建模在分离流预测中的应用[J]. 空气动力学学报, 2021, 39(2): 23-32. YIN Y H, LI H R, ZHANG Y F, et al. Application of machine learning assisted turbulence modeling in flow separation prediction[J]. Acta Aerodynamica Sinica, 2021, 39(2): 23-32. (in Chinese) |
| [6] |
张伟伟, 朱林阳, 刘溢浪, 等. 机器学习在湍流模型构建中的应用进展[J]. 空气动力学学报, 2019, 37(3): 444-454. ZHANG W W, ZHU L Y, LIU Y L, et al. Progresses in the application of machine learning in turbulence modeling[J]. Acta Aerodynamica Sinica, 2019, 37(3): 444-454. DOI:10.7638/kqdlxxb-2019.0036 (in Chinese) |
| [7] |
王怡星, 韩仁坤, 刘子扬, 等. 流体力学深度学习建模技术研究进展[J]. 航空学报, 2021, 42(4): 231-250. WANG Y X, HAN R K, LIU Z Y, et al. Progress of deep learning modeling technology for fluid mechanics[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(4): 231-250. (in Chinese) |
| [8] |
何磊, 钱炜祺, 汪清, 等. 机器学习方法在气动特性建模中的应用[J]. 空气动力学学报, 2019, 37(3): 470-479. HE L, QIAN W Q, WANG Q, et al. Applications of machine learning for aerodynamic characteristics modeling[J]. Acta Aerodynamica Sinica, 2019, 37(3): 470-479. DOI:10.7638/kqdlxxb-2019.0033 (in Chinese) |
| [9] |
RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707. DOI:10.1016/j.jcp.2018.10.045 |
| [10] |
PAZY A. Semigroups of linear operators and applications to partial differential equations[M]. New York, NY: Springer New York, 1983. doi: 10.1007/978-1-4612-5561-1.
|
| [11] |
HORMANDER L. The analysis of linear partial differential operators[M]. Springer-Verlag, 2005.
|
| [12] |
FRIEDMANN A. Partial difierential equations of parabolic type[M]. Dover Publications, 1964.
|
| [13] |
LESHNO M, LIN V Y, PINKUS A, et al. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function[J]. Neural Networks, 1993, 6(6): 861-867. DOI:10.1016/S0893-6080(05)80131-5 |
| [14] |
WEINAN E. The dawning of a new era in applied mathematics[J]. Notices of the American Mathematical Society, 2021, 68(4): 1. DOI:10.1090/noti2259 |
| [15] |
RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics informed deep learning (part I): data-driven solutions of nonlinear partial differential equations[EB/OL]. (2017-11-28). https://doi.org/10.48550/ arXiv.1711.10561
|
| [16] |
RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics informed deep learning (part II): data-driven discovery of nonlinear partial differential equations[EB/OL].(2017-11-28). https://doi.org/10.48550/ arXiv.1711.10566
|
| [17] |
LU L, MENG X H, MAO Z P, et al. DeepXDE: a deep learning library for solving differential equations[J]. SIAM Review, 2021, 63(1): 208-228. DOI:10.1137/19m1274067 |
| [18] |
刘顺, 徐惊雷, 俞凯凯. 基于PIV技术的压力场重构算法实现与研究[J]. 实验流体力学, 2016, 30(4): 56-65. LIU S, XU J L, YU K K. Implementation and research on the reconstruction algorithms of pressure fields based on PIV[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(4): 56-65. (in Chinese) |
| [19] |
ZHANG P, XIA Z. Contribution of viscous stress work to wall heat flux in compressible turbulent channel flows[J]. Physical Review E, 2020, 102(4-1): 043107. DOI:10.1103/physreve.102.043107 |
| [20] |
BAYDIN A G, PEARLMUTTER B A, RADUL A A, et al. Automatic differentiation in machine learning: a survey[J]. Journal of Machine Learning Research, 2018, 18(153): 1-43. |
| [21] |
RAISSI M, KARNIADAKIS G E. Hidden physics models: Machine learning of nonlinear partial differential equations[J]. Journal of Computational Physics, 2018, 357: 125-141. DOI:10.1016/j.jcp.2017.11.039 |
| [22] |
何伟峰, 基于融合物理模型的神经网络流场信息算法研究[D]. 浙江: 浙江大学, 2021. HE W F. Research on flow field reconstruction algorithm based on physics informed neural network[D]. Zhejiang: Zhejiang University, 2021. |
| [23] |
CALLAHAM J L, KOCH J V, BRUNTON B W, et al. Learning dominant physical processes with data-driven balance models[J]. Nature Communications, 2021, 12(1): 1016. DOI:10.1038/s41467-021-21331-z |
 2022, Vol. 40
2022, Vol. 40