2. 国家计算流体力学实验室,北京 100191
2. National Laboratory for Computational Fluid Dynamics, Beijing 100191, China
计算流体动力学技术的进步已经到了几乎所有流动问题都能在可接受时长内解决的阶段。网格是数值计算的基础。但高质量的网格生成所占的时间渐渐比求解流动方程更多。我国著名空气动力学家张涵信院士将CFD领域概括为5M1A模型,即网格(Mesh)、数值方法(Method)、计算机(Machine)、机理(Mechanics)、绘图(Mapping)和应用(Application)。经验丰富的CFD应用者,在生成网格时,是要将具体的流动应用背景、流动机理、数值方法以及后处理等多个方面通盘考虑,而CFD开发人员,则需要额外的计算机软硬件基础。
棱柱网格由于在某几个方面具有特殊的优势,因而广泛地应用在边界层网格的生成中:从网格生成的角度,物面三角化网格灵活性强,适用性高,边界层内棱柱网格生成自动化程度高,当面对复杂的外形时,可以大大减少人工交互;从流动机理上看,靠近物面的黏性区域在垂直物面方向上的网格具有方向性,在高雷诺数流动或者含湍流的流动中对黏性边界层的分辨至关重要;在数值方法上,在远离物面的方向,网格具有结构化编号,这种内在的网格结构可以应用到通量格式中以提高计算精度,也可以应用到隐式时间推进中以加速收敛。
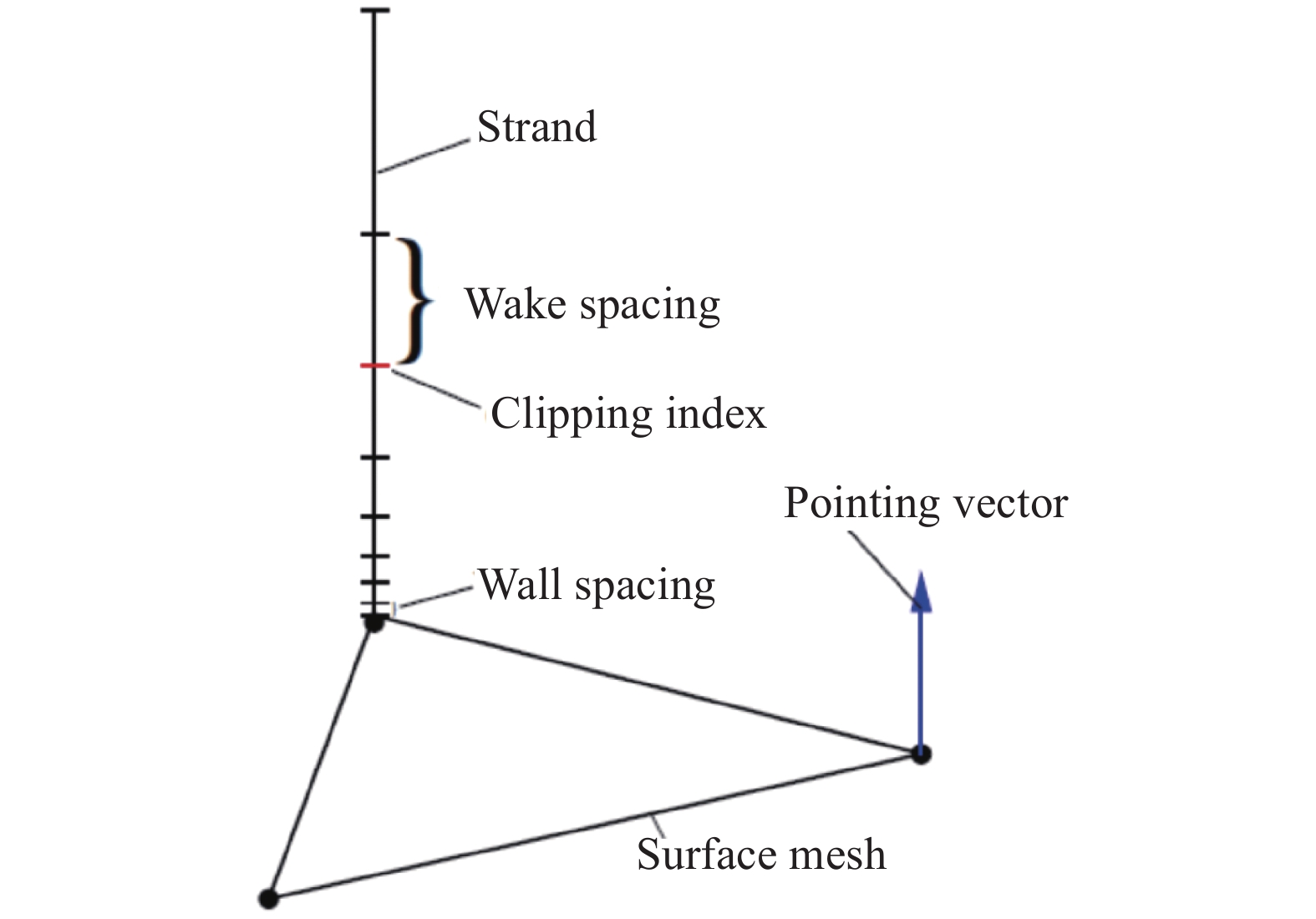
根据以上观察,Meakin等[1]于2007年引入了串网格划分方法。在这种方法中,通过直接从由三角形和四边形组成的离散曲面向外推进获得适合黏性捕捉的棱柱网格,这种体网格生成过程完全自动化。离散曲面的顶点向外生成一系列曲线,这些曲线称为“串”,通常是由指向向量和长度表示的直线(见图1),可以仅用几个参数来表示。边界层内捕捉流场细节的体网格是就是通过这些曲线上的点构建而成。
|
图 1 “串”的几何示意图[1] Fig.1 Geometry schematic of a strand |
串网格的生成,早期采用非结构网格边界层内棱柱网格生成的方法。棱柱网格的生成,可以分为基于几何的推进方法、基于各向异性四面体聚合的方法和基于场的推进方法。基于几何的方法,根据当地几何特征,确定推进方向和推进步长,重点解决在模型凹特征区域和邻近特征区域附近的边界层前沿面上可能出现的相交问题。基于网格聚合的方法[2]将自动生成的各向异性四面体网格基于一定的判定准则进行聚合,得到物面附近的棱柱网格单元。
基于场的方法,根据某种模型建立物面网格对空间网格影响的代数方程或者偏微分方程,由该方程确定的空间网格、网格推进方向或者网格推进步长自然满足网格的光滑性、正交性等条件,能够有效避免或者减轻基于几何的层推进方法中遇到的推进方向不确定或者可能出现的相交问题。基于场的方法的核心在于建立有效的控制方程,该方程能模拟计算出从物面到外部空间某种物理量,这个物理量自身的性质有助于确定网格推进中所需的推进方向、推进步长或者是直接的空间网格点。下边对已有的基于场的网格生成方法进行介绍。
Nakahashi[3]通过求解控制推进面总面积最小的变分方程,来确定推进方向上的网格步长,进而确定每一层的网格面。Sethian等[4]设计的水平集方法是通过求解Hamilton-Jacobi方程得到的一系列随时间演化的前沿面。Dawes等[5]将水平集方法应用到空间边界层网格的生成中。Park等[6]结合经典层进法和水平集方法,前沿点处的层进法向定义为水平集方法中隐式函数的梯度,并将前沿点沿着梯度方向投影到下一层前沿面上。在该方法中初始前沿面的几何信息得以借助前沿点的推进过程传递到各等值面上。Wang[7]将水平集方法的控制方程改为空间网格点距离物面最小欧氏距离所满足的Eikonal方程,通过求解该方程并计算其梯度确定推进方向,进而确定下一个前沿面。Sikara[8]通过类比静电场,建立势函数满足的拉普拉斯方程,使用边界积分方法求解拉普拉斯方程,势函数的梯度即电场方向,就是推进方向。Takanashi[9]在各个网格点放置不同的电荷,电荷量通过求解关于电场函数的最优化问题得到,进而通过电场方向确定推进方向。Zheng[10]利用快速多极子方法加速的边界积分方法求解三组拉普拉斯方程,确定推进方向场的三个分量,其本质为:势函数满足拉普拉斯方程,那么势函数梯度的每一个分量也满足拉普拉斯方程。孙岩[11]提出一种交互式棱柱网格生成方法,该方法交互地生成物面边界点的空间推进面网格,将边界点空间推进面网格的每层网格点看成边界网格点运动得到, 计算对应的边界网格点位移,利用径向基函数插值将边界网格点位移光滑传递给内部网格点,获得内部网格点的空间推进网格。
双曲网格生成方法历史悠久。Steger和Chan[12]提出并改进了双曲网格生成方法,采用中心差分加黏性耗散方式离散控制方程,成功应用到结构网格中。Tai[13]通过迎风格式离散双曲控制方程,并显式加入自适应的耗散。Steger[14]也提出了将双曲网格生成方法应用到非结构网格里去的思路,但由于非结构网格坐标转换所需的网格连接结构生成的困难,Steger的文章只有一个围绕简单球体的网格结果,没有证明能应用于复杂实用几何的外形。Matsuno[15]应用二阶迎风TVD的方法离散双曲控制方程,取代Steger和Chan方法中的中心差分加耗散,避免了耗散系数的人工调节。Matsuno[16]进一步将其应用到三角化网格面的棱柱网格生成中,前沿点是控制单元的格心,局部坐标通过与相邻单元格心的坐标数据计算得到,下一层格心点确定后,通过简单几何平均得到格点处的网格坐标。
Matsuno的方法有三个局限性:第一,基于格心的局部坐标系的指定具有随机性;第二,所能生成的网格仅限于三角形的网格;第三,所采用的三角形网格必须满足一定的条件,角度不能过分扭曲。此外,对于所有和球面同胚的多面体,根据欧拉公式[17],F+V = E+2,F为面元个数,V为顶点个数,E为面元边的个数,对于三角化的表面,2E = 3F,易得F = 2V−4,也就是说面元的个数是顶点个数的两倍。因此Matsuno方法中需要求解的以控制单元的格心坐标推进量为未知量,求解所需的内存和计算量都比较大。
本文基于Knupp[18]提出的定义在非结构网格局部离散点上的逻辑空间来近似计算坐标变换导数。进而将Steger和Chan的双曲网格生成方法[12]应用到非结构棱柱网格上。在非结构网格面上建立双曲型网格生成方程。通过隐式方法离散,得到线性方程组,调用Petsc库[19]中的广义最小残差算法(generalized mminimum RESidual,GMRES)求解。本质上讲,本文的方法是将双曲型网格生成方程在格点有限体积法的框架下离散并求解[20]。
1 双曲网格生成方法本文首先在结构网格的框架下描述三维双曲型网格生成原理,给出了双曲网格生成方程及数值求解方法。然后针对非结构网格面的格点,重新定义局部坐标来近似计算坐标变换导数,发展出非结构网格的框架下的双曲网格生成体系,利用格点有限体积法离散控制方程,并采用迎风方法和隐式推进求解。
1.1 双曲型结构网格生成方法用
| $ {{\boldsymbol{r}}_\xi } \cdot {{\boldsymbol{r}}_\zeta } = 0 $ | (1) |
| $ {{\boldsymbol{r}}_\eta } \cdot {{\boldsymbol{r}}_\zeta } = 0 $ | (2) |
| $ \left( {{{\boldsymbol{r}}_\xi } \times {{\boldsymbol{r}}_\zeta }} \right) \cdot {{\boldsymbol{r}}_\zeta } = V $ | (3) |
应用局部线化后,经过简单的代数运算,可以得到如下向量形式的网格生成方程:
| $ {Q_1}{\boldsymbol{r}}_\xi ^{} + {Q_2}{\boldsymbol{r}}_\eta ^{} + P{\boldsymbol{r}}_\zeta ^{} = {\boldsymbol{g}} $ | (4) |
| $\begin{split}& \boldsymbol r = \left[ {\begin{array}{*{20}{l}} x \\ y \\ z \end{array}} \right] \text{,} P = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{r}}_\xi }} \\ {{{\boldsymbol{r}}_\eta }} \\ {{{\boldsymbol{r}}_\xi } \times {{\boldsymbol{r}}_\eta }} \end{array}} \right] \text{,} {Q_1} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{r}}_\zeta }} \\ {\boldsymbol{0}} \\ {{{\boldsymbol{r}}_\eta } \times {{\boldsymbol{r}}_\zeta }} \end{array}} \right] \text{,}\\& {Q_2} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}} \\ {{{\boldsymbol{r}}_\zeta }} \\ {{{\boldsymbol{r}}_\zeta } \times {{\boldsymbol{r}}_\xi }} \end{array}} \right] \text{,} {\boldsymbol{g}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}} \\ {\boldsymbol{0}} \\ {V + 2\left( {{{\boldsymbol{r}}_\xi } \times {{\boldsymbol{r}}_\eta }} \right) \cdot {{\boldsymbol{r}}_\zeta }} \end{array}} \right] \end{split}$ | (5) |
由于物面单元面积均不为零,且单元格点排布方向使面法向朝向推进空间一侧,易知
| $ {\tilde Q_1}{\boldsymbol{r}}_\xi ^{} + {\tilde Q_2}{\boldsymbol{r}}_\eta ^{} + {\boldsymbol{r}}_\zeta ^{} = {P^{ - 1}}{\boldsymbol{g}} $ | (6) |
其中:
到目前为止,双曲网格生成控制方程的推导都是精确的。下一步需要将该方程离散,可以采用中心差分加人工黏性的方法[12],也可以使用迎风格式[13]。这里参考Chan[12]使用中心差分加人工黏性的方法,
| $ {\tilde Q_1}{\delta _\xi }\left( {{{\boldsymbol{r}}_{l + 1}} - {{\boldsymbol{r}}_l}} \right) + {\tilde Q_2}{\delta _\eta }\left( {{{\boldsymbol{r}}_{l + 1}} - {{\boldsymbol{r}}_l}} \right) + {\nabla _\zeta }{{\boldsymbol{r}}_{l + 1}} = {{\boldsymbol{h}}_{l + 1}} $ | (7) |
| $ {\delta _\xi }{{\boldsymbol{r}}_j} = \frac{{{{\boldsymbol{r}}_{j + 1}} - {{\boldsymbol{r}}_{j - 1}}}}{2},\quad {\delta _\eta }{{\boldsymbol{r}}_k} = \frac{{{{\boldsymbol{r}}_{k + 1}} - {{\boldsymbol{r}}_{k - 1}}}}{2} $ | (8) |
| $ {\nabla _\zeta }{{\boldsymbol{r}}_{l + 1}} = {{\boldsymbol{r}}_{l + 1}} - {{\boldsymbol{r}}_l} $ | (9) |
| $ {{\boldsymbol{h}}_{l + 1}} = {(0,0,{V_{l + 1}})^{\text{T}}} $ | (10) |
添加人工黏性后可以得到:
| $\begin{split}& \left[ {I + {{\tilde Q}_1}{\delta _\xi } - {\varepsilon _{i\xi }}{{(\Delta \nabla )}_\xi } + {{\tilde Q}_2}{\delta _\eta } - {\varepsilon _{i\eta }}{{(\Delta \nabla )}_\eta }} \right] \left( {{{\boldsymbol{r}}_{l + 1}} - {{\boldsymbol{r}}_l}} \right) = {{\boldsymbol{h}}_{l + 1}} + {{\boldsymbol{D}}_e} \end{split}$ | (11) |
其中:
| $ {(\Delta \nabla )_\eta }{\boldsymbol{r}} = {{\boldsymbol{r}}_{k + 1}} - 2{{\boldsymbol{r}}_k} + {{\boldsymbol{r}}_{k - 1}} $ | (12) |
通量格式大都可写作中心格式加耗散项的形式。如果双曲网格生成控制方程采用迎风格式,那么隐式耗散系数将会被
进一步的隐式顺滑可以通过将
| $\begin{split}& \left[ {I + (1 + \theta ){{\tilde Q}_1}{\delta _\xi } - {\varepsilon _{i\xi }}{{(\Delta \nabla )}_\xi } + (1 + \theta ){{\tilde Q}_2}{\delta _\eta } - {\varepsilon _{i\eta }}{{(\Delta \nabla )}_\eta }} \right]\cdot\\&\;\;\;\; \left( {{{\boldsymbol{r}}_{l + 1}} - {{\boldsymbol{r}}_l}} \right) = {{\boldsymbol{h}}_{l + 1}} + {{\boldsymbol{D}}_e} \end{split}$ | (13) |
该方程在结构化网格上是五块对角矩阵,可以通过近似分裂分别在两个方向化为三块对角矩阵分别求解。
接下来讨论右端耗散项:
| $ {{\boldsymbol{D}}_e} = - \left[ {{\varepsilon _{e\xi }}{{(\Delta \nabla )}_\xi } + {\varepsilon _{e\eta }}{{(\Delta \nabla )}_\eta }} \right]{r_l} $ | (14) |
| $ {\varepsilon }_{e\xi } = {\varepsilon }_{e}{R}_{\xi }{N}_{\xi }\text{,}{\varepsilon }_{e\eta } = {\varepsilon }_{e}{R}_{\eta }{N}_{\eta } $ | (15) |
| $ {R}_{\xi } = {S}_{l}{\tilde{d}}_{j,k,l}^{\;\xi }{a}_{j,k,l}^{\;\xi }\text{,}{R}_{\eta } = {S}_{l}{\tilde{d}}_{j,k,l}^{\;\eta }{a}_{j.k,l}^{\;\eta } $ | (16) |
其中
| $ {N}_{\xi } = \sqrt{\left|\right|{r}_{\zeta }|{|}^{2}/\left|\right|{r}_{\xi }|{|}^{2}}\text{,}{N}_{\eta } = \sqrt{\left|\right|{r}_{\zeta }|{|}^{2}/\left|\right|{r}_{\eta }|{|}^{2}} $ | (17) |
标量函数
网格分布感应器
| $ \begin{split}& \tilde d_{j,k.l}^{\;\xi} = \;{\text{max}}\;[\;{(d_{j.k,l}^{\;\xi} )^{2/{S_l}}},0.1\;] \\& \tilde d_{j,k,l}^{\;\eta} = \;{\text{max}}[\;{(d_{j,k,l}^{\;\eta} )^{2/{S_l}}},0.1\;] \end{split} $ | (18) |
| $ \begin{split}& d_{j,k,l}^{\;\xi }= \frac{{\left| {{{\boldsymbol{r}}_{j + 1,k,l - 1}} - {{\boldsymbol{r}}_{j,k,l - 1}}} \right| + \left| {{{\boldsymbol{r}}_{j - 1,k,l - 1}} - {{\boldsymbol{r}}_{j,k,l - 1}}} \right|}}{{\left| {{{\boldsymbol{r}}_{j + 1,k,l}} - {{\boldsymbol{r}}_{j,k,l}}} \right| + \left| {{{\boldsymbol{r}}_{j - 1,k,l}} - {{\boldsymbol{r}}_{j,k,l}}} \right|}} \\& d_{j,k,l}^{\;\eta }= \frac{{\left| {{{\boldsymbol{r}}_{j,k + 1,l - 1}} - {{\boldsymbol{r}}_{j,k,l - 1}}} \right| + \left| {{{\boldsymbol{r}}_{j,k - 1,l - 1}} - {{\boldsymbol{r}}_{j,k,l - 1}}} \right|}}{{\left| {{{\boldsymbol{r}}_{j,k + 1,l}} - {{\boldsymbol{r}}_{j,k,l}}} \right| + \left| {{{\boldsymbol{r}}_{j,k - 1,l}} - {{\boldsymbol{r}}_{j,k,l}}} \right|}} \end{split} $ | (19) |
网格角度感应器
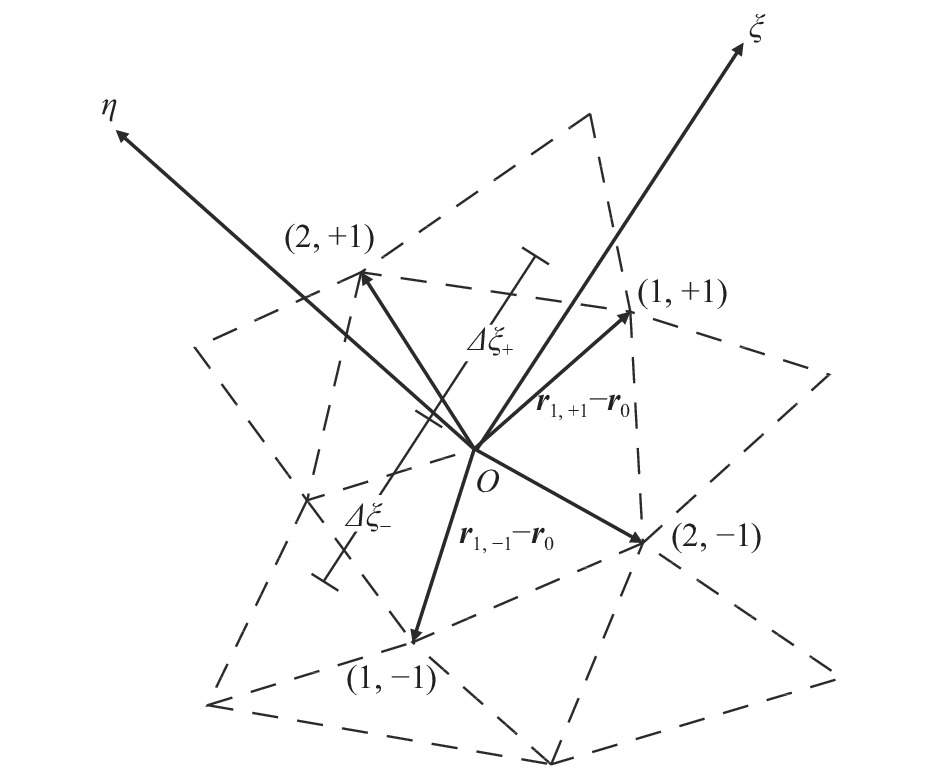
如引言所述,Steger[14]和Matsuno[16]都曾经将双曲型网格生成方法应用到非结构网格上。Steger的方法比较直接,如图2所示,在非结构的网格面上指定当地坐标系,然后找出可能存在的网格序号结构性,进而采用结构网格的方法进行网格生成。具体来讲,使用坐标为(1,+1)和(1,−1)的点计算ξ方向的坐标导数,使用坐标为(2,+1)和(2,−1)的点计算η方向的坐标导数。但由于这种坐标系指定的随机性以及网格潜在的结构性连接结构生成困难,Steger的文章只有一个围绕简单球体的网格结果,没有证明能应用于复杂实用几何的外形。
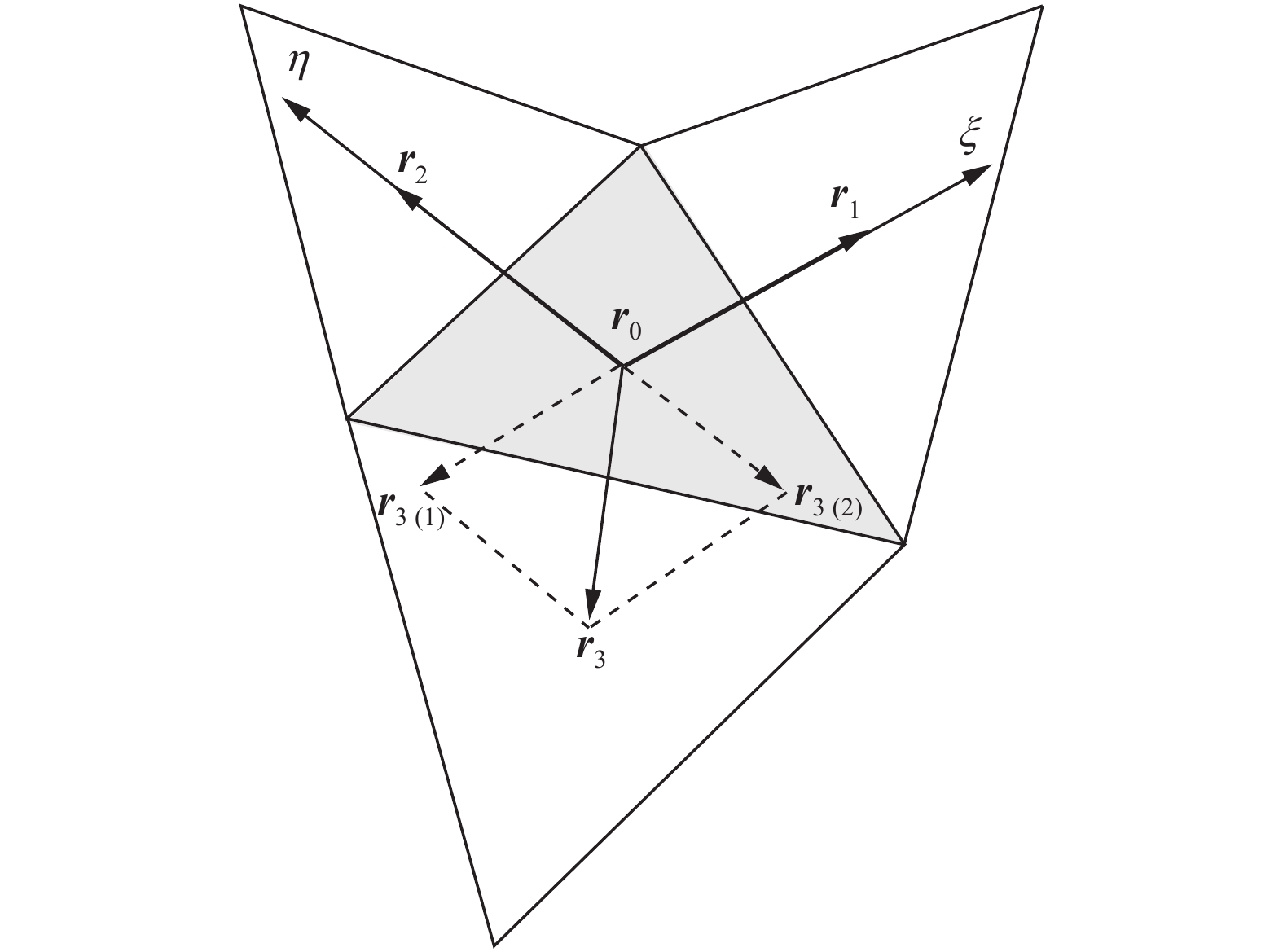
Matsuno[16]则在格心建立局部坐标系,通过单元和单元的连接关系指定局部坐标系的方向,即使用相邻单元格心的坐标计算得到,如图3所示。这样同样将非结构的问题转化为局部结构化问题进行双曲网格生成。下一层格心点确定后,通过简单几何平均得到格点处的网格坐标。他的方法,可以视为在非结构网格上构造通过将三角形剖分为四边形,从而构造出局部结构网格,开展双曲网格生成,也可以看为基于格心有限体积法的双曲网格生成。Matsuno方法的局限性已在引言中讲明。论文中算例的表面网格均为三角形网格,且三角形内角没有扭曲,单个顶点周围三角形的数量均为6个。可见他的方法适用性上是有限制的。在某些流动特征的数值模拟中,物面也会根据需要生成各向异性的网格,这个方法就会无能为力。
本文提出的方法则是完全适应于三角形、四边形混合表面网格,且对网格分布没有额外要求。因为本文的方法从根本上就是在基于格点有限体积法的框架下,对守恒型式的双曲方程进行推导离散。
将控制方程(6)改为守恒型:
| $ {\boldsymbol{r}}_\zeta ^{} + {\boldsymbol{F}}({\boldsymbol{r}})_\xi ^{} + {\boldsymbol{G}}({\boldsymbol{r}})_\eta ^{} = {\boldsymbol{S}} $ | (20) |
其中:
| $ {\boldsymbol{F}}({\boldsymbol{r}}) = {\tilde Q_1}{\boldsymbol{r}} ,\; {\boldsymbol{G}}({\boldsymbol{r}}) = {\tilde Q_2}{\boldsymbol{r}} , \;{\boldsymbol{S}} = {P^{ - 1}}{\boldsymbol{g}} $ | (21) |
应用高斯公式,转为积分型控制方程:
| $ \iint\limits_V {{\boldsymbol{r}}_\zeta ^{}{\text{d}}\varOmega } + \oint\limits_{\partial V} {[{\boldsymbol{F}},{\boldsymbol{G}}] \cdot {\boldsymbol{n}}{\text{d}}A} = \iint\limits_V {{\boldsymbol{S}}{\text{d}}V} $ | (22) |
其中:
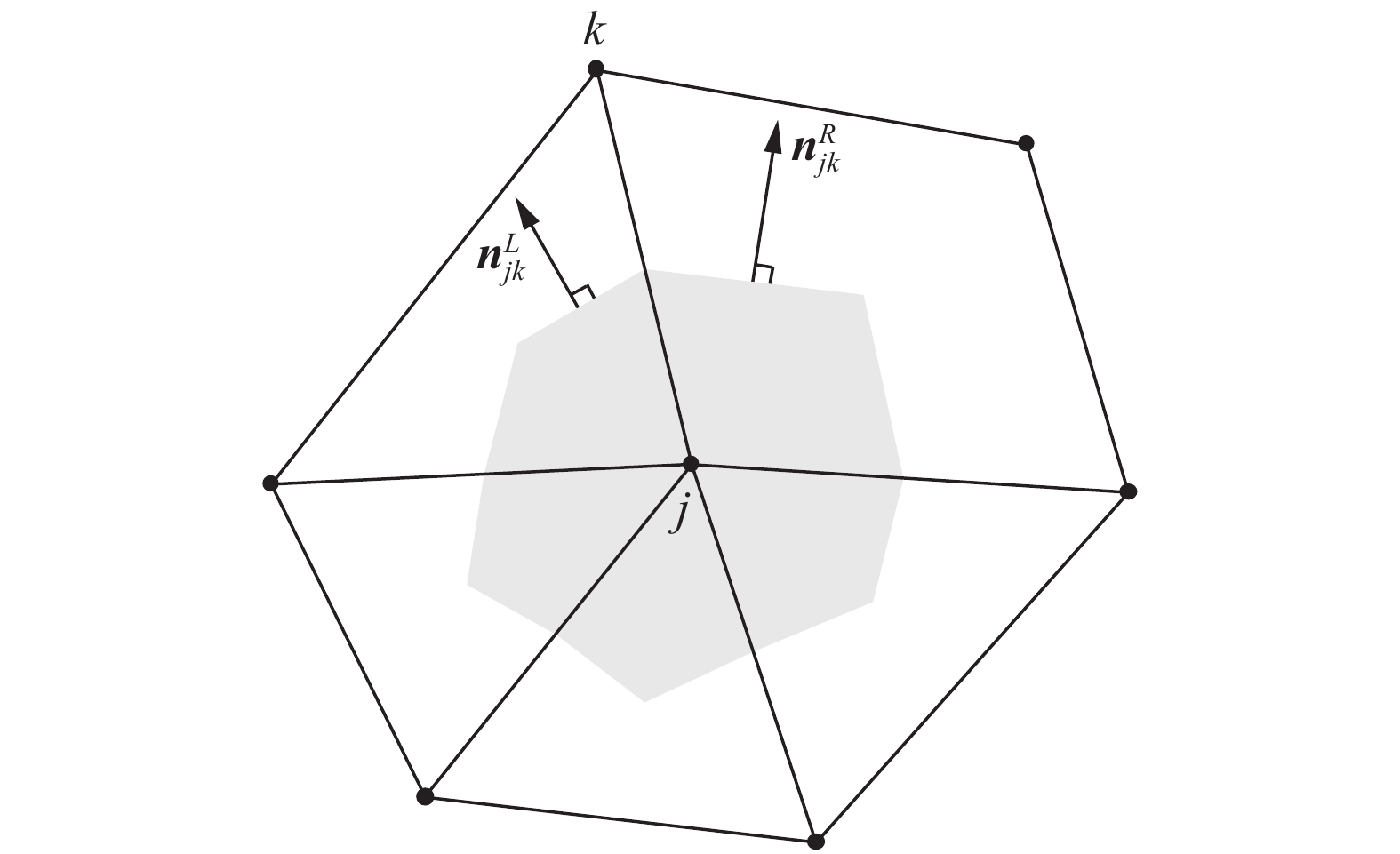
如图4所示,该方程在格点有限体积法的框架下可以离散为:
|
图 4 格点有限体积法控制体几何示意图 Fig.4 Schematic of dual control volume for node-centered finite-volume schemes with unit normals associated with an edge with an edge |
| $ \frac{{{\text{d}}{{\boldsymbol{r}}_j}}}{{{\text{d}}\zeta }} = - \frac{1}{{{V_j}}}\sum\limits_{k \in \left\{ {{N_j}} \right\}} {{{\boldsymbol{\varPhi }}_{jk}}({{\boldsymbol{r}}_j},{{\boldsymbol{r}}_k}){A_{jk}}} + {{\boldsymbol{S}}_j} $ | (23) |
其中:
数值通量采用迎风格式:
| $ {{\boldsymbol{\varPhi }}_{jk}}({{\boldsymbol{r}}_j},{{\boldsymbol{r}}_k}) = \frac{1}{2}\left[ {{{\boldsymbol{H}}_{jk}}\left( {{{\boldsymbol{r}}_j}} \right) + {{\boldsymbol{H}}_{jk}}\left( {{{\boldsymbol{r}}_k}} \right)} \right] - \frac{1}{2}{\lambda _{jk}}{\boldsymbol{I}}\left( {{{\boldsymbol{r}}_k} - {{\boldsymbol{r}}_j}} \right) $ | (24) |
| $ {{\boldsymbol{H}}_{jk}}\left( {{{\boldsymbol{r}}_j}} \right) = [{\boldsymbol{F}},{\boldsymbol{G}}] \cdot {\boldsymbol{n}_{jk}} = [{\tilde Q_1}{{\boldsymbol{r}}_j},{\tilde Q_2}{{\boldsymbol{r}}_j}] \cdot { {\boldsymbol{n}}_{jk}},\quad { {\boldsymbol{n}}_{jk}} = \frac{{{{\boldsymbol{n}}_{jk}}}}{{{A_{jk}}}} $ | (25) |
半离散方程的显式求解可以通过添加伪时间项,进行Runge-Kutta类型的求解[16]:
| $ \begin{split}& \frac{{\partial {\boldsymbol{r}}}}{{\partial \tau }} = - R({\boldsymbol{r}}) \\& R({{\boldsymbol{r}}_j}) \triangleq \frac{{{\rm{d}}{{\boldsymbol{r}}_j}}}{{{\rm{d}}\zeta }} + \frac{1}{{{V_j}}}\sum\limits_{k \in \left\{ {{N_j}} \right\}} {{{\boldsymbol{\varPhi }}_{jk}}({{\boldsymbol{r}}_j},{{\boldsymbol{r}}_k}){A_{jk}}} - {{\boldsymbol{S}}_j} \end{split}$ | (26) |
本文主要采用隐式求解。
| $ \Delta {{\boldsymbol{r}}_j} + \frac{1}{{{V_j}}}\sum\limits_{k \in \left\{ {{N_j}} \right\}} {{\boldsymbol{\varPhi }_{jk}}(\Delta {{\boldsymbol{r}}_j},\Delta {{\boldsymbol{r}}_k})} {A_{jk}} = {P^{ - 1}}{\boldsymbol{h}} $ | (27) |
| $ \begin{split}& \left\{ {{\boldsymbol{I}} + \sum\limits_{k \in \left\{ {{N_j}} \right\}} {\left[ {\frac{1}{2}{{\boldsymbol{H}}_{jk}}\left( {\Delta {{\boldsymbol{r}}_j}} \right) + \frac{1}{2}{\lambda _{jk}}{\boldsymbol{I}}} \right]\frac{{{A_{jk}}}}{{{V_j}}}} } \right\}\Delta {{\boldsymbol{r}}_j} \\&+ \sum\limits_{k \in \left\{ {{N_j}} \right\}} {\left\{ {{\boldsymbol{I}} + \left[ {\frac{1}{2}{{\boldsymbol{H}}_{jk}}\left( {\Delta {{\boldsymbol{r}}_k}} \right) - \frac{1}{2}{\lambda _{jk}}{\boldsymbol{I}}} \right]\frac{{{A_{jk}}}}{{{V_j}}}} \right\}} \Delta {{\boldsymbol{r}}_k} = {P^{ - 1}}{\boldsymbol{h}} \end{split} $ | (28) |
所有格点的代数方程可以组成一个线性方程组,通过PETSc库里的GMRES求解器,可以方便地实现并行求解,进而得到下一层的网格点
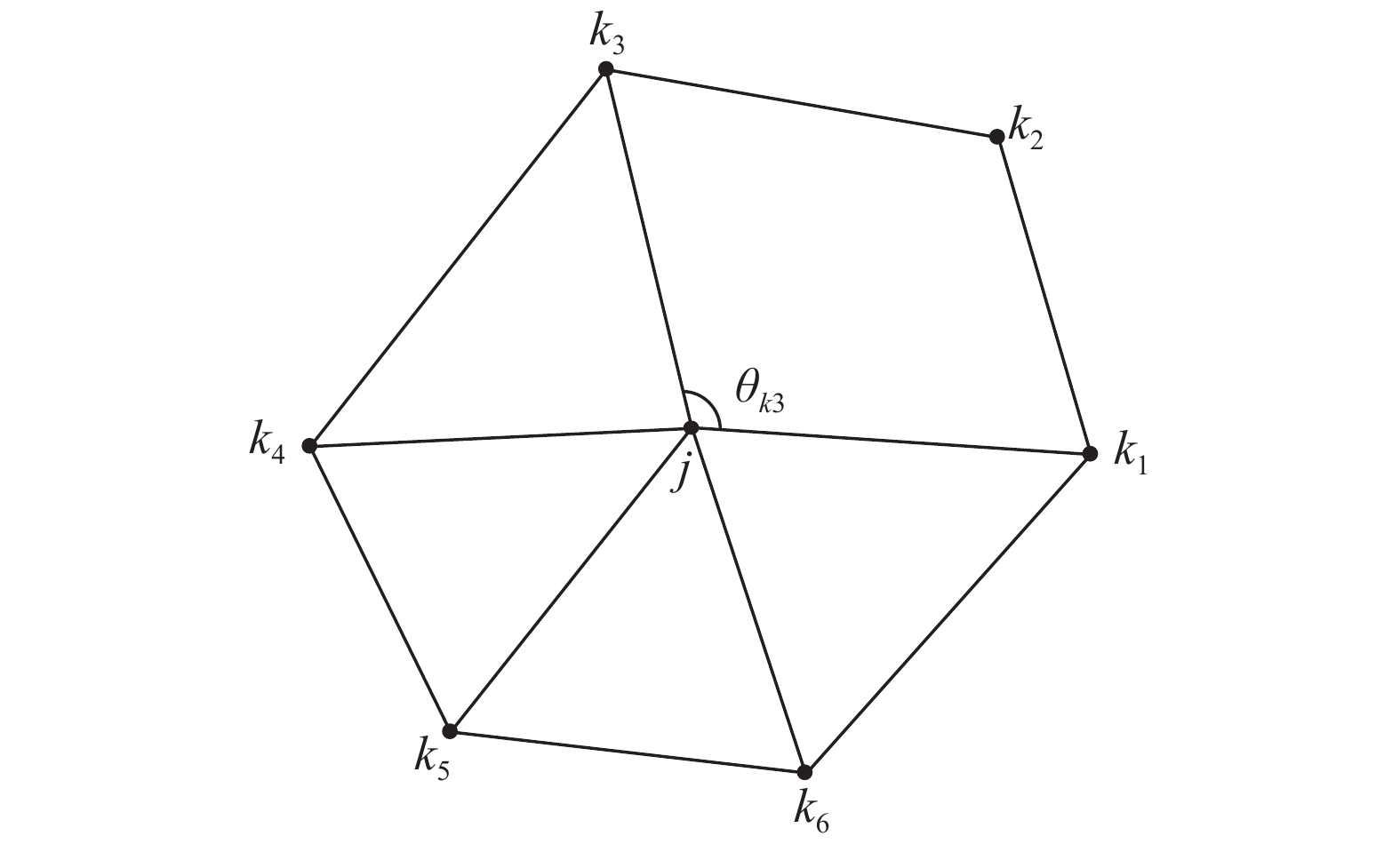
最后需要解决的一个问题是,在方程(5)系数矩阵
|
图 5 局部计算坐标变换导数所用模板示意图 Fig.5 Grid stencils for coordinate local transformation computation |
定义角度
| $ {{\boldsymbol{r}}_\xi } = \frac{2}{N}\sum\limits_{i = 1}^N {\left( {{{\boldsymbol{r}}_i} - {{\boldsymbol{r}}_0}} \right)\cos {\theta _i}} $ | (29) |
| $ {{\boldsymbol{r}}_\eta } = \frac{2}{N}\sum\limits_{i = 1}^N {\left( {{{\boldsymbol{r}}_i} - {{\boldsymbol{r}}_0}} \right)\sin {\theta _i}} $ | (30) |
通过方程(1~3),
| $ {{\boldsymbol{r}}_\zeta } = {P^{ - 1}} \cdot {[0,0,V_j^{l - 1}]^{\text{T}}} $ | (31) |
面通量计算所需的
| $ {\boldsymbol{n}}_{jk} = (\cos {\theta _i},\sin {\theta _i}) $ | (32) |
体积的指定在当前层格点控制体面积已知的情况下,就是沿推进方向的控制网格分布函数的指定,可以采用指数函数、双指数函数或者双曲正切函数,也可以从相似的简单参考外形体已有的网格上“拷贝”网格分布。作者所在课题组长期从事高超声速外形飞行器的设计及优化,我们的经验是采用球锥模型近似飞行器,根据近似公式得到激波位置并外扩作为远场边界,使用代数的方法生成参考网格。
为进一步提高网格的光滑性要求,对推进层的体积做拉普拉斯光顺:
| $ {V_j} = (1 - \upsilon ){V_j} + L({V_j}) $ | (33) |
其中:
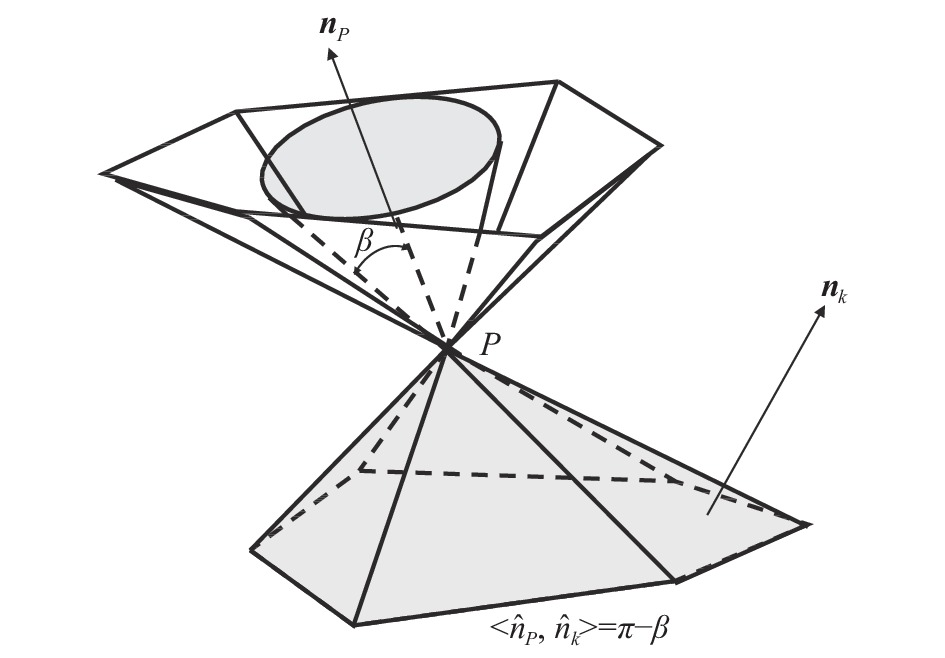
同样的,也可以在方程(28)右端加入显式的耗散项(14)。显式的耗散项从结构网格往非结构网格上扩展时,唯一需要注意的就是角度感受器中角度的定义。本文参考文献[22],如图6所示,将角度定义为平均法向与所有面法向夹角的最大值
|
图 6 角度感受器中角度的定义示意图 Fig.6 Illustration of angle definition in angle sensor function sensor function |
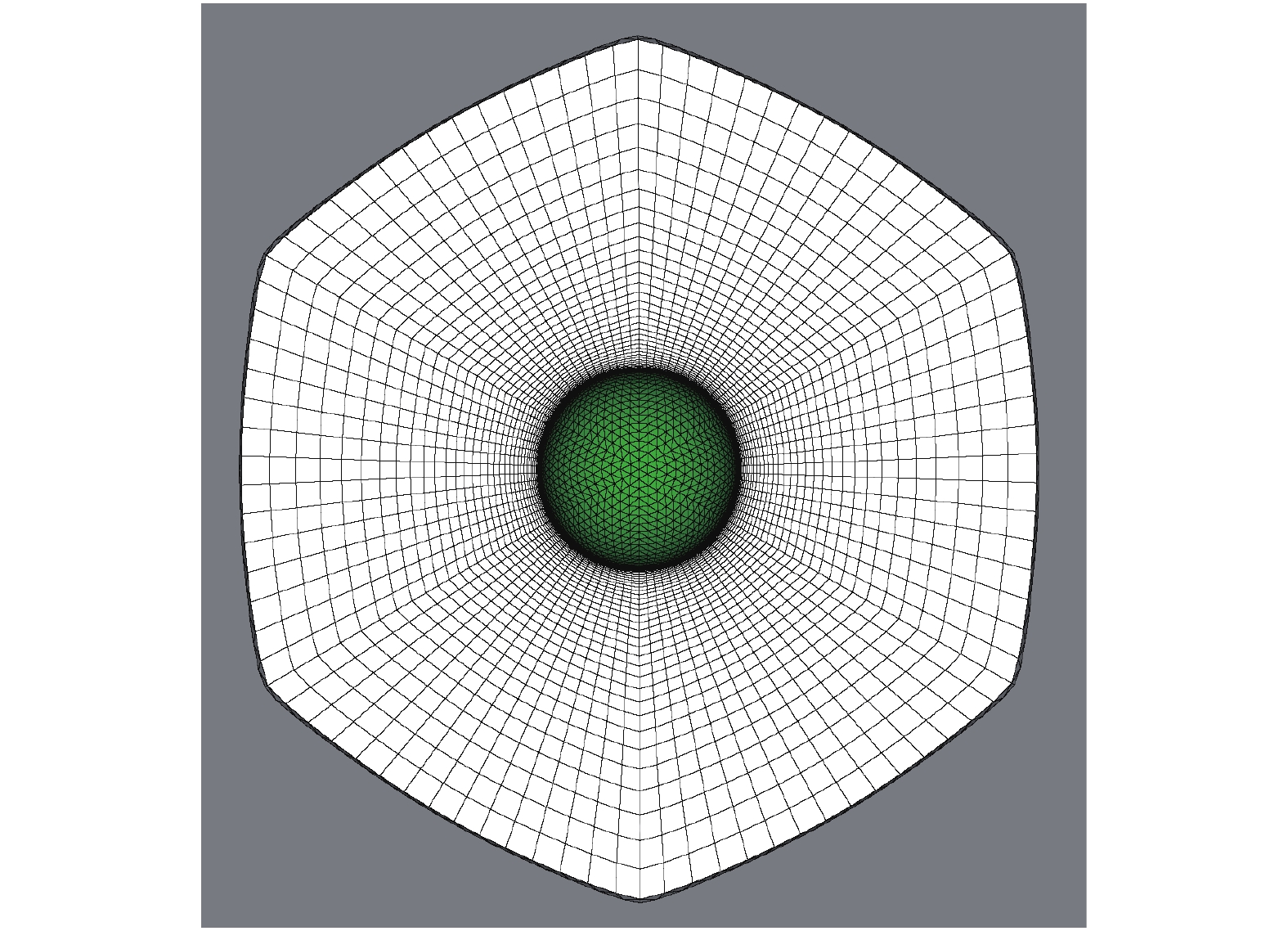
采用本文算法对几个典型外形生成了双曲型网格,验证本文方法的可行性。首先是最基本的球面,图7是圆球的表面网格,图8是本文方法生成的圆球双曲型非结构网格。从图8可以看出,表面光滑的圆球,由于表面网格点分布的非均匀性,也会导致生成的网格前沿面并非绝对球面。随着前沿面的继续推进,耗散将不再变化,最终会在足够远处得到比较圆的外边界,无论初始外形多么复杂。

|
图 7 圆球的表面网格 Fig.7 Surface mesh of sphere |
|
图 8 圆球的双曲型非结构网格y= 0切面图 Fig.8 Hyperbolic mesh slice at y = 0 cutting plane for sphere |
第二个网格生成例子是表面含有凹凸的旋成体,母线函数为:
| $ r = a\left[ {b\sqrt {{{0.5}^2} - {{(x - 0.5)}^2}} + {{\sin }^2}(k{\text {π}} x)} \right] $ | (34) |
其中:
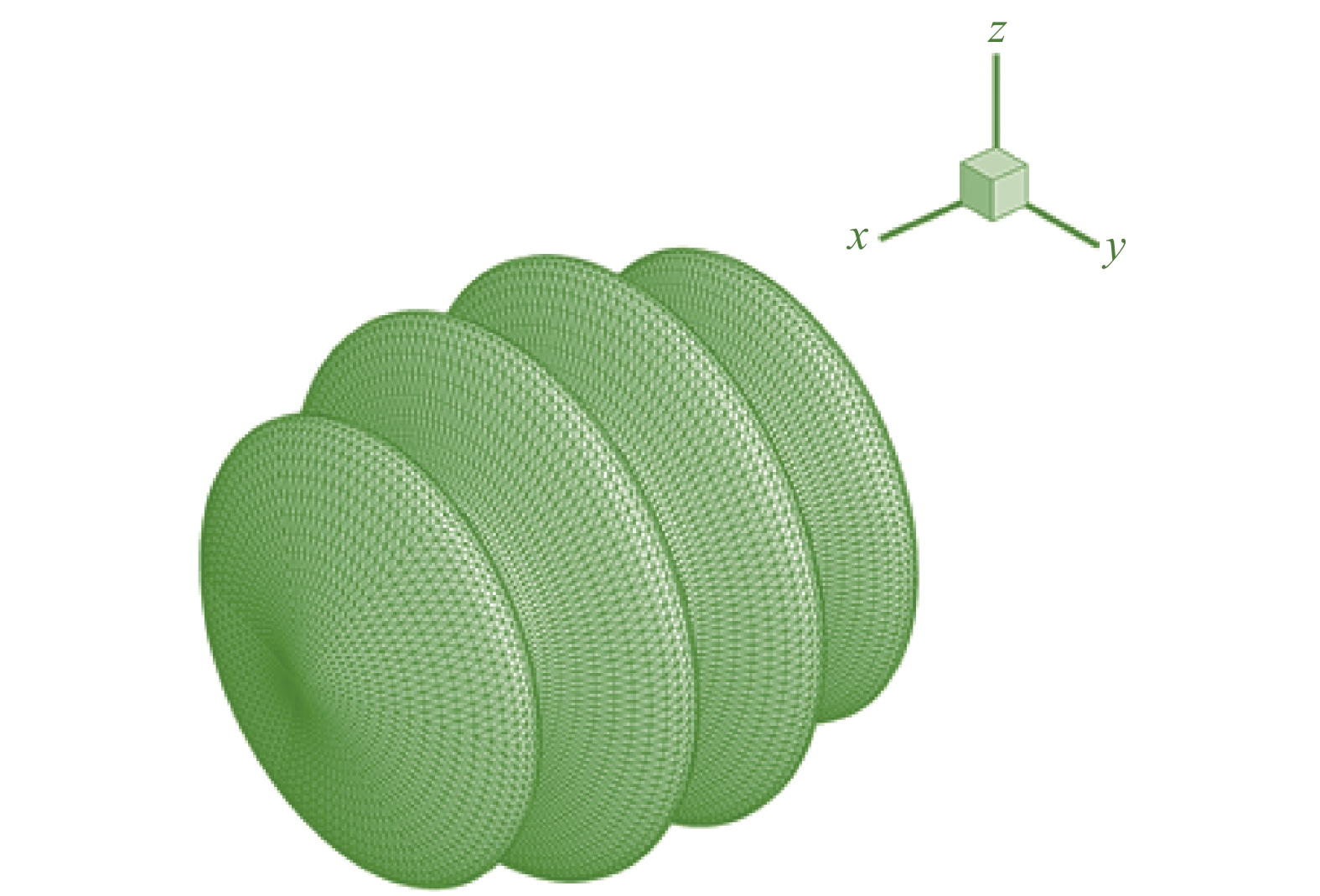
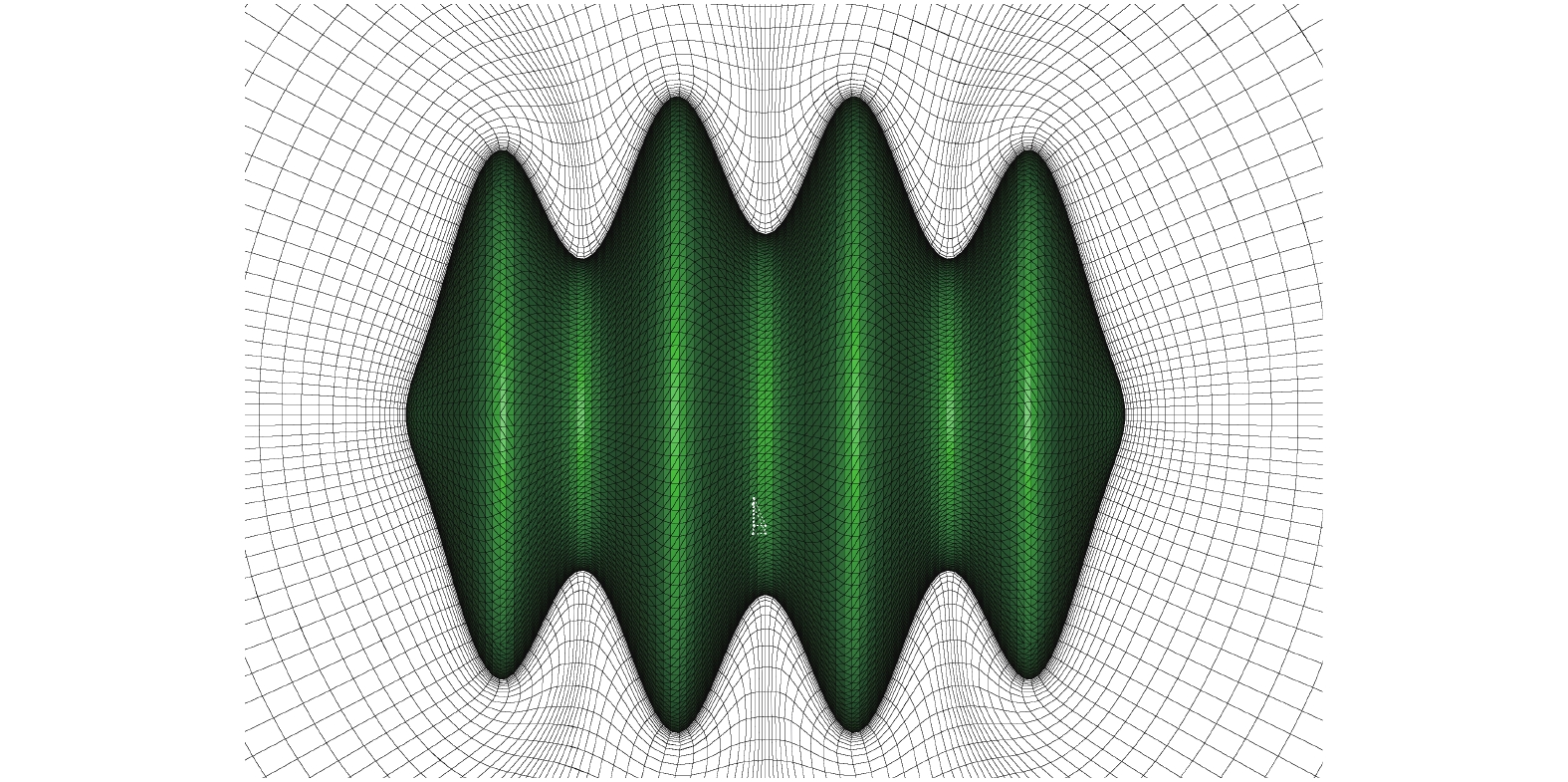
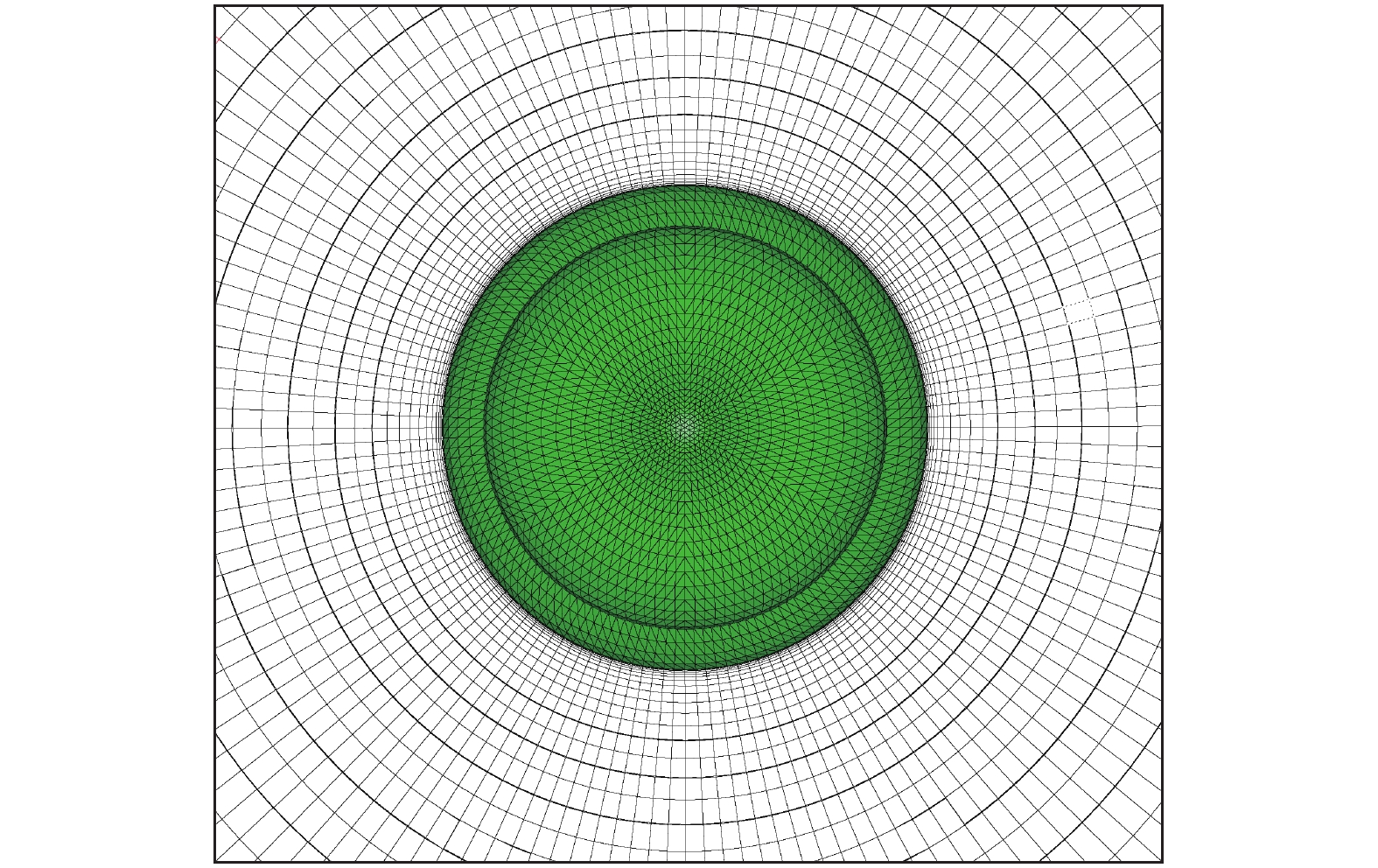
图9是含有凹凸结构的旋成体表面网格,图10是含有凹凸结构的旋成体双曲型网格y = 0切面图,图11是在物面附近的放大图,可以看出,无论是在外形的凸起处,还是在凹陷处,均可生成高质量的棱柱网格。图12是旋成体双曲型网格x切面图,由于旋成体周向网格分布均匀,生成的空间棱柱网格具有良好的对称性。
|
图 9 含有凹凸结构的旋成体表面网格 Fig.9 Surface mesh of the spiral body with extreme concave-convex structure |

|
图 10 含有凹凸结构的旋成体双曲型网格y = 0切面图 Fig.10 Hyperbolic mesh slice at y = 0 cutting plane of the spiral body with extreme concave-convex structure |
|
图 11 旋成体凹凸结构的处的双曲型网格y = 0切面放大图 Fig.11 Close up view of the hyperbolic mesh slice at y = 0 cutting plane of the spiral body with extreme concave-convex structure |
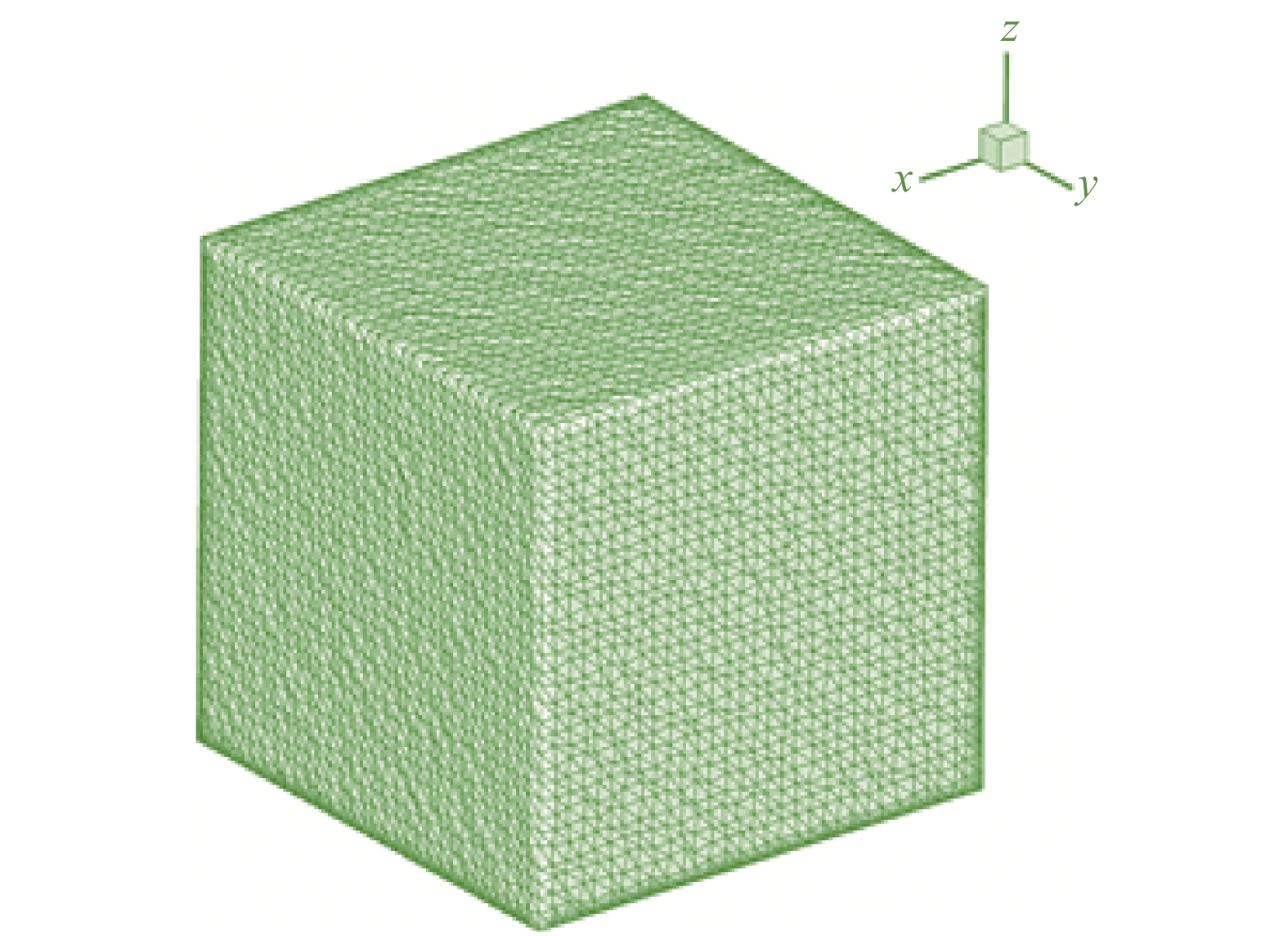
接下来是测试本文发展的双曲网格生成方法在含有尖角或尖锐边缘外形的适用情况,选取正方体外形进行测试。图13是立方体表面网格,在结构网格的基础上通过扰动并将四边形划分为三角形得到。图14、图15是本文方法生成的空间棱柱网格两个视角下的切面图,可以看出得到的网格结果令人满意。
|
图 12 含有凹凸结构的旋成体双曲型网格x切面图 Fig.12 Hyperbolic mesh slice at x cutting plane of the spiral body with extreme concave-convex structure |
|
图 13 立方体表面网格 Fig.13 Surface mesh of the cube with sharp edges |

|
图 14 立方体双曲型网格y切面图 Fig.14 Hyperbolic mesh slice at y const cutting plane of the cube |

|
图 15 立方体双曲型网格斜切面图 Fig.15 Oblique view of hyperbolic mesh slice at x+y = const cutting plane of the cube |
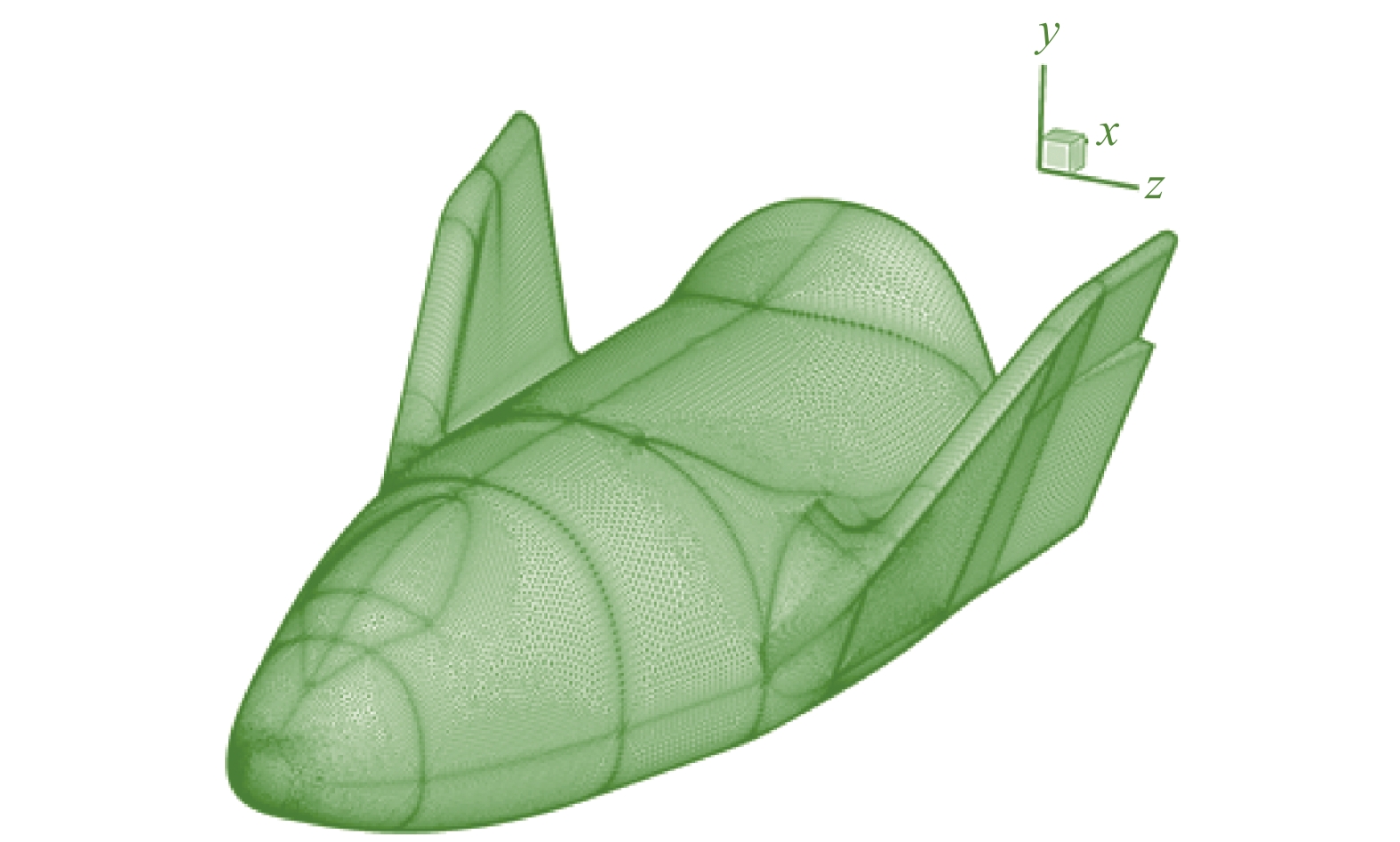
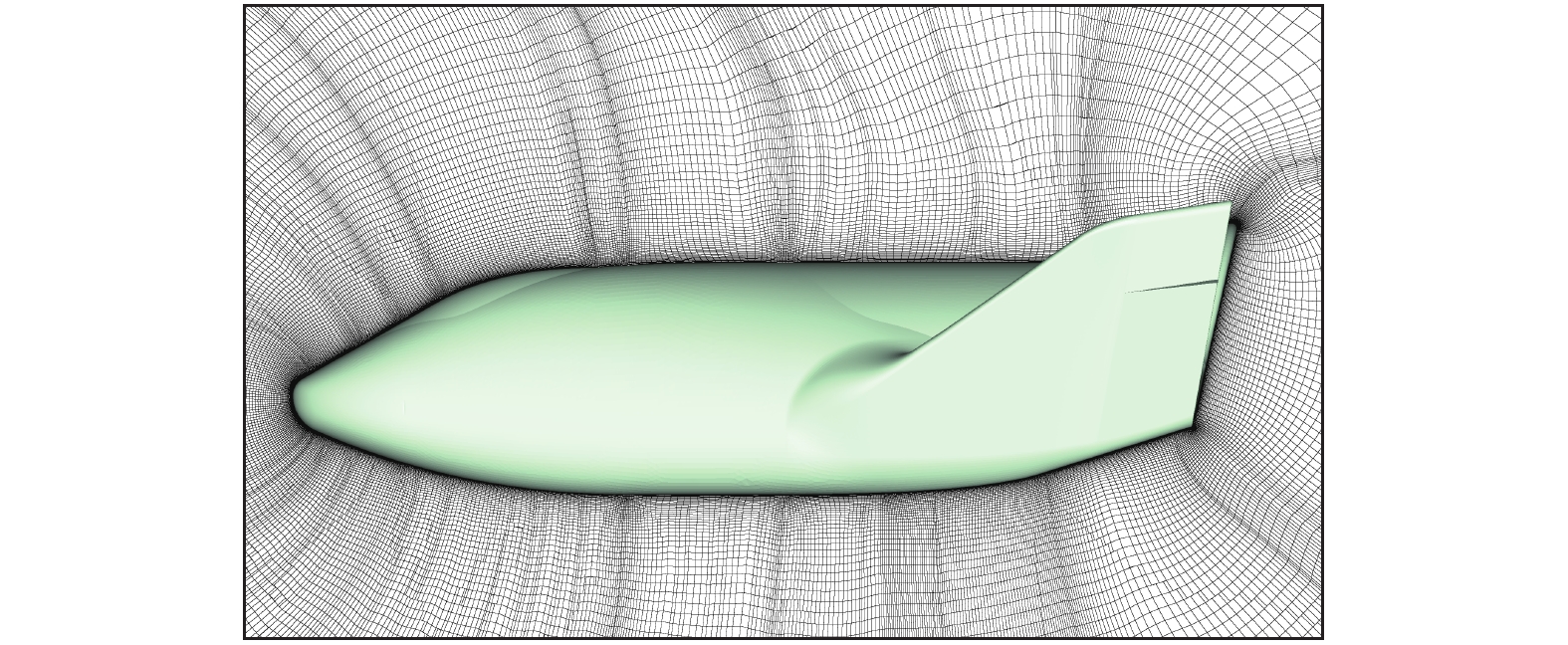
最后是复杂飞行器外形X38。图16为X38外形表面网格,根据流动特征进行了加密。邻居点的最大数量达到12,即在局部表面网格比较扭曲,三角形内角小于30°。表面一共有106138个点,212272个三角形网格。图17、图18分别展示了x切面和z切面下内部网格的正交性,图19、图20、图21分别展示了几个
|
图 16 X38飞行器表面网格示意图 Fig.16 Surface mesh of X38 Crew-Return-Vehicle |

|
图 17 X38双曲型网格x切面图 Fig.17 Hyperbolic mesh slice at x const cutting plane of X38 CRV |
|
图 18 X38双曲型网格z切面图 Fig.18 Hyperbolic mesh slice at z const cutting plane of X38 CRV |
|
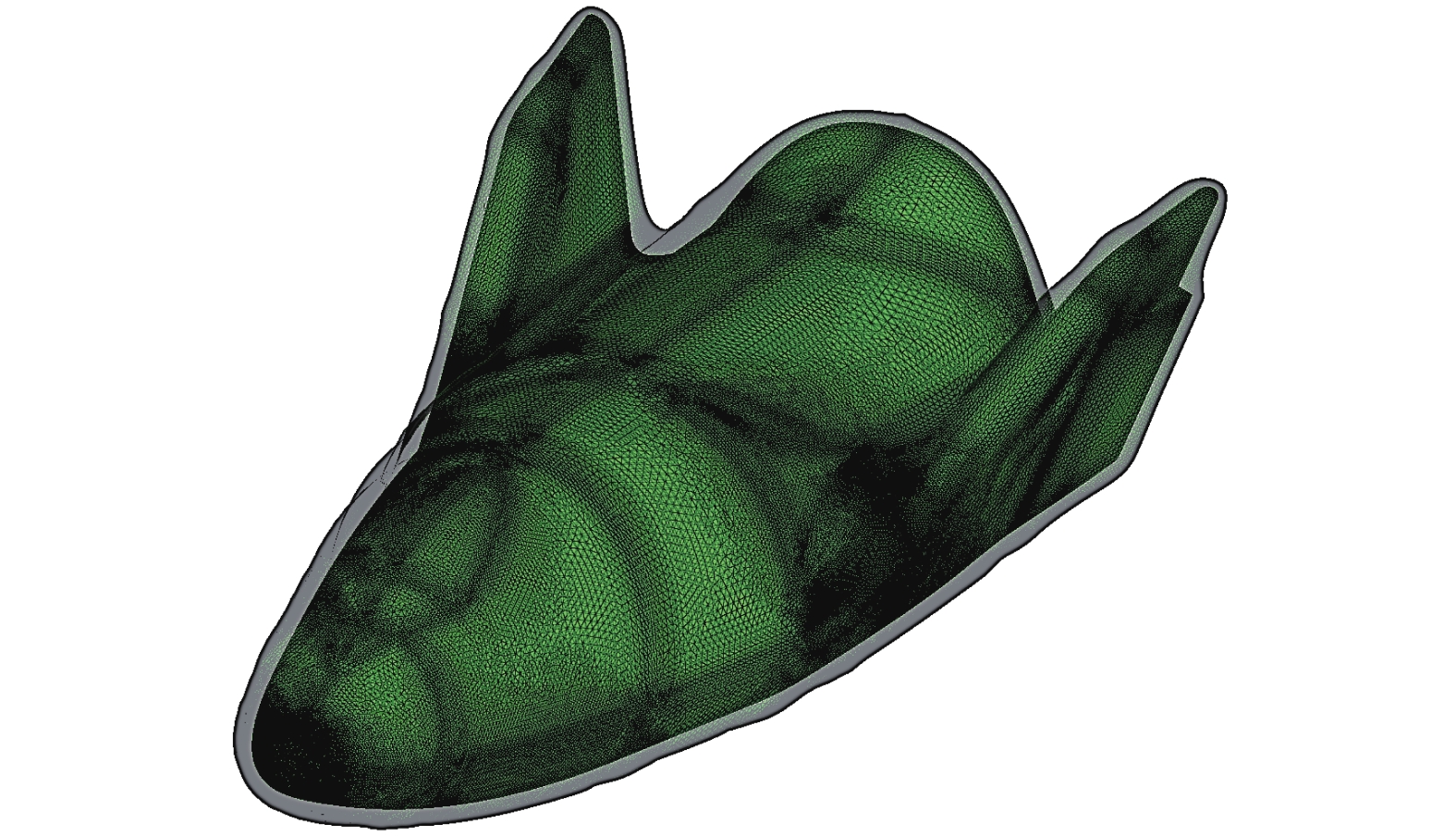
图 19 |

|
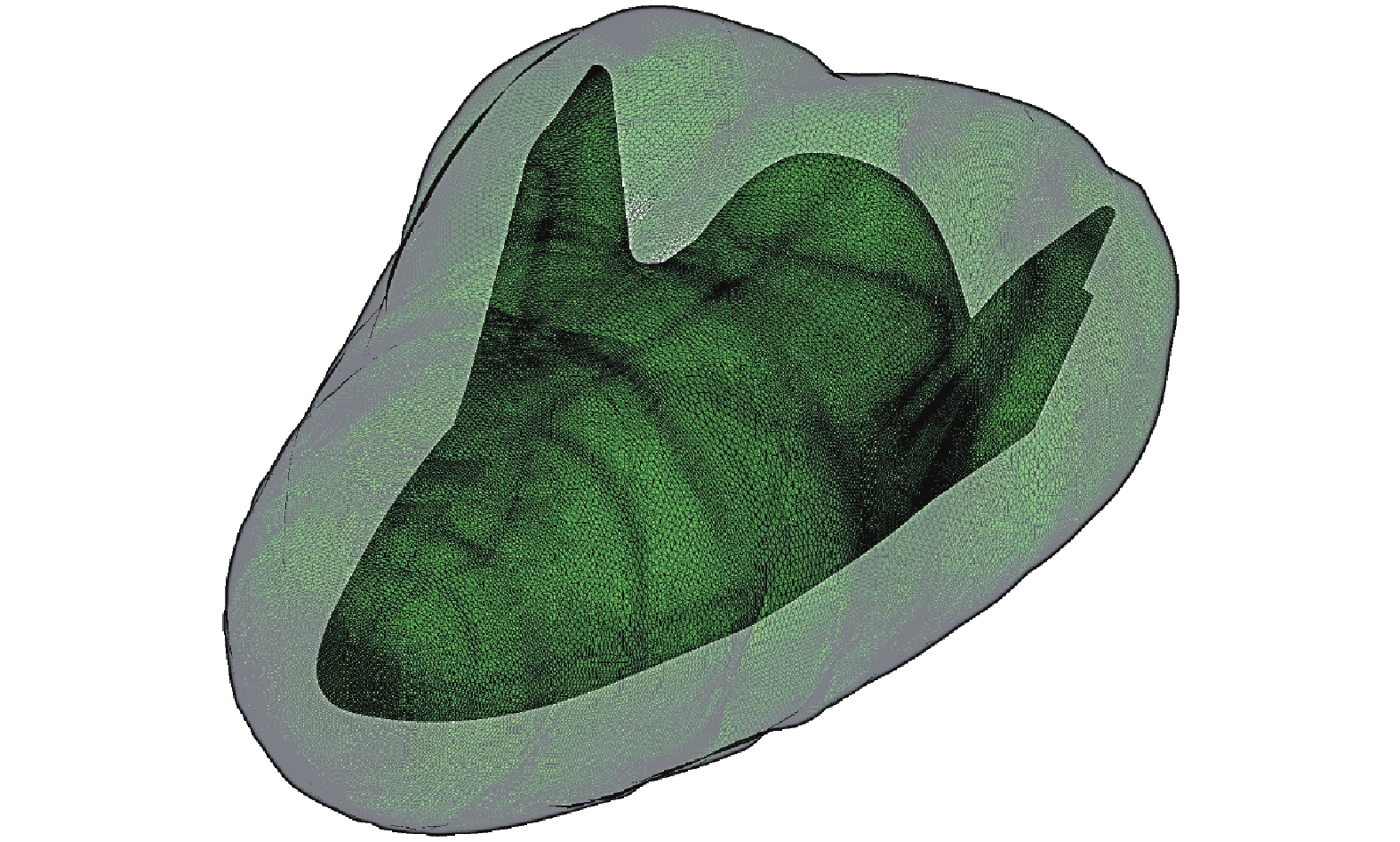
图 20 |
|
图 21 |
本文基于完全气体模型求解三维层流N-S 方程,使用格心有限体积法的隐式离散化,在通量计算上,利用本文网格的方向性,使用混合无黏通量格式。所采用的混合策略是,在壁面平行的面元上使用耗散足够小、能精确捕捉边界层的Godunov格式,在其他面元上使用耗散大、能抑制激波不稳定的旋转迎风格式。时间推进上采用线隐LUSGS求解。
3.1 X38外形气动力数值模拟X38飞机是为国际空间站研制的升力体再入式乘员往返飞行器的原型机,作为宇航员紧急逃逸装置使用,该模型主要用来考察本文发展的外形生成方法及数值仿真方法对型号外形基本气动力的模拟能力。
计算条件为:
如前所述,表面非结构网格在双曲网格生成中,生成的体网格在局部凹陷的区域会极度聚集。需要发展更合适的耗散参数感受器来进一步控制网格的质量。因此本文对X38外形进行数值计算时,使用的是混合网格,即在网格表面生成棱柱网格,远场生成四面体网格。
为了说明本文方法生成的附面层网格的优势,将本文方法生成的附面层网格与使用软件NNW-Gridstar生成的附面层网格进行了对比。图22为本文方法生成的X38飞行器附面层网格切面图。图23为Gridstar生成的X38飞行器附面层网格切面图。可以看出在大部分光滑物面,两种方法生成附面层网格都具备良好的正交性。而在机身和机翼之间的凹区域,以及在凹凸关联的区域,Gridstar为了避免棱柱网格相交,在局部停止生成棱柱网格,而本文的方法在这两个区域依然能够生成良好的棱柱网格。换而言之,本文方法生成棱柱网格,从外形表面到附面层网格外缘,每一条“串”上具有相等数量的棱柱网格,这对线隐格式的加速求解具有重要意义。

|
图 22 本文方法生成的X38飞行器附面层网格x切面图 Fig.22 Cut-out view of the prismatic mesh of X38 generated by proposed method |
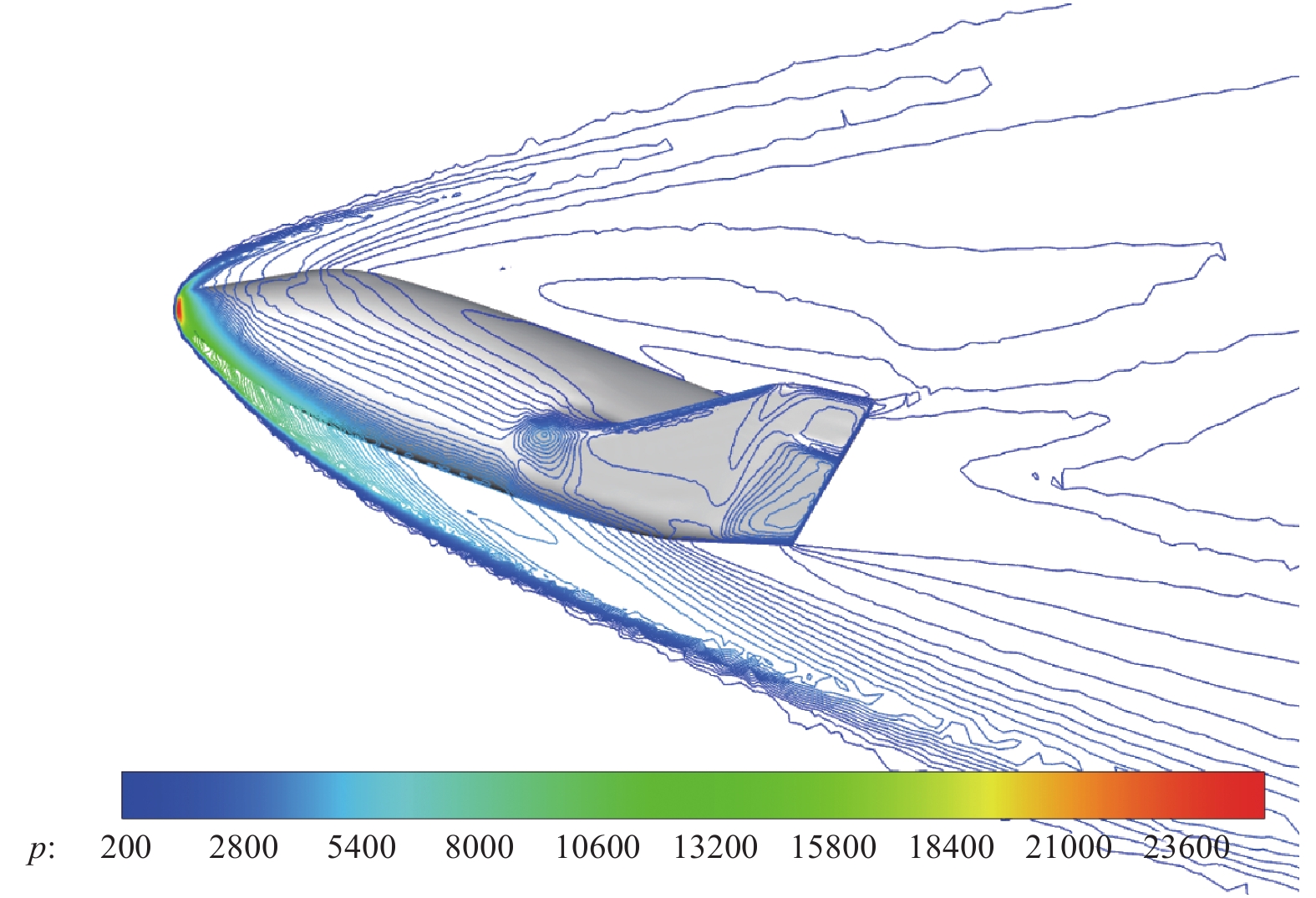
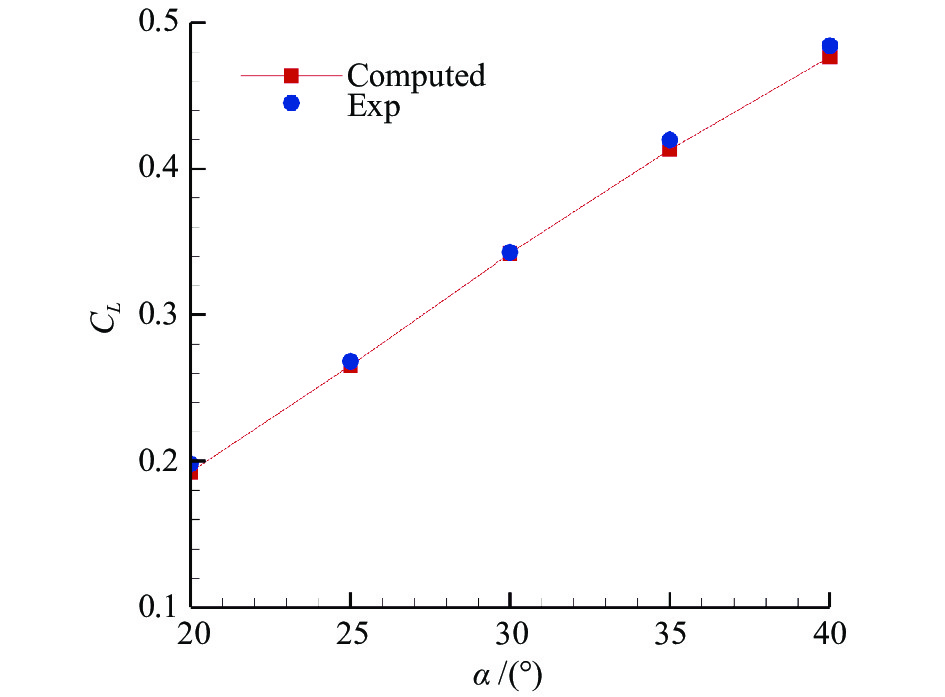
图24为本文计算所采用的混合网格,壁面法向第一层网格雷诺数为10,法向增长率为1.1,棱柱网格共30层。远场为四面体网格。图25为X38在攻角20°时有量纲压力场云图。图26为升力系数随攻角变化计算结果与实验值的对比图,两者符合得比较好。

|
图 23 Gridstar生成的X38飞行器附面层网格x切面图 Fig.23 Cut-out view of the prismatic mesh of X38 generated by Gridstar software |

|
图 24 X38飞行器混合网格z切面图 Fig.24 Cut-out view of the hybrid mesh of X38 |
|
图 25 X38攻角20°有量纲压力场云图 Fig.25 Pressure contour of the X38 at α = 20° |
|
图 26 X38升力系数随攻角的变化曲线 Fig.26 Comparison of experimental and CFD results on lift coefficient with angle of attack |
高超声速飞行器常采用简单组合体外形,相贯双椭球体是其中比较典型的一类,如美国航天飞机头部就具有典型双椭球特征。国内外对此外形开展的风洞实验研究较多,表面热流密度分布及流场内波系变化等实验数据较丰富,因此是研究高超声速大气再入问题的标准算例之一,以此可以考察本文方法生成的网格对相对复杂外形的气动热预测能力。本文对0°攻角的双椭球高超声速绕流进行了数值模拟。
计算条件为:
|
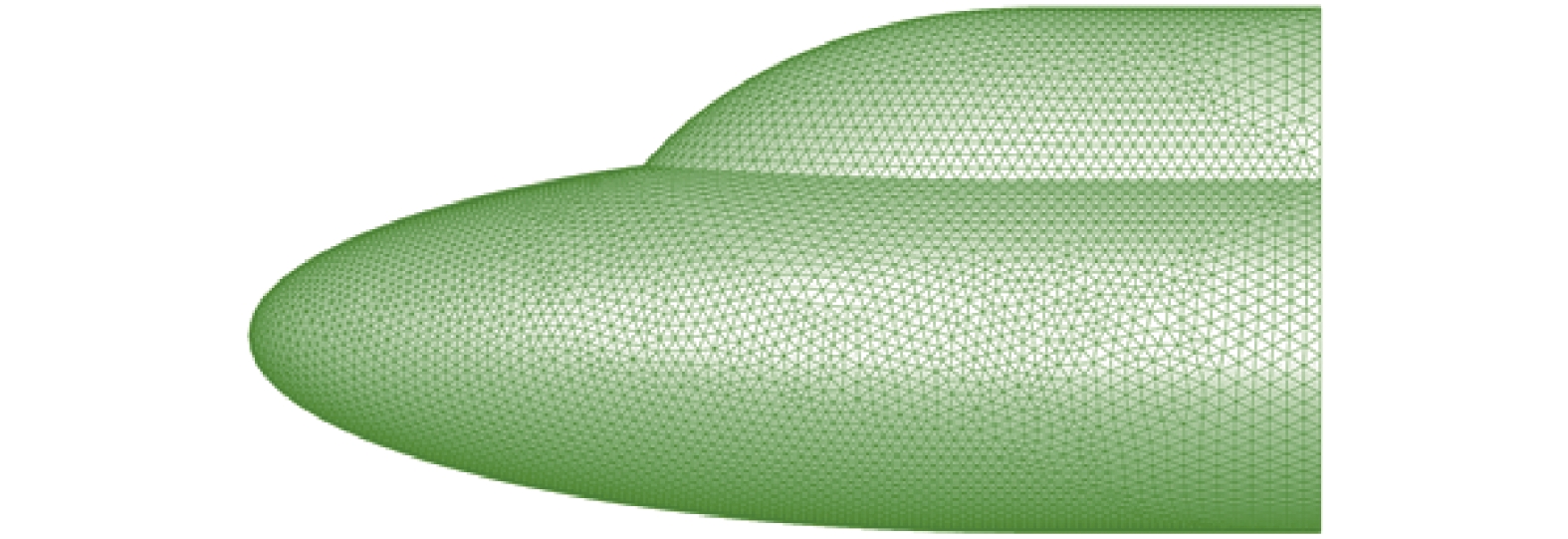
图 27 双椭球表面网格 Fig.27 Surface mesh of the double ellipsoid |

|
图 28 双椭球双曲型网格 Fig.28 3D mesh of the hyperbolic double ellipsoid |

|
图 29 双椭球模型无量纲压力场云图 Fig.29 Pressure contour of the double ellipsoid |
|
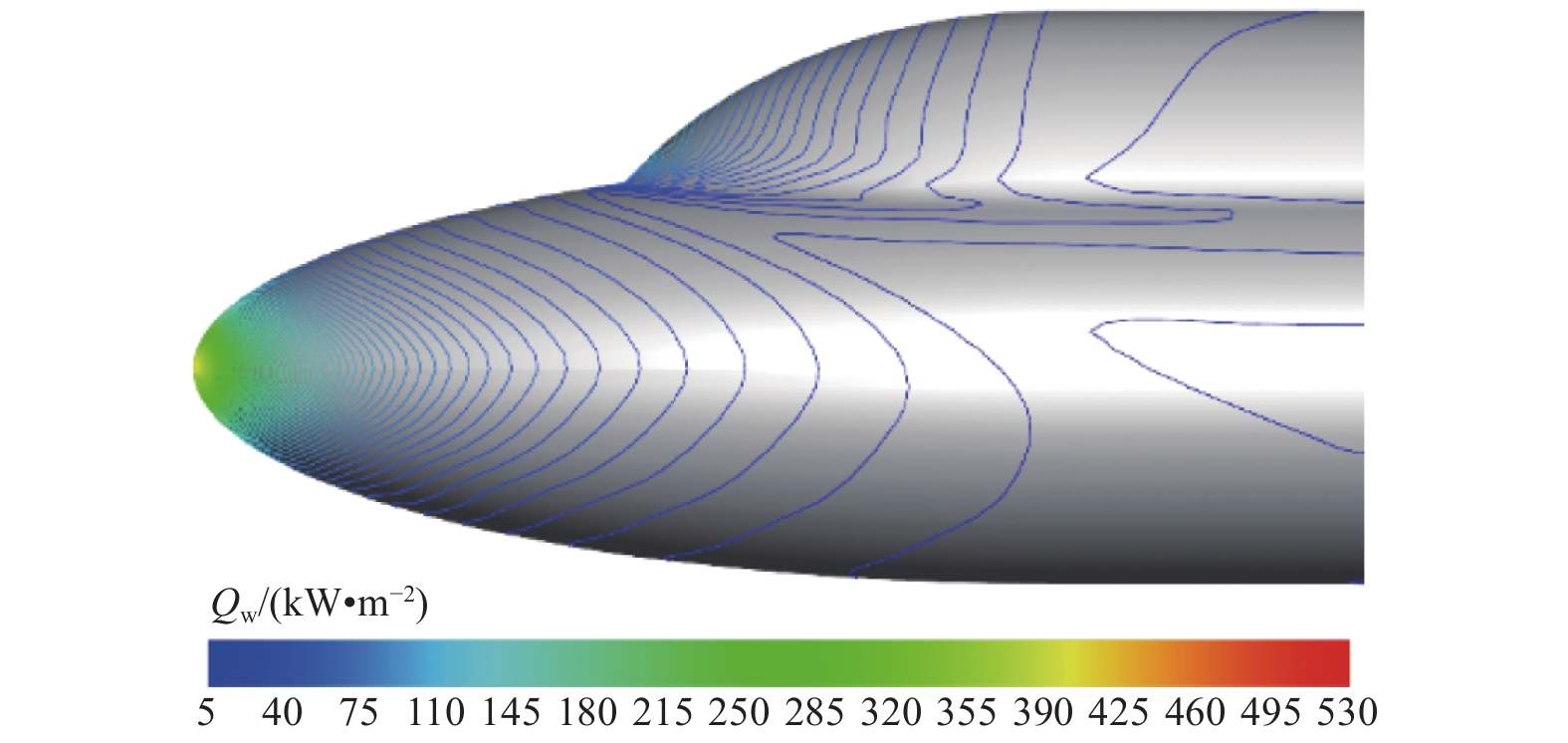
图 30 双椭球模型热流场云图 Fig.30 Heat flux contour of the double ellipsoid |
|
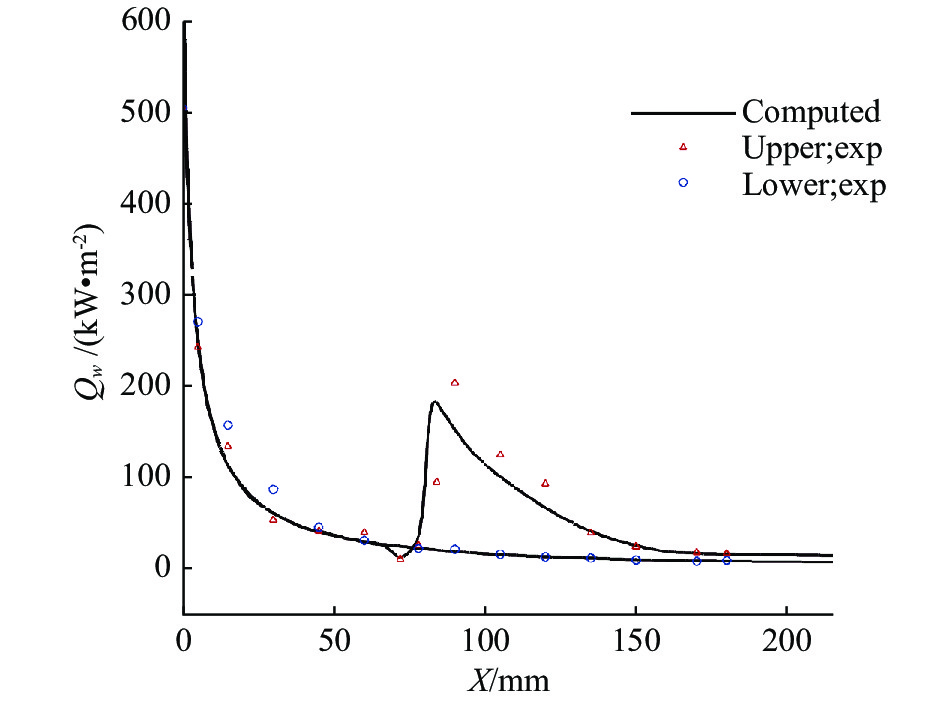
图 31 双椭球中心对称线热流分布 Fig.31 Heat flux distributions of upper and lower symmetric lines |
本文提出了一种基于格点有限体积法的非结构双曲网格生成的方法。建立了基于非结构网格面格点的局部坐标系,以在非结构网格下计算坐标变换导数。通过给控制方程右端添加人工耗散,并利用伪拉普拉斯权进行光顺,很好地控制非结构双曲型网格的自动生成。
本文发展的方法,在光滑的表面上、含有深凹高凸的外形上、含有尖锐边缘外形上,以及真实复杂三维高超声速飞行器外形上,均可自动生成良好的棱柱网格。在复杂外形上,亦可生成附面层网格,远场使用四面体网格。通过对X38外形的气动力数值模拟和对双椭球外形的气动热数值模拟,结果表明本文发展的双曲型网格可以满足高超声速流场气动力热数值仿真的需求。
下一步工作,可在以下方面展开:
1)在每一层推进过程中,发展适用于非结构网格面的椭圆型光顺方法,特别是针对有尖角的三维外形。
2)将本文发展的方法,进一步应用于含三角形、四边形物面网格的空间双曲型网格生成。
3)进一步发展适用于非结构网格的耗散控制感应器,提高双曲网格生成方法在非结构网格生成中的鲁棒性。
4)将双曲非结构网格生成方法与交互的棱柱网格生成算法、空间四面体网格生成算法、低质量网格重构方法或重叠网格技术结合,发展适用于CFD计算的混合网格自动生成技术。
| [1] |
MEAKIN R, WISSINK A, CHAN W, et al. On strand grids for complex flows[C]//18th AIAA Computational Fluid Dynamics Conference, Miami, Florida. Reston, Virigina: AIAA, 2007. doi: 10.2514/6.2007-3834
|
| [2] |
ZHANG L P, ZHAO Z, CHANG X H, et al. A 3D hybrid grid generation technique and a multigrid/parallel algorithm based on anisotropic agglomeration approach[J]. Chinese Journal of Aeronautics, 2013, 26(1): 47-62. DOI:10.1016/j.cja.2012.12.002 |
| [3] |
NAKAHASHI K. External viscous flow computations using prismatic grid[J]. Lecture Notes in Physics, 1970, 414: 280-284. DOI:10.1007/3-540-56394-6_232 |
| [4] |
SETHIAN J A . Level set methods and fast marching methods : Evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science[M]. Cambridge University Press, 1999.
|
| [5] |
DAWES W, HARVEY S, FELLOWS S, et al. Viscous layer meshes from level sets on Cartesian meshes[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2007. AIAA 2007-0555. doi: 10.2514/6.2007-555
|
| [6] |
PARK S, JEONG B, LEE J G, et al. Hybrid grid generation for viscous flow analysis[J]. International Journal for Numerical Methods in Fluids, 2013, 71(7): 891-909. DOI:10.1002/fld.3691 |
| [7] |
WANG Y L. Eikonal equation based front propagation technique and its applications[C]//AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virginia: AIAA, 2009. doi: 10.2514/6.2009-375
|
| [8] |
SIKARA J, MIRANDA R. Boundary integral grid generation technique[C]//3rd Applied Aerodynamics Conference, Colorado Springs, CO. Reston, Virginia: AIAA, 1985. doi: 10.2514/6.1985-4088
|
| [9] |
TAKANASHI S. A simple algorithm for structured-grid generation with application to efficient Navier-Stokes computation[J]. Computers & Fluids, 1991, 19(3-4): 393-399. DOI:10.1016/0045-7930(91)90064-O |
| [10] |
ZHENG Y, XIAO Z F, CHEN J J, et al. Novel methodology for viscous-layer meshing by the boundary element method[J]. AIAA Journal, 2017, 56(1): 209-221. DOI:10.2514/1.J056126 |
| [11] |
孙岩. 交互式棱柱网格生成方法[J]. 计算机辅助设计与图形学学报, 2016, 28(2): 247-254. SUN Y. Interactive prismatic grid generation method[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(2): 247-254. DOI:10.3969/j.issn.1003-9775.2016.02.006 (in Chinese) |
| [12] |
CHAN W M, STEGER J L. Enhancements of a three-dimensional hyperbolic grid generation scheme[J]. Applied Mathematics and Computation, 1992, 51(2-3): 181-205. DOI:10.1016/0096-3003(92)90073-A |
| [13] |
TAI C H, YIN S L, SOONG C Y. A novel hyperbolic grid generation procedure with inherent adaptive dissipation[J]. Journal of Computational Physics, 1995, 116(1): 173-179. DOI:10.1006/jcph.1995.1015 |
| [14] |
STEGER J L. Generation of three dimensional body fitted coordinates using hyperbolic partial differential equations[R]. Defense Technical Information Center, 1984. doi: 10.21236/ada148059
|
| [15] |
MATSUNO K. High-order upwind method for hyperbolic grid generation[J]. Computers & Fluids, 1999, 28(7): 825-851. DOI:10.1016/S0045-7930(98)00054-1 |
| [16] |
MATSUNO K. Hyperbolic upwind method for prismatic grid generation[C]//38th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 2000. doi: 10.2514/6.2000-1003
|
| [17] |
HATCHER A. Algebraic Topology[M]. Cambridge University Press, 2001.
|
| [18] |
KNUPP P M. Winslow smoothing on two-dimensional unstructured meshes[J]. Engineering With Computers, 1999, 15(3): 263-268. DOI:10.1007/s003660050021 |
| [19] |
BALAY S, ABHYANKAR S, ADAMS M, et al. PETSc users manual[R/OL]. https://publications.anl.gov/anlpubs/2017/11/139388.pdf
|
| [20] |
SAAd Y, SCHULTZ M H. GMRES: A generalized minimal residual algorithm for solving non-symmetric linear systems[J]. SIAM Journal on scientific and statistical computing, 1986, 7(3): 856-869. |
| [21] |
ROSSOW C C. A simple flux splitting scheme for compressible flows[R]// NITSCHE W, HEINEMANN H J, HILBIG R, eds. New results in numerical and experimental fluid mechanics II. Notes on Numerical Fluid Mechanics (NNFM), 1999, 72: 355-362. doi: 10.1007/978-3-663-10901-3_46
|
| [22] |
GARIMELLA R V, SHEPHARD M S. Boundary layer mesh generation for viscous flow simulations[J]. International Journal for Numerical Methods in Engineering, 2000, 49(1-2): 193-218. DOI:10.1002/1097-0207(20000910/20)49:1/2<193:AID-NME929>3.0.CO;2-R |
 2022, Vol. 40
2022, Vol. 40