2. 中国工程物理研究院 高性能数值模拟软件中心,北京 100088
2. CAEP Software Center for High Performance Numerical Simulation, Beijing 100088, China
数值模拟前,用户通常先定义CAD模型,然后生成计算网格,最后设置边界条件、材料和求解参数,这一过程被统称为前处理[1]。实际应用中,前处理过程用户交互频繁,易错且耗时长,是数值模拟的主要瓶颈[2],研究前处理自动化算法是解决这一瓶颈的关键,亟待解决的难题包括网格自动生成、模型自动修复和清理等[3-5]。
本文研究由多个部件“组装”而成的装配体模型的自动修复算法。随着软硬件性能的不断提高,以装配体模型为输入的多部件耦合数值模拟已成为发展趋势。相比传统的单部件模拟,这类模拟可以系统性和综合性地考虑不同部件之间的几何物理耦合关系,实现更高精度的数值模拟结果。当装配体模型具有成百上千、乃至更多数目部件时,为降低建模难度,普遍采用分部件建模的方式,导致部件和部件之间的共享区域在不同部件中存在多份几何表征。调用网格生成算法后,共享区域的网格也相应存在多份几何和拓扑上都不兼容的表征,无法在共享区域生成保形的网格,也即不能作为常规数值模拟的输入。
为此,本文提出利用“曲面嵌入”技术消除装配体不同部件交叠部分存在的多重定义。以图1所示两部件装配体为例,若直接在该模型的原始边界表征(如图1(a))上生成网格,曲面1和曲面2的网格不兼容,不符合数值模拟的需要;执行曲面嵌入操作后(如图1(b)),曲面2一分为二,部件2 (Volume2)和部件1 (Volume1)重叠部分直接引用曲面1,其余部分定义为新曲面2(含圆形孔洞的长方形)。显然,曲面嵌入消除了原曲面1和曲面2重叠区域的多重定义,在执行嵌入操作后获得的模型上可生成符合常规数值模拟输入要求的计算网格。

|
图 1 曲面嵌入操作示意 Fig.1 Illustration for surface imprinting operation |
已有曲面嵌入算法分两类:一类基于连续曲面,另一类基于离散曲面。连续曲面类算法其结果几何精度高,但几何计算复杂,数值稳定性差[6-8]。离散曲面类算法几何计算为线性计算,运算速度快,但其结果几何精度较低[9-14]。此外,离散曲面表征只涉及面片相邻等低层拓扑,应用于需高层拓扑支持的操作时,需构造连续曲面模型中常用的边界表征(B-rep)[15]。其中,第一类算法的代表有CADfix[16],其通过人工交互方式在连续B-rep直接进行相关的嵌入操作;第二类算法比较典型的如libigl[17],其提供在离散三角形网格上处理三角形相交的算法,此外,TetWild[18]提供一种通过四面体优化的方法来完成模型嵌入及修复的方法,其本质依然是一种基于离散面片的方法。
在前期研究中,陈建军等[3-4]提出一类将曲面连续表征和离散表征有机融为一体的曲面表征新方法,定义其为曲面的混合表征。本文针对错位装配体中几何重复表征问题,提出基于连续-离散混合曲面造型的装配体模型自动曲面嵌入算法。与前期研究工作[3-4]不同的是,该算法不仅消除曲面间曲线交缠等错误,更进一步消除模型实体间的曲面重叠、相交、错位等错误。
1 算法流程图2给出了本文所提面向错位装配体自动曲面嵌入算法的流程,该算法输入错位的装配体几何模型,输出曲面嵌入后可用于生成计算网格的B-rep几何。

|
图 2 算法流程图 Fig.2 The workflow of the algorithm |
本文所提算法主要包含如下步骤:
1)构建混合曲面表征。建立装配体模型的离散-连续表征数据结构,利用B-rep表征连续曲面模型,采用辐射边表征离散曲面模型,同时维护连续模型和离散模型两者之间的映射关系。
2)离散曲面嵌入。通过检测并计算离散模型上的共享边界区域相交,将边界线段嵌入相关的离散曲面中,进而在离散层面上计算出离散边界相交环图;而后通过拓扑操作移除其他区域的相交,完成在离散曲面嵌入。同时,在嵌入的过程中,同步更新离散-连续曲面表征的映射关系。
3)连续曲面嵌入。根据边界相交图、离散模型嵌入结果及维护的连续-离散映射关系,在自主的几何引擎中设计相应的嵌入、合并操作,自底向上依次完成曲线嵌入、曲面嵌入,生成共享区域表征一致的B-rep。
执行曲面嵌入算法后输出的装配体模型B-rep其不同部件边界曲面交叠部分不再存在多重定义问题,以其为输入,顺序执行单元尺寸计算[19-20]、曲面网格生成[21]和实体网格生成[22-23]等算法,即可最终获得符合通用数值模拟分析的计算网格模型。
2 算法实现本文算法在连续-离散混合曲面表征上进行曲面嵌入操作,需首先建立模型的混合曲面表征:给定CAD模型输入,将CAD模型逐条曲线、逐张曲面离散,继而根据离散模型和CAD模型的对偶关系建立初始的混合曲面表征[3]。
模型的连续-离散混合表征建立后,继而需解决离散模型的几何相交问题及求得边界相交图,同时更新连续曲面模型的B-rep。下文2.1节和2.2节分别介绍上述两个步骤的实现。为方便理解,文中引用图3所示的典型错位装配体展现本文算法各个过程中的处理效果,图3为模型的离散化形式,在曲面0和曲面7处发生重叠导致相交。

|
图 3 典型的错位装配体 Fig.3 Typical misaligned assembly |
本文中,离散模型中端点为B-rep中几何顶点离散对应的网格点,边界线段指代由B-rep中的曲线离散而成的网格边,而三条网格边中一条或者多条为边界线段的三角形被称为边界三角形。
2.1 离散曲面嵌入离散曲面嵌入的目标有两个:一是计算边界相交图;二是移除三角形相交。
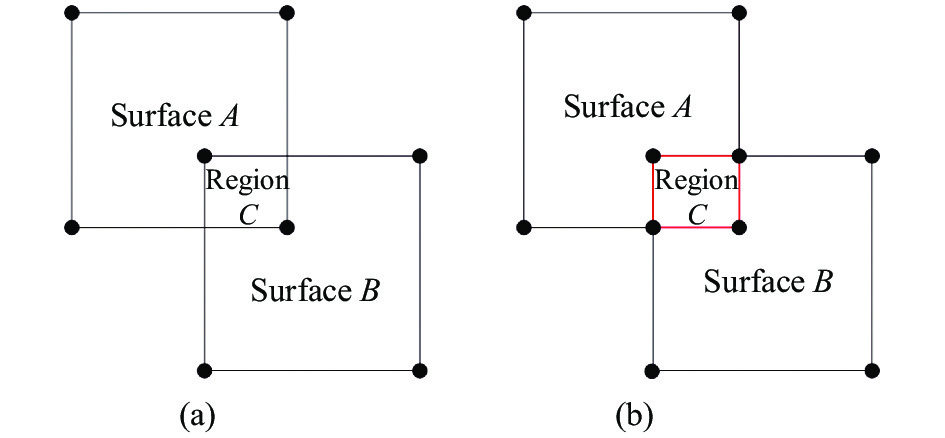
2.1.1 计算边界相交图边界相交图为一个曲面的边界(曲线)与其重叠的曲面求交形成的新的边界环图。如图4(a)所示,曲面A和B重叠于共享区域C,其边界相交图为图4(b),求交得到的交点及曲线形成新区域C的边界。
|
图 4 边界相交图示意 Fig.4 Intersected graph of boundary |
本文嵌入算法通过求解边界线段-三角形处相交以求得离散层面上的边界相交图,计算过程主要包括三个步骤:1)检测三角形相交;2)嵌入边界线段;3)边界线段一致化处理。
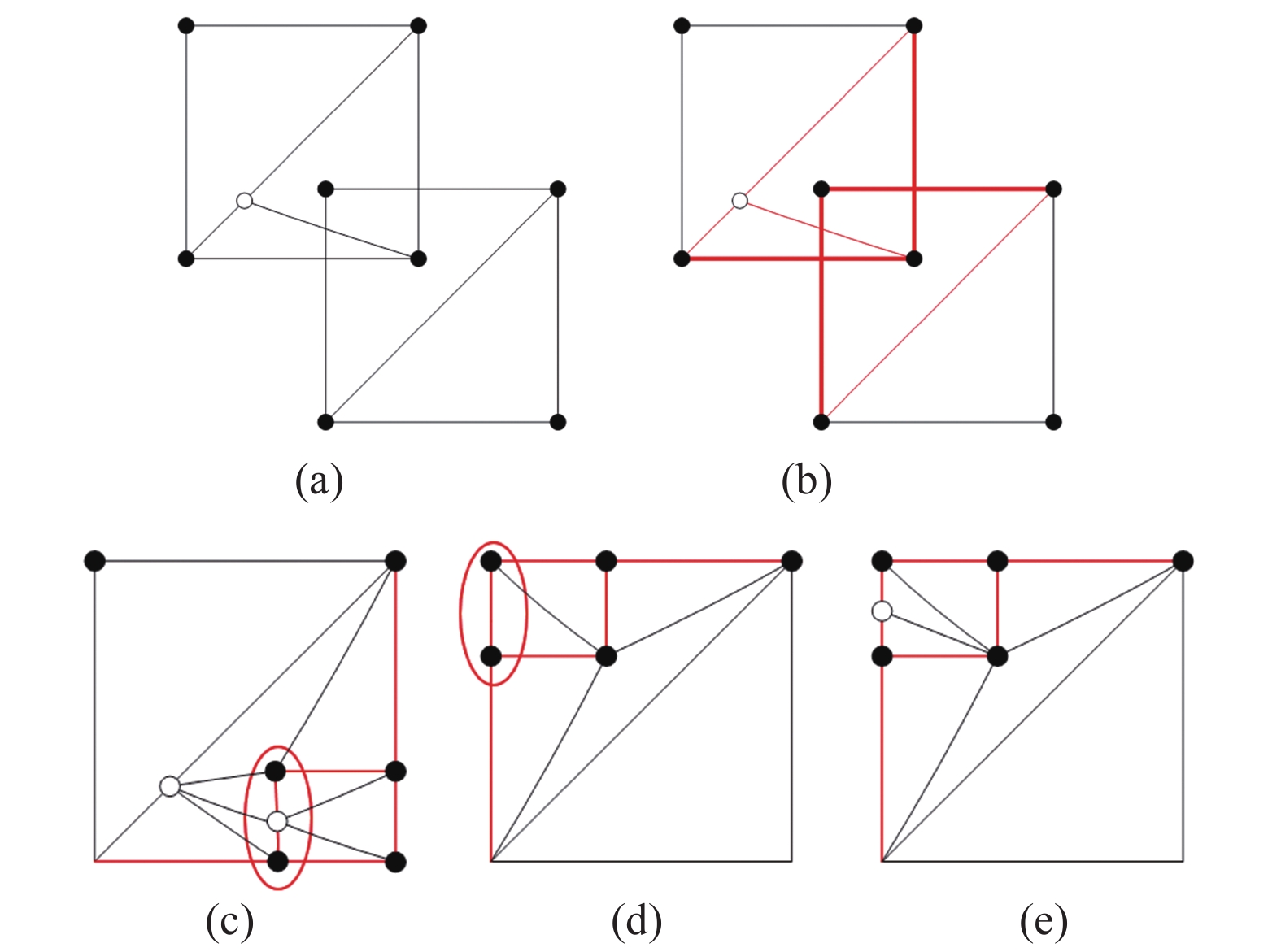
以图4中所示情形为例,详细介绍离散边界相交的计算,图5(a)为该情形的离散表征。
|
图 5 离散边界相交图计算 Fig.5 Computational process of intersection graph |
1)检测相交三角形相交。本文模型中的单个部件间不存在自相交问题,所有的三角形相交都存在于部件与部件的相邻处,所以本文通过计算部件相邻区域处的三角形距离来检测三角形相交。距离计算分为两类:第一类通过精确的三角形相交检测得到距离为零的三角形集合及其对应的曲面索引对;第二类针对相邻部件间在相邻曲面处存在细缝的情况,通过对部件、曲面、对应的面片集合层层进行误差
2)嵌入边界线段。根据相交检测得到相交曲面索引对,提取各自曲面的边界三角形上相交边界线段(图5(b)中红色较粗线段),将曲面B的边界线段通过线段-三角形求交嵌入进曲面A,同样,将曲面A中的边界线段嵌入进曲面B,结果分别如图5(c)和5(d)所示。
3)边界线段一致化处理。在相交曲面索引对中边界线段的嵌入过程中,因嵌入过程各自独立,此过程中可能产生图5(c)和5(d)中边界线段不一致的情形,因此在嵌入过程中需要追踪原始边界线段的分裂状态,在对应的边界线段上插入点使得相交曲面各自的边界线段一致,如图5(e)所示,通过插入点(空心点)得到一致的边界线段。
步骤2中线段-三角形相交计算中具体的相交形式可分类为5种:点点相交、点边相交、点面相交、边边相交、边面相交。除点点相交外,其余4类相交均存在退化情形,如点是边的端点、点是面片的端点、两条边相交于其中一条边的端点、边和面片相交于边或面片的端点等。但是,若按照上文所列顺序依次处理上述相交情形时,相应退化情形会预先得到处理。例如,点边相交的退化情形(点是边的端点)在点点相交时已处理完毕,因此,检测和解除点边相交时只需考虑点对边的投影位于边的中间这一非退化情形。同理,边面相交中,边和面片相交于边或面片的端点,这一退化情形会在点点相交、点边相交或点面相交对应的操作中得到处理;边和面片相交于面片的边界线段这一退化情形,会在边边相交对应的操作中得到处理。因此,在实现相交的检测和解除算法时,只要按顺序处理,就无需考虑退化情形,相应算法的实现得到大幅度简化。这里需要注意的是,处理相交的全过程中,我们需要及时更新和维护对应的混合曲面表征。基于上述思路,表1的算法1给出了处理所列5种相交以获得正确的边界离散曲面拓扑的算法流程。注意,因本文所考虑的输入不存在边界上边面相交情形,算法1并未包含边面相交情形的处理。另外,同一个点可能与多个点、边、面相交,边和面也类似。
| 表 1 算法1线段-三角形相交 Table 1 Algorithm 1 segment-triangle intersections |
|
|
求得离散边界相交图后,在相交曲面的重叠区域形成了一致的边界线段(图5(c、e)),然而在共享区域内部,三角形-三角形相交依然存在。本文在维护好的离散-连续映射关系的辅助下,通过拓扑关系移除共享区域的三角形相交。该拓扑方法避免了实际的三角形-三角形求交计算,也不存在浮点误差范围内面片求交的健壮性问题。移除共享区域的三角形相交在离散层面形成一致的几何表征,不仅可有效辅助后续的连续曲面上的嵌入及合并操作,而且可以将该离散表征直接作为文献[19]中定义尺寸函数的背景网格,与连续B-rep一起作为网格生成的两个完整的输入。
本文通过拓扑方式移除三角形-三角形相交主要分为两步:
1)遍历所有曲面,对单个曲面的三角面片根据边界线段进行“染色”,并根据染色结果进行区域划分。图6(a)和图6(b)分别展示了对图5(c)和图5(e)中三角面片进行区域划分的结果。

|
图 6 移除三角形相交 Fig.6 Removal of triangle-triangle intersections |
2)对相交曲面对中的区域进行拓扑比对,若两个区域拥有相同的边界线段,则该区域视为重叠区域,然后删掉一个区域内的一个三角面片,移除三角形相交,同时更新离散-连续映射关系。如图6所示,通过拓扑对比可得知,区域2与区域3有着相同的边界线段,因此这两个区域为共享区域,图6(c)中删掉了区域3中三角面片,移除了重叠区域的三角形相交。图6(d)为更新后的连续曲面表征示意,区域2处为原始曲面A和B的重叠区域,因此该区域三角面片对应的连续曲面索引为A、B。
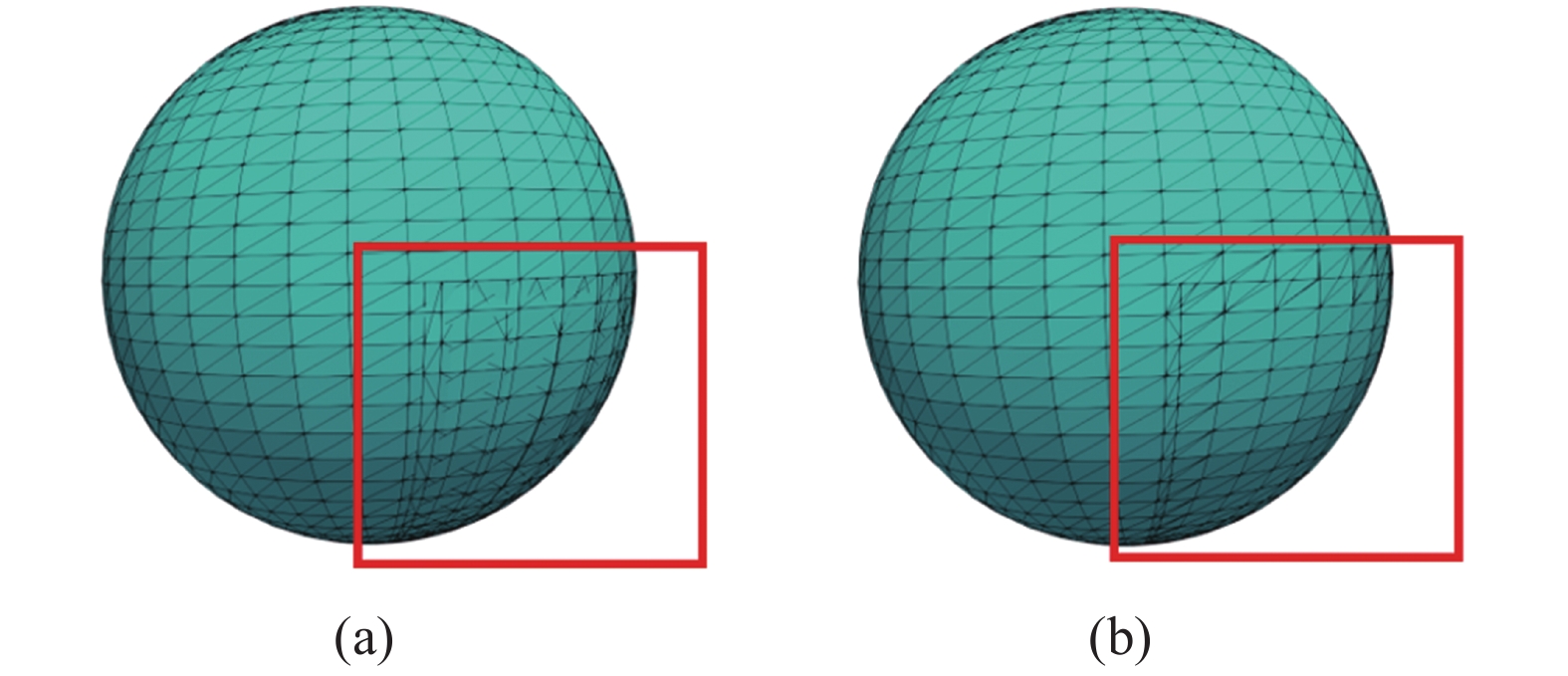
图7展示了图3例子经边界相交图计算和三角形相交移除后,在曲面0和曲面7相交区域的离散结果。图7(b)为嵌入后的结果,该区域三角形相交已被正确移除,曲面0中的边界线段也已成功嵌入新的曲面中。
|
图 7 离散曲面嵌入结果 Fig.7 Results of discrete imprinting |
本文算法意在获取一个完成曲面嵌入的连续B-rep,以支持后续的网格生成算法。离散曲面嵌入完成后,还需在连续B-rep上完成相应的自动曲面嵌入。
连续B-rep的曲面嵌入主要涉及两种基本操作:分裂与合并。其中分裂又分为曲线分裂和曲面分裂;合并分为顶点合并、曲线合并及曲面合并。根据离散曲面嵌入过程中得到的边界相交图及在重叠区域获得的一致的离散表征,在离散-连续映射关系的辅助下,本文设计了相应的分裂及合并操作,自底向上完成连续B-rep的自动曲面嵌入。本文中的连续几何采用文献[1]中具有完全自主知识产权的简化的几何引擎所提供的B-rep表征,其核心为基于Ferguson曲线和Conns曲面的裁剪曲面。本文所设计的分裂与合并操作均为拓扑操作,完全保留曲线/曲面的严格数学表达,故而能够最大程度地保留嵌入过程中的几何精度,也为后续的网格生成提供了精度保证。
2.2.1 分裂操作曲线分裂:对于一条曲线,遍历其对应的边界线段,若其对应的边界线段中包含多于2个端点,则根据这些端点对该曲线进行分裂。如图8(a)所示,曲线1对应的边界线段中包含有3个端点(黑色实心点),因此根据边界线段中间的端点对曲线1进行分裂,得到图8(b)中新的曲线1和曲线2,并同时更新离散-连续映射关系。

|
图 8 曲线分裂过程 Fig.8 Splitting of a curve |
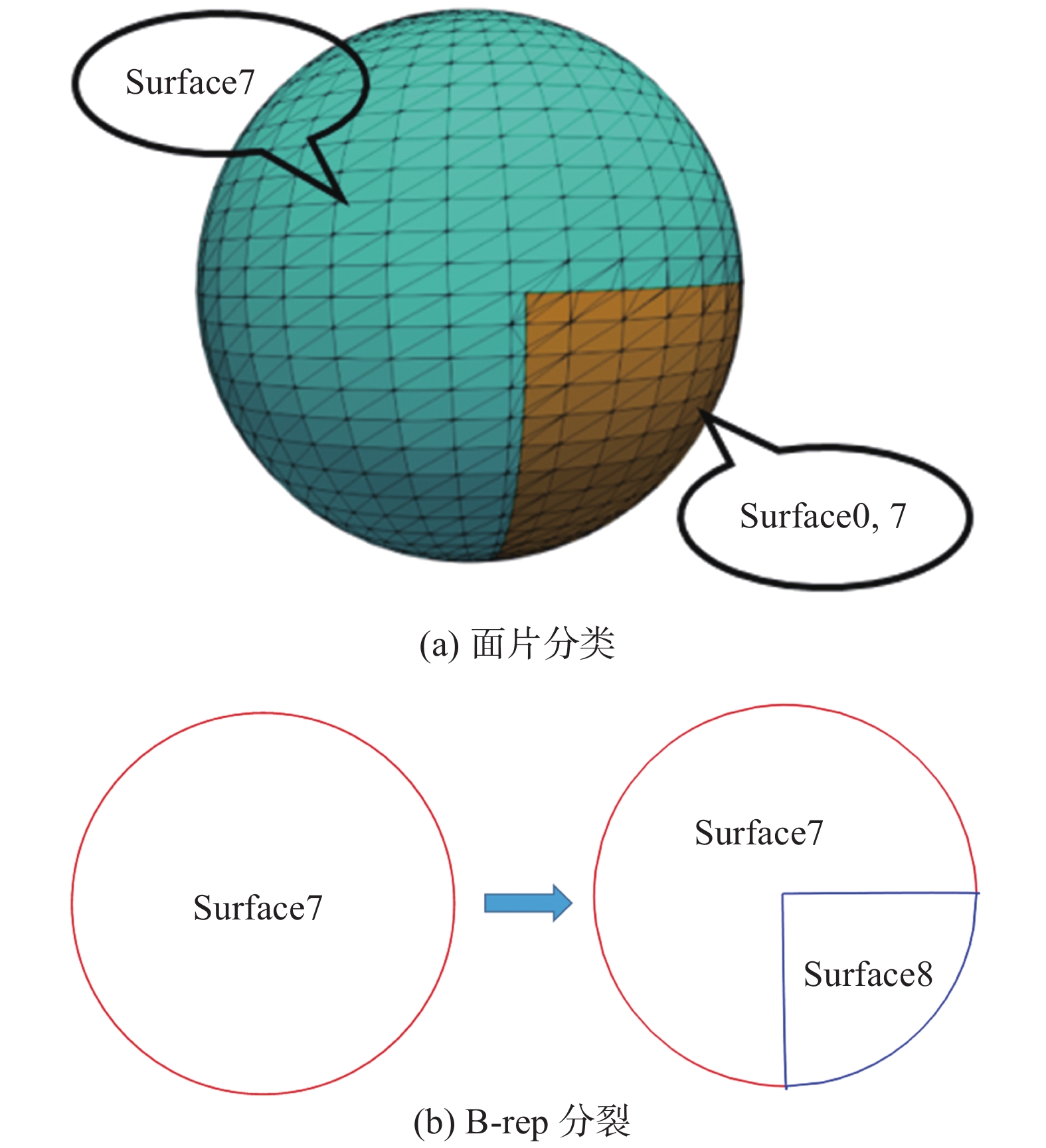
曲面分裂:对于一个曲面,首先对其所对应的三角面片根据其属性(曲面索引)进行分类,若该曲面包含多个种类的三角面片,则根据面片分类结果对该曲面进行分裂。分裂过程中,曲面的支撑曲面保持不变,根据分类的三角面片中包含的边界线段所对应的曲线属性形成新的环,完成曲面的分裂。图9为图3例子在重叠区域的曲面分裂过程,原始曲面7中包含有两种属性的三角面片,分别为属性7和属性0、7,根据不同种类三角面片上边界线段对应的曲线索引,保持支撑曲面不变的情况下形成新的环,分裂为新的曲面7和曲面8,其B-rep如图9(b)所示,并同时更新离散-连续映射关系。
|
图 9 曲面分裂过程 Fig.9 Splitting of a surface |
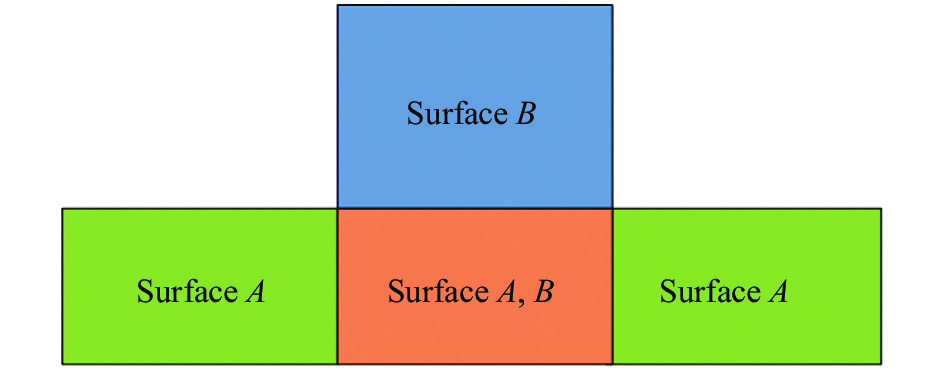
此外,在曲面分裂的过程中可能出现截断的多区域情形,如图10,曲面A和曲面B重叠于曲面AB区域(橙色),在三角面片分类过程中,曲面A中的面片将被分为三部分,共享区域AB和互不连通的两个A区域。鉴于此种情形,本文算法对每一类三角面片进行广度优先遍历(BFS),二次分类互不连通的同一属性的三角面片,之后完成曲面分裂。
|
图 10 多区域情况 Fig.10 Situation of multiple regions |
顶点合并:若多个几何顶点对应同一个端点,则删除多余顶点,只留一个顶点完成顶点合并。
曲线合并:若多条曲线对应同一个边界线段集合,则删掉多余曲线,只留一条曲线完成曲线合并。
曲面合并:若多个曲面对应同一个三角面片集合,则删掉多余曲面,只留一个曲面完成曲面合并。
在分裂及合并的基本操作的辅助下,本文采用自底向上的方法完成自动嵌入。根据表2中的算法2,从低维到高维依次完成顶点的合并、曲线的分裂及合并、曲面的分裂及合并、部件的曲面索引更新,最终完成连续曲面的自动嵌入,得到用于网格生成的连续B-rep模型。
| 表 2 算法2 自底向上自动嵌入 Table 2 Algorithm 2 bottom-up imprinting |
|
|
图11展示了以嵌入后的B-rep作为输入,在其几何上生成的网格结果,以验证本文嵌入方法的有效性。可见曲面0已被正确嵌入进曲面7,并保持了曲面0中的边界线段,生成了一致的保形网格。

|
图 11 网格细节 Fig.11 Details of the generated meshes |
本文选取了某型号火箭、靶球和大坝三个典型装配体CAD模型对算法进行数值验证,其分别包含13个、115个和1 884个部件,模型网格如图12所示。分部件建模获得的模型在不同部件的交界面处存在严重的几何重叠及错位,本文算法正确地消除了这些几何干涉,输出了几何、拓扑一致的模型,并在此模型上生成了高质量的计算网格。

|
图 12 典型的装配体模型 Fig.12 Typical assembly geometry |
图13展示了各模型曲面嵌入及网格生成结果的局部细节。其中,火箭模型中,共检测出1 656处相交,曲面嵌入算法花费时间34 s;靶球模型检测处15 177处相交,曲面嵌入算法花费时间1 047 s;大坝模型中,共检测出35 174处相交,曲面嵌入算法花费时间1 553 s。其中,连续曲面嵌入过程中只涉及到拓扑操作,所耗费时间基本可以忽略(大坝例子所耗时间最多,但亦不足1 s)。

|
图 13 曲面嵌入及网格细节 Fig.13 Details of imprinting and meshes |
本文方法时间花费主要在于离散曲面嵌入中的相交检测及相交处理过程(边界线段嵌入和边界一致化处理)中,表3统计了各个模型中此两个过程中所耗费时间数据。大坝例子中因其最多的部件以及更多的错位情形,其相交检测时间花费占比也最高,约为25%左右,而另外两个例子的占比分别约为6%和7%。
| 表 3 时间统计 Table 3 Statistics of time performance |
|
|
曲面嵌入算法中涉及到曲面的分裂及合并操作,这些操作会引起模型曲面和曲线数量的变化。如图3情形中,将有发生1次分裂、1次合并,则曲面总数不变;如图4情形中则发生2次分裂,1次合并则会导致曲面数量上升。若是曲面完全重复情形,则只发生合并操作,则其导致曲面数量下降。本文中,输入的火箭模型执行曲面嵌入算法后曲面和曲线数量保持不变,仍为124张曲面和248条曲线;靶球模型执行曲面嵌入算法后,曲面数由1 952张曲面和4 739条曲线减少到1 768张曲面和4 464条曲线;大坝模型曲面数由14 322减少到12 861,曲线数由31 676减少到22 029。
以执行曲面嵌入后的CAD模型以及适应模型几何特征与用户参数自动计算的单元尺寸函数为输入,即可生成几何与拓扑正确、单元形态和分布合理的高质量计算网格模型。针对火箭模型,测试中生成的曲面网格包含57 930个三角形单元,实体网格包含102 569个四面体单元;靶球模型的曲面网格和实体网格则分别包含5 146 056和19 542 658个单元;而大坝模型的对应数据为6 294 823和45 620 136个单元。
3.2 对比讨论如引言所述,曲面嵌入可分为直接在连续曲面B-rep上嵌入和在离散三角形网格上进行曲面嵌入,其相应代表有CADfix、libigl及TetWild等。本节中,我们将所提方法与上述程序进行了相关的对比以及讨论。
CADfix所提供的自动嵌入操作不能处理图3中这种部分嵌入的情况,需要通过布尔及分裂等操作完成最后的嵌入,该过程需要手工操作,对于图3所示简单例子可迅速完成,但对于大坝和靶球这种复杂例子,所涉及繁琐的手工操作往往令人难以忍受,因此本文算法的自动化具有明显优势。
libigl提供了一个在浮点误差内比较稳定健壮的三角形相交算法,但无法引入误差,在一些有狭小缝隙的地方无法完成嵌入,当然在相交中引入误差本身是个十分棘手的难题。如图14与之相比,本文通过在边界相交图的计算中引入误差,在曲面内部通过拓扑比较去除三角形相交,即可以正确完成在这些区域的自动嵌入。

|
图 14 本文方法与libigl嵌入对比 Fig.14 Comparison of imprinting between the proposed method and libigl |
TetWild通过四面体优化的方法来完成模型的嵌入及修复功能,并在该过程中引入误差,控制修复的精度,该方法亦可适用于本文所选取模型,但是存在着两个缺陷。其一,TetWild的相交运算是在有理数的辅助下完成的,远比浮点运算速度慢,另外四面体优化迭代过程也耗时较多;其二,TetWild修复仅仅基于离散表征,其网格结果中可能出现“锯齿”现象,使得网格精度降低。表4统计了TetWild和本文算法处理3个模型所耗时间。对比表明,本文算法所耗时间明显小于TetWild,且随着模型规模的增大,本文算法时间优势越来越凸显,对于3个测试样例,TetWild所耗时间是本文算法的2倍以上。
| 表 4 时间对比 Table 4 Comparison of computational time |
|
|
此外,在火箭和大坝模型(误差设置分别为0.5 mm和0.1 mm)中TetWild出现了“锯齿”现象,见图15,而本文算法通过连续-离散的双重表征,嵌入过程中保留了连续几何精确的数学表达而仅仅改变了B-rep的拓扑,严格保证了模型的几何精度。

|
图 15 本文方法与TetWild在“锯齿”处对比 Fig.15 Comparison between the proposed method and TetWild in zigzag region |
本文针对错位装配体在部件间重叠区域的多份表征问题,应用连续-离散混合曲面造型方法,开发了适用于分部件建模获得的装配体模型的自动曲面嵌入算法。在离散曲面上,通过引入误差计算边界线段-三角形相交以求得边界相交图,而后通过拓扑操作移除其余三角形相交问题,完成离散曲面嵌入;之后根据边界相交图及离散嵌入结果,在简化的几何引擎上设计了相应的曲线曲面分裂合并等操作,并在离散-连续映射关系的辅助下自动完成连续曲面B-rep上的自动曲面嵌入。在典型算例下用嵌入后的B-rep为输入,以其网格生成结果验证了该自动曲面嵌入算法的有效性。通过与其他嵌入方法的对比,展示了本文算法在自动化程度、嵌入有效性、精度保证及时间上的优势。本文算法的主要优点有:
1)曲面嵌入中的几何计算基于线性的离散模型,通过线段-三角形相交计算边界相交图,并运用拓扑比对移除三角形相交;
2)在离散-连续曲面的映射关系辅助下,根据边界相交图,在模型B-rep上完成嵌入和合并操作,该过程不更改模型B-rep的数学表达而只改变其拓扑,可有效保证嵌入后模型的几何精度;
3)保证修复后装配体模型B-rep的正确性和一致性,可直接复用已有的基于B-rep的主流曲面网格生成算法,生成保形的曲面网格。
本文算法目前尚不支持部件间互相贯穿的情形,在后续的工作中我们将尝试在B-rep上设置约束条件以处理贯穿情形下的曲面嵌入。
| [1] |
郑耀, 陈建军. 非结构网格生成: 理论、算法和应用[M]. 北京: 科学出版社, 2016. ZHENG Y, CHEN J. Unstructured mesh generation: theories, algorithms and applications[M]. Beijing: Science Press, 2016. |
| [2] |
HALPERN M. Industrial requirements and practices in finite element meshing: A survey of trends[C]// Proceedings of 6th International Meshing Roundtable, Sandia National Laboratories, October 1997: 399-411.
|
| [3] |
CHEN J J, CAO B W, ZHENG Y, et al. Automatic surface repairing, defeaturing and meshing algorithms based on an extended B-rep[J]. Advances in Engineering Software, 2015, 86: 55-69. DOI:10.1016/j.advengsoft.2015.04.004 |
| [4] |
曹秉万, 陈建军, 郑耀, 等. 面向混合曲面模型的自动拓扑生成算法[J]. 浙江大学学报(工学版), 2014, 48(5): 923-933. CAO B W, CHEN J J, ZHENG Y, et al. Automatic topology generation algorithm for hybrid surface models[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(5): 923-933. (in Chinese) |
| [5] |
曹秉万, 赵大伟, 陈建军, 等. 面向组合参数曲面扩展B-rep的特征简化和网格生成算法[J]. 计算机辅助设计与图形学学报, 2014, 26(1): 10-19. CAO B W, ZHAO D W, CHEN J J, et al. Defeaturing and meshing algorithms for extended B-rep of composite parametric surfaces[J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(1): 10-19. (in Chinese) |
| [6] |
CLARK B W. Removing small features with real CAD operations[C]// Proceedings of the 16th International Meshing Roundtable 2008: 183-198. doi: 10.1007/978-3-540-75103-8_11.
|
| [7] |
NOËL F. Global parameterization of a topological surface defined as a collection of trimmed bi-parametric patches: Application to automatic mesh construction[J]. International Journal for Numerical Methods in Engineering, 2002, 54(7): 965-986. DOI:10.1002/nme.454 |
| [8] |
DASSAULT SYSTEMES. ACIS[CP]. http://www.spatial.com
|
| [9] |
QUADROS W R, OWEN S J. Defeaturing CAD models using a geometry-based size field and facet-based reduction operators[C]//Proceedings of the 18th International Meshing Roundtable, 2009: 301-318. doi: 10.1007/978-3-642-04319-2_18
|
| [10] |
PATEL P S, MARCUM D L. Robust and efficient CAD topology generation using adaptive tolerances[J]. International Journal for Numerical Methods in Engineering, 2008, 75(3): 355-378. DOI:10.1002/nme.2263 |
| [11] |
PATEL P S, MARCUM D L, REMOTIGUE M G. Automatic CAD model topology generation[J]. International Journal for Numerical Methods in Fluids, 2006, 52(8): 823-841. DOI:10.1002/fld.1166 |
| [12] |
LAIDLAW D H, TRUMBORE W B, HUGHES J F. Constructive solid geometry for polyhedral objects[J]. ACM SIGGRAPH Computer Graphics, 1986, 20(4): 161-170. DOI:10.1145/15886.15904 |
| [13] |
MCLAURIN D, MARCUM D, REMOTIGUE M, et al. Repairing unstructured triangular mesh intersections[J]. International Journal for Numerical Methods in Engineering, 2013, 93(3): 266-275. DOI:10.1002/nme.4385 |
| [14] |
WHITE D R, SAIGAL S, OWEN S J. An imprint and merge algorithm incorporating geometric tolerances for conformal meshing of misaligned assemblies[J]. International Journal for Numerical Methods in Engineering, 2004, 59(14): 1839-1860. DOI:10.1002/nme.937 |
| [15] |
HAMRI O, DE LÉON J C, GIANNINI F, et al. Software environment for CAD/CAE integration[J]. Advances in Engineering Software, 2010, 41(10-11): 1211-1222. DOI:10.1016/j.advengsoft.2010.07.003 |
| [16] |
A WIPRO COMPANY. CADfix[CP]. https://www.cadfix.com
|
| [17] |
libig[CP]. https://libigl.github.io
|
| [18] |
HU Y X, ZHOU Q N, GAO X F, et al. Tetrahedral meshing in the wild[J]. ACM Transactions on Graphics, 2018, 37(4): 1-14. DOI:10.1145/3197517.3201353 |
| [19] |
CHEN J J, XIAO Z F, ZHENG Y, et al. Automatic sizing functions for unstructured surface mesh generation[J]. International Journal for Numerical Methods in Engineering, 2017, 109(4): 577-608. DOI:10.1002/nme.5298 |
| [20] |
CHEN J J, LIU Z W, ZHENG Y, et al. Automatic sizing functions for 3D unstructured mesh generation[J]. Procedia Engineering, 2017, 203: 245-257. DOI:10.1016/j.proeng.2017.09.804 |
| [21] |
ZHAO D W, CHEN J J, ZHENG Y, et al. Fine-grained parallel algorithm for unstructured surface mesh generation[J]. Computers & Structures, 2015, 154: 177-191. DOI:10.1016/j.compstruc.2015.04.004 |
| [22] |
CHEN J J, ZHENG J J, ZHENG Y, et al. Improved boundary constrained tetrahedral mesh generation by shell transformation[J]. Applied Mathematical Modelling, 2017, 51: 764-790. DOI:10.1016/j.apm.2017.07.011 |
| [23] |
CHEN J J, ZHAO D W, HUANG Z G, et al. Three-dimensional constrained boundary recovery with an enhanced Steiner point suppression procedure[J]. Computers & Structures, 2011, 89(5-6): 455-466. |
 2022, Vol. 40
2022, Vol. 40


