动网格生成技术是指网格做相应调整以适应模拟过程中计算区域的改变,是计算流体力学模拟运动界面流动问题的主要瓶颈之一。动网格方法在气动外形优化设计、流固耦合模拟和气动弹性计算等领域有着广泛的应用。为提升计算精度和结果可靠性,亟需一种高效健壮的动网格方法重新生成或移动网格以满足计算域的变化。第一种方法是直接在各时间步内重构整体或局部的计算网格,但复杂区域的网格生成十分耗时,且新旧网格间的插值传递会引入额外的误差[1]。第二种方法只变化网格节点坐标,但不改变连接关系,从而避免流场的插值传递,并能处理各种类型的网格单元,因此得到了广泛使用,但这种方法很难直接用于多体分离等大尺度运动问题。
在上述第二种方法中,超限插值法(transfinite interpolation,TFI)按网格方向顺序根据边界点与内部点的相对位置更新网格,该方法快速有效但只适用于结构网格[2]。对于没有规则方向的非结构网格运动,一般采用以下两类方法:第一类将网格边类比为弹簧[3]或弹性实体[4],根据网格拓扑构建力平衡系统,因此需反复求解规模为网格节点数目的线性方程组,计算成本很大。第二类只基于与边界点的距离计算各网格内部点的新坐标,由于计算量少且易于并行,近年来得到了广泛应用。基于Delaunay背景网格的插值方法先建立计算网格节点与背景单元的映射关系,边界运动后网格节点即可根据相应背景单元的边界点快速计算得到新坐标[5-7]。该方法效率较高且能推广至三维空间,但目前还只能用于凸区域的网格运动。逆距加权插值法(inverse distance weighting,IDW)通过显式函数移动网格内点,不需要求解隐式方程,但对于不同的运动形式和边界类型需采用不同的指数函数,健壮性较差[8-11]。径向基函数插值法(radial basis function,RBF)根据边界点坐标和运动位移拟合一个径向基函数来表示整个计算域内网格点位移的分布。由此需求解一个规模为边界点数目的线性方程组得到函数的待定系数[12]。为进一步提高其计算效率,可只选择部分边界点作为控制点来计算分布函数。主要思路是基于贪心思想,给定初始的控制点集合,由此得到拟合函数后计算剩余边界点的位移,然后再与其已知位移比较并将差异最大的若干个边界点加入该控制点集合,继而继续迭代直至满足设置的误差条件[13-14]。这种方法能够大幅度降低动网格的计算和存储成本,因此被广泛应用于各类问题。
IDW方法和RBF方法最初都是加权处理所有边界点对各内部点的影响,因此效率相对较低。而Delaunay背景网格插值法只基于背景单元的几个边界点影响相应内部点,变形能力又相对较弱。近年来,也出现了一些结合背景网格方法与IDW方法或RBF方法的研究[11,15],主要思路是先将IDW或RBF方法用于稀疏的背景网格运动变形,然后也维持计算网格节点与背景网格单元的相对位置不变,从而插值计算出网格节点的新坐标。该方法综合了两类算法的优点,但需要另外再生成一套计算域的稀疏背景网格。基于插值或拟合函数,尝试选择部分边界点与所有内部点、甚至不同边界点与不同内部点建立相应映射关系,从而优化和加速动网格方法,这是一个值得继续研究的方向。
本文基于上述思想,进一步放宽贪心选点的径向基函数插值法的约束条件,提出并完善了一种基于支持向量回归(support vector regression,SVR)的动网格方法,该方法将贪心选点的插值问题转化为自适应选点的优化问题。在前期的工作中,已初步基于高斯核函数与贪心RBF方法进行了对比,在保持网格运动健壮性的同时SVR方法具有更高的计算效率。本文进一步通过系统性测试分析,以高斯核函数的SVR方法为基准,针对SVR动网格方法给出了几个性质良好的核函数及其参数设置策略,并在若干典型二维/三维动网格案例上进行了成功应用,进一步优化和完善了SVR动网格算法。
1 方法描述 1.1 贪心选点RBF方法约束条件的放宽RBF动网格方法在各坐标方向分别采用一个RBF函数,以描述整个计算域内任意点在该方向将要移动的位移量,一般的表达形式如下:
| $ g\left( {\boldsymbol{x}} \right) = \sum\limits_{i = 1}^{{N_b}} {{\alpha _i}} \phi \left( {\left\| {{\boldsymbol{x}} - {{\boldsymbol{x}}_i}} \right\|} \right) $ | (1) |
其中,
| $ {d_i} = g\left( {{{\boldsymbol{x}}_i}} \right) $ | (2) |
将针对所有边界点的方程(2)联立形成方程组,有:
| $ D = \varPhi \alpha $ | (3) |
其中:
| $ D = \left( {\begin{array}{*{20}{c}} {{d_1}} \\ {{d_2}} \\ \vdots \\ {{d_{{N_b}}}} \end{array}} \right),\alpha = \left( {\begin{array}{*{20}{c}} {{\alpha _1}} \\ {{\alpha _2}} \\ \vdots \\ {{\alpha _{{N_b}}}} \end{array}} \right) $ | (4) |
| $ \varPhi = \left( {\begin{array}{*{20}{c}} {{\phi _{11}}}&{{\phi _{12}}}& \cdots &{{\phi _{1{N_b}}}} \\ {{\phi _{21}}}&{{\phi _{22}}}& \cdots &{{\phi _{2{N_b}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{\phi _{{N_b}1}}}&{{\phi _{{N_b}2}}}& \cdots &{{\phi _{{N_b}{N_b}}}} \end{array}} \right),{\phi _{ij}} = \phi \left( {\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|} \right) $ | (5) |
求解上述线性方程组确定RBF函数的系数后,从而得到了网格的运动函数。
为进一步提高RBF方法在求解大规模问题时的计算效率,贪心选点的思想是逐次新增若干边界点作为控制点,由此重新计算得到RBF插值函数,最终将其他非控制点的边界点位移量误差控制在一定范围内,从而减少待求方程组的规模。其数学内涵可以描述如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{d_i} = g\left( {{{\boldsymbol{x}}_i}} \right)},&{i \in \{ {N_b^{'}} \}} \\ {\left| {{d_i} - g\left( {{{\boldsymbol{x}}_i}} \right)} \right| \leqslant \varepsilon },&{i \in \{ {{N_b}} \} - \{ {N_b^{'}} \}} \end{array}} \right. $ | (6) |
其中,
若进一步将公式(6)的约束条件放宽,使得对所有边界点都允许计算得到的位移与已知位移存在一定误差,即:
| $ \begin{array}{*{20}{c}} {\left| {{d_i} - g\left( {{{\boldsymbol{x}}_i}} \right)} \right| \leqslant \varepsilon },&{i \in \left\{ {{N_b}} \right\}} \end{array} $ | (7) |
并在此基础上求解某个最值问题,则将贪心选点的RBF插值方法转换成了一个约束优化问题。而支持向量回归模型正是解决这类问题的高效方法,且其回归函数的表达形式也是由若干径向基函数线性组合而成。因此,完全可以尝试采用支持向量回归作为网格运动的位移分布函数。
1.2 支持向量回归支持向量回归的机器学习方法发展于统计学习的理论,提出近三十年来已广泛应用于诸多领域的模式识别、分类以及回归分析。如人脸识别、文本分类以及复杂工程分析的近似等[16-18]。SVR的核心原理是基于一个非线性核函数将样本空间映射到高维特征空间,并将原问题转化为在此高维空间求解一个线性拟合问题[19]。基于支持向量的概念,SVR所得到的拟合函数即要求所有样本点都落在给定的误差范围内,并使得函数在特征空间的斜率达到最小。
将SVR应用于求解网格运动时,本文提出的方法把所有边界点坐标及其某一坐标方向的已知位移量作为训练样本集,令其为:
| $ {\boldsymbol{T}} = \left\{ {\left( {{{\boldsymbol{x}}_1},{d_1}} \right),\left( {{{\boldsymbol{x}}_2},{d_2}} \right), \cdots ,\left( {{{\boldsymbol{x}}_{{N_b}}},{d_{{N_b}}}} \right)} \right\} \subset \aleph \times \Re $ | (8) |
其中
| $ \min \dfrac{1}{2}{\left\| \omega \right\|^2}\;\;{\text{ s}}{\text{.t}}{\text{. }}\begin{array}{*{20}{c}} {\left| {{d_i} - f\left( {{{\boldsymbol{x}}_i}} \right)} \right| \leqslant \varepsilon },&{i \in \left\{ {{N_b}} \right\}} \end{array} $ | (9) |
其中假设线性情况下的拟合函数为:
| $ f\left( {\boldsymbol{x}} \right) = \left\langle {\omega ,{\boldsymbol{x}}} \right\rangle + b, \omega \in \aleph ,b \in \Re $ | (10) |
如图1所示的样本集拟合函数,所有训练样本点都落在函数向两侧平移
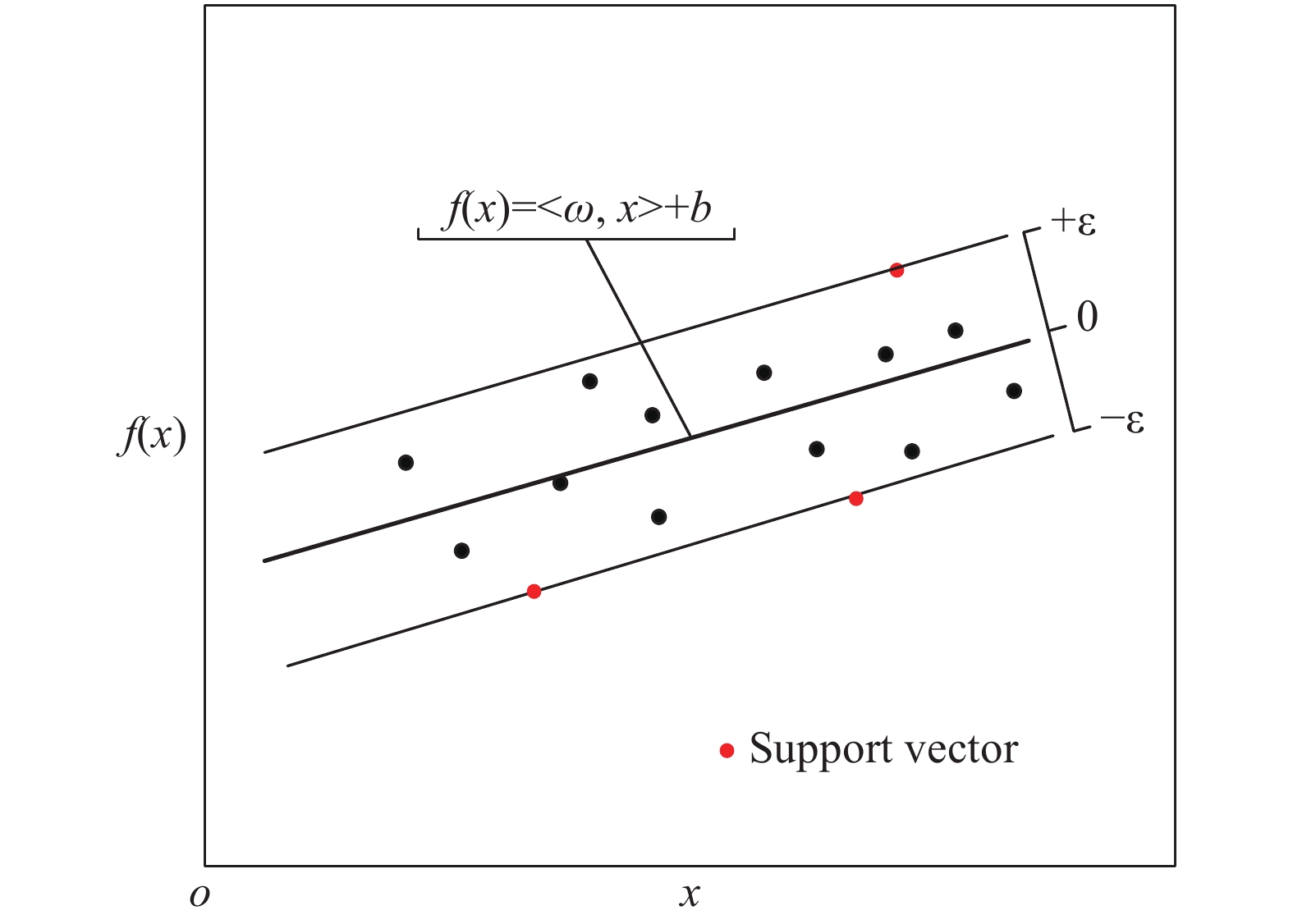
|
图 1 SVR在样本空间的示意图 Fig.1 Schematic of SVR in the sample space |
公式(9)的二次规划问题一般采用拉格朗日乘数法(Lagrange Multiplier)转化为对偶问题再更有效地求解。对偶后的函数可表示为如下形式:
| $ f\left( {\boldsymbol{x}} \right) = \sum\limits_{i = 1}^{{N_b}} {{\beta _i}\left\langle {{\boldsymbol{x}},{{\boldsymbol{x}}_i}} \right\rangle } + b $ | (11) |
此外,采用非线性核函数
| $ f\left( {\boldsymbol{x}} \right) = \sum\limits_{i = 1}^{{N_b}} {{\beta _i}k\left( {{\boldsymbol{x}},{{\boldsymbol{x}}_i}} \right)} + b $ | (12) |
关于支持向量回归对偶转化和非线性扩展更详细的推导,可参阅文献[21]。
1.3 SVR针对网格运动的适配针对网格运动,本方法与贪心选点的RBF插值法类似,也需要寻找合适的核函数
对于SVR方法的误差阈值
| $ \varepsilon = \lambda \frac{{{\Delta _{\min }}}}{s}\;\;{\text{ s}}{\text{.t}}{\text{. }}\;\;0 < \lambda \leqslant 1 $ | (13) |
在此基础上,误差阈值
通常而言,一般的SVR应用会采用归一化方法将样本各个维度的数据缩放至[0, 1]范围内。由于网格坐标各维度采用同一度量单位,且归一化还会降低数据的精度,因此针对网格运动不需要进行这一操作。除此之外,因为所有网格边界点都是有效数据,并且边界在运动形变中通常是连续的,故而不存在所谓的噪声数据,也就无需在算法模型中采取松弛变量处理例外[18]。
最后,针对SVR动网格方法对应的特殊二次规划问题,可采用序列最小最优化(sequential minimal optimization,SMO)算法[22]进行高效求解。SMO算法是在每次迭代中只选择两个变量而令其他为常数,从而将原问题分解为若干尽可能小的二次规划问题,再采用解析方法直接求解。因此在每个时间步内进行大规模网格运动时,相对于迭代求解规模递增方程组的贪心选点RBF方法,SVR方法有着很大的效率优势。此外,SMO算法从训练样本集全局考虑,自适应选择最合适的边界点作为支持向量,且无需选择若干边界点作为初始的控制点集合,进一步减少了人工干预。
2 基准测试SVR动网格方法总体分为两步,一是利用已知位移的边界点建立SVR模型,二是利用该模型预测计算内部点的位移。其中模型建立的时间开销通常更大,且直接决定第二步的网格质量,因此本节主要关注第一步的计算效率和对边界点位移值的拟合效果。对于内部点运动后的最终网格质量评估将在第3节通过案例应用测试分析。
2.1 测试案例设计为测试不同核函数针对网格边界运动规律的拟合能力、计算效率以及不同疏密网格下的健壮性,设计如图2所示的三套不同密度的二维笛卡尔网格。这些网格x、y方向的坐标范围为[−2, 2],z方向坐标为0,网格单元数分别为
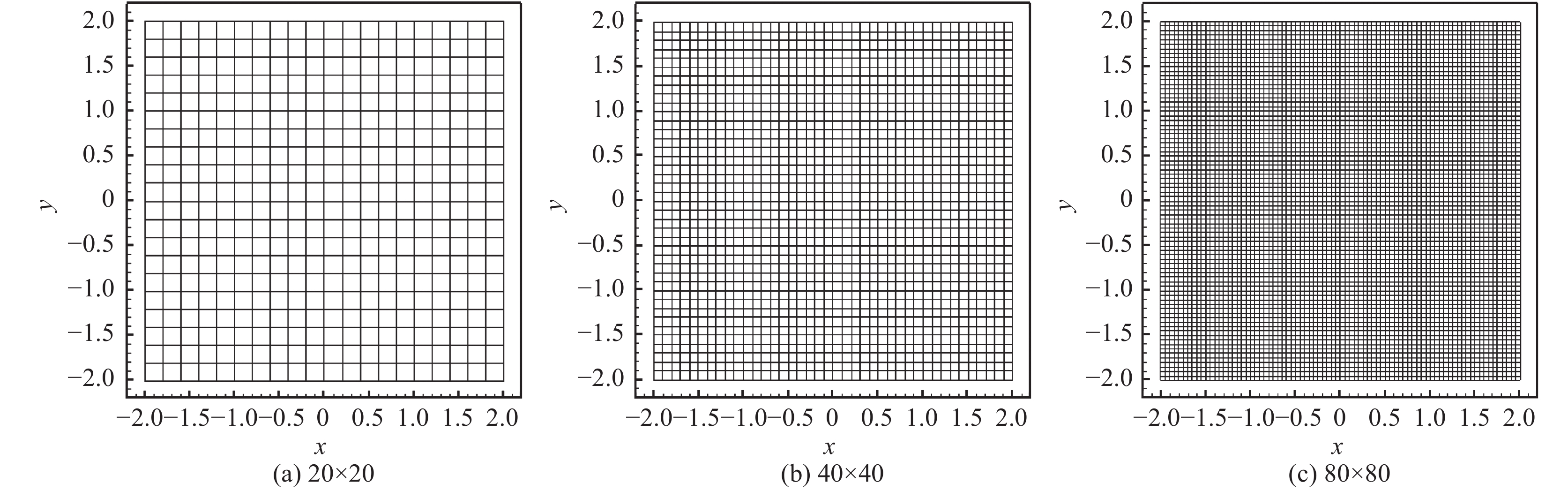
|
图 2 三套不同密度的二维笛卡尔网格 Fig.2 Three 2D Cartesian grids with different mesh densities |
在实际动网格案例中SVR方法是分别在三个方向独立建模,因此研究其拟合能力时只需针对某一方向测试即可。根据不同类型的网格运动,本节采用四个相对复杂的解析函数指导测试网格在z方向的变形,其z坐标的位移值等于用该点坐标代入相应函数所得。正值表示网格点沿z轴正向运动,负值表示沿z轴反向运动。4个运动函数如下:
| $ \begin{split}& F1(x,y) = {x^2} - {y^2} \\& F2(x,y) = 0.9\sqrt {{x^2} + {y^2}} + 0.3\cos \left( {{\text{9}}\sqrt {{x^2} + {y^2}} } \right) \\& F3(x,y) = 0.6\cos (4x)\sin (4y) \\& F4(x,y) = \frac{{3\sin \left( {4\sqrt {{x^2} + {y^2}} + 2.4} \right)}}{{4\sqrt {{x^2} + {y^2}} + 2.4}} \end{split} $ | (14) |
变形后的网格如图3所示,经F1
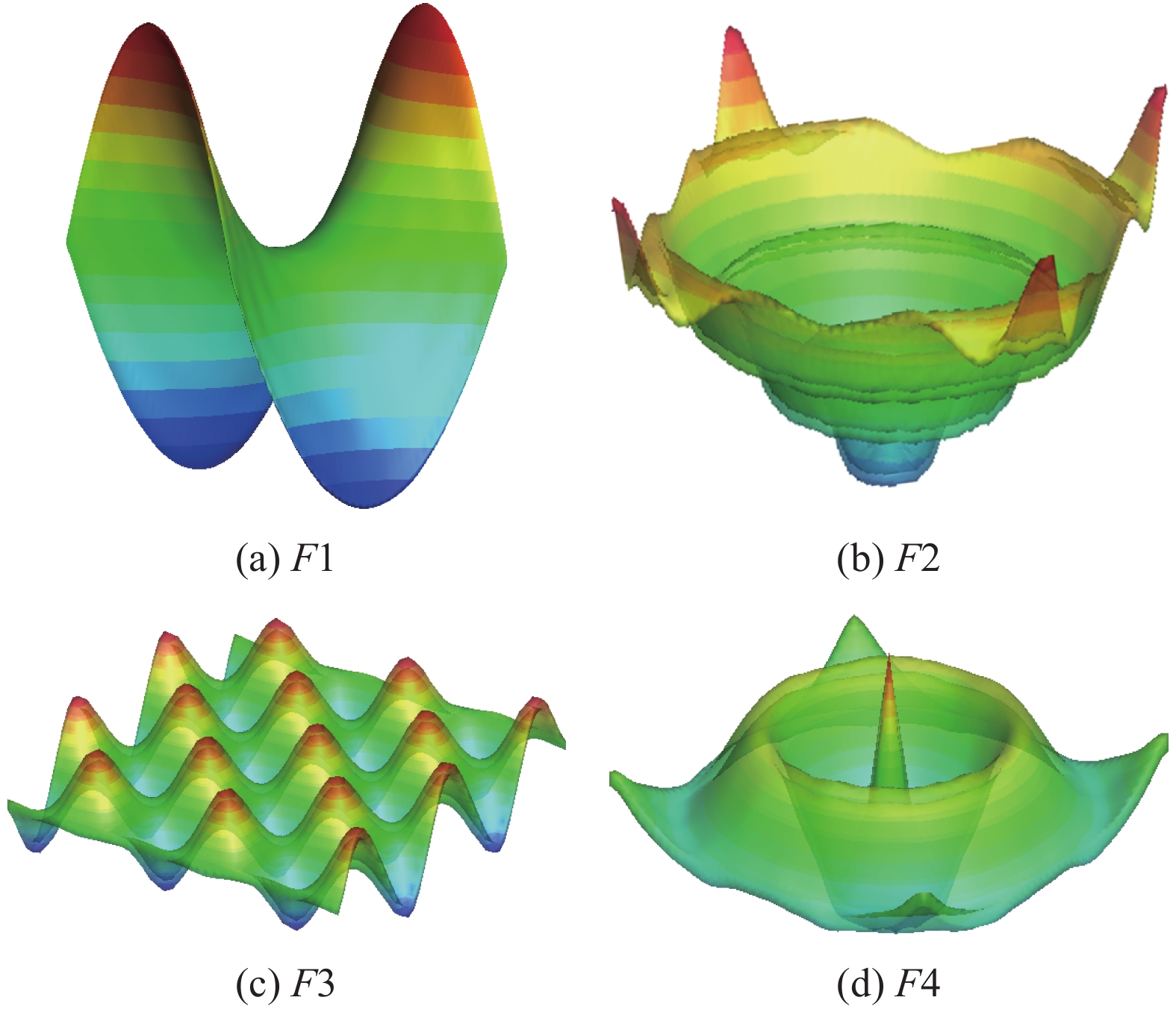
|
图 3 四种运动函数对应变形后的网格 Fig.3 Deformed grids for four motion functions |
将初始网格的坐标点和运动变形后的位移量作为不同核函数下SVR方法的训练样本,采用SMO算法训练得到相应的SVR模型。再将初始网格点代入这些SVR模型计算得到预测的位移量,从而可通过比较预测值和真实值的误差、选择的支持向量(控制点)考察不同核函数的拟合能力及训练开销等性能。
本文采用均方差(mean square error,MSE)来衡量回归拟合的精确度,其计算公式如下:
| $ {\text{MSE}} = \dfrac{{\displaystyle\sum\nolimits_{i = 1}^{{N_b}} {{{\left( {{z_i} - {{\widetilde z}_i}} \right)}^2}} }}{{{N_b}}} $ | (15) |
其中,
对于某个确定的回归问题,Vapnik等证明必然存在可行的核函数,且满足Mercer定理的函数均能作为核函数[16]。由于满足Mercer定理的函数较多,对于特定类型的问题,通常需要根据经验或大量实验对比才能给出更适合的核函数及其参数,从而能显著提高SVR的建模效率和质量。径向基核函数是处理无先验知识数据集首选的核函数类型,其以空间中两点的欧氏距离为自变量,影响周围区域的样本取值。
按照作用范围的不同,径向基函数可分为全支撑(Global Support)基函数和紧支撑(Compact Support)基函数两类。全支撑基函数在整个定义域内均为非零值,其常见的函数类型如表1所示,其中MQB和IMQB函数使用参数
| $ k\left( {{{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}} \right) = \phi (\xi ),{\text{ }}\xi = \frac{{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|}}{r} $ | (16) |
对于高斯核的内核宽度参数
| 表 1 常见的全支撑基函数 Table 1 Common global support basis functions |
|
|
与全支撑基函数不同,紧支撑基函数只作用在支撑半径
| $\begin{split} k\left( {{{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}} \right) =& \left\{ {\begin{array}{*{20}{l}} {\phi (\xi )}&,{0 \leqslant \xi \leqslant 1} \\ 0&,{\xi > 1} \end{array}} \right. \\&\xi = \frac{{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|}}{R} \end{split}$ | (17) |
表2给出了比较常规的紧支撑基函数。为方便论述,下文将缩放系数
| 表 2 常见的紧支撑基函数 Table 2 Common compact support basis functions |
|
|
新的SVR动网格方法将基于以上核函数进行测试,更多有关径向基函数的信息及其误差和收敛特性可参阅文献[23]。
2.3 结果分析除了前期研究采用的高斯核函数外,本节通过大范围调整核参数,对其余13个核函数进行了大量拟合测试,得到了7个能较好拟合公式(14)描述的四类网格运动的核函数及其核参数设置范围,结果如表3所示。其余核函数均不适用于SVR动网格方法,后续不再讨论。
| 表 3 成功拟合网格运动的核函数 Table 3 Kernel functions for successfully fitting mesh motions |
|
|
当SVR方法采用原来的高斯核函数时,基于测试案例
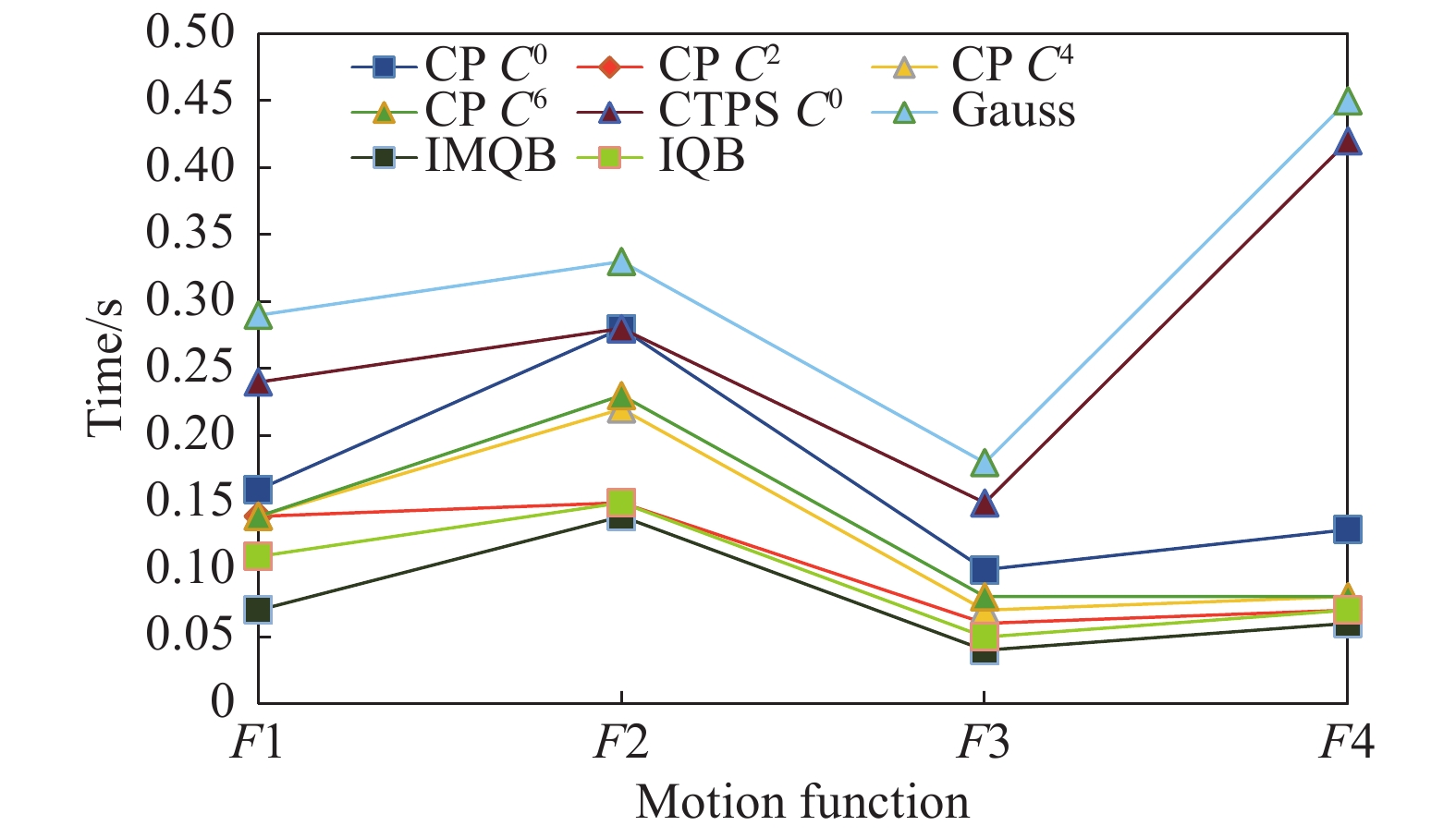
|
图 4 不同核函数在网格上的时间开销 Fig.4 Time cost on the grid for different kernel functions |
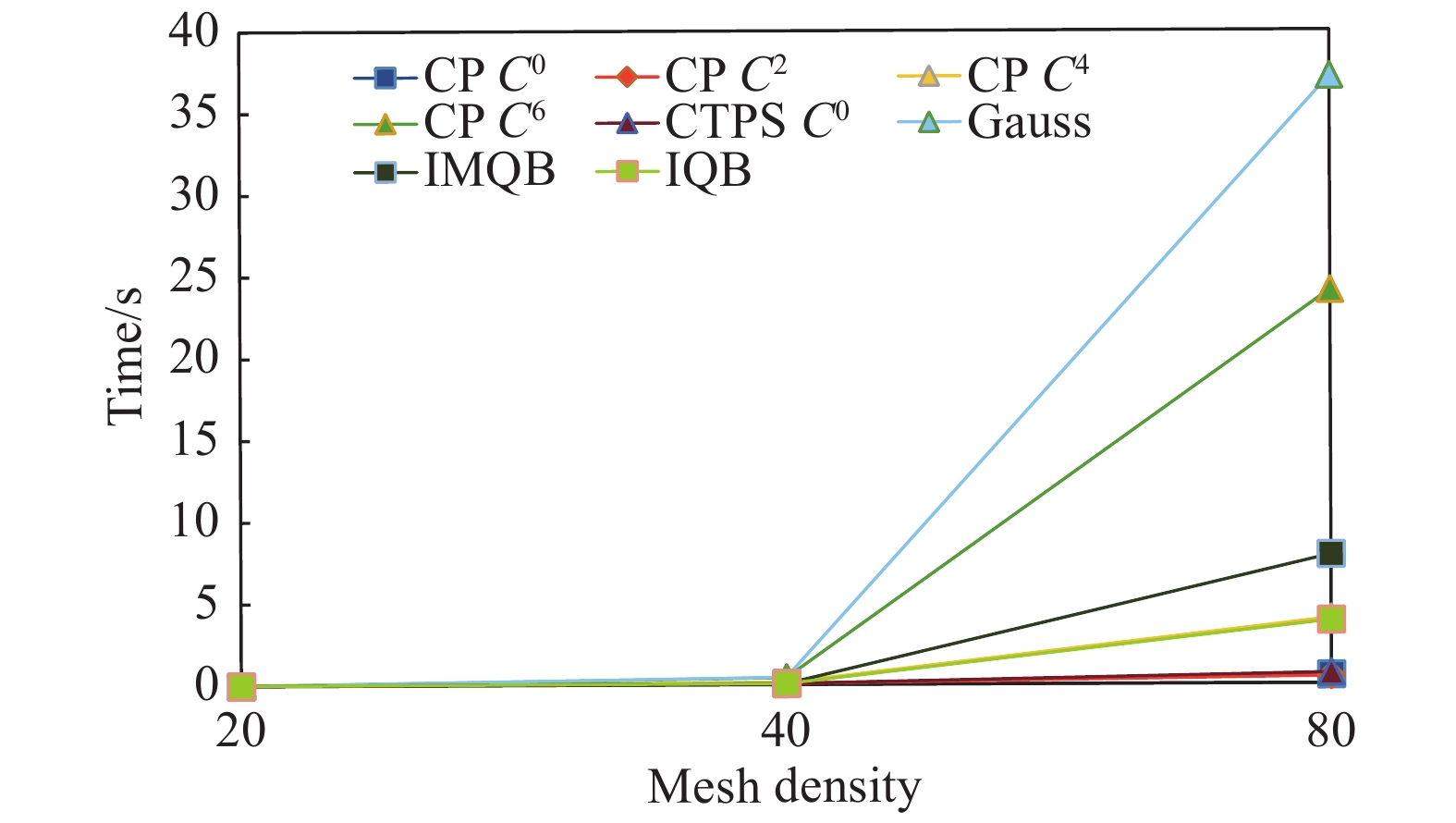
为考察边界点规模对SVR方法拟合性能的影响,采用运动特性较全面的F4函数测试了核函数在不同密度网格下(分别用20、40和80表示)完成变形的时间开销、控制点选择和均方差。图5给出了各类核函数在不同密度网格上的时间开销,从中可知边界点规模增大会明显降低建模的速度,但不同核函数的影响差异显著。高斯核函数和
|
图 5 不同密度网格上各类核函数时间开销 Fig.5 Time cost on different density grids for various kernel functions |
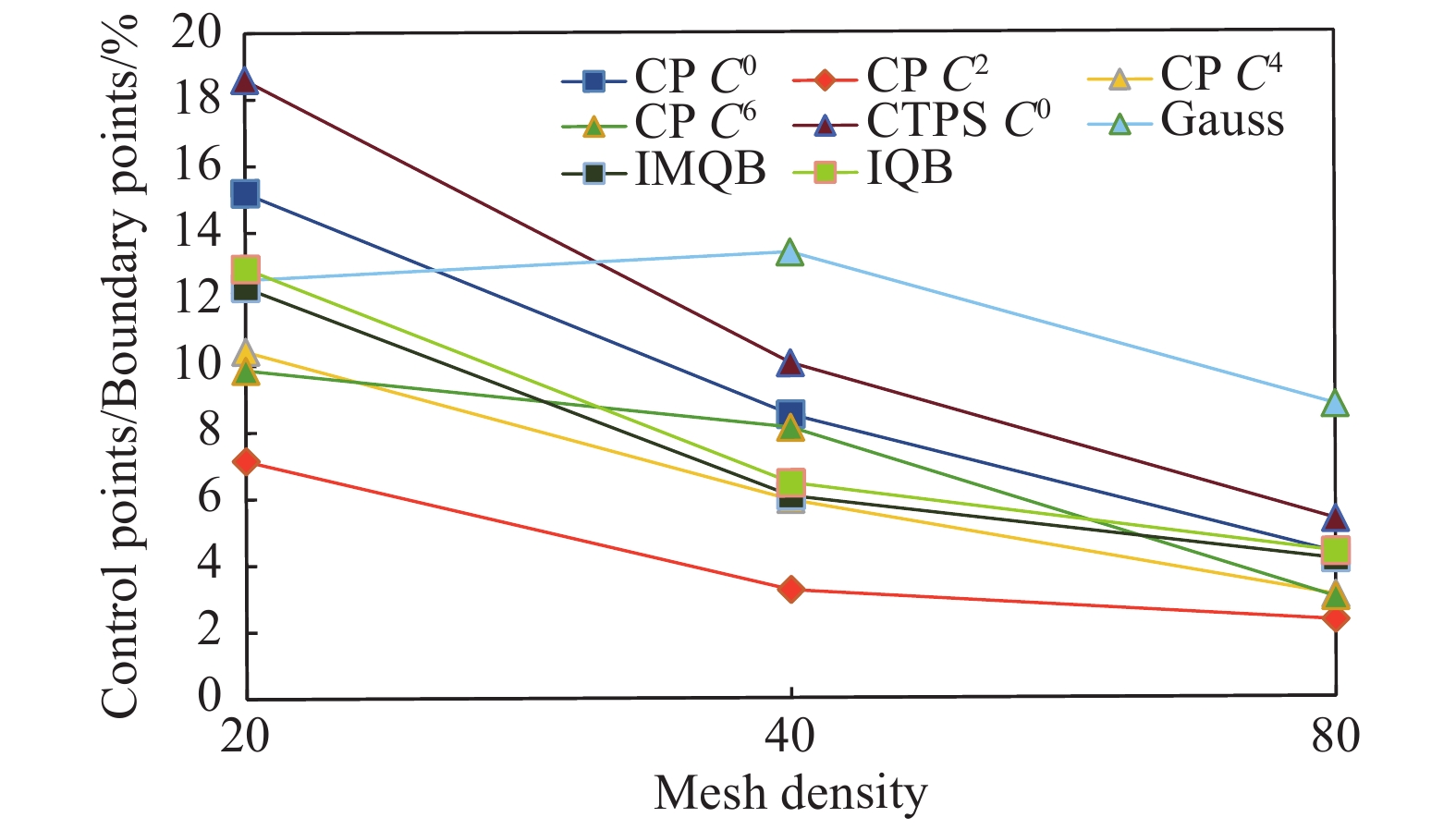
图6展示了不同核函数选择控制点占边界点数的比例,可以看出在处理较密两套网格时高斯核函数和
|
图 6 不同密度网格上各类核函数选择的控制点数量 Fig.6 Number of control points selected by various kernel functions on different density grids |
按照径向基函数分类,全支撑组和紧支撑组选择的控制点分布分别如图7(a)和图7(b)所示。从图中可明显看出,对于所有核函数,控制点的总体分布不会随网格密度增加而有明显改变。此外,不同核函数所选择的控制点虽然分布半径和密度有所区别,但基本都吻合同心圆样式的排列,这正是图3(d)中F4函数运动变化最剧烈的区域。由此反映出SVR方法能够自适应地选择位移最突出的边界点来表示边界运动。

|
图 7 不同密度网格上各类核函数的控制点分布 Fig.7 Distribution of control points for various kernel functions on different density grids |
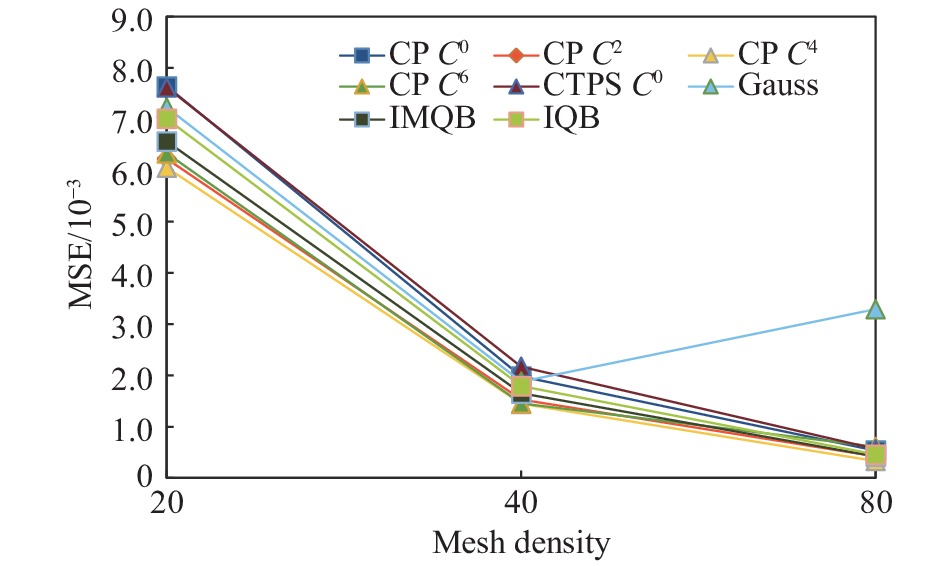
图8进一步给出了不同核函数拟合的均方差,说明所有被测核函数均能有效拟合边界的运动规律,但高斯核函数的拟合能力在密度最大的网格上有所下降,说明其健壮性较差。同时注意到
|
图 8 不同密度网格上各类核函数拟合的均方差 Fig.8 MSE of various kernel functions fitting on different density grids |
综合以上分析,针对SVR动网格方法,全支撑核函数IQB、IMQB和紧支撑核函数
本节通过三个典型案例测试分析核函数及其参数设置对SVR动网格方法的全面影响。对于变形运动后的网格质量,本文采用文献[12]提出的方法对三角形/四面体单元进行评估,并统计网格平均质量和最差单元质量。该方法通过函数
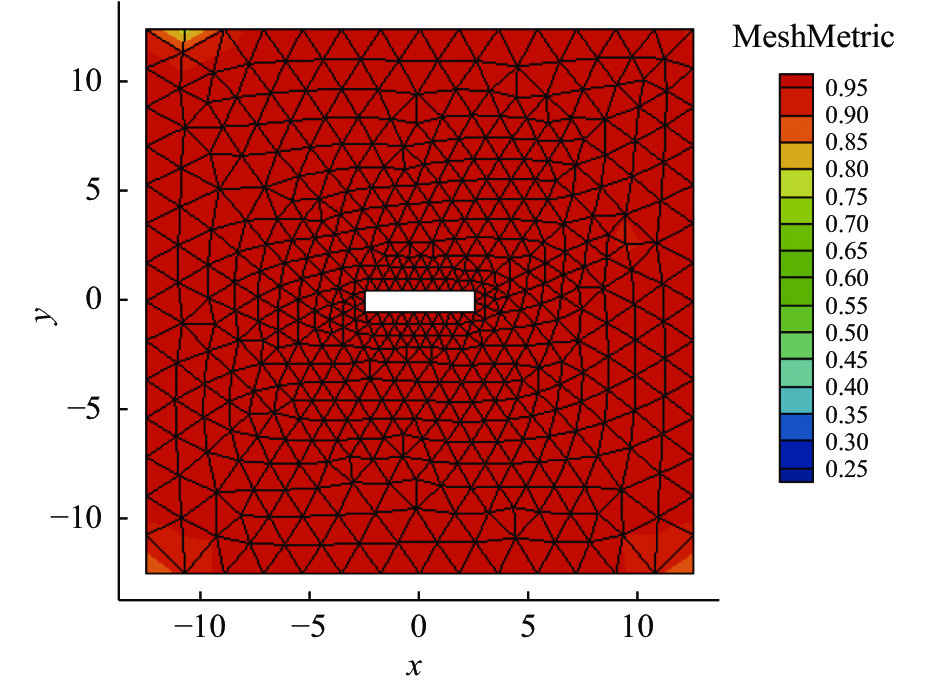
本案例主要考察在较大形变运动中采用SVR方法进行多步变形后的网格质量以及核函数的影响。初始网格如图9所示,其中外边界尺寸为
|
图 9 二维矩形块旋转平移案例的初始网格 Fig.9 Initial mesh for the 2D case of rectangular block rotation and translation |
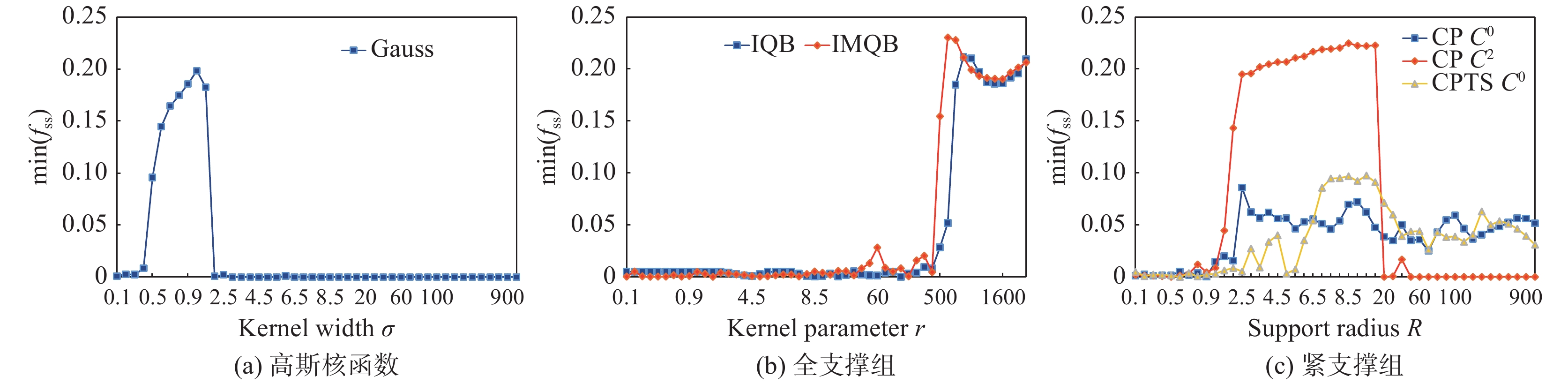
在进行实际动边界问题数值模拟时,从初始到最终状态往往需要计算多个时间步,因此也需要经过多步将初始网格变形到最终状态。首先设总的变形步数为20,研究不同核参数对网格变形后质量的影响。图10给出了最终网格的最差单元质量度量值,从中可知
|
图 10 分组对比不同核参数对最差单元质量的影响 Fig.10 Group comparison of the worst cell quality by different kernel parameters |
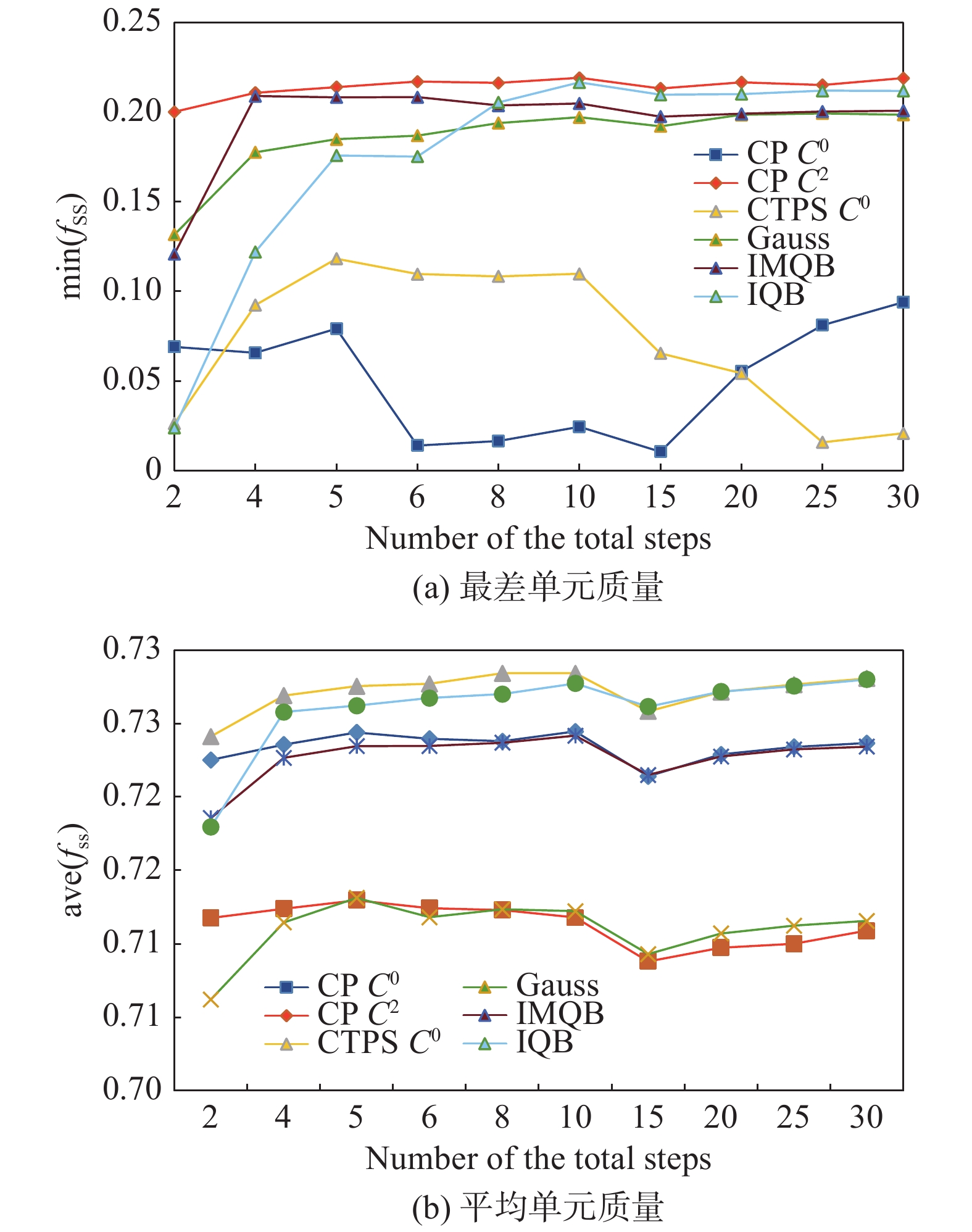
为考察网格整体质量,测试了不同步数下变形到最终状态的网格单元最差质量和平均质量,结果如图11所示。从中可知
|
图 11 不同核函数下多步变形后最终的网格质量对比 Fig.11 Comparison of the final mesh quality after multi-step deformation by different kernel functions |
图12直观展示了采用IMQB和高斯核函数通过4步变形到最终状态的网格及其质量度量分布。在矩形块经过大幅度旋转平移后,其周围的网格单元仍与之保持着较好的连接关系,且采用IMQB核函数变形后的网格质量明显更优。

|
图 12 采用4步变形的最终网格 Fig.12 Final mesh deformed after four steps by IMQB and Gaussian kernel function |
本案例通过多段翼的多体相对运动,进一步研究不同密度的网格变形质量受核函数的影响。初始网格的远场边界为圆形,半径长为25L,其中L为尾翼弦长,令内部边界中三段翼型的尾翼沿顺时针方向旋转

|
图 13 两套三段翼初始网格(局部) Fig.13 Two initial grids of the three-segment wing (partial in detail) |
本案例网格变形较缓和,取回归阈值系数
|
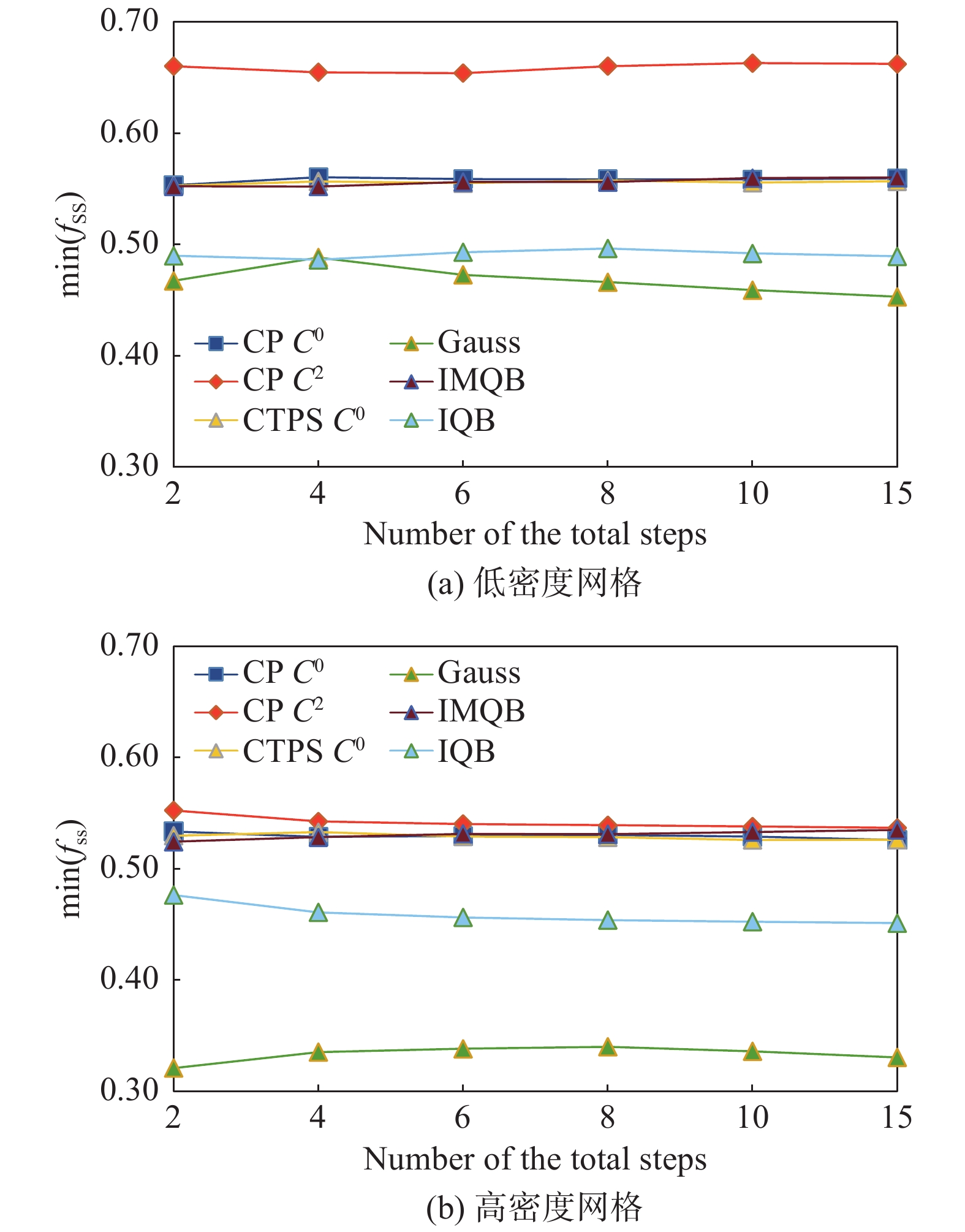
图 14 两套网格变形后的最差单元质量 Fig.14 Worst cell quality after deformation for two grids |
低密度和高密度网格的初始最差单元质量度量值分别为0.71和0.69,对比两套网格变形后的质量,可知在同一核参数下,网格密度的增加令高斯核函数的变形能力明显下降,但对其他核函数影响不大。图15分别展示了两套网格最终状态下动边界附近的网格单元质量分布,结果表明采用

|
图 15 三段翼动边界附近的最终网格质量分布 Fig.15 Final mesh quality distribution near the moving boundary of the three-segment wing |
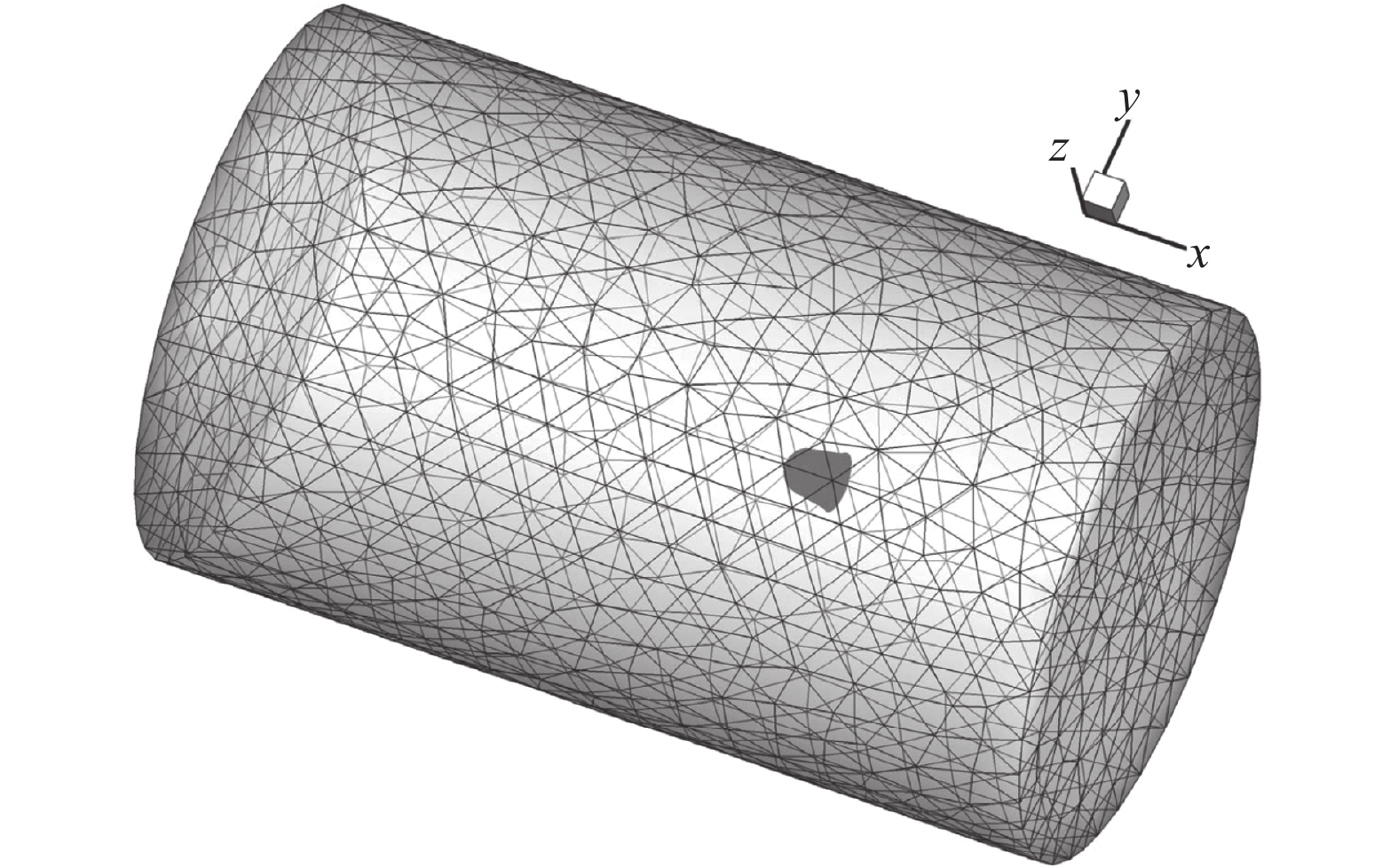
为进一步测试SVR方法在三维动网格上的表现,本案例对三维周期性运动后的网格质量稳定性进行研究。初始的四面体网格如图16所示,计算域的外边界成圆柱形,底部半径为5L,高约16L,L为返回舱中轴线长,返回舱最大半径为0.25L。共有61514个边界点,303927个内部点。
|
图 16 返回舱初始网格 Fig.16 Initial mesh of the return capsule |
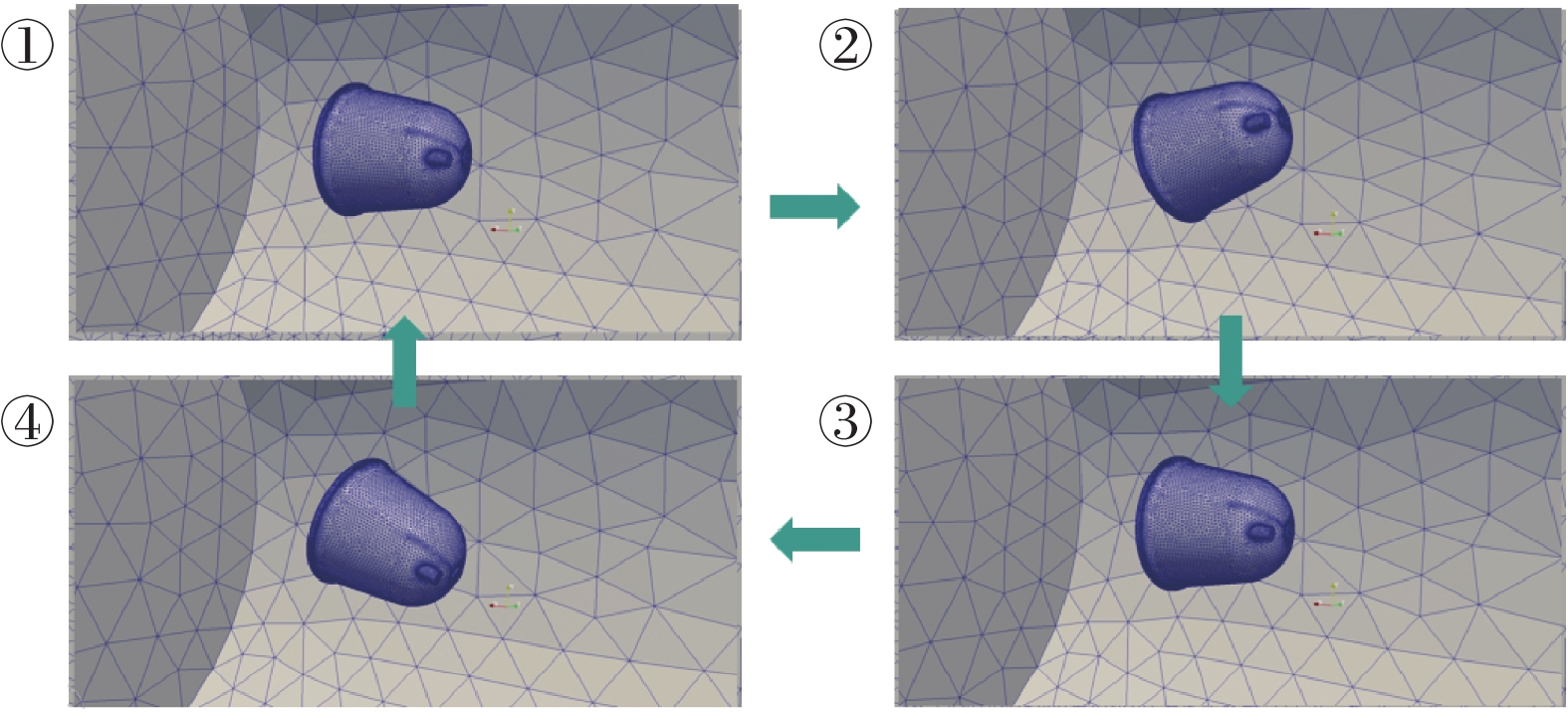
图17给出了采用本文方法变形返回舱一个周期的运动示意图,其俯仰中心位于中轴线尾部五分之一处,并在y轴方向以
|
图 17 返回舱的周期俯仰运动 Fig.17 Periodic pitching motion of the return capsule |
本案例动边界结构复杂,为减小潜在的插值累积误差,取较小的回归阈值系数
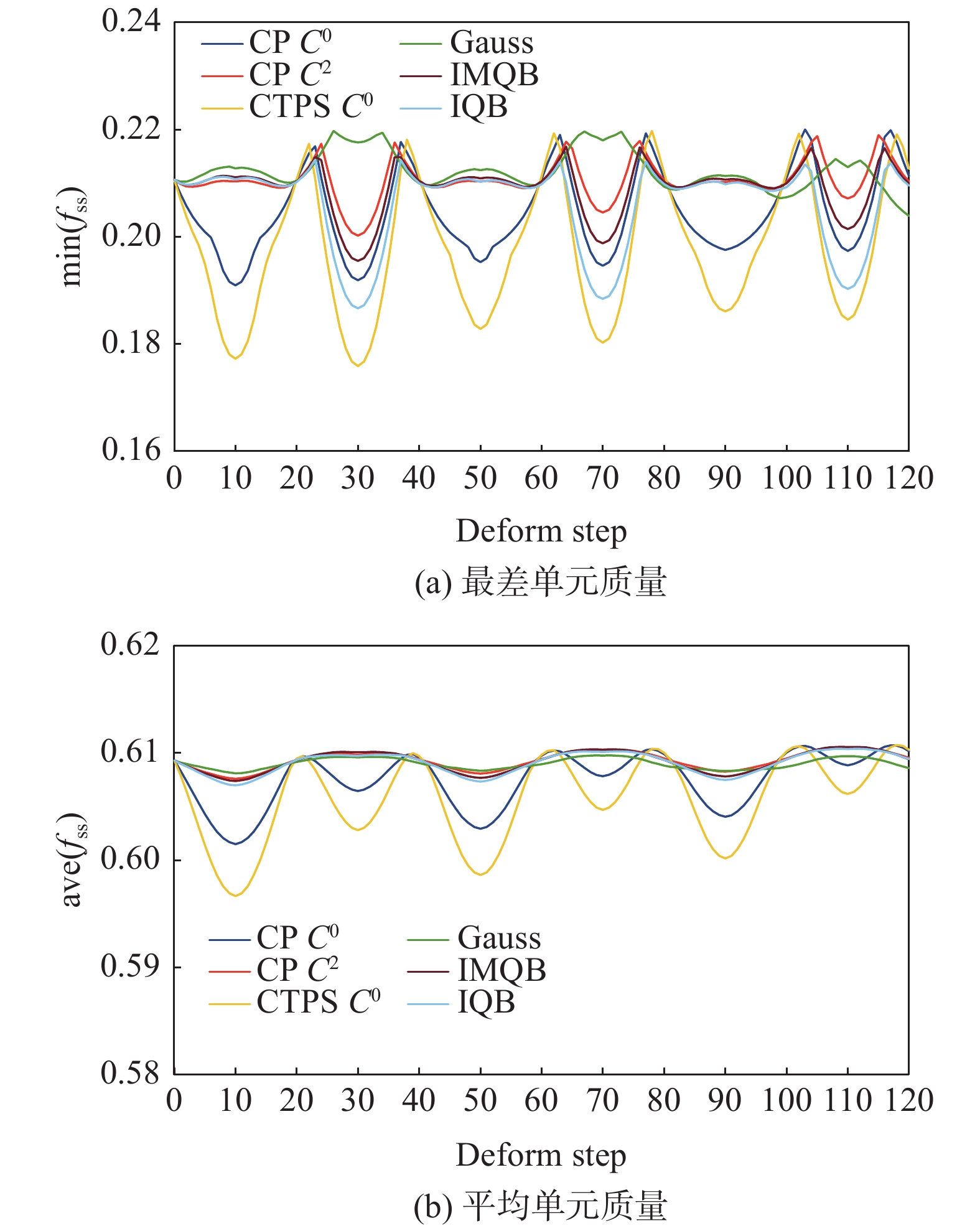
图18给出了每一变形步后四面体网格单元的最差质量和平均质量。当达到最大俯仰角时,高斯核函数相应的网格质量略好于其他核函数,但相差很小且网格质量均较好。另一方面从图17也可直观看出运动过程中保持了良好的网格质量。此外,之前实验表现最好的全支撑函数和
|
图 18 返回舱各变形步完成后的网格质量 Fig.18 Mesh quality after each deformation step of the return capsule |
表4进一步给出了采用不同核函数进行变形的总时间开销,并以高斯核函数为基准列出了其他函数所节省的时间比例。其中采用
| 表 4 不同核函数针对返回舱案例的时间开销 Table 4 Time cost of different kernel functions for the return capsule case |
|
|
本文通过进一步放宽贪心选点RBF插值法的约束条件,提出了一种更高效的基于支持向量回归的机器学习动网格技术,并以前期研究采用的高斯核函数为基准,总结了所提方法的核参数设置规律。对于常见运动形式,一般可将
在包含网格运动的大规模数值模拟中,动网格方法的计算效率始终是影响模拟周期的重要因素。在下一步的工作中,可以尝试将本文算法进行不同模式的并行化改造,使之适用于大规模复杂问题的工程实践。
| [1] |
庞宇飞, 卢风顺, 蔡云龙, 等. 基于网格框架的结构网格自动重构技术[J]. 空气动力学学报, 2017, 35(6): 807-811. PANG Y F, LU F S, CAI Y L, et al. Automatic remeshing technique for structured grid based on grid framework[J]. Acta Aerodynamica Sinica, 2017, 35(6): 807-811. (in Chinese) |
| [2] |
WANG Z, PRZEKWAS A. Unsteady flow computation using moving grid with mesh enrichment[C]//32nd Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 1994 doi: 10.2514/6.1994-285
|
| [3] |
朱冰, 祝小平, 周洲, 等. 基于非结构动网格的多体分离数值仿真研究[J]. 空气动力学学报, 2013, 31(2): 181-185. ZHU B, ZHU X P, ZHOU Z, et al. Simulation of unsteady multi-body flowfield involving relative movement based on unstructured mesh[J]. Acta Aerodynamica Sinica, 2013, 31(2): 181-185. DOI:10.7638/kqdlxxb-2011.0037 (in Chinese) |
| [4] |
LYNCH D R, ONEILL K. Elastic grid deformation for moving boundary problems in two space dimensions[R]. Finite elements in water resources, 1980, 2.
|
| [5] |
LIU X Q, QIN N, XIA H. Fast dynamic grid deformation based on Delaunay graph mapping[J]. Journal of Computational Physics, 2006, 211(2): 405-423. DOI:10.1016/j.jcp.2005.05.025 |
| [6] |
HASSAN O, MORGAN K, WEATHERILL N. Unstructured mesh methods for the solution of the unsteady compressible flow equations with moving boundary components[J]. Philosophical Transactions of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2007, 365(1859): 2531-2552. DOI:10.1098/rsta.2007.2020 |
| [7] |
肖天航, 昂海松, 仝超. 大幅运动复杂构形扑翼动态网格生成的一种新方法[J]. 航空学报, 2008, 29(1): 41-48. XIAO T H, ANG H S, TONG C. A new dynamic mesh generation method for large movements of flapping-wings with complex geometries[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(1): 41-48. DOI:10.3321/j.issn:1000-6893.2008.01.006 (in Chinese) |
| [8] |
WITTEVEEN J, BIJL H. Explicit mesh deformation using inverse distance weighting interpolation[C]//19th AIAA Computational Fluid Dynamics, San Antonio, Texas. Reston, Virigina: AIAA, 2009. doi: 10.2514/6.2009-3996
|
| [9] |
WITTEVEEN J. Explicit and robust inverse distance weighting mesh deformation for CFD[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virigina: AIAA, 2010. doi: 10.2514/6.2010-165
|
| [10] |
LUKE E, COLLINS E, BLADES E. A fast mesh deformation method using explicit interpolation[J]. Journal of Computational Physics, 2012, 231(2): 586-601. DOI:10.1016/j.jcp.2011.09.021 |
| [11] |
LI X H, GUO Z, HOU Z X, et al. Efficient mesh deformation method combined with the moving submesh approach[J]. Journal of Aerospace Engineering, 2017, 30(6): 04017069. DOI:10.1061/(asce)as.1943-5525.0000784 |
| [12] |
DE BOER A, VAN DER SCHOOT M S, BIJL H. Mesh deformation based on radial basis function interpolation[J]. Computers & Structures, 2007, 85(11-14): 784-795. DOI:10.1016/j.compstruc.2007.01.013 |
| [13] |
LI C, YANG W J, XU X H, et al. Numerical investigation of fish exploiting vortices based on the Kármán gaiting model[J]. Ocean Engineering, 2017, 140: 7-18. DOI:10.1016/j.oceaneng.2017.05.011 |
| [14] |
SHENG C H, ALLEN C B. Efficient mesh deformation using radial basis functions on unstructured meshes[J]. AIAA Journal, 2013, 51(3): 707-720. DOI:10.2514/1.j052126 |
| [15] |
LIU Y, GUO Z, LIU J. RBFs-MSA hybrid method for mesh deformation[J]. Chinese Journal of Aeronautics, 2012, 25(4): 500-507. DOI:10.1016/S1000-9361(11)60413-5 |
| [16] |
VAPNIK V. Support vector method for function approximation[J]. Advances in Neural Information Processing Systems, 1996, 9: 281-287. |
| [17] |
BURGES C J C. A tutorial on support vector machines for pattern recognition[J]. Data Mining and Knowledge Discovery, 1998, 2(2): 121-167. DOI:10.1023/A:1009715923555 |
| [18] |
VAPNIK V. The nature of statistical learning theory[M]. Springer Science & Business Media, 2013.
|
| [19] |
LI X, WANG H, GU B, et al. Data sparseness in linear SVM[C]// International Conference on Artificial Intelligence, 2015: 3628-3634.
|
| [20] |
DEBASISH B S, PATRANABIS D C. Support vector regression[J]. International Journal of Neural Information Processing-Letters and Reviews, 2007, 11(10): 203-224. |
| [21] |
GAO X, DONG Y D, XU C F, et al. Developing a new mesh deformation technique based on support vector machine[J]. International Journal of Computational Fluid Dynamics, 2017, 31(4-5): 246-257. DOI:10.1080/10618562.2017.1328734 |
| [22] |
PLATT J C. Sequential minimal optimization: a fast algorithm for training support vector machines[R]. Microsoft Research Technical Report, 1998.
|
| [23] |
BUHMANN M D. Radial basis functions[J]. Acta Numerica, 2000, 9: 1-38. DOI:10.1017/s0962492900000015 |
 2022, Vol. 40
2022, Vol. 40

