2. 中国工程物理研究院 高性能数值模拟软件中心,北京 100088;
3. 北京应用物理与计算数学研究所,北京 100094
2. CAEP Software Center for High Performance Numerical Simulation, Beijing 100088, China;
3. Institute of Applied Physics and Computational Mathematics, Beijing 100094, China
在数值模拟流程中,网格生成环节包括了几何建模、模型处理、网格剖分、设置边界/载荷参数、网格组装等阶段,最终得到计算所需要的求解域的离散网格。由于网格的精度和质量直接关系着求解的精度和质量,在上述阶段中,为得到满意的网格剖分结果,模型处理和网格剖分步骤需要反复的人工迭代修改,据美国圣地亚实验室统计,它们会占到整个算例工作量的50%以上[1] 。
高性能数值模拟应用是运行于高性能计算机上的复杂数值模拟应用,往往需要基于复杂模型生成十亿规模以上的网格[2-3] ,实现这一过程的高度自动化无疑有利于提高效率和避免人工失误。实现高度自动化的难点在于:首先是模型全自动处理难,数值模拟应用的模型(以下简称CAE几何模型)大多来自于CAD模型,而CAD模型和CAE几何模型的几何表达方式不同,技术关注的目标不同[4-5],实现CAD模型到CAE几何模型的自动处理一直是研究热点[4-6],目前,即使是成熟的商业前处理软件也不能实现任意模型的自动处理;其次是针对复杂模型的全自动网格生成算法难,尤其是六面体网格生成及高阶曲面网格生成仍然是众多研究关注的焦点[7-8]。
大规模网格生成本身对计算能力和内存的消耗也是巨大的,单机生成已无法满足需求。目前,并行求解器的研制正在逐步适应并行机体系结构,相比之下,网格生成方法的研究滞后很多,尝试在全自动网格生成算法的基础上实现并行化,达到“并行网格生成-并行求解”的一致并行,是突破大规模网格生成瓶颈的活跃的研究领域[3,9-12] 。并行网格生成的难点在于:首先,要得到高质量的网格划分,就要尽可能全局考虑几何,而在全局几何上的串行和紧耦合操作又会造成并行方面的瓶颈;其次,要支持自适应计算,就需要实现在求解过程中并行自适应调整网格[13-14],但又不能影响负载平衡;第三,需要考虑并行网格生成与并行求解器的耦合连接问题,外耦合文件连接方式存在巨大的I/O开销和网格量数据转换开销。这些都造成了网格生成算法并行化实现的困难。上述这些难点决定了必须发展和高性能数值模拟相适应的并行网格生成方法和相关软件工具。然而,相比于串行网格生成研究已有近50年的历史,且开源及商业的网格生成软件不断推出[15],并行网格生成研究起源于20世纪90年代,步入21世纪,才真正随着高性能计算的飞速发展而逐步展开。并行网格生成属于以计算数学、计算机图形学、并行计算等学科为支撑的交叉学科,在国内,缺乏长期投身这一技术研究的研究人员和对通用并行网格生成软件的持续研发投入,造成国产高性能数值模拟应用软件普遍存在“前处理弱”的问题,使得软件的可用性大打折扣,很大程度上影响了软件的推广。
1 国内外研究现状 1.1 CAD模型自动处理复杂数值模拟应用很少采用在数值模拟软件中建模的方式,而是采用在CAD软件中建立几何模型,然后导入到软件中。理想状态下,网格生成应能直接基于CAD模型进行,但实际情况是,导入的CAD模型需要进行一系列处理,才能得到可为后续网格生成算法使用的CAE几何模型。根本原因在于:CAD技术关注产品设计对象的几何外形,采用边界表示法(boundary representation,Brep)表示模型,即模型由一系列封闭解析曲面所包围的体所定义,体和体之间是拓扑分离,称为流形拓扑模型。而CAE几何模型关注数值模拟计算对象的物理性能和功能的分析,在拓扑上,不一定是封闭的且体与体之间也不一定拓扑分离,称为非流形拓扑模型,如图1所示,存在悬边、悬面等多维混合,以及共点、共边、共面等情况。

|
图 1 非流形拓扑示意 Fig.1 Examples of non-manifold topologies |
自20世纪90年代起,学术界和工业界就开始广泛关注CAD模型与CAE几何模型的数据不一致性问题[16],但直到现在,仍然缺乏业界认可的两者统一的数据标准,复杂模型的人工处理依然工作量巨大[1],全自动模型处理技术仍然是研究热点。
模型处理方法按处理对象,可分为自身错误处理和算法关联错误处理两类;按照实现方式,可分为对连续CAD模型处理[17-19]和对离散CAD模型处理[20-21]两类。
自身错误指模型的几何缺陷和拓扑缺陷,几何缺陷包括错位、曲线和曲面自相交、法向不连续等,拓扑缺陷包括存在孤立点、孤立边、非闭合面、邻接面相交或重叠等。算法关联错误指模型具有不适合特定网格生成算法的特征,例如:不适合Delaunay表面网格生成算法的短边、窄面、尖角等细小几何特征;算法关联错误还指模型具有对计算结果不产生影响的冗余特征,基于冗余特征生成网格,会造成多余的计算开销。算法关联错误的判定往往和具体的应用相关。
目前,绝大多数模型处理方法都是串行的。其中,全自动模型处理方法大多是针对自身错误的处理,首先通过自动的拓扑检测剔除孤立点、边和非闭合面,再以点/线/面间的容差为依据[17]进行缝隙、错位的缝合和重叠的解除等,采用合适的容差是自身错误处理算法的关键,过大的容差往往容易造成几何特征丢失。算法关联错误的处理由于有多种复杂因素影响,一般需要人工辅助来判定要处理的几何特征和选择处理方法,处理方法包括冗余细节移除[22]、局部降维[23-24]、对称处理[25]等,目前,也有学者尝试基于机器学习方法实现自动的判定和处理,已在单部件模型去细小特征方面取得了初步进展[6],但离工程实用仍有很大差距。
此外,将CAD模型信息无缝传递给CAE几何模型也是研究关注点,例如:通过传递CAD模型的装配信息给对应的CAE几何模型,实现自动设置接触对、运动副等边界条件,避免人工操作带来的失误。商业CAD平台UG、PTC、CATIA、AUTOCAD与其内置的CAE求解器之间已实现了这样的无缝对接,其他CAE软件只能通过采用商业转换插件[26]或在STEP等中间格式基础上研发信息传递机制[27]来实现。
1.2 并行网格生成及优化并行网格生成及优化方法需在串行自动网格生成算法基础上实现并行化。它要考虑并行机的特点,充分发挥机器计算能力的优势并具备良好的可扩展性,其研究内容涉及区域分解、网格并行剖分、网格自适应优化、并行网格数据结构等。
区域分解方法的目标是在保持子区域负载平衡的同时尽量减少通信,常用的实现方法分为静态图剖分和动态图剖分两类。静态图剖分方法主要有几何剖分、基于几何和拓扑的剖分、基于代数连通度的剖分和多层级剖分[28]等。动态图剖分方法用于负载发生变化后的分区调整,包括全局重剖分和增量重剖分,前者相对后者通信代价高但负载平衡效果能得到保障。当并行网格生成与并行求解器进行内耦合内存对接时,理想状态是并行求解的进程数与网格生成的分区数相当,这样会大大减少对接开销,但网格分区数如果过多,会在子区域内部插入过量的人工边界,导致子区域定义极易出错,网格生成无法顺利进行。
已有的网格并行剖分方法,按照实现方式不同可分为三类[9]:第一类是生成子区域交界面网格后,再生成各子区域内部网格;第二类是先生成各子区域内部网格,再生成子区域交界面网格;第三类是同步生成各子区域内部网格和交界面网格。
由于网格并行剖分方法的实现需建立在串行自动网格生成算法基础上,本文站在复用串行算法的角度,对网格并行剖分方法进行新的分类:第一类是零复用串行算法,需对串行算法的底层操作进行并行重构,例如,针对增量Delaunay四面体算法的插入点操作的并行化[29],此类方法需要重新设计算法的数据结构和逻辑;第二类是全复用串行算法,它通过区域分解,将整体区域分解为子区域,在子区域内部可全复用串行算法生成网格,对子区域交界面的处理有两种方式,一种是避免改动子区域交界面[30],但交界面附近网格质量难以保证,另一种是允许改动交界面但要进行少量通信;第三类是部分复用串行算法,它是前两类方法的混合[12]。第二、三类方法较容易扩展为能快速集成串行算法成果的网格并行生成框架[31-32]。
网格自适应优化指在求解器并行求解过程中,基于中间计算结果对网格的局部区域进行修改,从而不断提高计算精度。修改方法分为两类,一类是网格的重分或细化,一类是保持拓扑不变的网格节点移动。重分方法[3,14,33]删除修改区域的内部网格,保留区域边界,然后基于新定义的网格尺寸重新生成区域边界约束下的网格,当修改区域与分区交界面时,通常固定分区交界面不变,也有的方法是通过动态图剖分,使新分区的交界面避开修改区域。细化方法将修改区域的网格单元分裂为更细小单元,一般基于模板[34-36]实现,非结构网格常采用最长边中点分裂的模板,结构网格采用八叉树分裂模板,但相邻树节点深度差不超过1。网格节点移动方法先基于修改区域的网格质量度量构建目标优化函数,然后极小化求解,从而得到节点的较优位置[37],再移动节点。对分区交界面的优化可在完成内部网格优化后单独进行,首先需构建与相邻子区域至少1层单元重叠的虚(网格)区域(如图2所示),因为虚(网格)区域内单元也会对交界面上网格质量产生影响,优化后,再通过通信保持分区交界面的一致性。

|
图 2 虚(网格)区域示意(来自文献[38]) Fig.2 An illustration of ghost zones among sub-domains(courtesy of Ref.[38]) |
并行网格数据结构支撑了并行网格生成与优化算法的实现。目前,相比串行算法普遍采用的半边(Half-edge)、半面(Half-face)以及两者扩展的数据结构,并行网格数据结构的设计并无统一标准,主要从以下几个要素去考虑[39-40]:支持多样化的网格单元,支持存储和访问高效,易于并行扩展等。
1.3 并行网格生成软件网格生成是数值模拟前处理软件研发的基础,如图3所示,基于网格生成软件提供的核心数据结构和算法的支撑,再加上交互引擎、前处理界面方面的技术攻关和研发投入,可以快速形成各种专用及通用前处理软件,这种研发模式被商业前处理软件普遍采用。

|
图 3 基于网格生成软件开发前处理软件 Fig.3 Development of pre-processing softwares based on the mesh generation software |
受益于串行网格生成方法的多年发展,串行网格生成软件不断推出[15],国外研究机构、大学和商业公司在理论与工程实战经验积累上占有绝对优势[41],相比之下,无论从整个技术还是软件市场份额而言,国内外的并行网格生成软件都还不成熟,发展国产并行网格生成软件面临机遇。
目前,开源和自研的并行网格生成软件方面,国外的有美国阿贡实验室主持研制的SIGMA[42]和哥伦比亚大学研发的GRUMMP[43]等,SIGMA是并行网格生成及应用的框架软件,它提供并行网格数据结构和并行网格生成算法的基础框架,GRUMMP支持各向同性三角形和四面体网格并行生成。国内有浙江大学研发的HEDP-pre[44],能基于复杂外形并行生成大规模非结构网格;中国工程物理研究院研发的SuperMesh[45],具备非结构和结构网格并行生成能力,能支持百万亿次规模的并行计算;以及国防科技大学正在研制中的YHGrid[41]等。虽然大多数商业前处理软件还不支持并行前处理,但并行化趋势已显现,例如,近期Cubit开始推出并行扫掠六面体网格生成功能[46],ANSYS公司Fluent也推出了64核并行六面体核心网格生成功能[47]。
2 SuperMesh研制进展 2.1 软件概述中国工程物理研究院计算机应用研究所和中物院高性能数值模拟软件中心联合研制的并行网格生成软件,英文名称为“SuperMesh”[45],具备基于复杂几何模型的结构网格和非结构网格的并行生成功能,并通过无缝对接高性能科学与工程计算并行编程框架[48],支持高性能科学与工程计算中普适的三类计算:结构网格、非结构网格和无网格组合几何计算。目前,它已经支撑了结构力学、计算流体力学、辐射流体力学、分子动力学、燃烧学和电磁学,以及多物理过程耦合计算的多个应用。
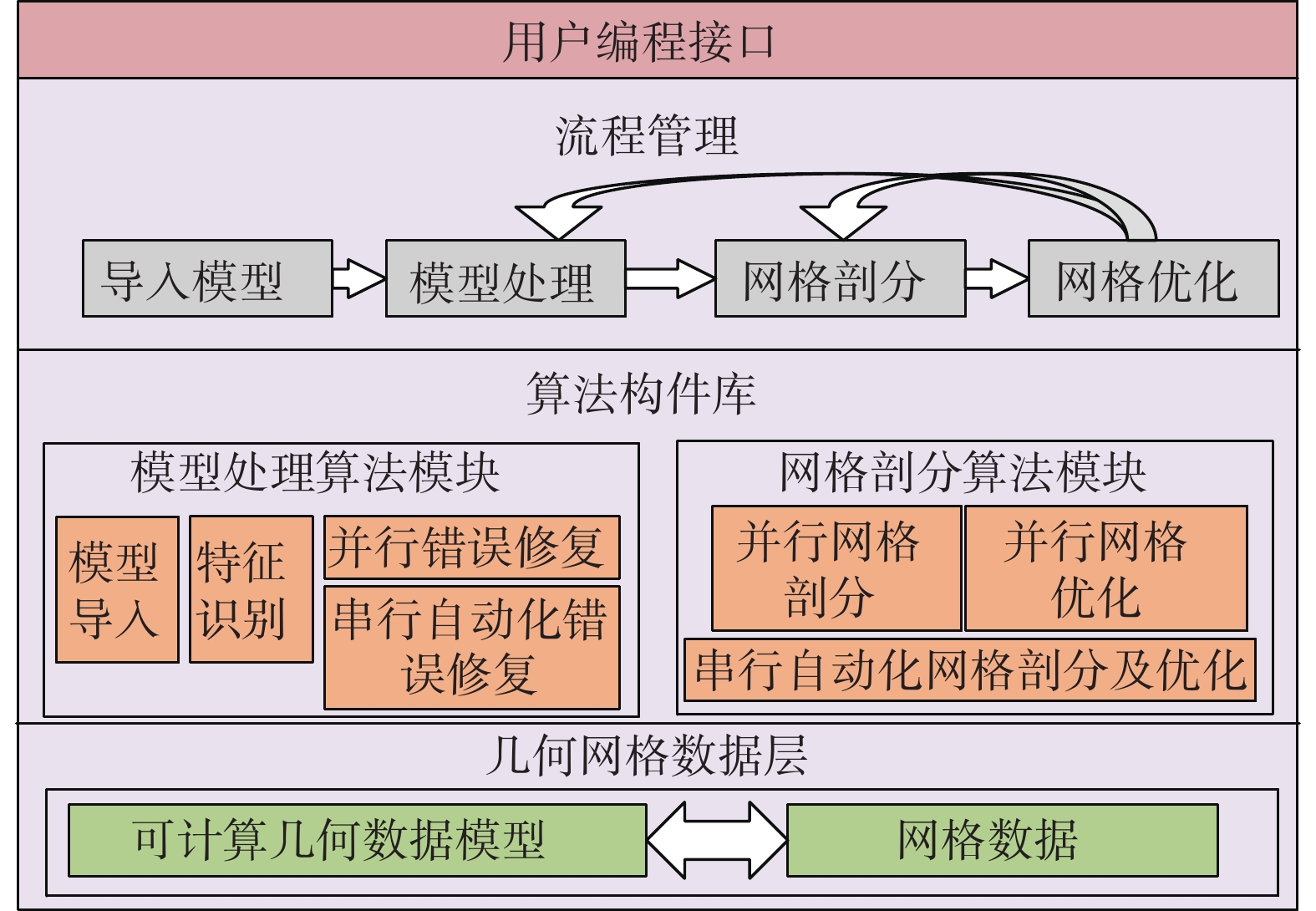
2.2 架构设计SuperMesh软件架构凝炼了并行网格生成过程的共性特征,设计了可复用的算法构件。软件架构如图4所示,自底向上分别是几何网格数据层、算法构件库、流程管理层、编程接口。
|
图 4 SuperMesh软件架构 Fig.4 The architecture of SuperMesh |
几何网格数据层包括可计算几何数据模型(computational geometry data model, CGDM)和它关联的网格数据;算法构件库包括模型处理和网格剖分两大模块,模型处理模块包括模型导入、特征识别、错误修复等算法构件,网格剖分模块包括网格剖分及网格优化构件;流程管理层负责算法构件库的管理和基于流程组装算法构件;编程接口是提供给用户的API接口,用户按上文图3中所述的开发方式,可直接调用API接口开发前处理功能。
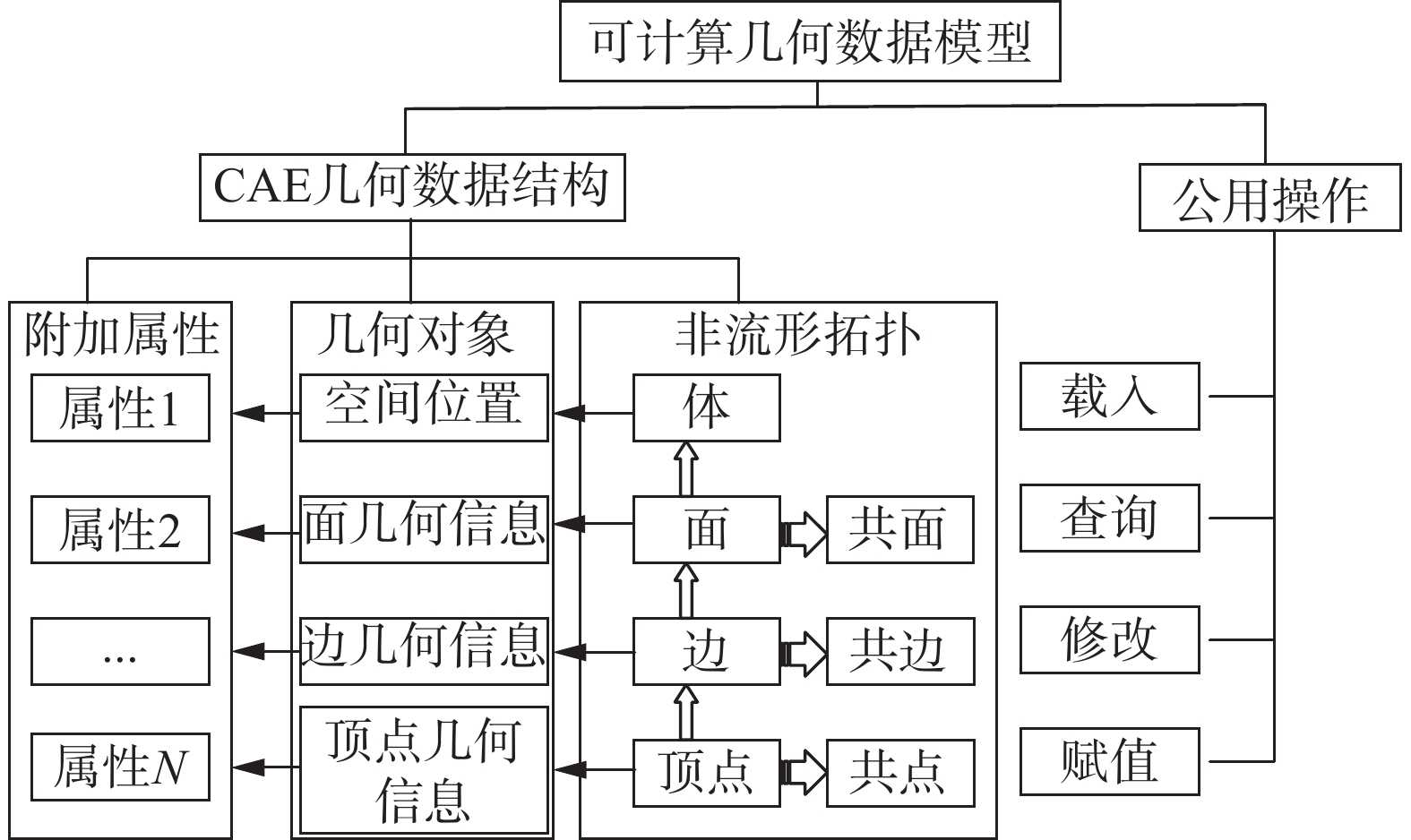
可计算几何数据模型包括CAE几何数据结构和其上定义的公用操作。如图5所示,CAE几何数据结构按照非流形拓扑关系来管理几何对象和附加属性。非流形拓扑关系在体/面/边/顶点等邻接关系的基础上增加了对共面/共边/共点邻接关系的支持。CAE几何数据上的公用操作包括载入、查询、修改、赋值四类:载入操作负责将不同表达格式的CAD模型在逻辑上映射为CAE几何数据结构,查询操作提供对CAE几何数据的访问,修改操作提供对CAE几何数据的编辑;赋值操作在几何对象上定义一些附加属性,例如:边界条件、网格尺寸参数、网格数据指针等。
|
图 5 可计算几何数据模型 Fig.5 An illustration of computable geometry data |
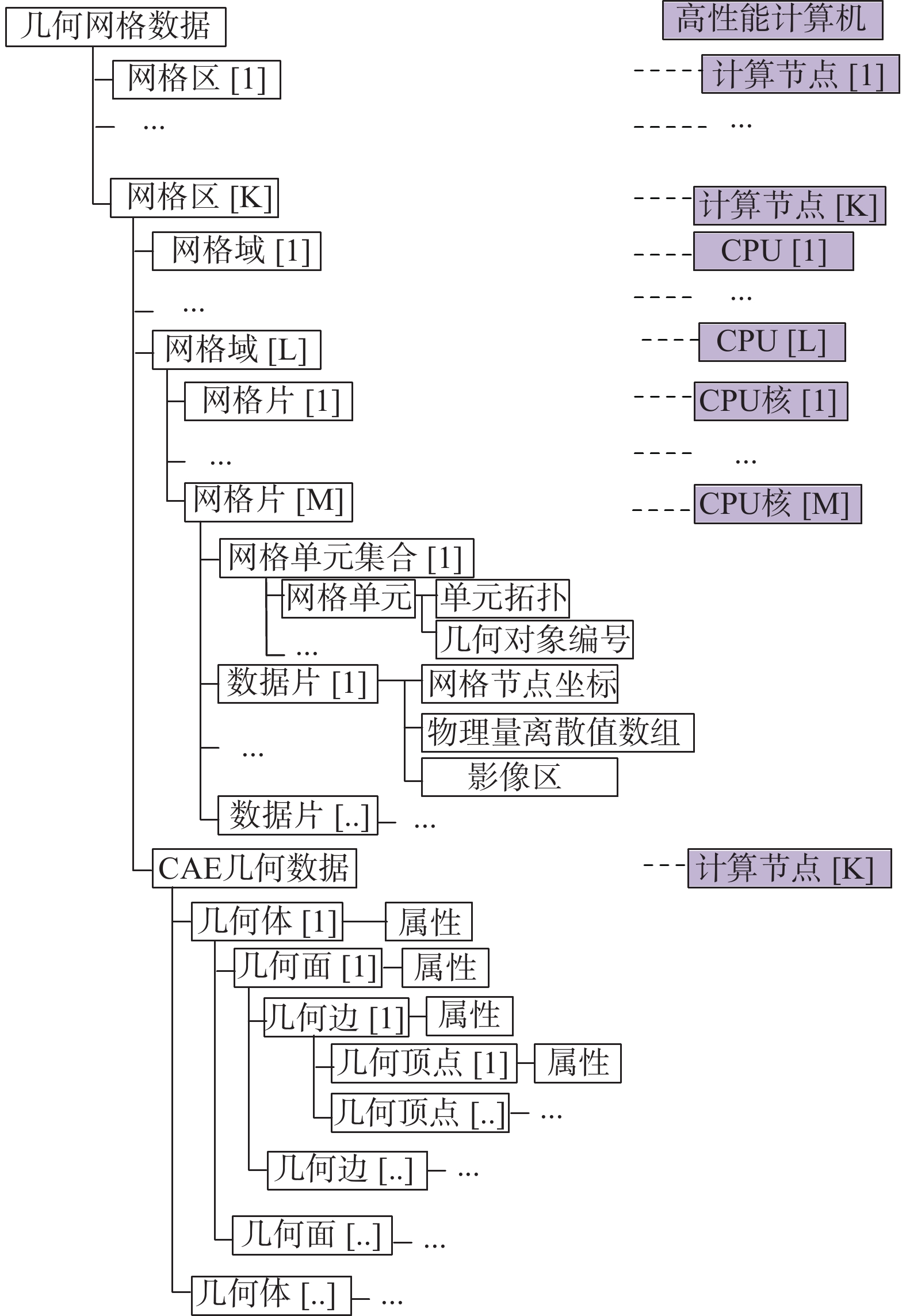
基于可计算几何数据模型和它关联的网格数据构成了与高性能计算机体系结构匹配的几何网格数据结构。数据结构运行时的内存映像如图6所示,CAE几何数据与计算节点对应,网格数据分为网格区、网格域和网格片,网格区与计算节点对应,网格域与计算节点内的CPU对应,网格片与计算节点内的CPU核对应。由于几何网格数据结构在“网格生成”和“数值计算”两阶段保持一致,实现了网格生成与并行编程框架[48]的内存对接,避免了长时间I/O开销和数据转换开销[49]。
基于几何网格数据结构实现了并行网格生成的算法构件化。算法构件的抽象模型如图7所示,包括构件接口、数据存储单元、数据并行通信单元、算法单元四部分。构件接口负责载入输入参数,并返回生成的数据;数据存储单元负责在进程私有空间存储几何网格数据;数据并行通信单元负责实现进程间拓扑相邻的几何网格数据的同步,确保相邻的网格单元是协调的;算法单元负责在进程内复用串行算法实现模型处理、网格剖分或优化。当用户按照构件抽象模型约定的规范扩展新的算法构件时,只需将算法构件注册到SuperMesh中,新增算法构件就可通过API接口提供给外部用户使用。
|
图 6 与高性能计算机体系结构匹配的几何网格数据结构 Fig.6 Data structure of geometry and mesh compatible with the architecture of high-performance computers |

|
图 7 算法构件抽象模型 Fig.7 Components of the parallel mesh-generation algorithm |
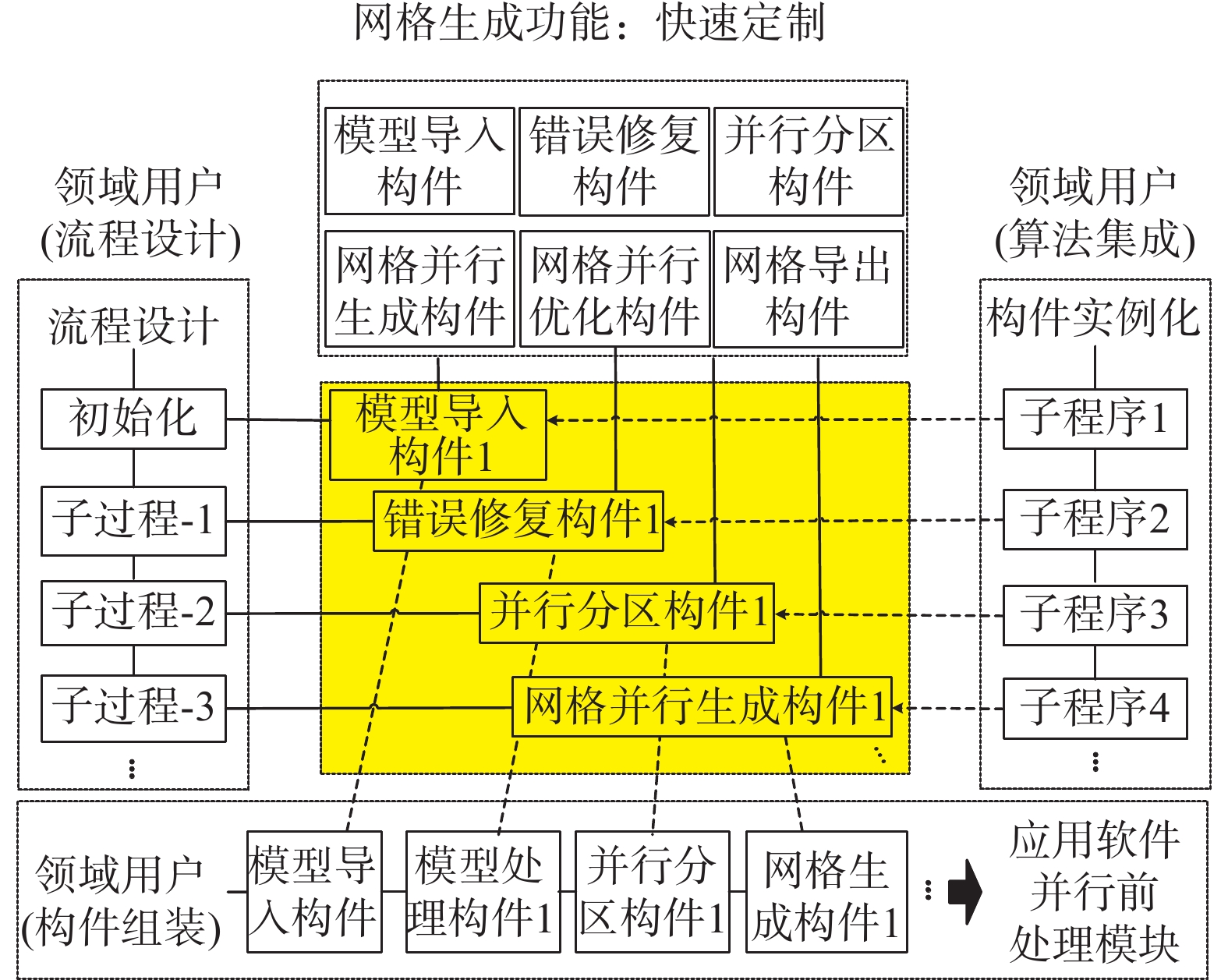
SuperMesh具有可配置的通用流程,用户按流程将不同的算法构件连接组装起来,如图8所示,就可快速研发前处理模块。
|
图 8 基于构件组装的并行前处理功能集成 Fig.8 An integration of parallel pre-processing components |
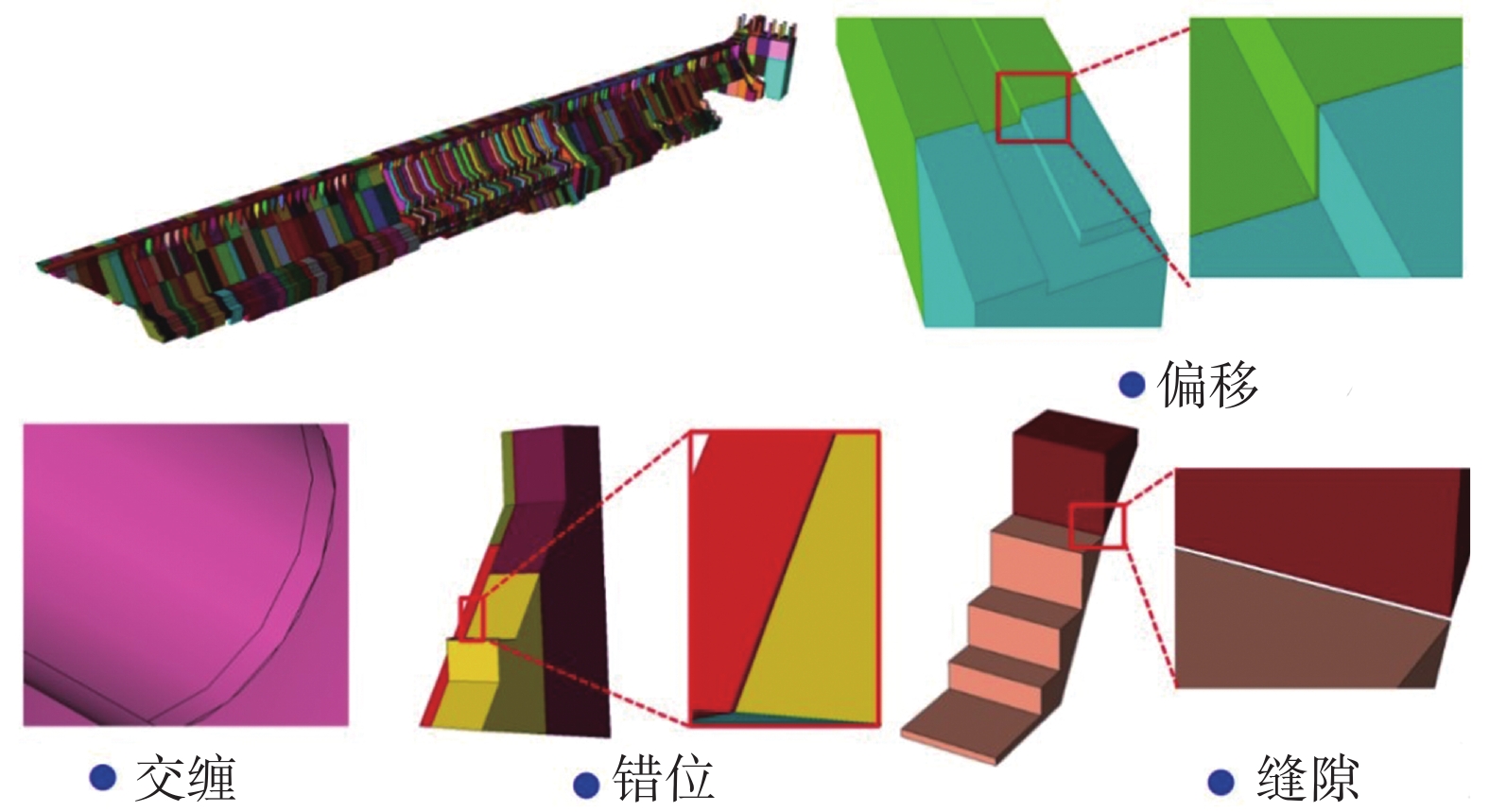
高性能数值模拟应用从部件级模拟跃升到多部件乃至整体模型的模拟,系统性、综合性地考虑不同部件之间的几何物理耦合关系,获得更高精度的数值模拟结果。在这类模拟中,典型输入是多个部件组装在一起的“装配体(Assembly Geometry)”,当装配体模型包含的部件数目成百上千、乃至更多时,为降低建模难度,普遍采用分部件建模的方式获得。分部件建模获得的装配体部件之间存在偏移、交缠、错位、缝隙等错误。
例如图9所示,某大坝模型按坝段装配时存在多种错误(模型由中国水利水电科学研究院张国新教授团队提供)。部件间的共享区域在不同部件中存在多份表征,如果直接在该模型的原始边界表征上生成网格,重叠区域的网格在几何和拓扑上都不兼容,不能用于数值模拟计算。针对上述重复表征问题,提出了适用于装配体模型的自动曲面嵌入算法[50],该算法首先建立连续表征与离散表征相互映射的混合表征模型,然后按照从低维向高维顺序处理的方式,依据表1设计的规则,先对装配模型的离散表征进行局部几何干涉解除,再更新连续表征,有效的实现了串行自动化的模型处理。
|
图 9 多部件装配模型错 Fig.9 Typical assembly errors of a multi-component model |
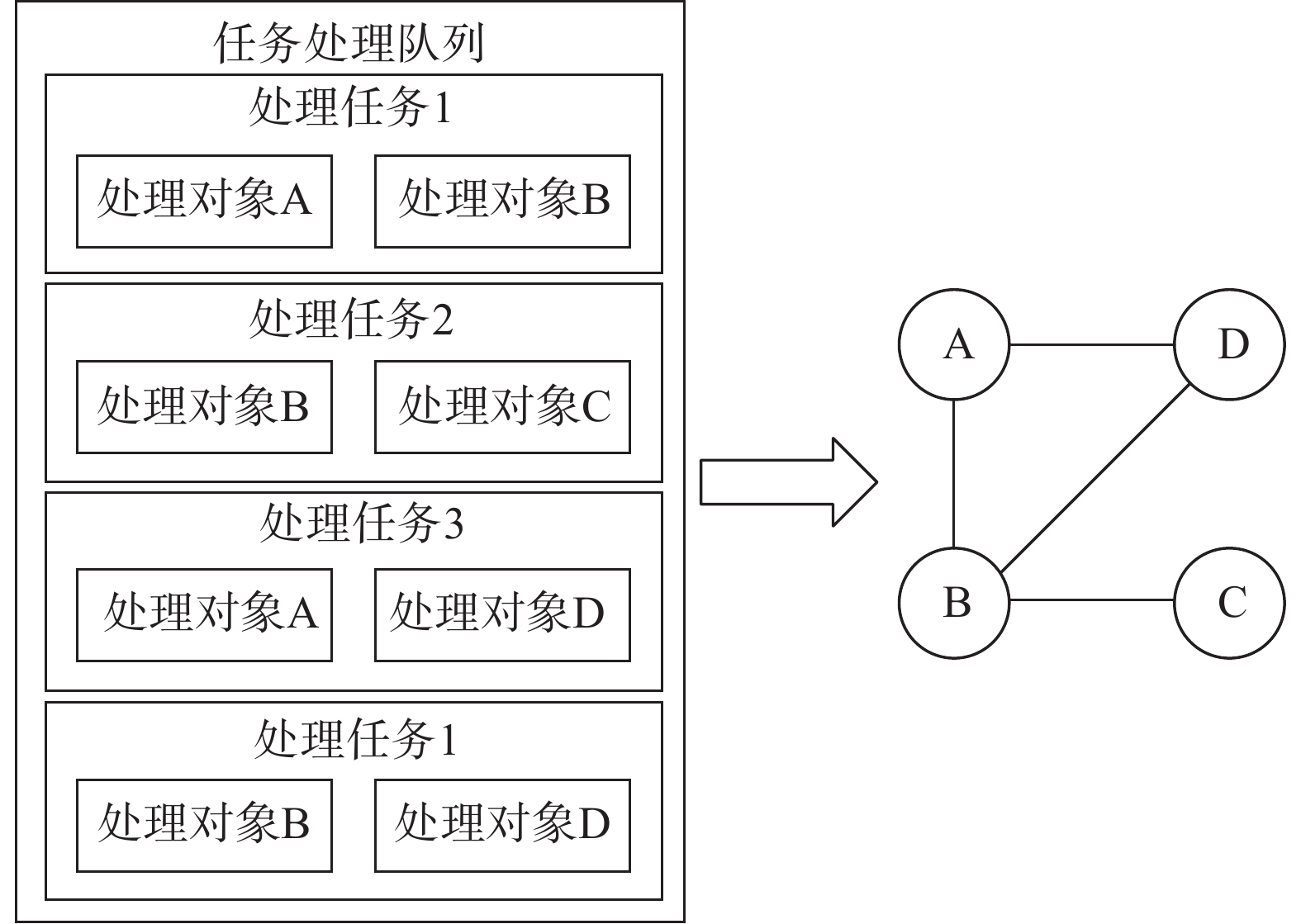
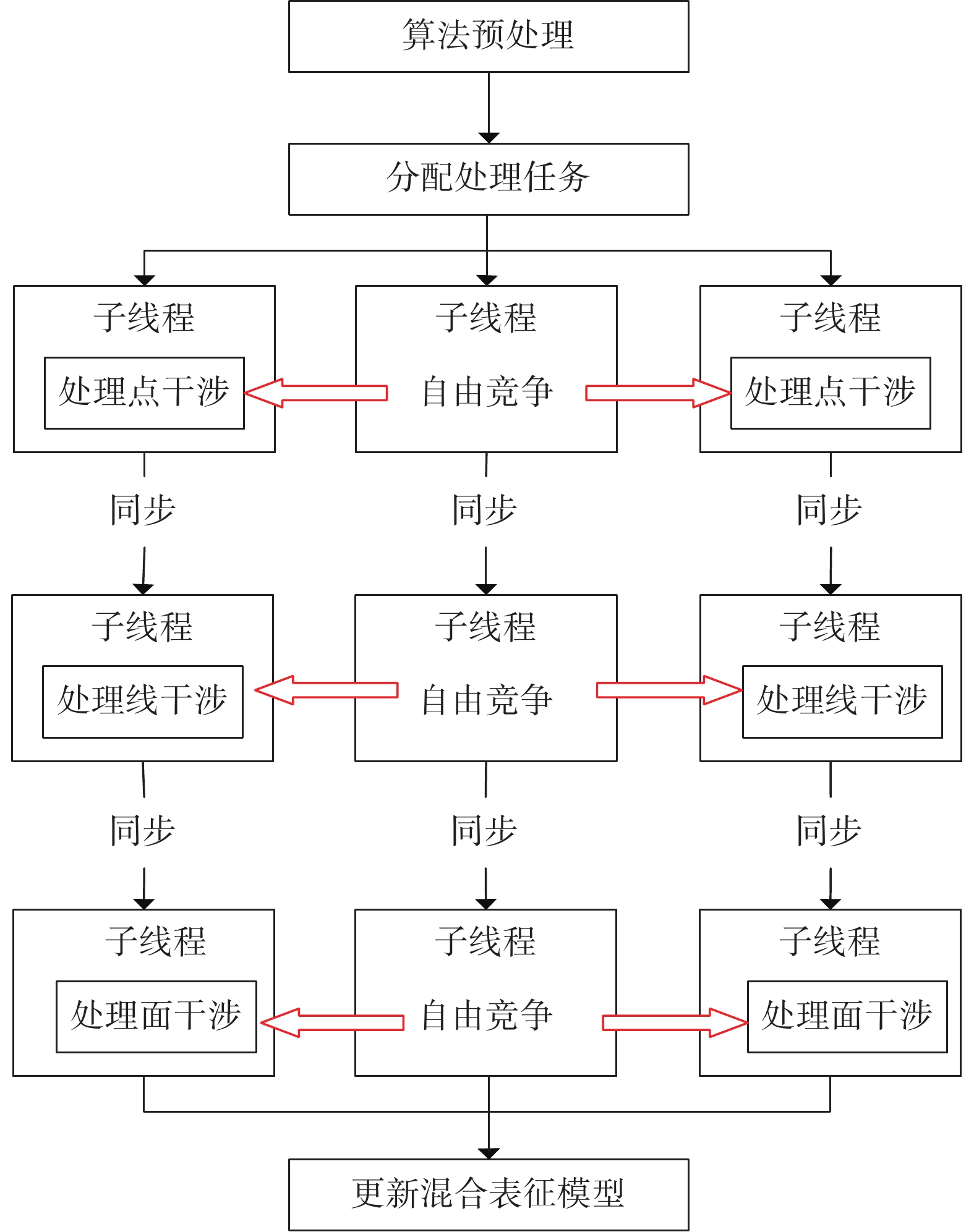
上述的串行方法,当几何对象的干涉数量上万时,处理时间接近半个小时,占据整个网格生成时间的一半以上,因此,我们进一步提出基于共享内存的并行化处理方法。其核心思路是:首先对所有要干涉处理任务,判定其所影响的几何对象,然后将处理任务依次分配给不同的线程进行处理。因此,在原串行算法的预处理环节中,增加建立任务影响邻接图步骤,该邻接图反映了待处理对象间的影响关系。如图10所示,任务队列中有4个任务,处理对象包括A、B、C、D四个,根据处理任务中的对象信息可以构建邻接图,该邻接图反应了待处理对象间的影响关系。在线程中执行处理任务时,先通过邻接图获取处理任务所影响的对象,为对象上锁,若对象已被上锁,则线程等待,接着,按串行算法执行处理任务,最后,为对象解锁。并行曲面嵌入算法流程如图11所示,详细步骤如表2所示。
| 表 1 自低维向高维的局部几何干涉解除规则 Table 1 Rules for resolving local interferences from lower dimensions to higher dimensions |
|
|
|
图 10 干涉处理任务邻接关系图 Fig.10 An adjacency graph of tasks |
|
图 11 并行曲面嵌入算法流程 Fig.11 Sketch for the parallel surface imprinting |
| 表 2 并行曲面嵌入算法 Table 2 The algorithm for parallel surface imprinting |
|
|
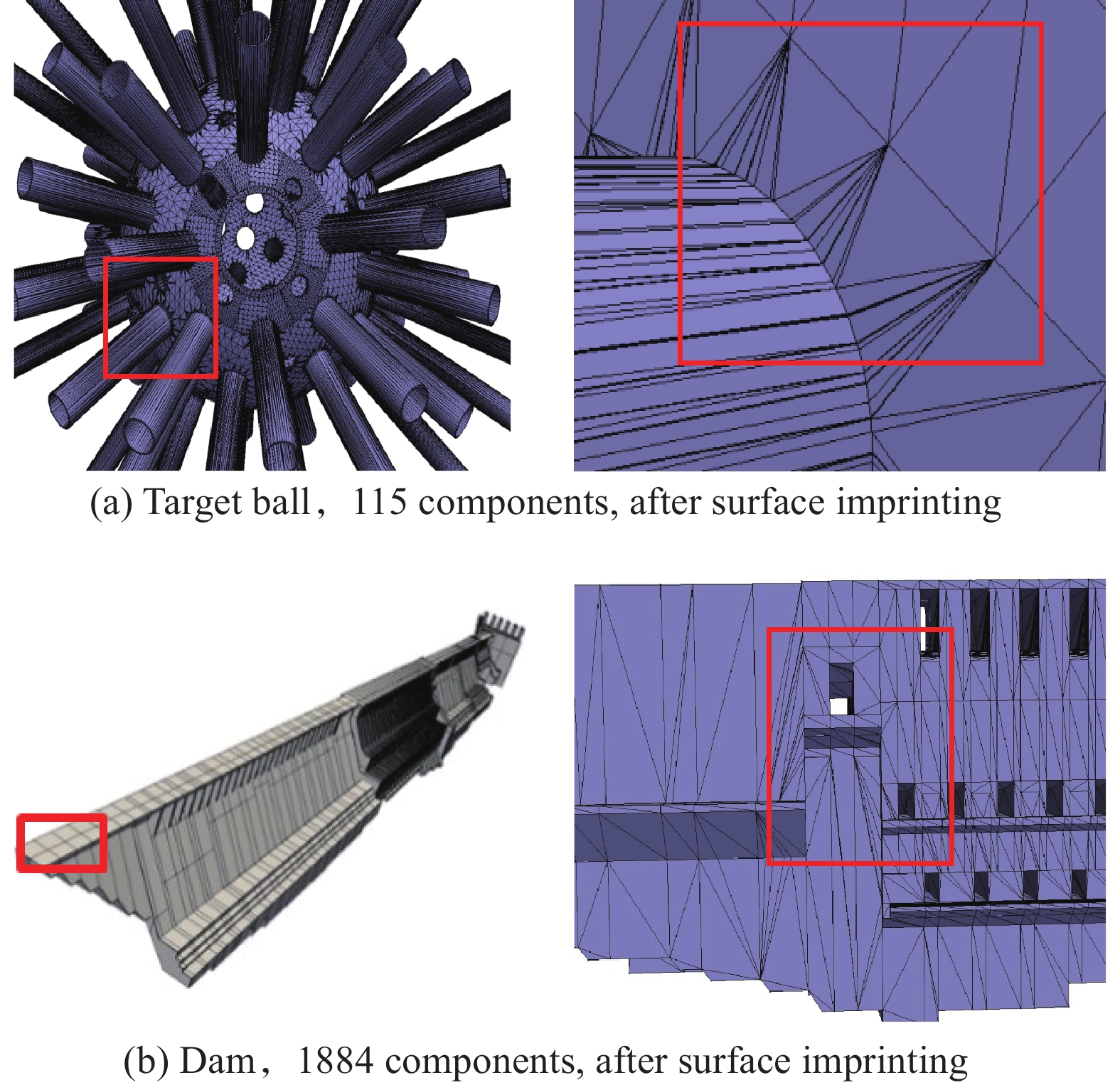
基于并行曲面嵌入方法对大坝模型和靶球模型分别进行了串行和多线程并行的测试,测试环境为中物院高性能数值模拟软件中心的高性能计算集群系统,采用Intel Xeon E5-2680v4(2.4 GHz)处理器,单节点28核,64G内存。如图12所示,输入的靶球模型包含115部件,1952张曲面和4739条曲线,检测出模型干涉数为15177个,执行曲面嵌入算法,串行耗时1047 s,多线程并行最低耗时457 s;大坝模型包含1884部件,检测出模型干涉数为35174个,执行曲面嵌入算法,串行耗时1521 s,多线程并行最低耗时696 s。测试结果如表3所示。
|
图 12 模型的曲面嵌入效果 Fig.12 Examples of surface imprinting |
| 表 3 并行曲面嵌入算法测试 Table 3 Parallel performance of the surface imprinting algorithm |
|
|
从表3可看出,我们提出的并行模型处理方法相比串行方法,能提高大概1倍的效率。但在可扩展性上并不理想,这是由于曲面嵌入算法的扩展性与模型干涉特征紧密相关,因此该方法依然有改进空间。
此外,针对CAD模型信息无缝传递给CAE几何模型的需求,我们提出基于离散CAD模型的信息自动重构方法。目前,已实现相似几何体自动识别算法和适用于任意曲面类型的接触关系自动识别算法。前者基于几何矩理论,采用一组满足平移、旋转、缩放不变性的几何矩不变量对三维几何体的形状特征进行描述,并根据形状特征向量的相似程度评估几何体之间的相似性[51],从而支持批量自动选取几何相似的对象,避免人工交互下的错选和漏选。针对复杂的离散CAD模型可能包含数千万甚至上亿三角面片,后者采用多线程并行加速筛选和接触检测过程,自动提取数百部件模型包含的接触关系只需15 s左右,同时,为了提高识别精度, 还根据模型特征计算几何对象间的局部容差, 基于局部容差进行接触检测,相比Ansys和Abaqus采用统一容差进行检测,检测结果更准确。
面向结构网格生成要对CAE几何模型进行分区处理的需求,我们实现了可复用的拓扑分区模板。通过将自动识别的几何构型特征点与拓扑分区模板自动匹配,实现将同一模板重复应用到同类几何构型上,提高了工作效率。例如图13所示,应用分区拓扑模板自动处理发动机三维风扇转子模型,生成结构网格。

|
图 13 可复用拓扑分区模板效果 Fig.13 Application of a reusable topology partition template |
当生成大规模网格时,串行网格生成和并行求解程序之间产生的输入、输出代价不可忽略。而当前的分布式并行网格生成与近万核并行求解器对接时,区域分解过程仍然存在分区数目过多造成的低质量人工边界等分区瓶颈问题。针对上述问题,我们提出多级并行网格生成与优化框架,该框架按照部分复用串行算法的方法,通过多级分区方式,克服分区瓶颈问题,并行可扩展性良好[12,52],可支持十亿量级以上网格并行生成。
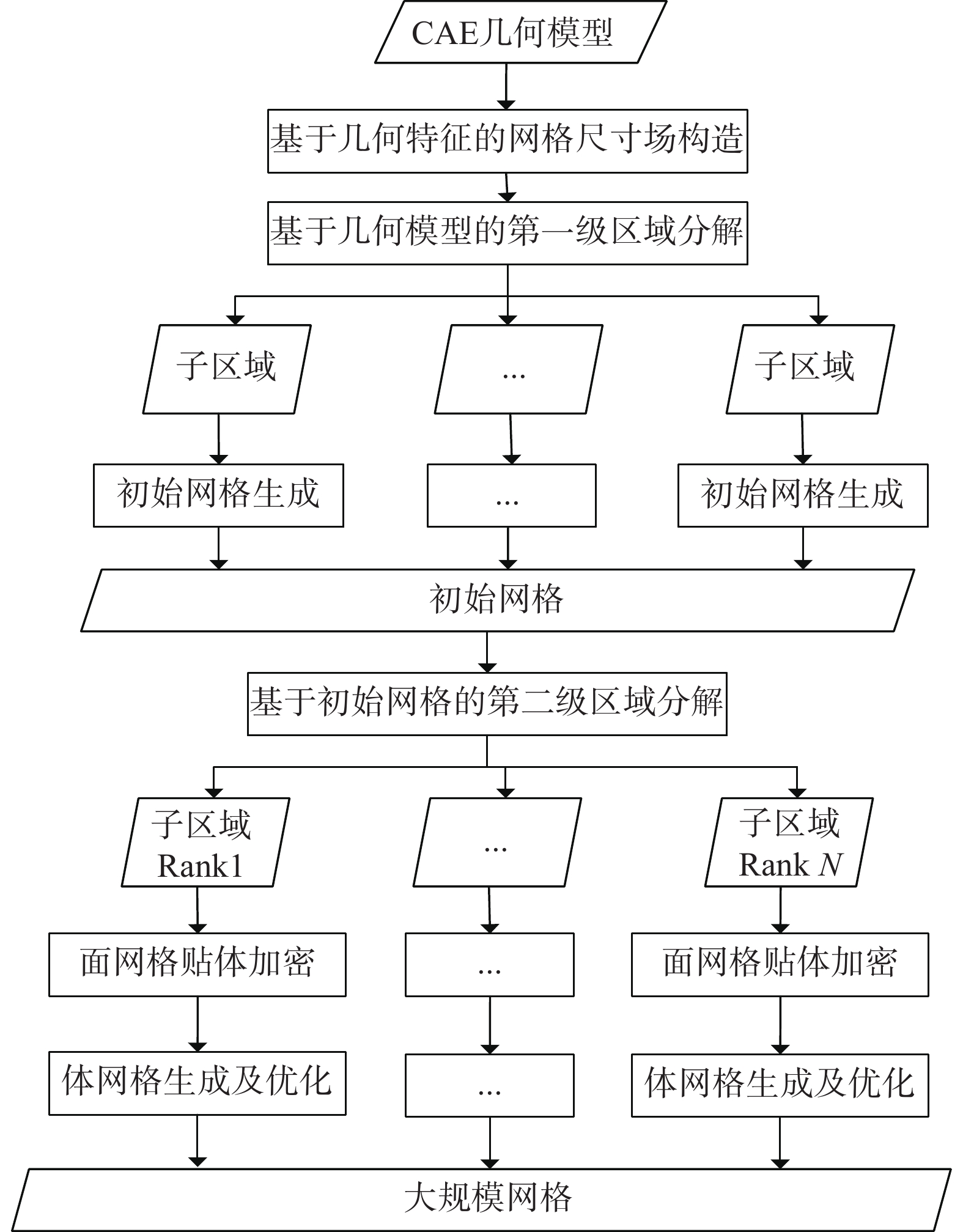
多级并行网格生成与优化的核心思路是:首先基于对网格分布情况的预估,对CAE几何模型进行第一级分解,将几何实体分配到不同的进程组中,在各进程中完成对初始网格的并行生成;接着,以初始网格为背景网格,进行第二级区域分解,再进行大规模网格的并行细化及优化[53],算法流程如图14,详细步骤如表4所示。
|
图 14 多级并行网格生成与优化流程 Fig.14 Diagram of multi-level parallel mesh generation and optimization |
| 表 4 多级并行网格生成与优化算法 Table 4 Mulit-level parallel mesh generation and optimization algorithm |
|
|
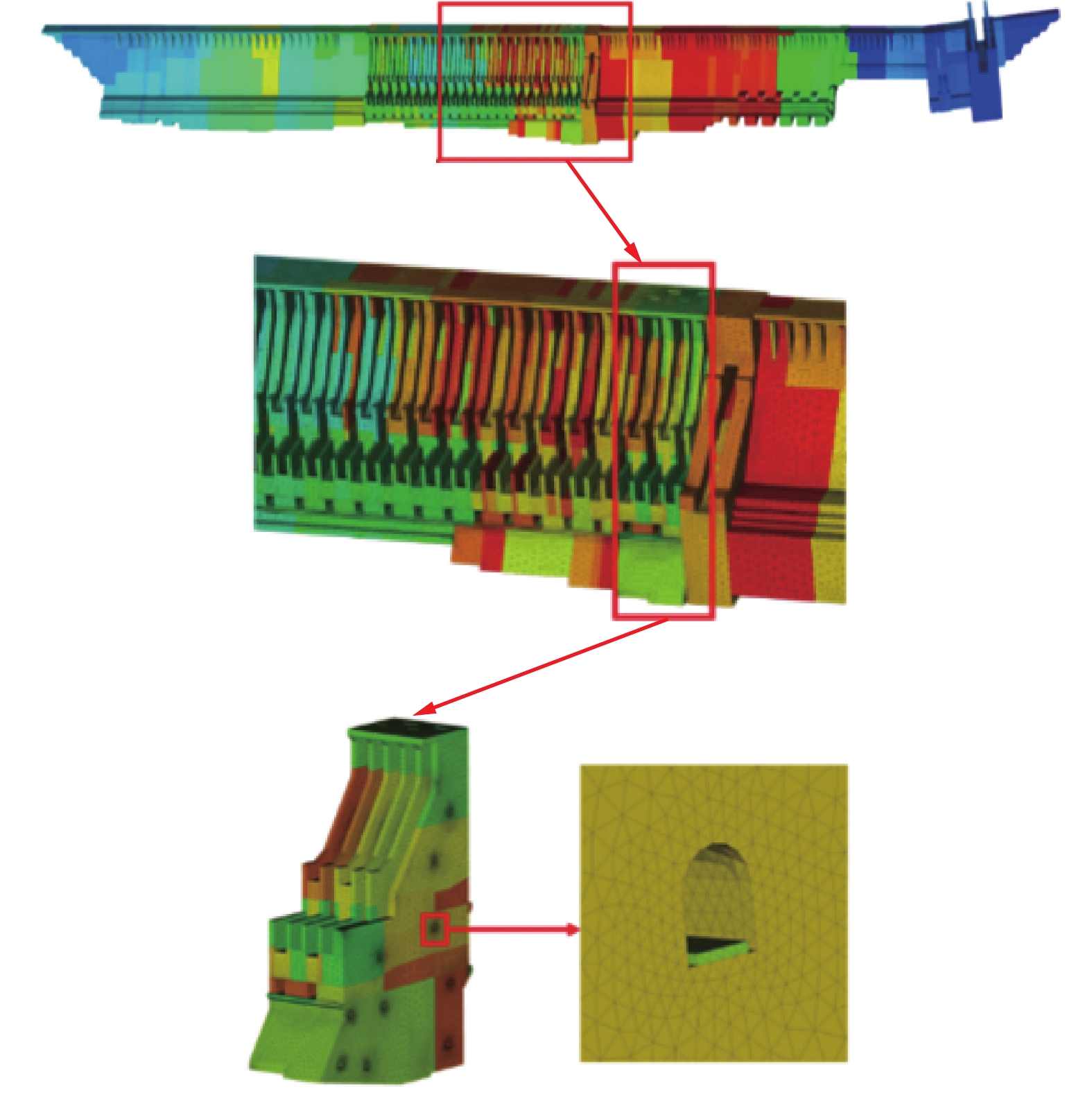
基于多级并行网格生成方法对上文中的大坝模型进行百亿网格生成,坝体初始网格结果如图15所示,测试环境为神威太湖之光超级计算机,可扩展结果如表5所示,可以看出该方法有较高的并行效率。基于多级并行网格生成方法对F6模型进行了混合网格剖分,初始网格如图16所示,混合网格在边界层采用半结构化的三棱柱单元,剩余区域采用四面体单元填充。
|
图 15 大坝模型的初始网格 Fig.15 The initial meshes for a dam model |
| 表 5 算法可扩展性测试 Table 5 Scalability test |
|
|

|
图 16 F6模型的初始网格 Fig.16 The initial meshes for F6 |
国产并行网格生成软件要能实现世界领先,核心竞争力在于并行网格生成技术的超越。过去十年,基于国产顶尖超算系统的大规模数值模拟应用取得了显著进步,服务于高性能数值模拟应用的并行网格生成技术也得到了很大发展。随着算力指数进入E级时代以及人工智能成为新一代超算系统重要的应用场景,并行网格生成需要适应新形势,未来可从以下两个方面把握技术的发展方向:
1)基于异构并行体系的并行网格生成方法。超算平台已发展为CPU和加速器(GPU)混合的异构并行体系,并行网格生成方法将以计算节点间分布式并行和计算节点内异构线程并行相结合的编程模型为主流,已有的方法需通过移植或改造,适应加速器等硬件,充分发挥超算平台的性能优势;此外,超大规模应用的复杂模型占用内存巨大,难以在单个计算节点上进行处理,需研究模型的分布式存储和表征方法,以及发展基于分布式内存的并行模型处理方法。
2)基于人工智能辅助实现高度自动化网格生成。在网格生成过程中,算法关联错误处理、设置网格尺寸等环节很大程度上依赖工程经验。基于人工智能技术能从经验数据中习得“模式”,然后依据“模式”实现处理的自动化,且对复杂问题的处理成功率将随着数据的积累而不断提高。例如,模型清理中,可基于模型的几何特征集和处理操作集构建神经网络的输入空间,再利用生成网格的质量度量不断反馈和修正网络,从而得到较优的操作组合;基于几何分解法的六面体占优网格生成中,通过大量样本训练可成功识别复杂模型的扫掠特征和拓扑六面体块特征,进而实现模型自动分解和网格生成;基于人工智能技术还能建立起几何外形或关键特征与网格密度分布之间的关系,为网格节点分布和自适应提供更好的依据,提高网格自适应的效率和计算结果的精准度。
4 结 束 语面向高性能数值模拟的网格生成与普通的网格生成不同,在求解问题的复杂度和规模不断增大的前提下,一方面需要实现网格生成的高度自动化,另一方面需要通过并行化来突破生成超大规模网格的内存和效率瓶颈,这就决定了必须发展相应的并行网格生成软件来满足需求。本文在分析国内外相关技术和软件的发展现状基础上,指出加强并行网格生成软件的研制既是挑战,也是机遇,详细介绍了自主可控并行网格生成软件SuperMesh的架构设计和关键技术,并对技术未来的发展方向进行了探讨,对相关技术研究和产品研发具有借鉴意义。
| [1] |
OWEN S J, CLARK B W, MELANDER D J, et al. An immersive topology environment for meshing[C]// 16th International Meshing Roundtable, 2008. doi: 10.1007/978-3-540-75103-8_31
|
| [2] |
LINTERMANN A, SCHLIMPERT S, GRIMMEN J H, et al. Massively parallel grid generation on HPC systems[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 277: 131-153. DOI:10.1016/j.cma.2014.04.009 |
| [3] |
LOSEILLE A, MENIER V, ALAUZET F. Parallel generation of large-size adapted meshes[J]. Procedia Engineering, 2015, 124: 57-69. DOI:10.1016/j.proeng.2015.10.122 |
| [4] |
GERTEISEN E A, HILBRINK N, MEZENTSEV A A, et al. CAD repair for finite element type simulation methods[C]//Proceedings of the Swiss CAD/CAM conference, Neuchatel University, Switzerland, 1999: 266-276.
|
| [5] |
HAMDI M, AIFAOUI N, LOUHICHI B, et al. Idealization of CAD model for a simulation by a finite element method[J]. European Journal of Computational Mechanics, 2010, 19(4): 419-439. DOI:10.3166/ejcm.19.419-439 |
| [6] |
DANGLADE F, PERNOT J P, VÉRON P. On the use of machine learning to defeature CAD models for simulation[J]. Computer-Aided Design and Applications, 2014, 11(3): 358-368. DOI:10.1080/16864360.2013.863510 |
| [7] |
王瑞, 高曙明, 吴海燕. 六面体网格生成和优化研究进展[J]. 计算机辅助设计与图形学学报, 2020, 32(5): 693-708. WANG R, GAO S M, WU H Y. Progress in hexahedral mesh generation and optimization[J]. Journal of Computer-Aided Design & Computer Graphics, 2020, 32(5): 693-708. (in Chinese) |
| [8] |
RUIZ-GIRONÉS E, SARRATE J, ROCA X. Generation of curved high-order meshes with optimal quality and geometric accuracy[J]. Procedia Engineering, 2016, 163: 315-327. DOI:10.1016/j.proeng.2016.11.108 |
| [9] |
CHRISOCHOIDES N. Parallel mesh generation[M]//Lecture Notes in Computational Science and Engineering. Berlin/Heidelberg: Springer-Verlag, : 237-264. doi:10.1007/3-540-31619-1_7
|
| [10] |
LÖHNER R. A 2nd generation parallel advancing front grid generator[C]// 21st International Meshing Roundtable, 2013. doi: 10.1007/978-3-642-33573-0_27
|
| [11] |
FOTEINOS P, CHRISOCHOIDES N. Dynamic parallel 3D delaunay triangulation[C]//Proceedings of the 20th International Meshing Roundtable, 2012. doi: 10.1007/978-3-642-24734-7_1
|
| [12] |
ZHENG P, YANG Y, LIU Z W, et al. Parallel and automatic isotropic tetrahedral mesh generation of misaligned assemblies[J]. CCF Transactions on High Performance Computing, 2020, 2(2): 149-163. DOI:10.1007/s42514-020-00024-x |
| [13] |
CHEN J J, LIU Z W, ZHENG Y, et al. Automatic sizing functions for 3D unstructured mesh generation[J]. Procedia Engineering, 2017, 203: 245-257. DOI:10.1016/j.proeng.2017.09.804 |
| [14] |
TREMEL U, SØRENSEN K A, HITZEL S, et al. Parallel remeshing of unstructured volume grids for CFD applications[J]. International Journal for Numerical Methods in Fluids, 2007, 53(8): 1361-1379. DOI:10.1002/fld.1195 |
| [15] |
Mesh generation and grid generation: Software[EB/OL]. [2020-06-03]. http://www.robertschneiders.de/meshgeneration/software.html
|
| [16] |
FAROUKI R T. Closing the gap between CAD model and downstream application[J]. SIAM News, 1999, 32(5): 303-319. |
| [17] |
BRONSART R. Automatic pre-mesh CAD data repairing[J]. International Journal of Mechanical Engineering and Applications, 2013, 1(1): 1-9. DOI:10.11648/j.ijmea.20130101.11 |
| [18] |
AYUSO L, JORDAN H, FAHRINGER T, et al. Parallelizing a CAD model processing tool from the automotive industry[C]//Euro-Par 2014: Parallel Processing Workshops, 2014. doi: 10.1007/978-3-319-14325-5_3
|
| [19] |
ANDERS N, KYLE P, CHAND K K. Detecting translation errors in CAD surfaces and preparing geometries for mesh generation[C]// Proceedings of 10th International Meshing Roundtable, Seattle, USA, 2001, 1: 363-371.
|
| [20] |
BISCHOFF S, KOBBELT L. Structure preserving CAD model repair[J]. Computer Graphics Forum, 2005, 24(3): 527-536. DOI:10.1111/j.1467-8659.2005.00878.x |
| [21] |
PIRET C, REMACLE J F, MARCHANDISE E. Mesh and CAD repair based on parametrizations with radial basis functions[C]//Proceedings of the 20th International Meshing Roundtable, 2012. doi: 10.1007/978-3-642-24734-7_23
|
| [22] |
李明. 工程仿真精度可信的CAD模型简化[J]. 计算机辅助设计与图形学学报, 2015, 27(8): 1363-1375. LI M. Review on engineering analysis reliable CAD model simplification[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(8): 1363-1375. DOI:10.3969/j.issn.1003-9775.2015.08.003 (in Chinese) |
| [23] |
LEE S H. A CAD-CAE integration approach using feature-based multi-resolution and multi-abstraction modelling techniques[J]. Computer-Aided Design, 2005, 37(9): 941-955. DOI:10.1016/j.cad.2004.09.021 |
| [24] |
LI M, ZHENG J Z, MARTIN R R. Quantitative control of idealized analysis models of thin designs[J]. Computers & Structures, 2012, 106-107: 144-153. DOI:10.1016/j.compstruc.2012.04.012 |
| [25] |
KAVEH A. Introduction to symmetry and regularity[M]//Optimal Analysis of Structures by Concepts of Symmetry and Regularity. Vienna: Springer Vienna, 2013: 1-14. doi: 10.1007/978-3-7091-1565-7_1
|
| [26] |
3DInterOP[EB/OL] [2021-10-29]. https://www.spatial.com/products/3d-interoperability.
|
| [27] |
KIRKWOOD R, SHERWOOD J A. Sustained CAD/CAE integration: integrating with successive versions of step or IGES files[J]. Engineering with Computers, 2018, 34(1): 1-13. DOI:10.1007/s00366-017-0516-z |
| [28] |
WALSHAW C, CROSS M. Mesh partitioning: a multilevel balancing and refinement algorithm[J]. SIAM Journal on Scientific Computing, 2000, 22(1): 63-80. DOI:10.1137/s1064827598337373 |
| [29] |
王俊吉, 朱朝艳, 陈建军, 等. 基于无锁原子操作的多线程并行Delaunay三角化算法[J]. 计算机工程与科学, 2018, 40(5): 773-779. WANG J J, ZHU C Y, CHEN J J, et al. A multithreaded parallel Delaunay triangulation algorithm based on lock-free atomic operations[J]. Computer Engineering and Science, 2018, 40(5): 773-779. DOI:10.3969/j.issn.1007-130X.2018.05.002 (in Chinese) |
| [30] |
LINARDAKIS L, CHRISOCHOIDES N. Delaunay decoupling method for parallel guaranteed quality planar mesh refinement[J]. SIAM Journal on Scientific Computing, 2006, 27(4): 1394-1423. DOI:10.1137/030602812 |
| [31] |
DIGNNET H , SILVA H, COUPEZ T. Massively parallel computation on anisotropic meshes[C]//Proceedings of 6th International Conference on Adaptive Modeling and Simulation, June, Lisbon, portugal, 2013, 1: 199-211.
|
| [32] |
LACHAT C, DOBRZYNSKI C, PELLEGRINI F. Parallel mesh adaption using parallel graph partitioning[C]//5th European conference on computational mechanics (ECCM V), July, Barcelone, Spain, 2014, 3: 2612-2613.
|
| [33] |
ALAUZET F, LI X R, SEOL E S, et al. Parallel anisotropic 3D mesh adaptation by mesh modification[J]. Engineering with Computers, 2006, 21(3): 247-258. DOI:10.1007/s00366-005-0009-3 |
| [34] |
JONES M T, PLASSMANN P E. Parallel algorithms for adaptive mesh refinement[J]. SIAM Journal on Scientific Computing, 1997, 18(3): 686-708. DOI:10.1137/S106482759528065X |
| [35] |
BALMAN M. Tetrahedral mesh refinement in distributed environments[C]//Proc of the 2006 International Conference on Parallel Processing Workshops (ICPPW'06), Columbus, OH, USA. IEEE, 2006: 8pp. -504. doi: 10.1109/ICPPW.2006.72
|
| [36] |
RANTAKOKKO J, THUNÉ M. Parallel structured adaptive mesh refinement[M]//Parallel Computing. London: Springer London, 2009: 147-173. doi: 10.1007/978-1-84882-409-6_5
|
| [37] |
ShONTZ S M , LOPEZ V, MAURIN A, et al. A parallel variational mesh quality improvement method for tetrahedral meshes[C]// Proceeding of the 28th International Meshing Roundtable (IMR), February, Buffalo, New York, USA, 2020: 30-42.
|
| [38] |
Parallel programming with Julia using MPI [EB/OL]. [2018-09-30]. http://www.claudiobellei.com/2018/09/30/julia-mpi
|
| [39] |
DYEDOV V, RAY N, EINSTEIN D, et al. AHF: array-based half-facet data structure for mixed-dimensional and non-manifold meshes[J]. Engineering with Computers, 2015, 31(3): 389-404. DOI:10.1007/s00366-014-0378-6 |
| [40] |
RAY N, GRINDEANU I, ZHAO X L, et al. Array-based hierarchical mesh generation in parallel[J]. Procedia Engineering, 2015, 124: 291-303. DOI:10.1016/j.proeng.2015.10.140 |
| [41] |
高翔, 张翔, 徐传福, 等. 面向科学工程计算的通用网格生成软件系统研究[J]. 计算机工程与科学, 2020, 42(10): 1897-1904. GAO X, ZHANG X, XU C F, et al. Research on general mesh generation software for scientific engineering computing[J]. Computer Engineering and Science, 2020, 42(10): 1897-1904. DOI:10.3969/j.issn.1007-130X.2020.10.023 (in Chinese) |
| [42] |
SIGMA[EB/OL]. [2021-10-29]. https://sigma.mcs.anl.gov
|
| [43] |
Grummp[EB/OL]. [2021-10-29]. http://tetra.mech.ubc.ca/GRUMMP
|
| [44] |
郑耀, 陈建军. 非结构网格生成: 理论、算法和应用[M]. 北京: 科学出版社, 2016. ZHENG Y, CHEN J J. Unstructured mesh generation: Theories, algorithms and applications[M]. Beijing: Science Press, 2016(in Chinese). |
| [45] |
SuperMesh[EB/OL]. [2021-10-29].http://www.caep-scns.ac.cn/SuperMesh.php
|
| [46] |
PÉBAY P P, STEPHENSON M B, FORTIER L A, et al. pCAMAL: an embarrassingly parallel hexahedral mesh generator[C]//Proceedings of the 16th International Meshing Roundtable, 2008. doi: 10.1007/978-3-540-75103-8_16
|
| [47] |
ANSYS FLuent[EB/OL]. [2021-10-29]. https://www.ansys.com/zh-cn/products/fluids/ansys-fluent
|
| [48] |
莫则尧. 面向高性能科学与工程计算的领域编程框架研究[J]. 中国计算机学会通讯, 2014, 10(1): 8-12. MO Z Y. Research on parallel programming framework for high performance scientific and engineering computing[J]. Communications of CCF, 2014, 10(1): 8-12. (in Chinese) |
| [49] |
莫则尧, 郑澎, 肖丽, 等. 高性能数值模拟的前后处理低开销连接数据结构及方法: CN111814384B[P]. 2020-12-11. MO Z Y, ZHENG P, XIAO L, et al. Front-back low-overhead connection data structure and method for high-performance numerical simulation: CN111814384B[P]. 2020-12-11 (in Chinese). |
| [50] |
刘智伟, 杨洋, 陈建军等. 面向错位装配体的自动曲面嵌入算法[J]. 空气动力学学报, 2022, 40(5): 166-174. LIU Z W, YANG Y, CHEN J J, et al. Automatic surface imprinting for misaligned assembly CAD models[J]. Acta Aerodynamica Sinica, 2022, 40(5): 166-174. DOI:10.7638/kqdlxxb-2021.0005 (in Chinese) |
| [51] |
冷珏琳, 张哲, 刘田田, 等. 基于几何矩的CAD模型形状匹配算法及应用[J]. 图学学报, 2021, 42(4): 608-614. LENG J L, ZHANG Z, LIU T T, et al. A shape matching algorithm based on geometric moments and its applications on CAD models[J]. Journal of Graphics, 2021, 42(4): 608-614. (in Chinese) |
| [52] |
徐权, 刘田田, 冷珏琳, 等. 面向复杂几何模型的多级并行四面体网格生成算法[J]. 国防科技大学学报, 2021, 43(2): 33-39. XU Q, LIU T T, LENG J L, et al. Multilevel parallel tetrahedral mesh generation for complex geometric models[J]. Journal of National University of Defense Technology, 2021, 43(2): 33-39. DOI:10.11887/j.cn.202102005 (in Chinese) |
| [53] |
郑澎, 方维, 徐权, 等. 面向JAUMIN的并行AFT四面体网格生成[J]. 计算机科学与探索, 2018, 12(4): 567-574. ZHENG P, FANG W, XU Q, et al. Parallel AFT tetrahedral mesh generation for JAUMIN[J]. Journal of Frontiers of Computer Science and Technology, 2018, 12(4): 567-574. DOI:10.3778/j.issn.1673-9418.1611083 (in Chinese) |
 2022, Vol. 40
2022, Vol. 40

