2. 国防科技大学 理学院 数学系,长沙 410073
2. Department of Mathematics, College of Science, National University of Defense Technology, Changsha 410073, China
高阶精度格式相比于低阶格式在精细结构模拟中更具优势,随着工程问题对于精细结构模拟要求的逐步提升,高阶精度格式成为计算流体力学中的一个重点研究方向[1-3]。在高阶精度格式中,重构修正方法(correction procedure via reconstruction, CPR)具有格式紧致、高效、可应用于复杂非结构网格的优点。它最初由Huynh[4]提出,并由王志坚等[5]推广至非结构网格上,现被较多应用到科学计算和工程预测之中。但CPR在捕捉激波时容易产生虚假的数值振荡[1],故CPR的激波捕捉技术成为研究焦点[1-2,4-5]。
舒其望等[6]在CPR方法中引入WENO限制器,保持了光滑区域上的高阶精度特性,并在间断附近有效抑制了数值振荡。李万爱等[7]通过提出一个p加权的过程,在间断Galerkin方法(discontinuous Galerkin, DG)上构造了新的光滑因子,提高了激波捕捉性能,然而间断附近的振荡现象未被完全消除。具有子单元分辨率的人工黏性法[8]也被提出,但是它依赖于参数的人工选择。
一个可行的解决办法是构造有限元方法(如CPR或DG)和有限差分法( finite difference method, FD)/有限体积法(finite volume method, FV)的混合格式,使得在间断附近具有更好的局部激波捕捉能力。这种方法的思路是,在光滑区域使用高阶有限元方法保持紧致和高分辨率的性质,在间断附近采用FD或FV提供鲁棒的激波捕捉能力。Dumbser等提出DG-FV混合格式[9]并使用二阶FV来捕捉激波。刘铁钢等[10]提出具有良好几何灵活性和高计算效率的Runge-Kutta间断Galerkin方法(the Runge-Kutta discontinuous Galerkin method, RKDG)和加权本质无振荡格式(weighted essentially non-oscillatory schemes, WENO)的区域混合格式。这些格式避免了高阶有限元方法直接处理激波,而是使用具有良好激波捕捉能力的格式进行激波捕捉,从而使得混合格式具有良好的激波捕捉特性。
朱华君等[11]构造了基于区域混合思路的混合WCNS-CPR格式,解决了混合格式的空间精度和几何守恒律等基础问题,该格式计算效率较高且易于应用到复杂曲网格中。最近,基于单元动态混合思想,郭嘉和朱华君等[12]构造了WCNS-CPR格式的激波捕捉技术。本文,我们在混合WCNS-CPR格式基础上,针对高阶CPR方法,通过引入激波侦测器和基于高阶WCNS插值的二阶格式来模拟带有激波的流动问题,进一步提高混合算法的计算效率并增强混合算法的激波捕捉能力。
1 数值方法以一维守恒律方程(1)为例,对三阶CPR方法和高分辨率二阶格式作简要的介绍。
| $ \frac{{\partial {\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial {\boldsymbol{F}}({\boldsymbol{U}})}}{{\partial x}} = 0 $ | (1) |
对于三阶CPR方法,第i个单元的三个求解点处的守恒变量
| $ \frac{{\partial {{\boldsymbol{U}}_{i,k}}}}{{\partial t}} + {\left. {\frac{{\partial {{\boldsymbol{F}}_i}(\xi )}}{{\partial \xi }}} \right|_{\xi = {\xi _k}}} + {\left. {\frac{{\partial {{\boldsymbol{\sigma }}_i}(\xi )}}{{\partial \xi }}} \right|_{\xi = {\xi _k}}} = 0,\;\;\xi \in [ - 1,1] $ | (2) |
式中:
| $ \begin{split}& {{\boldsymbol{F}}_i}(\xi ) = \sum\limits_{l = 1}^3 {{{\boldsymbol{F}}_{i,l}}} {\tilde L_l}(\xi ) \\& {{\boldsymbol{\sigma }}_i}({\xi _l}) = [{{\tilde {\boldsymbol{F}}}}( - 1) - {{\boldsymbol{F}}_i}( - 1)]{g_{\rm{L}}}({\xi _l}) + [{{\tilde {\boldsymbol{F}}}}(1) - {{\boldsymbol{F}}_i}(1)]{g_{\rm{R}}}({\xi _l}) \\ \end{split} $ | (3) |
其中,
| $ \begin{split} {{\tilde {\boldsymbol{F}}}}( - 1) = {{\tilde {\boldsymbol{F}}}}({{\boldsymbol{U}}_{i - 1}}(1),{{\boldsymbol{U}}_i}( - 1)) \\ {{\tilde {\boldsymbol{F}}}}(1) = {{\tilde {\boldsymbol{F}}}}({{\boldsymbol{U}}_i}(1),{{\boldsymbol{U}}_{i + 1}}( - 1)) \\ \end{split}$ | (4) |
这里
本文使用的求解点是高斯点:
| $ \begin{split}& {g_{\rm{L}}}(\xi ) = {g_{{\rm{DG,L}}}} = {{{( - 1)}^3}} \cdot ({\tilde L_3}(\xi ) - {\tilde L_2}(\xi ))/2 \\& {g_{\rm{R}}}(\xi ) = {g_{{\rm{DG,R}}}} =({\tilde L_3}(\xi ) + {\tilde L_2}(\xi )) /2 \end{split}$ |
其中:
WCNS格式[13-14]的构造过程主要包含三部分:非线性插值、数值通量以及通量导数的求解。文献[15]中指出,基于对称守恒型网格导数算法(symmetrical conservative metric method,SCMM)的WCNS可分解为多个二阶格式。本文采用了基于高阶WCNS插值的二阶格式,此格式为三阶WCNS的分解格式之一,即非线性插值为高阶WCNS插值,而通量导数使用二阶差分算子的格式,这里简称为高分辨率二阶格式(high-resolution second order finite difference scheme,HRFD2)。
1.2.1 三阶WCNS非线性插值基于网格点上的守恒变量
| $ {\boldsymbol{Q}}_k^{} = \sum\limits_{m{\text{ = 1}}}^n {{{\boldsymbol{l}}_{i,m}}{{\boldsymbol{U}}_{k,m}}} ,\;\;k = i - 1,i,i + 1 $ | (5) |
式中:n为方程和变量数目,
模板
| $ \begin{gathered} {{\boldsymbol{p}}^{(1)}}({x_{i + \frac{1}{2}}}) = \dfrac{3}{2}{{\boldsymbol{Q}}_i} - \frac{1}{2}{{\boldsymbol{Q}}_{i - 1}} \\ {{\boldsymbol{p}}^{(2)}}({x_{i + \frac{1}{2}}}) = \dfrac{1}{2}{{\boldsymbol{Q}}_i} + \frac{1}{2}{{\boldsymbol{Q}}_{i + 1}} \\ \end{gathered} $ | (6) |
进而,基于
| $ {\mkern 1mu} {\boldsymbol{Q}}_{i + \frac{1}{2},m}^{\rm{L}} = \sum\limits_{k = 1}^2 {\omega _{k,m}^{}{\boldsymbol{p}}_m^{(k)}({x_{i + \frac{1}{2}}})} $ | (7) |
式中
| $ {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \;\begin{array}{*{20}{c}} {{\beta _{k,m}} = {d_k}[{C_q} + {{(\frac{{\tau _5^m}}{{\varepsilon + {\boldsymbol{I}}{{\boldsymbol{S}}_{k,m}}}})}^{{p_z}}}],}&{k = 1,2} \end{array} $ | (8) |
其中:
| $ \begin{gathered} {\boldsymbol{I}}{{\boldsymbol{S}}_0} = \frac{1}{4}{(3{{\boldsymbol{Q}}_i} - 4{{\boldsymbol{Q}}_{i - 1}} + {{\boldsymbol{Q}}_{i - 2}})^2} + {({{\boldsymbol{Q}}_i} - 2{{\boldsymbol{Q}}_{i - 1}} + {{\boldsymbol{Q}}_{i - 2}})^2} \\ {\boldsymbol{I}}{{\boldsymbol{S}}_1} = \frac{1}{4}{(3{{\boldsymbol{Q}}_{i + 2}} - 4{{\boldsymbol{Q}}_{i + 1}} + 3{{\boldsymbol{Q}}_i})^2} + {({{\boldsymbol{Q}}_{i + 2}} - 2{{\boldsymbol{Q}}_{i + 1}} + {{\boldsymbol{Q}}_i})^2} \\ \end{gathered} $ | (9) |
最后,特征变量
数值通量
| $ {{\tilde {\boldsymbol{F}}}}_{i + \frac{1}{2}}^n = \frac{1}{2}[{\boldsymbol{F}}({\boldsymbol{U}}_i^n) + {\boldsymbol{F}}({\boldsymbol{U}}_{i + 1}^n) - {\alpha _n}({\boldsymbol{U}}_{i + 1}^n - {\boldsymbol{U}}_i^n)] $ | (10) |
其中,
本文采用二阶差分算子计算通量导数的近似值
混合格式在不光滑区域使用具有激波捕捉能力的HRFD2,而在光滑区域使用具有较高计算效率和较高分辨率的CPR格式。因此需要激波侦测器来侦测激波所在位置。本文使用NI激波侦测器[18]来判断激波所在单元,并将其标记为问题单元(Troubled cell)。NI的公式为:
| $\begin{split}& NI = \frac{1}{{{{[r(r + 1)]}^{1/2}}}}\cdot \\&\;\;\;\;\;\;\;\;\;\; {\Bigg[\sum\limits_{k = 0}^r {{{\Bigg(\frac{{[1/(r + 1)] - \Big[({\omega _k}/{d_k})\Big/\displaystyle\sum\limits_{k = 0}^r {({\omega _k}/{d_k})} \Big]}}{{[1/(r + 1)]}}\Bigg)^2}}} \Bigg]^{1/2}} \end{split}$ |
其中:r+1是非线性加权的候选模板个数,对于HRFD2,r =1。为了保证激波不会移动到光滑单元(Smooth cell),在问题单元附近引入缓冲单元(Buffer cell),如图1所示。

|
图 1 三种单元类型示意图 Fig.1 Illustration of three different types of cells |
所采用的格式切换策略如下:当激波侦测器侦测到激波时,在激波附近的单元格式切换为HRFD2。当激波离开后,这些单元的格式由HRFD2切换为CPR。综上,即根据激波侦测器的值,将所有单元分为不光滑单元(问题单元和缓冲单元)和光滑单元,在不光滑单元采用HRFD2,而在光滑单元采用CPR。
1.3.2 界面处理为了避免两种格式间出现错误的信息交换,我们需要仔细研究界面处理,主要的困难在于HRFD2-CPR界面的处理。下面以一维情况为例,给出界面处理方案。首先,如图2所示,第i+1单元的HRFD2需要其相邻的第i单元(CPR单元)的虚拟点信息
| $ {\boldsymbol{U}}({g_{i,k}}) = \sum\limits_{k = 1}^3 {\boldsymbol{U}} ({c_{i,k}}){\tilde L_k}({g_{i,k}}) $ | (11) |
其中

|
图 2 界面处理 Fig.2 Schematic of interface treatment |
其次,我们使用CPR单元的分布函数求得
| $ {{{\tilde {\boldsymbol{F}}}}_{i + \frac{1}{2}}} = {{\tilde {\boldsymbol{F}}}}\left( {{\boldsymbol{U}}_{i + \frac{1}{2}}^{ - ({\rm{cpr}})},{\boldsymbol{U}}_{i + \frac{1}{2}}^{ + ({\rm{HRFD2}})}} \right) $ | (12) |
此外,我们也要考虑格式切换时的信息传递。当第i个单元在第
1)将模板
2)分别在
| $ \begin{gathered} {{\boldsymbol{U}}_1}({c_{i,1}}) = {\boldsymbol{U}}({w_{i - 1,3}}){{\hat L}_1}({c_{i,1}}) + {\boldsymbol{U}}({w_{i,1}}){{\hat L}_2}({c_{i,1}}) \\ {{\boldsymbol{U}}_2}({c_{i,1}}) = {\boldsymbol{U}}({w_{i,1}}){{\hat L}_1}({c_{i,1}}) + {\boldsymbol{U}}({w_{i,2}}){{\hat L}_2}({c_{i,1}}) \\ \end{gathered} $ | (13) |
其中
3)计算非线性权。线性权可由
| $ \begin{split}& {d_1}{{\boldsymbol{U}}_1}({c_{i,1}}) + {d_2}{{\boldsymbol{U}}_2}({c_{i,1}}) = {\boldsymbol{U}}({w_{i - 1,3}}){{\hat L}_1}({c_{i,1}}) +\\& \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\boldsymbol{U}}({w_{i,1}}){{\hat L}_2}({c_{i,1}}) + {\boldsymbol{U}}({w_{i,2}}){{\hat L}_3}({c_{i,1}}) \end{split} $ | (14) |
得到,则非线性权由
4)最后得插值结果
本节中我们将会测试CPR与HRFD2的混合格式(简记为CPR-HRFD2)的空间精度、激波捕捉能力和计算效率。同时会进行CPR-HRFD2与HRFD2的对比。
我们首先在二维等熵涡问题中测试CPR-HRFD2的精度,简单对比了HRFD2和CPR的计算效率,并在一维激波管问题中验证格式的激波捕捉性能,在二维黎曼问题和双马赫反射问题测试激波捕捉能力以及对比计算效率,随后用高马赫数问题来测试格式的强激波捕捉能力,最后在激波-旋涡干扰问题中研究对于复杂流动问题的模拟。时间推进格式为显式三阶龙格库塔格式。
| $ {{\boldsymbol{e}}_{{L_2}}} = \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^N {({\boldsymbol{U}}_i^h - {\boldsymbol{U}}(} {r_i}){)^2}}}{N}} $ | (15) |
其中
我们在二维等熵涡问题中对构造的混合格式进行精度测试。下面考虑二维欧拉方程:
| $ \frac{\partial }{{\partial t}} \left[ \begin{array}{l} \rho \\ \rho u\\ \rho v\\ E \end{array} \right] + \frac{\partial }{{\partial x}}\left[ {\begin{array}{*{20}{c}} {\rho u}\\ {\rho {u^2} + p}\\ {\rho uv}\\ {u\left( {E + p} \right)} \end{array}} \right] + \frac{\partial }{{\partial y}}\left[ {\begin{array}{*{20}{c}} {\rho v}\\ {\rho uv}\\ {\rho {v^2} + p}\\ {v\left( {E + p} \right)} \end{array}} \right] = 0$ | (16) |
其中:
初值是均匀流
| $ \begin{split}& (\Delta u,\;\Delta v) = {\dfrac{\varepsilon }{{2\text {π} }}{{\rm{e}}^{0.5(1 - {r^2})}}( - y,x)}\\&{\Delta T = - \dfrac{{(\gamma - 1){\varepsilon ^2}}}{{8\gamma {{\text {π}} ^2}}}{{\rm{e}}^{(1 - {r^2})}}} \end{split}$ |
其中:
| 表 1 二维精度测试 Table 1 2D accuracy test |
|
|
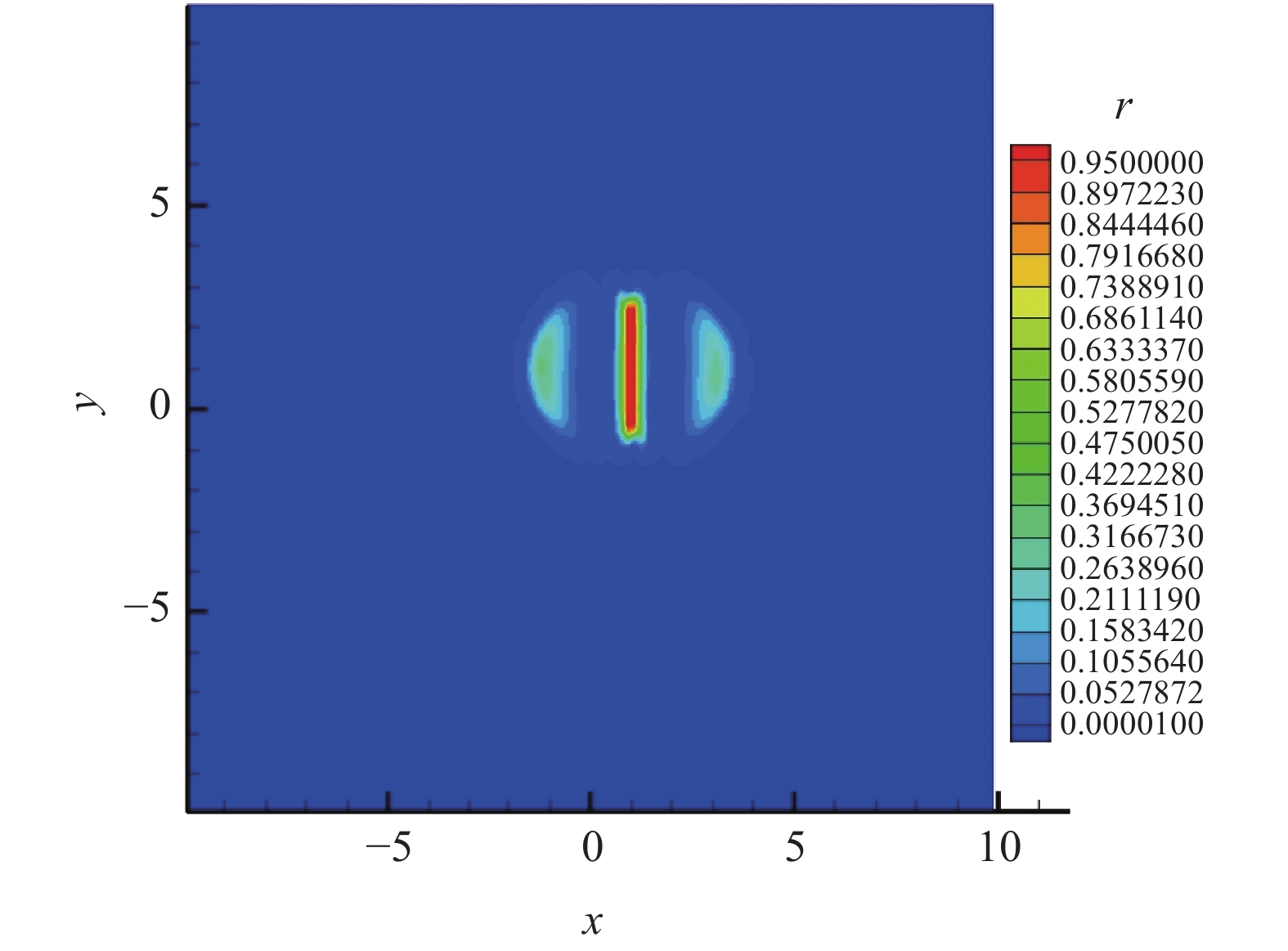
图3、图4、图5、图6分别展示了CPR-HRFD2的不同单元类型分布、x方向NI值、y方向NI值以及误差分布图。从图4、图5可看出,当NI值大于

|
图 3 不同单元分布(自由度为120) Fig.3 Distribution of different cells, DOFs = 120 |
|
图 4 x方向NI侦测结果分布(自由度为120) Fig.4 NI detection result in x-direction, DOFs = 120 |

|
图 5 y方向NI侦测结果分布(自由度为120) Fig.5 NI detection result in y-direction, DOFs = 120 |
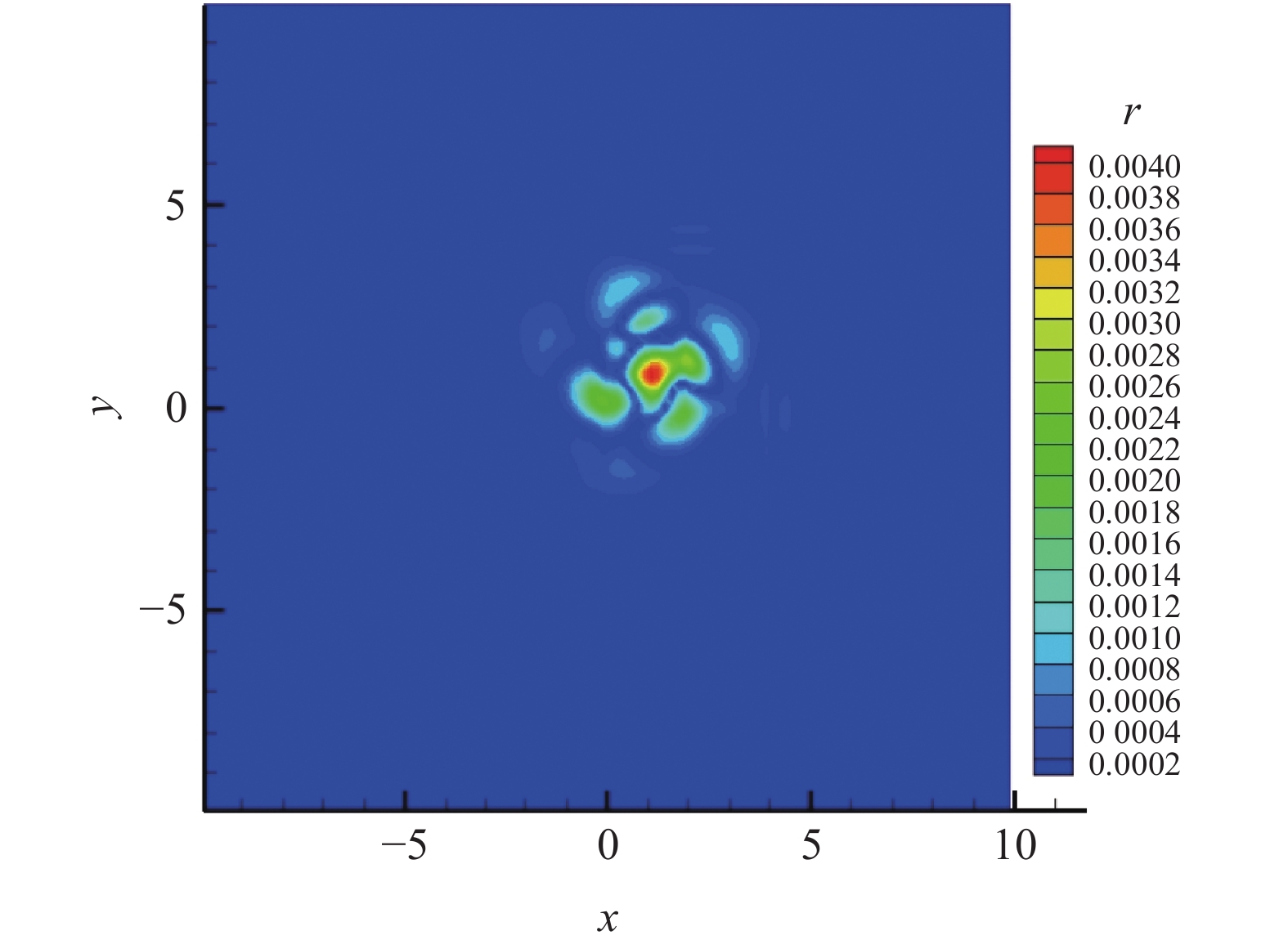
|
图 6 误差分布(自由度为120) Fig.6 Error distribution, DOFs = 120 |
此外,针对二维等熵涡问题,进行了HRFD2与CPR的计算时间对比测试,取相同的自由度,时间步长
| 表 2 二维等熵涡问题HRFD2与CPR计算时间对比 Table 2 CPU time of HRFD2 and CPR in isentropic vortex problem |
|
|
考虑一维欧拉方程:
| $\begin{split}& \qquad\qquad\qquad{{\boldsymbol{U}}_t} + {\boldsymbol{F}}{({\boldsymbol{U}})_x} = 0 \\& {\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho v} \\ E \end{array}} \right],{\mkern 1mu} {\mkern 1mu} {\boldsymbol{F}}{\mkern 1mu} ({\boldsymbol{U}}) = \left[ {\begin{array}{*{20}{c}} {\rho v} \\ {\rho {v^2} + p} \\ {v(E + p)} \end{array}} \right],E = \dfrac{p}{{\gamma - 1}} + \dfrac{1}{2}\rho {v^2} \\\end{split}$ | (17) |
其中:
初值为
这一算例,采用基于解析解的Dirichlet边界条件。
由图7可知,激波和接触间断都可以被高分辨率地捕捉到。在接触间断和激波附近,没有明显的振荡,这展现了CPR-HRFD2良好的激波捕捉能力。此外,大部分单元由CPR计算,保证具有更高的计算效率。
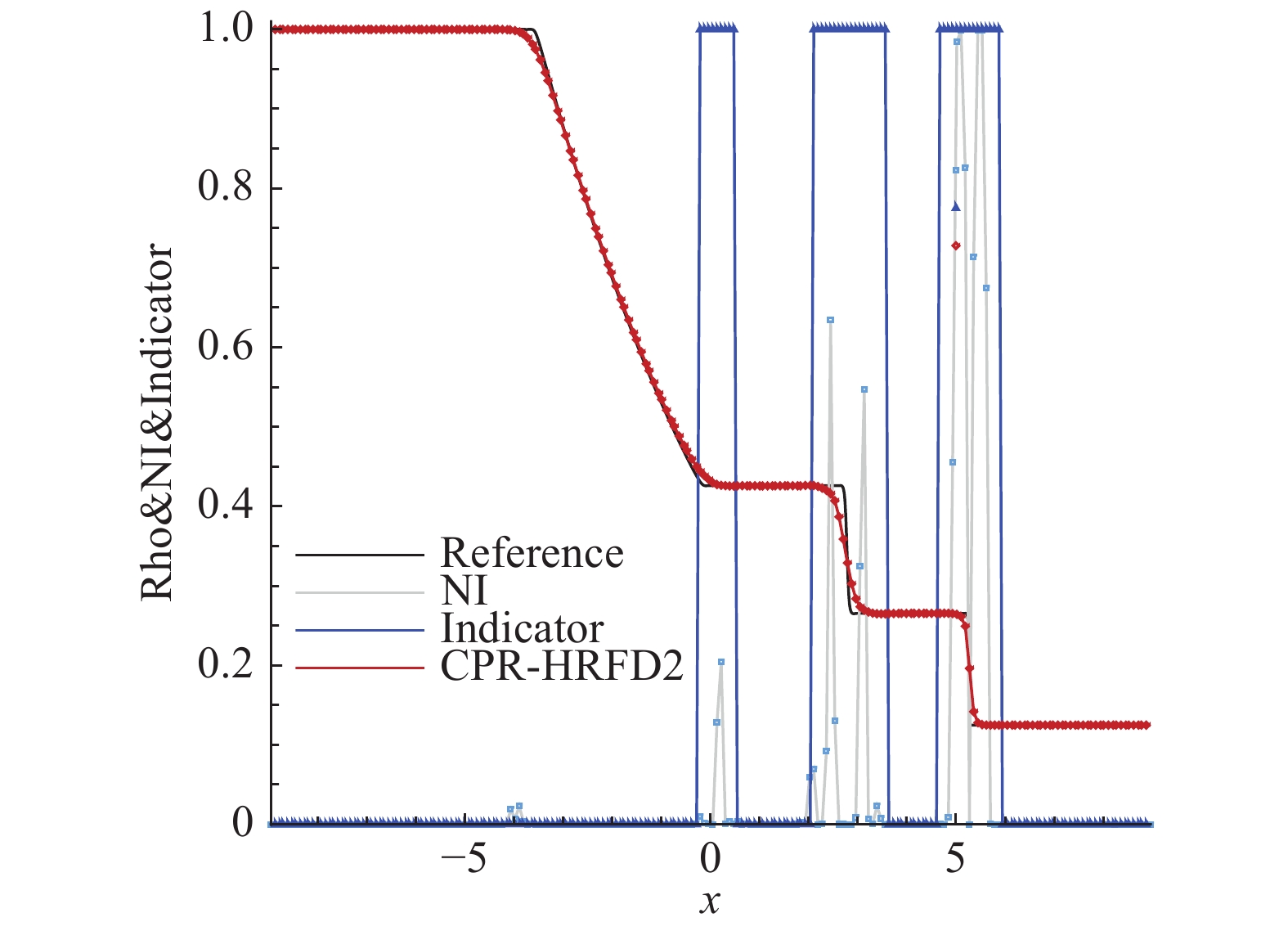
|
图 7 Sod激波管问题,自由度为120 Fig.7 Sod shock tube problem, DOFs = 120 |
初值为
这一算例,采用Dirichlet边界条件。时间步长为
由图8可知,在激波侦测器判别的充分光滑区域内使用了CPR。此外,CPR-HRFD2可以很好地捕捉激波和间断。密度的数值解贴近参考解,展现了高分辨率特点。
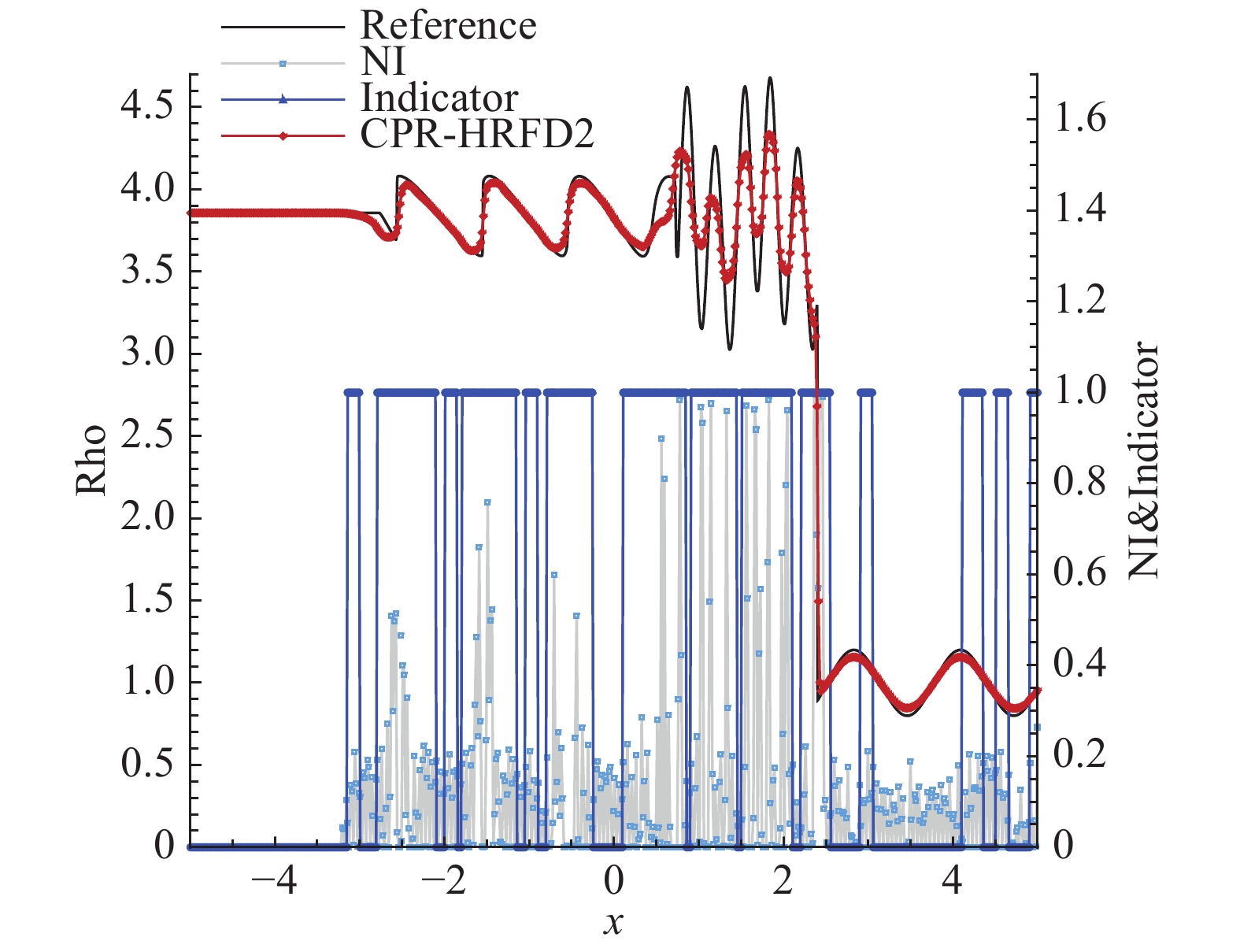
|
图 8 Shu-Osher激波管问题,自由度为600 Fig.8 Shu-Osher shock tube problem, DOFs = 600 |
初值为
这一算例,采用基于解析解的Dirichlet边界条件。时间步长为
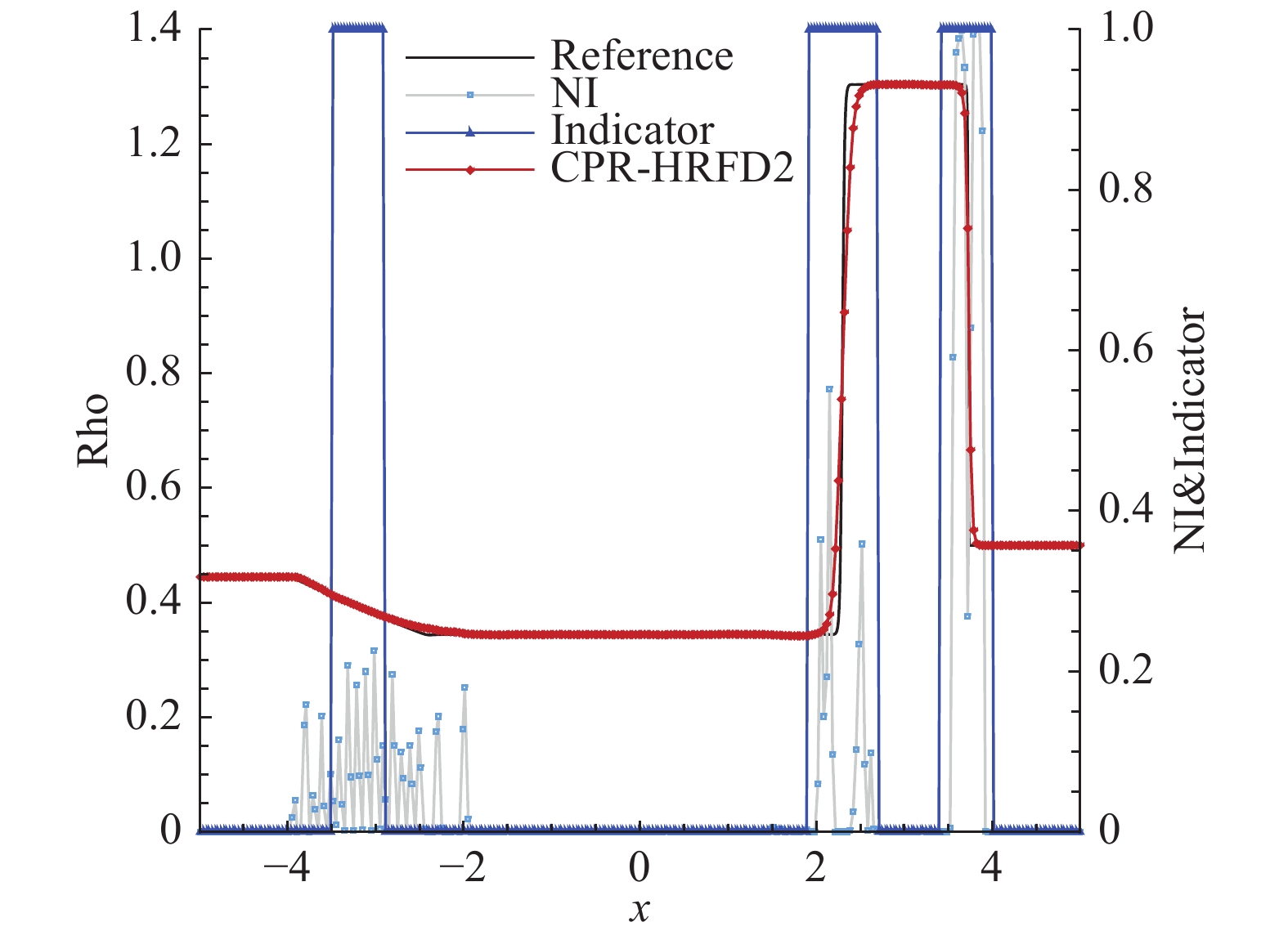
由图9可知,在
|
图 9 Lax 激波管问题,自由度为300 Fig.9 Lax shock tube problem, DOFs = 300 |
计算区域
| $ (\rho ,u,v,p)(x,y,0) = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {(1.5,\; 0,\; 0,\; 1.5),} \qquad\qquad\quad\\ \qquad\qquad {0.8 < x < {\text{1}}.{\text{0}},{\text{0}}.{\text{8}} < y < {\text{1}}.{\text{0}}} \\ {(0.5323,\; 1.206,\; 0,\; 0.3),} \qquad\qquad\quad\\ \;\;\; \qquad\qquad{0 < x \leqslant 0.8,0.8 < y < 1.0} \\ {(0.138,\; 1.206,\; 1.206,\; 0.029),} \qquad\qquad\quad\\ \;\;\;\;\;\;\; \qquad\qquad{0 < x \leqslant 0.8,0 < y \leqslant 0.8} \\ {(0.5323,\; 0,\; 1.206,\; 0.3),} \qquad\qquad\quad\\ \,\;\;\; \qquad\qquad{0.8 < x < {\text{1}}.{\text{0,0}} < y \leqslant {\text{0}}.{\text{8}}} \end{array}} \end{array}} \right. $ |
计算到
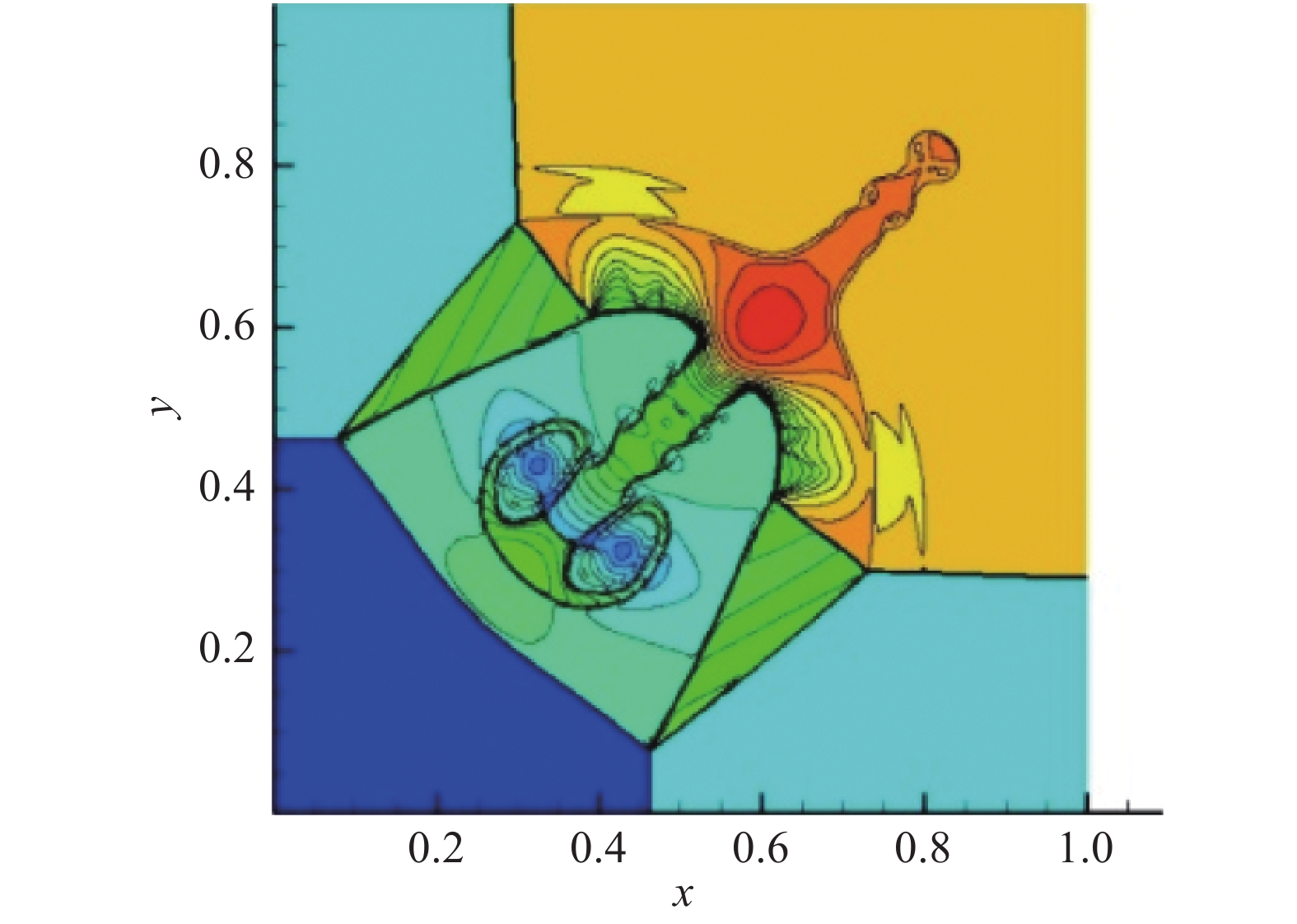
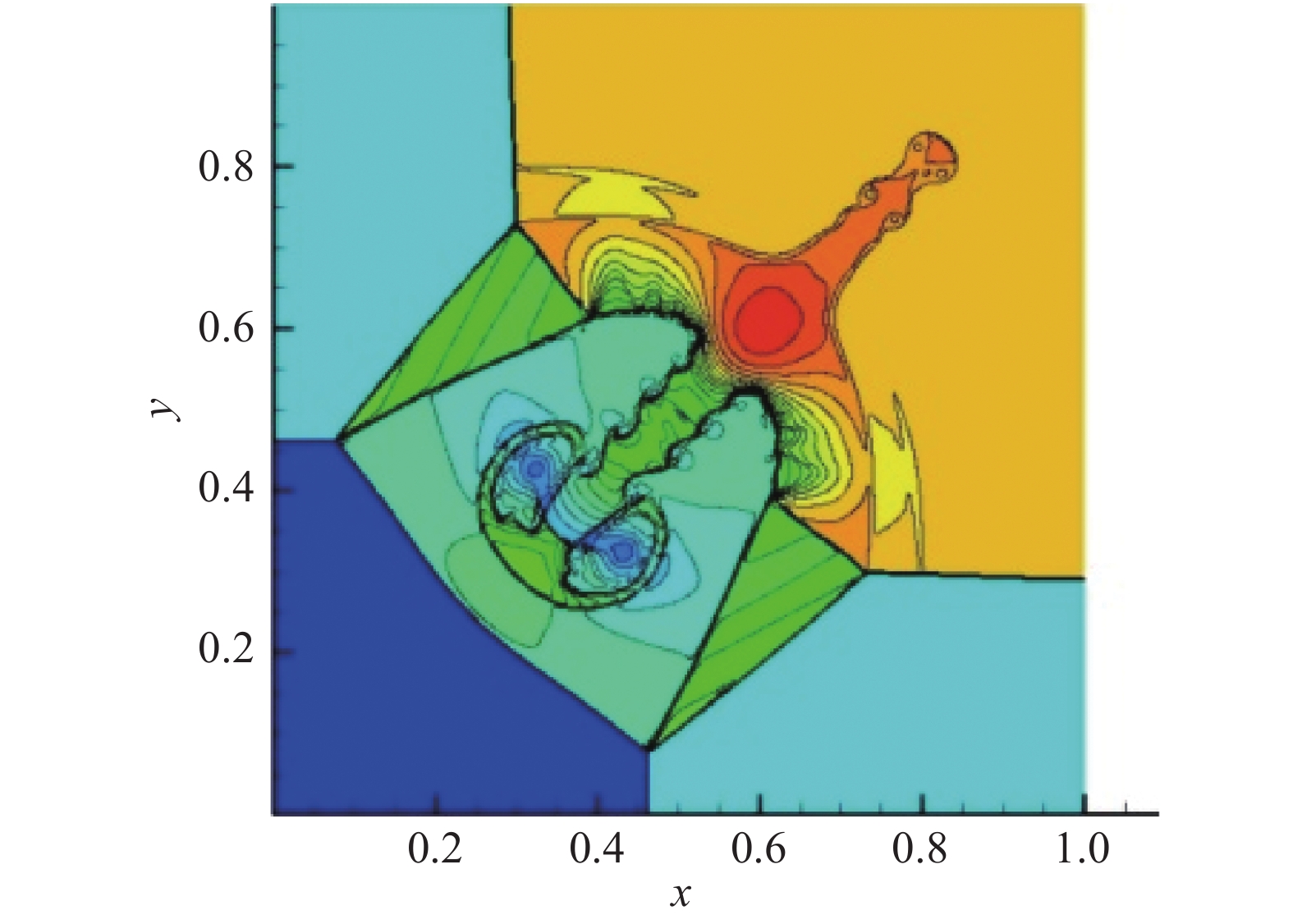
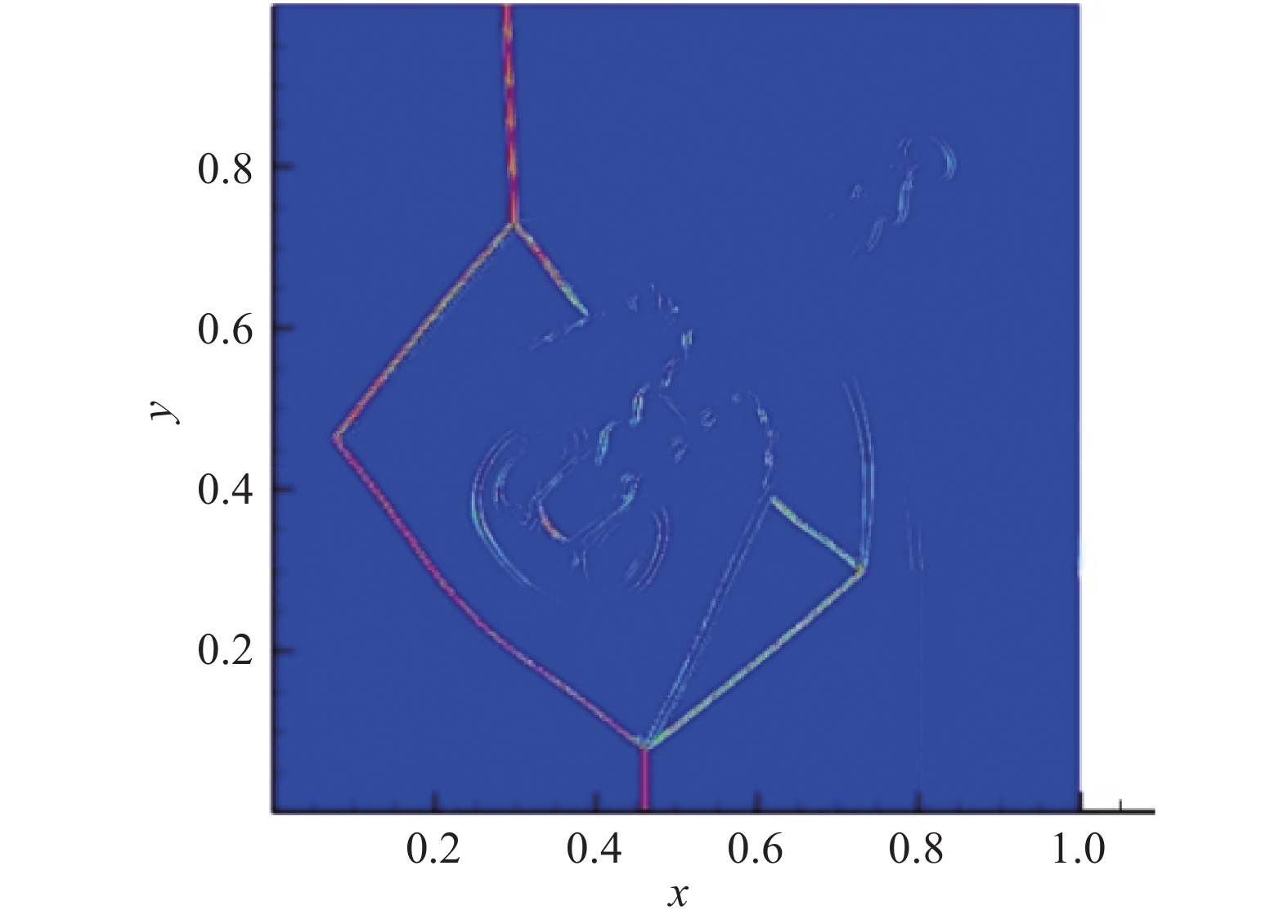
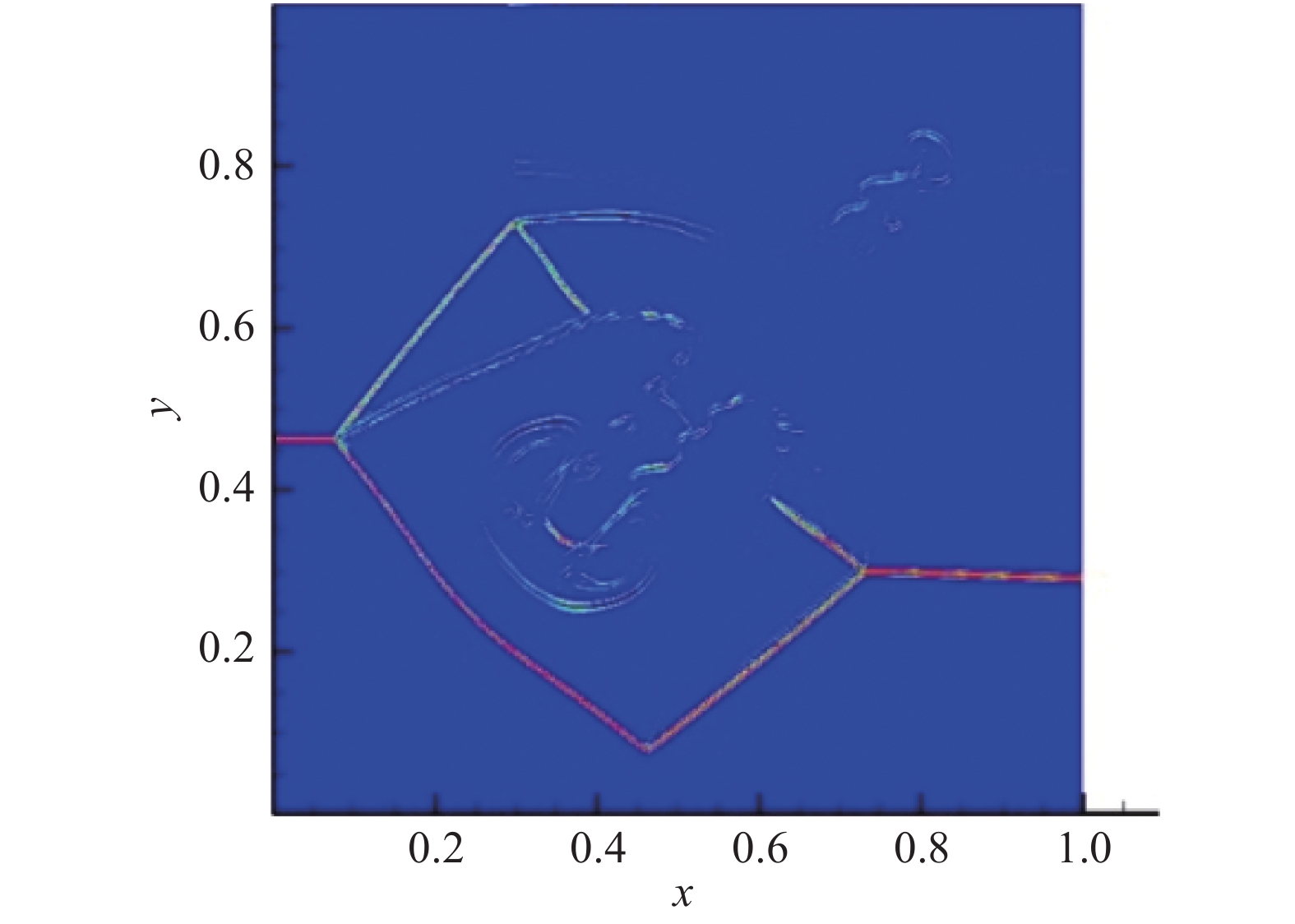
图10为HRFD2结果。由图11、图12和图13可知,在光滑区域,流场由CPR精确计算,且无明显振荡。此外,小尺度结构也被CPR-HRFD2高分辨率地捕捉到了,结果图(图11)和HRFD2的结果图(图10)相近。大部分区域由CPR计算,减少了计算代价。
|
图 10 HRFD2密度计算结果,自由度为960×960 Fig.10 Density result of HRFD2, DOFs = 960×960 |
|
图 11 CPR-HRFD2的计算密度结果,自由度为960×960 Fig.11 Density contour calculated by CPR-HRFD2 method,DOFs = 960×960 |
|
图 12 CPR-HRFD2的x方向NI侦测 Fig.12 NI detection contour by CPR-HRFD2 method in x direction |
|
图 13 CPR-HRFD2的y方向NI侦测 Fig.13 NI detection contour by CPR-HRFD2 method in y direction |
这个算例由Woodward提出,目的在于测试高分辨率格式的鲁棒特性。一个马赫数为10的激波设定在下边界
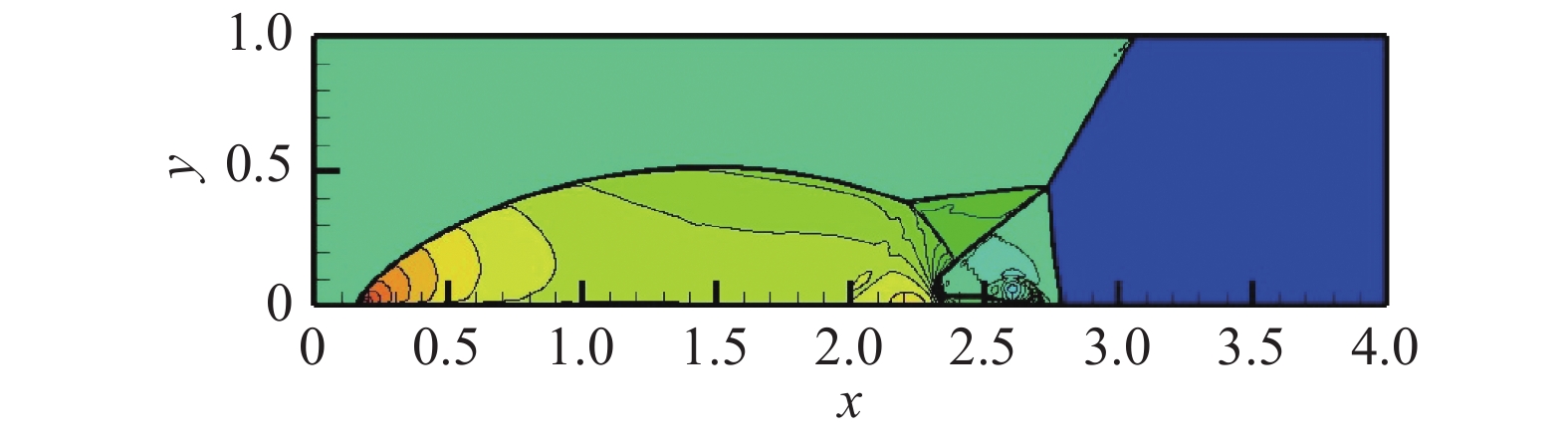
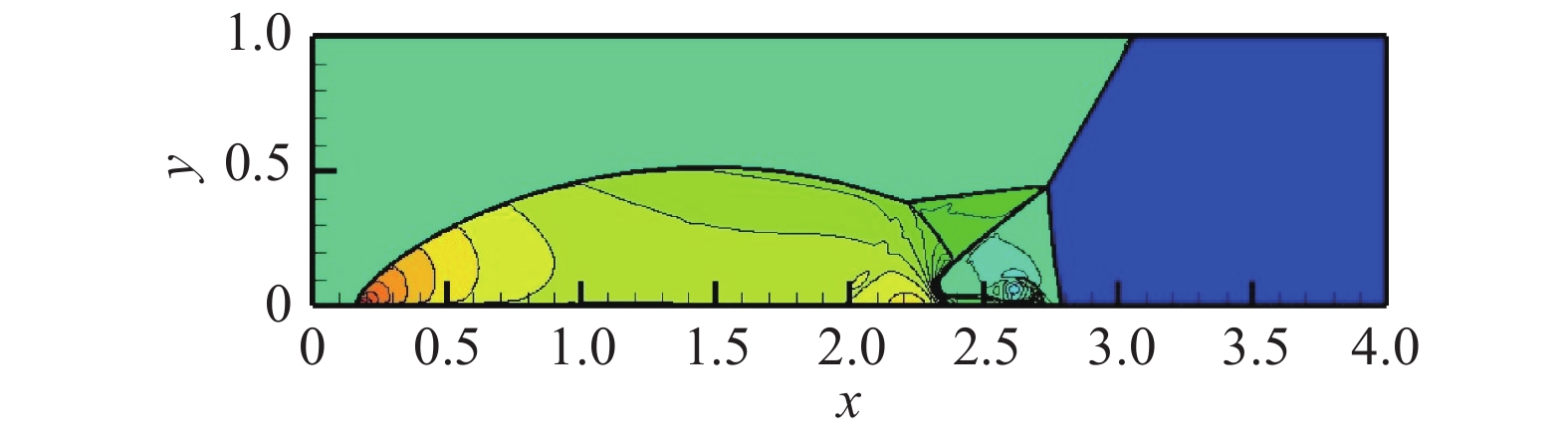
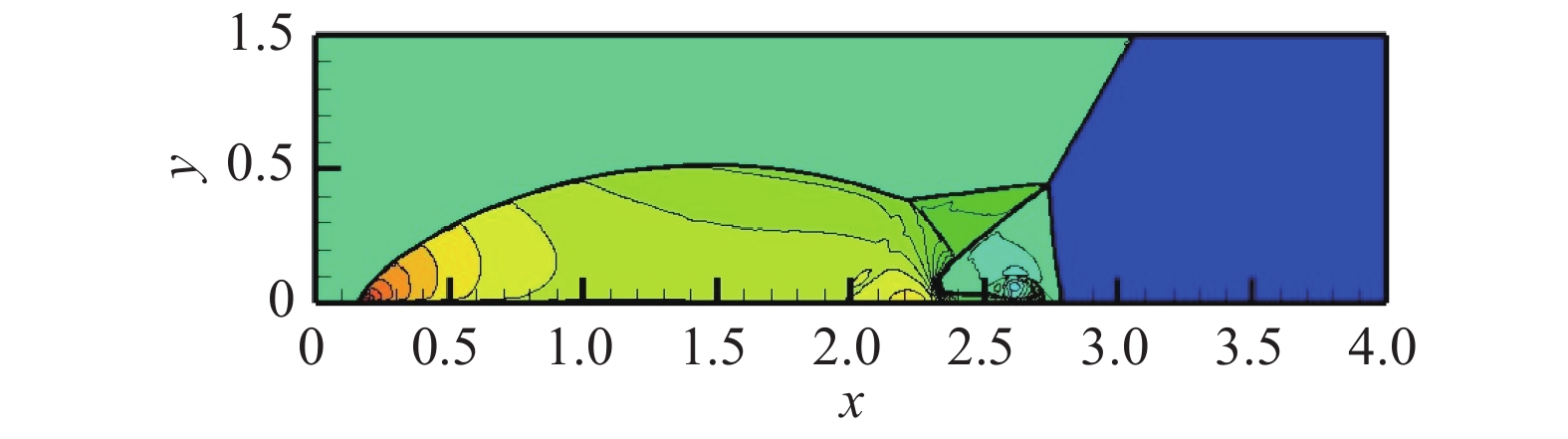
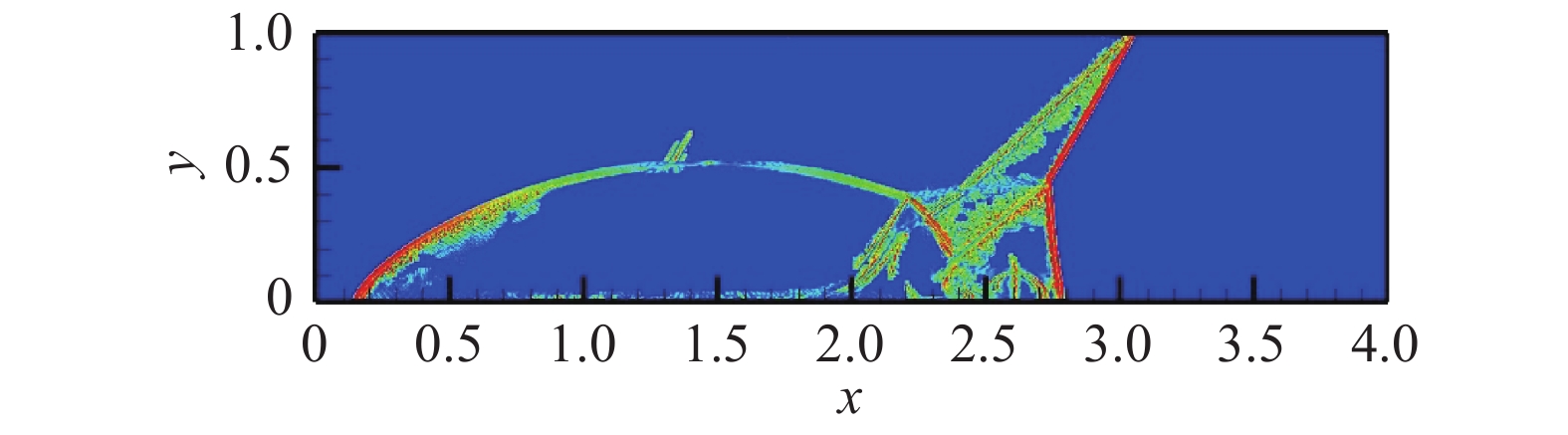
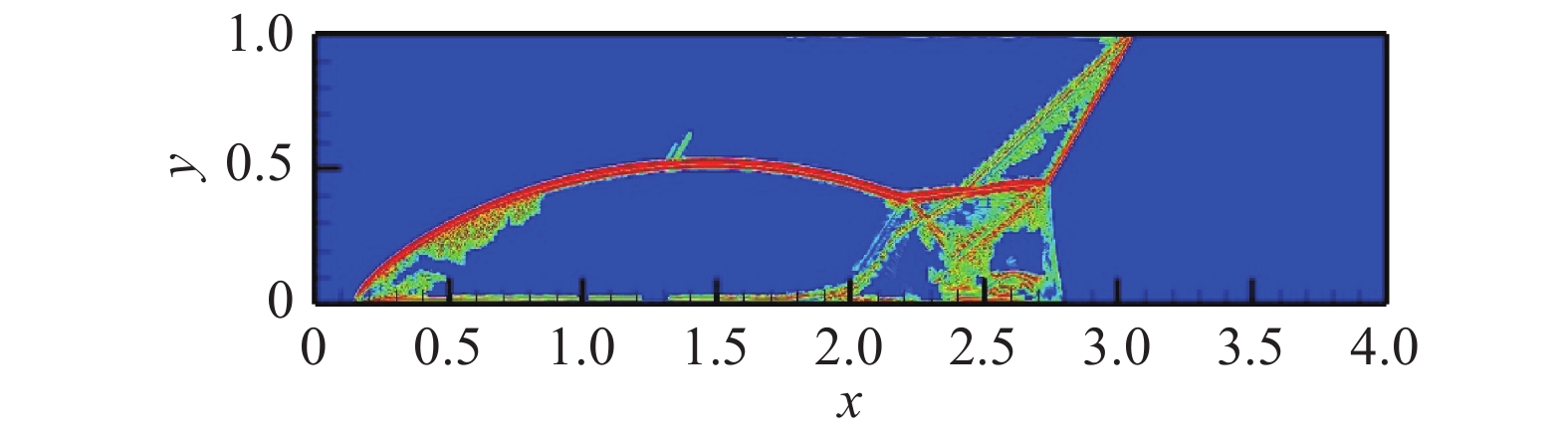
由图14、图15和图16知,CPR-HRFD2的结果图和HRFD2以及三阶WCNS的结果图基本相同,此外,重要的小尺度和大尺度结构都被CPR-HRFD2捕捉到了,其他区域也由CPR精确计算。由图17和图18知,整个区域CPR单元个数远超过HRFD2个数。另外,由表3知,CPR-HRFD2计算效率高于HRFD2(计算时间为18480 s)和三阶WCNS(计算时间为18840 s),当
|
图 14 三阶WCNS格式密度计算结果,自由度为1200×300 Fig.14 Density contour by WCNS3 method, DOFs = 1200×300 |
|
图 15 HRFD2密度计算结果,自由度为1 200×300 Fig.15 Density contour by HRFD2 method, DOFs = 1 200×300 |
|
图 16 CPR-HRFD2密度计算结果,自由度为1 200×300 Fig.16 Density contour by CPR-HRFD2 method, DOFs = 1 200×300 |
|
图 17 CPR-HRFD2的x方向NI侦测 Fig.17 NI detection contour by CPR-HRFD2 method in x direction |
|
图 18 CPR-HRFD2的y方向NI侦测 Fig.18 NI detection contour by CPR-HRFD2 method in y direction |
| 表 3 双马赫反射问题的CPU时间对比(自由度为1 200×300) Table 3 CPU time comparison of double Mach problem, DOFs = 1 200×300 |
|
|
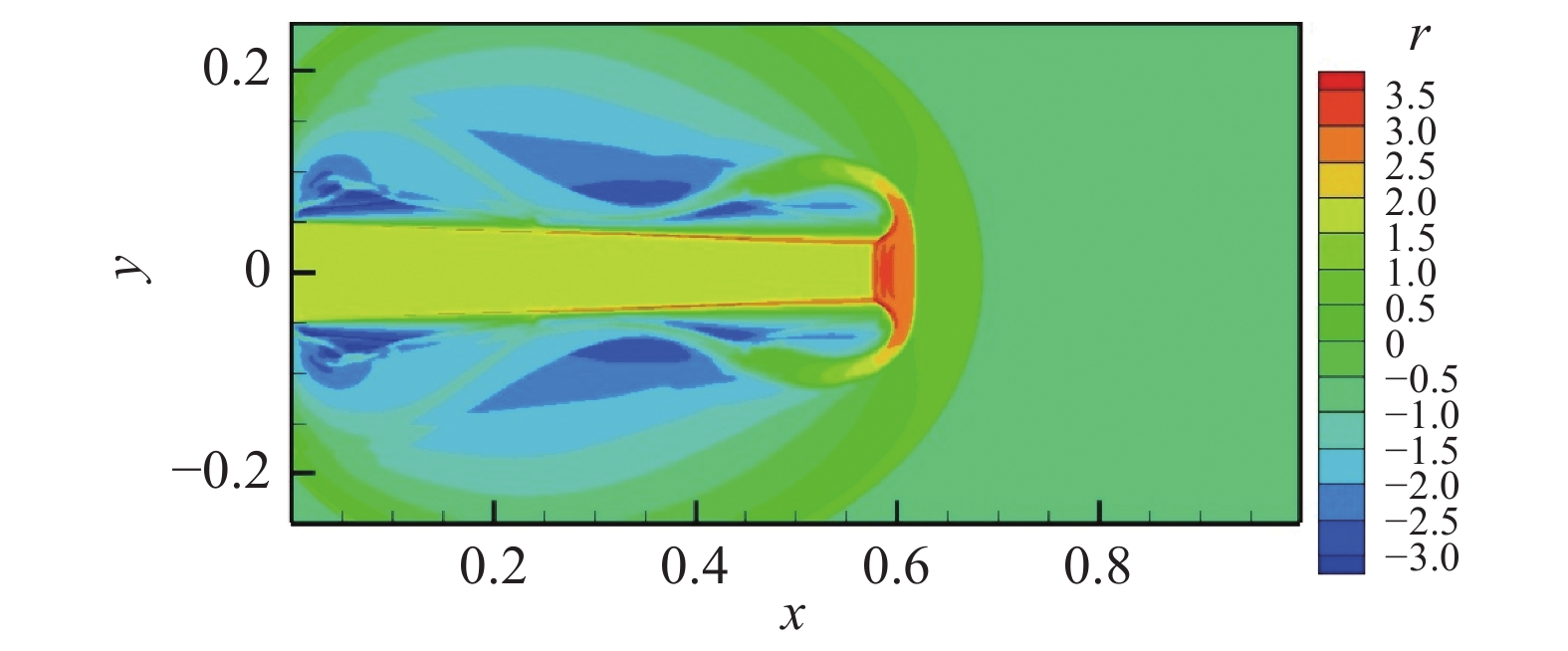
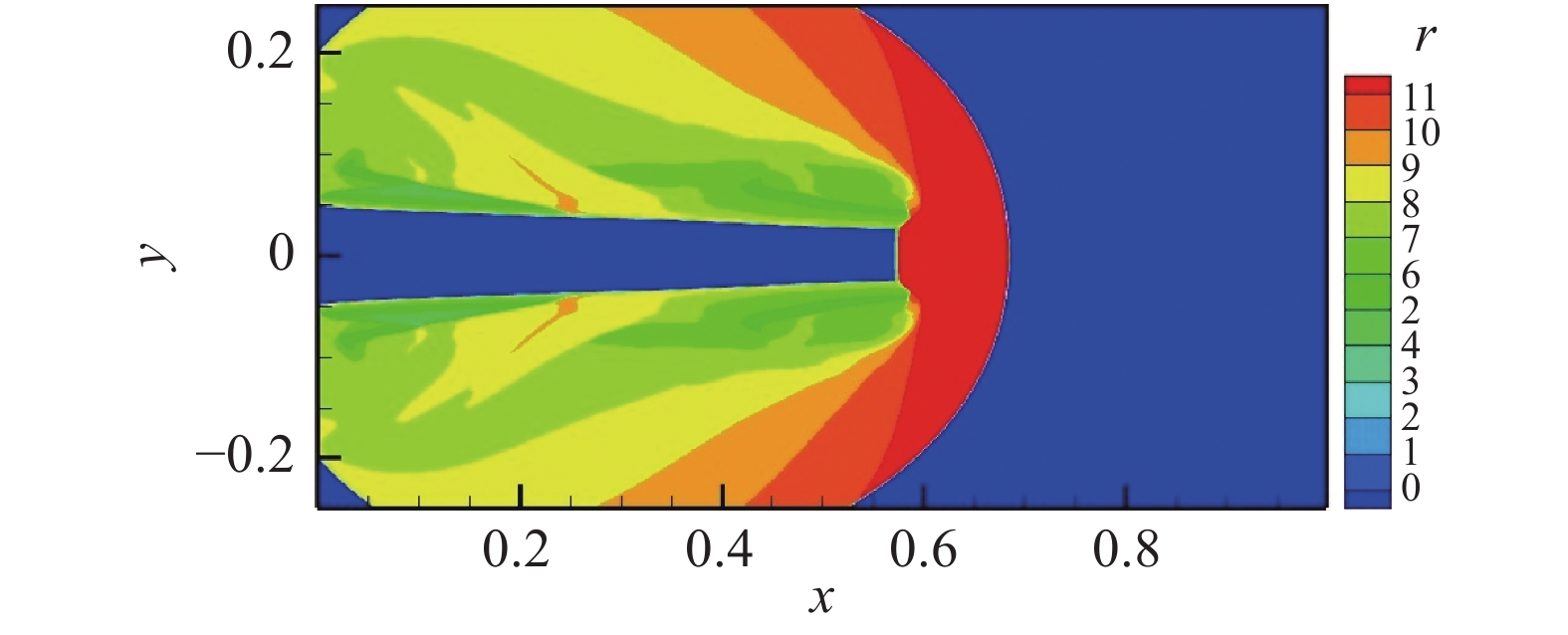
我们研究马赫数2000射流问题,计算域为
|
图 19 CPR-HRFD2密度计算结果,自由度1 710×855 Fig.19 Density contour by CPR-HRFD2 method, DOFs = 1 710×855 |
|
图 20 CPR-HRFD2压力计算结果,自由度1 710×855 Fig.20 Pressure contour by CPR-HRFD2 method, DOFs = 1 710×855 |
|
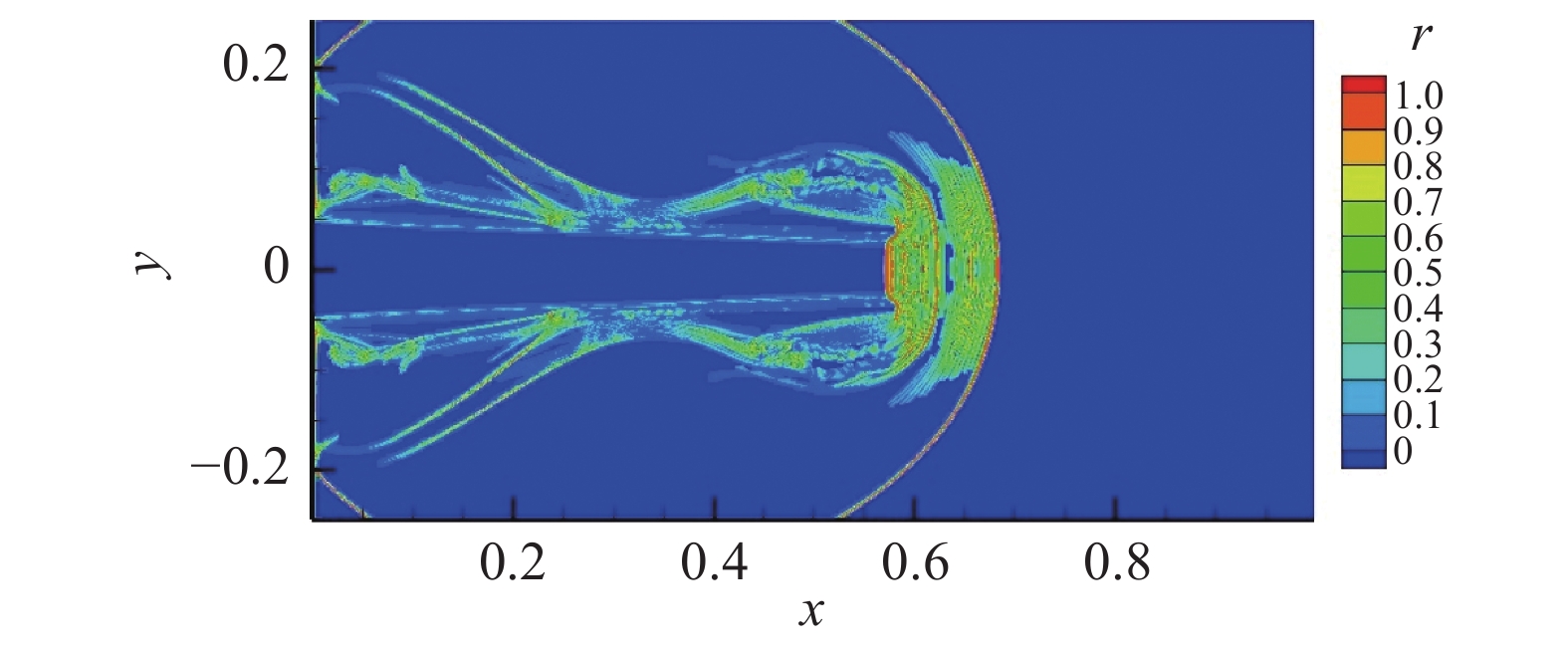
图 21 CPR-HRFD2的x方向NI侦测 Fig.21 NI detection contour by CPR-HRFD2 method in x direction |
|
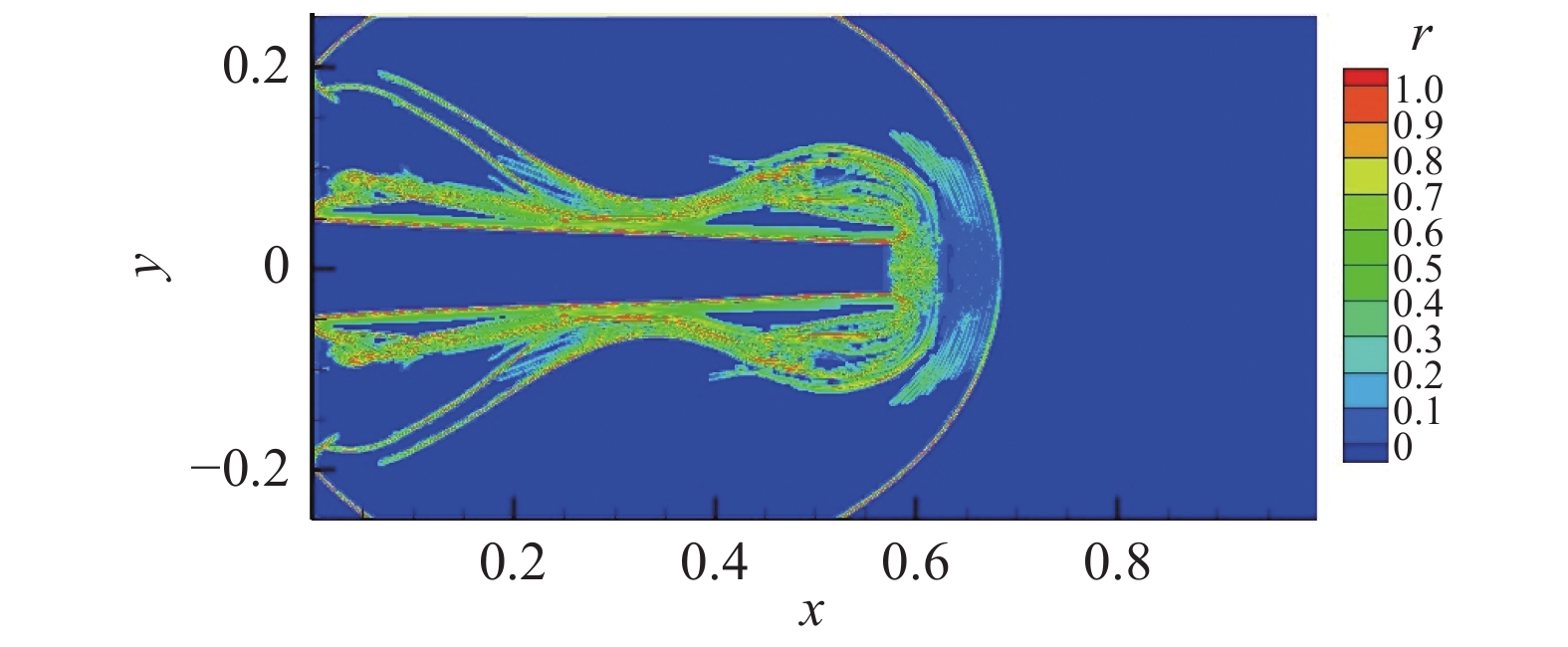
图 22 CPR-HRFD2的y方向NI侦测 Fig.22 NI detection contour by CPR-HRFD2 method in y direction |
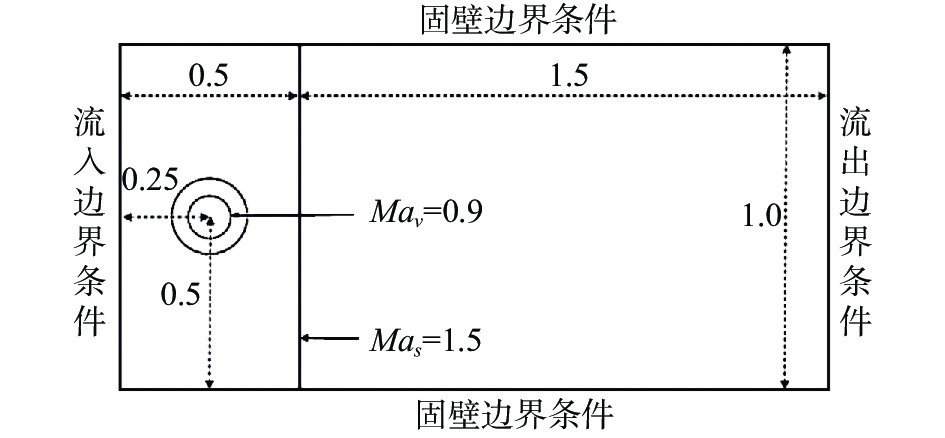
在最后,我们测试了激波-旋涡干扰问题[25]。该问题包含了一个运动的旋涡和一道静止正激波,可以发展出具有平滑特征和间断的复杂流动结构。如图23所示,该问题的计算域
|
图 23 激波-旋涡干扰的初始条件和边界条件 Fig.23 Initial and boundary conditions of shock-vortex |
左右边界分别设为流入、流出边界条件,上下边界设为滑移固壁边界条件。时间步长
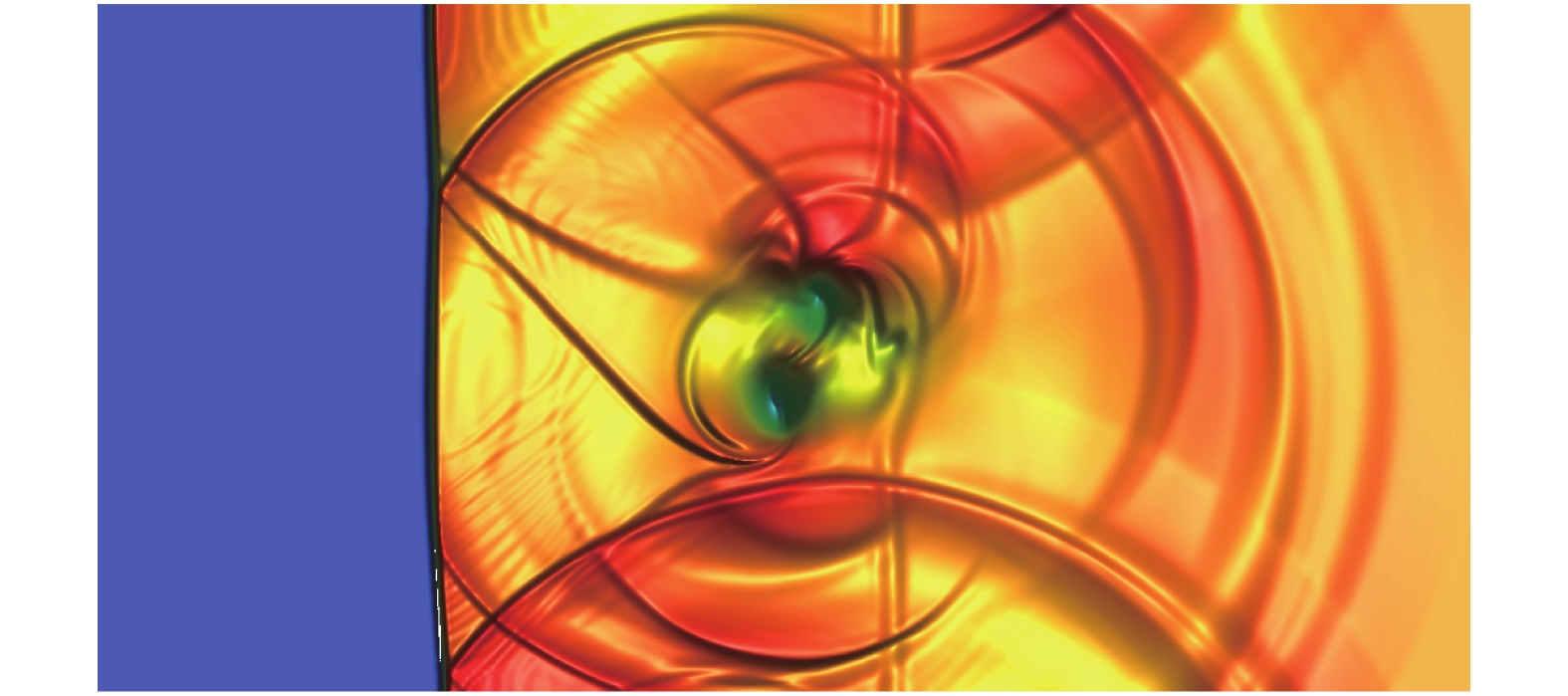
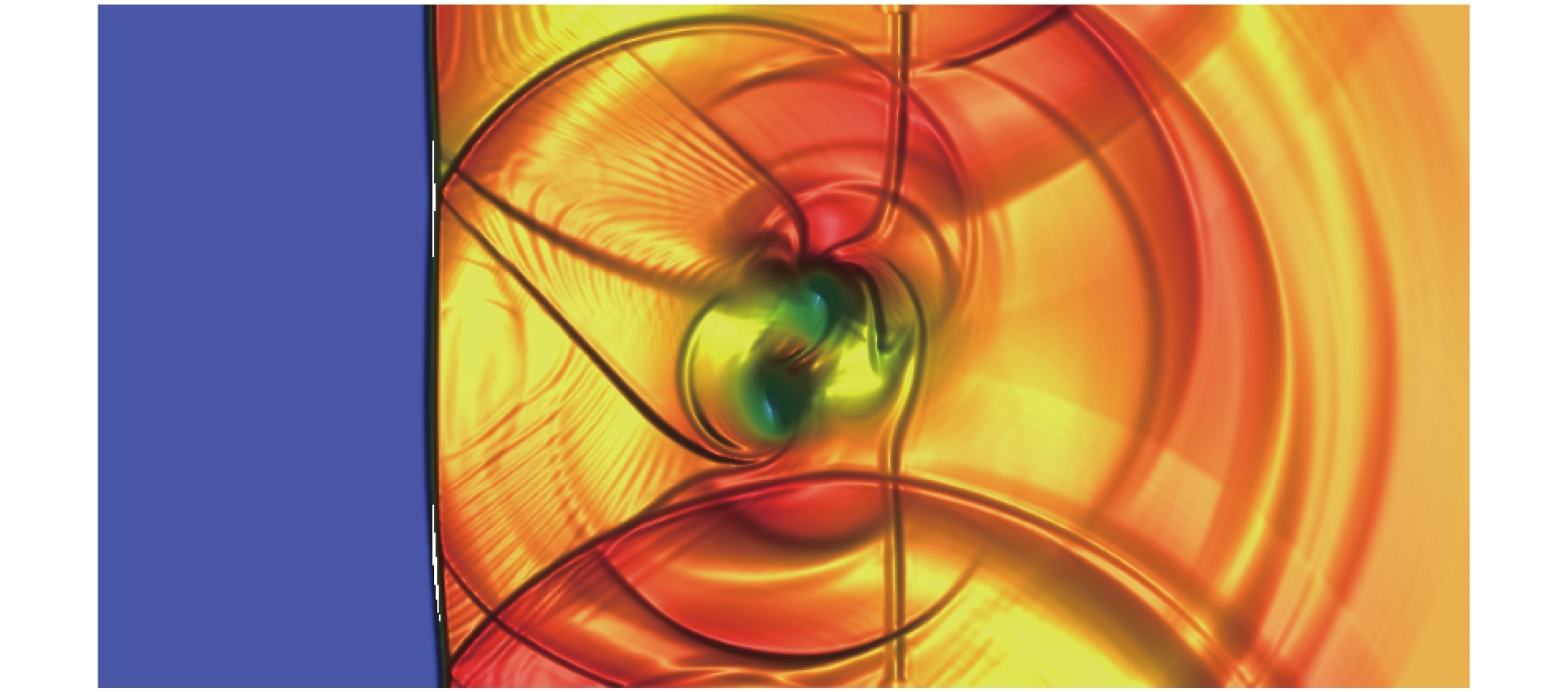
如图24、图25所示,CPR-HRFD2在保持激波捕捉能力的同时,对平滑旋涡产生的小尺度旋涡结构也有很好的捕捉能力,计算结果与文献[25]中的计算结果相符合。由图26和图27可知,大部分区域使用CPR计算,保持了较高的计算效率。
|
图 24 HRFD2密度计算结果,自由度960×480 Fig.24 Density contour by HRFD2 method, DOFs = 960×480 |
|
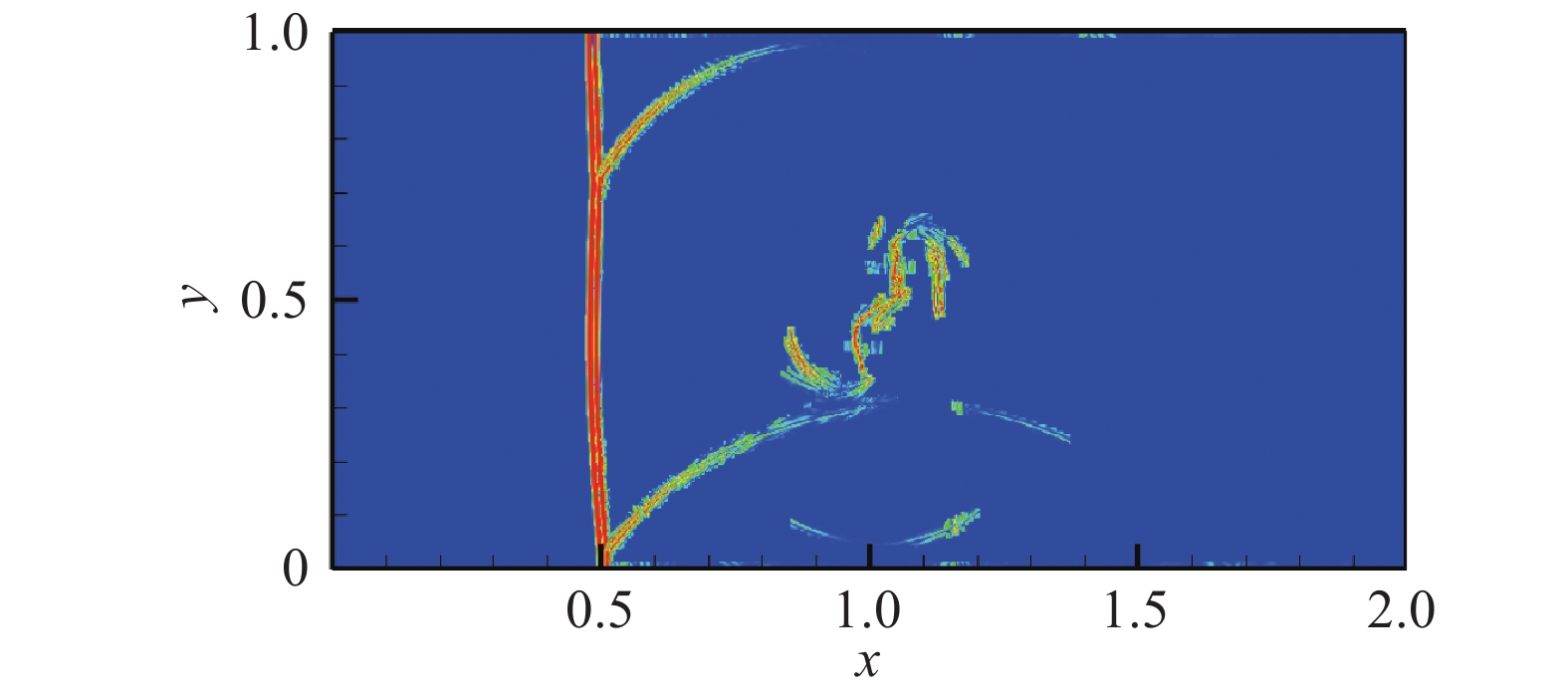
图 25 CPR-HRFD2密度计算结果,自由度960×480 Fig.25 Density contour by CPR-HRFD2 method, DOFs = 960×480 |
|
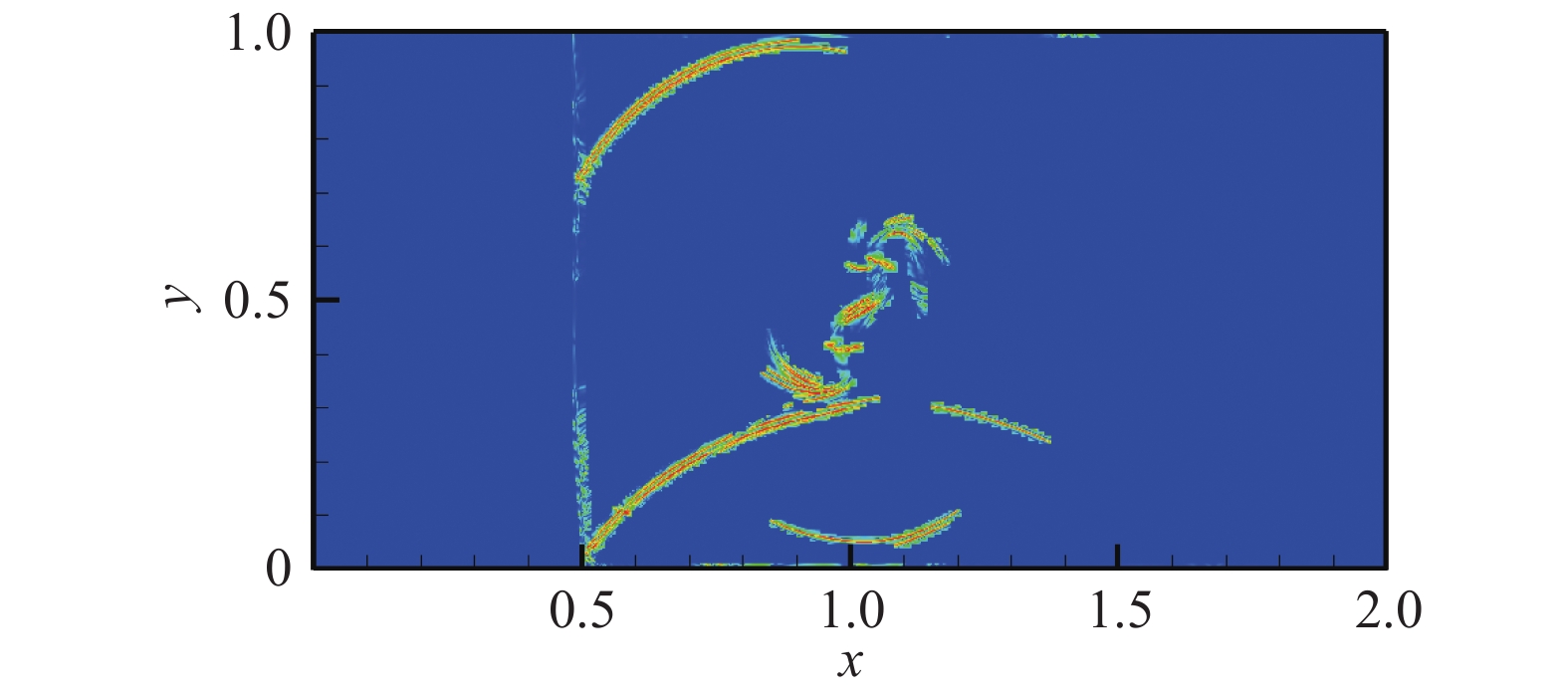
图 26 CPR-HRFD2的x方向NI侦测 Fig.26 NI detection contour by CPR-HRFD2method in x direction |
|
图 27 CPR-HRFD2的y方向NI侦测 Fig.27 NIdetection contour by CPR-HRFD2 method in y direction |
激波-旋涡干扰问题包含复杂的流动结构。按照如图28所示的切线位置,可以对不同结构特征进行定量分析[26]。不同参考线位置对应着不同的主要特征,见表4。
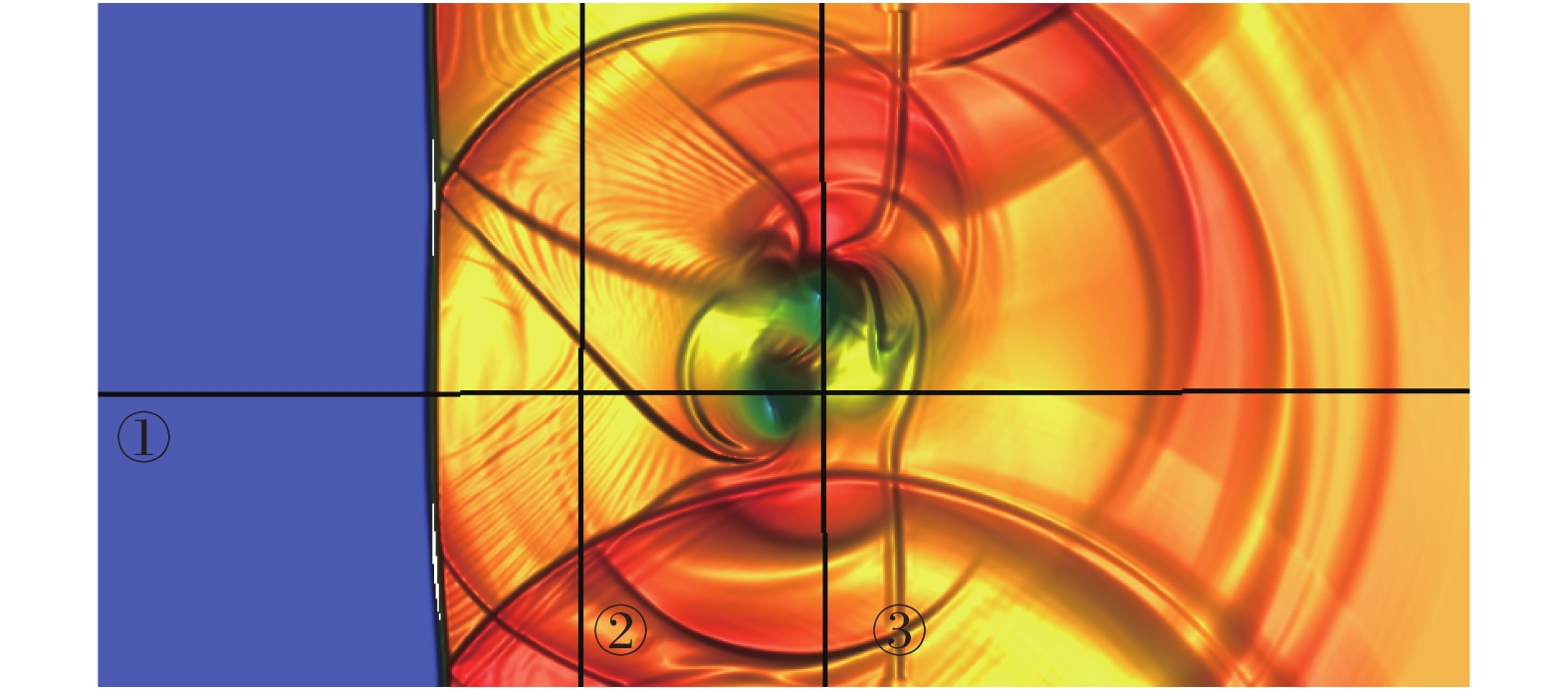
|
图 28 参考线位置 Fig.28 Illustration of the position of the reference lines |
| 表 4 参考线 Table 4 Reference lines |
|
|
为对比CPR-HRFD2和HRFD2的激波捕捉能力和分辨率特性,在此选取①②③参考线进行分析。
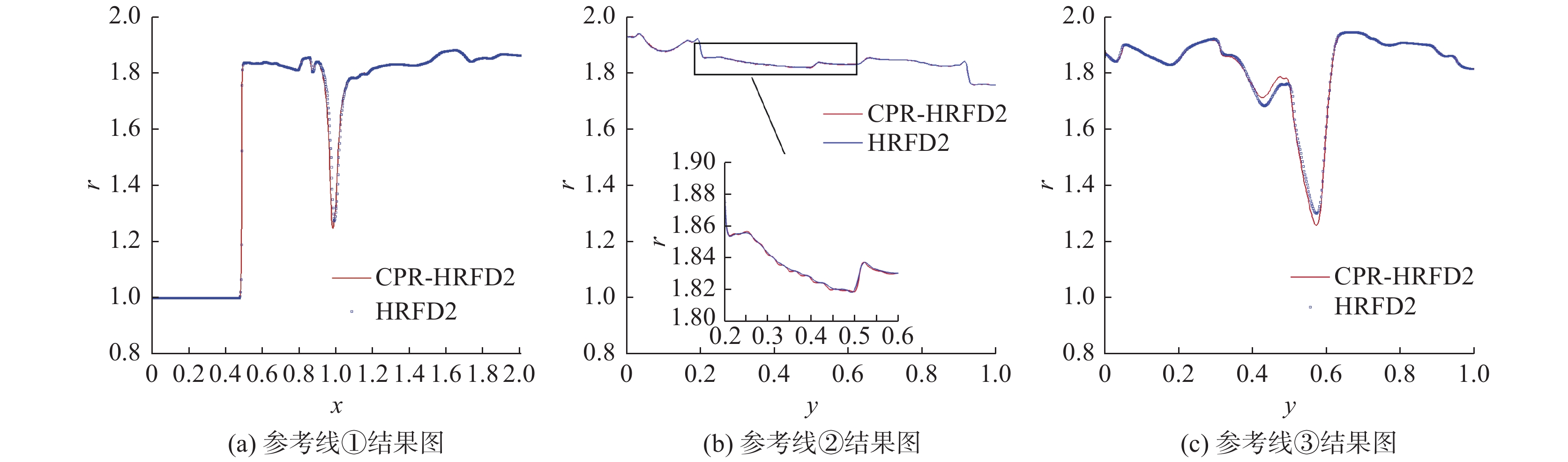
从图29中①可看出,CPR-HRFD2和HRFD2都有较强的激波捕捉能力,激波附近和波后区域流场光滑,无明显的振荡。从图29中①③则可以明显看出,对于旋涡的捕捉,HRFD2的分辨率不如CPR-HRFD2。从图26和图27侦测的结果来看,CPR-HRFD2在旋涡处也有使用HRFD2计算,但是与完全使用HRFD2相比,旋涡结构附近更多地使用CPR求解,且相比于HRFD2,CPR更高的精度避免了更大的耗散。如果增加
|
图 29 HRFD2和CPR-HRFD2的参考线结果 Fig.29 The reference lines calculated by HRFD2 and CPR-HRFD2 |
另外,文献[26]中采用基于无参数梯度限制器的三阶和四阶CPR方法对该问题进行了模拟,数值结果中观察到数值振荡,在定激波的右侧产生许多高频数值振荡。而在本文的数值结果中不管是密度图还是切线图都没有看到明显的数值振荡现象,说明了本文对高阶CPR方法所发展的基于混合算法的激波捕捉格式对激波旋涡问题具有更好的模拟能力。
3 结 论本文发展了三阶CPR与HRFD2的混合算法,使用基于非线性权的激波侦测器来判断问题单元和缓冲单元,提出了格式切换和界面处理策略。在问题单元和缓冲单元内,HRFD2用来捕捉激波,而在光滑单元内使用CPR,用于提高计算效率。文中进行了精度测试,激波捕捉能力测试,以及计算效率测试,得到了如下结论:
1)二维的精度测试结果表明CPR-HRFD2保持了精度;
2)通过对一维激波管问题,二维黎曼问题,双马赫反射问题,高马赫数射流问题和激波-旋涡干扰问题进行数值模拟,取得了比较好的结果,表明该混合格式具有强激波捕捉能力,可以应用于高超声速的高效数值模拟;
3)CPR-HRFD2是一种高分辨率激波捕捉格式,同时具有较高计算效率。相比于HRFD2,CPR-HRFD2计算量更小,计算效率更高。
本文的构造思想可以直接推广到更高阶的CPR方法与基于更高阶WCNS插值的二阶格式的混合算法中。
| [1] |
HUYNH H T, WANG Z J, VINCENT P E. High-order methods for computational fluid dynamics: a brief review of compact differential formulations on unstructured grids[J]. Computers & Fluids, 2014, 98: 209-220. DOI:10.1016/j.compfluid.2013.12.007 |
| [2] |
WANG Z J, LI Y, JIA F, et al. Towards industrial large eddy simulation using the FR/CPR method[J]. Computers & Fluids, 2017, 156: 579-589. DOI:10.1016/j.compfluid.2017.04026 |
| [3] |
DENG X G, MAO M L, TU G H, et al. High-order and high accurate CFD methods and their applications for complex grid problems[J]. Communications in Computational Physics, 2012, 11(4): 1081-1102. DOI:10.4208/cicp.100510.150511s |
| [4] |
HUYNH H T. A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods[C]//18th AIAA Computational Fluid Dynamics Conference, Miami, Florida. Reston, Virginia: AIAA, 2007. doi: 10.2514/6.2007-4079
|
| [5] |
WANG Z J, GAO H Y. A unifying lifting collocation penalty formulation including the discontinuous Galerkin, spectral volume/difference methods for conservation laws on mixed grids[J]. Journal of Computational Physics, 2009, 228(21): 8161-8186. DOI:10.1016/j.jcp.2009.07.036 |
| [6] |
DU J, SHU C W, ZHANG M P. A simple weighted essentially non-oscillatory limiter for the correction procedure via reconstruction (CPR) framework[J]. Applied Numerical Mathematics, 2015, 95: 173-198. DOI:10.1016/j.apnum.2014.01.006 |
| [7] |
LI W A, WANG Q, REN Y X. A p-weighted limiter for the discontinuous Galerkin method on one-dimensional and two-dimensional triangular grids[J]. Journal of Computational Physics, 2020, 407: 109246. DOI:10.1016/j.jcp.2020.109246 |
| [8] |
BARTER G E, DARMOFAL D L. Shock capturing with PDE-based artificial viscosity for DGFEM: Part I. Formulation[J]. Journal of Computational Physics, 2010, 229(5): 1810-1827. DOI:10.1016/j.jcp.2009.11.010 |
| [9] |
PERSSON P O, PERAIRE J. Sub-cell shock capturing for discontinuous Galerkin methods[C]//44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2006 doi: 10.2514/6.2006-112
|
| [10] |
CHENG J, LU Y W, LIU T G. Multi-domain hybrid RKDG and WENO methods for hyperbolic conservation laws[J]. SIAM Journal on Scientific Computing, 2013, 35(2): A1049-A1072. DOI:10.1137/110855156 |
| [11] |
ZHU H J, YAN Z G, LIU H Y, et al. High-order hybrid WCNS-CPR schemes on hybrid meshes with curved edges for conservation laws I: spatial accuracy and geometric conservation laws[J]. Communications in Computational Physics, 2018, 23(5): 1355-1392. DOI:10.4208/cicp.oa-2017-0032 |
| [12] |
GUO J, ZHU H J, YAN Z G, et al. High-Order Hybrid WCNS-CPR Scheme for Shock Capturing of Conservation Laws[J]. International Journal of Aerospace Engineering, 2020, Article ID 8825445. doi: 10.1155/2020/8825445
|
| [13] |
DENG X G, ZHANG H X. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165(1): 22-44. DOI:10.1006/jcph.2000.6594 |
| [14] |
毛枚良, 燕振国, 刘化勇, 等. 高阶加权非线性格式的拟线性频谱分析方法研究[J]. 空气动力学学报, 2015, 33(1): 1-9. MAO M L, YAN Z G, LIU H Y, et al. Study of quasi-linear spectral analysis method of high-order weighted nonlinear schemes[J]. Acta Aerodynamica Sinica, 2015, 33(1): 1-9. DOI:10.7638/kqdlxxb-2014.0115 (in Chinese) |
| [15] |
DENG X G. High-order finite difference schemes based on symmetric conservative metric method: decomposition, geometric meaning and connection with finite volume schemes[J]. Advances in Applied Mathematics and Mechanics, 2020, 12(2): 436-479. DOI:10.4208/aamm.oa-2017-0243 |
| [16] |
BORGES R, CARMONA M, COSTA B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J]. Journal of Computational Physics, 2008, 227(6): 3191-3211. DOI:10.1016/j.jcp.2007.11.038 |
| [17] |
燕振国, 刘化勇, 毛枚良, 等. 三阶HWCNS的构造及其在高超声速流动中的应用[J]. 航空学报, 2015, 36(5): 1460-1470. YAN Z G, LIU H Y, MAO M L, et al. Development of 3rd-order HWCNS and its application in hypersonic flow[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1460-1470. (in Chinese) |
| [18] |
WU M, MARTIN M P. Direct numerical simulation of supersonic turbulent boundary layer over a compression ramp[J]. AIAA Journal, 2007, 45(4): 879-889. DOI:10.2514/1.27021 |
| [19] |
SOD G A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws[J]. Journal of Computational Physics, 1978, 27(1): 1-31. DOI:10.1016/0021-9991(78)90023-2 |
| [20] |
PIROZZOLI S. On the spectral properties of shock-capturing schemes[J]. Journal of Computational Physics, 2006, 219(2): 489-497. DOI:10.1016/j.jcp.2006.07.009 |
| [21] |
LAX P D. Weak solutions of nonlinear hyperbolic equations and their numerical computation[J]. Communications on Pure and Applied Mathematics, 1954, 7(1): 159-193. DOI:10.1002/cpa.3160070112 |
| [22] |
WOODWARD P, COLELLA P. The numerical simulation of two-dimensional fluid flow with strong shocks[J]. Journal of Computational Physics, 1984, 54(1): 115-173. DOI:10.1016/0021-9991(84)90142-6 |
| [23] |
TANG L Y, SONG S H, ZHANG H. High-order maximum-principle-preserving and positivity-preserving weighted compact nonlinear schemes for hyperbolic conservation laws[J]. Applied Mathematics and Mechanics, 2020, 41(1): 173-192. DOI:10.1007/s10483-020-2554-8 |
| [24] |
ZHANG X X, SHU C W. On positivity-preserving high order discontinuous Galerkin schemes for compressible Euler equations on rectangular meshes[J]. Journal of Computational Physics, 2010, 229(23): 8918-8934. DOI:10.1016/j.jcp.2010.08.016 |
| [25] |
RAULT A, CHIAVASSA G, DONAT R. Shock-vortex interactions at high Mach numbers[J]. Journal of Scientific Computing, 2003, 19(1-3): 347-371. DOI:10.1023/A:1025316311633 |
| [26] |
LU Q L, LIU G M, MING P J, et al. A parameter-free gradient-based limiter for the FR/CPR method on mixed unstructured meshes[C]//Proc of the AIAA Aviation 2019 Forum, Dallas, Texas. Reston, Virginia: AIAA, 2019
|
 2022, Vol. 40
2022, Vol. 40


