2. 中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
飞机飞行过程中发生的结冰现象是飞行安全的重大威胁之一。大量研究表明,结冰不仅会影响飞机的气动性能,而且会降低飞行和控制性能,其中非对称结冰还会导致严重的飞行事故[1]。极端天气是导致飞行结冰的重要因素,其中92%由结冰引起的事故发生在飞行过程中[2]。因此开展飞行过程中结冰情况的识别研究,是提高飞行安全性,避免结冰事故的关键。
目前在民用飞机结冰适航要求中,结冰识别预警通常是基于传感器直接进行结冰探测[3-4],当探测到某部位结冰后,再启动电加热或除冰套等除冰装置确保飞行安全性,但这样的预警和防除冰系统通常只适合用于大型飞机,对于重量、体积和成本受限的无人机而言,传统的预警和防除冰系统并不完全适用。近年来随着材料技术的发展,基于超疏水涂层的防/除冰技术得到了较多关注和较快发展[5-7]。除此之外,随着计算机技术的进步,一些可用于结冰实时识别探测[8]、可重构控制和飞行包线保护[9-10]等的结冰探测和防护算法也得到了长足发展。相比于传统的防除冰方法和防除冰涂层技术,结冰识别和防护智能算法可搭载在飞机机载计算机上,直接处理飞行过程中实时测量得到的飞行状态参数,来探测结冰情况的发生和严重程度等,再结合除冰装置或容错控制算法来保证飞行安全性。因此,该方法具有灵活经济的特点,且能对飞机的整体飞行状态进行监控,仅受限于机载计算能力和算法效能,因此对于一些成本受限的无人机或无人侦察机,该方法具有较好的应用前景。
近年来,由于人工神经网络在数据分类和建模领域展现了强大的能力,神经网络在飞机结冰领域的研究和应用也引起了人们较多的关注。其中,除涉及气象条件与结冰相关性研究[11]、冰型参数与气动特性相关性研究[12]和结冰累积过程建模研究[13-14]等之外,在受结冰影响气动参数的辨识和结冰情况识别方面,神经网络的应用也较多。如,Caliskan[15]利用神经网络模型由飞行状态变量辨识出受结冰影响的气动稳定和控制导数,Aykan等[16]将这种方法应用于F16受结冰影响气动导数的辨识;为了进一步提高受结冰影响参数辨识精度,Melody等[17]建立了融合配平状态参数、铰链力矩测量数据和参数估计结果的神经网络模型;董一群[18]利用卷积神经网络和递归神经网络从飞行状态变量中辨识飞机受结冰影响气动导数;在结冰情况识别方面,BP神经网络[8]和概率神经网络[19-20]等均被用于对飞机结冰位置及结冰严重程度的识别,Johnson[21]和应思斌等[22]利用神经网络建模结合自组织映射对飞机飞行结冰进行识别。在以上研究工作中,飞行状态变量多用于对飞机受结冰影响参数或结冰严重性参数的拟合,对结冰情况的识别和分类多基于辨识得到的受结冰影响气动参数,而直接利用飞行状态进行结冰情况分类的研究还较少。直接利用飞行测量状态参数开展结冰情况识别分类,相对利用由状态量辨识得到的气动特性参数开展的结冰识别而言,省略了中间步骤,不仅能够简化计算,而且能够避免由于参数辨识偏差导致的识别精度降低等问题。但直接采用状态测量数据对结冰情况进行识别,中间缺乏特征提取的过程,虽然简化了流程,但在方法可行性、状态变量选取和识别精度等方面还需开展研究。
概率神经网络(probabilistic neural networks, PNN)是Specht博士[23-24]提出的一种结构简单、应用广泛的神经网络,特别是在模式分类问题中获得了较好的应用。概率神经网络可以视为一种径向基神经网络(radial basis function, RBF),在此基础上还融合了密度函数估计和贝叶斯决策理论,在某些易满足的条件下,以PNN实现的判别边界渐进地逼近贝叶斯最佳判定面[25]。大量研究表明,概率神经网络具有训练容易、收敛速度快的优点,可以实现任意的非线性逼近,隐含层采用径向基非线性映射函数,具有很强的容错性,只要样本充足,概率神经网络都能收敛到贝叶斯分类器。
针对以上情况,本文开展直接基于飞行状态测量的结冰情况识别研究,考虑利用非线性逼近能力较强的概率神经网络针对飞行状态测量量直接进行建模以识别飞机的不同结冰位置和严重程度。利用NASA双水獭结冰研究飞机的结冰飞行动力学仿真模型,生成不同结冰情况下的大量飞行仿真数据;基于该数据分析18个常规状态测量量受结冰影响的显著程度,选择受结冰影响显著的状态变量作为神经网络识别的输入;设计了一种能够提升分类精度的概率神经网络参数优化策略,并基于该策略针对六个受结冰影响显著的状态变量分别建立分类网络,利用三类评估数据(包括两种泛化性评估数据)对网络的性能进行评估;最后将本文提出的优化概率神经网络与两种支持向量机方法进行对比,进一步说明该方法的分类性能。通过本文的研究,初步验证了基于飞行状态开展神经网络结冰情况识别的可行性,结合分类精度和泛化性能评估,对不同状态变量的结冰分类适应性进行了总结,给出了针对这一结冰分类问题的状态变量最佳选择。
1 飞机结冰飞行动力学建模双水獭(DH-6)改进型飞机作为NASA结冰研究小组的结冰研究对象,已积累了较为完整的结冰数据,可作为本文方法研究开展的基础。下面对该飞机考虑结冰过程的飞行动力学模型进行简单介绍。
1.1 六自由度飞行动力学模型在机体坐标系下建立飞机的六自由度动力学模型,作为开展结冰飞行仿真的依据。六自由度动力学仿真模型如式(1)所示,式中飞机的质量惯量特性见表1,(u, v, w)T表示机体坐标系下的飞机速度分量,(p, q, r)T表示机体坐标系下的三个角速度分量,(θ, ψ, ϕ)T表示俯仰、偏航和滚转角,(xe, ye, ze)T为地面惯性系下的飞机位置坐标,(Cx, Cy, Cz)T为机体坐标系下的气动力系数分量,(Cl, Cm, Cn)T为机体坐标系下的气动力矩系数分量,分别为滚转力矩、俯仰力矩和偏航力矩系数,(Px, Py, Pz)T为机体坐标系下的三个推力分量,(gx, gy, gz)T为机体坐标系下的重力加速度分量,q∞为动压,Bbe表示由地面惯性系到机体坐标系的转换矩阵。
| 表 1 双水獭结冰研究飞机质量惯量特性 Table 1 Mass and inertial characteristics of the Twin Otter icing research aircraft |
|
|
NASA结冰研究小组在结冰研究飞机的水平和垂直尾翼上加上人工明冰,研究结冰对飞机纵横向气动特性的影响。根据大量风洞和飞行试验获得的飞机气动特性变化,给出飞机气动参数受结冰影响的数学模型(见式(2))[26],式中引入结冰严重性参数
| $\begin{split}& \dot u = rv - qw + \frac{{{q_\infty }S{C_x} + {P_x}}}{m} + {g_x}\\& \dot v = pw - ru + \frac{{{q_\infty }S{C_y} + {P_y}}}{m} + {g_y}\\& \dot w = qu - pv + \frac{{{q_\infty }S{C_z} + {P_z}}}{m} + {g_z}\\& \dot p = \left\{ {{I_{xz}}\left( {{I_{xx}} + {I_{zz}} - {I_{yy}}} \right)pq + \left[ {{I_{zz}}\left( {{I_{yy}} - {I_{zz}}} \right) - I_{xz}^2} \right]qr + } \right.\\& \;\;\;\;\;\left. {{I_{zz}}{q_\infty }Sl{C_l} + {I_{xz}}{q_\infty }Sl{C_n}} \right\}/D\\& \dot q = {{\left[ {\left( {{I_{zz}} - {I_{xx}}} \right)pr - {I_{xz}}\left( {{p^2} - {r^2}} \right) + {q_\infty }S{b_A}{C_m}} \right]} / {{I_{yy}}}}\\& \dot r = \left\{ {{I_{xz}}\left( {{I_{yy}} - {I_{xx}} - {I_{zz}}} \right)qr + \left[ {{I_{xx}}\left( {{I_{xx}} - {I_{yy}}} \right) + I_{xz}^2} \right]pq + } \right.\\& \;\;\;\;\;\left. {{I_{xx}}{q_\infty }Sl{C_n} + {I_{xz}}{q_\infty }Sl{C_l}} \right\}/D\\& \dot \theta = q\cos \phi - r\sin \phi \\& \dot \psi = {{\left( {q\sin \phi + r\cos \phi } \right)} / {\cos \theta }}\\& \dot \phi = p + \tan \theta \left( {q\sin \phi + r\cos \phi } \right)\\& \left[ {\begin{array}{*{20}{c}} {{{\dot x}_e}}\\ {{{\dot y}_e}}\\ {{{\dot z}_e}} \end{array}} \right] = {{B'}_{be}}\left[ {\begin{array}{*{20}{c}} u\\ v\\ w \end{array}} \right]\\& D = {I_{xx}}{I_{zz}} - I_{xz}^2 \end{split} $ | (1) |
| $ \begin{split}& {C_x} = {C_{x0}}\left( {{\delta _{{\rm{ice}}}}} \right) + {C_{x\alpha }}\left( {{\delta _{{\rm{ice}}}}} \right)\alpha + {C_{x{\alpha ^2}}}{\alpha ^2} \\& {C_y} = {C_{y\beta }}\left( {{\delta _{{\rm{ice}}}}} \right)\beta + {C_{yp}}\frac{l}{{2V}}p + {C_{yr}}\frac{l}{{2V}}r + {C_{y{\delta _r}}}\left( {{\delta _{{\rm{ice}}}}} \right){\delta _r} \\& {C_z} = {C_{z0}} + {C_{z\alpha }}\left( {{\delta _{{\rm{ice}}}}} \right)\alpha + {C_{zq}}\left( {{\delta _{{\rm{ice}}}}} \right)\frac{{{b_A}}}{V}q + {C_{z{\delta _e}}}\left( {{\delta _{{\rm{ice}}}}} \right){\delta _e} \\& {C_l} = {C_{l\beta }}\left( {{\delta _{{\rm{ice}}}}} \right)\beta + {C_{lp}}\left( {{\delta _{{\rm{ice}}}}} \right)\frac{l}{{2V}}p + {C_{lr}}\frac{l}{{2V}}r + \\& \qquad {C_{l{\delta _a}}}\left( {{\delta _{{\rm{ice}}}}} \right){\delta _a} + {C_{l{\delta _r}}}\left( {{\delta _{{\rm{ice}}}}} \right){\delta _r} \\& {C_m} = {C_{m0}} + {C_{m\alpha }}\left( {{\delta _{{\rm{ice}}}}} \right)\alpha + {C_{mq}}\left( {{\delta _{{\rm{ice}}}}} \right)\frac{{{b_A}}}{V}q + {C_{m{\delta _e}}}\left( {{\delta _{{\rm{ice}}}}} \right){\delta _e} \\& {C_n} = {C_{n\beta }}\left( {{\delta _{{\rm{ice}}}}} \right)\beta + {C_{np}}\frac{l}{{2V}}p + {C_{nr}}\left( {{\delta _{{\rm{ice}}}}} \right)\frac{l}{{2V}}r + \\&\qquad {C_{n{\delta _a}}}{\delta _a} + {C_{n{\delta _e}}}\left( {{\delta _{{\rm{ice}}}}} \right){\delta _r} \end{split} $ | (2) |
将式(2)中各气动系数的拟合导数按是否依赖结冰严重性参数δice分成了两类,一类不受结冰影响,另一类受结冰影响。对于受结冰影响的气动导数,目前常用于动力学仿真的是一种线化模型,这里将任意受结冰影响的气动导数
| $ {\dot C}\left( {{\delta _{{\rm{ice}}}}} \right) = \left( {1 + {\delta _{{\rm{ice}}}}{\dot K}} \right)\dot C^{{\rm{clean}}} $ | (3) |
式中,
| $ {\dot \delta _{{\rm{ice}}}} = {N_1}\left( {1 + {N_2}{\delta _{{\rm{ice}}}}} \right){d_\delta } $ | (4) |
| $ {d_\delta }\left( t \right) = \frac{1}{2}\left[ {1 - \cos \left( {\frac{{2\text{π} t}}{{{T_{{\rm{cld}}}}}}} \right)} \right] $ | (5) |
| $ \begin{split} {N_1} = \frac{2}{{{N_2}{T_{cld}}}}\ln \left[ {1 + {N_2}{\delta _{{\rm{ice}}}}\left( {{T_{{\rm{cld}}}}} \right)} \right] \\ {N_2}=\frac{{{\delta _{{\rm{ice}}}}\left( {{T_{{\rm{cld}}}}} \right) - 2{\delta _{{\rm{ice}}}}\left( {{{{T_{{\rm{cld}}}}} / 2}} \right)}}{{\delta _{{\rm{ice}}}^2\left( {{{{T_{{\rm{cld}}}}} / 2}} \right)}} \end{split} $ | (6) |
式中,t为当前时刻,Tcld表示结冰累积时间,当Tcld、
采用Dryden风场扰动模型近似实际飞行过程中阵风扰动的影响,Dryden模型利用限制带宽的白噪声经过合适的滤波器后产生的扰动信号来模拟风场对大气模型的扰动,可将风速假设为均值为零,方差为
| $ \begin{split} {S_{{u_w}}}\left( \omega \right) =& \frac{{\sigma _{{\rm{turb}}}^2{L_{{\rm{turb}}}}}}{\text{π} }\frac{1}{{1 + {{\left( {{\omega / V}} \right)}^2}L_{{\rm{turb}}}^2}} \\ {S_{{v_w}}}\left( \omega \right) =& \frac{{\sigma _{{\rm{turb}}}^2{L_{{\rm{turb}}}}}}{{2\text{π} }}\frac{{1 + 3{{\left( {{\omega / V}} \right)}^2}L_{{\rm{turb}}}^2}}{{{{\left[ {1 + {{\left( {{\omega / V}} \right)}^2}L_{{\rm{turb}}}^2} \right]}^2}}} \\ {S_{{w_w}}}\left( \omega \right) = &\frac{{\sigma _{{\rm{turb}}}^2{L_{{\rm{turb}}}}}}{{2\text{π} }}\frac{{1 + 3{{\left( {{\omega / V}} \right)}^2}L_{{\rm{turb}}}^2}}{{{{\left[ {1 + {{\left( {{\omega / V}} \right)}^2}L_{{\rm{turb}}}^2} \right]}^2}}} \end{split} $ | (7) |
式中,ω表示频率,Lturb表示扰动的波长,将单位强度的高斯白噪声经过线性滤波器就可得到风场扰动速度。在MATLAB飞行器动力学仿真工具箱中,风场扰动模块即采用了Dryden风场模型,仿真中可以直接调用来获得风场扰动,模块中可选择不同的扰动强度来生成风场扰动速度。
1.3 测量噪声模型实际飞行中的测量数据难免会受到噪声的污染,为了使仿真结果尽量接近真实情况,这里还需要考虑测量噪声的影响。将各测量噪声假设为独立静态的零均值高斯随机过程,其标准差取值参照双水獭飞机的传感器精度给出[26],如表2所示,表中(Nx, Ny, Nz)T为体轴系下三个方向的过载分量,h为飞行高度。
| 表 2 双水獭飞机测量噪声标准差取值 Table 2 Standard deviation values of the measured noise for the Twin Otter airplane |
|
|
通过动力学仿真生成大量仿真数据用于神经网络的训练和评估,考虑采用不同的仿真初值、风场扰动、测量噪声和结冰严重程度等产生仿真数据。为了充分分析神经网络的性能,在训练数据和评估数据之外,还额外生成了训练评估样本之外的数据用于验证网络的泛化性能。表3中给出了用于生成训练评估数据所采用的仿真初始参数取值情况,测量噪声以表2所给大小为标称值,以倍数cnoise的不同取值对噪声标准差进行放大或缩小,风场扰动强度以超越概率的形式给出,其中概率取值为1×10−2对应的风场扰动强度在模块中被定义为轻度扰动,数值越大代表扰动强度越低。
| 表 3 训练评估数据的不同参数取值 Table 3 Parameter values for the training and validation data |
|
|
结冰严重程度与
| 表 4 结冰严重性参数取值 Table 4 Values for the icing severity coefficient |
|
|
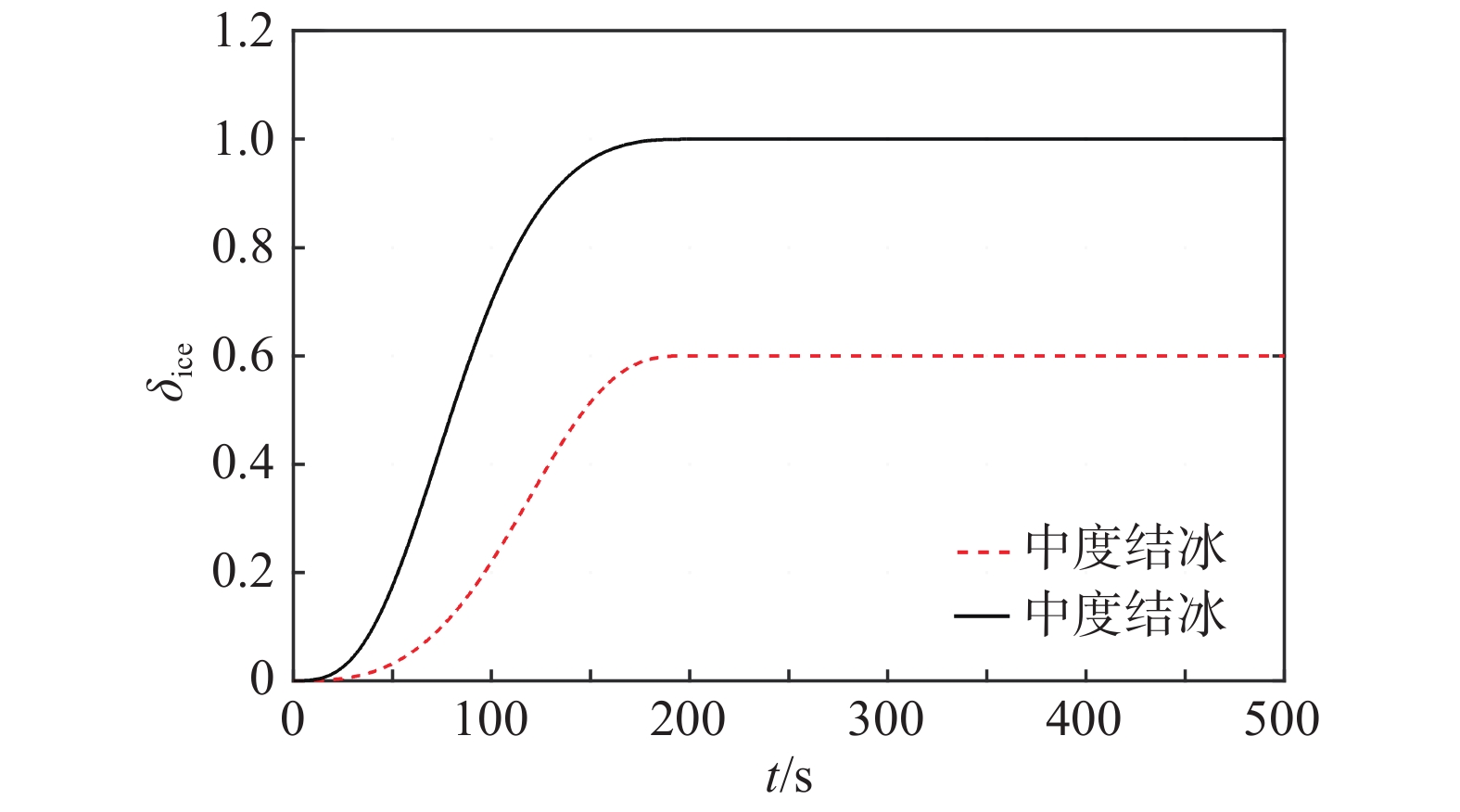
|
图 1 中度和重度结冰参数变化 Fig.1 Time variation for moderate and severe icing coefficients |
为了进一步说明网络的泛化能力,考虑在表3所给条件之外再生成一些仿真数据,用于对神经网络泛化能力的验证,仿真参数的取值见表5。表5中的参数取值同时考虑了对表3中训练评估数据取值的内插和外插情况,其中考虑了两种风场扰动超越概率,第一种取值与表3中一致,生成的数据可用于考核排除风场影响之外的泛化性能;另一取值为风场中等强度扰动,可用于考核加入风场影响后的模型泛化能力。
| 表 5 泛化能力评估数据的不同参数取值 Table 5 Parameter values for the generalization assessment data |
|
|
根据以上仿真条件,最后针对无冰、中度和重度机翼结冰以及中度和重度尾翼结冰五种结冰情况,分别生成1215条飞行数据作为神经网络训练评估的基础,并生成了72条飞行数据作为泛化性能验证的基础。
2.2 结冰影响分析通过分析仿真生成的大量飞行数据,分析结冰位置和严重性程度对飞行状态参数的影响,作为开展基于飞行状态结冰情况识别研究的基础。由于通过仿真得到的飞行状态变量较多,包括体坐标系下的三个速度分量(u, v, w)T、三个角速度分量(p, q, r)T、俯仰角θ、偏航角ψ、滚转角γ、惯性系下的三个位置分量(xe, ye, ze)T、过载分量(Nx, Ny, Nz)T、攻角α、侧滑角β和合速度V共18个变量。为了从这些飞行状态变量中选择受结冰影响较大的变量作为分类识别的依据,这里考虑通过对比结冰影响下的飞行状态相对无冰时的状态变化曲线的散布大小,来分析各状态变量受结冰影响的显著程度,为了保证变量之间的可比性,对所有状态变量统一进行了归一化处理。首先计算四种结冰情况导致的相对无冰情况的状态量偏差,再计算每一状态偏差曲线归一化后的方差表征偏差的散布,最后根据散布大小对18个状态变量在四种不同结冰情况下的1287次仿真结果进行排序,排序越小则表明方差散布越大,该变量受结冰影响越明显。
为了更为直观的呈现各状态量受结冰影响的程度,这里针对所有仿真结果中每一状态变量在任一排序出现的频次进行统计,并以色块图的形式对统计次数进行区分(见图2)。图2中分别给出了四种结冰情况下的统计结果,纵坐标表示方差散布大小排序,序号1表示方差最大,序号18表示方差最小,横坐标为18个状态变量,图中每一色块以从蓝到黄的色差表示状态变量在该排序上的统计次数。从图中可以看出,两种不同结冰位置导致状态量受影响程度呈现两种不同的变化规律,而相同结冰位置下的不同结冰严重程度分析结果呈现出较为一致的变化。对于机翼和尾翼结冰,受结冰影响程度较高的变量均为u、θ、xe、ze、Nx、α和V,说明机翼和尾翼结冰主要对飞机纵向运动参数产生影响。但由于结冰位置的不同,这些纵向参数的受影响程度排序存在较大区别,比如俯仰角θ在机翼结冰的影响下受影响程度高于尾翼结冰,而攻角α正好相反,通过对比发现θ、α和Nx三个变量在两种结冰位置下受影响程度排序存在差异,这也间接表明机翼和尾翼两种结冰位置对飞机动态特性具有不同的影响。
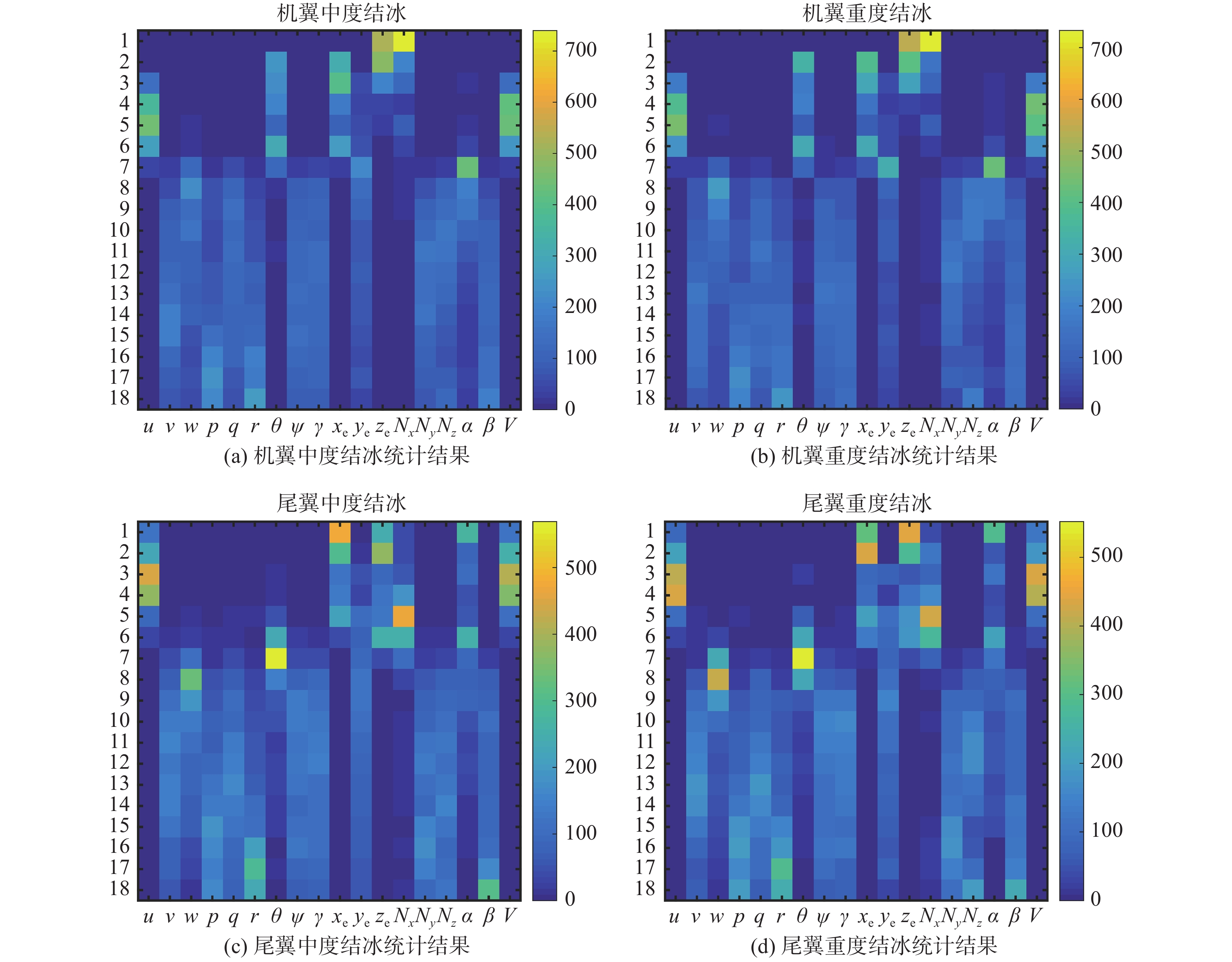
|
图 2 结冰对飞行状态变量的影响分析 Fig.2 Influence of icing on the flight state variables |
根据仿真数据的结冰影响分析结果,考虑基于受结冰影响程度较深的纵向状态变量u、θ、xe、ze、Nx和α建立结冰情况识别网络,由于u和V均表征飞行速度,因此这里不再特别针对合速度V开展研究。
3.1 网络参数优化策略概率神经网络中采用的径向基函数的传播速度对网络分类精度具有较为明显的影响,其取值越小,拟合程度越高,泛化性能越差,取值越大则相反。为了使设计的神经网络具有最优的性能,能够在具有较高的拟合精度的同时兼顾网络的泛化性能,本文设计了一种关于传播速度的优化策略,即在保证训练数据分类正确率100%的情况下使评估数据和泛化性能评估数据的误差最小,如图3所示。由于传播速度越小,训练数据分类精度越高,过拟合现象越明显,将会降低非训练数据的分类精度。因此首先利用一维搜索确定使训练数据分类精度达到100%的最大传播速度的取值bmax,再将评估数据和泛化性能评估数据分类误差之和作为优化指标,在[0, bmax]范围内寻找使误差最小的传播速度取值用于构建概率神经网络。
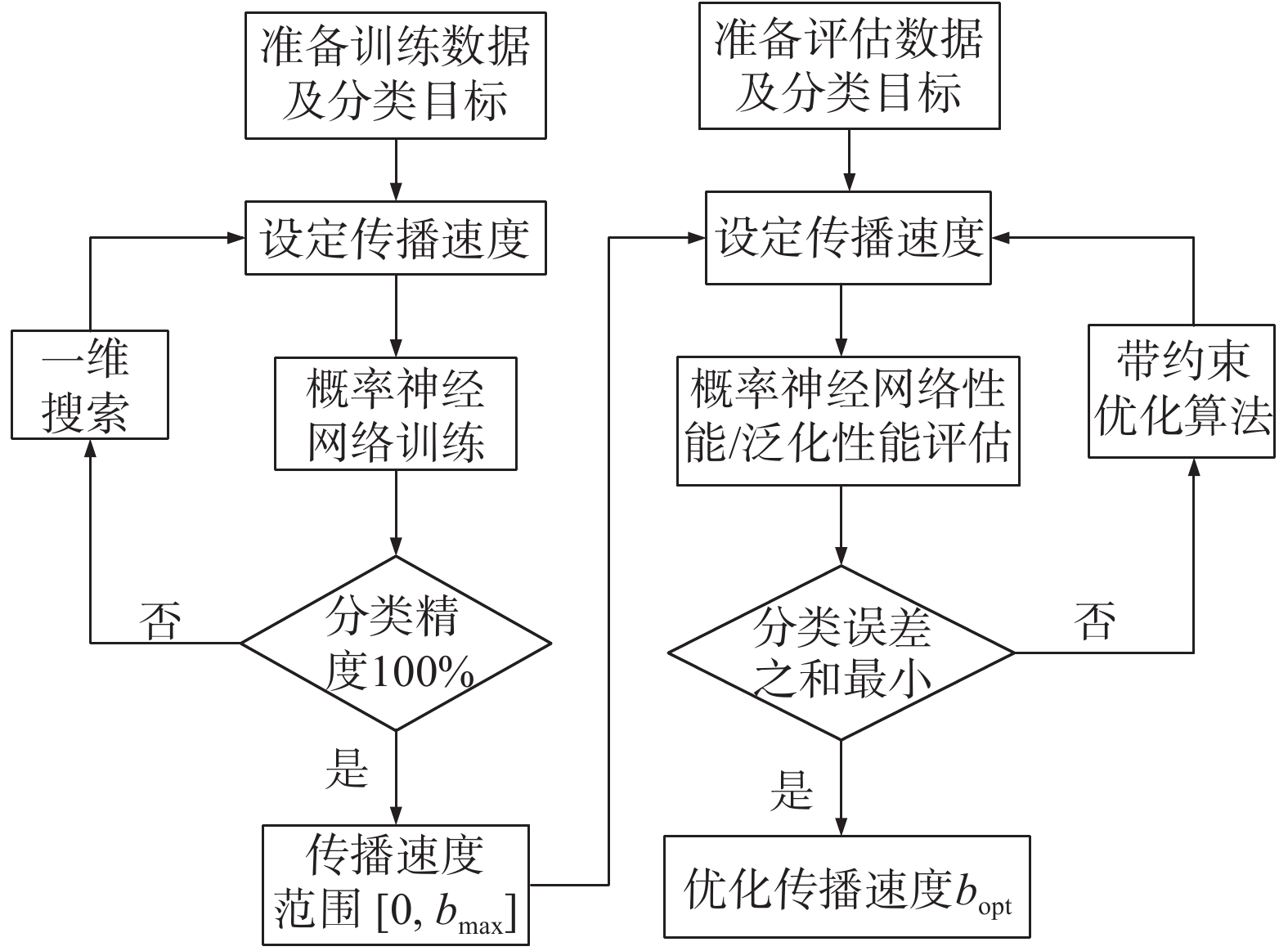
|
图 3 概率神经网络传播参数优化策略 Fig.3 Optimization scheme for the propagation parameter of probabilistic neural networks |
根据这一优化策略获得的概率神经网络能够达到基于该数据库的一种较佳的分类效果。
3.2 分类神经网络设计针对受结冰影响较大的u、θ、xe、ze、Nx和α共6个状态变量构建分类神经网络,首先在用于训练评估的数据中针对每一结冰情况按0.5的比例随机选取近一半数据作为网络的训练数据,另一半数据作为评估数据,这样可以有效避免“运动员-裁判员”的问题,保证评估的有效性。最后结合三种评估数据,利用上面的优化策略对基于状态变量的网络传播参数进行优化,最后得到了6个状态变量分别对应的传播参数优化结果(见表6)。表中给出了基于单一状态变量优化后得到的网络传播参数取值大小,考虑到位移分量相对量级较大,传播参数取值也较大,不便于算法优化计算,因此这里将x和z方向的位移分量做了线性映射处理(表中以“*”进行了标注),将数据通过线性变换投影到[0, 1]区间,这样可以缩小状态变量的搜索区间,以取得更好的分类效果。
| 表 6 不同状态变量的传播参数优化结果 Table 6 Optimized propagation parameter values for different state variables |
|
|
利用训练数据之外的评估数据和两种风场扰动对应的泛化性评估数据分析传播参数优化后的概率神经网络的性能,如图4所示。图中对比了6个状态变量在三种不同评估数据下的神经网络分类精度,其中评估数据指训练用数据库中用于评估网络性能的部分数据,两种泛化性评估数据分别对应表5中两种不同风场扰动数据,其中风场扰动超越概率取值为1×10−1对应的数据为泛化性评估数据一,由于该扰动取值已经包含在训练用数据库内,因此该数据可以用于评估PNN网络对于风场扰动之外的仿真条件和结冰条件的内插和外插性能;而泛化性评估数据二对应的风场扰动强度大于训练用数据库取值,因此这组数据可用于同时评估神经网络对仿真和结冰初始条件内插和外插以及风场扰动外插的能力。由图4中结果可知,基于攻角α的PNN网络对于评估数据有较高的分类精度,分类正确率高达99.1%,在不考虑风场扰动外插的情况下,对于不同仿真条件和结冰条件也具有较高的泛化能力,对泛化性评估数据一的分类正确率高于96%,但对于风场扰动外插的数据,几乎无法识别所有结冰情况,基于轴向速度u和过载Nx的分类结果也具有类似的特点。这是由于在飞机运动方程中风场扰动项的变化,会导致速度、攻角和过载等对加速度扰动敏感的变量呈现出较大的变化,导致基于这些参数的网络泛化性能降低;虽然风场扰动几乎不对姿态运动产生影响,但由于运动方程的耦合效应,风场扰动也会通过攻角等参数传递到姿态角,因此基于俯仰角θ的网络也呈现出评估精度较高(正确率超过97%),而泛化性能较低(正确率分别为52%和44%)的情况。从图4中可以看出,基于两个位移变量的分类网络,对于考虑风扰动后的数据泛化性能更强,这与风场扰动相对位移而言是小量,位移变量对参数小扰动变化不太敏感相关,因此基于两个位移变量的分类网络对于泛化性评估数据二的分类精度更高(正确率分别可达67%和53%),而基于xe的分类网络对于所有3类评估数据,其误差之和最小。
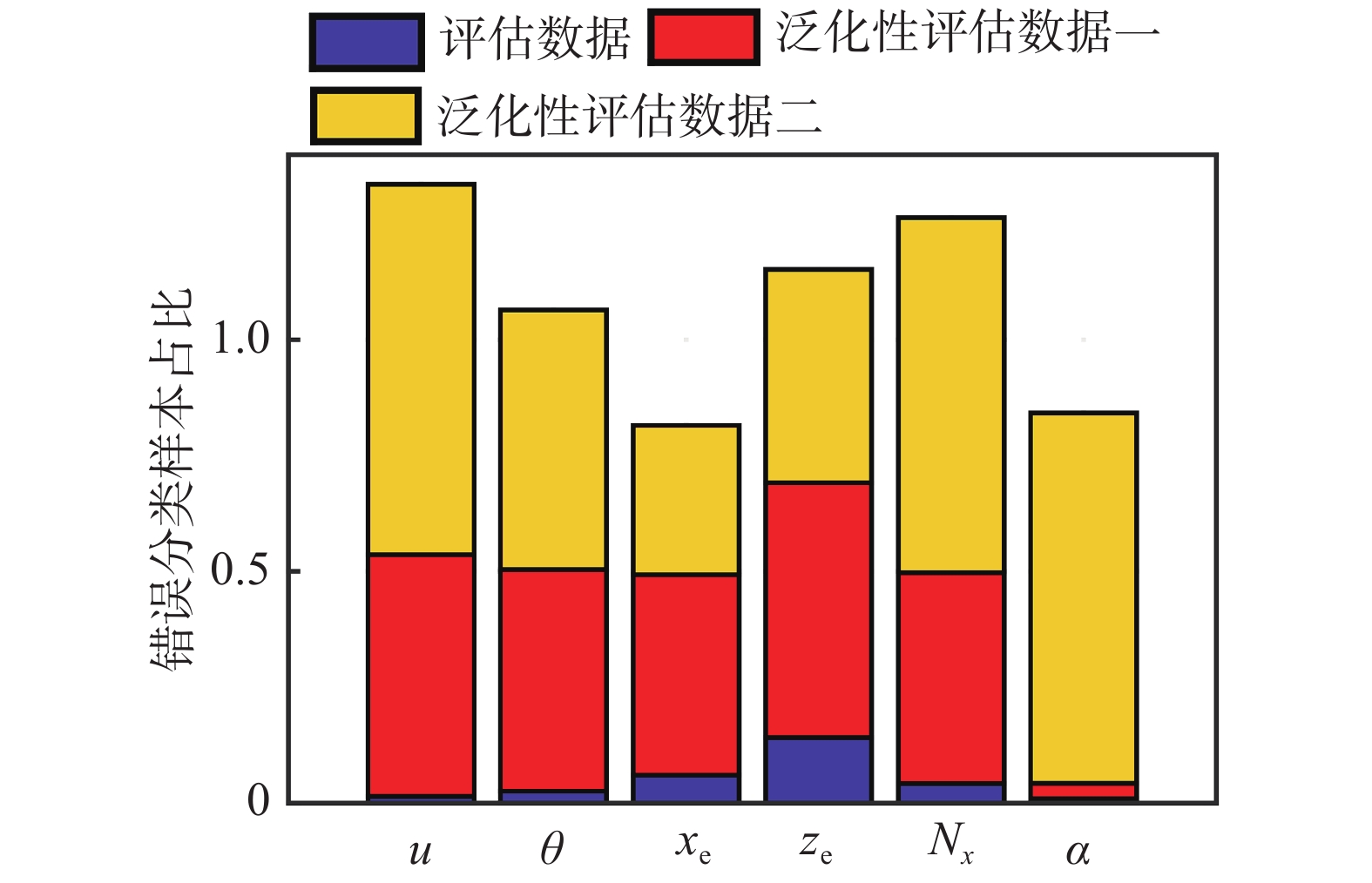
|
图 4 性能评估数据分类结果误差对比 Fig.4 Comparison of the classification errors of performance assessment data |
为了进一步对以上数据进行分析,这里引入物理学上的快/慢变量定义对状态变量进行划分,当系统受到干扰不稳定时,快变量是指使其回到稳定状态的阻尼大且衰减快的变量,慢变量是指使其离开稳定状态走向非稳定状态的衰减慢的变量。根据这一定义,飞机角速度、过载和姿态角等变量属于快变量,位置和速度属于慢变量。这两类变量在用于飞机结冰情况识别时分类效果区别较为明显,其中快变量能够更好的反应飞机的动态特性,对不同结冰情况反应更为灵敏,因此对于训练数据库中的数据,即使按0.5的比例选取训练-评估数据,均可获得较高的分类精度,但也同样因为变量的敏感性,导致风场之类的外部扰动同样对快变量有较大影响,因此基于快变状态变量的结冰分类网络普遍存在对加入风场扰动外插后的数据泛化性能较差的问题;而慢变状态变量对各种外部扰动的抗干扰能力更强,对结冰状态变化相对而言较为不敏感,因此对训练数据库中的评估数据分类误差较快变量大,但对泛化数据库中的数据分类效果整体更好。
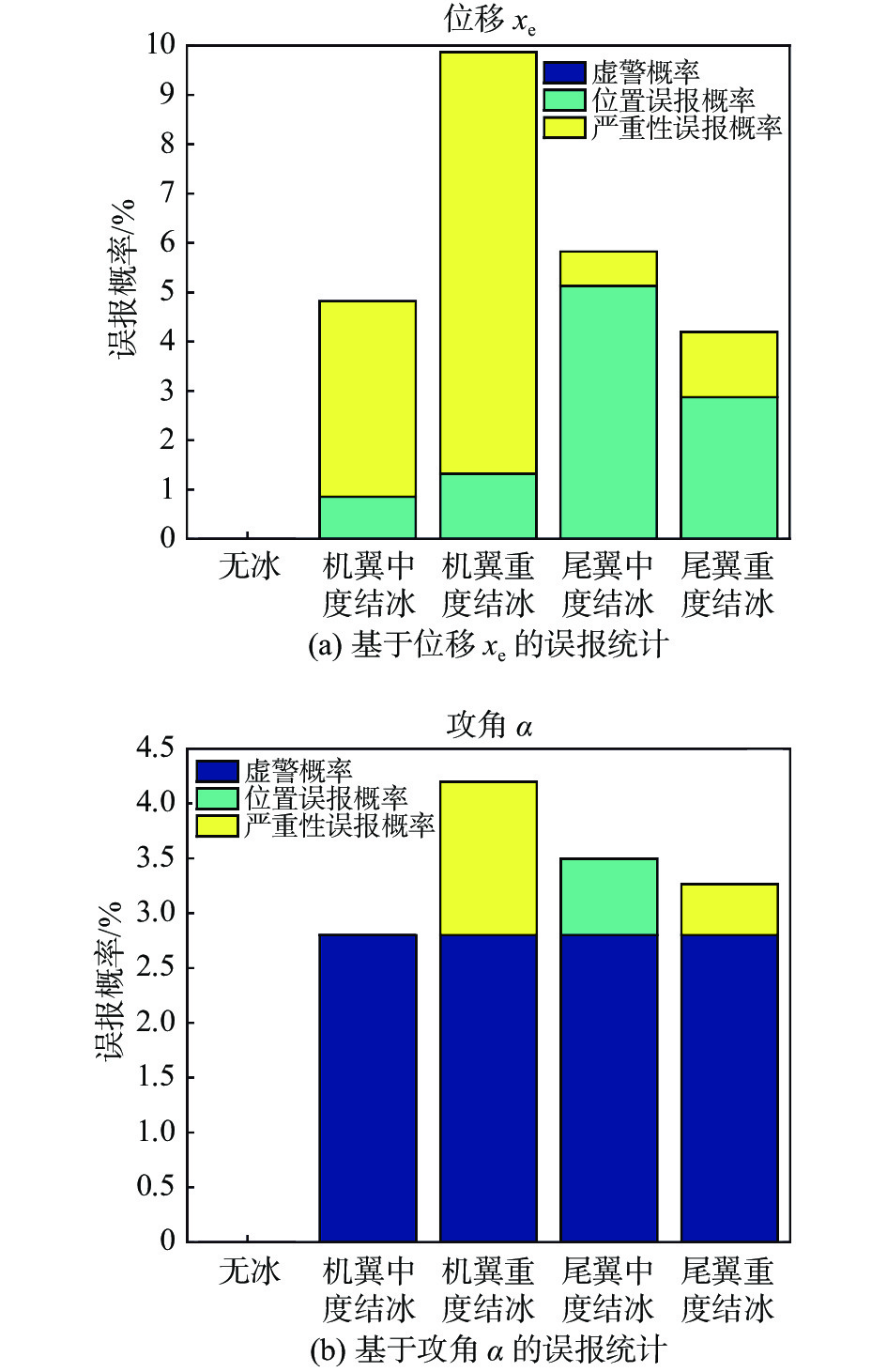
图5中针对分类精度较高的慢变量xe和快变量α的所有数据分类误报概率进行统计,分别按无冰、机翼中度结冰、机翼重度结冰、尾翼中度结冰和尾翼重度结冰五种情况进行统计。其中虚警概率指无冰情况中被当作结冰的样本,或结冰情况下被分类为无冰的样本在该情况下所有样本中的百分比。从图中可以看出这两种变量在无冰情况下均不会出现虚警,位移xe在结冰情况下也不存在虚警,但攻角α在四种结冰情况下出现了概率一致的虚警,这是由于网络对泛化性评估数据二中的所有结冰样本均被识别为无冰情况。位置误报概率和严重性误报概率均只针对四种结冰情况,结冰位置误报概率是指识别出的结冰位置,即机翼或尾翼出现错误的样本百分比,严重性误报概率是指对于同一结冰位置,错误判断为中度或重度结冰的样本百分比。从统计结果看,基于位移xe的机翼结冰出现严重性误报的概率明显超过位置误报,而尾翼结冰则正好相反,对于五种情况,整体上最大误报概率不超过10%;基于攻角α的位置和严重性误报概率均较小,在不考虑泛化性评估数据二出现的虚警情况下,最大误报概率为机翼重度结冰下出现的严重性误报,不超过1.4%,其中机翼中度结冰情况下没有出现除虚警之外的其他误报,说明排除风扰动的影响后,攻角α具有较高的结冰分类精度。
|
图 5 不同结冰情况下的神经网络分类误报概率统计 Fig.5 Statistics of the false alarming probability for neural network-based classification under different icing situations |
为了进一步说明所建立的神经网络对这一分类问题的性能,下面将网络分类精度与支持向量机(Support Vector Machine, SVM)的结果进行对比。支持向量机是一种经典的分类方法,在大多数分类问题中,支持向量机的分类精度通常可以超过各类神经网络、基因表达式编程分类器和k均值聚类分类器等[29]。这里利用基于两种不同核函数的支持向量机方法与本文提出的优化概率神经网络方法进行对比,说明该方法的性能。
分别选择立方核函数和高斯核函数作为支持向量机的内核函数,基于攻角α对五种情况进行分类,同样采用上面给出的训练数据和三种评估数据,分别计算四类数据的分类误差,见表7。由表中结果可知,基于立方核的SVM方法对所有四类数据的分类精度最高,对于相同的训练和评估数据,优化概率神经网络的分类精度接近立方核SVM方法,稍优于高斯核SVM方法;在泛化性评估方面,所有方法均存在泛化性能降低的现象,特别是对于第二类泛化性评估数据,优化概率神经网络的分类精度与高斯核SVM方法一致,低于立方核SVM方法。通过方法对比,说明无论是概率神经网络,还是性能更强的SVM方法,对于数据外推,均存在不同程度的泛化性能下降的问题,其中本文提出的优化概率神经网络,对于训练和评估数据其分类精度逼近立方核SVM方法,泛化性评估数据分类精度与高斯核SVM方法较为接近,这也说明了该方法具有较为优秀的分类性能。
| 表 7 不同方法的分类精度对比 Table 7 Comparison of the classification accuracy of different methods |
|
|
1) 通过对大量仿真数据分析发现,飞机机翼和尾翼结冰对u、θ、xe、ze、Nx和α六个飞机纵向运动参数的影响较为显著;同一结冰位置下状态变量受影响程度排序规律一致性较好,不同结冰位置影响程度排序规律有明显区别,说明对于机翼和尾翼两种不同结冰位置,飞机的动态特性具有不同的响应特点。
2) 基于六个受结冰影响较为显著的状态变量,在优化传播参数之后建立的概率神经网络模型,对训练评估数据具有较高的分类精度,即使在训练-评估数据选取比例为0.5的情况下,效果最差的网络对评估数据的分类错误样本占比仅为14%,效果最好的神经网络分类误差仅为0.9%;攻角和俯仰角等快变量对于评估数据分类精度较高,但由于对初值和风场等扰动更为敏感,导致对泛化评估数据的分类精度较低;虽然位移等慢变量对评估数据分类误差较快变量大,但由于其抗扰动能力更强,因此对泛化数据库中的数据分类效果更好。
3) 若不考虑风场扰动的变化,基于攻角α的分类网络是针对这一问题的最优分类网络,对于五种结冰情况的最大误报概率不超过1.4%;若综合考虑风场扰动变化的情况,则采用基于xe的分类网络分类误差更小,对于五种结冰情况,最大误报概率整体不超过10%。
4) 通过本文的研究工作说明直接基于飞行状态变量建立神经网络对飞行结冰情况进行识别分类具有一定的可行性,概率神经网络对于训练和评估数据分类精度较高,能够逼近立方核SVM方法,然而对于训练评估数据样本之外的数据,几种方法都存在泛化性能降低的问题,其分类精度与高斯核SVM方法相近。因此应尽量保证神经网络的训练库数据能够最大限度的覆盖研究关注的范围,以获得精度较高的神经网络分类结果。
本文的研究工作作为直接基于飞行状态变量进行结冰位置和严重程度分类识别的初步探讨,可作为传感器结冰探测的有益补充,对于飞机上无法安装传感器或传感器安装位置受限无法充分覆盖的情况,该方法具有较好的应用前景。下一步还有继续深化研究的空间,其一是可以结合动力学系统行为分析或飞行数据结冰信息提取等方法进一步提升该分类网络对不同飞行状态、复杂飞行环境和结冰情况等的识别能力;其二是进一步探讨神经网络模型和算法在基于状态变量的结冰情况分类中的能力和应用,如卷积神经网络和基于物理模型的神经网络等,以进一步改善分类精度和泛化能力。
| [1] |
CAO Y H, TAN W Y, WU Z L. Aircraft icing: an ongoing threat to aviation safety[J]. Aerospace Science and Technology, 2018, 75: 353-385. DOI:10.1016/j.ast.2017.12.028 |
| [2] |
CAO Y H, WU Z L, SU Y, et al. Aircraft flight characteristics in icing conditions[J]. Progress in Aerospace Sciences, 2015, 74: 62-80. DOI:10.1016/j.paerosci.2014.12.001 |
| [3] |
GORAJ Z. An overview of the de-icing and anti-icing technologies with prospects for the future[C]//24th International Congress of Aeronautical Sciences, Yokohama, Japan, 2004.
|
| [4] |
JARVINEN P. aircraft ice detection method[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2007. doi: 10.2514/6.2007-696
|
| [5] |
HUANG X, TEPYLO N, POMMIER-BUDINGER V, et al. A survey of icephobic coatings and their potential use in a hybrid coating/active ice protection system for aerospace applications[J]. Progress in Aerospace Sciences, 2019, 105: 74-97. DOI:10.1016/j.paerosci.2019.01.002 |
| [6] |
SHARIFI N, DOLATABADI A, PUGH M, et al. Anti-icing performance and durability of suspension plasma sprayed TiO2 coatings
[J]. Cold Regions Science and Technology, 2019, 159: 1-12. DOI:10.1016/j.coldregions.2018.11.018 |
| [7] |
LIU J P, WANG J, MEMON H, et al. Hydrophobic/icephobic coatings based on thermal sprayed metallic layers with subsequent surface functionalization[J]. Surface and Coatings Technology, 2019, 357: 267-272. DOI:10.1016/j.surfcoat.2018.10.002 |
| [8] |
SCHUCHARD E, MELODY J, BASAR T, et al. Detection and classification of aircraft icing using neural networks[C]// 38th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 2000. doi: 10.2514/6.2000-361
|
| [9] |
DING D, CHE J, QIAN W Q. Fault-tolerant flight control for aircraft wing icing based on icing detection method[C]// 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China. IEEE, 2018: 1-6. doi: 10.1109/GNCC42960.2018.9018871
|
| [10] |
WEI Y, XU H J, XUE Y. Adaptive neural networks-based dynamic inversion applied to reconfigurable flight control and envelope protection under icing conditions[J]. IEEE Access, 2020, 8: 11577-11594. DOI:10.1109/ACCESS.2020.2964728 |
| [11] |
MCCANN D W. NNICE - a neural network aircraft icing algorithm[J]. Environmental Modelling & Software, 2005, 20(10): 1335-1342. DOI:10.1016/j.envsoft.2004.09.027 |
| [12] |
CAO Y H, YUAN K G, LI G Z. Effects of ice geometry on airfoil performance using neural networks prediction[J]. Aircraft Engineering and Aerospace Technology, 2011, 83(5): 266-274. DOI:10.1108/00022661111159870 |
| [13] |
OGRETIM E, HUEBSCH W, SHINN A. Aircraft ice accretion prediction based on neural networks[J]. Journal of Aircraft, 2006, 43(1): 233-240. DOI:10.2514/1.16241 |
| [14] |
CHANG S N, LENG M Y, WU H W, et al. Aircraft ice accretion prediction using neural network and wavelet packet transform[J]. Aircraft Engineering and Aerospace Technology, 2016, 88(1): 128-136. DOI:10.1108/aeat-05-2014-0057 |
| [15] |
CALISKAN F. Neural network based icing identification and fault tolerant control of a 340 aircraft[J]. International Journal of Electrical, Computer, and Systems Engineering, 2007, 1(2): 98-103. |
| [16] |
AYKAN R, CALISKAN F, HAJIYEV C. F16 icing identification based on neural networks[J]. IFAC Proceedings Volumes, 2004, 37(19): 201-206. DOI:10.1016/S1474-6670(17)30683-3 |
| [17] |
MELODY J, POKHARIYAL D, MERRET J, et al. Sensor integration for inflight icing characterization using neural networks[C]// 39th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 2001. doi: 10.2514/6.2001-542
|
| [18] |
DONG Y Q. An application of Deep Neural Networks to the in-flight parameter identification for detection and characterization of aircraft icing[J]. Aerospace Science and Technology, 2018, 77: 34-49. DOI:10.1016/j.ast.2018.02.026 |
| [19] |
DONG Y Q, AI J L. Research on inflight parameter identification and icing location detection of the aircraft[J]. Aerospace Science and Technology, 2013, 29(1): 305-312. DOI:10.1016/j.ast.2013.03.012 |
| [20] |
DONG Y Q, AI J L. Inflight parameter identification and icing location detection of the aircraft: the time-varying case[J]. Journal of Control Science and Engineering, 2014, 2014: 1-11. DOI:10.1155/2014/396532 |
| [21] |
JOHNSON M D, ROKHSAZ K. Using artificial neural networks and self-organizing maps for detection of airframe icing[J]. Journal of Aircraft, 2001, 38(2): 224-230. DOI:10.2514/2.2779 |
| [22] |
YING S B, AI J L. Detection of aircraft in-flight icing in non-steady atmosphere using artificial neural network[C]// 2010 Third International Symposium on Intelligent Information Technology and Security Informatics, Jian, China. IEEE, 2010: 206-211. doi: 10.1109/IITSI.2010.146
|
| [23] |
SPECHT D F. Probabilistic neural networks[J]. Neural Networks, 1990, 3(1): 109-118. DOI:10.1016/0893-6080(90)90049-Q |
| [24] |
SPECHT. Probabilistic neural networks for classification, mapping, or associative memory[C]// IEEE 1988 International Conference on Neural Networks, San Diego, CA, USA. IEEE, 1988: 525-532. DOI: 10.1109/ICNN.1988.23887
|
| [25] |
陈明等. MATLAB神经网络原理与实例精解[M]. 北京: 清华大学出版社, 2013: 205-207
|
| [26] |
MELODY J W. Inflight characterization of aircraft icing[D]. Illinois Urbana: University of Illinois at Urbana-Champaign Graduate College, 2004: 17-46.
|
| [27] |
MELODY J W, HILLBRAND T, BAŞAR T, et al. H∞ parameter identification for inflight detection of aircraft icing: the time-varying case[J]. Control Engineering Practice, 2001, 9(12): 1327-1335. DOI:10.1016/S0967-0661(01)00081-8 |
| [28] |
赵元魁, 王耀力. 风场环境下四旋翼飞行器抗干扰研究[J]. 机械科学与技术, 2019, 38(4): 530-537. ZHAO Y K, WANG Y L. Research on anti-disturbance for quadrotor aircraft in wind field[J]. Mechanical Science and Technology for Aerospace Engineering, 2019, 38(4): 530-537. (in Chinese) |
| [29] |
KUSY M, ZAJDEL R. Probabilistic neural network training procedure based on Q(0)-learning algorithm in medical data classification[J]. Applied Intelligence, 2014, 41(3): 837-854. DOI:10.1007/s10489-014-0562-9 |
 2022, Vol. 40
2022, Vol. 40

