0 引　言

工业革命以来，煤炭、石油和天然气等传统燃料面临着资源日趋耗减的问题，大规模推动可再生能源技术部署被视为主要解决办法之一，而风能在2020年所有可再生资源中增幅最大，产能达到2750亿千瓦时^[1-2]。目前所使用的风能主要来自陆上。海上风电自20世纪90年代起才不断成熟，并逐渐向大规模商业化发展^[3]。然而，海上风电的引入给风能企业带来了成本挑战，海上风电的设计原理和相关策略尚不清楚^[4]。

风能未来的发展取决于风能技术的不断更新和成本的不断下降^[5]。为了降低风能成本，风力机产业最通用的措施之一，就是设计出尺寸更大、效率更高的风力机。通过增大叶片长度，使得扫风面积增大，可以捕获更多能量，在其他成本保持不变的同时，可以大幅降低单位能量成本^[6-7]。叶片延长后，为了降低整体重量并降低制造成本，大型风力机叶片通常采用杨氏模量和刚度较低的复合材料，造成叶片柔性显著增加，同时由于叶片几何形状也较为复杂，因此叶片气动载荷和结构动力学响应之间存在强烈的气动弹性耦合。同时，大挠度改变了有效扫风面积，进而导致功率输出、力矩和推力也受到影响。此外，由于非定常气动载荷与风力机结构之间的相互作用，容易发生叶片振动和颤振，严重时甚至可能影响风力机的使用寿命。

气动弹性预测是叶片设计中的重要步骤，非定常气动载荷和叶片变形之间复杂的相互作用对风力机性能和安全分析至关重要。相比于单独的结构或气动设计方法，结构动力学和空气动力学的联合分析可提供更全面和系统的数据，这将有助于提高叶片设计性能，同时保障整个风力机系统的安全可靠性，从而使风能发电更具竞争力。在风力机的结构动力学和空气动力学研究过程中，考虑到模拟复杂的真实海洋状态的困难性以及实验的高成本^[8-9]，数值模拟应用最为广泛。

气动弹性的数值分析已逐渐成为风电行业的重要研究内容，一些大型风能研究组织，如美国可再生能源国家实验室（NREL）、RisøDTU等，已经开发了多种气动弹性研究工具^[10-11]。这些工具大多采用叶素动量理论来模拟空气动力学，而结构动力学建模则采用刚体多体动力学、模态法和传统的线性有限元法。此外，来自其他学科领域（如航空航天、机械工程、土木工程）的许多研究人员也提出了不同的模型用于解决风力机气动弹性问题。Wang等^[12]基于ANSYS-FLUENT软件和壳单元，建立了风力机单向耦合模型，将CFD建模计算出的气动载荷作为边界条件映射到有限元模型，而叶片挠度未映射回气动模型。Li等^[13]对5 MW浮式风力机，将结构梁单元和精细CFD模型耦合，并采用显式风湍流模型进行求解。Mo等^[14]将一维梁单元和叶素动量理论耦合，模拟了5 MW风力机叶轮，结果表明叶片振动和变形对气动载荷有显著影响，与稳态气动模型相比，动态失速会导致叶片气动载荷的剧烈波动，从而对疲劳设计产生很大影响。Meng等^[15]结合致动线模型和Euler-Bernoulli梁理论，提出了一种弹性致动线模型，对风力机进行气动弹性模拟，分析叶片振动速度对攻角的影响。Ma等^[16]讨论了旋转刚化效应、应力加强效应、风力机叶片的非线性弯曲对风力机变形的影响，研究结果表明风力机的变形将影响远尾流区的速度分布。Li等^[17]结合变分渐近梁截面分析方法和Euler-Bernoulli梁模型，分析了弯扭耦合特性对风力机叶片动力学性能的影响。Qian等^[18]分别采用线性模态叠加法和非线性几何精确梁方法，计算了百米量级叶片在稳态来流（风）和湍流来流（风）条件下的动态响应，研究表明几何非线性效应对于大型风力机气动弹性分析不可忽略。

总的来说，学者们对风力机的气动弹性耦合研究已经进行了许多尝试，但仍然存在一些不容忽视的问题和困难。首先，三维叶片建模的复杂性和巨大的计算量仍然是一大挑战。风力机数值模拟的目标之一就是减少建模和计算时间，同时提供足够准确的预测，但传统的结构动力分析工具无法满足全面新设计的需求。同时，旋转运动引起的大位移和复合材料弹性耦合引起的几何非线性是不可忽略的，特别是对于大载荷下的柔性结构而言。另外，大多数现有的气动弹性模型是基于小叶片挠度假设的传统线性模型，但这些模型不再适用于经常经历大挠度变形的长柔性叶片设计。

因此，针对以上大型风力机发展中出现的问题，本文基于柔性多体动力学、致动线方法和大涡模拟，建立了一种新型的双向流固耦合模型，在避免了三维叶片建模的复杂性和巨大的计算量的同时，能够准确预测结构载荷及动力学响应，评估风力机的功率和负载，并对风力机尾迹和周围流场进行更详细的模拟和分析。

1 计算方法 1.1 致动线方法

目前，计算流体力学模拟风力机及其周围流场的方法主要有叶素动量法、致动盘法、致动线法和三维高保真模拟等。其中，致动线法凭借着计算量小、可以更好地解析叶片周围流动细节等优势，在风力机领域得到广泛应用。致动线模型可用于精确再现风力机叶片的涡流系统，并适用于简单的结构化网格，大量的研究证明了致动线法是预测风力机叶片非定常气动载荷的有效方法。

在致动线方法中，叶片被简化成一维的线，并被划分成有限个致动点，如图1所示。在获取每个致动点上的风速 $ {U}_{\mathrm{r}\mathrm{e}\mathrm{l}} $ 和攻角 $ {\alpha }_{\mathrm{r}\mathrm{e}\mathrm{l}} $ 后，通过查找相应的翼型数据表，获得对应的升力系数 $ {C}_{L} $ 和阻力系数 $ {C}_{D} $ ，并计算每个致动点的升力 $ L $ 和阻力 $ D $ ^[19]：

$ L = \frac{1}{2}{C}_{L}\left({\alpha }_{\mathrm{r}\mathrm{e}\mathrm{l}}\right)\rho {U}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{2}cw $

(1)

$ D = \frac{1}{2}{C}_{D}\left({\alpha }_{\mathrm{r}\mathrm{e}\mathrm{l}}\right)\rho {U}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{2}cw $

(2)

其中， $ \rho $ 为流场的密度， $ c $ 为弦长， $ w $ 为致动点所在截面宽度。

然后，根据高斯投影函数将升阻力分配到致动点周围相应球形区域内流体网格中心的体积力 $ f $ 上：

$ f\left(r\right) = \frac{F}{{\varepsilon }^{3}{\text{π} }^{\frac{3}{2}}}{\rm{exp}}{\Bigg[-\left(\frac{r}{\varepsilon }\right)\Bigg]}^{2} $

(3)

$ F = L+D $

(4)

其中， $ \varepsilon $ 为高斯函数的投影半径， $ r $ 为网格中心到投影致动点的距离， $ F $ 为升阻力的合力。

最后，将结果添加到Navier-Stokes方程中进行求解：

$ \frac{\partial {u}_{i}}{\partial t}+{u}_{j}\frac{\partial {u}_{i}}{{\partial x}_{j}} = -\frac{1}{\rho }\frac{\partial p}{\partial {x}_{i}}+\upsilon \frac{{\partial }^{2}{u}_{i}}{\partial {x}_{i}\partial {x}_{j}}+{f}_{i} $

(5)

其中， $ {u}_{i} $ 为 $ i $ 方向的流体速度， $ t $ 为时间， $ \rho $ 为流体密度， $ {x}_{i} $ 为流体网格坐标， $ p $ 为压强， $ {f}_{i} $ 为对应方向的体积力。

1.2 柔性多体动力学方程

柔性多体系统由多个弹性和刚性组件组成，其中柔性体的变形不可以忽略。系统的动力学方程如下^[20]：

$ \boldsymbol{M}\ddot{\boldsymbol{x}}\left(t\right)+\boldsymbol{C}\dot{\boldsymbol{x}}\left(t\right)+\boldsymbol{K}\boldsymbol{x}\left(t\right) = \boldsymbol{F}(\boldsymbol{x},\dot{\boldsymbol{x}},t) $

(6)

其中， $ \boldsymbol{x}\left(t\right) $ 是位移向量， $ \boldsymbol{M} $ 、 $ \boldsymbol{C} $ 、 $ \boldsymbol{K} $ 分别是质量矩阵、阻尼矩阵和刚度矩阵， $ \dot{\boldsymbol{x}} $ 是 $ \boldsymbol{x} $ 关于时间的导数， $ \boldsymbol{F} $ 是外部力向量。

为了方便求解，将动力学方程等价为如下一阶微分方程组：

$ \boldsymbol{M}\dot{\boldsymbol{x}} = \boldsymbol{\beta } $

(7)

$ \dot{\boldsymbol{\beta }}+{\boldsymbol{\phi }}_{/\boldsymbol{x}}^{\mathrm{T}}{\boldsymbol{\lambda }}_{\boldsymbol{\phi }}+{\boldsymbol{\psi }}_{/\dot{\boldsymbol{x}}}^{\mathrm{T}}{\boldsymbol{\lambda }}_{\boldsymbol{\psi }} = \boldsymbol{F} $

(8)

$ \boldsymbol{\phi }\left(\boldsymbol{x},t\right) = 0 $

(9)

$ \boldsymbol{\psi }\left(\boldsymbol{x},\dot{\boldsymbol{x}},t\right) = 0 $

(10)

其中， $ \boldsymbol{\beta } $ 为系统动量， $ \boldsymbol{\phi } $ 为完整约束， $ \boldsymbol{\psi } $ 为非完整约束， ${\boldsymbol{\lambda }}_{\boldsymbol{\phi }}$ 和 $ {\boldsymbol{\lambda }}_{\boldsymbol{\psi }} $ 分别是对应约束的拉格朗日乘子，下标 ${/\boldsymbol{x}}$ 为对 $ x $ 求导。

对方程组化简并省略高阶项，得到如下方程组：

$ \left[ {\begin{array}{*{20}{c}} {\boldsymbol{M}}&{ - h{b_0}{\boldsymbol{I}}}&0&0\\ { - (h{b_0}{F_{/x}} + {F_{/\dot x}})}&{\boldsymbol{I}}&{{\boldsymbol{\phi}} _{/{\boldsymbol{x}}}^{\rm{T}}}&{{\boldsymbol{\psi }}_{/\mathop {\boldsymbol{x}}\limits^. }^{\rm{T}}}\\ {{{\boldsymbol{\phi}} _{/x}}}&0&0&0\\ {{{\boldsymbol{\psi }}_{/\dot x}}}&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\partial \mathop {\boldsymbol{x}}\limits^. }\\ {\partial \mathop {\boldsymbol{\beta }}\limits^. } \end{array}}\\ {\begin{array}{*{20}{c}} {\partial \mathop {{{\boldsymbol{\lambda }}_{\boldsymbol{\phi}} }}\limits^. }\\ {\partial \mathop {{{\boldsymbol{\lambda }}_{\boldsymbol{\psi }}}}\limits^. } \end{array}} \end{array}} \right] = {\boldsymbol{R}} $

(11)

其中， $ h{b}_{0} $ 为常系数， $ \boldsymbol{I} $ 为单位矩阵， $ \boldsymbol{R} $ 为残差向量。

在线性化后，采用隐式线性多步积分法对动力学方程进行迭代求解，详细求解过程可参阅文献[20]。此外，在可再生能源领域，相比于传统梁模型，几何精确梁模型^[21-22]在分析细长柔性结构的几何非线性方面具有优越性^[23]，被逐渐应用到结构研究中^[24-25]，本文将叶片简化为几何精确梁模型，每个梁单元具有3个节点，每个节点具有6个自由度，可以用于模拟叶片的大范围旋转运动和几何非线性变形。

1.3 耦合机制

本文采用分区式耦合方法，将流体和结构求解器分别表示为算子 $ F $ 和 $ S $ ，求解器的输入和输出值分别对应结构运动学变量 $ s $ 如位移和速度，以及动力学变量 $ f $ 如升阻力，变量之间的关系如下：

$ F\left(s\right) = f $

(12)

$ S\left(f\right) = s $

(13)

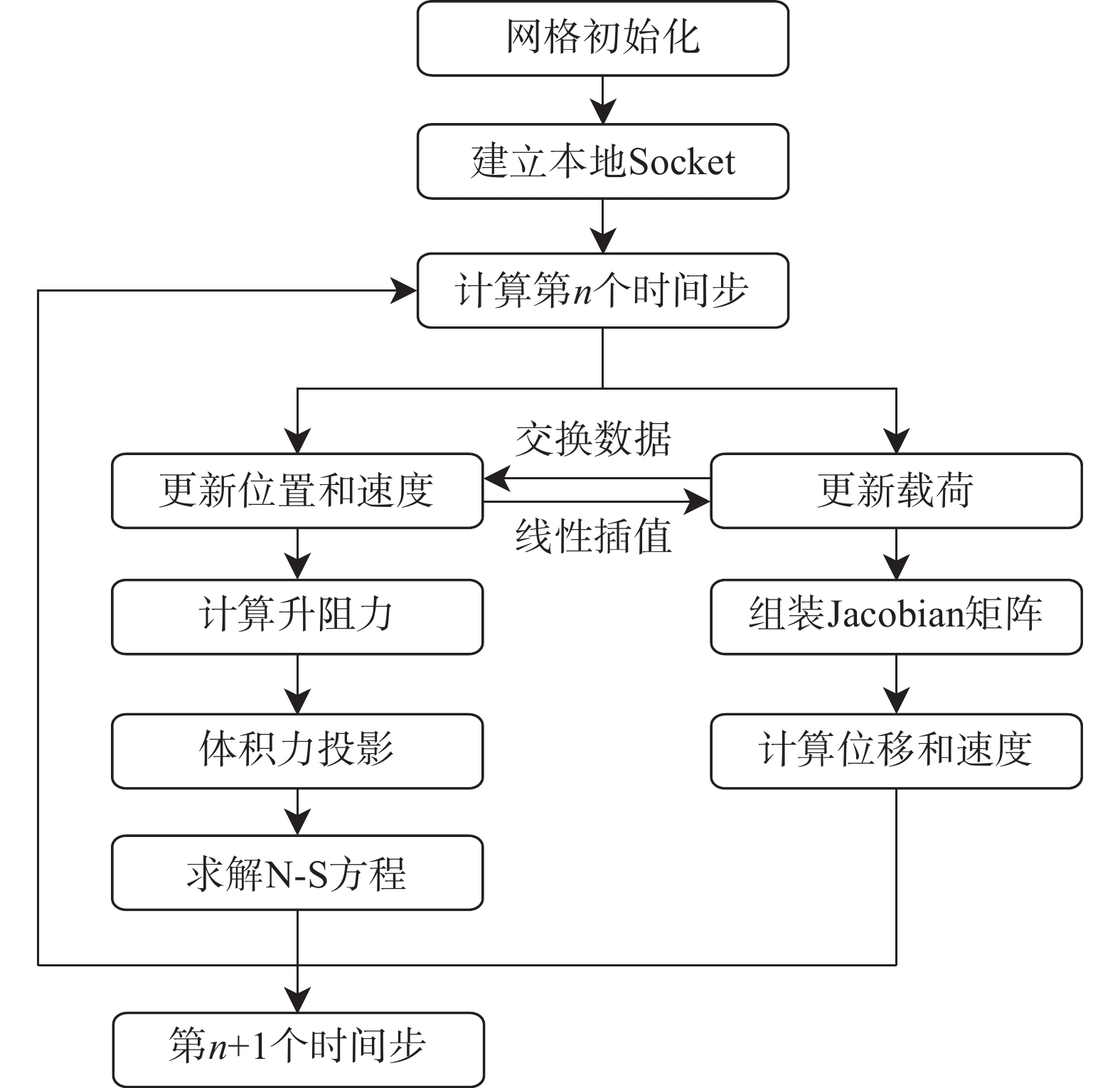
为了准确及时地交换和映射叶片结构和流场之间的耦合信息，双方求解器通过本地套接字在每个耦合时间步长交换数据。如图2所示，在每个耦合时间步长中，结构求解器向流体求解器发送预测的运动学数据，即位移和速度，并从流体求解器接收相关的力数据，通过线性插值，投影到结构单元上。同时，流体求解器接收映射过来的运动学数据，通过致动线方法求解升力和阻力，并将这两种体积力投影到每个致动点周围的流体网格上。本文数值计算基于柔性多体动力学程序MBDyn^[20]和计算流体力学软件OpenFOAM^[26]实现。

2 数值模型 2.1 NREL-5 MW风力机参数

本文选取的风力机模型为NREL提出的5 MW基准风力机，该风力机符合全球风力机产业尺度趋势，被广泛应用于数值模拟领域^[27]。其参数如表1所示。

2.2 数值模型

本文所有计算均在笛卡尔坐标系下进行，计算域为15D（长）×10D（宽）×10D（深），其中D为转子直径。总体布局如图3所示。顺流线方向，风力机上游为5D，风力机下游为10D，计算域足够长、利于尾流充分发展；风力机轮毂和横向边界之间的距离为5D，可以认为横向边界对风力机几乎没有影响。来流入口边界条件设为速度11.4 m/s的定常均匀来流，出口边界条件为速度梯度为0。底部、顶部和横向边界条件设置为滑移边界。如图3所示，六面体网格用于离散计算区域，风力机附近的区域在三个方向上依次加密，最大网格尺寸为20 m，最小网格尺寸为1.25 m，网格总数为6891528。

为了使预测出的体积力沿叶片分布足够光滑，每个叶片被划分为90个致动点。为了避免数值振荡，并确保网格可以投影上体积力， $ \varepsilon $ 应不小于最小网格尺寸的2倍^[28]，因此选择 $ \varepsilon = 3 $ 。湍流模型采用标准的Smagorinsky模型，并使用大涡模拟方法模拟风力机尾迹。考虑到使用笛卡尔网格的致动线模型时，每个时间步长内叶尖通过的距离不应超过一倍网格长度，因此本算例流体求解器的时间步长设为0.005 s。在结构模型中，每个叶片被简化为15个几何精确梁单元，时间步长为0.001 s。算例共采用112个计算节点，总计算时长为93 h，计算所得数据均基于初始状态60圈后达到稳定状态的20圈内的平均值。

3 结果分析 3.1 模型验证

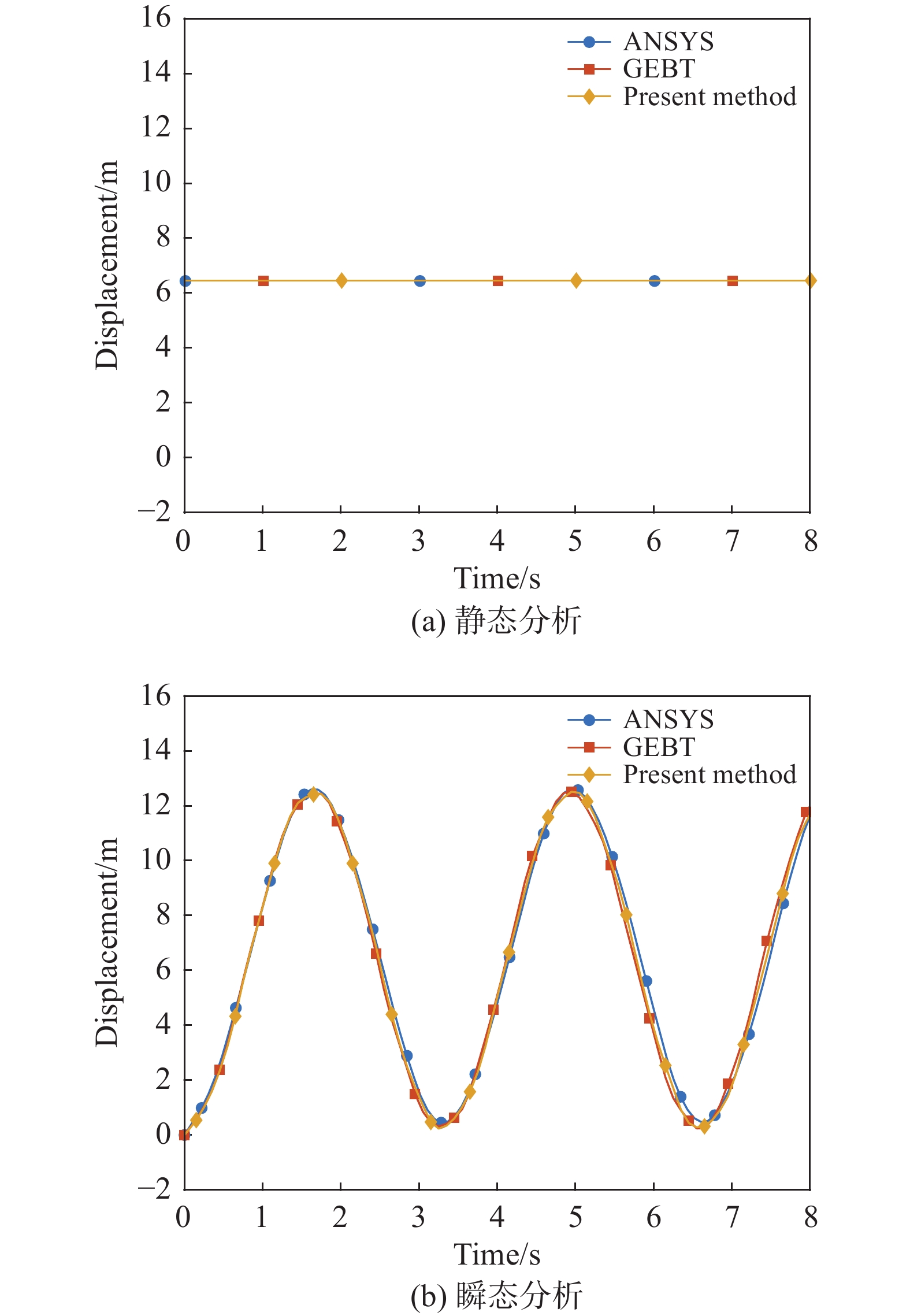
为了验证结构模型在静力学和瞬态分析中的准确性，将其与商业软件ANSYS和开源几何精确梁求解器GEBT进行了比较。验证模型为长60 m的悬臂梁，在梁的自由端施加100 kN的恒定荷载。选择参考文献[27]中的单个叶片横截面材料特性：叶片截面分布质量为294.734 kg/m；翼型截面弦长方向刚度为1102.38 × 10⁶ N·m²；宽度方向截面刚度为3447.14 × 10⁶ N·m²；扭转刚度为144.47 × 10⁶ N·m²；轴向拉伸刚度为1632.70×10⁶ N。梁在本文模型、GEBT和ANSYS中均划分为10个单元，时间步长为0.0001 s。静态和瞬态叶尖位移分别如图4（a）和图4（b）所示。可以看出，本文采用的结构模型所计算的结果与GEBT和ANSYS的结果吻合良好。

此外，将额定风速下5 MW风力机的本文气动弹性计算结果与NREL官方报告中FAST程序的计算结果^[27]进行了比较，结果列于表2。从数据可以看出：叶片结构变形、功率和推力均与FAST结果吻合较好；由于叶片的变形和振动，转子的扫风面积减小，转子功率和推力有所降低。

3.2 尾迹分析

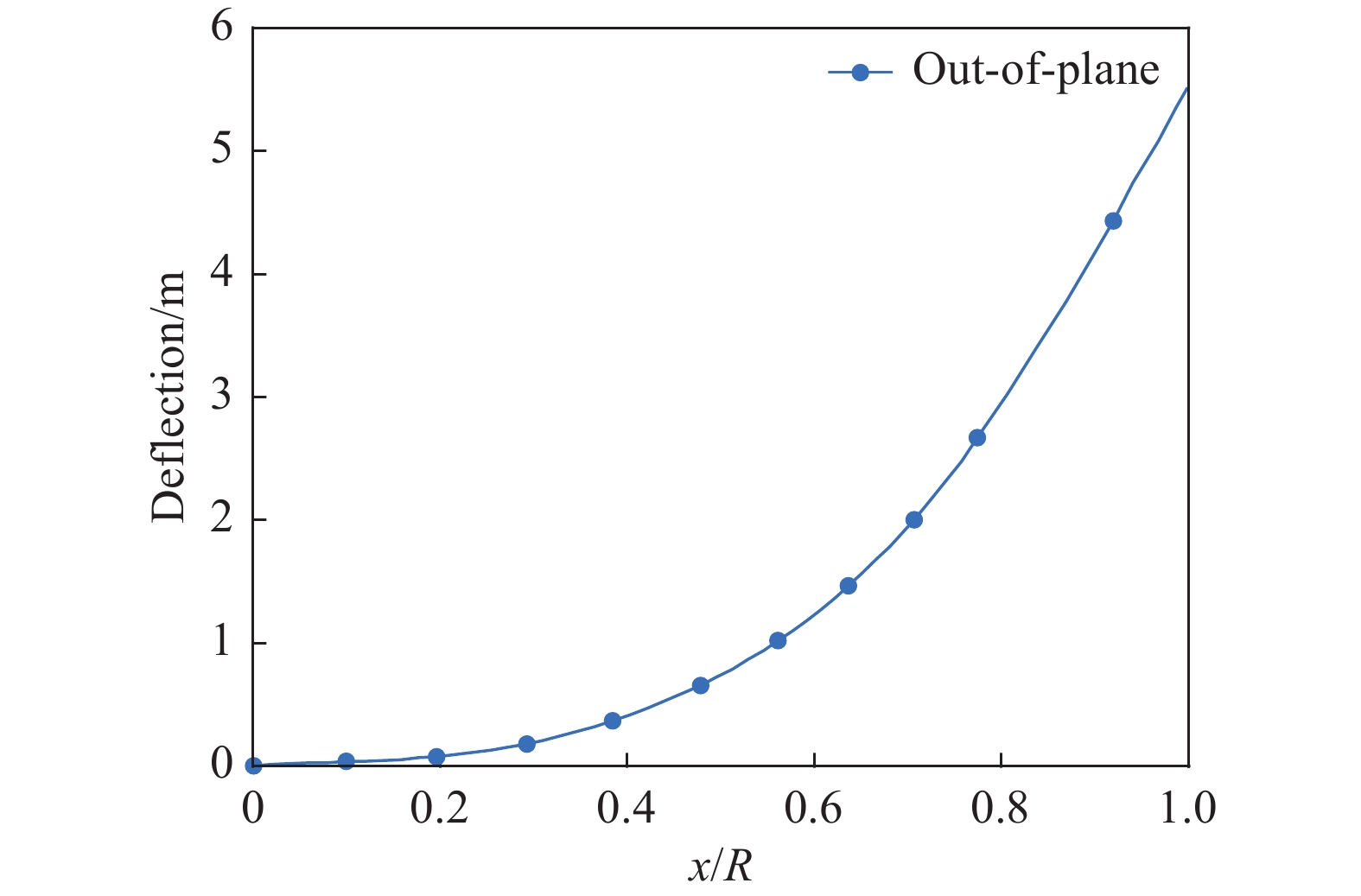
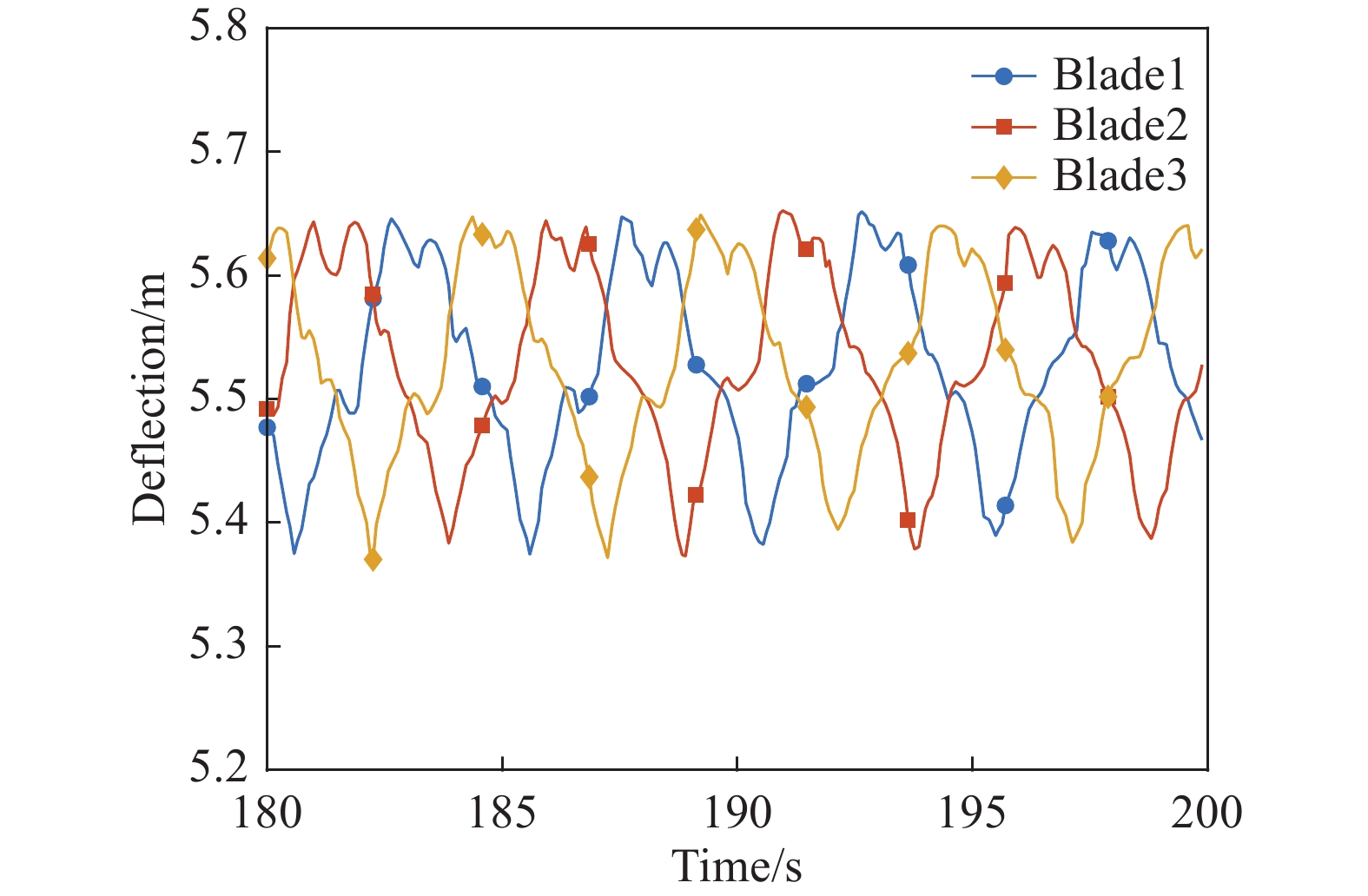
除了验证和计算风轮的变形和基本性能，本文也分析了叶片结构响应以及气动弹性对风力机尾迹的影响。图5给出了风力机三个叶片在流向上的变形沿径向分布情况，可以看出，叶尖处变形最大。图6给出了叶尖在流向上的振动响应。风力机的三个叶片在5.35～5.65 m范围内振动，其诱导的三个叶尖涡脱落，形成螺旋形尾迹，向下游移动，并在1D距离后略微破裂，如图7所示。

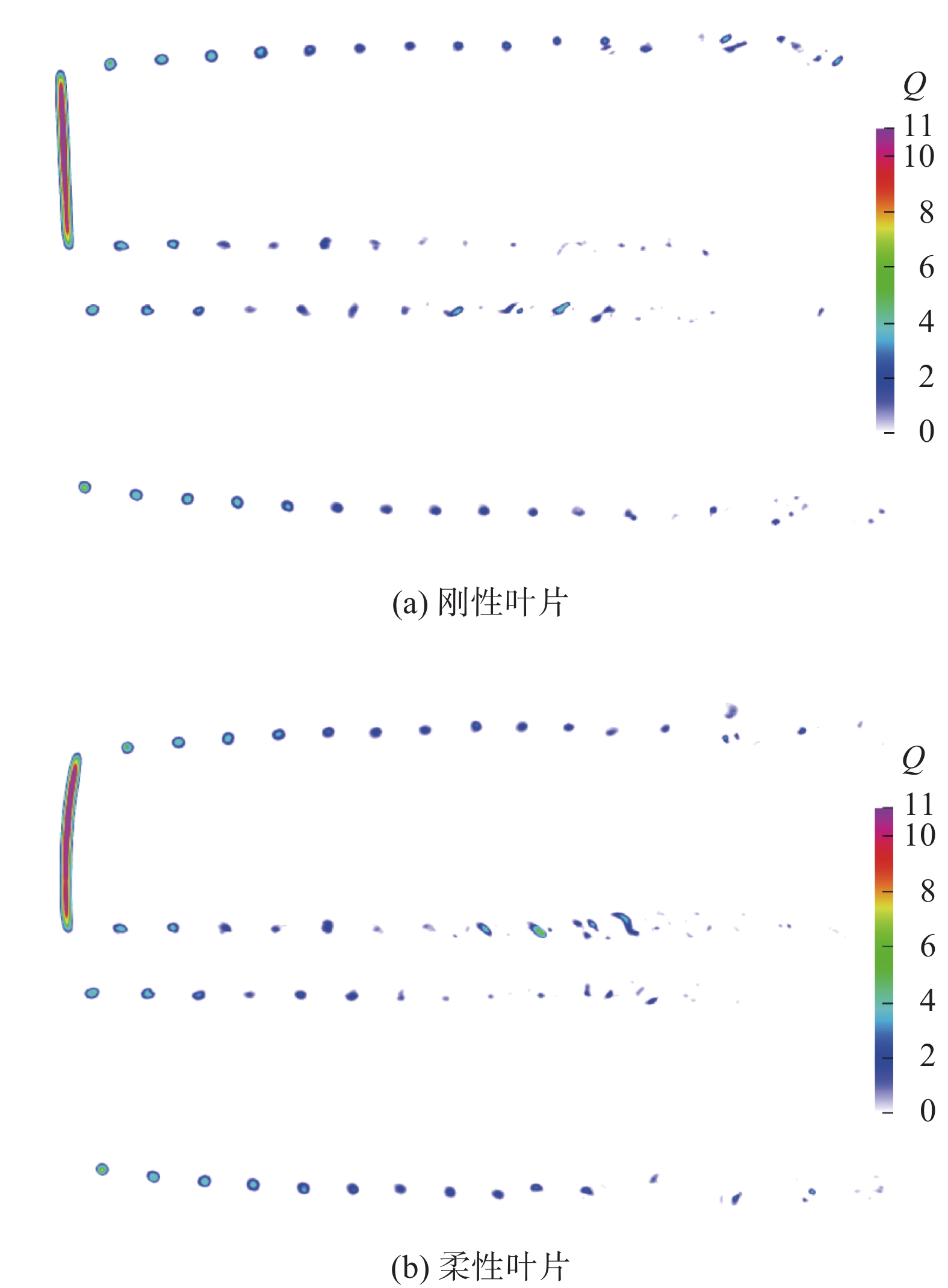
图8给出了刚性叶片和柔性叶片算例对应的Q沿流向剖面的云图。相比于图8（a）刚性叶片模拟结果，图8（b）中考虑叶片柔性后，叶片的变形影响了致动线的位置和体积力的分布，进而推迟了叶尖涡生成的原始位置。

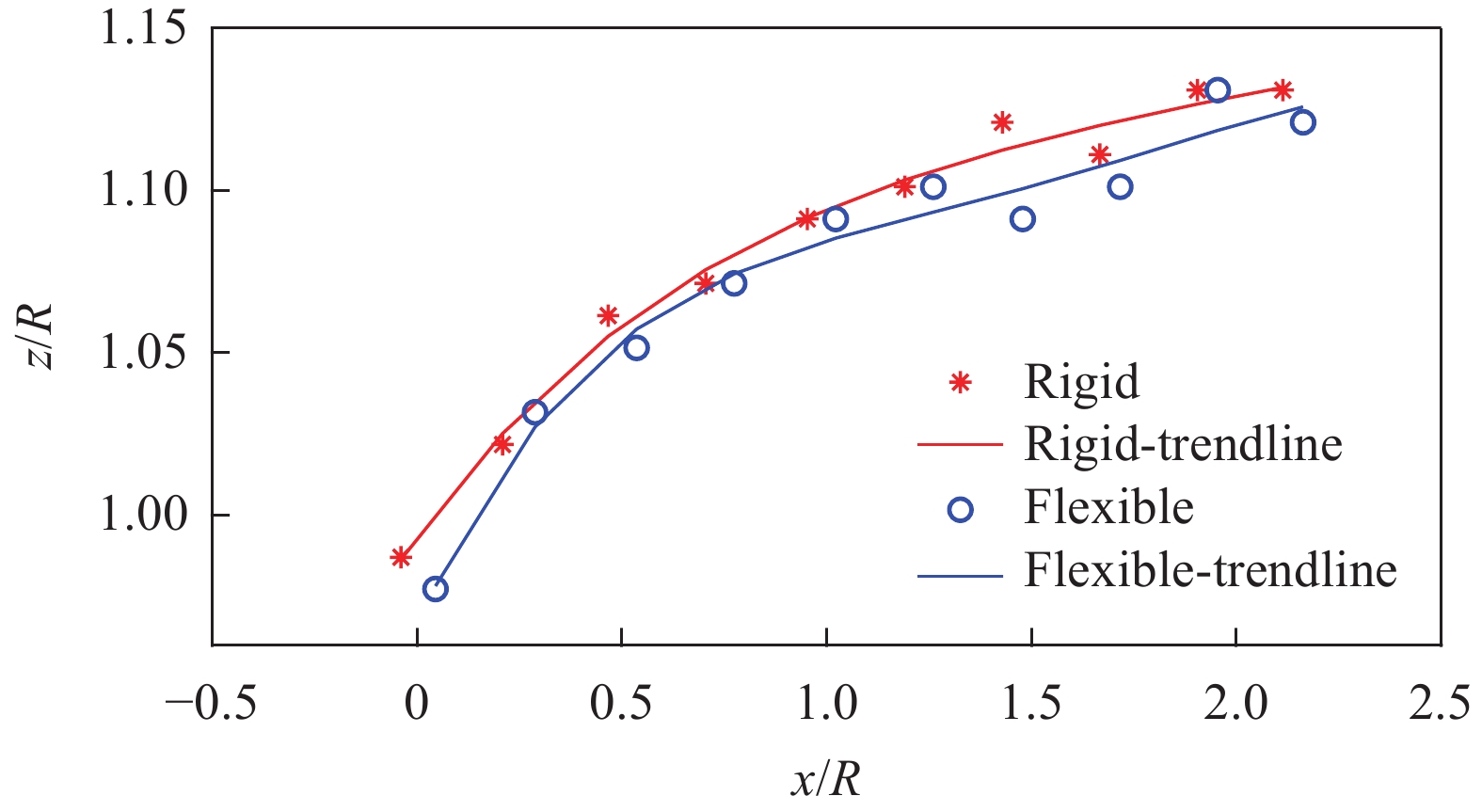
图9进一步分别提取了刚性叶片和柔性叶片模拟的叶尖涡位置，其中z用转子半径R参照。可以看出，叶片对叶尖涡的影响可持续到下游2D距离，并且在相同的轴向位置处，变形对叶尖涡涡强度的影响总是大于对根部涡附近的影响。

4 结　论

本文基于柔性多体动力学、致动线方法和大涡模拟，建立了一种用于风力机气动弹性和尾流分析的新型流固双向耦合数值模型。与传统致动线模型相比，本文气动弹性模型基于几何精确梁理论，进行了叶片自由度捕捉和重新建模，取代了传统的致动线模型单一刚体旋转运动描述，并保留了建模简单便捷的优点。

经过验证，本文流固双向耦合模型在转子功率、推力、结构变形等参数的计算上与其他方法所得结果相吻合。除此之外，本文模型通过和大涡模拟结合取代了叶素动量法，可以准确捕捉风力机的尾迹结构，包括叶尖涡和叶根涡。研究表明，叶片在风载荷作用下有显著的振动响应，同时，叶片的变形影响了致动点和体积力的分布，最终影响风力机的性能和尾迹特性。

综上所述，叶片的柔性在风力机气动弹性设计中不可忽略。本文方法可以通过简单的建模，避免三维建模的复杂性，并准确预测风力机性能和尾流特性，与传统方法相比，更适用于现代兆瓦级复合材料风力机流固耦合模拟和尾流分析。

由于致动线法在来流速度和投影函数的选取上有一定局限性，需要在未来的工作中进行改善，使得叶片体积力分布更贴近真实叶片形状。更具体的结构参数响应研究以及几何非线性对叶片气动的影响研究，也将在接下来的工作中展开。