当前我国海上风电行业方兴未艾,逐步由近海向资源更丰富的深远海发展,基础形式也由浅海的单桩基础向导管架基础过渡。为完成我国2030年碳排放达到峰值、2060年实现碳中和的目标,未来海上风电将迎来不短于30年的发展高潮期。然而我国沿海地区台风频发,严重威胁着风力机的结构安全。2003年台风“杜鹃”登陆广东,造成红海湾风电场9台风力机叶片损毁,6台风力机风向仪破坏,直接经济损失上千万[1]。2006年超强台风“桑美”袭击浙江苍南县,造成27台风力机故障,其中5座风力机塔倒塌,经济损失达7000万[2]。2013年台风“天兔”登陆广东,再次造成红海湾风电场8台机组倒塌、11台机组叶片折断,经济损失巨大[3]。这几起沿海陆上风力机事故调查表明,台风所诱发的狂风、暴雨等恶劣环境易引起风力机电网中断、控制系统故障、偏航系统失效,台风带来的极大气动载荷是造成风力机叶片、塔筒等结构破坏的主要原因[4]。海上风力机因建成及运营年代相对较短,暂时未见到台风引起风力机倒塌等重大事故的报道,但台风环境下的海上风力机,除要遭受更大的强风,还要面对极端海浪的威胁,若发生偏航系统失效,其破坏甚至倒塌的风险更高,因此对海上风力机在台风环境下的偏航失效时响应进行分析十分必要。
风力机所受载荷与风力机的状态(风力机偏航角、叶片桨距角、叶片停机位置)以及风、浪的强度、方向有关。当台风风速高于风力机切出风速时,风力机顺桨停机。偏航系统正常时,风力机风轮可实现风力机实时对风并使叶片处于顺桨状态,此时风轮所受风载荷的大小与叶片的停机位置基本无关[5],叶片的停机位置只对塔筒上风载荷分布及其响应造成一定程度的影响[6-7]。然而,当风力机偏航系统失效时,无法实现风力机实时对风,风轮受到的风载荷将显著增大,结构破坏概率显著增加。
目前风力机偏航失效时响应研究主要考虑风力机偏航角和叶片桨距角这两个参数的影响[6,8-9]。相关研究表明,风力机结构各部分响应及整体稳定性对偏航角和桨距角变化十分敏感。偏航角为0°时,叶片与塔筒的干涉作用最为明显;偏航角为45°时,风力机体系的稳定性能最为不利[9]。此外,通过对偏航失效时处于不同桨距角的风力机进行动力分析,发现当桨距角处于90°时,风力机在±90°偏航范围内的结构响应总体较小,有利于风力机结构安全[6,8]。
上述研究在考虑偏航失效时大多忽略了停机位置这一因素的影响。与正常状态不同,当偏航系统失效时,风力机无法对风,处于不同停机位置时叶片的风攻角会随风向改变而变化,且变化范围较大,因此风力机所受气动载荷及响应会受到显著影响[10]。对比分析不同停机位置下风力机的响应结果,有利于优化台风期间的停机策略,因此开展偏航失效时导管架式海上风力机在不同停机位置下的响应分析十分必要。
本文以目前广泛采用的5 MW导管架式海上风力机为研究对象,通过模拟随机风浪场,利用风力机计算分析软件FAST对偏航失效工况建立数值模型,对风力机停机时处于±90°偏航角范围内风力机的动力响应进行计算,对比了停机位置对叶片、塔筒及下部结构动力响应极值的影响。研究结论可为海上风力机应对台风等极端环境的停机策略以及抗台风设计提供一定的参考。
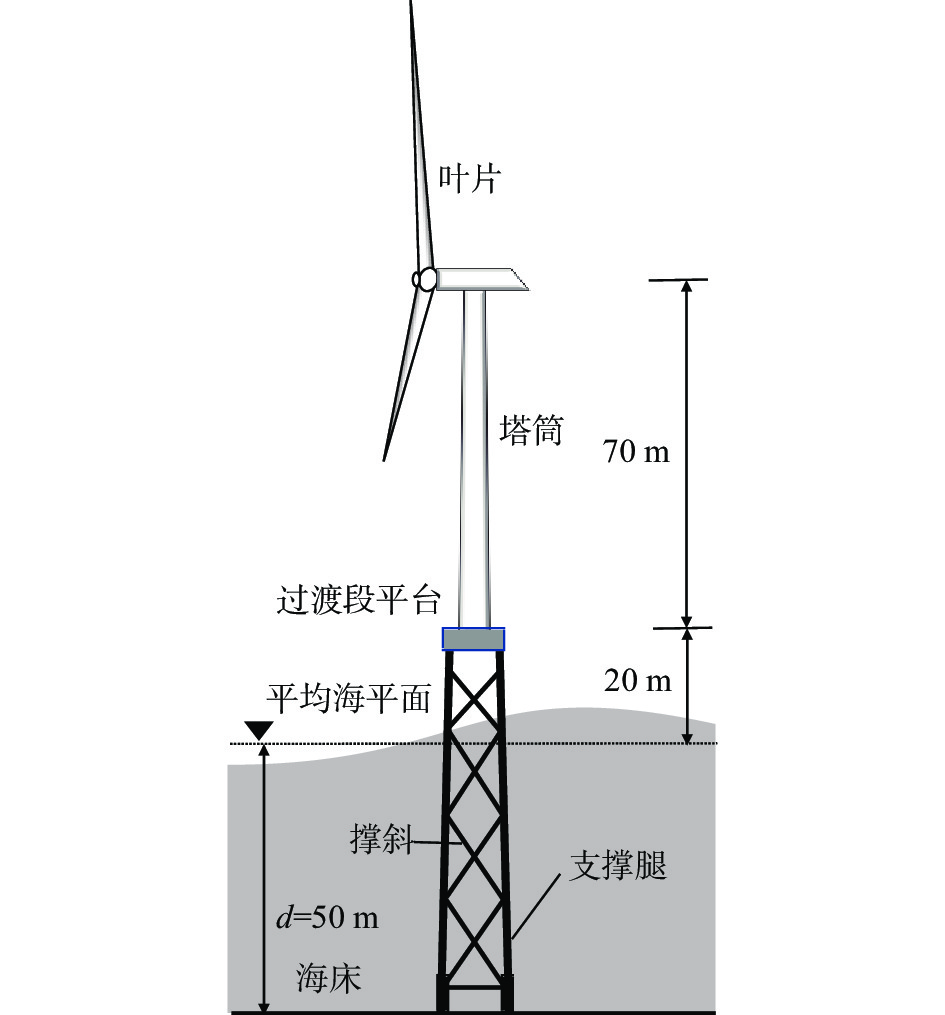
1 风力机模型及工况设置 1.1 风力机模型采用美国国家可再生能源实验室(NREL)提供的5 MW海上风力机标准机型[11],如图1所示,叶片长61.5 m,叶轮直径126 m。过渡段为高于海平面16 m的混凝土平台,长宽高为
|
图 1 NREL 5 MW导管架式海上风力机模型 Fig.1 NREL 5 MW OC4-jacket supported OWT model |
| 表 1 5 MW导管架式海上风力机主要参数 Table 1 Main properties of 5 MW OC4-jacket supported OWT |
|
|
| 表 2 风力机支撑系统模态及频率信息 Table 2 Mode and frequency information of the OWT support structure |
|
|
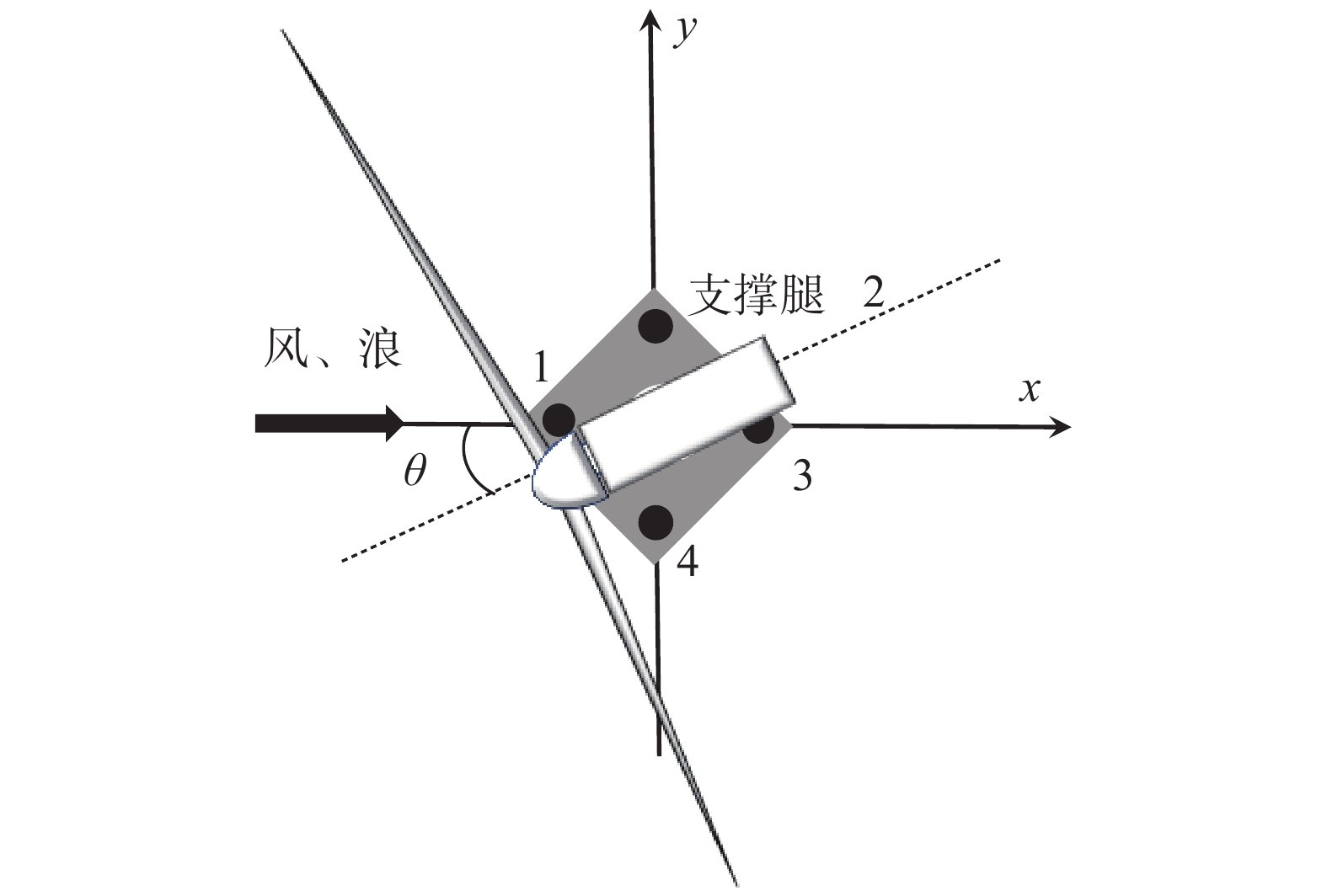
图2为该5 MW导管架式海上风力机偏航失效状态示意图。风力机偏航系统失效后,因无法实现风力机实时对风,来流风向改变时会与风力机旋转轴形成偏航角。本文通过固定风向、改变风力机机舱角度来实现不同偏航角工况,偏航角
|
图 2 海上风力机偏航失效示意图 Fig.2 Failure state of the yaw control system of OWTs |
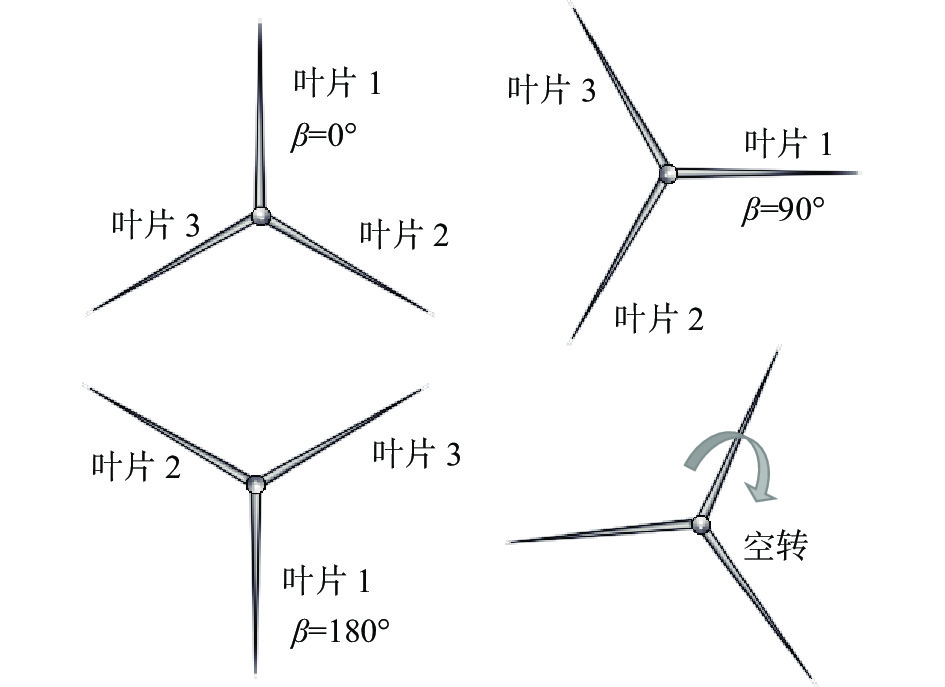
|
图 3 风力机叶片停机位置图 Fig.3 Parking positions of the OWT blades |
我国南海海域辽阔、风能资源丰富,本文研究风力机假定位于南海涠洲岛附近海域。基于该海域海洋站实测数据,周道成[12]利用Gumbel-logistic模型考虑了风、浪之间的相关性,对年极值风速和有效波高的联合分布进行统计分析,得到了不同重现期下极值风速与有效波高的组合。利用其研究结果,以该海域50年重现期下的风、浪强度作为各工况的环境载荷,其中10 m高度处风速为39.92 m/s,有效波高为10.47 m。风和浪均以最不利方向,即平行于导管架对角线方向[13],作用于风力机结构。
2 气动载荷与水动载荷计算 2.1 风场的模拟及气动载荷计算选用三维随机脉动风场来计算风力机叶片及塔筒所受气动载荷。顺风向风速由平均风速和脉动风速叠加而成:
| $ \bar u(z) = {V_{{\text{hub}}}}{\Bigg(\frac{z}{{{H_{{\text{hub}}}}}}\Bigg)^\alpha } $ | (1) |
式中:
脉动风速通过国际电工技术委员会(IEC)规范[14]推荐的Kaimal谱求得:
| $ \dfrac{{{S_k}\left( f \right)}}{{\sigma _k^2}} = \dfrac{{4\dfrac{{{L_k}}}{{{V_{{\text{hub}}}}}}}}{{{{\left( {1 + \dfrac{{6f{L_k}}}{{{V_{{\text{hub}}}}}}} \right)}^{\frac{5}{3}}}}} $ | (2) |
式中:
| $ {\sigma }_{k} = \left\{\begin{array}{l}0.11{V}_{{\rm{hub}}},\;k = u\\ 0.8{\sigma }_{u},\;\quad\; k = v\\ 0.5{\sigma }_{u},\;\quad\; k = w\end{array}\right.\text{;}\begin{array}{ll} {L}_{k}\text{ = }\left\{\begin{array}{l}8.10{\varLambda }_{U},\;k = u\\ 2.70{\varLambda }_{U},\;k = v\\ 0.66{\varLambda }_{U},\;k = w\end{array}\right.\end{array} $ | (3) |
| $ {\varLambda }_{U} = 0.7\; \mathrm{min}(60,{H_{{\text{hub}}}}) $ | (4) |
考虑到风速的空间相关性,两空间点风速互功率密度函数
| $ {S_{ij}}(f) = {\text{Coh}}(f,i,j)\sqrt {{S_{ii}}(f){S_{jj}}(f)} $ | (5) |
式中:
| $ {\text{Coh}}(f,i,j){\text{ = }}\exp \left[ { - a\sqrt {{{\Bigg(\frac{{fr}}{{{V_{{\text{hub}}}}}}\Bigg)}^2} + {{\Bigg(\frac{{0.12r}}{{{L_C}}}\Bigg)}^2}} } \right] $ | (6) |
式中:
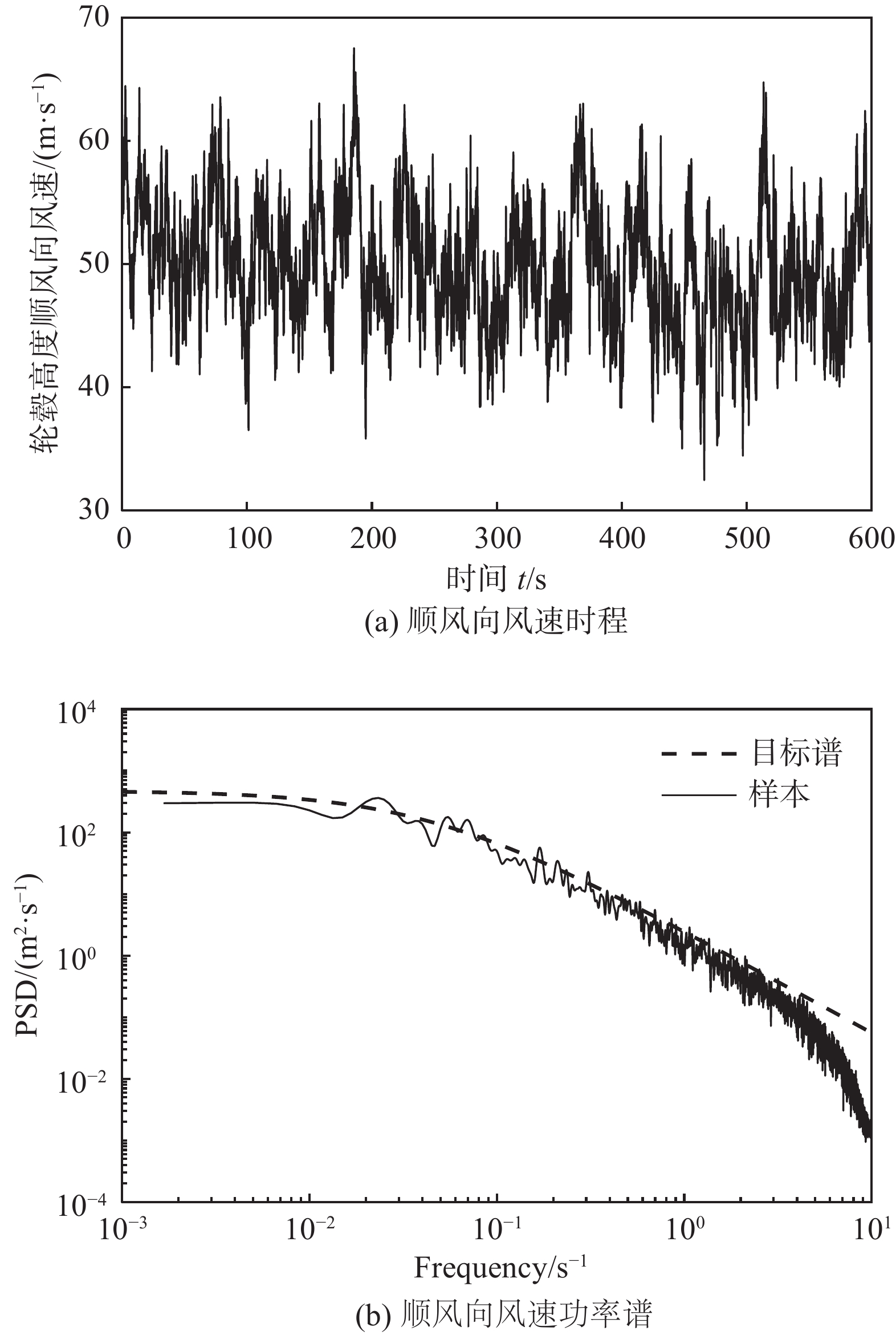
|
图 4 轮毂高度处顺风向风速时程及功率谱 Fig.4 Time history and PSD of the alongwindwind speed at the hub height |
对于处于停机状态的风力机,叶素上受到的升力
| $ \begin{split}& {F_L} = {C_L}(\alpha )\frac{1}{2}\rho {U_R}^2c{\text{d}}r \\& {F_D} = {C_D}(\alpha )\frac{1}{2}\rho {U_R}^2c{\text{d}}r \end{split} $ | (7) |
式中:
同理塔筒单位长度上的气动力由下式得到:
| $ \begin{split}& {F_{TL}} = {C_{TL}}(z)\cdot \frac{1}{2}\rho d(z){U^2_z}{\text{d}}z \\& {F_{TD}} = {C_{TD}}(z)\cdot \frac{1}{2}\rho d(z){U^2_z}{\text{d}}z \end{split} $ | (8) |
式中:
采用目前国内外广泛使用的JONSWAP谱模拟波浪场,此海浪谱由“联合北海波浪计划(The Joint North Sea Wave Project)”提出。IEC规范所推荐该谱的形式如下:
| $ \begin{split}{S}_{JS}\left(f\right) =& 0.3125{H}_{s}^{2}{T}_{p}{\left(\frac{f}{{f}_{p}}\right)}^{-5}\mathrm{exp}\left[-1.25{\left(\frac{f}{{f}_{p}}\right)}^{-4}\right]\cdot\\& \left(1-0.287 \; \mathrm{ln}\gamma \right)\gamma \; \mathrm{exp}\left[-0.5{\left(\dfrac{\dfrac{f}{{f}_{p}}-1}{\sigma }\right)}^{2}\right]\end{split} $ | (9) |
式中:
| $ \gamma = \left\{\begin{array}{ll}5& \text{,}\dfrac{{T}_{p}}{\sqrt{{H}_{s}}}\leqslant 3.6\\ \mathrm{exp}\left(5.75-1.15\dfrac{{T}_{p}}{\sqrt{{H}_{s}}}\right)& \text{,}3.6 < \dfrac{{T}_{p}}{\sqrt{{H}_{s}}}\leqslant 5\\ 1& \text{,}\dfrac{{T}_{p}}{\sqrt{{H}_{s}}} > 5\end{array}\right. $ | (10) |
| $ \sigma = \left\{\begin{array}{c}0.07\text{,}f\leqslant {f}_{p}\\ 0.09\text{,}f > {f}_{p}\end{array} \right.$ | (11) |
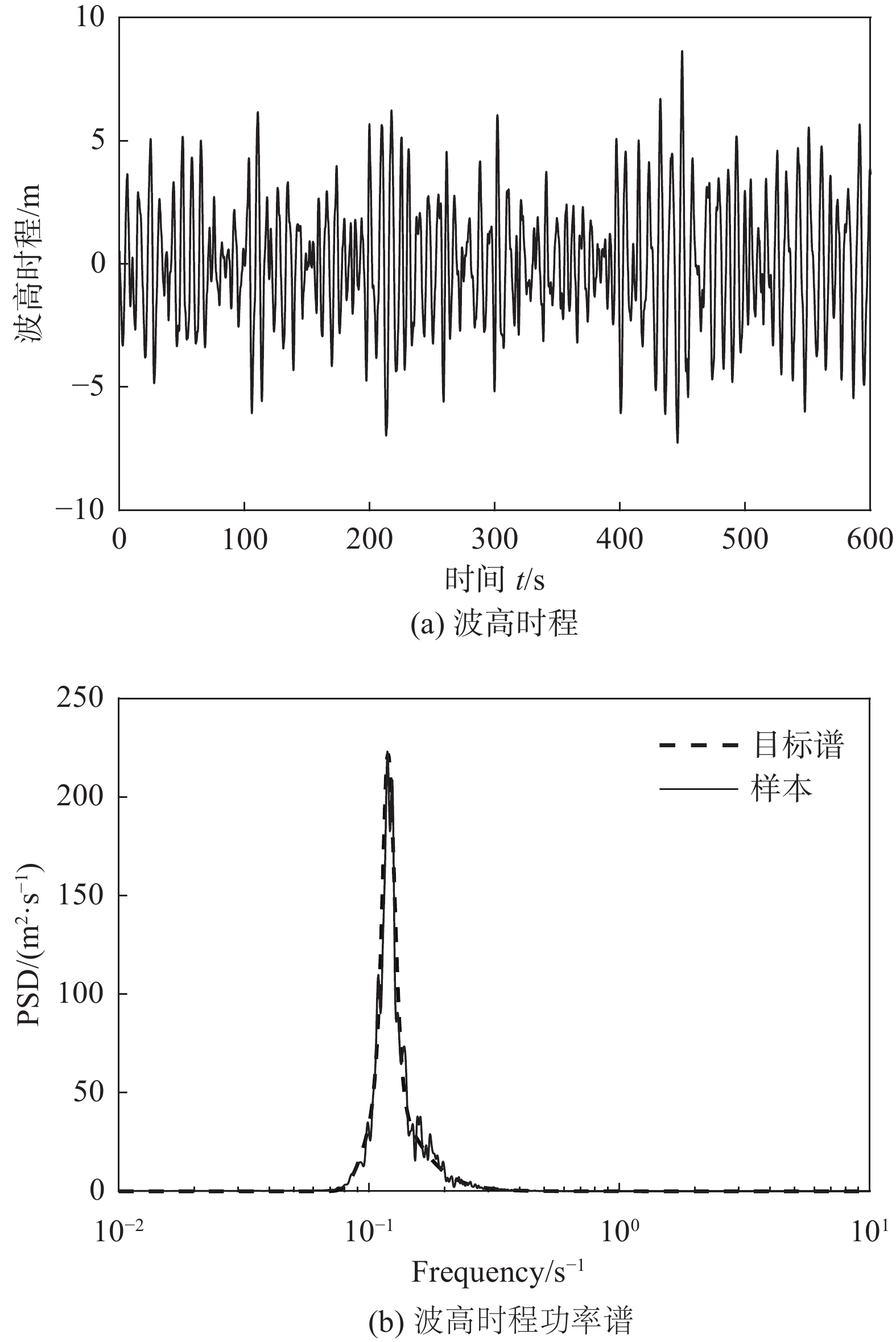
此外,以往的工程实践中,常基于Airy线性波理论来求解波浪运动方程,模拟生成不规则海浪。然而Marino等[15]的研究表明,采用线性波理论计算波浪载荷会低估风力机的极端响应,并不适用于中等程度以上海况。尤其对于风力机停机工况,气动阻尼仅为运行状态的十分之一,海浪的非线性成分对风力机响应的影响更为显著。因此为了更真实地模拟导管架所处的有限水深范围内的波浪场,本文采用二阶非线性不规则波浪模型[16]来求解水质点的运动状态。图5为模拟生成的海浪波高样本时程及其功率谱,与目标谱拟合良好。
|
图 5 海浪波高时程及功率谱 Fig.5 Time history and PSD of the wave height |
对于构件直径D与波长L之比小于0.2的导管架结构,波浪载荷采用Morison方程[17]计算。考虑到固-液相互作用及导管架构件的空间倾斜,作用在构件单位长度上的波浪力
| $ {\boldsymbol{f}} = \frac{1}{2}{C_D}{\rho _w}D{\boldsymbol{U}}\left| {\boldsymbol{U}} \right| + {C_M}{\rho _w}\frac{{{\text{π }}{D^2}}}{4}\frac{{\partial {\boldsymbol{U}}}}{{\partial t}} $ | (12) |
式中:
涉及风力机结构设计的参数包括叶根弯矩、风轮力矩、塔筒弯矩以及导管架基础各响应量等,其极值是影响风力机结构设计的关键参数。对4种停机位置下−90°~90°偏航范围内(13个偏航角度)共52种工况进行数值计算,每种工况计算6个30 min样本时程,取各工况下样本时程极值的均值作为响应统计量,研究其在偏航失效状态下的变化规律。
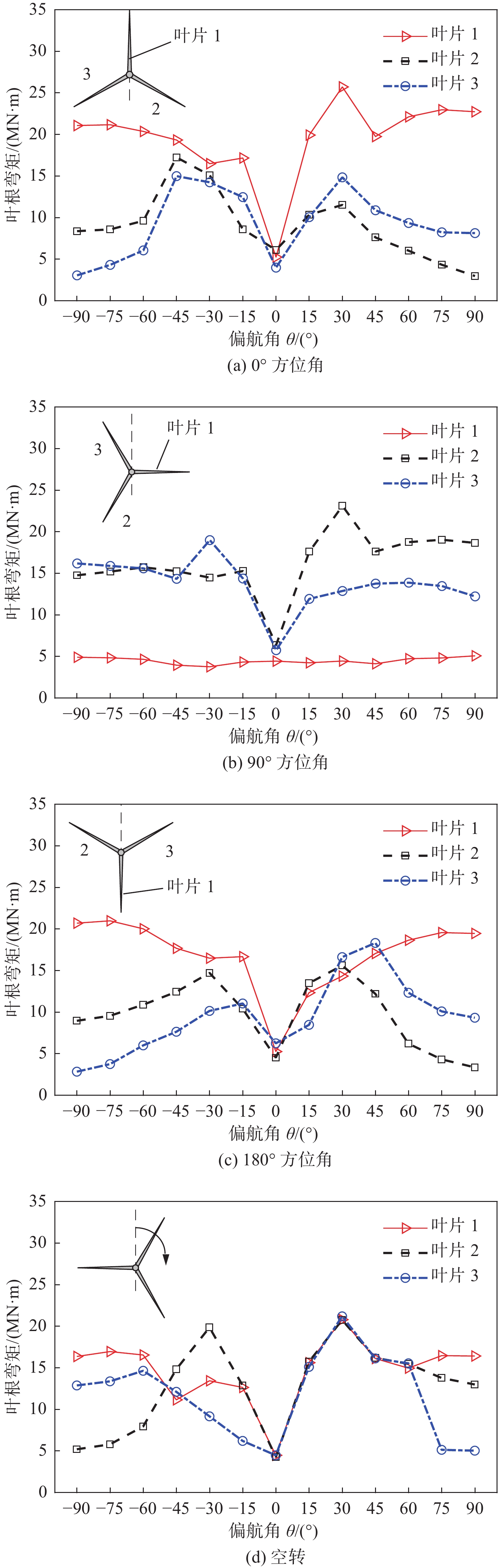
3.1 叶根弯矩图6为偏航失效时不同停机位置下风力机叶根弯矩极值。通过对比分析,得出偏航失效时偏航角度及停机位置对风力机叶片响应的影响:1)发生偏航失效后,叶片的叶根弯矩骤增,其值最高可达正常状态下(
|
图 6 偏航失效时不同停机位置下叶根弯矩极值 Fig.6 Maximum bending moment of the blade root under different parking positions with yaw control system failure |
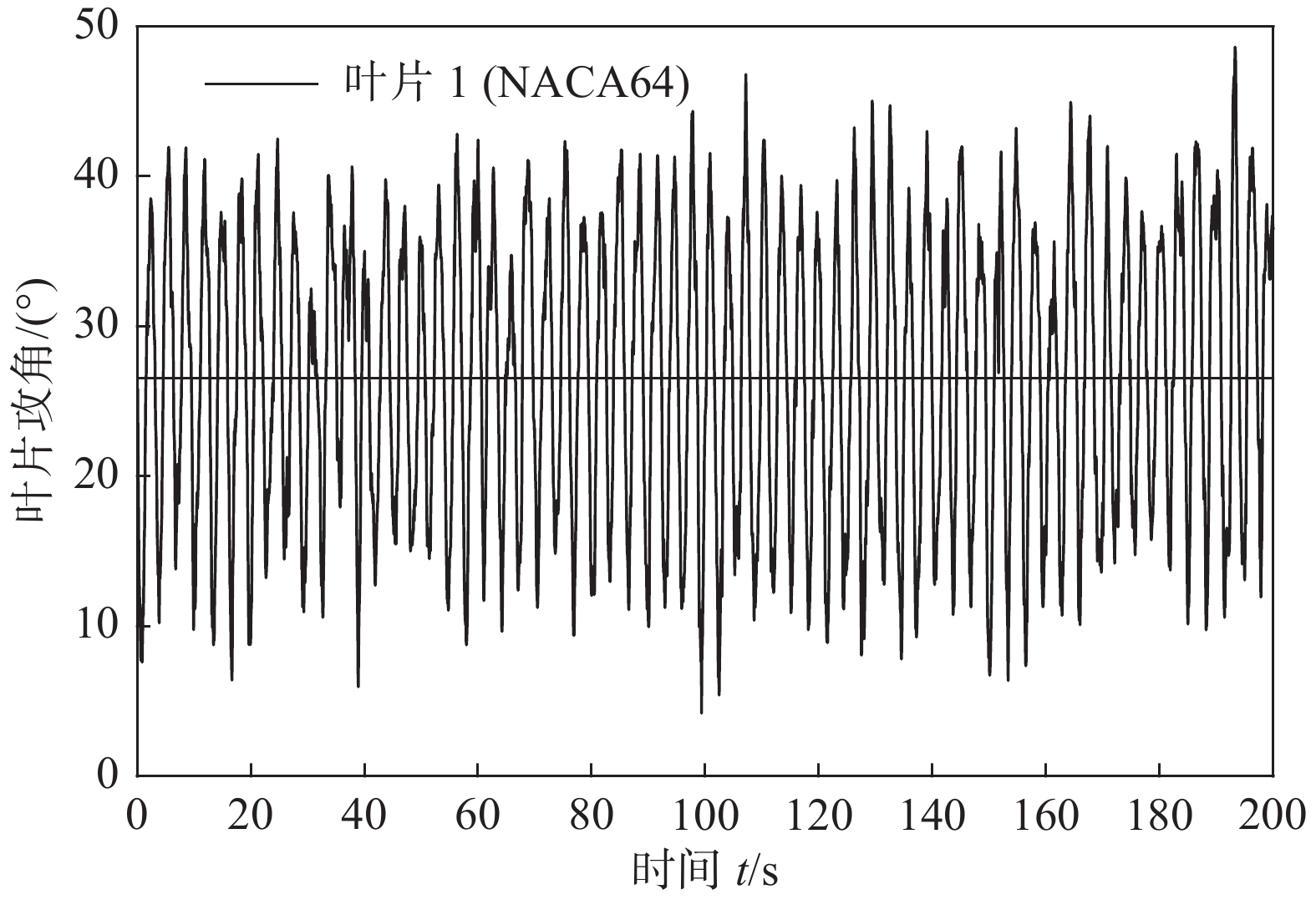
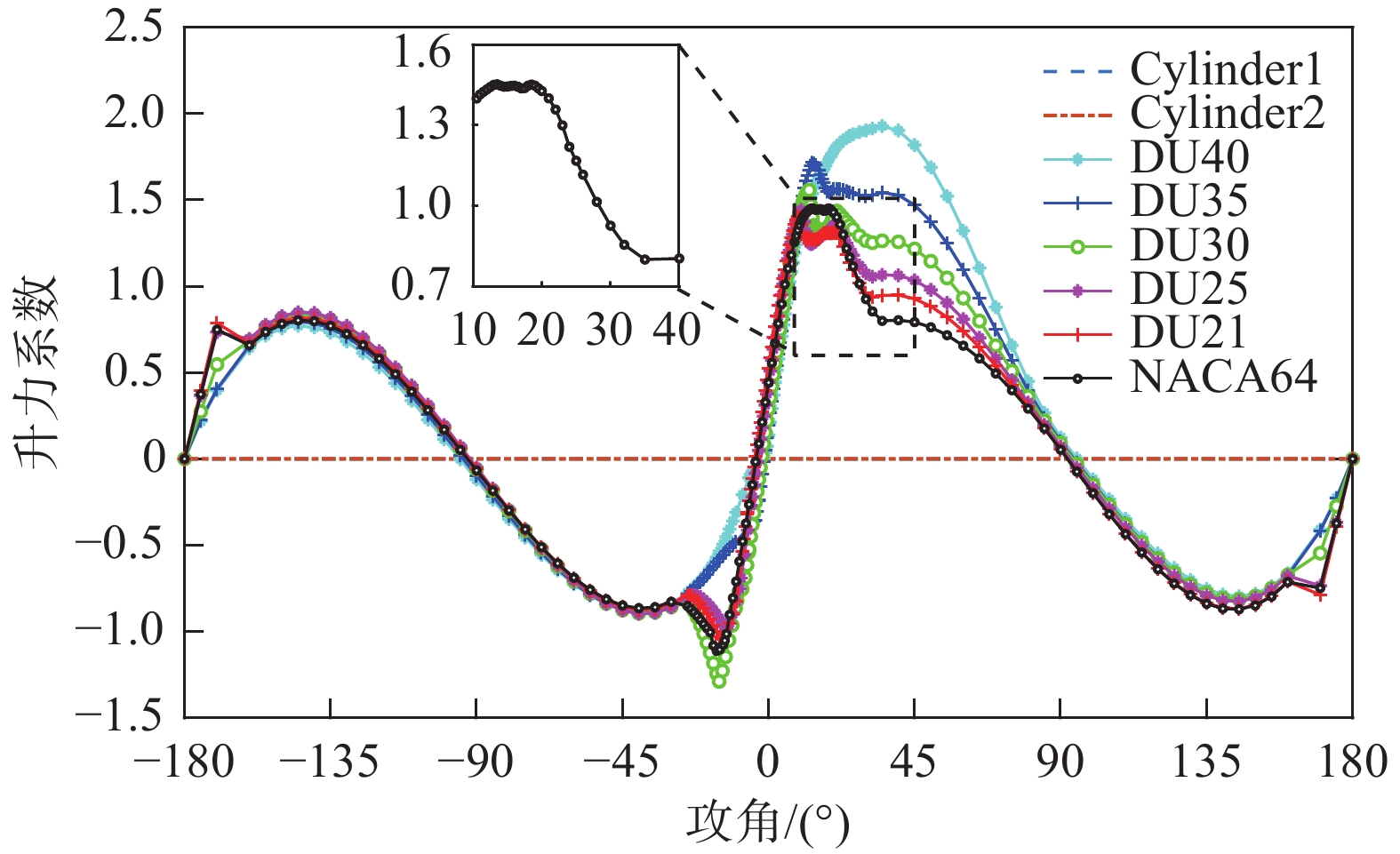
另外,可发现当偏航角处于±30°左右时,叶根弯矩的响应结果有明显突变(如图6a中叶片1在30°偏航角下的叶根弯矩响应极值等)。选取叶片三分之二处的NACA64翼型段,输出其在30°偏航角工况下的叶片攻角时程(图7),可见攻角在10°~40°范围附近波动。结合5 MW风力机叶片翼型的升力系数(图8),可知其攻角范围处于NACA64翼型升力系数失速段,因
|
图 7 叶片1的NACA64翼型的攻角时程 Fig.7 Time history of the attack angle for the NACA64 airfoil of blade 1 |
|
图 8 5 MW风力机叶片各翼型升力系数 Fig.8 Lift coefficients of different blade airfoils of the 5 MW OWT |
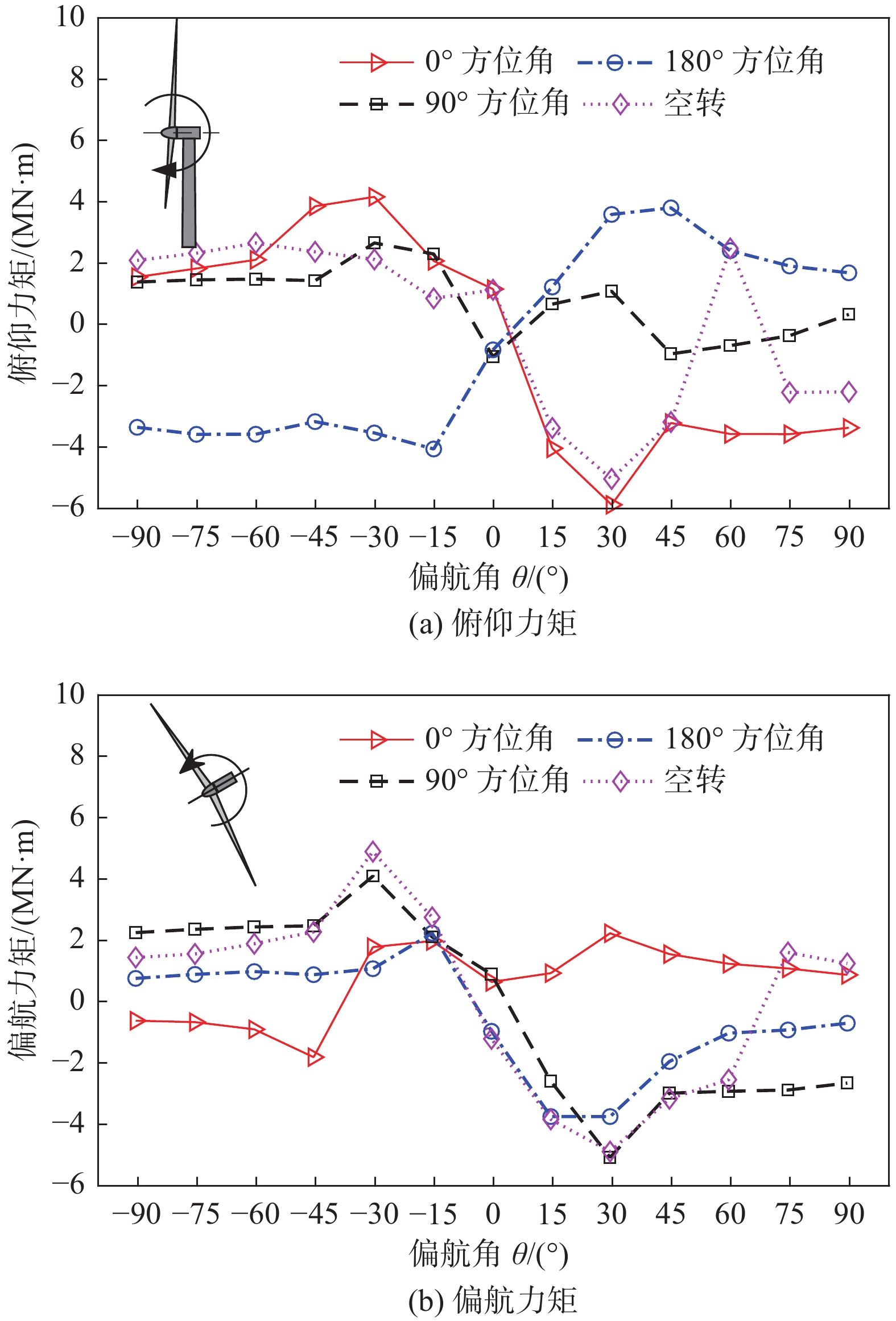
图9为偏航失效时不同停机位置下风力机风轮俯仰力矩和偏航力矩极值。可以看出,叶片停机位置对风力机风轮所受的俯仰力矩影响显著:当叶片处于0°、180°方位角和空转状态时,其俯仰力矩在0°偏航角附近异号,且幅值波动较大;当叶片处于90°方位角时,其俯仰力矩在整个偏航范围内幅值较小,更有利于轮毂安全。此外,当叶片处于90°、180°方位角和空转状态时,偏航力矩在0°偏航角附近异号,对于采用无源抗台风策略的风力机来说,有利于风轮在偏航力矩下回转到顺桨位置附近,可有效降低风轮载荷。
|
图 9 偏航失效时不同停机位置下风轮俯仰力矩和偏航力矩极值 Fig.9 Maximum values of the pitch and yaw moments of the OWT rotor under different parking positions with yaw control system failure |
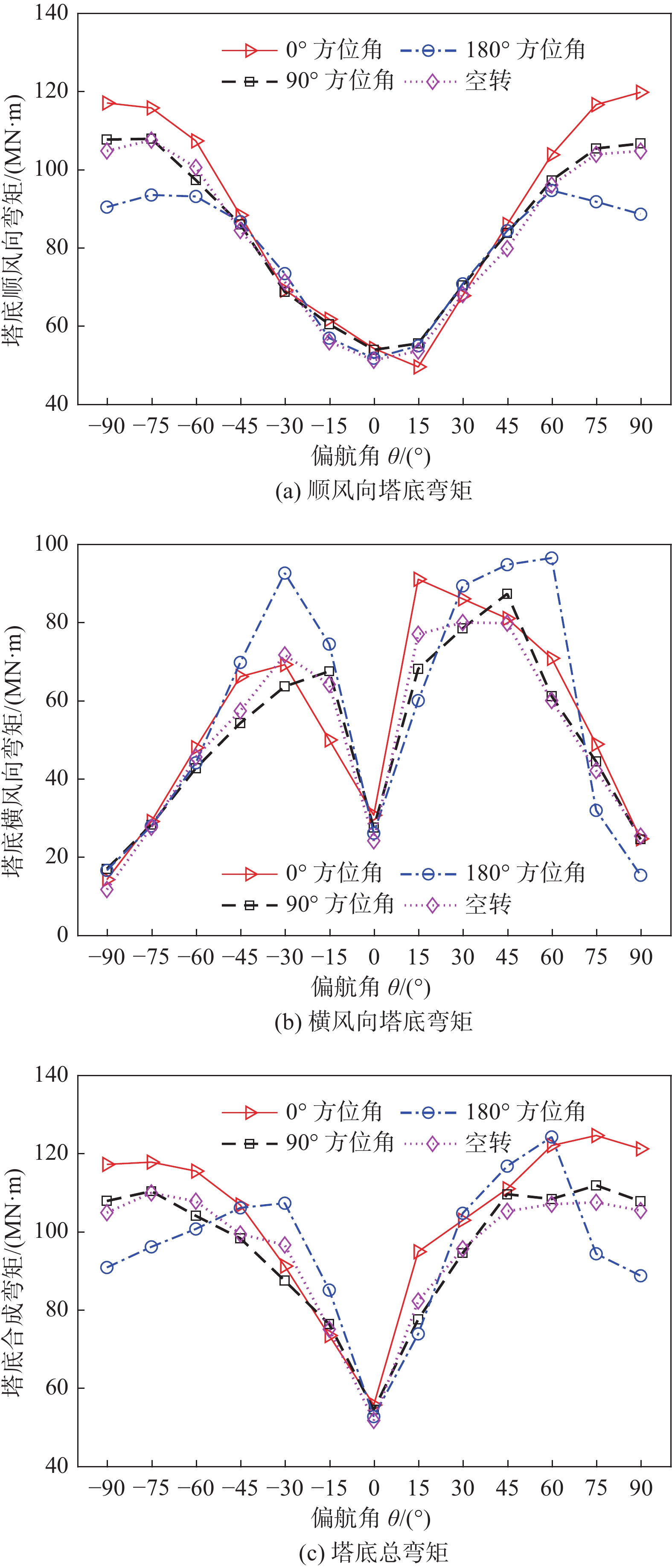
塔筒弯矩是风力机设计的关键控制参数。图10为偏航失效时不同停机位置下风力机塔底弯矩极值,可以发现:1)对于顺风向塔底弯矩,其值在偏航正常(
|
图 10 偏航失效时不同停机位置下风力机塔底弯矩极值 Fig.10 Maximum bending moment of the tower base under different parking positions with yaw control system failure |
对于传统的导管架式海上油气平台等海工结构物,其上部结构受风模式较为固定,且主要由海浪载荷控制。而海上风力机作为一种利用风能的捕风机构,其风载荷的大小与风力机的状态密切相关。对于导管架式海上风力机,其导管架基础不仅承受下部海浪的作用,而且还受到风力机上部结构所传递的复杂风载荷。选取偏航正常(
| 表 3 导管架基础平台位移及基底响应极值 Table 3 Maximum values of the platform displacement and base response of the jacket |
|
|
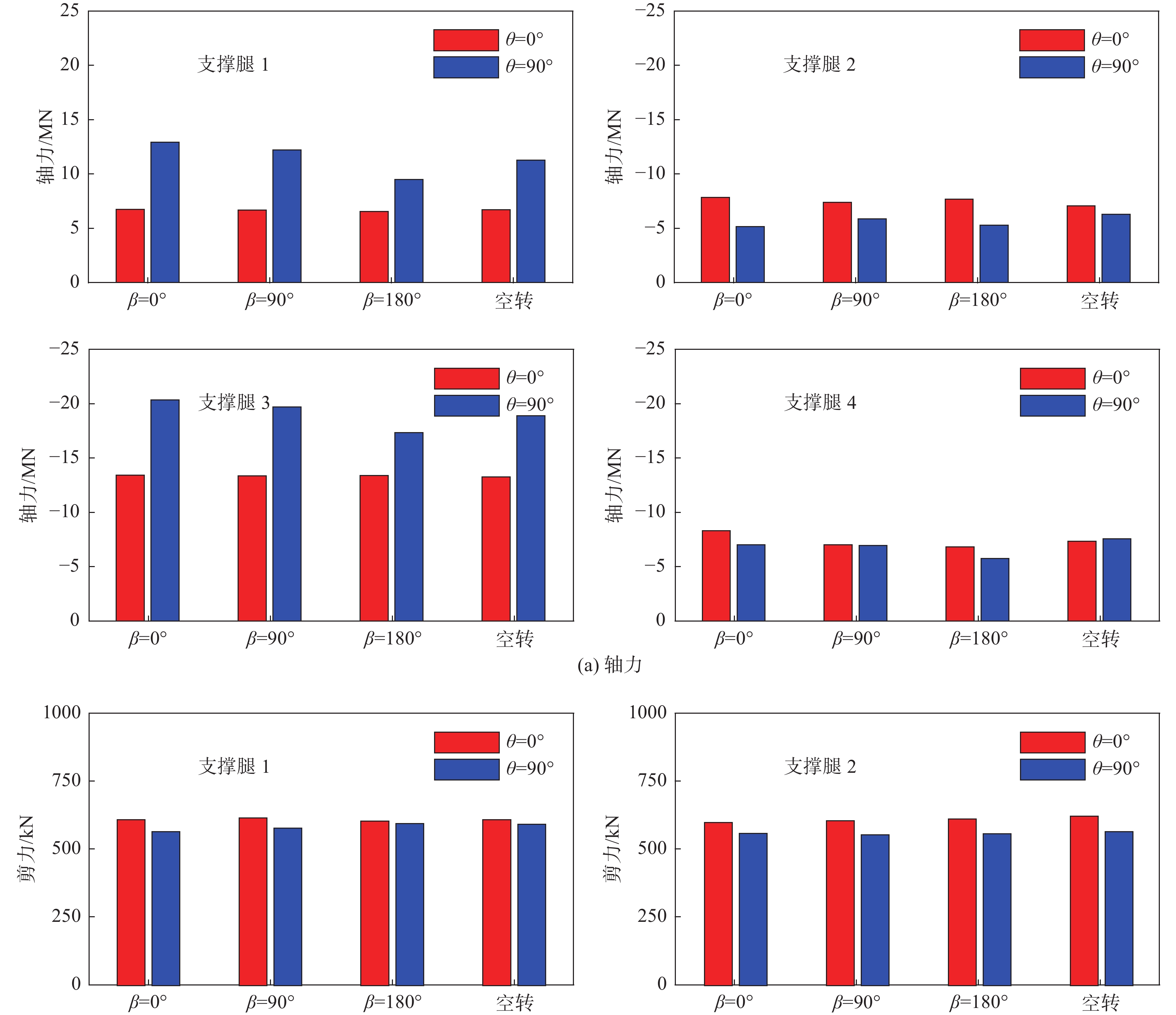
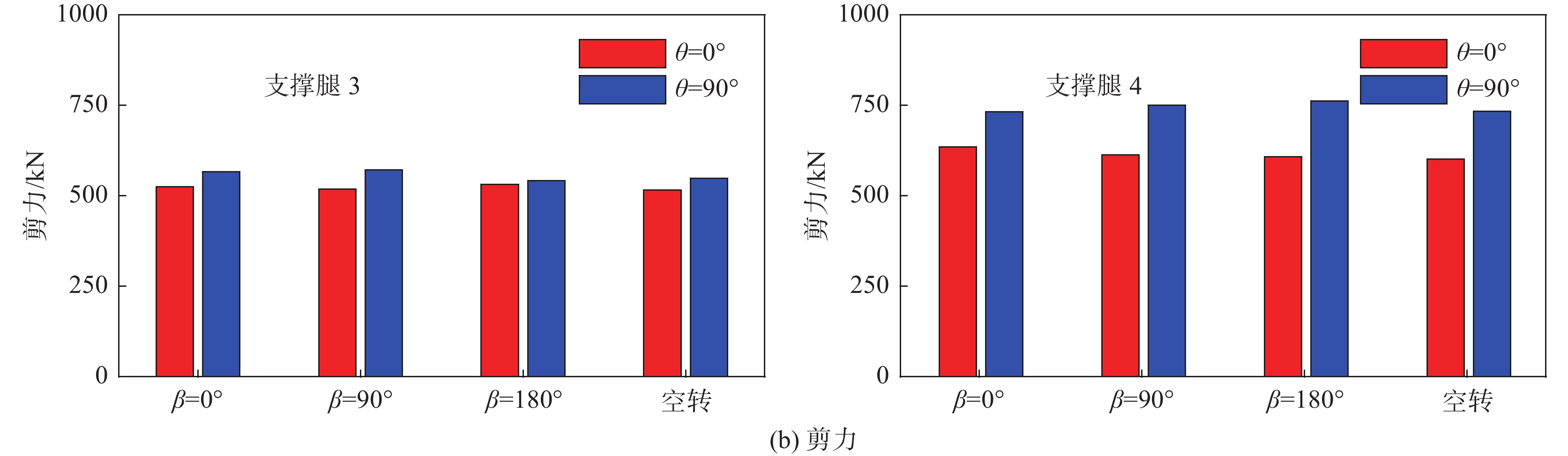
导管架基础多为群桩结构,在倾覆力矩的作用下,上风侧桩基础将承受较大的上拔力。图11为偏航正常与失效状态时不同停机位置下,导管架各支撑腿根部所受轴力和剪力极值。对于轴力,支撑腿1以受拉为主,其余各支撑腿以受压为主。由于受到倾覆力矩作用,支撑腿1和支撑腿3所受的轴力要远大于支撑腿2、支撑腿4,且偏航失效时其轴力显著增加,支撑腿1所受拉力可增至正常状态的1.91倍,支撑腿3所受压力可增至正常状态的1.51倍,对基础安全造成严重威胁。对于剪力,各导管架支撑腿差别不大,停机位置、偏航状态对其结果影响相对较小。
|
|
图 11 不同停机位置下导管架支撑腿底部轴力与剪力极值 Fig.11 Maximum axial and shear forces at the bottom of the jacket leg under different parking positions |
针对海上风力机台风环境下偏航失效的极端工况,通过模拟随机风、浪,对±90°偏航范围内处于不同停机位置的导管架式海上风力机进行动力响应计算,分析了风力机叶片、塔筒及下部结构响应随偏航角的变化规律以及停机位置对响应结果的影响。研究结果表明:
1)风力机结构各部分响应对偏航角的变化十分敏感。偏航系统失效时,风力机结构各部分响应骤增,部分偏航角下甚至会出现气弹失稳现象,大大增加了风力机结构的破坏概率。当偏航角处于
2)停机位置对于风力机叶片、风轮及塔筒的响应影响显著。在整个偏航范围内,采用空转策略或者叶片方位角处于90°停机位置的停摆策略时,风力机结构各部分响应值相对较小,应对偏航故障状态最为有利。
3)不同于传统受海浪载荷控制的导管架石油平台等海工结构,导管架式海上风力机受风、浪载荷的联合控制。对于导管架基础平台位移及基底弯矩,风载荷的贡献要大于浪载荷。当风力机偏航系统失效时,会大大增加导管架基础管桩受到的拉拔力。因此在设计时应充分考虑极端环境下风力机上部结构可能出现的偏航故障对其造成的影响。
| [1] |
王景全, 陈政清. 试析海上风力机在强台风下叶片受损风险与对策: 考察红海湾风电场的启示[J]. 中国工程科学, 2010, 12(11): 32-34. WANG J Q, CHEN Z Q. Analysis of risks and measures on the blade damage of offshore wind turbine during strong typhoons—enlightenment from Red Bay wind farm[J]. Engineering Sciences, 2010, 12(11): 32-34. DOI:10.3969/j.issn.1009-1742.2010.11.006 (in Chinese) |
| [2] |
LI Z Q, CHEN S J, MA H, et al. Design defect of wind turbine operating in typhoon activity zone[J]. Engineering Failure Analysis, 2013, 27: 165-172. DOI:10.1016/j.engfailanal.2012.08.013 |
| [3] |
吴远伟. 台风对沿海风电机组的危害及对策[J]. 风能, 2015(2): 88-93. DOI:10.3969/j.issn.1674-9219.2015.02.023 |
| [4] |
HALLOWELL S T, MYERS A T, ARWADE S R, et al. Hurricane risk assessment of offshore wind turbines[J]. Renewable Energy, 2018, 125: 234-249. DOI:10.1016/j.renene.2018.02.090 |
| [5] |
练继建, 贾娅娅, 王海军. 台风作用下2.5 MW风力机风载荷特性研究[J]. 太阳能学报, 2018, 39(3): 611-618. LIAN J J, JIA Y Y, WANG H J. Numerical simulation for characteristics of wind loads of 2.5 MW wind turbine under typhoon[J]. Acta Energiae Solaris Sinica, 2018, 39(3): 611-618. (in Chinese) |
| [6] |
KIM E, MANUEL L. Hurricane-induced loads on offshore wind turbines with considerations for nacelle yaw and blade pitch control[J]. Wind Engineering, 2014, 38(4): 413-423. DOI:10.1260/0309-524x.38.4.413 |
| [7] |
KE S T, YU W, WANG T G, et al. Wind loads and load-effects of large scale wind turbine tower with different halt positions of blade[J]. Wind and Structures, 2016, 23(6): 559-575. DOI:10.12989/was.2016.23.6.559 |
| [8] |
YIN L L, LO K H, WANG S S. Effects of blade pitch, rotor yaw, and wind–wave misalignment on a large offshore wind turbine dynamics in western gulf of Mexico shallow water in 100-year return hurricane[J]. Journal of Offshore Mechanics and Arctic Engineering, 2017, 139(1): 011901. DOI:10.1115/1.4034330 |
| [9] |
柯世堂, 王晓海. 考虑叶片偏航和干扰效应大型风力机体系风振响应与稳定性分析[J]. 湖南大学学报(自然科学版), 2018, 45(7): 61-70. KE S T, WANG X H. Analysis on wind-induced response and stability of large wind turbine systems considering blade yaw and interference effects[J]. Journal of Hunan University (Natural Sciences), 2018, 45(7): 61-70. (in Chinese) |
| [10] |
LIAN J J, JIA Y Y, WANG H J, et al. Numerical study of the aerodynamic loads on offshore wind turbines under typhoon with full wind direction[J]. Energies, 2016, 9(8): 613. DOI:10.3390/en9080613 |
| [11] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. NREL/TP-500-38060. National Renewable Energy Laboratory, Golden, CO, 2009. https://www.nrel.gov/docs/fy09osti/38060.pdf doi: 10.2172/947422
|
| [12] |
周道成, 段忠东. 耿贝尔逻辑模型在极值风速和有效波高联合概率分布中的应用[J]. 海洋工程, 2003, 21(2): 45-51. ZHOU D C, DUAN Z D. The Gumbel-logistic model for joint probability distribution of extreme-value wind speeds and effective wave heights[J]. The Ocean Engineering, 2003, 21(2): 45-51. DOI:10.3969/j.issn.1005-9865.2003.02.008 (in Chinese) |
| [13] |
WEI K, ARWADE S R, MYERS A T, et al. Effect of wind and wave directionality on the structural performance of non-operational offshore wind turbines supported by jackets during hurricanes[J]. Wind Energy, 2017, 20(2): 289-303. DOI:10.1002/we.2006 |
| [14] |
International Electrotechnical Commision (IEC). Wind turbines Wind Turbines-part 1: Design Requirements-Part 1: Design requirements[S]. IEC 61400-1, 2009.
|
| [15] |
MARINO E, GIUSTI A, MANUEL L. Offshore wind turbine fatigue loads: the influence of alternative wave modeling for different turbulent and mean winds[J]. Renewable Energy, 2017, 102: 157-169. DOI:10.1016/j.renene.2016.10.023 |
| [16] |
SHARMA J N, DEAN R G. Second-order directional seas and associated wave forces[J]. Society of Petroleum Engineers Journal, 1981, 21(1): 129-140. DOI:10.2118/8584-PA |
| [17] |
MORISON J R, JOHNSON J W, SCHAAF S A. The force exerted by surface waves on piles[J]. Journal of Petroleum Technology, 1950, 2(5): 149-154. DOI:10.2118/950149-G |
 2022, Vol. 40
2022, Vol. 40


