0 引　言

对于高超声速飞行器，较高的阻力和强烈的气动加热是必须考虑的两个关键问题^[1]。飞行器在高马赫数飞行时，强烈的激波会使飞行器表面热流显著攀升，这可能导致飞行器壁面烧蚀甚至飞行器内部电子电路失效^[2]。因此，能否有效降低气动加热是高超声速飞行器能否成功应用于工程实际的关键之一。

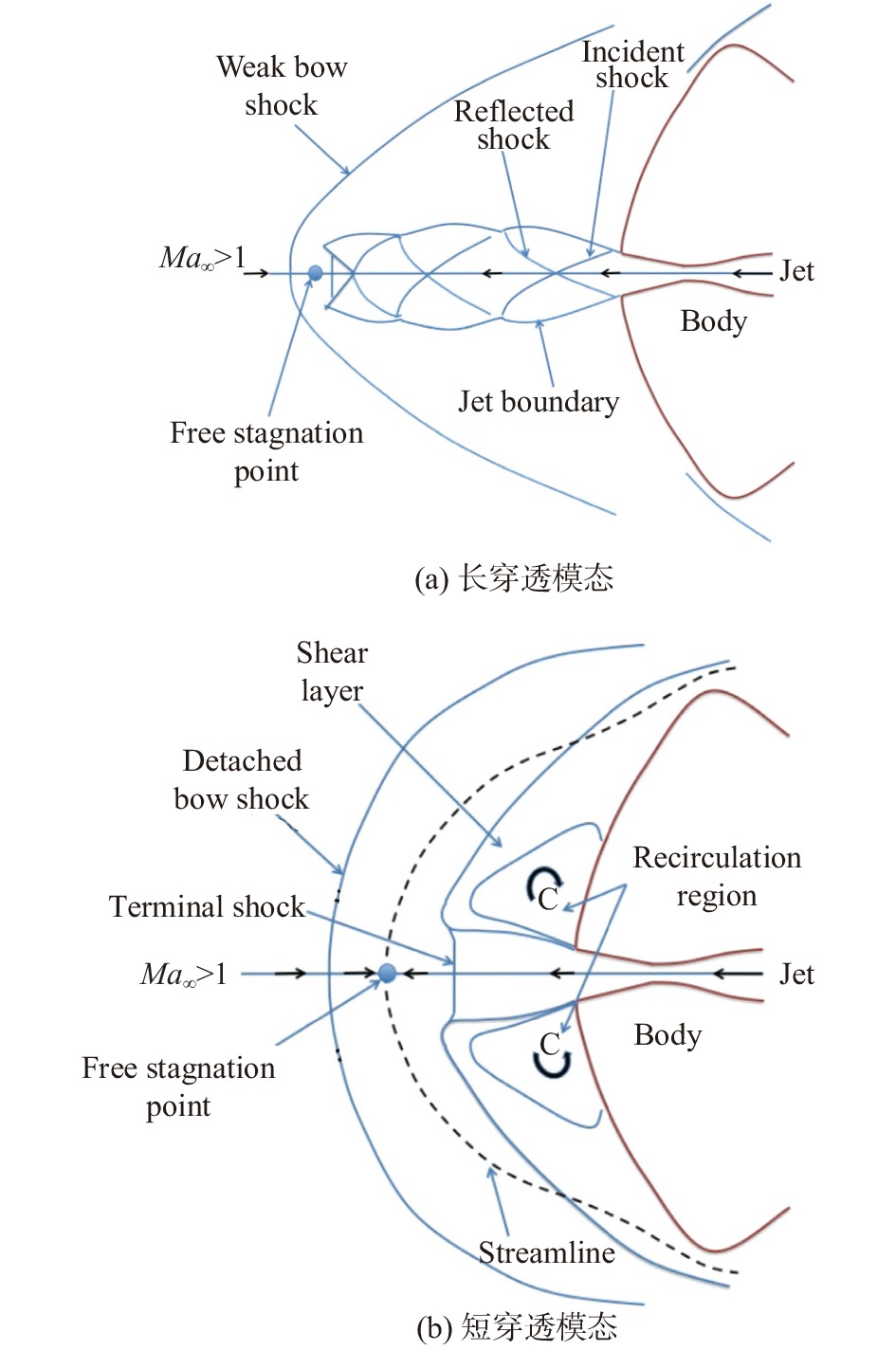
基于此，Laptoff等^[3]提出使用逆向喷流技术来达到降低高超声速飞行器表面热流的目的。逆向喷流一般情况是从飞行器头部喷出与来流方向相反的喷流，以此将激波推离飞行器表面，而喷流接触来流后会反向附着于物面并在喷口附近形成回流区，来流则在回流区外流动并再附。其典型流场结构可分为长穿透和短穿透两种模态，如图1所示^[4]。

影响逆向喷流流场结构的参数包括来流条件（马赫数、总压、总温等）和喷流条件（喷流工质、喷口几何形状、喷流马赫数、喷流质量流率等）。关联起二者的重要参数为压比 $ {P}_{R} $ ，即喷流总压与来流总压之比^[5]。目前，国内外许多学者^[6-10]已经对此进行了大量研究。其中，黄龙呈等^[6]总结了目前主要的主动减阻方法及原理，提出可对喷流开关进行控制以及将喷流发生器置于飞行器内部，研究发现该方法可以在避免改变飞行器气动外形的同时有效地减小波阻。Love^[7]研究了逆向喷流试验相关的问题，考虑了喷流马赫数、喷管扩张角、喷流静压比对喷流结构、喷流波长、喷流边界形状和曲率的影响。Finley等^[8]针对超声速来流下的逆向喷流展开试验，提出稳态流动的气动特性主要包括喷流压力和喷流马赫数。Romeo等^[9]结合试验数据分析了喷流激波和接触面尺寸，并建立了预测喷流激波距离和接触面半径的理论方法。Deng等^[10-11]对来流马赫数8条件下带有逆向喷流的升力体飞行器进行了数值模拟，重点研究了长穿透模态的减阻效果及其周期振荡特性，结果显示，在小迎角范围内逆向喷流可以有效降低飞行器阻力，而自维持振荡过程表明锥形剪切层呈现离轴拍打运动。Warren^[12]试验对比了冷却气体以涡流形式喷出和直接喷出的降热效果，发现直喷式冷却的效果更好，但是由于该试验中冷却气体喷流的总压较小，导致实际的绝对降热量较小。Hayashi K等^[13]对来流马赫数为3.98时不同喷流压比状态下的钝头体头部流场结构和喷流降热效果进行了风洞试验研究，利用纹影法观察到长穿透模态和短穿透模态这两种逆向喷流的经典流场，并通过对模型表面斯坦顿数分布的分析，指出在较大喷流压比状态下出现的短模态流场对降热有着显著效果，并且减阻降热效果随着压比的增大而越好。王立强等^[14]数值模拟研究了喷流质量流量以及喷口尺寸对钝头体逆向喷流降热效果的影响，分析了三种可能出现的流场（长穿透模态、振荡模态和短穿透模态）的形成机理。结果显示，随着喷流质量流量和喷口尺寸的增大，表面热流均减小。Meyer等^[15]对来流马赫数为6.5条件下的钝体逆向喷流进行了数值模拟，发现逆向喷流可以降低钝体前缘的激波阻力、表面热流以及表面摩擦阻力。黄喜元等^[16] 通过数值模拟，对比研究了单喷管和多喷管逆向喷流技术，提出多喷管逆向喷流降热更具鲁棒性和工程适用性。

然而，上述研究中，对于高超声速来流条件下逆向喷流技术降热效果的风洞试验研究较少，缺乏数值模拟和试验结果的相互校验。同时，对于不同来流马赫数条件下逆向喷流降热效果的对比研究也不够完善。因此，本文选取半球体钝体模型作为研究对象，通过数值模拟及风洞试验，研究不同高马赫数来流条件下逆向喷流对钝头体附近流场以及热流分布的影响。

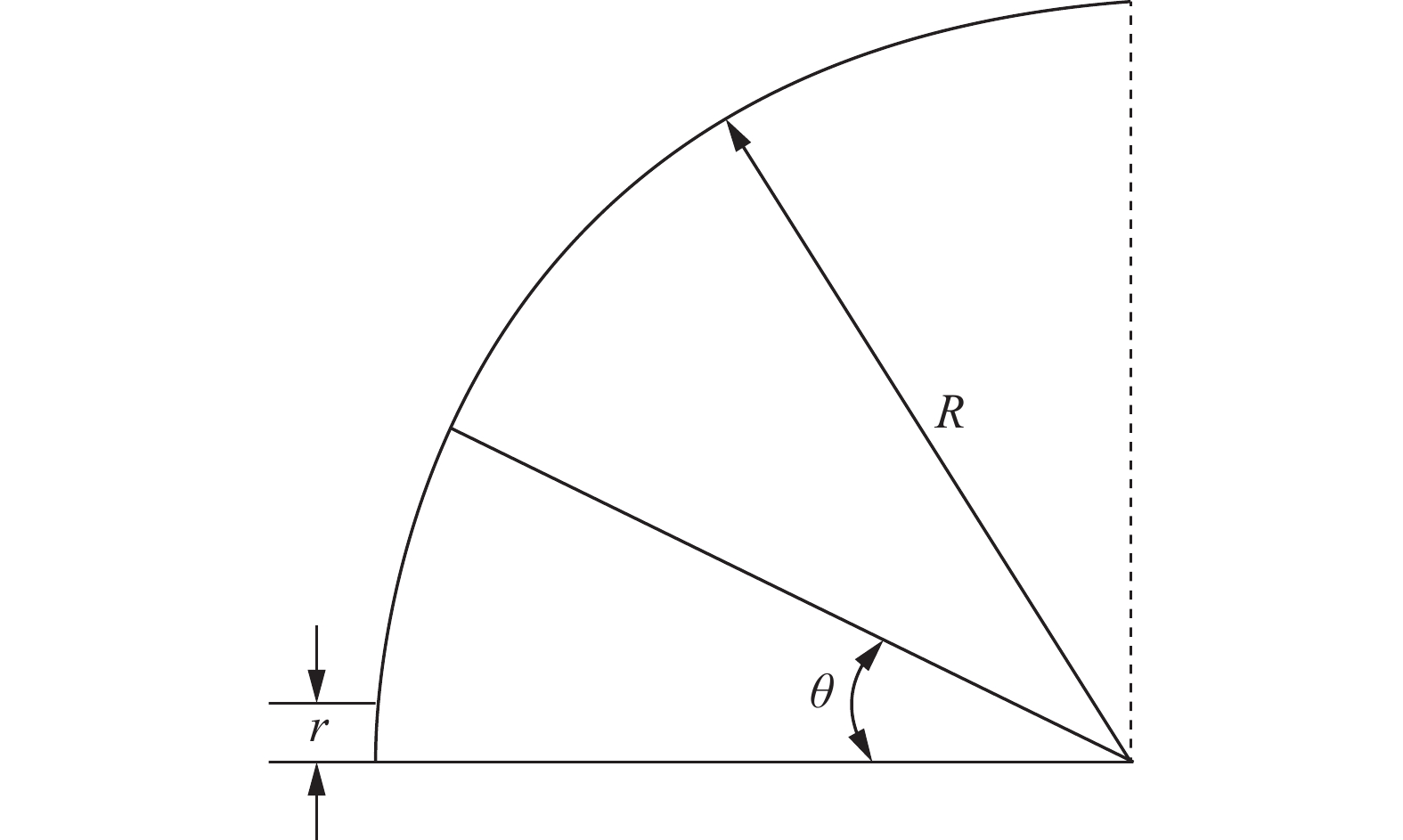
1 物理模型和数值方法 1.1 物理模型

研究对象采用半径为25 mm的半球体钝体模型。头部驻点处设置逆向喷流喷口，喷口半径r = 2 mm，定义周向角为θ，如图2所示。

1.2 数值模拟

数值模拟中，控制方程采用可压缩雷诺平均的Navier-Stokes方程，如式（1）所示。

$ \frac{\partial }{\partial t}{\int }_{\varOmega }{{\boldsymbol{W}}}\mathrm{d}\varOmega +{\oint }_{\partial \varOmega }^{}\Big({{{\boldsymbol{F}}}}_{c}-{{{\boldsymbol{F}}}}_{v}\Big)\mathrm{d}S=0 $

(1)

式中， ${\boldsymbol{W}}$ 为守恒变量矢量， ${{{\boldsymbol{F}}}}_{c}$ 为对流通量矢量， ${{{\boldsymbol{F}}}}_{v}$ 为黏性通量矢量。

采用有限体积法进行空间离散，时间项采用隐式格式离散，对流项使用AUSM差分格式处理，湍流模型选取SSTk-ω模型。

物面边界条件采用无滑移条件，并假设物面为等温壁。自由来流边界设为压力远场边界，喷口采用压力入口边界，出口边界设为压力出口边界，由流场内部线性外推得到。

计算网格采用二维轴对称结构网格，对称边界设置为中心轴对称边界，对喷口区域及壁面处网格进行加密，如图3所示。

1.3 算例验证

为验证计算方法的可靠性，选取了Hayashi K等^[13]的逆向喷流试验结果进行对比。选取 $ {P}_{R} $ = 0.6状态，喷流介质为N₂，计算条件见表1，计算网格量分别取25600、38400和57600。 $ {P}_{R} $ 定义如下：

$ {P}_{R} = \frac{{P}_{j}}{{P}_{0}} $

(2)

其中， $ {P}_{j} $ 为是逆向喷流总压， $ {P}_{0} $ 为是自由来流总压。

选取无量纲参数斯坦顿数 ${S t}$ 来表征钝头体壁面热流。斯坦顿数表示传递到流体中的热量与流体的热容量之比，其定义如下：

$ {S t}=\frac{q}{\left({T}_{{\rm{aw}}}-{T}_{{\rm{w}}}\right){\rho }_{\infty }{c}_{p\infty }{u}_{\infty }} $

(3)

$ {T}_{{\rm{aw}}}={T}_{\infty }\left\{1+\sqrt[3]{{P}{r}}\left[\frac{\left(\gamma -1\right)}{2}\right]{M}_{\infty }^{2}\right\} $

(4)

式（3）中， $ q $ 为表面热流密度， $ {T}_{{\rm{aw}}} $ 为绝热壁温， $ {T}_{{\rm{w}}} $ 为实际壁温， $\; {\rho }_{\mathrm{\infty }} $ 为自由来流密度， $ {c}_{p\infty } $ 为自由来流的比定压热容， $ {u}_{\infty } $ 为自由来流速度。式（4）中， $ {T}_{\infty } $ 为自由来流温度， ${P}{r}$ 为普朗特数， $ \gamma $ 为比热比。

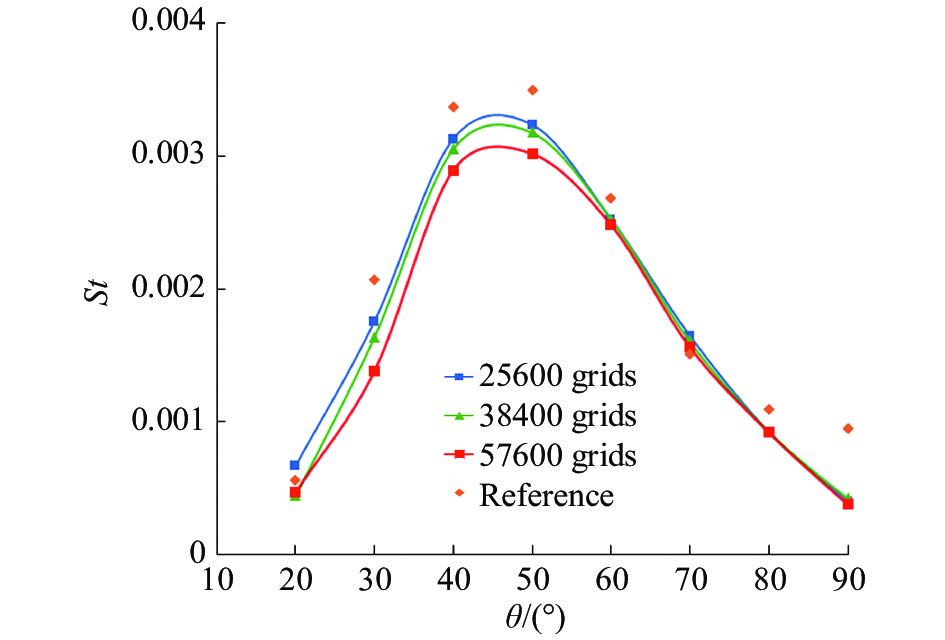
计算结果与文献试验结果的对比如图4和图5所示，其中图4给出了计算得到的密度云图与试验纹影图^[13]的对比；图5给出了模型表面斯坦顿数分布的对比。从流场结构来看，计算和文献试验结果有较好的一致性，喷口处产生膨胀波，喷流与自由来流相互作用形成了结构稳定且密度较大的马赫盘结构，头部脱体激波被喷流推离并在下游处到达物面形成再附激波。从模型表面斯坦顿数分布来看，计算结果与文献试验的结果较为接近，且误差不超过10%。参考Hayashi等文献[17]中的数值模拟部分以及Sun等^[18]对数值模拟湍流模型的对比研究，可以证实ASUM离散格式以及SST k-ω湍流模型可用于高超声速气动热计算。而文献[13]中试验测得的模型表面热流可能存在误差，导致计算网格越密，计算结果与文献数据差距越大。

计算选用的三种网格均能较好地体现出逆向喷流的流场结构，且相对误差较小。为兼顾计算的精度和效率，本文选用网格量为38400的计算模型进行后续研究。

2 风洞试验 2.1 试验设备及试验方法

试验在南京航空航天大学高超声速风洞（NHW）中开展。NHW是一座喷管出口直径 $\phi$ = 500 mm的高压下吹—真空抽吸暂冲式高超声速风洞，如图6所示。NHW风洞有5对轴对称超声速喷管，名义马赫数为4、5、6、7、8，每车次试验时间为7～10 s。试验段及真空驻室上方各有一个 350 mm×350 mm的观察窗，通过观察窗可以使用CCD相机或高速摄影设备对模型和流场进行光学测量。

试验采用高速纹影拍摄流场，获得定性的流场结构，同时采用红外热成像测量技术对试验模型表面温度进行监测。在模型表面沿周向每5°设置一个测温点，通过红外热成像技术测得模型壁面的实时温度。将数据进行处理后可以得到模型表面的热流密度分布，进一步得到模型壁面斯坦顿数分布。

2.2 试验模型及试验状态

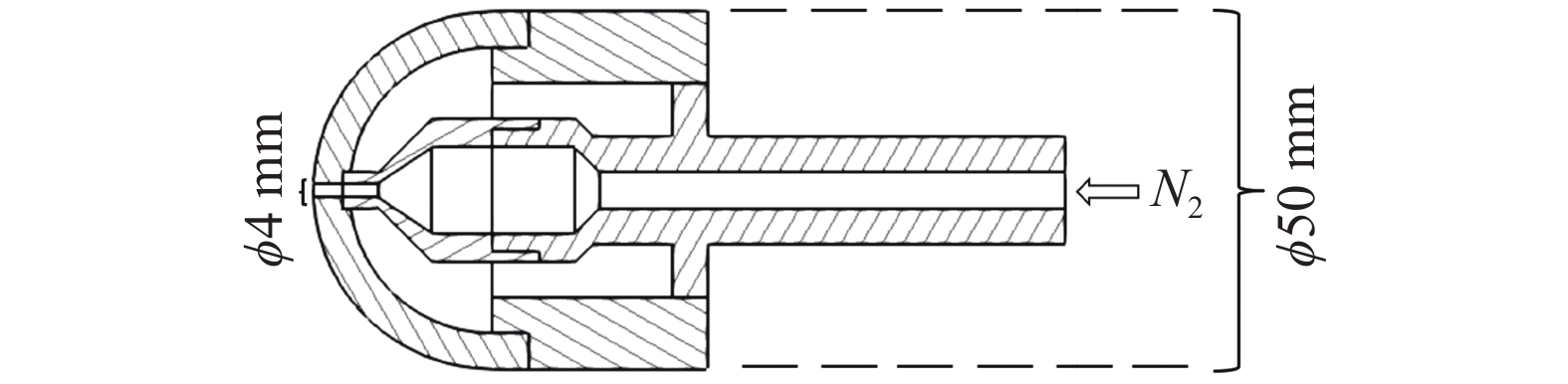
逆向喷流系统如图7所示。模型尾部连接充有N₂的高压气罐，以保证试验时N₂以规定的喷流总压 $ {P}_{j} $ 注入头部喷口。试验采用的模型与数值模拟保持一致。半球体钝体模型由聚醚醚酮加工而成，如图8所示。试验在0°迎角下开展，风洞试验状态见表2。喷流工质为N₂，喷流马赫数为1。

2.3 热流密度计算方法

试验利用红外热像仪采集模型表面温度数据，结合一维热传导假设，获取模型表面的温度分布，最后基于求得的温度分布利用傅里叶传热定律计算出模型表面热流密度。具体如下。

根据一维热传导方程：

$ \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial {\varsigma }^{2}} $

(5)

其中α表示热扩散系数，定义为：

$ \alpha =\frac{\kappa }{\rho {c}_{p}} $

(6)

其中 $\kappa $ 、ρ、c_p分别表示材料的热传导系数、密度和比热容。热传导方程的离散采用时间前差、空间中心差分格式。有限差分离散结果为：

$ \frac{{T}_{i+1,j}-{T}_{i,j}}{\mathrm{\Delta }t}=\frac{\alpha ({T}_{i,j-1}-2{T}_{i,j}+{T}_{i,j+1})}{\mathrm{\Delta }{\varsigma }^{2}}+{O}(\delta {\varsigma }^{2}) $

(7)

其中 $ \mathrm{\Delta }t $ 表示时间步长，本文中红外热像采样频率为30 Hz，因此时间步长为 $ \dfrac{1}{30} $ s。 $ \mathrm{\Delta }\varsigma $ 为空间步长，其取值满足稳定性要求。通过计算获取模型表面的温度分布后，采样点每个时间节点处的热流密度可以通过傅里叶定律获得：

$ q=-\kappa \frac{\partial T}{\partial \varsigma } $

(8)

将温度梯度利用三点格式近似表示，则近似热流密度可表示为：

$ q=-\kappa \dfrac{-\dfrac{3}{2}{T}_{n,0}+2{T}_{n,1}-\dfrac{1}{2}{T}_{n,2}}{\Delta \varsigma } $

(9)

将计算得到的热流密度代入式（3）中，便可得到风洞试验中模型表面的斯坦顿数分布。

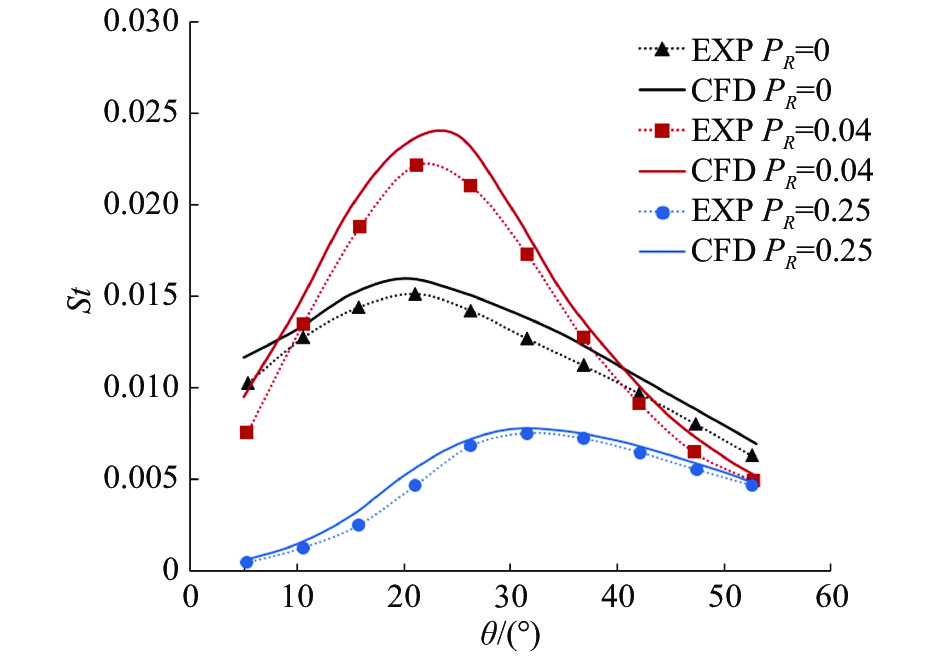
3 结果与分析 3.1 典型流场结果对比

图9和图10给出了来流马赫数6条件下不同喷流压比（ $ {P}_{R}=0{\text{、}}0.04{\text{、}}0.25 $ ）的结果，其分别对应无喷流状态、长穿透模态、短穿透模态三种典型流场结构。图9给出了数值模拟得到的流场云图（密度梯度）与试验拍摄的纹影图的对比，由图可见，计算与试验所得到的流场结构吻合较好，弓形激波、马赫盘、回流区以及再附激波等典型结构的大小、位置大致相同。图10给出了三个喷流压比下计算和试验得到的模型壁面斯坦顿数的分布情况，可以看出，计算与试验得到的模型表面热流分布趋势基本一致，数据误差基本不超过10%。

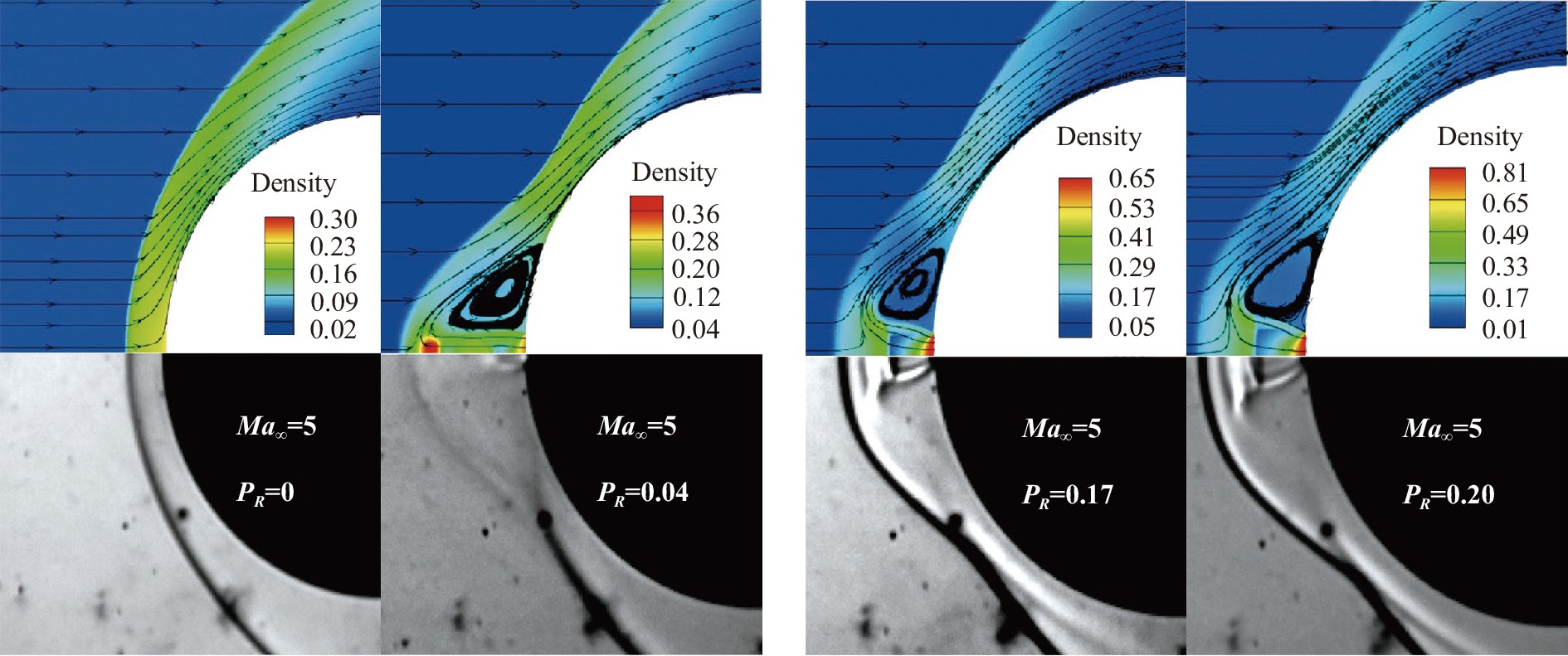
参照文献[5，14]可给出长穿透模态和短穿透模态流场成因：当喷流压比较小时，喷流出口压力较小，喷口呈过度膨胀状态，此时喷流穿透能力强，导致喷口小角度范围内弓形激波被推离地更远，形成不稳定的斜激波系结构，流场为长穿透模态；当喷流压比逐渐增大至某临界值，此时喷流出口压力大，喷口呈欠膨胀状态，弱激波结构崩溃，喷流被主流弓形激波中止形成马赫盘结构，形成短穿透模态流场，流场结构趋于稳定。

对比数值模拟和风洞试验结果可知，本文采用的数值模拟方法吻合度较高，可以用于对高超声速逆向喷流的降热效果研究。

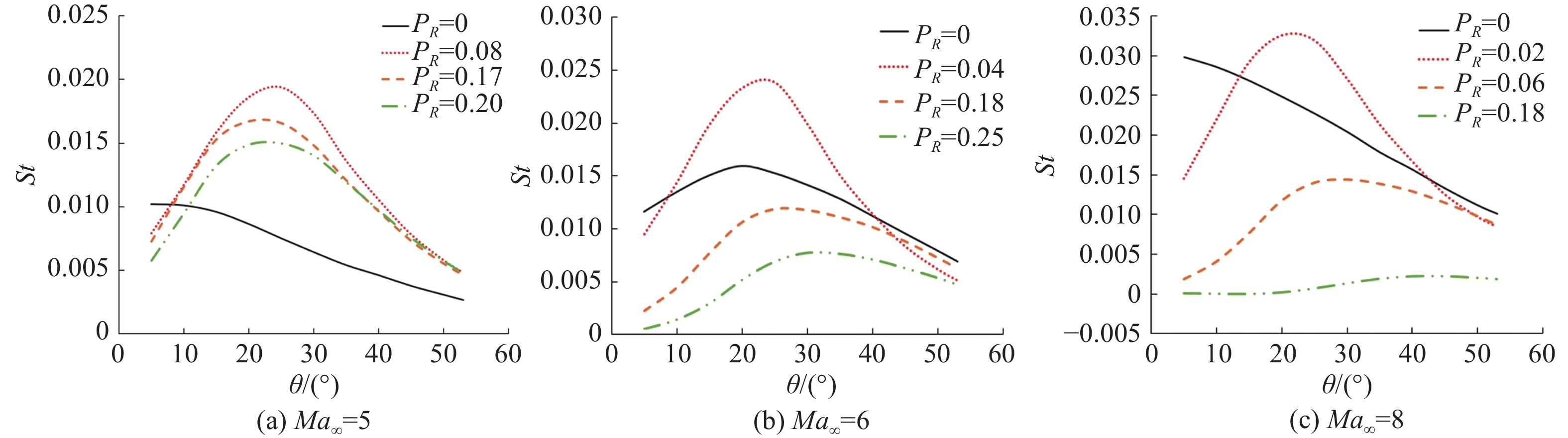
3.2 喷流压比影响

图11和图12分别给出了三种来流马赫数中不同喷流压比下的流场结构对比以及壁面斯坦顿数分布。

从图中可以看出，同一来流马赫数下，喷流压比较小时，模型表面热流不降反增，此时对应的流场为长穿透模态或者结构较小的短穿透模态。随着喷流压比增大，流场变为稳定的短穿透模态，此时逆向喷流对模型表面的降热效果显著，尤其在靠近驻点处表现得更为明显；继续增大喷流压比，可以发现逆向喷流降热效果越来越好。

结合流场结构以及壁面斯坦顿数分布可以分析高超声速来流条件下逆向喷流的降热机理。当来流马赫数一定时，对于稳定的短穿透模态流场，随着喷流压比增大，马赫盘距驻点距离以及弓形激波离体距离增大，因此降低了钝头体表面热流。同时，回流区在模型表面的范围不断扩大，冷却气体回流使得模型表面热流不断降低，即对应图12曲线图中St逐渐增大的部分。再附激波的位置则对应曲线图中St的最大值点，随着喷流压比增大，短模态流场结构扩大，再附激波位置后移，曲线图中St的最大值点随之变化。基于此，可认为弓形激波远离物面以及喷流回流区共同作用达到了降热的效果。而当喷流压比较小，形成长穿透模态流场或无法覆盖较大的壁面回流区时，则无法获得较好的降热效果。

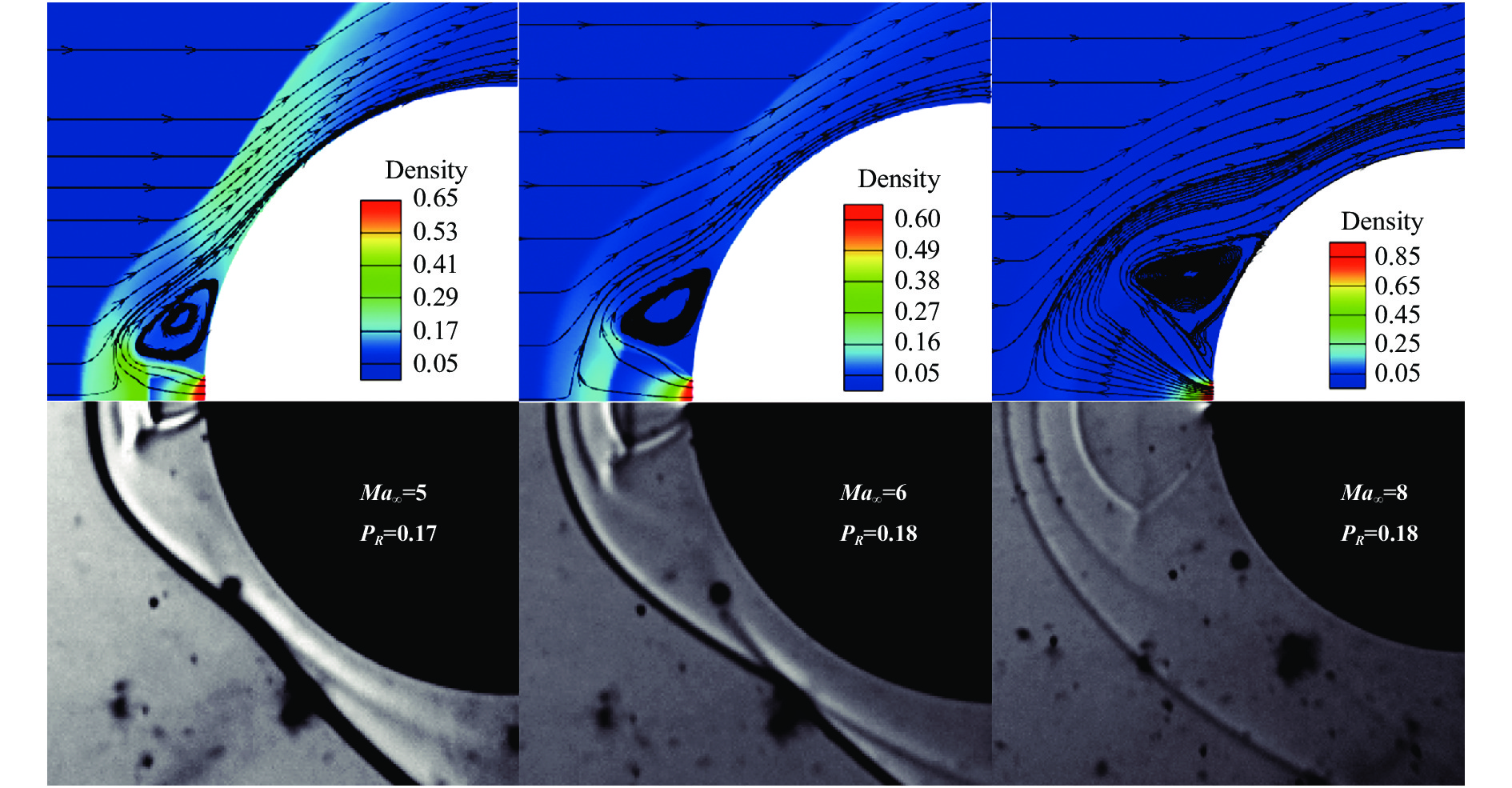
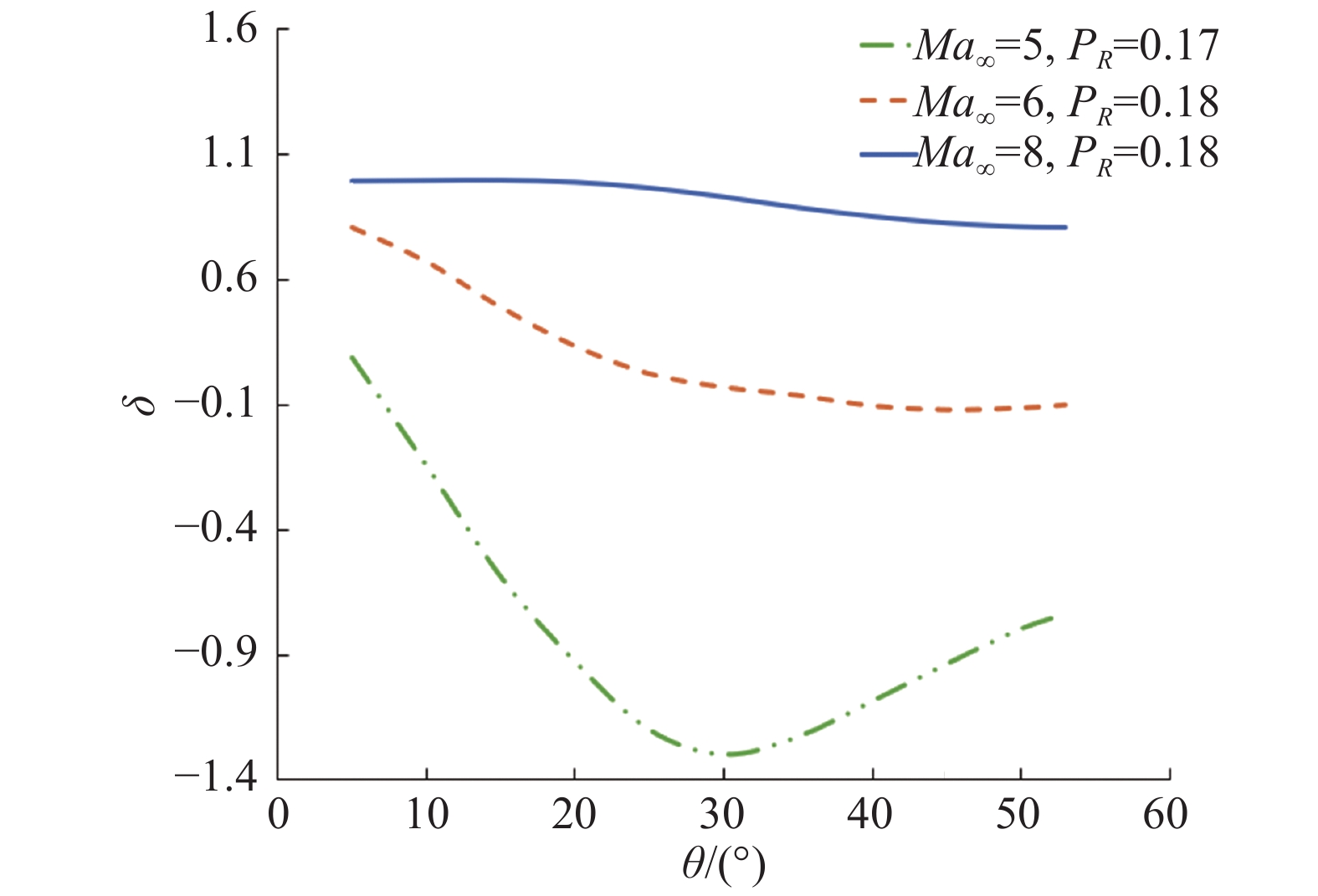
3.3 来流马赫数影响

图13和图14分别给出了在不同来流马赫数 ${Ma}_{\infty }$ 状态下，喷流压比相近时，逆向喷流形成的流场以及模型壁面降热效果对比。引入 $ \delta $ 来直观地反映各状态的降热效果。 $ \delta $ 定义如式（10）所示：

$ \delta =\frac{{S t}_{0}-{S t}_{{j}}}{{S t}_{0}} $

(10)

其中， ${S t}_{0}$ 指的是无逆向喷流状态下的模型壁面斯坦顿数， ${S t}_{{j}}$ 指的是带有逆向喷流时的模型壁面斯坦顿数。因此， $ \delta $ 为正，说明逆向喷流起到了降热效果，并且 $ \delta $ 的数值越大，说明降热效果越好。

从图14可以看出，在喷流压比相近时，随着来流马赫数的提高，逆向喷流的降热效率也越高。进一步结合图13中的流场可以很明显地看出，这是因为短穿透模态的结构在不断扩大，模型壁面被喷流回流所覆盖的面积增大，弓形激波整体被逆向喷流推离得更远，再附激波的位置更加远离驻点甚至消失。这也进一步验证了前文对逆向喷流降热机理的分析。

4 结　论

通过数值模拟及风洞试验获得了自由来流，马赫数分别为5、6、8时不同逆向喷流压比条件下半球体钝体的流场结构和表面热流分布，进行了对比和相互校验，分析了高超声速来流中逆向喷流的降热规律和相关机理，得到以下结论：

1）通过对逆向喷流流场结构及模型表面热流分布的分析可知，逆向喷流产生的降热效果是冷却气体回流以及喷流推离弓形激波共同作用的结果。

2）较小喷流压比形成的长穿透模态或结构较弱的短穿透模态无法达到降热的效果。而随着喷流压比的增大，短穿透模态流场结构逐渐增强，此时逆向喷流的降热效果较为明显，并且喷流压比越大，降热效果也越好。

3）喷流压比相近时，来流马赫数越大，逆向喷流的降热效率越高。这与回流区的覆盖面积、弓形激波被推离距离、再附激波位置等相关。

4）本文研究结论可为高超声速逆向喷流技术的实际应用提供参考。实际中，可以根据飞行器的飞行马赫数对喷流压比进行调整，在达到预期降热效果的同时，降低能源和工质的消耗。