0 引　言

运动边界和流固耦合（Fluid-structure interaction，FSI）问题是航空航天工程、船舶和海洋工程、土木和交通工程等领域经常面临的多场耦合问题^[1-2]。数值模拟FSI问题目前已发展大量方法。近些年，随着技术进步，以微纳米机电系统（micro-electro-mechanical-systems，MEMS）和超低轨道航天器为代表的应用领域面临跨流域运动边界和流固耦合问题，如MEMS中微尺度梁的振动问题^[3]、航天器返回过程^[4]和超低轨道航天器与外层稀薄大气相互作用问题^[5]。在这类问题中，由于特征尺度的显著减小或气体密度显著降低，流体的稀薄气体效应是这类流固耦合问题需要考虑的重要影响因素之一。根据克努森数（Kn）定义^[6]，流动可划分为连续流、滑移流、过渡流和自由分子流四个流域。由于上述新问题中流体流域通常处于滑移流域或过渡流域，而传统的流固耦合求解方法中流体部分通常采用基于Navier-Stokes方程的适用于连续流域的宏观方法，因此有必要发展可考虑稀薄气体效应影响的流固耦合求解新方法。

近年来，在跨流域流动数值模拟方法方面，离散统一气体动理学格式（discrete unified gas kinetic scheme，DUGKS）^[7]这一新兴数值方法得到了广泛关注。该方法在格式通量计算部分，借鉴了格子Boltzmann方法（lattice Boltzmann method，LBM）^[8]的特征线构造思想，较统一气体动理学格式（unified gas kinetic scheme，UGKS）^[9]显著简化，计算效率进一步提升。在网格实施方面，由于标准LBM采用迁移-碰撞模式，Boltzmann方程的对流项隐藏在分布函数沿特征线的迁移过程中^[10]，因此计算网格需采用均匀笛卡尔网格；而DUGKS在实施过程中由于采用对流项显式求解思想，尽管计算复杂度有所提升，数值耗散也有所增加，但可采用的网格也更加灵活，结构、非结构及混合网格均可，对不规则计算域的适用性显著提高。在数值耗散方面，与传统的有限体积LBM^[11-12]相比，由于对流项计算过程中引入迁移-碰撞思想，因此数值耗散小，对网格尺度和时间步长约束小。目前该类方法已具有全流域流动计算能力，并在快速发展中^[13-14]。考虑到运动边界问题的重要性，目前已有开展少量工作^[15]，仍需进一步完善。

在运动边界数值模拟方面，网格技术通常分为基于动网格技术的任意拉格朗日-欧拉法（arbitrary Lagrangian-Eulerian，ALE）^[16]和基于笛卡尔网格的浸入边界法（immersed boundary method，IBM）^[17]。ALE可采用贴体网格，在模拟高雷诺数流动及结构运动模式相对简单的FSI问题时有较大优势，计算效率较高，如航空工程中的颤振数值模拟。IBM由于壁面附近采用笛卡尔网格，适用于雷诺数较低的流动问题，模拟大变形动边界问题有显著优势。目前，基于DUGKS的ALE^[15]和IBM^[18]均有发展，其中ALE-DUGKS在模拟考虑稀薄气体效应影响的运动边界问题时有良好表现。而在低速连续流域范围，以LBM、DUGKS为代表的介观数值方法，由于无需求解宏观方法中的压力泊松方程^[19]，方法实施也相对简单。ALE-DUGKS在低速连续流和稀薄流的独特优势是为进一步发展低速跨流域运动边界和流固耦合数值方法奠定基础。在流固耦合数值模拟方面，发展较为成熟的是松耦合计算方法^[20]，即在每个数值模拟时间步长内采用计算流体力学（computational fluid dynamics，CFD）和计算结构动力学（computational structural dynamics，CSD）各自成熟的求解方法，并在流-固耦合界面进行数据交换实现流体域和固体域的耦合推进。

综上，本文的主要工作是针对MEMS和航天工程面临的跨流域流动运动边界和流固耦合问题，采用新兴跨流域数值方法DUGKS，将已发展的运动边界ALE-DUGKS扩展至低速，同时兼顾高速流动的流固耦合计算框架，利用网格的贴体性采用较少的网格量更高效地模拟边界层流动。针对连续流域圆柱绕流强迫振动和自由振动两个典型算例进行模拟，验证方法的计算能力，并进一步采用跨流域求解方法验证方法的跨流域计算能力和拓展性。

1 基于DUGKS的流固耦合求解方法 1.1 ALE-DUGKS格式

ALE-DUGKS是王勇等^[15]在原始DUGKS^[7]基础上构造的跨流域流动运动边界求解格式。原始DUGKS格式构造基于Boltzmann-BGK方程：

$ \frac{{\partial f}}{{\partial t}} + \boldsymbol{\xi} \cdot \nabla f = \varOmega = - \frac{1}{\tau }\left( {f - {f^{{\rm{eq}}}}} \right) $

(1)

式中， $ f = f\left( {{\boldsymbol{x}},\boldsymbol{\xi} ,t} \right) $ 为在 $t$ 时刻位置 $ \boldsymbol{x} $ 、离散速度 $\boldsymbol{\xi} $ 的分布函数， $\varOmega$ 为碰撞项， $\tau = \mu /p$ 为松弛时间（ $\mu $ 和 $p$ 分别为流体的动力黏度和压强）， ${f^{{\rm{eq}}}}$ 为平衡态分布函数。对于连续流模拟，可采用LBM的D2Q9离散速度模型^[8]， ${f^{eq}}$ 为：

$ f_{{\alpha}} ^{{\rm{eq}}} = \rho {{\omega} _{{\alpha}} }\left[ {1 + \frac{{{{\boldsymbol{e}}_{{\alpha}} } \cdot {\boldsymbol{u}}}}{{c_s^2}} + \frac{{{{\left( {{{\boldsymbol{e}}_{{\alpha}} } \cdot {\boldsymbol{u}}} \right)}^2}}}{{2c_s^4}} - \frac{{{\boldsymbol{u}^2}}}{{2c_s^2}}} \right] $

(2)

式中， $\;\rho $ 为流体密度， ${\boldsymbol{u}}$ 为流体速度， ${c_s}$ 为格子声速， ${{\omega} _{{\alpha}} }$ 为权系数：

$ {\omega _{{\alpha}} } = \left[ {\begin{array}{*{20}{c}} {\dfrac{4}{9}}&{\dfrac{1}{9}}&{\dfrac{1}{9}}&{\dfrac{1}{9}}&{\dfrac{1}{9}}&{\dfrac{1}{{36}}}&{\dfrac{1}{{36}}}&{\dfrac{1}{{36}}}&{\dfrac{1}{{36}}} \end{array}} \right] $

(3)

${{\boldsymbol{e}}_{\alpha} }$ 为格子速度（物理意义与 ${\boldsymbol{\xi}} $ 相同）：

$ {{\boldsymbol{e}}_{\alpha} } = \sqrt {3RT} \left[ {\begin{array}{*{20}{c}} 0&1&0&{ - 1}&0&1&{ - 1}&1&{ - 1} \\ 0&0&1&0&{ - 1}&1&1&{ - 1}&{ - 1} \end{array}} \right] $

(4)

式中R和T分别为气体常数和气体温度（本文RT = 1/3）。对于稀薄流模拟， ${f^{{\rm{eq}}}}$ 为Maxwell平衡态分布函数，二维流动为：

$ {f^{{\rm{eq}}}} = \frac{\rho }{{2\text{π} RT}}\exp \left( { - \frac{{{{\left| {\boldsymbol{\xi} - \boldsymbol{u}} \right|}^2}}}{{2RT}}} \right) $

(5)

对于离散速度模型，通常采用Gauss-Hermit或Newton-Cotes积分及非结构网格积分法^[21]，并将积分点设置成离散速度点。最后，宏观量计算为：

$ \rho = \int {f{\rm{d}}\boldsymbol{\xi} } ,\;\;\;\rho {\boldsymbol{u}} = \int {\boldsymbol{\xi} f{\rm{d}}\boldsymbol{\xi} } ,\;\;\;p = \rho RT $

(6)

ALE-DUGKS格式在构造过程中将式（1）修改为：

$ \frac{{\partial f}}{{\partial t}} + \left( {\boldsymbol{\xi} - {\boldsymbol{v}}} \right) \cdot \nabla f = - \frac{1}{\tau }\left( {f - {f^{eq}}} \right) $

(7)

式中， ${\boldsymbol{v}}$ 为网格运动速度。网格在运动过程中只需对对流项进行修正，不影响平衡态分布函数更新，具体分析参见文献[22]。

式（7）采用非结构网格有限体积法进行离散，分布函数存储在控制体格心处，对流项采用中点公式，碰撞项采用梯形公式：

$ \begin{split}& f_j^{n + 1}\left| {V_j^{n + 1,*}} \right| - f_j^n\left| {V_j^{n,*}} \right| + \Delta t{F^{n + 1/2}} = \\& \qquad{\text{ }}\frac{{\Delta t}}{2}\left[ {\varOmega _j^{n + 1}\left| {V_j^{n + 1,*}} \right| + \varOmega _j^n\left| {V_j^{n,*}} \right|} \right] \end{split} $

(8)

式中， $\Delta t$ 为时间步长，下标j为离散控制体编号，二维可为三角形或四边形控制体，上标n为离散时间层。 ${F^{n + 1/2}}$ 为介观界面通量：

$ \begin{split} {F^{n + 1/2}} =& \int_{\partial {V_j}} {\left( {\boldsymbol{\xi} - {\boldsymbol{v}}} \right)} \cdot {\boldsymbol{n}}f\left( {{{\boldsymbol{x}}_b},{t^{n + 1/2}}} \right){\rm{d}}S \\=& {\text{ }}\sum\limits_k {\left( {\boldsymbol{\xi} - {\boldsymbol{v}}_{b,k}^{n + 1/2}} \right) \cdot {\boldsymbol{n}}_{b,k}^*f\left( {{{\boldsymbol{x}}_b},{t^{n + 1/2}}} \right)S_{b,k}^*} \end{split} $

(9)

式中，下标k为控制体界面编号，下标b为界面中点处相应变量值。式（8）和式（9）中的V和S分别为控制体体积和界面面积，在实际计算中采用有向界面面积 ${{\boldsymbol{S}}_b} = {{\boldsymbol{n}}_b}{S_b}$ ，上标*表示相应变量需由离散几何守恒律确定（discretized geometric conservation law，DGCL）。文献[15]详细讨论了DGCL在ALE-DUGKS的实现方法，本文具体为：

$ \begin{split}& {\boldsymbol{v}}_b^{n + 1/2} = \frac{{{\boldsymbol{x}}_b^{n + 1} - {\boldsymbol{x}}_b^n}}{{\Delta t}}, \\& V_j^{n + 1,*} = V_j^{n + 1}, \;\;\;\;V_j^{n,*} = V_j^n ,\\& {\boldsymbol{S}}_b^* = {\boldsymbol{S}}_b^{n + 1/2} = \frac{{{\boldsymbol{S}}_b^{n + 1} + {\boldsymbol{S}}_b^n}}{2} \end{split} $

(10)

式（8）消去隐式碰撞项 ${\varOmega ^{n + 1}}$ ，引入两组辅助分布函数：

$ \begin{split}& \tilde f = f - \frac{{\Delta t}}{2}\varOmega = \frac{{2\tau + \Delta t}}{{2\tau }}f - \frac{{\Delta t}}{{2\tau }}{f^{{\rm{eq}}}} \\& {{\tilde f}^ + } = f + \frac{{\Delta t}}{2}\varOmega = \frac{{2\tau - \Delta t}}{{2\tau + \Delta t}}\tilde f + \frac{{2\Delta t}}{{2\tau + \Delta t}}{f^{{\rm{eq}}}} \end{split} $

(11)

可改写为：

$ \tilde f_j^{n + 1} = \left| {\frac{{V_j^{n,*}}}{{V_j^{n + 1,*}}}} \right|\tilde f_j^{ + ,n} - \frac{{\Delta t}}{{\left| {V_j^{n + 1,*}} \right|}}{F^{n + 1/2}} $

(12)

即，与原始DUGKS相同，ALE-DUGKS在计算过程中更新 $\tilde f$ 。对于式（9）中界面分布函数 $ f\left( {{\boldsymbol{x}_b},{t^{n + 1/2}}} \right) $ 计算，将式（1）在半个时间步长 $s = \Delta t/2$ 沿特征线积分：

$ \begin{split}& f\left( {{{\boldsymbol{x}}_b},{t^{n + 1/2}}} \right) - f\left( {{{\boldsymbol{x}}_b} - \boldsymbol{\xi} s,{t^n}} \right) = \\& \qquad{\text{ }}\frac{s}{2}\left[ {\varOmega \left( {{{\boldsymbol{x}}_b},{t^{n + 1/2}}} \right) + \varOmega \left( {{{\boldsymbol{x}}_b} - \boldsymbol{\xi} s,{t^n}} \right)} \right] \end{split} $

(13)

同时，进一步引入两组辅助分布函数：

$ \begin{split}& {\bar {f}} = f - \frac{s}{2}{\varOmega} = \frac{{2{\tau} + s}}{{2{\tau} }}f - \frac{s}{{2{\tau} }}{f^{{\rm{eq}}}} \\& {{\bar {f}}^ {+} } = f + \frac{s}{2}{\varOmega} = \frac{{2{\tau} - s}}{{2{\tau} + s}}{\bar {f}} + \frac{s}{{2{\tau} + s}}{f^{{\rm{eq}}}} \end{split} $

(14)

则式（13）可改写为：

$ \bar f\left( {{{\boldsymbol{x}}_b},{t^{n + 1/2}}} \right) = {\bar f^ + }\left( {{{\boldsymbol{x}}_b} - \boldsymbol{\xi} s,{t^n}} \right) $

(15)

将式（15）带入式（14）第一个方程后，式（9）的界面原始分布函数为：

$ f\left( {{{\boldsymbol{x}}_b},{t^{n + 1/2}}} \right) = \frac{{2\tau }}{{2\tau + s}}\bar f\left( {{{\boldsymbol{x}}_b},{t^{n + 1/2}}} \right) + \frac{s}{{2\tau + s}}{f^{{\rm{eq}}}}\left( {{{\boldsymbol{x}}_b},{t^{n + 1/2}}} \right) $

(16)

由关系式：

$ {\bar f^ + } = \frac{{2\tau - s}}{{2\tau + \Delta t}}\tilde f + \frac{{3s}}{{2\tau + \Delta t}}{f^{{\rm{eq}}}} $

(17)

将格心处 $\tilde f$ 换算成 ${\bar f^ + }$ ，并采用Taylor展开和最小二乘法插值获得 $ {{\boldsymbol{x}}_b} - \boldsymbol{\xi} s $ 处 ${\bar f^ + }$ 。最后，根据碰撞不变性及式（6），格心和界面中点处宏观量可由相应的辅助分布函数 $\tilde f$ 和 $\bar f$ 积分得出。

1.2 流固耦合计算方法

ALE-DUGKS具备运动边界问题求解能力，耦合计算结构动力学并采用松耦合求解方法后，可将DUGKS发展成可考虑稀薄气体效应的跨流域流固耦合计算框架。在实施过程中，流体域网格变形采用Laplace光顺法^[23]，结构域控制方程为：

$ {\boldsymbol{M}}\ddot {\boldsymbol{y}} + {\boldsymbol{C}}\dot {\boldsymbol{y}} + {\boldsymbol{Ky}} = {{\boldsymbol{F}}_{{\rm{ext}}}} $

(18)

式中， $\boldsymbol{\ddot y} $ 、 $\boldsymbol{\dot y} $ 和 $\boldsymbol{y} $ 分别为结构各自由度的加速度、速度和位移矩阵，M为质量矩阵，C为阻尼矩阵，K为刚度矩阵， ${\boldsymbol{F}_{{\rm{ext}}}}$ 为流体施加在结构上的外力矩阵。式（18）时间离散采用Newmark隐式求解方法^[24]。由于Newmark算法需给定n+1时刻外力矩阵后才能更新结构位移矩阵，而流体域在已知结构新位置后才能获得外力矩阵。因此，在算法实施过程中采用二阶外插格式预估n+1时刻 $\boldsymbol{F}_{{\rm{ext}}}^{n + 1}$ ：

$ {\boldsymbol{F}}_{{\rm{ext}}}^{n + 1} = 2{\boldsymbol{F}}_{{\rm{ext}}}^n - {\boldsymbol{F}}_{{\rm{ext}}}^{n - 1} $

(19)

综上，针对FSI的计算流程为：

Step1：式（19）预估n+1时刻外力矩阵；

Step2：Newmark格式计算n+1时刻位移矩阵y；

Step3：根据新时刻结构位移，采用Laplace方法更新流体域网格；

Step4：式（12）更新n+1时刻分布函数 ${\tilde f^{n + 1}}$ 。

当前ALE-DUGKS采用显式求解方法，推进过程中 $\Delta {t_{_{{\rm{CFD}}}}} = \Delta {t_{_{{\rm{CSD}}}}}$ ，每个时间步长内重复一次计算流程即可获得系统收敛解。此外，对于强迫运动的单向FSI问题，由于新时刻结构位移已知，忽略Step 1～2步即可。

2 算例验证 2.1 静止圆柱绕流算例

为了验证DUGKS方法并为后续算例提供对比数据，首先进行静止圆柱绕流模拟。离散速度模型采用D2Q9模型。参考文献[25，26]的算例设置，计算域见图1，此处D为圆柱直径，根据阻塞率5%布置上、下边界远场距离。计算域左侧边界和上、下边界设置为入口边界条件，边界外法线为 $ {\boldsymbol{n}_b} $ ；对于进入计算域的分布函数方向 $ {\boldsymbol{e}_{\alpha} } \cdot {\boldsymbol{n}_b} < 0 $ ，分布函数给定为平衡态；离开计算域的分布函数方向由内场分布函数插值获得。计算域右侧边界设置为出口边界条件，分布函数由内场插值获得。图2为计算网格，总网格单元为37506，其中壁面附近采用四边形贴体网格，最小网格尺度为D/256，其余为三角形网格。初始化来流速度为 ${u} = {U_\infty } = 0.05$ ， ${v} = 0$ ；初始密度 $\;{\rho _\infty } = 1.0$ 。雷诺数范围为Re = 60～150。升力系数 $C_L$ 定义为：

$ C_L = \frac{{2F_L}}{{{\rho _\infty }U_\infty ^2D}} $

(20)

式中F_L为圆柱所受升力。图3是雷诺数为60、100和150时，升力系数 $C_L$ 的时间发展历程。雷诺数较高时，经过较短的无量纲数值模拟时间即可发展为稳定的周期性流动，即出现卡门涡街现象。图4为无量纲涡脱落频率St对比，其中St定义为：

$ S t = fD/{U_\infty } $

(21)

式中f为自然涡脱落频率。本文与Prasanth^[25]和He^[26]的数值模拟结果以及Williamson^[27]的平行涡脱落模型吻合良好。在雷诺数Re = 60～80范围内数值结果略高于平行涡脱落模型，主要原因是随着雷诺数降低，黏性影响范围增大，远场边界条件对结果影响显著。减小阻塞率后，可明显改善数值结果和模型之间的差异。

2.2 Re = 100圆柱横向强迫振动算例

在静止圆柱绕流算例基础上，进一步模拟圆柱横向强迫振动算例以验证算法的运动边界模拟能力。计算参数与算例1相同，雷诺数Re = 100。圆柱y方向运动方程为：

$ \begin{array}{l}y = A\mathrm{sin}(2\text{π} {f}_{y}t),\\ A = {A}^{*}D\text{，}{f}_{y} = {f}^{*}{f}_{Re = 100}\end{array} $

(22)

式中，A为圆柱振幅，f_y为圆柱结构频率，f_{Re = 100}为静止圆柱绕流自然涡脱落频率，A^*为圆柱无量纲振幅，f ^*为与自然涡脱落频率的比值。在文献[28]中，Kumar等将圆柱涡脱落分为非锁频区、过渡区和锁频区。图5为各区分界线图，与Kumar等结果整体十分吻合。图6为五组A^*和f ^*组合下的升阻力系数时间发展历程和升力系数功率谱图，其中阻力系数C_D为将式（20）中 $ F_L $ 替换成 $ {F_D} $ 。当无量纲频率f ^*<1时，非锁频区（图6（a））和锁频区（图6（b））有清晰的分界线。在非锁频区，由于流体自然涡脱落频率和结构频率接近，升阻力系数出现类似“拍”现象，功率谱图中流动自然涡脱落频率占优且包含其他无规律频率信息；在锁频区，涡脱落频率锁定在结构频率，同时其他频率与主频呈现清晰的倍频现象。当无量纲频率f ^* > 1时，非锁频区和锁频区之间存在过渡区。在非锁频区和过渡区，升阻力系数同样出现“拍”现象（ 图6（c）和图6（d））。当流动自然涡脱落频率占优时，流动呈现非锁频现象；当结构自然频率占优时，流动则处在过渡区范围。对于功率谱图，非锁频区和过渡区除主频外，还包含其他无规律频率信息，锁频区其他频率信息则呈现清晰的倍频现象（图6（e））。

2.3 Re = 100圆柱自由振动算例

为验证ALE-DUGKS模拟流固耦合问题的能力，首先对Re = 100圆柱自由振动进行模拟。结构自由振动控制方程为x和y方向两自由度无阻尼振动方程，对应于式（18）中的质量矩阵M、刚度矩阵K和外力矩阵F_ext分别为：

$ \boldsymbol{M} = \left[ {\begin{array}{*{20}{c}} {{m^*}{m_f}}&0 \\ 0&{{m^*}{m_f}} \end{array}} \right] $

(23)

$ \boldsymbol{K} = \left[ {\begin{array}{*{20}{c}} {{m^*}{m_f}{{\left( {2\text{π} {f_x}} \right)}^2}}&0 \\ 0&{{m^*}{m_f}{{\left( {2\text{π} {f_y}} \right)}^2}} \end{array}} \right] $

(24)

$ {\boldsymbol{F}_{{\rm{ext}}}} = {\left[ {\begin{array}{*{20}{{c}}} {{F_D}}&{{F_L}} \end{array}} \right]^T} $

(25)

式中， ${m^*}$ 为圆柱截面面积内的流体和结构质量比值，取为10； ${m_f} = {\rho _\infty }\text{π} {D^2}/4$ 则为流体质量。 ${f_x} = {f_y}$ 为结构自然频率，取为 ${f_y} = {U_\infty }/\left( {D{U^*}} \right)$ ； ${U^*}$ 为无量纲折减速度； ${F _s} = 1/{U^*} = {f_y}D/{U_\infty }$ 为无量纲频率。该算例主要分析来流风速固定时，结构频率的变化对流致振动最大位移和锁频的影响。模拟过程中，在100个无量纲时间内，圆柱处在锁定状态，流场发展成周期性流动后释放圆柱。图7为U^* = 6.25时两个方向位移时间发展历程和收敛后的耦合位移，其中x和y为圆柱在两个方向的位移值。可以发现周期性非定常升力使得圆柱在y方向产生较大位移，非定常阻力则使圆柱在x方向运动到平衡位置后以较小振幅振动，且两方向耦合位移呈现类似“8”的结构；圆柱在其他折减速度时有类似现象。图8为圆柱y方向最大位移和涡致振动频率对比，其中y_max /D为无量纲最大位移，St = 0.166为静止圆柱绕流的无量纲涡脱落频率。本文与Singh^[29]、Zhang^[30]等数值结果吻合良好，主要差异在锁频和非锁频的过渡区间。图9为U^* = 4.0时y方向位移时间历程，与图7结果不同，此时流动处在非锁频状态，圆柱位移很小。图10则为流动处在锁频和非锁频的过渡状态，需要较长的数值模拟时间获得周期性振动结果。此外，数值模拟发现，阻塞率较小时，圆柱最大位移偏高，即远场距离对圆柱位移有压缩效应。这也是本文与文献[29]相同，取5%阻塞率的原因。

2.4 Re = 60～150圆柱自由振动算例

与Re = 100圆柱自由振动算例不同，该算例主要验证结构自然频率固定时来流风速变化对结构位移和频率的影响。结构参数仍为式（23）～式（25），此时无量纲频率给定为F_s = 16.6/Re，其中16.6使得Re = 100时结构无量纲频率约等于静止圆柱绕流无量纲涡脱落频率。图11为y方向最大位移和涡脱落频率对比，与Prasanth等^[25]的数值结果十分吻合，仅在锁频和非锁频的过渡区间有差异。主要原因是Prasanth等在计算过程中通过动态调节雷诺数（增加或减小）以分析风速的动态变化对过渡区流动机理的影响；本文主要为方法验证，忽略动态影响机理分析，计算中每给定一个雷诺数获得收敛结果后完成计算。对于y方向位移和升阻力系数，在非锁频和锁频区与算例2.3的Re = 100自由振动算例类似，但在过渡区较为复杂。图12为Re = 130的时间历程，经过频谱分析，当无量纲时间小于1800时，y方向位移不断增加，此时涡脱落频率中圆柱的自然涡脱落频率占优；当时间大于1800后，涡脱落频率锁定在结构自然频率，圆柱位移也收敛到稳定的周期性振动状态。

2.5 Re = 60圆柱横向强迫振动连续流和稀薄流对比

为验证算法的扩展能力，采用跨流域计算框架对Re = 60圆柱横向强迫振动进行数值模拟。跨流域计算中，克努森数Kn、马赫数Ma和雷诺数Re关系为^[31]：

$ Kn = \sqrt {\frac{\gamma }{\text{π} }} \frac{{\sqrt 2 \left( {5 - 2\omega } \right)\left( {7 - 2\omega } \right)}}{{15}}\frac{{Ma}}{{Re}} $

(26)

式中， $\gamma = 5/3$ ，为单原子气体比热比； $\omega = 0.5$ ，为传热指数。前述连续流算例根据LBM格子声速取值，当来流速度 ${U_\infty } = 0.05 $ 时Ma = 0.0866，则Re = 60时Kn = 2.382×10⁻³，处在（近）连续流范围。作为对比分析，连续流离散速度模型仍采用D2Q9模型，跨流域计算框架则采用式（5）的平衡态分布函数，并采用8×8高斯点作为离散速度点。式（22）为结构运动方程，并将 ${f_{Re = 100}}$ 替换为 ${f_{Re = 60}}$ ，即Re = 60时的自然涡脱落频率。图13为两组计算方法获得的升力系数时间发展历程对比。与Re = 100相同，（A^*，f ^*） = （0.025，0.9）时流动处在非锁频状态，（A^*，f ^*） = （0.1，0.9）时流动处在锁频状态。两种方法结果吻合良好，说明跨流域计算框架数值结果可收敛于连续流结果。此外，进一步模拟了Ma = 0.4的流动状态，此时Kn约为0.011，处于滑移流域。因流动具有可压缩性，除式（7）密度分布函数外，需额外求解能量分布函数h：

$ \frac{{\partial h}}{{\partial t}} + \left( {\boldsymbol{\xi} -\boldsymbol{v}} \right) \cdot \nabla h = - \frac{1}{\tau }\left( {h - {h^{{\rm{eq}}}}} \right) $

(27)

式中符号与式（7）相同，二维单原子h^eq和 ${f^{{\rm{eq}}}}$ 关系为：

$ {h^{{\rm{eq}}}} = RT{f^{{\rm{eq}}}} $

(28)

针对弱可压缩流动，式（7）和式（27）求解见文献[15]。离散速度采用28×28高斯点。Ma = 0.4时圆柱自然涡脱落频率St = 0.132，与Canuto等^[32]结果吻合，略低于Ma = 0.0866时的结果。图14为两组马赫数下升力系数时间发展历程对比，随着马赫数增加，稀薄程度增加，升力系数呈减小趋势。Canuto等^[32]采用宏观方法和无滑移边界分析了压缩性对静止圆柱绕流的流动特性影响，因方法的局限性无法考虑稀薄气体效应影响，数值结果在低雷诺数时存在一定偏差。但与本文静止圆柱和振动圆柱趋势一致，即Re = 60时马赫数对St影响较小，但最大升力系数降低。

2.6 Ma = 5.0圆柱横向强迫振动稀薄流算例

2.2～2.5节的算例验证了算法的低速跨流域运动边界求解能力。本文虽主要关注低速流动问题，但考虑到跨流域高速流动中也面临大量的运动边界问题，为验证算法的进一步拓展能力以及ALE-DUGKS的全流域、全速域求解能力，对Ma = 5.0圆柱横向强迫振动进行了数值模拟。克努森数取Kn = 0.1和1.0两组条件。根据文献[21]设置，来流气体为氩气， $\omega = 0.81$ （式（26）），自由来流速度和温度给定为1538.18 m/s和273 K，参考温度和参考速度则为 ${T_{{\text{ref}}}} = 273\;{\text{K}}$ 和 ${U_{{\text{ref}}}} = \sqrt {2R{T_{{\text{ref}}}}} = $ 337.0 m/s。在实际计算中无量纲密度和温度设置为 $\;{\rho _0} = 1.0$ 和 ${T_0} = 1.0$ ，无量纲速度为 ${U_0} = 4.56$ 。图15（a）为计算中采用的物理空间计算网格，网格量64×61，其中壁面第一层网格尺度在Kn = 0.1时为0.005D，在Kn = 1.0时为0.01D。离散速度空间采用图15（b）的非结构速度空间^[21]，总离散速度为3052，其中每个非结构网格控制体的中心坐标为式（6）中的微观粒子离散速度分量（积分点），控制体面积为积分权重。考虑到粒子速度主要集中在来流高速粒子和壁面附近的低速粒子，速度空间网格在相应位置进行了加密。经过算例测试，非结构速度空间网格技术相比于传统的用于高速稀薄流的Newton-Cotes积分法，计算效率提升约3～4倍，部分算例提升约1个量级^[21]。图16为静止圆柱绕流的表面压力和剪切力分布对比，与文献[33]的UGKS和DSMC方法数值结果吻合良好。从图中可以发现，当马赫数固定时，来流越稀薄，雷诺数越低，黏性影响范围越大，圆柱所受阻力也越高，这一结论与文献[34]吻合。本文结果中，当Kn = 1.0时阻力系数为1.92，Kn = 0.1时则阻力系数为1.52。

对于强迫振动状态，圆柱运动方程为：

$ y = {A^*}D\sin \Bigg(2\text{π} \frac{{{U_0}}}{{{U^*}}}\frac{1}{D}t\Bigg) $

(29)

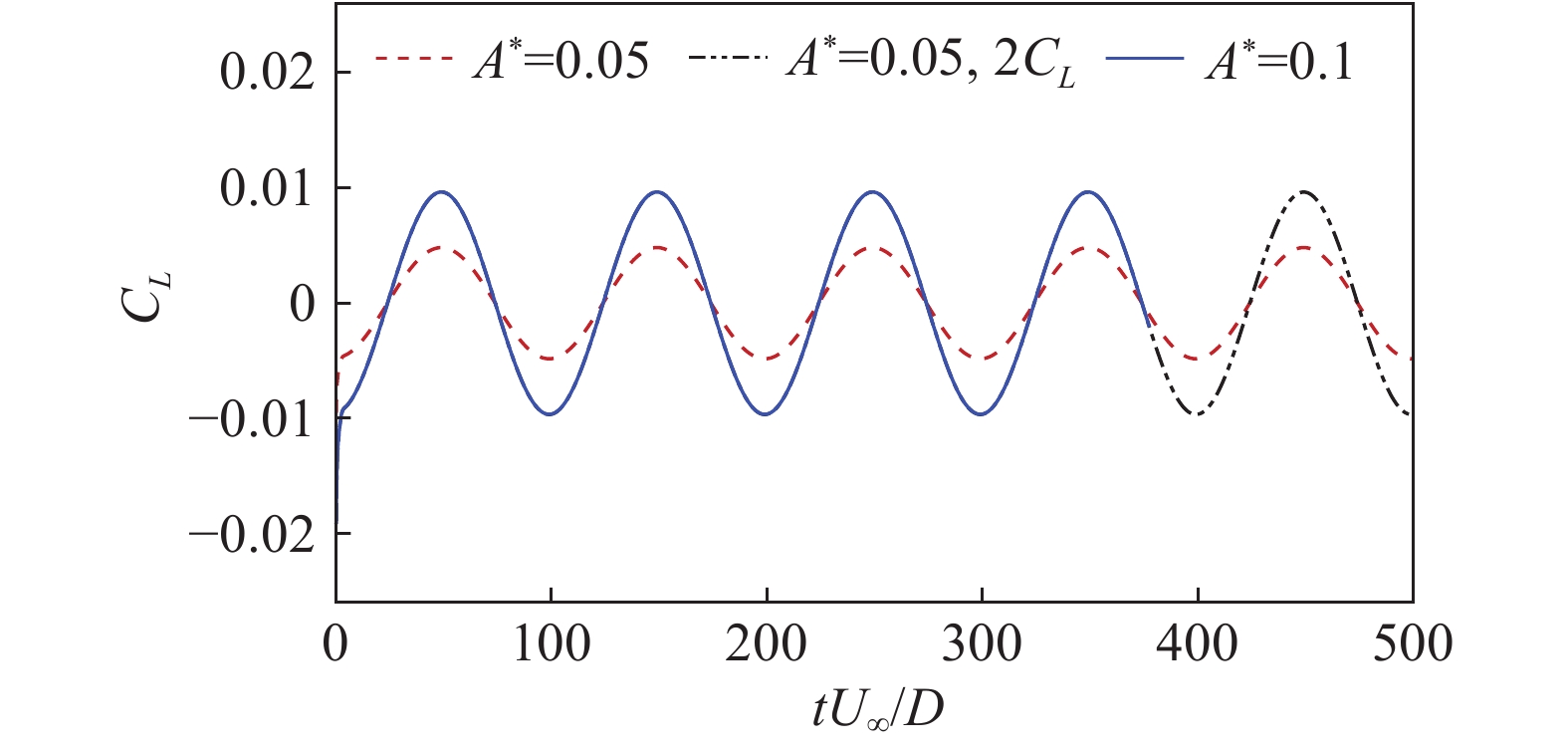
其中，A^*为圆柱无量纲振幅，U^* = 100为折减速度。图17为A^* = 0.05时的升力系数时间发展历程。由于振幅较小，振动频率较低，圆柱所受升力系数较小。此外，与静止圆柱绕流相同，马赫数固定时，来流越稀薄，升力越大。图18为Kn = 0.1、A^*分别取0.05和0.1时的升力系数时间发展历程对比。由于来流为稀薄流，圆柱表面无分离涡和涡脱落现象，流动呈现为附着流的未失稳状态，此时升力系数与振幅表现为线性增长关系。考虑到不同马赫数、克努森数、振幅A^*和折减速度U^*组合下的圆柱强迫振动流动分析超出了本文的讨论范围，课题组将会在接下来的论文中进行系统讨论。

3 结　论

本文在原始DUGKS基础上，耦合任意拉格朗日-欧拉方法和计算结构动力学，实现了可考虑稀薄气体效应的低速兼顾高速流动的流固耦合问题数值模拟框架。针对低速连续流域的圆柱强迫振动和自由振动两个典型算例，采用LBM中高效的D2Q9离散速度模型，该框架可获得与宏观方法一致的数值结果。鉴于DUGKS的全流域、全速域计算能力，更改离散速度模型后，即可具备模拟跨流域运动边界模拟能力。在算法实施方面，本文初步验证了显式ALE-DUGKS模拟流固耦合问题能力，未来可发展隐式格式，进一步提高其计算效率。在应用方面，考虑到稀薄气体效应对新型跨流域飞行器低雷诺数可压缩绕流场的显著影响^[35]，以及国内外较少开展低雷诺数可压缩圆柱绕流分析，本文后续将深入研究圆柱静、动态气动特性数值模拟。