2. 南方科技大学 工学院 力学与航空航天系,深圳 518055
2. Department of Mechanics and Aerospace Engineering, College of Engineering, Southern University of Science and Technology, Shenzhen 518055, China
诞生于格子气自动机[1]的格子Boltzmann方法(LBM),与传统直接求解宏观量的计算流体力学(CFD)方法相比,由于避开了Navier-Stokes方程非线性项的处理,且没有求解压力泊松方程这一繁重过程,使得LBM具有程序编制简单、并行计算效率高的优点[2],在湍流、多相流、多孔介质流动及渗流、颗粒流、微流动、气动声学等领域的模拟中得到了广泛应用[3-6]。早期的LBM离散模型都是基于半经验理论推导,其约束条件往往局限于满足质量和动量守恒方程,并以低马赫数假设为基础,能量方程无法正确还原,使得LBM方法只适用于等温低速弱可压流动成为了较普遍的观点[2,7]。
随着航空航天科技发展,高速流动的数值模拟在飞行器设计验证中起到越来越重要的作用[8],CFD领域涌现了多种可压缩流动的处理格式与方法,例如黎曼问题求解器和TVD格式[9]、用于高精度激波捕捉的WENO格式[10],以及计算激波-湍流相互作用的Compact-WENO混合格式[11];这些数值方法在理论研究和工程应用领域都取得了可观的成果[12-13]。不可否认的是,尽管传统CFD方法已经过了多年的发展和完善,在具体问题中要同时准确解析流动小尺度结构和激波间断,实现模拟方法的精度、耗散、稳定性和计算效率等因素的最佳平衡,仍然存在着诸多挑战[14]。另一方面,工程传热流动问题中,高效换热器普遍具有形状复杂的管腔结构,处理复杂几何边界、并兼顾精度和计算效率也对流动模拟方法提出了更高的要求。
LBM源自于气体动理学理论,对气体运动描述的物理背景清晰,且在处理复杂几何外形、特别是多孔结构时具有独特优势,理论上LBM在模拟可压缩流动和复杂结构的传热流动问题方面拥有巨大潜力。研究者们对传统LBM模型进行了诸多改进,以期突破LBM在计算可压缩流动和热力学流动时的局限性,其基本思想是增加LBM离散模型的自由度和约束条件以还原能量守恒方程。改进方案大致分为两类,一类是额外增加一个能量(内能或总能)分布函数以满足能量方程约束[15-20],称之为双分布函数模型。然而,根据气体动理学理论,气体的密度、动量和能量都是气体分子热运动的统计结果,其动力学状态也应当只需由单一的分布函数描述(对于单组分、单原子气体而言),因此引入能量的分布函数必然需要与密度分布函数进行耦合,该耦合关系带有一定的经验性,在增加复杂度的同时也对模型的广泛适用性带来了一定的限制。另一种方案是构造更高阶的单一平衡态分布函数,在平衡态分布函数中引入更多的待定系数,并使用更多的离散速度点,通过增加离散点数量(未知数个数)的方案来满足额外的能量方程约束,典型做法是在每个离散速度方向上使用2个以上的速度大小模态,称之为多层速度模型。与双分布函数模型类似,多层速度模型在能量方程约束条件、分布函数的形式和离散速度点选取上也具有一定的经验性,自Qian[21]和Alexander等[22]提出以来,出现了形式多样的方案且各有优缺点。
多层速度模型按平衡态分布函数展开式的构造方法主要分为三类:第一类遵循传统LBM模型的思路,将Maxwell-Boltzmann分布函数泰勒展开至更高阶数[23-26]。第二类由Shan等[27]提出,他们发展了Grad[28-29]的早期工作思路,认为平衡态分布函数可由Hermite多项式级数展开,只需要将展开级数保留足够的截断阶数,即可分别还原到Navier-Stokes方程的质量、动量和能量方程,而密度、动量、能量等宏观统计量均可由Hermite展开式的各阶系数组合表达,并在进一步的工作中阐明传统等温弱可压LBM是Hermite多项式模型的低阶形态,且离散速度是五阶精度Gauss-Hermite积分公式的积分点的事实[30]。第三类由Xu等[31]提出,其基本思想是不预设平衡态分布函数的展开形式,而是将离散模型还原质量、动量和能量方程的约束条件视为平衡态分布函数离散点的线性代数方程组,直接求解方程组得出离散分布函数。
由于Maxwell-Boltzmann分布函数的各阶Hermite多项式展开是确定的,Gauss-Hermite积分公式的积分点也具有确定性,使得上述第二类基于Hermite多项式构造的多层速度模型不依赖于经验而具有普适性。然而,由于该模型的数学基础理论较为晦涩,各部分细节的阐述散落于跨度接近20年的多篇文献中,使得科研工作者对该模型进行深入理解存在一定的困难。为了弥补这个缺点,使读者连贯、系统地理解Hermite多项式模型的构造原理和方法,同时也在与其他LBM模型的对比中全面认识各类方案的优劣,我们对Hermite多项式模型重新梳理归纳的同时,也一并列出了其他多层速度模型的构造思想,作为LBM多层速度模型的一个简要总结性工作。
本文的各部分内容为:第1节为Boltzmann方程和LBM的基础理论。由于多层速度模型起源于经典的等温弱可压LBM,且经典LBM模型的很多思想在多层速度模型中仍然适用,故第2节对等温弱可压LBM进行简单介绍。第3节介绍各类多层速度LBM模型(除Hermite多项式模型以外)的基本思想。第4节详细描述Hermite多项式模型的理论和平衡态分布函数的具体形式,以及基于Gauss-Hermite积分公式的离散速度模型及其构造方法。第5节对LBM和传统CFD方法的结合进行了简要介绍,例如LBM有限差分、LBM有限体积和LBM有限元方法。第6节对现有的多层速度模型存在的问题进行总结,并提出未来需要完善和发展的方向。
1 Boltzmann-BGK方程我们考虑D维(D = 1、2、3)空间中的气体,其中气体分子的位置空间坐标为x,速度为
| $ \rho ({{\boldsymbol{x}}},t) = \int {f\;{\text{d}}{\boldsymbol\xi }} $ | (1) |
| $ {{\boldsymbol{u}}}({{\boldsymbol{x}}},t) = \frac{1}{\rho }\int {f{\boldsymbol\xi }\;{\text{d}}{\boldsymbol\xi }} $ | (2) |
| $ e({{\boldsymbol{x}}},t) = \frac{1}{\rho }\int {f{\mkern 1mu} \frac{{|{\boldsymbol\xi } - {{\boldsymbol{u}}}{|^2}}}{2}\;{\text{d}}{\boldsymbol\xi }} $ | (3) |
以上各式中积分范围为
| $ \int {f{\xi _i}{\xi _j}{\text{d}}{\boldsymbol\xi = }\rho {u_i}{u_j} + } \int {f{v_i}{v_j}{\text{d}}{\boldsymbol\xi }} = \rho {u_i}{u_j} - {P_{ij}} $ | (4) |
| $ \begin{split} \frac{1}{2}\int {f{\xi _i}{\xi _j}{\xi _j}{\text{d}}{\boldsymbol\xi}=}&{\rho E{u_i} - } {P_{ij}}{u_j} + \frac{1}{2}\int {f{v_i}{v_j}{v_j}{\text{d}}{\boldsymbol\xi }} \\ =&\rho E{u_i} - {P_{ij}}{u_j} + {q_i} \end{split} $ | (5) |
其中:
| $ {P_{ij}} = - \int {f{v_i}{v_j}{\text{d}}{\boldsymbol\xi }} ,\;\;{q_i} = \frac{1}{2}\int {f{v_i}{v_j}{v_j}{\text{d}}{\boldsymbol\xi }} $ | (6) |
分别为动量输运项(切应力)和能量扩散项(热流),
根据分子动理学理论和内能e的定义(式(3)),流体的压强p定义为:
| $ p = - \frac{1}{D}{P_{ii}} = \frac{1}{D}\int {fv_i^2{\text{d}}{\boldsymbol\xi }} = \frac{2}{D}\rho e $ | (7) |
能均分定理可表达为:
| $ e = \frac{{D{k_B}T}}{{2{m_M}}} = \frac{D}{2}\theta $ | (8) |
其中,T为气体温度,
结合式(7)与式(8)可得到理想气体状态方程:
| $ p = \rho \frac{{{k_B}}}{{{m_M}}}T = \rho \theta $ | (9) |
Boltzmann-BGK方程可表达为:
| $ \frac{{\partial f}}{{\partial t}} + {\boldsymbol{\xi} } \cdot {\nabla} f + \frac{{{\boldsymbol{F}}}}{\rho } \cdot {\nabla _{\boldsymbol{\xi}} }f = \varOmega = - \frac{{f - {f^{(0)}}}}{\tau } $ | (10) |
其中,F为单位体积流体所受的外力,
| $ {f^{(0)}}({{\boldsymbol{x}}},{\boldsymbol\xi },t) = \frac{\rho }{{{{(2\text{π} \theta )}^{D/2}}}}{{\text{e}}^{ - {{({\boldsymbol\xi } - {u})}^2}/(2\theta )\;}} $ | (11) |
为了方便之后的分析,我们定义参考尺度
| $ \begin{split}& V_0^* = 1 \\& {f^*} = fV_0^D/{\rho _0} \\& {{\boldsymbol\xi }^*} = {\boldsymbol\xi }/{V_0} \\& {{{\boldsymbol{x}}}^*} = {{\boldsymbol{x}}}/{L_0} \\& {{{\boldsymbol{u}}}^*} = {{\boldsymbol{u}}}/{V_0} \\& {{{\boldsymbol{v}}}^*} = {{\boldsymbol{v}}}/{V_0} \\& {{{\boldsymbol{F}}}^*} = {{\boldsymbol{F}}}{L_0}/({\rho _0}V_0^2) \\& {t^*} = t{L_0}/{V_0} \\& {\theta ^*} = \theta /V_0^2 \\& {p^*} = p/({\rho _0}V_0^2) \\& {\rho ^*} = \rho /{\rho _0} \end{split} $ | (12) |
由于无量纲化的Boltzmann-BGK方程和平衡态分布函数分别与式(10)和式(11)形式上完全一致。因此后文无明确标识时,各物理量均为无量纲量,并略去星号标识。对于等温流动,如果取参考温度
对
| $ \int {{f^{(0)}}{\text{d}}{\boldsymbol\xi = }\rho } $ | (13) |
| $ \int {{f^{(0)}}{\boldsymbol\xi }{\text{d}}{\boldsymbol\xi }} = \rho {{\boldsymbol{u}}} $ | (14) |
| $ \int {{f^{(0)}}{\xi _i}{\xi _j}{\text{d}}{\boldsymbol\xi }} = \rho {u_i}{u_j} + \rho \theta {\delta _{ij}} $ | (15) |
| $ \begin{split}& \int {{f^{(0)}}{\xi _i}{\xi _j}{\xi _k}{\text{d}}{\boldsymbol\xi }} = \rho {u_i}{u_j}{u_k} +\\&\qquad \quad \rho \theta ({u_i}{\delta _{jk}} + {u_j}{\delta _{ik}} + {u_k}{\delta _{ij}}) \end{split} $ | (16) |
其中
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}} = 0 $ | (17) |
| $ \frac{{\partial \rho {u_i}}}{{\partial t}} + \frac{{\partial (\rho {u_i}{u_j})}}{{\partial {x_j}}} = \frac{{\partial {P_{ij}}}}{{\partial {x_j}}} $ | (18) |
| $ \frac{{\partial (\rho E)}}{{\partial t}} + \frac{{\partial (\rho {u_i}E)}}{{\partial {x_i}}} = \frac{{\partial ({P_{ij}}{u_j})}}{{\partial {x_i}}} - \frac{{\partial {q_i}}}{{\partial {x_i}}} $ | (19) |
可以看到,式(17)~式(19)已经十分接近Navier-Stokes方程。LBM中选定f的离散模型,将决定
等温弱可压LBM模型是最早提出的LBM模型,并在不可压流动计算中得到广泛应用。严格意义上,包括气体、液体在内的所有流体都具有可压缩性,例如液体的压缩性可用Tait方程描述[34]。传统求解压力泊松方程的不可压流计算方法将导致无限大声速,也就是压力扰动的无限速度传播,这与物理事实是相悖的。采用弱可压方法计算“不可压流动”理论上更加接近物理本质。本节对等温弱可压LBM模型进行简要陈述,这也将成为多层速度LBM模型修正和拓展的基础。
2.1 速度空间离散模型LBM的核心是将连续的Boltzmann方程离散化,即用速度空间离散的分布函数
将平衡态分布函数
| $ \begin{split} {f}^{(0)} =& \frac{\rho }{{(2\text{π} \theta )}^{D/2}}{\text{e}}^{-\text{}\text{}\text{}\text{}\frac{{(\xi -u)}^{2}}{2\theta }}\\ =& \frac{\rho }{{(2\text{π} \theta )}^{D/2}}{\text{e}}^{-\frac{{\xi}^{2}}{2\theta }}\mathrm{exp}\left(\frac{\xi\cdot {\boldsymbol{u}}}{\theta }-\frac{{u}^{2}}{2\theta }\right)\\ =& \frac{\rho }{{(2\text{π} \theta )}^{D/2}}{\text{e}}^{-\frac{{\xi}^{2}}{2\theta }}\left[1+\frac{\xi\cdot {\boldsymbol{u}}}{\theta }+\frac{{\left(\xi\cdot {\boldsymbol{u}}\right)}^{2}}{2{\theta }^{2}}-\frac{{{u}}^{2}}{2\theta }\right] \end{split}$ | (20) |
将
| $ f_a^{(0)} = \rho {w_a}\left[ {1 + \frac{{{{\boldsymbol\xi }_a} \cdot {{\boldsymbol{u}}}}}{\theta } + \frac{{{{\left( {{{\boldsymbol\xi }_a} \cdot {{\boldsymbol{u}}}} \right)}^2}}}{{2{\theta ^2}}} - \frac{{{{{\boldsymbol{u}}}^2}}}{{2\theta }}} \right] $ | (21) |
其中,
| $ \rho = \sum\limits_{a = 1}^d {f_a^{(0)} = \int {{f^{(0)}}{\mkern 1mu} {\text{d}}{{\boldsymbol{\xi}} }} } $ | (22) |
| $ \rho {{\boldsymbol{u}}} = \sum\limits_{a = 1}^d {f_a^{(0)}{{{\boldsymbol{\xi}} }_a} = \int {{f^{(0)}}{{\boldsymbol{\xi}} }{\mkern 1mu} {\text{d}}{{\boldsymbol{\xi}} }} } $ | (23) |
| $ \rho {u_i}{u_j} + \rho \theta {\delta _{ij}} = \sum\limits_{a = 1}^d {f_a^{(0)}{\xi _{ai}}{\xi _{aj}} = \int {{f^{(0)}}{\xi _i}{\xi _j}{\mkern 1mu} {\text{d}}{{\boldsymbol{\xi}} }} } $ | (24) |
将式(21)代入式(22)~式(24),可得到关于
| $ \sum\limits_{a = 1}^d {{w_a} = 1} $ | (25) |
| $ \sum\limits_{a = 1}^d {{w_a}{\xi _{ai}}{\xi _{aj}} = \theta {\delta _{ij}}} $ | (26) |
| $ \sum\limits_{a = 1}^d {{w_a}{\xi _{ai}}{\xi _{aj}}{\xi _{ak}}{\xi _{al}} = {\theta ^2}({\delta _{ij}}} {\delta _{kl}} + {\delta _{ik}}{\delta _{jl}} + {\delta _{il}}{\delta _{jk}}) $ | (27) |
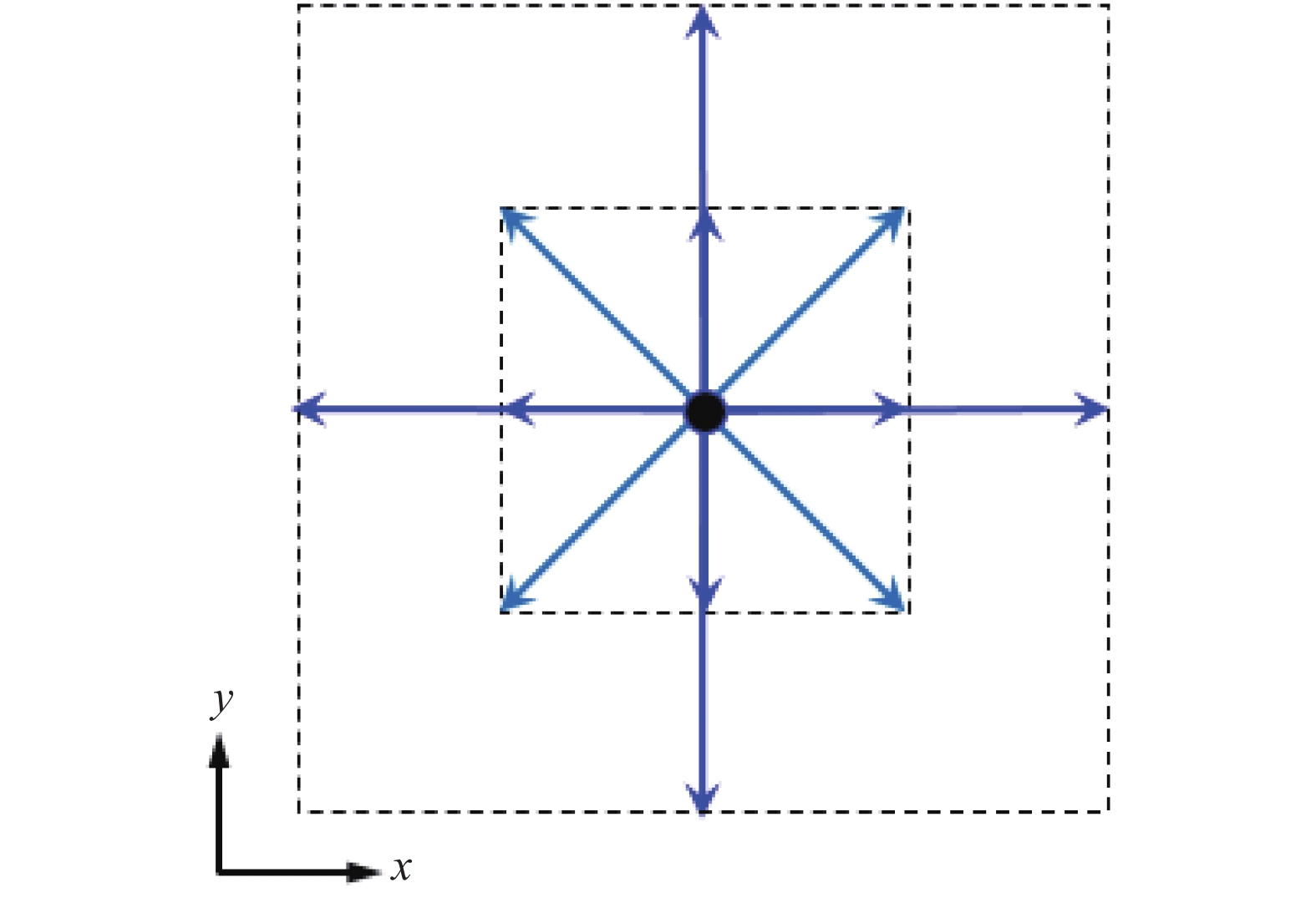
此时我们根据经验预设对称性的离散速度模型,例如图1所示的D1Q3(

|
图 1 等温弱可压流动LBM的一维和二维离散速度模型 Fig.1 One- and two-dimensional discrete velocity models for isothermal weakly compressible flows |
在获得离散速度
| $ \begin{split}& {f_a}({{\boldsymbol{x}}} + {{\boldsymbol\xi }_a}\Delta t,t + \Delta t) - {f_a}({{\boldsymbol{x}}},t) = \int_t^{t + \Delta t} {{\varOmega _a}({{\boldsymbol{x}}},t){\text{d}}t} \end{split} $ | (28) |
使用梯形积分公式达到二阶时间精度,式(28)可表达为:
| $ \begin{split}&\quad {f_a}({{\boldsymbol{x}}} + {{\boldsymbol\xi }_a}\Delta t,t + \Delta t) - {f_a}({{\boldsymbol{x}}},t) \\& = \frac{{\Delta t}}{2}[{\varOmega _a}({{\boldsymbol{x}}},t) + {\varOmega _a}({{\boldsymbol{x}}} + {{\boldsymbol\xi }_a}\Delta t,t + \Delta t)] \\& = - \frac{{\Delta t}}{{2\tau }}[{f_a}({{\boldsymbol{x}}},t) - f_a^{(0)}({{\boldsymbol{x}}},t) + \\&\quad {f_a}({{\boldsymbol{x}}} + {{\boldsymbol\xi }_a}\Delta t,t + \Delta t) - f_a^{(0)}({{\boldsymbol{x}}} + {{\boldsymbol\xi }_a}\Delta t,t + \Delta t)] \end{split} $ | (29) |
为使得式(29)变为显式方法,定义中间时刻的分布函数[16]:
| $ {\overline f _a} = {f_a} + \frac{{\Delta t}}{{2\tau }}({f_a} - f_a^{(0)}) $ | (30) |
则式(29)变为:
| $ \begin{split}& {\overline f _a}({{\boldsymbol{x}}} + {{\boldsymbol\xi }_a}\Delta t,t + \Delta t) - {\overline f _a}({{\boldsymbol{x}}},t) = - \frac{{\Delta t}}{{\bar \tau }}[{\overline f _a}({{\boldsymbol{x}}},t) - f_a^{(0)}({{\boldsymbol{x}}},t)] \end{split} $ | (31) |
其中:
| $ \bar \tau = \tau + \Delta t/2 $ | (32) |
使用Chapman-Enskog展开分析,并对离散速度模型和平衡态分布函数添加额外约束条件:
| $ \begin{split} \sum\limits_{a = 1}^d {f_a^{(0)}{\xi _{ai}}{\xi _{aj}}{\xi _{ak}} =}& {\int {{f^{(0)}}{\xi _i}{\xi _j}{\mkern 1mu} {\xi _k}{\mkern 1mu} {\text{d}}{\boldsymbol\xi }} - \rho {u_i}{u_j}{u_k}} \\= & \rho \theta ({u_i}{\delta _{jk}} + {u_j}{\delta _{ik}} + {u_k}{\delta _{ij}}) \end{split} $ | (33) |
可证明式(31)恢复了Navier-Stokes方程的质量和动量方程[33,36],且流体的运动学黏性系数为:
| $ \nu = \frac{p}{\rho }\Bigg(\bar \tau - \frac{{\Delta t}}{2}\Bigg) $ | (34) |
需要注意的是,由于约束条件式(33)成立的前提是u的三阶量可忽略,因此Chapman-Enskog展开也只能在忽略
常用的D1Q3和D2Q9等离散速度模型中,
| $ f_a^{(0)} = \rho {w_a}\left[ {1 + \frac{{{\boldsymbol{c}_a} \cdot {{\boldsymbol{u}}'}}}{{c_s^2\theta }} + \frac{{{{\left( {{\boldsymbol{c}_a} \cdot {{\boldsymbol{u}}'}} \right)}^2}}}{{2c_s^4{\theta ^2}}} - \frac{{{{\boldsymbol{u}}}{{'}^2}}}{{2c_s^2\theta }}} \right] $ | (35) |
相应于归一化速度,我们定义归一化时间
| $ {f}_{a}^{(0)} = \rho {w}_{a}\left[1+\frac{\boldsymbol{c}_{a}\cdot {\boldsymbol{u}}}{{c}_{s}^{2}}+\frac{{\left(\boldsymbol{c}_{a}\cdot {\boldsymbol{u}}\right)}^{2}}{2{c}_{s}^{4}}-\frac{{{\boldsymbol{u}}}^{2}}{2{c}_{s}^{2}}\right] $ | (36) |
相应的无量纲时间和空间离散式也写为:
| $ \begin{split}& {\bar f _a}({{\boldsymbol{x}}} + {\boldsymbol{c}_a},t + 1) - {\bar f _a}({{\boldsymbol{x}}},t) = - \frac{1}{{\bar \tau }}\big[{\bar f _a}({{\boldsymbol{x}}},t) - f_a^{(0)}({{\boldsymbol{x}}},t)\big] \end{split} $ | (37) |
其中:
| $ \bar \tau = \tau + 1/2 $ | (38) |
相应的无量纲黏性系数为:
| $ \upsilon = c_s^2\Bigg(\bar \tau - \frac{1}{2}\Bigg) $ | (39) |
| $ \rho = \sum\limits_{a = 1}^d {{f_a}} $ | (40) |
| $ {{\boldsymbol{u}} = }\frac{1}{\rho }\sum\limits_{a = 1}^d {{f_a}{{{\boldsymbol{c}}}_a}} $ | (41) |
式(40)~式(41)的合理性将在第4节详细说明。
3 多层速度LBM模型从第2节可以看到,等温弱可压流动LBM模型,其离散速度在每个方向都只有一个值(分布函数信息只传播到相邻的网格点),因此称之为单层速度模型。推导该模型时,只约束了离散模型的质量、动量和动量输运量,故无法准确还原能量方程。受此启发,业内学者开始对离散模型施加能量相关(
Qian[21]和Alexander等[22]分别在1993年提出了最早的多层速度模型。他们均指出,
| $ \begin{split} f_{pa}^{(0)} =& \rho \big[{A_p} + {B_p}{{\boldsymbol\xi }_a} \cdot {{\boldsymbol{u}} + }{C_p}{({{\boldsymbol\xi }_a} \cdot {{\boldsymbol{u}}})^2} + {D_p}{u^2} { + } \\& {E_p}{({{\boldsymbol\xi }_a} \cdot {{\boldsymbol{u}}})^3} + {F_p}{u^2}{{\boldsymbol\xi }_a} \cdot {{\boldsymbol{u}}}\big] \end{split} $ | (42) |
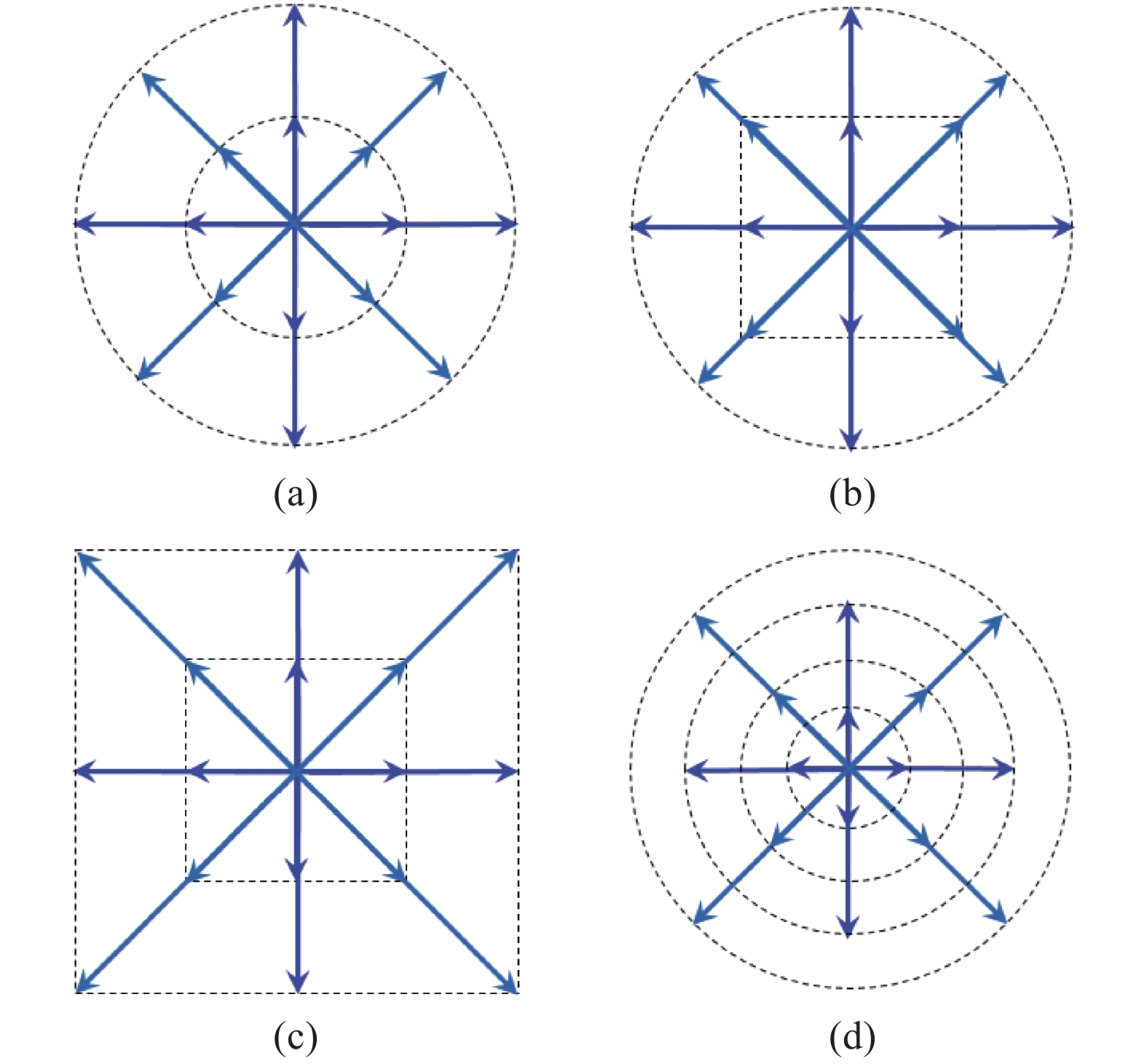
其中,p = 0,1,2为预设离散速度模型的网格层数,p = 0为中心网格,p = 1,2为中心周围第1、第2层网格;a = 1, 2, 3,···m为该层网格上的离散点编号。相应的二维离散速度模型D2Q13如图2~图3所示。
对
| $ {q_i} = \frac{1}{2}\sum\limits_{p,a}^{} {{f_{pa}}} {({\xi _{paj}} - {u_j})^2}({\xi _{pai}} - {u_i}) $ | (43) |
在Chapam-Enskog展开中,
Chen等[23]认为,Qian和Alexander等提出的模型,在还原Navier-Stokes的能量方程后会额外多出非线性误差项
| $ \boldsymbol{T}_{pk{\alpha _1}{\alpha _2}{\alpha _2} \cdots {\alpha _n}}^{(n)} = \sum\limits_{i = 1}^m {{\xi _{pki{\alpha _1}}}} {\xi _{pki{\alpha _2}}}{\xi _{pki{\alpha _3}}} \cdots {\xi _{pki{\alpha _n}}} $ | (44) |
其中:(p,k)为组编号,代表该组离散速度的大小均为
| $ \begin{split} f_{pka}^{(0)} =& {A_{pk}} + {M_{pk}}{{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}} + }{J_{pk}}{({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})^2} + \\& {G_{pk}}{u^2}{ + }{H_{pk}}{({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})^3} + {Q_{pk}}{u^2}{{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}} { + } \\& {R_{pk}}{u^2}{({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})^2} + {S _{pk}}{u^4} \end{split} $ | (45) |
对
| $ \begin{split} \sum\limits_{p,k,a}^{} {f_{pka}^{(0)}{\xi _{ai}}{\xi _{aj}}{\xi _{ak}}} =& \int {{f^{(0)}}{\xi _i}{\xi _j}{\mkern 1mu} {\xi _k}{\mkern 1mu} {\text{d}}{\boldsymbol\xi }} \\ =& \rho {u_i}{u_j}{u_k} + \rho \theta ({u_i}{\delta _{jk}} + {u_j}{\delta _{ik}} + {u_k}{\delta _{ij}}) \end{split} $ | (46) |
此时离散模型与连续的
| $ \begin{split}& \sum\limits_{p,k,a}^{} {f_{pka}^{(0)}\xi _a^2{\xi _{ai}}{\xi _{aj}}} = \rho \left[ {\frac{{4(D + 2)}}{{{D^2}}}} \right.{e^2}{\delta _{ij}} +\\&\qquad \frac{2}{D}e{u^2}{\delta _{ij}} + \left. {\frac{{2(D + 4)}}{D}e{u_i}{u_j} + {u^2}{u_i}{u_j}} \right] \end{split} $ | (47) |
在以上约束条件下,预设一维多层速度模型1D5V,其离散点为
Watari和Tsutahara的计算试验发现[24-25],Chen等的模型在计算热流和可压缩问题时仍然不能令人满意。例如在计算平板Couette流动时,一旦松弛时间
| $ \begin{split} f_{pka}^{(0)} =& \rho {F_{pk}}\left[ {\left( {1 - \frac{D}{{4e}}{u^2} + \frac{{{D^2}}}{{32{e^2}}}{u^4}} \right)} \right. \\& + \frac{D}{{2e}}\left( {1 - \frac{D}{{4e}}{u^2}} \right){{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}} + }\frac{{{D^2}}}{{8{e^2}}}\left( {1 - \frac{D}{{4e}}{u^2}} \right){({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})^2} \\& + \frac{{{D^3}}}{{48{e^3}}}{({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})^3} + \left. {\frac{{{D^4}}}{{384{e^4}}}{{({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})}^4}} \right] \end{split} $ | (48) |
另一种是在Chen等的模型,即式(45)中再添加
| $ \begin{split} f_{pka}^{(0)} =& \rho [{A_{pk}} + {M_{pk}}{{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}} + }{J_{pk}}{({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})^2} \\& + {G_{pk}}{u^2}{ + }{H_{pk}}{({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})^3} + {Q_{pk}}{u^2}{{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}} \\& + {R_{pk}}{u^2}{({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})^2} + {S _{pk}}{u^4} + {T_{pk}}{({{\boldsymbol\xi }_{pka}} \cdot {{\boldsymbol{u}}})^4}] \end{split} $ | (49) |
需要说明的是,在Watari和Tsutahara[25]的原文中,将

|
图 5 Watari-Tsutahara二维多层速度模型[24-25] Fig.5 Two-dimensional discrete velocity model of Watari-Tsutahara[24-25] |
本小节之前介绍的几类多层速度模型,事实上都是基于单原子气体动理学理论,这些模型会导致还原的气体比热比为固定值,不适用于双原子和多原子分子气体。为了弥补这一缺陷,Kataoka和Tsutahara提出[26],以
| $ \rho (b{k_B}T/{m_M} + {u^2}) = \sum\limits_{a = 1}^d {{f_a}(\xi _a^2 + \eta _a^2)} $ | (50) |
对离散速度和
| $ \rho (b{k_B}T/{m_M} + {u^2}) = \sum\limits_{a = 1}^d {f_a^{(0)}(\xi _a^2 + \eta _a^2)} $ | (51) |
| $ \rho {u_i}{u_j}{u_k} + \rho \theta ({u_i}{\delta _{jk}} + {u_j}{\delta _{ik}} + {u_k}{\delta _{ij}}) = \sum\limits_{a = 1}^d {f_a^{(0)}{\xi _{ai}}{\xi _{aj}}{\xi _{ak}}} $ | (52) |
| $ \rho [(b + 2){k_B}T/{m_M} + {u^2}]{u_i} = \sum\limits_{a = 1}^d {f_a^{(0)}(\xi _a^2 + \eta _a^2)} {\xi _{ai}} $ | (53) |
| $ \begin{split}& \rho \Big\{ (b + 2){({k_B}T/{m_M})^2}{\delta _{ij}} + \big[(b + 4){u_i}{u_j} + {u^2}{\delta _{ij}}\big]{k_B}T/{m_M} \\&\qquad + {u^2}{u_i}{u_j}\Big\} = \sum\limits_{a = 1}^d {f_a^{(0)}(\xi _a^2 + \eta _a^2)} {\xi _{ai}}{\xi _{aj}} \\[-12pt] \end{split}$ | (54) |
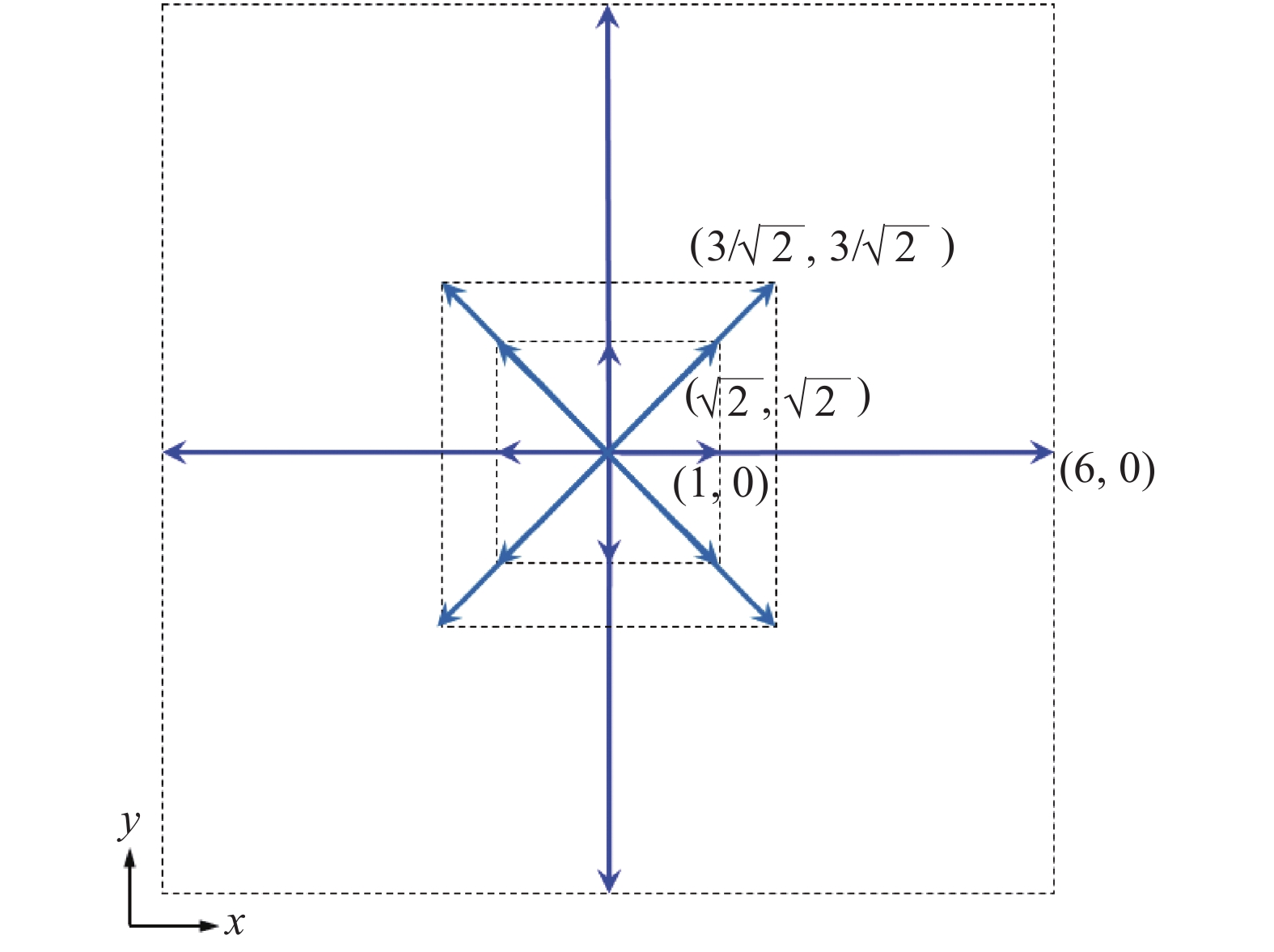
Kataoka和Tsutahara给出了二维情况下一个16点离散速度模型,如图6所示。而
| $ {\eta }_{a}/{c}_{s} = \Bigg\{\begin{array}{l}5/2,\;\;\;1\leqslant a\leqslant 4\\ 0,\;\;\;\;\;\;\;5\leqslant a\leqslant 16\end{array} $ | (55) |
|
图 6 Kataoka-Tsutahara[26]二维多层速度模型,图中的坐标代表离散速度点 |
其
| $ \begin{split} f_a^{(0)} =& \rho \big[{A_{0a}} + {A_{1a}}T + {A_{2a}}{T^2} + ({A_{3a}} + {A_{4a}}T)u_a^2 + \\& {A_{5a}}{(u_a^2)^2} + ({B_{0a}} + {B_{1a}}T + {B_{2a}}{u^2}){{\boldsymbol\xi }_{a}} \cdot {{\boldsymbol{u}}} + \\& ({D_{0a}} + {D_{1a}}T + {D_{2a}}{u^2}){({{\boldsymbol\xi }_{a}} \cdot {{\boldsymbol{u}}})^2} + {E_a}{({{\boldsymbol\xi }_{a}} \cdot {{\boldsymbol{u}}})^3}\big] \end{split} $ | (56) |
根据约束条件可求出
Xu等[31,38-39]则在Kataoka-Tsutahara模型的基础上,发展了离散Boltzmann方法(DBM)。传统多层速度模型往往先预设含待定系数的平衡态分布函数展开形式,根据约束条件求得待定系数,再将离散速度点代入
| $ {{{\boldsymbol{f}}}^{(0)}} = {(f_1^{(0)},f_2^{(0)},f_3^{(0)}, \cdots ,f_I^{(0)})^{\text{T}}} $ | (57) |
将约束条件的等式左边部分视为方程组的右端项向量
| $ C{{\boldsymbol{f}}}^{(0)} = {{\boldsymbol{M}}} $ | (58) |
求解方程组即可得到分布函数的离散形式
从第3节的介绍可以看出,大部分多层速度模型还是沿袭了单层速度模型“预设平衡态分布函数离散形式—预设离散速度模型—待定系数法求解”的思路。这种思路可以针对每一类特定问题都构造相对优化的多层速度模型,但经验性较强,对于开始接触多层速度模型的学者而言,面对种类繁多的离散模型、平衡态分布函数形式和约束条件,如何选择最优方案往往无所适从;即便获得了对某一问题的优化组合,当流动参数改变后,计算结果不一定同样令人满意,无法保证模型的普适性。
Shan等[27,30]在Grad[28-29]工作的基础上,发展了Hermite多项式模型,该模型基于Hermite多项式级数展开的数学性质,使平衡态分布函数的展开形式和离散速度模型都不再依赖于经验而具有确定性,且可以证明单层速度模型事实上是多层速度模型的低阶形态。这正是本节将详述的内容。
参照Grad的定义,D维空间的n阶Hermite多项式定义为n阶张量:
| $ \boldsymbol{H}_{{i_1}{i_2} \cdots {i_n}}^{(n)}({\boldsymbol\xi }) = \frac{{{{( - 1)}^n}}}{{\omega ({\boldsymbol\xi })}}\nabla _{{i_1}{i_2} \cdots {i_n}}^n\omega ({\boldsymbol\xi }) $ | (59) |
其中:
| $ \nabla _{{i_1}{i_2} \cdots {i_n}}^n = \frac{\partial }{{\partial {\xi _{{i_1}}}}}\frac{\partial }{{\partial {\xi _{{i_2}}}}} \cdots \frac{\partial }{{\partial {\xi _{{i_n}}}}} $ | (60) |
| $ \omega ({\boldsymbol\xi }) = \frac{1}{{{{(2\text{π} )}^{D/2}}}}\exp \left( { - \frac{{{\boldsymbol\xi } \cdot {\boldsymbol\xi }}}{2}} \right) $ | (61) |
不同阶数之间的Hermite多项式之间有递推关系:
| $ {\xi _i}\boldsymbol{H}_{{i_1}{i_2} \cdots {i_n}}^{(n)} = \boldsymbol{H}_{{i_1}{i_2} \cdots {i_n}i}^{(n + 1)} + \sum\limits_{k = 1}^n {{\delta _{{i_k}i}}\boldsymbol{H}_{{i_1}{i_2} \cdots {i_{k - 1}}{i_{k + 1}} \cdots {i_n}}^{(n - 1)}} $ | (62) |
以及正交关系:
| $ \int {\omega ({\boldsymbol\xi })\boldsymbol{H}_{\alpha }^{(m)}({\boldsymbol\xi })\boldsymbol{H}_{\beta }^{(n)}({\boldsymbol\xi }){\text{d}}\boldsymbol\xi } = \prod\limits_{i = 1}^D {{n_i}!} \;{\delta _{mn}}{\delta _{{\alpha \beta }}} $ | (63) |
其中,
根据Hermite多项式的定义和递推关系,零到四阶Hermite多项式为:
| $ {H^{(0)}}({{\boldsymbol{\xi}} }) = 1 $ | (64) |
| $ H_i^{(1)}({{\boldsymbol{\xi}} }) = {\xi _i} $ | (65) |
| $ H_{ij}^{(2)}({{\boldsymbol{\xi}} }) = {\xi _i}{\xi _j} - {\delta _{ij}} $ | (66) |
| $ H_{ijk}^{(3)}({{\boldsymbol{\xi}} }) = {\xi _i}{\xi _j}{\xi _k} - {\xi _i}{\delta _{jk}} - {\xi _j}{\delta _{ik}} - {\xi _k}{\delta _{ij}} $ | (67) |
| $ \begin{split} H_{ijkl}^{(4)}({{\boldsymbol{\xi}} }) =& {\xi _i}{\xi _j}{\xi _k}{\xi _l} - ({\xi _i}{\xi _j}{\delta _{kl}} + {\xi _i}{\xi _k}{\delta _{jl}} + \\& {\xi _i}{\xi _l}{\delta _{jk}} + {\xi _j}{\xi _k}{\delta _{il}} + {\xi _j}{\xi _l}{\delta _{ik}} + {\xi _k}{\xi _l}{\delta _{ij}}) + \\& {\delta _{ij}}{\delta _{kl}} + {\delta _{ik}}{\delta _{jl}} + {\delta _{il}}{\delta _{jk}} \end{split} $ | (68) |
由于Hermite多项式序列为一组完备基,对于任意在
| $ \begin{split} f({{\boldsymbol{\xi}} }) =& \omega ({{\boldsymbol{\xi}} })\sum\limits_{n = 0}^\infty {\frac{1}{{n!}}{{\boldsymbol{a}}}_{}^{(n)} \cdot {{\boldsymbol{H}}}_{}^{(n)}({{{\boldsymbol{\xi}}} })} = \omega ({{\boldsymbol{\xi}} })\sum\limits_{n = 0}^\infty {\frac{1}{{n!}}\sum\limits_{i} {a_{i}^{(n)}H_{i}^{(n)}({{\boldsymbol{\xi}} })} } \end{split} $ | (69) |
| $ a_{i}^{(n)} = \int {f({{\boldsymbol{\xi}} })} H_{i}^{(n)}({{\boldsymbol{\xi}} }){\text{d}}{{\boldsymbol{\xi}} } $ | (70) |
在一维情况下,n阶Hermite多项式具有唯一表达式;多维n阶Hermite多项式则是由下标排列
容易证明,
| $ {p_{_N}}({{\boldsymbol{\xi}} }) = \sum\limits_{n = 0}^N {{{\boldsymbol{b}}}_{}^{(n)} \cdot {{\boldsymbol{H}}}_{}^{(n)}({{\boldsymbol{\xi}} })} $ | (71) |
其中,系数
| $ \begin{split}& \int {f({{\boldsymbol{\xi}} }){\xi _{{i_1}}}{\xi _{{i_2}}}{\xi _{{i_3}}} \cdots {\xi _{{i_N}}}} {\mkern 1mu} {\text{d}}{{\boldsymbol{\xi}} } \\& \qquad = \int {\omega ({{\boldsymbol{\xi}} })\sum\limits_{n = 0}^N {\frac{1}{{n!}}{{\boldsymbol{a}}}_{}^{(n)} \cdot {{\boldsymbol{H}}}_{}^{(n)}({{\boldsymbol{\xi}} })} } \sum\limits_{m = 0}^N {{{\boldsymbol{b}}}_{}^{(m)} \cdot {{\boldsymbol{H}}}_{}^{(m)}({{\boldsymbol{\xi}} })} {\text{d}}{{\boldsymbol{\xi}} } { + } \\& \qquad \sum\limits_{n = N + 1}^\infty {\sum\limits_{m = 0}^N {{{\boldsymbol{a}}}_{}^{(n)}{{\boldsymbol{b}}}_{}^{(m)} \cdot \frac{1}{{n!}}} } \int {\omega ({{\boldsymbol{\xi}} }){{\boldsymbol{H}}}_{}^{(n)}({{\boldsymbol{\xi}} }){{\boldsymbol{H}}}_{}^{(m)}({{\boldsymbol{\xi}} })} {\text{d}}{{\boldsymbol{\xi}} } \end{split} $ | (72) |
由于Hermite多项式的正交性,式(72)右边第二项级数为0,因此有:
| $ \begin{split}& \int {f({{\boldsymbol{\xi}} }){\xi _{{i_1}}}{\xi _{{i_2}}}{\xi _{{i_3}}} \cdots {\xi _{{i_N}}}} {\mkern 1mu} {\text{d}}{{\boldsymbol{\xi}} } \\& = \int {\omega ({{\boldsymbol{\xi}} })\sum\limits_{n = 0}^N {\frac{1}{{n!}}{{\boldsymbol{a}}}_{}^{(n)} \cdot {{\boldsymbol{H}}}_{}^{(n)}({{\boldsymbol{\xi}} }){p_{_N}}({{\boldsymbol{\xi}} })} } {\text{d}}{{\boldsymbol{\xi}} } = \int {{f_N}({{\boldsymbol{\xi}} }){p_{_N}}({{\boldsymbol{\xi}} }){\text{d}}{{\boldsymbol{\xi}} }} \end{split} $ | (73) |
其中,定义函数
| $ {f_N}({{\boldsymbol{\xi}} }) \equiv \omega ({{\boldsymbol{\xi}} })\sum\limits_{n = 0}^N {\frac{1}{{n!}}{{\boldsymbol{a}}}_{}^{(n)} \cdot {{\boldsymbol{H}}}_{}^{(n)}({{\boldsymbol{\xi}} })} $ | (74) |
从式(73)可以看出,函数
对于Boltzmann-BGK方程(式(10)),其理论上的精确解
| $ f = {f^{(0)}} + \varepsilon {f^{(1)}} + O({\varepsilon ^2}) $ | (75) |
| $ {f^{(0)}} = \omega ({{\boldsymbol{\xi}} })\sum\limits_{n = 0}^\infty {\frac{1}{{n!}}{{\boldsymbol{a}}}_0^{(n)} \cdot {{\boldsymbol{H}}}_{}^{(n)}({{\boldsymbol{\xi}} })} $ | (76) |
| $ {f^{(1)}} = \omega ({{\boldsymbol{\xi}} })\sum\limits_{n = 0}^\infty {\frac{1}{{n!}}{{\boldsymbol{a}}}_1^{(n)} \cdot {{\boldsymbol{H}}}_{}^{(n)}({{\boldsymbol{\xi}} })} $ | (77) |
注意式(76)~式(77)中的
| $ {{{\boldsymbol{a}}}^{(n)}} = {{\boldsymbol{a}}}_0^{(n)} + \varepsilon {{\boldsymbol{a}}}_1^{(n)} + O({\varepsilon ^2}),n = 0,1,2, \cdots $ | (78) |
在此基础上,我们考察Boltzmann-BGK方程还原到各类方程需要的Hermite展开级数。
Euler方程:取
| $ {P_{ij}} = - \int {{f^{(0)}}{v_i}{v_j}{\text{d}}{{\boldsymbol{\xi}} }} = - p{\delta _{ij}} $ | (79) |
| $ {q_i} = \frac{1}{2}\int {f{v_i}{v_j}{v_j}{\text{d}}{{\boldsymbol{\xi}} }} = \frac{1}{2}\int {{f^{(0)}}{v_i}{v_j}{v_j}{\text{d}}{{\boldsymbol{\xi}} }} = 0 $ | (80) |
于是式(17)~式(19)还原到Euler方程。在此过程中最高计算到
Navier-Stokes方程:从式(79)~式(80)看到,
| $ \frac{\partial }{{\partial t}} = \varepsilon \frac{\partial }{{\partial {t_1}}} + {\varepsilon ^2}\frac{\partial }{{\partial {t_2}}} + {O}({\varepsilon ^3}) $ | (81) |
| $ \frac{\partial }{{\partial {x_i}}} = \varepsilon \frac{\partial }{{\partial {x_i}}} + {O}({\varepsilon ^2}) $ | (82) |
将分布函数
| $ \begin{split}& \varepsilon \left[ {\frac{{\partial {f^{(0)}}}}{{\partial {t_1}}} + {{\boldsymbol{\xi}} } \cdot \nabla {f^{(0)}} + \frac{{{f^{(1)}}}}{\tau }} \right] + {\varepsilon ^2}\left[ {\frac{{\partial {f^{(0)}}}}{{\partial {t_2}}}} \right. + \\& \qquad \frac{{\partial {f^{(1)}}}}{{\partial {t_1}}} + {{\boldsymbol{\xi}} } \cdot \nabla {f^{(1)}} + \left. {\frac{{{f^{(2)}}}}{\tau }} \right] + {O}({\varepsilon ^3}) = 0 \end{split} $ | (83) |
忽略
| $ \frac{{{f^{(1)}}}}{\tau } + \frac{{\partial {f^{(0)}}}}{{\partial {t_1}}} + {\xi _i}\frac{{\partial {f^{(0)}}}}{{\partial {x_i}}} = 0 $ | (84) |
进一步分析可指出[37, 44],如果
将
| $ \begin{split}& \omega ({{\boldsymbol{\xi}} })\sum\limits_{n = 0}^\infty {\frac{1}{{n!}}} \left[ {\frac{{{{\boldsymbol{a}}}_1^{(n)}}}{\tau } \cdot {{{\boldsymbol{H}}}^{(n)}}({{\boldsymbol{\xi}} }) + \frac{{\partial {{\boldsymbol{a}}}_0^{(n)}}}{{\partial {t_1}}} \cdot {{{\boldsymbol{H}}}^{(n)}}({{\boldsymbol{\xi}} })} \right. + \\& \qquad \left. {\frac{{\partial {{\boldsymbol{a}}}_0^{(n)}}}{{\partial {x_i}}} \cdot {\xi _i}{{{\boldsymbol{H}}}^{(n)}}({{\boldsymbol{\xi}} })} \right] = 0 \end{split} $ | (85) |
将式(85)的第三项所含的
| $ \begin{split}& \omega ({{\boldsymbol{\xi}} })\sum\limits_{n = 0}^\infty {\frac{1}{{n!}}} \left[ {\frac{{{{\boldsymbol{a}}}_1^{(n)}}}{\tau } \cdot {{{\boldsymbol{H}}}^{(n)}}({{\boldsymbol{\xi}} }) + \frac{{\partial {{\boldsymbol{a}}}_0^{(n)}}}{{\partial {t_1}}} \cdot {{{\boldsymbol{H}}}^{(n)}}({{\boldsymbol{\xi}} })} \right. + \\& \qquad \left. {\frac{{\partial {{\boldsymbol{a}}}_0^{(n)}}}{{\partial {x_i}}} \cdot ({{\boldsymbol{H}}}_i^{(n + 1)}({{\boldsymbol{\xi}} }) + n{\delta }{{{\boldsymbol{H}}}^{(n - 1)}})} \right] = 0 \end{split} $ | (86) |
其中:
| $ n{\delta }{{{\boldsymbol{H}}}^{(n - 1)}} = \sum\limits_{k = 1}^n {{\delta _{{i_k}i}}H_{{i_1}{i_2} \cdots {i_{k - 1}}{i_{k + 1}} \cdots {i_n}}^{(n - 1)}} $ | (87) |
将式(86)整理后,合并同阶Hermite多项式系数,有:
| $ \begin{split}& \omega ({{\boldsymbol{\xi}} })\left[ {\sum\limits_{n = 0}^\infty {\frac{1}{{n!}}} \left( {\frac{{{{\boldsymbol{a}}}_1^{(n)}}}{\tau } + \frac{{\partial {{\boldsymbol{a}}}_0^{(n)}}}{{\partial {t_1}}}} \right)} \right. + \sum\limits_{n = 1}^\infty {\frac{1}{{n!}}} n\nabla {{\boldsymbol{a}}}_0^{(n - 1)} + \\&\qquad \left. {\quad \sum\limits_{n = - 1}^\infty {\frac{1}{{n!}}} \nabla \cdot {{\boldsymbol{a}}}_0^{(n + 1)}} \right] \cdot {{{\boldsymbol{H}}}^{(n)}}({{\boldsymbol{\xi}} }) = 0 \end{split} $ | (88) |
由于Hermite多项式的正交性,式(88)成立的条件为各阶
| $ {{\boldsymbol{a}}}_1^{(n)} = - \tau \left[ {\frac{{\partial {{\boldsymbol{a}}}_0^{(n)}}}{{\partial {t_1}}} + n\nabla {{\boldsymbol{a}}}_0^{(n - 1)} + \nabla \cdot {{\boldsymbol{a}}}_0^{(n + 1)}} \right] $ | (89) |
式(89)指出:对于Boltzmann-BGK方程精确解的零阶和一阶近似
| $ \tilde{f} = {f}_{{N}_{0}}^{(0)}+\epsilon {\tilde{f}}^{(1)} = {\tilde{f}}^{(0)}+\epsilon {\tilde{f}}^{(1)} $ | (90) |
其中,
| $ {\tilde f^{(0)}} = \omega \sum\limits_{n = 0}^\infty {\frac{1}{{n!}}{\tilde {\boldsymbol{a}}}_0^{(n)} \cdot {{{\boldsymbol{H}}}^{(n)}}({{\boldsymbol{\xi}} })} $ | (91) |
| $ {\tilde f^{(1)}} = \omega \sum\limits_{n = 0}^\infty {\frac{1}{{n!}}{\tilde {\boldsymbol{a}}}_1^{(n)} \cdot {{{\boldsymbol{H}}}^{(n)}}({{\boldsymbol{\xi}} })} $ | (92) |
显然
| $\tilde{\boldsymbol{a}}_{0}^{(n)} = {{{\boldsymbol{a}}}}_{0}^{(n)},\;\;\;\;0\leqslant n \leqslant N+1 $ | (93) |
即
根据上述讨论,在Chapman-Enskog展开一阶小量近似下,如需
| $ {\tilde {\boldsymbol{a}}}_1^{(N + 2)} \ne 0 $ | (94) |
这也就是说,
在以上讨论的基础上,我们可以回到具体需还原的方程类型中考察N的值。对于等温弱可压Navier-Stokes方程,只需要准确还原质量和动量方程,故需
关于积分内核的多项式阶数,也可以从另一个方面去解释[45]:对于等温弱可压Navier-Stokes方程,需
综上,我们将具体还原的方程类型和其多项式阶数列在表1中。
| 表 1 不同流动分布函数的Hermite截断式最低阶数 Table 1 Lowest order of truncated Hermite distribution function for different types of flows |
|
|
| $ {{\boldsymbol{a}}}_0^{(0)} = \rho ,\quad {{\boldsymbol{a}}}_0^{(1)} = \rho {{\boldsymbol{u}}} $ | (95) |
| $ {{\boldsymbol{a}}}_0^{(2)} = \rho\big [{{{\boldsymbol{u}}}^2} + (\theta - 1)\boldsymbol{\delta} \big] $ | (96) |
| $ {{\boldsymbol{a}}}_0^{(3)} = \rho \big[{{{\boldsymbol{u}}}^3} + (\theta - 1){\boldsymbol{\delta} {\boldsymbol{u}}}\big] $ | (97) |
| $ {{\boldsymbol{a}}}_0^{(4)} = \rho \big[{{{\boldsymbol{u}}}^4} + (\theta - 1){{\boldsymbol{\delta}} }{{{\boldsymbol{u}}}^2} + {(\theta - 1)^2}{{{\boldsymbol{\delta}} }^2}\big] $ | (98) |
其中,矢量或张量并列(
| $\qquad\qquad \begin{split} f_2^{(0)}({{\boldsymbol{\xi}} }) =& \rho \omega ({{\boldsymbol{\xi}} })\Big\{ 1 + {{\boldsymbol{\xi}} } \cdot {{\boldsymbol{u}}}+ \\& \frac{1}{2}\big[{({{\boldsymbol{\xi}} } \cdot {{\boldsymbol{u}}})^2} - {u^2} + (\theta - 1)({\xi ^2} - D)\big]\Big\} \end{split} $ | (99) |
| $\qquad\qquad \begin{split} f_3^{(0)}({{\boldsymbol{\xi}} }) =& f_{2}^{(0)}({{\boldsymbol{\xi}} }) + \rho \omega ({{\boldsymbol{\xi}} })\bigg\{ \frac{{{{\boldsymbol{\xi}} } \cdot {{\boldsymbol{u}}}}}{6}\Big[{({{\boldsymbol{\xi}} } \cdot {{\boldsymbol{u}}})^2} - \\&3{u^2} + 3(\theta - 1)({\xi ^2} - D - 2)\Big]\bigg\} \end{split} $ | (100) |
| $ \begin{split}& f_4^{(0)}({{\boldsymbol{\xi}} }) = f_{3}^{(0)}({{\boldsymbol{\xi}} }) + \rho \omega (\boldsymbol{\xi })\cdot \\& \Bigg\{\frac{1}{{24}}\Big[{(\boldsymbol{\xi } \cdot {{\boldsymbol{u}}})^4} - 6{(\boldsymbol{\xi } \cdot {{\boldsymbol{u}}})^2}{u^2} + 3{u^4}\Big] + \\& \frac{{\theta - 1}}{4}\Big\{ ({\xi ^2} - D - 2)\Big[{(\boldsymbol{\xi } \cdot {{\boldsymbol{u}}})^2} - {u^2}\Big] - 2{(\boldsymbol{\xi } \cdot {{\boldsymbol{u}}})^2}\Big\} +\\& \frac{{{{(\theta - 1)}^2}}}{8}\Big[{\xi ^4} - 2(D + 2){\xi ^2} + D(D + 2)\Big]\;\Bigg\} \end{split} $ | (101) |
在表1的指导下,可根据实际计算的流动类型选用对应阶数的
| $ \int {\omega ({{\boldsymbol{\xi}} })g({{\boldsymbol{\xi}} })} {\mkern 1mu} {\text{d}}{{\boldsymbol{\xi}} = }\sum\limits_{a = 1}^d {{w_a}g(} {{{\boldsymbol{\xi}} }_a}) $ | (102) |
这里K阶精度的意义是对于
定义分布函数的离散形式:
| $ {f_a} = \frac{{{w_a}\tilde f({{{\boldsymbol{\xi}} }_{{\boldsymbol{a}}}})}}{{\omega \left( {{{{\boldsymbol{\xi}} }_{{\boldsymbol{a}}}}} \right)}},\;f_a^{(0)} = \frac{{{w_a}f_{N + 1}^{(0)}({{{\boldsymbol{\xi}} }_{{\boldsymbol{a}}}})}}{{\omega \left( {{{{\boldsymbol{\xi}} }_{{\boldsymbol{a}}}}} \right)}} $ | (103) |
在Boltzmann-BGK方程(10)中用近似解
| $ \frac{{\partial {f_a}}}{{\partial t}} + {{{\boldsymbol{\xi}} }_{a}} \cdot \nabla {f_a} = - \frac{{{f_a} - f_a^{(0)}}}{\tau } $ | (104) |
附录B中我们将证明,只要
在离散化
| $ \begin{split} \rho =& \int {f\;{\text{d}}{{\boldsymbol{\xi}} }} = \int {\tilde f\;{\text{d}}{{\boldsymbol{\xi}} }} = \int {\omega (\xi )\frac{{\tilde f\;}}{{\omega (\xi )}}{\text{d}}{{\boldsymbol{\xi}} }} \\ = &\sum\limits_{a = 1}^d {\frac{{{w_a}\tilde f({\xi _a})\;}}{{\omega ({\xi _a})}}} = \sum\limits_{a = 1}^d {{f_a}} \end{split} $ | (105) |
| $ \rho u = \int {\tilde f{{\boldsymbol{\xi}} }\;{\text{d}}{{\boldsymbol{\xi}} }} = \sum\limits_{a = 1}^d {\frac{{{w_a}\tilde f({\xi _a}){{{\boldsymbol{\xi}} }_a}\;}}{{\omega ({\xi _a})}}} = \sum\limits_{a = 1}^d {{f_a}{{{\boldsymbol{\xi}} }_a}} $ | (106) |
| $ \begin{split} \rho {u^2} + pD = &\rho ({u^2} + \theta D) = \int {\tilde f{\xi _i}{\xi _i}{\text{d}}{{\boldsymbol{\xi}} }} \\=& \sum\limits_{a = 1}^d {\frac{{{w_a}\tilde f({\xi _a})\xi _a^2\;}}{{\omega ({\xi _a})}}} = \sum\limits_{a = 1}^d {{f_a}\xi _a^2} \end{split} $ | (107) |
在等温弱可压流动中,
多层速度模型的离散Boltzmann方程(式(104))与等温弱可压流动相同,因此可以沿用2.2节类似的思路,在特征线
| $ \frac{\mu }{{{\mu _0}}} = {\left( {T/{T_0}} \right)^{3/2}}\frac{{1 + S/{T_0}}}{{T/{T_0} + S/{T_0}}} $ | (108) |
其中,S为随气体类型变化的常数,对于空气S = 110.4 K;
| $ \bar \tau - \frac{{\Delta t}}{2} = \frac{\mu }{p} $ | (109) |
对于给定雷诺数Re和马赫数Ma的可压缩热流问题(以及指定了定义雷诺数、马赫数的尺度L和速度U),如果在尺度
| $ \bar \tau _0^{} = \frac{{{N_L}{{Ma}}}}{{{c_s}{{Re}} }} + \frac{1}{2} $ | (110) |
事实上式(110)也适用于等温弱可压流动。对于流场中任意一点的分布函数
| $ \frac{T}{{{T_0}}} = \frac{{p/\rho }}{{p_0^{}/\rho _0^{}}} = p/\rho $ | (111) |
代入式(108)中求得
| $ \bar \tau = \frac{\mu }{{{\mu _0}p}}\left( {\bar \tau _0^{} - \frac{1}{2}} \right) + \frac{1}{2} $ | (112) |
即为适应于温度变化的松弛时间。
4.3 离散速度模型在之前的讨论中,有一个重要的问题没有展开——如何获得具有K阶精度的数值积分公式(式(102))。我们指出,对于任意的m阶多项式
| $ \sum\limits_{a = 1}^d {{w_a}H_{j}^{(i)}(} {\xi _a}) = {\delta _{0i}},\quad i = 0,1,2, \cdots ,m $ | (113) |
其证明见附录C,求解该式即可获得
| $ \begin{array}{l}{\displaystyle \sum _{a = 1}^{d}{w}_{a}{H}_{11}^{(2)}(}{\xi }_{a}) = 0,\;\;\;\;{\displaystyle \sum _{a = 1}^{d}{w}_{a}{H}_{12}^{(2)}(}{\xi }_{a}) = 0,\\ {\displaystyle \sum _{a = 1}^{d}{w}_{a}{H}_{22}^{(2)}(}{\xi }_{a}) = 0\end{array} $ |
为了求解式(113),我们预设解的四个性质:
(1)均匀性。一维情况下,
(2)对称性。关于坐标轴对称和原点对称的
(3)正定性。权重
(4)经济性。对于同样阶数的积分精度可能存在多个解,我们倾向于选择积分点数d最少的解,这样可以最大化节约计算资源。
在这些预设条件下,求解式(113)过程分为三步:
(1)根据积分精度确定方程。奇数阶的Hermite多项式至少是
(2)求解步骤(1)中的p个方程,得到
(3)确定特征常数c。只要所有
该求解过程已在Shan[30]中初步给出了思路,并由Nie[45]和Shan[46-47]对求解过程进行了更详细地描述。Spiller等[48-50]则将求解方法编制成了Python程序包。以下在一维和二维情况下以实例说明该过程。
一维情况下,我们考察一到九阶精度的积分公式。对求解
| $ \begin{array}{l} \begin{array}{ccc cccc} \quad \quad \quad & {w}_{0}& {w}_{1}& {w}_{2}& {w}_{3}& {w}_{4}& {w}_{5} \end{array}\\ \begin{array}{c} {H}^{(0)}:\\ {H}^{(2)}:\\ {H}^{(4)}:\\ {H}^{(6)}:\\ {H}^{(8)}: \end{array} \left[ \begin{array}{cccccc} 1& ~~2& ~~2& ~~2& ~~2& 2\\ 0& ~~1& ~~4& ~~9& ~~16& 25\\ 0& ~~0& ~~1& ~~6& ~~20& 50\\ 0& ~~0& ~0& ~~1& ~~8& 35\\ 0& ~~0& ~0& ~~0& ~~1& 10 \end{array} \right] \cdot {{\boldsymbol{w}}} = {{\boldsymbol{r}}}\\ \end{array} $ | (114) |
其中,
右端项
| $\boldsymbol {r} = \left[ \begin{array}{l} 1 \\ 1/2{c^2} \\ - ({c^2} - 3)/24{c^2} \\ (4{c^4} - 15{c^2} + 15)/720{c^6} \\ - (12{c^6} - 49{c^4} + 70{c^2} - 35)/13440{c^8} \\ \end{array} \right] $ | (115) |
为了方便对照,我们在式(114)系数矩阵的左侧和顶端分别列出了各系数对应的Hermite多项式和未知数。如需要五阶积分公式,需要考察
| $\begin{split} & {w_0} = (7{c^2} - {c^4} - 4)/(4{c^2})\\ & {w_1} = ({c^4} - 3{c^2} + 3)/(6{c^2})\\ & {w_2} = (3 - {c^2})/{24} \end{split} $ | (116) |
此时,只要给定任意使
进一步地,我们考虑使用积分点
| $ \begin{split}& {w_0} = (36{c^6} - 49{c^4} + 42{c^2} - 15)/36{c^6} \\& {w_1} = (12{c^4} - 13{c^2} + 5)/16{c^6} \\& {w_2} = ( - 3{c^4} - 10{c^2} + 5)/40{c^6} \\& {w_3} = (4{c^4} - 15{c^2} + 15)/720{c^6} \end{split} $ | (117) |
此时
多维情况下,对于2n阶Hermite多项式
| $\boldsymbol{i} = (\underset{2\alpha 个}{\underbrace{1,\cdots 1}},\underset{2\beta 个}{\underbrace{2,\cdots 2}},\underset{2\gamma 个}{\underbrace{3,\cdots 3}}) = ({1}^{2\alpha }{2}^{2\beta }{3}^{2\gamma }) $ | (118) |
其中,
二维情况下,对于一到九阶精度积分公式,有效的Hermite多项式依次为
| $ \begin{array}{l} \begin{array}{ccccc ccccc c} \quad\quad\quad\quad& {w}_{0}& {w}_{10}& {w}_{11}& {w}_{20}& {w}_{21}& {w}_{22}& {w}_{30}& {w}_{31}& {w}_{32}& {w}_{33} \end{array}\\ \begin{array}{c} {H}^{(0)}:\\ {H}_{11}^{(2)}:\\ {H}_{{1}^{2}{2}^{2}}^{(4)} :\\ {H}_{{1}^{4}}^{(4)}:\\ {H}_{{1}^{4}{2}^{2}}^{(6)} :\\ {H}_{{1}^{6}}^{(6)}:\\ {H}_{{1}^{4}{2}^{4}}^{(8)} :\\ {H}_{{1}^{6}{2}^{2}}^{(8)} :\\ {H}_{{1}^{8}}^{(8)}: \end{array} \left[ \begin{array}{ccccc ccccc} ~~~1& ~~~~4& ~~~~4& ~~~~4& ~~~8& ~~4& ~~~4& ~~~8& ~~8& ~4\\ ~~~0& ~~~~1& ~~~~2& ~~~~4& ~~~10& ~~8& ~~~9& ~~~20& ~~26& ~18\\ ~~~0& ~~~~0& ~~~~1& ~~~~0& ~~~8& ~~16& ~~~0& ~~~18& ~~72& ~81\\ ~~~0& ~~~~0& ~~~~0& ~~~~1& ~~~2& ~~2& ~~~6& ~~~12& ~~14& ~12\\ ~~~0& ~~~~0& ~~~~0& ~~~~0& ~~~1& ~~4& ~~~0& ~~~6& ~~33& ~54\\ ~~~0& ~~~~0& ~~~~0& ~~~~0& ~~~0& ~~0& ~~~1& ~~~2& ~~2& ~2\\ ~~~0& ~~~~0& ~~~~0& ~~~~0& ~~~0& ~~1& ~~~0& ~~~0& ~~12& ~36\\ ~~~0& ~~~~0& ~~~~0& ~~~~0& ~~~0& ~~0& ~~~0& ~~~1& ~~4& ~9\\ ~~~0& ~~~~0& ~~~~0& ~~~~0& ~~~0& ~~0& ~~~0& ~~~0& ~~0& ~0 \end{array} \right] \end{array} $ |
右端项r为:
| $ \boldsymbol{r} = \left[ \begin{array}{l} 1 \\ 1/2{c^2} \\ 1/4{c^4} \\ (3 - {c^2})/24{c^4} \\ (3 - {c^2})/48{c^6} \\ (4{c^4} - 15{c^2} + 15)/720{c^6} \\ {({c^2} - 3)^2}/576{c^8} \\ (4{c^4} - 15{c^2} + 15)/1440{c^8} \\ 12{c^6} - 49{c^4} + 70{c^2} - 35 \end{array} \right] $ | (119) |
对于五阶积分公式,需满足
| $\begin{split}& {w_0} = 1 - \frac{5}{{2{c^2}}} + \frac{5}{{2{c^4}}} \\& {w_{10}} = \frac{{2{c^2} - 3}}{{3{c^4}}} \\& {w_{11}} = \frac{1}{{4{c^4}}} \\& {w_{20}} = - \frac{{{c^2} - 3}}{{24{c^4}}} \end{split} $ | (120) |
此时取
| 表 2 二维积分公式的积分点与权重 Table 2 Quadrature abscissas and weights of the 2D integral formula |
|
|
对于七阶积分公式,需要满足
| $ \begin{split}& {w_0} = \frac{{144{c^6} - 392{c^4} + 525{c^2} - 255}}{{144{c^6}}} \\& {w_{10}} = \frac{{36{c^4} - 71{c^2} + 39}}{{48{c^6}}} \\& {w_{11}} = \frac{{4{c^2} - 3}}{{12{c^6}}} \\& {w_{20}} = - \frac{{36{c^4} - 125{c^2} + 75}}{{480{c^6}}} \\& {w_{22}} = \frac{{3 - {c^2}}}{{192{c^6}}} \\& {w_{30}} = \frac{{4{c^4} - 15{c^2} + 15}}{{720{c^6}}} \end{split} $ | (121) |
此时再选择合适的c使得其中某一个权重为零。由于
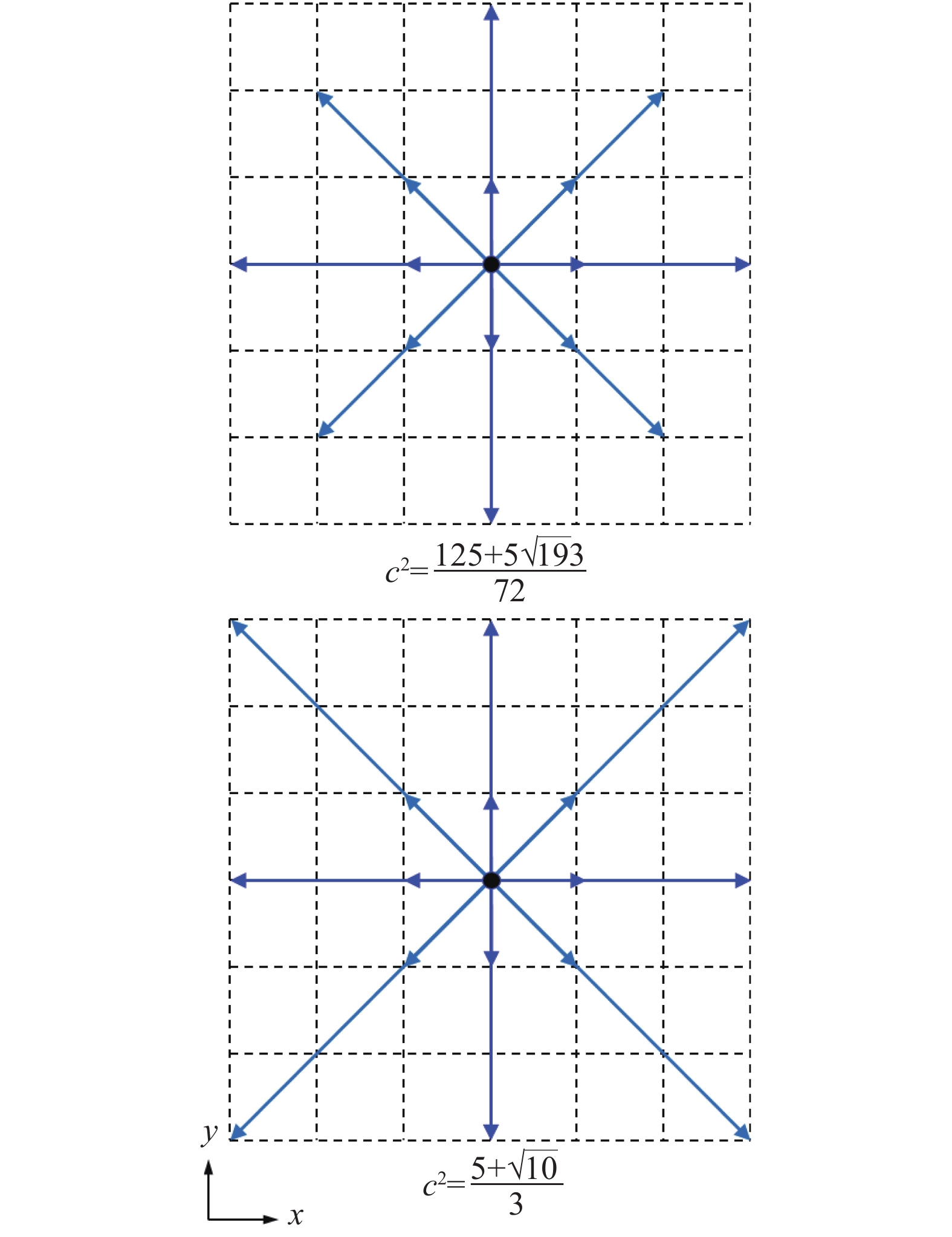
|
图 8 2种D2V17离散速度模型 Fig.8 Two types of D2V17 discrete velocity models |
对于九阶积分公式,此时需要使用到
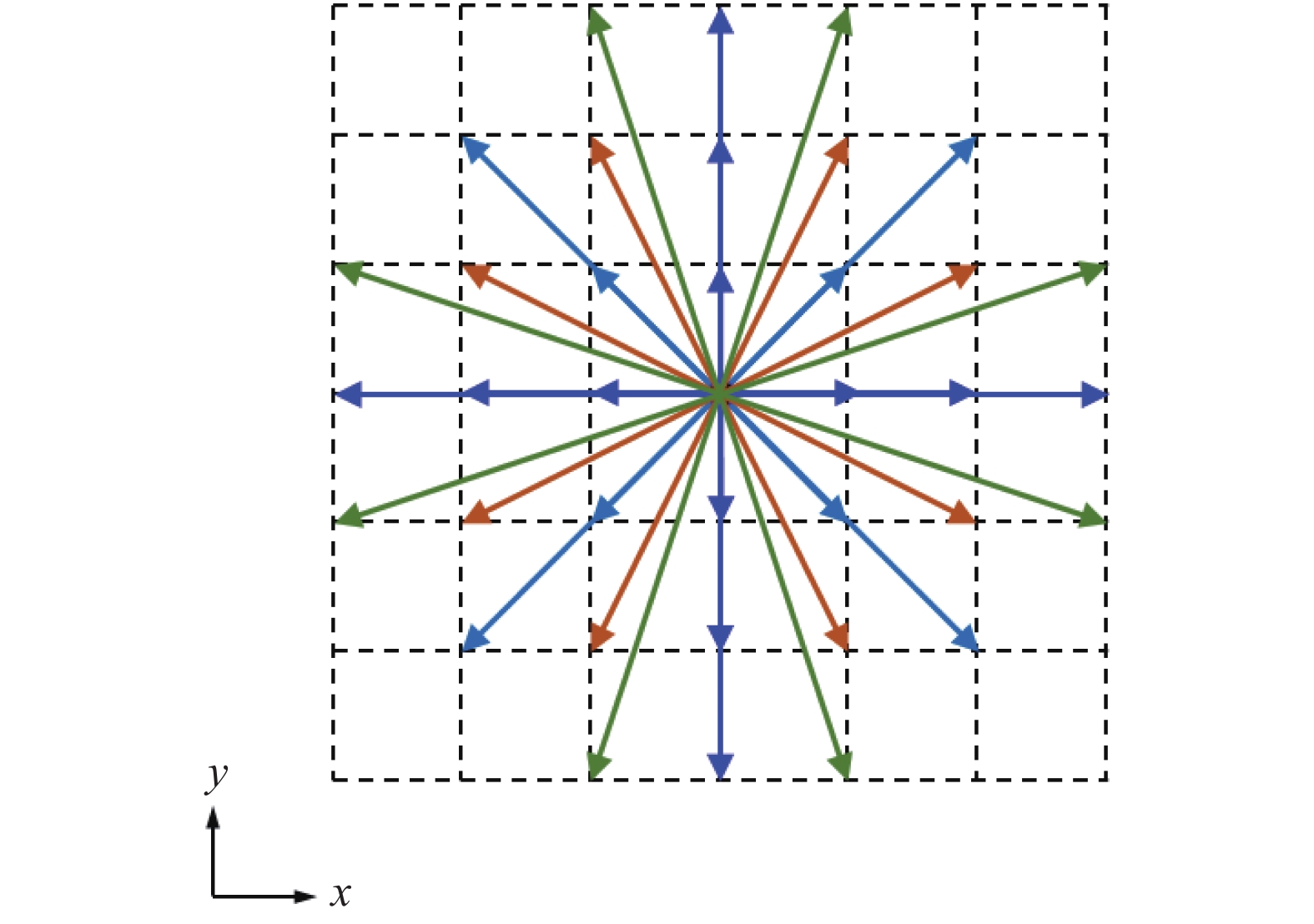
|
图 9 D2V37离散速度模型 Fig.9 D2V37 discrete velocity models |
对于三维情况下的积分公式,也可以遵循同样的思路求解。相关的细节过程可参考文献[47]。
4.4 等温弱可压模型的推导对于截断到二阶Hermite多项式级数的平衡态分布函数 (式(99)),如果令
| $ f_2^{(0)}({{\boldsymbol{\xi}} }) = \rho \omega ({{\boldsymbol{\xi}} })\Big\{ 1 + {\boldsymbol\xi } \cdot {{\boldsymbol{u}}} + \frac{1}{2}\big[{(\boldsymbol{\xi } \cdot {{\boldsymbol{u}}})^2} - {u^2}\big]\Big\} $ | (122) |
与等温弱可压模型的平衡态分布函数展开式(20)一致。
对于离散速度模型,在4.3节的一维和二维情况已经证实,D1Q3、D2Q9模型的
同时,Hermite多项式模型也同时指出(见表1),如需要准确还原动量方程,模拟等温弱可压流动,
经典的LBM中时间和空间离散均为沿特征线积分(参考2.2节和4.2节),并设置归一化的
1)由于
2)无法使用贴体网格。在倾斜方向边界,或者曲面边界上,需要同时使用笛卡尔网格和浸没边界法[53],以锯齿形边界近似斜边界或者曲面边界。这种非贴体网格由于精度较低,且在对流扩散问题中易造成收敛性困难[54]和稳定性问题,往往需要与局部加密网格和多松弛时间模型(MRT)结合[55]。
3)计算稳定性。经验表明,经典LBM方法在雷诺数较大时只能使用较小的物理时间步长才能获得稳定的数值解;当使用Zhou-He非平衡态反弹边界条件[56]时稳定性问题更加突出,这对实际工程湍流的计算会形成较大的障碍。
由于传统CFD方法可以使用边界层加密贴体网格,使用合适的时间与空间格式时,数值稳定性良好,将传统CFD方法与LBM结合成为了解决以上问题的一种思路。Reider和Sterling[57]、Cao等[58]将有限差分法与LBM模型结合,提出了FDLBM方法。FDLBM的基本思路是将LBM方程(式(104))视为关于各个离散分布函数
使用隐式时间离散是传统CFD方法中提高数值稳定性的常用方法,伴随而来的是需要迭代求解线型代数方程组,这往往使得计算量和实施难度显著增加。在FDLBM中,Guo和Zhao[62]使用了与经典LBM类似的隐式时间处理办法,即类似于式(30)定义一个中间时刻的
为了适应复杂几何构型和不规则形状网格的计算需求,Nannell和Succi[64]、Benzi等[65]将有限体积方法引入LBM,提出了FVLBM方法。FVLBM的基本思想是,将LBM方程(式(104))对流场中任意一个控制体单元
| $ \frac{\partial }{{\partial t}}\int_\varOmega {{f_a}} {\text{d}}\varOmega + \oint_{\partial \varOmega } {({\boldsymbol{\xi }_{a}} \cdot {{\boldsymbol{n}}}){f_a}} {\text{d}}S = - \int_\varOmega {\frac{1}{\tau }} ({f_a} - f_a^{(0)}){\text{d}}\varOmega $ | (123) |
其中,
| $ {f_{a,\varOmega }} = \frac{1}{\varOmega }\int_\varOmega {{f_a}} {\text{d}}\varOmega $ | (124) |
以及单元面对流通量:
| $ {L_{a,\varOmega }} = \oint_{\partial \varOmega } {({\boldsymbol{\xi }_{a}} \cdot {{\boldsymbol{n}}}){f_a}} {\text{d}}S $ | (125) |
则式(123)可写为关于分布函数单元体平均量和单元面对流通量的方程。求解该方程的过程即与传统有限体积方法类似。Chen[66]和Peng等[67]将FVLBM的理论和其在非均匀网格上的应用进行了完善。为了提高稳定性,Stiebler等[68]使用迎风型格式重构单元面通量。Patil和Lakshmisha[69]则将TVD格式应用于单元面通量的重构。
随着计算流体力学有限元方法日趋成熟[70-71],Lee和Lin[72]、Shi等[73]将有限元方法引入LBM,发展了有限元LBM方法。近年来,MacMeccan等[74]、Krüger等[75]使用混合型有限元LBM方法模拟了可变形颗粒流动并应用于生物流计算领域。由于主题和篇幅所限,此处不对有限元LBM方法作进一步展开。有兴趣的读者可参阅有关文献了解相关细节。
6 总结与展望LBM多层速度模型起源于单层速度模型,在热流和可压缩流动应用需求下不断发展,经历了平衡态分布函数展开从二阶提高到四阶、离散速度模型从单层网格提高到2层或者更多层网格、约束条件也逐步增多的过程。Hermite多项式模型则提供了一个既理论又实用的判定框架:要想准确还原能量方程,平衡态分布函数必须展开到速度四阶量。Watari-Tsutahara预设的多层速度模型[24-25]与该结论殊途同归。Hermite多项式模型也同时指出,离散速度模型事实上为相应阶数积分公式的积分点和权重,只需查表(或用程序包计算)找出这些积分点和权重,选出一组应用即可,而不是根据经验预设和优化。尽管Hermite多项式模型给出了较为简洁和确定的形式,但是依照经验理论进行马赫展开或待定系数得到的其他多层速度模型,在特定范围和领域内仍具有一定的应用价值。
必须承认,相对于计算等温弱可压流动的经典单层速度模型而言,多层速度模型仍然是一种尚不成熟的模型,在很多方面仍然需要改进和完善。这主要在以下几个方面:
1)模型的误差、色散与耗散、稳定性分析。目前对单层速度模型的误差和稳定性分析已有不少工作,例如:Sterling和Chen[76]对D2Q7(六边形模型)、D2Q9和D3Q15进行线性稳定性分析后得出
对多层速度模型而言,McNamara等[80]对D3Q21模型(D3Q15加上
值得注意的是,在Hermite多项式模型框架下,经典D3Q15、D3Q19和D3Q27模型从积分精度角度来讲,并不存在差别,因为都具有五阶积分精度;从计算经济性原则来讲,应该选择积分点最少的D3Q15模型。然而Silva等[78]和Bauer等[79]的工作提示我们,在选择离散模型时还需要考虑各向同性、截断误差等更多方面的因素,即计算最经济的模型不一定是最优的计算结果。Sieber等[82]将Hermite多项式模型与D2Q9模型、Chen等[23]的多层速度模型进行了线性稳定性分析对比,发现对等温弱可压流动而言,将平衡态分布函数展开到三阶Hermite多项式级数,或使用D2V17、D2V37模型都能显著提高稳定性;对于可压缩热流而言,使用四阶Hermite展开的
2)边界条件。LBM单层速度模型在经过多年发展后,其边界条件处理方法已经日趋完善,有关工作可谓汗牛充栋[33,36,83],对于壁面反弹边界条件[56,84]、周期边界条件[85]、适用于流动出入口的无反射边界条件[86-87]以及其他类型的边界条件等都已有充分的研究工作,可满足绝大多数计算工况的需求。然而,当使用多层速度模型时,一方面由于离散速度点跨越多层网格,使得边界附近的内部结点与边界结点区分变得模糊;另一方面平衡态分布函数的形式也变得更为复杂,如何恰当处理边界条件成为了一个难点,相关的工作也屈指可数[83]。Malaspinas等提出[88],将边界节点的分布函数离散点按内部和边界分为已知量和未知量,将离散分布函数各阶矩的约束条件构成方程组,通过求解方程组构造一种“通用”的边界条件处理方法。他们在D2Q9和D3Q19模型中进行了测试,并指出该方法可适用于多层速度模型的边界条件(但没有后续验证)。Meng和Zhang[89]提出了适用于多层速度模型的扩散-反弹边界条件格式,并应用到D2V16、D2V17、D2V37和D3V121[45]这四种模型,对等温流动和热流进行了测试计算。Lee等[90]将Hecht和Harting针对D3Q19的非平衡态壁面反弹边界条件[91],推广到了用多层速度模型计算等温弱可压流动的情况,并用D2V17模型进行了验算。Klass等[92]进一步延续了Lee等的工作,并将其应用到了弱可压热流中,使用D2V17和D2V37模型进行了验证,计算结果比Meng和Zhang的扩散-反弹边界条件表现更优。总体来看,针对多层速度模型的边界条件研究工作还处于起步阶段,且大部分局限于弱可压热流和Dirichlet边界类型;对于压缩性较强的跨声速、超声速流动,以及流动出入口涉及的无反射边界条件,尚无相关工作涉足。将单层速度模型中的各类边界条件处理方法扩展到多层速度模型,并在各类流动中广泛验证测试,仍是今后需要较多投入的方向。
3)高性能算法。LBM最大优势是计算速度和高度并行特性,然而它也有一个众所周知的缺点:由于需要存储数量众多的离散分布函数,对计算机内存的使用量比传统CFD方法更多,因此有不少工作聚焦于如何改进算法,减少内存消耗并提高计算效率[93-95]。另外,正如上一节所述,经典的LBM(相对于FDLBM和FVLBM及其他混合方法而言)一般使用均匀网格,当涉及到边界层计算时,将LBM与自适应局部加密网格(AMR)结合[96-98]是更加经济有效的方案。这些算法与目前流行的GPU高性能计算相结合,能发挥LBM的最大计算潜力[99-101]。然而,目前这些高性能算法都是集中应用在单层速度模型中。对于多层速度模型而言,特别是三维情况,准确模拟可压缩热流的最经济模型是D3V103,但其分布函数离散点的数量已经是D3Q27的4倍。这一方面使其内存占用问题更加突出;另一方面,在并行化和局部自适应加密网格时,不同块之间的界面数据交互量也更大,需要相当谨慎地处理。然而这些往往是工程实际应用中决定算法效率的制约因素。发展适用于多层速度模型的高性能算法,包括内存节约算法、高效率通信和AMR方法、CPU+GPU异构高效算法,并在各类复杂几何外形、复杂流动中广泛测试,应引起业内学者的广泛关注。
总体来说,LBM模型,特别是多层速度模型,仍然需要诸多补充和完善才能成为一种可靠、高效的流体力学研究手段和应用技术。正如1998年Chen和Doolen[2]在文章结尾中提到,LBM多相流和复杂反应系统模型主要集中于等温弱可压流问题,适应于可压缩热流的LBM模型仍待开发。20余年后的今天,这些方面虽然取得了一些进步,但是离可靠性要求还有不少差距。我们期望多层速度模型能够百花齐放,特别是具有较完备数学理论框架的Hermite多项式模型,能在这些方面继续发展壮大并做出应有的贡献。
| [1] |
FRISCH U, HASSLACHER B, POMEAU Y. Lattice-gas automata for the Navier-Stokes equation[J]. Physical Review Letters, 1986, 56(14): 1505-1508. DOI:10.1103/physrevlett.56.1505 |
| [2] |
CHEN S Y, DOOLEN G D. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 329-364. DOI:10.1146/annurev.fluid.30.1.329 |
| [3] |
AIDUN C K, CLAUSEN J R. Lattice-Boltzmann method for complex flows[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 439-472. DOI:10.1146/annurev-fluid-121108-145519 |
| [4] |
SHAO W D, LI J. Review of lattice Boltzmann method applied to computational aeroacoustics[J]. Archives of Acoustics, 2019, 44: 215-238. DOI:10.24425/aoa.2019.128486 |
| [5] |
李军, 邵卫东. 格子Boltzmann方法与计算气动声学[M]. 北京: 科学出版社, 2021. LI J, SHAO W D. Lattice Boltzmann Method and Computational Aeroacoustics[M]. Beijing: Science Press, 2021. |
| [6] |
HUANG H B, SUKOP M C, LU X Y. Multiphase lattice Boltzmann methods: theory and application[M]. Chichester, UK: John Wiley & Sons, Ltd, 2015. doi: 10.1002/9781118971451
|
| [7] |
冉政, 陈健. 关于格子Boltzmann方法的几个问题(I)[J]. 空气动力学学报, 2016, 34(3): 333-340. RAN Z, CHEN J. Several problems on the lattice Boltzmann method(I)[J]. Acta Aerodynamica Sinica, 2016, 34(3): 333-340. DOI:10.7638/kqdlxxb-2015.0058 (in Chinese) |
| [8] |
SPALART P R, VENKATAKRISHNAN V. On the role and challenges of CFD in the aerospace industry[J]. The Aeronautical Journal, 2016, 120(1223): 209-232. DOI:10.1017/aer.2015.10 |
| [9] |
LEVEQUE R J. Finite volume methods for hyperbolic problems[M]. Cambridge: Cambridge University Press, 2002. doi: 10.1017/cbo9780511791253
|
| [10] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [11] |
WANG J, WANG L P, XIAO Z, et al. A hybrid numerical simulation of isotropic compressible turbulence[J]. Journal of Computational Physics, 2010, 229(13): 5257-5279. DOI:10.1016/j.jcp.2010.03.042 |
| [12] |
WANG J C, SHI Y P, WANG L P, et al. Scaling and statistics in three-dimensional compressible turbulence[J]. Physical Review Letters, 2012, 108(21): 214505. DOI:10.1103/physrevlett.108.214505 |
| [13] |
ECONOMON T D, PALACIOS F, COPELAND S R, et al. SU2: an open-source suite for multiphysics simulation and design[J]. AIAA Journal, 2016, 54(3): 828-846. DOI:10.2514/1.j053813 |
| [14] |
LONGO J M A, HANNEMANN K, HANNEMANN V. The challenge of modeling high speed flows[R]. German Aerospace Center, 2007.
|
| [15] |
SHAN X W. Simulation of Rayleigh-Bénard convection using a lattice Boltzmann method[J]. Physical Review E, 1997, 55(3): 2780-2788. DOI:10.1103/physreve.55.2780 |
| [16] |
HE X Y, CHEN S Y, DOOLEN G D. A novel thermal model for the lattice Boltzmann method in incompressible limit[J]. Journal of Computational Physics, 1998, 146(1): 282-300. DOI:10.1006/jcph.1998.6057 |
| [17] |
SHI Y, ZHAO T S, GUO Z L. Thermal lattice Bhatnagar-Gross-Krook model for flows with viscous heat dissipation in the incompressible limit[J]. Physical Review E, 2004, 70: 066310. DOI:10.1103/PhysRevE.70.066310 |
| [18] |
GUO Z L, ZHENG C, SHI B. Thermal lattice Boltzmann equation for low Mach number flows: Decoupling model[J]. Physical Review E, 2007, 75: 036704. DOI:10.1103/physreve.75.036704 |
| [19] |
LI Q, HE Y L, WANG Y, et al. Coupled double-distribution-function lattice Boltzmann method for the compressible Navier-Stokes equations[J]. Physical Review E, 2007, 76(5): 056705. DOI:10.1103/physreve.76.056705 |
| [20] |
LI Q, LUO K H, HE Y L, et al. Coupling lattice Boltzmann model for simulation of thermal flows on standard lattices[J]. Physical Review E, 2012, 85: 016710. DOI:10.1103/physreve.85.016710 |
| [21] |
QIAN Y H. Simulating thermohydrodynamics with lattice BGK models[J]. Journal of Scientific Computing, 1993, 8(3): 231-242. DOI:10.1007/BF01060932 |
| [22] |
ALEXANDER F J, CHEN S, STERLING J D. Lattice Boltzmann thermohydrodynamics[J]. Physical Review E, 1993, 47(4): R2249. DOI:10.1103/physreve.47.r2249 |
| [23] |
CHEN Y, OHASHI H, AKIYAMA M. Thermal lattice Bhatnagar-Gross-Krook model without nonlinear deviations in macrodynamic equations[J]. Physical Review E, 1994, 50(4): 2776. DOI:10.1103/physreve.50.2776 |
| [24] |
WATARI M, TSUTAHARA M. Two-dimensional thermal model of the finite-difference lattice Boltzmann method with high spatial isotropy[J]. Physical Review E, 2003, 67(3): 036306. DOI:10.1103/physreve.67.036306 |
| [25] |
WATARI M, TSUTAHARA M. Possibility of constructing a multispeed Bhatnagar-Gross-Krook thermal model of the lattice Boltzmann method[J]. Physical Review E, 2004, 70(1): 016703. DOI:10.1103/physreve.70.016703 |
| [26] |
KATAOKA T, TSUTAHARA M. Lattice Boltzmann model for the compressible Navier-Stokes equations with flexible specific-heat ratio[J]. Physical Review E, 2004, 69(3): 035701. DOI:10.1103/physreve.69.035701 |
| [27] |
SHAN X W, HE X Y. Discretization of the velocity space in the solution of the Boltzmann equation[J]. Physical Review Letters, 1998, 80(1): 65-68. DOI:10.1103/physrevlett.80.65 |
| [28] |
GRAD H. Note on N-dimensional Hermite polynomials[J]. Communications on Pure and Applied Mathematics, 1949, 2(4): 325-330. DOI:10.1002/cpa.3160020402 |
| [29] |
GRAD H. On the kinetic theory of rarefied gases[J]. Communications on Pure and Applied Mathematics, 1949, 2(4): 331-407. DOI:10.1002/cpa.3160020403 |
| [30] |
SHAN X W, YUAN X F, CHEN H D. Kinetic theory representation of hydrodynamics: a way beyond the Navier–Stokes equation[J]. Journal of Fluid Mechanics, 2006, 550: 413-441. DOI:10.1017/s0022112005008153 |
| [31] |
XU A G, ZHANG G C, GAN Y B, et al. Lattice Boltzmann modeling and simulation of compressible flows[J]. Frontiers of Physics, 2012, 7(5): 582-600. DOI:10.1007/s11467-012-0269-5 |
| [32] |
GUO Z L, ZHENG C G, SHI B C. Discrete lattice effects on the forcing term in the lattice Boltzmann method[J]. Physical Review E, 2002, 65: 046308. DOI:10.1103/physreve.65.046308 |
| [33] |
郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009. GUO Z L, ZHENG C G. Theory and applications of lattice Boltzmann method[M]. Beijing: Science Press, 2009. (in Chinese) |
| [34] |
HAYWARD A J. Compressibility equations for liquids: a comparative study[J]. British Journal of Applied Physics, 1967, 18(7): 965-977. DOI:10.1088/0508-3443/18/7/312 |
| [35] |
WOLF-GLADROW D A. Lattice-gas cellular automata and lattice Boltzmann models-an introduction[M]. Springer, 2000
|
| [36] |
何雅玲, 王勇, 李庆, 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2009. HE Y L, WANG Y, LI Q, Lattice Boltzmann Method: Theory and Application[M]. Beijing: Science Press, 2009. |
| [37] |
VIGGEN E. The lattice Boltzmann method: fundamentals and acoustics[D]. Norwegian University of Science and Technology , 2014. https://ntnuopen.ntnu.no/ntnu-xmlui/bitstream/handle/11250/2370925/697490_FULLTEXT01.pdf?sequence = 1&isAllowed = y
|
| [38] |
GAN Y B, XU A G, ZHANG G C, et al. Lattice BGK kinetic model for high-speed compressible flows: Hydrodynamic and nonequilibrium behaviors[J]. EPL (Europhysics Letters), 2013, 103(2): 24003. DOI:10.1209/0295-5075/103/24003 |
| [39] |
许爱国, 张广财, 李英骏, 等. 非平衡与多相复杂系统模拟研究: Lattice Boltzmann动理学理论与应用[J]. 物理学进展, 2014, 34(3): 136-167. XU A G, ZHANG G C, LI Y J, et al. Modeling and simulation of nonequilibrium and multiphase complex systems: lattice Boltzmann kinetic theory and application[J]. Progress in Physics, 2014, 34(3): 136-167. (in Chinese) |
| [40] |
LIN C D, LUO K H. Discrete Boltzmann modeling of unsteady reactive flows with nonequilibrium effects[J]. Physical Review E, 2019, 99: 012142. DOI:10.1103/physreve.99.012142 |
| [41] |
许爱国, 张广财, 应阳君. 燃烧系统的离散Boltzmann建模与模拟研究进展[J]. 物理学报, 2015, 64(18): 184701. XU A G, ZHANG G, YING Y. Progess of discrete Boltzmann modeling and simulation of combustion system[J]. Acta Physica Sinica, 2015, 64(18): 184701. DOI:10.7498/aps.64.184701 (in Chinese) |
| [42] |
许爱国, 陈杰, 宋家辉, 等. 多相流系统的离散玻尔兹曼研究进展[J]. 空气动力学学报, 2021, 39(3): 138-169. XU A G, CHEN J, SONG J H, et al. Progress of discrete Boltzmann study on multiphase complex flows[J]. Acta Aerodynamica Sinica, 2021, 39(3): 138-169. DOI:10.7638/kqdlxxb-2021.0021 (in Chinese) |
| [43] |
SHAN X W. Central-moment-based Galilean-invariant multiple-relaxation-time collision model[J]. Physical Review E, 2019, 100(4): 043308. DOI:10.1103/physreve.100.043308 |
| [44] |
HUANG K. Statistical mechanics[M]. John Wiley & Sons, 1987.
|
| [45] |
NIE X B, SHAN X, CHEN H. Galilean invariance of lattice Boltzmann models[J]. EPL (Europhysics Letters), 2008, 81(3): 34005. DOI:10.1209/0295-5075/81/34005 |
| [46] |
SHAN X W. General solution of lattices for Cartesian lattice Bhatanagar-Gross-Krook models[J]. Physical Review E, 2010, 81: 036702. DOI:10.1103/physreve.81.036702 |
| [47] |
SHAN X W. The mathematical structure of the lattices of the lattice Boltzmann method[J]. Journal of Computational Science, 2016, 17: 475-481. DOI:10.1016/j.jocs.2016.03.002 |
| [48] |
SPILLER D, DÜNWEG B. Semiautomatic construction of lattice Boltzmann models[J]. Physical Review E, 2020, 101: 043310. DOI:10.1103/PhysRevE.101.043310 |
| [49] |
DÜNWEG B. Lattice-Boltzmann-weights[CP]. https://github.com/BDuenweg/Lattice-Boltzmann-weights
|
| [50] |
DOMBROWSKI M. Lattice-Boltzmann weights[CP]. https://i10git.cs.fau.de/ed52egek/lbmweights
|
| [51] |
PHILIPPI P C, HEGELE L A, DOS SANTOS L O E, et al. From the continuous to the lattice Boltzmann equation: The discretization problem and thermal models[J]. Physical Review E, 2006, 73(5): 056702. DOI:10.1103/physreve.73.056702 |
| [52] |
GUZIK S M, WEISGRABER T H, COLELLA P, et al. Interpolation methods and the accuracy of lattice-Boltzmann mesh refinement[J]. Journal of Computational Physics, 2014, 259: 461-487. DOI:10.1016/j.jcp.2013.11.037 |
| [53] |
MITTAL R, IACCARINO G. Immersed boundary methods[J]. Annual Review of Fluid Mechanics, 2005, 37(1): 239-261. DOI:10.1146/annurev.fluid.37.061903.175743 |
| [54] |
黄俊涛. 格子Boltzmann方法的边界和界面格式[M]. 北京: 清华大学出版社, 2021. HUANG JT. Boundary and interface schemes for the lattice Boltzmann method[M]. Beijing: Tsinghua University Press, 2021. |
| [55] |
PENG Y, SHU C, CHEW Y T, et al. Application of multi-block approach in the immersed boundary-lattice Boltzmann method for viscous fluid flows[J]. Journal of Computational Physics, 2006, 218(2): 460-478. DOI:10.1016/j.jcp.2006.02.017 |
| [56] |
ZOU Q S, HE X Y. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids, 1997, 9(6): 1591-1598. DOI:10.1063/1.869307 |
| [57] |
REIDER M B, STERLING J D. Accuracy of discrete-velocity BGK models for the simulation of the incompressible Navier-Stokes equations[J]. Computers & Fluids, 1995, 24(4): 459-467. DOI:10.1016/0045-7930(94)00037-Y |
| [58] |
CAO N Z, CHEN S Y, JIN S, et al. Physical symmetry and lattice symmetry in the lattice Boltzmann method[J]. Physical Review E, 1997, 55(1): R21. DOI:10.1103/physreve.55.r21 |
| [59] |
SOFONEA V, SEKERKA R F. Viscosity of finite difference lattice Boltzmann models[J]. Journal of Computational Physics, 2003, 184(2): 422-434. DOI:10.1016/S0021-9991(02)00026-8 |
| [60] |
WANG Y, HE Y L, ZHAO T S, et al. Implicit-explicit finite-difference lattice Boltzmann method for compressible flows[J]. International Journal of Modern Physics C, 2007, 18(12): 1961-1983. DOI:10.1142/s0129183107011868 |
| [61] |
张涵信. 无波动、无自由参数的耗散差分格式[J]. 空气动力学学报, 1988, 6(2): 143-165. ZHANG H X. Non-oscillatory and non-free-parameter dissipation difference scheme[J]. Acta Aerodynamica Sinica, 1988, 6(2): 143-165. (in Chinese) |
| [62] |
GUO Z, ZHAO T S. Explicit finite-difference lattice Boltzmann method for curvilinear coordinates[J]. Physical Review E, 2003, 67: 066709. DOI:10.1103/physreve.67.066709 |
| [63] |
PARESCHI L, RUSSO G. Implicit-explicit Runge-Kutta schemes and applications to hyperbolic systems with relaxation[J]. Journal of Scientific Computing, 2005, 25(1): 129-155. DOI:10.1007/s10915-004-4636-4 |
| [64] |
NANNELLI F, SUCCI S. The lattice Boltzmann equation on irregular lattices[J]. Journal of Statistical Physics, 1992, 68(3-4): 401-407. DOI:10.1007/BF01341755 |
| [65] |
BENZI R, SUCCI S, VERGASSOLA M. The lattice Boltzmann equation: theory and applications[J]. Physics Reports, 1992, 222(3): 145-197. DOI:10.1016/0370-1573(92)90090-M |
| [66] |
CHEN H D. Volumetric formulation of the lattice Boltzmann method for fluid dynamics: Basic concept[J]. Physical Review E, 1998, 58(3): 3955-3963. DOI:10.1103/physreve.58.3955 |
| [67] |
PENG G W, XI H W, DUNCAN C, et al. Lattice Boltzmann method on irregular meshes[J]. Physical Review E, 1998, 58(4): R4124. DOI:10.1103/physreve.58.r4124 |
| [68] |
STIEBLER M, TÖLKE J, KRAFCZYK M. An upwind discretization scheme for the finite volume lattice Boltzmann method[J]. Computers & Fluids, 2006, 35(8-9): 814-819. DOI:10.1016/j.compfluid.2005.09.002 |
| [69] |
PATIL D V, LAKSHMISHA K N. Finite volume TVD formulation of lattice Boltzmann simulation on unstructured mesh[J]. Journal of Computational Physics, 2009, 228(14): 5262-5279. DOI:10.1016/j.jcp.2009.04.008 |
| [70] |
DONEA J, HUERTA A. Finite element methods for flow problems[M]. John Wiley & Sons, 2003DOI:10.1002/0470013826
|
| [71] |
LÖHNER R. Applied computational fluid dynamics techniques: an introduction based on finite element methods[M]. John Wiley & Sons, 2008
|
| [72] |
LEE T, LIN C L. A characteristic Galerkin method for discrete Boltzmann equation[J]. Journal of Computational Physics, 2001, 171(1): 336-356. DOI:10.1006/jcph.2001.6791 |
| [73] |
SHI X, LIN J Z, YU Z S. Discontinuous Galerkin spectral element lattice Boltzmann method on triangular element[J]. International Journal for Numerical Methods in Fluids, 2003, 42(11): 1249-1261. DOI:10.1002/fld.594 |
| [74] |
MACMECCAN R M, CLAUSEN J R, NEITZEL G P, et al. Simulating deformable particle suspensions using a coupled lattice-Boltzmann and finite-element method[J]. Journal of Fluid Mechanics, 2009, 618: 13-39. DOI:10.1017/s0022112008004011 |
| [75] |
KRÜGER T, VARNIK F, RAABE D. Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice Boltzmann finite element method[J]. Computers & Mathematics with Applications, 2011, 61(12): 3485-3505. DOI:10.1016/j.camwa.2010.03.057 |
| [76] |
STERLING J D, CHEN S Y. Stability analysis of lattice Boltzmann methods[J]. Journal of Computational Physics, 1996, 123(1): 196-206. DOI:10.1006/jcph.1996.0016 |
| [77] |
MARIÉ S, RICOT D, SAGAUT P. Comparison between lattice Boltzmann method and Navier-Stokes high order schemes for computational aeroacoustics[J]. Journal of Computational Physics, 2009, 228(4): 1056-1070. DOI:10.1016/j.jcp.2008.10.021 |
| [78] |
SILVA G, SEMIAO V. Truncation errors and the rotational invariance of three-dimensional lattice models in the lattice Boltzmann method[J]. Journal of Computational Physics, 2014, 269: 259-279. DOI:10.1016/j.jcp.2014.03.027 |
| [79] |
BAUER M, SILVA G, RÜDE U. Truncation errors of the D3Q19 lattice model for the lattice Boltzmann method[J]. Journal of Computational Physics, 2020, 405: 109111. DOI:10.1016/j.jcp.2019.109111 |
| [80] |
MCNAMARA G R, GARCIA A L, ALDER B J. Stabilization of thermal lattice Boltzmann models[J]. Journal of Statistical Physics, 1995, 81(1-2): 395-408. DOI:10.1007/BF02179986 |
| [81] |
WISSOCQ G, SAGAUT P, BOUSSUGE J F. An extended spectral analysis of the lattice Boltzmann method: modal interactions and stability issues[J]. Journal of Computational Physics, 2019, 380: 311-333. DOI:10.1016/j.jcp.2018.12.015 |
| [82] |
SIEBERT D N, HEGELE L A, PHILIPPI P C. Lattice Boltzmann equation linear stability analysis: Thermal and athermal models[J]. Physical Review E, 2008, 77(2): 026707. DOI:10.1103/physreve.77.026707 |
| [83] |
KRÜGER T, KUSUMAATMAJA H, KUZMIN A, et al. . The Lattice Boltzmann method: principles and practice[M]. Switzerland: Springer International Publishing, 2017. DOI:10.1007/978-3-319-44649-3
|
| [84] |
LADD A J C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation[J]. Journal of Fluid Mechanics, 1994, 271: 285-309. DOI:10.1017/s0022112094001771 |
| [85] |
KIM S H, PITSCH H. A generalized periodic boundary condition for lattice Boltzmann method simulation of a pressure driven flow in a periodic geometry[J]. Physics of Fluids, 2007, 19(10): 108101. DOI:10.1063/1.2780194 |
| [86] |
IZQUIERDO S, FUEYO N. Characteristic nonreflecting boundary conditions for open boundaries in lattice Boltzmann methods[J]. Physical Review E, 2008, 78(4): 046707. DOI:10.1103/physreve.78.046707 |
| [87] |
HEUBES D, BARTEL A, EHRHARDT M. Characteristic boundary conditions in the lattice Boltzmann method for fluid and gas dynamics[J]. Journal of Computational and Applied Mathematics, 2014, 262: 51-61. DOI:10.1016/j.cam.2013.09.019 |
| [88] |
MALASPINAS O, CHOPARD B, LATT J. General regularized boundary condition for multi-speed lattice Boltzmann models[J]. Computers & Fluids, 2011, 49(1): 29-35. DOI:10.1016/j.compfluid.2011.04.010 |
| [89] |
MENG J P, ZHANG Y H. Diffuse reflection boundary condition for high-order lattice Boltzmann models with streaming-collision mechanism[J]. Journal of Computational Physics, 2014, 258: 601-612. DOI:10.1016/j.jcp.2013.10.057 |
| [90] |
LEE H C, BAWAZEER S, MOHAMAD A A. Boundary conditions for lattice Boltzmann method with multispeed lattices[J]. Computers & Fluids, 2018, 162: 152-159. DOI:10.1016/j.compfluid.2017.12.011 |
| [91] |
HECHT M, HARTING J. Implementation of on-site velocity boundary conditions for D3Q19 lattice Boltzmann simulations[J]. Journal of Statistical Mechanics:Theory and Experiment, 2010, 2010(1): P01018. DOI:10.1088/1742-5468/2010/01/p01018 |
| [92] |
KLASS F, GABBANA A, BARTEL A. A non-equilibrium bounce-back boundary condition for thermal multispeed LBM[J]. Journal of Computational Science, 2021, 53: 101364. DOI:10.1016/j.jocs.2021.101364 |
| [93] |
GEIER M, SCHÖNHERR M. Esoteric twist: an efficient in-place streaming algorithmus for the lattice Boltzmann method on massively parallel hardware[J]. Computation, 2017, 5(4): 19. DOI:10.3390/computation5020019 |
| [94] |
PEREPELKINA A, LEVCHENKO V, ZAKIROV A. New compact streaming in LBM with ConeFold LRnLA algorithms[C]//6th Russian Supercomputing Days, Springer, 2020: 50-62. DOI:10.1007/978-3-030-64616-5_5
|
| [95] |
ZAKIROV A, PEREPELKINA A, LEVCHENKO V, et al. Streaming techniques: revealing the natural concurrency of the lattice Boltzmann method[J]. The Journal of Supercomputing, 2021, 77(10): 11911-11929. DOI:10.1007/s11227-021-03762-z |
| [96] |
TÖLKE J, FREUDIGER S, KRAFCZYK M. An adaptive scheme using hierarchical grids for lattice Boltzmann multi-phase flow simulations[J]. Computers & Fluids, 2006, 35(8-9): 820-830. DOI:10.1016/j.compfluid.2005.08.010 |
| [97] |
EITEL-AMOR G, MEINKE M, SCHRÖDER W. A lattice-Boltzmann method with hierarchically refined meshes[J]. Computers & Fluids, 2013, 75: 127-139. DOI:10.1016/j.compfluid.2013.01.013 |
| [98] |
姚皆可, 钟诚文, 李凯. 基于四叉树网格下的浸入边界-格子Boltzmann方法[J]. 空气动力学学报, 2013, 31(4): 525-532. YAO J K, ZHONG C W, LI K. Immersed boundary-lattice Boltzmann method based on quadtree grids[J]. Acta Aerodynamica Sinica, 2013, 31(4): 525-532. (in Chinese) |
| [99] |
XIAN W, TAKAYUKI A. Multi-GPU performance of incompressible flow computation by lattice Boltzmann method on GPU cluster[J]. Parallel Computing, 2011, 37(9): 521-535. DOI:10.1016/j.parco.2011.02.007 |
| [100] |
OBRECHT C, KUZNIK F, TOURANCHEAU B, et al. Multi-GPU implementation of the lattice Boltzmann method[J]. Computers & Mathematics with Applications, 2013, 65(2): 252-261. DOI:10.1016/j.camwa.2011.02.020 |
| [101] |
VALERO-LARA P, JANSSON J. Heterogeneous CPU+GPU approaches for mesh refinement over Lattice-Boltzmann simulations[J]. Concurrency and Computation:Practice and Experience, 2017, 29(7): e3919. DOI:10.1002/cpe.3919 |
 2022, Vol. 40
2022, Vol. 40