2. 中国航空工业集团 成都飞机设计研究所,成都 610091
2. Chengdu Aircraft Design & Research Institute, Aviation Industry Corporation of China, Chengdu 610091, China
内埋式武器在投放分离过程中,弹舱将演变为(带舱门)大尺度空腔。大尺度空腔是航空航天武器装备必不可少且普遍采用的一种典型结构形式,主要用于作战武器装载、动力燃油存储和起落架存放等,具有尺度大、结构复杂等特点。在动载荷激励下,空腔薄壁结构容易产生严重的振动和噪声,不仅影响武器装备的作战效能,甚至危及武器装备安全。因此,空腔绕流是空气动力学领域的一个重要且典型问题。
针对空腔中流动和噪声的复杂现象与物理机理,国内外科研工作者通过风洞试验和计算手段对干净弹舱(空腔)模型[1-4]进行了广泛深入的研究。具体包括分析流致振荡现象的成因[5-6],对空腔类型[7]、来流马赫数、边界层厚度等[3, 8]参数进行详细研究,并探讨了多种不同的控制措施[2, 9],对空腔设计具有重要的指导意义。Rossiter[10]提出了预测空腔噪声模态频率的半经验模型;Heller等[11]改进了此模型,将其推广到高马赫数(Ma = 2、3)的可压缩流动中。
空腔是弹舱的一种理想模型,实际中舱门的存在会使得空腔内非定常流动更加复杂,因而研究学者们对带舱门的空腔流动开展了研究和分析。首先是对带有静态舱门的空腔流动的研究:Blair和Stallings[12]采用风洞试验研究了不同舱门开度和舱门高度对导弹类物体在超声速空腔中投放的影响,结果表明舱门开度对弹体的气动载荷有显著影响,并且降低舱门高度会减少弹体的气动载荷;Lawson和Barakos[13]采用脱体涡模拟(DES)方法对舱门开启90°的空腔标模M219和1303无人机模型进行了模拟,并分析了舱门打开对弹体抛投的影响。Casper等[14]采用试验的方式模拟了带有舱门的复杂空腔中弹体抛投的流固耦合问题,发现增加空腔复杂度会引发弹体展向共振。其次在动态舱门的研究上,Sheta等[15]采用RANS/LES混合方法,模拟了超声速(Ma = 1.44)空腔舱门从5°打开到35°过程中的流动,发现在舱门运动到30°时,剪切层和舱内声波产生较强的相互作用,腔内壁面出现强的压力脉动;Loupy等[16]对比分析了固定开度舱门和动态舱门对马赫数为0.85的空腔流动、载荷和气动噪声的影响,发现舱门打开过程中的过渡阶段,舱门气动载荷增大,流动的脉动和总声压级增强,对空腔结构产生显著影响。
国内多位学者采用RANS方法模拟分析静态舱门[17]和舱门开启过程中[18]空腔动态气动特性和载荷的变化。吴继飞等[19-20]对Ma = 0.6空腔舱门的开闭问题开展了研究,设计了不同的运动方式,发现舱门运动时气动载荷发生明显变化,舱门打开30°时气动载荷最大,并分析了腔内和舱门的总声压级和声压谱特性。由于带舱门的空腔流动非定常效应显著,且流动的湍流结构复杂,所以传统的RANS方法捕捉复杂流动结构比较困难。闫盼盼等[21]采用基于
考虑运动舱门时,空腔中气动与噪声特性会变得更加复杂,预测难度增加,而国内对带运动舱门的复杂空腔流动与噪声的研究较少。为了研究舱门运动情况下的空腔复杂流动现象,深入分析静、动态舱门对空腔复杂流动的影响,本文采用嵌套重叠网格方法对舱门和空腔分别生成网格,采用改进的脱体涡模拟方法对亚声速(Ma = 0.6)空腔流场进行数值模拟,从流场特性、湍流结构、脉动特性上分析舱门对湍流流场和腔内噪声的影响。
1 数值方法采用有限体积方法求解三维非定常Navier-Stokes方程:
| $ \frac{\partial }{{\partial t}}\iiint_\varOmega {{\boldsymbol W}{\rm{d}}\varOmega + \iint_S {\left[ {{{\boldsymbol F}_{{c}}}({\boldsymbol W}) + {{\boldsymbol F}_{{v}}}({\boldsymbol W})} \right]{\rm{d}}S = }}0 $ | (1) |
式中,
| $ {\boldsymbol W} = {(\rho ,\rho u,\rho v,\rho w,\rho E)^{\rm{T}}} $ | (2) |
其中,ρ为密度,u、v、w是速度
| $ {{\boldsymbol F}_{{c}}}({\boldsymbol W}) = {\boldsymbol F}_{{c}}^{S}({\boldsymbol W}) - {V_{gn}}{\boldsymbol W} $ | (3) |
其中,
针对空腔流动强脉动、强湍流的特点,采用RANS/LES混合方法进行计算,本文采用改进的脱体涡湍流模拟方法(Improved Delayed DES,IDDES)[22],解析空腔内分离区域的湍流结构和脉动特性。基于以上的数值方法,本文发展了一套基于有限体积方法的多块结构网格求解器,并通过多种复杂流动问题验证其准确性和可靠性[23-26]。
1.1 高精度低耗散格式双时间步推进方法用于非定常问题的计算,采用无矩阵形式的LU-SGS格式。流场求解空间格式采用一种高精度低耗散混合格式[27]离散对流项。该格式由无耗散的中心格式和AUSMDV[28]迎风格式组成,其通量
| $ {q_{_{{L/R}}}} = \alpha q_{_{{L/R}}}^{{\rm{MUSCL}}} + (1 - \alpha )q_{_{{L/R}}}^{{\rm{SYM4}}} $ | (4) |
式中,
| $ q_{_{i + 1/2,{L/R}}}^{{\rm{SYM4}}} = \frac{7}{{12}}({q_{_i}} + {q_{_{i + 1}}}) - \frac{1}{{12}}({q_{_{i - 1}}} + {q_{_{i + 2}}}) $ | (5) |
加权系数
| $ {\alpha _{i + 1/2}} = \max (0.1,{\rm{ }}{\phi _i},{\rm{ }}{\phi _{i + 1}}) $ | (6) |
式中,
| $ \phi = \frac{{{{(\nabla \cdot {\boldsymbol V})}^2}}}{{\left| {\nabla \times {\boldsymbol V}} \right| + {{(\nabla \cdot {\boldsymbol V})}^2} + {\varepsilon ^2}}} $ | (7) |
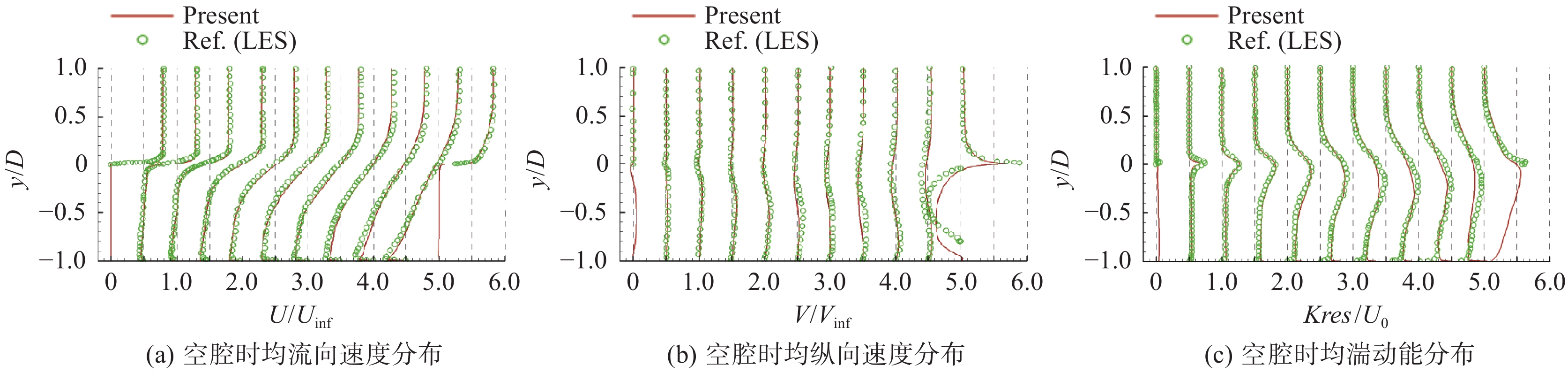
为验证高精度数值格式在空腔问题中的有效性,采用本文提出的格式对马赫数0.85空腔标模M219进行模拟分析,并与参考文献[32]的LES计算结果进行对比。网格单元总数量约800万,空腔内部与附近的网格数量约380万。对于马赫数为0.85的流动,时间步长为
|
图 1 空腔标模M219在Ma = 0.85时均速度与湍动能分布 Fig.1 Wall-normal profiles of the mean velocity and turbulence kinetic energy in canonical cavity M219 at Ma = 0.85 |
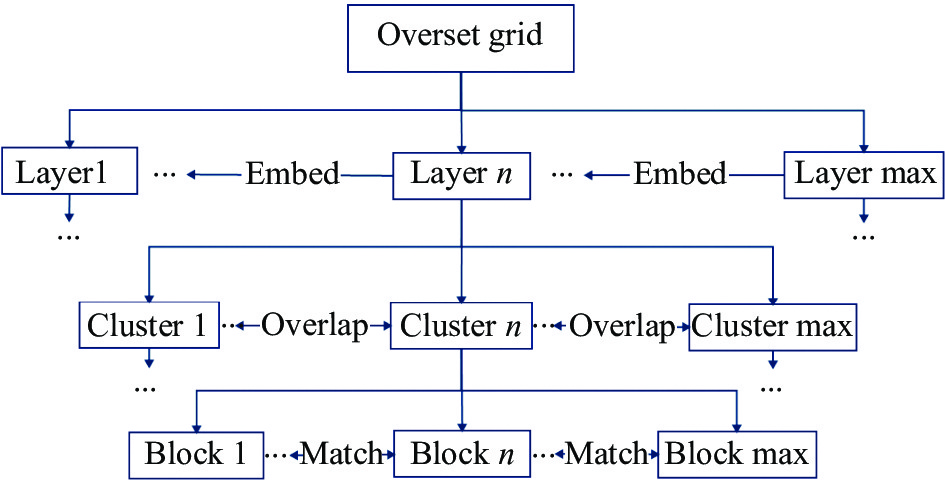
针对运动物体的网格生成问题,发展了快速的动态嵌套重叠网格方法[33]。首先通过采用分层嵌套重叠网格策略(如图2)对网格进行划分,然后采用自适应树结构完成网格切割和贡献单元搜索。引入壁面距离概念,设计了统一的分层嵌套重叠策略,同时实现了重叠网格切割和嵌套网格切割两个功能,完成重叠最小化的功能,使得重叠网格组装质量得到了改善。
|
图 2 分层嵌套重叠网格策略 Fig.2 Hierarchically embedded strategy of overset grids |
根据运动规律的不同,可将所有运动物体分为若干动态组,而所有静态物体归为唯一的静态组。各组分别构造独立的二叉树和八叉树辅助网格,并且每个组内的流场网格和二/八叉树网格的坐标均保持不变。即,各个动态分组仍然用各自原有的局部坐标系,但在每个时间步上记录下各动态组运动的位移。而在更新切割信息时,将所有被切割的坐标点变换到切割物体所在的局部坐标内,从而完成运动问题的网格切割。对于同一组内的切割,由于相对位置不变,只需进行一次切割,后续不需再改变。此方法使得二叉树和八叉树在运动过程中不必重新构造,只需进行坐标变换操作,大大节省了计算时间。表1给出了舱门运动时网格组装时间的对比。对于总计2 100多万的网格单元来说,两种动态嵌套重叠网格组装方法均可满足该类非定常流动计算的效率要求。
| 表 1 考虑运动舱门的空腔动态重叠网格组装的耗时统计 Table 1 Assembly time of overset grids for a cavity with moving doors |
|
|
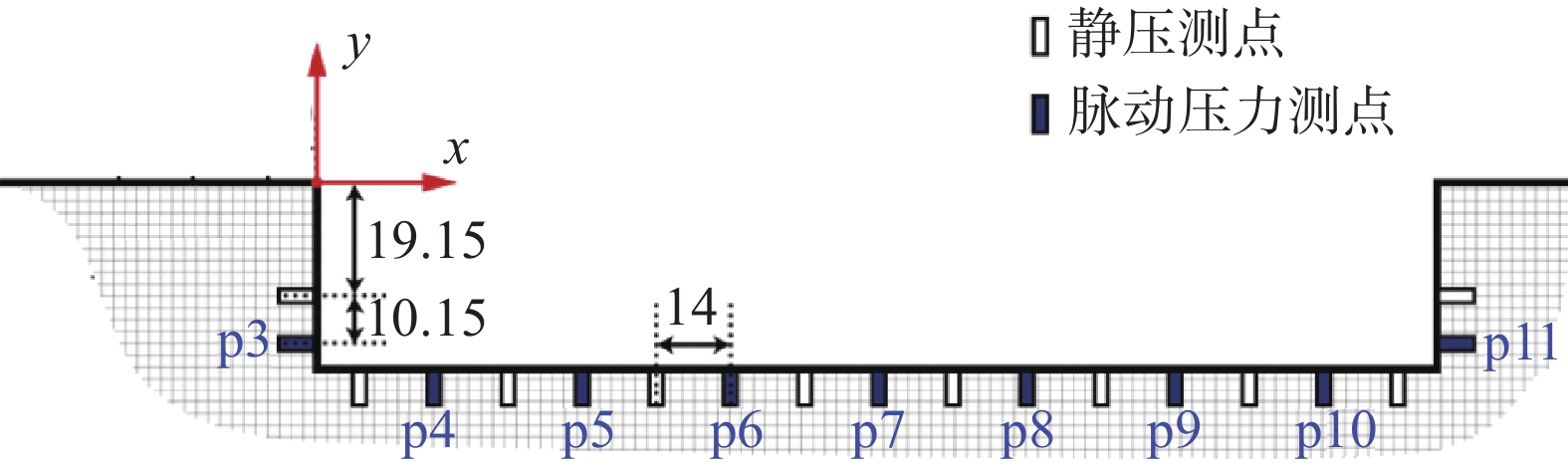
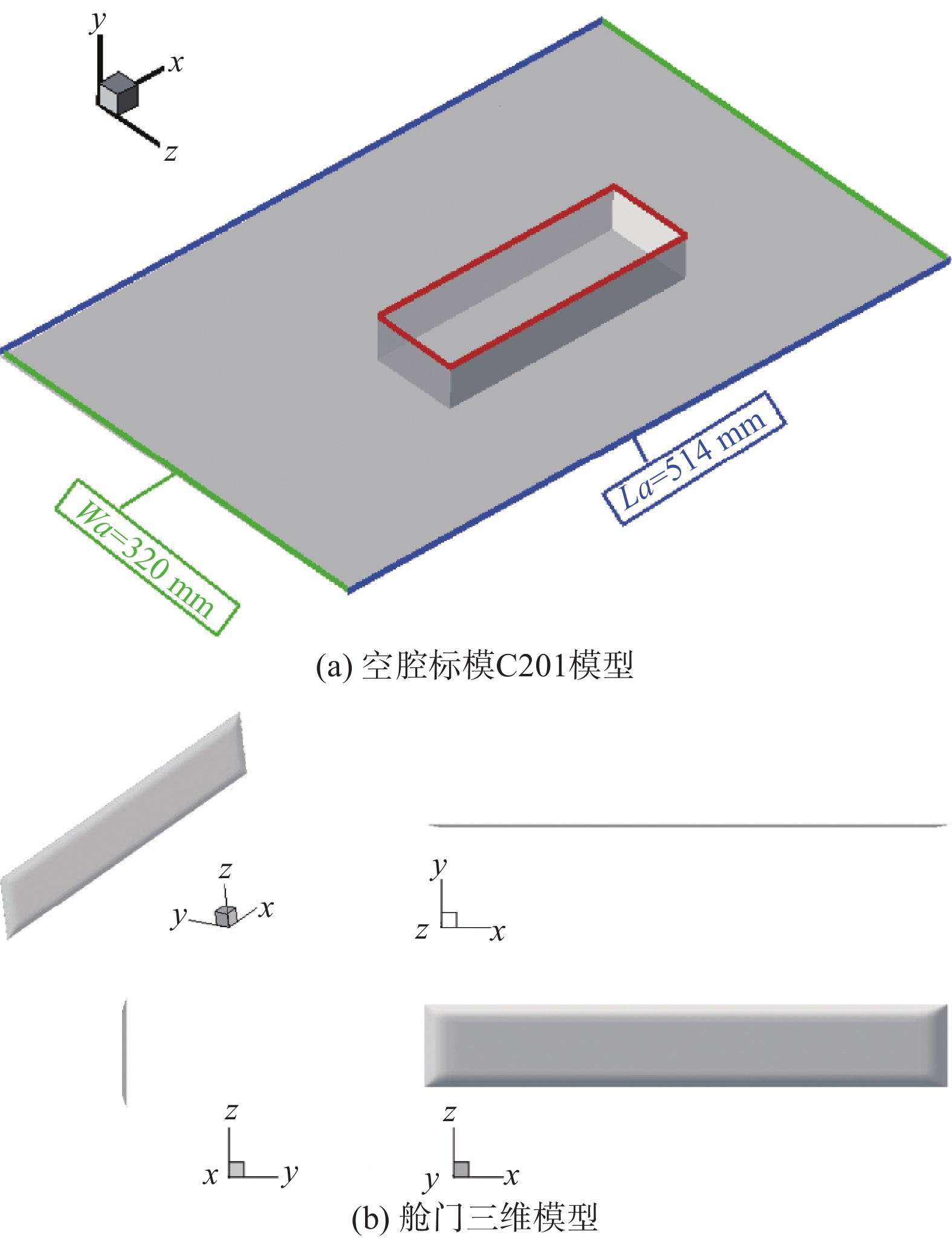
空腔标模C201由中国空气动力研究与发展中心设计,空腔底部、前后壁分别布置了静压测点和脉动压力测点(见图3)。本文采用的计算模型如图4(a)所示,与试验的模型外形一致。空腔长度(L)为200 mm,深度(D)为33.3 mm,宽度(W)为66.7 mm,空腔长深比L/D为6,宽深比W/D为2;与空腔相连壁面的长度和宽度分别是Wa和La。
|
图 3 空腔标模C201中截面的压力测点 Fig.3 Distribution of pressure probes in the central section of canonical cavity C201 |
参照文献[1]的数据选取舱门,舱门厚度1.5 mm,舱门四周采用弧形物面进行过渡。此构型与空腔标模M219的舱门外形有一定相似性。在舱门与空腔、舱门与舱门之间保留1 mm(约为舱门深度的3%)缝隙,这样可以保证缝隙处保留足够的网格用于数值模拟。舱门三维模型如图4(b)所示。
|
图 4 空腔标模C201与舱门计算模型 Fig.4 Geometry of canonical cavity C201 and doors |
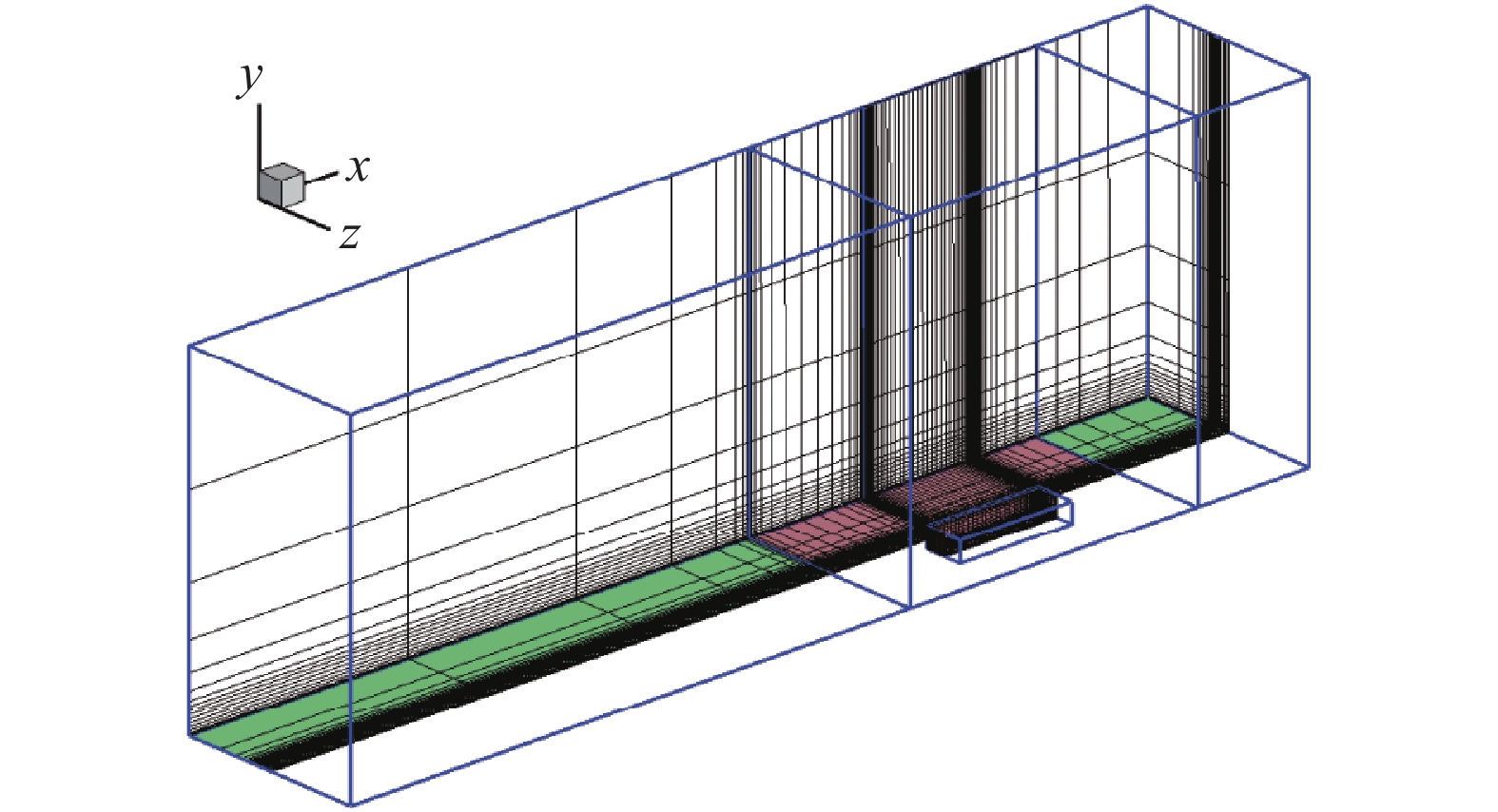
整个模型网格采用一个网格层,包含三个网格簇:空腔网格簇(其中包含背景网格)和两个舱门网格簇。图5给出了空腔的网格,由于网格在展向(z方向)是对称的,所以图中显示了一半网格。边界条件设置如下:在图5给出的模型中,红色为无滑移物面边界条件;绿色表示的是空腔前后的自由端,采用对称边界条件;展向的两个边界均采用对称边界条件;最上面的外场边界设置为入口/出口边界;前后外场分别为入口/出口边界。空腔网格采用结构网格,共计约1600万网格单元。
|
图 5 空腔标模C201计算模型与网格(每4个点显示一个网格点) Fig.5 Computational domain and grids for canonical cavity C201 |
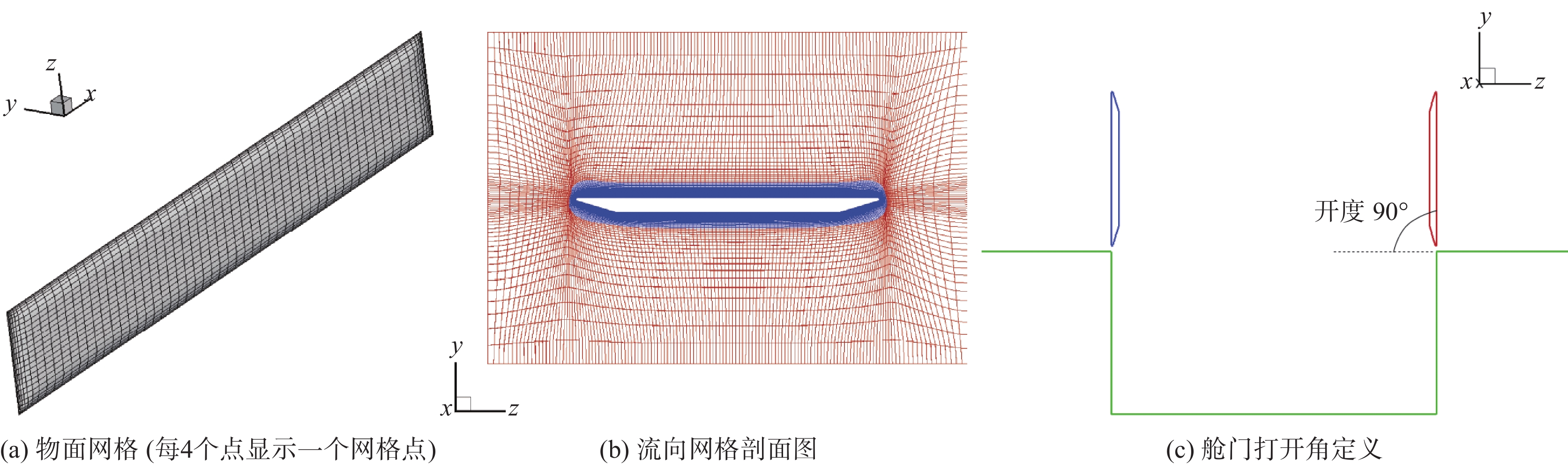
舱门采用沿着物面法向将物面网格向外推进的方法生成贴体网格,然后在外围采用矩形外场,使得外场网格的周向尺寸得到控制。单个舱门的网格单元共计约454万,图6(a)给出了舱门的物面网格,舱门的前向剖视图如图6(b)所示。舱门壁面的第一层网格厚度由
|
图 6 舱门计算网格与舱门打开角度(开度)定义 Fig.6 Computational grids for cavity doors and the definition of the door-opening angle |
剪切层流动是空腔复杂流场的重要因素之一,所以需要保留高质量的空腔剪切层网格。通过改进空腔壁面距离的计算方法,使得在四种不同舱门打开角度下均能保留空腔剪切层网格(见图7),从而保证剪切层流动计算的精细和准确。

|
图 7 四种不同舱门开度在 |
对无舱门的空腔标模C201亚声速流动(Ma = 0.6)进行模拟,来流条件为
图13(a)给出了中截面时均流场的压强系数分布和流线形状,在空腔后部存在一个较小的第二环流。在较低速来流条件下,剪切层厚度增长较大,大范围冲击到后壁、角落和底部。冲击后壁与角落的气流较为靠近剪切层核心区,流速较高,形成局部高压环流;而冲击底部的气流较为远离剪切层核心区,流速较低,被角落的高压环流所阻碍,提前回流形成了主环流。
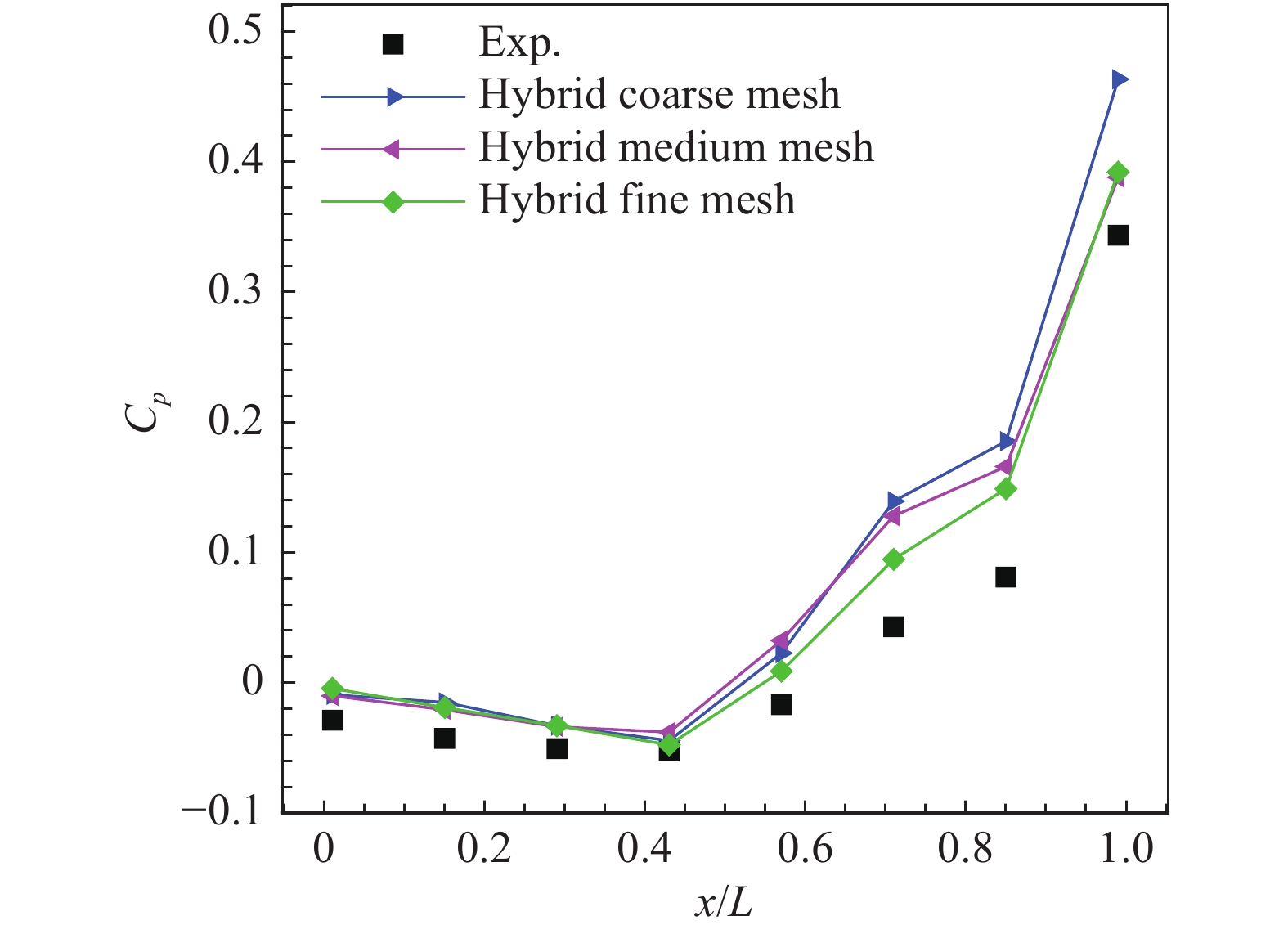
图8对比了三种不同网格尺度下腔内底部压力系数的分布与试验值的比较。随着网格的加密,计算结果趋于稳定。尽管其值高于试验结果,但是计算结果可以较好地预测压力系数的变化。从图中可以看出,底部压强分布表现为前段平缓下降、中段增长和后段快速上升,最后气流冲击后壁形成高压区域。
|
图 8 三种网格对腔内底部压力系数时均分布的影响 Fig.8 Grid convergence of the mean pressure coefficients at cavity floor compared to experimental distribution |
总声压级(overall sound pressure level,OASPL)可以通过湍流模拟得到的压力脉动来获得,其定义如下:
| $ {\rm{OASPL}} = 20\;\lg\ {\frac{{{p_{{{\rm{rms}}}}}}}{{p_{{\rm{ref}}}}}} $ | (8) |
式中,
| $ {p_{{{\rm{rms}}}}} = \mathop {\lim }\limits_{T \to \infty } \sqrt {\frac{1}{T}\int\limits_0^T {{{p'}^2}} {\rm{d}}t} = \sqrt {\frac{1}{N}\sum\limits_N {{{p'}^2}} } $ | (9) |
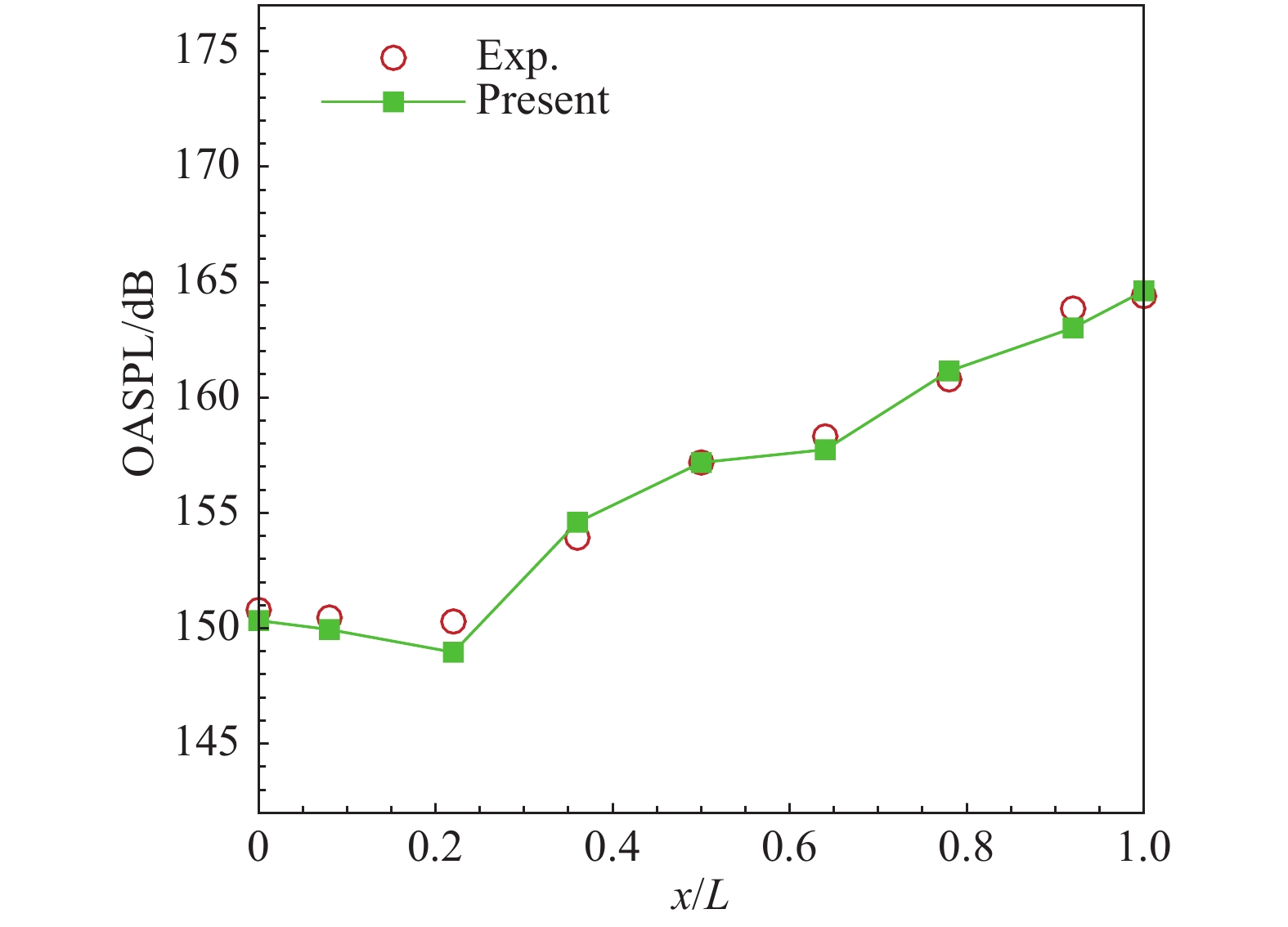
图9给出了C201空腔底部总声压级计算和试验结果,两者吻合较好。总声压级分布曲线表现出以下特点:在
|
图 9 空腔标模C201腔内底部总声压级 Fig.9 OASPL distribution at the floor of canonical cavity C201 without doors |

|
图 10 空腔标模C201底部声压级成分合成示意图 Fig.10 Sketch of the development of OASPL in canonical cavity C201 |
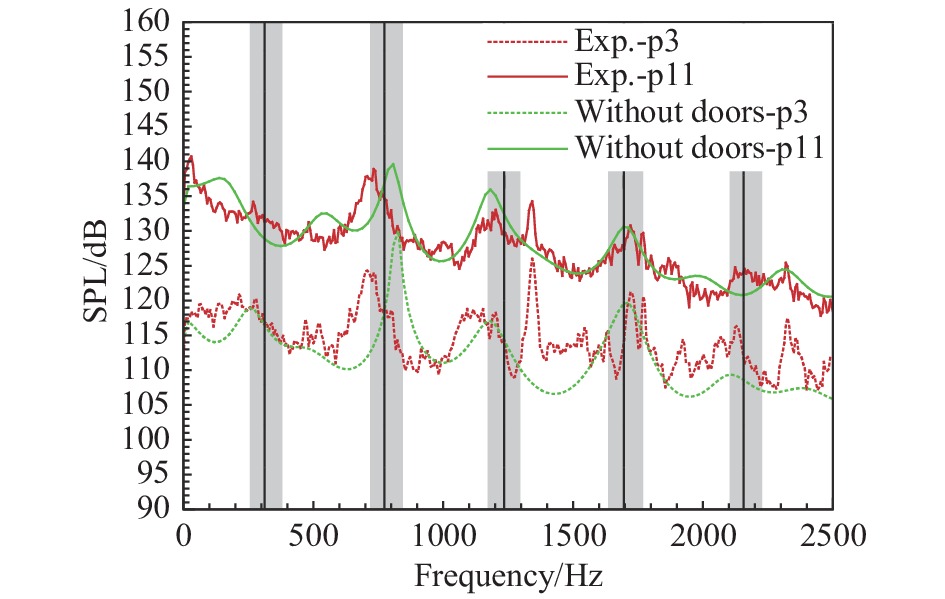
通过脉动压力功率谱分析空腔底部的频谱特性,对脉动压力
|
图 11 空腔标模C201腔内底部p3和p11测点脉动压强功率谱 Fig.11 Comparison of SPL of fluctuating pressure at probes p3 and p11 between numerical simulation and experiment |
在满足准定常假设时,可以对静态舱门直接模拟分析。采用发展的嵌套重叠网格方法和IDDES湍流模拟方法,对舱门开度分别为30°、60°、90°和120°的四种工况进行准定常流动模拟,分析其流动时均特性和流场动态特性。从时均流场(中截面时均流场和底部压力分布)、流场的动态特性(总声压级、脉动压强功率谱)和瞬时场湍流结构三个方面分析舱门对空腔流场产生的影响。本节采用的数值方法、计算方式与干净空腔模拟方法一致。
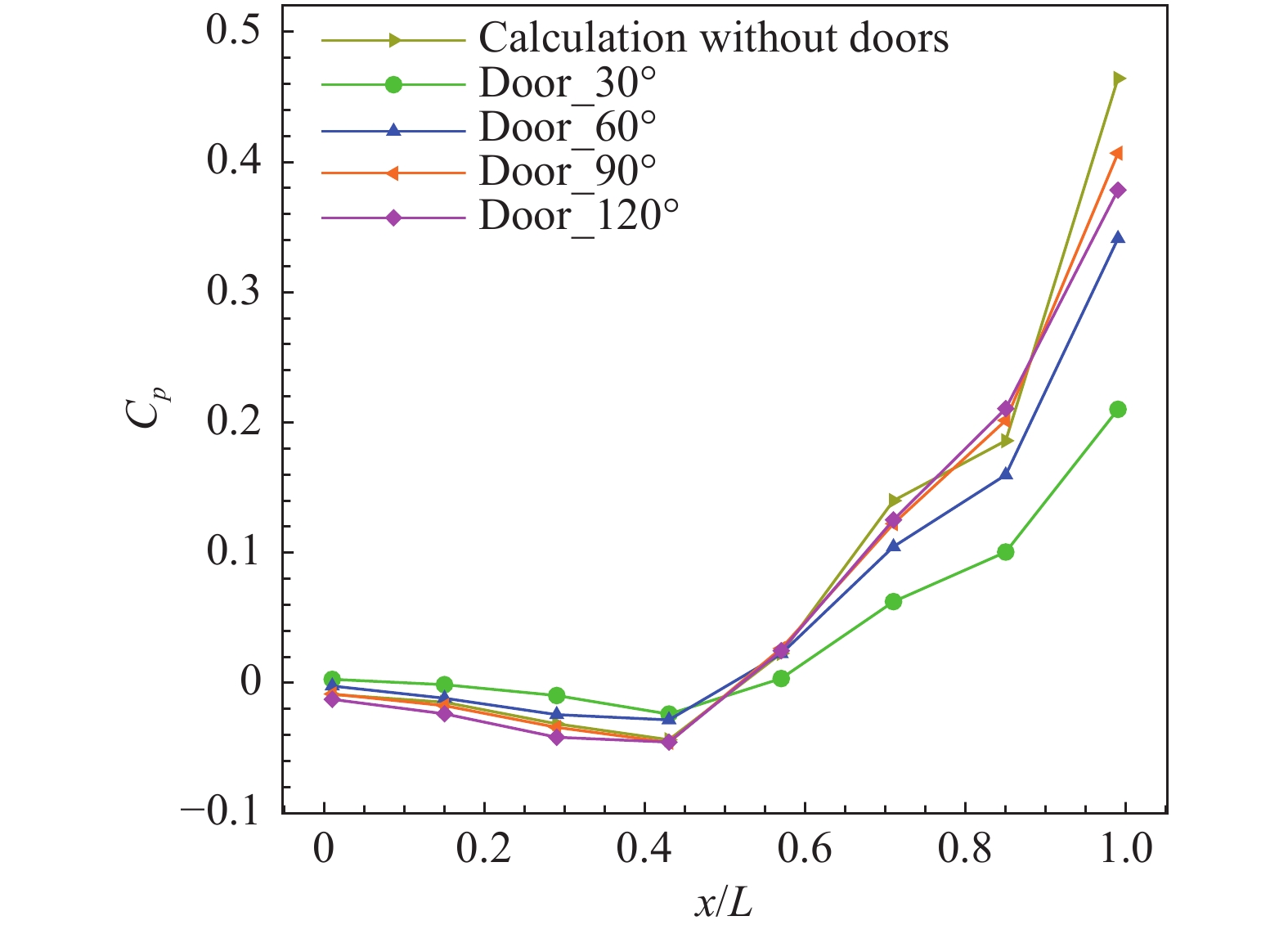
5.1 时均场特性分析将空腔底部的静压测点时均压力与干净空腔的结果进行对比分析,图12给出了不同状态下底部压力系数的分布。从腔内底部压力分布来看,舱门打开30°时,底部压力系数的分布与干净空腔的差别较大,前部压强有所升高,后部压强明显降低。在舱门打开60°、90°、120°时,腔内前半部分底部压力系数基本与干净空腔的计算结果一致,后半部分压力系数随着舱门打开角度的增加逐渐趋于干净空腔。开启角度为90°和120°时,时均压强系数分布与干净空腔基本一致。
图13给出了干净空腔和不同舱门开度的中截面时均流场压力系数云图和流线分布情况。从图中可以看出在舱门打开角度为30°时,空腔前缘附近的平板上,压力系数会升高,这是由于舱门的阻碍使得流动减速造成的。这种压强升高作用也使得空腔前部的负压区域的压强系数相对干净空腔要偏高。同时,对于30°开启角度,外流与空腔附近的流动受到舱门的阻挡,只能通过中截面附近的开口相互作用。特别是阻碍外流对剪切层的能量供给,使得后壁附近的压强相对干净空腔明显降低,导致30°时,空腔底面后部压强系数水平整体降低。此外,后壁附近的高压也受到舱门阻碍,在纵向方向只能在中截面开口处泄压,后部流线有更加明显地向上弯曲。
|
图 12 四种舱门开度(30°、60°、90°、120°)对空腔底部压力系数的影响 Fig.12 Impacts of the door-opening angle on mean pressure coefficients at the cavity floor |

|
图 13 干净空腔和四种舱门开度下中截面平均流场压力系数与流线分布 Fig.13 Impacts of door-opening angles on the streamlines and mean pressure contours in the middle section of cavity C201 |
舱门开度为60°、90°和120°时,空腔前缘平板同一位置的压力系数逐渐降低,且后壁高压区和后壁拐角处低压区的范围较舱门开度为30°时逐渐变大,并与干净空腔的结果趋于一致。这与“舱门打开角度越大,对流动的限制明显越小”的物理原因是一致的。
另外,相比于干净空腔,随着舱门打开角的不断增大,主涡位置沿流向不断地后移并靠近干净空腔主涡位置。舱门打开120°时,湍流结构基本上与干净空腔的一致,但是在前壁附近的流场结构与干净空腔有所区别。由此可知,随着空腔打开角度的增加,腔内时均流场的形态、涡的结构与干净空腔的结果逐渐趋于一致。
5.2 总声压级图14给出了四种舱门开度下空腔底部总声压级的分布。从图中可以看出,舱门开度30°时,底部各个位置的总声压级较干净空腔均明显下降,但变化趋势与干净空腔的结果基本一致。舱门打开90°时,总声压级与120°的变化趋势一致,前者的值略高1~2 dB。舱门开度为60°时,总声压级腔内前半部分的分布特点与90°、120°的结果基本一致;而在腔内后半部分,其总声压级明显有所改变。
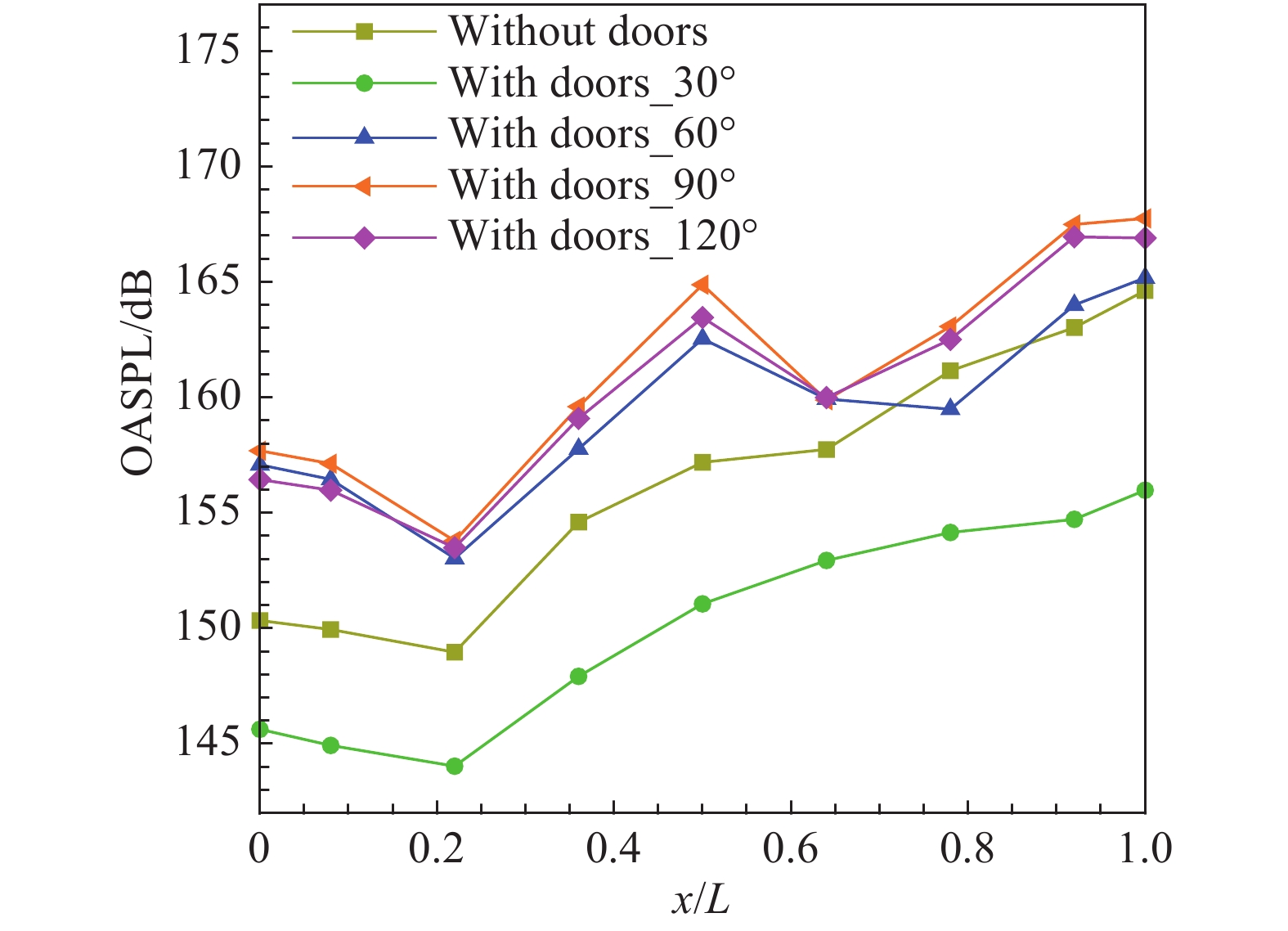
|
图 14 干净弹舱与四种舱门开度下的弹舱底部总声压级分布 Fig.14 Impacts of door-opening angles on OASPL at the cavity floor |
本文认为导致噪声升高的原因在于舱门阻碍了腔内噪声向外传播。从图14可以看出,舱门分别开启60°、90°、120°时,三种条件下的声压级分布几乎一致,因此可知噪声升高与舱门开启角度无关,只与舱门的存在有关。舱门的存在使得空腔内部的脉动能量无法以声波的形式沿展向传播,只能沿着两舱门开口方向传播,第二阶模态的能量无法得到有效释放,这样就导致腔内噪声强度升高。本文中舱门开度为90°时,总声压级的计算结果与空腔标模M219在马赫数0.85下的试验结果[1]分布特点相似,呈现出“W”形态的分布。
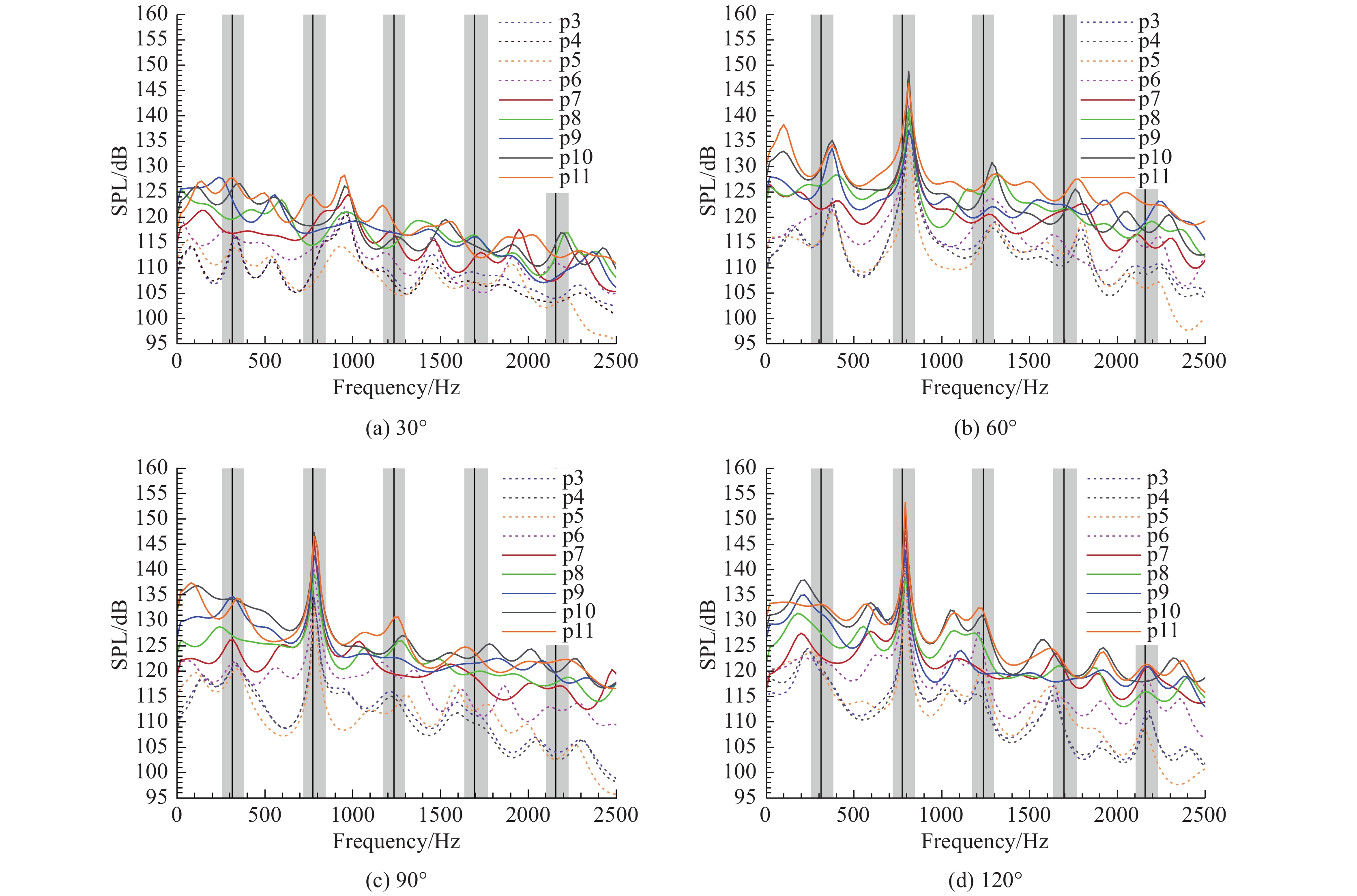
5.3 脉动压强功率谱空腔中的噪声主要由宽频白噪声和窄频噪声(Rossiter模态)两部分组成[13]。白噪声是由流动结构产生,其来源为自由来流的脉动、剪切层和湍流等。第二部分也称为Rossiter模态,是不同流场结构直接相互作用产生的,其特点为幅值大且集中在某几个频率。图15给出了四种不同舱门开启角度下,腔内9个脉动测点的脉动压强功率谱曲线,柱状条带是Heller公式计算的峰值频率。从图中可以看出:
|
图 15 不同舱门开度下腔内9个脉动测点脉动压强功率谱 Fig.15 SPL of fluctuating pressure at nine probes on cavity floors for cases with different door-opening angles |
1)舱门开度为30°时,二阶Rossiter所占优势显著减弱,并且该模态频率偏高,其他高频(第三、第四)模态已经不再明显。这是由于舱门打开较小时,空腔流动中剪切层与回传压缩波的相互作用受到限制,所以流场结构相互作用的强度减弱,致使声压幅值降低。
2)60°、90°和120°舱门开度下,各脉动压力测点的Rossiter模态明显,且模态频率与经验公式基本一致。这说明此时流场中的结构与干净空腔一致。二阶Rossiter模态占主导,幅值明显比其他模态高10 dB以上。
3)图中虚线、实线分别表示腔内前、后半部分采样点的结果。从图中可以看出,四种不同舱门开启角度下,后半部分的脉动强度明显高于前半部分。
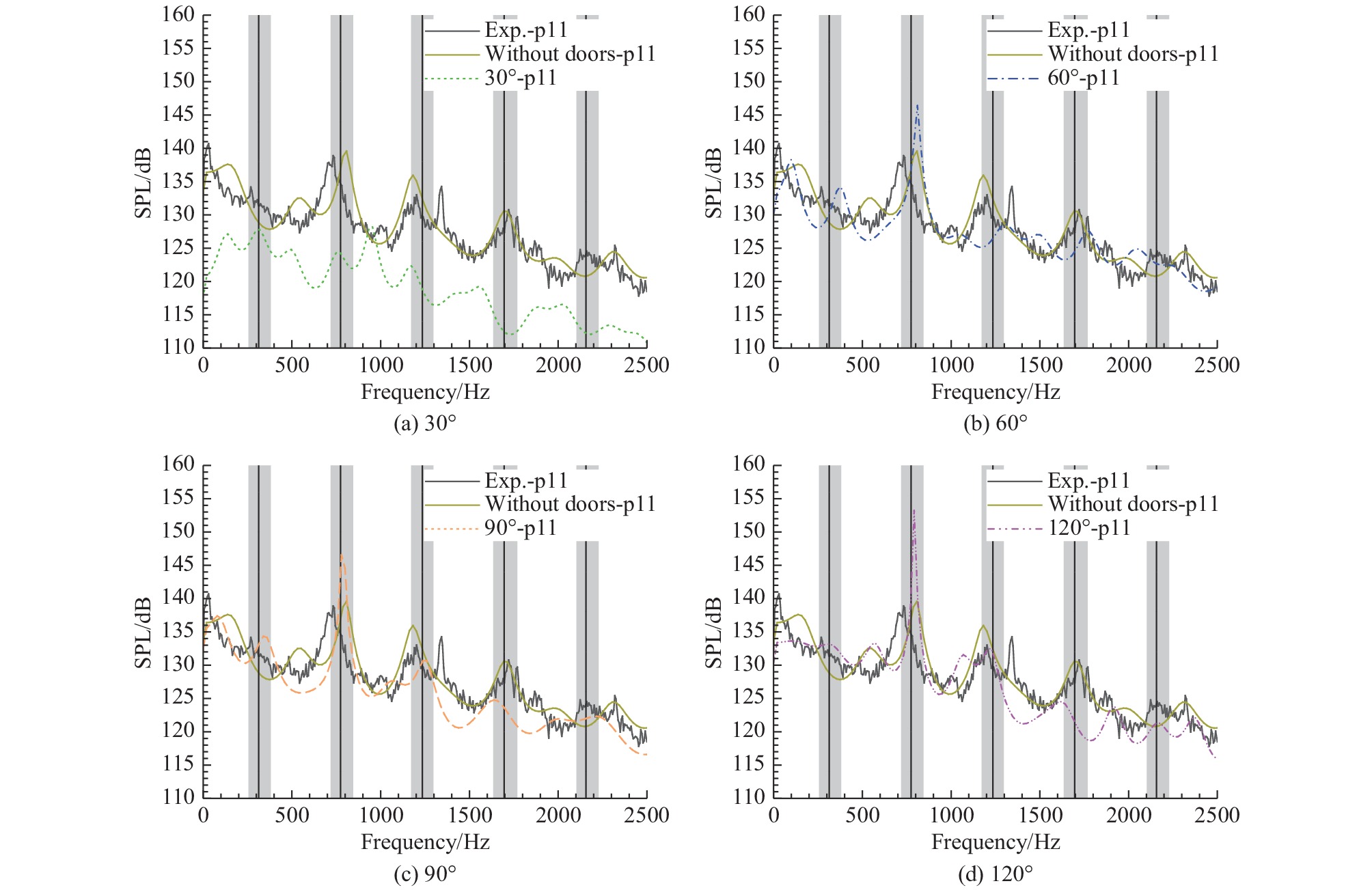
为研究舱门对腔内脉动特性的影响,进一步选取后壁(p11)的脉动压强测点上的脉动压强功率谱进行比较分析,如图16所示。各图中黑色曲线为干净空腔试验曲线,褐色曲线为干净空腔计算曲线,其他彩色曲线为各角度情况下的计算曲线。
|
图 16 不同舱门开度腔内后壁测点p11脉动压强功率谱 Fig.16 SPL of fluctuating pressure at probe p11 on cavity floors for cases with different door-opening angles |
对于后壁测点p11来说,当开启角为30°时,功率水平明显低于干净空腔,其主峰频率比干净空腔的主峰频率偏高。这可能是由于小角度开启情况下,空腔构型更接近封闭腔体,其展向或者纵向的共振成分加强。而在其他开启角度情况下,变化基本一致,峰值频率大致和干净空腔一致,但是第二模态峰值都显著升高,三、四模态峰值没有升高甚至幅值降低。这也印证了第二阶模态被强化的观点。同时这也说明,当打开角度较大时,在各处,舱门对主模态的影响是一致的,是通过改变流场的主结构来影响噪声的产生。在前壁和腔内底部测点的脉动压强功率谱中,出现了相似的变化和影响,不在此赘述。
整体来看,出现不同的变化的原因是,在舱门打开小角度时,空腔内的法向(y向)和展向(z向)流动均受到限制,流场脉动会受到抑制,噪声也会减小。舱门打开角度较大(60°以后)时,舱门的限制主要在展向,对法向的限制已经不明显;但是此时舱门的存在会增加空腔流动的复杂性,阻断空腔近壁面噪声沿展向向外传播,从而会增强腔内的噪声。
5.4 湍流结构为了进一步分析不同舱门开度下空腔流动的特点,通过Q等值面比较瞬时场中湍流结构的异同。正的Q值区域表示涡张量比应变率张量大的流动区域,是与旋涡有关的部分,是常被用作判断旋涡区域的标准[34]。图17给出了干净空腔和四种不同舱门开度下,瞬时流场中的Q = 3000等值面,采用来流方向的无量纲速度

|
图 17 瞬时流场的Q = 3000等值面(用 |
从瞬时图中可以看出,由于舱门的存在,空腔内的流动会受到不同程度的影响,具体表现为:
1)30°的湍流结构明显受到舱门的限制,从而使得流场的湍流结构较干净空腔要小,舱内涡结构很稀疏,尤其是空腔前部区域。
2)在舱门打开60°时,涡结构变得密集,可以明显看到舱内的流动结构沿法向(y向)向外运动,但是空腔前部仍然比较稀疏。
3)到90°和120°时,涡结构的丰富程度变得相似。在舱门开度为120°时,舱门仍然会限制空腔展向的流动。这从侧面反映了舱门的存在会阻碍空腔周围噪声的传播,从而使得腔内噪声一定程度地增大。
4)相比干净空腔的瞬时Q准则等值面图,可以看出,有舱门时空腔上方的剪切层涡结构运动高度更高,这仍然是剪切层在展向受舱门限制的结果。而随着舱门开度的不断增大,展向的空腔流动会受到不同程度的限制。
5)流动经过前缘平板后形成的剪切层,在流场结构中会出现大尺度的剪切层涡结构。舱门对腔内前半部分湍流结构的相互作用较弱;对后腔内半部分不同流动结构之间相互作用的影响较大,从而影响空腔流动的脉动和噪声特性。
6 运动舱门空腔模拟为进一步模拟真实舱门打开过程对空腔流动和声场的影响,本节采用前文的空腔和舱门,在考虑舱门运动的情况下,对空腔的湍流流动进行模拟。对考虑运动的非稳态非定常流动问题,采用经验模态分解(empirical mode decomposition,EMD)方法提取非稳定特征,定量分析其噪声特性的变化。
6.1 舱门运动设计舱门运动规律的选取由条件相似准则确定,而斯特劳哈尔数(St)是非定常流动中须考虑的相似准则,物理上代表非定常运动与定常运动的惯性力之比,其定义为:
| $ {S t} = \frac{{{L_{D}}}}{{\Delta T{\rm{ }}{V_\infty }}} $ | (10) |
式中,
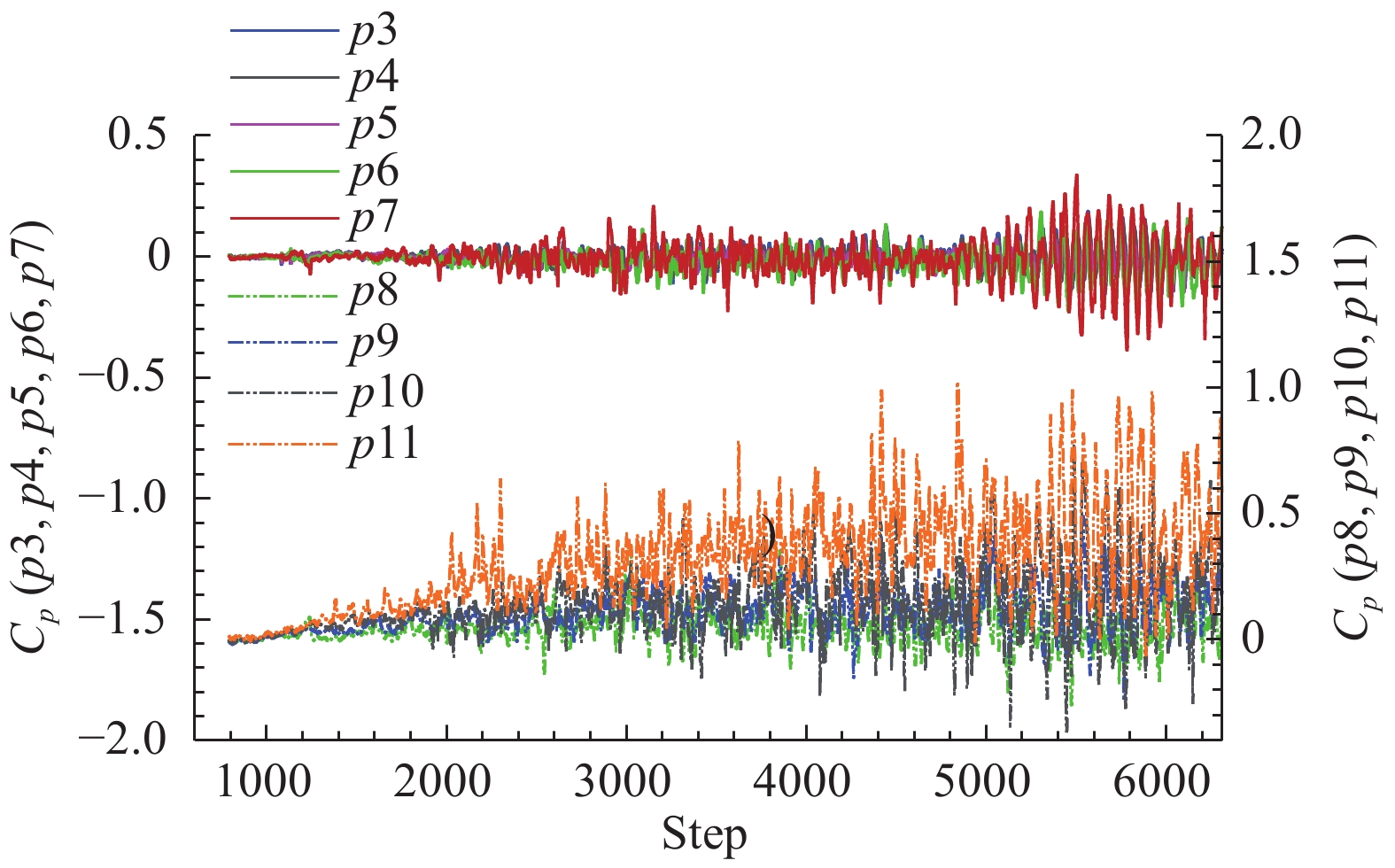
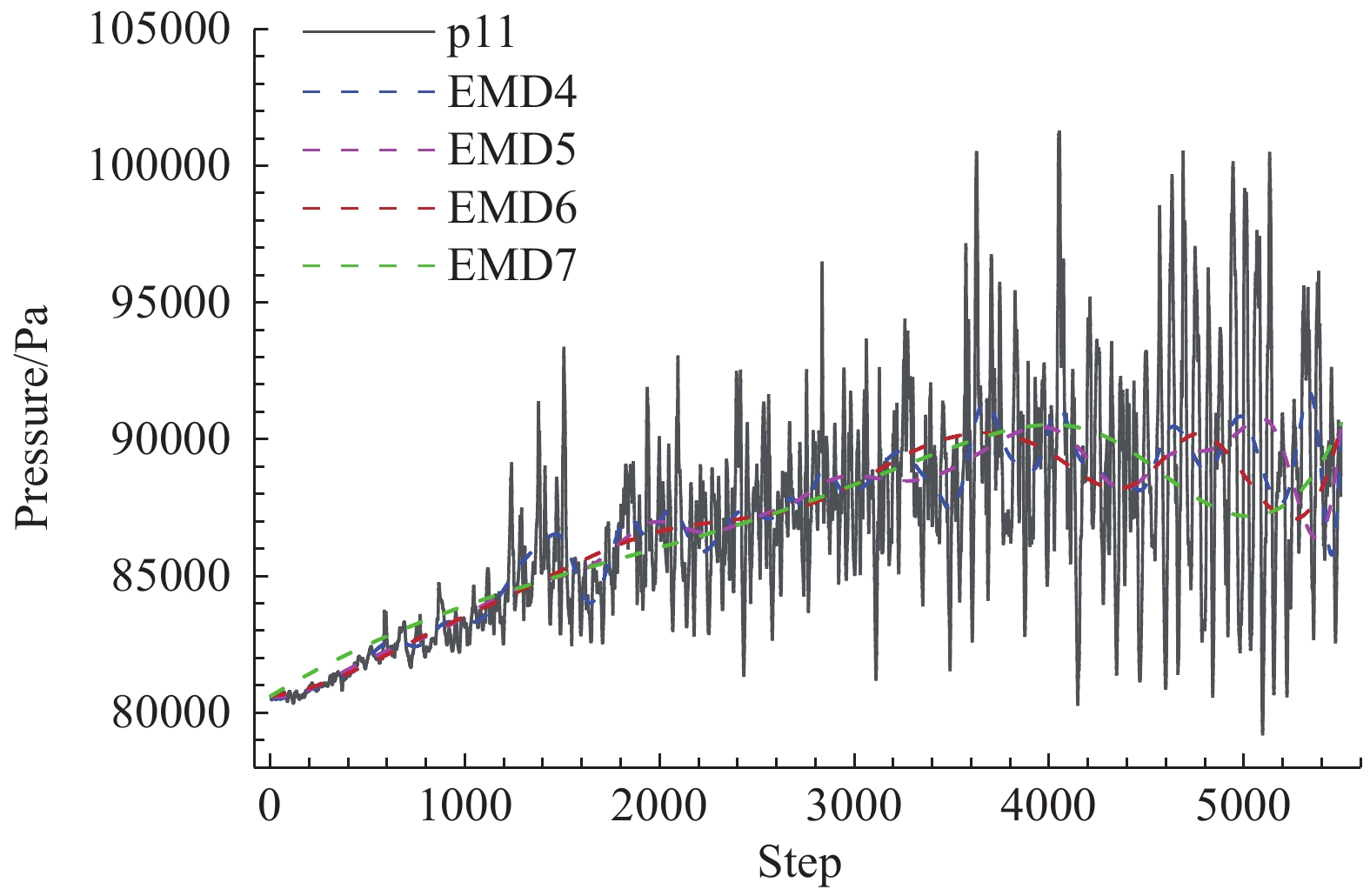
首先对舱门关闭状态进行非定常计算,保证流动充分发展;然后舱门开始运动,进行完整的非稳态非定常流动模拟。图18给出了舱门从0°打开到100°过程中,空腔内动态测点的压力系数变化。从图中可以看出,整个流动大致分为三个阶段:初期的小幅稳定阶段(≤30°)、过渡阶段(30°~60°)、充分发展阶段(≥60°)。同时空腔前半区域各动态采集点(p3~p7)的压力系数呈对称摆动趋势,而空腔后半区域动态采集点的压力系数呈增长趋势。以p11测点为例,图19展示了其压力值的变化情况。
由于舱门运动使得空腔内流动呈现非稳态的变化,即压力脉动(
|
图 18 舱门打开过程中各动态采集点的压力系数变化 Fig.18 Variations of pressure coefficients at different probes during the opening of cavity doors |
|
图 19 舱门开启过程中弹舱后壁测点p11处压力变化与EMD模态曲线 Fig.19 Variation of pressure and its EMD modes at probe p11 during the opening of cavity doors |
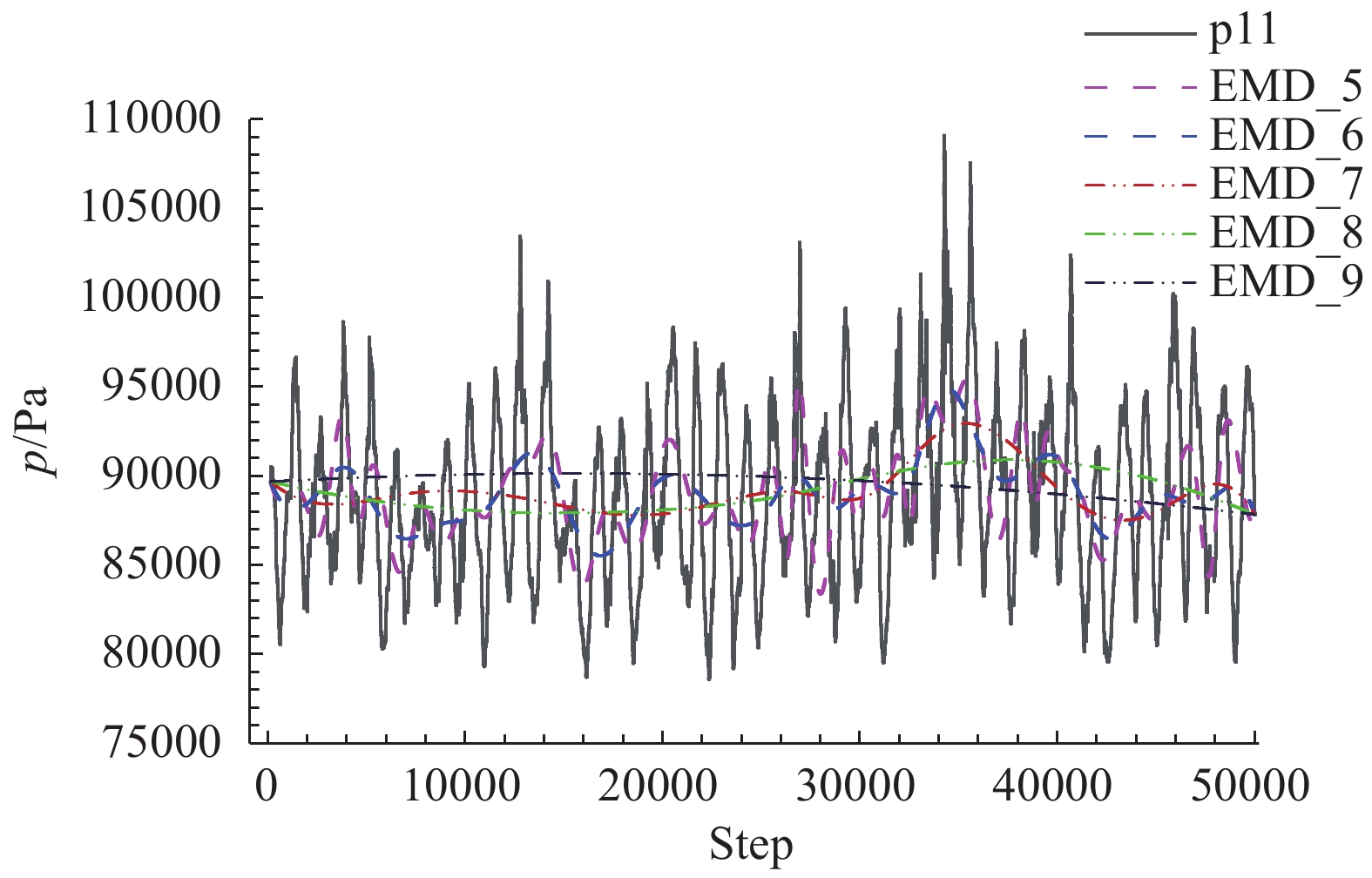
为证明该方法的有效性,采用舱门打开90°的准定常流动进行分析,并用代数平均的计算结果进行对比验证。以测压点p11为例,图20给出了不同EMD模态的分布曲线。分析结果表明,低阶EMD模态分析包含较多高频信息,与原始数据分布具有一致性,无法直接用于捕捉非稳态的信息;高阶的EMD模态多数与低频流场信息有关,可用于描述舱门运动引起的非稳态流场的变化。从图20中,EMD5和EMD6模态的分布差异可以观察到此特征。而更高阶的EMD模态(如EMD9)基本与代数平均值一致。从而说明EMD方法具有与代数平均计算方式相同的功能。
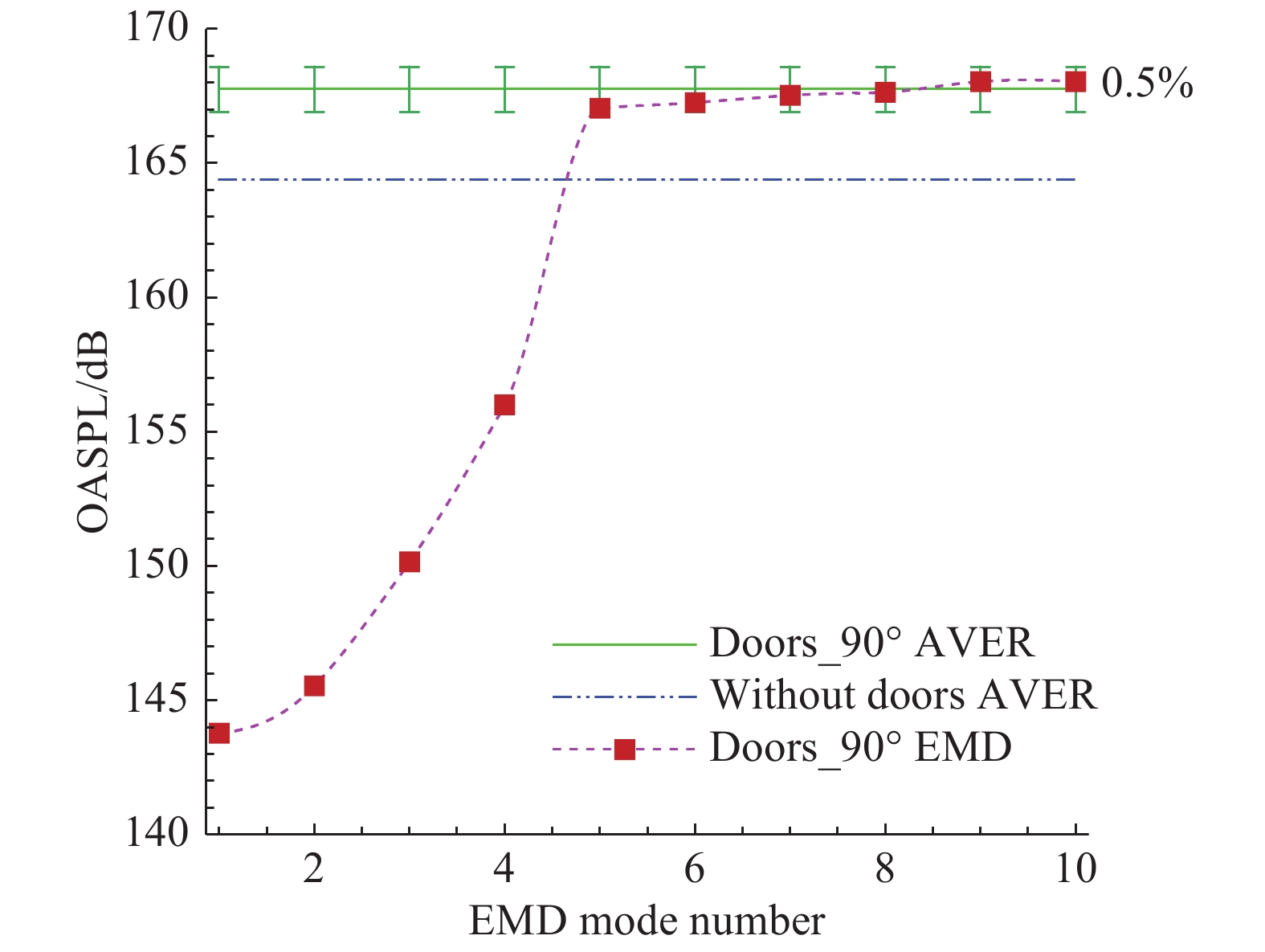
图21中给出了采用不同EMD模态作为时均值时,p11点总声压级的变化。结果表明,采用低阶EMD模态所得的OASPL远低于采用代数平均值方式计算的值。而提高采用的EMD模态,OASPL会逐渐收敛于代数平均计算的值(相差在0.5%以内)。这说明采用EMD模态进行OASPL计算是有效可行的。尽管EMD模态的选取无统一标准,但可以采用OASPL的收敛性判断选取的EMD模态。
|
图 20 舱门打开90°时p11点压力变化与不同EMD模态曲线 Fig.20 Time histories of pressure and its EMD modes at probe p11 in the cavity with vertical doors |
|
图 21 舱门打开90°时考虑不同EMD模态的p11点OASPL计算结果 Fig.21 OASPL computed using different EMD modes at probe p11 in the cavity with vertical doors |
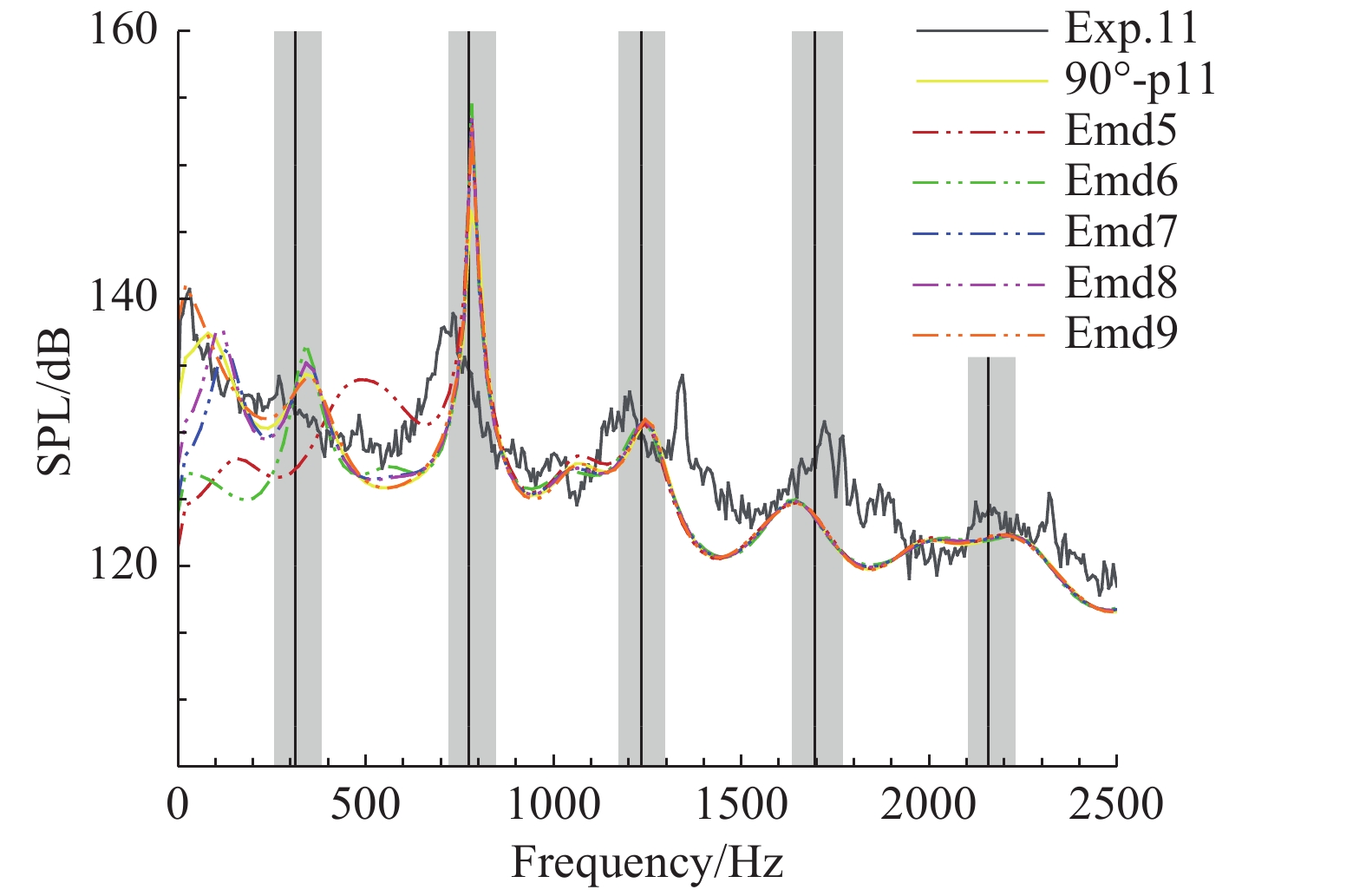
图22给出了EMD模态对p11测点功率谱的影响,主要特点为低频区域有差别,高频区域无明显差异。由于EMD本身就是对高频滤波的结果,不同的EMD曲线代表不同的低频模态,所以会对低阶频率产生影响。计算结果中的典型Rossiter频率与采用平均值计算的方式一致,可见采用EMD模态对压力功率谱的计算方式是可行的。
|
图 22 舱门打开90°时在不同EMD模态下p11点的脉动压强功率谱 Fig.22 SPL computed using different EMD modes at probe p11 in the cavity with vertical doors |
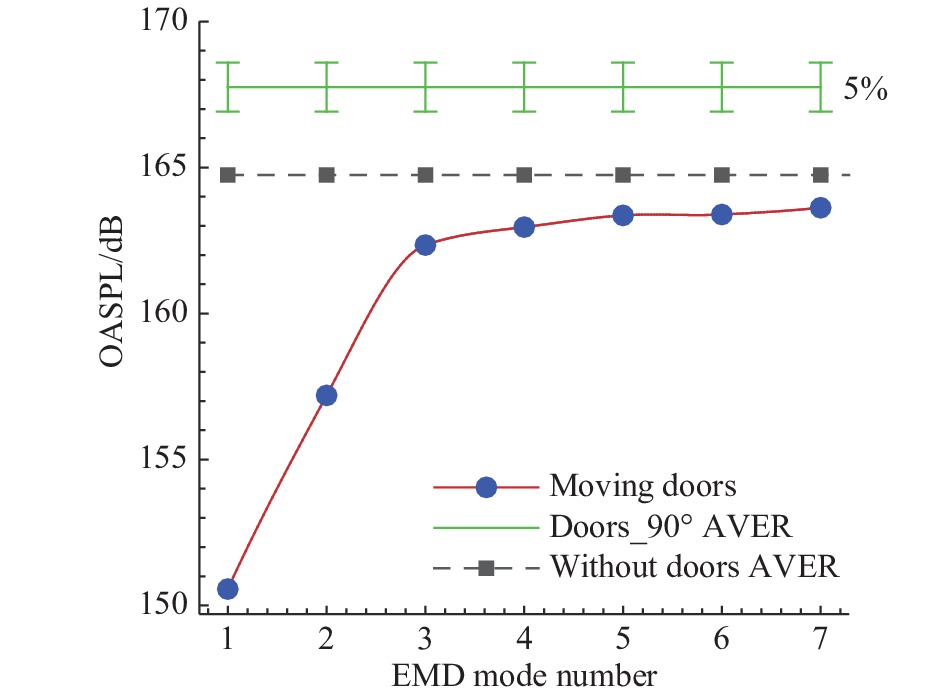
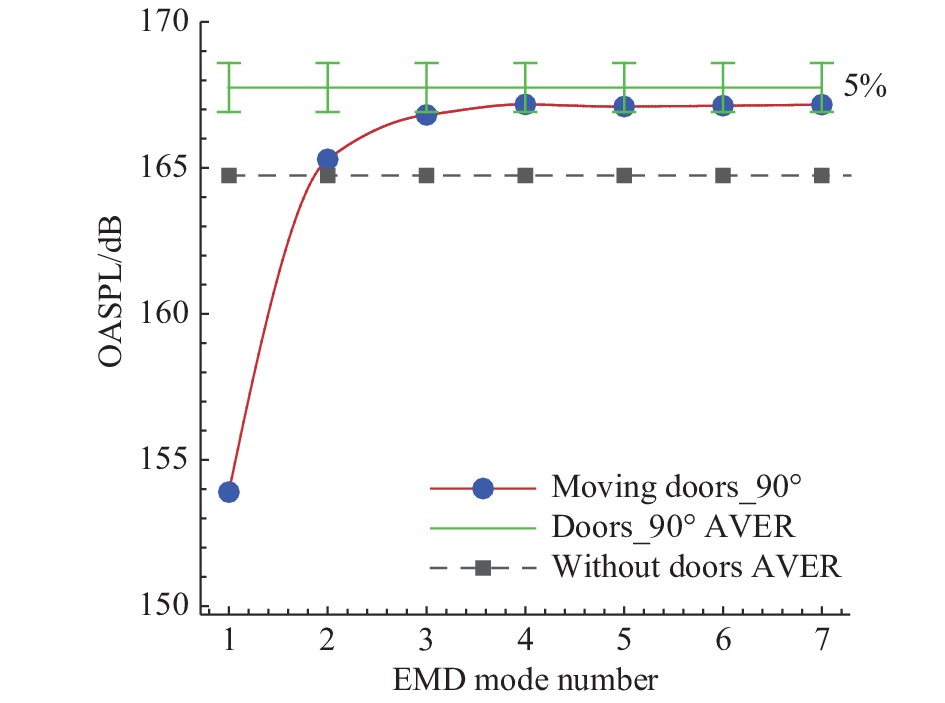
采用经验模态分解方法,对亚声速空腔舱门开启过程中的非稳态动态特性进行分析。图23给出了空腔后壁p11测点的OASPL随着选取不同EMD模态所产生的变化。当取到EMD5模态时,计算得到的OASPL开始趋于稳定,收敛值为舱门运动过程中的OASPL。值得注意的是,该值低于静态舱门的计算值。这是因为,在舱门的开启过程中,当舱门打开角度小时,流动的脉动较小,舱门打开后期的脉动变大(见图19),空腔内流动与声场逐渐产生相互作用并增强,进而产生了流动的振荡现象。图24给出了采用舱门开启到90°附近的数据进行分段动态分析的OASPL计算结果。此时的结果与静态舱门计算值相当,说明对静态舱门打开90°的准定常计算跟真实运动过程中的状态吻合,这对工程问题的分析具有指导意义。
|
图 23 舱门开启过程中不同EMD模态的p11点OASPL计算结果 Fig.23 OASPL computed using different EMD modes at probe p11 during the opening of cavity doors |
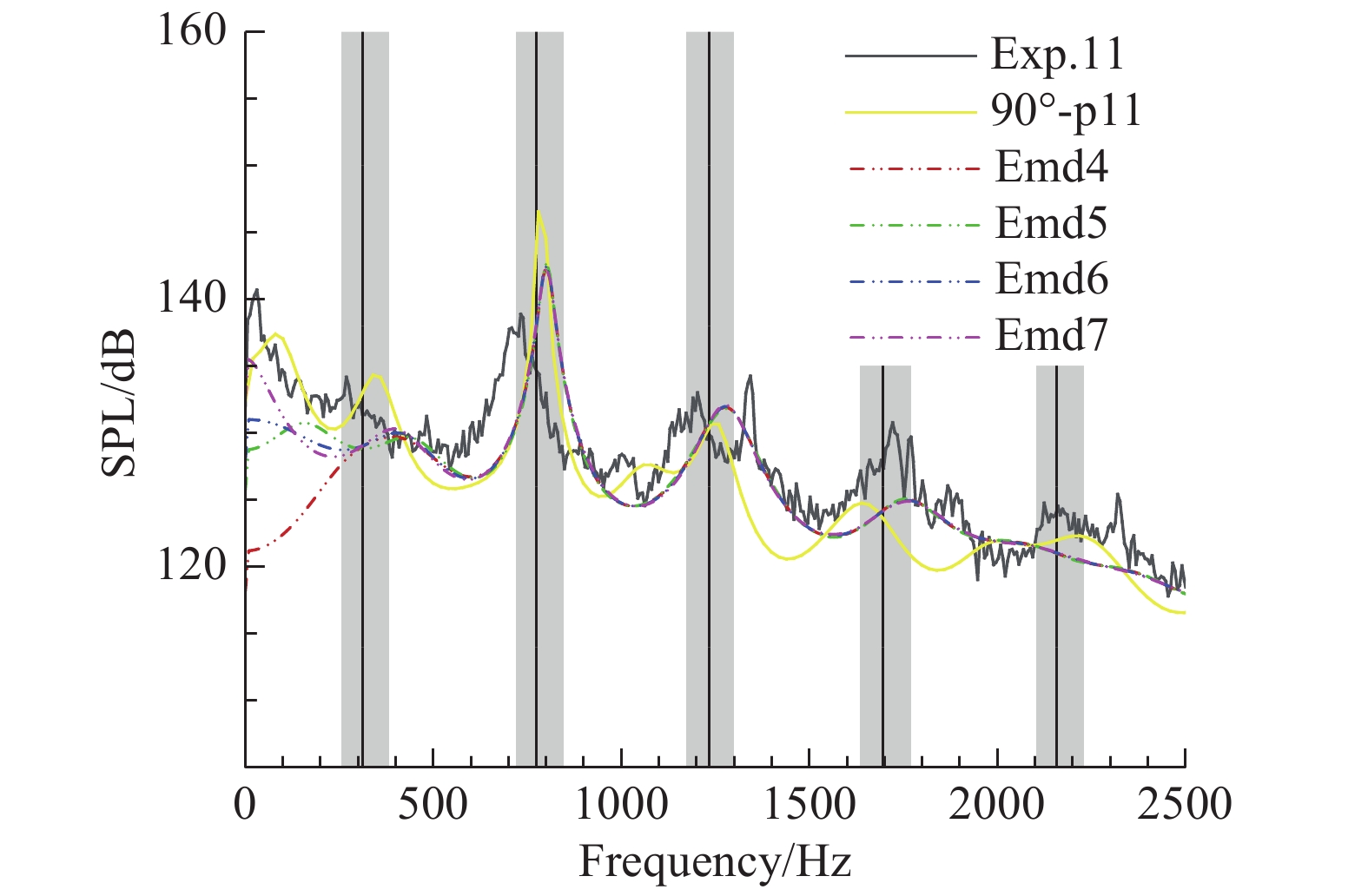
图25给出了采用不同EMD模态时,对应的脉动压力功率谱分析结果。舱门运动过程中,二阶Rossiter模态仍为主导模态,幅值明显高于其他模态10 dB以上,但低于静态舱门打开90°的分析结果,此处与总声压级降低的原因一致。一阶Rossiter模态强度降低,而三、四阶Rossiter模态略有升高。
|
图 24 舱门开启到90°时不同EMD模态的p11点的OASPL分析结果 Fig.24 OASPL computed using different EMD modes at probe p11 when cavity doors are opened to 90° |
|
图 25 舱门开启过程中不同EMD模态的p11点的功率谱比较 Fig.25 SPL computed using different EMD modes at probe p11 during the opening of cavity doors |
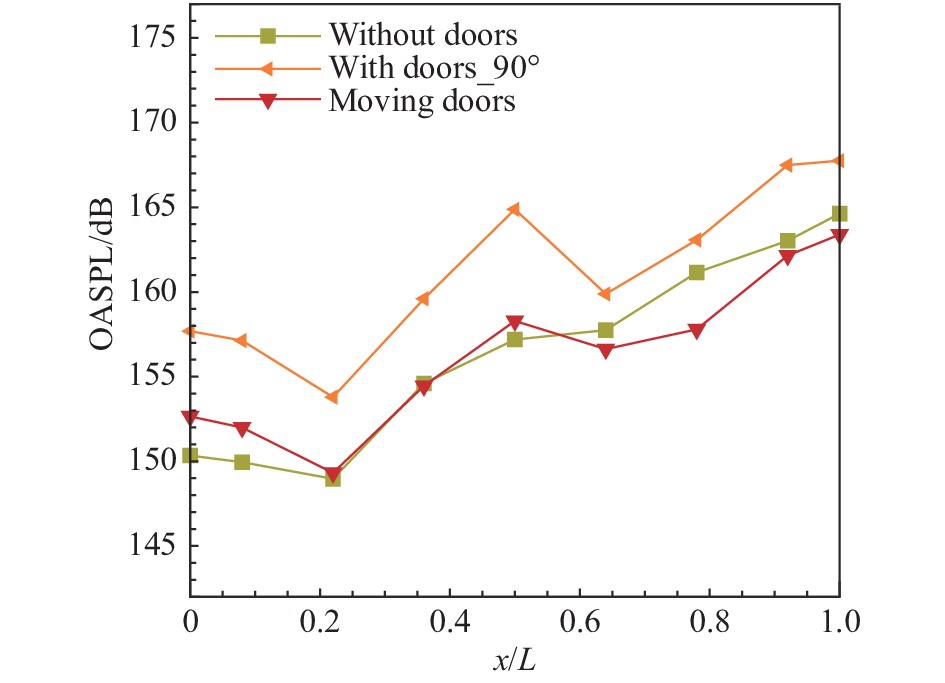
采用EMD方法对空腔内全部脉动测点进行OASPL分析,如图26所示。计算结果表明,舱门开启过程中,OASPL分布状态仍呈现“W”形状,但其值比静态大开度舱门整体降低5 dB左右。这是由于舱门开启过程中,存在由小幅脉动到强脉动的发展过程。小角度的舱门开启过程中,流场的脉动较小,还没有完全发展;强脉动的完全发展需要一定的时间。在舱门的整个运动过程中流动呈现过渡发展的特点,因此出现OASPL的降低。
|
图 26 舱门开启过程中空腔底部总声压级分布 Fig.26 OASPL at cavity floor during the opening of cavity doors |
图27给出了舱门开启过程中,舱门打开到不同角度时,物面压力系数的分布情况。从图中可以看出,压力分布具有一定对称性,两侧舱门承受的压力相当。在舱门打开小角度时,舱门限制了空腔内部与外部流场的掺混与交换,压力变化较小。随着舱门的逐渐打开,空腔与外流场发生混合,空腔内压力变化增大。舱门打开角度较大(60°以后)时,空腔内流动出现大幅度振荡现象,流场与声场出现强相互作用,从而造成流场脉动增强,噪声特性变得显著。与前文OASPL分析和功率谱分析结果一致。

|
图 27 舱门开启过程中物面压力系数变化 Fig.27 Instantaneous wall pressure coefficients during the opening of cavity doors |
针对考虑舱门的多尺度、强湍流、高雷诺数、强脉动的空腔流动问题,采用本文发展的嵌套重叠网格方法对带运动舱门的空腔生成网格,用IDDES湍流模拟方法对亚声速(Ma = 0.6)空腔流动进行模拟,分析了静、动态舱门对空腔复杂流动和噪声特性的影响。具体结论如下:
1)发展的动态嵌套重叠网格方法,可自动高效生成大幅度运动物体的计算网格,用于运动舱门的空腔复杂流场模拟。
2)采用四阶对称重构和三阶MUSCL 混合的格式,在不明显增加计算量的前提下,明显降低了数值耗散,提升了计算的准确度,可以捕捉空腔中的湍流结构。对标模M219的计算结果与文献给的结果吻合。对空腔标模C201腔内噪声的预测和对脉动压力功率谱的分析结果与试验数据一致。
3)亚声速空腔标模C201腔内底部压强分布表现出三段分布:前段平缓负压区;中段压力增长过渡区;后段高度增加区,形成后壁的高压区域。腔内主导峰值频率为第二峰值。
4)与干净空腔相比,当舱门为静态时,舱门小开度(30°)时,时均流场中截面上腔内的流态变得更加复杂,并且腔内底部压力系数的值均会明显减小。舱门开度较大(60°以后)时,时均流场中截面的腔内涡结构与干净空腔一致,底部压力分布趋于干净空腔的计算结果;但是舱门的存在,会使得底部后半部分的压力较干净空腔出现一定程度上的降低。舱门开度为90°时,腔内总声压级较干净空腔有所升高,最大升高值近9 dB,呈现出“W”形态的分布;二阶Rossiter模态占主导。舱门与空腔后半部分的不同流动结构之间相互作用,从而对空腔流动的脉动和噪声特性产生影响。
5)针对舱门运动的非稳态非定常特点,本文采用经验模态分解方法对噪声特性进行分析,计算结果表明该方法有效可行。舱门开启过程中,整体的OASPL有所下降,主导频率依然为二阶Rossiter模态。对于小开度的舱门,静态舱门模拟与运动舱门结果相差较大,因而此类情况需要考虑运动舱门的影响。在舱门开度较大(90°)时,两者的分析结论一致,说明可采用准定常来分析此状态的流场与噪声特性,指导内埋弹舱的设计。
| [1] |
LAWSON S J, BARAKOS G N. Review of numerical simulations for high-speed, turbulent cavity flows[J]. Progress in Aerospace Sciences, 2011, 47(3): 186-216. DOI:10.1016/j.paerosci.2010.11.002 |
| [2] |
ROWLEY C W, WILLIAMS D R. Dynamics and control of high-Reynolds-number flow over open cavities[J]. Annual Review of Fluid Mechanics, 2006, 38: 251-276. DOI:10.1146/annurev.fluid.38.050304.092057 |
| [3] |
李晓东, 刘靖东, 高军辉. 空腔流激振荡发声的数值模拟研究[J]. 力学学报, 2006, 38(5): 599-604. LI X D, LIU J D, GAO J H. Numerical simulation of flow-induced oscillation and sound generation in a cavity[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 599-604. DOI:10.3321/j.issn:0459-1879.2006.05.004 (in Chinese) |
| [4] |
万振华, 周林, 孙德军. 方腔流致振荡及噪声的数值研究[J]. 空气动力学学报, 2012, 30(3): 291-298. WAN Z H, ZHOU L, SUN D J. Numerical investigation of flow-induced oscillations and noise from a rectangular cavity[J]. Acta Aerodynamica Sinica, 2012, 30(3): 291-298. DOI:10.3969/j.issn.0258-1825.2012.03.003 (in Chinese) |
| [5] |
ROCKWELL D, NAUDASCHER E. Review —self-sustaining oscillations of flow past cavities[J]. Journal of Fluids Engineering, 1978, 100(2): 152-165. DOI:10.1115/1.3448624 |
| [6] |
王显圣, 杨党国, 刘俊, 等. 空腔可压缩流致噪声问题研究进展[J]. 实验流体力学, 2018, 32(3): 1-16. WANG X S, YANG D G, LIU J, et al. Progress of research on noise induced by compressible flow over cavities[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(3): 1-16. DOI:10.11729/syltlx20170132 (in Chinese) |
| [7] |
PLENTOVICH E, STALLINGS Jr R L, TRACY M B. Experimental cavity pressure measurements at subsonic and transonic speeds static-pressure results[R/OL]. NASA TP-3358, 1993. https://cs.odu.edu/~mln/ltrs-pdfs/tp3358.pdf
|
| [8] |
刘俊, 杨党国, 王显圣, 等. 湍流边界层厚度对三维空腔流动的影响[J]. 航空学报, 2016, 37(2): 475-483. LIU J, YANG D G, WANG X S, et al. Effect of turbulent boundary layer thickness on a three-dimensional cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 475-483. DOI:10.7527/S1000-6893.2015.0112 (in Chinese) |
| [9] |
ILLINGWORTH S J, MORGANS A S, ROWLEY C W. Feedback control of cavity flow oscillations using simple linear models[J]. Journal of Fluid Mechanics, 2012, 709: 223-248. DOI:10.1017/jfm.2012.330 |
| [10] |
ROSSITER J E. Wind tunnel experiments on the flow overrectangular cavities at subsonic and transonic speeds[R]. ARC/R&M-3438, 1964. https://naca.central.cranfield.ac.uk/bitstream/handle/1826.2/4020/arc-rm-3438.pdf?sequence = 1&isAllowed = y
|
| [11] |
HELLER H H, HOLMES D G, COVERT E E. Flow-induced pressure oscillations in shallow cavities[J]. Journal of Sound and Vibration, 1971, 18(4): 545-553. DOI:10.1016/0022-460X(71)90105-2 |
| [12] |
BLAIR A B, STALLINGS R L. Cavity door effects on aerodynamic loads of stores separating from cavities[J]. Journal of Aircraft, 1989, 26(7): 615-620. DOI:10.2514/3.45811 |
| [13] |
LAWSON S J, BARAKOS G N. Computational fluid dynamics analyses of flow over weapons-bay geometries[J]. Journal of Aircraft, 2010, 47(5): 1605-1623. DOI:10.2514/1.C000218 |
| [14] |
CASPER K M, WAGNER J L, BERESH S J, et al. Fluid-structure interactions on a tunable store in complex cavity flow[J]. Journal of Aircraft, 2019, 56(4): 1501-1512. DOI:10.2514/1.C035050 |
| [15] |
SHETA E F, HARRIS R E, GEORGE B, et al. Loads and acoustics prediction on deployed weapons bay doors[J]. Journal of Vibration and Acoustics, 2017, 139(3): 31007. DOI:10.1115/1.4035701 |
| [16] |
LOUPY G J M, BARAKOS G N, TAYLOR N J. Cavity flow over a transonic weapons bay during door operation[J]. Journal of Aircraft, 2017, 55(1): 339-354. DOI:10.2514/1.C034344 |
| [17] |
史爱明, 叶正寅, 杨永年. 内埋式弹舱舱门气动载荷计算分析研究[J]. 航空计算技术, 2007, 37(3): 5-6,16. SHI A M, YE Z Y, YANG Y N. Calculation and analysis for aerodynamic loads acting on interior weapon cabin's door[J]. Aeronautical Computing Technique, 2007, 37(3): 5-6,16. DOI:10.3969/j.issn.1671-654X.2007.03.002 (in Chinese) |
| [18] |
张培红, 王明, 邓有奇, 等. 武器分离及舱门开启过程数值模拟研究[J]. 空气动力学学报, 2013, 31(3): 277-281,293. ZHANG P H, WANG M, DENG Y Q, et al. Numerical simulation of store separation and door operation[J]. Acta Aerodynamica Sinica, 2013, 31(3): 277-281,293. (in Chinese) |
| [19] |
吴继飞, 徐来武, 范召林, 等. 内埋弹舱舱门气动特性研究[J]. 空气动力学学报, 2012, 30(6): 744-748. WU J F, XU L W, FAN Z L, et al. Investigation on aerodynamic characteristics of internal bay's door[J]. Acta Aerodynamica Sinica, 2012, 30(6): 744-748. (in Chinese) |
| [20] |
吴继飞, 徐来武, 郭洪涛, 等. 内埋武器舱舱门开闭动态模拟试验技术研究[J]. 实验流体力学, 2015, 29(4): 88-94. WU J F, XU L W, GUO H T, et al. Investigation on dynamic simulation technology of internal weapons bay's doors opening and closing[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(4): 88-94. DOI:10.11729/syltlx20140131 (in Chinese) |
| [21] |
闫盼盼, 张群峰, 金明. 舱门对内埋武器分离特性影响分析[J]. 兵工学报, 2017, 38(6): 1120-1130. YAN P P, ZHANG Q F, JIN M. Effect of bay door on separation characteristics of internal store[J]. Acta Armamentarii, 2017, 38(6): 1120-1130. DOI:10.3969/j.issn.1000-1093.2017.06.011 (in Chinese) |
| [22] |
SHUR M L, SPALART P R, STRELETS M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649. DOI:10.1016/j.ijheatfluidflow.2008.07.001 |
| [23] |
CHEN S Y, CHEN Y C, XIA Z H, et al. Constrained large-eddy simulation and detached eddy simulation of flow past a commercial aircraft at 14 °s angle of attack[J]. Science China Physics, Mechanics and Astronomy, 2013, 56(2): 270-276. DOI:10.1007/s11433-013-4990-z |
| [24] |
XU J, CAI J S, LIU Q H, et al. Flow simulations by enhanced implicit-hole-cutting method on overset grids[J]. Journal of Aircraft, 2014, 51(5): 1401-1409. DOI:10.2514/1.C032283 |
| [25] |
CAI J S, PAN S C, LI W F, et al. Numerical and experimental investigations of a nonslender delta wing with leading-edge vortex flap[J]. Computers & Fluids, 2014, 99: 1-17. DOI:10.1016/j.compfluid.2014.03.011 |
| [26] |
XU J, QU K, CAI J S. Flow simulations for NASA CRM wing-body-tail with implicit hole cutting method[J]. Applied Mechanics and Materials, 2013, 378: 355-361. DOI:10.4028/www.scientific.net/amm.378.355 |
| [27] |
WHITE J, BAURLE R, FISHER T, et al. Low-dissipation advection schemes designed for large eddy simulations of hypersonic propulsion systems[C]//48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, Georgia. Reston, Virginia: AIAA, 2012. doi: 10.2514/6.2012-4263
|
| [28] |
WADA Y, LIOU M S. A flux splitting scheme with high-resolution and robustness for discontinuities[C]//32nd Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 1994: 83.
|
| [29] |
DUCROS F, FERRAND V, NICOUD F, et al. Large-eddy simulation of the shock/turbulence interaction[J]. Journal of Computational Physics, 1999, 152(2): 517-549. DOI:10.1006/jcph.1999.6238 |
| [30] |
BLAZEK J. Computational fluid dynamics: Principles and applications[M]. Oxford, UK: ELSEVIER, 2001. doi: 10.1016/C2013-0-19038-1
|
| [31] |
潘书诚. 基于多尺度湍流数值模拟的流动控制机理研究[D]. 西安: 西北工业大学, 2013. PAN S C. Investigation of flow control and mechanism based on multi-scale numerical simulation of turbulence[D]. Xi'an: Northwestern Polytechinical University, 2013 (in Chinese). |
| [32] |
LARCHEVêQUE, LIONEL, SAGAUT, et al. Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number[J]. Journal of Fluid Mechanics, 516, 265-301. doi: 10.1017/S0022112004000709
|
| [33] |
李晓东, 屈崑, 蔡晋生. 分层嵌套重叠网格自适应树结构动态组装方法[J]. 航空学报, 2017, 38(3): 120243. LI X D, QU K, CAI J S. A dynamic assembling method based on adaptive tree structure for hierarchical overset grids[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 120243. DOI:10.7527/S1000-6893.2016.0135 (in Chinese) |
| [34] |
HUNT J C R, WRAY A A, MOIN P. Eddies, streams, and convergence zones in turbulent flows[R]//Studying Turbulence Using Numerical Simulation Databases, 2. Proceedings of the 1988 Summer Program, 1988: 193-208. N89-24555. https://ntrs.nasa.gov/api/citations/19890015184/downloads/19890015184.pdf
|
| [35] |
冯金富, 杨松涛, 刘文杰. 战斗机武器内埋关键技术综述[J]. 飞航导弹. 2010(7): 71-74.
|
 2022, Vol. 40
2022, Vol. 40


