2. 西北工业大学 力学与土木建筑学院,西安 710072;
3. 中国空气动力研究与发展中心 气动噪声控制重点实验室,绵阳 621000;
4. 中国科学技术大学 近代力学系,合肥 230027
2. School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi’an 710072, China;
3. Key Laboratory of Aerodynamic Noise Control, China Aerodynamics Research and Development Center, Mianyang 621000, China;
4. Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
自然界和工业生产过程中存在大量声波与剪切层流动相互作用的物理现象。1858年Leconte[1]发现音乐会上的蜡烛会随着乐器的声音“随音起舞”,即声波对燃烧射流的影响。在声学风洞实验中,声波穿过开口声学风洞与周围流体形成的剪切层,会产生折射、反射现象,从而导致测量结果失真[2]。因此,声波与剪切层的相互作用的机理研究可用于提升人们对燃烧、湍流涡环的控制能力,亦或是准确的声源定位技术,具有重要的科学与工程价值。
声激励对流动发展的影响存在于大量流动稳定性研究之中。1878年Rayleigh[3]研究了射流的稳定性问题,探讨了流动失稳的数学原理。在大量关于射流或混合层稳定性研究的实验[4-6]中,声波被用于充当初始小扰动。Sato和Sakao[7]使用纵向声波激励平面射流,通过流场结构变化确定出二维平面射流失稳的临界雷诺数;Ho和Huang[8]通过实验发现使用与混合层不稳定波频率呈一定数值关系的声波激励混合层,可以控制流场中涡的融合,并依此提出亚谐频反馈回路机制。在一些实验[9-10]中为凸显出相干结构的演化规律,研究人员对流场施加弱声波激励使其结构变得清晰可见。
尽管声波影响流动的现象被广泛研究,但流动稳定性研究的关注重点是不稳定波的演化,声波只被简单当作初始扰动引入,而缺乏更精细的过程描述;声波与剪切层失稳波的耦合也在大部分工作中被忽略。Tam的报道[11-12]指出关于声波如何激励起不稳定波的机理问题是感受性问题,通过建立波束与二维剪切层相互作用的数学模型,求解得到声波激励剪切层失稳的两个条件:1)声波与不稳定波频率需要匹配;2)二者在流向上的相速度需要匹配。吴介之[13]亦在文中指出感受性与稳定性的不同之处,即感受性是激励声波在流场中的表现。目前关于声波在剪切层中的演化规律研究较少。
另一方面,流动对声传播的影响被广泛关注。许多学者针对声波穿过剪切层的物理过程开展了大量研究。从Miles[14]研究穿过有相对运动速度流体的声波传播规律开始,研究者对波动方程做了诸多修正并提出多种模型,如Amiet[15]创建的剪切层修正理论以及Padios等[16]修正了对流引起的声源偏移。在数值模拟方面,张雪等[17]通过求解线化Euler方程数值模拟了二维单极子在剪切层中的声传播,对比验证了Amiet理论修正剪切层声折射现象的准确性。尽管线性Euler方程可以捕捉声传播的过程,但由于其未考虑黏性和非线性项,预测的剪切层Kelvin-Helmholtz(K-H)不稳定波的发展并不符合物理规律,也就无法精确描述声波与剪切层之间的相互作用。更进一步地,关于K-H不稳定性现象的研究是流体力学中的一个经典问题[18],尽管近年来其在可压缩流[19-20]、磁流体[21]、多相流[22]等环境下有长足的进展,但对于声激励条件下剪切流动失稳机理尚不十分明确。即,从剪切层对声传播干扰方面来看,现有理论只注重了剪切层外的传播规律及接收信号的变化,只有剪切层对声传播单方面的影响,而较少关注声波在剪切层内部是如何与流动相互作用(声波激励起剪切层中复杂的涡系结构)的。
格子Boltzmann方法(lattice Boltzmann method,LBM)[23]是20世纪90年代发展起来的一种介观计算流体力学方法,备受关注。它具有编程简单、并行性好等特征,适用于大规模计算。研究表明,它能够很好地对具有复杂固壁边界、湍流等的流动现象进行准确预测。在1998年Buick等[24]采用LBM成功地获得了声信号传播的线性与非线性行为,而关于LBM方法在声学领域适用性的论证源自于Lallemand和Luo[25]对LBM数值耗散、色散特性的分析。Marié等[26]进一步分析了多种LBM数值格式并指出:LBM可以近乎理想地模拟声学现象。Najafi-Yazdi和Mongeau[27]将完美匹配层方法(perfect match layer,PML)添加到LBM框架中,这是一种效果较好的声学无反射边界条件。上述工作为LBM方法在声学模拟领域的发展奠定了坚实的基础,使其得以用于很多流场模拟领域。以LBM为核心求解方案的流体力学商业软件PowerFlow,已成功地应用于轿车气动声音的分析。Viggen[28]研究了流体的剪切黏性、体黏性对声传播的影响,其研究进一步确定了LBM对声传播捕捉的精确性。对中高雷诺数流动[29]、非线性声学现象[30]以及涡运动噪声及其与壁面相互作用[31]的研究也证实了LBM对流动噪声问题的模拟具有令人满意的效果。
综上所述,声波穿过剪切层的前期研究大都没有考虑双向耦合。剪切层稳定性受声场影响,并进一步给声传播提供复杂流动背景,改变声传播特征,其内在规律有待研究。因此本文采用LBM直接数值模拟了不同波数声波穿过剪切层的传播规律,以及在其影响下剪切层K-H波的激励与发展过程。本文后续部分中,将首先介绍所采用的数值方法和计算模型,然后结合剪切层稳定性理论,展示和讨论剪切层对声传播的影响以及声波激励剪切层流动失稳的机理,最后给出结论。本文相关研究成果可用于声学风洞声信号解读、指导流动控制等技术的发展,具有重要的学术意义和工程应用价值。
1 数值方法与计算模型 1.1 数值方法LBM基于经典Boltzmann方程,是一种基于气体动理论的介观方法。采用指标法以及Einstein求和约定表达(下文相同)的控制方程为:
| $ \frac{\partial f}{\partial t}+{\xi }_{i}{\partial }_{i}f = \mathrm{\varOmega }\left(f\right) $ | (1) |
其中,
| $ \mathrm{\varOmega }\left(f\right) = -\frac{f-{f}^{{\rm{eq}}}}{\tau } $ | (2) |
其中
| $ {f}^{{\rm{eq}}} = \rho {\left(\frac{1}{2\text{π} RT}\right)}^{D/2}\mathrm{exp}\left[-{\left|\boldsymbol{v}\right|}^{2}/\left(2RT\right)\right] $ | (3) |
式中,
不同于传统计算流体力学方法,LBM首先对速度相空间进行离散(
| $ {\partial }_{t}{f}_{i}+{c}_{i\alpha }{\partial }_{\alpha }{f}_{i} = -\frac{1}{\tau }({f}_{i}-{f}_{i}^{{\rm{eq}}}) $ | (4) |
文中,希腊字母(
| $ {f}_{i}^{{\rm{eq}}}\approx {w}_{i}\rho \left[1+\frac{{c}_{i\alpha }{u}_{\alpha }}{{c}_{s}^{2}}+\frac{{A}^{\left(2\right)}}{2{c}_{s}^{4}}+\frac{{A}^{\left(3\right)}}{2{c}_{s}^{6}}++\frac{{A}^{\left(4\right)}}{4{c}_{s}^{8}}+O\left({u}^{5}\right)\right] $ | (5) |
| $ {A}^{\left(2\right)} = {H}_{i\alpha \beta }^{\left(2\right)}{u}_{\alpha }{u}_{\beta } $ | (6) |
| $\begin{split} {A}^{\left(3\right)} =& {H}_{ixxy}^{\left(3\right)}{u}_{x}^{2}{u}_{y}+{H}_{ixxz}^{\left(3\right)}{u}_{x}^{2}{u}_{z}+{H}_{ixyy}^{\left(3\right)}{u}_{y}^{2}{u}_{x}+{H}_{ixzz}^{\left(3\right)}{u}_{z}^{2}{u}_{x} +\\&{H}_{iyzz}^{\left(3\right)}{u}_{z}^{2}{u}_{y}+{H}_{iyyz}^{\left(3\right)}{u}_{y}^{2}{u}_{z}+{H}_{ixyz}^{\left(3\right)}{u}_{x}{u}_{y}{u}_{z} \end{split}$ | (7) |
| $ \begin{split}&{A}^{\left(4\right)} = {H}_{ixxyy}^{\left(4\right)}{u}_{x}^{2}{u}_{y}^{2}+{H}_{ixxyy}^{\left(4\right)}{u}_{x}^{2}{u}_{y}^{2}+{H}_{ixxzz}^{\left(4\right)}{u}_{x}^{2}{u}_{z}^{2}+{H}_{iyyzz}^{\left(4\right)}{u}_{z}^{2}{u}_{y}^{2} +\\&2\left({H}_{ixyzz}^{\left(4\right)}{u}_{x}{u}_{y}{u}_{z}^{2}+{H}_{ixyyz}^{\left(4\right)}{u}_{x}{u}_{y}^{2}{u}_{z}+{H}_{ixxyy}^{\left(4\right)}{u}_{x}^{2}{u}_{y}^{2}+{H}_{ixxyz}^{\left(4\right)}{u}_{x}^{2}{u}_{y}{u}_{z}\right) \end{split}$ | (8) |
其中,
本文模拟的是二维问题(D = 2),选用D2Q9速度模型,其中离散粒子速度定义为:
| $ {\boldsymbol{c}}_{i} = \left\{\begin{array}{ll}\left(\mathrm{0,0}\right),& i = 0\\ \left[\mathrm{sin}\left(\dfrac{i-1}{2}\text{π} \right),\mathrm{cos}\left(\dfrac{i-1}{2}\text{π} \right)\right],& i = 1~4\\ \sqrt{2}\left[\mathrm{sin}\left(\dfrac{2i-1}{4}\text{π} \right),\mathrm{cos}\left(\dfrac{2i-1}{4}\text{π} \right)\right],& i = 5~8\end{array}\right. $ | (9) |
速度权重为:
| $ {w}_{i} = \left\{\begin{array}{ll}4/9,& i = 0\\ 1/9,& i = 1~4\\ 1/36,& i = 5~8\end{array}\right. $ | (10) |
格子声速为
| $ {f}_{i}\left(\boldsymbol{x}+{\boldsymbol{c}}_{i}\mathrm{\Delta }t,t+\mathrm{\Delta }t\right) = {f}_{i}\left(\boldsymbol{x},t\right)-\frac{\mathrm{\Delta }t}{\tau }[{f}_{i}\left(\boldsymbol{x},t\right)-{f}_{i}^{{\rm{eq}}}(\boldsymbol{x},t\left)\right] $ | (11) |
其中,
本文涉及点声源在流场中的叠加,采用Viggen[36]提出的多极子声源方法。该方法可以统一描述多极子声源作用,并以源项
| $ \left[\begin{array}{c}{s}_{0}\\[16.4pt] {s}_{1}\\[15.5pt] {s}_{2}\\[16.2pt] {s}_{3}\\ {s}_{4}\\ {s}_{5}\\[19.2pt] {s}_{6}\\ {s}_{7}\\ {s}_{8}\end{array}\right] = \left[\left.\begin{array}{ccccccccc}{w}_{0}& 0& 0& -1& -1& 0& 0& -\dfrac{1}{2}& -\dfrac{1}{2}\\ {w}_{1}& \dfrac{1}{2}& 0& \dfrac{1}{2}& 0& 0& 0& 0& 0\\ {w}_{2}& 0& \dfrac{1}{2}& 0& \dfrac{1}{2}& 0& 0& 0& 0\\ {w}_{3}& -\dfrac{1}{2}& 0& \dfrac{1}{2}& 0& 0& 0& 0& 0\\ {w}_{4}& 0& -\dfrac{1}{2}& 0& \dfrac{1}{2}& 0& 0& 0& 0\\ {w}_{5}& 0& 0& 0& 0& \dfrac{1}{\sqrt{8}}& 0& \dfrac{1}{4}& 0\\ {w}_{6}& 0& 0& 0& 0& 0& \dfrac{1}{\sqrt{8}}& 0& \dfrac{1}{4}\\ {w}_{7}& 0& 0& 0& 0& -\dfrac{1}{\sqrt{8}}& 0& \dfrac{1}{4}& 0\\ {w}_{8}& 0& 0& 0& 0& 0& -\dfrac{1}{\sqrt{8}}& 0& \dfrac{1}{4}\end{array}\right]\right.\left[\begin{array}{c}{M}_{0}\\ {M}_{x}\\ {M}_{y}\\ {M}_{xx}\\ {M}_{yy}\\ {M}_{{x}'}\\ {M}_{{y}'}\\ {M}_{{x}'{x}'}\\ {M}_{{y}'{y}'}\end{array}\right] $ | (12) |
其中,
点声源声波影响下的剪切层发展计算模型如图1所示。计算域上下两个区域分别有水平速度
| $ \left\{\begin{array}{l}u(x,y) = \dfrac{{u}_{1}+{u}_{2}}{2}+\dfrac{{u}_{1}-{u}_{2}}{2}\mathrm{tanh}\left(\dfrac{2y}{{\theta }_{m}}\right)\\ v(x,y) = 0\end{array}\right. $ | (13) |
式中
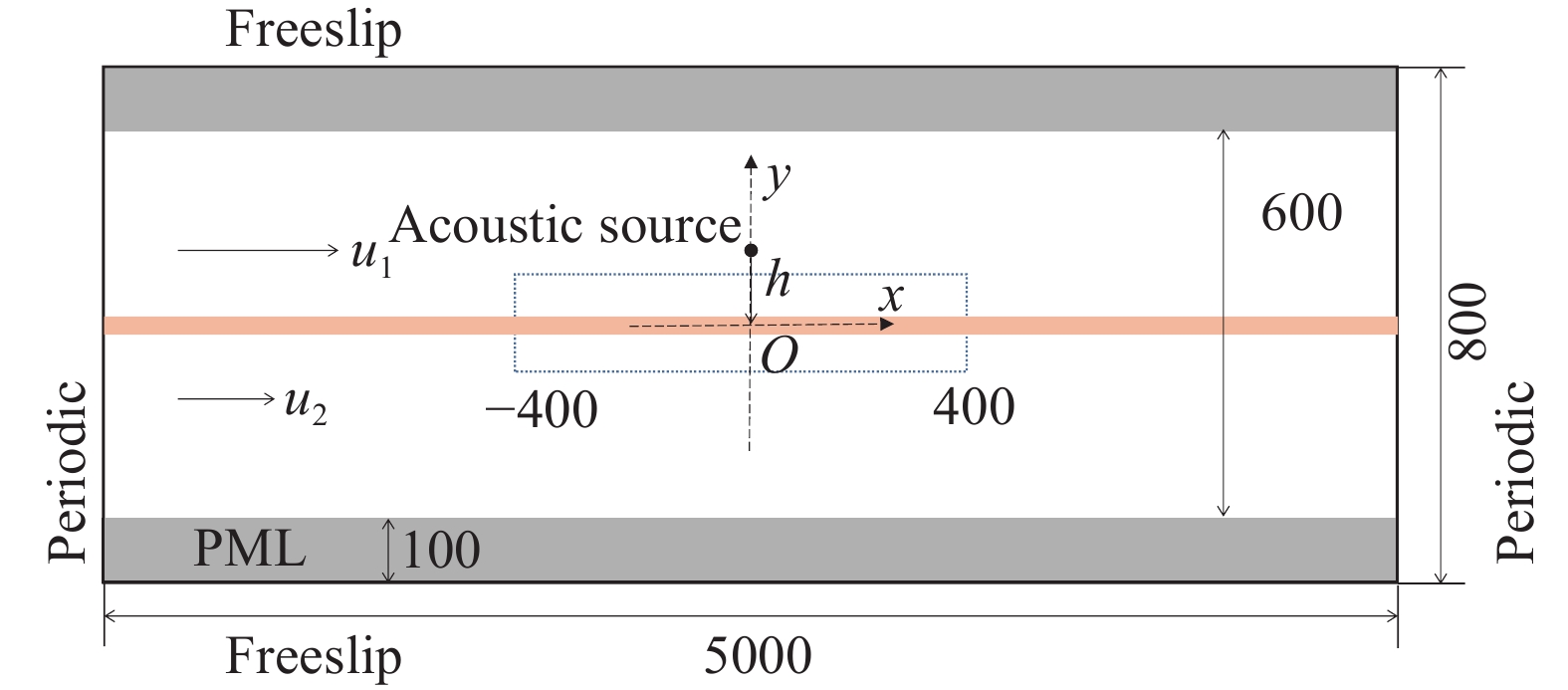
|
图 1 计算模型示意图 Fig.1 Schematic of the computational setup |
计算域上下两边设置声波吸收条带,采用PML技术实现[27],这主要为了吸收计算域中的传出声波,不使边界反射波污染流场。在PML层中,额外增加起吸波效果的碰撞项:
| $ {\mathrm{\varOmega }}^{{\rm{PML}}}\left({f}_{i}\right) = -\left[\epsilon{c}_{i\alpha }{\partial }_{\alpha }{Q}_{i}+2\epsilon{\tilde f}_{i}^{{\rm{eq}}}+{\epsilon}^{2}{Q}_{i}\right] $ | (14) |
| $ \begin{split}\\{\partial }_{t}{Q}_{i} = {\tilde f}_{i}^{{\rm{eq}}} = {f}_{i}^{{\rm{{\rm{eq}}}}}\left(\rho ,\boldsymbol{u},t\right)-{f}_{i}^{{\rm{eq}}}\left(\bar{\rho },\bar{\boldsymbol{u}},t\right) \end{split}$ | (15) |
其中,
| $ \epsilon = {\epsilon}_{0}\frac{{l}^{2}}{{L}_{{\rm{PML}}}^{2}} $ |
在本文计算中,计算域尺度为
计算结果表明,在初始无扰动情况下,剪切层可以在声波穿越过程中维持一段时间的稳定。在这段时间中,声传播方向满足Amiet理论的描述[15],即背景流场具有稳定的速度剖面时,多普勒效应导致声传播在剪切层上发生偏折。Amiet公式为:
| $ \mathrm{t}\mathrm{a}\mathrm{n}{\theta }_{c} = \frac{\chi }{M a+(1-{M a}^{2})\mathrm{c}\mathrm{o}\mathrm{s}\theta } $ | (16) |
| $ \chi = \sqrt{{\left(1-M a\;\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)}^{2}-{\mathrm{cos}}^{2}\theta } $ | (17) |
其中,
图2给出某一时刻流场压力脉动(压力与密度成正比)分布云图,红线标记了剪切层位置,可以看到声场在剪切层两侧的偏折现象明显。进一步在图中取三个测点:(-40,-40)、(80,-40)、(120,-40),进行声波波前到达时间以及密度脉动幅度的测量。结果显示,LBM的计算结果与Amiet理论预测吻合较好(见表1),证实了本文数值方法的准确性。
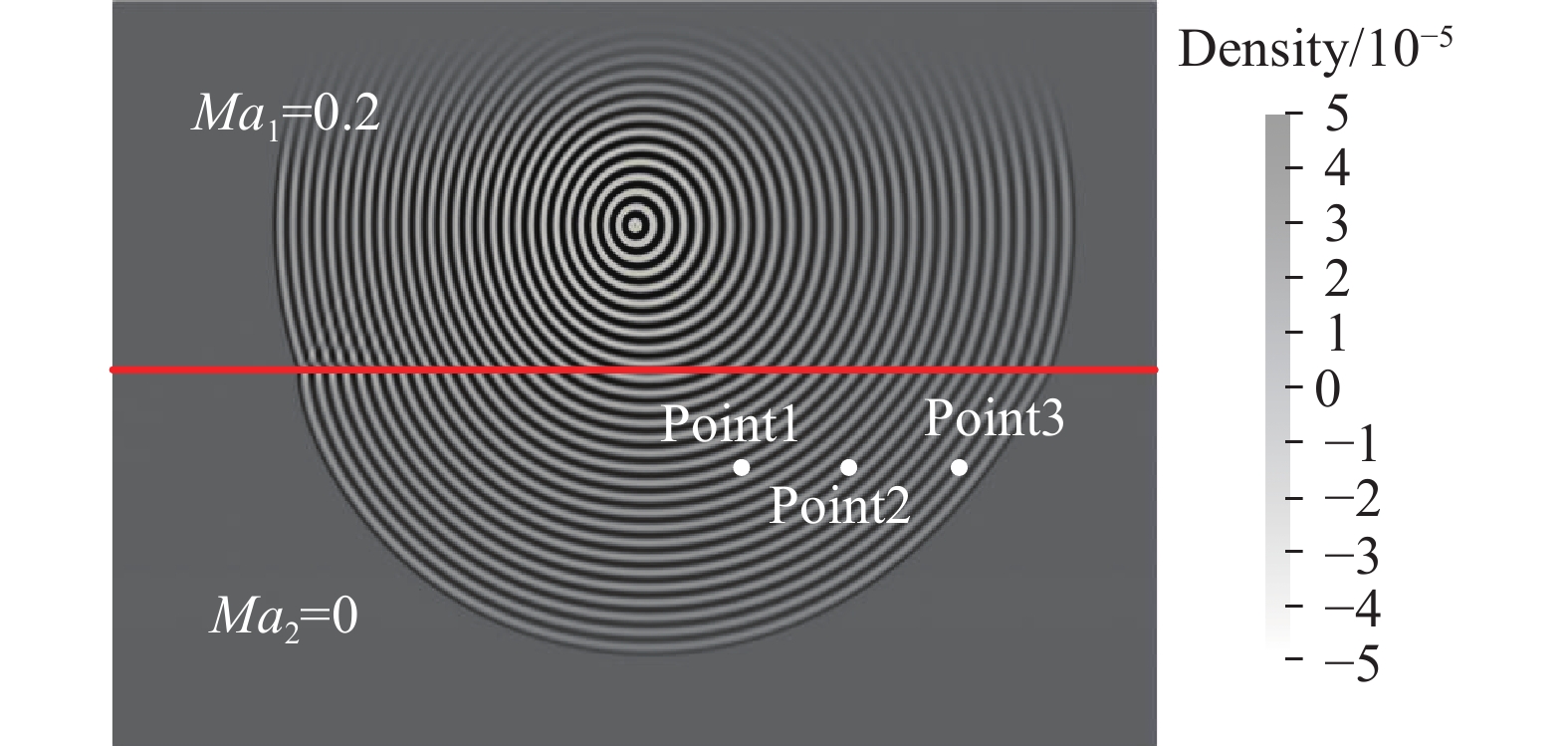
|
图 2 声波穿过薄剪切层密度分布云图 Fig.2 Sound field induced by waves propagatingthrough a thin shear layer |
| 表 1 LBM计算与Amiet理论预测结果比较 Table 1 Comparison between LBM results and Amiet’s prediction |
|
|
本文研究不同波数声波与有一定厚度的水平剪切层相互作用后的流场和声场的变化。根据流向速度可将流场划分为3个部分:剪切层上侧(声源一侧)、剪切层区域以及剪切层下侧(声波接收区)。受速度梯度的影响,声波传播会发生反射与折射,剪切层上侧的声场同时受入射波与反射波影响,剪切层下侧基本只有折射声波。剪切层中不仅存在3种声波的叠加,还包含由声波激励起的K-H波造成的流场、压力场变化。
计算结果显示,在声传播过程中流场声场演化基本分为三个阶段:初始阶段,平直剪切层稳定,声波穿越剪切层过程主要具有折射特征,满足Amiet理论预测;第二阶段,随着流动的发展,剪切层对声传播的影响进一步显现,声压分布在不同的区域表现出一些特殊结构,其局部的流动参量分布开始偏离稳定流状态,此时剪切流场仍然没有可见的变化;第三阶段,在声场分布特殊结构的作用下,剪切层开始失稳,并进一步迅速发展为不稳定流动,其中剪切层的波动分布与前述声波的特殊结构相匹配。研究同时表明,声场对剪切层不稳定性的发展起到诱发作用,在剪切层不稳定性进一步发展的过程中则摆脱了声场的影响。
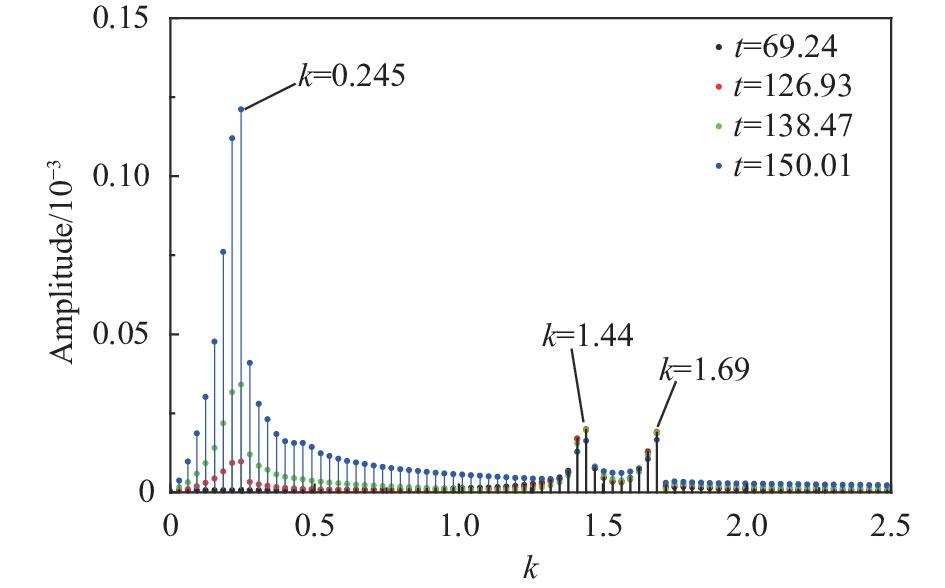
数值模拟发现,在演化过程中激励声波波数
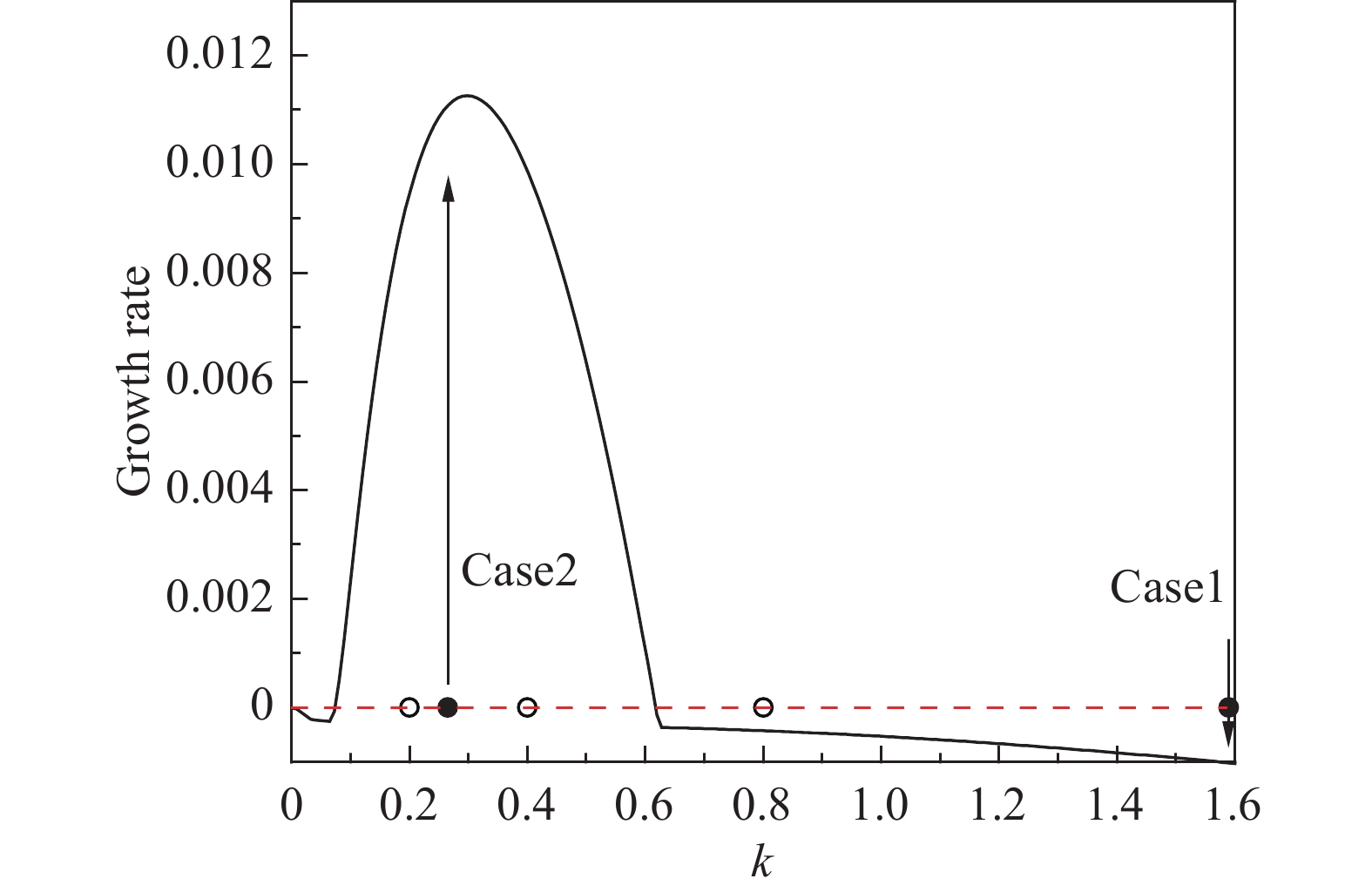
|
图 3 剪切层不稳定波波数与增长率关系 Fig.3 Growth rate of unstable waves in the shear layer |
测算结果表明,以
本节主要针对短波长声波传播与剪切层发展耦合现象(算例1)开展分析。图4给出了

|
图 4 算例1短波长条件下,剪切层附近的密度分布 Fig.4 Density distribution near the shear layer in case 1 (short-wave mode) |
上述描述表明,区域1中的流动具有较为丰富的物理内涵,而区域2中的声场-流动演化与2.3节所述内容相近。因此,下面的内容主要针对区域1的声场分布与不稳定性演化过程加以展开。
图5给出了
| $ \theta \left({M}_{1}\right) = \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\left[-\frac{1}{1+{M}_{1}}\right] $ |
当前算例中,

|
图 5 算例1流场密度场演化云图 Fig.5 Temporal evolution of density in case 1 (short-wave mode) |
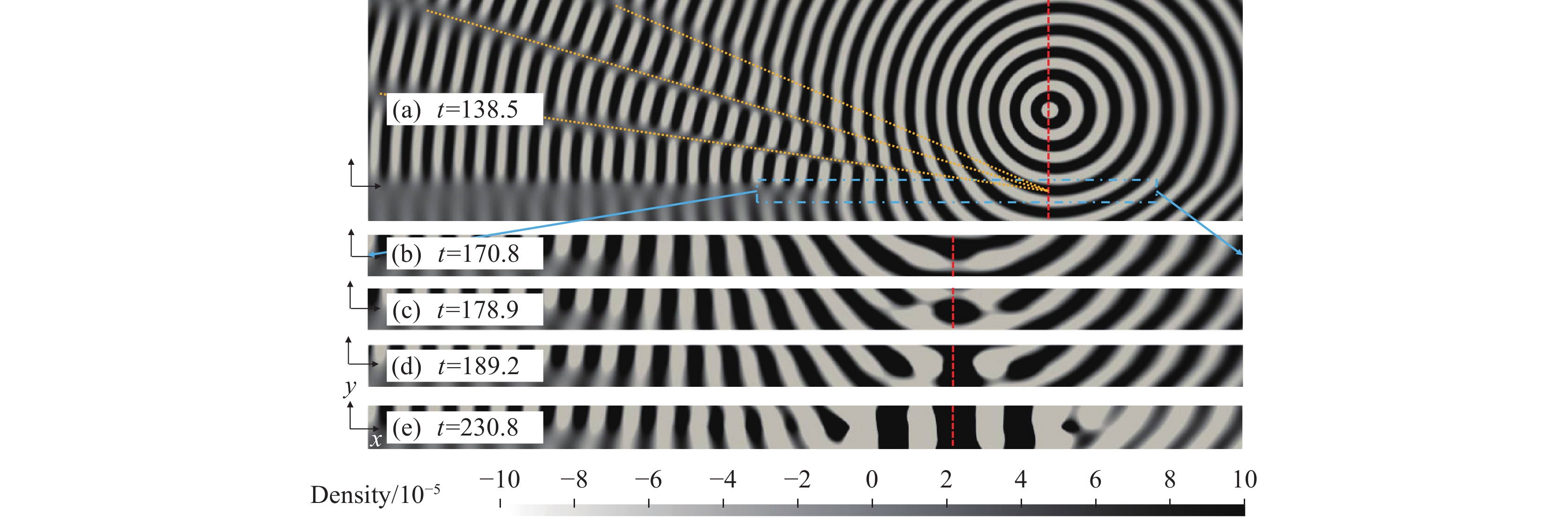
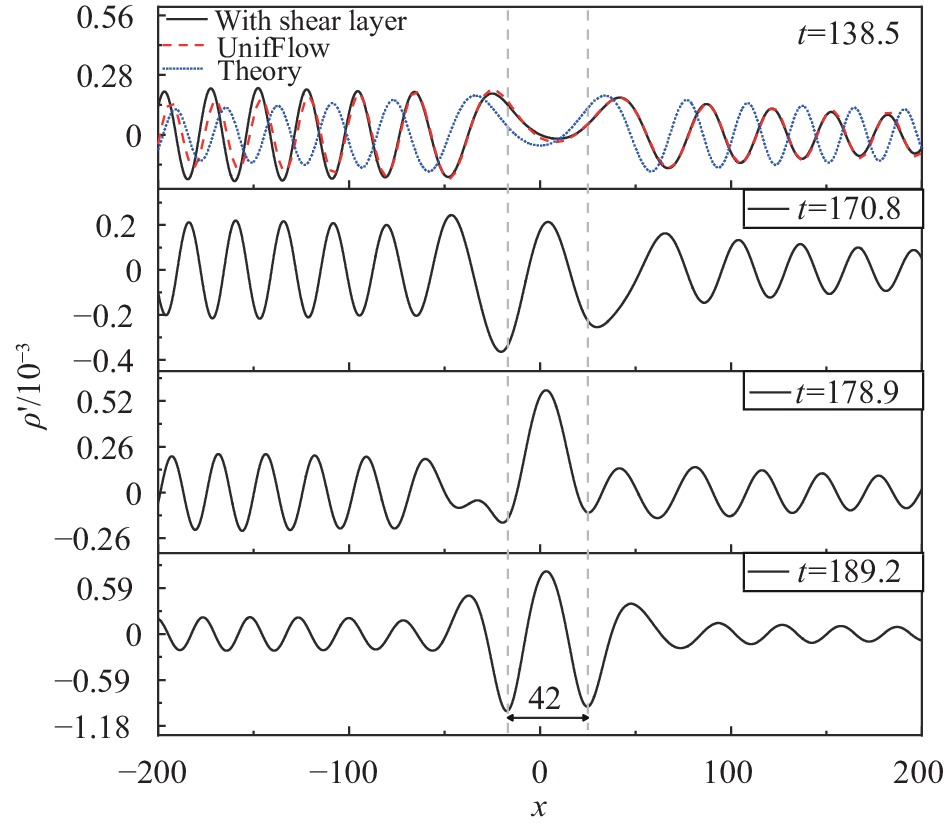
为了进一步看清压力波包结构的发展,我们提取了剪切层附近一条水平线
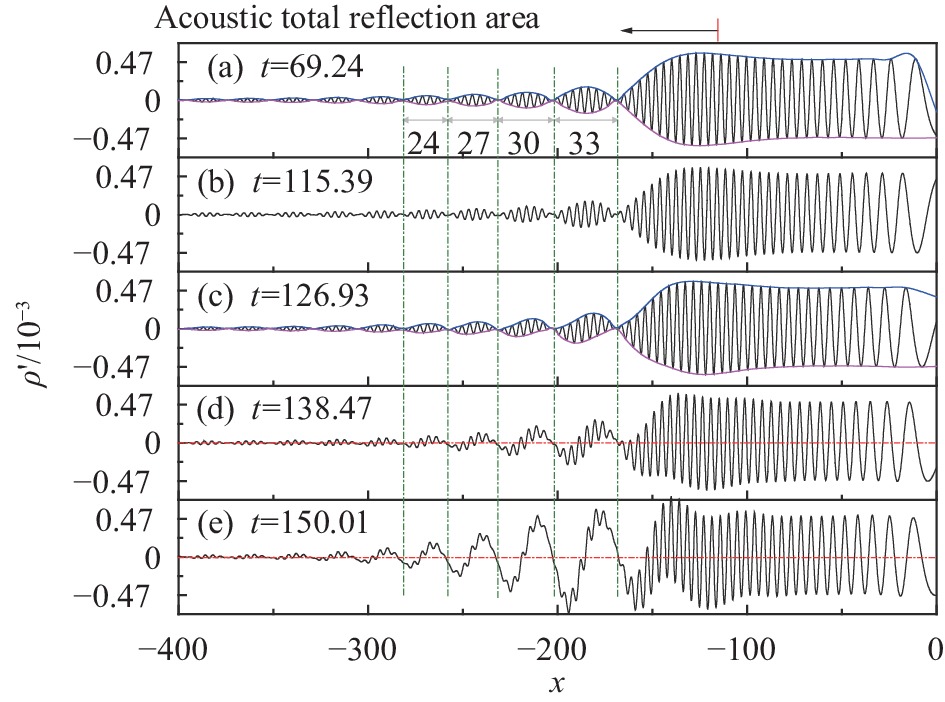
|
图 6 算例1中 |
图6进一步显示,在时刻
|
图 7 算例1中 |
最后需要指出两点:
1) 结合区域3的声场压力分布(图4)以及声波在剪切层全反射的条件判据可知,区域3中,声波以穿越剪切层为主,因而不存在区域1中的波叠加现象,也就无法诱导出类似于区域1中的波包结构;并且声波脉动本身的空间尺度又明显小于K-H最不稳定波的尺度。因而此区域的K-H波发展缓慢,流动相对稳定。
2) 尽管区域1剪切层中波包结构较为规整,但从图6可以看出靠近声源区域的波包波长(点划线指示部分)仍然存在变化,这主要是由声波、背景流动速度、剪切层的夹角在这个区域变化较大所造成的。
2.3 长波长声波作用下的剪切层失稳图8给出了算例2中,
在当前算例中,区域2的剪切流动首先失稳,其表现为剪切层中,剪切层上声波垂直入射位置的两侧出现压力极小值区(图8(b)中的亮斑)。该压力极值区将进一步发展出剪切层变形,并最终失稳(图8(e))。对于其他大波长声波(
|
图 8 算例2中不同时刻密度场分布演化云图 Fig.8 Temporal evolution of density in case 2 (long-wave mode) |

|
图 9 算例2中失稳后的涡量分布 Fig.9 Instantaneous vorticity field in unstable flow in case 2 (long-wave mode) |
与2.2节中区域1的声波入射条件不同,区域2中声波入射角度受水平位置影响更大。二维平面内点声源的传播有理论解,其分布可以用Bessel函数加以描述(本文采用第一类0阶Bessel函数:
|
图 10 算例2中 |
上述现象表明,含剪切层和背景流空间中,声波的传播发展具有特殊性。为了区分两者的作用,计算了声波在均匀流场中(即
1) 均匀流条件下声波波幅在垂直入射点两侧呈衰减趋势,且衰减速率与经典声学理论解(Bessel函数)预测一致;
2) 剪切层条件下,声场在垂直入射点右侧与均匀流一致,但左侧声脉动幅值明显提高,且在远场方向上的衰减微弱(或不衰减);
3) 剪切层条件下,声波垂直入射点左侧剪切层中压力波动波长发生了变化。
上述现象是在剪切层没有明显失稳的前提下被观察到的,由此我们可以判断:尽管在区域2中声波的演化、传播仍然具有行波特征,但剪切层的反射作用加剧了区域2左半部分的声压脉动幅值;并且由于非线性效应,压力波动的波长逐步减小,幅值随时间增加。剪切层对声波的透射和反射作用具有指向的选择性,这进一步使得剪切层上压力波动分布左右不对称,加剧了流动的不均匀性。综合2.2节所得结果,我们可以得到声场波动幅值的空间不均匀性,促使剪切层流动的不稳定发展。
本节结果表明区域2中的声波传播受更多因素的影响,比如剪切层对不同角度入射声波的折射/反射规律、声-流耦合;而现有理论模型、数值和实验结果仍然不足以支撑对有关现象的精确描述,因此有待将来开展更深入的物理机理研究。
3 结 论本文采用格子Boltzmann数值方法,对声波传播与平行剪切流稳定性发展的声作用机理开展了研究。探讨了声波在剪切流界面上的折射、反射现象,发现剪切层对声波的反射具有方向选择性。发现多普勒效应—声波在上下两层流体中的波长变化是导致流动稳定性的一个重要诱因。最终结合平行剪切流动稳定性分析,探讨了声压幅值分布对流动稳定性的影响;发现声场对剪切层稳定影响可以分为(声波)长波模式和短波模式。基于声源一侧流动方向,剪切层不稳定性发展可分为上游区、声波近垂直入射区和下游区。三个区域的失稳原因和失稳条件存在不同。研究结果表明:
1)在背景流动下游,声传播方向与流动方向夹角较小,声波透过剪切层成分较高,其传播规律服从经典Amiet理论,声场作用对剪切层稳定性影响较小。在背景流动上游区域,随着声波传播方向与来流方向夹角的增长,剪切层上的声反射作用增强,直至全反射出现,反射波与入射波在声源一侧区域形成干涉条纹结构。
2)在短波长声波情况下,剪切层上侧声波与下侧声波形成干涉。由于其波长不同,叠加声波构成稳定的波包结构,该结构的波长如果与剪切层失稳波长吻合,会诱导产生流动失稳。在流动失稳形成后,流动与声波发展可以解耦。
3)在长波长声波条件下,前述剪切层上游的干涉波包结构较弱,声源垂直入射区扰动增长占优。剪切层的反射作用使得该区域上游部分声压脉动增强,造成剪切层内声扰动分布对称性的缺失,同时压力波动波长随时间减小;当这样的波长落入失稳波长区域后,K-H波被诱导产生,并逐渐进入相对独立的发展阶段。
本研究揭示了不同波长声波作用下,平行剪切流动失稳的机理,可以为流动稳定性控制、声探测、流动噪声调制等研究提供借鉴。研究同时也显示,在声场作用下,剪切层内部流动、剪切层的声反射、声传播机制等方面的研究工作仍然亟待开展。
| [1] |
LECONTE J. On the influence of musical sounds on the flame of a jet of coal-gas[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1858, 15(99): 235-239. DOI:10.1080/14786445808642470 |
| [2] |
王李璨, 陈荣钱, 尤延铖, 等. 剪切层形态对声波传播与声源定位的影响研究[J]. 西北工业大学学报, 2019, 37(6): 1148-1157. WANG L C, CHEN R Q, YOU Y C, et al. Effects of shear layer characteristics on acoustic propagation and source localization[J]. Journal of Northwestern Polytechnical University, 2019, 37(6): 1148-1157. DOI:10.3969/j.issn.1000-2758.2019.06.008 (in Chinese) |
| [3] |
RAYLEIGH L. On the instability of jets[J]. Proceedings of the London Mathematical Society, 1878, s1-10(1): 4-13. DOI:10.1112/plms/s1-10.1.4 |
| [4] |
CROW S C, CHAMPAGNE F H. Orderly structure in jet turbulence[J]. Journal of Fluid Mechanics, 1971, 48(3): 547-591. DOI:10.1017/s0022112071001745 |
| [5] |
ZAMAN K B M Q, HUSSAIN A K M F. Vortex pairing in a circular jet under controlled excitation. Part 1. General jet response[J]. Journal of Fluid Mechanics, 1980, 101(3): 449-491. DOI:10.1017/s0022112080001760 |
| [6] |
OLSEN J F, RAJAGOPALAN S, ANTONIA R A. Jet column modes in both a plane jet and a passively modified plane jet subject to acoustic excitation[J]. Experiments in Fluids, 2003, 35(3): 278-287. DOI:10.1007/s00348-003-0663-4 |
| [7] |
SATO H, SAKAO F. An experimental investigation of the instability of a two-dimensional jet at low Reynolds numbers[J]. Journal of Fluid Mechanics, 1964, 20(2): 337-352. DOI:10.1017/s0022112064001264 |
| [8] |
HO C M, HUANG L S. Subharmonics and vortex merging in mixing layers[J]. Journal of Fluid Mechanics, 1982, 119: 443-473. DOI:10.1017/s0022112082001438 |
| [9] |
BIRBAUD A L, DUROX D, DUCRUIX S, et al. Dynamics of free jets submitted to upstream acoustic modulations[J]. Physics of Fluids, 2007, 19(1): 013602. DOI:10.1063/1.2432156 |
| [10] |
HSIAO F B, HUANG J M. On the evolution of instabilities in the near field of a plane jet[J]. Physics of Fluids A:Fluid Dynamics, 1990, 2(3): 400-412. DOI:10.1063/1.857735 |
| [11] |
TAM C K W. Excitation of instability waves in a two-dimensional shear layer by sound[J]. Journal of Fluid Mechanics, 1978, 89(2): 357-371. DOI:10.1017/s0022112078002645 |
| [12] |
TAM C K W. Excitation of instability waves by sound: a physical interpretation[J]. Journal of Sound and Vibration, 1986, 105(1): 169-172. DOI:10.1016/0022-460X(86)90228-2 |
| [13] |
吴介之. 波涡相互作用研究的某些进展(I)[J]. 力学进展, 1991, 21(4): 430-443. WU J Z. Wave-vortex interactions(I)[J]. Advances in Mechanics, 1991, 21(4): 430-443. DOI:10.6052/1000-0992-1991-4-J1991-050 (in Chinese) |
| [14] |
MILES J W. On the reflection of sound at an interface of relative motion[J]. The Journal of the Acoustical Society of America, 1957, 29(2): 226-228. DOI:10.1121/1.1908836 |
| [15] |
AMIET R K. Refraction of sound by a shear layer[J]. Journal of Sound and Vibration, 1978, 58(4): 467-482. DOI:10.1016/0022-460X(78)90353-X |
| [16] |
PADOIS T, PRAX C, VALEAU V. Numerical validation of shear flow corrections for beamforming acoustic source localisation in open wind-tunnels[J]. Applied Acoustics, 2013, 74(4): 591-601. DOI:10.1016/j.apacoust.2012.09.013 |
| [17] |
张雪, 陈宝, 卢清华. Amiet剪切层理论的角度折射验证研究[J]. 应用声学, 2014, 33(5): 433-438. ZHANG X, CHEN B, LU Q H. Verification of angle refraction correction based on Amiet's shear layer theory[J]. Applied Acoustics, 2014, 33(5): 433-438. DOI:10.11684/j.issn.1000-310X.2014.05.009 (in Chinese) |
| [18] |
MASSON A, NYKYRI K. Kelvin-Helmholtz instability: lessons learned and ways forward[J]. Space Science Reviews, 2018, 214(4): 1-18. DOI:10.1007/s11214-018-0505-6 |
| [19] |
LIN C D, LUO K H, GAN Y B, et al. Kinetic simulation of nonequilibrium Kelvin-Helmholtz instability[J]. Communications in Theoretical Physics, 2019, 71(1): 132. DOI:10.1088/0253-6102/71/1/132 |
| [20] |
LIN C, LUO K H, XU A, et al. Multiple-relaxation-time discrete Boltzmann modeling of multicomponent mixture with nonequilibrium effects[J]. Physical Review E, 2021, 103(1-1): 013305. DOI:10.1103/physreve.103.013305 |
| [21] |
MIURA A, PRITCHETT P L. Nonlocal stability analysis of the MHD Kelvin-Helmholtz instability in a compressible plasma[J]. Journal of Geophysical Research:Space Physics, 1982, 87(A9): 7431-7444. DOI:10.1029/JA087iA09p07431 |
| [22] |
HSIEH D Y. Kelvin-Helmholtz stability and two-phase flow[J]. Acta Mathematica Scientia, 1989, 9(2): 189-197. DOI:10.1016/S0252-9602(18)30344-8 |
| [23] |
CHEN S Y, DOOLEN G D. Lattice boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 329-364. DOI:10.1146/annurev.fluid.30.1.329 |
| [24] |
BUICK J M, CAMPBELL D M, GREATED C A. Lattice Boltzmann methods in acoustics[J]. The Journal of the Acoustical Society of America, 1998, 103(5): 2975. DOI:10.1121/1.422412 |
| [25] |
LALLEMAND P, LUO L S. Theory of the lattice Boltzmann method: acoustic and thermal properties in two and three dimensions[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2003, 68(3 pt 2): 036706. DOI:10.1103/physreve.68.036706 |
| [26] |
MARIÉ S, RICOT D, SAGAUT P. Comparison between lattice Boltzmann method and Navier-Stokes high order schemes for computational aeroacoustics[J]. Journal of Computational Physics, 2009, 228(4): 1056-1070. DOI:10.1016/j.jcp.2008.10.021 |
| [27] |
NAJAFI-YAZDI A, MONGEAU L. An absorbing boundary condition for the lattice Boltzmann method based on the perfectly matched layer[J]. Computers & Fluids, 2012, 68: 203-218. DOI:10.1016/j.compfluid.2012.07.017 |
| [28] |
VIGGEN E M. Viscously damped acoustic waves with the lattice Boltzmann method[J]. Philosophical Transactions of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2011, 369(1944): 2246-2254. DOI:10.1098/rsta.2011.0040 |
| [29] |
LIU M, CHEN X P, PREMNATH K N. Comparative study of the large eddy simulations with the lattice Boltzmann method using the wall-adapting local eddy-viscosity and vreman subgrid scale models[J]. Chinese Physics Letters, 2012, 29(10): 104706. DOI:10.1088/0256-307x/29/10/104706 |
| [30] |
CHEN X P, REN H. Acoustic flows in viscous fluid: a lattice Boltzmann study[J]. International Journal for Numerical Methods in Fluids, 2015, 79(4): 183-198. DOI:10.1002/fld.4045 |
| [31] |
GUO R Q, CHEN X P. Sound generation by two dimensional vortex pair motion and the influence of viscosity[J]. Computers & Mathematics With Applications, 2019, 78(8): 2761-2771. DOI:10.1016/j.camwa.2019.04.022 |
| [32] |
HE X Y, LUO L S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation[J]. Physical Review E, 1997, 56(6): 6811-6817. DOI:10.1103/physreve.56.6811 |
| [33] |
SHAN X W, YUAN X F, CHEN H D. Kinetic theory representation of hydrodynamics: a way beyond the Navier–Stokes equation[J]. Journal of Fluid Mechanics, 2006, 550: 413. DOI:10.1017/s0022112005008153 |
| [34] |
COREIXAS C, CHOPARD B, LATT J. Comprehensive comparison of collision models in the lattice Boltzmann framework: theoretical investigations[J]. Physical Review E, 2019, 100(3): 033305. DOI:10.1103/physreve.100.033305 |
| [35] |
DE ROSIS A, LUO K H. Role of higher-order Hermite polynomials in the central-moments-based lattice Boltzmann framework[J]. Physical Review E, 2019, 99: 013301. DOI:10.1103/physreve.99.013301 |
| [36] |
VIGGEN E M. Acoustic multipole sources for the lattice Boltzmann method[J]. Physical Review E, 2013, 87(2): 023306. DOI:10.1103/physreve.87.023306 |
| [37] |
BARRIOS G, RECHTMAN R. Dynamics of an acoustically levitated particle using the lattice Boltzmann method[J]. Journal of Fluid Mechanics, 2008, 596: 191-200. DOI:10.1017/s0022112007009548 |
| [38] |
LAGRAVA D, MALASPINAS O, LATT J, et al. Advances in multi-domain lattice Boltzmann grid refinement[J]. Journal of Computational Physics, 2012, 231(14): 4808-4822. DOI:10.1016/j.jcp.2012.03.015 |
| [39] |
YE H Y, YANG L J, FU Q F. Spatial instability of viscous double-layer liquid sheets[J]. Physics of Fluids, 2016, 28(10): 102101. DOI:10.1063/1.4962872 |
 2022, Vol. 40
2022, Vol. 40


