2. 上海市动力工程多相流动与传热重点实验室,上海 200093
2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China
气泡在复杂微通道内的流动现象广泛存在于自然界和工业生产过程,如沸腾现象、页岩气开采、燃料电池的使用等。例如在燃料电池中气泡间的碰撞和合并时常发生,气泡在液体中的运动和相互作用直接影响相间的接触时间和接触面积,并改变气液间的传热传质[1],进而影响其使用性能[2-4]。因此对气泡进行微通道内的流动研究以及工业生产过程中的优化具有十分重要的意义。
学者们对复杂微通道内的气泡流动问题进行了大量的实验研究。Chen等[5]研究了高黏度流体中气泡在孔板通道内上升时的形状变化,发现气泡穿过孔板通道后变为“月牙状”。Corapcioglu等[6]提出采用定量方法预测气泡在粗糙多孔介质中的上升速度,其预测结果表明气泡的上升速度经过很短的时间后会达到平衡。Dawson等[7]研究了在恒定体积流量中孔板微通道内气泡的流动过程,发现随着流速的增加,气泡的后尖端速度发散且气泡尾部变薄向中间收缩回主体。
以上实验结果得到了气泡运动过程中的直观现象和宏观规律,为人们认识气泡在通道内的运动规律提供了理论基础。然而由于实验方法难以捕获微孔内的流动细节,采用数值模拟来研究两相流动问题也逐渐成为人们研究气泡运动的一种常用方法[8-9]。Sussman等[10]应用Level-set方法,研究了单个气泡上升过程中的界面形变以及破裂现象,发现随着表面张力和黏度比的增加,气泡越不容易发生变形和破裂现象;而随着雷诺数的增加气泡的变形会越来越剧烈。Sun等[11]利用格子Boltzmann方法模拟了单个气泡在含三个半圆形障碍物的通道内上升的问题,发现了障碍物的存在可以影响气泡的运动形态,使其运动轨迹发生偏转。Lou等[12]通过两相流格子Boltzmann模型,模拟研究了气泡在浮力作用下上升并通过复杂微通道的问题。研究发现障碍物表面润湿性越强,气泡变形越剧烈、气泡终端速度越小;且随着障碍物半径的增大,气泡的终端速度呈线性减小。
以上研究揭示了一些气泡在复杂微通道内的运动机理,但主要集中于单气泡的研究,较少涉及多气泡在复杂微通道内的运动行为,且大部分研究只能考虑较小的气液密度比。因此,本文选用Liang等[13]基于Allen-Cahn相场理论提出的大密度比格子Boltzmann模型,对两个上下排列的气泡在含孔板结构的微通道内的运动形态进行研究;主要调查了
Liang等[13]提出的大密度比LBM模型采用了两个分布函数描述指标参数和速度/压力的演化过程,其中指标函数满足如下Allen-Cahn方程:
| $ \begin{array}{c}\dfrac{\partial \phi }{\partial t}+\nabla \cdot \left(\phi \boldsymbol{u}\right) = \nabla \cdot \left[M\left(\nabla \phi -\mathrm{\lambda }\boldsymbol{n}\right)\right]\end{array} $ | (1) |
式中:
| $ \begin{array}{c}{f}_{i}\left(\boldsymbol{x} + \boldsymbol{e}_{i}{\delta }_{t},t + {\delta }_{t}\right)-{f}_{i}\left(\boldsymbol{x},t\right) = -\dfrac{{f}_{i}\left(\boldsymbol{x},t\right)-{f}_{i}^{{\rm{eq}}}\left(\boldsymbol{x},t\right)}{{\tau }_{f}}+{\delta }_{t}{{{F}}}_{i}\left(\boldsymbol{x},t\right)\end{array} $ | (2) |
| $ \begin{array}{c}{g}_{i}\left(\boldsymbol{x}+\boldsymbol{e}_{i}{\delta }_{t},t + {\delta }_{t}\right) - {g}_{i}\left(\boldsymbol{x},t\right) = -\dfrac{{g}_{i}\left(\boldsymbol{x},t\right)-{g}_{i}^{{\rm{eq}}}\left(\boldsymbol{x},t\right)}{{\tau }_{g}}+{\delta }_{t}{\mathit{G}}_{i}\left(\boldsymbol{x},t\right)\end{array} $ | (3) |
在两相流系统中,由于气液相界面的存在,运动黏度
平衡态分布函数
| $ \begin{array}{c}{f}_{i}^{{\rm{eq}}} = {\omega }_{i}\phi \left(1+\dfrac{\boldsymbol{c}_{i}\cdot \boldsymbol{u}}{{c}_{s}^{2}}\right)\end{array} $ | (4) |
| $ \begin{array}{l}{g}_{i}^{{\rm{eq}}}\left\{\begin{array}{l}\dfrac{p}{{c}_{s}^{2}}\left({\omega }_{i}-1\right)+\rho {s}_{i}\left(\boldsymbol{u}\right),\qquad i = 0\\ \dfrac{p}{{c}_{s}^{2}}{\omega }_{i}+\rho {s}_{i}\left(\boldsymbol{u}\right),\;\qquad\qquad i = 1~8\end{array}\right.\end{array} $ | (5) |
| $ \begin{array}{c}{s}_{i}\left(\boldsymbol{u}\right) = {\omega }_{i}\left[\dfrac{\boldsymbol{c}_{i}\cdot \boldsymbol{u}}{{c}_{s}^{2}}+\dfrac{{\left(\boldsymbol{c}_{i}\cdot \boldsymbol{u}\right)}^{2}}{2{c}_{s}^{2}}-\dfrac{\boldsymbol{u}\cdot \boldsymbol{u}}{2{c}_{s}^{2}}\right]\end{array} $ | (6) |
其中:
| $ \begin{array}{l}\boldsymbol{c}_{i} = \left\{ \begin{array}{l}c\left(\mathrm{0,0}\right),\qquad\qquad\qquad\qquad\qquad\qquad\qquad i = 0\\ c\left\{\mathrm{cos}\left[\left(i-1\right)\dfrac{{\text{π}} }{2}\right],\mathrm{sin}\left[\left(i-1\right)\dfrac{{\text{π}} }{2}\right]\right\},\;\qquad\qquad i = 1~4\\ \sqrt{2}c\left\{\mathrm{cos}\left[\left(2i-1\right)\dfrac{{\text{π}} }{4}\right],\mathrm{sin}\left[\left(2i-1\right)\dfrac{{\text{π}} }{4}\right]\right\},\qquad i = 5~8\end{array}\right.\end{array} $ | (7) |
式中,
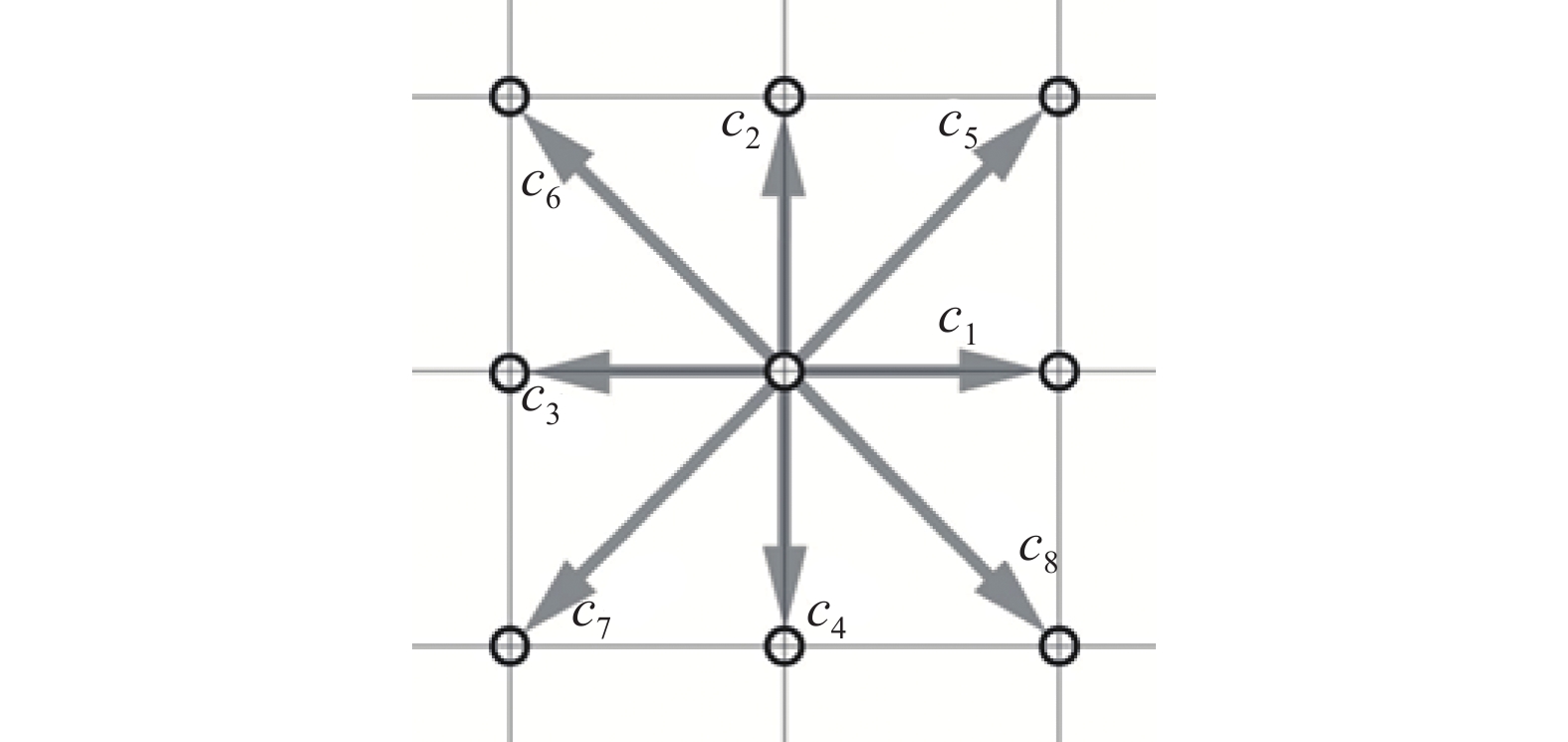
|
图 1 D2Q9速度模型示意图 Fig.1 Discrete velocities for D2Q9 model |
力项
| $ {\mathit{F}}_{i}\left(\boldsymbol{x},t\right) = \left(1-\dfrac{1}{2{\tau }_{f}}\right)\frac{{\omega }_{i}\boldsymbol{c}_{i}\cdot \left[{\partial }_{t}\left(\phi \boldsymbol{u}\right)+{c}_{s}^{2}\lambda \boldsymbol{n}\right]}{{c}_{s}^{2}} $ | (8) |
| $ {\mathit{G}}_{i}\left(\boldsymbol{x},t\right) = \left(1-\frac{1}{2{\tau }_{g}}\right)\times {\omega }_{i}\left[ \frac{{\boldsymbol{c}_{i}\cdot (\boldsymbol{F}}_{s}+\boldsymbol{G})}{{c}_{s}^{2}}+\left({\rho }_{l}-{\rho }_{g}\right)\boldsymbol{u}\nabla \phi :\dfrac{\boldsymbol{c}_{i}\boldsymbol{c}_{i}}{{c}_{s}^{2}}\right] $ | (9) |
式(8)中的
| ${\partial }{t}\left(\phi \boldsymbol{u}\right) = \frac{\phi \left(x,t\right)\boldsymbol{u}\left(x,t\right)-\phi \left(x,t-{\delta }_{t}\right)\boldsymbol{u}\left(x,t-{\delta }_{t}\right)}{{\delta }_{t}}$ | (10) |
式(9)中:
| $ \begin{split}\phi =& \sum _{i}{f}_{i} \\ \rho =& \phi \left({\rho }_{l}-{\rho }_{g}\right)+{\rho }_{g} \\ \rho \boldsymbol{u} =& \sum _{i = 0}^{8}\boldsymbol{c}_{i}{g}_{i}+0.5{\delta }_{t}\left({\boldsymbol{F}}_{s}+\boldsymbol{G}\right)\end{split} $ | (11) |
本文所研究的物理问题如图2所示。在计算区域为
| $ {v}_{b} = \frac{\mathrm{\Sigma }{V}_{z}\phi }{\mathrm{\Sigma }\phi } $ | (12) |
另外,取
| $ {t}^{\mathrm{*}} = t\sqrt{\frac{g}{\sqrt{{d}_{1}^{2}+{d}_{2}^{2}}}} $ | (13) |
| $ {v}^{\mathrm{*}} = \frac{{v}_{b}}{\sqrt{{g}\sqrt{{d}_{1}^{2}+{d}_{2}^{2}}}} $ | (14) |
对计算时间和速度进行无量纲化,其中:
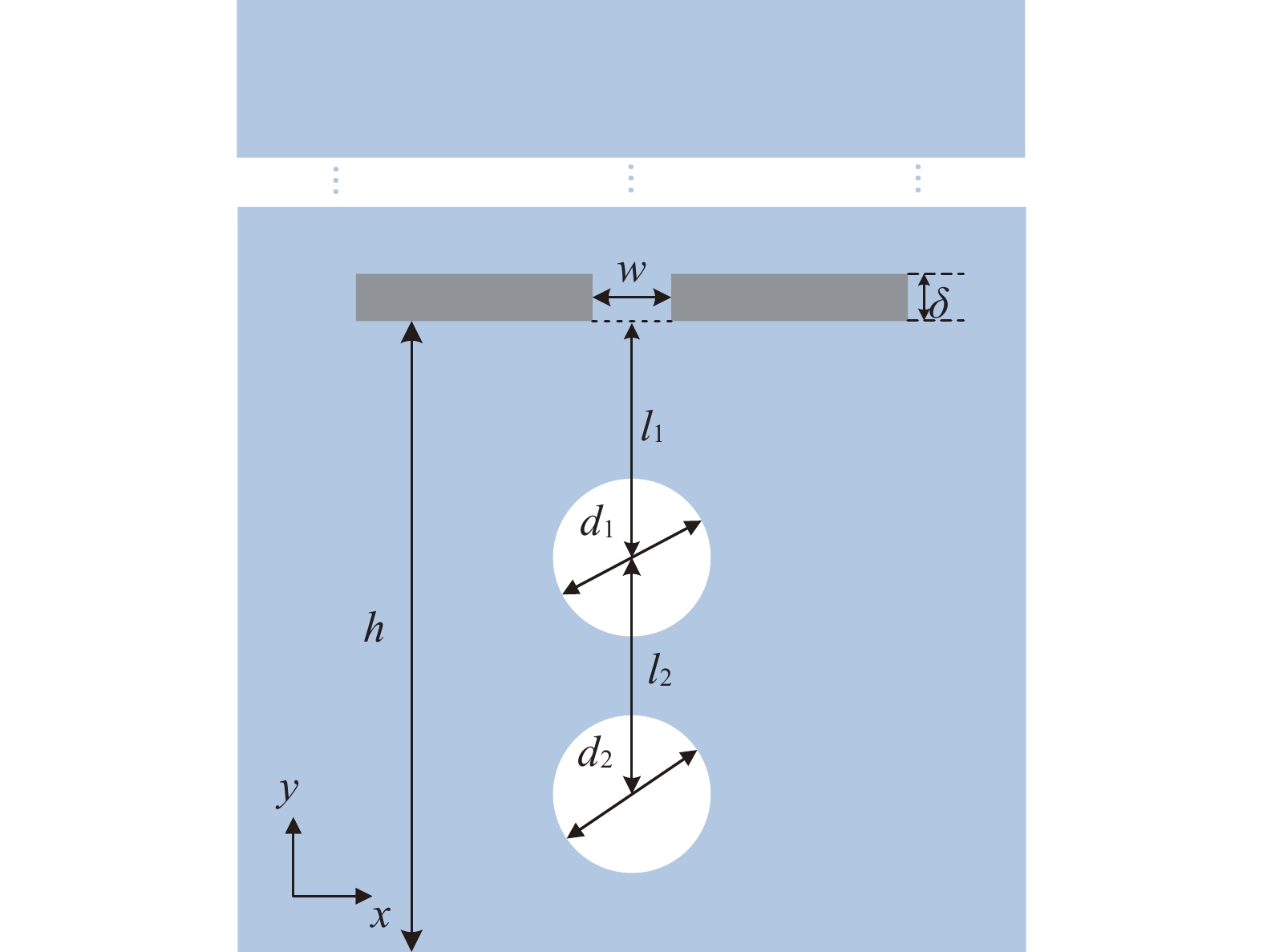
|
图 2 模型示意图 Fig.2 Model sketch |
首先通过Laplace定律验证模型的正确性。Laplace定律指出,当系统达到平衡态时,气泡内部压力与液相压力的差和表面张力成正比,和气泡半径
| $ \Delta p = {p}_{{\rm{inside}}}-{p}_{{\rm{outside}}} = \frac{\sigma }{r}$ | (15) |
其中
在本文验证中,初始气泡半径选20、25、30、35、40这五种情况,并考虑不同表面张力σ = 0.2、0.4、0.6、0.8、1.0,模拟结果如图3显示。气泡半径的倒数与表面张力成正比,模拟结果与Laplace定律吻合,证明了本文所使用模型的准确性。
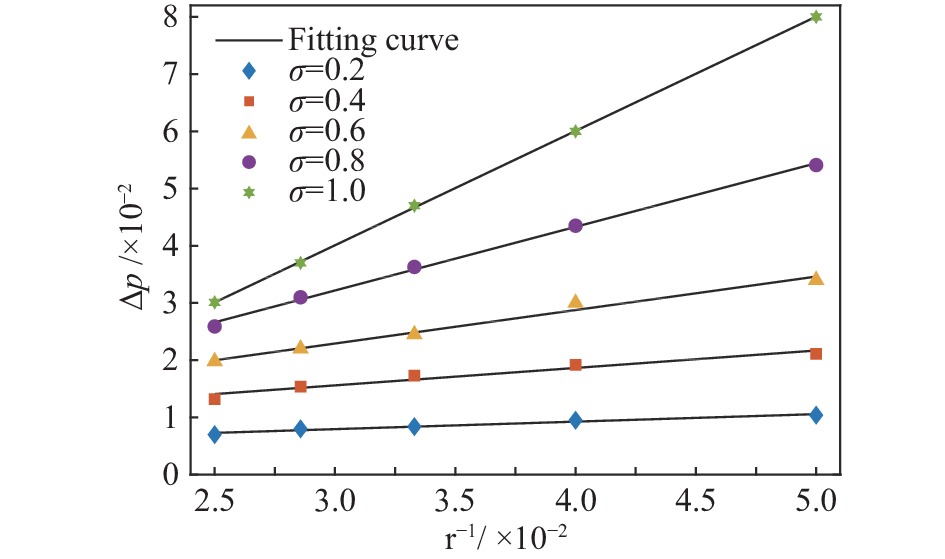
|
图 3 Laplace验证 Fig.3 Numerical validation |
气泡在光滑壁面通道内受浮力上升的问题与本文所要研究的问题相似, 且已有学者对该问题进行了大量研究, 因此本小节将采用该算例验证模型的正确性。模拟计算区域为
考虑
|
表 1 不同
|
|
|
|
表 2 不同
|
|
|
本文中主要研究Eötvös数(Eo)、气泡之间的相对大小和气泡的初始相对位置对气泡在孔板微通道内流动过程的影响。
4.1图4给出了四种
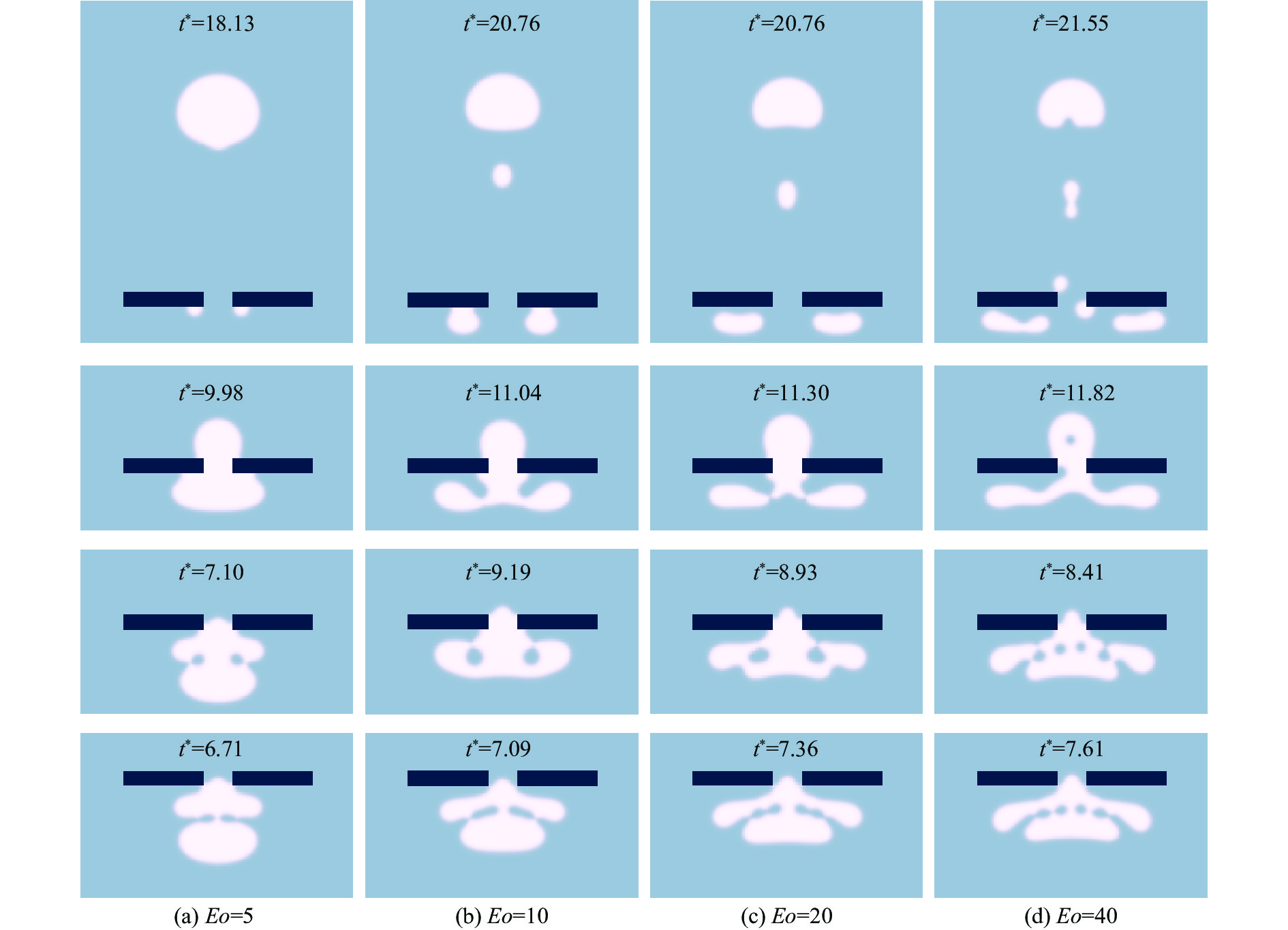
|
图 4 不同 |
图4(b)所示为
图4(c)为
上述四种工况下,
|
图 5 不同 |
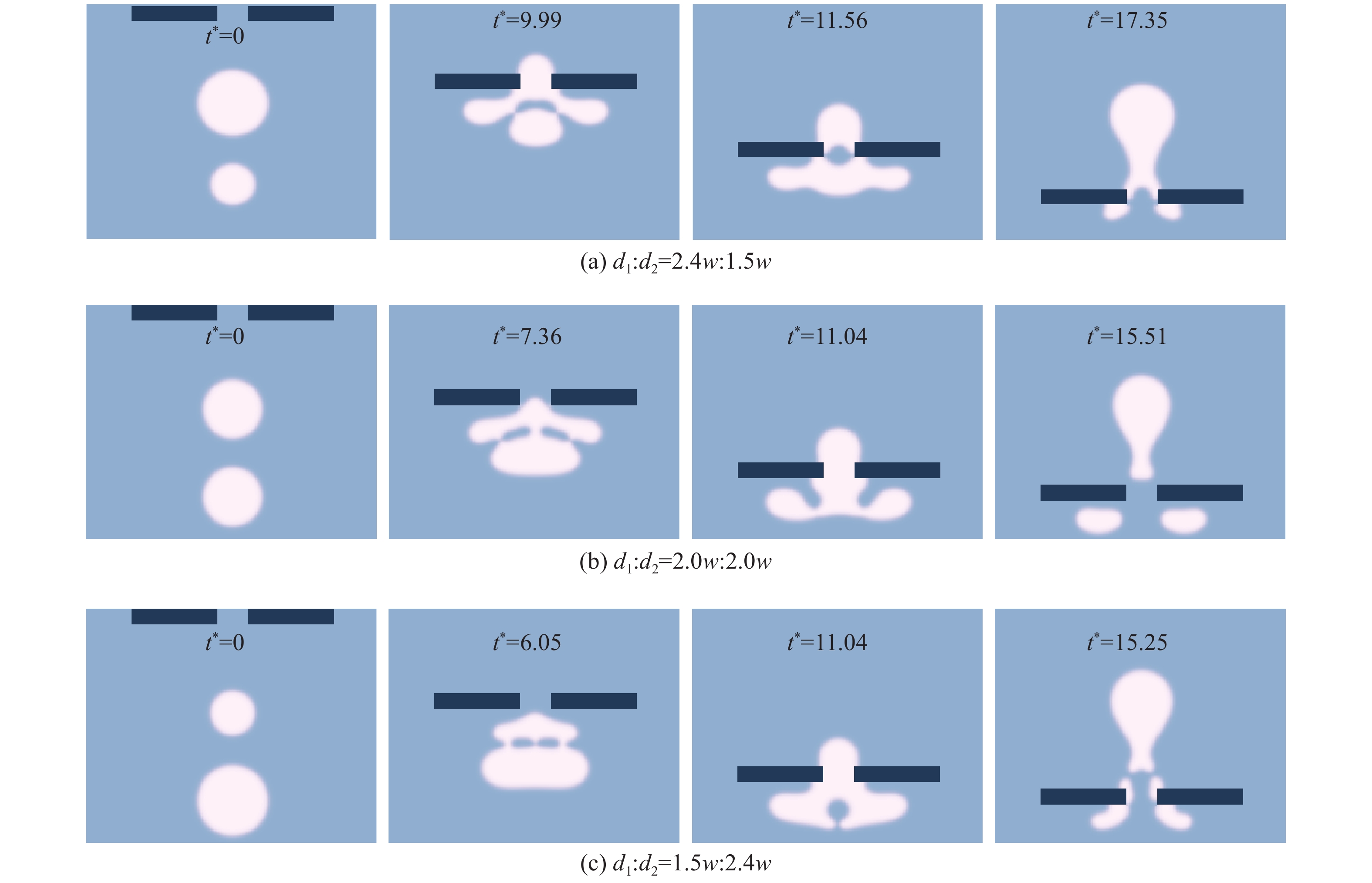
本小节研究了气泡相对大小对气泡通过孔板微通道的影响。数值模拟中参数设置为
图6(a)展示了
|
图 6 不同气泡直径下气泡运动过程 Fig.6 The temporal evolution of bubbles with different diameters |
图6(b)给出了上下两气泡直径相等时(
上方气泡直径小于下方气泡(
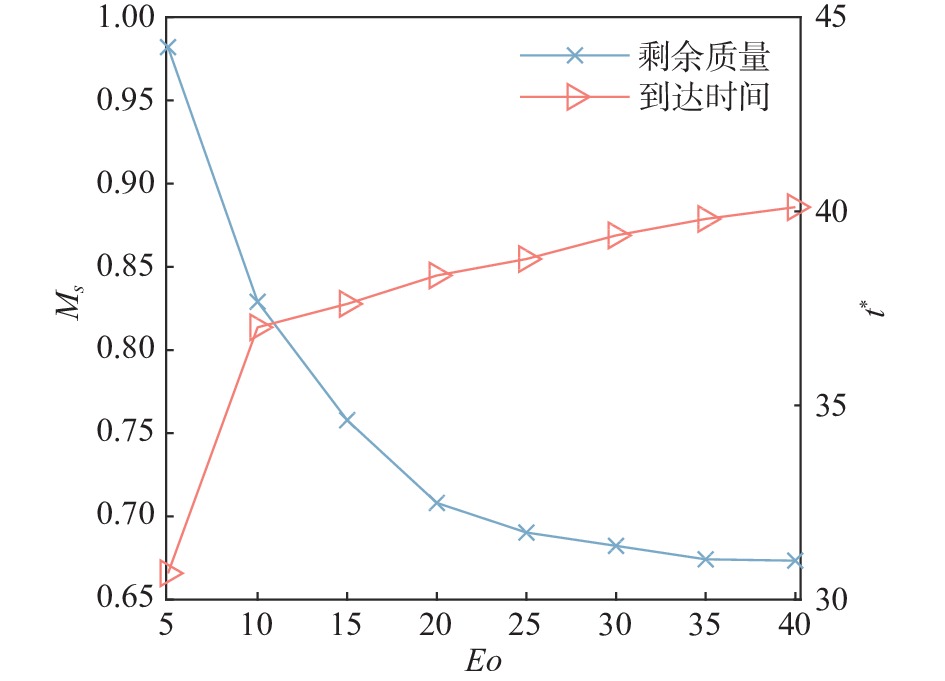
为了研究气泡相对大小对气泡通过孔板通道后剩余气泡质量的影响,增加了几组气泡直径比不同的工况以便比较。图7给出了三组相同变化比例但不同初始质量和的情况,统计了气泡穿过孔板后的剩余质量以及气泡运动到计算区域上方的时刻。从图7中间组可以看出,当上气泡质量大于下气泡质量时,上气泡位于孔板正下方部分质量接触到下气泡后在表面张力作用下向中间收缩,最终有较多的剩余质量可以达到顶部。而当下方气泡大于上方气泡时,两气泡发生合并的时间和位置提前,尽管下方气泡是从两侧汇入上气泡,但两个气泡形变程度较小,合并的气泡质量向孔口方向移动,故最终穿过孔板通道的质量比前者情况少。从中间组可以看出上下气泡直径对比度越大,剩余质量越多;而当上下两个气泡大小相等,穿过孔板到达通道上半部分的剩余质量最少,为0.82。在相反的直径比例下,质量大的气泡处在上方的情况最终的剩余质量始终比处在下方的情况多。另外,随着下方气泡相对上方气泡直径增大,气泡通过孔板到达顶部所需时间变短。结合图7上下两组可以看出气泡尺寸相对孔径越小,其通过得越完整,即剩余质量越多;而较小的质量也导致其受到的浮力相对较小,到达顶部时间变慢,在不同直径比下的剩余质量和到达时间也与中间组的变化趋势相似。
|
图 7 不同气泡直径下的剩余质量比和达到时间 Fig.7 Residual mass and the time for bubbles to reach the top for different diameters |
本小节研究两气泡之间的距离以及气泡与孔板的距离对双气泡运动行为的影响。首先研究不同气泡之间距离的情况,为了方便比较,此算例也以孔板间距
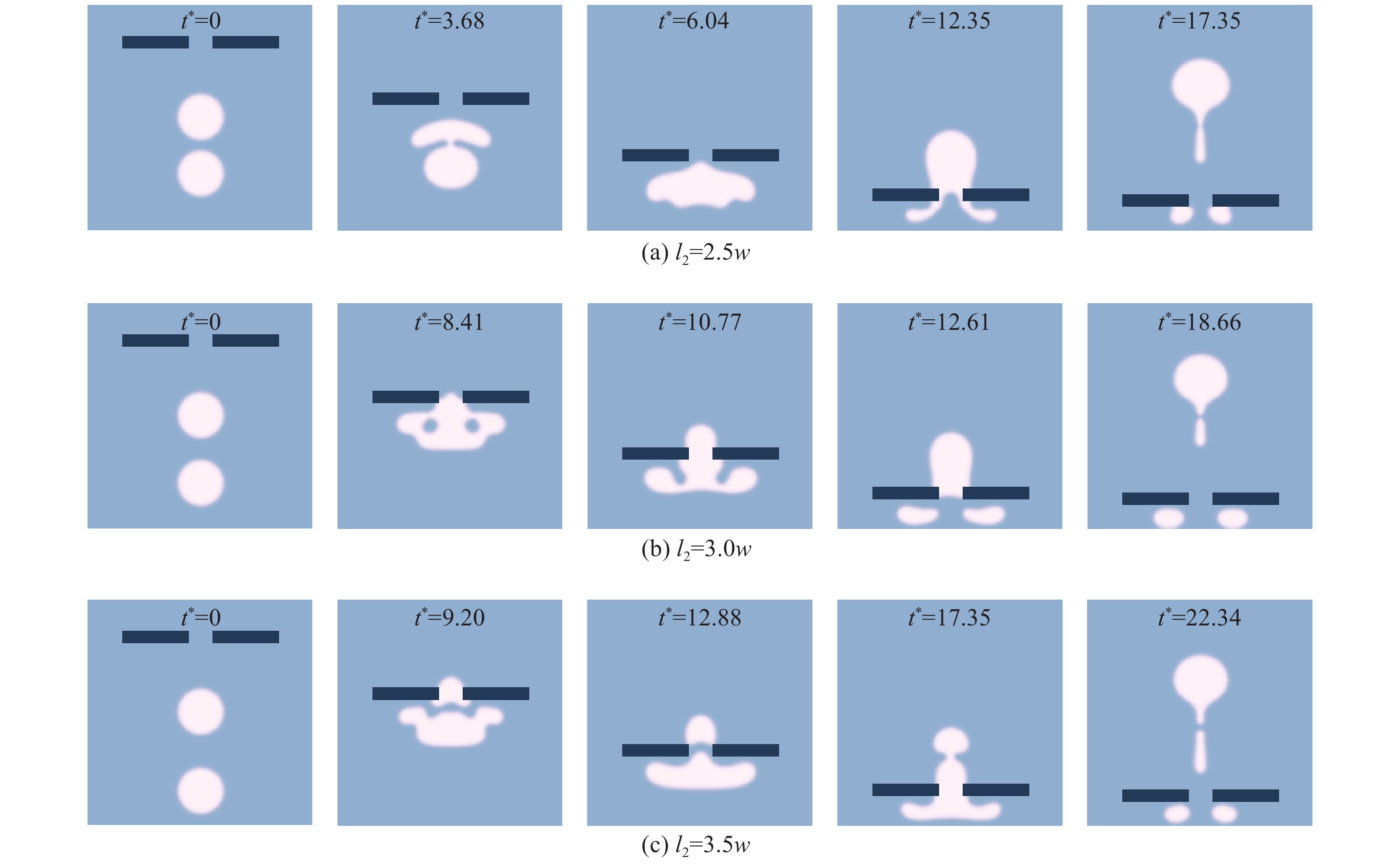
当两个气泡圆心距离
|
图 8 气泡不同初始位置情况下气泡运动过程 Fig.8 The temporal evolution of bubbles under different initial positions |
当两个气泡圆心距离
图8(c)给出了两个气泡圆心距离
经模拟计算发现,当
图9展示了两个气泡从不同位置开始上升时统计得到的速度变化曲线。从图9可以看出,在气泡未到达障碍物通道前,气泡的上升速度变化趋势基本相同;但当上气泡与孔板的距离
接下来研究上方气泡与孔板间的距离对双气泡运动行为的影响,这里固定两气泡间距,通过改变上气泡的位置来改变气泡与孔板的间距
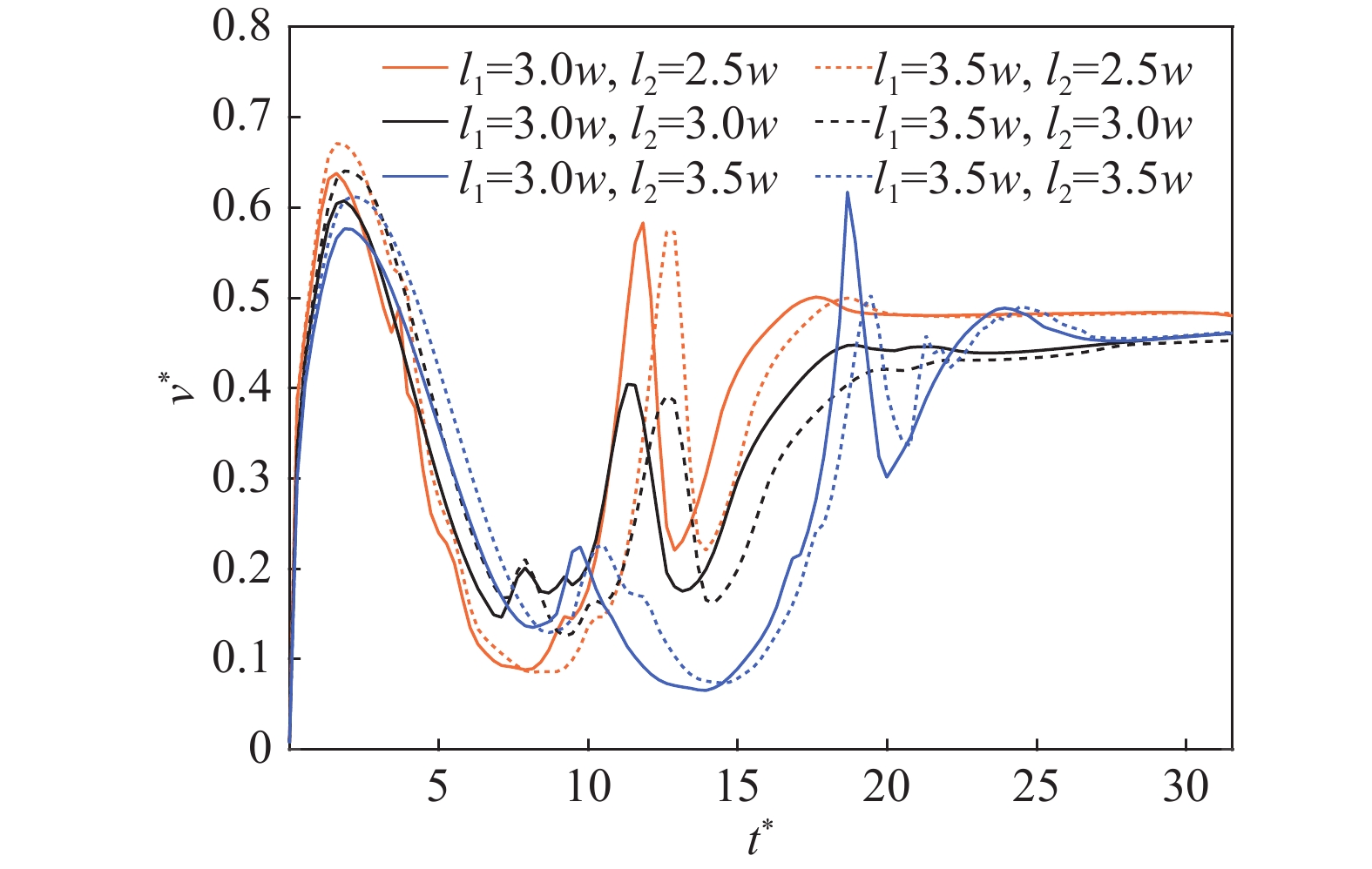
|
图 9 不同初始位置下气泡上升的平均速度 |
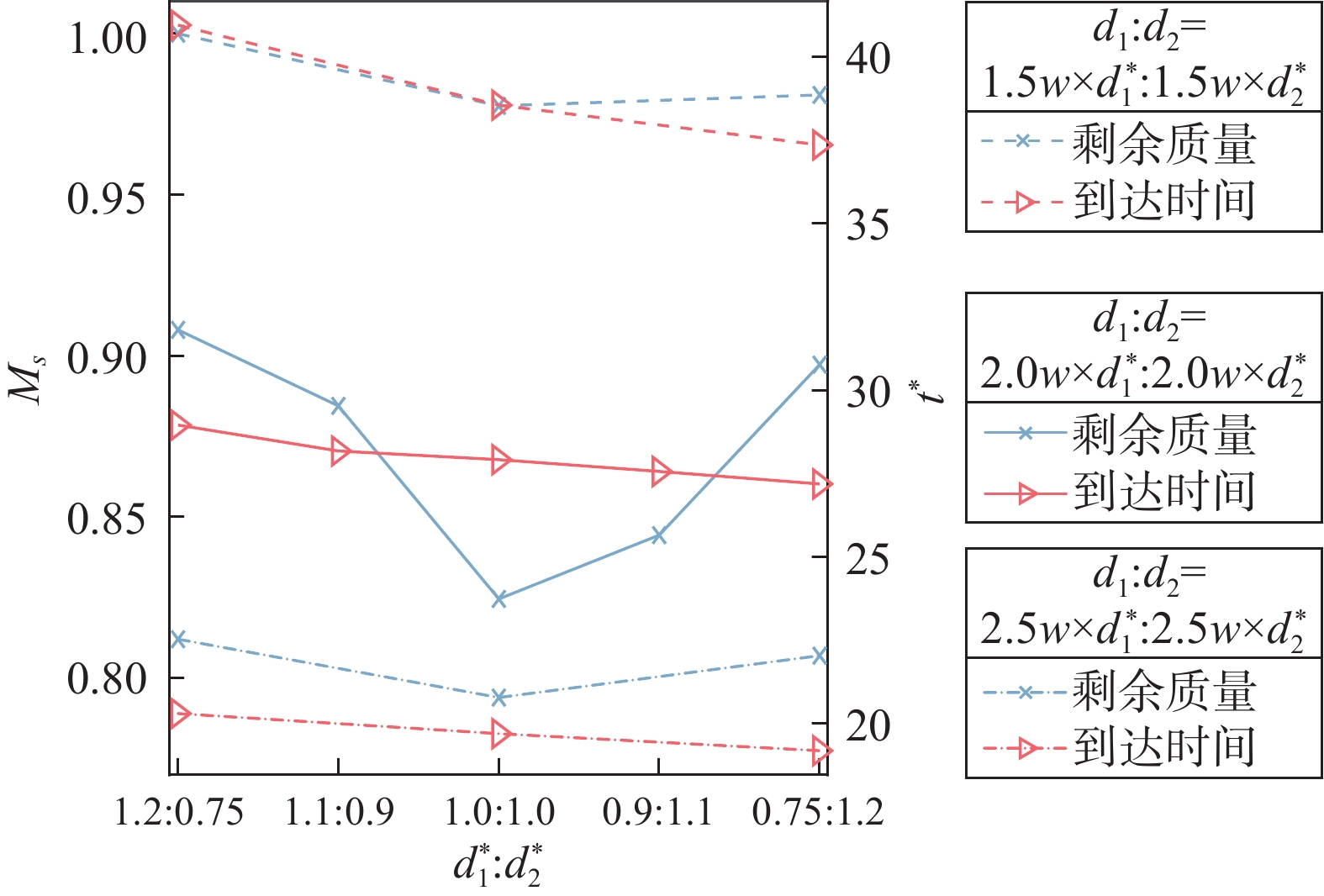
为了分析气泡初始位置和初始间距对气泡通过孔板通道后剩余气泡质量的影响,本文在上述三种工况的基础上,通过改变
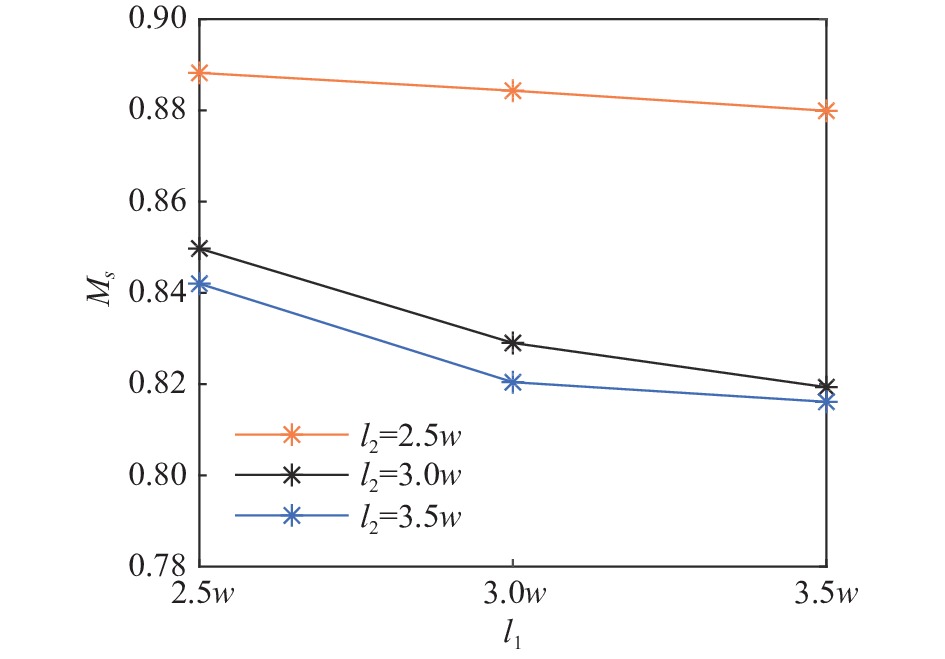
|
图 10 气泡初始位置与剩余质量的关系 Fig.10 The relationship between the residual massand the position of the bubble |
本文基于大密度比两相流LBM模型,对双气泡在含孔板微通道内的运动过程进行了研究。分别考虑了
(1)随着
(2)大气泡在上、小气泡在下时,运动过程中气泡受到的阻力更大,表现为上方气泡通过孔板的过程中形变更明显,两个气泡在孔口附近合并得更充分,通道内的残留质量较少;但到达通道顶部需要的时间更长。大气泡在下、小气泡在上时,气泡到达孔板附近的时间更快,此种情况两气泡的形变最小,气泡到达顶部所需要的时间最短。而当上下两气泡相等时,穿过孔板到达通道上半部分的剩余质量相对于其他两种情况最少。
(3)当两个气泡初始距离相近时,两气泡之间的合并通常发生在上方气泡到达孔板通道之前,此时通过的剩余质量最多;随着两个气泡之间的距离拉大,两气泡之间的合并更容易发生在上方气泡经过孔板通道时,通过的剩余质量次之;当两气泡之间的距离增加到一定程度,上方气泡穿过孔板通道并发生断裂之后,下方气泡才追上并与之合并,到达计算区域上方的剩余质量最小。另外,上下气泡初始位置同时升高也可以提高通过孔道的剩余质量。
| [1] |
赵建福, 张良, 杜王芳, 等. 单气泡池沸腾传热中的重力效应数值模拟[J]. 空气动力学学报, 2021, 39(3): 121-129. ZHAO J F, ZHANG L, DU W F, et al. Numerical simulation of gravity effect on heat transfer in single bubble pool boiling[J]. Acta Aerodynamica Sinica, 2021, 39(3): 121-129. DOI:10.7638/kqdlxxb-2021.0039 (in Chinese) |
| [2] |
赵寅廷, 刘冲, 梁军生, 等. 微型直接甲醇燃料电池CO2气泡排除问题研究
[J]. 传感技术学报, 2008, 21(2): 199-202. ZHAO Y T, LIU C, LIANG J S, et al. Research on CO2 gas bubble elimination in μDMFC anode flow field [J]. Chinese Journal of Sensors and Actuators, 2008, 21(2): 199-202. DOI:10.3969/j.issn.1004-1699.2008.02.002 (in Chinese) |
| [3] |
何健烽, 章渊昶, 朱菊香, 等. 直接甲醇燃料电池阳极通道内气泡行为[J]. 化工进展, 2010, 29(5): 831-838. HE J F, ZHANG Y C, ZHU J X, et al. Experimental investigation on bubble behavior in anode channel of DMFC[J]. Chemical Industry and Engineering Progress, 2010, 29(5): 831-838. (in Chinese) |
| [4] |
KANG S M, ZHOU B, JIANG M C. Bubble behaviors in direct methanol fuel cell anode with parallel design[J]. International Journal of Hydrogen Energy, 2017, 42(31): 20201-20215. DOI:10.1016/j.ijhydene.2017.06.149 |
| [5] |
CHEN C H, HALLMARK B, DAVIDSON J F. The motion and shape of a bubble in highly viscous liquid flowing through an orifice[J]. Chemical Engineering Science, 2019, 206: 224-234. DOI:10.1016/j.ces.2019.05.021 |
| [6] |
CORAPCIOGLU M Y, CIHAN A, DRAZENOVIC M. Rise velocity of an air bubble in porous media: Theoretical studies[J]. Water Resources Research, 2004, 40(4): W04214. DOI:10.1029/2003WR002618 |
| [7] |
DAWSON G, HÄNER E, JUEL A. Extreme deformation of capsules and bubbles flowing through a localised constriction[J]. Procedia IUTAM, 2015, 16: 22-32. DOI:10.1016/j.piutam.2015.03.004 |
| [8] |
BRUCE STEWART H, WENDROFF B. Two-phase flow: Models and methods[J]. Journal of Computational Physics, 1984, 56(3): 363-409. DOI:10.1016/0021-9991(84)90103-7 |
| [9] |
张慧生. 气泡和液滴在上升或下降时大变形的数值模拟[J]. 空气动力学学报, 1994, 12(1): 51-59. ZHANG H S. The NumericaI simulation of large deformation of bubbles and drops during their rlsing or descending[J]. Acta Aerodynamica Sinica, 1994, 12(1): 51-59. (in Chinese) |
| [10] |
SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow[J]. Journal of Computational Physics, 1994, 114(1): 146-159. DOI:10.1006/jcph.1994.1155 |
| [11] |
孙涛, 刘志斌, 范伟, 等. 过热液体中蒸汽泡上升过程的格子Boltzmann三维数值模拟[J]. 计算物理, 2019, 36(6): 659-664. SUN T, LIU Z B, FAN W, et al. Three-dimensional numerical simulation of vapor bubble rising in superheated liquid by lattice boltzmann method[J]. Chinese Journal of Computational Physics, 2019, 36(6): 659-664. DOI:10.19596/j.cnki.1001-246x.7925 (in Chinese) |
| [12] |
娄钦, 李涛, 杨茉. 复杂微通道内气泡在浮力作用下上升行为的格子Boltzmann方法模拟[J]. 物理学报, 2018, 67(23): 234701. LOU Q, LI T, YANG M. Lattice Boltzmann simulations of rising bubble driven by buoyancy in a complex microchannel[J]. Acta Physica Sinica, 2018, 67(23): 234701. DOI:10.7498/aps.67.20181311 (in Chinese) |
| [13] |
LIANG H, XU J, CHEN J, et al. Phase-field-based lattice Boltzmann modeling of large-density-ratio two-phase flows[J]. Physical Review E, 2018, 97(3-1): 033309. DOI:10.1103/physreve.97.033309 |
| [14] |
LIANG H, SHI B C, GUO Z L, et al. Phase-field-based multiple-relaxation-time lattice Boltzmann model for incompressible multiphase flows[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2014, 89(5): 053320. DOI:10.1103/physreve.89.053320 |
| [15] |
ZHANG C H, YANG K, GUO Z L. A discrete unified gas-kinetic scheme for immiscible two-phase flows[J]. International Journal of Heat and Mass Transfer, 2018, 126: 1326-1336. DOI:10.1016/j.ijheatmasstransfer.2018.06.016 |
| [16] |
TAKADA N, MISAWA M, TOMIYAMA A, et al. Simulation of bubble motion under gravity by lattice boltzmann method[J]. Journal of Nuclear Science and Technology, 2001, 38(5): 330-341. DOI:10.1080/18811248.2001.9715037 |
| [17] |
REN F, SONG B W, SUKOP M C. Terminal shape and velocity of a rising bubble by phase-field-based incompressible Lattice Boltzmann model[J]. Advances in Water Resources, 2016, 97: 100-109. DOI:10.1016/j.advwatres.2016.08.012 |
| [18] |
ALIZADEH M, SEYYEDI S M, TAEIBI RAHNI M, et al. Three-dimensional numerical simulation of rising bubbles in the presence of cylindrical obstacles, using lattice Boltzmann method[J]. Journal of Molecular Liquids, 2017, 236: 151-161. DOI:10.1016/j.molliq.2017.04.009 |
| [19] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
 2022, Vol. 40
2022, Vol. 40














