操纵面嗡鸣是飞行器在跨声速阶段飞行时发生的一种气动弹性不稳定现象,通常表现为操纵面绕其刚轴的不衰减单自由度高频自激振动,有的学者也将其称为单自由度颤振[1]。
嗡鸣的发生对于飞行器来说是非常不利的,轻则降低操纵面效率,重则导致操纵面甚至安定面结构破坏,发生灾难性的飞行事故[2]。自飞行器进入跨声速飞行时代,因操纵面嗡鸣引发的飞行事故时有发生。早在二战期间,美国洛克希德公司在P-80喷气式战斗机飞行试验中首次观察到操纵面嗡鸣现象,高马赫数试飞中操纵面嗡鸣直接导致副翼完全损坏[3-4]。贝尔公司的X-1超声速飞机在Ma = 0.86~0.95范围内出现了副翼嗡鸣,后续的X-1A飞机也存在类似问题;飞行员甚至观察到激波在操纵面上来回移动,同时感受到操纵面的剧烈振动[4]。20世纪90年代初,美国海军研制的T-45“苍鹰”高级舰载教练机在Ma = 0.95、高度为2×104 ft(约6096 m)及Ma = 0.9、高度为1×104 ft(约3048 m)试飞过程中,均出现了方向舵嗡鸣问题[5]。诺斯洛普·格鲁门公司的高空长航时全球鹰无人机在高空飞行试验过程中,左右机翼内/外侧副翼同时出现了明显的嗡鸣现象,机载测试仪器清晰记录了典型的振动及载荷数据[6]。
在国内,操纵面嗡鸣问题同样困扰着飞行器设计部门,多型高速歼击机在飞行试验过程中出现操纵面嗡鸣问题,如图1所示,某飞机在试飞过程中方向舵发生嗡鸣导致破坏,严重影响了型号的研制进程[7]。
随着现代飞行器性能的不断提升、结构重量的不断下降及新材料的广泛应用,操纵面嗡鸣已成为除颤振外,型号设计部门另一重点关注的气动弹性问题。例如在F/A-22战斗机气动弹性设计过程中就着重关注了操纵面的防嗡鸣设计[8]。目前快速发展的高速无人机,无法像有人机一样第一时间感受到操纵面的振动并进行判断,一旦出现嗡鸣将难以实施改错措施,很可能发生严重的飞行事故[9]。操纵面嗡鸣涉及激波与边界层的相互作用,气动力情况复杂,并且存在强烈的非线性效应,至今尚没有准确预测嗡鸣的计算方法,通常采用风洞试验来获取有关数据[10-11]。
本文通过整理国内外操纵面嗡鸣风洞试验相关资料,结合我们开展嗡鸣风洞试验的经验,对嗡鸣发生机理、试验风洞选取、试验模型设计、试验方法流程等问题进行梳理总结;同时针对颤振风洞试验中可能出现的嗡鸣问题提供了判别手段,供型号设计部门及同行参考借鉴。
1 国内外研究进展飞行器进入跨声速飞行时代后,操纵面嗡鸣引发的系列飞行事故驱动着操纵面嗡鸣理论研究及试验技术的快速发展。为研究前文所述P-80飞机试飞过程中出现的副翼嗡鸣问题,1947年美国NASA的Erikson等在艾姆斯中心的16英尺高速风洞开展了该飞机全尺寸机翼模型的嗡鸣试验,研究了扰流条、翼型厚度、副翼质量、阻尼等对副翼嗡鸣特性的影响,并进行了较详细的理论分析[12]。图2给出了全尺寸机翼在风洞中的安装照片。
1990年前后,美国洛克希德公司的Parker等[13]在NASA兰利研究中心的TDT风洞针对国家空天飞机(NASP)机翼系列模型开展了嗡鸣试验,研究了操纵刚度、机翼后掠角度、翼型厚度、操纵面与安定面之间缝隙的密封方式等因素对操纵面嗡鸣的影响,由于对模型及结果的详细描述使其成为诸多嗡鸣数值仿真研究的标准验证算例。图3给出了典型的试验结果和模型安装照片。
1994年前后,洛克希德公司在加利福尼亚州的4 ft × 4 ft (约1.22m × 1.22m)三声速风洞中开展了F/A-22 战斗机垂尾的颤振风洞试验,如图4所示,方向舵在Ma = 1.41时出现了典型的嗡鸣现象并导致方向舵损坏[8]。
2012年,日本宇宙航空研究开发机构(JAXA)在2 m × 2 m跨声速风洞采用半模型开展了下一代超声速客机在Ma = 0.9~1.15范围内的副翼嗡鸣验证试验。图5给出了模型在风洞内的安装照片,试验结果表明副翼有发生“C”型嗡鸣的可能性[14]。
除了典型的型号风洞试验研究外,美国、英国、日本等国家的科研人员为研究操纵面嗡鸣的发生机理,还开展了大量的翼型风洞试验,甚至采用飞机搭载或火箭助推的方法进行了飞行试验[15-18]。
国内操纵面嗡鸣相关研究起步较晚,且主要集中在数值仿真方面。20世纪90年代末刘千刚、代捷等[19-20]针对操纵面嗡鸣问题进行了数值研究,并与飞行试验结果进行了对比。21世纪初杨国伟、史爱明、张伟伟等[7, 21-23]针对跨声速嗡鸣的数值模拟方法及嗡鸣抑制方法开展了系列研究。近年来张伟伟、许军、贺顺、高传强等[1, 24-30]针对嗡鸣的诱发机理、飞翼布局无人机嗡鸣特性、操纵面间隙非线性影响等问题进行了大量研究。
国内操纵面嗡鸣风洞试验相关文献较少且均是较早期做的试验。通过查找历史档案,发现中国空气动力研究与发展中心的申超峰、陈忠实等在20世纪70年代开展过嗡鸣风洞试验相关研究,且在FL-21风洞(0.6 m×0.6 m跨超声速风洞)完成了两型飞机方向舵的嗡鸣试验[31-32]。不过受风洞尺寸、采集设备、模型设计加工能力的限制,当时的嗡鸣风洞试验技术还处于初级探索阶段。
鉴于现代新型飞行器研制过程中对操纵面嗡鸣风洞试验的迫切需求,得益于国内2 m量级高速风洞及气动弹性风洞试验技术的快速发展,近年来作者所在团队在FL-26风洞(2.4 m×2.4 m跨声速风洞)初步建立了工程实用的操纵面嗡鸣风洞试验技术,完成了多个型号的操纵面嗡鸣试验,并开展了系列研究工作。
2 操纵面嗡鸣的发生机理伴随着飞行器的发展,国内外科研人员对操纵面嗡鸣的发生机理及触发条件开展了大量的研究工作,总结下来主要有以下观点:
1)操纵面嗡鸣的发生与来流马赫数及翼面上激波的运动密切相关,翼面上激波运动与操纵面振动之间的相位差是嗡鸣发生的主要原因[4, 12, 16-17];
2)激波并非操纵面嗡鸣发生的必要条件,流动分离才是嗡鸣发生的主要原因[3, 15];
3)操纵面嗡鸣不仅与来流马赫数有关,还与迎角及来流速压有关[13, 17];
4)操纵面嗡鸣本质上是一种单自由度非线性颤振[27-28];
5)操纵面嗡鸣的发生是操纵面结构模态和最不稳定流动模态间的耦合导致的[1, 29-30]。
在上述观点中,“激波说”是被广泛认可的。不过受当时试验条件及理论基础的限制,以上不同论述可能存在一定的局限性,也可能是同一种物理内涵的不同呈现方式,尚需开展进一步研究以期达成统一意见。其中,英国国家物理实验室科学家Lambourne于1964年结合前人研究成果及翼型风洞试验数据,发表了一篇对操纵面嗡鸣研究至今仍有深远影响的文章。他根据操纵面嗡鸣发生时马赫数和激波与操纵面的相对位置,将嗡鸣分为A、B、C三种类型[17],具体如图6所示。A、B型嗡鸣主要发生在跨声速范围,区别在于A型嗡鸣激波位于操纵面铰链前,B型嗡鸣激波强于A型,且已位于操纵面上。C型嗡鸣主要发生在低超声速,激波已移动至操纵面后缘。Lambourne对操纵面嗡鸣的分类及嗡鸣抑制措施的建议在现代飞机设计中依旧具有重要意义。
通过对嗡鸣发生机理和触发条件的梳理,可以为开展操纵面嗡鸣风洞试验提供依据,为操纵面嗡鸣抑制提供参考;同时嗡鸣风洞试验的结果也可以不断验证和发展现有的理论。
3 操纵面嗡鸣风洞试验 3.1 操纵面嗡鸣风洞试验目的操纵面嗡鸣风洞试验的主要目的是研究操纵面嗡鸣的发生机理,验证飞行器防嗡鸣设计效果,研究操纵面的嗡鸣特性、影响因素和抑制手段[2]。
1)研究操纵面嗡鸣的发生机理。通过风洞试验开展机理研究,推动理论和学科发展,从根本上指导飞行器防嗡鸣设计、数值方法及试验技术改进、操纵面嗡鸣抑制等工作。
2)研究飞行器操纵面的嗡鸣特性。通过风洞试验验证飞行器操纵面的防嗡鸣设计。如果存在嗡鸣问题,则需要研究操纵面嗡鸣发生的马赫数、迎角、速压范围,定位激波位置,判断嗡鸣类型,研究关键影响因素对嗡鸣特性的影响,为飞行器试飞提供依据。
3)研究飞行器操纵面嗡鸣的抑制方法。对于试验或试飞过程中出现操纵面嗡鸣的飞行器,可以通过风洞试验研究改变气动外形、操纵刚度、操纵系统阻尼等手段对操纵面嗡鸣的抑制效果,为飞行器改型提供技术支撑。
3.2 操纵面嗡鸣试验风洞操纵面嗡鸣的发生跟激波与操纵面的相对位置有密切关系,而试验模型的气动外形和试验雷诺数能够显著影响激波的位置和强度。因此,在操纵面嗡鸣风洞试验中要尽可能精确地模拟飞行器的外形及试验雷诺数。
风洞的尺寸越大,试验模型就可以做得越大,飞行器的细节就可以模拟得更精确,这是显而易见的。通常情况下,风洞试验雷诺数要低于飞行雷诺数。根据式(1)可知,为了使嗡鸣试验雷诺数尽可能接近飞行雷诺数,可以通过增加模型尺寸、降低来流介质总温、提高来流总压来有效提高试验雷诺数。
| $ \begin{split} Re =& \frac{{\rho v{l_{{\rm{Re}}}}}}{\mu } \\=& 0.0479 \times {10^6} \frac{{\left[ {{{\left( {1 + 0.2M {a^2}} \right)}^{ - 1}} + \dfrac{{110.4}}{{{T_0}}}} \right]}}{{{{\left( {1 + 0.2 M {a^2}} \right)}^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}}{T_0}}} {P_0}M a{l_{{\rm{Re}}}} \end{split}$ | (1) |
其中,
此外,操纵面嗡鸣不仅对来流马赫数较为敏感,而且与模型迎角及来流速压也有关。这就需要风洞对试验马赫数有较高的控制精度,且能实现模型迎角及速压的变化。综合上述需求,建议尽量在2 m量级及以上低温增压风洞开展操纵面嗡鸣试验。
中国空气动力研究与发展中心的FL-26风洞是试验段横截面为2.4 m×2.4 m的半回流、暂冲引射式跨声速风洞。试验马赫数范围为0.3~1.4(如图7所示),控制精度为0.002~0.003,达到国军标先进指标。该风洞可以进行变速压试验,速压可达到正常值的2~3倍,实现不同试验雷诺数的模拟[33]。FL-26风洞能满足除低温外的所有需求,是目前国内最适合开展操纵面嗡鸣试验的风洞。
3.3 操纵面嗡鸣试验模型操纵面嗡鸣试验模型同属气动弹性模型,相似参数同颤振试验模型,同样包含长度比例尺
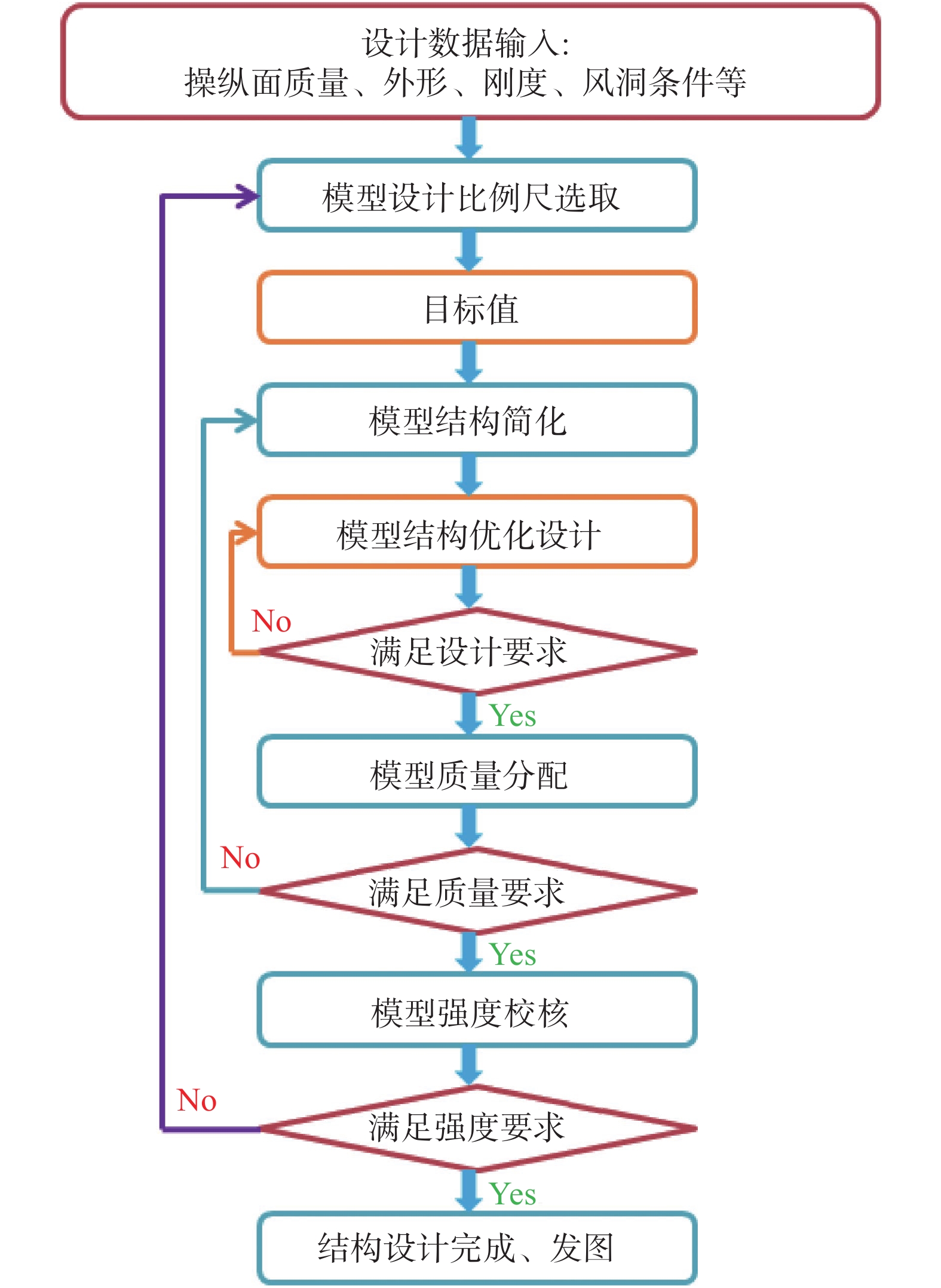
操纵面嗡鸣与结构模态相互耦合的经典颤振有所区别,前者主要受操纵面旋转模态的影响,与飞行器其余模态关系不大,因此嗡鸣模型的设计要比颤振模型简单。图8给出了嗡鸣试验模型的设计流程,以下进行简要介绍。
|
图 8 操纵面嗡鸣试验模型设计流程 Fig.8 Flow chart of the model design of the buzz wind tunnel test |
同提高外形模拟精度及试验雷诺数对模型的要求一样,嗡鸣试验模型的动力学特性模拟同样要求模型的尺寸越大越好。嗡鸣试验模型尺寸越大,动力学相似操纵面的模拟精度越高,模型的设计加工难度也相应降低。在试验对象及风洞尺寸确定的前提下,考虑到风洞堵塞度及翼面宽度的要求,长度比例尺
为了精确模拟翼面上激波的位置及强度,嗡鸣试验模型安定面及操纵面的气动外形要与原型严格相似;此外还要注意安定面与操纵面之间缝隙的模拟,避免窜流影响翼面激波位置。半模型或者部件模型的整流部分要经过详细设计,保证来流与全机模型基本一致。
3.3.3 动力学特性嗡鸣的发生与操纵面的旋转模态密切相关,与飞行器其余模态关系不大。因此嗡鸣模型的安定面可以设计成刚模,操纵面则只需要模拟操纵刚度及质量/惯量分布。
综合考虑飞行器的飞行包线、风洞速压范围、变参数研究、试验安全性等方面,选取合适的速压比例尺
| $ 频率比例尺 {k_\omega } = {\left( {{k_q}/{k_\rho }} \right)^{1/2}}/{k_L} $ | (2) |
| $ 质量比例尺 {k_m} = {k_\rho }k_L^3 $ | (3) |
| $ 转动惯量比例尺 {k_I} = {k_\rho }k_L^5 $ | (4) |
其中,频率比例尺是操纵刚度设计的依据,质量/惯量比例尺是操纵面设计的依据。由于不需要模拟安定面的动力学特性及操纵面的刚度特性,嗡鸣模型可选取的材料库相对颤振模型来说要丰富得多,且实现难度大大降低。例如20世纪70年代中国空气动力研究与发展中心开展的垂尾嗡鸣风洞试验,试验模型垂尾安定面采用刚模,方向舵则用轻质核桃木、胶合板等材料模拟,安定面和方向舵之间采用不同厚度的弹簧片模拟不同的操纵刚度[32]。
颤振试验模型不但满足嗡鸣模型所有的相似参数,还满足刚度相似,因此采用颤振模型开展嗡鸣试验是可行的。事实上,出于研制成本、进度考虑,或颤振试验中出现了预期外的嗡鸣问题,型号设计部门往往采用颤振模型或者改造颤振模型来进行操纵面嗡鸣试验,例如NASP系列机翼嗡鸣试验的基准模型就是由颤振试验模型改造而来[13]。
得益于高速风洞颤振试验技术及材料科学的快速发展,近年来国内气动弹性模型设计加工能力有了长足的进步,形成了较为完善的设计体系及材料库[34-37],为操纵面嗡鸣试验模型的设计、加工提供了强有力的支撑和有益的参考。图9给出了某平尾全复材颤振试验模型加工过程。
3.4 操纵面嗡鸣风洞试验方法操纵面嗡鸣风洞试验的试验流程、信号采集、关车触发条件与颤振风洞试验基本类似,但流场控制方式有所不同,且暂时没有可靠的亚临界预测方法,一般采用直吹的方式。
试验流程上,嗡鸣试验前,同样要先开展地面振动试验来确定操纵面的动力学特性是否符合设计要求。试验中每个试验车次结束后,需采用敲击的方式检查模型频率来确认模型状态。
信号采集上,在操纵面远离转轴位置安装加速度传感器,在模拟操纵刚度的弹簧片或者转轴上粘贴应变片,试验过程中采用动态采集设备实时测量上述传感器的振动响应信号。
关车触发条件上,由于没有可靠的亚临界预测方法,直吹嗡鸣可能导致试验模型或风洞设备受损,此时快速触发风洞关车尤为重要。同颤振试验类似,可以采用计算机实时监测单位时间内超过设定振幅的波形个数来程控关车。
流场控制上,总体上把握“粗吹、细吹”相结合的方式。先采用定总压定迎角阶梯变马赫数的开车方式进行粗吹,建议马赫数跨度0.05为一个阶梯,获得操纵面嗡鸣发生的大致马赫数范围;再采用定马赫数定迎角阶梯变速压的开车方式或者定马赫数定速压变迎角的开车方式进行细吹,此时马赫数跨度0.01较为合适,进而获得操纵面嗡鸣发生的精确马赫数、速压、迎角范围。
4 颤振试验中操纵面嗡鸣的判别对于仅模拟操纵面动力学特性、安定面使用刚模的嗡鸣模型,或者由颤振模型改造而来的嗡鸣模型,操纵面是否出现嗡鸣是显而易见的。但采用颤振模型开展嗡鸣试验时或者颤振试验中出现嗡鸣问题时,如何对试验结果进行判别?例如F/A-22战斗机在NTS风洞开展颤振试验时出现的方向舵嗡鸣问题[8],S3反潜机在TDT风洞开展颤振试验时出现的副翼嗡鸣问题等[38]。近年来作者单位在含操纵面部件颤振试验过程中曾多次遇到确认或者疑似操纵面嗡鸣问题,耗费了大量精力进行排查。
操纵面嗡鸣对试验马赫数较为敏感,颤振对试验速压更为敏感,但在暂冲式跨声速风洞中仅通过以上特性对二者进行辨识是难以奏效的。因为颤振边界跨声速凹坑的存在或模型颤振速压接近风洞速压下边界时,在某个马赫数,操纵面嗡鸣和颤振很可能呈现相似现象:均表现为流场初步建立模型便出现等幅或发散振动,触发风洞关车,无法继续增压或者开展后续马赫数试验。同时二者的振动形式非常相似,难以通过传感器的响应信号进行辨识。最直观有效的辨识方法就是将颤振模型的安定面替换为刚模,但这需要付出额外的时间及经费,耽误型号研制进度。以下结合作者经验,主要针对试验现场对操纵面嗡鸣和颤振的判别方法进行介绍。
4.1 流动显示判别方法阴影仪/纹影仪是风洞流场观测最常用的流动显示设备,通常被用来确定激波的形状和位置,显示湍流和边界层特性[39]。颤振/嗡鸣试验时,利用阴影/纹影设备观察操纵面发散时有无激波震荡,以及激波与操纵面的相对位置,来判断是否发生嗡鸣及嗡鸣的类型。在P80飞机及系列二元翼型嗡鸣试验中,均采用纹影设备记录激波的位置。
不过无论是传统的阴影/纹影设备,或近年新发展的背景纹影技术,均只能获得激波在翼面弦向或展向的投影,无法对激波的形态进行精确刻画,更无法获得激波的空间分布情况。即便如此,阴影/纹影的结果也为嗡鸣的判别提供重要参考。通过阴影/纹影确定操纵面出现嗡鸣的情况下,还可以通过油流试验获得激波沿翼面展向的分布情况。
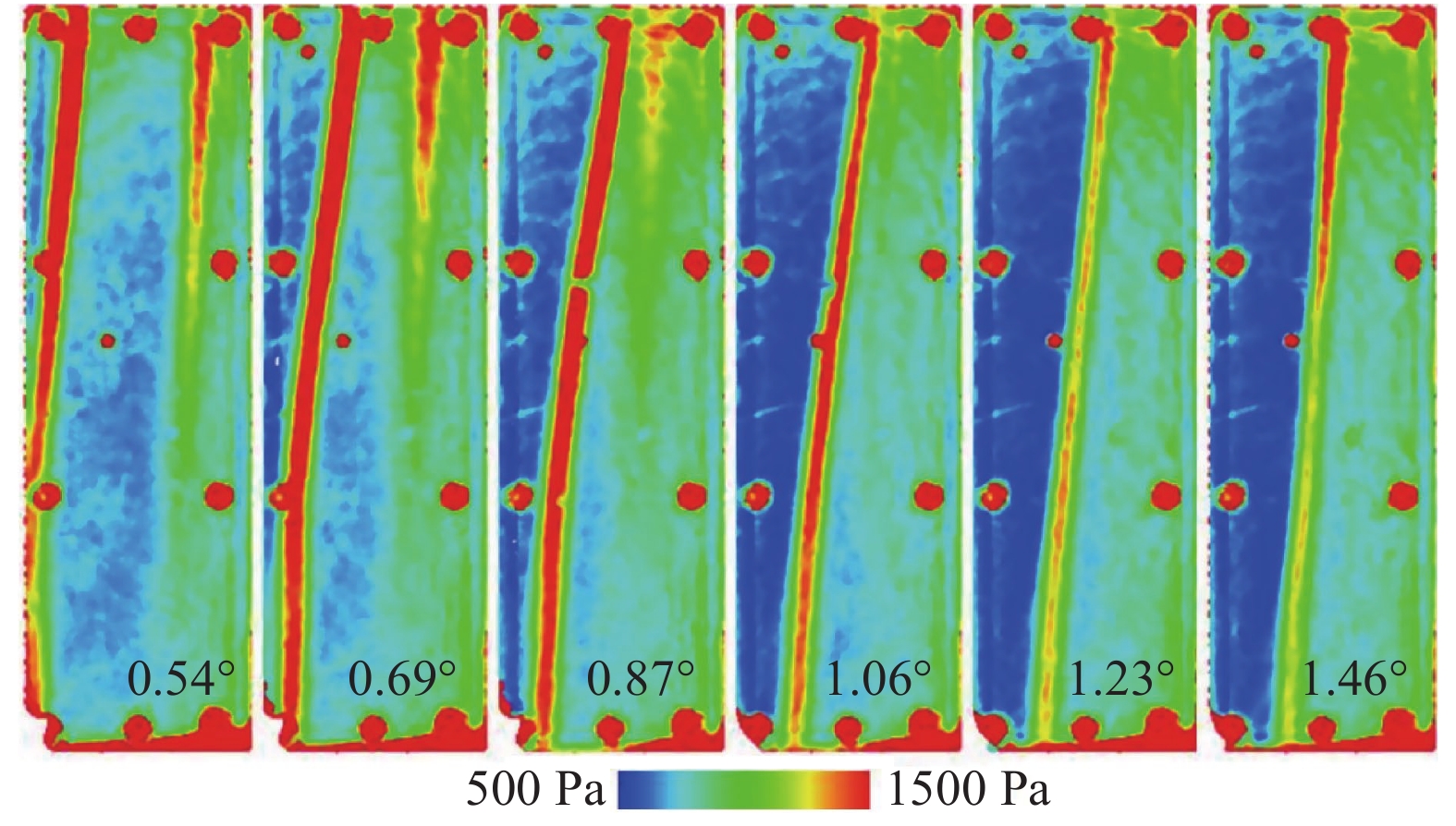
快速响应PSP技术作为近年迅猛发展的流动显示技术,在动态流场的测量方面有着良好的应用前景[40]。颤振/嗡鸣试验时,可以在模型表面喷涂快速响应压敏涂料,其响应时间可以达到毫秒甚至微秒量级,再通过高速摄影及图像处理的方法获得翼面上激波的位置分布及动态变化信息。法国ONERA的MC.Merienne等[41]在S2MA跨声速风洞采用快速响应PSP技术研究了某民机的抖振特性并定位激波位置,图10给出了典型的试验结果。
与阴影/纹影技术相比,快响PSP技术可以实现翼面全区域测量,显示出激波在翼面上的分布及变化情况,不过试验成本相对高昂。
上述流动显示方法并非十全十美,各有各的局限,但若条件具备,无论采用何种形式的流动显示手段都对操纵面嗡鸣判别具有重要意义,记录的激波位置也能为操纵面嗡鸣抑制提供重要参考。
4.2 模态耦合判别方法经典颤振是由结构模态之间的相互耦合产生的,而操纵面嗡鸣的发生与安定面的动力学特性无关。因此可以根据经典颤振与嗡鸣发生机理的不同,采用排除法进行判别,这也是试验现场最常用的判别手段。
与操纵面嗡鸣容易混淆的通常是安定面的一弯模态与操纵面的旋转模态耦合发生的颤振,因此可以通过改变颤振模型安定面动力学特性来进行判别。把安定面替换为刚模也是改变安定面动力学特性的极端情况;此外还可以采取安定面翼尖增加配重、改变安定面弯曲刚度、约束安定面翼尖振动等方法改变安定面的动力学特性。如果操纵面出现等幅振动,且流场参数无明显变化,则发生操纵面嗡鸣的可能性较大;反之则是颤振。
此外,操纵面等幅振动的速压随马赫数的变化趋势也可以做为判别操纵面嗡鸣与颤振的辅助手段,但这需要对模型的颤振特性有较深刻的理解。
5 结束语操纵面嗡鸣风洞试验可以利用风洞再现嗡鸣现象,研究嗡鸣特性,是飞行器研制阶段检验操纵面防嗡鸣设计最行之有效的手段。国内外主要航空强国均已建立工程实用的操纵面嗡鸣风洞试验技术,尤其是近年来气动弹性风洞试验技术的迅猛发展,推动了操纵面嗡鸣风洞试验在各方面均取得长足进步,但依旧存在以下典型共性问题:
1)近年来国内外的操纵面嗡鸣风洞试验主要针对型号研制过程中的具体工程问题,很少深入开展机理性的研究工作。操纵面嗡鸣的发生机理和触发条件主要依靠数值模拟开展相关研究,缺乏风洞试验结果进行验证,以致于现有观点依然存在分歧,尚未形成统一意见。
2)大型生产型跨声速风洞受空间限制,很少配备光路复杂的纹影/阴影设备,即使近年来快速发展的背景纹影技术,也仅能获得激波沿翼面弦向或展向的投影,无法直接观察到激波在翼面上的运动情况,难以对操纵面嗡鸣进行判别和分型。
鉴于国内外操纵面嗡鸣风洞试验技术存在的共性问题,为更好地推动学科发展,服务于型号研制,国内相关院所还需在以下几个方面共同努力:
1)型号设计部门在型号研制过程中鲜有规划操纵面嗡鸣风洞试验,往往在试验或试飞过程中出现操纵面嗡鸣问题才开展试验研究,很可能耽误型号研制进度。建议依托含操纵面的部件颤振试验,改造或更换安定面模型,同步开展操纵面嗡鸣试验研究。有限的车次就可能获得有益的结果。
2)结合数值仿真与风洞试验,推动操纵面嗡鸣发生机理及抑制方法的研究,为型号设计建立工程实用的防嗡鸣设计准则,为嗡鸣抑制提供切实可行的手段方法。
3)建立健全大型生产型风洞的非接触测量手段,例如空间纹影技术、快速响应PSP技术等,为操纵面嗡鸣的鉴别、分型提供直观依据。
| [1] |
张伟伟, 高传强, 叶正寅. 复杂跨声速气动弹性现象及其机理分析[J]. 科学通报, 2018, 63(12): 1095-1110. ZHANG W W, GAO C Q, YE Z Y. The complex transonic aeroelastic phenomena and it's mechanisms[J]. Chinese Science Bulletin, 2018, 63(12): 1095-1110. DOI:10.1360/N972018-00151 (in Chinese) |
| [2] |
王发祥. 高速风洞试验[M]. 北京: 国防工业出版社, 2003: 437.
|
| [3] |
STEGER J L, BAILEY H E. Calculation of transonic aileron buzz[J]. AIAA Journal, 1980, 18(3): 249-255. DOI:10.2514/3.50756 |
| [4] |
BENDIKSEN O. Nonclassical aileron buzz in transonic flow[C]//34th AIAA, ASME, ASCE, AHS, and ASC, Structures, Structural Dynamics and Materials Conference. AIAA and ASME, Adaptive Structures Forum. La Jolla, CA, 1993: 19-22. AIAA-93-1479. doi: 10.2514/6.1993-1479
|
| [5] |
FUGLSANG D, BRASE L, AGRAWAL S. A numerical study of control surface buzz using computational fluid dynamic methods[C]//10th Applied Aerodynamics Conference, Palo Alto, CA, USA. Reston, Virigina: AIAA, 1992. AIAA-92-2654. doi: 10.2514/6.1992-2654
|
| [6] |
HUTTSELL L, SCHUSTER D, VOLK J, et al. Evaluation of computational aeroelasticity codes for loads and flutter[C]//39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2001. AIAA-01-0569. doi: 10.2514/6.2001-569
|
| [7] |
史爱明, 杨永年, 叶正寅. 跨音速单自由度非线性颤振: 嗡鸣的数值分析[J]. 西北工业大学学报, 2004, 22(4): 525-528. SHI A M, YANG Y N, YE Z Y. Investigation of control surface buzz in transonic flow[J]. Journal of Northwestern Polytechnical University, 2004, 22(4): 525-528. DOI:10.3969/j.issn.1000-2758.2004.04.028 (in Chinese) |
| [8] |
ANDERSON W, MORTARA S. F-22 aeroelastic design and test validation[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, Hawaii. Reston, Virigina: AIAA, 2007. AIAA 2007-1764. doi: 10.2514/6.2007-1764
|
| [9] |
邓俊艳, 周伟, 易军, 等. 操纵面嗡鸣工程判别及预防[C]//第十六届全国空气弹性学术交流会会议, 2019: 624-625.
|
| [10] |
杨超, 主编. 飞行器气动弹性原理[M]. 北京: 北京航空航天大学出版社, 2011: 123.
|
| [11] |
李周复, 主编. 风洞特种试验技术[M]. 北京: 航空工业出版社, 2010: 201-207.
|
| [12] |
ERICKSON A L, STEPHENSON J D. A suggested me-thod of analyzing for transonic flutter of control surfaces based on available experimental evidence [R]. NACA-RM-A7F30, 1947. https://ntrs.nasa.gov/api/citations/19930085716/downloads/19930085716.pdf
|
| [13] |
PARKER E, SPAIN C, SOISTMANN D. Aileron buzz investigated on several generic NASP wing configurations[C]//32nd Structures, Structural Dynamics, and Materials Conference, Baltimore, MD, USA. Reston, Virigina: AIAA, 1991. AIAA-91-0936-CP. doi: 10.2514/6.1991-936
|
| [14] |
SAITON K, TAMAYAMA M, KIKUCHI T, et al. An aileron flutter experiment and analysis using Semi-Span model for the small supersonic experimental aircraft[C]//Japan Society of Aeronautical Space Sciences, 2012, 60: 108-113. https://www.jstage.jst.go.jp/article/jjsass/60/2/60_2_108/_pdf/-char/en doi: 10.2322/jjsass.60.108
|
| [15] |
PHILLIPS W H, ADAMS J J. Low-speed tests of a model simulating the phenomenon of control-surface buzz[R]. NACA-RM-L50F19, 1950. https://ntrs.nasa.gov/api/citations/19930087842/downloads/19930087842.pdf
|
| [16] |
HENNING A B. Results of a rocket-model investiga-tion of control-surface buzz and flutter on a 4-percent-thick unswept wing and on 6-, 9-, and 12-percent-thick swept wings at transonic speeds[C]. NACA-RM-L53I29, 1953. https://ntrs.nasa.gov/api/citations/19930089146/downloads/19930089146.pdf
|
| [17] |
LAMBOURNE N C. Control-surface buzz[R]. ARC/R&M-3364, 1963. https://naca.central.cranfield.ac.uk/bitstream/handle/1826.2/3947/arc-rm-3364.pdf?sequence = 1&isAllowed = y
|
| [18] |
NAKAMURA Y. Some contributions on a control-surface buzz at high subsonic speeds[J]. Journal of Aircraft, 1968, 5(2): 118-125. DOI:10.2514/3.43918 |
| [19] |
代捷, 刘千刚. 跨声速操纵面嗡鸣的数值研究[J]. 空气动力学学报, 1997, 15(3): 366-371. DAI J, LIU Q G. Calculation of transonic control surface buzz[J]. Acta Aerodynamica Sinica, 1997, 15(3): 366-371. (in Chinese) |
| [20] |
刘千刚, 代捷, 白俊强. 跨音速操纵面嗡鸣Hopf分叉分析及结构参数对嗡鸣特性影响的研究[J]. 航空学报, 1999, 20(6): 527-532. LIU Q G, DAI J, BAI J Q. Hopf bifurcation analysis of transonic control surface buzz and investigation of the influence of structural parameters on buzz characteristics[J]. Acta Aeronautica et Astronautica Sinica, 1999, 20(6): 527-532. DOI:10.3321/j.issn:1000-6893.1999.06.011 (in Chinese) |
| [21] |
YANG G W, OBAYASHI S, NAKAMICHI J. Aileron buzz simulation using an implicit multiblock aeroelastic solver[J]. Journal of Aircraft, 2003, 40(3): 580-589. DOI:10.2514/2.3134 |
| [22] |
史爱明, 杨永年, 叶正寅. 跨音速三维操纵面嗡鸣数值方法研究[J]. 西北工业大学学报, 2006, 24(5): 537-540. SHI A M, YANG Y N, YE Z Y. Relatively accurate calculation of 3-D control surface buzz in transonic flow[J]. Journal of Northwestern Polytechnical University, 2006, 24(5): 537-540 (in Chinese). |
| [23] |
张伟伟, 叶正寅, 史爱明, 等. 基于Euler方程的B型和C型嗡鸣特性数值研究[J]. 振动工程学报, 2005, 18(4): 458-464. ZHANG W W, YE Z Y, SHI A M, et al. Numerical analysis for B-type buzz and C-type buzz basing on Euler codes[J]. Journal of Vibration Engineering, 2005, 18(4): 458-464. DOI:10.3969/j.issn.1004-4523.2005.04.012 (in Chinese) |
| [24] |
许军, 马晓平. 飞翼无人机嗡鸣气动弹性响应分析[J]. 西北工业大学学报, 2015, 33(4): 588-595. XU J, MA X P. Buzz aeroelastic responses analysis for a flying wing UAV[J]. Journal of Northwestern Polytechnical University, 2015, 33(4): 588-595. DOI:10.3969/j.issn.1000-2758.2015.04.012 (in Chinese) |
| [25] |
XU J, MA X P. Transonic rudder buzz investigated on a tailless flying wing UAV[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2015, 32(1): 61-69. DOI:10.16356/j.1005-1120.2015.01.061 |
| [26] |
许军, 马晓平. 考虑气动结构耦合的飞翼无人机嗡鸣振动[J]. 空军工程大学学报(自然科学版), 2016, 17(3): 6-10. XU J, MA X P. Research on flying wing UAV buzz vibration considering the aerodynamic structural coupling effects[J]. Journal of Air Force Engineering University (Natural Science Edition), 2016, 17(3): 6-10. DOI:10.3969/j.issn.1009-3516.2016.03.002 (in Chinese) |
| [27] |
贺顺. 机翼跨音速非线性颤振研究[D]. 西安: 西北工业大学, 2017: 27-49. HE S. Study on wing nonlinear flutter in transonic flow[D]. Xi'an: Northwestern Polytechnical University, 2017: 27-49 (in Chinese). |
| [28] |
HE S, YANG Z C, GU Y S. Limit cycle oscillation behavior of transonic control surface buzz considering free-play nonlinearity[J]. Journal of Fluids and Structures, 2016, 61: 431-449. DOI:10.1016/j.jfluidstructs.2015.11.014 |
| [29] |
GAO C Q, ZHANG W W, YE Z Y. A new viewpoint on the mechanism of transonic single-degree-of-freedom flutter[J]. Aerospace Science and Technology, 2016, 52: 144-156. DOI:10.1016/j.ast.2016.02.029 |
| [30] |
高传强, 张伟伟. 跨声速嗡鸣诱发机理及其失稳参数研究[J]. 空气动力学学报, 2019, 37(1): 99-106. GAO C Q, ZHANG W W. Study on the mechansim and instability parameters of transonic buzz[J]. Acta Aerodynamica Sinica, 2019, 37(1): 99-106. DOI:10.7638/kqdlxxb-2018.0204 (in Chinese) |
| [31] |
申超峰. 某飞机方向舵振动试验报告[R]. 绵阳: 中国空气动力研究与发展中心, 1974.
|
| [32] |
陈忠实. 某飞机方向舵嗡鸣试验报告[R]. 绵阳: 中国空气动力研究与发展中心, 1977.
|
| [33] |
寇西平. 大展弦比机翼高速静气动弹性模型设计研究[D]. 绵阳: 中国空气动力研究与发展中心, 2013: 44. KOU X P. Research on high speed static aeroelastic model design of high-aspect-ratio wing[D]. Mianyang: CARDC, 2013: 44 (in Chinese). |
| [34] |
罗务揆, 谭申刚, 谢怀强, 等. 确定颤振模型设计参数的方法研究[J]. 航空学报, 2013, 34(10): 2383-2390. LUO W K, TAN S G, XIE H Q, et al. Research on methods used to determine flutter model design factors[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(10): 2383-2390. DOI:10.7527/S1000-6893.2013.0076 (in Chinese) |
| [35] |
钱卫, 张桂江, 刘钟坤. 飞机全动平尾颤振特性风洞试验[J]. 航空学报, 2015, 36(4): 1093-1102. QIAN W, ZHANG G J, LIU Z K. Flutter characteristics for aircraft all-movable horizontal tail through wind tunnel test[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1093-1102. DOI:10.7527/S1000-6893.2014.0250 (in Chinese) |
| [36] |
孙亚军, 梁技, 杨飞, 等. 超临界机翼跨音速颤振风洞试验研究[J]. 振动与冲击, 2014, 33(4): 190-194. SUN Y J, LIANG J, YANG F, et al. Transonic flutter wind tunnel tests for an aircraft with a supercritical wing[J]. Journal of Vibration and Shock, 2014, 33(4): 190-194. DOI:10.3969/j.issn.1000-3835.2014.04.034 (in Chinese) |
| [37] |
冉玉国, 李秋彦, 杨兴华. 静不安定飞机缩比模型跨声速颤振试验技术[J]. 四川理工学院学报(自然科学版), 2017, 30(1): 49-54. RAN Y G, LI Q Y, YANG X H. Review of transonic flutter test techniques for statically unstable aircraft scaled model[J]. Journal of Sichuan University of Science & Engineering (Natural Science Edition), 2017, 30(1): 49-54. DOI:10.11863/j.suse.2017.01.09 (in Chinese) |
| [38] |
RIVERA J A, FLORANCE J R. Contributions of transonic dynamic tunnel testing to airplane flutter clearance[R]. AIAA 2000-1768, 2000. https://ntrs.nasa.gov/api/citations/20000037720/downloads/20000037720.pdf
|
| [39] |
杨祖清, 主编. 流动显示技术[M]. 北京: 国防工业出版社, 2002: 101-131.
|
| [40] |
高丽敏, 吴亚楠, 胡小全, 等. 基于光强的快速响应PSP动态测量技术及其应用[J]. 航空学报, 2014, 35(3): 607-623. GAO L M, WU Y N, HU X Q, et al. Intensity-based fast response PSP technique and its applications[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 607-623. DOI:10.7527/S1000-6893.2013.0532 (in Chinese) |
| [41] |
MERIENNE M C, LE SANT Y, LEBRUN F, et al. Transonic buffeting investigation using unsteady pressure-sensitive paint in a large wind tunnel[C]//51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine (Dallas/Ft. Worth Region), Texas. Reston, Virginia: AIAA, 2013. doi: 10.2514/6.2013-1136
|
 2022, Vol. 40
2022, Vol. 40