2. 同济大学 上海地面交通工具风洞中心,上海 201804;
3. 北京民用飞机技术研究中心,北京 102211
2. Shanghai Automotive Wind Tunnel Center, Tongji University, Shanghai 201804, China;
3. Beijing Aeronautical Science & Technology Research Institute, Beijing 102211, China
列车是贴地高速运行、外形细长的运动物体,气流沿列车表面的发展会受到转向架区域、车厢间隙以及地面效应等影响[1],使得列车底部和尾部流场非线性发展,呈现出复杂的三维非定常特性,包含剪切层、涡脱落、分离泡以及反旋流向涡对等多尺度流动结构的相互耦合。随着高速列车速度的不断提升,列车尾部非定常尾迹引起的列车风安全问题越来越凸显[1-3]。列车风是指列车高速运行时诱导周围气流运动,形成沿列车逐渐增厚的边界层以及具有复杂三维湍流特性的尾迹流动,而过高的列车风速度会使站台的乘客、设备和轨道旁人员失稳甚至被卷入尾迹中,造成人员伤亡或列车受损[3-5]。为了降低列车风峰值,保证列车运行时的安全性,就必须在充分了解列车尾迹结构的基础上理解其与列车风之间的关系,以提供更加准确的列车风评估手段和控制方法。
之前的研究已经得到典型的列车风分布[4-5],并发现列车风的峰值主要出现在近尾迹区域,且呈现强烈的间歇性特征[5-7]。目前学者普遍认为该峰值是由列车尾涡的非定常特性引起的[7-9]。近年来,关于列车尾迹的研究,学者们做了大量的探索。2016年,Bell等[9]通过缩比风洞实验的方法,采用多孔探头对ICE3两节编组列车的尾迹进行了测量,研究指出高速列车的时均尾涡以一对反旋的对称流向涡对为主导,且呈现出正弦式的展向不对称周期性振荡。2018年,Xia等[10]进行风洞缩比试验,采用粒子图像测速和本征正交分解(POD)相结合的方法剖析了尾涡动力学演化特性,提出CRH3列车的三维瞬时尾涡是以交替脱落的半环形流向涡对为主导。
以往的研究还表明底部转向架结构引起的底部流场扰动对尾流的非定常特性有很大的影响[11-13]。2018年,Wang等[11]基于ICE3列车模型,数值模拟研究了转向架对高速列车列车风速度的影响,发现转向架的存在可以显著改变气动载荷的预测,增加列车风速度,特别是在轨道侧位置。同时指出转向架并不是引起尾迹展向振荡的直接原因,认为展向运动可能是由于流向涡对的自然对流不稳定性引起的。2019年,Dong等[12]通过对四种不同简化转向架结构流场的数值模拟比较,论证了过于简化转向架(只有转向架舱,无转向架结构)会导致过高估计车体下流速,同时会增加底部的湍流度。2019年,Liu等[13]利用数值模拟和动力学模态分解(DMD)相结合,研究转向架对非定常尾迹的影响,研究表明对于无转向架模型,尾涡的产生有两个固有的来源,即排障器和尾车车头;而对于有转向架模型,尾涡主要是由尾车的排障器产生的。
如上所述,高速列车尾迹呈现出复杂的三维湍流特性,尾涡的动力学演化特性尚不明确,同时其与近尾迹列车风峰值的相关性还未被完全建立,此外转向架对尾涡的产生和演化的影响仍未达成共识。
近年来,为理解复杂的湍流结构和相关机理,学者结合各种数据驱动算法发展了多种非定常流场的模态分解方法[14-18]。通过模态分解方法得到的降阶模型可以直观的展现非定常流动随时间和空间的演化规律,因此对于湍流尾迹的非定常流动机理分析具有重要意义。目前应用广泛的是POD和DMD[14-15]。其本质都是寻找一组低维的子空间(流动模态或相干结构),将高维、复杂非定常流场表示为这些子空间在低维坐标系上的叠加,从而在低维空间中描述流场随时间和空间的演化规律[16]。然而,当流动的相干结构出现在低能量或多频率时,传统的POD并不能得到很好的结果[17]。2016年,Sieber等[17]提出Spectral POD方法,通过对相关矩阵沿对角线应用低通滤波器来增加矩阵的对角线相似度,既而增强底层信号动力学的相似度。相较于POD,SPOD更有利于分离发生在多个频率和能量的流动现象。自从该SPOD方法被提出,它已经成功应用于多种基础湍流流场的分析[17, 19-21],如Chu等[19]将SPOD应用于圆柱和海豹胡须柱的尾涡动力学演化分析中,发现了海豹胡须柱尾迹中存在着四种典型的涡脱落模式,并阐明了其可以有效抑制卡门涡脱落的机制。然而,SPOD方法在更复杂三维湍流尾迹流场,如高速列车三维尾迹中的应用还鲜有涉及。
因此本文采用增强型延迟分离涡数值模拟方法(IDDES)和SPOD方法相结合,研究三种不同转向架构型对高速列车列车风和非定常尾涡动力学特性的影响。
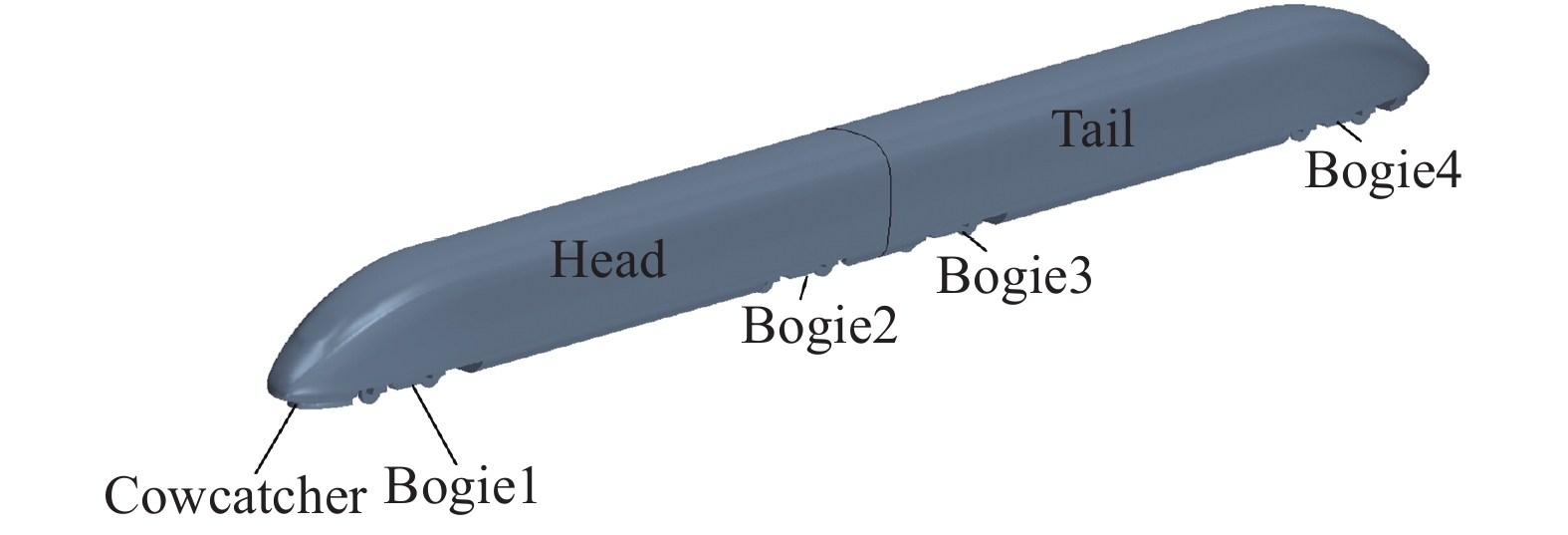
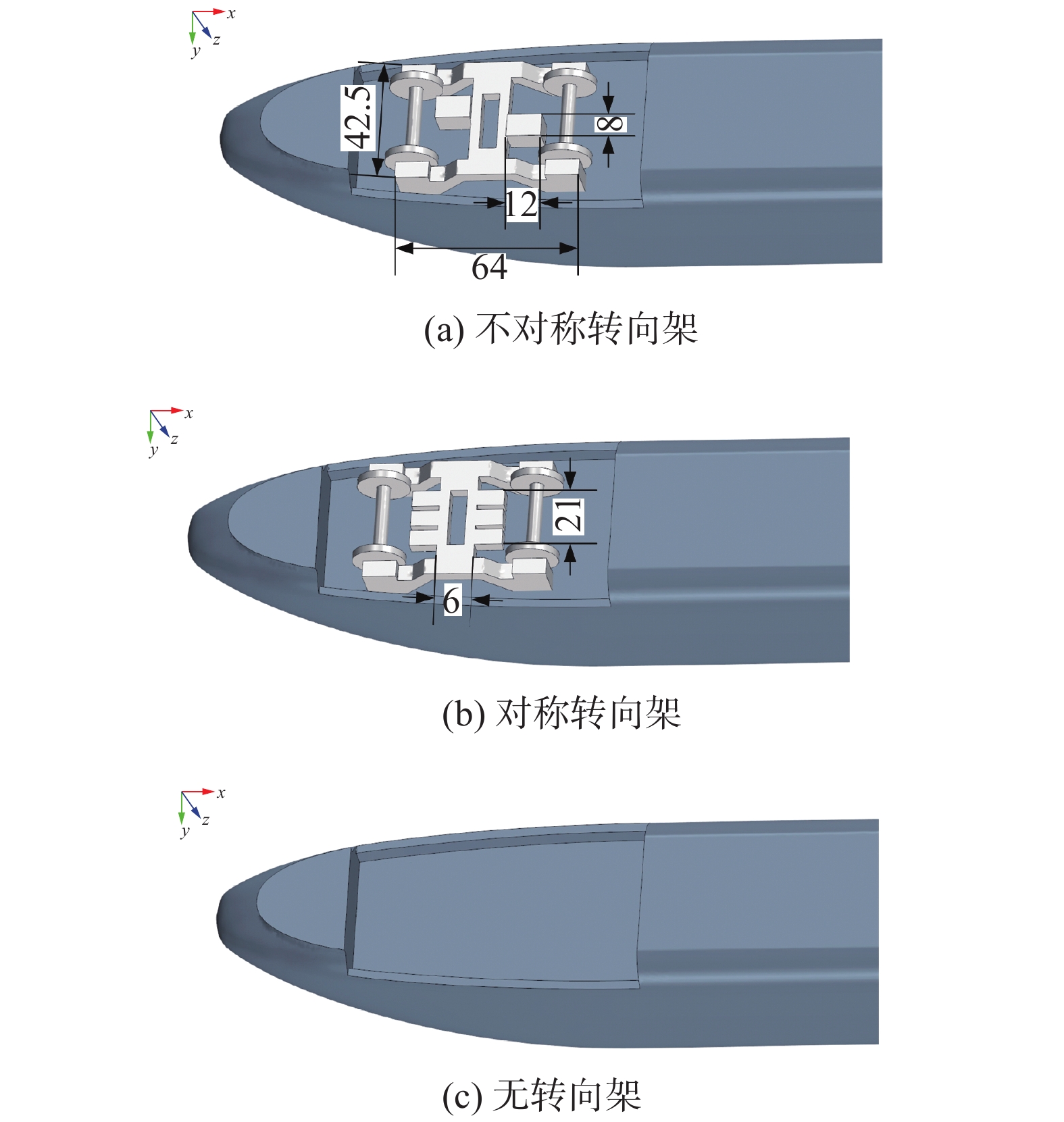
1 方 法 1.1 高速列车模型本文的研究对象为1/50缩比两节编组的CRH3高速列车模型,尺寸为15.7W×1.0W×1.1W(长L×宽W×高H),W = 0.065 m,包含2个排障器,4个转向架。三种不同转向架构型分别为:不对称转向架(Asymmetric Bogies,AB)、对称转向架(Symmetric Bogies,SB)和无转向架(Without Bogie,WoB;带有转向架空腔)。高速列车模型的三维图如图1所示,三种转向架构型如图2所示。不对称转向架和对称转向架分别对应动车和拖车转向架结构,车轮、轮轴及轮对支撑框架均相同,其中车轮的直径为d = 20 mm,宽度为2.6 mm,其他相关尺寸如图2所示(单位为mm)。
|
图 1 1/50两节编组CRH3高速列车模型 Fig.1 1/50 scaled high-speed train model CRH3 with two cars |
|
图 2 三种不同转向架构型 Fig.2 Bogie configurations:(a) asymmetric bogies (AB);(b) symmetric bogies (SB);(c) without bogies (WoB) |
本文采用了基于k-

|
图 3 计算域和边界条件 Fig.3 Computational domain and boundary conditions |
| 表 1 网格信息 Table 1 Grids information |
|
|

|
图 4 高速列车模型网格分布 Fig.4 Grid distribution around a high-speed train model |
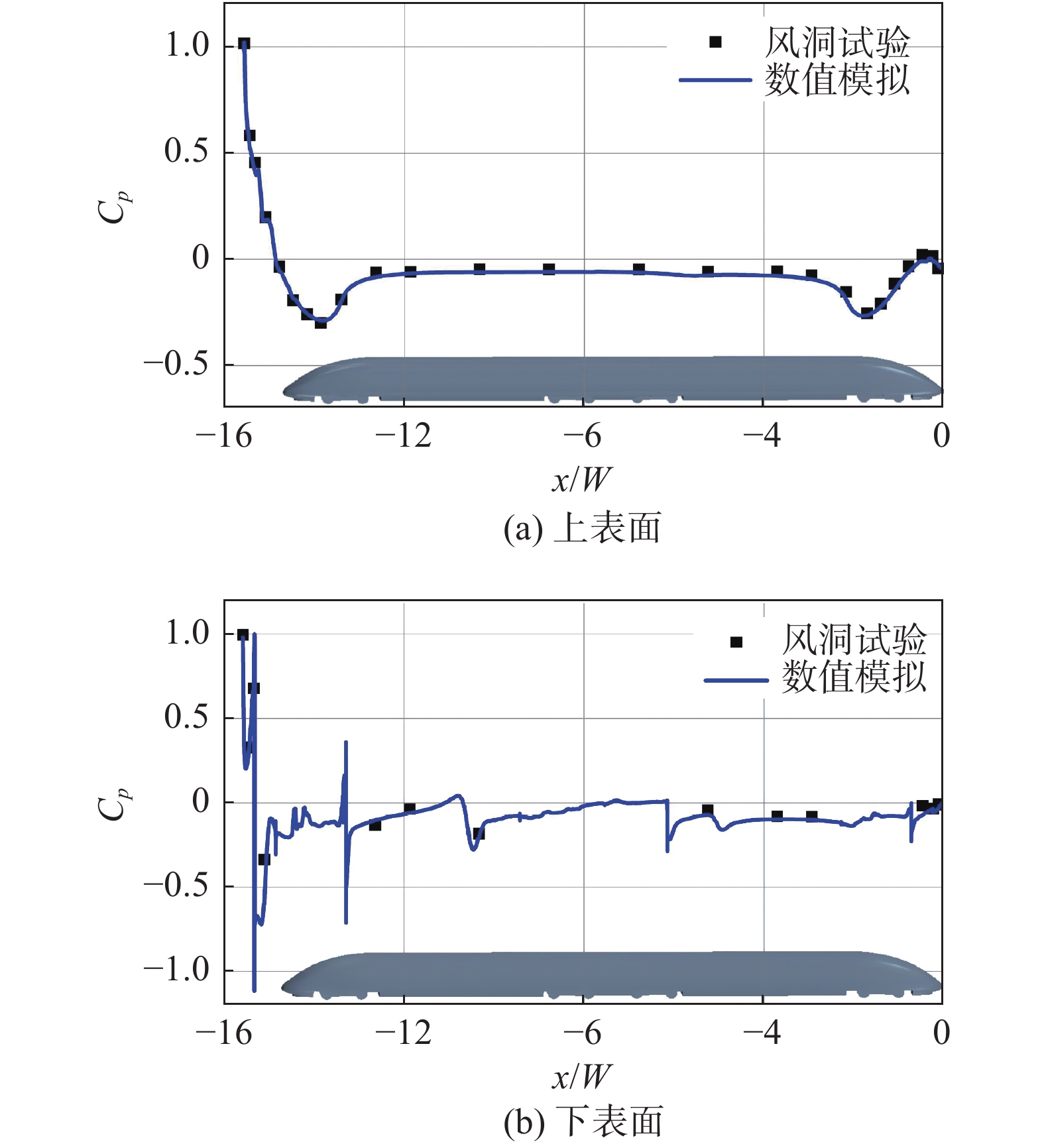
为了验证数值模拟计算的准确性,将不对称转向架模型在静止地面边界条件下的计算结果与风洞试验结果进行了对比。该风洞试验的模型以及地面条件均与数值模型一致,有关实验的其他细节可参考之前的研究[10]。图5展示了中截线上列车上下表面时均压力系数分布的试验和数值结果。压力系数的定义如公式(1)所示:
|
图 5 风洞试验与数值模拟中截线上时均压力系数对比 Fig.5 Comparison of time-averaged pressure coefficients along the longitudinal centreline between IDDES and experiment |
| $ {C_p}=\frac{{p - {p_\infty }}}{{\dfrac{1}{2}\rho U_\infty ^2}} $ | (1) |
式中,p为时均表面压力,
如图5所示,对于上表面和下表面,除了尾部的个别测点外,数值模拟和风洞试验的结果均吻合较好,此外气动力和尾迹速度场的验证结果也较合理,这里因为篇幅限制不再展示,可以参考之前的研究[23]。
1.4 SPOD方法SPOD方法是在POD方法的基础上增加了额外的时间约束,能够分离发生在多个频率的能量和流动现象,通过改变滤波长度
SPOD将速度矢量
| $ u(x,t)=\bar u(x) + u'(x,t)=\bar u(x) + \sum\limits_{i=1}^N {{\alpha _i}(t){\phi _i}(x)} $ | (2) |
相关矩阵R为:
| $ {R_{i,j}}=\frac{1}{N}\left\langle {u'(x,{t_i}),u'(x,{t_j})} \right\rangle $ | (3) |
其中
与传统的POD算法不同,SPOD沿着对角线应用一个简单的低通滤波器来增加矩阵R的对角线相似度,过滤后的相关矩阵S为:
| $ {S_{i,j}}=\sum\limits_{k= - {N_f}}^{{N_f}} {{g_k}} {R_{i + k,j + k}} $ | (4) |
其中
后面的步骤和传统的POD相同,
| $ S{a_i}={\lambda _i}{a_i} $ | (5) |
式中:
| $ \frac{1}{N}({a_i},{a_j})={\lambda _i}{\delta _{ij}} $ | (6) |
式中,(,)代表向量积,
空间模态由速度快照投影到时间系数上得到:
| $ {\phi _i}(x)=\frac{1}{{N{\lambda _i}}}\sum\limits_{j=1}^N {{a_i}({t_j})} u'(x,{t_j}) $ | (7) |
在数值仿真中,由于列车采用静止处理,因此得到的瞬时速度是以列车为参考系,通常先经过来流速度归一化处理后转换成以地面为参考系的速度,列车风速度的定义如下:
| $ {U_{{\rm{TF}}}}=\frac{{{U_{{\rm{TF}}}}}}{{{U_\infty }}},{V_{{\rm{TF}}}}=\frac{{{V_{{\rm{TF}}}}}}{{{U_\infty }}} $ | (8) |
| $ {U_{{\rm{GF}}}}=1 - {U_{{\rm{TF}}}},{V_{{\rm{GF}}}}={V_{{\rm{TF}}}} $ | (9) |
| $ {U_{{\rm{slipstream}}}}=\sqrt {(U_{{\rm{GF}}}^2 + V_{{\rm{GF}}}^2)} $ | (10) |
其中,TF表示列车参考系,GF表示地面参考系;U为流体x方向的速度,V为流体y方向的速度。
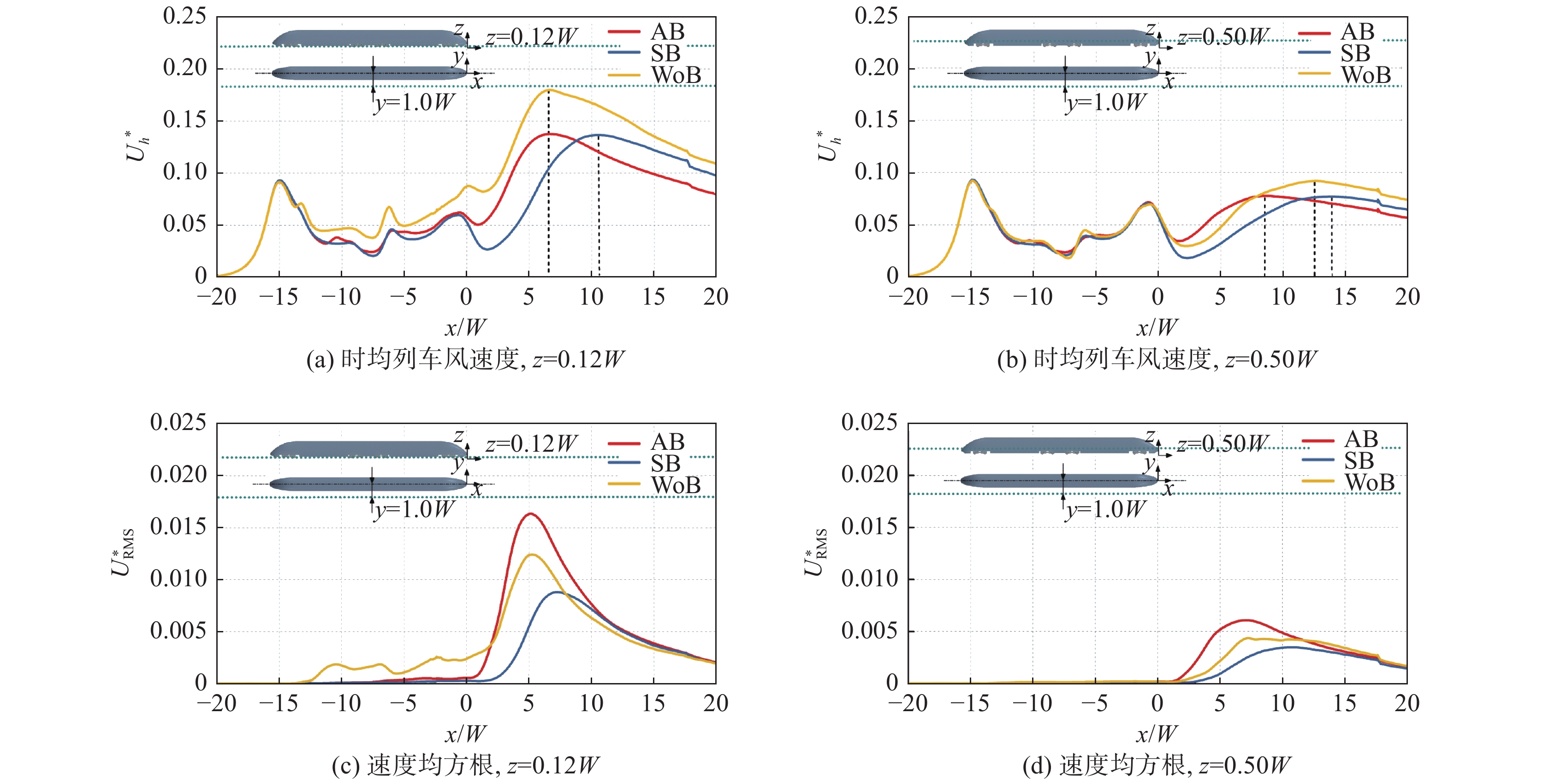
图6展示了三种转向架结构列车模型在TSI[3]要求的两个监控位置处(轨侧位置(y = 1.0W, z = 0.12W)和站台位置(y = 1.0W, z = 0.50W))沿x轴方向的时均列车风速度
与时均列车风速度不同,图6(c、d)显示不对称转向架的列车风速度的均方根峰值最大,对称转向架的列车风速度的均方根峰值最小。
|
图 6 三种转向架结构沿x轴方向的列车风速度分布(y = 1.0W) Fig.6 Slipstream velocity distributions for three bogie configurations alongx direction at y = 1.0W |
图7展示了三种转向架构型的第一个转向架腔内的瞬时流场拓扑结构。可见不对称转向架的分离涡结构较为丰富且不对称。对于无转向架结构,空腔内的涡结构尺度更大且转向架空腔及其后缘流动分离产生大尺度的流向涡脱落,导致了第一个转向架空腔后(x ≈ −13.5W)相对较高的列车风速度,如图6(a)所示。

|
图 7 转向架腔内的瞬时流场结构 Fig.7 Instantaneous flow structures in the bogie cavity |
图8展示了Q准则中Q= 1000时的三种转向架构型的时均尾迹流场。由图可知,三种转向架的尾迹均是由一对反向旋转的流向涡主导;其中,无转向架和不对称转向架的涡结构强度更大,尾车底部两侧的涡脱落结构更加明显。
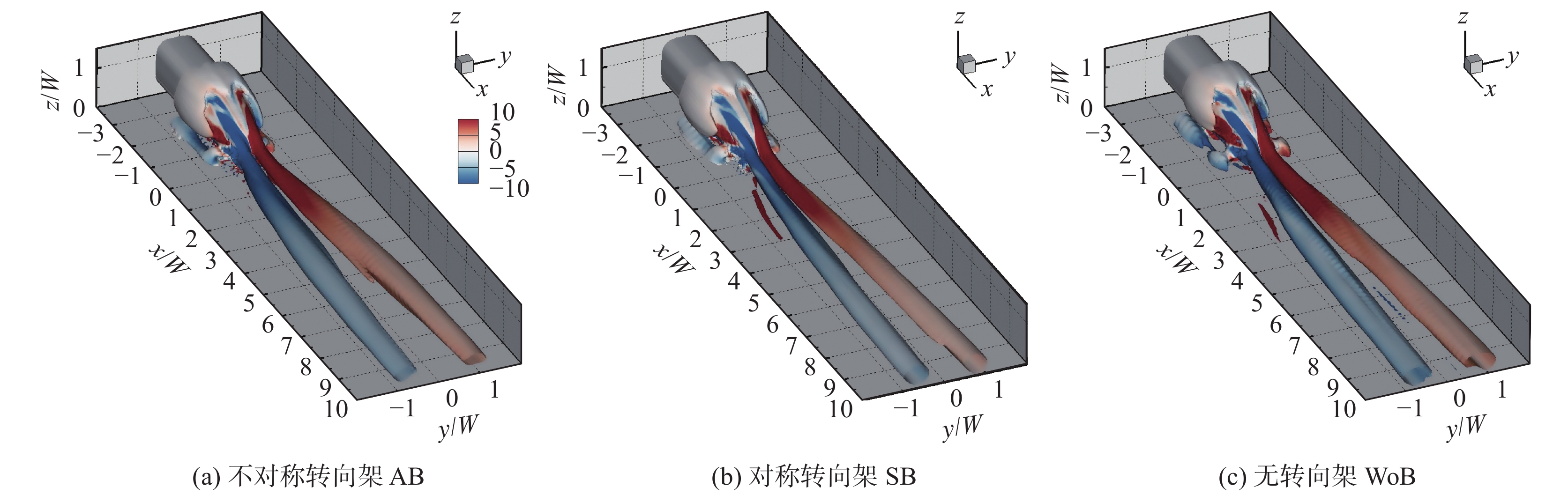
|
图 8 时均尾迹结构(Q= 1000) Fig.8 Time-averaged wake flow structures (Q = 1000) |
图9展示了尾迹瞬态压力p = −3.5 Pa表示的三种转向架构型的瞬时流场拓扑结构。可以观察到,对于三种转向架构型,尾迹中的主导结构均是大尺度的半环形流向交替涡脱落,涡腿紧贴地面。三种转向架构型在瞬时尾迹拓扑结构上的主要区别在于尾迹的展向宽度和涡脱落左右交替或同步出现的程度。与对称转向架相比,无转向架和不对称转向架的尾迹展向宽度更宽,当流向涡脱落更大概率地经过轨道侧和站台侧的测点位置时,就会引起较大的列车风速度。对于不对称转向架,如 图9(a)所示,由于不对称转向架构型带来的底部扰动与流向涡对的相互作用,使得半环形流向涡交替脱落程度更强。
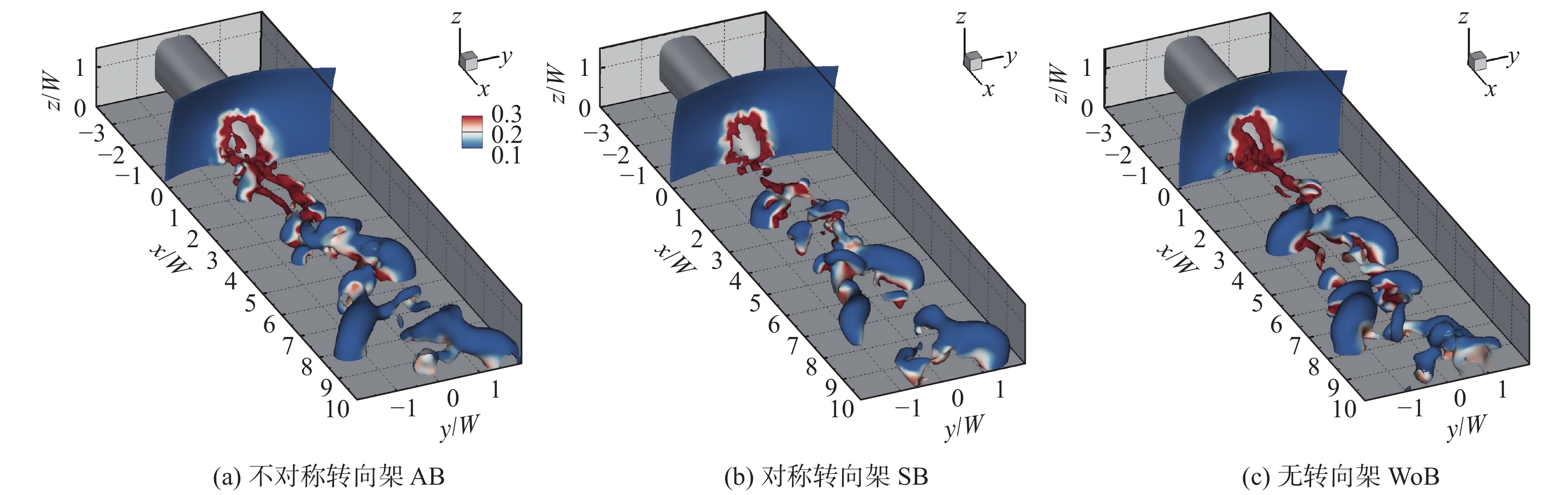
|
图 9 瞬时尾迹结构(p = −3.5 Pa) Fig.9 Instantaneous wake flow structures (p = −3.5 Pa) |
SPOD方法一个重要的参数就是滤波器的大小即
首先选取
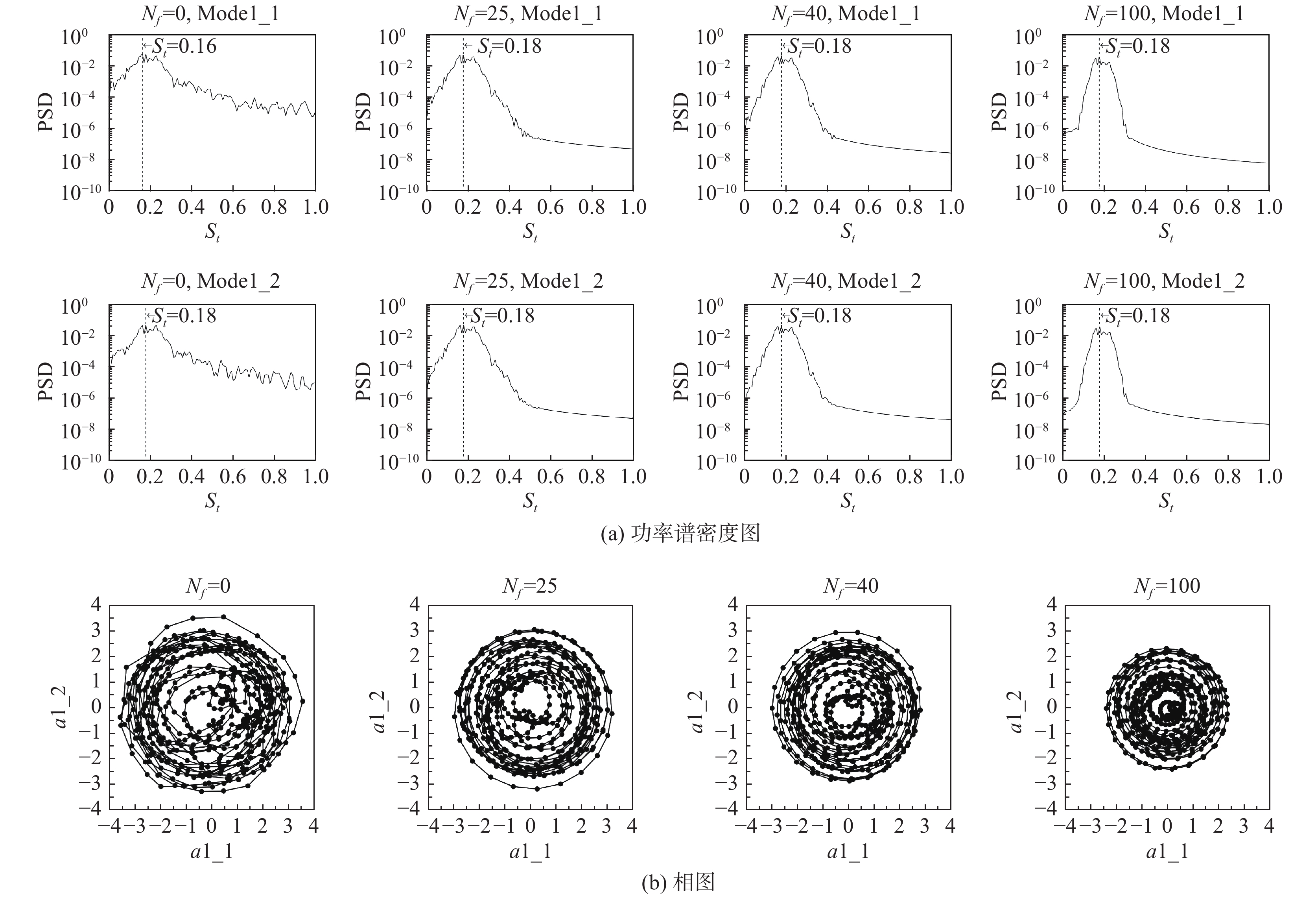
|
图 10 不同 |
先前的研究[17, 19]表明
| $ {S_t}=\frac{{fD}}{{{U_\infty }}} $ | (11) |
| $ {N_f}=(1 \sim 2){T / {\Delta t}} $ | (12) |
式中:f为频率;D为特征长度,此处为列车宽度此处为列车宽度W = 0.065 m;
图11展示了不对称转向架前50个模态的能量占比情况,随着
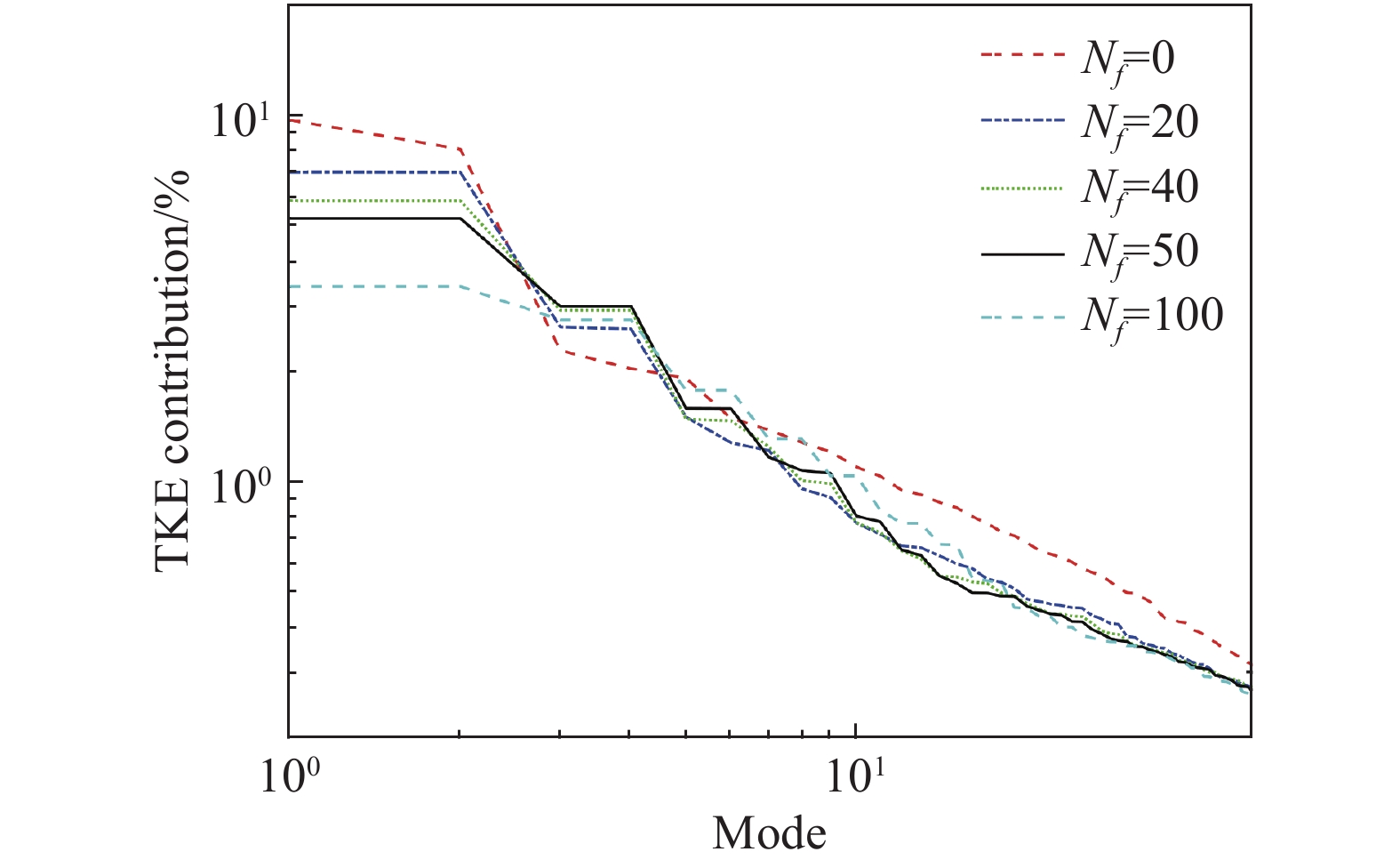
|
图 11 不对称转向架前50个模态能量占比 Fig.11 Energy fraction of the first 50 modes for the AB configuration |
以不对称转向架为例,图12展示了流场速度U(流向速度,即x方向速度)和速度V(展向速度,即y方向速度)分别用POD(

|
图 12 不对称转向架速度U和V的前两对模态云图 Fig.12 Contours of the first two pairs of modes for velocities U and V of the AB configuration |
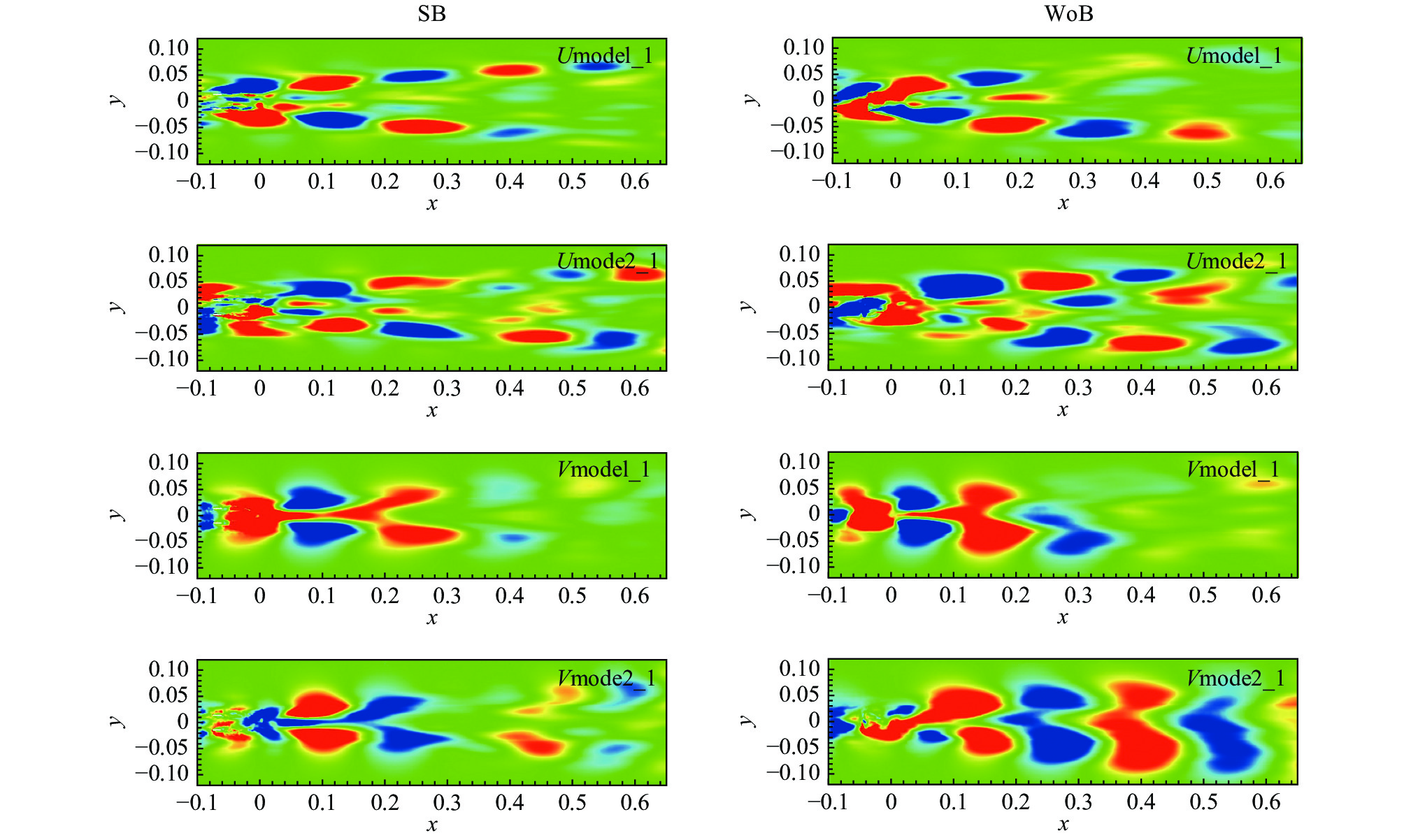
图13展示了对称转向架和无转向架构型速度U和速度V的SPOD(
|
图 13 对称转向架和无转向架速度U和V的前两对模态云图 Fig.13 Contours of the first two pairs of modes for velocities U and V of the SB and WoB configurations |
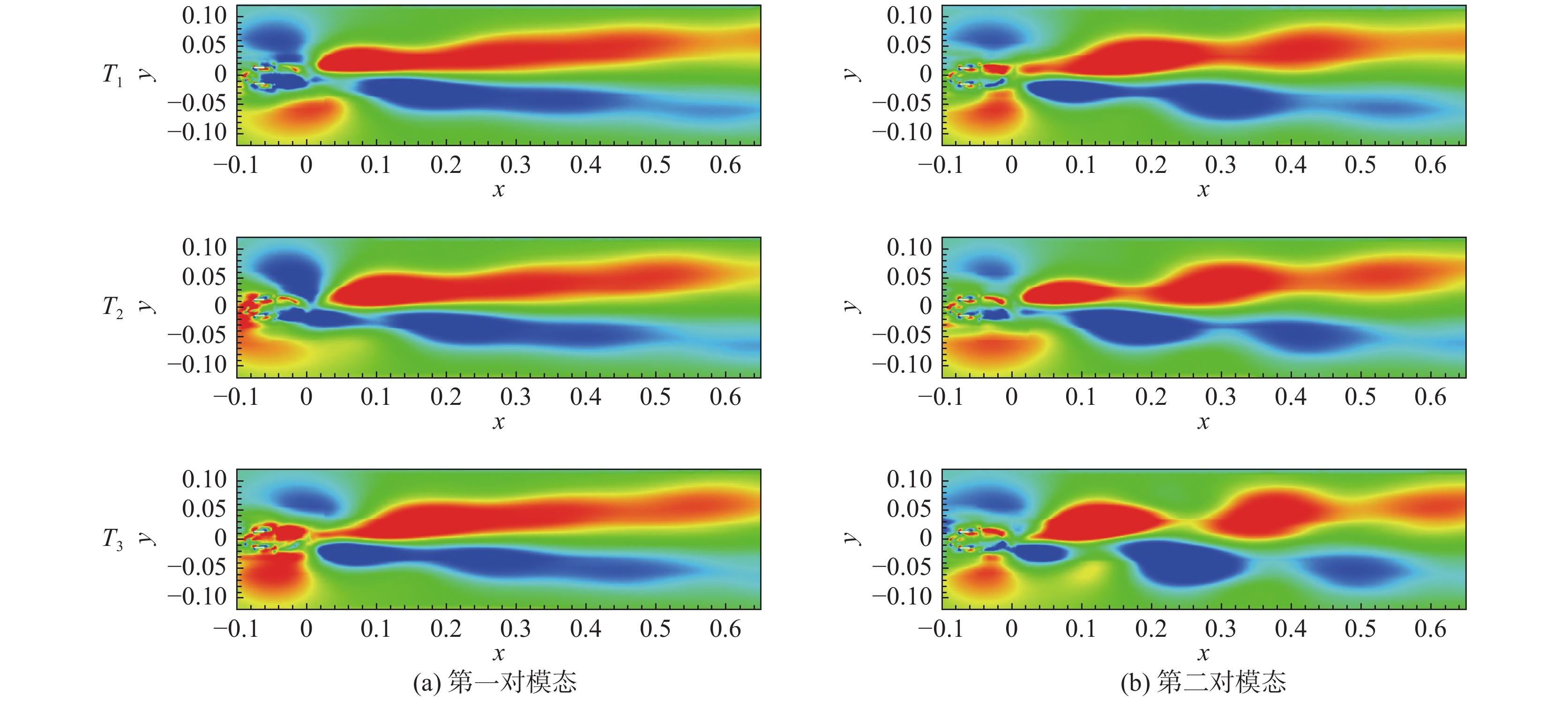
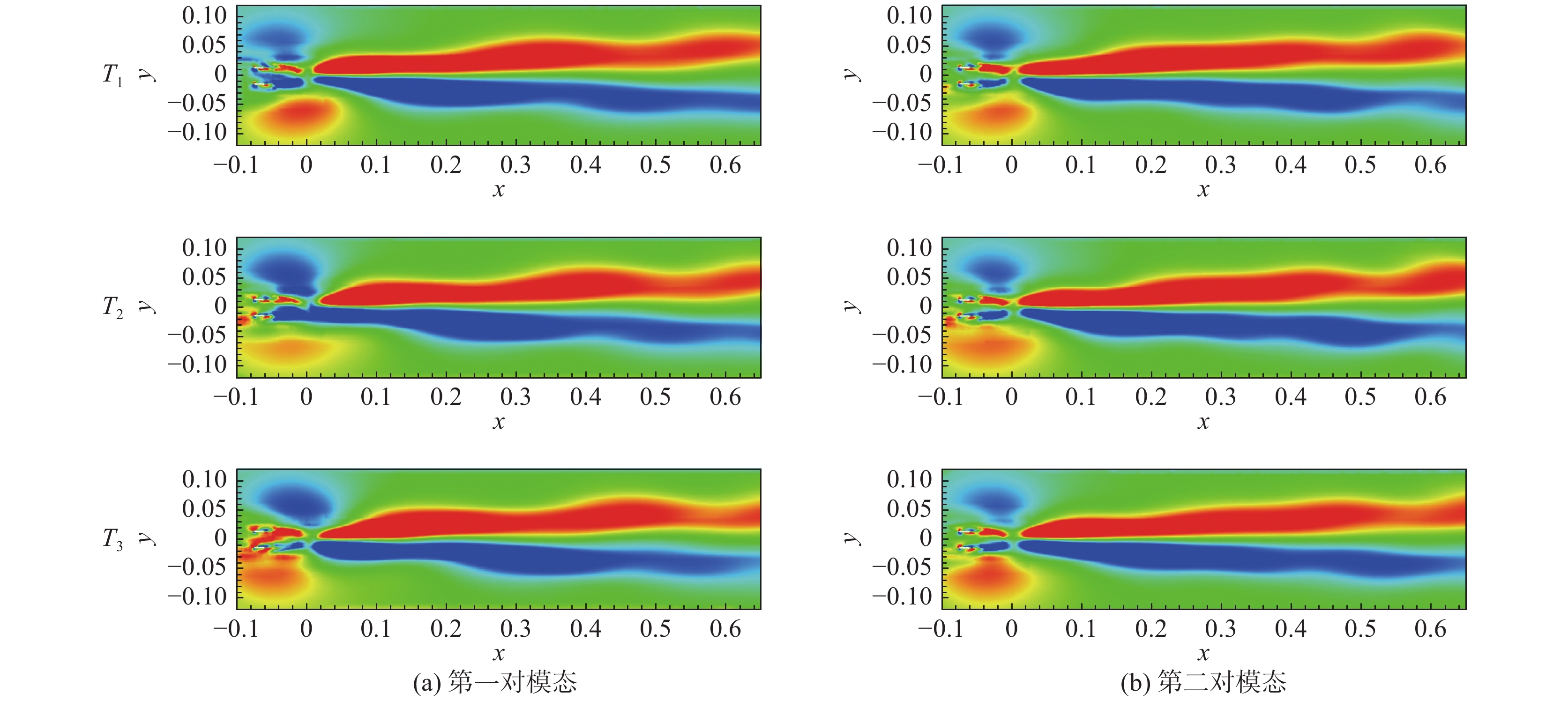
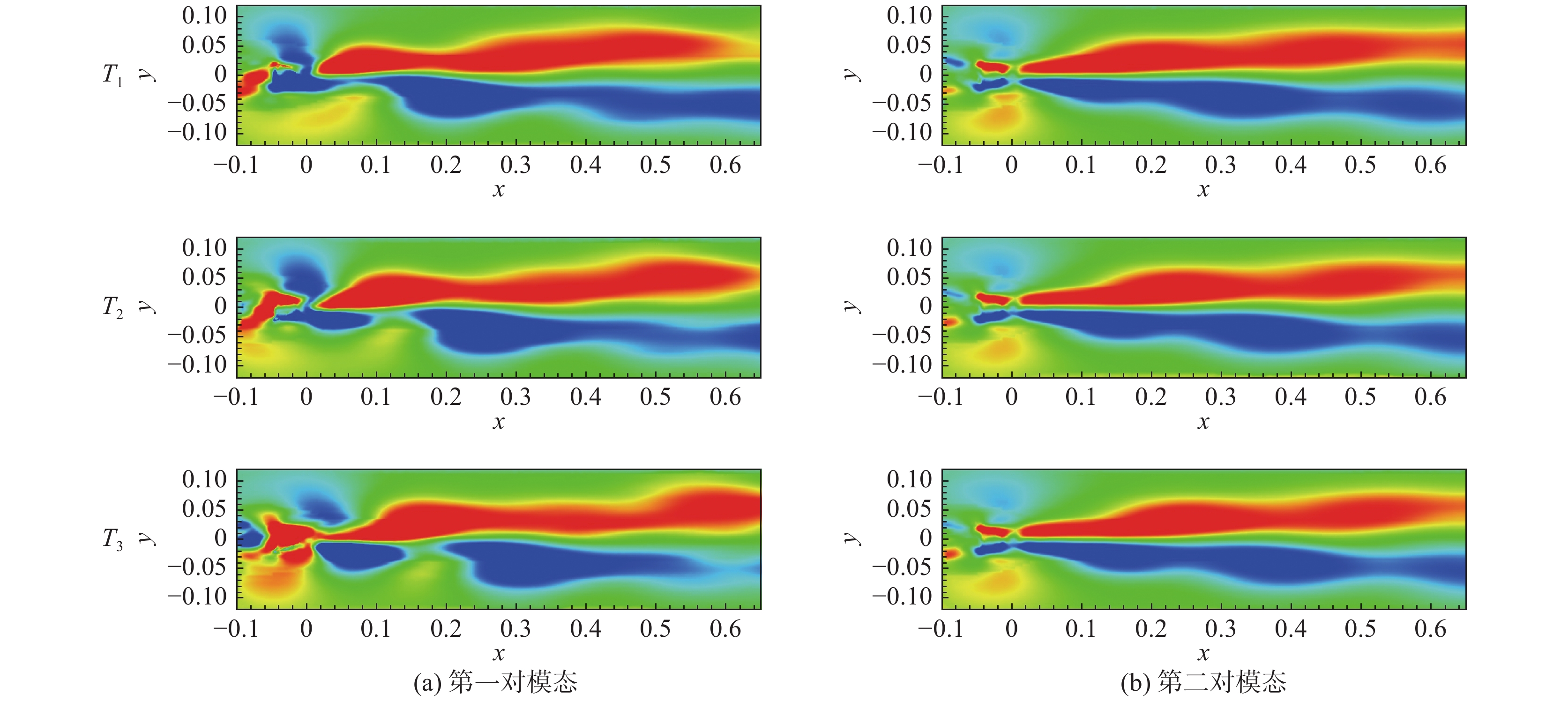
图14~图16分别展示了不对称转向架、对称转向架和无转向架三种转向架构型的第一对模态和第二对模态的涡量重构结果。从不对称转向架结果来看,对于第一对模态重构结果,可以看到从近尾迹区的交替涡脱落,向下游发展与流向向涡对相互作用后相融合;对于第二对模态重构结果,T1时刻尾迹的主要特征为正弦式震荡,而T3时刻为交替涡脱落,T2时刻则为二者的一个过渡。因此第一对模态表示交替的涡脱落特征,而第二对模态表示涡脱落与正弦式震荡交替出现的双稳态特征[10],故两对模态在模态图上差别不大。从对称转向架结果来看,如图15所示,相比不对称转向架,第一对模态重构结果的展向范围更窄;第二对模态的的涡脱落不明显,正弦式震荡也不如不对称转向架强烈。从无转向架结果来看,如图16所示,第一对模态的重构结果也能观察到涡脱落,但在近尾迹区较为混乱,与其他两种转向架差别较大,主要是由于空腔后缘流动分离产生的大尺度涡脱落造成的;第二对模态重构结果的涡脱落和正弦式震荡的强度均介于不对称转向架和对称转向架之间。
|
图 14 不对称转向架瞬时流场重构结果 Fig.14 Reconstructed instantaneous flow fields for the AB configuration |
|
图 15 对称转向架瞬时流场重构结果 Fig.15 Reconstructed instantaneous flow fields for the SB configuration |
|
图 16 无转向架瞬时流场重构结果 Fig.16 Reconstructed instantaneous flow fields for the WoB configuration |
本文采用IDDES数值模拟方法结合SPOD方法研究了三种不同转向架结构对高速列车列车风和非定常尾迹的影响,主要结论如下:
1)三种转向架构型的高速列车尾迹均是由一对反向旋转的半环形流向交替涡脱落主导,当流向涡脱落经过轨道侧和站台侧的测点位置时,会引起较大的列车风速度;
2)对于不对称转向架,由于其不对称结构所带来的扰动与流向涡对较强的相互作用导致交替脱落程度更强,尾涡宽度更宽,进而诱导更高的列车风脉动速度;
3)对于对称转向架,其涡脱落及展向震荡程度均最小,故而列车风在尾迹出现峰值的位置明显延后,时均和脉动速度均最小;
4)对于无转向架,由于空腔后缘的大尺度涡脱落与流向涡对的相互作用,加剧了流向涡对的正弦震荡,扩宽了尾迹宽度,从而产生了最高的列车风时均速度;
5)相比于POD方法,SPOD方法通过对相关矩阵的对角滑动滤波,增强其对角相似性,使得其从复杂湍流中提取主导流动模态的能力更强;随着
| [1] |
杨国伟, 魏宇杰, 赵桂林, 等. 高速列车的关键力学问题[J]. 力学进展, 2015, 45(1): 217-460. YANG G W, WEI Y J, ZHAO G L, et al. Research progress on the mechanics of high speed rails[J]. Advances in Mechanics, 2015, 45(1): 217-460. DOI:10.6052/1000-0992-13-091 (in Chinese) |
| [2] |
SUZUKI M, NAKADE K, IDO A. Countermeasures for reducing unsteady aerodynamic force acting on high-speed train in tunnel by use of modifications of train shapes[J]. Journal of Mechanical Systems for Transportation and Logistics, 2009, 2(1): 1-12. DOI:10.1299/jmtl.2.1 |
| [3] |
BAKER C J, QUINN A, SIMA M, et al. Full-scale measurement and analysis of train slipstreams and wakes. Part 1: Ensemble averages[J]. Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit, 2014, 228(5): 451-467. DOI:10.1177/0954409713485944 |
| [4] |
BAKER C J, DALLEY S J, JOHNSON T, et al. The slipstream and wake of a high-speed train[J]. Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit, 2001, 215(2): 83-99. DOI:10.1243/0954409011531422 |
| [5] |
STERLING M, BAKER C J, JORDAN S C, et al. A study of the slipstreams of high-speed passenger trains and freight trains[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2008, 222(2): 177-193. DOI:10.1243/09544097jrrt133 |
| [6] |
BELL J R, BURTON D, THOMPSON M C, et al. Moving model analysis of the slipstream and wake of a high-speed train[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 136: 127-137. DOI:10.1016/j.jweia.2014.09.007 |
| [7] |
XIA C, WANG H F, SHAN X Z, et al. Effects of ground configurations on the slipstream and near wake of a high-speed train[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 168: 177-189. DOI:10.1016/j.jweia.2017.06.005 |
| [8] |
BELL J R, BURTON D, THOMPSON M C, et al. Dynamics of trailing vortices in the wake of a generic high-speed train[J]. Journal of Fluids and Structures, 2016, 65: 238-256. DOI:10.1016/j.jfluidstructs.2016.06.003 |
| [9] |
BELL J R, BURTON D, THOMPSON M C, et al. Flow topology and unsteady features of the wake of a generic high-speed train[J]. Journal of Fluids and Structures, 2016, 61: 168-183. DOI:10.1016/j.jfluidstructs.2015.11.009 |
| [10] |
XIA C, WANG H F, BAO D, et al. Unsteady flow structures in the wake of a high-speed train[J]. Experimental Thermal and Fluid Science, 2018, 98: 381-396. DOI:10.1016/j.expthermflusci.2018.06.010 |
| [11] |
WANG S B, BURTON D, HERBST A, et al. The effect of bogies on high-speed train slipstream and wake[J]. Journal of Fluids and Structures, 2018, 83: 471-489. DOI:10.1016/j.jfluidstructs.2018.03.013 |
| [12] |
DONG T Y, LIANG X F, KRAJNOVIĆ S, et al. Effects of simplifying train bogies on surrounding flow and aerodynamic forces[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 191: 170-182. DOI:10.1016/j.jweia.2019.06.006 |
| [13] |
LIU W, GUO D L, ZHANG Z J, et al. Effects of bogies on the wake flow of a high-speed train[J]. Applied Sciences, 2019, 9(4): 759. DOI:10.3390/app9040759 |
| [14] |
ROWLEY C W, DAWSON S T M. Model reduction for flow analysis and control[J]. Annual Review of Fluid Mechanics, 2017, 49(1): 387-417. DOI:10.1146/annurev-fluid-010816-060042 |
| [15] |
TAIRA K, BRUNTON S L, DAWSON S T M, et al. Modal analysis of fluid flows: an overview[J]. AIAA Journal, 2017, 55(12): 4013-4041. DOI:10.2514/1.J056060 |
| [16] |
寇家庆, 张伟伟. 动力学模态分解及其在流体力学中的应用[J]. 空气动力学学报, 2018, 36(2): 163-179. KOU J Q, ZHANG W W. Dynamic mode decomposition and its applications in fluid dynamics[J]. Acta Aerodynamica Sinica, 2018, 36(2): 163-179. DOI:10.7638/kqdlxxb-2017.0134 (in Chinese) |
| [17] |
SIEBER M, PASCHEREIT C O, OBERLEITHNER K. Spectral proper orthogonal decomposition[J]. Journal of Fluid Mechanics, 2016, 792: 798-828. DOI:10.1017/jfm.2016.103 |
| [18] |
KAISER E, NOACK B R, CORDIER L, et al. Cluster-based reduced-order modelling of a mixing layer[J]. Journal of Fluid Mechanics, 2014, 754: 365-414. DOI:10.1017/jfm.2014.355 |
| [19] |
CHU S J, XIA C, WANG H F, et al. Three-dimensional spectral proper orthogonal decomposition analyses of the turbulent flow around a seal-vibrissa-shaped cylinder[J]. Physics of Fluids, 2021, 33(2): 025106. DOI:10.1063/5.0035789 |
| [20] |
RIBEIRO J H M, WOLF W R. Identification of coherent structures in the flow past a NACA0012 airfoil via proper orthogonal decomposition[J]. Physics of Fluids, 2017, 29(8): 085104. DOI:10.1063/1.4997202 |
| [21] |
KADU P A, SAKAI Y, ITO Y, et al. Application of spectral proper orthogonal decomposition to velocity and passive scalar fields in a swirling coaxial jet[J]. Physics of Fluids, 2020, 32(1): 015106. DOI:10.1063/1.5131627 |
| [22] |
SHUR M L, SPALART P R, STRELETS M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649. DOI:10.1016/j.ijheatfluidflow.2008.07.001 |
| [23] |
ZHOU Z W, XIA C, SHAN X Z, et al. The impact of bogie sections on the wake dynamics of a high-speed train[J]. Flow, Turbulence and Combustion, 2020, 104(1): 89-113. DOI:10.1007/s10494-019-00052-w |
 2022, Vol. 40
2022, Vol. 40


