表面介质阻挡放电等离子体激励(surface dielectric barrier discharge,SDBD)[1-3]是一种典型的主动流动控制技术,具有结构简易、易布设、响应迅速、作用频带宽等优势,被广泛应用于分离流动控制[4-5]、边界层控制[6-7]和噪声控制[8-9]等领域。
表面介质阻挡放电等离子体激励对流场的作用效果取决于激励电源形式,对于正弦交流电源驱动的表面介质阻挡放电等离子体激励(AC-SDBD),主要是通过“动量效应”,即向流场中注入体积力,进而诱导气流加速、提升流场动量,达到流动控制的目的[2]。基于AC-SDBD的流动控制作用与其诱导气流加速的能力直接相关,已有研究表明,AC-SDBD在静止空气中诱导形成的壁面射流,最大速度在10 m/s附近,难以在高速环境下取得显著的流动控制效果。因此,提升AC-SDBD诱导气流加速的能力,是实现工程应用的技术瓶颈之一。围绕这一问题,国内外学者展开了一系列探索,已有研究表明使用多组等离子体激励器组合形成的阵列式等离子体激励,是提升AC-SDBD流动控制能力的有效手段。在机翼流动分离抑制方面,Roth 等[10]证明了阵列式AC-SDBD 激励器控制机翼流动分离和增大失速攻角的能力;杨雷雷[11]等利用阵列式AC-SDBD 激励器有效削弱襟翼吸力面流动分离;在压气机内流流动控制方面,张海灯等[12-13]使用阵列式AC-SDBD有效控制了叶尖泄漏流动和叶片角区分离;GE公司Saddoughi 等[14]则使用阵列式AC-SDBD拓宽了跨声速压气机失速裕度。
从已有研究结果来看,阵列式AC-SDBD可以在高速环境下取得一定流动控制效果,但其流动控制能力并不是随着激励器数目的增加而线性增大的[15-18],尤其是阵列式AC-SDBD对流场作用效果对流动状态的依赖性仍有待揭示。
针对上述问题,本文在直流风洞中测试了不同来流速度下阵列式AC-SDBD对流场的作用。通过对等离子体激励下游流场速度和总压进行测量,分析获得了阵列式AC-SDBD“动量效应”随来流速度的变化规律,所得结论可为基于AC-SDBD的高速等离子体流动控制方案设计提供支撑。
1 实验系统 1.1 实验电源及测量系统实验中所使用的交流高压电源为苏曼CTP-2000K型低温等离子体电源,输出电压波形为正弦波形,峰值电压0到30 kV连续可调,实验中电极电压的频率固定为11 kHz,最大输出功率为150 W。
使用皮托管和附面层总压探针测量流向速度和附面层总压,皮托管头部直径为1.5 mm,附面层总压探针头部厚度为0.5 mm;使用精度为0.01 mm的三坐标位移台来控制探针移动;压力传感器型号为DAQ-DAX-16A,量程为±10 kPa,精度为0.25% FS。
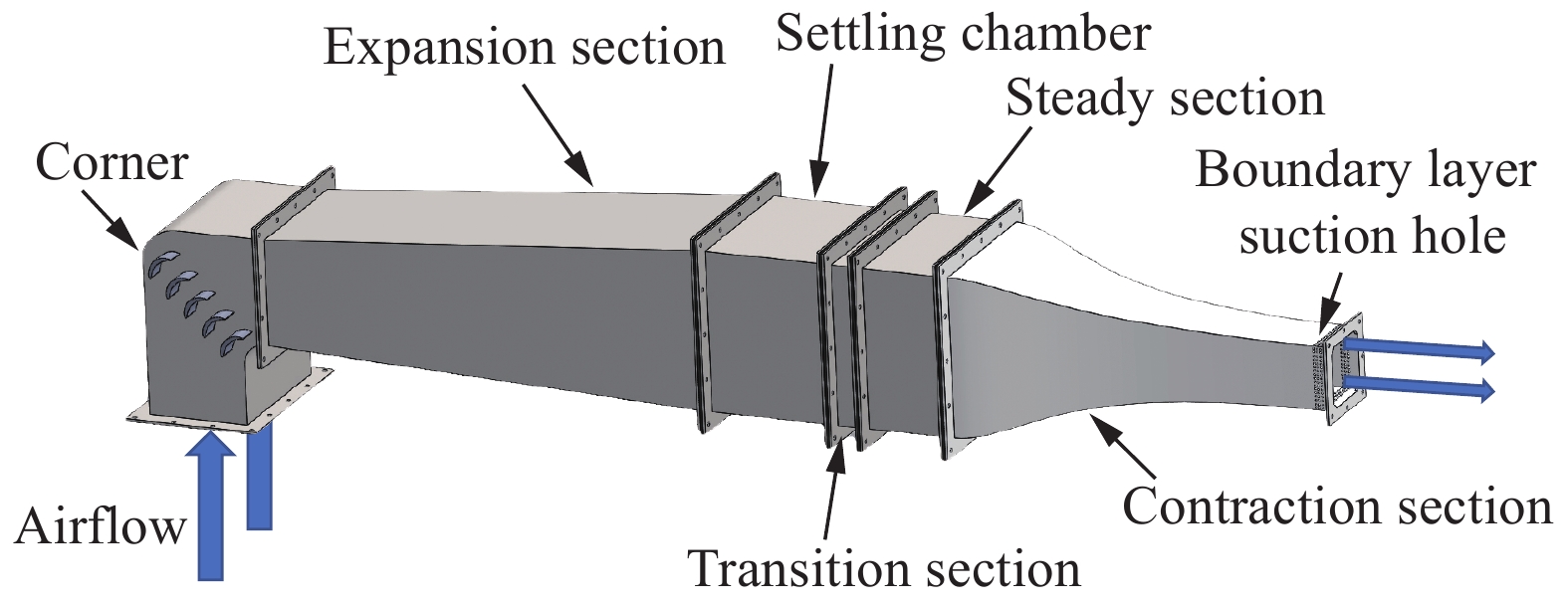
1.2 直流风洞如图1所示,直流风洞由以下七部分构成:动力系统、拐角段、扩张段、稳流段、过渡段、静流段和收缩段。动力系统由离心风机和控制柜组成;拐角段设有五个导流叶片,气流经过拐角导流后方向向右偏折90°,拐角段出口设有一道30目阻尼网;由于拐角出口气流仍有向上运动的趋势,扩张段下壁更容易产生分离现象,经仿真验证,最终确定扩张段下壁扩张角为2°,上壁扩张角为7°,两侧壁扩张角为5°,扩张段总长1000 mm,扩张面积比为3.2;稳流段横截面为340 mm×340 mm矩形,稳流段入口和出口各设有40目阻尼网,中段内嵌长细比为10,厚度为100 mm的不锈钢蜂窝器;在稳流段之后设置长度为85 mm过渡段,在过渡段出口布设一道40目阻尼网以进一步降低湍流度;在过渡段之后设置长度为170 mm静流段,目的是使稳流段出口气流得到充分掺混,提升收缩段入口速度均匀度;综合考虑出口动压稳定性系数,动压系数及实验段轴向静压梯度等流场评定参数,最终确定收缩段采用维氏曲线,长度为600 mm,收缩比为11.5。在近出口壁面设有三排直径为1 mm的附面层吸除孔,对出口附面层进行吸除。值得说明的一点,稳定段及其下游风洞段各截面四个直角均用45°切角以改善直角处产生的二次流动现象。
|
图 1 直流风洞示意图 Fig.1 Schematic of the open circuit wind tunnel |
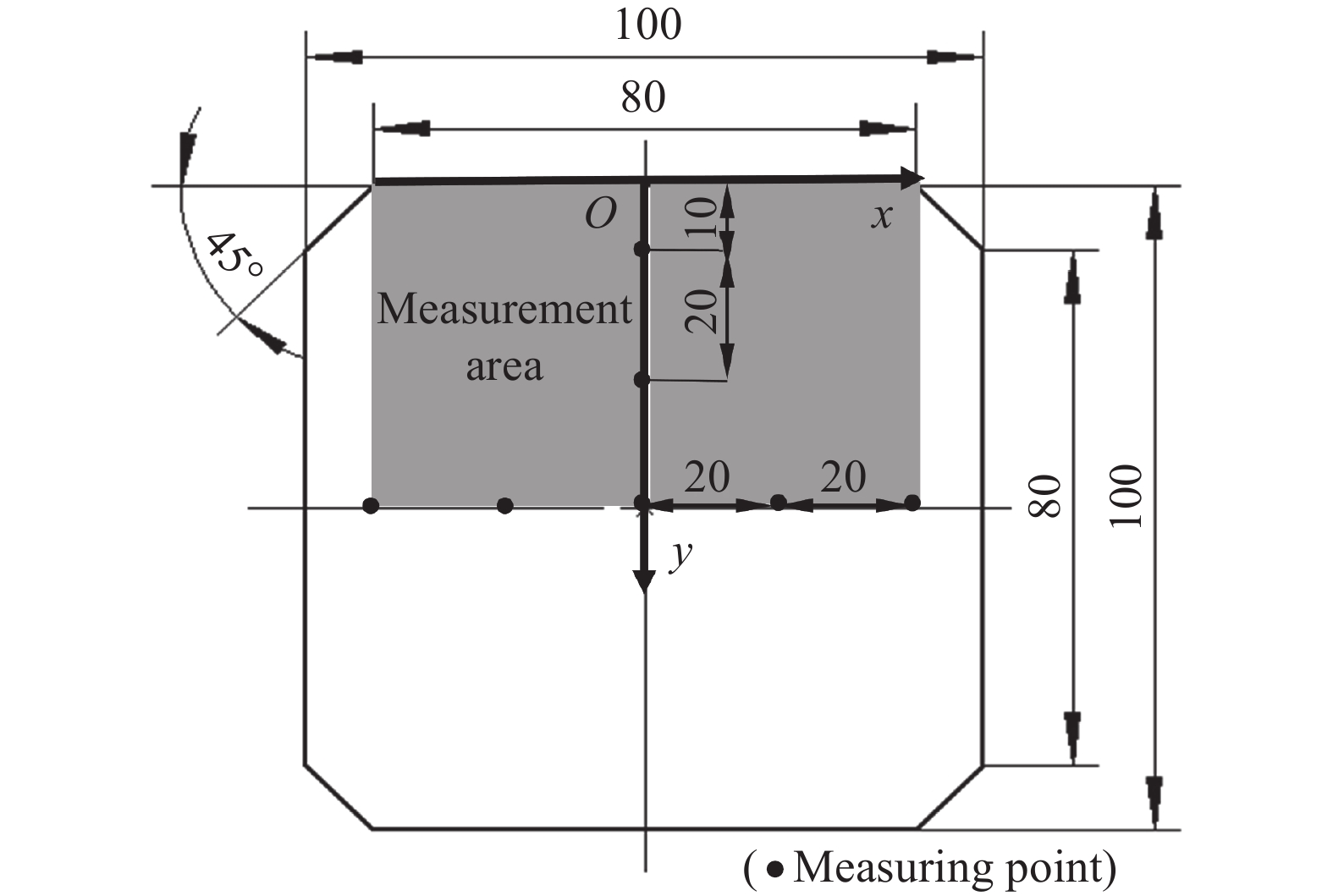
为了判断出口流场品质能否满足实验要求,使用皮托管对风洞出口(实验段入口)流场的总压和速度进行测量,出于简化测量的目的,仅对出口上半区域(80 mm×50 mm)进行测量,原点位于出口上壁面几何中心位置。具体测试方案如图2所示。
|
图 2 测试方案示意图 Fig.2 Schematic diagram of the measurement scheme |
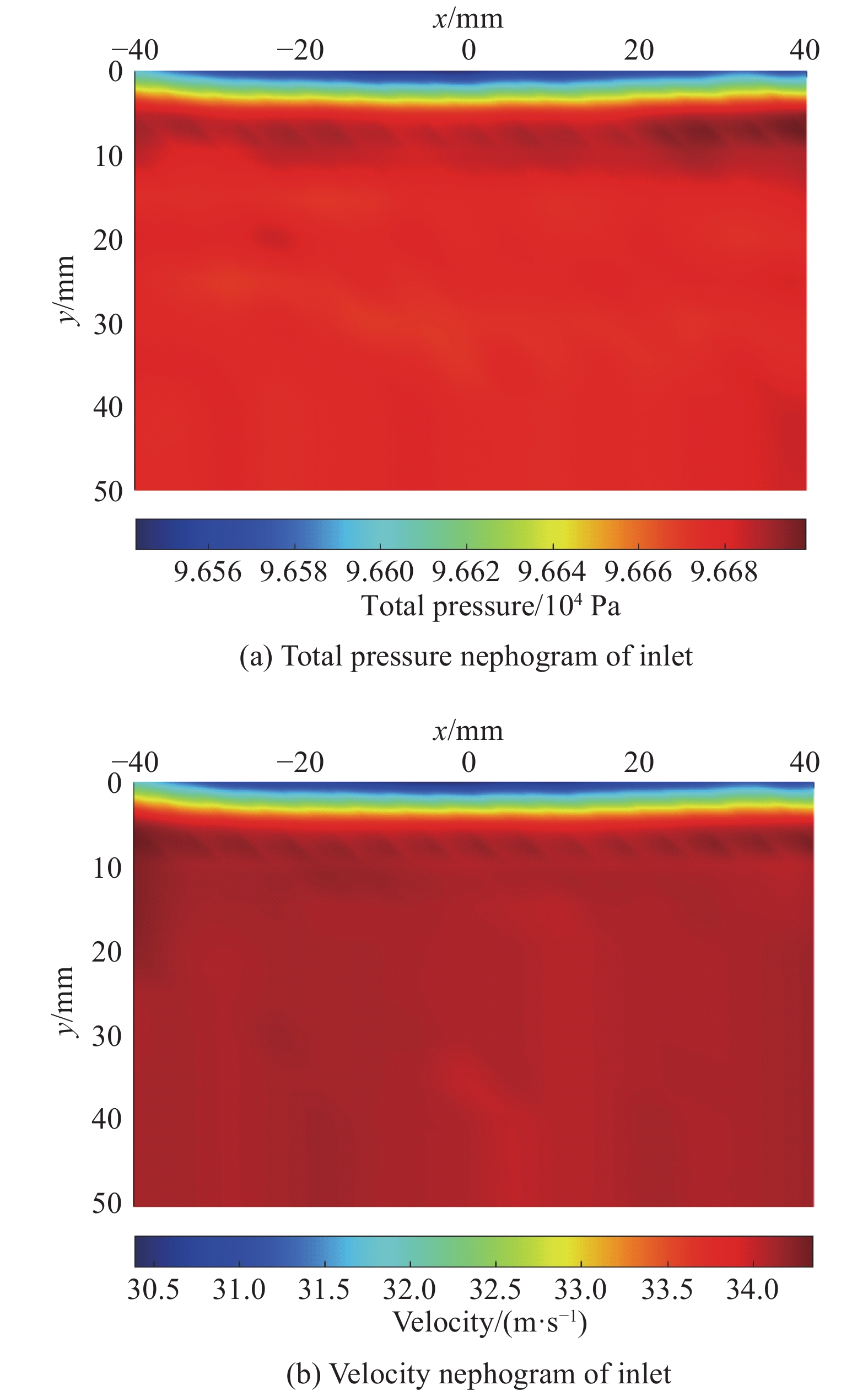
图3为测得总压与速度云图,在主流风速v∞ = 35 m/s条件下,上壁面测量中心位置附面层厚度在3.5 mm左右,近切角区域附面层略薄。定义动压稳定性系数η和动压系数μ定量评定风洞流场品质:
|
图 3 出口截面流场 Fig.3 Flow field at the outlet cross-section |
| $\eta {\rm{ = }}\frac{{{q_{\max }} - {q_{\min }}}}{{{q_{\max }} + {q_{\min }}}}$ | (1) |
| $\mu {\rm{ = }}{\frac{{1}}{{n}}}\sum\limits_1^n {\left. {\left| {\frac{{{q_i} - \overline q }}{{\overline q }}} \right.} \right|} $ | (2) |
式中,
经测量,主流区域内动压稳定性系数η为0.1%,动压系数μ为0.29%,湍流度在0.09%左右,综合以上技术指标评定出口流场品质满足实验要求。
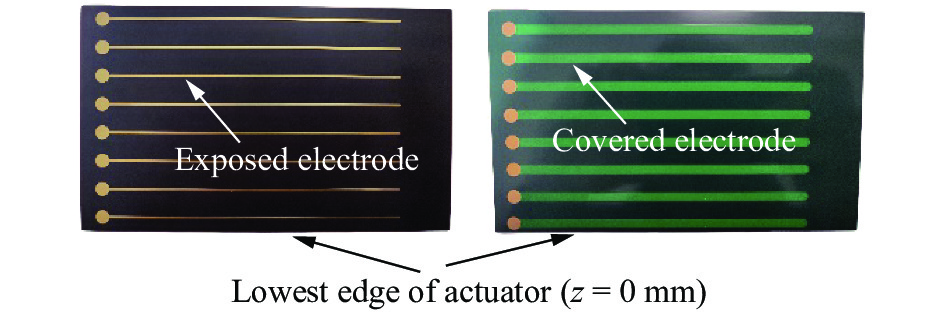
1.3 阵列式AC-SDBD激励器图4和图5分别为阵列式AC-SDBD激励器实物图和激励示意图。阵列式AC-SDBD激励器绝缘介质的绝缘材料为聚酰亚胺,绝缘介质厚度为1 mm,电极材料为铜,暴露电极(高压电极)宽度为1 mm,掩埋电极(低压电极)宽度为4 mm,掩埋电极上覆有绝缘绿油,每组电极间距为12.5 mm,第8组暴露电极距激励器下缘的距离为6.5 mm,将激励器下缘定义为初始位置(流向坐标z = 0 mm),阵列式AC-SDBD激励器可以由不同组数的电极组成,如无特殊说明,本文所述阵列式AC-SDBD激励器均为8组电极构型。
|
图 4 阵列式AC-SDBD激励器实物图 Fig.4 Images of the AC-SDBD actuator array |

|
图 5 激励示意图 Fig.5 Schematics of the AC-SDBD actuators |
在v∞ = 40 m/s条件下,距收缩段出口300 mm流向位置处的附面层厚度达到8 mm,为了减小附面层厚度,设置插板使得平板附面层重新发展,附面层厚度降至5 mm。实验段如图6所示。
2 实验测试结果 2.1 静止工况下激励的诱导速度特性为了找到阵列式AC-SDBD激励器最大诱导速度对应的激励电压,定义z = 5 mm、y = 2 mm、x= −20 mm(即距激励器下缘流向距离5 mm、距上壁高度2 mm、展向中心位置处)为 P处,对不同峰值电压下该位置诱导速度进行测量,以测量范围内最大速度vmax对所测速度进行无量纲化,具体实验结果见图7。

|
图 6 实验段安装图 Fig.6 Experimental set-up of the test section |
|
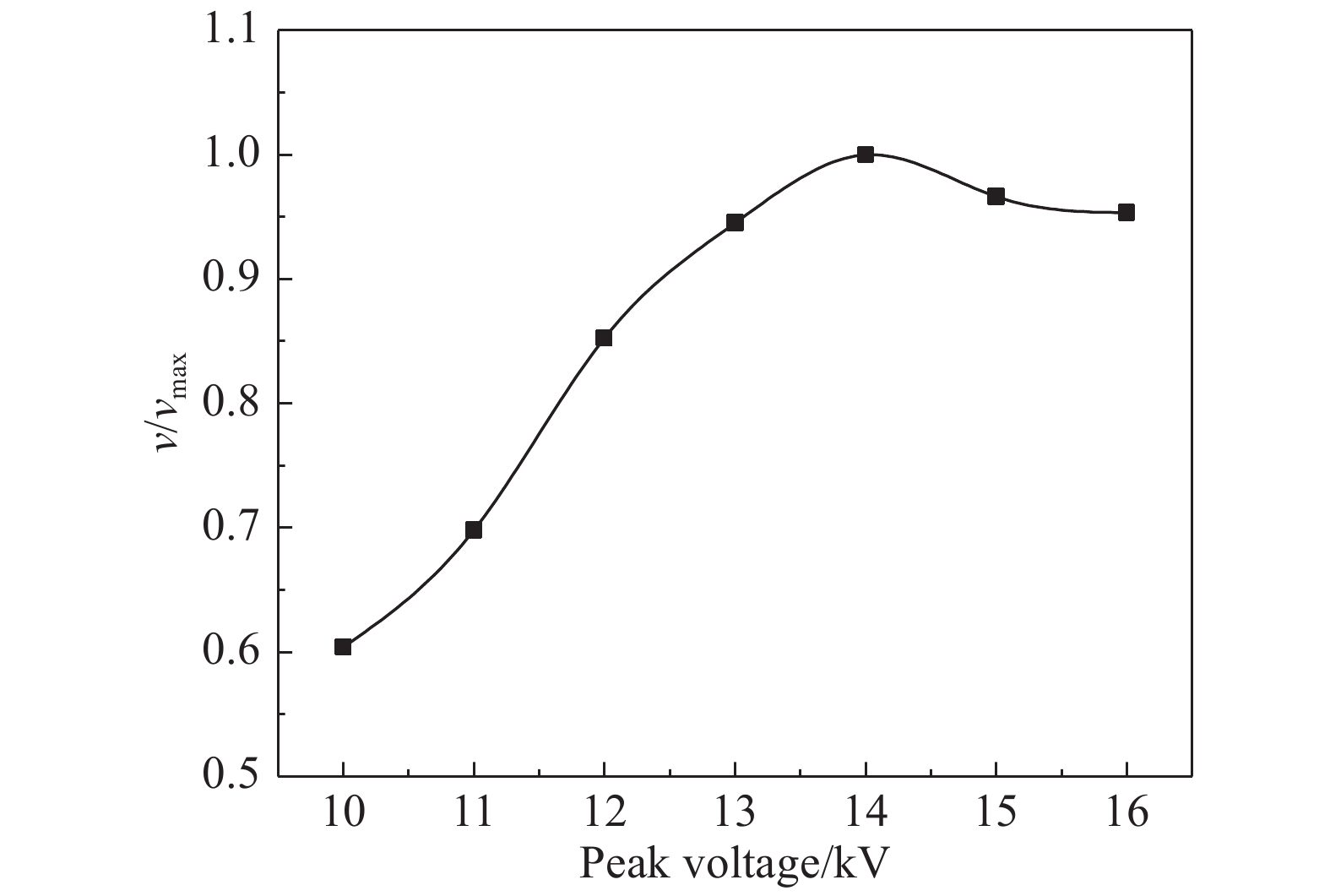
图 7 阵列式AC-SDBD诱导速度随峰值电压变化图 Fig.7 Variation of the induced velocity with the peak voltage for the AC-SDBD actuator array |
图7显示,峰值电压在10~16 kV范围内时,随着激励电压的提高,诱导速度随之上升,在峰值电压为14 kV左右达到最大值,当激励电压超过峰值电压时诱导速度下降。
在保证阵列式AC-SDBD激励器不击穿的条件下,阵列式AC-SDBD激励器以峰值电压为14 kV工作时产生诱导速度最大,下文所有实验将14 kV峰值电压作为放电参数。
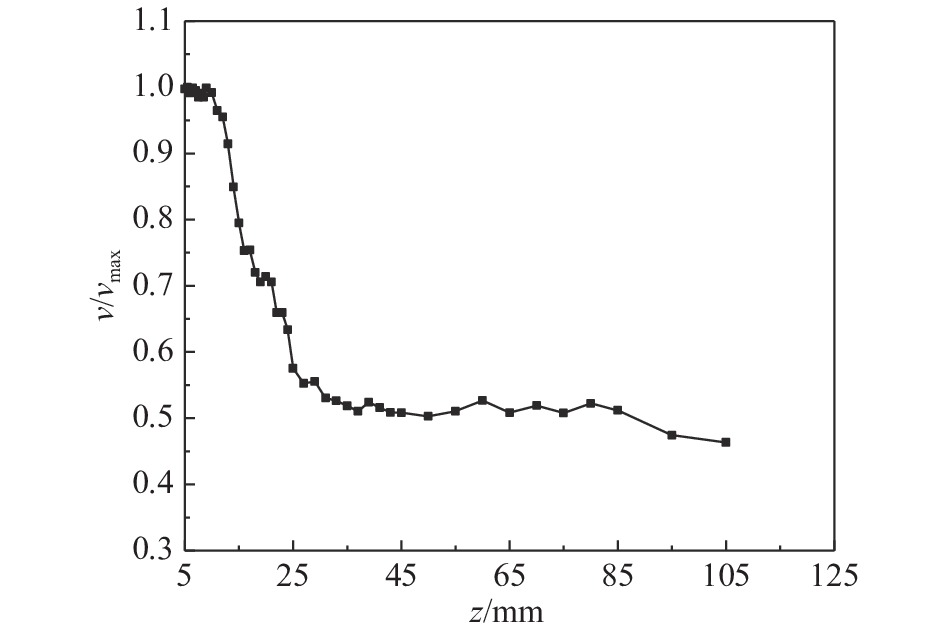
下面使用14 kV峰值电压,在展向位置x = −20 mm、高度位置y = 2 mm沿流向进行诱导速度测量,以最大诱导速度vmax对所测速度进行无量纲化,如图8所示。从图8可以看到,阵列式AC-SDBD激励器下游15 mm以内的诱导速度维持在较高水平,基本上没有衰减;15 mm ≤ z ≤ 35 mm时,诱导速度快速亏损到最大诱导速度的50%左右;z > 35 mm之后,诱导速度缓慢下降。
|
图 8 AC-SDBD诱导速度沿流向变化图 Fig.8 Variation of the induced velocity along the streamwise direction for the AC-SDBD actuator |
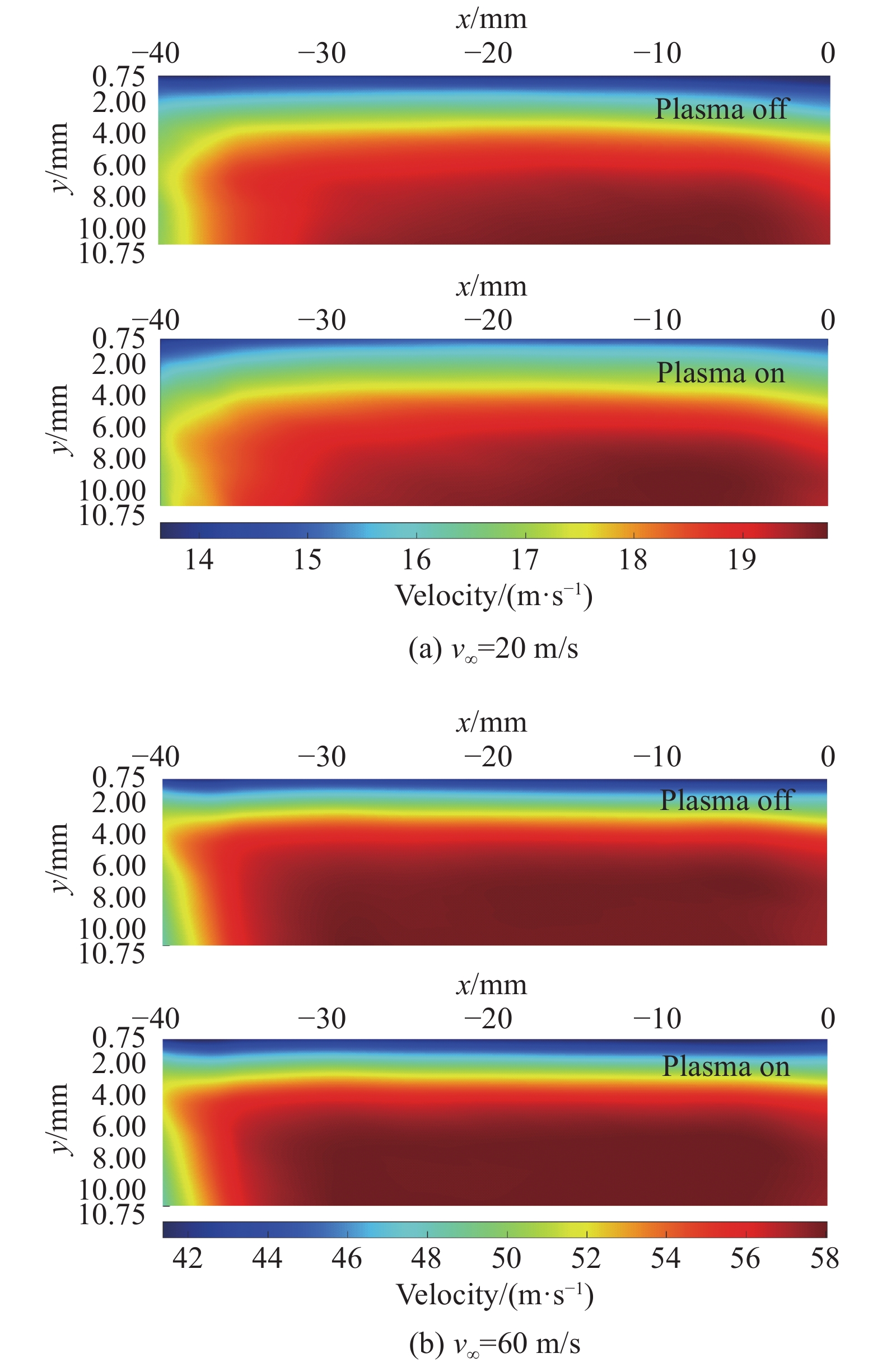
为了排除激励后流场的展向均匀性和可能产生的流场畸变对测试结果产生干扰,选取两个典型速度v∞ = 20 m/s和60 m/s进行研究。以P处(x = −20 mm处)展向位置为中心,对−40 mm ≤ x ≤ 0 mm,0.75 mm ≤ y ≤ 10.75 mm速度场进行测量,测量截面流向位置为z = 5 mm,结果如图9所示。
|
图 9 激励前后速度云图对比 Fig.9 Comparison between the velocity contours with and without actuation |
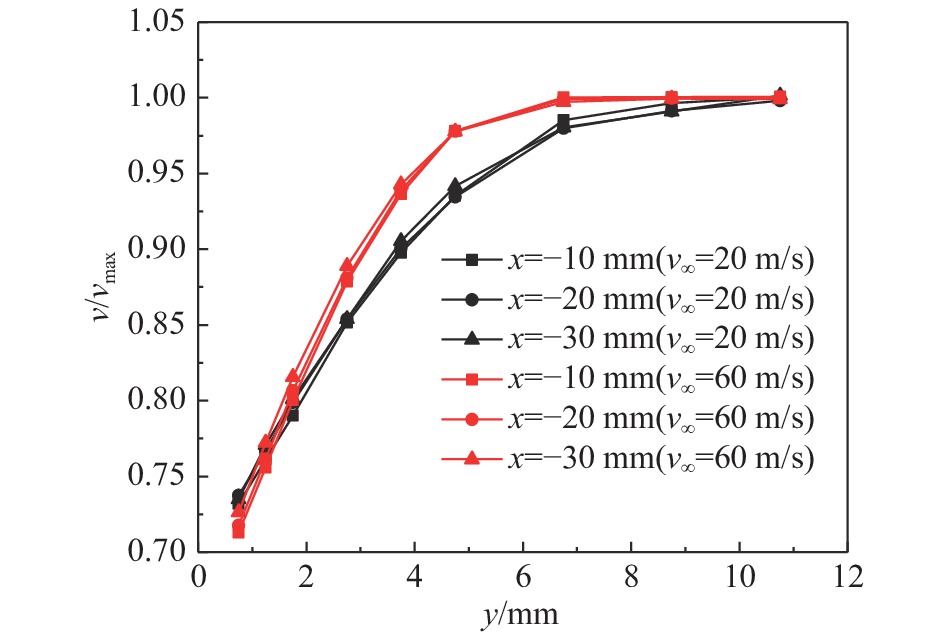
从图9可以看到,两种工况测量中心位置区域激励后速度沿展向分布均匀,无明显速度畸变。为了定量分析激励后不同展向位置速度分布,将展向位置x = −10 mm、−20 mm和−30 mm处速度以测量范围最大速度vmax进行无量纲化,数据处理结果如图10所示。
|
图 10 激励后不同展向位置速度分布 Fig.10 Velocity profiles at different spanwise locations with actuation |
从图10可以看到,在不同工况下3个展向位置速度分布规律相同,即−30 mm ≤ x≤ −10 mm展向范围内流动均匀性较好。
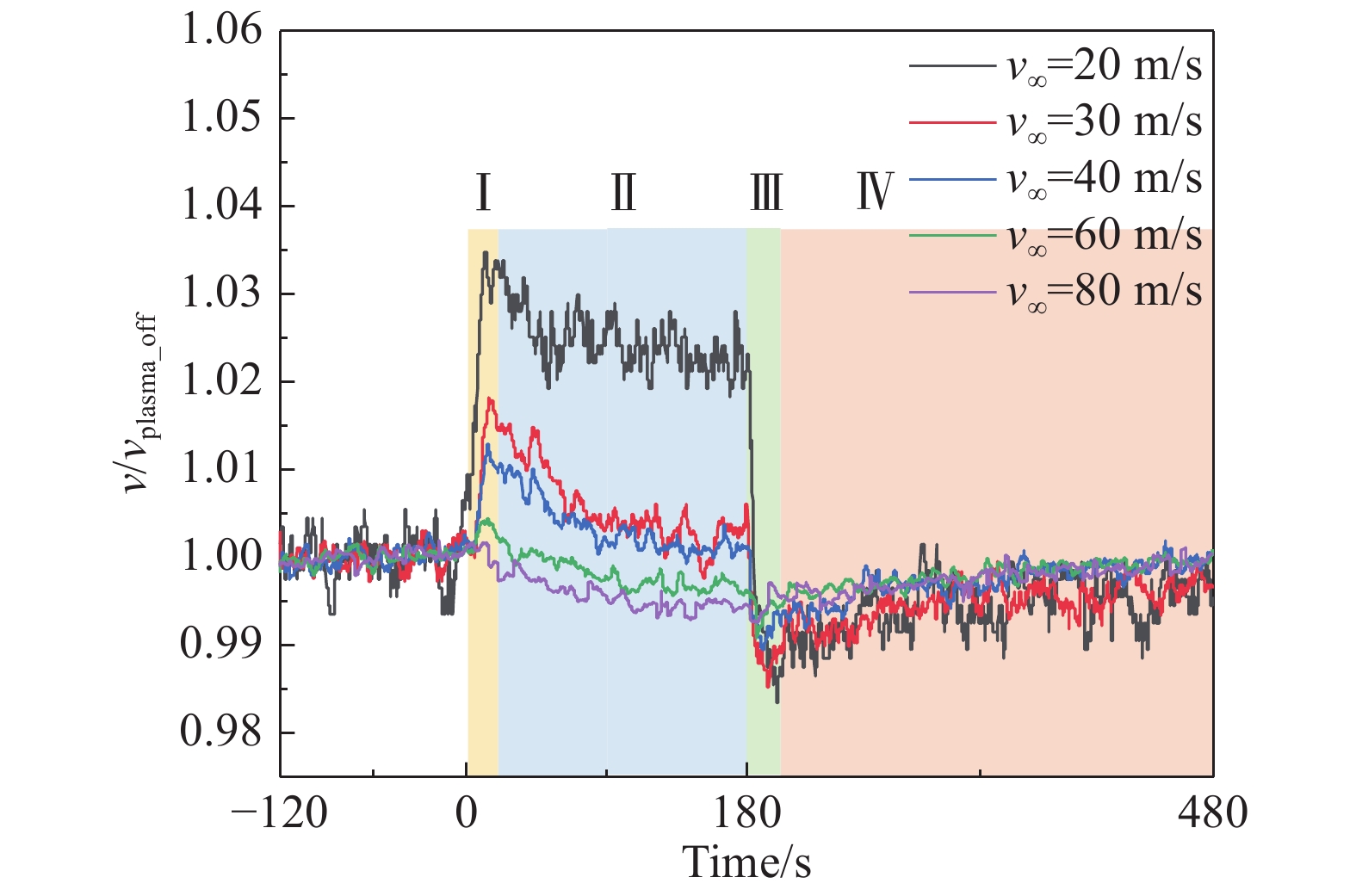
对v∞ = 20 m/s、30 m/s、40 m/s、60 m/s和80 m/s不同来流速度下P处速度随时间变化进行测量,实验中对未激励状态持续采样120 s后施加等离子体激励180 s,最后静置300 s。以
|
图 11 P处流速随时间变化图 Fig.11 Time evolution of the local velocity at position P |
施加阵列式AC-SDBD激励后,近壁流速与激励时间有关。不同工况速度变化规律可以分为以下四个阶段:阶段Ⅰ:刚开始施加激励时,近壁流体在电场力的加速作用下,产生贴壁射流使得近壁速度瞬间提升,激励瞬时速度提升量与来流风速密切相关,v∞ = 20 m/s时瞬时速度提升达基准速度的3.5%,随着主流速度的提高,激励瞬时速度提升幅值下降明显,80 m/s来流下瞬时速度提升基本为零。以上现象主要是由于主流速度的提高使近壁流体受到体积力加速作用的时间变短,从而造成动量提升效果减弱;阶段Ⅱ:随着时间的推进,速度逐渐下降,在激励180 s内,各主流速度工况下,近壁速度基本达到平衡速度,主流速度越大,相对应的平衡速度相对提升量越低,在v∞ = 60 m/s和80 m/s工况下,平衡速度低于基准速度,激励对流场有减速作用,此阶段中激励对流场的减速作用可能与近壁区域被加热的空气引发的高流动损失有关;阶段Ⅲ:关闭激励器后,体积力的诱导加速效应消失,近壁速度陡然下降,各工况速度下降幅值和施加激励瞬间速度提升幅值基本一致;阶段Ⅳ:随着时间推进,近壁流速逐渐提升并趋向于基准状态。
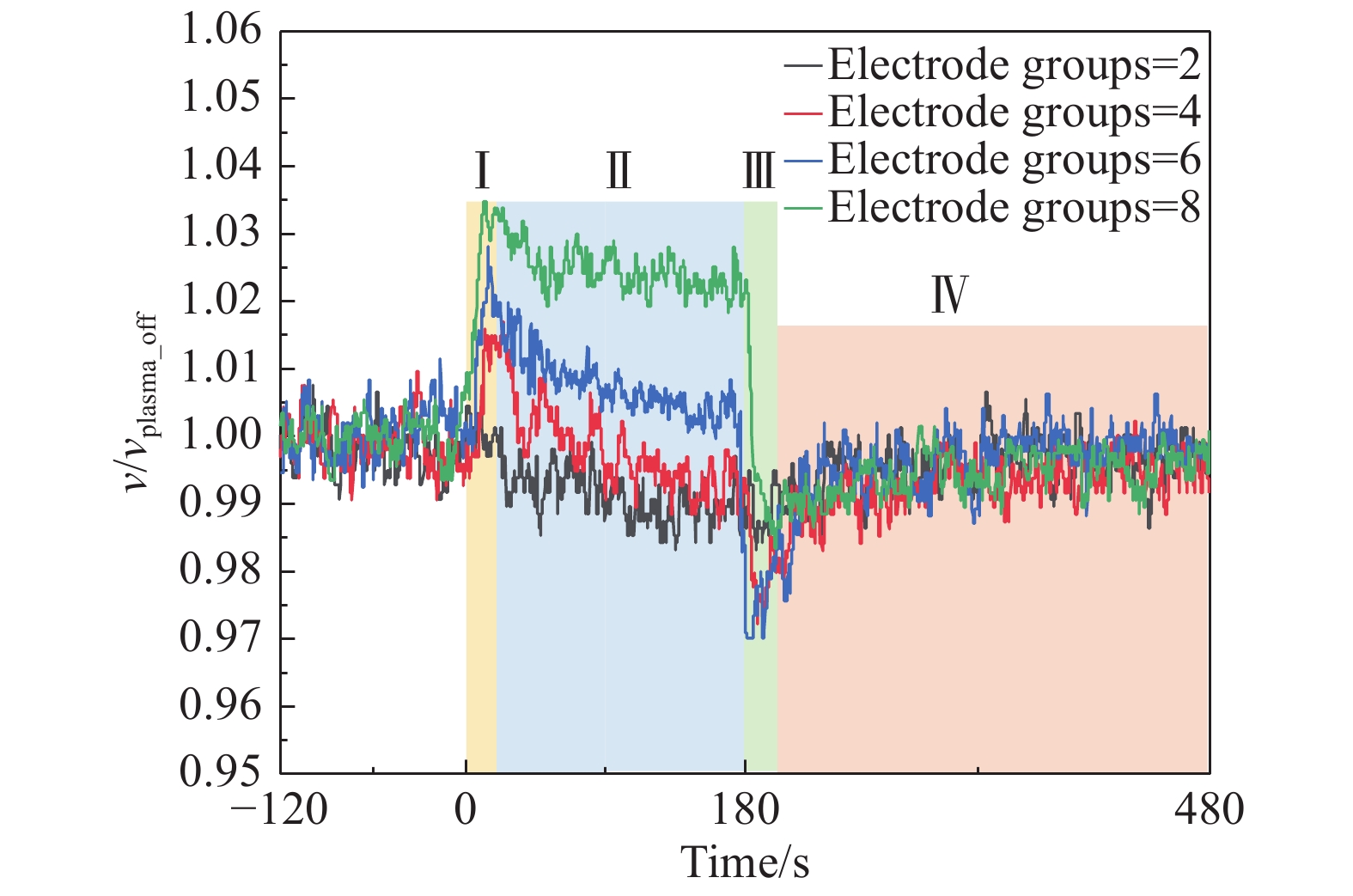
为了确定上述规律对不同组数的阵列式激励器激励后流场的适用性,针对 v∞ = 20 m/s工况,在P处测量了2、4、6和8组电极激励后单点瞬时速度变化,以
|
图 12 激励组数对瞬态流速的影响(v∞= 20 m/s) Fig.12 Influence of the number of excited plasma actuators on the time evolution of the local velocity (v∞= 20 m/s) |
实验结果表明,与上述对激励后流场瞬态速度变化规律的研究结论相似,不同激励组数速度变化规律同样可以分为四个阶段,随着激励组数的增加,激励对近壁流场加速现象越明显且激励后近壁区速度随时间的阶段性变化规律愈发显著。
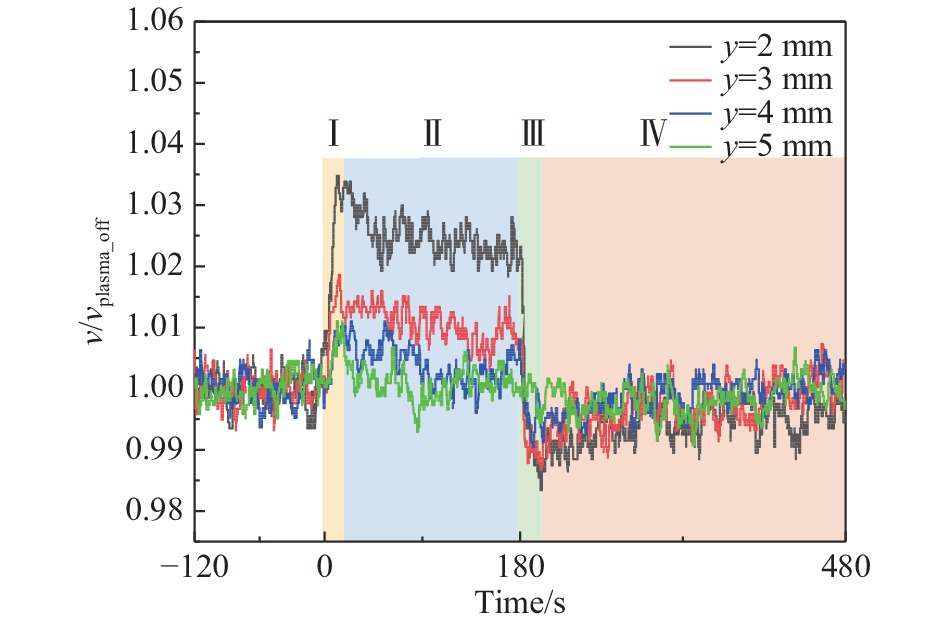
为了确定上述规律对激励后不同高度流场的适用性,针对 v∞ = 20 m/s工况,固定测量展向位置x= −20 mm、流向位置z = 5 mm,在y = 2 mm、3 mm、4 mm和5 mm共4个不同高度位置进行速度测量。以
|
图 13 不同高度下流速随时间变化图(v∞= 20 m/s) Fig.13 Time evolution of the local velocity at different wall-normal locations (v∞= 20 m/s) |
从图13中可以看到,随着高度的増加,阶段Ⅰ中瞬时速度提升减小;在扩散和黏滞效应下,阶段Ⅱ中随高度的提高激励后平衡速度相对提升量越低,且速度缓降相对幅值减小。
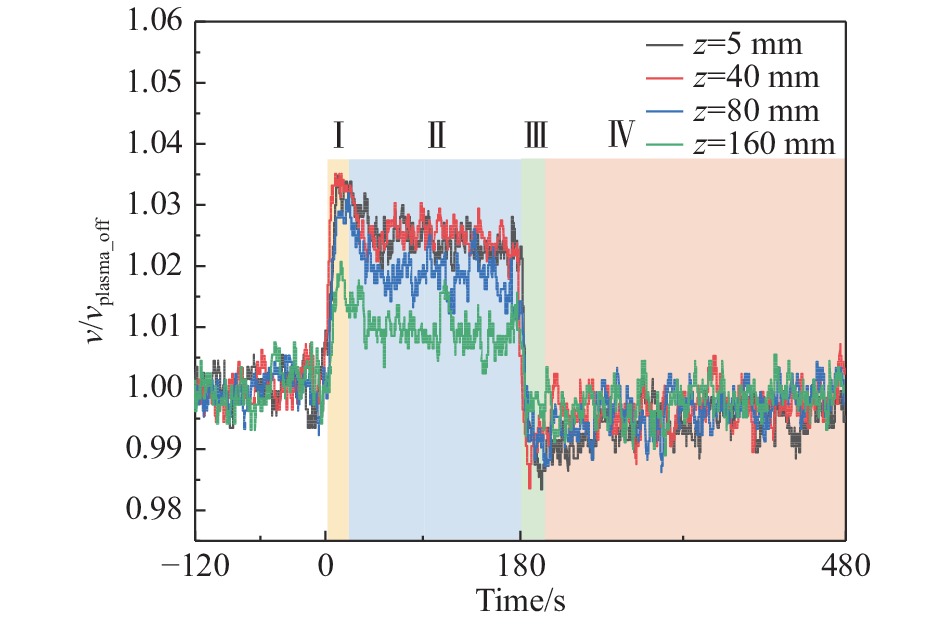
为了研究激励后不同流向位置流场速度变化规律,针对v∞ = 20 m/s工况,在固定测量展向位置x = −20 mm、高度位置y = 2 mm,在z = 5 mm、40 mm、80 mm、160 mm共4个流向位置进行速度测量。以
|
图 14 不同流向位置下流速随时间变化图(y = 2 mm) Fig.14 Time evolution of the local velocity at different streamwise locations (y= 2 mm) |
对于不同流向位置来说,激励后速度随时间变化过程同样可分成四个阶段。z ≤ 40 mm区域激励对流场加速能力基本没有衰减。当z > 40 mm后,随着流向距离的增大,激励对当地流场的影响逐渐减弱,此现象与2.1节静止工况激励后速度沿流向变化规律类似。
2.2.2 激励对流场压力的影响为了研究激励后流场总压和速度变化的关联性,以z = 5 mm流向截面为研究对象,定义速度比
| $\gamma {\rm{ = }}\frac{{{v_{{\rm{plasma\_on}}}}}}{{{v_{{\rm{plasma\_off}}}}}}$ | (3) |
| $\omega {\rm{ = }}\frac{{p_{{\rm{total\_plasma\_off}}} - {p_{{\rm{total\_plasma\_on}}}}}}{{0.5\rho {v_\infty }^2}}$ | (4) |
式中:
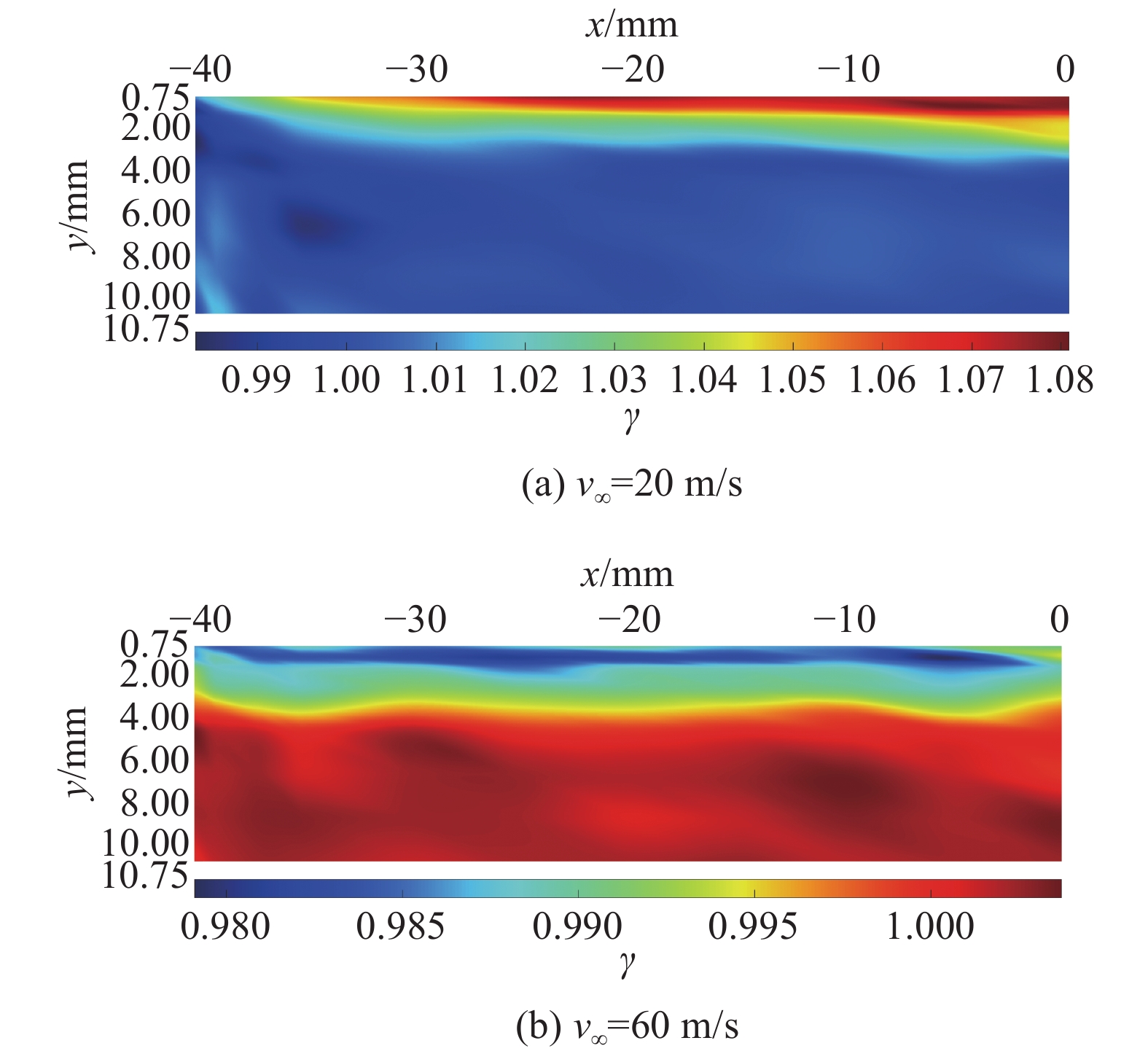
|
图 15 激励前后速度比云图对比(z= 5 mm) Fig.15 Comparison between the velocity ratio contours with and without actuation (z= 5 mm) |
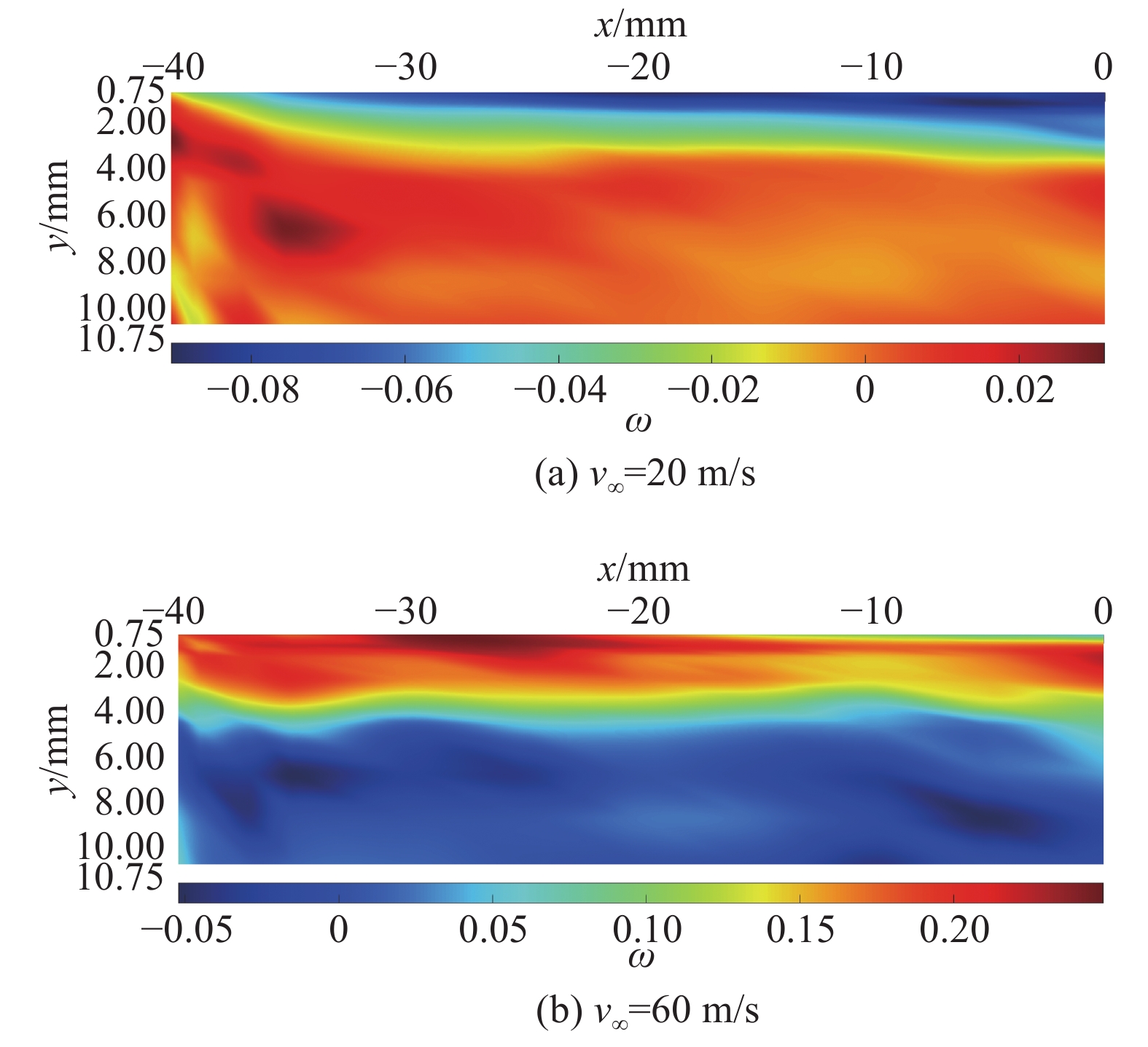
|
图 16 激励前后总压损失系数分布云图对比(z = 5 mm) Fig.16 Comparison between the total pressure loss coefficient contours with and without actuation (z= 5 mm) |
从图15可以发现,对于v∞ = 20 m/s工况来说,阵列式AC-SDBD激励对高度0.75 mm ≤ y ≤ 3 mm以内有明显的加速作用,由于角区及端壁流场影响,使得从展向位置−40 mm ≤ x ≤ −30 mm近壁加速区域范围逐渐扩大;对于v∞ = 60 m/s工况来说,激励对0.75 mm ≤ y ≤ 4 mm的流体有明显减速效应,并且随着高度的增加,减速效应逐渐减弱。
图16展现的是激励前后总压损失系数的变化云图,其中正值代表激励后总压损失增加,负值代表激励使总压恢复。通过对比图15和图16,可以发现,总压损失系数变化规律和速度比变化规律一致。以上研究表明,通过激励前后当地总压的变化能准确反应激励前后速度的变化。
为了精细化研究激励前后附面层内总压的变化,使用头部较细的附面层探针进行v∞ = 20 m/s和60 m/s两种工况的总压测量工作。测量位置为x = −20 mm、z = 5 mm,0 ≤ y≤ 10 mm,使用9 mm < y <10 mm范围内平均表总压对测得表总压进行无量纲化,具体实验结果见图17和图18。
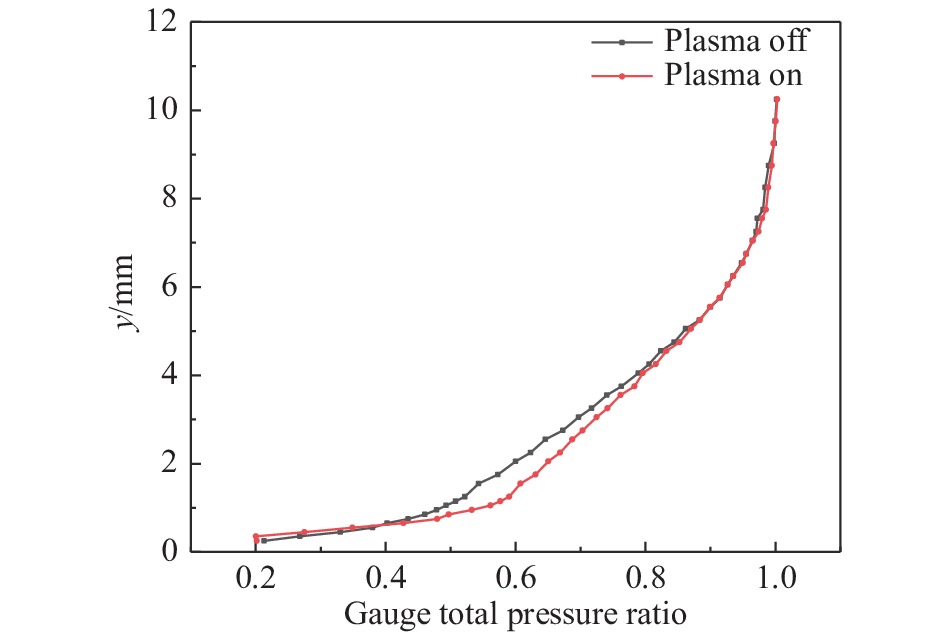
|
图 17 激励前后附面层总压分布(v∞= 20 m/s) Fig.17 Total pressure distributions in the boundary layer with and without actuation (v∞= 20 m/s) |
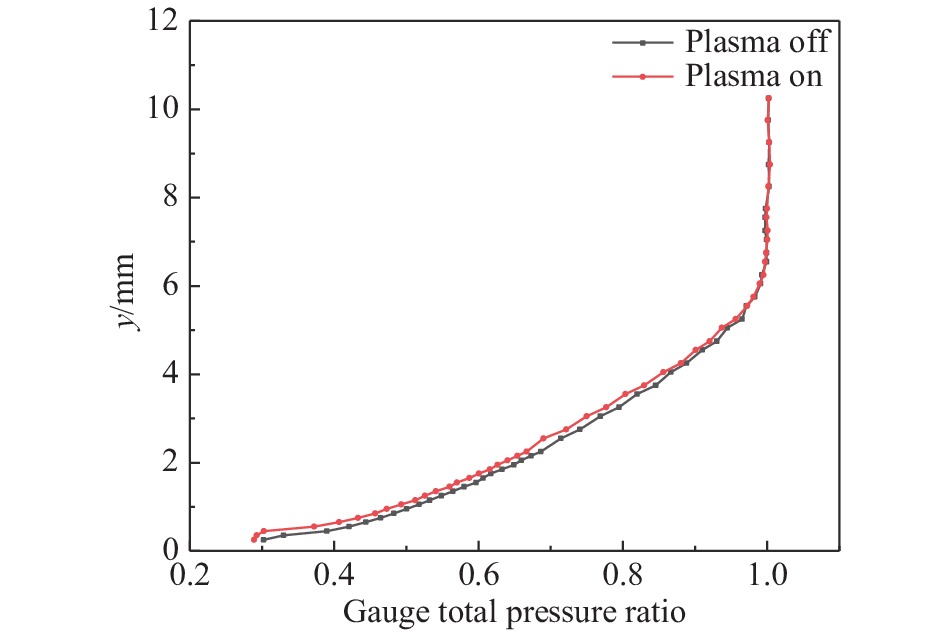
|
图 18 激励前后附面层总压分布(v∞= 60 m/s) Fig.18 Total pressure distributions in the boundary layer with and without actuation (v∞= 60 m/s) |
为了更加清晰地对比两种工况下附面层总压变化规律,使用总压恢复系数
| $\sigma {\rm{ = }}\frac{{p_{{\rm{total\_plasma\_on}}} - p_{{\rm{total\_plasma\_off}}}}}{{p_{{\rm{total}}\_\infty }}}$ | (5) |
式中:
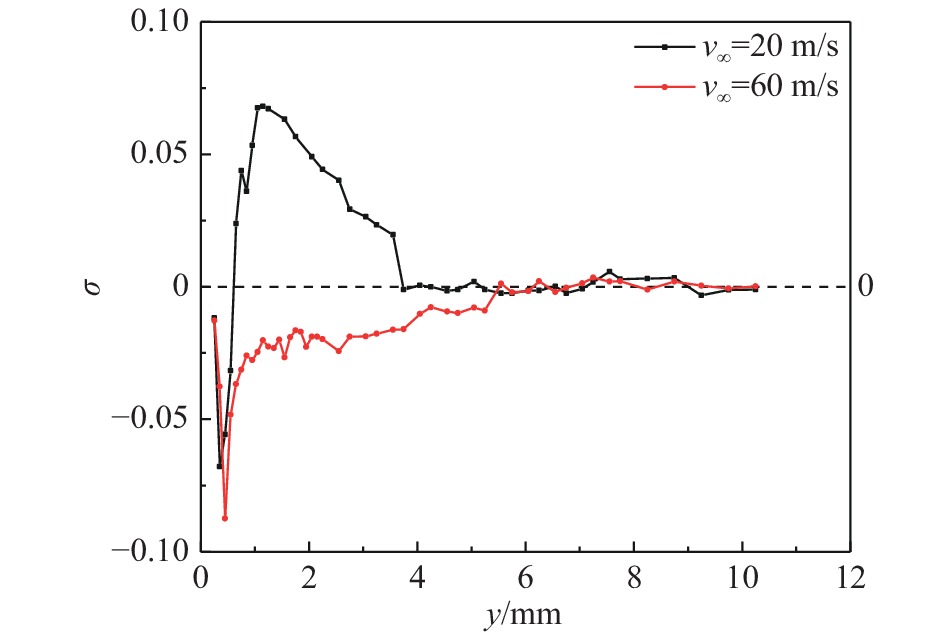
图19为主流速度对激励后附面层总压恢复系数影响曲线。v∞ = 20 m/s工况,相对于基准状态,激励后沿远离壁面方向,总压先降低,再升高,最后不变;在v∞ = 60 m/s工况下,整个附面层内总压水平均低于激励前状态。两种工况高度y≤ 0.65 mm区域内的
|
图 19 主流速度对激励后附面层总压恢复系数分布影响(z = 5 mm) Fig.19 Effect of the mainstream velocity on the total pressure recovery coefficient of the boundary layer under plasma actuation (z= 5 mm) |
由于低速来流条件下激励器向流场注入动量更多, v∞ = 20 m/s工况中
阵列式AC-SDBD激励使v∞ = 60 m/s高速工况y ≤ 6 mm区域内附面层总压降低,即减速效应,随着高度的提升,
可见,阵列式AC-SDBD激励对附面层总压的影响规律不仅和主流速度有关,与距壁面高度也有关。
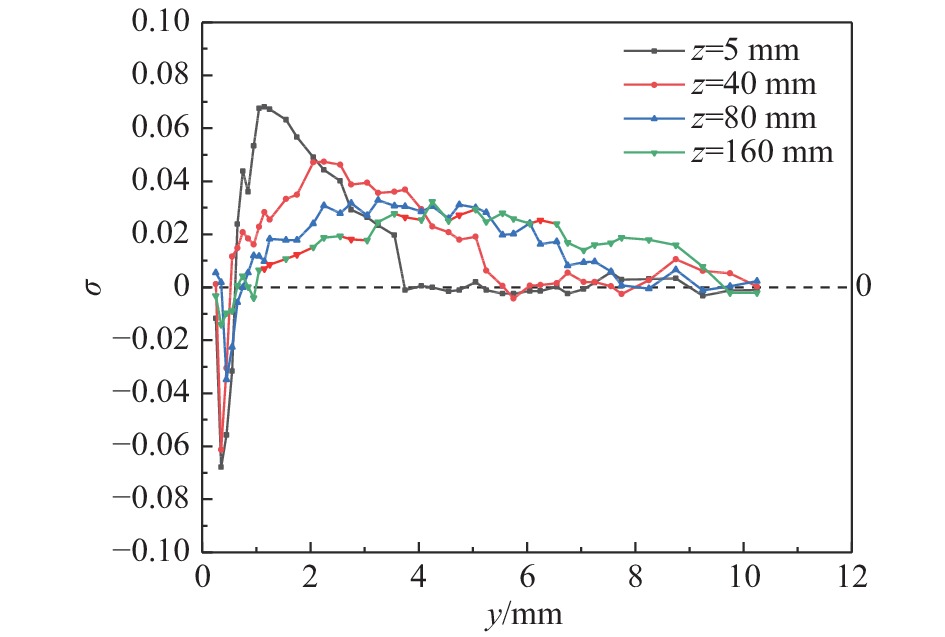
不同流向距离附面层内总压恢复系数分布如图20所示。随着流向距离的增加,由于激励产生的贴壁高能射流逐渐与附近低能流体掺混,流体加速的区域变大,使得y≤ 0.65 mm以内最低总压恢复系数逐渐恢复,附面层内最大总压恢复系数有减小趋势,且最大总压恢复系数对应的法向位置逐渐增大。在v∞ = 20 m/s工况下,激励沿法向的影响范围达到了y = 10 mm高度位置,伴随着法向影响范围扩大的同时激励对流场最大影响能力逐渐减弱。
|
图 20 激励后不同流向位置附面层总压恢复系数分布 Fig.20 Total pressure recovery coefficient of boundary layer at different streamwise locations under plasma actuation |
对v∞ = 20 m/s、30 m/s、40 m/s、60 m/s和80 m/s工况下x = −20 mm、y = 2 mm位置处激励后稳态速度场进行测量,使用相对速度提升系数
| $\Delta v = \frac{{{v_{{\rm{plasma}}\_{\rm{on}}}} - {v_{{\rm{plasma}}\_{\rm{off}}}}}}{{{v_{{\rm{plasma}}\_{\rm{off}}}}}} \times 100{\text{%}} $ | (6) |
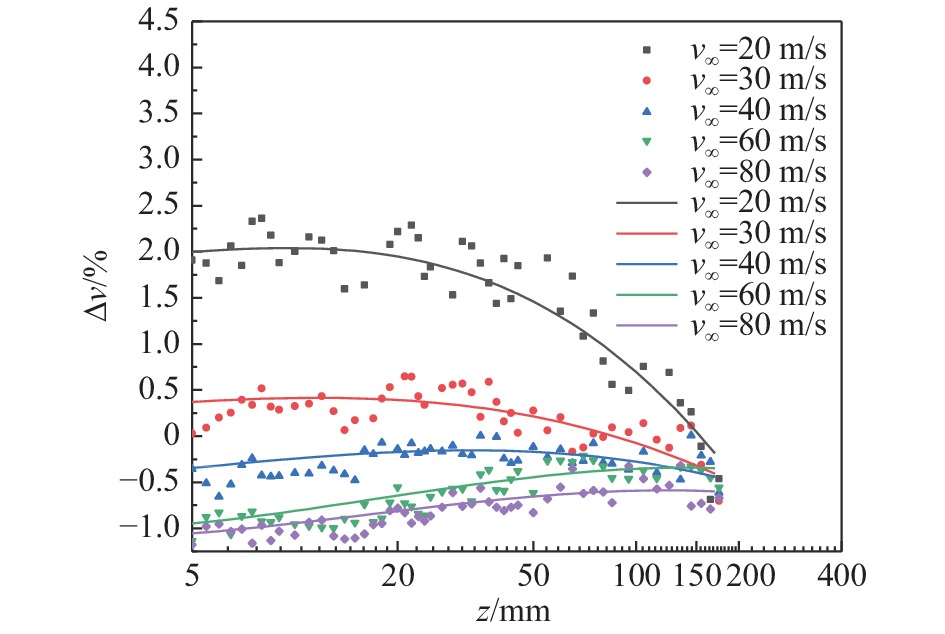
图21为不同主流速度下激励后沿流向
|
图 21 主流速度对激励后速度分布影响(y = 2 mm) Fig.21 Effect of the mainstream velocity on the velocity distribution along the streamwise direction under plasma actuation (y = 2 mm) |
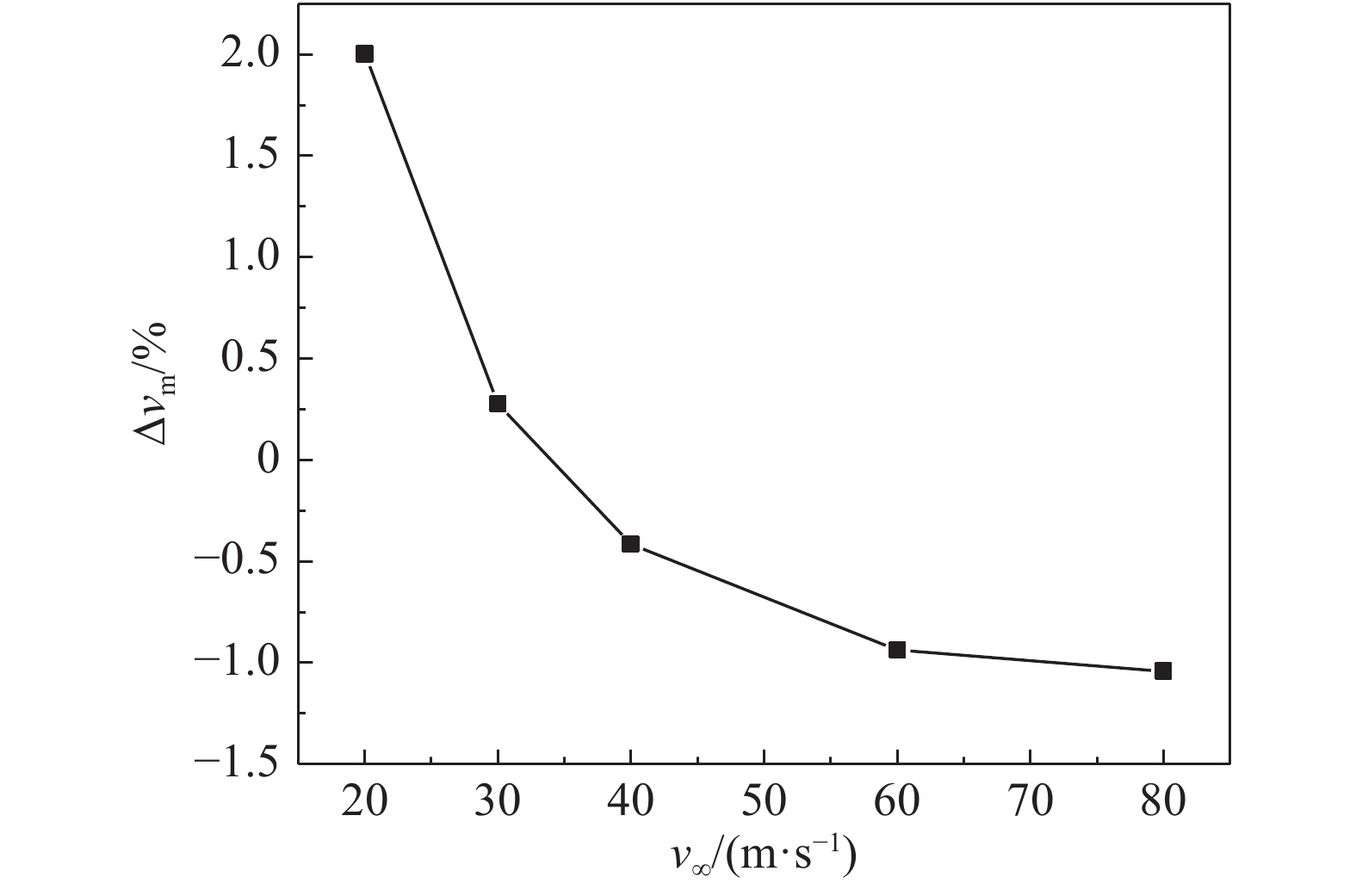
为直观比较主流速度对激励后速度分布影响,
|
图 22 激励后 |
从图22中可以看到,阵列式AC-SDBD激励对近壁流场加速能力随着主流速度的提高非线性降低,v∞ ≤ 30 m/s时,激励使得稳定后的近壁区速度增大。v∞从20 m/s提高到30 m/s过程中,
1)阵列式AC-SDBD激励诱导近壁气流加速规律与激励时间有关。在施加激励的瞬间,近壁区速度明显增大,随着时间的推移,近壁区速度有所下降,最后趋于稳定。
2)多组阵列式AC-SDBD激励器的动量效应显著,随着激励组数的增加,激励诱导近壁流场加速能力越强,且激励后近壁区速度随时间的阶段性变化规律愈发显著。
3)阵列式AC-SDBD激励对近壁流速的影响规律与距壁面高度和流向距离相关。随着距激励器流向距离的增大,激励影响流体能力逐渐减弱,在法向上受激励影响范围逐渐扩大,且受最大影响法向位置逐渐远离壁面。
4)阵列式AC-SDBD激励对近壁流速的影响规律与主流速度相关。随着主流速度的提高,阵列式AC-SDBD动量效应减弱且对近壁流场加速能力非线性降低,在主流速度从20 m/s提高到80 m/s的过程中,
| [1] |
吴云, 李应红. 等离子体流动控制研究进展与展望[J]. 航空学报, 2015, 36(2): 381-405. WU Y, LI Y H. Progress and outlook of plasma flow control[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 381-405. (in Chinese) |
| [2] |
CORKE T C, ENLOE C L, WILKINSON S P. Dielectric barrier discharge plasma actuators for flow control[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 505-529. DOI:10.1146/annurev-fluid-121108-145550 |
| [3] |
WANG J J, CHOI K S, FENG L H, et al. Recent developments in DBD plasma flow control[J]. Progress in Aerospace Sciences, 2013, 62: 52-78. DOI:10.1016/j.paerosci.2013.05.003 |
| [4] |
JIA Y H, LIANG H, HE Q K, et al. Flow separation control of nacelle in crosswind by microsecond pulsed surface dielectric barrier discharge plasma actuator[J]. Flow, Turbulence and Combustion, 2021, 1-21. DOI:10.1007/s10494-021-00247-0 |
| [5] |
KADIVAR A, AMANIFARD N, DEYLAMI H M, et al. Flow separation control in an axial compressor cascade using various arrangement of plasma actuator[J]. Journal of Electrostatics, 2021, 112: 103580. DOI:10.1016/j.elstat.2021.103580 |
| [6] |
YATES H B, MATLIS E H, JULIANO T J, et al. Plasma-actuated flow control of hypersonic crossflow-induced boundary-layer transition[J]. AIAA Journal, 2020, 58(5): 2093-2108. DOI:10.2514/1.J058981 |
| [7] |
KIM D, DO H, CHOI H. Drag reduction on a three-dimensional model vehicle using a wire-to-plate DBD plasma actuator[J]. Experiments in Fluids, 2020, 61(6): 1-14. DOI:10.1007/s00348-020-02961-3 |
| [8] |
PEREIRA GOUVEIA DA SILVA G, EGUEA J P, GARCIA CROCE J A, et al. Slat aerodynamic noise reduction using dielectric barrier discharge plasma actuators[J]. Aerospace Science and Technology, 2020, 97: 105642. DOI:10.1016/j.ast.2019.105642 |
| [9] |
THOMAS F O, KOZLOV A, CORKE T C. Plasma actuators for cylinder flow control and noise reduction[J]. AIAA Journal, 2008, 46(8): 1921-1931. DOI:10.2514/1.27821 |
| [10] |
REECE ROTH J, DAI X. Optimization of the aerodynamic plasma actuator as an electrohydrodynamic (EHD) electrical device[C]// 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2006. doi: 10.2514/6.2006-1203
|
| [11] |
YANG L L, LI J, CAI J S, et al. Lift augmentation based on flap deflection with dielectric barrier discharge plasma flow control over multi-element airfoils[J]. Journal of Fluids Engineering, 2016, 138(3): 031401. DOI:10.1115/1.4031613 |
| [12] |
ZHANG H D, WU Y, LI Y H, et al. Control of compressor tip leakage flow using plasma actuation[J]. Aerospace Science and Technology, 2019, 86: 244-255. DOI:10.1016/j.ast.2019.01.009 |
| [13] |
吴云, 张海灯, 于贤君, 等. 轴流压气机等离子体流动控制[J]. 工程热物理学报, 2017, 38(7): 1396-1414. WU Y, ZHANG H D, YU X J, et al. Plasma flow control of axial compressor[J]. Journal of Engineering Thermophysics, 2017, 38(7): 1396-1414. (in Chinese) |
| [14] |
SADDOUGHI S, BENNETT G, BOESPFLUG M, et al. Experimental investigation of tip clearance flow in a transonic compressor with and without plasma actuators[C]//Proceedings of ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany. 2014. doi: 10.1115/GT2014-25294
|
| [15] |
赵小虎, 李应红, 吴云, 等. 等离子体气动激励的加速特性研究[J]. 空气动力学学报, 2010, 28(2): 168-173, 196. ZHAO X H, LI Y H, WU Y, et al. Investigation on the acceleration characteristic by plasma aerodynamic actuation[J]. Acta Aerodynamica Sinica, 2010, 28(2): 168-173, 196. DOI:10.3969/j.issn.0258-1825.2010.02.008 (in Chinese) |
| [16] |
CHERNYSHEV S L, GAMIRULLIN M D, KURYACHII A P, et al. Simple design of multiple aerodynamic plasma actuator[C]// Progress in Flight Physics, Krakow, Poland. Les Ulis, France: EDP Sciences, 2017. doi: 10.1051/eucass/2016090253
|
| [17] |
GAMIRULLIN M D, KURYACHII A P, LITVINOV V M, et al. Investigation of a simplified scheme of multiple plasma actuator for boundary layer control[J]. TsAGI Science Journal, 2014, 45(8): 889-901. DOI:10.1615/tsagiscij.2015013547 |
| [18] |
SATO S, OZAWA Y, KOMURO A, et al. Experimental demonstration of low-voltage operated dielectric barrier discharge plasma actuators using SiC MOSFETs[J]. Journal of Physics D: Applied Physics, 2020, 53(43): 43LT01. DOI:10.1088/1361-6463/aba0e1 |
 2022, Vol. 40
2022, Vol. 40


