2. 南方科技大学 复杂流动及软物质研究中心,深圳 518055
2. Center for Complex Flows and Soft Matter Research, Southern University of Science and Technology, Shenzhen 518055, China
湍流广泛存在于各种自然现象和工程应用当中。由于其多尺度耦合、强非线性、强非平衡等复杂特性,关于湍流的研究充满了挑战。其中一个焦点是如何通过准确便捷的速度场测量,来同时获取湍流系统中的大尺度流动结构和小尺度统计特性,这对于理解湍流的能量级串过程,即能量如何在大、小尺度流动结构之间传递并最终耗散,有着重要的意义[1]。因此,研究人员一直在探索并发展着各种流体测速技术方法。
目前最为盛行的流体测速技术是粒子成像测速技术(particle image velocimetry,PIV)[2-3]。自20世纪90 年代[4]以来,尽管PIV 在硬件和软件上都得到了显著的发展,但该技术在实际应用中依然存在许多局限,例如无法有效地分辨小尺度流动结构,也很难准确地计算与强速度梯度相关的物理量等[5-6]。这些局限的根本原因在于,PIV并非直接测量流体速度,而是基于一定大小的问询域内一定数量的示踪粒子运动,通过计算相邻两张粒子图像在傅里叶空间的相关性来获得相应问询域内的流体速度。因此,PIV速度场的准确性和空间分辨率会受限于示踪粒子浓度尤其是问询域的大小(通常不小于16 pixel × 16 pixel)。尽管研究人员提出了各种办法来解决这个困难,包括亚像素插值、多网格迭代、可变形问询域等,这一由算法原理本身决定的困难依然被认为是PIV的重要挑战[7-8]。在实际应用中,为了同时获得大、小尺度流动特性,研究人员一般会采用多台相机进行全场和局部场的同步拍摄,而这对实验硬件以及大量数据的存储和后期分析提出了较高的要求。所以,PIV 在同时测量大尺度流动结构和小尺度统计特性方面并不实用。
另一方面,光流测速法(optical flow velocimetry,OFV)在进行超高空间分辨率的大区域速度场测量上具有天然的优势[9]。该方法起源于计算机视觉领域,Horn和Schunck[10]基于连续图像光强不变的假设,提出了图像光强亮度限制方程以及相应的变分方程,从而将连续图像中刚体运动的速度与光流建立了联系。随后,研究人员采用不同的光流限制方程对OFV进行了完善[11-12]。由于OFV获得的速度场分辨率与图像分辨率一致(即单像素分辨率),所以该方法早年也曾被尝试用于处理PIV的粒子图像,以期获得高分辨的速度场[13-15]。然而,不同于刚体运动,流体运动遵循Navier-Stokes方程,而上述的光强限制方程并未考虑流体问题的实际背景,所以光流与流场之间的关联缺乏合理的物理依据。因此,早期的OFV在流体力学领域并未得到关注。
为了解决OFV存在的非物理问题,Liu等[16-18]通过一系列的理论推导和实验工作,成功地建立了光流与实际流体运动间的定量联系,并给出了明确的误差分析。鉴于OFV在获取流体速度上有了物理基础,这个方法逐渐引起了流体力学领域的关注[9]。相比于PIV,OFV可以处理的图像种类非常丰富,除了粒子图像,还包括阴影图和纹影图[16,19],甚至是卫星云图[20-21]。需要特别指出的是,阴影图(纹影图)等图像实质上是光强变化在投影方向上路径积分的结果,所以这类图像通过OFV得到的结果一般只能做定性或半定量的分析。虽然粒子图像可以用OFV进行定量分析,但当粒子浓度不够高或在相邻两帧图像中的位移过大时,光流方程中的光强时间导数通常难以准确获得[16],从而无法给出准确的流体速度场。
注意到用于PIV的互相关算法对一定范围内的粒子浓度和位移大小并不敏感,Liu和Shen认为可以发展一种兼容PIV和OFV优势的混合测速法[16]。这个提议近年来被Yang 等[22]和Liu等[23-24]先后独立实现,在此称之为基于互相关的光流测速法(cross-correlation based optical flow velocimetry,cOFV)。简单地说,cOFV首先利用互相关算法处理粒子图像,然后将获得的粗粒化速度场作为初始约束,最后通过光流法给出高分辨率的速度场(见图1)。可见,cOFV兼容了PIV的准确性和OFV的高分辨率,具备同时准确测量大、小尺度流动特性的可能性。类似的思路和方法在近年来的其他一些工作亦有体现[25-28],但大多数工作都只关注这类方法与传统方法在获取流场结构及速度分布上的比较,很少有研究对其获取小尺度统计特性的准确性进行仔细检验。
本文选取Rayleigh-Bénard(RB)对流作为测试系统,考察cOFV在同时测量大尺度流场结构和小尺度湍流统计特性上的有效性和准确性。RB对流是通过对系统上、下边界施加温差而驱动流体运动的理想系统。作为一个边界条件明确的封闭系统,RB对流不仅在实验和数值模拟上容易实现和控制,而且兼具壁湍流和各向同性湍流的特性,因此经常被用于研究热对流现象和湍流的基本机理[29-31]。此外,RB对流内部的能量耗散率与系统的控制参数有明确的标度关系[32],这为进行理论或技术方法的定量检验提供了可靠的参考标准。事实上,目前关于RB对流的主流理论[33]的一个重要假设,就是系统内部中央区域的能量是由大尺度流动结构注入并最终耗散。为了验证这个假设,就必须同时测量大、小尺度的流动统计特性。这也是我们选取RB对流作为测试系统考察cOFV的主要动机。
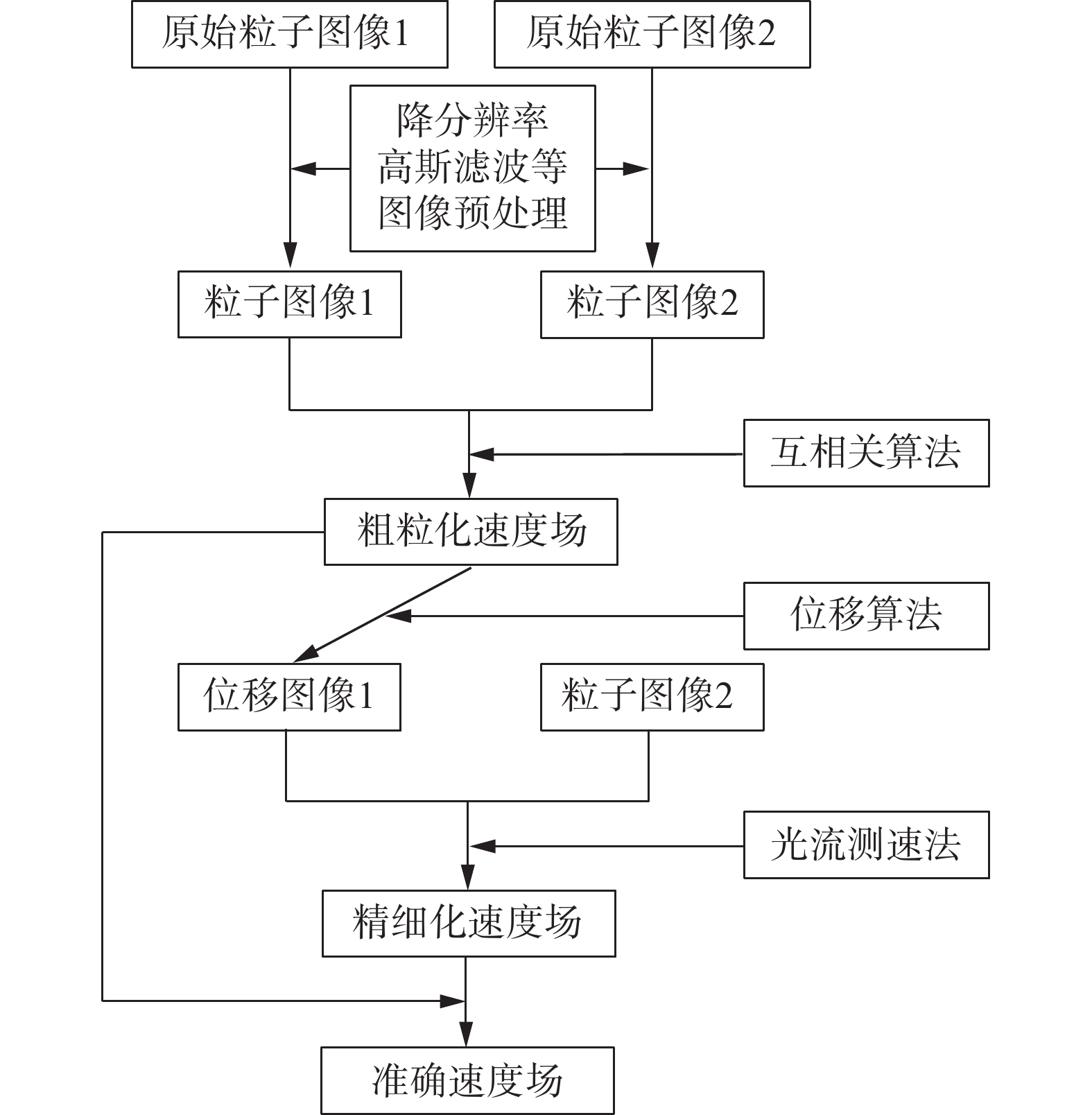
|
图 1 cOFV的分析流程图 Fig.1 Flow chart of cOFV |
本文往后章节的结构如下:我们先介绍本工作中所采用的RB对流实验装置、测量技术、以及cOFV的原理和数据处理流程;然后展示基于cOFV得到的平均场和流动强度,并与PIV的结果进行比较;最后展示通过cOFV得到的速度结构函数和能量耗散率,并进行讨论和总结。
1 实验装置和技术方法 1.1 实验装置和测量技术本研究采用的对流槽与Li等[34]所使用的几乎相同,是一个长宽高(对应笛卡尔坐标系下的x、y、z三个方向)分别为L = 25.1 cm、D= 7.6 cm、H = 24.8 cm的窄方腔对流槽。由于cOFV对光强变化十分敏感,所以对流槽的导热铜板表面被均匀地喷涂上了一薄层黑色的铁氟龙,用以避免表面反光带来的影响。同时,为了减小周围环境的影响,整个对流槽放置在温度变化小于0.1℃的恒温箱中。RB 对流的系统控制参数为衡量浮力驱动强度的Rayleigh数(Ra = αgΔTH3/υκ)及反映工作流体物性的Prandtl数(Pr = υ/κ),其中g是重力加速度,ΔT是系统上、下边界的温差,α、υ和κ分别是流体的热膨胀系数、运动黏度和热扩散率。在本实验中,Ra数的范围是9.5×108 ≤ Ra ≤ 4.1×109,而Pr数保持不变为5.4。
本实验获取粒子图像的方法与标准的PIV技术一致,在此仅作简要介绍。我们首先将直径为50 μm、密度为1.03 g/cm3 的示踪粒子(斯托克斯数
由于PIV技术已经非常成熟,所以在此不作赘述,我们主要介绍cOFV的方法原理。Liu等[17]曾定量给出OFV应用于粒子图像的误差来源,主要包括粒子位移、粒子直径、粒子速度梯度和粒子光照强度。其中,粒子位移与总误差成正比,且存在一个使总误差最小的最佳光强。该误差分析同样适用于cOFV[24]。据此,我们在使用cOFV分析粒子图像之前,首先通过降采样将初始粒子图像缩小为原来的一半,从而尽可能降低粒子位移带来的影响。此外,考虑到相邻两帧粒子图像之间的光强可能存在变化,我们先将二者的平均光强提升(或降低)至相同值,以此控制总体光强不变,再通过高斯滤波使局部光强的变化更为平滑。这些图像处理可以极大地降低误差,提高结果的可信度。
cOFV的分析流程如图1所示[23]。在完成原始粒子图像的预处理之后,我们先采用开源程序PIVlab[37]的互相关算法,获取粗粒化速度场。基于此粗粒化速度场,我们通过位移算法(空间插值)获得粒子图像1的位移图像1。鉴于重构后的位移图像1与粒子图像2之间的粒子位移已经足够小,我们便可以应用OFV计算二者之间的精细化速度场。为求解光流方程,本文采用Horn-Schunck估计[10]作为初始解,然后借鉴Liu-Shen估计[16, 18]计算精细解。最终获得的准确速度场是空间插值后的粗粒化速度场与OFV输出的精细化速度场的叠加。区别于Yang等的cOFV[22],本文的cOFV包含了迭代过程。通常情况下,一次迭代足以获得准确的速度场[23]。
2 结果与讨论 2.1 平均流场和Reynolds数我们首先对比cOFV和PIV获得的平均速度场(图2,Ra = 2.0×109)。两种方法均能清晰地观察到RB对流的典型流态[38]:一个呈椭圆形状的大尺度结构和两个反向的角涡。从云图的颜色分布及色标范围来看,两种方法得到的速度分布和大小基本一致,最大速度的差别仅为2%(如图2各子图中的色标最大值所示)。鉴于PIV在测量速度场上的应用十分广泛,而且认可度高,这些半定性半定量的比较在一定程度上说明了cOFV的可靠性。这一结论和之前的研究一致[22-23, 25, 27]。
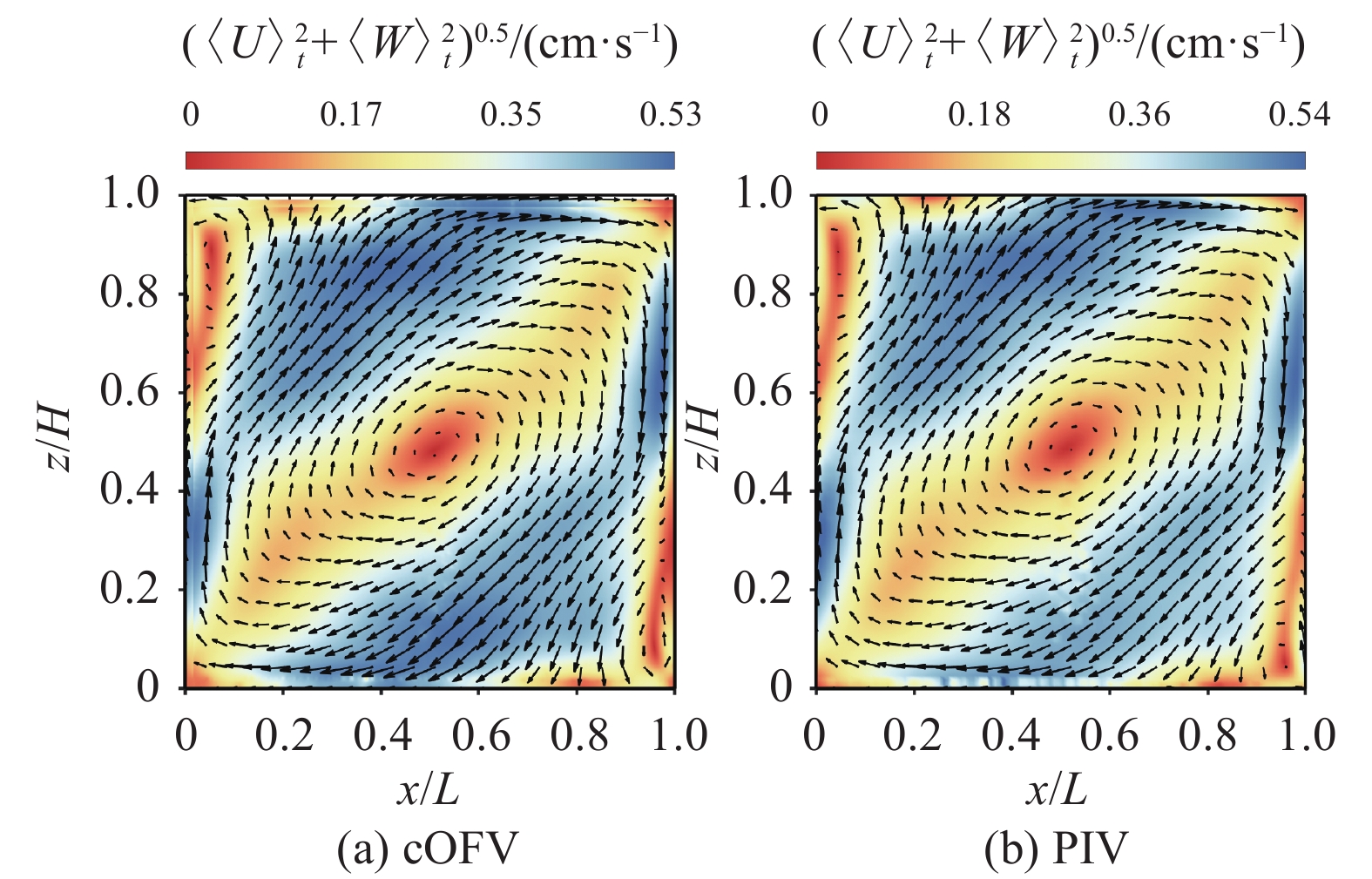
|
图 2 Ra = 2.0×109下的平均速度场 Fig.2 Time-averaged velocity fields at Ra = 2.0 × 109 注:图中的速度及其大小分别通过矢量和背景颜色表示。 |
为了定量比较cOFV和PIV在获取平均场以及瞬时场上的区别,我们考察反映流动强度的Reynolds数,即Re = VH/υ,其中V为系统内部流动的特征速度。对于平均场,选取速度最大值
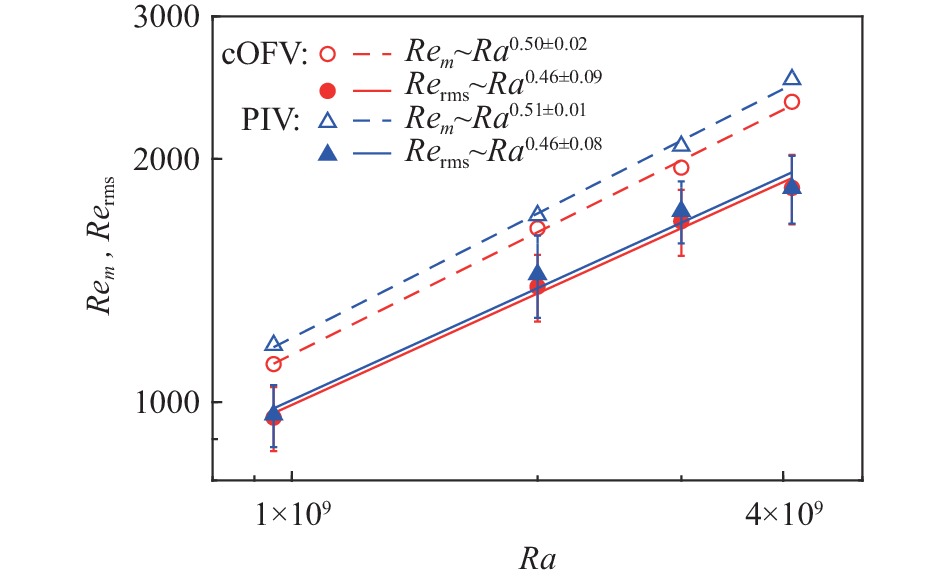
|
图 3 Re数与Ra数的依赖关系 Fig.3 Log-log plot of Re as a function of Ra |
为了验证cOFV获取小尺度统计量的准确性,我们考察二阶速度结构函数在湍流耗散区的行为。前人研究表明[35, 42-44],RB对流中央区域的流动统计特性与均匀各向同性湍流相符。对于均匀各向同性湍流,其二阶纵向速度结构函数DLL和横向速度结构函数DNN在湍流耗散区满足以下关系:
| $ D_{LL}/r^{2} = D_{NN}/(2r^{2}) =\left\langle \varepsilon \right\rangle /(15\upsilon) $ | (1) |
其中r为空间两点的间隔尺度,
我们首先比较基于cOFV和PIV获得的二阶速度结构函数(Ra = 2.0×109)。图4展示了根据公式(1)进行数据补偿后的结果,其中横坐标采用Kolmogorov尺度ηc = υ0.75/(
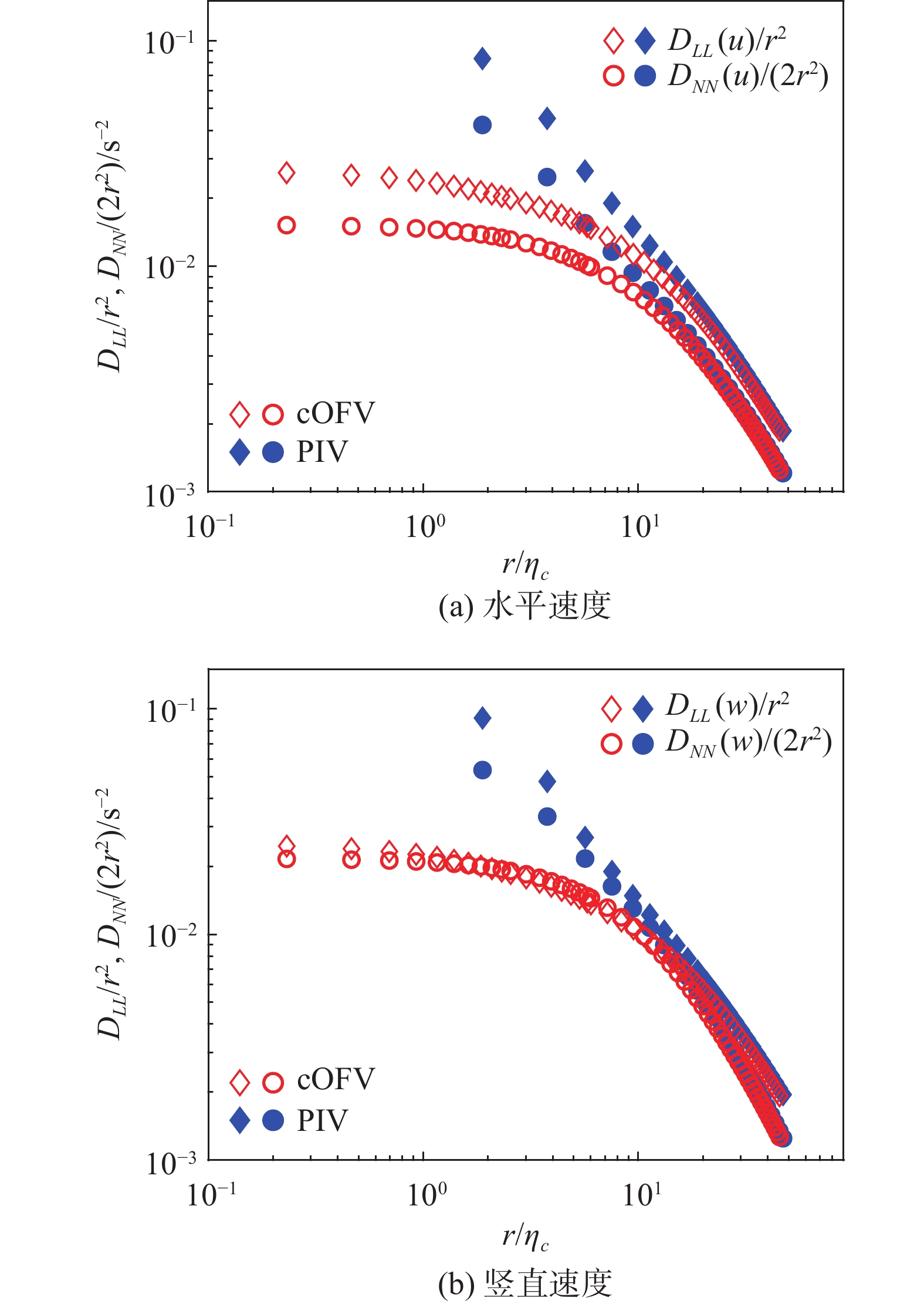
|
图 4 Ra = 2.0×109下二阶速度结构函数 Fig.4 Second-order velocity structure functions at Ra = 2.0×109 |
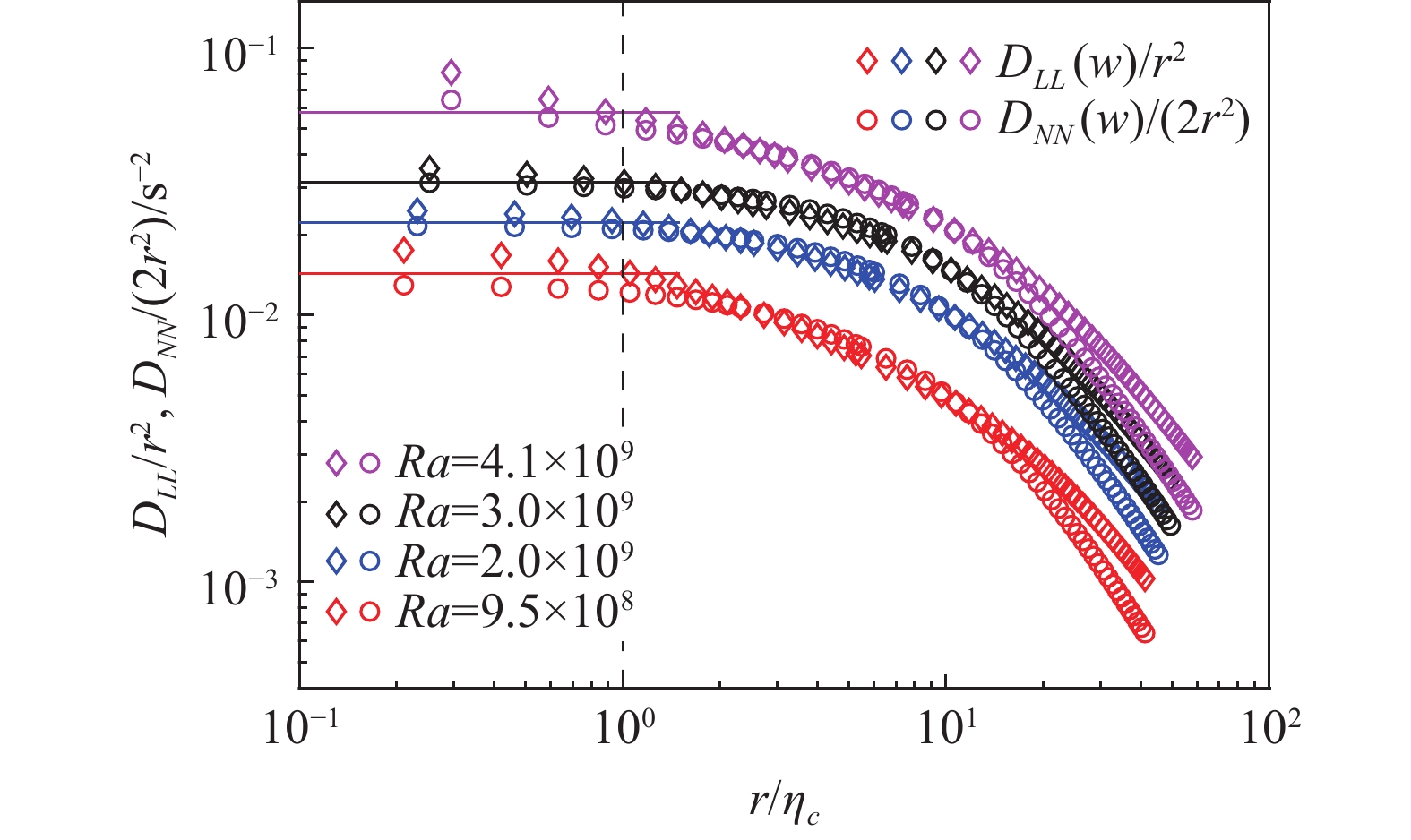
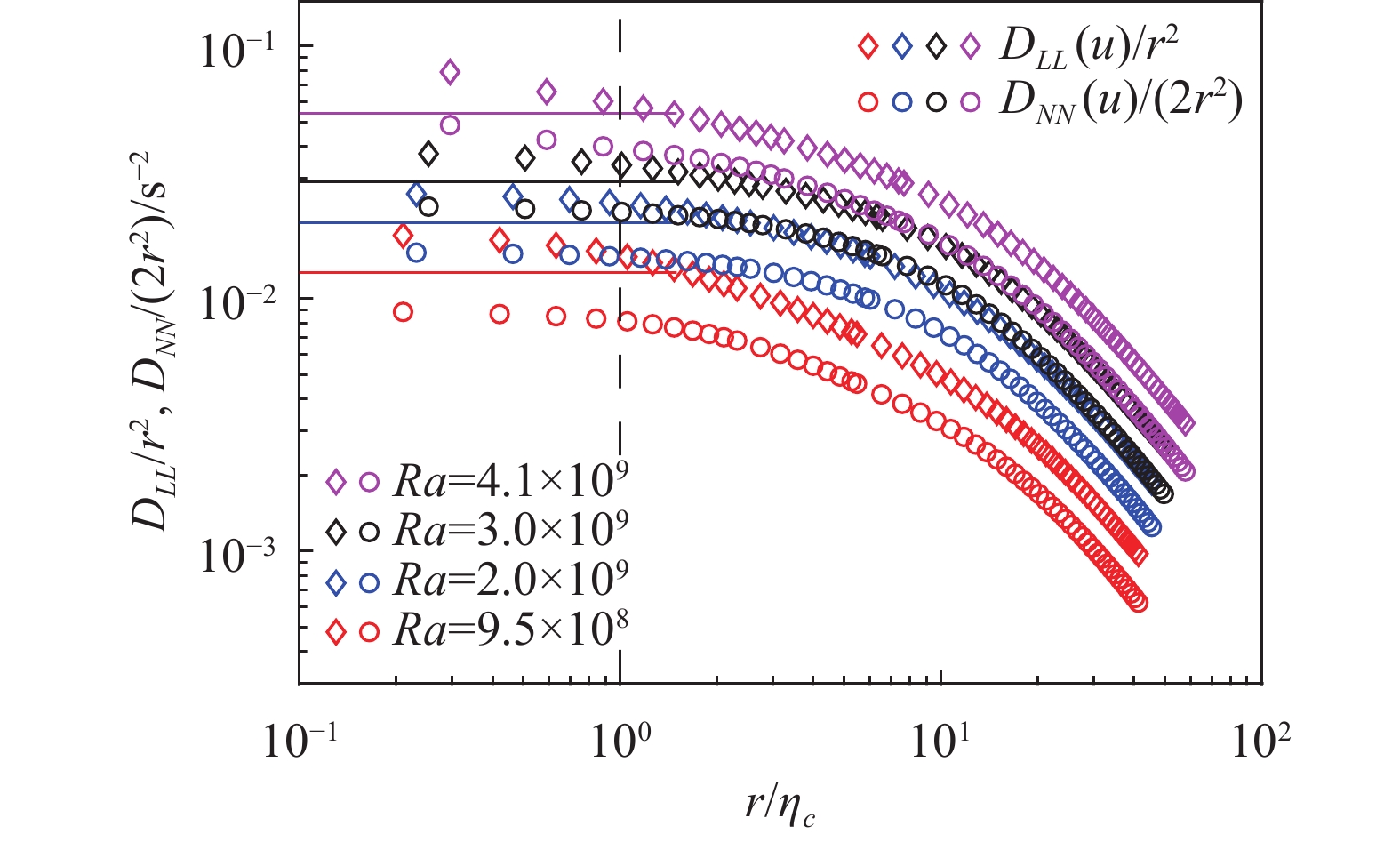
图5和图6分别展示了cOFV获得的不同Ra数下竖直和水平速度的二阶速度结构函数。这些结果也按图4的方式进行了补偿和无量纲化处理。从结构函数的形态上看,D [w(r)] 和D [u(r)]在Kolmogorov尺度以下都存在一定的“平台”,但不同于D [w(r)] 的纵向和横向分量在湍流耗散区几乎重合,D [u(r)]的两个分量有一定程度的错开。这说明在本实验装置中,中央区域的竖直脉动速度更接近均匀各向同性湍流的特性,而水平脉动速度则有可能受到了窄方腔对流槽的空间约束的影响[45]。尽管如此,我们依然可以结合公式(1),通过耗散区的“平台”(如图5和图6中的水平实线所示,其中图6的水平实线是相同Ra数下纵向和横向结构函数对应“平台”的平均)获得相应的平均能量耗散率
|
图 5 不同Ra数下竖直速度二阶结构函数与r的依赖关系 Fig.5 Log-log plot of second-order structure functions of vertical velocity versus r for different Ra |
|
图 6 不同Ra数下水平速度二阶结构函数与r的依赖关系 Fig.6 Log-log plot of second-order structure functions of horizontal velocity versus r for different Ra |
另一方面,我们也可以根据定义直接计算能量耗散率,并和基于速度结构函数获得的能量耗散率进行对比验证。考虑到本实验中获得的速度场是一个二维场,所以我们需要通过现有的二维数据重构出三维的耗散场。为此,我们借鉴Doron等[46]和Luznik等[47]的做法,假设三维耗散场中缺失的项与二维耗散场中对应的项相近,由此得到的能量耗散率重构公式如下:
| $ \begin{split} {\langle \varepsilon \rangle _D} =& \nu \left\langle {4{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + 4{{\left( {\frac{{\partial w}}{{\partial z}}} \right)}^2} + 3{{\left( {\frac{{\partial u}}{{\partial z}}} \right)}^2} + 3{{\left( {\frac{{\partial w}}{{\partial x}}} \right)}^2}} \right\rangle + \\& \nu \left\langle {4\left( {\frac{{\partial u}}{{\partial x}}\frac{{\partial w}}{{\partial z}}} \right) + 6\left( {\frac{{\partial u}}{{\partial z}}\frac{{\partial w}}{{\partial x}}} \right)} \right\rangle \end{split} $ | (2) |
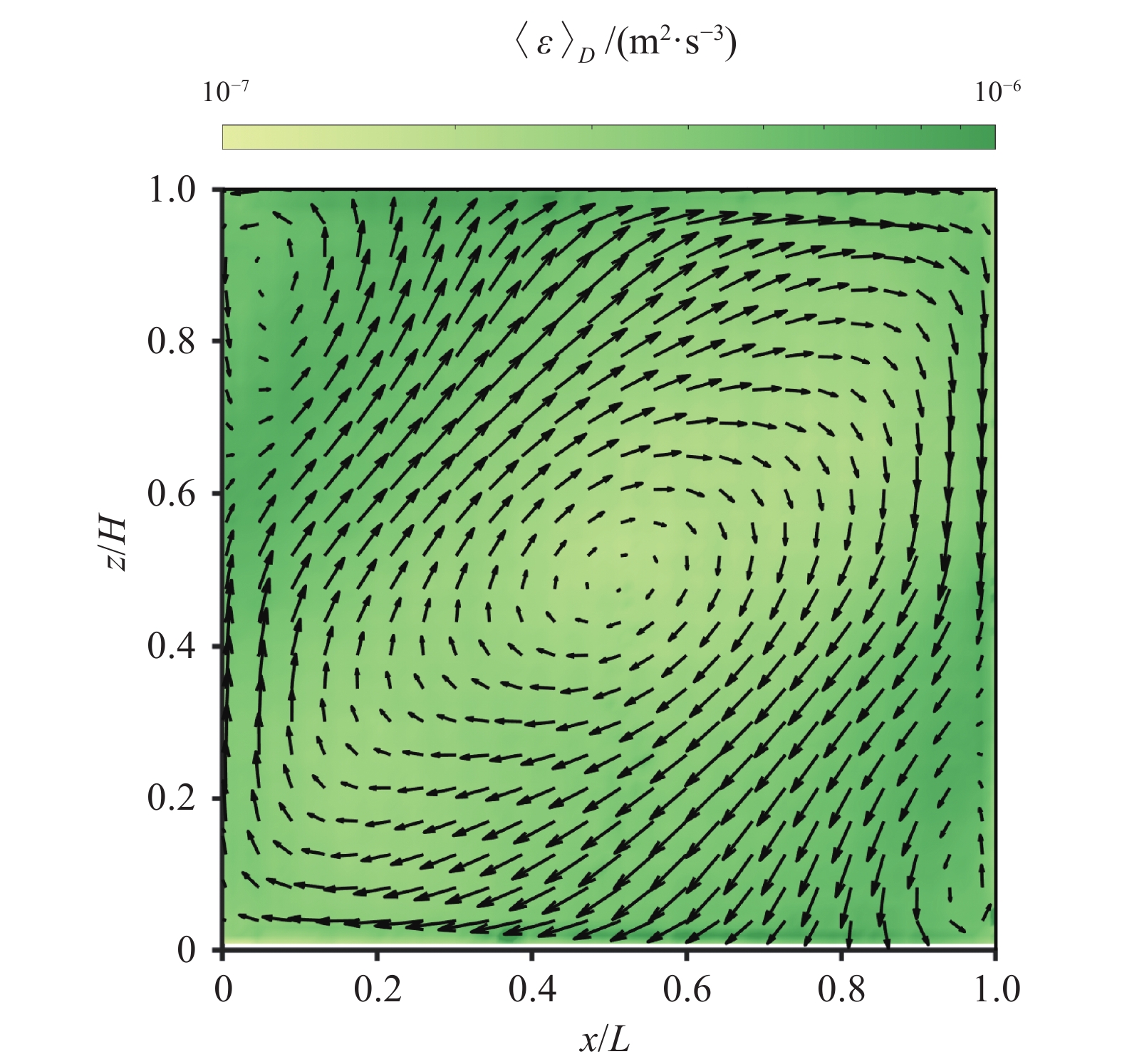
图7展示了通过公式(2)重构的能量耗散率场(Ra = 2.0×109)。根据叠加的平均速度场,我们可以看到中央区域的能量耗散率明显小于靠近边界区域的强度,且耗散率较大的地方主要集中在大尺度流动结构即剪切较强的区域。需要指出的是,由于RB系统在边界附近存在强烈的温度涨落,其引起的局部光强不均匀使得相应区域的光折射率变化极大,进而导致局部光强非常不均匀。而cOFV对光强的变化十分敏感,在计算边界附近的速度场尤其是速度梯度时会存在较大误差。为了避免边界效应带来的影响,下文只对RB系统中央区域(即远离边界处)的能量耗散率进行定量分析。
|
图 7 Ra = 2.0×109下的能量耗散率场 Fig.7 The reconstructed energy dissipation field at Ra = 2.0×109 注:图中的速度矢量为平均速度场。 |
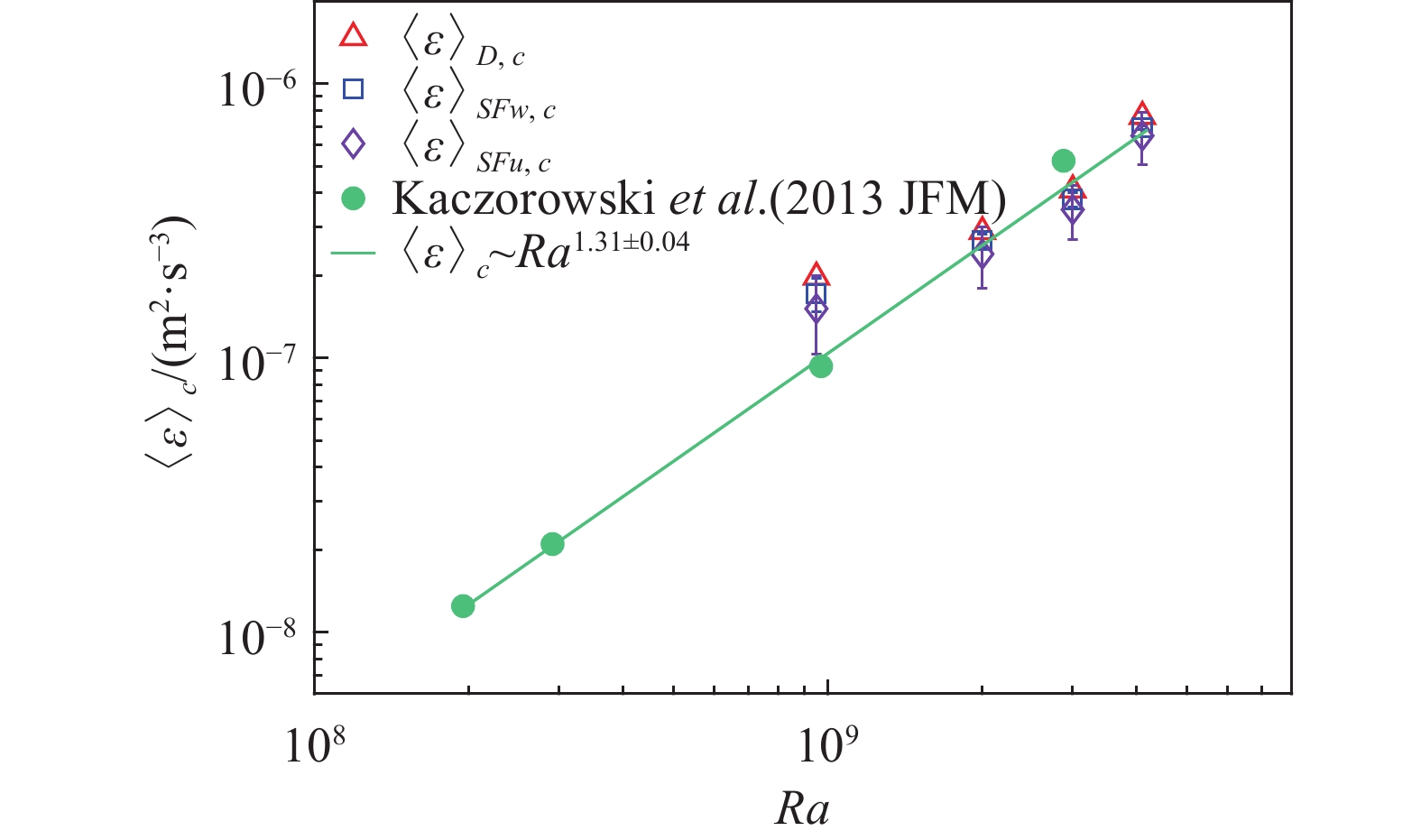
根据重构后的能量耗散场,我们便可以得到中央区域的平均能量耗散率
为了检验这些实验结果的正确性,我们选取对流槽几何参数与本研究接近的直接数值模拟的结果[44]一起画在图8中作为参考标准。需要指出的是,对于RB对流这类封闭系统,系统的能量耗散率和传热效率有明确的对应关系,而能量耗散率的空间分布则和大尺度流动结构有关。以往的研究[44-45,48-49]表明,RB系统在窄方腔和立方体对流槽中的传热效率基本相同,大尺度流动结构也非常相似,并没有表现出明显的空间约束效应。因此,采用立方体RB系统的数值模拟结果进行对比,具有合理性。可以看到,本研究的实验结果和数值结果符合得很好,除了Ra = 9.5×108那组数据有所偏离。可能原因是对于这个Ra数,统一选取的中央区域(0.25 ≤ x/L ≤0.75,0.25 ≤z/H ≤ 0.75)偏大,导致部分大尺度流动结构亦有贡献。如果对图8中的结果进行拟合,我们得到的标度关系为
|
图 8 中央区域的平均能量耗散率与Ra数的依赖关系 Fig.8 The energy dissipation rate in the central region as a function of Ra |
本文采用基于互相关的光流测速法(cOFV),对窄方腔RB对流系统中的大尺度流动结构和小尺度湍流统计特性进行了同时测量和研究。实验中的Pr数保持不变为5.4,Ra数的变化范围是9.5×108 ≤ Ra ≤ 4.1×109,主要结果如下:
1)在大尺度流动结构方面,cOFV与PIV给出的流场形态相同。定量地,两种测速方法给出的流场强度互相吻合,其中基于均方根速度定义的Rerms数无论在数值大小还是与Ra数的标度关系上都完全一致,相应的标度指数也与前人的实验和理论工作相符合。这些结果表明,cOFV在测量全局场上具备与PIV技术同等的能力。
2)为了探究cOFV在测量小尺度湍流统计量上的准确性,我们考察了RB系统中央区域的速度结构函数和能量耗散率。我们根据均匀各向同性湍流在耗散区的特性,通过二阶速度结构函数间接得到了能量耗散率,并与根据定义直接计算获得的能量耗散率进行对比,发现二者和已有的直接数值模拟结果相吻合,且它们与Ra数的标度关系也和主流理论预测一致。
这些结果表明基于互相关的光流测速法在同时测量大、小尺度流动特性上有很好的应用潜力。我们今后将会把此方法应用到其它湍流系统中,通过把不同尺度的流动结构和能量耗散率的空间分布建立关联,来检验湍流理论的一些重要假设[1]。
致谢:感谢刘天舒教授把基于互相关的光流测速法介绍给我们,并提供了开源程序(
| [1] |
MONIN A S, YAGLOM A M. Statistical fluid mechanics: Mechanics of turbulence, vol. 2[M]. Cambridge: The MIT Press, 1975.
|
| [2] |
ADRIAN R J, WESTERWEEL J. Particle image velocimetry[M]. Cambridge: Cambridge University Press, 2011.
|
| [3] |
RAFFEL M, WILLERT C E, SCARANO F, et al. Particle image velocimetry: A practical guide[M]. 3rd ed. Berlin: Springer, 2018.
|
| [4] |
ADRIAN R J. Particle-imaging techniques for experimental fluid mechanics[J]. Annual Review of Fluid Mechanics, 1991, 23: 261-304. DOI:10.1146/annurev.fl.23.010191.001401 |
| [5] |
WANG F, HUANG S D, ZHOU S Q, et al. Laboratory simulation of the geothermal heating effects on ocean overturning circulation[J]. Journal of Geophysical Research:Oceans, 2016, 121(10): 7589-7598. DOI:10.1002/2016JC012068 |
| [6] |
WANG F, HUANG S D, XIA K Q. Contribution of surface thermal forcing to mixing in the ocean[J]. Journal of Geophysical Research:Oceans, 2018, 123(2): 855-863. DOI:10.1002/2017JC013578 |
| [7] |
STANISLAS M, OKAMOTO K, KÄHLER C J, et al. Main results of the third international PIV Challenge[J]. Experiments in Fluids, 2008, 45(1): 27-71. DOI:10.1007/s00348-008-0462-z |
| [8] |
KÄHLER C J, ASTARITA T, VLACHOS P P, et al. Main results of the 4th international PIV challenge[J]. Experiments in Fluids, 2016, 57(6): 1-71. DOI:10.1007/s00348-016-2173-1 |
| [9] |
MENDES L P N, RICARDO A M C, BERNARDINO A J M, et al. A comparative study of optical flow methods for fluid mechanics[J]. Experiments in Fluids, 2021, 63(1): 1-26. DOI:10.1007/s00348-021-03357-7 |
| [10] |
HORN B K P, SCHUNCK B G. Determining optical flow[J]. Artificial Intelligence, 1981, 17(1-3): 185-203. DOI:10.1016/0004-3702(81)90024-2 |
| [11] |
BARRON J L, FLEET D J, BEAUCHEMIN S S. Performance of optical flow techniques[J]. International Journal of Computer Vision, 1994, 12(1): 43-77. DOI:10.1007/BF01420984 |
| [12] |
HAUSSECKER H W, FLEET D J. Computing optical flow with physical models of brightness variation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(6): 661-673. DOI:10.1109/34.927465 |
| [13] |
QUÉNOT G M, PAKLEZA J, KOWALEWSKI T A. Particle image velocimetry with optical flow[J]. Experiments in Fluids, 1998, 25(3): 177-189. DOI:10.1007/s003480050222 |
| [14] |
RUHNAU P, KOHLBERGER T, SCHNÖRR C, et al. Variational optical flow estimation for particle image velocimetry[J]. Experiments in Fluids, 2005, 38(1): 21-32. DOI:10.1007/s00348-004-0880-5 |
| [15] |
CORPETTI T, HEITZ D, ARROYO G, et al. Fluid experimental flow estimation based on an optical-flow scheme[J]. Experiments in Fluids, 2006, 40(1): 80-97. DOI:10.1007/s00348-005-0048-y |
| [16] |
LIU T S, SHEN L X. Fluid flow and optical flow[J]. Journal of Fluid Mechanics, 2008, 614: 253-291. DOI:10.1017/s0022112008003273 |
| [17] |
LIU T S, MERAT A, MAKHMALBAF M H M, et al. Comparison between optical flow and cross-correlation methods for extraction of velocity fields from particle images[J]. Experiments in Fluids, 2015, 56(8): 1-23. DOI:10.1007/s00348-015-2036-1 |
| [18] |
WANG B, CAI Z M, SHEN L X, et al. An analysis of physics-based optical flow[J]. Journal of Computational and Applied Mathematics, 2015, 276: 62-80. DOI:10.1016/j.cam.2014.08.020 |
| [19] |
OZAWA Y, IBUKI T, NONOMURA T, et al. Single-pixel resolution velocity/convection velocity field of a supersonic jet measured by particle/schlieren image velocimetry[J]. Experiments in Fluids, 2020, 61(6): 1-18. DOI:10.1007/s00348-020-02963-1 |
| [20] |
HÉAS P, MÉMIN E, PAPADAKIS N, et al. Layered estimation of atmospheric mesoscale dynamics from satellite imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(12): 4087-4104. DOI:10.1109/TGRS.2007.906156 |
| [21] |
LIU T S, WANG B, CHOI D S. Flow structures of Jupiter's Great Red Spot extracted by using optical flow method[J]. Physics of Fluids, 2012, 24(9): 096601. DOI:10.1063/1.4752227 |
| [22] |
YANG Z F, JOHNSON M. Hybrid particle image velocimetry with the combination of cross-correlation and optical flow method[J]. Journal of Visualization, 2017, 20(3): 625-638. DOI:10.1007/s12650-017-0417-7 |
| [23] |
LIU T S, SALAZAR D M, FAGEHI H, et al. Hybrid optical-flow-cross-correlation method for particle image velocimetry[J]. Journal of Fluids Engineering, 2020, 142(5). doi: 10.1115/1.4045572
|
| [24] |
LIU T S, SALAZAR D M. OpenOpticalFlow_PIV: an open source program integrating optical flow method with cross-correlation method for particle image velocimetry[J]. Journal of Open Research Software, 2021, 9. DOI:10.5334/jors.326 |
| [25] |
SEONG J H, SONG M S, NUNEZ D, et al. Velocity refinement of PIV using global optical flow[J]. Experiments in Fluids, 2019, 60(11): 1-13. DOI:10.1007/s00348-019-2820-4 |
| [26] |
SCHMIDT B E, SUTTON J A. Improvements in the accuracy of wavelet-based optical flow velocimetry (wOFV) using an efficient and physically based implementation of velocity regularization[J]. Experiments in Fluids, 2020, 61(2): 1-17. DOI:10.1007/s00348-019-2869-0 |
| [27] |
WANG H P, HE G W, WANG S Z. Globally optimized cross-correlation for particle image velocimetry[J]. Experiments in Fluids, 2020, 61(11): 1-17. DOI:10.1007/s00348-020-03062-x |
| [28] |
OUYANG Z X, YANG H, HUANG Y A, et al. A circulant-matrix-based hybrid optical flow method for PIV measurement with large displacement[J]. Experiments in Fluids, 2021, 62(11): 1-18. DOI:10.1007/s00348-021-03317-1 |
| [29] |
AHLERS G, GROSSMANN S, LOHSE D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection[J]. Reviews of Modern Physics, 2009, 81(2): 503-537. DOI:10.1103/revmodphys.81.503 |
| [30] |
LOHSE D, XIA K Q. Small-scale properties of turbulent Rayleigh-Bénard convection[J]. Annual Review of Fluid Mechanics, 2010, 42: 335-364. DOI:10.1146/annurev.fluid.010908.165152 |
| [31] |
XIA K Q. Current trends and future directions in turbulent thermal convection[J]. Theoretical and Applied Mechanics Letters, 2013, 3(5): 052001. DOI:10.1063/2.1305201 |
| [32] |
SHRAIMAN B I, SIGGIA E D. Heat transport in high-Rayleigh-number convection[J]. Physical Review A, 1990, 42(6): 3650-3653. DOI:10.1103/physreva.42.3650 |
| [33] |
GROSSMANN S, LOHSE D. Scaling in thermal convection: a unifying theory[J]. Journal of Fluid Mechanics, 2000, 407: 27-56. DOI:10.1017/s0022112099007545 |
| [34] |
LI X M, HE J D, TIAN Y, et al. Effects of Prandtl number in quasi-two-dimensional Rayleigh–Bénard convection[J]. Journal of Fluid Mechanics, 2021, 915: A60. DOI:10.1017/jfm.2021.21 |
| [35] |
NI R, HUANG S D, XIA K Q. Local energy dissipation rate balances local heat flux in the center of turbulent thermal convection[J]. Physical Review Letters, 2011, 107(17): 174503. DOI:10.1103/PhysRevLett.107.174503 |
| [36] |
LI X M, HUANG S D, NI R, et al. Lagrangian velocity and acceleration measurements in plume-rich regions of turbulent Rayleigh-Bénard convection[J]. Physical Review Fluids, 2021, 6(5): 053503. DOI:10.1103/physrevfluids.6.053503 |
| [37] |
THIELICKE W, STAMHUIS E J. PIVlab–towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB[J]. Journal of Open Research Software, 2014, 2: 30. DOI:10.5334/jors.bl |
| [38] |
XIA K Q, SUN C, ZHOU S Q. Particle image velocimetry measurement of the velocity field in turbulent thermal convection[J]. Physical Review E, 2003, 68(6): 066303. DOI:10.1103/PhysRevE.68.066303 |
| [39] |
SUN C, CHEUNG Y H, XIA K Q. Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection[J]. Journal of Fluid Mechanics, 2008, 605: 79-113. DOI:10.1017/s0022112008001365 |
| [40] |
HUANG S D, WANG F, XI H D, et al. Comparative experimental study of fixed temperature and fixed heat flux boundary conditions in turbulent thermal convection[J]. Physical Review Letters, 2015, 115(15): 154502. DOI:10.1103/PhysRevLett.115.154502 |
| [41] |
CHEN X, HUANG S D, XIA K Q, et al. Emergence of substructures inside the large-scale circulation induces transition in flow reversals in turbulent thermal convection[J]. Journal of Fluid Mechanics, 2019, 877: R1. DOI:10.1017/jfm.2019.624 |
| [42] |
SUN C, ZHOU Q, XIA K Q. Cascades of velocity and temperature fluctuations in buoyancy-driven thermal turbulence[J]. Physical Review Letters, 2006, 97(14): 144504. DOI:10.1103/PhysRevLett.97.144504 |
| [43] |
ZHOU Q, SUN C, XIA K Q. Experimental investigation of homogeneity, isotropy, and circulation of the velocity field in buoyancy-driven turbulence[J]. Journal of Fluid Mechanics, 2008, 598: 361-372. DOI:10.1017/s0022112008000189 |
| [44] |
KACZOROWSKI M, XIA K Q. Turbulent flow in the bulk of Rayleigh–Bénard convection: small-scale properties in a cubic cell[J]. Journal of Fluid Mechanics, 2013, 722: 596-617. DOI:10.1017/jfm.2013.74 |
| [45] |
HUANG S D, XIA K Q. Effects of geometric confinement in quasi-2-D turbulent Rayleigh–Bénard convection[J]. Journal of Fluid Mechanics, 2016, 794: 639-654. DOI:10.1017/jfm.2016.181 |
| [46] |
DORON P, BERTUCCIOLI L, KATZ J, et al. Turbulence characteristics and dissipation estimates in the coastal ocean bottom boundary layer from PIV data[J]. Journal of Physical Oceanography, 2001, 31(8): 2108-2134. DOI:10.1175/1520-0485(2001)031<2108:tcadei>2.0.co;2 |
| [47] |
LUZNIK L, ZHU W, GURKA R, et al. Distribution of energy spectra, Reynolds stresses, turbulence production, and dissipation in a tidally driven bottom boundary layer[J]. Journal of Physical Oceanography, 2007, 37(6): 1527-1550. DOI:10.1175/jpo3076.1 |
| [48] |
HUANG S D, KACZOROWSKI M, NI R, et al. Confinement-induced heat-transport enhancement in turbulent thermal convection[J]. Physical Review Letters, 2013, 111(10): 104501. DOI:10.1103/PhysRevLett.111.104501 |
| [49] |
KACZOROWSKI M, CHONG K L, XIA K Q. Turbulent flow in the bulk of Rayleigh–Bénard convection: aspect-ratio dependence of the small-scale properties[J]. Journal of Fluid Mechanics, 2014, 747: 73-102. DOI:10.1017/jfm.2014.154 |
 2022, Vol. 40
2022, Vol. 40


