2. 浙江大学 航空航天学院,杭州 310027;
3. 南方科技大学 广东省湍流基础研究与应用重点实验室,深圳 518055;
4. 北京大学 湍流与复杂系统国家重点实验室,北京 100871
2. School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China;
3. Guangdong Provincial Key Laboratory of Turbulence Research and Applications, Southern University of Science and Technology, Shenzhen 518055, China;
4. State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing 100871, China
热对流是一种常见的物理现象,与人们的日常生活、生产息息相关[1]。其不仅存在于北极夏季融冰湖[2]、大气及海洋环流[3-4]、地球内部地幔形成[5]等自然现象中;还广泛应用于核反应堆冷却[6]、新型储能材料[7]、芯片散热[8]、磁流体传热[9]等工业工程问题中。而Rayleigh-Bénard对流(Rayleigh-Bénard convection,RBC)系统,则是从众多复杂的自然现象及工程问题中抽象简化出来的研究对流问题的经典模型。同时,由于RBC系统中可以同时存在多种热量传递方式,因此它也是传热领域非常经典的课题,研究RBC系统对认识实际情况下各种各样对流过程中的传热机制有着非常重要的意义。
狭义上的RBC通常指在一个封闭腔体内,上表面冷却,下表面加热,形成恒定温差,从而导致腔体内流体产生特殊流动的系统,如图1(来源van der Poel等[10])所示。当系统充分发展后,上下壁面附近会形成温度边界层[11],同时不断生成冷热羽流,并在腔体中形成稳定的大尺度环流(large-scale circulation,LSC)结构。除了对经典标度律[12-15]、拟序结构[16-17]及能量耗散[18-19]等的研究,科研工作者在近二十年对LSC的反转问题也进行了深入的研究[20-22]。最近Jiang等[23]通过设置上下壁面的非对称棘轮状粗糙度和引入较小倾角对热对流系统中的LSC和传热进行控制;Zhang等[24-25]通过增加侧壁局部恒温条件也实现了对LSC反转及强弱的有效控制。
由于经典的RBC系统假设上下边界温度恒定且分布均匀,这与一些实际系统的热边界条件并不相符。例如在地球物理研究中模拟地幔对流时,需要考虑热传导性差异较大的大陆板块与海洋板块,此时热边界条件就不再均匀。另一方面,工程应用中一些对流换热优化问题也需要考虑非均匀热边界条件。在对流换热的优化问题研究中,已有的增加对流传热效率的途径主要分为两种:一是改变换热板表面的粗糙度,该方法已被证明可在有限Rayleigh数(
但目前已有文献中非均匀热边界条件主要考虑简单对称分布情况,所以进一步研究非对称分布的复杂热边界条件对高Rayleigh数热湍流系统流动结构及传热规律的影响是必要的。本文参考Zhang等[24-25]算例设置,基于
假设方腔高为H,满足宽高比
| $ \nabla \cdot {{\boldsymbol{u}}} = 0 $ |
| $ \frac{\partial \boldsymbol{u}}{\partial t}+{{\boldsymbol{u}}}\cdot \nabla \boldsymbol{u} = -\nabla p+\frac{1}{\sqrt{Ra/Pr}}{\nabla }^{2}\boldsymbol{u}+\theta \boldsymbol{j} $ |
| $ \frac{\partial \theta }{\partial t}+\boldsymbol{u}\cdot \nabla \theta = \frac{1}{\sqrt{RaPr}}{\nabla }^{2}\theta $ | (1) |
其中Ra和Pr为RBC系统的无量纲控制参数,其定义如下:
| $ Ra = \frac{g\beta \Delta \theta {H}^{3}}{\upsilon \kappa },Pr = \frac{\upsilon }{\kappa } $ |
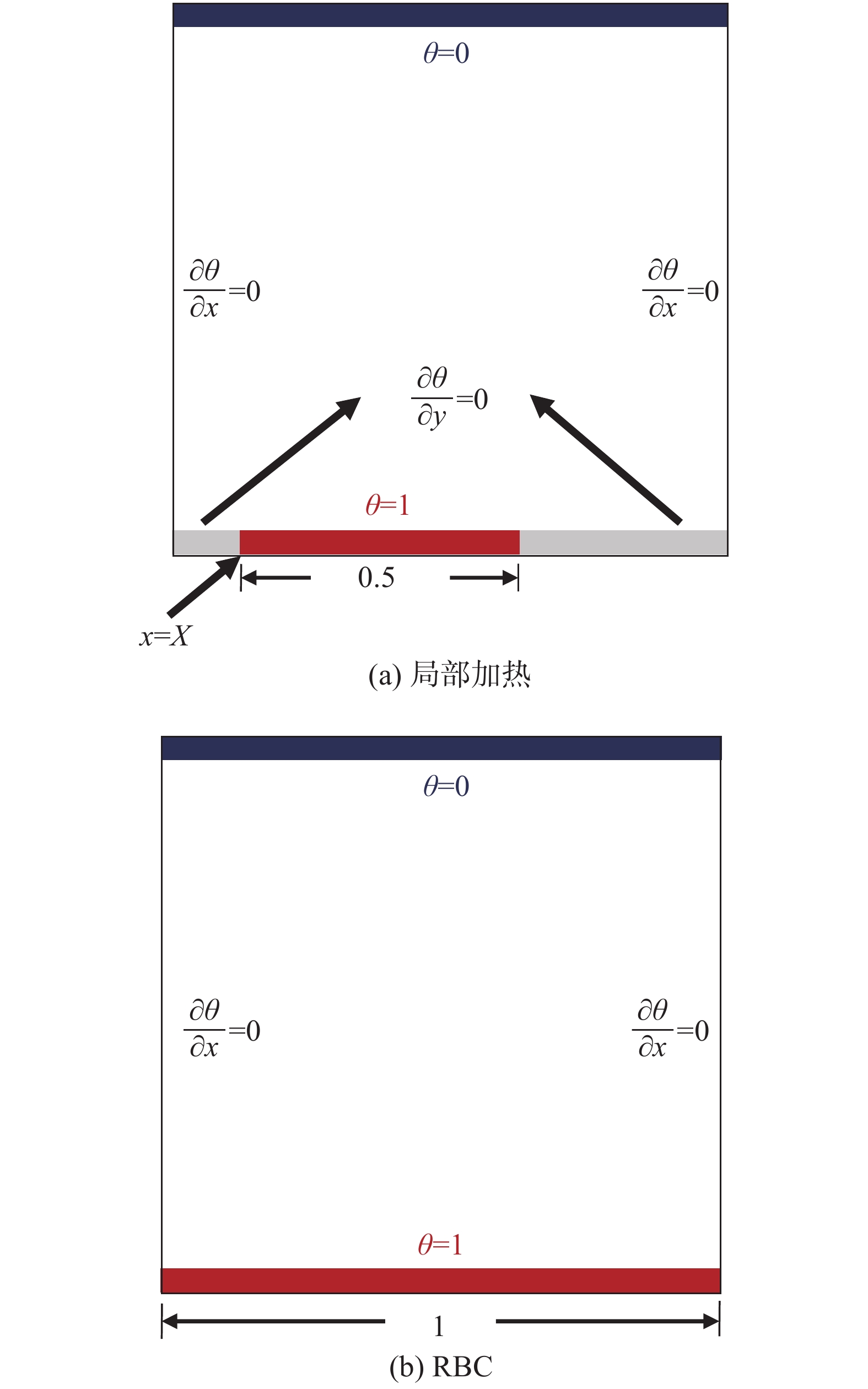
后文中变量如无特别说明,均已无量纲化。图2为本文计算的三种局部加热系统及RBC系统示意图。左右壁面为绝热条件,即
|
图 2 局部加热系统及RBC系统计算示意图 Fig.2 Sketches of local heating and RBC cases |
本文数值模拟均采用经过部分修改的二阶有限差分法代码AFiD[10]进行计算,其中离散Poisson方程通过水平方向的离散余弦变换解耦并采用三对角求解器进行求解,时间推进采用二阶显式Adams-Bashforth格式实现。与de Vahl Davis等[36]的方腔自然对流结果对比,文献在 Pr = 0.71、Ra = 1×104 、1×105 、1×106 条件下的壁面时均
本文在Pr= 2、Ra = 1×108条件下,以加热左端点无量纲坐标X为位置参数,对全局加热(经典RBC)系统和局部加热系统(加热位置分别为X= 0、0.125、0.25,加热长度
所有算例中,水平方向为均匀网格,竖直方向为非均匀网格(靠近壁面处细化),保证边界层内网格大小
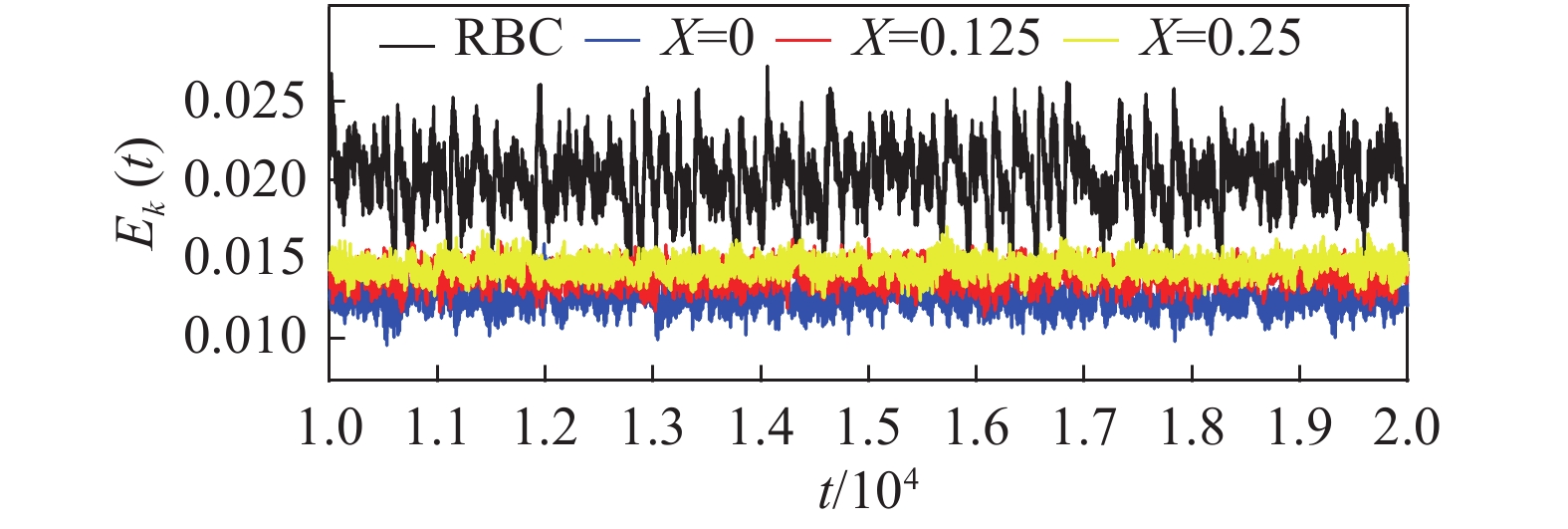
首先考虑不同位置局部加热条件对热湍流达到统计稳态后的流动影响,分析总动能的时间演化情况。本文计算总动能为:
| $ {E}_{k}\left(t\right) = {\frac{1}{2}\left\langle{{u}^{2}+{v}^{2}}\right\rangle}_{S} $ | (2) |
其中下角标
|
图 3 不同加热位置及经典RBC的Ek(t)变化情况 Fig.3 Time series of Ek(t) of local heating cases and traditional RBC case |
其中RBC系统的总动能均值
根据前文所提,传统RBC具有的流场结构特性之一便是当流动充分发展后,流场内会形成较为稳定的LSC结构且会发生反转现象。为了分析局部加热是否会影响LSC的反转,本文采用角动量符号对此进行判断。计算平均角动量定义如下[38]:
| $ L\left(t\right) = {\left\langle{\left(x-\frac{1}{2}\right) v-\left(y-\frac{1}{2}\right) u}\right\rangle}_{x,y} $ |
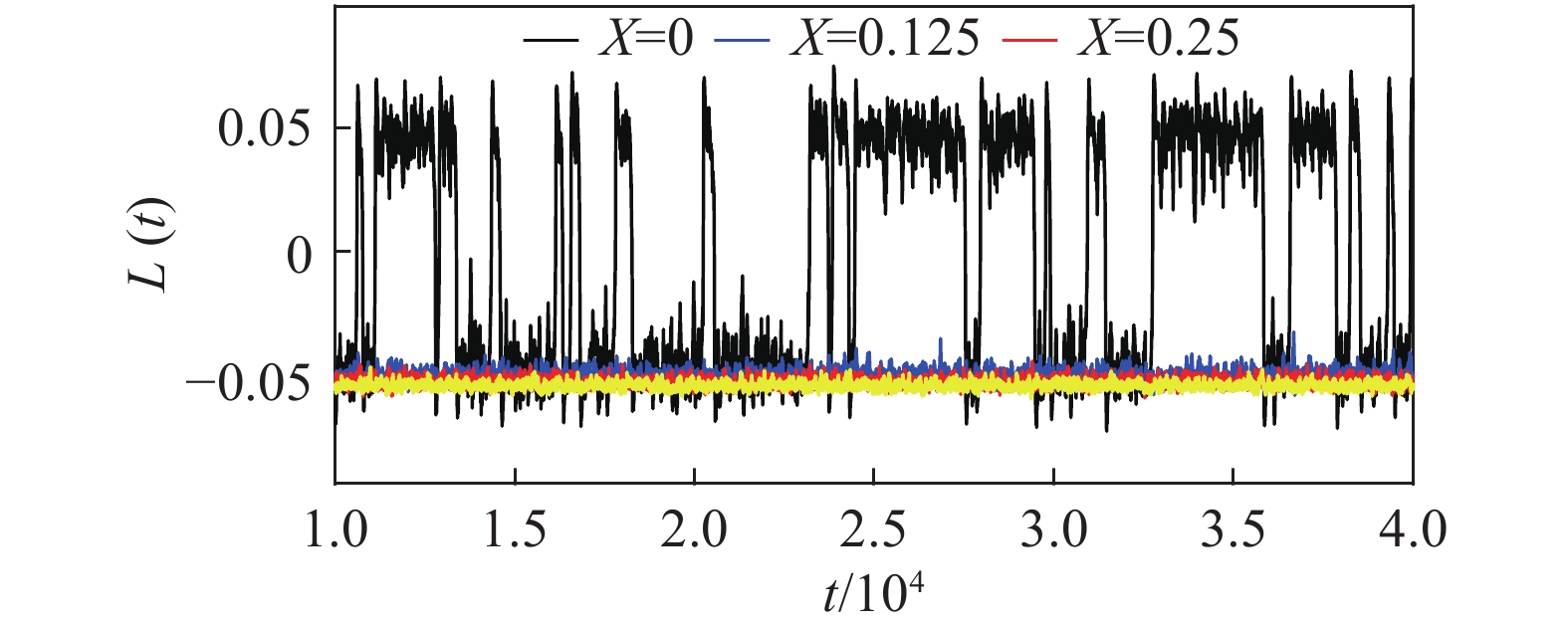
图4给出局部加热系统及RBC的
|
图 4 不同加热位置及经典RBC的L(t)变化情况 Fig.4 Time series of L(t) of local heating cases and traditional RBC case |
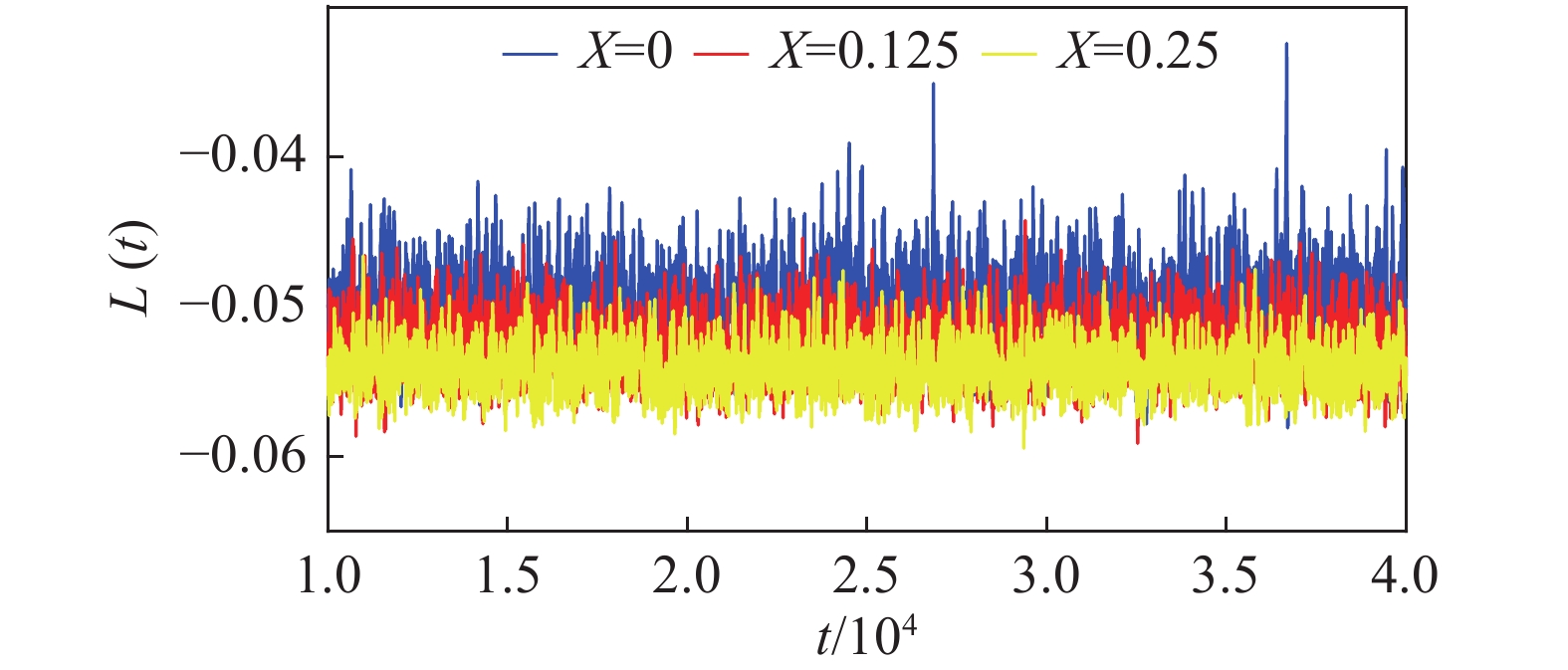
|
图 5 不同加热位置的L(t)变化情况 Fig.5 Time series of L(t) of local heating cases |
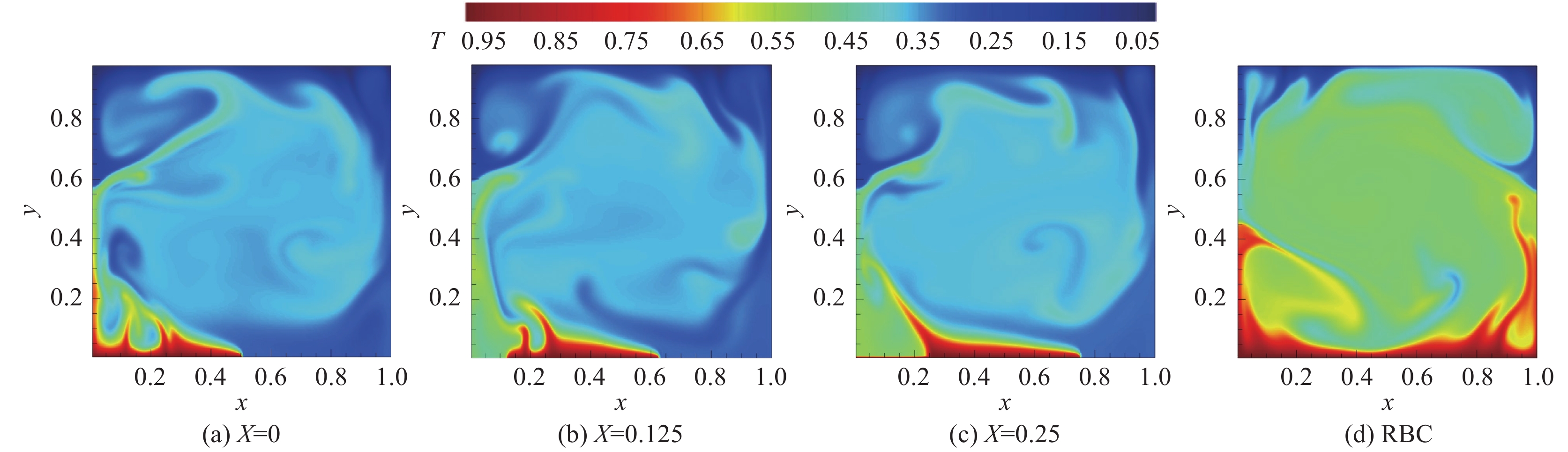
Sugiyama等[38]曾描述了角涡在LSC反转过程中的作用,即由于角落边界层分离羽流的能量补给,小的角涡会逐渐增大,直至达到腔体高度的一半,然后破坏主体LSC结构,并在相反方向上建立另一个新的LSC。由此我们知道反转现象的产生与角涡的生长密不可分,为了观察角涡及中心大涡的变化情况,绘制了流场云图及动画(在网刊资源附件中提供)。从动画及图6中可看出无论是否局部加热,其基本流场结构均主要由中心大涡及角涡组成。其中局部加热系统中下壁面角涡不稳定,且大小受限。虽然RBC系统中的角涡关于方腔中心的对称性更强,
|
图 6 不同加热位置及经典RBC瞬时温度云图 Fig.6 Temperature contours of local heating cases and traditional RBC case |
由于左右壁面均为绝热条件,故只考虑竖直方向传热情况,通过
| $ Nu\left(t\right) = -\frac{1}{2}{\left\langle{{\left.\frac{\partial \theta }{\partial y}\right|}_{y = 0}+{\left.\frac{\partial \theta }{\partial y}\right|}_{y = 1}}\right\rangle}_{x} $ |
其中下边界绝热壁面
|
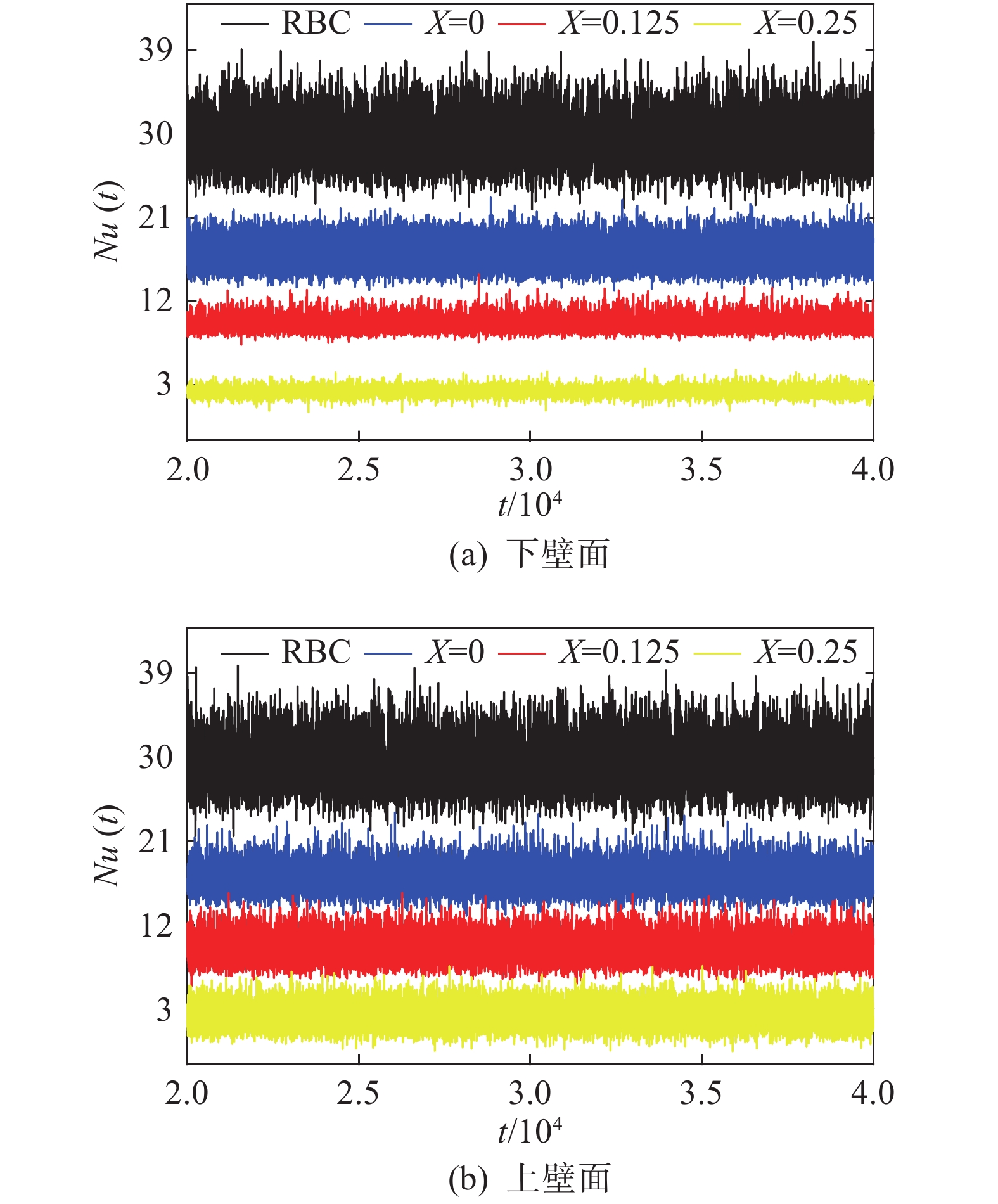
图 7 不同加热位置及经典RBC的上下壁面Nu(t)变化情况 Fig.7 Time series of Nu(t) at the bottom wall (a) and top wall (b) from different cases |
其中RBC系统
观察图7(b)并与图7(a)作对比,可以看出在达到统计稳态后,RBC系统上下壁面
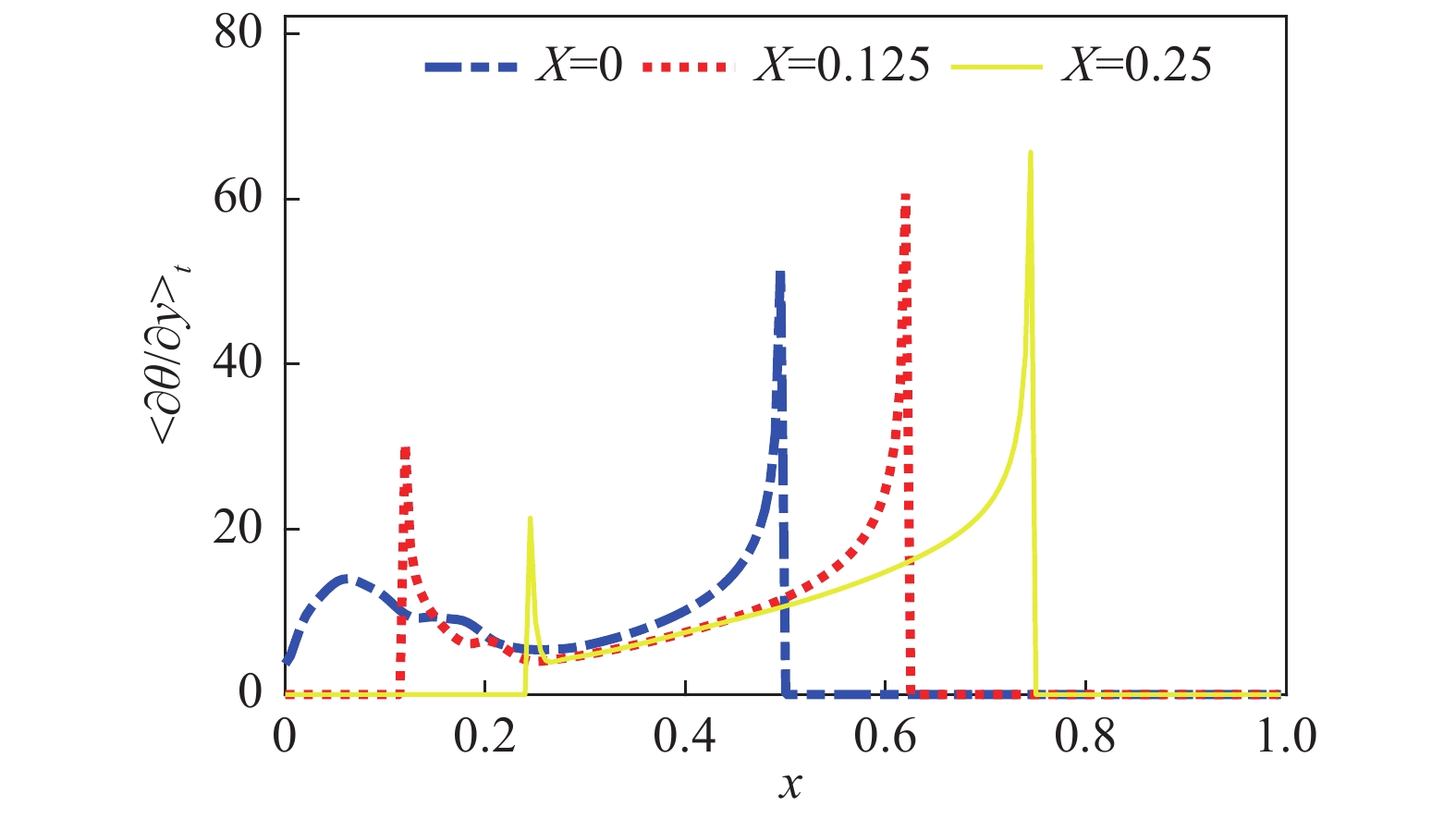
图8展示了统计稳态时,下壁面加热区域的时均温度梯度分布,其证明加热位置越靠近冷羽流冲击点,其受冷羽流影响端温度梯度就越大,即冷羽流作用程度越强。而中心加热系统中,加热位置最靠近冷羽流发生变向运动区域,其受影响最大,热羽流生成数量始终维持在1~2个,因此热羽流可以以近似一簇的状态快速从左侧壁上升进而与冷羽流进行相互作用,又因为其对于方腔中心而言具有更稳定的LSC结构,因此具有更高效率的对流换热,故整体传热效率更高。
|
图 8 不同加热位置系统的下壁面时均温度梯度 Fig.8 Temperature gradient of the bottom wall of different heating position cases |
本文以二维方腔RBC系统为基础,通过直接数值模拟计算了
1)局部加热系统中,加热位置越靠近下壁面中心,其总动能和角动量绝对值越大、振幅越小,系统主体LSC稳定性越高;
2)局部加热条件会对系统下壁面角涡的生长产生限制,进而抑制LSC反转;
3)虽然加热长度为RBC系统的一半,但局部加热系统总动能
4)在一定的加热长度下,可以通过调整加热位置令传热效率最大化,其中
5)在没有热羽流上升侧,冷羽流下降后到达壁面处改为横向运动,该位置与加热区域越近则对热羽流数量和对应温度脉动影响越明显,其对应端点温度梯度也越大。
由于本文计算选取局部加热位置数量有限,因此想要得到更为确切的定量关系,还需大量不同加热位置及加热长度的计算结果。本文初步证明了加热长度确定的情况下,可以通过加热位置来控制传热效率。关于局部加热条件对LSC反转的影响,后续还会深入研究。除此之外,本文作为对非对称局部加热问题的初步研究,目前仅开展了二维直接数值模拟研究,后续我们将进一步开展三维问题的直接数值模拟与分析,以及相应的实验研究。
| [1] |
周全, 夏克青. Rayleigh-Bénard湍流热对流研究的进展、现状及展望[J]. 力学进展, 2012, 42(3): 231-251. ZHOU Q, XIA K Q. Advances and outlook in turbulent Rayleigh-Bénard convection[J]. Advances in Mechanics, 2012, 42(3): 231-251. (in Chinese) |
| [2] |
POLASHENSKI C, PEROVICH D, COURVILLE Z. The mechanisms of sea ice melt pond formation and evolution[J]. Journal of Geophysical Research:Oceans, 2012, 117(C1): C01001. DOI:10.1029/2011JC007231 |
| [3] |
CIESZELSKI R. A case study of Rayleigh-Bénard convection with clouds[J]. Boundary-Layer Meteorology, 1998, 88(2): 211-237. DOI:10.1023/a:1001145803614 |
| [4] |
RIEHL H, YEH T C, MALKUS J S, et al. The north-east trade of the Pacific Ocean[J]. Quarterly Journal of the Royal Meteorological Society, 1951, 77(334): 598-626. DOI:10.1002/qj.49707733405 |
| [5] |
HENSHALL T. Mantle convection in super-earths[J]. Nature Reviews Physics, 2019, 1(3): 181. DOI:10.1038/s42254-019-0035-5 |
| [6] |
SATO T, MAEDA K, NAGATAKI S, et al. High-entropy ejecta plumes in Cassiopeia A from neutrino-driven convection[J]. Nature, 2021, 592(7855): 537-540. DOI:10.1038/s41586-021-03391-9 |
| [7] |
ZHANG S, FENG D L, SHI L, et al. A review of phase change heat transfer in shape-stabilized phase change materials (ss-PCMs) based on porous supports for thermal energy storage[J]. Renewable and Sustainable Energy Reviews, 2021, 135: 110127. DOI:10.1016/j.rser.2020.110127 |
| [8] |
王迪, 闵春华, 杨旭光, 等. 电子元件散热器翅片自然对流散热性能研究[J]. 热科学与技术, 2021, 20(4): 313-317. WANG D, MIN C H, YANG X G, et al. Research on natural convection heat dissipation performance of electronic component radiator fins[J]. Journal of Thermal Science and Technology, 2021, 20(4): 313-317. (in Chinese) |
| [9] |
LI M G, ZHENG C, ZHAO Q, et al. Anisotropic heat transfer of Ferro-nanofluid in partially heated rectangular enclosures under magnetic field[J]. Case Studies in Thermal Engineering, 2021, 26: 101145. DOI:10.1016/j.csite.2021.101145 |
| [10] |
VAN DER POEL E P, OSTILLA-MÓNICO R, DONNERS J, et al. A pencil distributed finite difference code for strongly turbulent wall-bounded flows[J]. Computers & Fluids, 2015, 116: 10-16. DOI:10.1016/j.compfluid.2015.04.007 |
| [11] |
AHLERS G, GROSSMANN S, LOHSE D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection[J]. Reviews of Modern Physics, 2009, 81(2): 503-537. DOI:10.1103/revmodphys.81.503 |
| [12] |
CIONI S, CILIBERTO S, SOMMERIA J. Strongly turbulent Rayleigh-Bénard convection in mercury: comparison with results at moderate Prandtl number[J]. Journal of Fluid Mechanics, 1997, 335: 111-140. DOI:10.1017/s0022112096004491 |
| [13] |
AHLERS G, XU X. Prandtl-number dependence of heat transport in turbulent Rayleigh-Bénard convection[J]. Physical Review Letters, 2001, 86(15): 3320-3323. DOI:10.1103/PhysRevLett.86.3320 |
| [14] |
QIU X L, TONG P. Onset of coherent oscillations in turbulent Rayleigh-Bénard convection[J]. Physical Review Letters, 2001, 87(9): 094501. DOI:10.1103/PhysRevLett.87.094501 |
| [15] |
SILANO G, SREENIVASAN K R, VERZICCO R. Numerical simulations of Rayleigh–Bénard convection for Prandtl numbers between 10–1 and 104 and Rayleigh numbers between 105 and 109[J]. Journal of Fluid Mechanics, 2010, 662: 409-446. DOI:10.1017/s0022112010003290 |
| [16] |
GROSSMANN S, LOHSE D. Fluctuations in turbulent Rayleigh-Bénard convection: the role of plumes[J]. Physics of Fluids, 2004, 16(12): 4462-4472. DOI:10.1063/1.1807751 |
| [17] |
XI H D, LAM S, XIA K Q. From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection[J]. Journal of Fluid Mechanics, 2004, 503: 47-56. DOI:10.1017/s0022112004008079 |
| [18] |
BAILEY S C C, HULTMARK M, SCHUMACHER J, et al. Measurement of local dissipation scales in turbulent pipe flow[J]. Physical Review Letters, 2009, 103: 014502. DOI:10.1103/physrevlett.103.014502 |
| [19] |
ZHOU Q, XIA K Q. Universality of local dissipation scales in buoyancy-driven turbulence[J]. Physical Review Letters, 2010, 104(12): 124301. DOI:10.1103/PhysRevLett.104.124301 |
| [20] |
BENZI R. Flow reversal in a simple dynamical model of turbulence[J]. Physical Review Letters, 2005, 95(2): 024502. DOI:10.1103/PhysRevLett.95.024502 |
| [21] |
ASSAF M, ANGHELUTA L, GOLDENFELD N. Rare fluctuations and large-scale circulation cessations in turbulent convection[J]. Physical Review Letters, 2011, 107(4): 044502. DOI:10.1103/PhysRevLett.107.044502 |
| [22] |
WANG Q, XIA S N, WANG B F, et al. Flow reversals in two-dimensional thermal convection in tilted cells[J]. Journal of Fluid Mechanics, 2018, 849: 355-372. DOI:10.1017/jfm.2018.451 |
| [23] |
JIANG H C, ZHU X J, MATHAI V, et al. Controlling heat transport and flow structures in thermal turbulence using ratchet surfaces[J]. Physical Review Letters, 2018, 120(4): 044501. DOI:10.1103/PhysRevLett.120.044501 |
| [24] |
ZHANG S Q, XIA Z H, ZHOU Q, et al. Controlling flow reversal in two-dimensional Rayleigh–Bénard convection[J]. Journal of Fluid Mechanics, 2020, 891: R4. DOI:10.1017/jfm.2020.210 |
| [25] |
ZHANG S Q, CHEN X, XIA Z H, et al. Stabilizing/destabilizing the large-scale circulation in turbulent Rayleigh-Bénard convection with sidewall temperature control[J]. Journal of Fluid Mechanics, 2021, 915: A14. DOI:10.1017/jfm.2021.58 |
| [26] |
TOPPALADODDI S, SUCCI S, WETTLAUFER J S. Roughness as a route to the ultimate regime of thermal convection[J]. Physical Review Letters, 2017, 118(7): 074503. DOI:10.1103/PhysRevLett.118.074503 |
| [27] |
ZHU X J, STEVENS R J A M, VERZICCO R, et al. Roughness-facilitated local 1/2 scaling does not imply the onset of the ultimate regime of thermal convection[J]. Physical Review Letters, 2017, 119(15): 154501. DOI:10.1103/PhysRevLett.119.154501 |
| [28] |
XIE Y C, XIA K Q. Turbulent thermal convection over rough plates with varying roughness geometries[J/OL]. Journal of Fluid Mechanics, 2017, 825: 573-599
|
| [29] |
ZHU X, VERSCHOOF R A, BAKHUIS D, et al. Wall roughness induces asymptotic ultimate turbulence[J]. Nature Physics, 2018, 14(4): 417-423. DOI:10.1038/s41567-017-0026-3 |
| [30] |
WANG F, HUANG S D, XIA K Q. Thermal convection with mixed thermal boundary conditions: effects of insulating lids at the top[J]. Journal of Fluid Mechanics, 2017, 817: R1. DOI:10.1017/jfm.2017.121 |
| [31] |
COOPER C M, MORESI L N, LENARDIC A. Effects of continental configuration on mantle heat loss[J]. Geophysical Research Letters, 2013, 40(11): 2647-2651. DOI:10.1002/grl.50547 |
| [32] |
RIPESI P, BIFERALE L, SBRAGAGLIA M, et al. Natural convection with mixed insulating and conducting boundary conditions: low- and high-Rayleigh-number regimes[J]. Journal of Fluid Mechanics, 2014, 742: 636-663. DOI:10.1017/jfm.2013.671 |
| [33] |
BAKHUIS D, OSTILLA-MÓNICO R, VAN DER POEL E P, et al. Mixed insulating and conducting thermal boundary conditions in Rayleigh–Bénard convection[J]. Journal of Fluid Mechanics, 2018, 835: 491-511. DOI:10.1017/jfm.2017.737 |
| [34] |
VASILIEV A, SUKHANOVSKII A. Turbulent convection in a cube with mixed thermal boundary conditions: low Rayleigh number regime[J]. International Journal of Heat and Mass Transfer, 2021, 174: 121290. DOI:10.1016/j.ijheatmasstransfer.2021.121290 |
| [35] |
NANDUKUMAR Y, CHAKRABORTY S, VERMA M K, et al. On heat transport and energy partition in thermal convection with mixed boundary conditions[J]. Physics of Fluids, 2019, 31(6): 066601. DOI:10.1063/1.5095242 |
| [36] |
DE VAHL DAVIS G, JONES I P. Natural convection in a square cavity: a comparison exercise[J]. International Journal for Numerical Methods in Fluids, 1983, 3(3): 227-248. DOI:10.1002/fld.1650030304 |
| [37] |
SHISHKINA O, STEVENS R J A M, GROSSMANN S, et al. Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution[J]. New Journal of Physics, 2010, 12(7): 075022. DOI:10.1088/1367-2630/12/7/075022 |
| [38] |
SUGIYAMA K, NI R, STEVENS R J A M, et al. Flow reversals in thermally driven turbulence[J]. Physical Review Letters, 2010, 105(3): 034503. DOI:10.1103/PhysRevLett.105.034503 |
 2022, Vol. 40
2022, Vol. 40



