2. 南方科技大学 力学与航空航天工程系,复杂流动及软物质研究中心,深圳 518055
2. Center for Complex Flows and Soft Matter Research, Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, China
湍流多重态是近期湍流研究的热点问题[1]。湍流多重态通常是指在相同控制参数下,湍流系统会出现不同的流动结构和统计特性,比如在von Kármán旋转湍流[2-5]、Taylor-Couette流动[6-9]、展向旋转平板Couette流动[10-11]、球形Couette流动[12]和Taylor-Green湍流[13]中,人们均发现湍流系统会出现以不同的大尺度湍流结构为典型特征的多态现象。上述系统中观察到的多态现象可以分为以下两类:一类多态现象源于系统驱动力对称性的改变或者驱动力在控制参数空间路径的改变,例如Von Kármán旋转湍流、Taylor-Couette流动和Taylor-Green湍流;另一类多态现象源于不同的初始条件,例如展向旋转平板Couette流动。作为湍流的重要模型之一,浮力驱动的热湍流(热对流)是否也存在类似的多态现象备受关注。
热对流现象广泛存在于自然界和工程应用中,如海洋[14]和大气[15]中的热对流及核聚变反应堆包层[16]中的热对流等。Rayleigh-Bénard(RB) 热湍流是从众多自然现象中抽象出来研究浮力驱动湍流的经典模型[17-19]。在RB系统中,通过加热封闭对流腔体的下边界,同时冷却其上边界,使流体在浮力的作用下产生对流。当上下边界的温差足够大时,RB系统会进入湍流状态,此时系统的温度梯度主要集中于上下边界处很薄的温度边界层内。温度边界层由于不稳定性生成冷(热)羽流,羽流通过自组织,形成大尺度湍流结构[20]。
在Oberbeck-Boussinesq(OB)近似下,RB系统的控制方程为:
不可压缩连续性方程
| $ {\partial _i}{u_i} = 0 $ | (1) |
加入浮力项的Navier-Stokes(N-S)方程
| $ {\partial _t}{u_i} + {u_j}{\partial _j}{u_i} = - {\partial _i}p + \upsilon {\partial _j}{\partial _j}{u_i} + \alpha g{\delta _{i3}}\theta $ | (2) |
热输运方程
| $ {\partial _t}\theta + {u_j}{\partial _j}\theta = \kappa {\partial _j}{\partial _j}\theta $ | (3) |
其中,ui (i = 1,2,3)为速度场,θ 为温度场,p 为广义压强场;
| $ Ra = \frac{{\alpha g\varDelta {H^3}}}{{\kappa \upsilon }},{\text{ }}Pr = \frac{\upsilon }{\kappa } $ | (4) |
式中,Δ为上下边界温差,H为对流腔体高度。Ra数是无量纲化的温差,用来衡量驱动浮力的大小;Pr数表征流体的物性参数。从实验的角度,还需要引入系统的宽高比 Γ = D/H来表征给定几何形状下对流腔体的空间约束程度,这里D为对流腔体的水平特征尺度。
RB系统的响应参数为Nusselt数(Nu)和Reynolds数(Re)。它们的定义分别如下:
| $ Nu = \frac{{\langle {u}_{3}\theta \rangle }_{\text{A}}-\kappa {\partial }_{3}{\langle \theta \rangle }_{\text{A}}}{\kappa \varDelta {H}^{-1}}\text{,}Re = \frac{U}{\upsilon {H}^{-1}} $ | (5) |
其中,<···>A表示对任意一水平面的面平均,u3为竖直方向的速度,U 为系统的特征速度。Nu数表示RB系统传热效率与流体处于静止状态时热传导传热效率的比值,用于衡量系统的热输运效率。Re数衡量系统的动量输运效率。
已有研究发现在圆柱对流腔体内的热湍流会出现单环结构和双环结构的大尺度湍流结构[21-22]。近期谢毅超等发现随着Ra数在6.0×107~1.3×109范围内的增加,圆环对流腔体中的RB热湍流会从高传热效率的四极子湍流态演化到低传热效率的偶极子湍流态,这种流态转变对应着系统的自发对称破缺[23]。在转变区间,系统呈现出多重态现象,即系统会在四极子态和偶极子态两个亚稳态之间自主随机的转变。如果Ra继续增加,系统会出现什么样的流态,其又遵循什么样的输运规律是本文将要研究的问题。
需要指出的是四极子流态和偶极子流态与单环结构(双环结构)湍流态[21-22]有着明显的区别。单双环结构的转变存在于实验所包括的所有Ra数工况下,并且这两个状态的持续时间均和大尺度湍流结构的特征时间相当;而偶极子流态和四极子流态的转变只发生在有限的Ra数范围内,且系统处在各态的时间远大于大尺度湍流结构的特征时间;其次,单双环结构流态转变并未导致系统的Nu数等响应参数出现明显的双峰结构。
1 实验装置和测量方法实验采用了圆环对流腔体。为了表征圆环体的空间约束效应,除了宽高比Γ 以外,还需要引入内外径比γ = Di /Do ,这里Di是圆环体内圆柱的外径,Do 是圆环体外圆柱的内径。实验中采用了两套几何参数接近、但特征高度不同的对流腔体,它们的高度分别为H = 150 mm(大对流腔体)和H = 104 mm(小对流腔体)。大对流腔体和小对流腔体的宽高比和内外径比分别为Γ = 2、γ = 0.9和Γ = 1.88、γ = 0.9。
实验装置卡通图见图1,每个对流腔体由三部分组成,分别是无氧紫铜(TU1)制作的冷却上板、加热下板和有机玻璃制作的边壁。上下板和流体接触的表面镀了镍薄层保护紫铜。上板内部刻有圆环形的流道,深20 mm,宽度5 mm,来自恒温水浴(Julabo DD1000)的冷却水流经流道,冷却上板。下板内埋有两层镍铬电阻丝(Omega,NI80-012-200),由99.99%电压稳定性的直流电源(Armetex,XG300-5)提供恒定的加热。为了实现高精度的热输运测量,实验使用了边壁保温罩和底部保温罩等辅助保温装置。整个对流腔体放置于保温装置内,并将保温装置和对流腔体之间的空隙填满保温棉。
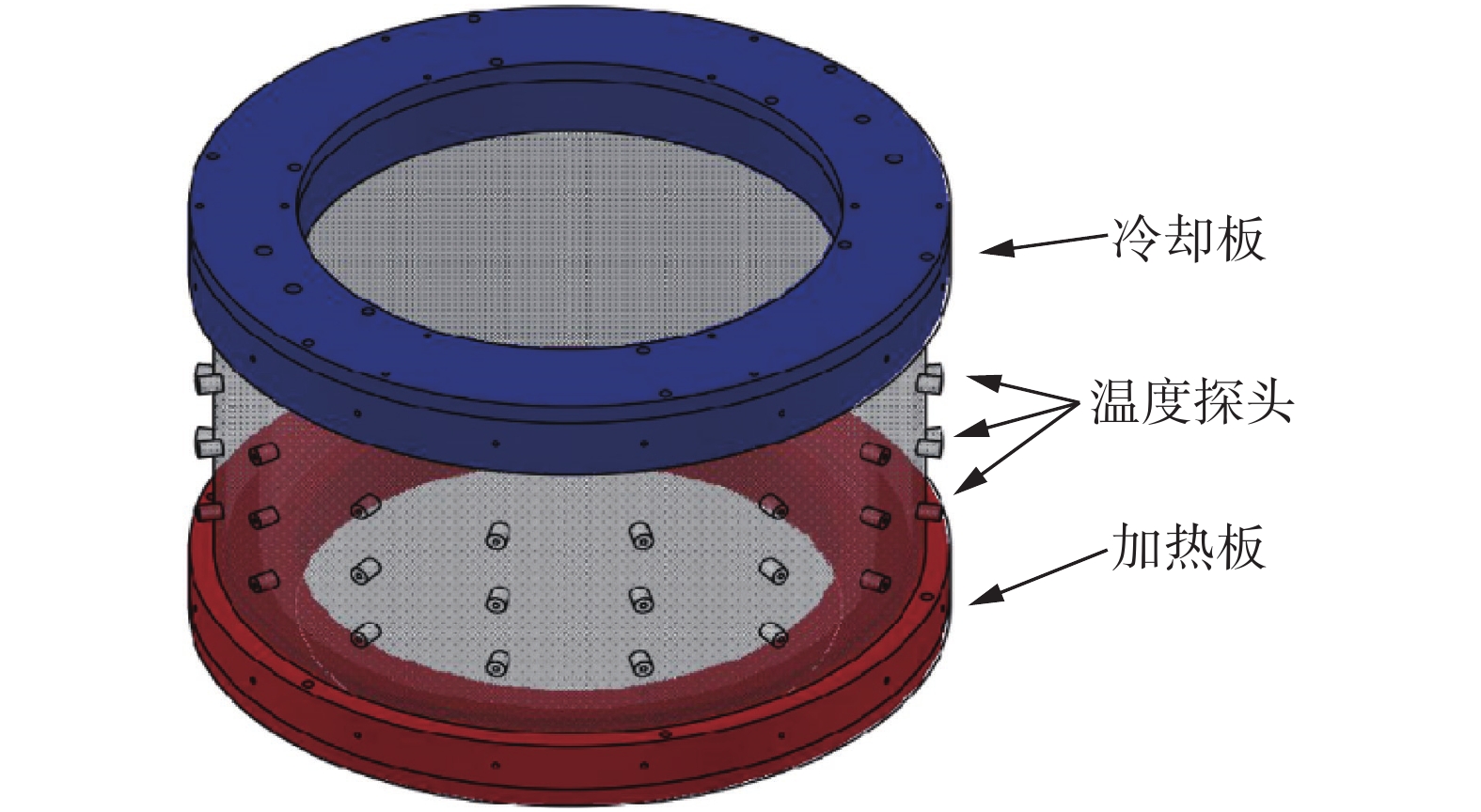
|
图 1 圆环对流腔体示意图和温度探头布置图 Fig.1 Sketch of the annulus convection cell and the distribution of thermistors |
实验采用热敏电阻(Omega Inc,44031)实现高精度的温度测量:分别在上下板中沿角向均匀布置8个温度探头,测量其温度。结合同步测量的加热板输入电压U和电流I,可以计算系统的Nu数,
实验使用去离子水作为工作物质。大对流腔体上下板的温差范围为2.4 K ≤ Δ ≤ 34.3 K , 对应的Ra数范围为 2.0×108 ≤ Ra ≤ 2.9×109。流体的平均温度设定为30℃,对应的Prandtl数为Pr = 5.4。通过PID调制,使得上板的温度为恒定值,其近似地满足恒温边界条件;下板为恒热流边界条件;边壁为绝热边界条件。对于每一个Ra工况,先通过PID温控程序调制下板输入功率和上板温度,使系统收敛到预设的Ra值,随后固定加热板的输入功率并且等待系统稳定2.5 h以后,开始采集数据。根据Ra数的不同,实验测量的时间不同,当处于最大的Ra数时,测量时间最短,为12 h;在后文提到的转变区间内的工况,测量时间最长,为72 h。
实验中,使用粒子图像测速仪(particle image velocimetry, PIV,Lavision)直接测量了小对流腔体内的大尺度湍流结构。为了实现PIV测量,将上板用透明的蓝宝石代替,激光光片从水平方向射入对流腔体,将摄像机置于对流腔体正上方,从而获得对流腔体不同高度的水平二维速度矢量场。实验中分别测量了四极子流态和偶极子流态的空间结构;对于每一个流态,测量了5个不同高度;每个高度的测量时长为20 min,其采样频率为15 Hz。
2 结果分析 2.1 大尺度湍流结构直接测量通过测量对流腔体 z= H/2 处的温度空间分布,文献[23]在小对流腔体中发现热湍流会出现偶极子流态和四极子流态。在本文中,利用PIV直接测量了小对流腔体中这两种流态的空间结构。
图2(a)展示了偶极子流态时对流腔体五个高度的时均速度矢量场和部分流线。从流线方向可以看出封闭对流腔体内存在两个大尺度涡结构,其路径分别为(abcdefa)和(agcdhfa)。图2(b)和图2(c)分别展示了时间和径向平均后的角向速度与径向速度分布。与文献[23]温度测量中观察到的偶极子流态类似,角向速度分布呈现偶极子结构,同时径向速度比角向速度小一个数量级,因此圆环腔体内的偶极子流态近似地看作沿着角向和轴向的准二维流动。
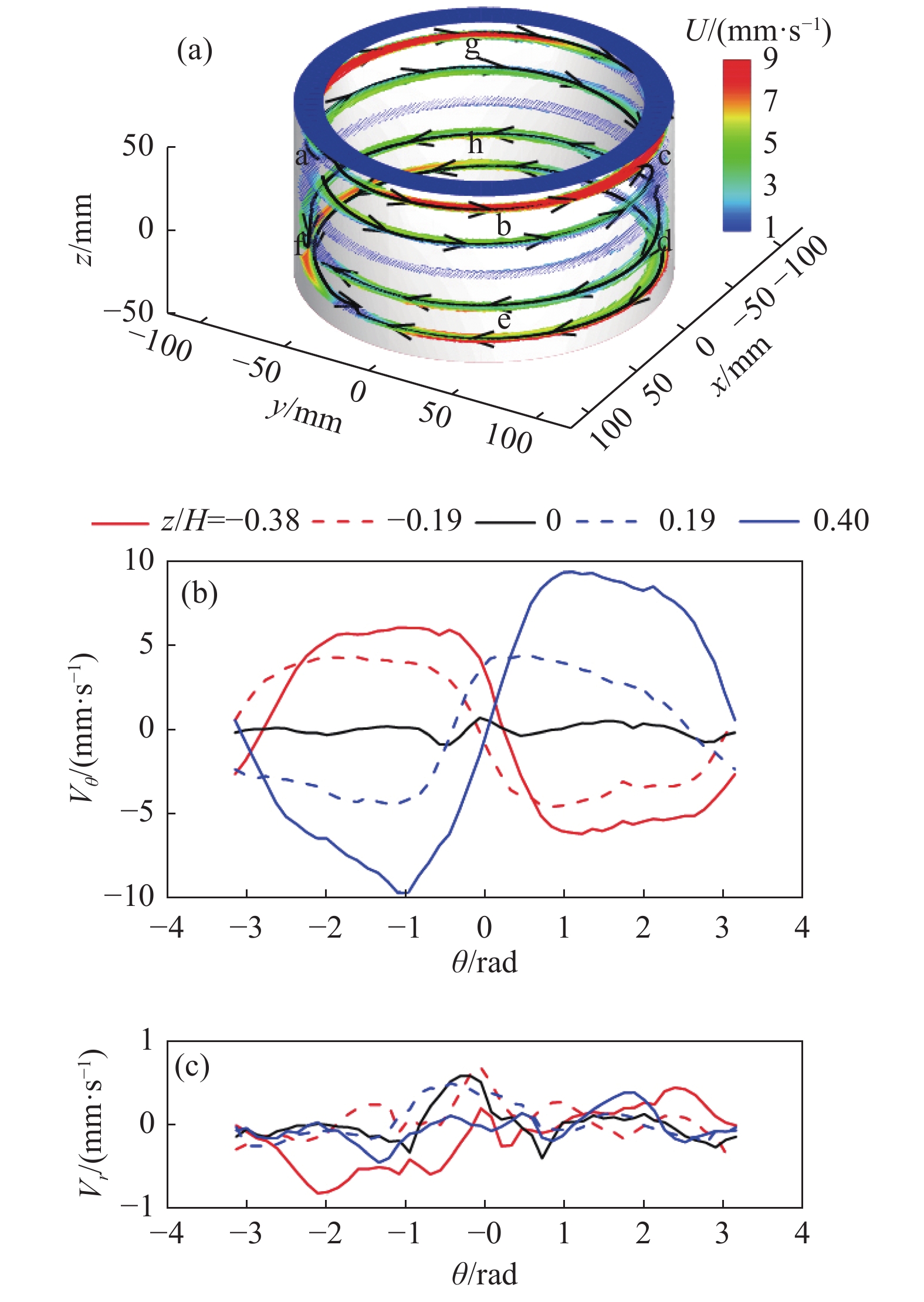
|
图 2 (a)偶极子流态时的空间时均速度矢量图与部分流线;(b)时均角向速度分布图;(c)时均径向速度分布图 Fig.2 (a) Mean velocity field and streamlines of the dipole mode; (b) mean angular velocity; (c) mean radial velocity |
图3(a)展示了四极子流态时对流腔体五个高度时均速度矢量场和部分流线。图3(b)和图3(c)分别展示了时间和径向平均后的角向速度与径向速度分布。结合图3(a、b) 可以看出圆环对流腔体中存在4个大小不等且上下贯穿的大尺度涡结构,这与文献[23]中温度测量得到的四极子流态一致。比较图3(b)和图3(c)可以看出四极子流态的径向速度比角向速度小一个数量级,因此圆环对流腔体中的四极子流态也可以看作沿角向和轴向的准二维流动。由于温度场和速度场反映的大尺度结构是一致的,因此可以通过长时间的温度测量来研究大尺度湍流涡结构的动力学特性。
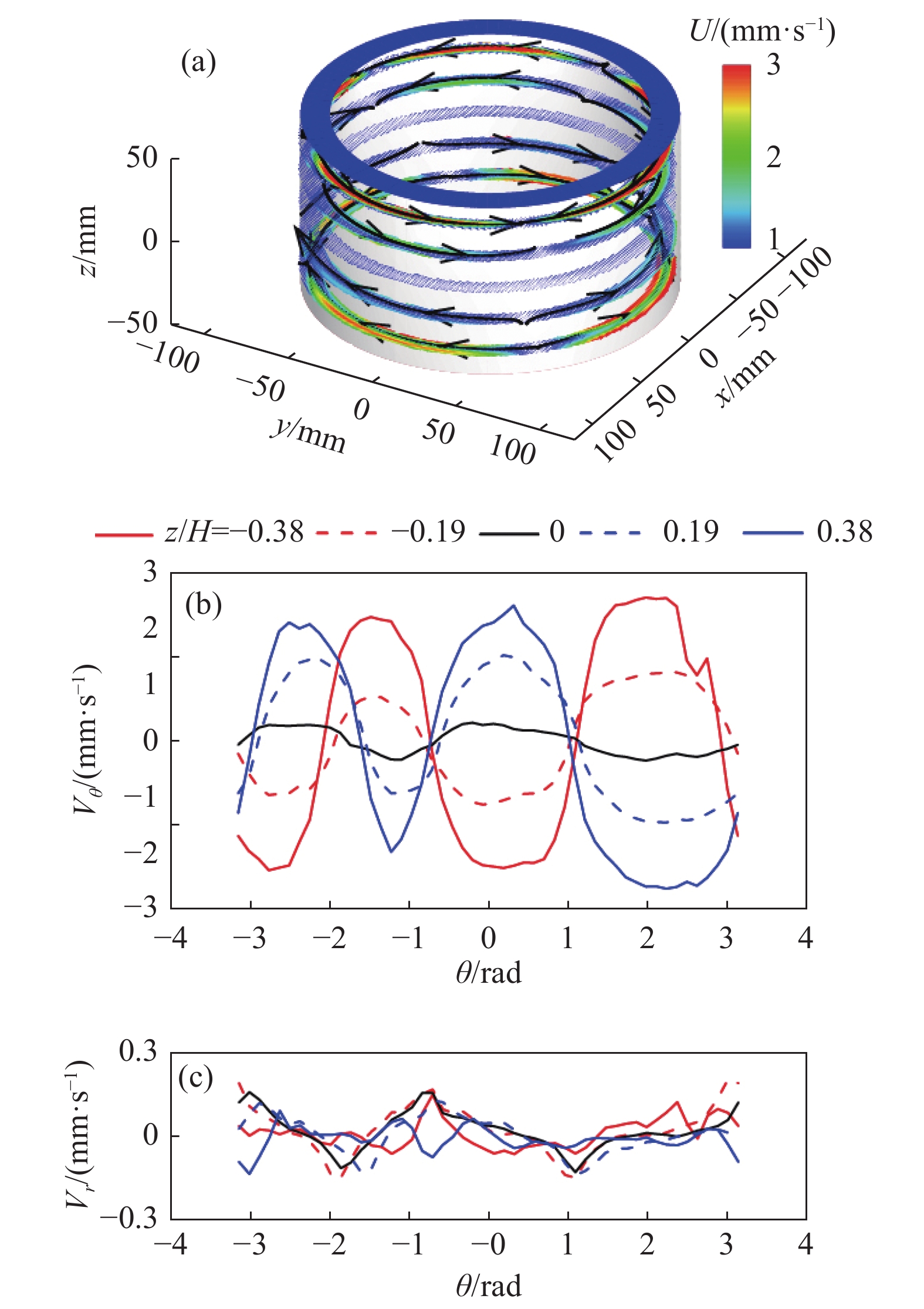
|
图 3 (a) 四极子流态时的均速度矢量图与部分流线 ;(b) 时均角向速度分布图;(c) 时均径向速度分布图 Fig.3 (a) Mean velocity field and streamlines of the quadrupole mode; (b) mean angular velocity; (c) mean radial velocity |
这部分主要讨论RB热湍流中的多重态现象。由2.1节中的结论可知,在RB湍流中速度场和温度场呈现的信息一致,因此可以通过直接测量温度场,得到对流腔体中的大尺度湍流结构信息。小对流腔体的结果已经在参考文献[23]中予以报道,本文将主要关注大对流腔体中的多重态现象。实验中采用多温度探头技术[24-25]测量大尺度流动结构动力学特性。在每一时刻,将对流腔体边壁z = H/2处的温度空间分布进行离散傅里叶展开:
| $ {T_l} = \bar T + \sum\limits_{k = 1}^8 {{A_k}\sin \Bigg(\frac{{k{\text{π}} }}{8}l + {\theta _k}\Bigg)} $ | (6) |
其中,
图4(a~d)分别展示一阶至四阶傅里叶模态主导时z = H/2处的温度分布和对应阶的三角函数拟合曲线。与文献[23]中的结果一致,大尺度湍流结构会出现一阶模态和二阶模态主导的湍流态 (图4(a、b));不同的是,在大对流腔体中还观测到了三阶傅里叶模态(图4(c)) 和四阶傅里叶模态(图4(d)) 占主导的情况。傅里叶模态与流态的对应关系为:一阶模态对应偶极子流态,二阶模态对应四极子流态,三阶和四阶模态对应高阶流态。
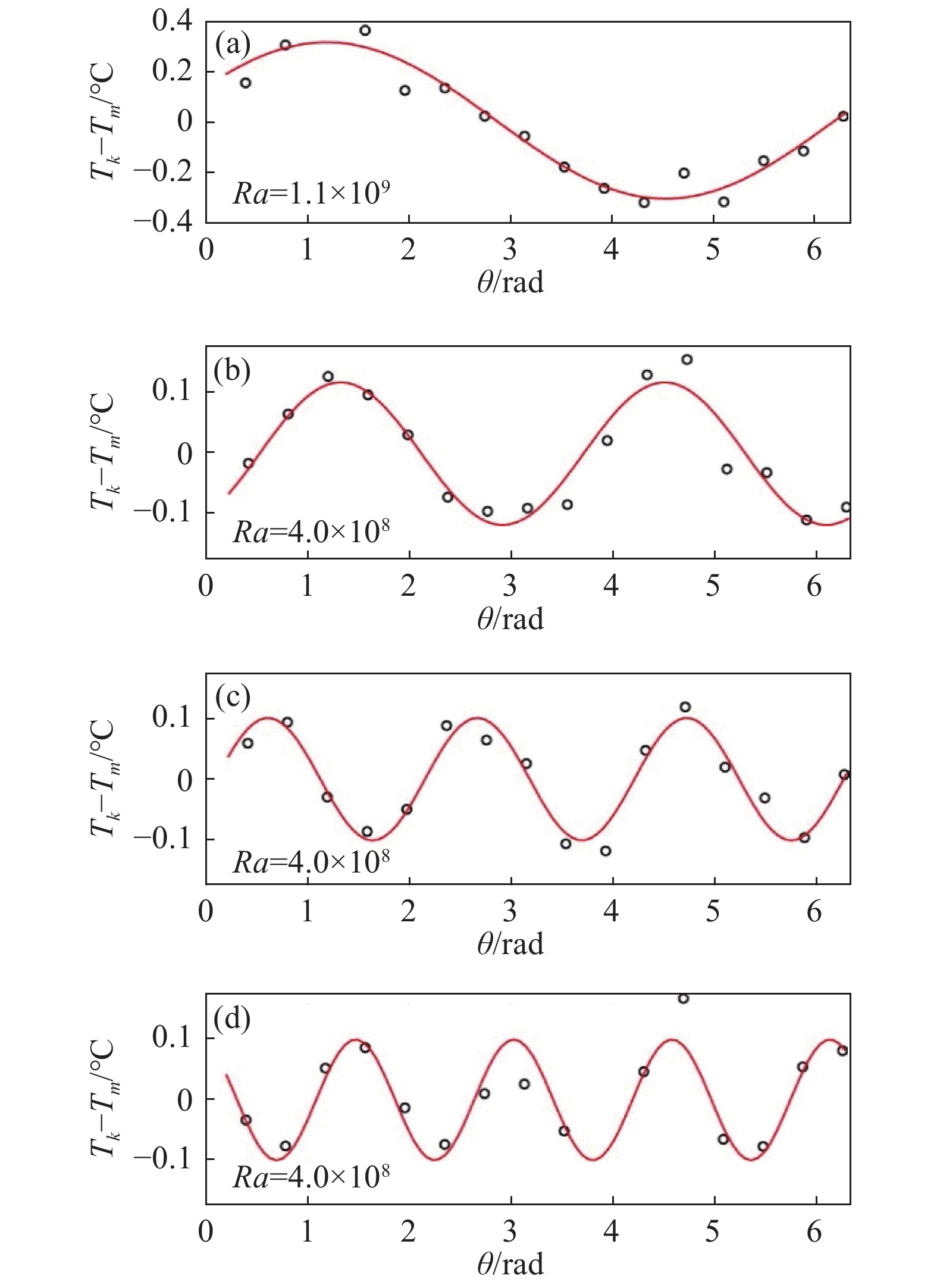
|
图 4 对流腔体z = H/2处不同模态主导时对应的温度分布:(a)一阶,(b) 二阶,(c) 三阶,(d) 四阶 Fig.4 Fourier modes of the azimuthal temperature profile measured at half-height of the convection cell: (a) the first mode, (b) the second mode, (c) the third mode and (d) the fourth mode |
为研究流态随Ra数的变化规律,引入模态相对强度Sk[26],其定义为:
| $ {S_k} = \max \left( {\left( {\frac{{A_k^2}}{{\displaystyle\sum\limits_{i = 1}^4 {A_i^2} }} - \frac{1}{4}} \right)\left/\left( {1 - \frac{1}{4}} \right)\right.,\;\;0} \right)$ | (7) |
这里k为1到4的整数。当第k阶模态的能量
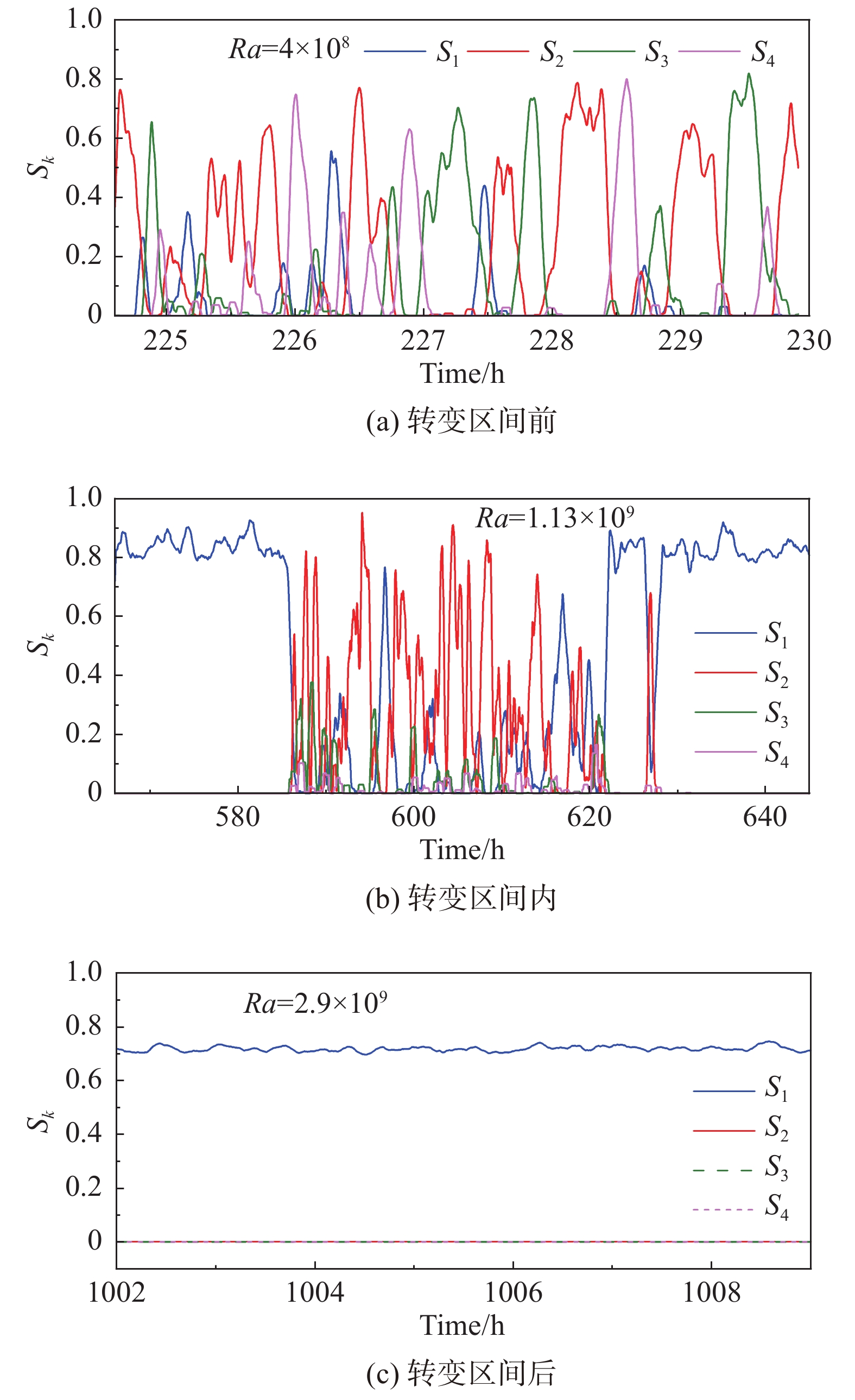
图5(a) 展示了Ra = 4×108时模态相对强度Sk的时间序列。为了更加清晰的看到大尺度湍流结构的动力学特性,图中的时间序列经过了一个低通滤波,后文将使用相同的方法处理数据。从中可以清晰地看到一阶模态到四阶模态阵发主导的现象。图5(b) 展示了Ra = 1.13×109时的模态相对强度的时间序列,可以看出此时系统先从偶极子流态主导的状态转变到了四极子流态主导的状态,四极子流态持续了接近30个小时,偶极子流态又重新成为了主导流态。这个流态转变过程与文献[23]中报道的类似,说明大对流腔体中也存在以不同大尺度湍流结构为典型特征的多重态现象。进一步分析给出大对流腔体流态的转变区间为1.0×109 ≤ Ra ≤ 1.4×109(见图11和图12)。
|
图 5 转变区间前 、转变区间内 、转变区间后前四阶傅里叶模态相对强度Sk的时间序列 Fig.5 Time series of Sk ( k = 1,2,3,4 ) : (a) before, (b) during and (c) after the transition |
图5(c) 展示的是Ra = 2.9×109的相对模态强度。由于此时大尺度结构完全由偶极子流态主导,其它阶流态的相对强度始终为0。综合图5(a~c),发现随着Ra数的增加,大尺度湍流结构从高阶模态主导的流态转变到了最低阶的一阶模态,这与文献[23]中的发现是一致的;与文献[23]不同的是在大对流腔体中Ra比较小的时候,大尺度湍流结构呈现出一阶到四阶模态交替随机出现的状态(图5(a))。而在文献[23]中,转变之前的大尺度湍流结构只存在偶极子流态。
从图5的分析中可以清楚地看出在大对流腔体中也存在多重态现象,那么不同流态出现的机率随Ra是如何变化的呢?图6反映的是不同流态主导时间占总时间的比重随Ra数的变化。在转变区间之前,偶极子流态主导时间比小于8%,而四极子流态主导时间比重相对快速上升,此外高阶模态占据了大约50%的时间,且高阶模态比重随Ra增大而减少。进入转变区间时,高阶模态相对一阶和二阶模态的占比已可以忽略。转变区间内,偶极子流态主导时间占比开始骤升,而四极子流态占比骤降。转变区间过后,全时域由偶极子流态主导。因此,图6反映了大尺度湍流结构随着Ra数的增加是如何从高阶流态动态地演化到了最低阶的湍流态。

|
图 6 不同模态时间占比随Ra数的变化 Fig.6 Time fractions of different flow modes versus Ra |
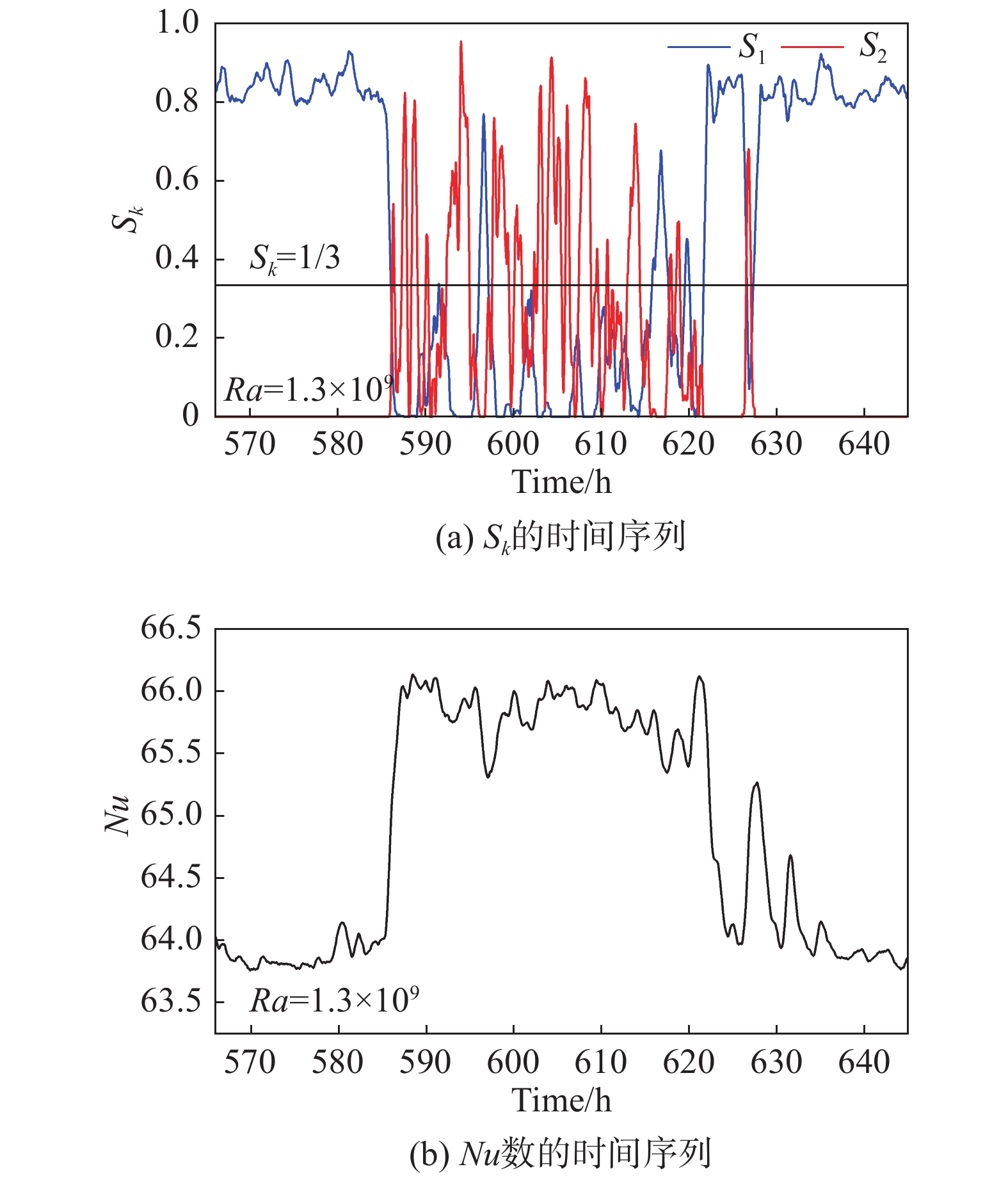
图7(a)为流态转变区间内S1、S2的时间序列,图7(b) 为对应Nu数的时间序列,可以看出偶极子流态主导时,RB系统的时均Nu数为Nu = 64 ± 0.12;而四极子流态主导时,系统的时均Nu数为Nu = 66 ± 0.21。由此可见,流态与输运效率存在明确的一一对应关系,且四极子流态的热输运效率高于偶极子流态。
|
图 7 转变区间Sk与对应的Nu数的时间序列 Fig.7 Time series of S1, S2 and the corresponding Nu during the transition |
图8给出了Ra = 1.06×109长时间采样的S1 、S2和Nu数的时间序列。可以看出偶极子流态和四极子流态随机交替成为系统的主导大尺度湍流结构,与此对应的是系统的Nu数也在两个状态之间变化。这与图7给出的例子是一致的。此外,在整个流态转变区间内(1.0×109 ≤ Ra ≤ 1.4×109)都观察到了类似于图8中所展示的现象,说明热湍流多态现象以及流态和输运效率一一对应是转变区间的普遍现象。

|
图 8 Ra = 1.06×109时S1、S2与 对应的Nu数的长时间序列 Fig.8 Long time series of S1, S2, and the corresponding Nu at Ra = 1.06×109 |
为了从统计上分析流态与输运效率的关系,分析
| $ {C_{x,y}}\left( {\Delta t} \right) = \frac{{\left\langle {\left( {x(t + \Delta t) - \left\langle x \right\rangle } \right)\left( {y(t) - \left\langle y \right\rangle } \right)} \right\rangle }}{{\sigma (x)\sigma (y)}} $ | (8) |
其中<···>表示时间平均。互相关函数表征的是两个时间序列在Δt间隔下的相关程度,其峰值代表两个时间序列相关程度达到极值的情况。峰值对应的时间延迟Δt如果是正值,表示x、y两组序列中的相关信号,在y序列中发生要先于在x序列;反之同理。
图9(a)和图9(b)分别展示了Ra = 1.13×109时,偶极子流态相对强度S1和Nu数以及四极子流态相对强度S2和Nu数的互相关函数。可以看出S1和Nu呈负相关,而S2和Nu呈正相关,说明偶极子流态越强,系统的热输运效率越低;四极子流态越强,系统的热输运效率越高;同时两个互相关函数的峰值均对应于负的时间延迟,说明大尺度湍流结构的变化引起了系统热输运效率的变化。

|
图 9 S1与Nu、S2与Nu的互相关函数 Fig.9 The cross-correlation function between (a)S1 and Nu and (b)S2 and Nu |
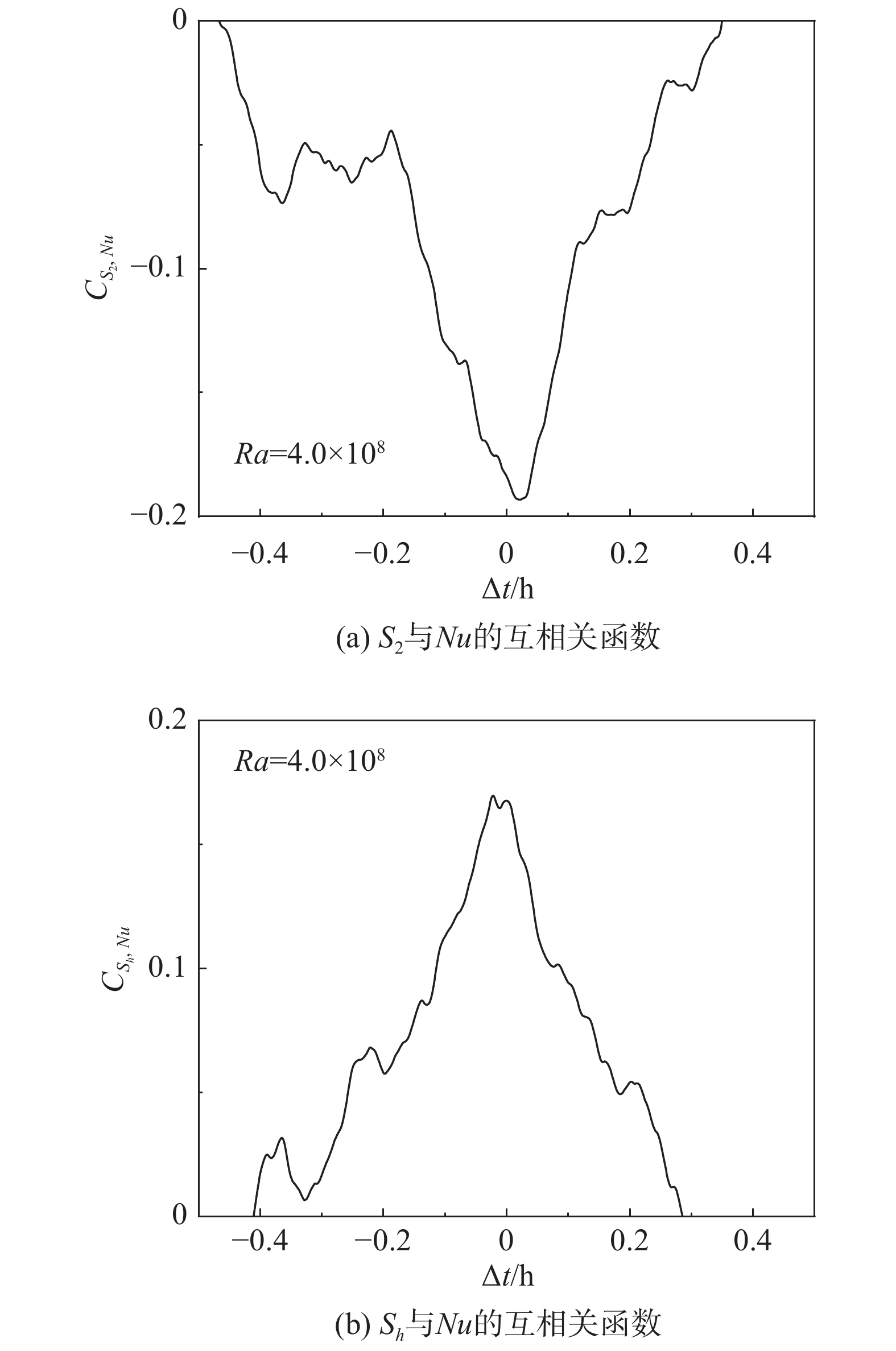
从图6中可以看出Ra = 4.0×108时,大尺度湍流结构主要由四极子流态和高阶模态占主导的流态主导。将它们的相对强度S2、Sh分别和Nu做互相关分析,这里Sh = S3+S4是高阶模态占主导的流态的相对强度。图10(a)和图10(b)分别展示了S2和Nu数以及Sh和Nu数的互相关函数。可以看出,四极子流态与热输运效率呈现负相关,同时高阶模态占主导的流态与热输运效率呈现正相关,再次说明高阶模态越强,热湍流系统的热输运效率越高。与图9不同的是,图10中互相关函数峰值的时间偏移并不明显,且其相关系数较小,这主要是由于Ra较小时,各阶模态主导时间尺度较短,且Nu数有较强的涨落。
|
图 10 S2与Nu、Sh与Nu的互相关函数 Fig.10 The cross-correlation function between (a) S2 and Nu and (b)Sh and Nu |
结合图9和图10可以得出:高阶模态主导湍流态的输运效率高于低阶模态主导湍流态,即高对称性流态热输运效率高于低对称性流态,这为通过主动调控湍流态从而调控系统的热输运效率提供了基础。目前,我们正在开展这方面的工作。
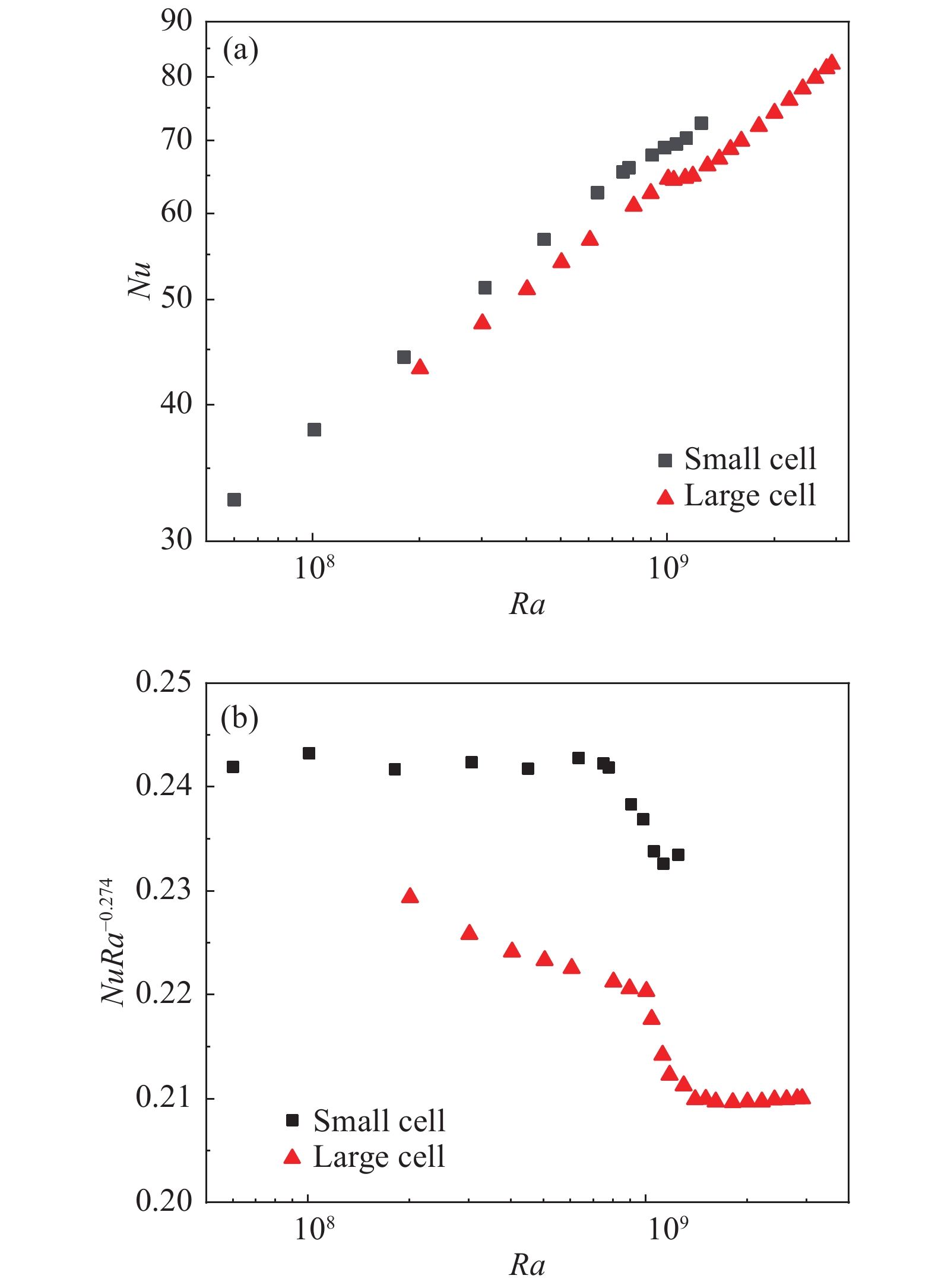
2.4 传热标度率图11(a)展示的是Nu数随Ra数的变化关系,横坐标和纵坐标都为对数坐标;图11(b)是使用补偿画法绘制的半对数图,纵轴是Nu·Ra−0.274,横轴是Ra的对数坐标,其中黑色方块和红色三角分别对应小对流腔体和大对流腔体中测得的Nu数。小对流腔体的数据已经发表于文献[23]。
|
图 11 (a)时均Nu与Ra的函数关系;(b) 补偿画法下的时均Nu~Ra关系图 Fig.11 (a) Time-averagedNu as a function of Ra; (b) time-averagedNu compensated by Ra−0.274 as a function of Ra |
从图11(a)可以看出大对流腔体的传热效率整体低于小对流腔体,造成这一区别的主要原因可能是对流腔的尺寸越小,漏热对其热输运效率的影响越大。对比图11(b) 中的补偿画法图可以看出,Nu数在两个对流腔体中都发生了一个明显的转变,但是转变的Ra数区间略有不同:在小对流腔体中,热输运转变的区间为6.4×108≤Ra≤1.1×109,而在大对流腔体中是1.0×109≤ Ra ≤1.4×109。结合2.2节中流动模态分析发现,在大对流腔体中系统传热效率出现明显转变的区间内,湍流大尺度流动结构在四极子流态和偶极子流态之间发生频繁的转变(见图8),此时热湍流出现多重态,这与小对流腔体中观察到的现象是一致的。
由于小对流腔体能够承受的最大温差的限制,其最大的Ra数约为1.2×109,此时系统刚刚进入由偶极子流态主导的区间。在大对流腔体中,通过增加腔体高度,在和小腔体相同的温差下,可以实现更大的Ra数,从而可以在更加宽的Ra数范围内研究RB热湍流系统的输运特性。从图11(b)可以看出,在大腔体中,系统在进入偶极子流态主导的参数区间以后(Ra > 1.4×10 9),其热输运的标度率为Nu~Ra0.274,这个标度律指数与系统单纯由四极子流态主导时是一致的(Nu~Ra0.274)。由于在大腔体中转变区间前的流态既包括四极子流态又包括高阶流态,且高阶流态的时间比重随着Ra数的增加而减小,因此转变区间之前的标度律为Nu~Ra0.25,小于系统由单一流态主导时的标度律指数。
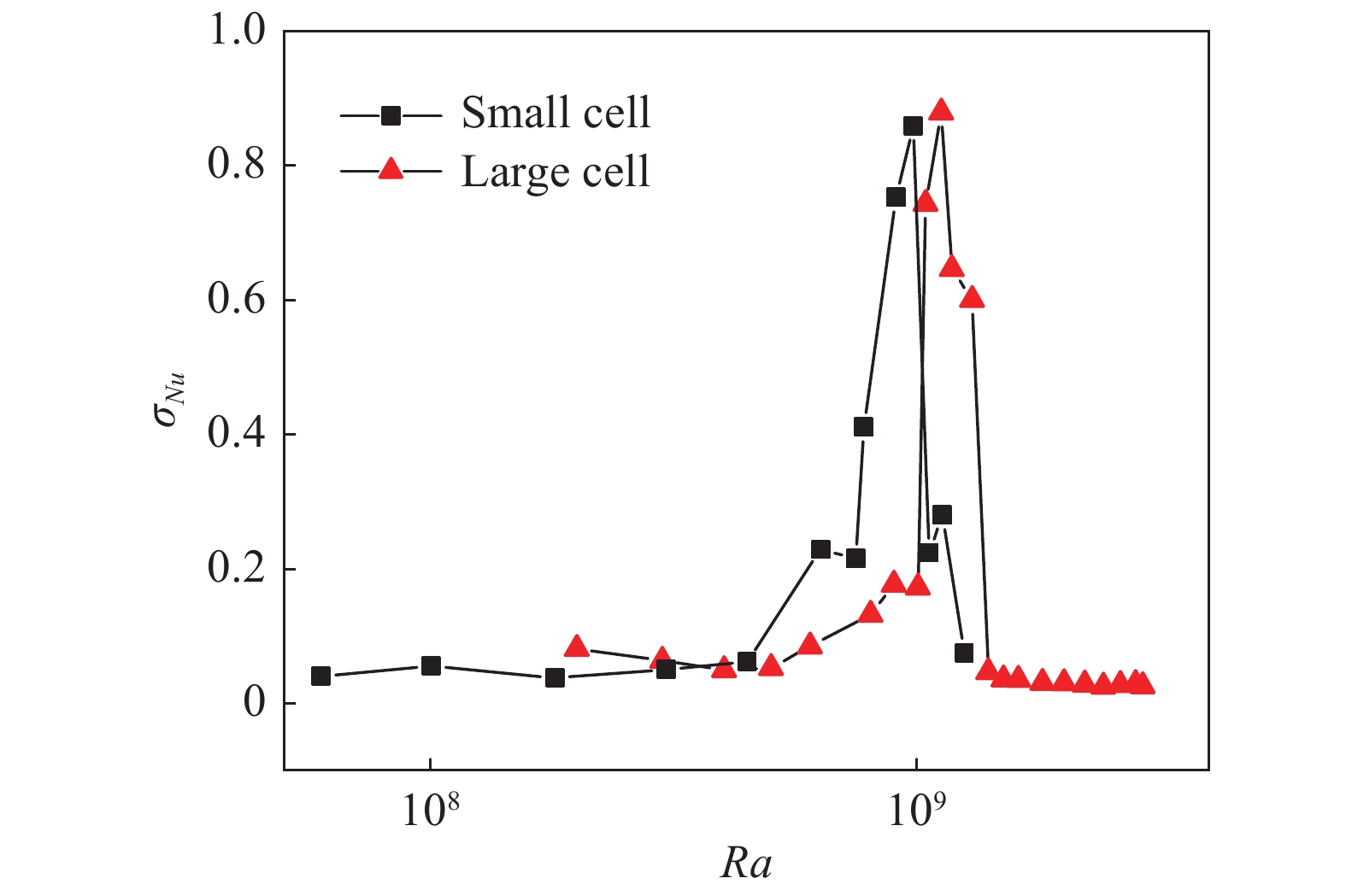
由于偶极子流态和四极子流态具有不同的热输运效率,因此湍流大尺度流动在这两个流态之间转变时,系统的Nu数会呈现出强烈的脉动。利用Nu数的标准差σNu (
|
图 12 半对数坐标下Nu的标准差σNu与Ra的关系图 Fig.12 The standard deviation of Nu as a function of Ra on a semilog plot |
从图6可以看出,随着Ra数的增加,RB系统会进入流态转变区间,此时偶极子流态和四极子流态交替成为主导流态,系统呈现出多重态。随着Ra数的进一步增加,偶极子流态成为唯一主导的流态,因此这一节主要研究偶极子流态在转变区间和转变之后的动力学特性。
图13(a) 展示的是转变区间内(Ra = 1.13×109)偶极子流态强度和相位随着时间演化的一个例子。图中不同的颜色代表不同的时刻;径向坐标轴代表偶极子流态的强度A1;角向坐标轴代表偶极子流态的相位 θ1,其定义为大尺度流动结构上行处的角向位置。图13(b)是转变区间不同Ra数下偶极子流态强度和相位随时间变化曲线,图中的箭头代表时间演化的方向。从图13(a)可以看出,偶极子流态主导时具有一个偏好的相位角。当偶极子流态逐渐增强时,如果其相位不处于偏好位置,它将通过角向游走运动到偏好位置。图13(b)是不同Ra数下的偶极子流态相位游走图,与图13(a)中的情况类似,当偶极子流态逐渐增强时,其相位会靠近并最终停留在偏好位置附近,这是偶极子流态在转变区间时的普遍现象。

|
图 13 转变区间偶极子流态强化过程:(a) 相位游走与时间的关系;(b) 不同Ra下的相位游走 Fig.13 The azimuthal meandering of the dipole mode (a) at Ra = 1.13 ×109 and (b) at various Ra |
当系统经过转变区间后(Ra>1.4×109),大尺度湍流结构完全由偶极子流态占据。图14(a) 是由偶极子流态完全主导时其强度和相位分布图;图14(b) 是偶极子流态强度A1的概率密度函数,黑色实线为标准高斯分布,插入图是A1的标准差

|
图 14 (a) 转变区间后偶极子流态强度和相位分布;(b,c) 偶极子流态幅值A1与相位θ1的概率分布函数,嵌入图为对应量的标准差随Ra数的变化 Fig.14 (a) The phase θ1 and amplitude A1 of the dipole mode after transition; (b) the PDFs of A1 and its standard deviation σA1 as a function of Ra; (c) the PDFs of θ1 and its standard deviation σθ1as a function of Ra |
从图14(a) 可以看出偶极子流态强度随着Ra数增加而增加,且其相位的涨落范围逐渐减小:Ra = 1.6×109时θ1的涨落范围为27°,而Ra = 2.9×109时θ1的涨落范围为7°。此外,不同时刻的θ1都汇聚于系统偏好的相位角处,表明偶极子流态具有明确的相位偏好,并且该方向与转变区间偶极子流态的偏好方向吻合。留意到在圆柱对流腔体中,大尺度湍流结构也存在相位偏好现象[21,25,27],同时相位存在周期性振荡[28]。而在大圆环对流腔体中由偶极子流态主导时,并没有观测到明显的周期振荡特性,说明强空间约束不但会改变大尺度湍流结构的空间结构,也会影响其动力学特性。
从图14(b) 和图14(c) 可以看出,不同Ra数时标准化以后的偶极子流态强度和相位大致重叠在一起,且可以用高斯函数来近似描述,说明偶极子流态在占主导以后其动力学特性不再依赖Ra。此外,偶极子流态强度A1的标准差
已有研究发现,通过在RB系统中引入空间约束可以实现热输运的强化,例如文献[29]中发现将矩形对流腔体沿着一个水平方向压缩,RB系统的热输运效率最高可以提升17%。在本文研究的圆环对流腔体中,内外径比γ 就是用来衡量系统空间约束强度的一个重要参数。图15展示了宽高比Γ = 2,内外径比 γ 分别为0.5和0.9的两个圆环对流腔体的Nu数。图中Γ = 2、γ = 0.5的数据来源于文献[30],其大尺度湍流结构一直处于四极子流态。

|
图 15 半对数坐标下时均Nu与Ra的补偿画法图 Fig.15 Time-averaged Nu compensated by Ra−0.274 as a function ofRa on semilog scale |
由图15可以看出空间约束究竟是增强还是抑制湍流热输运与Ra数(即湍流态)相关。当Ra<1×109的时候,强空间约束条件下(γ = 0.9),系统出现更高阶的流态。由2.3节的讨论可知更高阶的流态对应更强的输运效率,因此强空间约束可以增强系统的热输运效率。当Ra>1×109的时候,强空间约束下(γ = 0.9) 热湍流的流动结构已经被偶极子流态占主导;而此时 γ = 0.5的对流腔体中流动结构仍然是四极子流态,因此 在这种情况下γ = 0.5的对流腔体热输运效率更高。
3 结 论本文以水为工作流体,通过实验研究了Rayleigh-Bénard(RB)热湍流中的多重态现象和热输运效率。通过系统地测量两个宽高比和内外径比接近,但是特征高度不同的圆环对流腔体中的大尺度湍流结构和热输运效率,得出以下结论:
1)利用PIV直接测量了偶极子流态和四极子流态的空间结构,明确了圆环对流腔体RB热湍流中大尺度结构的速度分布和温度分布高度一致。因此可以通过直接测量温度空间分布得到大尺度流动的空间结构。此外,在内外径比γ = 0.9时,圆环对流腔体中的大尺度流动结构可以近似地看作沿角向和轴向的准二维流动。
2)在文献[23]的基础上,再次确认了热湍流存在多重态现象,即在相同的控制参数Ra数下,RB系统会出现不同的大尺度湍流结构和热输运效率。
3)通过同步测量大尺度湍流结构和热输运效率,发现了大尺度湍流结构与热输运效率存在一一对应关系,并且由高阶模态主导的湍流态的热输运效率高于由低阶模态主导的湍流态。为通过调控大尺度湍流结构从而调控热湍流输运效率提供理论基础。
4)随着Ra数的增加,偶极子流态强度的相对涨落和相位涨落降低,说明偶极子流态变得更加稳定。与圆柱对流腔体中大尺度湍流结构(大尺度环流)类似,偶极子流态也存在偏好的相位角,但是圆柱对流腔体中大尺度结构相位的周期性振荡在圆环对流腔体中并不存在,说明空间约束不仅会改变大尺度湍流结构的空间结构,也会影响其动力学特性。
5)通过对比不同空间约束程度的圆环对流腔体的热输运效率,发现空间约束增强或抑制湍流热输运效率取决于其对对流腔体中的流动状态的调控:当空间约束导致系统出现更高阶流动模态主导的流态时,空间约束会增强热输运;反之,当空间约束导致系统出现更低阶流动模态主导的流态时,空间约束则会抑制湍流热输运。
| [1] |
夏振华. 湍流中的多态现象[J]. 科学通报, 2019, 64(4): 373-383. XIA Z H. Multiple states in turbulence[J]. Chinese Science Bulletin, 2019, 64(4): 373-383. DOI:10.1360/n972018-01042 (in Chinese) |
| [2] |
FARANDA D, SATO Y, SAINT-MICHEL B, et al. Stochastic chaos in a turbulent swirling flow[J]. Physical Review Letters, 2017, 119(1): 014502. DOI:10.1103/PhysRevLett.119.014502 |
| [3] |
RAVELET F, MARIÉ L, CHIFFAUDEL A, et al. Multistability and memory effect in a highly turbulent flow: experimental evidence for a global bifurcation[J]. Physical Review Letters, 2004, 93(16): 164501. DOI:10.1103/physrevlett.93.164501 |
| [4] |
RAVELET F, CHIFFAUDEL A, DAVIAUD F. Supercritical transition to turbulence in an inertially driven von Kármán closed flow[J]. Journal of Fluid Mechanics, 2008, 601: 339-364. DOI:10.1017/s0022112008000712 |
| [5] |
CORTET P P, CHIFFAUDEL A, DAVIAUD F, et al. Experimental evidence of a phase transition in a closed turbulent flow[J]. Physical Review Letters, 2010, 105(21): 214501. DOI:10.1103/PhysRevLett.105.214501 |
| [6] |
HUISMAN S G, VAN DER VEEN R C A, SUN C, et al. Multiple states in highly turbulent Taylor-Couette flow[J]. Nature Communications, 2014, 5: 3820. DOI:10.1038/ncomms4820 |
| [7] |
Van Der VEEN R C A, HUISMAN S G, DUNG O Y, et al. Exploring the phase space of multiple states in highly turbulent Taylor-Couette flow[J]. Physical Review Fluids, 2016, 1(2): 024401. DOI:10.1103/physrevfluids.1.024401 |
| [8] |
GROSSMANN S, LOHSE D, SUN C. High–Reynolds number Taylor-Couette turbulence[J]. Annual Review of Fluid Mechanics, 2016, 48: 53-80. DOI:10.1146/annurev-fluid-122414-034353 |
| [9] |
GUL M, ELSINGA G E, WESTERWEEL J. Experimental investigation of torque hysteresis behaviour of Taylor-Couette Flow[J]. Journal of Fluid Mechanics, 2018, 836: 635-648. DOI:10.1017/jfm.2017.809 |
| [10] |
HUANG Y H, XIA Z H, WAN M P, et al. Numerical investigation of plane Couette flow with weak spanwise rotation[J]. Science China Physics, Mechanics & Astronomy, 2019, 62(4): 1-13. DOI:10.1007/s11433-018-9310-4 |
| [11] |
XIA Z H, SHI Y P, CAI Q D, et al. Multiple states in turbulent plane Couette flow with spanwise rotation[J]. Journal of Fluid Mechanics, 2018, 837: 477-490. DOI:10.1017/jfm.2017.869 |
| [12] |
ZIMMERMAN D S, TRIANA S A, LATHROP D P. Bi-stability in turbulent, rotating spherical Couette flow[J]. Physics of Fluids, 2011, 23(6): 065104. DOI:10.1063/1.3593465 |
| [13] |
YOKOYAMA N, TAKAOKA M. Hysteretic transitions between quasi-two-dimensional flow and three-dimensional flow in forced rotating turbulence[J]. Physical Review Fluids, 2017, 2(9): 092602. DOI:10.1103/physrevfluids.2.092602 |
| [14] |
MARSHALL J, SCHOTT F. Open-ocean convection: observations, theory, and models[J]. Reviews of Geophysics, 1999, 37(1): 1-64. DOI:10.1029/98rg02739 |
| [15] |
HARTMANN D L, MOY L A, FU Q. Tropical convection and the energy balance at the top of the atmosphere[J]. Journal of Climate, 2001, 14(24): 4495-4511. DOI:10.1175/1520-0442(2001)014<4495:tcateb>2.0.co;2 |
| [16] |
倪明玖. 磁约束核聚变关键能量转换部件的磁流体力学研究[J]. 力学与实践, 2010, 32(5): 1-9. NI M J. Magnetohydrodynamics relevant to liquid blanket of fusion[J]. Mechanics in Engineering, 2010, 32(5): 1-9. DOI:10.6052/1000-0879-lxysj2010-348 (in Chinese) |
| [17] |
AHLERS G, GROSSMANN S, LOHSE D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection[J]. Reviews of Modern Physics, 2009, 81(2): 503-537. DOI:10.1103/revmodphys.81.503 |
| [18] |
LOHSE D, XIA K Q. Small-scale properties of turbulent Rayleigh-Bénard convection[J]. Annual Review of Fluid Mechanics, 2010, 42: 335-364. DOI:10.1146/annurev.fluid.010908.165152 |
| [19] |
XIA K Q. Current trends and future directions in turbulent thermal convection[J]. Theoretical and Applied Mechanics Letters, 2013, 3(5): 052001. DOI:10.1063/2.1305201 |
| [20] |
XI H D, LAM S, XIA K Q. From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection[J]. Journal of Fluid Mechanics, 2004, 503: 47-56. DOI:10.1017/s0022112004008079 |
| [21] |
XI H D, XIA K Q. Flow mode transitions in turbulent thermal convection[J]. Physics of Fluids, 2008, 20(5): 055104. DOI:10.1063/1.2920444 |
| [22] |
STRINGANO G, VERZICCO R. Mean flow structure in thermal convection in a cylindrical cell of aspect ratio one half[J]. Journal of Fluid Mechanics, 2006, 548: 1-16. DOI:10.1017/s0022112005007378 |
| [23] |
XIE Y C, DING G Y, XIA K Q. Flow topology transition via global bifurcation in thermally driven turbulence[J]. Physical Review Letters, 2018, 120(21): 214501. DOI:10.1103/PhysRevLett.120.214501 |
| [24] |
XI H D, XIA K Q. Cessations and reversals of the large-scale circulation in turbulent thermal convection[J]. Physical Review E, 2007, 75(6 Pt 2): 066307. doi: 10.1103/PhysRevE.75.066307
|
| [25] |
XIE Y C, WEI P, XIA K Q. Dynamics of the large-scale circulation in high-Prandtl-number turbulent thermal convection[J]. Journal of Fluid Mechanics, 2013, 717: 322-346. DOI:10.1017/jfm.2012.574 |
| [26] |
KUNNEN R P J, STEVENS R J A M, OVERKAMP J, et al. The role of Stewartson and Ekman layers in turbulent rotating Rayleigh-Bénard convection[J]. Journal of Fluid Mechanics, 2011, 688: 422-442. DOI:10.1017/jfm.2011.383 |
| [27] |
BROWN E, NIKOLAENKO A, AHLERS G. Reorientation of the large-scale circulation in turbulent Rayleigh-Bénard convection[J]. Physical Review Letters, 2005, 95(8): 084503. DOI:10.1103/PhysRevLett.95.084503 |
| [28] |
XI H D, ZHOU S Q, ZHOU Q, et al. Origin of the temperature oscillation in turbulent thermal convection[J]. Physical Review Letters, 2009, 102(4): 044503. DOI:10.1103/PhysRevLett.102.044503 |
| [29] |
HUANG S D, XIA K Q. Effects of geometric confinement in quasi-2-D turbulent Rayleigh-Bénard convection[J]. Journal of Fluid Mechanics, 2016, 794: 639-654. DOI:10.1017/jfm.2016.181 |
| [30] |
ZHU X, ZHOU Q. Flow structures of turbulent Rayleigh-Bénard convection in annular cells with aspect ratio one and larger[J]. Acta Mechanica Sinica, 2021, 37(8): 1291-1298. DOI:10.1007/s10409-021-01104-z |
 2022, Vol. 40
2022, Vol. 40

