0 引　言

在自然界与实际工程应用中，流体局部温度的差异会产生一定的密度差，因密度差而产生的浮力会驱动流体产生热对流现象。常见的热对流现象包括热水沸腾、大气及海洋环流^[1-4]、地球内部浅层地幔对流^[5-6]、决定地磁场产生和变化的外地核对流^[7-10]等；热对流现象也应用于热核反应堆冷却^[11]、晶体制作^[12]、芯片散热^[13]等工业生产中。研究热对流的经典模型是底部加热、顶部冷却的Rayleigh-Bénard（RB）系统。图1展示了RB系统的示意图。在浮力驱动作用下，热流体上升而冷流体下降形成对流。对于充分发展的热对流而言，在上下导板附近会形成很薄的温度边界^[14-16]，冷热羽流分别从上下边界层中生成，并在浮力作用下自组织运动形成大尺度环流^[17]。

RB湍流热对流是一个复杂的非线性系统。在系统温差不大的情况下可以通过Oberbeck-Boussinesq近似^[18]简化模型，得到RB系统的控制方程：

$ \frac{\partial \boldsymbol{u}}{\partial t}+\left(\boldsymbol{u}\cdot \nabla \right)\boldsymbol{u} = -\frac{1}{\rho }\nabla p+\nu {\nabla }^{2}\boldsymbol{u}+\alpha g\delta T\hat{{\boldsymbol{z}}} $

(1)

$ \nabla \cdot \boldsymbol{u} = 0 $

(2)

$ \frac{\partial T}{\partial t}+\left(\boldsymbol{u}\cdot \nabla \right)T = \kappa {\nabla }^{2}T $

(3)

式中， $\boldsymbol{u}$ 和 $ T $ 分别代表速度和温度场， $ p $ 为压强场， $\hat{{\boldsymbol{z}}}$ 为竖直方向单位矢量， $ g $ 为重力加速度， $\; \rho $ 、 $ \nu $ 、 $ \alpha $ 和 $ \kappa $ 分别是槽内流体的密度、运动黏性系数、热膨胀系数和热扩散系数。 $ \delta T = T-{T}_{0} $ ， $ {T}_{0} $ 是对流槽的平均温度。以上方程将速度场、温度场和压力场联系起来，分别描述了RB封闭系统中的动量守恒、质量守恒和能量守恒。上述方程组经过无量纲化后，得到RB系统的两个重要控制参数Rayleigh数（Ra）和Prandtl数（Pr）：

$ Ra = \frac{\alpha g\Delta T{H}^{3}}{\nu \kappa } $

(4)

$ Pr = \frac{\nu }{\kappa } $

(5)

其中，Ra代表无量纲化的温差，Pr是流体本身的物理性质，代表动量扩散与热扩散之间的比值。对流槽的几何特征则通过宽高比 $ \varGamma = L/H $ 来描述，L和H分别是对流槽的水平宽度和高度。RB系统中的两个重要响应参数分别是Nusselt数（Nu）和Reynolds数（Re）：

$ Nu = \frac{J}{\lambda \mathrm{\Delta }T/H} $

(6)

$ Re = \frac{UH}{\nu } $

(7)

式中， $ J $ 是通过对流槽的实际热通量， $ \lambda $ 是流体的热传导系数， $ \mathrm{\Delta }T $ 是上下板之间的温差， $ U $ 是流动的特征速度。Nu用于描述系统的传热效率，Re表征对流的强度。

在RB系统研究领域中，湍流传热规律一直是人们关心的问题。其中，Grossmann-Lohse (GL) 理论^[19-20]是目前应用最为广泛的理论基础，该理论预测了Nu、Ra和Pr之间的标度律关系，定量地描述了湍流流动输运热量的内在机理。此外，在工程应用中，需要考虑如何通过被动或主动的方式控制热传输过程。经典的GL理论和大量的实验数值研究结果表明：在RB系统中，温度边界层特性与羽流结构的生成及演化过程关系密切，并决定了系统的热输运效率^[19-20]。在过去十多年中，研究者们尝试了许多控制对流传热以及流动结构演化的方法^[21-25]，例如在下板壁面加入粗糙元实现对系统传热的调制作用^[26]，通过侧壁温度控制实现对RB系统流动反转的调制^[27-28]，以及通过改变底板温度时间和空间分布实现对系统传热以及流动的调制作用^[29-30]。其背后的机理是通过改变边界层特性激发或抑制羽流结构的生成及演化，实现对系统传热以及流动的调制。其中，改变边界层特性主要有以下两个途径：一是改变上下板壁面的几何形状；二是改变壁面温度边界条件。本文将从以上两个方面，介绍近年来的最新进展。

1 边界粗糙元调制 1.1 边界粗糙元对传热的影响

粗糙边界作为一个调制传热的方法广泛应用于湍流热对流中。在过去的研究中，国内外学者曾采用不同粗糙元构型研究粗糙边界是如何调制湍流传热的（见图2）。Shen等^[26]以水为对流介质，在对流槽上下导板表面均匀地排布了金字塔状的粗糙元，实验发现当Ra超过某一临界值时，系统的整体热输运效率有约20%的增强。Stringano等^[31]通过数值模拟的方法，研究“V”形粗糙单元的对流槽对传热的影响，并与相关实验结果^[26]进行了对比。发现当平均热边界层厚度小于沟槽高度时，传热增加，这与实验研究结果一致。Wagner 和 Shishkina^[32-33]研究了具有扁平长方体粗糙元的三维矩形平行六面体对流槽，探究了规则壁面粗糙度对系统传热的影响，并观察到不同Ra时粗糙元对系统传热存在两种不同的调制效应：低Ra时，粗糙壁面与光滑壁面相比Nu-Ra的标度律指数增加；高Ra时，标度律指数趋于光滑壁面的标度律指数。Toppaladodddi等^[34]通过直接数值模拟方法，对带有正弦形状粗糙元的RB系统进行研究，通过改变粗糙元波长，发现存在一个最优波长使得Nu和Ra满足接近1/2的标度律指数。Zhu等^[36]又采用多尺度粗糙元，成功实现了Ra在更广的范围内保持1/2的标度率，Xia^[37]评价Zhu等^[36]提出的多尺度粗糙元方法，为边界粗糙元调制传热提供了一种新思路。Jiang等^[38]在对流槽上下板做了相反的棘齿粗糙元结构，发现非对称的粗糙元结构中，传热对大尺度环流的方向很敏感。

1.2 边界粗糙元调制传热机理

在上述研究中，一个值得讨论的问题是：对于不同几何构型，是否存在统一的传热调制机理？Shen等^[26]通过实验研究发现，粗糙元的高度是一个重要的物理参数。当粗糙元高度小于热边界层厚度时（h < δ_th），系统传热不受影响；当粗糙元高度h大于热边界层δ_th的厚度时（h > δ_th），对于 $ Nu = A(Pr,\varGamma ){Ra}^{\beta } $ 的前置因子 $ A(Pr,\varGamma ) $ 增加了大约20%。后续研究表明，当h > δ_th时，由于粗糙元尖端释放了更多的热羽流结构，导致了热输运的增强^[39]（如图3所示）。Du和Tong^[40]通过增加粗糙元的高度h，发现前置因子 $A(Pr,\varGamma )$ 快速增加。这是因为大尺度环流引发的强水平剪切流动与粗糙元相互作用使得相邻粗糙元之间形成二次涡，促进了羽流的生成，从而极大地提高了系统的整体热输运效率（Nu增加了超过76%）。综上所述，当粗糙元高度小于温度边界层时（h < δ_th），粗糙边界RB系统与光滑相比传热不会改变，此时称之为粗糙元湍流对流的Ⅰ区；当粗糙元高度大于温度边界层时（h > δ_th），此时湍流热对流进入传热增强区，称之为Ⅱ区（如图4（a）所示）。

随着研究的深入，研究者们发现粗糙元对系统传热调制规律不仅取决于粗糙元高度与温度边界层厚度的相对大小，而且与粗糙元与速度边界层的比值也有着紧密关系。Xie和Xia^[41]在实验中使用一系列不同粗糙度的粗糙边界，引入不同程度的边界层扰动，并通过粒子图像测速（PIV）技术获得了边界层附近流场并计算出速度边界层厚度。根据粗糙元高度与边界层厚度（温度边界层厚度δ_th、速度边界层厚度δ_u）之间的关系，在两个分区域（图4（a））的基础上，进一步将流动区域划分为三个区域（图4（b））：区域Ⅰ（h < δ_th< δ_u），此区域粗糙元边界不改变系统整体传热；区域Ⅱ（δ_th < h < δ_u），随着粗糙元相对高度的增加，粗糙元开始对系统传热产生影响转向Ⅱ区域；区域Ⅲ（δ_th< δ_u< h），当粗糙元高度大于速度边界层厚度（Pr > 1, δ_th< δ_u）流动进入区域Ⅲ，区域Ⅲ中Nu与Ra的标度律明显大于区域Ⅱ中的标度律（如图4（b））。需注意的是上述区域划分是在Pr > 1即 δ_th< δ_u的情况下进行的。随着Pr的减小，速度边界层与温度边界层的相对大小发生变化，传热规律也会发生变化，图4（b）中可以发现，在区域Ⅱ中随着Pr的减小，Nu增强有减小的趋势。Stringano 和 Shishkina等^[31,33]也观察到当粗糙元的高度较小时，它会降低系统传热效率。Zhang等^[35]数值计算了Pr = 0.7下粗糙元对系统传热的影响，解释了这种传热效率下降的机理。当粗糙元的高度较小时，流体黏性起主导作用，致使温度边界层变厚，热量被限制在粗糙元间的腔体之内，无法有效传进湍流体区间，导致传热效率下降（如图5所示）。

此外，研究人员也讨论了粗糙边界是否引起对流进入到“终极区间”。Toppaladoddi^[34]通过直接数值模拟，发现Nu～Ra的标度律指数约为1/2，与Kraichnan提出的“终极区间”指数相符合。Zhu^[24,36]在Toppaladoddi的研究基础上，采用相同的粗糙元并将Ra提高到Ra =10¹²。他们发现Nu与Ra标度律由1/2重回1/3。这说明Toppaladoddi等观察到Nu～Ra^1/2不是完全湍流状态的“终极区间”。

2 边界温度调制

在经典RB热对流系统中，上下导板之间在时间上和空间上都保持着恒定的温度差，即其上下导板的温度是定常且均匀的。然而，非定常非均匀温度边界条件下的湍流热对流现象比比皆是。例如，地表温度由于太阳辐射不均匀、陆地和海洋比热差异等使得地球表面温度分布不均匀^[42-44]。此外，局部受热不均引起的非均匀加热加也是非恒温的典型例子。在热湍流系统中，温度作为主动标量对速度场有反馈作用，因此当温度边界在时空分布上发生变化时，系统流动结构以及热输运效率均会受到边界条件调制作用的影响。

2.1 边界温度时间调制

温度时间调制是指控制边界温度随时间进行周期性的变化。早期的研究主要集中在流动对边界温度变化的响应。Lohse^[45-46]基于衰减湍流的平均场理论，建立了周期脉冲流动的平均场理论，通过该理论描述实验液氦流中能量的衰减，进而从理论上理解不同的流动状态，探索间歇性调制对这些流动状态的影响。研究发现对于足够大振幅A和频率f，雷诺数呈指数增长，然后达到饱和Re^sat。Re^sat可以通过衰减平均场理论解析获得，当雷诺数足够大时，满足Re^sat～Af的关系。Niemela等^[47]，在对流槽下导板施加扰动，以产生正弦变化的下导板温度边界条件, 他们发现当 Ra较低时，正弦变化的温度扰动将会以指数的形式向对流槽中央区域衰减，这一衰减方式类似于Stokes 流动；而当 Ra达到 10¹³ 以上时, 扰动将会无衰减地传递到对流槽的中央区域，他们认为这是因为对流槽中央区域形成了所谓的“超导”核心。Jin 和 Xia ^[48]通过实验在RB系统中的下导板施加周期脉动温度调制，发现周期脉动温度边界条件与恒温边界条件下的振荡频率f₀（大尺度环流周期T_LSC = 1/f₀）相等（图6（a）所示），并通过f₀定义了大尺度环流的雷诺数（Re_f = 4H²f₀/v），发现恒定温度和脉动温度边界条件的Re_f彼此吻合（图6（b）所示），说明了周期脉动温度不会破坏大尺度环流的结构。

在传热方面，由于在底板施加随时间变化的温度脉动，底板附近温度边界层受时间调制的影响而对系统传热产生影响。Jin 和 Xia^[48]在实验（下导板施加周期温度脉动）中发现在这种周期温度脉动调制热湍流中，与恒定的能量输入相比，传热效率（Nu）提高了约7%。一个重要因素是能量输入的反冲周期与湍流内在时间尺度同步。当输入能量脉冲的周期等于大尺度环流周期时间的一半时，系统产生了共振现象，导致了明显的传热增强。另一个重要的因素是脉冲信号的形状，尖峰脉冲比相同能量的平脉冲更有利于传热。近期，Yang等^[29]采用直接数值模拟方法对温度时间调制进行了研究。他们对RB系统的下导板施加正弦调制，调制频率跨越五个数量级。其研究发现传热显著增强（～25%），并通过Stokes热边界层的概念，将系统流动对调制频率f的响应分成了三个区域（如图7所示）：区域Ⅰ（δ_stokes<δ_th <δ_u），在区域Ⅰ内周期调制下Stokes边界层在温度边界层以内，此时由于调制频率较高，系统感受不到边界温的时间变化；区域Ⅱ（δ_th< δ_stokes<δ_u），在区域Ⅱ中系统传热对周期调制开始响应；区域Ⅲ（δ_th<δ_u<δ_stokes），在区域Ⅲ中调制频率进一步减小，系统中心温度开始受到不同时间相位差调制的影响。通过三个流动区域的划分，解释了Nu增强的开始频率和最大Nu的最佳频率，以及它们如何依赖于瑞利数Ra和普朗特数Pr。综上所述，在固定振幅的情况下，边界温度时间调制对系统传热的影响取决于调制频率。相较于低频的温度周期变化，高频调制衰减迅速，对系统流动调制作用有限。

2.2 边界温度空间调制

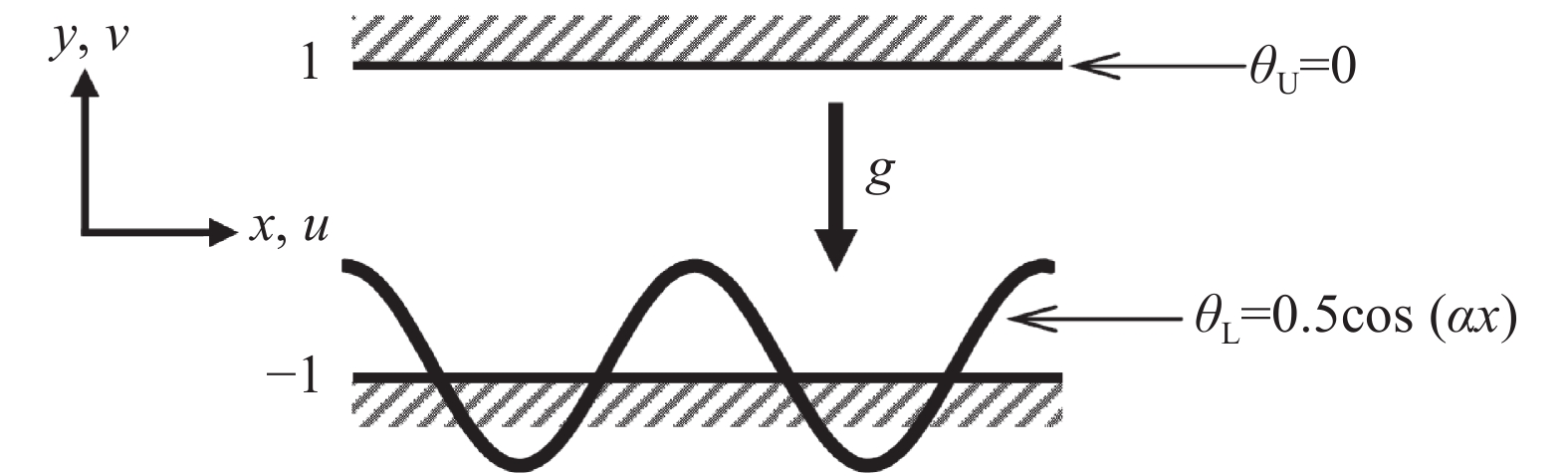
温度空间调制是指在导热板施加特定的温度分布。与响应时间调制单一维度不同的是，RB对空间调制的响应是多维度的，并存在着较宽范围的共振波数^[49-52]。这使得可以通过改变调制波数来实现对系统的不同调制模式^[53]。Kelly和Pal^[54]发现当Ra接近临界值时，小振幅且波长为系统失稳的临界波长的空间调制作用将会被放大。Curado等^[55]在调制波长与经典RB系统失稳的临界波长不相等时发现了对流具有准周期性。Walton^[56]研究了在下导板施加非均匀温度调制的对流系统。发现扰动主要局限于下导板温度最高点（“热点”）附近；同时采用局部分析预测了非均匀温度调制对临界瑞利数的影响。Schmitz 等^[57]研究了上下导板均施加周期性温度边界调制的二维热对流。导板间温差的非均匀性破坏了对流槽水平方向上的平移不变性；两种温度调制之间的相位差会使对流在水平方向发生移动。Mullarney等^[58]对下导板一半进行加热和另一半进行冷却，考虑大宽高比的对流槽，发现高Ra下，在冷板上方温度稳定分层，在热板上失稳产生羽流，在冷热板间非均匀温度产生的浮力作用下，系统形成大尺度环流，促进冷热板间的水平输运。Hossain等^[50]研究了下板施加一个正弦函数变化的温度调制，同时保证两壁面之间的平均温度相等的对流问题（如图8所示）。研究发现非均匀加热产生的对流强度随着调制波数的增加而减小（如图9所示）。除了采用单纯的温度空间调制，Reiter等^[59]在二维和三维对流系统中，在下导板施加行波温度边界条件，使得下导板同时受到空间和时间调制作用。结果表明行波可以引起系统的水平流动。Zhang等^[27-28]在RB对流统中提出侧壁温度控制的方法，通过改变温度控制区域的位置以及面积实现对大尺度环流反转的调制。

在传热方面，由于边界温度空间分布不均匀，局部高温会促进羽流的生成，进而影响传热。詹靖华、周全^[30,60]通过实验研究了空间线性非均匀加热对RB湍流热对流系统传热效率的影响。实验采用长方形对流槽并以水为流体介质，通过调节下导板加热片的输入功率，使得下导板温度呈线性分布，改变系统注入能量的空间分布。通过对比非均加热与均匀加热传热效率（Nu），发现在非均匀加热条件下对流强度和湍流传热效率都明显增强，如图10所示。吴磊等^[61]在文献[30、60]的基础上，通过实验研究了宽高比分别为0.99和0.25，以水为对流介质的矩形RB湍流热对流系统，通过改变下导板加热片输入功率的空间分布，使空间非均匀加热线性分布强度δ等于0、1/6、1/4和1/3，研究了空间非均匀加热对湍流流动结构的影响。实验中Ra从1.8×10⁹变化到9.1×10⁹，Pr固定为5.4。研究结果表明：非均匀加热提高了流体流动速度，并使羽流向边壁附近聚集，从而增强了系统的整体热输运效率。

3 结论与展望

本文介绍了近年来通过改变边界几何形状或温度边界条件对RB热对流系统进行调制的相关研究成果。研究结果表明：边界条件的改变对RB系统边界层的作用存在一个特征尺度——调制深度，系统传热对边界调制的响应规律则取决于该调制深度与温度和速度边界层厚度之间的几何关系。对于边界几何调制，调制深度与粗糙元的形状和几何尺寸有关。对于温度边界时间调制，调制深度取决于频率的大小，可通过斯托克斯边界层厚度δ_stokes来定量描述。与边界温度时间调制类似，调制深度与空间波数的息息相关，但调制深度与空间波数间的具体关系有待进一步研究。

尽管目前有关湍流热对流的边界调制及其机理的相关研究成果较为丰富，但仍有很多问题有待进一步深入的研究：

1）目前提出的边界调制机理是否具有普适性？如该调制机理在不同Pr下是否仍然成立？是否可以应用于其他典型的湍流系统？

2）不同的边界调制方式相结合，其调制结果能否产生叠加的效果？其调制机理是否发生变化？

3）如何利用现有的边界调制机理，提出相应的流动控制策略，以及通过机器学习方法实现对湍流热对流的控制？