2. 西北工业大学 航空学院,西安 710072;
3. 西北工业大学 极端力学研究院,西安 710072
2. School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China;
3. Institute of Extreme Mechanics, Northwestern Polytechnical University, Xi’an 710072, China
由温度梯度引发的湍流称为热湍流。热湍流在自然界和生产生活中普遍存在并起着至关重要的作用:在自然界中引起天气、气候变化的大气环流、海洋环流,引起大陆板块漂移的地幔对流,决定地磁场产生和变化的外地核对流等;在日常生活中的烧开水以及室内供暖;在工业生产中影响单晶晶体生长和金属制备过程中的对流、核反应堆内部及其乏燃料池中的对流等。人们针对这一类流动现象提出了一种模型系统,称之为瑞利-伯纳德(Rayleigh-Bénard,RB)热湍流系统[1-3]。
图1为矩形瑞利-伯纳德热湍流系统的示意图。瑞利-伯纳德热湍流系统是一个高度为H的封闭湍流系统,加热其下壁,保持温度T+ΔT,冷却其上壁,保持温度T,侧壁为绝热壁。整个热湍流系统中充满了流体介质,流体介质在上、下壁间温差ΔT的作用下,下(上)壁附近的流体受热膨胀(遇冷收缩),密度减小(变大),受到浮力的作用,从下(上)壁附近热(冷)的热边界层中脱落,形成高(低)于湍流背景温度的蘑菇状羽流结构。当系统的控制参数Rayleigh数(Ra)、Prandtl数(Pr)、宽高比(Γ = L/H)进入一定的参数空间时,羽流由于羽流之间的相互作用最终自组织形成大尺度的相干结构,即大尺度环流(Large-Scale Circulation,LSC)[4-5]。理解热湍流系统中相干结构的动力学特征有助于理解湍流热输运、边界层结构以及湍流脉动等重要问题。

|
图 1 矩形瑞利-伯纳德热湍流系统和流动示意图(红色代表高温流体,蓝色代表低温流体,绿色箭头指明了大尺度环流的流动方向) Fig.1 (Color online) Sketch of a rectangular turbulent RB convection(The red-arrows and blue arrows indicate the hot and cold plumes respectively. The green arrow represents the direction of the large-scale circulation) |
2008年,郗恒东与夏克青首次在圆柱形瑞利-伯纳德热湍流系统中通过实验发现了热湍流系统中的多湍流态现象[6],即在相同的控制参数下,系统的大尺度流动存在不同的湍流状态(结构),而且不同的湍流状态可以自发地切换。对于流动在某一确定的控制参数下所处的流动状态,Kolmogorov在1941年提出的湍流理论[7]认为,对于充分发展的湍流,其脉动足够大以至于流动会遍历所有的相空间,因而这种充分发展湍流的小尺度统计特性应只存在一种统计稳定的状态。经典的湍流理论假设湍流是各态遍历的,也就是说即使某些中间状态可能会受到例如初始条件等因素的影响,但是其统计平均量是不依赖于初始流场的。各态遍历假设是湍流理论的一个重要基础。大尺度流动的多湍流态的发现及其进一步的研究,势必会为经典的湍流理论提供一个强有力的补充。近年来这种多湍流态现象陆续在不同的湍流系统中被发现并且被广泛且细致的研究,除了本文所描述的热湍流系统[6, 8-20],还包括泰勒-库埃特湍流系统[21-22]、双扩散对流湍流系统[23]、冯·卡门湍流系统[24]、旋转球壳库埃特流动系统[25]、展向旋转平板库埃特湍流系统[26]、二维强迫剪切流动[27]、二维槽道流动[28]、风洞中流经作钟摆运动的圆盘后的流动[29]以及T型混合器中的流动[30]等。在上述的研究中,一个普遍的发现是当系统处于不同的湍流状态时,系统中的大尺度相干结构存在显著的差异,同时系统的某些输出参数,例如系统整体的能量输运效率、动量输运效率或者流动的掺混效率等,也有显著的不同。早先对于湍流相干结构的研究告诉我们,湍流结构是湍流基本物理过程的流场时空分布表征,湍流结构的时空演化直接主导了流体的动量、能量和物质的输运特性,因而对湍流中力、热的产生及其非定常输运起着决定性的作用。因此,知晓在某一控制参数下,系统处于何种流动状态对理解、进而调控此时系统的动量、能量以及物质的输运特性是十分关键的。
此外,多湍流态现象在自然界的流动中也有展现。在海洋环流中,一个典型的例子是日本东海岸的“黑潮”,这是与北大西洋湾流齐名的一支强大的暖性海流。“黑潮”时不时会改变其沿着日本东海岸自南向北的流动方向,转头回流,出现所谓的“大蛇行”现象[31],进而引发西太平洋地区一系列的海洋生态问题,最近一次“大蛇行”发生在2017年8月。再者,例如在地球的大气环流中,中纬度地区的大气以西风为主且几乎是带状流动,然而,这种西风流动会被突然出现并可以持续很长时间的反气旋流动阻挡,从而向极地明显偏移[32]。此外,外地核中的液态金属的对流[33]也存在着流动反向的现象。多湍流态现象不仅在地球上的大气、海洋和外地核的流动中出现,在木星大气中也有出现,其对流层中的条带状的射流流动在1939年至1940年间失去了其中一股,取而代之的是三个呈现白色的反气旋流动,这一事件被称为木星气候突变事件[34],这也可以认为是一种新的湍流状态。
本文将就瑞利-伯纳德热湍流系统中多湍流态现象的研究成果进行综述。通过近些年的研究发现,多湍流态现象大致可以分为两类:一类是在相同的初始条件下,随着流动的发展,流动在不同的湍流状态下自发地、随机地切换,上一段中提到的自然界中的多湍流态现象目前来看也均属于这一类;另一类则是由于在流动初始时刻给定了不同的初始条件进而导致系统演化为不同的流动状态,并且该流动状态十分的稳定,可以保持很长的一段时间。下文中,我们将就瑞利-伯纳德热湍流系统中这两类多湍流态现象分别展开介绍。在本文的最后,我们将给出总结与展望。
1 相同参数条件下自发产生的多湍流态现象我们首先讨论相同参数条件下自发产生的多湍流态现象。郗恒东与夏克青[6]最早在圆柱形热湍流系统中通过实验发现了该类型的多湍流态现象。他们通过实验分别研究了宽高比为1、1/2和1/3的热湍流系统中的流动结构随时间的演化规律,发现在这三个宽高比的热湍流系统中,单环的大尺度环流模态(single-roll state, SRS,可见图2(c)、图3 (a))和上下堆叠排列的双环模态(double-roll state,DRS,可见图2(c)、图3 (b))均可以稳定存在,且这两种流动状态可以自发地、随机地相互转换。
图2展示了在对流腔体的上(3H/4)、中(H/2)、下(H/4)三个不同高度上通过多点温度测量方法测得的流动在单环模态与双环模态之间的一次转变。多点温度测量方法是由Cioni等[35]提出并在之后相关的研究中被广泛使用[36-38]。众所周知,大尺度环流实际上是冷、热羽流的自组织运动[39],基于此,对于圆柱形热湍流系统,我们可以在某一横截面周向均匀地布置若干(此处使用8个)温度探头,通过使用函数Tn = T0+Acos(nΠ/4−ϕ),n = 0,···,7,拟合某一瞬时时刻测得的8个周向温度值,可以获得大尺度环流的瞬时方位角ϕ以及大尺度环流的瞬时强度A。从图2可以看到,在150 s之前,我们可以观察到上、中、下三层测得的大尺度环流平面的方位角几乎重合,说明此时系统内的流动呈现一个尺寸与系统尺寸相若的单环结构,如图2(c)中的左侧示意图所示。在150 s左右,Atop的值降低至0附近,紧接着,ϕtop的值突变了180°,即当地大尺度环流的方位角发生了反向。结合Atop、ϕtop的变化,说明原先的大尺度环流在系统的上部出现了分裂,形成了一个新的相反流动的涡结构。我们还注意到ϕmid、ϕbot的值从始至终都较为接近,这说明分裂之后的上、下两个涡并非是对称的,下方的涡结构尺寸要大于上方的涡结构,如图2(c)中的中间示意图所示。流动在双环模态下保持了一段时间之后再次回到了原先方向的单环模态。当然,这里新形成的单环模态也不总是保持原先的流动方向,有时也会形成相反方向的单环流动。

|
图 2 Ra = 3.3×1010,Γ = 1/2,利用多点温度测量方法测得的流动状态随时间的演化[6]:(a)上、中、下三层分别测得的大尺度环流方位角ϕtop、ϕmid、ϕbot的时间序列;(b) 与(a)对应时刻的上、中、下三层分别测得的大尺度环流的流动强度Atop、Amid、Abot的时间序列;(c)流动状态演化的卡通示意图,其中箭头分别代表不同层温度探头所处的高度 Fig.2 (Color online) Flow mode transition in Γ = 1/2 cell at Ra = 3.3×1010[6]: (a) segments of time traces of the orientation angles ϕtop, ϕmid, ϕbot; (b) corresponding time traces of the flow strengths Atop, Amid, Abot; (c) cartoons depicting the flow structure before, during, and after a flow mode transition. The arrows indicate the positions of the three rows of thermistor |
图3是利用粒子图像测速技术(PIV)测得的速度场,展示了一次单环模态-双环模态-单环模态的转变过程。从图中可以清晰地看到在t = 0s时,流动呈现一个倾斜的大尺度环流,即单环结构;随后,在t = 72 s时,流动自单环模态破裂为上、下堆叠的两个涡,并且下方的涡结构尺寸更大;在t = 184 s时,流动又恢复到单环结构。这样的转变过程与通过多点温度测量方法测得的结果一致。

|
图 3 Ra = 5.3×1010, Γ = 1/2,利用粒子图像测速技术(PIV)测得的流动状态随时间演化的瞬时速度场[6]:(a) 单环模态(SRS);(b) 双环模态(DRS);(c) 再次回到单环模态 Fig.3 (Color online) PIV-measured instantaneous velocity vector fields showing a flow mode transition in Γ = 1/2 cell at Ra = 5.3×1010[6]: (a) single-roll mode (SRM); (b) double-roll mode (DRM); and (c) single-roll mode again |
此外,该工作还研究了宽高比对多湍流态的影响,发现宽高比影响不同湍流态(结构)持续存在的时间。Γ = 1时,约87.1%的时间系统流动处于单环模态,仅有0.8%的时间流动处于双环模态;而当Γ = 1/2时,单环模态所占的时间降低至69.5%,双环模态则上升至7.9%;当Γ = 1/3时,单环模态所占的时间进一步下降,至26.7%,双环模态则进一步上升,并超越单环模态,达到了34.1%。此外,通过细致地测量系统的传热效率,他们发现当流动在不同的流动状态之间切换时,系统的传热效率也相应地变化。通过直接比较系统处于不同流动状态时的传热效率(无量纲的热输运效率Nusselt数(Nu)),他们发现,单环模态相较于双环模态更有利于传热。
随后,Weiss和Ahlers[10]延续了郗恒东和夏克青的工作,单独针对Γ = 1/2的热湍流系统进行了更为细致且系统的研究。首先,他们在实验中同样观测到了郗恒东和夏克青[6]发现的多湍流态现象。之后,他们研究了不同湍流态存在的时间与Ra数之间的依赖关系,他们发现单环模态所占的时间随着Ra数的增长逐渐从12%(Ra = 2×108)提升至80%(Ra = 1011),双环模态则相应的由40%降低至6%。此外,他们也证实了郗恒东等[6]提出的单环模态相较于双环模态更有利于热量输运的结论。图4(a)展示了系统传热效率Nu(t)与流动所处湍流态之间的互相关,从图中可以发现单环模态的强度与传热效率呈现正相关,证明单环模态更有利于传热,而双环模态的强度则与传热效率呈现负相关,证明其不利于传热。图4(b)则进一步定量地给出了单环模态相较于双环模态传热效率增加的幅度,在Ra = 1010(1011)时,单环模态的传热效率比双环模态的传热效率高1.6%(0.9%)。

|
图 4 (a) Ra = 9.0×1010,Γ = 1/2,系统传热效率Nu(t)与流动状态参数S(t)之间的互相关,红色实线代表单环结构(SRS),蓝色虚线代表双环结构(DRS);(b) 归一化后的单环结构传热效率与双环结构传热效率的差别,图中实线为对数据的幂律拟合,得到的幂指数为–0.25±0.07. 图取自参考文献[10] Fig.4 (Color online) (a) Time cross-correlation functions between Nu(t) and the state function S(t) for the SRS (solid red line) and the DRS (dashed blue line), These results are for Ra = 9.0×1010,Γ = 1/2; (b) Normalized differences in Nu between the SRS and the DRS on logarithmic scales. The solid line is a power-law fit which yielded the exponent –0.25±0.07. The figure is adapted from Ref.[10] |
Zwirner等[18]在更小宽高比(Γ = 1/5)的圆柱形热湍流系统中利用直接数值模拟同样发现,在相同的控制参数下,存在单环模态以及双环模态两种可以稳定存在的流动状态,并且他们指出双环模态的传热效率仅为单环模态的80%,这个数值比实验中测量得到的数值(约1%~2%)要大很多。最近,Zwirner等[19]进一步利用直接数值模拟探索了在Γ = 1/5的圆柱形热湍流系统中的多湍流态现象及其产生的原因。他们发现在Ra = 5×106,Pr = 0.1,Γ = 1/5时,不仅存在单环模态、双环模态,还会存在上下堆叠排列的三环、四环模态(可见图5(a~d))。同时,他们发现流动中涡环的数量越多,传热效率也相应的越低,在Ra = 5×106时,单环模态的传热效率是四环模态传热效率的2.5倍。此外,他们还发现此时的流动更倾向于处在双环模态,其存在的时间占比达到了40.6%。在该参数下,单环、双环、三环以及四环模态平均存活时间(以系统特征时间归一化)、各种流动模态平均存在时间占比以及传热效率可见表1。

|
图 5 Ra = 5×106,Pr = 0.1,Γ = 1/5,大尺度环流的瞬时流线图[19]:(a) 单环结构;(b) 双环结构;(c) 三环结构;(d) 四环结构;(e) 由于椭圆不稳定性而产生的强烈的周向流动 Fig.5 (Color online) Instantaneous flow fields, for a LSC composed of a different number n of rolls[19]: (a)n = 1; (b) n = 2; (c) n = 3; (d)n = 4; (e) a snapshot illustrating a strong azimuthal motion, due to the elliptical instability. Parameters are Ra = 5×106, Pr = 0.1, Γ = 1/5 |
| 表 1 Ra = 5×106,Pr = 0.1,Γ = 1/5,单环、双环、三环以及四环模态平均存活时间(使用系统特征时间归一化)、平均存在时间占比以及传热效率Nu [19] Table 1 Mean lifetime, probabilities, and mean heat transport efficiency Nu of n-roll flow modes (n = 1, 2, 3, 4), for Ra = 5×106, Pr = 0.1, Γ = 1/5 |
|
|
关于多湍流态发生的原因,Zwirner等认为是由于单环结构大尺度环流的椭圆不稳定性,定量的分析也支持他们这一结论。椭圆不稳定性是指由具有椭圆形流线的二维平面流动破裂产生三维流动的失稳机理(可见综述论文[40])。在Γ = 1/5的热湍流系统中,当流动处于单环模态时(如图5(a)所示),可以被认为是一个具有椭圆形流线的二维平面流动,当其受到一定的扰动时,椭圆不稳定性将会引起其破裂,从而产生多环模态。图5(e)展示了一个单环流动破裂过程中的瞬时场,从该流场中可以看到很强烈的周向运动,正是这样的周向运动破坏了单环结构的大尺度环流。针对这样的模态间转变机制,Zwirner等认为只有当椭圆不稳定性的增长率远大于系统中黏性耗散引起的阻尼(可简单认为是维持当前流动状态的稳定项)时才能发生。事实上也正是如此,Zwirner等发现在该参数下,椭圆不稳定性的增长率要远远大于其他的稳定性项。
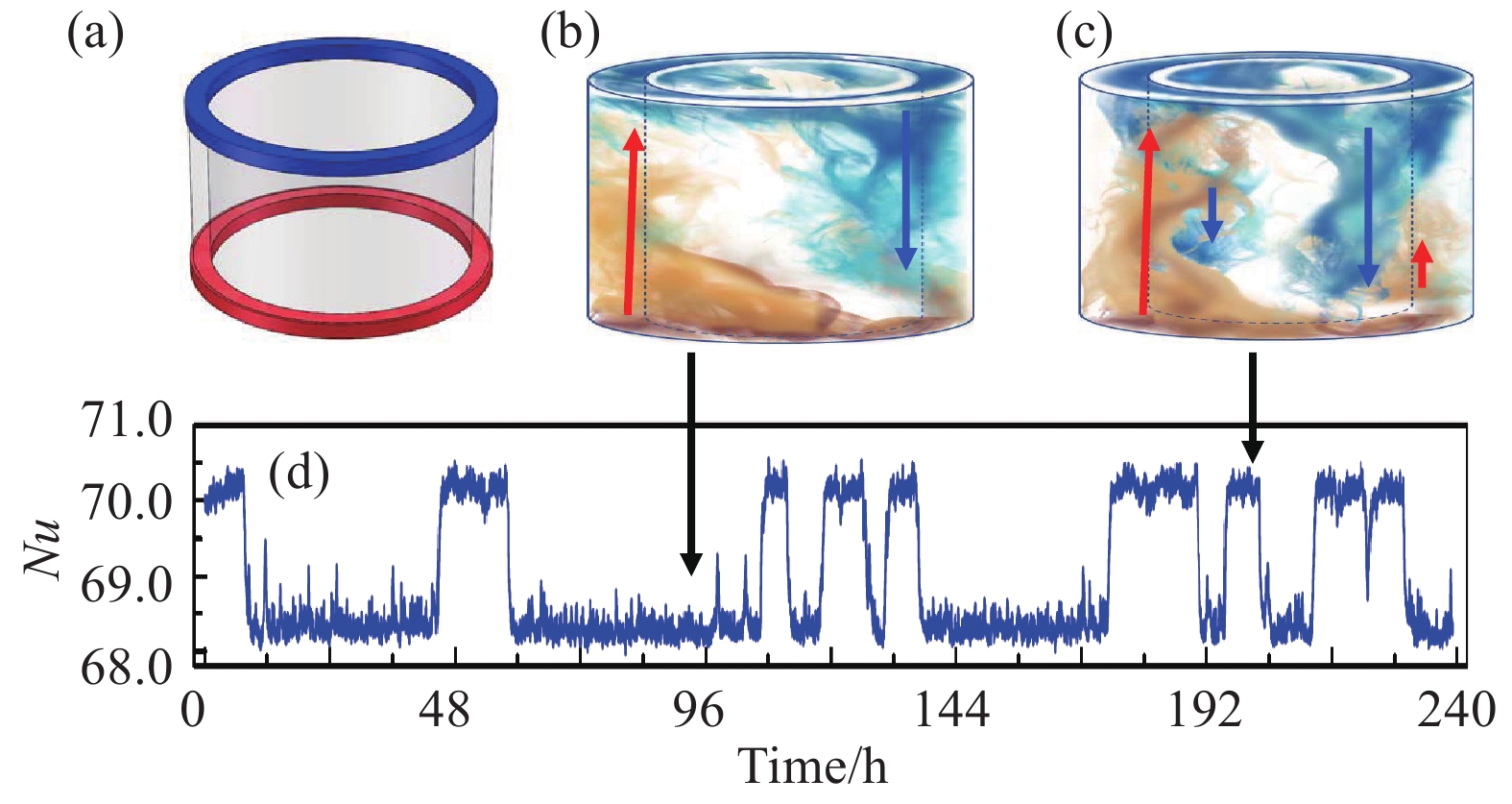
最近,谢毅超等[12]设计了一种两个同轴空心圆筒形成的圆环型的热湍流系统(见图6(a)),并在这种热湍流系统中同样发现了多湍流态现象。通过长时间的流场结构与传热效率的同步测量,发现系统的传热效率会在两种稳定状态下自发且随机地转换,见图6(d),而且这种传热效率的转换与流场结构的转换一一对应。这种一一对应的关系表明,对称性更高的四极子流动状态(见图6(c))有着更高的传热效率,而对称性相对较低的偶极子流动状态(见图6(b))的传热效率也相对较低。通过这个实验,他们认为在热湍流系统中存在通过全局分叉实现的流动状态自发且随机地转换,并且整个系统中的流动状态由于自发的对称破缺使得系统整体流动变得更加混乱。
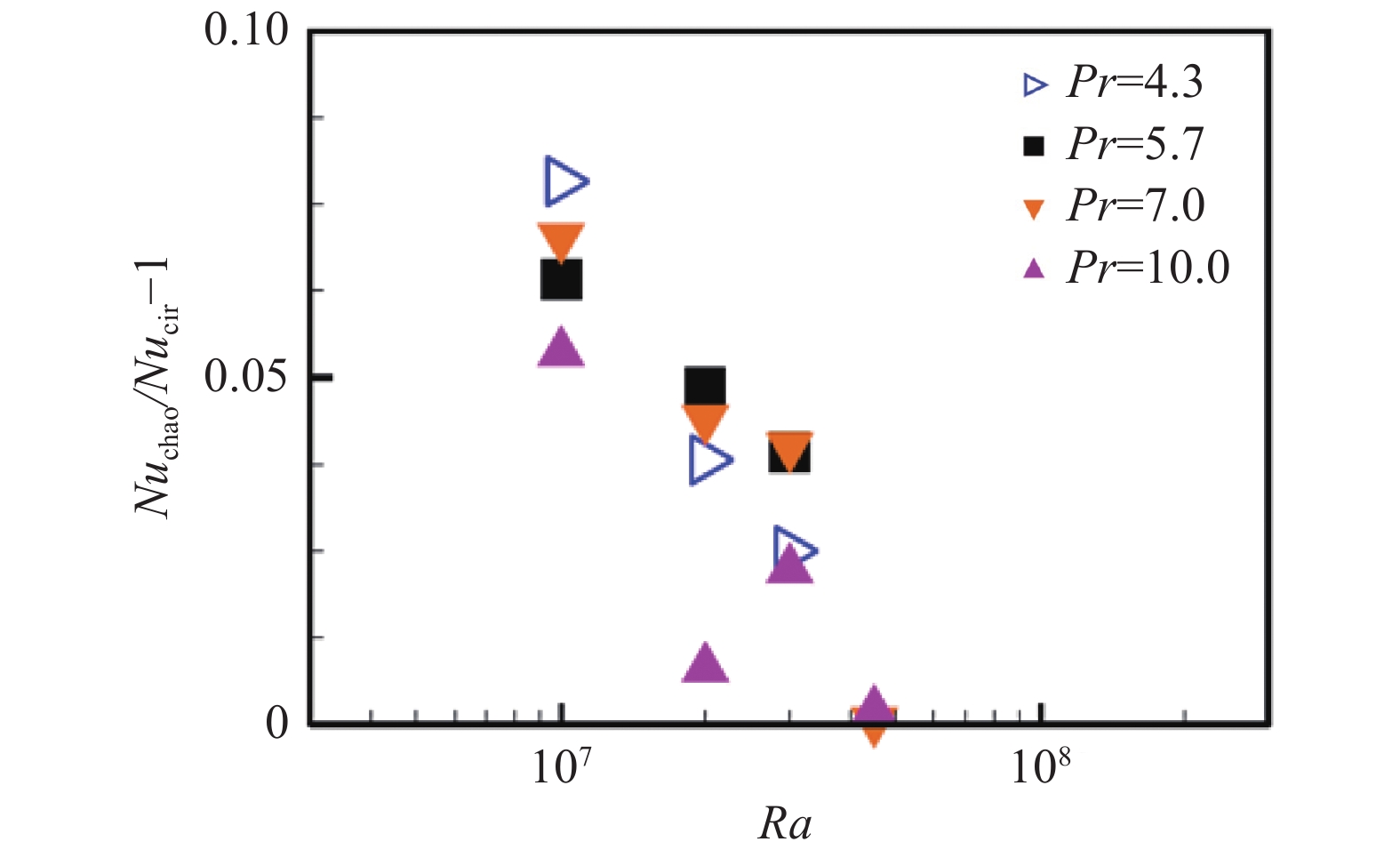
此外,徐翱和陈鑫等[20]最近在圆盘形热湍流系统中也发现多湍流态的存在。我们发现在该种热湍流系统中,除了已知的呈现为大尺度环流的流动状态之外,还存在着一种混乱无序的流动状态,此时,羽流不会沿着边壁上升(下降),而会随机地发射,大量的羽流选择经过系统的中心区域抵达对面边界,无法自组织形成大尺度环流。通过定量地分析系统处于不同流动状态时的传热效率,我们同样发现这两种流动状态的传热效率有着明显的区别,如图7所示,处于混乱无序的流动状态时,根据Pr的不同,系统的传热效率相较于处于大尺度环流状态时最高可提升8%。
|
图 6 (a) 谢毅超等设计的一种圆环型热湍流系统的示意图;(b) 偶极子流动状态示意图;(c) 四极子流动状态示意图;(d) Ra = 9.84×108时,系统传热效率Nu的时间序列. 图取自参考文献[12],图中箭头代表一一对应关系 Fig.6 (Color online) (a) Schematic of the annular convection cell. Sketches of (b) dipole state and (c) quadrupole state. (d) Time series of Nu at Ra = 9.84×108. The figure is adapted from Ref.[12]. The arrows represent the one-to-one correspondences between the flow states and Nu |
|
图 7 在不同的Pr下Nuchao/Nucir – 1随Ra数的变化[20],这里的Nuchao和Nucir分别为流动处于混乱无序的流动状态以及处于大尺度环流时热输运效率Nu的条件平均 Fig.7 (Color online) Values of Nuchao/Nucir – 1 as function of Ra for various Pr[20]. Here, Nuchao, Nucir are the conditional average Nu when the flow is in the chaotic state and the circulation states respectively. The figure is adapted from Ref.[20] |
实际上,还有一类特殊的多湍流态现象,即热湍流系统中大尺度环流的流向反转现象[38, 41]。在热湍流系统中,正如我们在前文中一直提到的,一个重要的湍流结构是与系统尺寸相若的大尺度环流。大尺度环流的流动方向可以沿着顺时针方向,也可以沿着逆时针方向。在流动过程中,顺时针、逆时针方向运动的大尺度环流可以自发且随机地切换,经过长时间的统计测量,这两种流动状态出现的概率几乎相同。流向反转一向是流体力学中极为重要的一类问题,同时也是一类小概率(极端)流动事件,一直吸引着众多研究者的目光。但需要指出的是,对于大尺度环流流动方向的反转是否也会带来某些系统输出参数例如热输运效率Nu显著的变化,在目前的研究中并没有发现这样的特征。因此,我们将不把流动的反转列入本文的讨论范围,不在这里进行过多的描述,感兴趣的读者可以参考笔者相关的论文[42]。
2 不同初始条件引发的多湍流态现象我们接着讨论不同初始条件引发的多湍流态现象。王启等[13]在这个方面做了最为系统的探索。他们利用二维直接数值模拟,在1≤Pr≤100,107≤Ra≤1010的参数空间内,研究了在较大宽高比Γ(最高到32)二维矩形热湍流系统中流动对于不同初始条件的响应。对于不同初始条件的给定,他们使用傅里叶模态基函数
| $ \begin{split}&u\left(x,z\right) = \mathrm{sin}\left({n}^{\left(i\right)}{\text{π}} x/{\varGamma }\right)\mathrm{cos}\left({\text{π}} z\right) \\& w(x,z) = -\mathrm{c}\mathrm{o}\mathrm{s}\left({n}^{\left(i\right)}{\text{π}} x/{\varGamma }\right)\mathrm{s}\mathrm{i}\mathrm{n}\left({\text{π}} z\right) \end{split}$ | (1) |
来产生不同数量的对流涡结构,这里的n(i)表示在系统水平方向上排列的处于湍流状态的对流涡的数量。此外,系统的初始温度为具有随机扰动的线性剖面,系统的初始速度则是根据当前控制参数下的雷诺数确定。
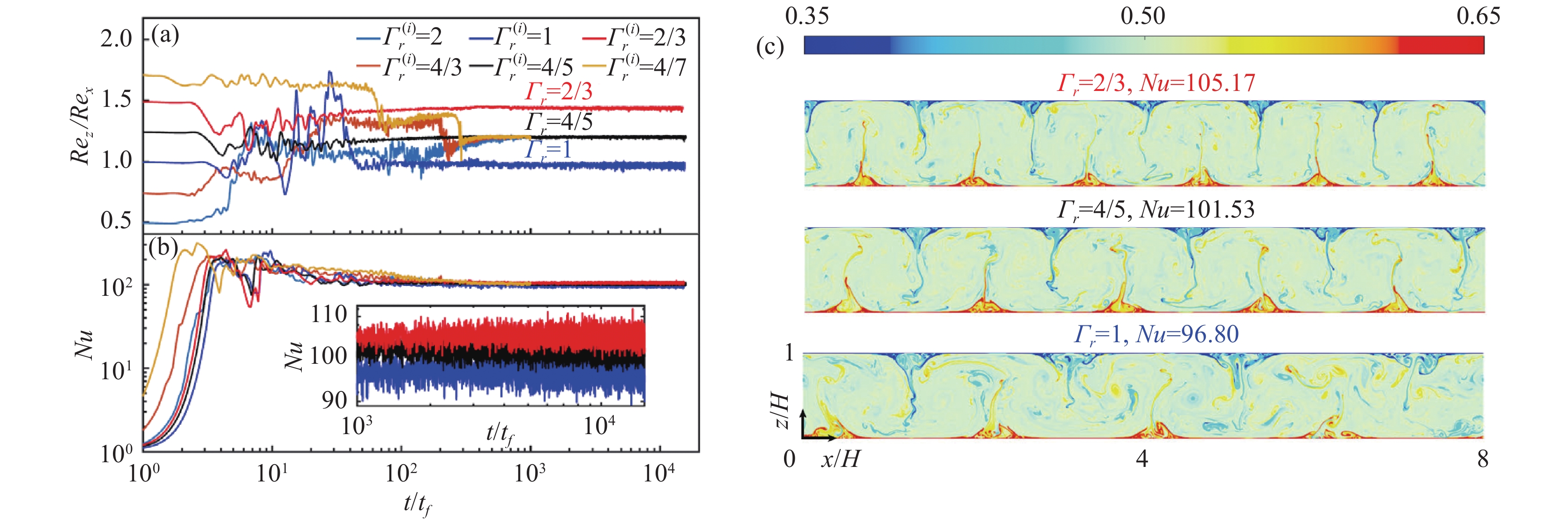
图8给出了在Ra = 1010、Pr = 10、Γ = 8时,给定不同的初始条件(初始对流涡数量n(i) = 4~14,对应图2中Γr(i) = Γ/n(i) = 2~4/7)系统中的流动状态随时间的演化。我们可以看出,对于六个不同的初始条件,经过长时间演化(数千个流动特征时间)后,系统最终演化出三种截然不同的湍流状态,并表现出不同的系统热输运效率,如图8(c)所示。对多湍流态形成的机理,王启等利用椭圆形平面涡结构维持的条件即应变-涡量平衡关系并借助椭圆不稳定性理论中应变-涡量-涡的长宽比之间的定量关系[40]成功地预测了不同的湍流态在控制参数空间上的分布规律。
|
图 8 在Ra = 1010,Pr = 10,Γ = 8时,不同初始条件(对流涡的数目不同)下流动随时间的演化[13]:(a) 雷诺数比值Rez/Rex随时间的演化,这里 |
王启等[11]还利用二维直接数值模拟研究了宽高比以及热湍流系统的倾角(温度梯度的方向与重力方向之间的夹角)对于多湍流态存在与否的影响。他们发现,在宽高比为2的矩形热湍流系统中,当系统保持水平时,系统中的流动是在水平方向上排列的双环模态。当系统存在倾斜,倾角为9°时,由于浮力的作用,系统内的流动为单环模态。如果以此时的单环模态作为初值,连续地减小系统的倾角至系统水平,他们发现单环模态在系统水平时仍然可以稳定存在。另外,他们还指出在系统保持水平且在相同的控制参数下,双环模态下的Nu比单环模态下的Nu大13%。进一步的研究发现,这种多湍流态现象在更大的宽高比下也同样存在,并且不同的湍流态表现出不同的热输运效率。这个现象与Huisman等[21]在泰勒-库埃特湍流系统中发现的多湍流态一致。
3 结论与展望以上我们详细讨论了关于瑞利-伯纳德热湍流系统中的多湍流态现象研究的最新进展。多湍流态在热湍流系统中以两种形式呈现,一类则是流动在发展过程中自发产生并且自由切换的多湍流态,另一类是由于流动初始条件不同而产生的多湍流态现象。两类多湍流态的研究中均发现当系统处于不同湍流态时,系统整体的热输运效率也相应改变,这也为之后探索相应的湍流调控方法提供了理论支持。下面,笔者就多湍流态的相关问题进行讨论并给出展望。
在实验室中进行湍流的研究是为了更好地理解自然界中、工程实际中的湍流问题,然而这些真实的湍流问题往往伴随着极高的系统控制参数,如Re、Ra等。因此能否将实验室中研究的成果顺利地推广至这些实际问题中要求我们对于流动处于何种流动状态、是否还存在不同的流动状态等等这些问题有清晰的认知。经典的湍流理论中认为,对于湍流流动,流动中大量的自由度被激发且湍流脉动足够大,以至于所有的高维空间都被遍历,此时流动的小尺度统计特性不再受到流动边界或者外界的影响,然而这是否意味着大尺度流动状态(结构)同样只能存在唯一的一种流动状态呢?对于这个问题,从本文综述的内容角度来看,应该不是唯一的。
此外,20世纪中期,Kolmogorov及其学派[43]开始将湍流状态下的流动视作类似于统计学角度的随机场。换句话说,每一个真实的流场都被考虑成是“所有可能的场的统计集合”中抽取的一个“样本”。时至今日,这种对于湍流场的处理已被大家广为接受。任何变量的平均化都可以理解为相对于相应统计集合的概率平均化,这样的处理一个最根本的前提在于各态遍历假设。各态遍历假设是统计研究的基石,其保证了我们在有限时间、有限空间、有限实现下得到的统计结果可以无限接近于理论的、真实的、期望的数值。在湍流理论中,认为当平均的范围(时间、空间或者事件)足够大时,对于该范围上的均值将会趋同于统计概率的均值。正是因为这样的一个假设存在,经典的湍流理论普遍认为湍流流动在给定某个初始条件以及边界条件下应该仅仅存在一种流动状态,与之对应的也仅仅存在一种系统输出参数。此时,我们来回顾上文中综述的两类多湍流态现象,对于第二类多湍流态现象,部分观点认为其与上述的统计学概念是自洽的,即在某一初始条件或者边界条件下是一种确定的流动,有着确定的系统输出参数;但是,也有部分学者认为各态遍历假设已然要求湍流系统遍历相空间中的任意状态点,从某种意义上来讲,系统应很快忘记初始状态的信息,系统最终所处的状态也应该与初始状态无关。对于这一方面的讨论,本文作者更倾向于认为第二类多湍流态现象是与各态遍历假设是相符的。然而对于第一类多湍流态现象,笔者则认为其与Kolmogorov的理论不一致。在该类多湍流态现象中,一个明显的特征是不同的湍流态对应着不同的系统输出参数,这便会带来一个问题,如何来定义上文中所说的足够大的平均范围呢?如果平均范围(时间段)内流动未发生转变,此时得到的系统的平均输出参数会是该湍流态对应的系统输出参数;而如果在平均范围(时间段)内流动发生了转变,此时的系统的平均输出参数会受到不同湍流态所对应的不同系统输出参数的影响。那么我们如何通过有限时间、有限空间、有限实现的实验、数值模拟得到趋同于真值的结果呢? 因此,需要我们进一步的探索如何解释这类自发的、随机的湍流态之间的转换。
另外,从N-S方程的角度出发,其作为一类极其复杂的非线性系统,多解现象以及多解之间的相互转换又是普遍且可预期的。关于多湍流态的真实存在与否以及其产生的机理还有待进一步深入的研究,然而这并不妨碍笔者对多湍流态现象进行展望。
1) 目前众多的关于多湍流态的研究大都集中于封闭的湍流系统。封闭湍流系统具有几个突出的优点:第一,作为一个封闭系统,其整体响应参数和湍流内部能量耗散率有着精确的对应关系;第二,作为一个统计上的稳态系统,可以进行长时间测量来提高被测量参数的统计特性,例如可以精确地测量系统的整体热传输效率、系统的外加阻力等。然而,封闭湍流系统也存在着尺度效应的问题。因此,使用封闭湍流系统来研究多湍流态问题也极大地限制了对这个问题的理解。那么,在非封闭的湍流系统如壁湍流中是否同样存在类似的多湍流态现象?
2) 对于热湍流系统中多湍流态现象的产生,Zwirner等[19]和王启等[13]将目光锁定在了椭圆不稳定性;郗恒东等[44]则认为高阶的流动状态参与其中。第一类多湍流态现象中不同的湍流态为什么会自发形成?什么因素促使不同的湍流态自发的转换?如果可以解答这一问题将极大地提升对于湍流问题的理解。
3) 另一个疑问是通过给定不同的初始条件引起的第二类多湍流态现象是否会在长时间演化后同样出现自发地、向不同的湍流状态切换,两类多湍流态现象是否从根源上来说是一致的,这也需要将来进一步的研究。
4) 湍流是否存在对大尺度湍流结构的选择性?如何主动选择流动的状态进而调控湍流系统的输运特性?
5) 针对第二类多湍流态现象,现有少量的研究结果主要集中于直接数值模拟的研究,缺乏相关实验的证实。当然,不同初始条件的给定在实验中存在一定的挑战,这也需要进一步的探索。
实际上还有大量的问题值得进一步的探索,笔者希望通过本篇文章向更多的湍流研究工作者介绍相关的最新研究进展,一同推进理解相关的湍流问题。
| [1] |
AHLERS G, GROSSMANN S, LOHSE D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection[J]. Reviews of Modern Physics, 2009, 81(2): 503-537. DOI:10.1103/revmodphys.81.503 |
| [2] |
LOHSE D, XIA K Q. Small-scale properties of turbulent Rayleigh-Bénard convection[J]. Annual Review of Fluid Mechanics, 2010, 42: 335-364. DOI:10.1146/annurev.fluid.010908.165152 |
| [3] |
XIA K Q. Current trends and future directions in turbulent thermal convection[J]. Theoretical and Applied Mechanics Letters, 2013, 3(5): 052001. DOI:10.1063/2.1305201 |
| [4] |
XI H D, LAM S, XIA K Q. From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection[J]. Journal of Fluid Mechanics, 2004, 503: 47-56. DOI:10.1017/s0022112004008079 |
| [5] |
KRISHNAMURTI R, HOWARD L N. Large-scale flow generation in turbulent convection[J]. Proceedings of the National Academy of Sciences of the United States of America, 1981, 78(4): 1981-1985. DOI:10.1073/pnas.78.4.1981 |
| [6] |
XI H D, XIA K Q. Flow mode transitions in turbulent thermal convection[J]. Physics of Fluids, 2008, 20(5): 055104. DOI:10.1063/1.2920444 |
| [7] |
KOLMOGOROV A N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers[J]. Proceedings:Mathematical and Physical Sciences, 1991, 434(1890): 9-13. |
| [8] |
VAN DER POEL E P, STEVENS R J A M, SUGIYAMA K, et al. Flow states in two-dimensional Rayleigh-Bénard convection as a function of aspect-ratio and Rayleigh number[J]. Physics of Fluids, 2012, 24(8): 085104. DOI:10.1063/1.4744988 |
| [9] |
VAN DER POEL E P, STEVENS R J A M, LOHSE D. Connecting flow structures and heat flux in turbulent Rayleigh-Bénard convection[J]. Physical Review E, 2011, 84(4): 045303. DOI:10.1103/physreve.84.045303 |
| [10] |
WEISS S, AHLERS G. Turbulent Rayleigh-Bénard convection in a cylindrical container with aspect ratio Γ = 0.50 and Prandtl number Pr = 4.38
[J]. Journal of Fluid Mechanics, 2011, 676: 5-40. DOI:10.1017/s0022112010005963 |
| [11] |
WANG Q, WAN Z H, YAN R, et al. Multiple states and heat transfer in two-dimensional tilted convection with large aspect ratios[J]. Physical Review Fluids, 2018, 3(11): 113503. DOI:10.1103/physrevfluids.3.113503 |
| [12] |
XIE Y C, DING G Y, XIA K Q. Flow topology transition via global bifurcation in thermally driven turbulence[J]. Physical Review Letters, 2018, 120(21): 214501. DOI:10.1103/physrevlett.120.214501 |
| [13] |
WANG Q, VERZICCO R, LOHSE D, et al. Multiple states in turbulent large-aspect ratio thermal convection: what determines the number of convection rolls?[J]. Physics Review Letters, 2020, 125(7): 074501. DOI:10.1103/PhysRevLett.125.074501 |
| [14] |
FAVIER B, GUERVILLY C, KNOBLOCH E. Subcritical turbulent condensate in rapidly rotating Rayleigh-Bénard convection[J]. Journal of Fluid Mechanics, 2019, 864: R1. DOI:10.1017/jfm.2019.58 |
| [15] |
MANNIX P M, MESTEL A J. Bistability and hysteresis of axisymmetric thermal convection between differentially rotating spheres[J]. Journal of Fluid Mechanics, 2021, 911: A12. DOI:10.1017/jfm.2020.1042 |
| [16] |
AHLERS G, FUNFSCHILLING D, BODENSCHATZ E. Heat transport in turbulent Rayleigh-Bénard convection for Pr ≃ 0.8 and Ra ≲ 1015
[J]. Journal of Physics:Conference Series, 2011, 318(8): 082001. DOI:10.1088/1742-6596/318/8/082001 |
| [17] |
GROSSMANN S, LOHSE D. Multiple scaling in the ultimate regime of thermal convection[J]. Physics of Fluids, 2011, 23(4): 045108. DOI:10.1063/1.3582362 |
| [18] |
ZWIRNER L, SHISHKINA O. Confined inclined thermal convection in low-Prandtl-number fluids[J]. Journal of Fluid Mechanics, 2018, 850: 984-1008. DOI:10.1017/jfm.2018.477 |
| [19] |
ZWIRNER L, TILGNER A, SHISHKINA O. Elliptical instability and multiple-roll flow modes of the large-scale circulation in confined turbulent Rayleigh–Bénard convection[J]. Physical Review Letters, 2020, 125(5): 054502. DOI:10.1103/PhysRevLett.125.054502 |
| [20] |
XU A, CHEN X, XI H D. Tristable flow states and reversal of the large-scale circulation in two-dimensional circular convection cells[J]. Journal of Fluid Mechanics, 2021, 910: A33. DOI:10.1017/jfm.2020.964 |
| [21] |
HUISMAN S G, VAN DER VEEN R C A, SUN C, et al. Multiple states in highly turbulent Taylor-Couette flow[J]. Nature Communications, 2014, 5: 3820. DOI:10.1038/ncomms4820 |
| [22] |
WEN J, ZHANG W Y, REN L Z, et al. Controlling the number of vortices and torque in Taylor-Couette flow[J]. Journal of Fluid Mechanics, 2020, 901: A30. DOI:10.1017/jfm.2020.561 |
| [23] |
YANG Y, CHEN W, VERZICCO R, et al. Multiple states and transport properties of double-diffusive convection turbulence[J]. Proceedings of the National Academy of Sciences of the United States of America, 2020, 117(26): 14676-14681. DOI:10.1073/pnas.2005669117 |
| [24] |
RAVELET F, MARIÉ L, CHIFFAUDEL A, et al. Multistability and memory effect in a highly turbulent flow: experimental evidence for a global bifurcation[J]. Physical Review Letters, 2004, 93(16): 164501. DOI:10.1103/physrevlett.93.164501 |
| [25] |
ZIMMERMAN D S, TRIANA S A, LATHROP D P. Bi-stability in turbulent, rotating spherical Couette flow[J]. Physics of Fluids, 2011, 23(6): 065104. DOI:10.1063/1.3593465 |
| [26] |
XIA Z H, SHI Y P, CAI Q D, et al. Multiple states in turbulent plane Couette flow with spanwise rotation[J]. Journal of Fluid Mechanics, 2018, 837: 477-490. DOI:10.1017/jfm.2017.869 |
| [27] |
DALLAS V, SESHASAYANAN K, FAUVE S. Transitions between turbulent states in a two-dimensional shear flow[J]. Physical Review Fluids, 2020, 5(8): 084610. DOI:10.1103/physrevfluids.5.084610 |
| [28] |
MARKEVICIUTE V K, KERSWELL R R. Degeneracy of turbulent states in two-dimensional channel flow[J]. Journal of Fluid Mechanics, 2021, 917: A57. DOI:10.1017/jfm.2021.336 |
| [29] |
GAYOUT A, BOURGOIN M, PLIHON N. Rare event-triggered transitions in aerodynamic bifurcation[J]. Physical Review Letters, 2021, 126(10): 104501. DOI:10.1103/physrevlett.126.104501 |
| [30] |
SCHIKARSKI T, TRZENSCHIOK H, PEUKERT W, et al. Inflow boundary conditions determine T-mixer efficiency[J]. Reaction Chemistry & Engineering, 2019, 4(3): 559-568. DOI:10.1039/c8re00208h |
| [31] |
SCHMEITS M J, DIJKSTRA H A. Bimodal behavior of the Kuroshio and the Gulf Stream[J]. Journal of Physical Oceanography, 2001, 31(12): 3435-3456. DOI:10.1175/1520-0485(2001)031<3435:bbotka>2.0.co;2 |
| [32] |
RAHMSTORF S. Ocean circulation and climate during the past 120, 000 years[J]. Nature, 2002, 419(6903): 207-214. DOI:10.1038/nature01090" |
| [33] |
GLATZMAIERS G A, ROBERTS P H. A three-dimensional self-consistent computer simulation of a geomagnetic field reversal[J]. Nature, 1995, 377(6546): 203-209. DOI:10.1038/377203a0 |
| [34] |
BOUCHET F, ROLLAND J, SIMONNET E. Rare event algorithm links transitions in turbulent flows with activated nucleations[J]. Physical Review Letters, 2019, 122(7): 074502. DOI:10.1103/physrevlett.122.074502 |
| [35] |
CIONI S, CILIBERTO S, SOMMERIA J. Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number[J]. Journal of Fluid Mechanics, 1997, 335: 111-140. DOI:10.1017/s0022112096004491 |
| [36] |
BROWN E, AHLERS G. Rotations and cessations of the large-scale circulation in turbulent Rayleigh-Bénard convection[J]. Journal of Fluid Mechanics, 2006, 568: 351. DOI:10.1017/s0022112006002540 |
| [37] |
XI H D, ZHOU Q, XIA K Q. Azimuthal motion of the mean wind in turbulent thermal convection[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2006, 73(5 Pt 2): 056312. DOI:10.1103/PhysRevE.73.056312 |
| [38] |
XI H D, XIA K Q. Cessations and reversals of the large-scale circulation in turbulent thermal convection[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2007, 75(6 Pt 2): 066307. DOI:10.1103/PhysRevE.75.066307 |
| [39] |
周全, 夏克青. Rayleigh-Bénard湍流热对流研究的进展、现状及展望[J]. 力学进展, 2012, 42(3): 231-251. ZHOU Q, XIA K Q. Advances and outlook in turbulent Rayleigh-Bénard convection[J]. Advances in Mechanics, 2012, 42(3): 231-251. (in Chinese) |
| [40] |
KERSWELL R R. Elliptical instability[J]. Annual Review of Fluid Mechanics, 2002, 34: 83-113. DOI:10.1146/annurev.fluid.34.081701.171829 |
| [41] |
CHEN X, HUANG S D, XIA K Q, et al. Emergence of substructures inside the large-scale circulation induces transition in flow reversals in turbulent thermal convection[J]. Journal of Fluid Mechanics, 2019, 877: R1. DOI:10.1017/jfm.2019.624 |
| [42] |
陈鑫. 瑞利-伯纳德热湍流中大尺度环流及其反转的实验研究 [D]. 西安: 西北工业大学, 2021.
|
| [43] |
MONIN A S, YAGLOM A M. Statistical fluid mechanics: The mechanics of turbulence[R]. Defense Technical Information Center, 1999. doi: 10.21236/ada398728
|
| [44] |
XI H D, ZHANG Y B, HAO J T, et al. Higher-order flow modes in turbulent Rayleigh-Bénard convection[J]. Journal of Fluid Mechanics, 2016, 805: 31-51. DOI:10.1017/jfm.2016.572 |
 2022, Vol. 40
2022, Vol. 40


